Highlights
What are the main findings?
- A lightweight multi-scale framework, Crater-MASN, is proposed to balance high accuracy with computational efficiency.
- A novel training and post-processing pipeline enables robust detection in dense, nested regions and demonstrates an exceptional capability for discovering previously uncatalogued craters.
What is the implication of the main finding?
- Crater-MASN provides a scalable and efficient tool for planetary scientists to perform large-scale, high-precision crater cataloging and planetary surface analysis.
- The model’s proven ability to identify uncatalogued craters demonstrates its significant potential for scientific discovery and the completion of existing lunar databases.
Abstract
Automatic crater detection is crucial for planetary science, but still faces several long-standing challenges. The morphological characteristics of craters exhibit significant variability; combined with complex lighting conditions, this makes feature extraction difficult, especially for small or severely degraded features. These difficulties are further compounded by incomplete ground truth annotations, which limit the effectiveness of supervised learning. In addition, achieving a balance between detection accuracy and computational efficiency remains a critical bottleneck, especially in large-scale planetary surveys. Traditional postprocessing algorithms also often struggle to resolve complex spatial hierarchies in densely cratered regions, leading to substantial omissions and misclassifications. To address these interrelated challenges, we propose Crater-MASN, a lightweight adaptive detection framework specifically designed for lunar crater analysis. The architecture employs a compact GhostNet backbone to balance efficiency and accuracy, while enhancing multi-scale feature representation through a novel bidirectional integration and fusion module (BIFM) to better capture the morphological diversity of craters. To mitigate the impact of incomplete annotations, we introduce an adaptive semantic contrastive sampling (ASCS) mechanism which dynamically mines unlabeled craters through semantic clustering and contrastive learning. Additionally, we design the hierarchical soft NMS (H-SoftNMS) algorithm, a geometry-aware postprocessing method that selectively suppresses non-hierarchical overlaps to preserve nested craters, thereby achieving more accurate crater retention in dense regions. Experiments on a dedicated lunar crater dataset demonstrate the effectiveness of Crater-MASN. The model achieves an mAP50 of 91.0% with only 2.1 million parameters. When combined with H-SoftNMS, it achieves a recall rate of 95.0% and new discovery rate of 89.6%. These results highlight the potential of Crater-MASN as a scalable and reliable tool for high-precision crater cataloging and planetary surface analysis.
1. Introduction
Impact craters are one of the most common geological structures on the Moon and represent an important research topic in planetary science and exploration. They have profound implications for understanding the Moon’s geological history, estimating surface age, and selecting safe landing sites [1,2,3,4,5]. Accurate detection and characterization of lunar craters is crucial for geological mapping, topographic age estimation, and the selection of landing sites for future exploration missions. For example, analyzing the size–frequency distribution of craters can effectively estimate the age of a planetary surface [2], while the presence of water ice in permanently shadowed craters near the lunar poles holds significant implications for future lunar missions. While traditionally reliable, manual annotation of craters from lunar imagery is time-consuming, subjective, and infeasible at planetary scales. This challenge has motivated the development of automated crater detection algorithms (CDAs) over the past two decades [1,6]. Furthermore, automatic crater detection is crucial for efficiently extracting this information from the vast amount of lunar images obtained from missions such as Clementine, SELENE, the Lunar Reconnaissance Orbiter (LRO), and China’s Chang’e mission [1,6]. Early automated crater detection algorithms primarily relied on mathematical morphology and geometric matching techniques. For instance, Ding et al. [7] introduced an embedded framework that utilized mathematical morphology to identify potential crater regions in planetary images, focusing on feature selection and boosting strategies to effectively classify crater candidates. Similarly, Chen et al. [8] proposed a geometric matching approach that modeled craters as circular shapes, employing edge detection and grouping techniques to align detected edges with template features. As the need for efficient crater detection grew, researchers began integrating machine learning techniques into their methodologies. Ding et al. [9] expanded on their previous work by incorporating transfer learning to enhance detection performance in varying surface morphologies. Their framework achieved an impressive F1 score above 0.85, demonstrating significant improvements over traditional methods. Yu et al. [10] introduced a novel sequence detection algorithm utilizing digital elevation model (DEM) data, which allowed for the identification of elliptical crater shapes and effectively filtered out pseudo-edges, thereby enhancing the accuracy of crater detection. Luo et al. [11] also developed a method for global detection of large lunar craters using terrain attributes, which facilitated the automatic cataloging of craters based on topographic data. Early CDAs typically involved image preprocessing (including noise reduction, contrast enhancement, and geometric correction), feature extraction (identifying edges, circular shapes, and shadow patterns, such as “shady and sunny” patterns in low-sun-angle images, or seeking curves and circles from thinned and connected edge lines, sometimes employing fuzzy Hough transforms for discrete or broken circular edges [1]), crater candidate selection, and crater verification (filtering out spurious detections based on morphological criteria, for instance by using the isolation forest algorithm to eliminate falsely detected craters [12]). Chen et al. [2] proposed a CDA based on terrain analysis and mathematical morphology methods. They utilized DEMs to identify crater boundaries and provided methods to detect different types of craters, including dispersal craters, connective craters, and con-craters. Duan et al. [13] introduced an automated lunar crater detection algorithm (CDA) based on DEM data, which extracts the lowest points on the DEM as potential crater centers, then detects the rim of craters using a maximum curvature detection method and a watershed algorithm. Sawabe et al. [1] improved upon their previous algorithm, testing it on images captured by Clementine and Apollo, and was reported to detect 80% more craters without parameter tuning.The integration of deep learning models has led to significant advancements in detection accuracy and efficiency. Deep learning techniques have gained prominence in lunar crater detection over recent years, particularly convolutional neural networks (CNNs) [14]. These methods can automatically learn relevant features from lunar images, often outperforming traditional approaches [15]. Among these, Silburt et al. [16] pioneered lunar crater identification using deep learning, demonstrating the ability of convolutional neural networks to automate this process. Jia et al. [15] proposed an automatic crater extraction method utilizing an enhanced U-Net model, where crater features were parameterized by a deep convolutional neural network. Mao et al. [17] presented a dual-path convolutional neural network (Dual-Path) built upon a U-NET architecture, which they designed for effective feature integration from both elevation (DEM) and orthographic projection (WAC) maps. Tang et al. [18] showcased the efficacy of the YOLOv5 one-stage object detection network for lunar crater detection using LRO camera CCD data. Furthermore, Fan et al. [4] developed an efficient lunar crater detection (ELCD) algorithm, leveraging a novel crater edge segmentation network (AFNet) for DEM-based crater detection. Wang et al. [19] introduced CraterIDNet, an end-to-end fully convolutional neural network designed for simultaneous crater detection and identification, which demonstrated state-of-the-art performance by effectively mapping craters in remotely sensed images. Additionally, Wu et al. [20] proposed a compact crater extraction network optimized for resource-constrained platforms, showcasing the versatility of deep learning applications in this domain. Zang et al. [21] proposed a new crater detection model (Crater R-CNN) and trained it using a semi-supervised deep learning method to address the challenge of limited labeled data. Lin et al. [22] proposed a complete workflow including an end-to-end deep learning pipeline for lunar crater detection, particularly for craters smaller than 50 km in diameter. Miao et al. [5] proposed a novel lunar crater detection neural network called LCD-Net. This network incorporates a reserved negative sampling module and an adaptive non-maximum suppression module to optimize the detection of overlapping craters and reduce the miss rate. Sinha et al. [23] presented a crater-based U-Net model with Resnet18 as the backbone for automated lunar crater identification with Chandrayaan-2 Terrain Mapping Camera-2 (TMC-2) images. Myojin et al. [24] explored the use of Monte Carlo dropout to quantify the uncertainty of Deep Neural Network (DNN) predictions, thereby improving the reliability of crater detection. Wang et al. [25] presented a method for detecting small lunar craters, incorporating statistically constrained path morphologies and unsupervised discriminate correlation filters. Dai et al. [26] proposed a two-stream fusion crater detection network (TFCDNet) and utilized near-infrared (IR) images and DEMs in the feature domain to boost crater detection performance. Recent studies have continued to push the boundaries of crater detection technology. Tewari et al. [27] utilized a combination of optical images, DEMs, and slope maps to enhance lunar surface crater detection, achieving high precision and recall rates. Additionally, Zhao et al. [21] employed the Segment Anything Model (SAM) to detect craters in high-resolution images from the Tianwen-1 mission, successfully extracting over 841,000 craters. The integration of super-resolution techniques has also emerged as a promising avenue for improving crater detection. La Grassa et al. [28] introduced YOLOLens, a deep learning model based on super-resolution, which significantly enhanced crater detection performance in low-resolution images. Tewari et al. [29] further advanced this concept by proposing an arbitrary-scale super-resolution approach, enabling effective crater detection across multiple resolutions.
Automated lunar crater detection technology has evolved significantly over the years, with deep learning methods now offering state-of-the-art performance. These algorithms are essential for analyzing the vast amounts of lunar imagery and extracting valuable information about the Moon’s history and evolution. Continued research and development in this field will further improve the accuracy, efficiency, and robustness of crater detection, enabling a more comprehensive understanding of our nearest celestial neighbor. The ongoing efforts to map and characterize lunar craters contribute significantly to our understanding of the solar system and inform future lunar exploration missions.
Despite significant progress, automated crater detection faces a confluence of inherent challenges. The immense variability in crater morphology, covering a wide range of sizes, shapes, and degradation states, is further complicated by variable illumination conditions, making robust feature extraction difficult [12]. This issue is exacerbated by the presence of quasi-circular geological features, such as volcanic calderas, which act as natural distractors and lead to false positives. The difficulty is particularly acute for small-scale craters, which include subtle features that are often lost in low-resolution imagery [4,23]. Addressing these issues demands sophisticated models capable of processing enormous volumes of high-resolution data, which introduces a practical bottleneck due to high computational costs. Furthermore, the deep learning models that currently dominate the field are fundamentally constrained by the quality of their training data; existing ground-truth catalogs are known to be incomplete, causing a large number of true but unlabeled craters to be erroneously penalized as negatives during training. Finally, even when craters are correctly identified, standard postprocessing algorithms such as non-maximum suppression (NMS) often fail in dense regions, erroneously suppressing valid smaller craters nested within larger ones [5].
To address these challenges, this paper proposes Crater-MASN, a lightweight and high-performance crater detection network. By systematically integrating an efficient architecture with advanced training and postprocessing strategies, Crater-MASN is designed to achieve an optimal balance between efficiency and accuracy.
The main contributions of this work are summarized as follows:
- 1.
- To address the tradeoff between efficiency and accuracy, we design and validate a lightweight architecture combining a GhostNet backbone with a BIFM neck, significantly reducing model parameters while enhancing multi-scale feature representation.
- 2.
- To overcome the detrimental effects of incomplete annotations, we propose a novel Adaptive Semantic Contrast Sampling (ASCS) training strategy that intelligently mines unlabeled craters, substantially improving model recall and generalization.
- 3.
- To resolve ambiguous detections in dense and nested regions, we design a H-SoftNMS algorithm. In conjunction with our proposed New Discovery Rate () metric, this provides a robust solution for scientific catalog completion by correctly handling complex spatial relationships and quantifying the value of new discoveries.
2. Materials and Methods
In this section, we describe our proposed workflow with details, including the steps of data preparation, crater detection process, postprocessing, and model evaluation.
2.1. Data Sources and Preprocessing
To construct a robust dataset for lunar crater detection, we employed the global lunar mosaic generated from over 15,000 images acquired by the wide-angle camera (WAC) of the Lunar Reconnaissance Orbiter (LRO) between November 2009 and February 2011 [30]. This mosaic, encompassing the full longitude range [−180°, 180°] and latitude range [−90°, 90°], utilizes a cylindrical projection with a spatial resolution of 100 m per pixel, and is represented in 8-bit grayscale [31,32]. For ground truth, we utilized the Robbins crater catalog [33]. This catalog was specifically chosen as our foundational dataset for several key reasons. First, it is a comprehensive, global database containing approximately 1.3 million craters, providing the scale necessary for training a robust model. Second, and most importantly, it is a manually annotated catalog. This human-verified ground truth is considered a high-quality and reliable benchmark, making it an ideal source for supervising the training of our network and ensuring that the model learns from an accurate representation of crater features. Its widespread acceptance and use in the planetary science community further establish it as a standard for such studies. To ensure consistency with the WAC mosaic, the catalog’s native coordinates, expressed in a cylindrical system with longitudes from 0° to 360°, were first transformed into the [−180 °, 180 °] range.
To capture multi-scale features of craters across diverse sizes and enhance the model’s generalizability, we devised a hierarchical sampling strategy. For each randomly selected lunar location, three image regions of distinct physical dimensions at native resolution were sequentially extracted: (1) a base-scale region of 416 × 416 pixels (corresponding to 41.6 × 41.6 km2 at 100 m/pixel); (2) a medium-scale region of 832 × 832 pixels (83.2 × 83.2 km2); and (3) a large-scale region of 1664 × 1664 pixels (166.4 × 166.4 km2). To standardize the input dimensions, the medium- and large-scale patches were downsampled by factors of two and four, respectively, then resized to 416 × 416 pixels. This resulted in three versions of each region, all sharing the same pixel dimensions but representing spatial resolutions of 100, 200, and 400 m per pixel, respectively. Through this combination of hierarchical sampling and controlled downsampling, we were able to generate a set of training samples that reflect identical lunar terrain at varying spatial scales.
This strategy offers two critical advantages. First, it compels the model to learn crater-relevant features that are invariant to absolute pixel size, promoting scale-robust representations. Second, it enhances the model’s ability to detect small craters—which may occupy only a few pixels in high-resolution images—while simultaneously preserving broader spatial context through coarser representations. Together, these benefits significantly strengthen the model’s capacity to recognize craters across the full spectrum of sizes and morphological conditions.
Following orthorectification, crater locations from the Robbins catalog were converted from geographic coordinates to image pixel coordinates corresponding to each tile. To maintain data quality and ensure effective model training, a rigorous filtering protocol was applied in which tiles exhibiting significant projection distortion (particularly near the lunar poles) or containing fewer than 45 mapped craters were excluded. Additionally, to avoid ambiguous partial annotations, craters with diameters exceeding the actual tile dimensions (41.6 km for the 100 m/pixel tiles) were discarded. The remaining valid crater annotations within each tile were then encoded into the YOLO format: , with all values normalized to the interval.
Through this preprocessing pipeline, a final dataset was obtained comprising 10,302 tiles. This dataset was partitioned into training and validation sets at an 80:20 ratio, ensuring that only high-quality and low-distortion tiles were utilized for model training. All samples were stored in a YOLO-compatible format, facilitating an end-to-end learning pipeline for lunar crater detection and enabling global-scale inference across the lunar surface.
2.2. Overall Network Architecture
To achieve both efficient and accurate detection of lunar craters, we propose a novel lightweight multi-scale detection network named Crater-MASN. The model is an advanced one-stage detector, and its overall architecture is illustrated in Figure 1. Crater-MASN is composed of three carefully-designed core components: a lightweight backbone network for efficient feature extraction, an efficient feature fusion neck for enhanced multi-scale information interaction, and a standard detection head for precise localization and classification. During the training phase, we employed our proposed ASCS strategy to handle incomplete annotations. For postprocessing, we also evaluated a specialized H-SoftNMS algorithm designed for nested craters. The design principles and functionality of each component are detailed in the subsequent sections.
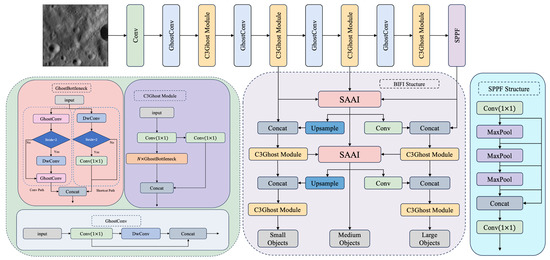
Figure 1.
The overall architecture of our proposed Crater-MASN. The model consists of three core components: a lightweight Backbone based on GhostNet for efficient feature extraction; a Neck featuring our BIFM for enhanced multi-scale feature interaction; and a standard detection Head for final localization and classification. The data flow from the input image through these stages to produce the final detection results for small, medium, and large objects.
2.3. Lightweight Backbone Network
In modern object detectors, the backbone network undertakes the primary feature extraction task [34] while also accounting for the majority of computational overhead. To meet the combined requirements of model compactness, inference speed, and detection accuracy in lunar exploration tasks, we adopt GhostNet [35] as the backbone of Crater-MASN. GhostNet leverages the concept of information flow decoupling to construct an efficient feature generation path, significantly reducing model size while preserving semantic representation capability. Its core principle is to address the feature map redundancy inherent in deep neural networks. It decomposes the standard convolution operation into a two-stage process. First, a standard convolution is used to generate a small number of information-dense intrinsic feature maps. Subsequently, a series of computationally inexpensive linear operations such as depth-wise convolutions [36] are applied to these intrinsic features in order to produce a larger set of complementary ghost feature maps. Furthermore, the architecture is well-suited for deployment on ARM-based or embedded devices, making it an ideal choice for lightweight detection systems in resource-limited environments. Our backbone encapsulates this mechanism within the C3Ghost module, which serves as the fundamental building block of the network. As demonstrated in our ablation results (Table 1, Experiment 2), adopting the GhostNet backbone successfully reduced the model’s parameter count by 40%. Although this gain in efficiency is accompanied by a slight decrease in performance, the performance is effectively recovered and even surpassed through the introduction of advanced fusion modules (BIFM) and our contrastive sampling strategy (ASCS), thereby validating the effectiveness of our backbone design.

Table 1.
Ablation study of different components on our crater dataset. A checkmark (✓) indicates that the module is included. P, R, and mAP are reported in percentage (%). The best results for each metric are highlighted in bold.
2.4. The Bidirectional Integration and Fusion Module
In biological neural networks, sophisticated information processing emerges from the dynamic bidirectional interplay between specialized brain regions. This principle of reciprocal reinforcement, in which different components mutually inform and refine one another, offers a compelling model for overcoming a key challenge in object detection: the effective reconciliation of high-level semantic abstractions with fine-grained spatial details. Conventional feature pyramid networks are often limited by unidirectional or simplistic two-way information flow and struggle to achieve a truly synergistic integration, akin to a dialogue with constrained feedback [37,38].
To address this limitation, we introduce a novel fusion architecture, the BIFM, designed to facilitate a rich and iterative dialogue between feature scales. As detailed in Figure 2, the BIFM integrates two synergistic components: a Spatial-Aware Attention Injection (SAAI) unit and a cross-scale semantic diffusion mechanism. Let be a set of feature maps from a pyramid, where represents the features at the i-th scale, with C, H, and W denoting the channels, height, and width of the feature map, respectively. The BIFM improves each feature map by aggregating the context from all other scales j. This integration is formulated as
where is a learnable affinity weight that governs the contribution of information from scale j to scale i. The SAAI unit first transforms the source feature into a more potent representation, which is then weighted and fused.
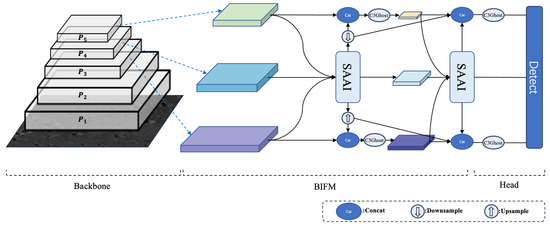
Figure 2.
The architecture of the Bidirectional Integration and Fusion Module (BIFM), which promotes rich, iterative interactions across feature scales through a Spatial-Aware Attention Injection (SAAI) unit and a semantic diffusion mechanism that propagates high-level context.
Spatially-Aware Attention and Semantic Diffusion
The SAAI unit [39] serves as the foundational stage of the BIFM, preparing features for effective cross-scale communication. As detailed in Figure 3, the SAAI module is built to process three adjacent feature maps from different scales: the high-level semantic feature , the low-level detailed feature , and the current-level feature . All features are resized via convolution and interpolation to match the spatial resolution. First, we divide each feature map along the channel dimension into four equal segments. Subsequently, each of these three aligned maps is partitioned into non-overlapping segments along the channel axis, yielding the respective feature groups , , and .
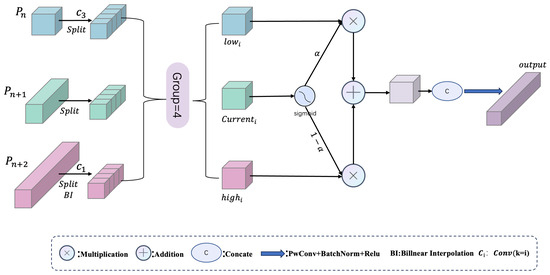
Figure 3.
Detailed architecture of the Scale-Aware Attentive Integration (SAAI) module. Guided by a dynamic attention weight , the module adaptively merges semantically rich high-level features and spatially detailed low-level features to improve small object detection.
For each channel group i, a dynamic gating weight is generated by applying a sigmoid function to the current-layer feature group :
where for each channel group i, a dynamic gating weight is generated by applying a sigmoid function to the current-layer feature group . This gate adaptively controls the fusion of the low-level group and the high-level group . A higher value for emphasizes the contribution of fine-grained spatial details from , whereas a lower value favors the contextual information from . After this parallel processing, the fused feature groups are reassembled via channel-wise concatenation and passed through a final convolutional block to produce the enhanced output :
where represents a standard sequence of batch normalization and represents the ReLU activation function.
This enhanced feature set enables the cross-scale semantic diffusion mechanism, which performs the final critical step of intelligent fusion. As formalized in Equation (5), this mechanism operates as a dynamic message passing system governed by the learned affinity weights . These weights function as adaptive gates, controlling the flow of information between scales based on their semantic relevance. This allows the network to selectively amplify complementary information, such as injecting precise localization cues into semantic features, as well as to suppress conflicting signals. In this way, the resulting fused feature map possesses superior discriminative power, enhancing robustness to variations in object size and morphology.
2.5. Adaptive Semantic Contrast Sampling
A principal challenge in the automated detection of planetary impact craters arises from the inherently incomplete nature of existing crater catalogs. Within these incompletely annotated datasets (IADs), a substantial number of true but unannotated craters, denoted as unlabeled positives (UPs), are erroneously treated as hard negatives during training. This misinterpretation leads to suppressive gradient updates that severely impair model recall. Furthermore, the simple morphology of craters often causes visual confusion with other geological features or illumination artifacts, demanding a higher level of semantic discrimination.
Inspired by the retaining-based negative sampling (RNS) strategy from LCDNet [5], our work aims to resolve two of its core limitations: first, its reliance on a static confidence threshold, which lacks adaptability to the dynamic training process, and second, the absence of semantic-level verification allowing for the distinguishing of true UPs from well-structured false positives.
To address the dual challenges of data incompleteness and semantic ambiguity in crater detection, we propose an advanced training paradigm: Adaptive Semantic Contrast Sampling (ASCS). ASCS is a dynamic sampling strategy implemented in a fully vectorized manner. It employs a two-stage mechanism, featuring multi-prototype semantic validation to generate a loss mask , precisely identifying and masking potential unlabeled craters to guide the model towards more robust learning.
2.5.1. Adaptive Candidate Filtering
The initial stage of ASCS aims to identify a high-quality set of candidate UPs from the pool of background predictions . We employ a dynamic confidence threshold that adapts to the training epoch e:
where represents the predefined number of ramp-up epochs, while and are the initial and final threshold values. A background prediction is included in the candidate set if it satisfies both confidence and spatial non-overlap criteria:
where is the class score vector of prediction , is its bounding box, and is the set of ground truth boxes.
2.5.2. Multi-Prototype Semantic Contrast and Validation
To effectively address the high intra-class variance inherent in crater morphologies, the semantic validation stage of ASCS is built upon a multi-prototype strategy. This approach adaptively discovers multiple dominant feature patterns within the true positives of each training batch.
First, for the set of feature embeddings from all confirmed true positives within a batch, we apply a lightweight online clustering algorithm (e.g., K-Means with K = 2) to partition them into K clusters. The choice of K = 2 is based on the primary morphological dichotomy observed in lunar craters: relatively “fresh” craters with distinct sharp rims, and “degraded” or ancient craters with heavily eroded and ambiguous features. Setting K = 2 allows the model to form two distinct semantic prototypes that effectively represent these two dominant classes, capturing the most significant intra-class variance without adding undue computational complexity to the training pipeline. A separate semantic centroid is then computed for each cluster, forming a prototype set :
where is the set of true positive samples in the k-th cluster.
A candidate sample is ultimately retained if and only if the cosine similarity of its feature with any of the prototype centroids exceeds the threshold .
This multi-prototype strategy enables ASCS to simultaneously identify unlabeled samples that are similar to either of the “fresh” or “eroded” crater prototypes, significantly enhancing the robustness and accuracy of the validation process.
2.5.3. Efficient Implementation and Loss Masking
To seamlessly integrate ASCS into modern detector training pipelines, we have designed and implemented a fully vectorized version that avoids the performance bottlenecks associated with per-sample loops. The core of this implementation lies in flattening all prediction and target tensors within a batch and utilizing a batch index tensor to maintain the correspondence between each element and its source image.
Batched Semantic Centroid Computation: For each image k in a batch, its semantic centroid is computed in parallel. We leverage the efficient scatter_mean operation, which groups and averages the features of all TPs based on the batch index tensor , yielding all per-image semantic centroids in a single operation.
Loss Masking: Following semantic validation, we obtain a final set of indices for samples to be retained. From this, we construct a Boolean loss mask , where each element is defined as shown below.
This mask is then applied to the standard loss function of the baseline detector, which typically comprises three components: a classification loss (), a bounding box regression loss (), and a distribution focal loss (). The final total loss is the weighted sum of these three components, each modulated by the ASCS strategy:
where are the respective loss weights. The primed loss terms denote that their computation is modulated by the loss mask . Specifically, the classification loss is computed over all non-retained samples, whereas the regression-related losses and are computed on the subset of samples that are both true positives and not retained.
In our experimental setup, the dynamic confidence threshold parameters were set to , , and . The semantic similarity threshold was set to 0.70.
2.6. Hierarchical Soft-NMS (H-SoftNMS)
Non-maximum suppression (NMS) is a fundamental postprocessing step in object detection pipelines. NMS is designed to eliminate redundant bounding boxes; however, conventional NMS as well as variants such as Soft-NMS [40] face fundamental challenges when applied to crater detection. First, their reliance on rectangular intersection over union (IoU) fails to accurately quantify the true overlap between circular craters. More critically, they are incapable of distinguishing between two distinct spatial relationships, namely, adjacent overlap and hierarchical containment. This often leads to the erroneous suppression of valid smaller craters located entirely within larger ones due to high IoU values, thereby compromising recall.
To address this issue, we propose a novel postprocessing algorithm called Hierarchical Soft-NMS (H-SoftNMS). H-SoftNMS is not a learnable module but rather an efficient rule-based suppression strategy. By incorporating circular geometric metrics and a differential suppression policy based on hierarchical spatial relationships, it is designed to precisely preserve nested structures while gracefully resolving adjacent overlaps.
2.6.1. Geometric Representation and Hierarchical Relationship Judgment
The first step in H-SoftNMS is to convert all predicted rectangular boxes into a more geometrically appropriate circular representation , where the radius is estimated as . All overlap metrics are based on this circular representation.
The core of the algorithm lies in judging the hierarchical relationship between two detections, and . We define detection as being nested in if the Euclidean distance between their centers, i.e., , plus the radius of , i.e., , is less than the radius of , i.e., . This condition is formally expressed as follows:
2.6.2. The H-SoftNMS Algorithm
The iterative process of H-SoftNMS is as follows. Given a set of detections sorted in descending order by their confidence scores s, we iteratively select the highest-scoring detection and use it to update the scores of the remaining detections in the set. An innovative differential suppression policy determines the updated score for any overlapping detection , as follows:
where is a Gaussian penalty function, . In our implementation, the parameter was empirically set to 0.5, a standard value in Soft-NMS implementations that provides a graceful score decay for overlapping detections. The detailed procedure of H-SoftNMS is described in Algorithm 1.
| Algorithm 1 Hierarchical Soft-NMS (H-SoftNMS) Procedure. | ||
| 1: | Input: | |
| 2: | : a set of predicted bounding boxes | |
| 3: | : corresponding confidence scores | |
| 4: | : final confidence threshold | |
| 5: | : IoU threshold for overlap check | |
| 6: | : sigma for Gaussian penalty function | |
| 7: | Output: | |
| 8: | : a set of final, filtered detections | |
| 9: | ||
| 10: | begin | |
| 11: | ▹ Initial filtering by score | |
| 12: | ▹ Convert boxes to circular representations | |
| 13: | ▹ Initialize final set of kept detections | |
| 14: | ||
| 15: | while do | |
| 16: | ▹ Select index of max score detection | |
| 17: | ; | |
| 18: | ||
| 19: | Remove , , from their respective sets | |
| 20: | ||
| 21: | for each detection in do | |
| 22: | if then | |
| 23: | if not ( or ) then | |
| 24: | ||
| 25: | end if | |
| 26: | end if | |
| 27: | end for | |
| 28: | ▹ Remove detections where | |
| 29: | end while | |
| 30: | ||
| 31: | return | |
| 32: | end | |
This policy explicitly distinguishes between two scenarios:
- 1.
- Nested Relationship: If one detection is contained within another, regardless of which is larger, their confidence scores remain unaffected. This critical mechanism protects “crater-in-crater” structures, ensuring that smaller craters inside larger ones are not suppressed.
- 2.
- Adjacent Overlap Relationship: If two detections merely overlap without being nested, a standard Gaussian soft-suppression penalty is applied. This gracefully resolves redundancy for neighboring independent craters by decaying scores rather than eliminating detections.
After all iterations, detections with updated scores remaining above a final confidence threshold are retained.
2.7. Postprocessing
Following inference with our proposed model on large-scale image tiles covering the lunar surface, an initial set of crater candidates is generated, each associated with a bounding box in image pixel coordinates and a confidence score. However, this raw output contains significant redundancies. A single physical crater may be detected multiple times in different image tiles due to our data generation strategy, which involves overlapping regions and multi-scale sampling. This precludes a direct assessment of the model’s global detection performance. Therefore, a systematic postprocessing pipeline is essential for refining these disparate pixel-based predictions into a precise, non-redundant, and globally georeferenced final crater catalog against which the model’s performance can be quantitatively assessed.
First, we perform preliminary filtering on the detection results. Candidate boxes with confidence scores below a predefined threshold are discarded. Furthermore, predictions with boundaries extending beyond the image patch are eliminated to mitigate inaccuracies arising from edge effects.
Second, to address multiple detections of the same crater, a non-maximum suppression (NMS) algorithm is applied. Unlike traditional NMS, which operates on rectangular pixel-space boxes, our approach is designed for circular targets defined by geographic coordinates, as illustrated in Figure 4.
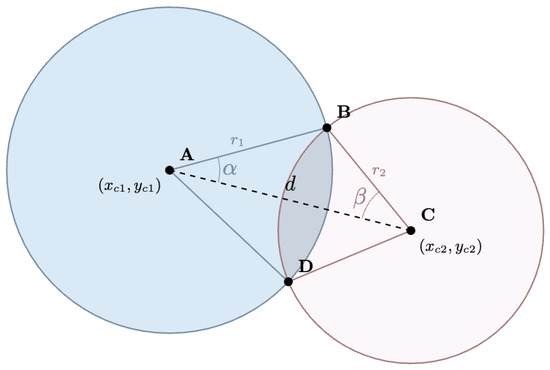
Figure 4.
Circular IoU structure of a two impact crater.
To achieve this step, we first need to perform a coordinate transformation. The native output of the model is typically a rectangular bounding box . To better reflect the physical morphology of the craters, we convert this representation to a circular format. The center coordinates and radius r (in pixels) are calculated using the following equations.
Subsequently, following [16] we convert the pixel-based coordinates to geographic coordinates (Longitude, Latitude, Radius). This conversion relies on the georeferencing information of the image, such as its center coordinates and latitude span , along with the lunar radius :
where is the pixel height at the image center and is the conversion factor between degrees and kilometers on the Moon.
Due to our overlapping tile strategy for data processing, the same physical crater may be detected multiple times. Therefore, a final deduplication stage is crucial after merging all initial detections into a global list. This process employs a method conceptually similar to NMS, but is specifically adapted for circular targets on a spherical surface.
The core of this method is a specialized IoU metric, denoted as . For any two craters defined by their geographic coordinates and radii, the is calculated as follows:
The term “overlap” represents the precise geometric intersection area of the two circular craters. Its calculation is defined by a piecewise function that considers three distinct spatial scenarios based on the crater radii () and the distance d between their centers:
In the case of partial overlap, the area is determined by summing the areas of the two circular sectors () and subtracting the area of the quadrilateral formed by the crater centers and the intersection points (). These components are calculated using the angles and , which are derived from the law of cosines.
Computation of the overlap area requires the crater radii r and the center-to-center distance d to be in consistent angular units. These values are derived from the geographic coordinates and and the physical radii . The distance d is calculated with a cosine correction based on the mean latitude in order to accurately model the separation on a spherical body:
The crater radii are converted from kilometers to the working angular unit using a conversion factor :
By employing this physically-grounded metric, our final NMS stage can accurately resolve duplicate detections to produce a clean and globally consistent crater catalog. We acknowledge that this coordinate transformation relies on a simplified cylindrical projection and uses a cosine correction for longitude scaling, which serves as a computationally efficient approximation. This approach does not account for more complex topographic variations or projection distortions, which can be more pronounced near the lunar poles. For studies requiring the highest degree of positional accuracy, a more rigorous photogrammetric solution would be necessary. However, for the purpose of global-scale cataloging, this method provides a well-established and effective tradeoff between geometric precision and computational feasibility.
2.8. Model Evaluation
To quantitatively evaluate the crater detection efficacy of our proposed model, we benchmark its performance against the ground-truth Robbins catalog. We measure detection correctness and completeness using precision and recall while also assessing the localization and sizing accuracy through normalized longitude, latitude, and radius errors. To quantify the model’s ability to identify valid craters beyond the established ground truth, we employ the new discovery rate ().
The foundational step of our evaluation is to establish a correspondence between predicted detections and ground truth (GT) annotations. We utilize the intersection over union (IoU) as the primary matching criterion. A prediction is classified as a true positive (TP) if its IoU with an unmatched GT box is greater than or equal to a predefined threshold, which is set to 0.5 in our primary analysis. Any prediction failing to meet this criterion is considered a false positive (FP), while any GT crater not matched by a prediction is counted as a false negative (FN). Precision and recall: These fundamental metrics quantify the correctness of predictions and the completeness of detection, respectively.
In the context of crater detection, a detection labeled as a false positive (FP) is inherently ambiguous. Such a result could be a genuine misidentification, for instance a rock or shadow mistaken for a crater, or it could be a true crater that was simply not included in our ground truth (GT) dataset, representing a potential new discovery. Standard evaluation metrics cannot distinguish between these two cases.
To more deeply assess the scientific value of the false positives generated by our model, we introduce a new evaluation metric called the new discovery rate, .
We define as the proportion of all false positives (FPs) generated by the model that can be successfully matched to an entry in an external, comprehensive, and authoritative master catalog. An FP detection is reclassified as a new discovery and counted as a verified false positive () if a corresponding entry is found for it within the master catalog.
Therefore, the formula to calculate is
where is the total number of false positives produced by the model and is the number of those false positives that are verified against the external master catalog.
This metric provides a means of quantifying the “quality” of errors. A high value indicates that a significant fraction of what are conventionally considered errors (FPs) in fact consists of scientifically valuable detections that serve as valid additions to existing catalogs.
In addition to standard performance indicators like precision and recall, a thorough assessment of a crater detection algorithm necessitates quantifying the geometric deviation between the model’s predictions and the ground-truth labels. To facilitate this, we use three normalized error metrics to measure the discrepancies in the fundamental properties of a crater: its longitude, latitude, and radius. These metrics provide a more granular analysis of the model’s localization and sizing accuracy.
The normalized longitude error () and latitude error () are formulated as the absolute difference in their respective geographic coordinates, scaled by the average radius of the predicted and true craters. Similarly, the relative radius error () is computed as the absolute difference in radii, normalized by the same factor. The formal definitions are as follows:
where the subscript p denotes a value predicted by the model, while the subscript t indicates the corresponding ground-truth value from the manually annotated dataset. Specifically, , , and r respectively represent the longitude, latitude, and radius of a given crater. This normalization ensures that the calculated errors are relative to the crater’s size, providing a scale-invariant measure of performance.
3. Results
3.1. Implementation Details
All experiments were conducted on a server equipped with a single NVIDIA GeForce RTX 3090 GPU 24 GB with 90 GB RAM. The entire experimental procedure, including all comparative and ablation studies, was implemented within the PyTorch framework (version 2.1.2) under the Ubuntu 22.04 operating system, utilizing Python 3.10 and CUDA 11.8 to ensure a fair and consistent evaluation.
The models were trained for a total of 150 epochs. A batch size of 16 was used, and input images from all datasets were resized to a resolution of pixels. To enhance model generalization, a set of light data augmentation techniques was employed, including random scaling, translation, and horizontal flipping. The models were optimized using the Stochastic Gradient Descent (SGD) optimizer with a momentum of 0.937 and a weight decay of 0.0005. The initial learning rate was set to 0.01 and scheduled using a cosine annealing strategy, decaying to a final value of zero over the training duration.
3.2. Ablation Study
To systematically evaluate the independent contributions and synergistic effects of our proposed components on model performance, we conducted a series of comprehensive ablation studies. As detailed in Table 1, we integrated lightweight backbone (GhostNet), efficient feature fusion neck (BIFM), Adaptive Semantic Contrast Sampling strategy (ASCS), and Hierarchical Soft-NMS (H-SoftNMS) in a progressive and isolated manner. All experiments were conducted on our crater validation set to ensure a fair comparison.
- (1)
- Baseline: To establish a reliable performance benchmark, we first constructed a model based on a mature architecture. It leverages the DarkNet53 network to generate multi-scale feature maps from the input images, which are subsequently fused by a feature pyramid network (FPN) to produce semantically rich feature representations for detection. A consistent set of hyperparameters was maintained throughout all experiments to provide a fair basis of comparison for all subsequent methods. Ultimately, this baseline model achieved a precision of 84.1% and a recall of 78.8% on our validation set.
- (2)
- Effect of the Lightweight Backbone: The GhostNet module is designed to create a more efficient backbone by generating more feature maps from cheaper operations. When integrated into our baseline, it leads to a significant improvement in model efficiency, reducing the parameter count by 40% from 3.0M to 1.8M. However, this reduction in complexity comes at a slight cost to performance, with mAP50 and mAP95 decreasing by 0.9% and 0.4%, respectively. This highlights the classic tradeoff between model size and accuracy.
- (3)
- Effect of BIFM: In Experiment 3, the addition of BIFM to the GhostNet backbone resulted in a comprehensive performance leap over Experiment 2, with mAP50 increasing significantly from 85.9% to 89.7% and mAP95 from 68.1% to 73.8%. This demonstrates its superior cross-scale weighted feature fusion capabilities, which provide higher-quality feature maps for subsequent processing compared to the standard neck.
- (4)
- Synergistic Effect of BIFM and ASCS: A critical observation arises from comparing Experiments 4 and 6. When the ASCS strategy is applied directly to the GhostNet backbone in Experiment 4, the performance improvement is modest, with mAP50 increasing by only 1.3%. In contrast, Experiment 6 shows that applying ASCS to the model already enhanced by BIFM yields substantial performance gains, boosting mAP50 by 5.1% and mAP95 by 7.0%. This significant difference in performance uplift reveals a powerful synergistic effect between BIFM and ASCS. The underlying reason for this is that the ASCS strategy is not a standalone improvement; rather, its efficacy is fundamentally dependent on the quality of the features it receives. The BIFM module acts as an essential enabler. By enriching the multi-scale features, the BIFM creates a feature space in which crater representations are more semantically consistent and discriminative. This provides the ideal conditions for ASCS to accurately compute representative centroids and distinguish true unlabeled craters from hard negatives, thereby unlocking its full potential. In this way, the significant performance increase seen in Experiment 6 is not merely an additive effect of two independent components but a synergistic improvement born from their powerful interaction.
- (5)
- Effect of H-SoftNMS: Experiments 5 and 7 clearly demonstrate the characteristics of H-SoftNMS. Applying this postprocessing algorithm to two different model bases consistently resulted in a dramatic increase in recall, rising by 9.9 and 12 percentage points, respectively, at the cost of a significant drop in precision. This validates that H-SoftNMS, as an independent postprocessing module, has a stable and predictable effect: it minimizes false negatives by protecting nested and adjacent objects at the expense of potentially retaining more false positives. This highlights the inherent tradeoff between recall and precision for applications with different priorities.
- (6)
- Synergistic Effects and Final Model Performance: Experiment 6 demonstrates our optimal configuration, combining GhostNet, BIFM, and ASCS, which achieved the best results in precision, mAP50, and mAP95. This confirms the positive and progressive synergy among these three components. In turn, Experiment 7 provides a high-recall alternative by applying H-SoftNMS, which is suitable for specific applications where minimizing false negatives is the primary objective.
3.3. Performance Comparison of Crater Detection Models
For the performance comparison against other state-of-the-art algorithms, we selected our final representative Crater-MASN model from Experiment 6 of our ablation study, as this configuration integrates GhostNet, BIFM, and ASCS and exhibited the best overall performance. This decision was based on two primary considerations.
First, our primary innovations lie in a lightweight architectural design based on GhostNet, an enhancement of feature fusion known as BIFM, and an optimization of the training strategy, termed ASCS. These components synergistically constitute a high-performance detector that achieves an excellent balance between precision and recall, with its comprehensive performance being objectively reflected by the mAP metrics. The results from Experiment 6, with an mAP50 of 91.0% and mAP95 of 75.1%, represent the optimal performance achievable by our core methodology.
Second, we consider H-SoftNMS to be an advanced postprocessing algorithm specifically designed for extreme overlap and nesting scenarios. Its unique performance profile, characterized by exceptionally high recall at the expense of precision, warrants a more focused analysis in a targeted context. Therefore, to ensure a fair and generalizable comparison against existing methods that typically employ standard NMS, we have chosen to use our model without H-SoftNMS in this main comparison section. This allows for a more direct demonstration of the inherent advantages of our Crater-MASN core architecture in feature extraction and fusion as well as its learning strategy. The performance of H-SoftNMS will be specifically discussed and evaluated in a subsequent section dedicated to its application in a specific complex and overlapping crater field scene.
To comprehensively evaluate the effectiveness of our proposed Crater-MASN model, we conducted a performance comparison against a series of representative previously published crater detection algorithms. These include both segmentation-based methods and detection-based methods. As presented in Table 2, all models were assessed across several key metrics, including precision, recall, localization errors, and model parameter count. Finally, Figure 5 shows three random tiles extracted from the test set, comparing all the craters detect by the baseline (first column) and the predicted craters using Crater-MASN (second column). The yellow circles denote those craters successfully matched with the manually labeled catalog, the red circles indicate newly discovered craters, and the blue circles represent missed detections. This comparison clearly highlights the advantages of Crater-MASN over the baseline. Across all examples, Crater-MASN consistently reduces the number of missed detections while identifying a greater number of potential new discoveries. This is especially clear in subfigures c and d of the middle row, where the baseline model struggles significantly while our proposed model performs effectively. This demonstrates the enhanced robustness of Crater-MASN to challenging geological and lighting conditions and its superior capability for catalog completion.

Figure 5.
Qualitative comparison of detection results on three representative test set tiles. The left column (a,c,e) displays predictions from the YOLOv8n baseline, while the right column (b,d,f) shows the corresponding results from our proposed Crater-MASN. Detections are color-coded as follows: yellow circles denote TPs matched to the ground-truth catalog, red circles indicate potential new discoveries (FPs), and blue circles represent missed ground-truth craters (FNs).
- (1)
- Overall Performance Analysis: Our Crater-MASN model demonstrates exceptional overall performance while maintaining high efficiency. Compared to the YOLOv8n [41], our model achieves substantial improvements of 3.1% in precision and 4.2% in recall, reaching 87.2% and 83.0%, respectively. This result provides strong evidence for the synergistic effectiveness of our integrated GhostNet, BIFM, and ASCS strategies. Notably, this performance enhancement is achieved alongside a significant reduction in model parameters from 3.0M to 2.1M, amounting to a 30% decrease.When compared with existing crater detection models, Crater-MASN exhibits distinct advantages. Although YOLOLens5x achieves the highest scores in precision (89.9%) and recall (87.2%), it does so at the cost of an extremely large model size (101.2M parameters), making it impractical for deployment on resource-constrained edge devices. In contrast, our Crater-MASN model achieves highly competitive precision and recall with a parameter count that is merely one-fiftieth of YOLOLens5x. Furthermore, while segmentation-based methods like SqUNet attain high precision (87.5%), their recall (80.7%) is notably lower than that of our model.
- (2)
- Error Analysis: The conversion of model predictions from pixel space to a scientifically viable geographic catalog inevitably introduces errors. These discrepancies primarily stem from two sources: first, quantization errors arise from the transformation of discrete pixel coordinates into continuous geographic coordinates; second, map projections, such as the orthographic projection used in our work, can cause geometric distortions at the peripheries of the images, potentially affecting the precise measurement of crater size and morphology. Consequently, evaluating the accuracy of the prediction results generated by different methods is crucial. As presented in Table 2, we report the average errors between the predicted geographic coordinates of TP results and the corresponding entries in the manual crater catalog for various detection methods on the validation set. It is noteworthy that among the methods compared, our proposed Crater-MASN achieves the lowest fractional errors across all three metrics: longitude (8.0%), latitude (7.3%), and radius (3.1%). The radius error (Errorr) is particularly significant, as the 3.1% value achieved by our model is substantially lower than the 3.6% from the baseline as well as the values (typically exceeding 6%) from most other approaches. This superior localization accuracy can be primarily attributed to the advanced BIFM feature fusion neck used in our architecture, which works in concert with the GhostNet backbone and the ASCS training strategy to enhance the precision of bounding box regression. Overall, the predictions from Crater-MASN exhibit strong consistency with the ground truth recorded in the manual catalog, affirming its reliability as a tool for scientific analysis.

Table 2.
Performance comparison between our proposed model and other methods available in the literature. Error metrics (Errorlo, Errorla, Errorr) represent the fractional errors for longitude, latitude, and radius, respectively. The best results are highlighted in bold.
Table 2.
Performance comparison between our proposed model and other methods available in the literature. Error metrics (Errorlo, Errorla, Errorr) represent the fractional errors for longitude, latitude, and radius, respectively. The best results are highlighted in bold.
| Model | Precision (%) | Recall (%) | Errorlo (%) | Errorla (%) | Errorr (%) | Params (M) |
|---|---|---|---|---|---|---|
| DeepMoon [16] | 81.0 | 56.0 | 9.3 | 7.5 | 6.6 | 10.3 |
| ERU-Net [42] | 72.9 | 81.2 | 8.9 | 8.7 | 7.8 | 23.7 |
| D-LinkNet [43] | 71.7 | 68.2 | 11.0 | 9.2 | 9.2 | 21.0 |
| SqUNet [44] | 87.5 | 80.7 | 8.9 | 8.4 | 6.8 | 11.8 |
| ELCD [4] | 80.6 | 81.9 | 12.0 | 9.8 | 6.6 | 21.8 |
| Faster R-CNN [22] | 80.9 | 81.2 | 6.2 | 9.4 | 6.0 | 41.5 |
| YOLOLens5x [28] | 89.9 | 87.2 | 10.2 | 8.9 | 8.8 | 101.2 |
| Yolov9t [45] | 84.5 | 77.7 | 9.1 | 8.9 | 3.5 | 2.0 |
| Yolov10n [46] | 83.9 | 78.9 | 8.7 | 8.8 | 3.4 | 2.7 |
| Yolov11n [47] | 84.3 | 77.8 | 8.4 | 8.5 | 3.4 | 2.6 |
| Yolov12n [48] | 83.8 | 77.7 | 8.6 | 8.3 | 3.5 | 2.6 |
| YOLOv8n [41] | 84.1 | 78.8 | 8.9 | 8.6 | 3.6 | 3.0 |
| Ours (H-SoftNMS) | 69.3 | 95.0 | 8.3 | 7.8 | 3.3 | 2.1 |
| Ours | 87.2 | 83.0 | 8.0 | 7.3 | 3.1 | 2.1 |
3.4. Performance Analysis in a Specific Complex and Overlapping Crater Field Scene
To assess the efficacy of our proposed H-SoftNMS postprocessing strategy in handling extreme conditions, we selected 500 test samples from the validation set that contained overlapping scenes and dense meteorite crater scenes. A subset of these selected samples is presented in Figure 6. In such scenarios, maximizing recall by minimizing missed detections is often more critical than suppressing false positives. Consequently, we adopted recall and our newly defined new discovery rate metric, , as the primary evaluation metrics. measures the proportion of all FPs that can be verified against an authoritative external catalog, reflecting the model’s ability to discover unlabeled true objects.
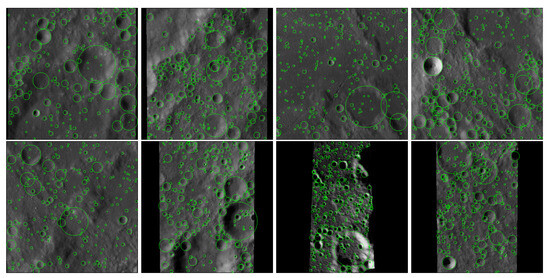
Figure 6.
Visualization of some complex and overlapping crater scene testing samples.
As shown in Table 3, our optimal model equipped with H-SoftNMS demonstrates outstanding performance. First, in terms of recall, our method achieved 91.6%, attaining the best performance among all compared methods. This result significantly surpasses the standard Yolov8n baseline (74.5%) and also exceeds other advanced methods such as LCD-Net (90.6%). The substantial improvement in recall provides strong evidence for the effectiveness of the core mechanisms within H-SoftNMS. Its containment-aware logic accurately identifies and preserves smaller craters nested within larger ones, while its soft-suppression nature retains adjacent overlapping craters, thereby enabling superior object detection capability in complex scenes characterized by density and nesting.
More remarkably, our method also achieved the best performance in terms of the new discovery rate (). To rigorously validate the scientific merit of these potential discoveries, we employed a two-stage cross-referencing process. First, we performed an internal consistency check by comparing the FPs generated on our validation set against the entire Robbins catalog. The Robbins catalog was chosen for this initial step because it served as our foundational dataset; this allowed us to verify whether the model could successfully rediscover known craters that were simply not part of the held-out validation split. This step is crucial in order to confirm that the model’s FPs are not random noise and correspond to genuine crater-like features present in our source data. When cross-referenced against the established Robbins crater catalog, our method reached a of 89.6%. This implies that nearly 90% of the false positives generated by our method are in fact true craters present in the authoritative catalog but that were unlabeled in our training set. As shown in Table 3, this figure is substantially higher than most compared methods. However, a definitive external validation was essential in order to confirm these findings independently, particularly given the known limitations of the Robbins catalog. While a valuable benchmark, the Robbins catalog is manually annotated, a process that is prone to subjectivity and omissions; in addition, its scope is primarily limited to craters with diameters greater than 1–2 km. To address these limitations, we chose the LU5M812TGT catalog [49] for our final validation. In contrast to Robbins, the LU5M812TGT is a more recent AI-powered global database with a more comprehensive scope that includes craters with diameters greater than 0.4 km. Its systematic methodology and more inclusive size range make it a superior independent authority for verifying our model’s discoveries, especially for smaller craters that fall outside the annotation scope of our original ground truth. The results of this rigorous external validation were even more compelling, with reaching an exceptional 94.01%. This reveals a key synergistic effect in which the ASCS training strategy had already endowed the model with the potential to recognize unlabeled objects, then the lenient H-SoftNMS postprocessing fully unleashed this potential. Consequently, a seemingly high false positive rate, when examined through the lens of the metric, is transformed into powerful evidence of the model’s capability for scientific exploration and catalog completion.

Table 3.
Performance comparison in a specific complex and overlapping crater field scene compared to the model reported in [5]. The best results for each metric are highlighted in bold.
Table 3.
Performance comparison in a specific complex and overlapping crater field scene compared to the model reported in [5]. The best results for each metric are highlighted in bold.
| Model | Recall (%) | (%) |
|---|---|---|
| DeepMoon [16] | 84.1 | 71.87 |
| Mask R-CNN [50] | 73.4 | 83.90 |
| SqUNet [44] | 86.9 | 79.18 |
| R-FCN [51] | 88.9 | 65.71 |
| Faster R-CNN [22] | 88.1 | 68.36 |
| LCD-Net [5] | 90.6 | 63.02 |
| Yolov8n | 74.5 | 85.72 |
| Yolov9t | 70.9 | 85.36 |
| Yolov10n | 74.9 | 84.96 |
| Yolov11n | 72.3 | 85.93 |
| Yolov12n | 75.2 | 83.88 |
| Ours | 91.6 | 89.6 |
Finally, to qualitatively assess the practical performance of our proposed Crater-MASN model (equipped with H-SoftNMS) in complex scenarios, we visualized the detection results on representative images from our test set. As illustrated in Figure 7, we employ a color-coded scheme to distinguish different categories of detection outcomes: yellow circles denote TPs that were successfully matched to the ground truth; blue circles represent FNs, which are ground-truth craters missed by the model; and red circles indicate FPs, which are predictions that do not correspond to any ground-truth annotation in our dataset.
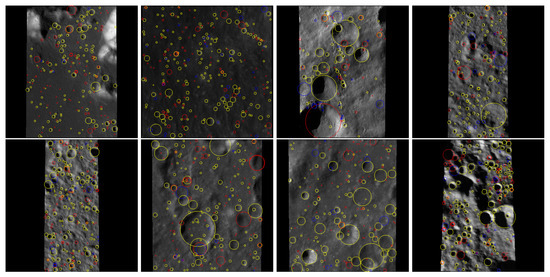
Figure 7.
Visualization of detection results on representative testing samples with dense and overlapping craters. The yellow, blue, and red circles denote TPs, FNs, and FPs, respectively.
The visualization clearly demonstrates the robust detection capability of our model, particularly in regions characterized by high crater density and significant overlap. The prevalence of yellow circles, covering the vast majority of ground-truth craters of various sizes, provides intuitive corroboration for the exceptional 91.6% recall rate reported in our quantitative analysis. Of particular note is the model’s ability to successfully identify both the outer larger craters and the smaller inner ones in areas with nested crater-in-crater structures, as evidenced by multiple yellow circles. This directly validates the effectiveness of the H-SoftNMS algorithm in preserving hierarchical relationships.
Furthermore, an analysis of the error types offers profound insights. The blue circles (FNs) are predominantly associated with two challenging cases: either extremely small craters approaching the resolution limit of the imagery, or ancient heavily-eroded craters with highly ambiguous rim features. This indicates that the model’s missed detections are concentrated on the most challenging samples. On the other hand, while red circles (FPs) are present, a significant portion of them also exhibit clear crater-like morphology. This observation aligns strongly with our of 89.6%, providing compelling evidence that the majority of these FPs are not model errors but rather valid new discoveries of true craters that were unlabeled in our ground-truth dataset.
4. Discussion
In this study, we have proposed and validated Crater-MASN, a network designed to systematically overcome key obstacles in crater detection. The experimental results confirm its efficacy across multiple fronts.
Our work first tackled the dual challenges of computational efficiency and robust multi-scale representation. By employing a GhostNet backbone, we were able to reduce the parameter count by 30% compared to a standard baseline, addressing the need for efficiency in large-scale analysis. While this incurs a slight initial performance tradeoff, the integration of our BIFM fusion neck not only recovers this loss but significantly surpasses the baseline. Bidirectional information flow, a key aspect of the BIFM, proves crucial for reconciling semantic and spatial features. This reconciliation enhances the detection of small variably-degraded craters and directly addresses the challenge of high data variability.
A cornerstone of our contribution is the ASCS training strategy, which is designed to confront the issue of incomplete ground-truth catalogs. Our ablation study revealed a powerful synergy between BIFM and ASCS in which the high-quality features from BIFM enabled ASCS to more accurately distinguish true unlabeled craters from hard negatives. This synergy transformed the data incompleteness problem from a liability into an opportunity for discovery, ultimately elevating our model’s mAP50 to 91.0% and enabling a remarkable new discovery rate of 89.6%.
Finally, we addressed the long-standing problem of resolving complex spatial structures. Our proposed H-SoftNMS algorithm demonstrates unique value in specific complex scenarios such as dense crater fields, maximizing the recall rate to 95.0%. By differentiating between hierarchical containment and simple adjacency, H-SoftNMS successfully preserves “crater-in-crater” structures that are typically suppressed by conventional NMS algorithms, providing a more accurate catalog of these challenging regions. However, this high recall rate appears to come at the expense of precision. A nuanced discussion is warranted regarding the practical applicability of the high-recall and low-precision mode enabled by H-SoftNMS. It is crucial to interpret the term “low precision” in this context not as a measure of failure but as a reflection of both the algorithm’s design and the limitations of existing ground-truth catalogs. The drop in precision is a direct consequence of the algorithm’s intentional leniency and the incompleteness of the Robbins catalog used for evaluation. As demonstrated by the high of 89.6%, a vast majority of what are metrically classified as “false positives” are in fact scientifically valuable true craters. Therefore, this configuration should be understood not as an inaccurate mode but as a high-sensitivity discovery mode. A scientist would prefer this mode for several specific scenarios, including the initial creation of catalogs covering newly surveyed regions, exploratory science when searching for rare features, and generating training data for future models.
Nevertheless, our work has certain limitations. First, although the proposed ASCS strategy performs exceptionally well in handling incomplete annotations, its effectiveness is still constrained by the number and diversity of TPs within each training batch, which can lead to instability in the online clustering of prototypes. For practical applications, we recommend that users aim for batch sizes that ensure a sufficient number of TPs, such as greater than 5–10 on average, to ensure robust prototype generation. Second, the high false positive rate associated with H-SoftNMS, despite its high recall, necessitates a more complex subsequent manual verification process. To make this more manageable, we suggest a two-stage workflow: first, automatically cross-reference the model’s FPs with other established crater catalogs to filter out known discoveries; second, prioritize manual review for the remaining unverified FPs that have the highest confidence scores. Future work could explore semi-supervised or self-supervised learning methods to pre-train a more robust feature extractor on vast amounts of unlabeled data, thereby reducing the dependency on in-batch TPs. Additionally, investigating model quantization and pruning techniques to further compress the model while maintaining its current performance is another important direction.
5. Conclusions
In this paper, we have proposed and validated Crater-MASN, a lightweight network designed to systematically address the multifaceted challenges of crater detection such as efficiency, data incompleteness, and complex spatial scenarios. By integrating an efficient GhostNet backbone, a novel BIFM fusion neck, and an ASCS training strategy, our model achieves a state-of-the-art balance between accuracy and computational cost, reaching an mAP50 of 91.0% with only 2.1M parameters. Furthermore, the introduction of our H-SoftNMS algorithm specifically targets nested crater structures, boosting recall to an exceptional 95.0% and achieving a new discovery rate () of 89.6%. This research provides planetary science with a powerful and scalable tool for both high-precision cataloging and scientific discovery. The methodologies presented in this paper can also offer valuable insights for other computer vision tasks grappling with similar data and object complexity challenges. Future work will focus on enhancing model robustness and extending its application to other planetary bodies. While the trained model is specific to its training data, the fundamental architecture of Crater-MASN is not specific to any planetary body. This architectural generality makes it a promising candidate for adaptation to Martian or Mercury crater detection by retraining on relevant datasets.
Author Contributions
Conceptualization, R.Y.; methodology, R.Y.; software, R.Y.; validation, R.Y.; formal analysis, R.Y.; investigation, Z.X. and R.Y.; resources, Z.X. and R.Y.; data curation, Z.X. and R.Y.; writing—original draft preparation, R.Y.; writing—review and editing, Z.X. and R.Y.; visualization, R.Y.; supervision, Z.X. and R.Y.; project administration, R.Y.; funding acquisition, Z.X. and R.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number No. 62271303; Pujiang Talents Plan, grant number No. 22PJD029.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sawabe, Y.; Matsunaga, T.; Rokugawa, S. Automated detection and classification of lunar craters using multiple approaches. Adv. Space Res. 2006, 37, 21–27. [Google Scholar] [CrossRef]
- Chen, M.; Liu, D.; Qian, K.; Li, J.; Lei, M.; Zhou, Y. Lunar crater detection based on terrain analysis and mathematical morphology methods using digital elevation models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3681–3692. [Google Scholar] [CrossRef]
- Zang, S.; Mu, L.; Xian, L.; Zhang, W. Semi-supervised deep learning for lunar crater detection using ce-2 dom. Remote Sens. 2021, 13, 2819. [Google Scholar] [CrossRef]
- Fan, L.; Yuan, J.; Zha, K.; Wang, X. Elcd: Efficient lunar crater detection based on attention mechanisms and multiscale feature fusion networks from digital elevation models. Remote Sens. 2022, 14, 5225. [Google Scholar] [CrossRef]
- Miao, D.; Yan, J.; Tu, Z.; Barriot, J.P. LCDNet: An Innovative Neural Network for Enhanced Lunar Crater Detection Using DEM Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 11034–11049. [Google Scholar] [CrossRef]
- Salamunićcar, G.; Lončarić, S.; Mazarico, E. LU60645GT and MA132843GT catalogues of Lunar and Martian impact craters developed using a Crater Shape-based interpolation crater detection algorithm for topography data. Planet. Space Sci. 2012, 60, 236–247. [Google Scholar] [CrossRef]
- Ding, W.; Stepinski, T.F.; Bandeira, L.; Vilalta, R.; Wu, Y.; Lu, Z.; Cao, T. Automatic detection of craters in planetary images: An embedded framework using feature selection and boosting. In Proceedings of the 19th ACM international Conference on Information and Knowledge Management, Toronto, ON, Canada, 26–30 October 2010; pp. 749–758. [Google Scholar]
- Chen, J.Q.; Cui, P.Y.; Cui, H.T. Automated detection and classification for craters based on geometric matching. In International Symposium on Photoelectronic Detection and Imaging 2011: Space Exploration Technologies and Applications, Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2011, Beijing, China, 24–26 May 2011; SPIE: Bellingham, WA, USA, 2011; Volume 8196, pp. 543–548. [Google Scholar]
- Ding, W.; Stepinski, T.F.; Mu, Y.; Bandeira, L.; Ricardo, R.; Wu, Y.; Lu, Z.; Cao, T.; Wu, X. Subkilometer crater discovery with boosting and transfer learning. ACM Trans. Intell. Syst. Technol. (TIST) 2011, 2, 39. [Google Scholar] [CrossRef]
- Yu, Z.; Zhu, S.; Cui, P. Sequence detection of planetary surface craters from DEM data. In Proceedings of the 10th World Congress on Intelligent Control and Automation, Beijing, China, 6–8 July 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 4775–4779. [Google Scholar]
- Luo, L.; Mu, L.; Wang, X.; Li, C.; Ji, W.; Zhao, J.; Cai, H. Global detection of large lunar craters based on the CE-1 digital elevation model. Front. Earth Sci. 2013, 7, 456–464. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, H.; Huang, Q.; Feng, Y.; Yan, X.; Tong, X.; Liu, S.; Liu, S.; Xu, X.; Wang, C.; et al. A novel approach for multiscale lunar crater detection by the use of path-profile and isolation forest based on high-resolution planetary images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4601424. [Google Scholar] [CrossRef]
- Duan, Q.; Liu, R.; Liu, Y. Automatic Lunar Crater Detection Based on DEM Data Using a Max Curvature Detection Method. IEEE Geosci. Remote Sens. Lett. 2024, 21, 8001205. [Google Scholar] [CrossRef]
- Hashimoto, S.; Mori, K. Lunar crater detection based on grid partition using deep learning. In Proceedings of the 2019 IEEE 13th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 29–31 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 75–80. [Google Scholar]
- Jia, Y.; Wan, G.; Liu, L.; Wu, Y.; Zhang, C. Automated detection of lunar craters using deep learning. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020; IEEE: Piscataway, NJ, USA, 2020; Volume 9, pp. 1419–1423. [Google Scholar]
- Silburt, A.; Ali-Dib, M.; Zhu, C.; Jackson, A.; Valencia, D.; Kissin, Y.; Tamayo, D.; Menou, K. Lunar crater identification via deep learning. Icarus 2019, 317, 27–38. [Google Scholar] [CrossRef]
- Mao, Y.; Yuan, R.; Li, W.; Liu, Y. Coupling complementary strategy to U-net based convolution neural network for detecting lunar impact craters. Remote Sens. 2022, 14, 661. [Google Scholar] [CrossRef]
- Tang, K.; Liang, J.; Yan, P.; Tian, X. Lunar crater detection based YOLOV5 using CCD data. In Proceedings of the 2022 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 24–26 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 511–514. [Google Scholar]
- Wang, H.; Jiang, J.; Zhang, G. CraterIDNet: An end-to-end fully convolutional neural network for crater detection and identification in remotely sensed planetary images. Remote Sens. 2018, 10, 1067. [Google Scholar] [CrossRef]
- Wu, Y.; Wan, G.; Liu, L.; Wei, Z.; Wang, S. Intelligent crater detection on planetary surface using convolutional neural network. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; IEEE: Piscataway, NJ, USA, 2021; Volume 5, pp. 1229–1234. [Google Scholar]
- Zhao, Y.; Ye, H. Crater Detection and Population Statistics in Tianwen-1 Landing Area Based on Segment Anything Model (SAM). Remote Sens. 2024, 16, 1743. [Google Scholar] [CrossRef]
- Lin, X.; Zhu, Z.; Yu, X.; Ji, X.; Luo, T.; Xi, X.; Zhu, M.; Liang, Y. Lunar crater detection on digital elevation model: A complete workflow using deep learning and its application. Remote Sens. 2022, 14, 621. [Google Scholar] [CrossRef]
- Sinha, M.; Paul, S.; Ghosh, M.; Mohanty, S.N.; Pattanayak, R.M. Automated Lunar Crater Identification with Chandrayaan-2 TMC-2 Images using Deep Convolutional Neural Networks. Sci. Rep. 2024, 14, 8231. [Google Scholar] [CrossRef]
- Myojin, T.; Hashimoto, S.; Mori, K.; Sugawara, K.; Ishihama, N. Improving reliability of object detection for lunar craters using Monte Carlo dropout. In Artificial Neural Networks and Machine Learning–ICANN 2019: Image Processing, Proceedings of the 28th International Conference on Artificial Neural Networks, Munich, Germany, 17–19 September 2019; Proceedings, Part III 28; Springer: Cham, Switzerland, 2019; pp. 68–80. [Google Scholar]
- Wang, Y.; Xie, H.; Huang, Q.; Yan, X.; Liu, S.; Ye, Z.; Wang, C.; Xu, X.; Liu, S.; Jin, Y.; et al. Small Lunar Crater Detection from LROC NAC using Statistically Constrained Path-morphologies and Unsupervised Discriminate Correlation Filters. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4601124. [Google Scholar] [CrossRef]
- Dai, Y.; Xue, C.; Du, A. Boosting crater detection via vit-based feature fusion from near-ir images and dems. IEEE Geosci. Remote Sens. Lett. 2023, 20, 8002505. [Google Scholar] [CrossRef]
- Tewari, A.; Verma, V.; Srivastava, P.; Jain, V.; Khanna, N. Automated crater detection from co-registered optical images, elevation maps and slope maps using deep learning. Planet. Space Sci. 2022, 218, 105500. [Google Scholar] [CrossRef]
- La Grassa, R.; Cremonese, G.; Gallo, I.; Re, C.; Martellato, E. YOLOLens: A deep learning model based on super-resolution to enhance the crater detection of the planetary surfaces. Remote Sens. 2023, 15, 1171. [Google Scholar] [CrossRef]
- Tewari, A.; Khanna, N. Arbitrary Scale Super-Resolution Assisted Lunar Crater Detection in Satellite Images. arXiv 2024, arXiv:2402.05068. [Google Scholar] [CrossRef]
- Robinson, M.S.; Brylow, S.; Tschimmel, M.e.; Humm, D.; Lawrence, S.; Thomas, P.; Denevi, B.W.; Bowman-Cisneros, E.; Zerr, J.; Ravine, M.; et al. Lunar reconnaissance orbiter camera (LROC) instrument overview. Space Sci. Rev. 2010, 150, 81–124. [Google Scholar] [CrossRef]
- Speyerer, E.; Robinson, M.; Denevi, B.; LROC Science Team. Lunar Reconnaissance Orbiter Camera global morphological map of the Moon. In Proceedings of the 42nd Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 7–11 March 2011; p. 2387, Number 1608 in LPI Contribution. [Google Scholar]
- Sato, H.; Robinson, M.; Hapke, B.; Denevi, B.; Boyd, A. Resolved Hapke parameter maps of the Moon. J. Geophys. Res. Planets 2014, 119, 1775–1805. [Google Scholar] [CrossRef]
- Robbins, S.J. A new global database of lunar impact craters > 1–2 km: 1. Crater locations and sizes, comparisons with published databases, and global analysis. J. Geophys. Res. Planets 2019, 124, 871–892. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28, 1–9. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.; Tian, Q.; Guo, J.; Xu, C.; Xu, C. Ghostnet: More features from cheap operations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1580–1589. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar] [CrossRef]
- Liu, S.; Qi, L.; Qin, H.; Shi, J.; Jia, J. Path Aggregation Network for Instance Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 8759–8768. [Google Scholar]
- Tan, M.; Pang, R.; Le, Q.V. EfficientDet: Scalable and Efficient Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 10781–10790. [Google Scholar]
- Xu, S.; Zheng, S.; Xu, W.; Xu, R.; Wang, C.; Zhang, J.; Teng, X.; Li, A.; Guo, L. Hcf-net: Hierarchical context fusion network for infrared small object detection. In Proceedings of the 2024 IEEE International Conference on Multimedia and Expo (ICME), Niagara Falls, ON, Canada, 15–19 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–6. [Google Scholar]
- Bodla, N.; Singh, B.; Chellappa, R.; Davis, L.S. Soft-NMS–improving object detection with one line of code. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5561–5569. [Google Scholar]
- Jocher, G.; Chaurasia, A.; Qiu, J. Ultralytics YOLOv8. 2023. Available online: https://github.com/ultralytics/ultralytics (accessed on 10 June 2024).
- Wang, S.; Fan, Z.; Li, Z.; Zhang, H.; Wei, C. An effective lunar crater recognition algorithm based on convolutional neural network. Remote Sens. 2020, 12, 2694. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, C.; Wu, M. D-LinkNet: LinkNet with pretrained encoder and dilated convolution for high resolution satellite imagery road extraction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 182–186. [Google Scholar]
- Zhao, Y.; Ye, H. Squnet: An high-performance network for crater detection with dem data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 8577–8585. [Google Scholar] [CrossRef]
- Wang, C.Y.; Yeh, I.H.; Mark Liao, H.Y. Yolov9: Learning what you want to learn using programmable gradient information. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Cham, Switzerland, 2024; pp. 1–21. [Google Scholar]
- Wang, A.; Chen, H.; Liu, L.; Chen, K.; Lin, Z.; Han, J. Yolov10: Real-time end-to-end object detection. Adv. Neural Inf. Process. Syst. 2024, 37, 107984–108011. [Google Scholar]
- Khanam, R.; Hussain, M. Yolov11: An overview of the key architectural enhancements. arXiv 2024, arXiv:2410.17725. [Google Scholar] [CrossRef]
- Tian, Y.; Ye, Q.; Doermann, D. Yolov12: Attention-centric real-time object detectors. arXiv 2025, arXiv:2502.12524. [Google Scholar]
- La Grassa, R.; Martellato, E.; Cremonese, G.; Re, C.; Tullo, A.; Bertoli, S. LU5M812TGT: An AI-Powered global database of impact craters ≥ 0.4 km on the Moon. ISPRS J. Photogramm. Remote Sens. 2025, 220, 75–84. [Google Scholar] [CrossRef]
- Ali-Dib, M.; Menou, K.; Jackson, A.P.; Zhu, C.; Hammond, N. Automated crater shape retrieval using weakly-supervised deep learning. Icarus 2020, 345, 113749. [Google Scholar] [CrossRef]
- Yang, C.; Zhao, H.; Bruzzone, L.; Benediktsson, J.A.; Liang, Y.; Liu, B.; Zeng, X.; Guan, R.; Li, C.; Ouyang, Z. Lunar impact crater identification and age estimation with Chang’E data by deep and transfer learning. Nat. Commun. 2020, 11, 6358. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).