A Machine Learning Model Integrating Remote Sensing, Ground Station, and Geospatial Data to Predict Fine-Resolution Daily Air Temperature for Tuscany, Italy
Abstract
1. Introduction
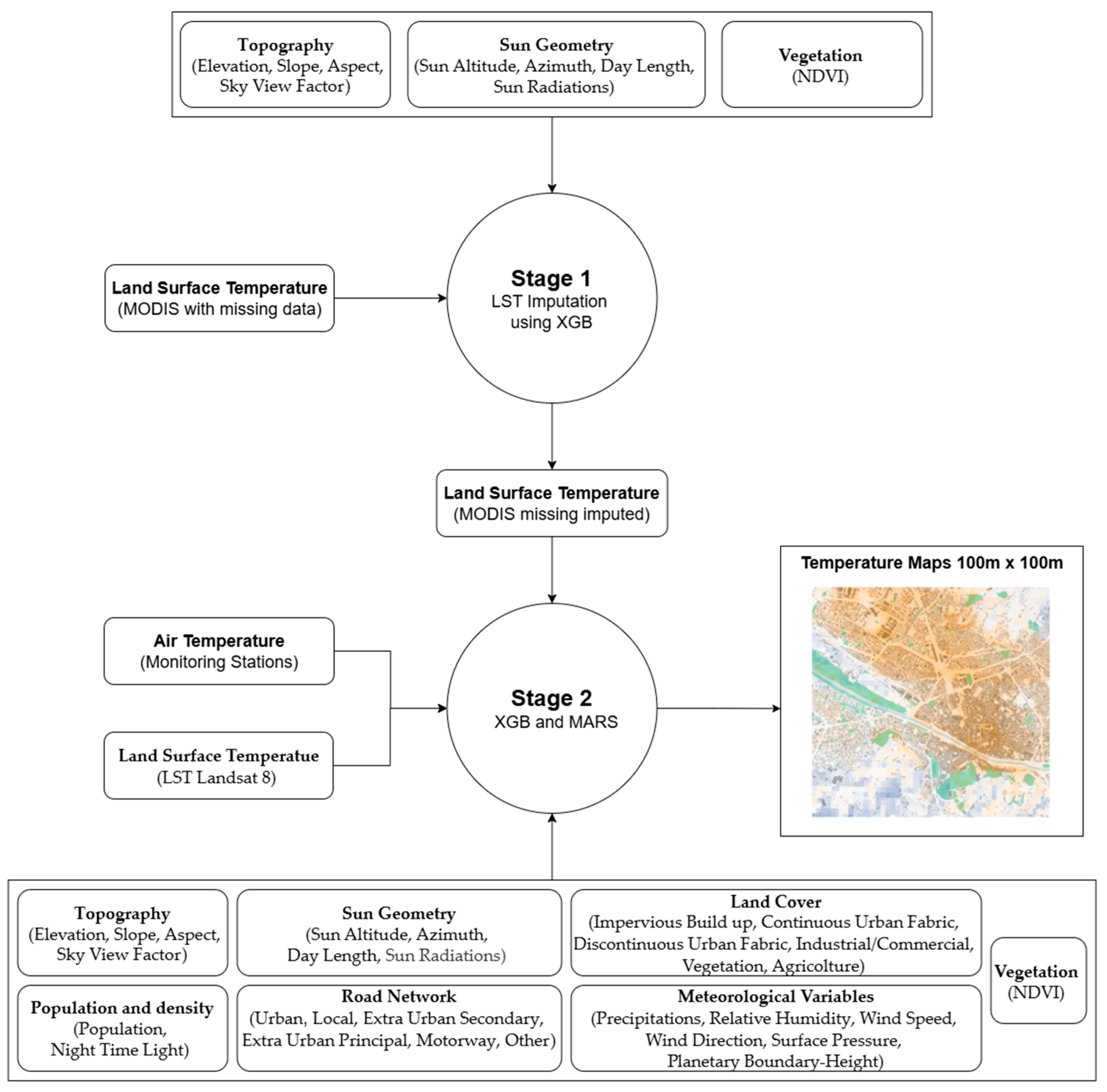
2. Materials and Methods
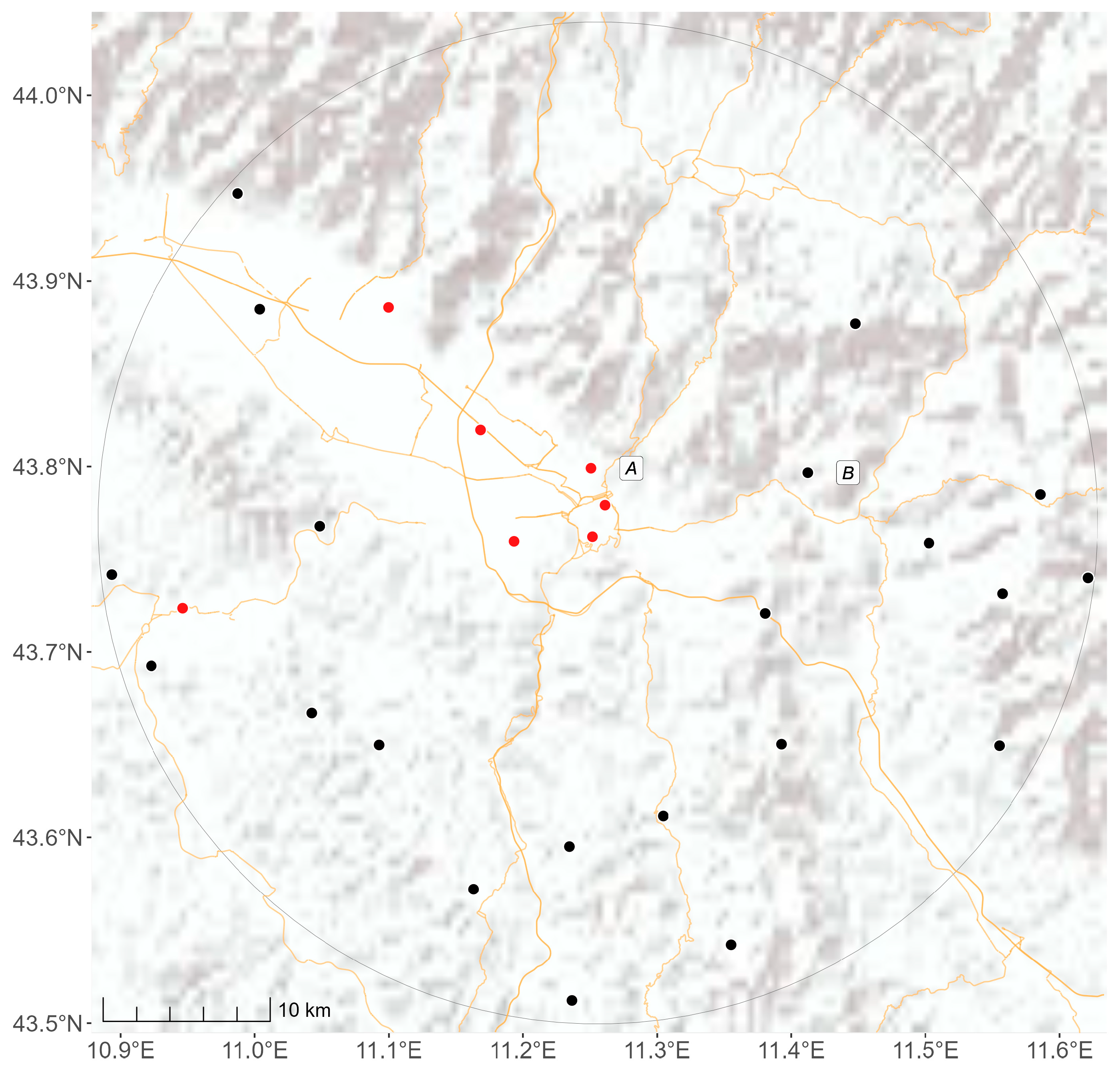
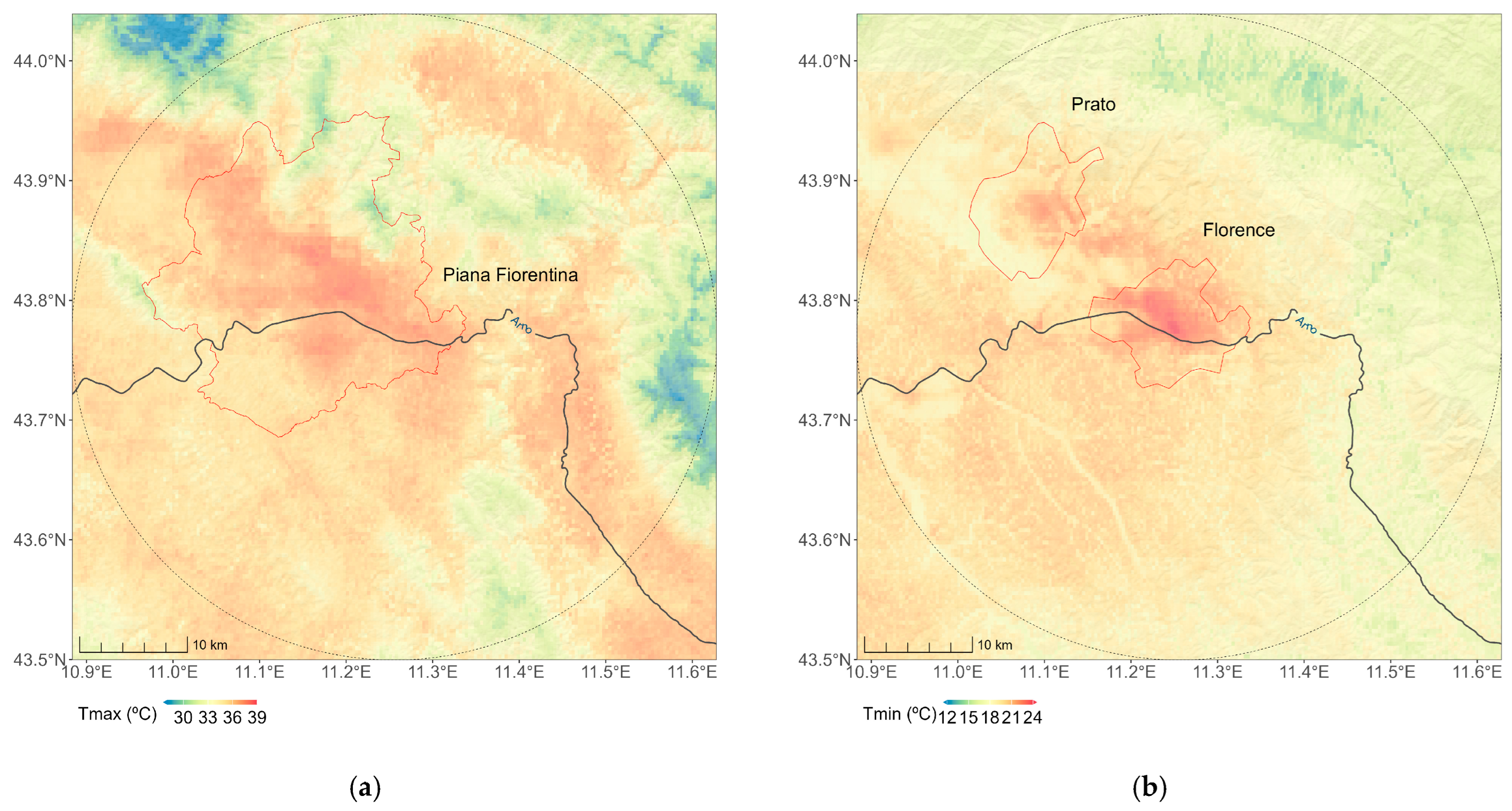
2.1. The Study Area
2.2. Data
2.2.1. Meteorological Observations

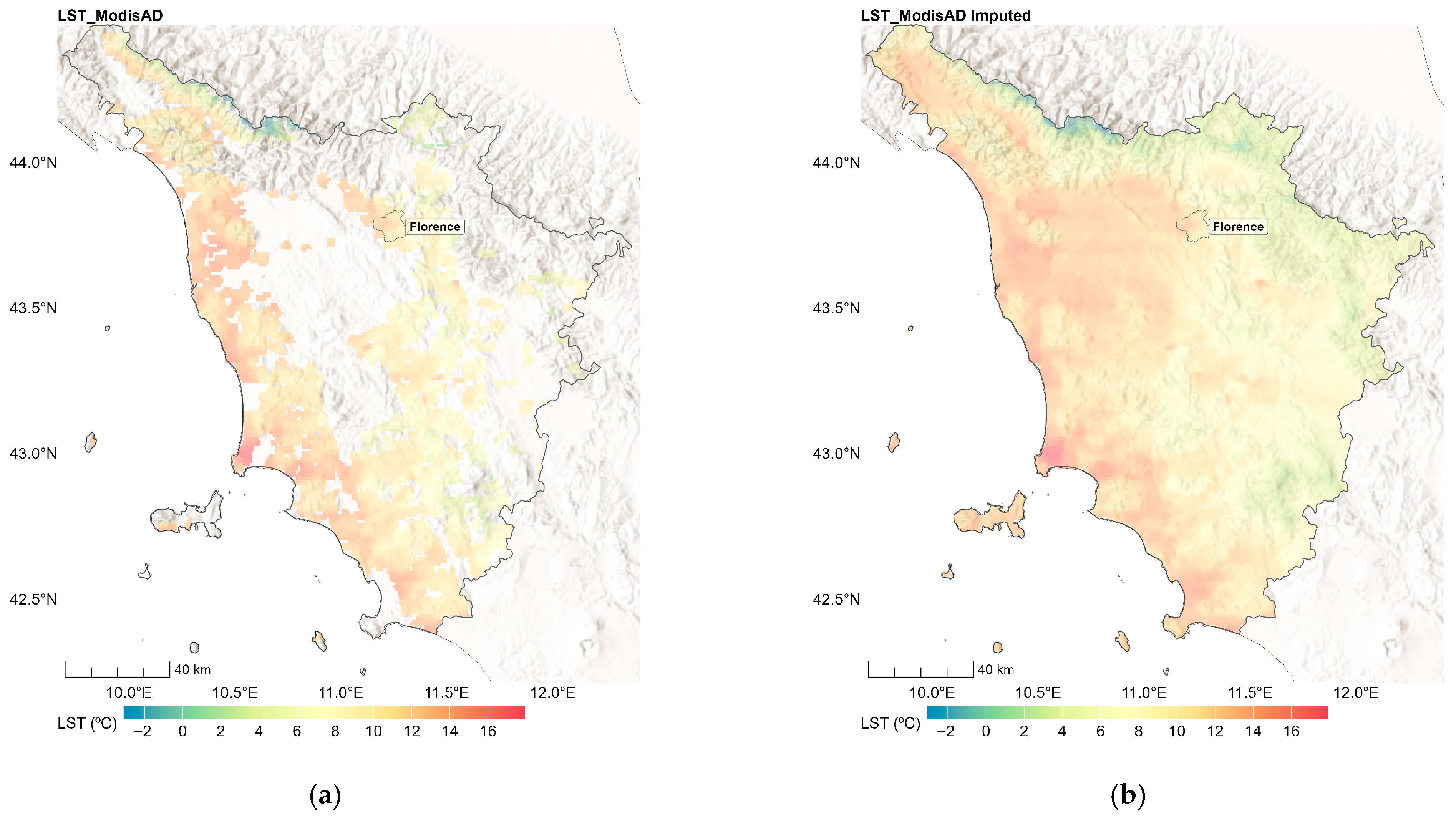
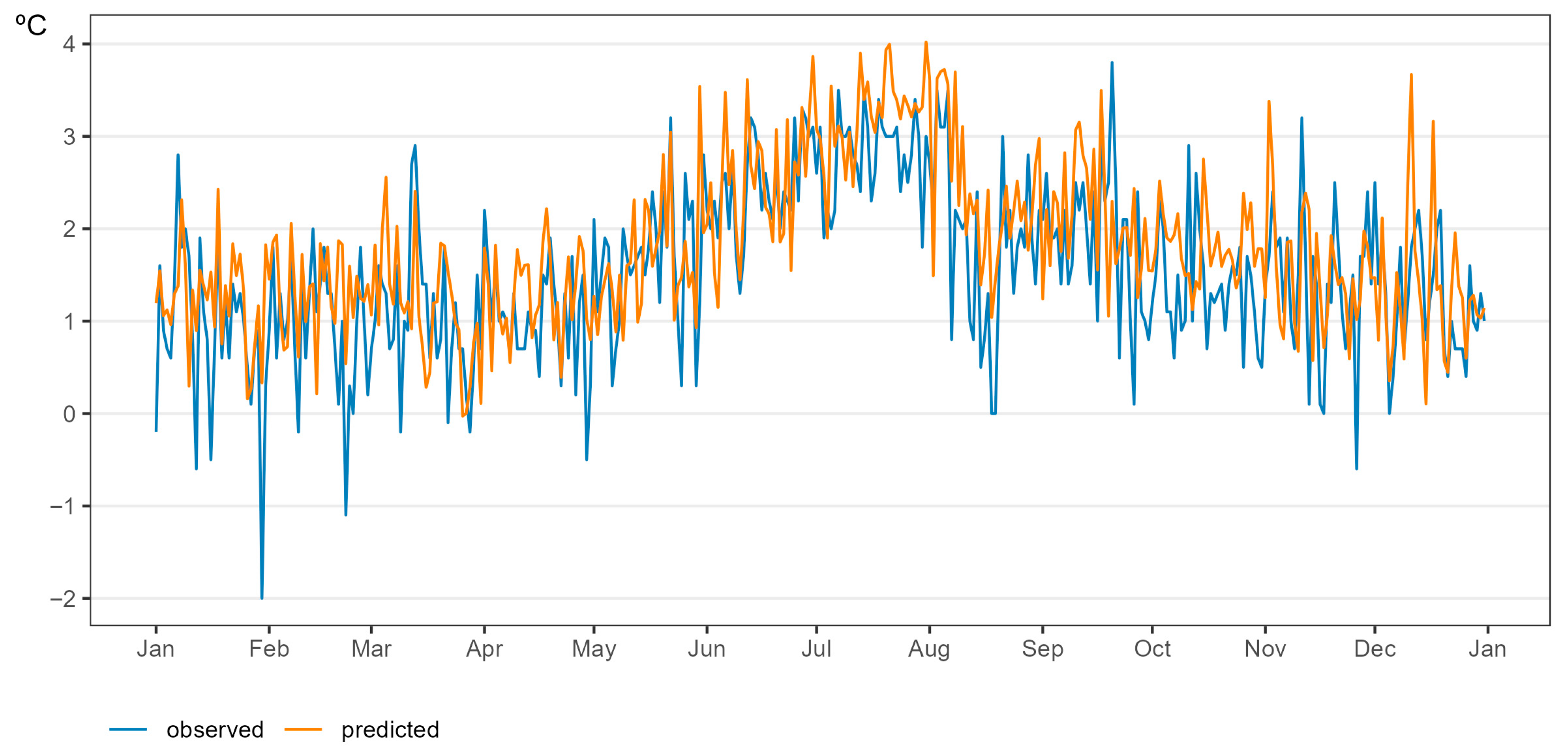
2.2.2. Land Surface Temperature Data
2.3. Spatial and Spatio-Temporal Predictors
2.4. Statistical Methods
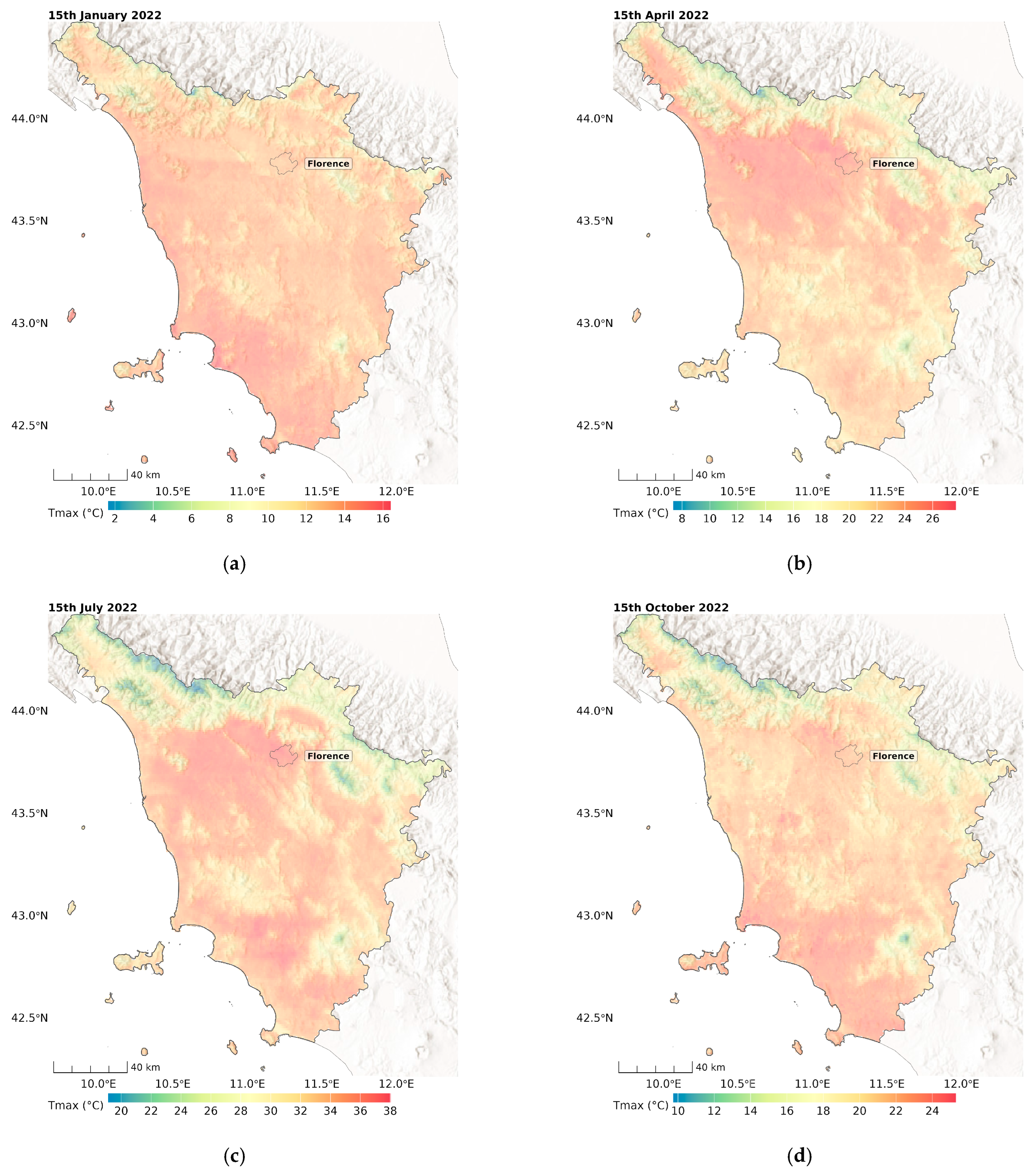
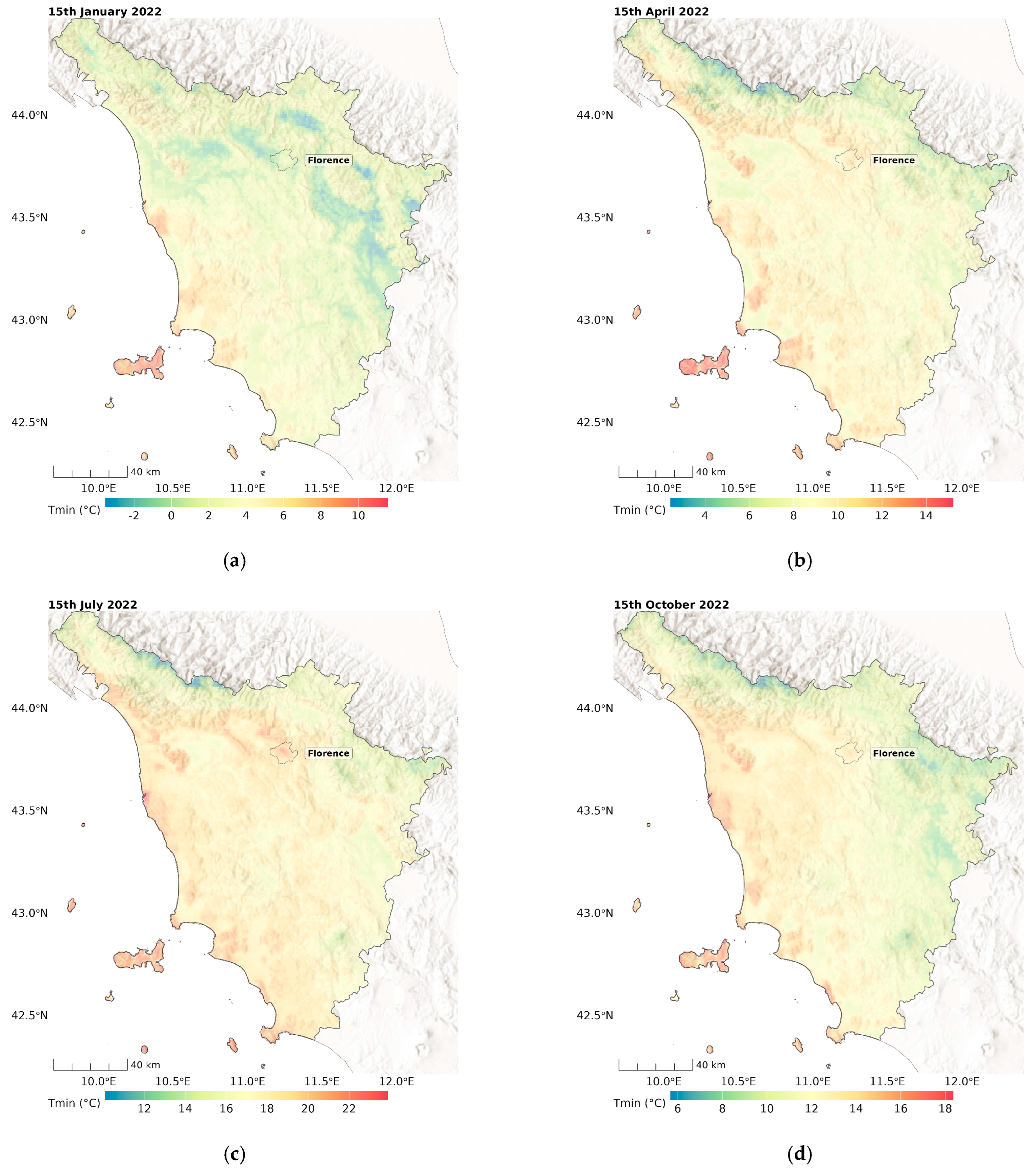
3. Results
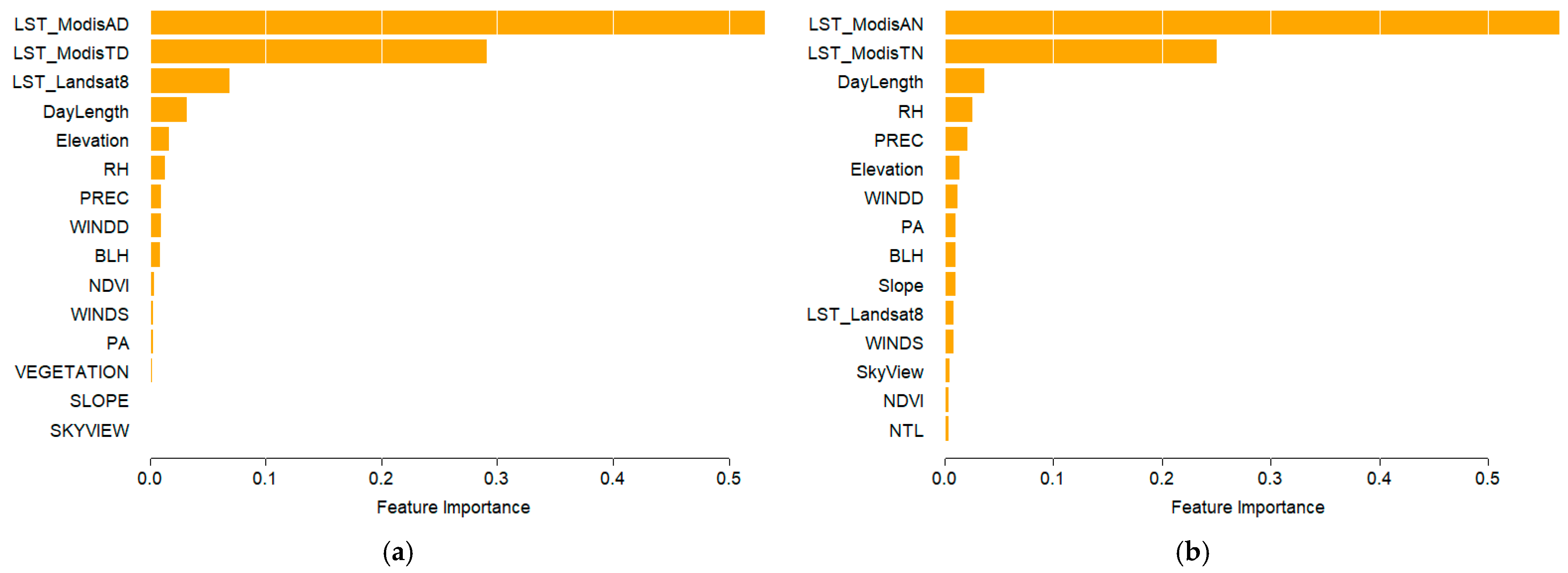
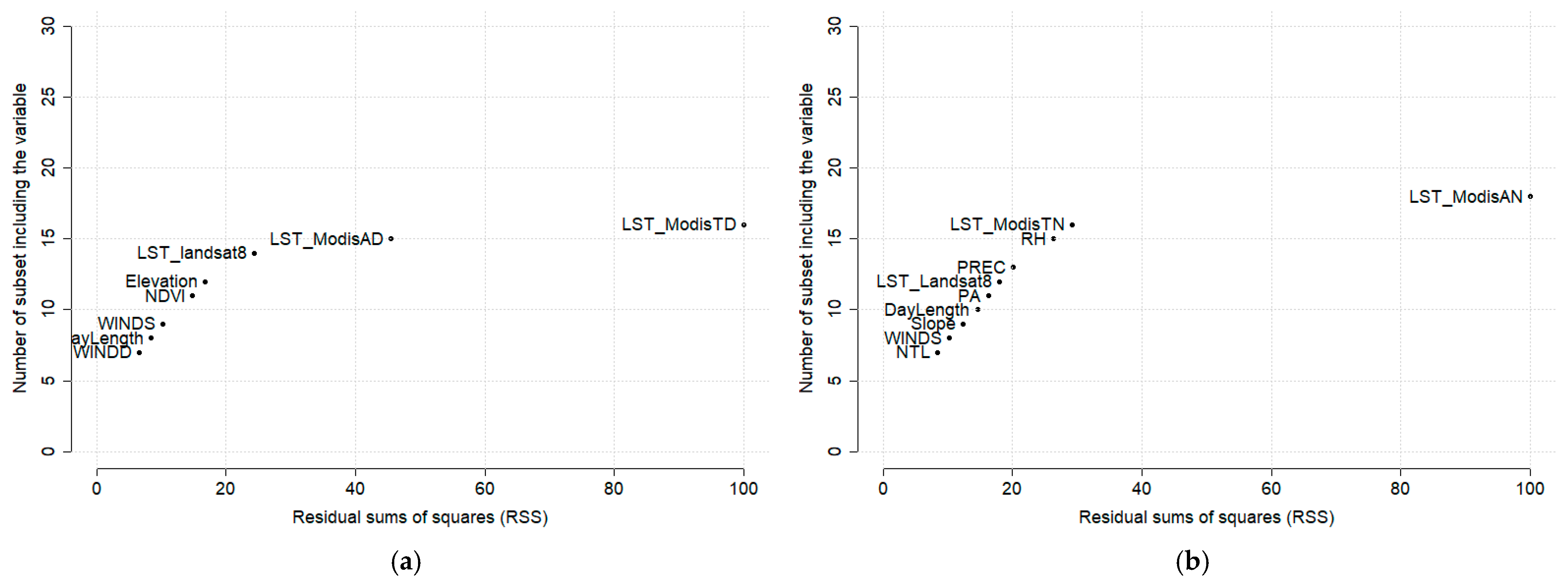
3.1. Stage 1
3.2. Stage 2
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AD | Aqua Day |
| AN | Aqua Night |
| BLH | Planetary Boundary Layer Height |
| CLC | Corine Land Cover |
| CV | Cross-Validation |
| DAYL | Day Length |
| DEM | Digital Elevation Model |
| DIFSUNRAD | Diffuse Solar Radiation |
| DIRSUNRAD | Direct Solar Radiation |
| EO | Earth Observation |
| GNN | Graph Neural Network |
| HHAP | Heat Health Action Plans |
| IBU | Impervious Build-up |
| LST | Land Surface Temperature |
| MAE | Mean Absolute Error |
| MARS | Multivariate Adaptive Regression Splines |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| NDVI | Normalized Difference Vegetation Index |
| NTL | Nighttime Light |
| OOB | Out-of-Bag |
| PA | Surface Pressure |
| PM2.5 | Particulate Matter < 2.5 μm |
| POP | Population |
| PREC | Total Precipitation |
| RDS | Road Network Dataset |
| RH | Relative Humidity |
| RMSE | Root Mean Square Error |
| SLP | Slope |
| ST-GAT | Spatio-Temporal Graph Attention Network |
| SUNALT | Sun Altitude |
| SVF | Sky View Factor |
| TD | Terra Day |
| Tmax | Maximum Temperature |
| Tmin | Minimum Temperature |
| TN | Terra Night |
| UHI | Urban Heat Island |
| WINDD | Wind Direction |
| WINDS | Wind Speed |
| XGB | Extreme Gradient Boosting |
References
- Basu, R. High ambient temperature and mortality: A review of epidemiologic studies from 2001 to 2008. Environ. Health 2009, 8, 40. [Google Scholar] [CrossRef] [PubMed]
- Basu, R.; Samet, J.M. Relation between Elevated Ambient Temperature and Mortality: A Review of the Epidemiologic Evidence. Epidemiol. Rev. 2002, 24, 190–202. [Google Scholar] [CrossRef]
- Masselot, P.; Mistry, M.; Vanoli, J.; Schneider, R.; Iungman, T.; Garcia-Leon, D.; Ciscar, J.-C.; Feyen, L.; Orru, H.; Urban, A.; et al. Excess mortality attributed to heat and cold: A health impact assessment study in 854 cities in Europe. Lancet Planet. Health 2023, 7, e271–e281. [Google Scholar] [CrossRef] [PubMed]
- Gasparrini, A.; Guo, Y.; Hashizume, M.; Lavigne, E.; Zanobetti, A.; Schwartz, J.; Tobias, A.; Tong, S.; Rocklöv, J.; Forsberg, B.; et al. Mortality risk attributable to high and low ambient temperature: A multicountry observational study. Lancet Lond. Engl. 2015, 386, 369–375. [Google Scholar] [CrossRef]
- Gasparrini, A.; Guo, Y.; Sera, F.; Vicedo-Cabrera, A.M.; Huber, V.; Tong, S.; de Sousa Zanotti Stagliorio Coelho, M.; Nascimento Saldiva, P.H.; Lavigne, E.; Matus Correa, P.; et al. Projections of temperature-related excess mortality under climate change scenarios. Lancet Planet. Health 2017, 1, e360–e367. [Google Scholar] [CrossRef]
- Masselot, P.; Mistry, M.N.; Rao, S.; Huber, V.; Monteiro, A.; Samoli, E.; Stafoggia, M.; de’Donato, F.; Garcia-Leon, D.; Ciscar, J.-C.; et al. Estimating future heat-related and cold-related mortality under climate change, demographic and adaptation scenarios in 854 European cities. Nat. Med. 2025, 31, 1294–1302. [Google Scholar] [CrossRef]
- World Meteorological Organization. WMO Confirms 2024 as Warmest Year on Record at About 1.55 °C Above Pre-Industrial Level. 2025. Available online: https://wmo.int/news/media-centre/wmo-confirms-2024-warmest-year-record-about-155degc-above-pre-industrial-level (accessed on 27 June 2025).
- Armstrong, B.G. Effect of measurement error on epidemiological studies of environmental and occupational exposures. Occup. Environ. Med. 1998, 55, 651–656. [Google Scholar] [CrossRef]
- Mistry, M.N.; Schneider, R.; Masselot, P.; Royé, D.; Armstrong, B.; Kyselý, J.; Orru, H.; Sera, F.; Tong, S.; Lavigne, É.; et al. Comparison of weather station and climate reanalysis data for modelling temperature-related mortality. Sci. Rep. 2022, 12, 5178. [Google Scholar] [CrossRef]
- MCC Collaborative Research Network. Home. Available online: https://mccstudy.lshtm.ac.uk/ (accessed on 27 June 2025).
- Heaviside, C.; Macintyre, H.; Vardoulakis, S. The Urban Heat Island: Implications for Health in a Changing Environment. Curr. Environ. Health Rep. 2017, 4, 296–305. [Google Scholar] [CrossRef]
- Qian, Y.; Chakraborty, T.C.; Li, J.; Li, D.; He, C.; Sarangi, C.; Chen, F.; Yang, X.; Leung, L.R. Urbanization Impact on Regional Climate and Extreme Weather: Current Understanding, Uncertainties, and Future Research Directions. Adv. Atmos. Sci. 2022, 39, 819–860. [Google Scholar] [CrossRef] [PubMed]
- Cheval, S.; Amihăesei, V.-A.; Chitu, Z.; Dumitrescu, A.; Falcescu, V.; Irașoc, A.; Micu, D.M.; Mihulet, E.; Ontel, I.; Paraschiv, M.-G.; et al. A systematic review of urban heat island and heat waves research (1991–2022). Clim. Risk Manag. 2024, 44, 100603. [Google Scholar] [CrossRef]
- Jänicke, B.; Holtmann, A.; Kim, K.R.; Kang, M.; Fehrenbach, U.; Scherer, D. Quantification and evaluation of intra-urban heat-stress variability in Seoul, Korea. Int. J. Biometeorol. 2019, 63, 1–12. [Google Scholar] [CrossRef]
- Hajat, S.; Kosatky, T. Heat-related mortality: A review and exploration of heterogeneity. J. Epidemiol. Community Health 2010, 64, 753–760. [Google Scholar] [CrossRef] [PubMed]
- Lauwaet, D.; Berckmans, J.; Hooyberghs, H.; Wouters, H.; Driesen, G.; Lefebre, F.; De Ridder, K. High resolution modelling of the urban heat island of 100 European cities. Urban Clim. 2024, 54, 101850. [Google Scholar] [CrossRef]
- Kloog, I.; Chudnovsky, A.; Koutrakis, P.; Schwartz, J. Temporal and spatial assessments of minimum air temperature using satellite surface temperature measurements in Massachusetts, USA. Sci. Total Environ. 2012, 432, 85–92. [Google Scholar] [CrossRef]
- Kloog, I.; Nordio, F.; Coull, B.A.; Schwartz, J. Predicting spatiotemporal mean air temperature using MODIS satellite surface temperature measurements across the Northeastern USA. Remote Sens. Environ. 2014, 150, 132–139. [Google Scholar] [CrossRef]
- Shi, L.; Liu, P.; Kloog, I.; Lee, M.; Kosheleva, A.; Schwartz, J. Estimating daily air temperature across the Southeastern United States using high-resolution satellite data: A statistical modeling study. Environ. Res. 2016, 146, 51–58. [Google Scholar] [CrossRef]
- Kloog, I.; Nordio, F.; Lepeule, J.; Padoan, A.; Lee, M.; Auffray, A.; Schwartz, J. Modelling spatio-temporally resolved air temperature across the complex geo-climate area of France using satellite-derived land surface temperature data. Int. J. Climatol. 2017, 37, 296–304. [Google Scholar] [CrossRef]
- Oyler, J.W.; Ballantyne, A.; Jencso, K.; Sweet, M.; Running, S.W. Creating a topoclimatic daily air temperature dataset for the conterminous United States using homogenized station data and remotely sensed land skin temperature. Int. J. Climatol. 2015, 35, 2258–2279. [Google Scholar] [CrossRef]
- Kloog, I. Use of earth observations for temperature exposure assessment in epidemiological studies. Curr. Opin. Pediatr. 2019, 31, 244–250. [Google Scholar] [CrossRef]
- Flückiger, B.; Kloog, I.; Ragettli, M.S.; Eeftens, M.; Röösli, M.; de Hoogh, K. Modelling daily air temperature at a fine spatial resolution dealing with challenging meteorological phenomena and topography in Switzerland. Int. J. Climatol. 2022, 42, 6413–6428. [Google Scholar] [CrossRef]
- Hough, I.; Just, A.C.; Zhou, B.; Dorman, M.; Lepeule, J.; Kloog, I. A multi-resolution air temperature model for France from MODIS and Landsat thermal data. Environ. Res. 2020, 183, 109244. [Google Scholar] [CrossRef]
- Jin, Z.; Ma, Y.; Chu, L.; Liu, Y.; Dubrow, R.; Chen, K. Predicting spatiotemporally-resolved mean air temperature over Sweden from satellite data using an ensemble model. Environ. Res. 2022, 204, 111960. [Google Scholar] [CrossRef] [PubMed]
- Nikolaou, N.; Dallavalle, M.; Stafoggia, M.; Bouwer, L.M.; Peters, A.; Chen, K.; Wolf, K.; Schneider, A. High-resolution spatiotemporal modeling of daily near-surface air temperature in Germany over the period 2000–2020. Environ. Res. 2023, 219, 115062. [Google Scholar] [CrossRef]
- Zheng, M.; Zhang, J.; Wang, J.; Yang, S.; Han, J.; Hassan, T. Reconstruction of 0.05° all-sky daily maximum air temperature across Eurasia for 2003–2018 with multi-source satellite data and machine learning models. Atmos. Res. 2022, 279, 106398. [Google Scholar] [CrossRef]
- Zhang, Z.; Du, Q. Merging framework for estimating daily surface air temperature by integrating observations from multiple polar-orbiting satellites. Sci. Total Environ. 2022, 812, 152538. [Google Scholar] [CrossRef]
- Gutiérrez-Avila, I.; Arfer, K.B.; Wong, S.; Rush, J.; Kloog, I.; Just, A.C. A spatiotemporal reconstruction of daily ambient temperature using satellite data in the Megalopolis of Central Mexico from 2003 to 2019. Int. J. Climatol. J. R. Meteorol. Soc. 2021, 41, 4095–4111. [Google Scholar] [CrossRef]
- Zeng, Q.; Li, Y.; Tao, J.; Fan, M.; Chen, L.; Wang, L.; Wang, Y. Full-coverage estimation of PM2.5 in the Beijing-Tianjin-Hebei region by using a two-stage model. Atmos. Environ. 2023, 309, 119956. [Google Scholar] [CrossRef]
- Bussalleu, A.; Hoek, G.; Kloog, I.; Probst-Hensch, N.; Röösli, M.; de Hoogh, K. Modelling Europe-wide fine resolution daily ambient temperature for 2003-2020 using machine learning. Sci. Total Environ. 2024, 928, 172454. [Google Scholar] [CrossRef] [PubMed]
- Pirotti, F.; Toffah, F.E.; Guarnieri, A. Correlation Analysis of Vertical Ground Movement and Climate Using Sentinel-1 InSAR. Remote Sens. 2024, 16, 4123. [Google Scholar] [CrossRef]
- Temperature, Precipitation and Drought Code at 1 km Resolution over Italy from Start of 2017 to End of 2022 (6 Years). Available online: https://zenodo.org/records/13358521 (accessed on 14 July 2025).
- Bonafoni, S.; Anniballe, R.; Gioli, B.; Toscano, P. Downscaling Landsat Land Surface Temperature over the urban area of Florence. Eur. J. Remote Sens. 2016, 49, 553–569. [Google Scholar] [CrossRef]
- Treccani. Toscana—Enciclopedia. Available online: https://www.treccani.it/enciclopedia/toscana/ (accessed on 21 February 2025).
- Marine Areas (Sea)—Tuscany Region. Available online: https://www.regione.toscana.it/it/aree-marine-mare- (accessed on 21 February 2025).
- Resident Population on 1 January: All Municipalities. Available online: https://demo.istat.it/app/?i=POS (accessed on 31 August 2025).
- SIR-DATA/Thermometry. Available online: https://sir.toscana.it/termometria-pub (accessed on 21 February 2025).
- Aybar, C. Rgee: R Bindings for Calling the “Earth Engine” API. 2025. Available online: https://github.com/r-spatial/rgee/issues/ (accessed on 21 February 2025).
- Google/Earth Engine-API. Google. 2025. Available online: https://github.com/google/earthengine-api (accessed on 21 February 2025).
- EarthExplorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 21 February 2025).
- Baston, D. Exactextract. 2025. Available online: https://github.com/isciences/exactextract (accessed on 21 February 2025).
- Ecosystem CDS. Copernicus DEM—Global and European Digital Elevation Model|Copernicus Data Space Ecosystem. Available online: https://dataspace.copernicus.eu/explore-data/data-collections/copernicus-contributing-missions/collections-description/COP-DEM (accessed on 21 February 2025).
- Häntzschel, J.; Goldberg, V.; Bernhofer, C. GIS-based regionalisation of radiation, temperature and coupling measures in complex terrain for low mountain ranges. Meteorol. Appl. 2005, 12, 33–42. [Google Scholar] [CrossRef]
- Böhner, J.; Antonić, O. Land-Surface Parameters Specific to Topo-Climatology. Dev. Soil Sci. 2009, 33, 195–226. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Routledge: London, UK, 2002; 464p. [Google Scholar]
- Seyednasrollah, B. Solrad: Calculating Solar Radiation and Related Variables Based on Location, Time and Topographical Conditions. 2018. Available online: https://cran.r-project.org/web/packages/solrad/index.html (accessed on 21 February 2025).
- ERA5 Hourly Data on Single Levels from 1940 to Present. Available online: https://cds.climate.copernicus.eu/datasets/reanalysis-era5-single-levels?tab=overview (accessed on 21 February 2025).
- Cai, J. Humidity: Calculate Water Vapor Measures from Temperature and Dew Point. 2019. Available online: https://cran.r-project.org/web/packages/humidity/index.html (accessed on 21 February 2025).
- Fernández-López, J.; Schliep, K. rWind: Download, edit and include wind data in ecological and evolutionary analysis. Ecography 2019, 42, 804–810. [Google Scholar] [CrossRef]
- rWind: Download, Edit and Include Wind and Sea Currents Data in Ecological and Evolutionary Analysis Version 1.1.7 from CRAN. Available online: https://rdrr.io/cran/rWind/ (accessed on 21 February 2025).
- Imperviousness Density 2018 (Raster 10 m and 100 m), Europe, 3-Yearly—Copernicus Land Monitoring Service. Available online: https://land.copernicus.eu/en/products/high-resolution-layer-imperviousness/imperviousness-density-2018 (accessed on 21 February 2025).
- Google for Developers. MOD13Q1.061 Terra Vegetation Indices 16-Day Global 250 m|Earth Engine Data Catalog. Available online: https://developers.google.com/earth-engine/datasets/catalog/MODIS_061_MOD13Q1 (accessed on 21 February 2025).
- GEOSTAT-GISCO-Eurostat. Available online: https://ec.europa.eu/eurostat/web/gisco/geodata/population-distribution/geostat (accessed on 21 February 2025).
- VIIRS Nighttime Light. Available online: https://eogdata.mines.edu/products/vnl/ (accessed on 21 February 2025).
- Elvidge, C.; Li, X.; Zhou, Y.; Cao, C.; Warner, T.A. (Eds.) Remote Sensing of Night-Time Light; Routledge: London, UK, 2021; 310p. [Google Scholar]
- Grafo Stradale, Numeri Civici, Cippi Chilometrici—Grafo Ferroviario, Stazioni, Scali-OpenData-Regione Toscana. Available online: https://dati.toscana.it/dataset/grafo-civici (accessed on 21 February 2025).
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Alvarez, I.; Quesada-Ganuza, L.; Briz, E.; Garmendia, L. Urban Heat Islands and Thermal Comfort: A Case Study of Zorrotzaurre Island in Bilbao. Sustainability 2021, 13, 6106. [Google Scholar] [CrossRef]
- Ambrosini, D.; Galli, G.; Mancini, B.; Nardi, I.; Sfarra, S. Evaluating Mitigation Effects of Urban Heat Islands in a Historical Small Center with the ENVI-Met® Climate Model. Sustainability 2014, 6, 7013–7029. [Google Scholar] [CrossRef]
- Biggart, M.; Stocker, J.; Doherty, R.M.; Wild, O.; Carruthers, D.; Grimmond, S.; Han, Y.; Fu, P.; Kotthaus, S. Modelling spatiotemporal variations of the canopy layer urban heat island in Beijing at the neighbourhood scale. Atmos. Chem. Phys. 2021, 21, 13687–13711. [Google Scholar] [CrossRef]
- Bokwa, A.; Geletič, J.; Lehnert, M.; Žuvela-Aloise, M.; Hollósi, B.; Gál, T.; Skarbit, N.; Dobrovolný, P.; Hajto, M.J.; Kielar, R.; et al. Heat load assessment in Central European cities using an urban climate model and observational monitoring data. Energy Build. 2019, 201, 53–69. [Google Scholar] [CrossRef]
- Chew, L.W.; Liu, X.; Li, X.-X.; Norford, L.K. Interaction between heat wave and urban heat island: A case study in a tropical coastal city, Singapore. Atmos. Res. 2021, 247, 105134. [Google Scholar] [CrossRef]
- Garbero, V.; Milelli, M.; Bucchignani, E.; Mercogliano, P.; Varentsov, M.; Rozinkina, I.; Rivin, G.; Blinov, D.; Wouters, H.; Schulz, J.-P.; et al. Evaluating the Urban Canopy Scheme TERRA_URB in the COSMO Model for Selected European Cities. Atmosphere 2021, 12, 237. [Google Scholar] [CrossRef]
- Giannaros, C.; Agathangelidis, I.; Papavasileiou, G.; Galanaki, E.; Kotroni, V.; Lagouvardos, K.; Giannaros, T.M.; Cartalis, C.; Matzarakis, A. The extreme heat wave of July–August 2021 in the Athens urban area (Greece): Atmospheric and human-biometeorological analysis exploiting ultra-high resolution numerical modeling and the local climate zone framework. Sci. Total Environ. 2023, 857, 159300. [Google Scholar] [CrossRef] [PubMed]
- Holec, J.; Feranec, J.; Šťastný, P.; Szatmári, D.; Kopecká, M.; Garaj, M. Evolution and assessment of urban heat island between the years 1998 and 2016: Case study of the cities Bratislava and Trnava in western Slovakia. Theor. Appl. Climatol. 2020, 141, 979–997. [Google Scholar] [CrossRef]
- Hürzeler, A.; Hollósi, B.; Burger, M.; Gubler, M.; Brönnimann, S. Performance analysis of the urban climate model MUKLIMO_3 for three extreme heatwave events in Bern. City Environ. Interact. 2022, 16, 100090. [Google Scholar] [CrossRef]
- Venter, Z.S.; Brousse, O.; Esau, I.; Meier, F. Hyperlocal mapping of urban air temperature using remote sensing and crowdsourced weather data. Remote Sens. Environ. 2020, 242, 111791. [Google Scholar] [CrossRef]
- Wu, Y.; Li, S.; Zhao, Q.; Wen, B.; Gasparrini, A.; Tong, S.; Overcenco, A.; Urban, A.; Schneider, A.; Entezari, A.; et al. Global, regional, and national burden of mortality associated with short-term temperature variability from 2000–19: A three-stage modelling study. Lancet Planet. Health 2022, 6, e410–e421. [Google Scholar] [CrossRef]
- Giannico, O.V.; Sardone, R.; Bisceglia, L.; Addabbo, F.; Pirotti, F.; Minerba, S.; Mincuzzi, A. The mortality impacts of greening Italy. Nat. Commun. 2024, 15, 10452. [Google Scholar] [CrossRef] [PubMed]
- White, E.; Armstrong, B.K.; Saracci, R. Principles of Exposure Measurement in Epidemiology; Oxford University Press: New York, NY, USA, 2008; Available online: https://academic.oup.com/book/6327 (accessed on 13 March 2025).
- Eisenman, D.P.; Wilhalme, H.; Tseng, C.-H.; Chester, M.; English, P.; Pincetl, S.; Fraser, A.; Vangala, S.; Dhaliwal, S.K. Heat Death Associations with the built environment, social vulnerability and their interactions with rising temperature. Health Place 2016, 41, 89–99. [Google Scholar] [CrossRef]
- Benmarhnia, T.; Kihal-Talantikite, W.; Ragettli, M.S.; Deguen, S. Small-area spatiotemporal analysis of heatwave impacts on elderly mortality in Paris: A cluster analysis approach. Sci. Total Environ. 2017, 592, 288–294. [Google Scholar] [CrossRef]
- Williams, A.; Allen, J.; Catalano, P.; Spengler, J. The Role of Individual and Small-Area Social and Environmental Factors on Heat Vulnerability to Mortality Within and Outside of the Home in Boston, MA. Climate 2020, 8, 29. [Google Scholar] [CrossRef] [PubMed]
- Cleland, S.E.; Steinhardt, W.; Neas, L.M.; Jason West, J.; Rappold, A.G. Urban heat island impacts on heat-related cardiovascular morbidity: A time series analysis of older adults in US metropolitan areas. Environ. Int. 2023, 178, 108005. [Google Scholar] [CrossRef] [PubMed]
- Nawaro, J.; Gianquintieri, L.; Pagliosa, A.; Sechi, G.M.; Caiani, E.G. Neighborhood determinants of vulnerability to heat for cardiovascular health: A spatial analysis of Milan, Italy. Popul. Environ. 2024, 46, 25. [Google Scholar] [CrossRef]
- Jung, J.; Uejio, C.K.; Kintziger, K.W.; Duclos, C.; Reid, K.; Jordan, M.; Spector, J.T. Heat illness data strengthens vulnerability maps. BMC Public Health 2021, 21, 1999. [Google Scholar] [CrossRef]
- Tewari, K.; Tewari, M.; Niyogi, D. Need for considering urban climate change factors on stroke, neurodegenerative diseases, and mood disorders studies. Comput. Urban Sci. 2023, 3, 4. [Google Scholar] [CrossRef]

| Dimension | Variable (Acronym) | Description | Unit of Measurement | Spatial or Spatio- Temporal | Original Spatial Resolution | Temporal Resolution | Stage |
|---|---|---|---|---|---|---|---|
| Topography | Elevation (DEM) | Digital Elevation Model | m | Spatial | 25 m × 25 m | Constant (2016) | 1;2 |
| Slope (SLP) | Steepest slope | Degree (angle) | Spatial | 25 m × 25 m | Constant (2016) | 1;2 | |
| Aspect (Aspect) | Direction of the steepest slope, clockwise starting north | Degree (angle) | Spatial | 25 m × 25 m | Constant (2016) | 1;2 | |
| Skyview (SVF) | Ratio of the visible sky (sky view factor) | Proportion | Spatial | 25 m × 25 m | Constant (2016) | 1;2 | |
| Sun geometry | SunAltitude (SUNALT) | Sun altitude | Degree | Spatio- temporal | 100 m × 100 m | Daily (constant through years) | 1 |
| Azimuth (Azimuth) | Azimuth | Degree | Spatio- temporal | 100 m × 100 m | Daily (constant through years) | 1 | |
| DayLength (DAYL) | Day length | h | Spatio- temporal | 100 m × 100 m | Daily (constant through years) | 1;2 | |
| DiffuseSunRadiation (DIFSUNRAD) | Diffuse solar radiation | Spatio- temporal | 100 m × 100 m | Daily (constant through years) | 1 | ||
| DirectSunRadiation (DIRSUNRAD) | Direct solar radiation | Spatio- temporal | 100 m × 100 m | Daily (constant through years) | 1 | ||
| Meteorological Variables | Precipitations (PREC) | Total precipitation | m | Spatio- temporal | 9 km × 9 km | Daily | 2 |
| RelativeHumidity (RH) | Relative humidity | Percentage | Spatio- temporal | 9 km × 9 km | Daily | 2 | |
| WindSpeed (WINDS) | Wind speed | ms−1 | Spatio- temporal | 9 km × 9 km | Daily | 2 | |
| WindDirection (WINDD) | Wind direction | Degree (angle) | Spatio- temporal | 9 km × 9 km | Daily | 2 | |
| SurfacePressure (PA) | Surface pressure | Pa | Spatio- temporal | 9 km × 9 km | Daily | 2 | |
| PlanetaryBoundaryHeight (BLH) | Planetary boundary height | m | Spatio- temporal | 31 km × 31 km | Daily | 2 | |
| Land cover | ImperviousBuildup (IBU) | Impervious build-up | Proportion | Spatial | 100 m × 100 m | Constant (2018) | 2 |
| Continuous- UrbanFabric (CLC: Continuous Urban fabric) | Proportion of area covered by continuous urban fabric (from Corine Land Cover) | Proportion | Spatial | 100 m × 100 m | Constant (2018) | 2 | |
| Discontinuous- UrbanFabric (CLC: Discontinuous Urban fabric) | Proportion of area covered by discontinuous urban fabric (from Corine Land Cover) | Proportion | Spatial | 100 m × 100 m | Constant (2018) | 2 | |
| Industrial/Commercial (CLC: Industrial/ Commercial) | Proportion of area covered by industrial/commercial (from Corine Land Cover) | Proportion | Spatial | 100 m × 100 m | Constant (2018) | 2 | |
| Vegetation (CLC: Vegetation) | Proportion of area covered by vegetation (from Corine Land Cover) | Proportion | Spatial | 100 m × 100 m | Constant (2018) | 2 | |
| Agriculture (CLC: Agriculture) | Proportion of area covered by agriculture (from Corine Land Cover) | Proportion | Spatial | 100 m × 100 m | Constant (2018) | 2 | |
| NDVI | NDVI (NDVI) | Normalized difference vegetation index | Ratio (−1;1) | Spatio- temporal | 250 m × 250 m | Every 16 days | 1;2 |
| Population and density | Population (POP) | Population | Persons/ Area | Spatial | 1 km × 1 km | Constant (2018) | 2 |
| NightTimeLight | Nighttime light | Spatial | 15 arc seconds (~500 m × 500 m at the equator) | Constant (2022) | 2 | ||
| Road network | UrbanRoad (RDS: Urban Road) | Length of urban roads | m | Spatial | - | Constant (2020) | 2 |
| LocalRoad (RDS: Local Road) | Length of local roads | m | Spatial | - | Constant (2020) | 2 | |
| ExtraUrbanSecondaryRoad (RDS: Extra UrbanSecondary Road) | Length of extra urban secondary road | m | Spatial | - | Constant (2020) | 2 | |
| ExtraUrbanPrincipalRoad (RDS: Extra UrbanPrincipal Road) | Length of extra urban principal road | m | Spatial | - | Constant (2020) | 2 | |
| Motorway (RDS: Motorway) | Length of motorway | m | Spatial | - | Constant (2020) | 2 | |
| OtherRoad (RDS: Other Road) | Length of other road | m | Spatial | - | Constant (2020) | 2 | |
| Land surface temperature | LST_ModisAD | Land surface temperature from MODIS aqua day | K | Spatio- temporal | 1 km × 1 km | Daily | 2 Tmax |
| LST_ModisTD | Land surface temperature from MODIS terra day | K | Spatio- temporal | 1 km × 1 km | Daily | 2 Tmax | |
| LST_ModisAN | Land surface temperature from MODIS aqua night | K | Spatio- temporal | 1 km × 1 km | Daily | 2 Tmin | |
| LST_ModisTN | Land surface temperature from MODIS terra night | K | Spatio- temporal | 1 km × 1 km | Daily | 2 Tmin | |
| LST_Landsat8 | Land surface temperature from LANDSAT8 | K | Spatio- temporal | 30 m × 30 m | Every 16 days | 2 |
| Variables | Observation Period | Number of Days with 100% NA | % NA | RMSE (°C) | R2 | MAE (°C) |
|---|---|---|---|---|---|---|
| LST_ModisAD | All Year | 35 | 76.8 | 0.317 | 0.992 | 0.221 |
| Winter | 3 | 83.2 | 0.229 | 0.993 | 0.158 | |
| Spring | 24 | 84.6 | 0.344 | 0.992 | 0.241 | |
| Summer | 1 | 67.0 | 0.461 | 0.992 | 0.330 | |
| Autumn | 7 | 73.0 | 0.278 | 0.992 | 0.199 | |
| LST_ModisAN | All Year | 42 | 78.9 | 0.162 | 0.994 | 0.113 |
| Winter | 6 | 76.3 | 0.162 | 0.995 | 0.111 | |
| Spring | 25 | 90.2 | 0.173 | 0.994 | 0.120 | |
| Summer | 0 | 65.8 | 0.159 | 0.993 | 0.110 | |
| Autumn | 11 | 78.7 | 0.160 | 0.995 | 0.114 | |
| LST_ModisTD | All Year | 33 | 81.4 | 0.250 | 0.994 | 0.174 |
| Winter | 3 | 82.2 | 0.181 | 0.995 | 0.123 | |
| Spring | 6 | 82.5 | 0.285 | 0.993 | 0.201 | |
| Summer | 3 | 77.6 | 0.358 | 0.994 | 0.253 | |
| Autumn | 21 | 84.3 | 0.206 | 0.994 | 0.150 | |
| LST_ModisTN | All Year | 44 | 82.1 | 0.148 | 0.995 | 0.101 |
| Winter | 15 | 82.5 | 0.133 | 0.996 | 0.093 | |
| Spring | 15 | 87.0 | 0.147 | 0.995 | 0.102 | |
| Summer | 0 | 82.2 | 0.143 | 0.995 | 0.097 | |
| Autumn | 14 | 76.8 | 0.155 | 0.994 | 0.110 |
| Variable | Model | RMSE (°C) | R2 | MAE (°C) | Spatial R2 | Temporal R2 |
|---|---|---|---|---|---|---|
| Tmax | XGB | 1.458 | 0.972 | 1.098 | 0.915 | 0.954 |
| MARS | 2.991 | 0.881 | 2.329 | 0.906 | 0.880 | |
| Ensemble | 1.954 | 0.950 | 1.518 | 0.915 | 0.954 | |
| Tmin | XGB | 1.715 | 0.938 | 1.314 | 0.715 | 0.941 |
| MARS | 2.559 | 0.858 | 2.030 | 0.679 | 0.878 | |
| Ensemble | 1.961 | 0.920 | 1.530 | 0.715 | 0.941 |
| Variable | Season | RMSE (°C) | R2 | MAE (°C) |
|---|---|---|---|---|
| Tmax | Winter | 1.704 | 0.752 | 1.274 |
| Spring | 2.306 | 0.896 | 1.839 | |
| Summer | 1.790 | 0.769 | 1.401 | |
| Autumn | 1.958 | 0.908 | 1.561 | |
| Tmin | Winter | 2.024 | 0.757 | 1.592 |
| Spring | 2.187 | 0.850 | 1.719 | |
| Summer | 1.723 | 0.647 | 1.350 | |
| Autumn | 1.883 | 0.845 | 1.465 |
| Variable | Area | RMSE (°C) | R2 | MAE (°C) |
|---|---|---|---|---|
| Tmax | Urban | 2.001 | 0.944 | 1.577 |
| Non-urban | 1.938 | 0.952 | 1.504 | |
| Tmin | Urban | 1.863 | 0.935 | 1.464 |
| Non-urban | 1.959 | 0.919 | 1.528 |
| Month | Tmax (°C) | Tmin (°C) |
|---|---|---|
| January | 10.6 | 2.4 |
| February | 12.6 | 3.4 |
| March | 14.6 | 2.9 |
| April | 17.9 | 6.3 |
| May | 23.9 | 12.1 |
| June | 30.1 | 16.9 |
| July | 32.8 | 18.8 |
| August | 30.0 | 18.1 |
| September | 23.4 | 14.0 |
| October | 21.2 | 12.1 |
| November | 15.3 | 7.3 |
| December | 11.4 | 6.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Limoncella, G.; Feurer, D.; Roye, D.; de Hoogh, K.; de la Cruz, A.; Gasparrini, A.; Schneider, R.; Pirotti, F.; Catelan, D.; Stafoggia, M.; et al. A Machine Learning Model Integrating Remote Sensing, Ground Station, and Geospatial Data to Predict Fine-Resolution Daily Air Temperature for Tuscany, Italy. Remote Sens. 2025, 17, 3052. https://doi.org/10.3390/rs17173052
Limoncella G, Feurer D, Roye D, de Hoogh K, de la Cruz A, Gasparrini A, Schneider R, Pirotti F, Catelan D, Stafoggia M, et al. A Machine Learning Model Integrating Remote Sensing, Ground Station, and Geospatial Data to Predict Fine-Resolution Daily Air Temperature for Tuscany, Italy. Remote Sensing. 2025; 17(17):3052. https://doi.org/10.3390/rs17173052
Chicago/Turabian StyleLimoncella, Giorgio, Denise Feurer, Dominic Roye, Kees de Hoogh, Arturo de la Cruz, Antonio Gasparrini, Rochelle Schneider, Francesco Pirotti, Dolores Catelan, Massimo Stafoggia, and et al. 2025. "A Machine Learning Model Integrating Remote Sensing, Ground Station, and Geospatial Data to Predict Fine-Resolution Daily Air Temperature for Tuscany, Italy" Remote Sensing 17, no. 17: 3052. https://doi.org/10.3390/rs17173052
APA StyleLimoncella, G., Feurer, D., Roye, D., de Hoogh, K., de la Cruz, A., Gasparrini, A., Schneider, R., Pirotti, F., Catelan, D., Stafoggia, M., de’Donato, F., Biscardi, G., Marzi, C., Baccini, M., & Sera, F. (2025). A Machine Learning Model Integrating Remote Sensing, Ground Station, and Geospatial Data to Predict Fine-Resolution Daily Air Temperature for Tuscany, Italy. Remote Sensing, 17(17), 3052. https://doi.org/10.3390/rs17173052











