Abstract
Geosynchronous satellite maneuver detection is critical for enhancing space situational awareness and inferring satellite intent. However, traditional methods often require high-quality orbital sequence data and heavily rely on hand-crafted features, limiting their effectiveness in complex real-world environments. While recent neural network-based approaches have shown promise, they are typically trained in scene or task-specific settings, resulting in limited generalization and adaptability. To address these challenges, we propose MC-MD, a pre-training framework that integrates Masked and Clustered learning strategies to improve the robustness and transferability of geosynchronous satellite Maneuver Detection. Specifically, we introduce a masked prediction module that applies both time- and frequency-domain masking to help the model capture temporal dynamics more effectively. Meanwhile, a cluster-based module guides the model to learn discriminative representations of different maneuver patterns through unsupervised clustering, mitigating the negative impact of distribution shifts across scenarios. By combining these two strategies, MC-MD captures diverse maneuver behaviors and enhances cross-scenario detection performance. Extensive experiments on both simulated and real-world datasets demonstrate that MCMD achieves significant performance gains over the strongest baseline, with improvements of 8.54% in Precision and 7.8% in F1-Score. Furthermore, reconstructed trajectories analysis shows that MC-MD more accurately aligns with the ground-truth maneuver sequence, highlighting its effectiveness in satellite maneuver detection tasks.
1. Introduction
Geosynchronous satellite maneuver detection involves monitoring satellites in geosynchronous orbit and identifying maneuvers [1], such as orbital transfers [2], position adjustments [3,4], and emergency maneuvers [5]. As maneuvering technologies advance, the frequency of such activities in high-altitude orbits has increased, thereby raising the risk of losing track of observed satellites. Consequently, maneuver detection is a key research focus in space situational awareness. This process relies on the integration of multi-source remote sensing data (e.g., optical, radar, and LiDAR) to monitor satellite positions, velocities, and maneuvering intentions [6,7]. This research advances remote sensing technologies in space object identification and data fusion, while also providing essential support for space security [8,9,10], underscoring its importance within remote sensing.
Geosynchronous satellite maneuver detection presents several challenges in modern operational contexts [11,12]. First, the maneuvering behavior of geosynchronous satellites is highly time-sensitive, complex, and uncertain, making it difficult for traditional passive monitoring systems to meet real-time accuracy requirements. Second, the increasing congestion of geosynchronous orbit, coupled with limited sensor resources, intensifies challenges in object tracking and data acquisition. Third, the maneuvering intentions of geosynchronous satellites are difficult to predict, further hindering detection [13]. Overcoming these challenges and achieving the precise detection of satellite maneuvers is of great research importance [14]. Hence, the development of artificial intelligence algorithms can foster innovation in remote sensing, offering more efficient monitoring solutions.
Sampled data from geosynchronous satellite maneuver missions are typically represented as time series [5,15], which vary dynamically with satellite maneuvers. Traditional studies mainly employ handcrafted feature methods [2,3]. For example, Dehadraya et al. [16] proposed a feature-engineering approach using astrometric data to characterize maneuver behavior. Kelecy et al. [17] detected anomalous orbital parameters by smoothing and differencing two-line element (TLE) time series. Gong et al. [18] introduced a maneuver signature based on relative angular momentum with a sliding window to predict orbital maneuver timing. Mukundan et al. [19] detected deorbiting by comparing orbital parameters from TLE Keplerian elements with those from a propagation model. Solera et al. [20] computed longitudes to detect transition events in high-orbit satellites, while Beer et al. [21] used passive radio frequency data with a sliding-window least-squares method for maneuver detection. However, these approaches depend on high-quality orbital data and manual features, limiting their applicability in real-world scenarios.
Geosynchronous satellite maneuver detection data are typically represented as time series, recording temporal variations in satellite position, velocity, and attitude [22,23]. In recent years, deep learning methods for maneuver detection have attracted growing interest [24,25]. Unlike traditional models that require manual feature extraction, deep learning can automatically learn representations, reducing reliance on expert knowledge [26,27]. For example, DiBona et al. [28] developed a probabilistic spatial threat assessment system using neural networks for maneuver classification, while Roberts et al. [29] applied one-dimensional CNNs with TLE data. Kelecy et al. [30] adopted a Transformer model to extract relative motion features from electro-optical imagery, identifying various rendezvous and proximity operations. However, current deep learning models for geosynchronous satellite maneuver sequences are mostly trained in specific scenarios, limiting cross-scenario detection [31,32]. As the volume of satellite and scenario data grows, developing pre-trained models in diverse scenarios is crucial to improving generalization and applicability [25,33].
To address the aforementioned challenges, we propose a pre-training model based on Masked prediction and a Cluster-based strategy for geosynchronous satellite Maneuver Detection (MC-MD) across diverse scenarios. Specifically, a masked prediction strategy is designed by randomly masking a portion of maneuver sequence data and training the model to recover missing values in both time and frequency domains, inspired by masked reconstruction methods in computer vision [34,35] and natural language processing [36,37]. This unsupervised reconstruction captures temporal dependencies and strengthens maneuver behavior modeling. In parallel, a cluster-based strategy is introduced, where sequence data under each maneuver mode are treated as clusters, encouraging the model to separate distinct distributions and learn inter-cluster relationships [12,38]. By integrating masked prediction and clustering, MC-MD not only models temporal dependencies within sequences but also learns evolving maneuver patterns, thereby enhancing its generalization capacity for cross-scenario detection.
The primary contributions of this paper are summarized as follows:
- We propose a masked prediction pre-training strategy for geosynchronous satellite maneuver detection. This strategy performs unsupervised pre-training by predicting missing values in the time and frequency domains from unmasked observations, thereby modeling temporal dependencies in the sequence data.
- We introduce a cluster-based pre-training strategy for maneuver detection. This strategy employs unsupervised clustering to separate clusters of different maneuver modes, effectively mitigating the impact of complex scenarios on training.
- Experimental results on simulated and real datasets show that the proposed MC-MD model consistently outperforms baseline methods in maneuver detection. Furthermore, reconstructed trajectories analysis further confirms the model’s effectiveness.
2. Materials and Methods
2.1. Background on Geosynchronous Satellite Maneuvers
The maneuvers of geosynchronous satellites play a critical role in the successful execution of their missions, encompassing a wide array of operations such as orbit transfer, position adjustment, position holding, emergency maneuvers, decommissioning maneuvers, and longitude offset maneuvers [39]. These maneuvers not only address the diverse mission requirements related to satellite avoidance, orbit adjustment, and object detection, but also ensure the stable operation of satellites throughout their lifecycle. Beginning with their launch into low-Earth orbit or geostationary transfer orbit, satellites increase their velocity through engine ignition to facilitate orbit transfer and are ultimately captured by the Earth’s gravity into a higher orbit. Geosynchronous satellites must make both east-west and north-south position adjustments to maintain precise coverage of the designated service area. In response to non-spherical gravitational influences and the perturbing effects of the Sun and Moon’s gravitational forces, periodic position-holding maneuvers are employed to counteract orbital drift. These maneuver behaviors fine-tune the orbit using small thrusters, ensuring the satellite’s stable operation. When faced with the risk of collision with space debris or other celestial objects, emergency maneuvers become an effective means of mitigating potential threats. Upon the conclusion of a satellite’s operational life, decommissioning maneuvers, such as transitioning to a graveyard orbit or lowering the satellite’s altitude for natural atmospheric re-entry and burn-up, are implemented to reduce space debris and make room for future satellites. Longitude offset maneuvers, by contrast, enable GEO satellites to shift their mission areas and are typically accomplished in three stages: removal, natural drift, and repositioning.
The aforementioned maneuvers can be categorized into three primary types: conventional maneuvers, passive maneuvers, and active maneuvers. Conventional maneuvers, such as orbit transfer, position adjustment, and decommissioning, are predefined and deterministic in nature. Passive maneuvers, including position holding and emergency avoidance, exhibit a degree of randomness and uncertainty. Active maneuvers, such as longitude bias, proximity reconnaissance, and collision avoidance, are typically triggered by specific missions and exhibit a higher level of uncertainty. These active maneuvers are particularly challenging and crucial in the context of maneuver detection for geosynchronous satellites. Currently, research efforts are divided into two main approaches: one focuses on the real-time detection of active or passive maneuvers with known intent, while the other involves the detection and prediction of maneuvers in geosynchronous satellites using observation data. However, due to the limited availability of sensor resources, geosynchronous satellite maneuvers often occur in the intervals between observations, which significantly increases the difficulty of detection.
Task-driven active maneuver behaviors of geosynchronous satellites, such as orbiting, formation flying, skimming, rendezvous and docking, and approach maneuvers, involve complex orbital control and precise maneuvers that necessitate highly accurate monitoring and prediction. The detection of geosynchronous satellite maneuvers typically relies on remote sensing technologies, which, through the fusion and analysis of multi-source data, facilitate high-precision monitoring of satellite positions, velocities, and maneuvering behaviors. This approach not only advances the development of remote sensing technologies in areas such as space object identification, data fusion, and pattern recognition but also provides critical technological support for space security and satellite operations management.
2.2. Datasets
2.2.1. The Simulation Dataset
To construct a simulation dataset for a geosynchronous satellite maneuver detection task, we utilize a high-fidelity satellite orbital dynamics model and generate data through the satellite simulation software (v3.0). The specific steps involved are as follows: First, a three-dimensional spatial distribution of satellite orbital scenario is created within the simulator, and multiple satellites are modeled as shown in Figure 1, with their initial orbital parameters set. Second, orbit change operations are introduced through scripting to simulate the effect of approach maneuvers, such as approaching a satellite in two segments (the first segment approaching to 5000 km and the second to 2000 km). Subsequently, the export information and coordinate system are selected to generate the simulation data in CSV format. Finally, the satellite trajectory data were generated using satellite trajectory simulation software. This dataset comprises approximately 21,000 satellite motion trajectories, with each trajectory sampled at a 2-h interval over a total observation period of 45 days. Each sample contains 540 data points across 16 variables; detailed descriptions of these variables are provided in Table 1. In addition, the timing of satellite maneuvering is randomized to control the proportion of maneuvering points within trajectories at approximately 1%. Labels correspond to the maneuver status at each timestamp, where a label of 0 indicates no maneuvering state and a label of 1 represents the presence of a maneuvering state. For experimental analysis, after data screening and alignment with practical application requirements, each trajectory sequence was preprocessed into input sequences of length 128 for model input. Statistical details regarding the quantity of these preprocessed trajectory samples are summarized in Table 2.
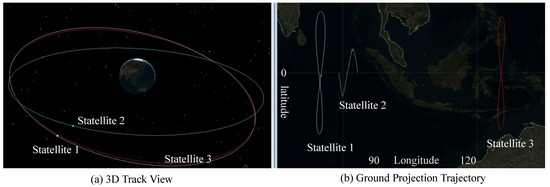
Figure 1.
Three-dimensional spatial distribution of satellite orbital scenario and ground-projected trajectories. (a) A three-dimensional orbital view illustrates the elliptical orbital distributions of three satellites within the Earth’s gravitational field, with Satellites 1, 2, and 3 operating on distinct orbital planes to form a configuration with varying inclinations and eccentricities. (b) The associated ground-projected trajectories highlight the geometric projection patterns of each satellite’s path onto the Earth’s surface.

Table 1.
The detailed information regarding the channels of simulated and real-world datasets.

Table 2.
The detailed information about the datasets.
The simulation dataset offers considerable advantages in supporting satellite maneuver prediction tasks. Firstly, high-precision simulations are capable of modeling complex physical effects, including the Earth’s non-spherical gravitational field, solar and lunar gravitational influences, atmospheric drag, and solar radiation pressure. These simulations ensure a high degree of accuracy and confidence in the orbital simulation results. Secondly, simulations generate a wide range of data types, encompassing various parameters such as position, velocity, and attitude, thereby providing diverse features for machine learning models. Furthermore, long-term simulation extrapolation can generate extensive historical data, establishing a robust foundation for model pre-training.
2.2.2. The Real-World Dataset
The real-world dataset utilized in this study is derived from the SSA AI Challenge competition, organized by the MIT ARC Lab from October 2023 to March 2024 [40]. This dataset comprises 1945 motion trajectories from over 10 high-orbit satellites, with a sampling period of 2 h for each trajectory, a total observation duration of 6 months, and an average of 2160 data points per trajectory. The dataset is accessible through the link https://github.com/ARCLab-MIT/splid-devkit/tree/main, accessed on 10 December 2023. The entire training set contains approximately 4 million sample points. Each sample point is characterized by 16-dimensional input features, similar to the simulated dataset in Table 1, which includes the object’s trajectory hex and state data, and four-dimensional output labels that specify the maneuver time, maneuver direction, maneuver state, and propulsion mode. Training samples are constructed at 2 h intervals, covering two days of observations. If a maneuver occurs at a specific moment, the corresponding sample is labeled as a positive sample; otherwise, it is labeled as a negative sample. The real-world samples are cleaned using an identical preprocessing methodology as that applied to the synthetic dataset, with sample information summarized in Table 2.
The real-world dataset provides timestamp indices of the points where the behavior pattern of each trajectory sequence sample changes, as well as the direction, nodes, and types of the changes. This paper only used timestamp indexing in the experiment. In addition, this dataset provides valuable real-world data support for the detection of geosynchronous satellite maneuver behaviors, encompassing a variety of maneuver types and complex scenarios. It thus lays a solid foundation for the training and validation of the model. This study employs time series analysis techniques to learn feature representations of high-dimensional sequences for satellite maneuvering. The robust feature representation learning capability of deep neural networks is expected to substantially enhance the accuracy of maneuver detection and behavior analysis, providing critical technical support for spatial situational awareness and satellite operation management.
2.3. Architecture Overview
The proposed MC-MD model is illustrated in Figure 2 and is mainly divided into three components: (1) the general training process, consisting of pre-training, fine-tuning and testing; (2) pre-training based on a masked process (unsupervised reconstruction pre-training) and (3) pre-training based on a clustered process.
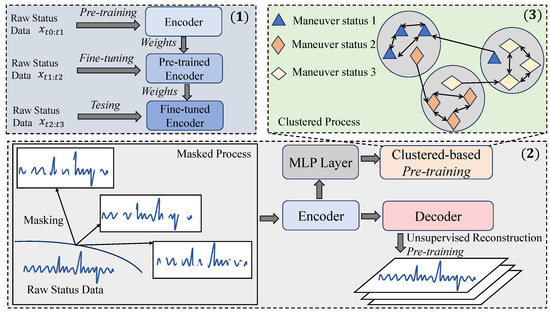
Figure 2.
The overall architecture of the proposed MC-MD model.
In component (1), we first pre-train the encoder using the original, extensive state data from different simulation scenes, resulting in a pre-trained encoder with fixed weight parameters. Subsequently, we fine-tune the pre-trained encoder using the test scenario data corresponding to the satellite’s location, updating the encoder’s weight parameters. Finally, we evaluate the fine-tuned encoder’s performance on the test set for geosynchronous satellite state detection. For component (2), we apply multiple random masking operations to the original state sequence data, generating a time- and frequency-domain time series that contains missing values. This masked sequence is then fed into the encoder to obtain a feature representation of the corresponding samples. These feature representations are subsequently input into a decoder, specifying the model for unsupervised reconstruction pre-training using the real observations from the original complete sequence data. In component (3), the feature representation obtained from the encoder is passed through a multi-layer perception layer for clustering-based pre-training, based on the process outlined in (2). Specifically, we use the categories of motorized behaviors in the original sequence state data as the number of clusters for the clustering task, and perform unsupervised clustering pre-training using the designed clustering loss function.
2.4. Mask Prediction Pre-Training
Let X represent a multivariate time series describing the state and maneuver information of a geosynchronous satellite over a given observation period. The geosynchronous satellite time series can be defined as follows:
where T is the total length of the time series, and each time step t corresponds to an observation vector , which is an m-dimensional vector:
where m represents the number of variables included in the dataset, and each corresponds to the value of the i-th variable at time t. These variables encompass various physical and dynamic properties of the satellite, such as position, velocity, and other state indicators. In particular, as shown in Figure 3, the data sequence consists of two main components:

Figure 3.
The description of information on geosynchronous satellite maneuver detection sequences based on observed data.
Normal State Information: The majority of the sequence points primarily reflect the regular operational status of the satellite. These values describe nominal orbital behaviors and expected state transitions under non-maneuvering conditions.
Maneuver Information: A subset of time points within the sequence corresponds to maneuver events, which are represented by specific values in that indicate abnormal variations in satellite motion due to control actions such as station-keeping, repositioning, or collision avoidance maneuvers. These maneuvers are sparse in the dataset compared to normal states. The input and output representations of such maneuver time series are illustrated in Figure 4.
Figure 4.
Input and output maneuver time series data of the geosynchronous satellite maneuver detection model.
To formally distinguish between these two types of states, we define a binary indicator function:
Thus, the full dataset can be represented as the tuple:
where M provides the labels for maneuver detection tasks. Since maneuvers are rare, the distribution of is highly imbalanced, with most values being zero. This presents a challenge for maneuver detection in satellite monitoring applications. Hence, for the describing the state of a geosynchronous satellite, we apply a masking strategy to introduce missing values for unsupervised pre-training. To generate masked training data, we perform random masking on X multiple times [12]. Let be a masking function for the k-th masked sequence, where
We generate M masked of X by setting a fraction r of the time steps to zero:
where ⊙ denotes element-wise multiplication. The resulting dataset consists of the original time series and M augmented masked time series samples:
where N is the total number of time series samples in the dataset.
To leverage the masked time series samples for self-supervised learning, we employ an encoder-decoder framework that reconstructs the missing values.
Encoder : The encoder maps the masked sample into a latent representation Z:
where captures high-level features of the sequence.
Decoder : The decoder reconstructs the original time series sample from the latent space:
The reconstructed sequence should approximate the unmasked ground truth X.
Since we have access to the true values in the masked regions, we define a reconstruction loss that only applies to the masked portions in the time domain:
Recent studies [41,42] have demonstrated that incorporating frequency-domain information alongside time-domain signals enables models to more effectively capture the complex dynamic patterns inherent in time series data. In addition to time-domain reconstruction, we also transform the original time-domain sequences into the frequency domain using the discrete Fourier transform [43]. Let and denote the frequency-domain representations of the original and reconstructed sequences, respectively. We define the frequency-domain reconstruction loss as follows:
The total reconstruction loss used for masked pre-training is the weighted sum of both domains:
This time- and frequency-domain objective encourages the model to capture both local temporal dynamics and global spectral patterns, thereby learning more robust and generalizable representations of satellite maneuver behavior.
2.5. Similarity-Based Cluster Pre-Training
To enhance the robustness of the model for maneuver detection in geosynchronous satellite time series, a similarity-based clustering pre-training module is introduced. This approach groups different types of status information and maneuver information into multiple clusters, improving detection granularity. After warming up the self-supervised masked reconstruction pre-training for epochs, the model’s outputs are used as representations of the satellite’s status at each time step. These representations are then clustered using K-means [44] to obtain C clusters, representing different maneuver and status categories. To achieve effective clustering, K-means is applied to the learned representations from time steps . The clustering objective is defined as follows:
where represents the cluster centroid matrix, and is a one-hot encoded cluster assignment vector. The optimal assignments and centroids Q are obtained through an iterative optimization process, ensuring that each representation is assigned to a well-defined cluster.
For a newly observed time-step representation , its cluster assignment is determined by measuring the cosine similarity with each cluster center , where :
ensuring that is associated with the most similar cluster. This step enables the model to categorize unseen time-series representations based on previously learned cluster structures.
To improve clustering consistency, a clustering loss is introduced, inspired by DeepCluster. This loss function refines the learned feature representations by aligning them with the pseudo-labels obtained from K-means clustering. The clustering optimization objective is formulated as follows:
where is updated dynamically using cosine similarity-based assignments. This loss function enforces feature representations to form well-separated clusters, enhancing maneuver classification performance.
The overall pre-training process consists of four key steps. First, the masked reconstruction model undergoes warm-up training for epochs. Second, K-means clustering is applied to the learned representations to obtain C cluster centers Q. Third, newly observed time-series representations are assigned to clusters based on cosine similarity with cluster centers. Finally, clustering loss optimization is conducted to refine feature representations and improve cluster separation. By distinguishing multiple maneuver and status types, this method overcomes the limitations of binary reconstruction loss and provides a more fine-grained classification of satellite maneuvers.
2.6. Overall Training
To effectively learn the maneuver patterns of geosynchronous satellites, we propose a two-stage pre-training framework that consists of unsupervised masked reconstruction pre-training and similarity-based clustering pre-training. The overall training objective is formulated as follows:
where the weighting coefficient is used to balance the contribution of the clustering loss. To ensure effective initialization of the clustering process, we set for the first epochs, relying solely on to learn discriminative features before introducing clustering-based optimization. The training of the MC-MD model consists of four main stages, as detailed in the Pseudocode Algorithm 1.
| Algorithm 1 Our proposed MC-MD model |
|
3. Results
3.1. Experimental Settings
To evaluate the effectiveness of our proposed MC-MD model for maneuver detection, we conduct experiments on both the simulated dataset and real-world geosynchronous satellite dataset (as described in Section 2.2). These two datasets are designed to reflect realistic orbital behaviors and include various maneuvering events for detection. For each dataset, both MC-MD and the baseline models are trained using a reconstruction-based time series learning approach. Specifically, the training process involves learning to reconstruct multivariate time series sequences under a masked prediction setting. During the testing phase, we compute the model’s reconstruction error to determine whether a particular time point corresponds to a maneuver event.
To quantify the detection accuracy, we introduce a tolerance window parameter , which defines an acceptable range around the ground-truth maneuver time index. A predicted maneuver timestamp is considered correct if it satisfies the condition:
where denotes the true maneuver event timestamp. In other words, the prediction is deemed accurate if it falls within the interval . This tolerance accounts for temporal uncertainty in maneuver detection and provides a more flexible evaluation metric. As illustrated in Figure 5, we provide a visualization of one geosynchronous satellite time series sample that contains two maneuver points, where the anomalous values are visibly separated from the distribution of normal states. In our experiments, we conduct comparative evaluations using three different tolerance levels: , , and , to comprehensively assess the detection performance under varying levels of temporal strictness.
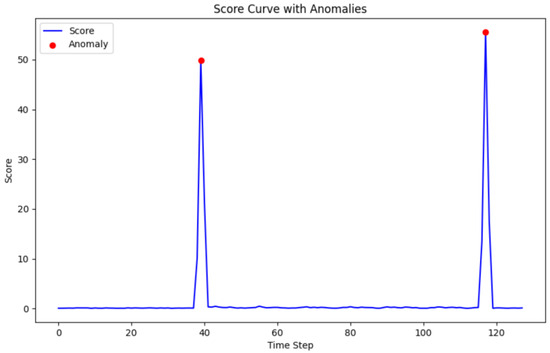
Figure 5.
A geosynchronous satellite time series sample showing two distinctly different anomalous maneuvering events.
3.1.1. Baselines
We compare the MC-MD model with nine baseline models: two classical filtering approaches and five deep learning-based time series models, which are detailed as follows:
- Interactive Multiple Model (IMM) [45]: It maintains multiple Kalman filters, each representing a different motion model. It updates their probabilities using Bayesian inference and combines predictions. For maneuver detection, sharp changes in mode probabilities or filter residuals are treated as indicators of abnormal motion.
- Kalman Filter [46]: It estimates system states by predicting and updating with new observations. Maneuvers are identified by detecting significant or persistent residuals that deviate from expected motion.
- LSTM [47]: It models sequence dependencies through gated recurrent units. We use it to reconstruct satellite time series and compute the mean squared error between predicted and true values. High errors typically correspond to maneuver points.
- TS2Vec [48]: It learns timestamp-level representations through hierarchical contrastive learning on augmented context views, producing robust contextual embeddings. Sub-sequence representations are obtained by aggregating the embeddings of corresponding timestamps.
- TimesNet [49]: It captures multi-periodic patterns using 2D convolutions across time series. It reconstructs regular orbital behavior, and anomalies are identified based on large deviations from expected patterns.
- GPT4TS [50]: It fine-tunes selected part parameters of a pre-trained Transformer for time series prediction. It learns to complete masked sequences; prediction errors signal unexpected behavior such as satellite maneuvers.
- ModernTCN [51]: It applies temporal convolutions with large kernels to model dependencies. Maneuver points are identified via high reconstruction or prediction error.
- iTransformer [52]: It applies attention and feed-forward layers on inverted dimensions, where time points are represented as variate tokens. This design enables the model to capture cross-variable dependencies and learn nonlinear token representations, yielding strong performance in time series forecasting.
- TimeMixer [53]: It uses multiscale mixing blocks to separate local and global temporal patterns. It forecasts future values, and discrepancies between predicted and observed data indicate potential maneuvers.
3.1.2. Implementation Details
The MC-MD model is trained using the Adam optimizer, with a learning rate set to 0.001 and a batch size of 32. The maximum number of training epochs is fixed at 100. For the encoder architecture, we adopt the Transformer structure, and design the decoder as a symmetric counterpart to the encoder. In the total loss function , the weighting coefficient for the clustering-based pre-training objective is set to 0.01. In addition, the cluster count C used in the simulated and real-world datasets is set to 12. All experiments are conducted using two NVIDIA RTX 4090 GPUs, and each experiment is run with five different random seeds to reduce the effects of randomness; the final performance is reported as the average across these runs.
To evaluate the effectiveness of the proposed method, we use four standard performance metrics: Accuracy, Precision, Recall, and F1-Score. These metrics are defined as follows. Let , , , and denote the number of true positives, true negatives, false positives, and false negatives, respectively. Then
- Accuracy measures the proportion of correct predictions over all predictions:
- Precision evaluates the correctness of positive predictions:
- Recall measures the ability to capture true positive instances:
- F1-Score is the harmonic mean of Precision and Recall:
Each of these metrics yields values in the range , where higher values indicate better detection performance. These metrics offer complementary insights: Accuracy indicates overall correctness, while Precision and Recall capture the trade-off between false positives and false negatives. F1-Score balances both and is especially important in imbalanced settings that are common in maneuver detection. Given the class imbalance in this task, Accuracy serves as a reference, but evaluation primarily relies on Precision, Recall, and particularly the F1-score. Finally, the core architectural components defining the MC-MD model are presented in Table 3.

Table 3.
Network configuration setting of the MC-MD Model. Among them, B denotes batch size; T (the length of the input time series sequence); N (the number of input channels, with variable dimensionality); P (the number of patches extracted from the input); (the dimensionality of hidden representations in the transformer layers) and patch_size (the size of frequency-domain patches applied for signal decomposition).
3.2. Main Results in Maneuver Detection
To validate the effectiveness of the proposed MC-MD method, we conduct a comprehensive evaluation under three temporal tolerance settings: , , and . The evaluation begins with experiments on a simulation dataset, which is first used for self-supervised pre-training. Upon completion of the pre-training phase, fine-tuning is performed using the labeled instances from the same simulation data to align the model with the maneuver detection task. As shown in Table 4, Table 5 and Table 6, MC-MD consistently achieves the highest Accuracy across all tolerance levels, highlighting its robustness in distinguishing maneuver events from normal orbital behavior. In most cases, our proposed MC-MD method also delivers the highest Precision, Recall, and F1-Score, reflecting both high confidence and strong overall balance in detection performance, with minimal false positives. These results underscore the advantage of combining time-frequency masking with clustering-based representation learning in modeling complex satellite dynamics.

Table 4.
Maneuver detection results comparison on the simulated dataset with . The best results are in bold.

Table 5.
Maneuver detection results comparison on the simulated dataset with . The best results are in bold.

Table 6.
Maneuver detection results comparison on the simulated dataset with . The best results are in bold.
Figure 6 compares MC-MD’s performance with and without pre-training on the real-world dataset. In the pre-training setup, the model is first pre-trained on a simulated dataset and then fine-tuned on a real dataset. In contrast, the no-pre-training variant is trained directly on the real dataset. The results show consistent performance gains. Precision improves from 0.9616 to 1.0000 (+3.98%), indicating a clear reduction in false positives. Recall increases slightly from 0.7220 to 0.7362 (+1.97%), reflecting improved sensitivity despite distributional differences between simulated and real data. F1-Score also improves from 0.8247 to 0.8480 (+2.83%), demonstrating better balance between precision and recall. These improvements can be attributed to the benefits of simulation-based pre-training, which allows the model to learn generalizable temporal and structural features, accelerates fine-tuning, and provides a more robust parameter initialization. This is particularly valuable in real-world scenarios with limited labeled data. Moreover, pre-training improves the model’s ability to handle edge cases and noisy inputs. Overall, these findings confirm that combining simulated pre-training with real-data fine-tuning significantly enhances cross-scene maneuver detection performance.
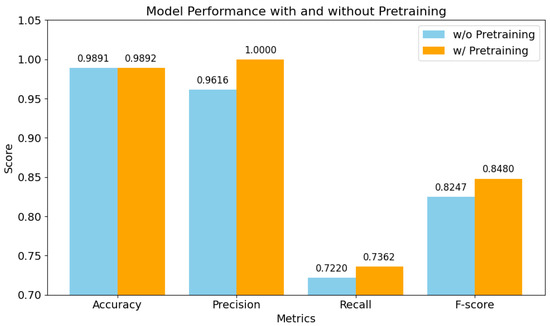
Figure 6.
Maneuver detection results of MC-MD comparison on the real-world dataset with .
In summary, the strong performance of MC-MD is primarily driven by two key architectural innovations. First, the dual-view masking strategy jointly perturbs time-domain and frequency-domain signals during pre-training, encouraging the model to learn robust and transferable representations that capture both temporal dynamics and spectral patterns. Second, the unsupervised clustering module introduces structural regularization in the latent space by grouping similar representations through similarity-based assignments, enhancing the model’s ability to distinguish between different maneuver behaviors. Further, compared with baseline methods, MC-MD leverages the synergy between masked prediction and clustering, which not only mitigates overfitting to specific maneuver scenarios but also improves generalization to unseen conditions. Moreover, the explicit integration of spectral cues with temporal dependencies allows MC-MD to detect subtle maneuver variations that are often overlooked by conventional temporal models. Hence, the experimental results consistently demonstrate that MC-MD achieves state-of-the-art performance across varying tolerance thresholds, confirming its adaptability to both strict and relaxed detection requirements.
3.3. Ablation Study
To further assess the effectiveness of each component in MC-MD for geosynchronous satellite maneuver detection, we conduct ablation studies with . This setting requires exact temporal alignment between predicted and ground-truth maneuver events, making it particularly suitable for evaluating the contribution of individual modules. We consider the following four ablation variants of our full model:
- w/o pre-training: This variant removes the entire pre-training stage, and directly trains the model on the downstream maneuver detection task. This setting assesses the overall importance of our self-supervised pre-training strategy.
- w/o frequency mask loss (freq loss): We remove the frequency-domain loss component from the masked reconstruction pre-training. Only time-domain masking is applied. This allows us to evaluate the contribution of frequency masking.
- w/o cluster loss: This strategy eliminates the similarity-based clustering loss used during pre-training. The model is still trained with dual-view masked reconstruction, but without unsupervised cluster-based pre-training.
- w/o frequency mask and cluster loss (freq and cluster loss): Both the frequency-domain masking loss and the clustering loss are removed. The model is trained only with time-domain masked reconstruction, aiming to assess the joint impact of both components.
As shown in Table 7, removing the entire pre-training phase (w/o pre-training) leads to a noticeable drop in F1-Score from 0.8886 to 0.8712, confirming the overall importance of the masked and clustered pre-training strategy for enhancing maneuver detection performance. Further, eliminating the frequency-domain masking loss (w/o freq loss) results in a slight performance degradation (F1-Score drops from 0.8886 to 0.8818), indicating that frequency-based masking complements time-domain information by helping the model capture global periodic or abrupt variations associated with satellite maneuvers. The cluster loss plays a more significant role: removing it (w/o cluster loss) causes a larger drop in both Precision (from 0.9444 to 0.8812) and F1-Score (from 0.8886 to 0.8292), suggesting that the unsupervised clustering pre-training module substantially improves performance. Finally, removing both the frequency-domain loss and the cluster loss (w/o freq and cluster loss) leads to the lowest F1-Score (0.8288), reinforcing the complementary contribution of these two components. Collectively, these results validate that both time-frequency dual-view masking and similarity-based clustering are essential for achieving robust and accurate maneuver detection for geosynchronous satellites.

Table 7.
Maneuver detection results of ablation study with . The best results are in bold.
3.4. Reconstructed Trajectories Analysis
Figure 7 and Figure 8 present reconstruction results on simulated and real-world test sequences, respectively. In the simulated case, the anomaly occurs at time step 36; in the real-world case, it appears at step 69. In both scenarios, the blue solid line denotes the ground truth trajectory, which all baseline models aim to reconstruct. The sequences exhibit periodic behavior with distinct deviations at the maneuver points. Our proposed MC-MD method yields reconstructions that most closely follow the ground truth, effectively capturing both the underlying periodic structure and the abrupt deviations associated with maneuvers. It achieves the lowest Mean Squared Error (MSE) among all models, highlighting its superior reconstruction accuracy. TimeMixer also demonstrates reasonable performance by capturing general periodic trends. However, it deviates near anomaly points, indicating limited sensitivity to sharp transitions. Other baseline methods perform noticeably worse, with significant reconstruction errors—particularly around anomalous segments—suggesting insufficient capacity to model the complex temporal dynamics of satellite maneuvers. These results confirm the advantage of MC-MD in reconstructing high-fidelity sequences, particularly in scenarios involving both smooth orbital trends and sudden behavioral shifts, which are critical for accurate maneuver detection.
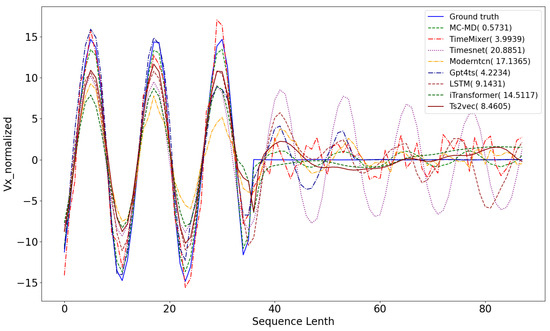
Figure 7.
Comparative analysis of the results of different methods for reconstructing the input data on a test set of simulation-generated sequence.
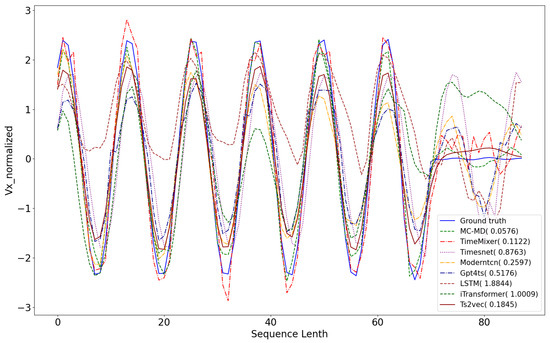
Figure 8.
Comparative analysis of the results of different methods for reconstructing the input data on a test set of real-world sequence.
3.5. Frequency Modeling and Clustering Analysis
To further validate the effectiveness of our proposed MC-MD, we conducted comparative experiments to evaluate the performance of multiple frequency analysis methods, including the Hilbert–Huang Transform (HHT), Short-Time Fourier Transform (STFT), Wavelet Packet Transform (WPT), Short-Time Wavelet Packet Transform (STWPT), and our focal method used for time-frequency mask pre-training, Discrete Fourier Transform (DFT). Table 8 reveals notable disparities in performance: HHT is the lowest among all methods, while STF and WPT exhibit moderate improvements. STWPT slightly outperforms STFT but lags behind WPT. Notably, DFT (Ours) demonstrates a clear advantage, achieving the highest accuracy, precision, recall, and F1-score across all evaluated methods. This consistent superiority underscores that DFT, when integrated into the MC-MD framework, effectively captures the characteristic patterns of satellite maneuvers, enabling more precise and reliable detection compared with alternative time-frequency techniques. These findings validate DFT as the optimal choice for enhancing maneuver detection within MC-MD.

Table 8.
Using different frequency domain analysis techniques for MC-MD modeling on the simulated dataset with .
To evaluate the impact of cluster center initialization strategies on MC-MD performance, three methods were compared: K-means + Att (K-means on low-dimensional encoder representations with Transformer attention optimization), K-means+Raw (K-means on raw high-dimensional sequence data), and Random (random initialization). As shown in Table 9, K-means + Att outperforms the others across all metrics. K-means + Raw follows with lower performance, while Random yields the lowest metrics. Notably, K-means + Att exhibits a drastically shorter training time than K-means + Raw and Random, with consistent inference time across methods. The superiority of K-means + Att may stem from low-dimensional encoder representations capturing discriminative features, reducing noise and enhancing clustering quality.

Table 9.
The results of the k-means analysis. K-means + Att denotes K-means combines the attention of the transformer for training, and K-means + Raw represents combining the raw data for cluster initialization.
3.6. Hyperparameter Analysis
The hyperparameter governs the relative contribution of the clustering loss within the overall training objective of the MC-MD model. To evaluate its effect, Figure 9 analyzes the model’s F1-Score across a range of values, spanning from to . When is set to a small value (e.g., or ), the model achieves its highest F1-Score (0.8886), indicating optimal performance in maneuver detection. In this regime, the clustering loss exerts minimal influence, allowing the model to focus primarily on learning global temporal structures through masked reconstruction—an essential factor for capturing anomalous behavior in satellite motion. As increases to a moderate range (e.g., to 1), the F1-Score gradually declines. This suggests that assigning greater weight to the clustering loss may lead the model to overfit local structural patterns in the latent space, while underemphasizing broader temporal dependencies necessary for accurately identifying maneuver events. With large values (e.g., 10 to 1000), the degradation becomes more pronounced, with the clustering loss dominating the training objective. This imbalance reduces the model’s reconstruction quality and negatively impacts overall detection performance. In summary, the analysis indicates that a small value provides a well-calibrated trade-off between structural regularization and representation generalization. Excessive weighting of the clustering loss undermines model robustness and impairs its ability to generalize for complex maneuver dynamics.
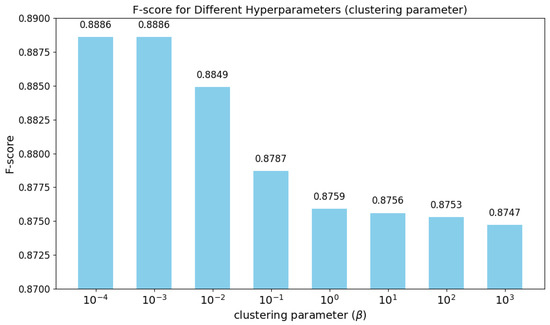
Figure 9.
The hyperparameter analysis of the weighting coefficient for the clustering loss.
4. Discussion
The experimental results clearly demonstrate the superior performance and practical advantages of the proposed MC-MD model in maneuver detection for geosynchronous satellites. Compared with both traditional filtering techniques and recent deep learning baselines, MC-MD consistently achieves state-of-the-art results across a range of temporal tolerance settings () and evaluation metrics (Accuracy, Precision, Recall, F1-Score). This strong performance can be attributed to the core architectural innovations embedded within the model. Specifically, the dual-perspective masking strategy and the unsupervised clustering pre-training module. The masked strategies, which simultaneously apply masks in the time and frequency domains, enable the model to learn comprehensive representations that are sensitive to both local temporal anomalies and global periodic structures, two patterns that are highly characteristic of satellite motion data. Meanwhile, the clustering-based pre-training component enforces a high-level structure in the latent space, grouping similar maneuver behaviors and thereby improving the model’s ability to generalize to previously unseen or rare satellite actions. This is particularly crucial in scenarios where the lack of labeled data and heterogeneous maneuver patterns poses significant challenges to traditional and supervised approaches.
Beyond performance metrics, the design of MC-MD also addresses key limitations of current remote sensing methodologies. Traditional model-based detectors, such as IMM and Kalman Filters, rely heavily on precise physical modeling assumptions and are sensitive to measurement noise and nonlinear maneuvers. Meanwhile, many deep learning-based methods assume a supervised training regime on data that closely resemble the deployment domain. In contrast, MC-MD’s pre-training-finetuning paradigm leverages large-scale, synthetically generated maneuver sequences to build transferable representations, which are then fine-tuned on real-world observations with minimal supervision. This aligns well with the realities of space-based remote sensing, where simulated orbital data are often more abundant and less costly to obtain than high-quality labeled real-time datasets. Moreover, the ability of MC-MD to encode both statistical anomalies and structural dynamics makes it particularly well-suited for integration with remote sensing pipelines that involve time series analysis of telemetry, tracking, and other Earth observation streams. Notably, the strong reconstruction performance observed on both simulated and real datasets highlights the robustness of the MC-MD model. This capability to recover subtle patterns in telemetry sequences is essential for accurate remote diagnostics and behavior prediction in space operations.
5. Conclusions
In this paper, we propose MC-MD (Masked and Clustered Pre-training for Maneuver Detection), a novel framework for detecting maneuvers in geosynchronous satellites. By integrating time-frequency masked reconstruction with clustering-guided pre-training, MC-MD effectively learns both local and global patterns in satellite time series. The masking strategy enhances sensitivity to temporal anomalies, while clustering enforces structural consistency in the latent space, improving generalization across varied maneuver types. Experimental results on both simulated and real-world datasets confirm that MC-MD consistently outperforms traditional model-based filters and advanced deep learning baselines across all evaluation metrics and tolerance settings. Importantly, MC-MD aligns well with remote sensing practice, leveraging synthetic pre-training to reduce dependence on labeled real-world data. Its architecture is adaptable to various orbital dynamics and data distributions, making it a practical and scalable solution for satellite monitoring systems. In future work, we plan to extend MC-MD to the task of maneuver prediction, enabling proactive modeling of satellite behavior and further enhancing space situational awareness.
Author Contributions
Conceptualization, S.-H.T. and Y.-Q.F.; Data curation, S.-H.T.; Formal analysis, Y.-Q.F.; Investigation, S.-H.T.; Methodology, S.-H.T.; Project administration, Y.-S.Z.; Resources, Y.-S.Z.; Software, S.-H.T. and D.L.; Supervision, Y.-Q.F. and Y.-S.Z.; Validation, Y.-Q.F. and H.-F.D.; Visualization, D.L.; Writing—original draft, S.-H.T.; Writing—review and editing, Y.-Q.F. and H.-F.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was approved by the institutional review board of Space Engineering University.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Roberts, T.G.; Linares, R. A survey of longitudinal-shift maneuvers performed by geosynchronous satellites from 2010 to 2021. In Proceedings of the 73rd International Astronautical Congress, Paris, France, 18–22 September 2022. [Google Scholar]
- Peng, H.; Bai, X. Improving orbit prediction accuracy through supervised machine learning. Adv. Space Res. 2018, 61, 2628–2646. [Google Scholar] [CrossRef]
- Peng, H.; Bai, X. Machine learning approach to improve satellite orbit prediction accuracy using publicly available data. J. Astronaut. Sci. 2020, 67, 762–793. [Google Scholar] [CrossRef]
- Han, H.; Dang, Z. Game-theoretic maneuvering strategies for orbital inspection of non-cooperative spacecraft in cislunar space. Chin. J. Aeronaut. 2025, 103574. [Google Scholar] [CrossRef]
- Roberts, T.G.; Solera, H.E.; Linares, R. Geosynchronous satellite behavior classification via unsupervised machine learning. In Proceedings of the 9th Space Traffic Management Conference, Austin, TX, USA, 1–2 March 2023; Volume 3. [Google Scholar]
- Zhou, H.; Wang, X.; Zhong, S. A satellite orbit maneuver detection and robust multipath mitigation method for GPS coordinate time series. Adv. Space Res. 2024, 74, 2784–2800. [Google Scholar] [CrossRef]
- Wang, S.A.; Zhang, H.; Cai, L.; Wang, Z.; An, Y. Research on Mass Center Identification for Gravitational Wave Detection Spacecraft with Guaranteed Laser Link Pointing Accuracy. Remote Sens. 2025, 17, 296. [Google Scholar] [CrossRef]
- Dai, X.; Lou, Y.; Dai, Z.; Hu, C.; Peng, Y.; Qiao, J.; Shi, C. Precise orbit determination for GNSS maneuvering satellite with the constraint of a predicted clock. Remote Sens. 2019, 11, 1949. [Google Scholar] [CrossRef]
- Sun, C.; Sun, Y.; Yu, X.; Fang, Q. Rapid Detection and Orbital Parameters’ Determination for Fast-Approaching Non-Cooperative Target to the Space Station Based on Fly-around Nano-Satellite. Remote Sens. 2023, 15, 1213. [Google Scholar] [CrossRef]
- Wang, L.; Sun, Z.; Wang, Y.; Wang, J.; Yan, C. Virtual-Integrated Admittance Control Method of Continuum Robot for Capturing Non-Cooperative Space Targets. Biomimetics 2025, 10, 281. [Google Scholar] [CrossRef]
- Maestrini, M.; Di Lizia, P. Guidance strategy for autonomous inspection of unknown non-cooperative resident space objects. J. Guid. Control. Dyn. 2022, 45, 1126–1136. [Google Scholar] [CrossRef]
- Qin, Z.; Zhang, Q.; Huang, G.; Tang, L.; Wang, J.; Wang, X. BDS Orbit Maneuver Detection Based on Epoch-Updated Orbits Estimated by SRIF. Remote Sens. 2023, 15, 2558. [Google Scholar] [CrossRef]
- Yihan, L.; Dong, S.; Han, Y.; Mu, Q.; Liu, X.; Qi, P. Research on Intent Recognition Method for Non-Cooperative Satellite Based on LSTM Network. In Proceedings of the 2023 China Automation Congress (CAC), Chongqing, China, 17–19 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 3854–3859. [Google Scholar]
- Wang, S.; Zhao, D.; Hong, H.; Sun, K. A Review of Space Target Recognition Based on Ensemble Learning. Aerospace 2025, 12, 278. [Google Scholar] [CrossRef]
- Roberts, T.G.; Rodriguez-Fernandez, V.; Siew, P.M.; Solera, H.E.; Linares, R. End-to-end behavioral mode clustering for geosynchronous satellites. In Proceedings of the 2023 Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 19–22 September 2023. [Google Scholar]
- Dehadraya, A.; Paliwal, V.; Malhotra, Y.; Vatsal, V. Geosynchronous Satellite Pattern-of-Life Characterization Through Machine Learning-based Mode Change Detection and Classification. In Proceedings of the 2024 IEEE Space, Aerospace and Defence Conference (SPACE), Bangalore, India, 22–23 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 235–239. [Google Scholar]
- Kelecy, T.; Hall, D.; Hamada, K.; Stocker, D. Satellite maneuver detection using Two-line Element (TLE) data. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference; Maui Economic Development Board (MEDB): Maui, HA, USA, 2007; pp. 1–10. [Google Scholar]
- Gong, B.; Jin, X.; Jiang, L.; Ren, M. Space-based passive orbital manoeuvre detection algorithm via a new characterization. In Proceedings of the Aerospace Europe Conference 2023—10th EUCASS—9th CEAS, Ecublens, Switzerland, 9–13 July 2023; pp. 1–16. [Google Scholar]
- Mukundan, A.; Wang, H.C. Simplified approach to detect satellite maneuvers using TLE data and simplified perturbation model utilizing orbital element variation. Appl. Sci. 2021, 11, 10181. [Google Scholar] [CrossRef]
- Solera, H.E.; Roberts, T.G.; Linares, R. Geosynchronous satellite pattern of life node detection and classification. In Proceedings of the 9th Space Traffic Management Conference, Austin, TX, USA, 1–2 March 2023. [Google Scholar]
- Austin Beer, K.S. Geosynchronous Satellite Maneuver Identification and Characterization using Passive RF Ranging. In Proceedings of the dvanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 14–17 September 2021; pp. 1–12. [Google Scholar]
- Pastor, A.; Escribano, G.; Sanjurjo-Rivo, M.; Escobar, D. Satellite maneuver detection and estimation with optical survey observations. J. Astronaut. Sci. 2022, 69, 879–917. [Google Scholar] [CrossRef]
- Cipollone, R.; Leonzio, I.; Calabrò, G.; Di Lizia, P. An LSTM-based Maneuver Detection Algorithm from Satellites Pattern of Life. In Proceedings of the 2023 IEEE 10th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Milan, Italy, 19–21 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 78–83. [Google Scholar]
- Huo, Y.; Li, Z.; Fang, Y.; Zhang, F. Classification for geosynchronous satellites with deep learning and multiple kernel learning. Appl. Opt. 2019, 58, 5830–5838. [Google Scholar] [CrossRef]
- Mello, C.; Mendoza, M.; Camacho, L.; Eberhardt, D. Advancing Geosynchronous Satellite Classification Utilizing Spectral Data via Fine-Tuned Pretrained Deep Learning Models. In Proceedings of the Advanced Maui Optical and Space Surveillance (AMOS) Technologies Conference, Maui, HI, USA, 17–20 September 2024; p. 32. [Google Scholar]
- Wang, Z.; Han, Y.; Zhang, Y.; Hao, J.; Zhang, Y. Classification and recognition method of non-cooperative objects based on deep learning. Sensors 2024, 24, 583. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, P.; Chen, D.; Pei, W.; Ma, Q. Scale-teaching: Robust multi-scale training for time series classification with noisy labels. Adv. Neural Inf. Process. Syst. 2023, 36, 33726–33757. [Google Scholar]
- DiBona, P.; Foster, J.; Falcone, A.; Czajkowski, M. Machine learning for RSO maneuver classification and orbital pattern prediction. In Proceedings of the 2019 Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 17–20 September 2019. [Google Scholar]
- Roberts, T.G.; Linares, R. Geosynchronous satellite maneuver classification via supervised machine learning. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 14–17 September 2021. [Google Scholar]
- Kelecy, T.; Abernethy, S.; Jones, F.; Gerber, E.; Wurzel, H. Predicted intent inferred from real-time rendezvous and proximity behavior. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 27–30 September 2022. [Google Scholar]
- Li, F.; Zhao, Y.; Zhang, J.; Zhang, Z.; Wu, D. A station-keeping maneuver detection method of non-cooperative geosynchronous satellites. Adv. Space Res. 2024, 73, 160–169. [Google Scholar] [CrossRef]
- Tang, C.; Chen, Y.; Chen, G.; Du, L.; Liu, H. A Dynamic and Collaborative Spectrum Sharing Strategy Based on Multi-Agent DRL in Satellite-Terrestrial Converged Networks. IEEE Trans. Veh. Technol. 2024, 74, 7969–7984. [Google Scholar] [CrossRef]
- Ma, Q.; Liu, Z.; Zheng, Z.; Huang, Z.; Zhu, S.; Yu, Z.; Kwok, J.T. A Survey on Time-Series Pre-Trained Models. IEEE Trans. Knowl. Data Eng. 2024, 36, 7536–7555. [Google Scholar] [CrossRef]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked autoencoders are scalable vision learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16000–16009. [Google Scholar]
- Li, Y.; Fan, H.; Hu, R.; Feichtenhofer, C.; He, K. Scaling language-image pre-training via masking. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 23390–23400. [Google Scholar]
- Jawahar, G.; Sagot, B.; Seddah, D. What Does BERT Learn about the Structure of Language? In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 3651–3657. [Google Scholar]
- Zhou, C.; Li, Q.; Li, C.; Yu, J.; Liu, Y.; Wang, G.; Zhang, K.; Ji, C.; Yan, Q.; He, L.; et al. A comprehensive survey on pretrained foundation models: A history from bert to chatgpt. Int. J. Mach. Learn. Cybern. 2024, 1–65. [Google Scholar] [CrossRef]
- Araguz, C.; Bou-Balust, E.; Alarcón, E. Applying autonomy to distributed satellite systems: Trends, challenges, and future prospects. Syst. Eng. 2018, 21, 401–416. [Google Scholar] [CrossRef]
- Dong, J.; Liu, P.; Wang, B.; Jin, Y. Detection of Flight Target via Multistatic Radar Based on Geosynchronous Orbit Satellite Irradiation. Remote Sens. 2024, 16, 4582. [Google Scholar] [CrossRef]
- MIT ARCLab Prize for AI Innovation in Space 2024. 2024. Available online: https://eval.ai/web/challenges/challenge-page/2164/overview (accessed on 10 December 2023).
- Liu, Z.; Ma, Q.; Ma, P.; Wang, L. Temporal-frequency co-training for time series semi-supervised learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 8923–8931. [Google Scholar]
- Wu, X.; Qiu, X.; Li, Z.; Wang, Y.; Hu, J.; Guo, C.; Xiong, H.; Yang, B. CATCH: Channel-Aware multivariate Time Series Anomaly Detection via Frequency Patching. In Proceedings of the International Conference on Learning Representations, Singapore, 24–28 April 2025. [Google Scholar]
- Wang, Z. Fast algorithms for the discrete W transform and for the discrete Fourier transform. IEEE Trans. Acoust. Speech, Signal Process. 1984, 32, 803–816. [Google Scholar] [CrossRef]
- Ahmed, M.; Seraj, R.; Islam, S.M.S. The k-means algorithm: A comprehensive survey and performance evaluation. Electronics 2020, 9, 1295. [Google Scholar] [CrossRef]
- Johnston, L.A.; Krishnamurthy, V. An improvement to the interacting multiple model (IMM) algorithm. IEEE Trans. Signal Process. 2001, 49, 2909–2923. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Yue, X.; Dempster, A.G. GPS-based onboard real-time orbit determination for LEO satellites using consider Kalman filter. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 769–777. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Yue, Z.; Wang, Y.; Duan, J.; Yang, T.; Huang, C.; Tong, Y.; Xu, B. Ts2vec: Towards universal representation of time series. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 22 February–1 March 2022; Volume 36, pp. 8980–8987. [Google Scholar]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis. In Proceedings of the The Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Zhou, T.; Niu, P.; Wang, X.; Sun, L.; Jin, R. One fits all: Power general time series analysis by pretrained lm. Adv. Neural Inf. Process. Syst. 2023, 36, 43322–43355. [Google Scholar]
- Luo, D.; Wang, X. Moderntcn: A modern pure convolution structure for general time series analysis. In Proceedings of the The Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024; pp. 1–43. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. In Proceedings of the The Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Wang, S.; Wu, H.; Shi, X.; Hu, T.; Luo, H.; Ma, L.; Zhang, J.Y.; Zhou, J. TimeMixer: Decomposable Multiscale Mixing for Time Series Forecasting. In Proceedings of the The Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).