Improving the Assimilation of T-TREC-Retrieved Wind Fields with Iterative Smoothing Constraints During Typhoon Linfa
Abstract
1. Introduction
2. Case and Methodologies
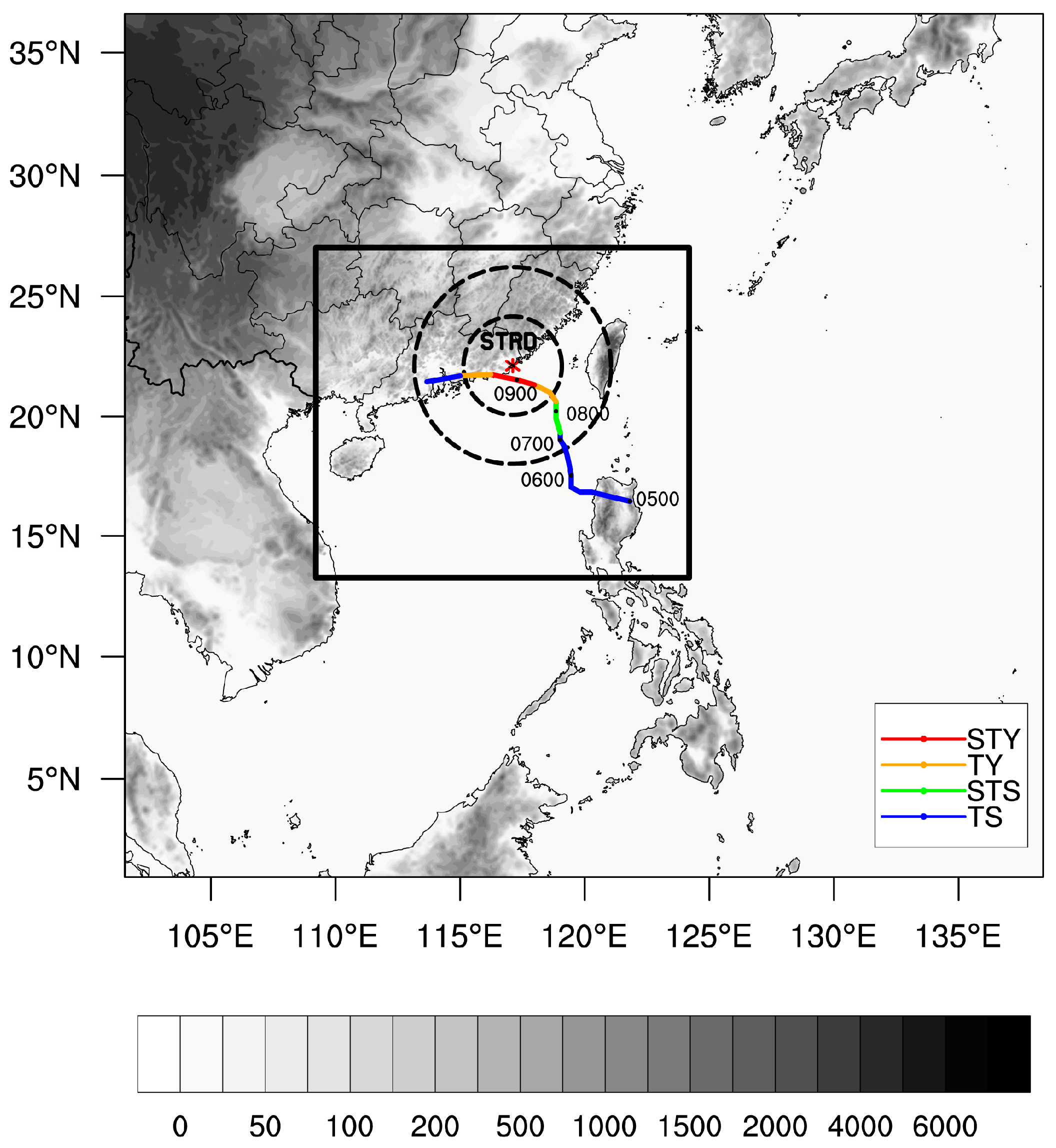
2.1. Overview of Typhoon Linfa
2.2. Radar Data Preprocessing
2.3. Introduction to the T-TREC-IS Algorithm
2.4. Assimilation Methodology
3. Results and Analysis
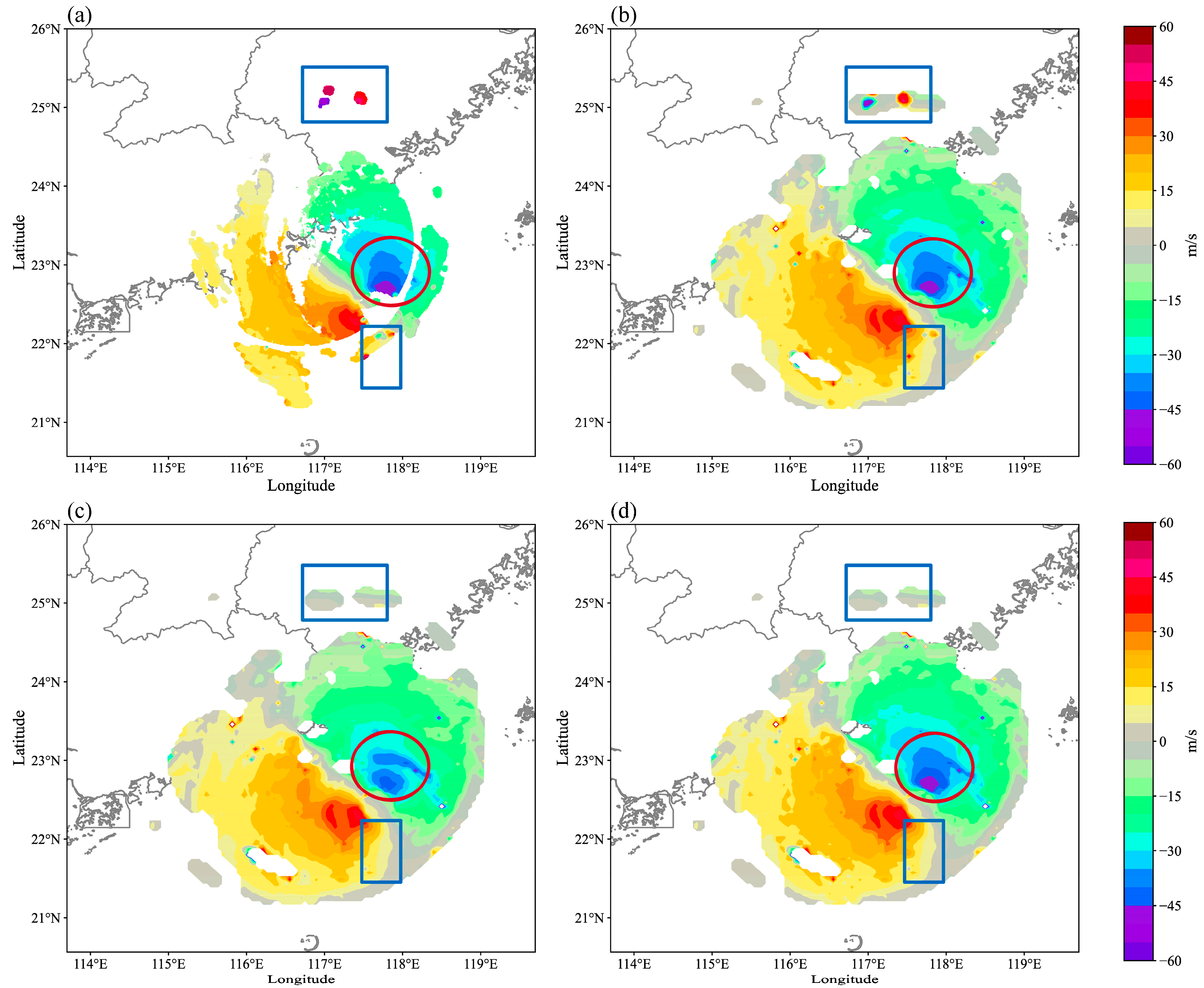
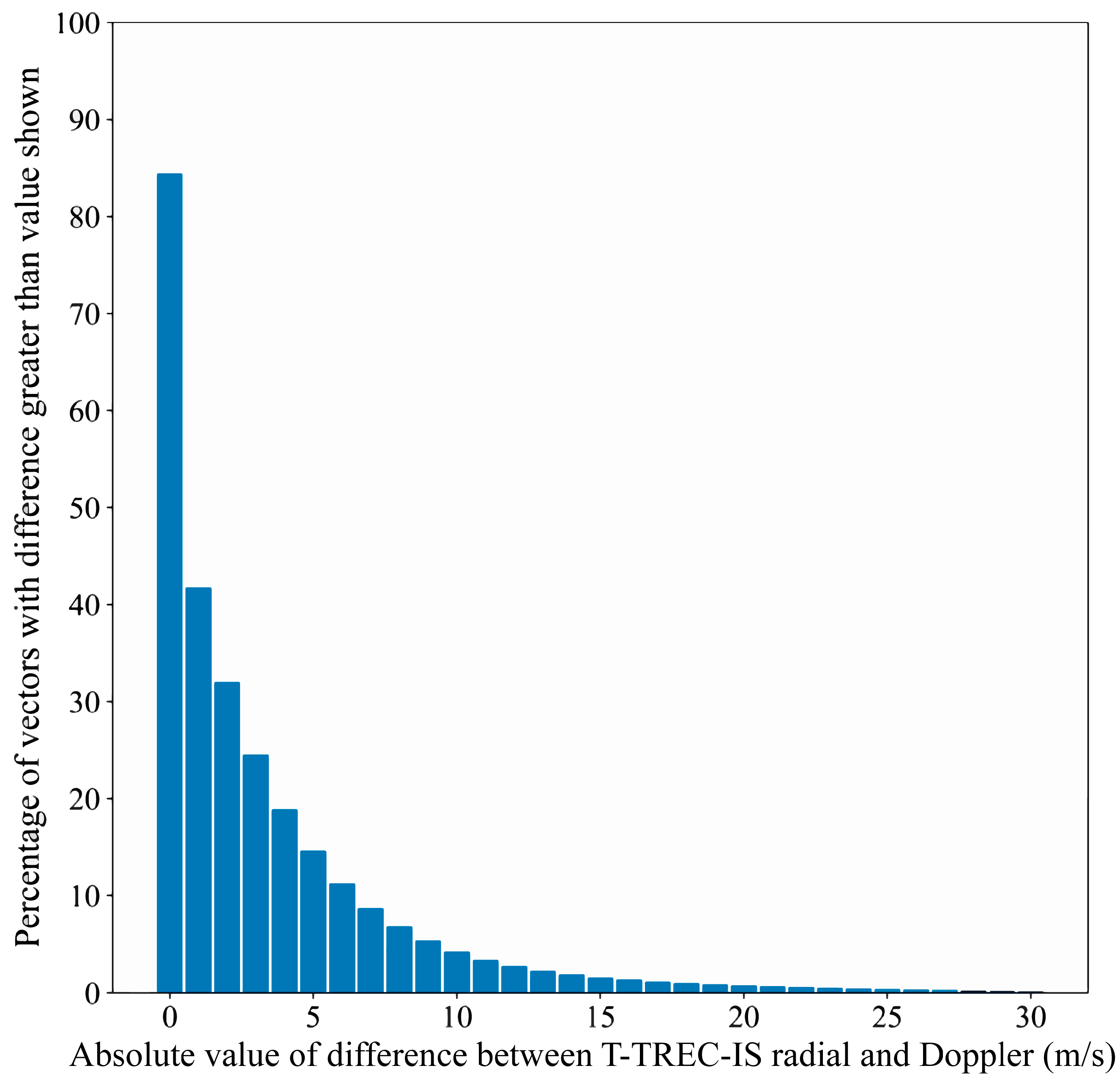
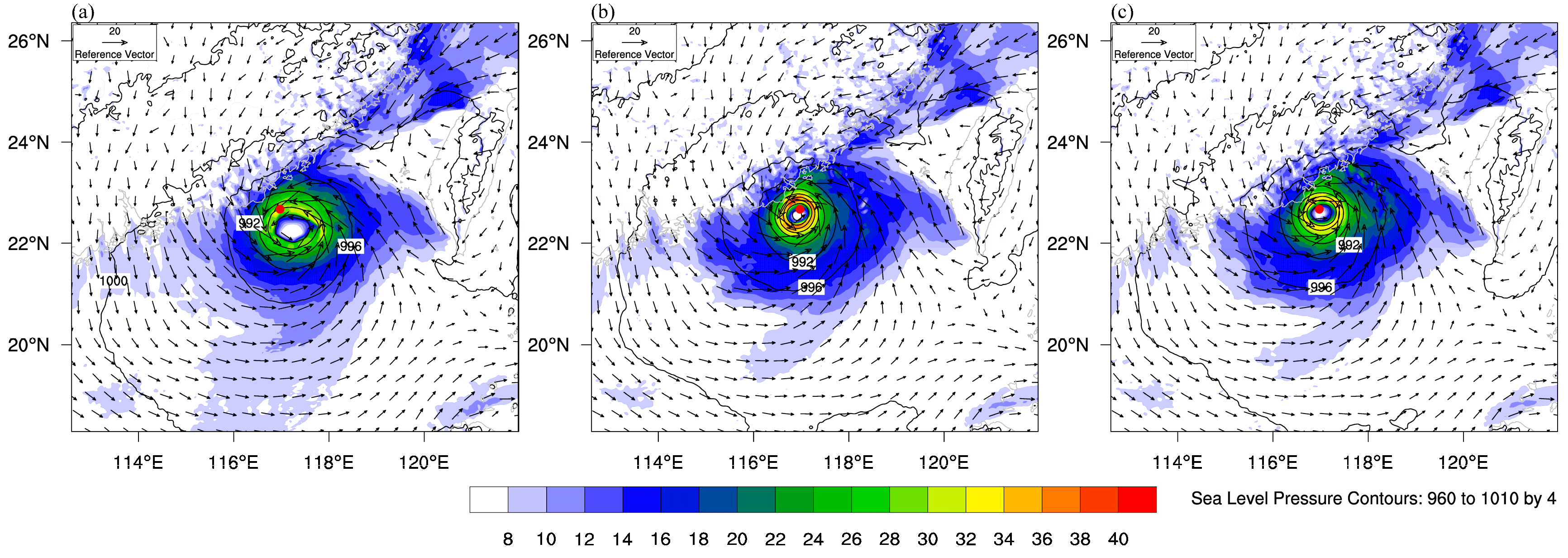
3.1. Evaluation of the Retrieved Wind Field Quality
3.2. Experimental Setup
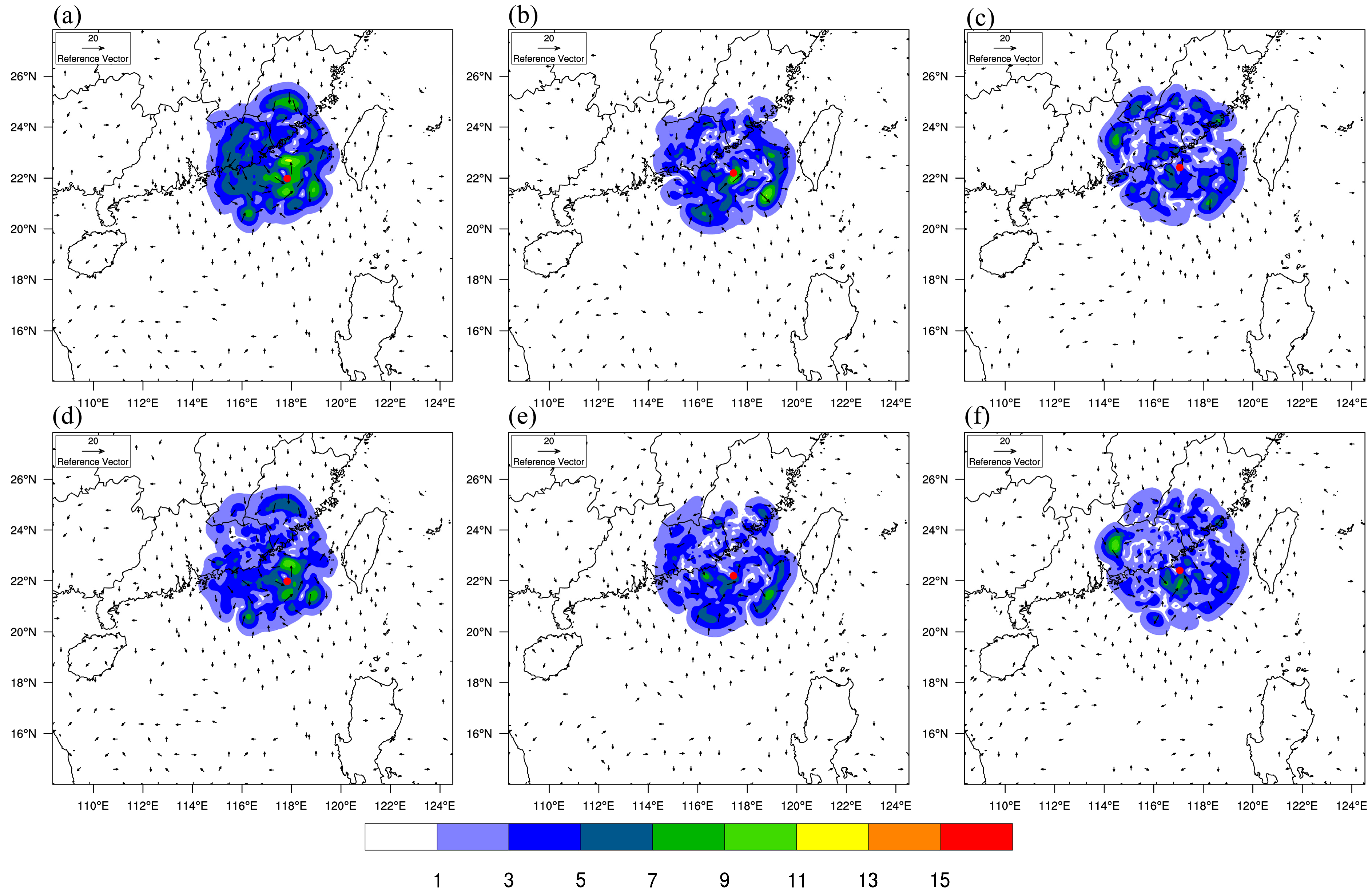
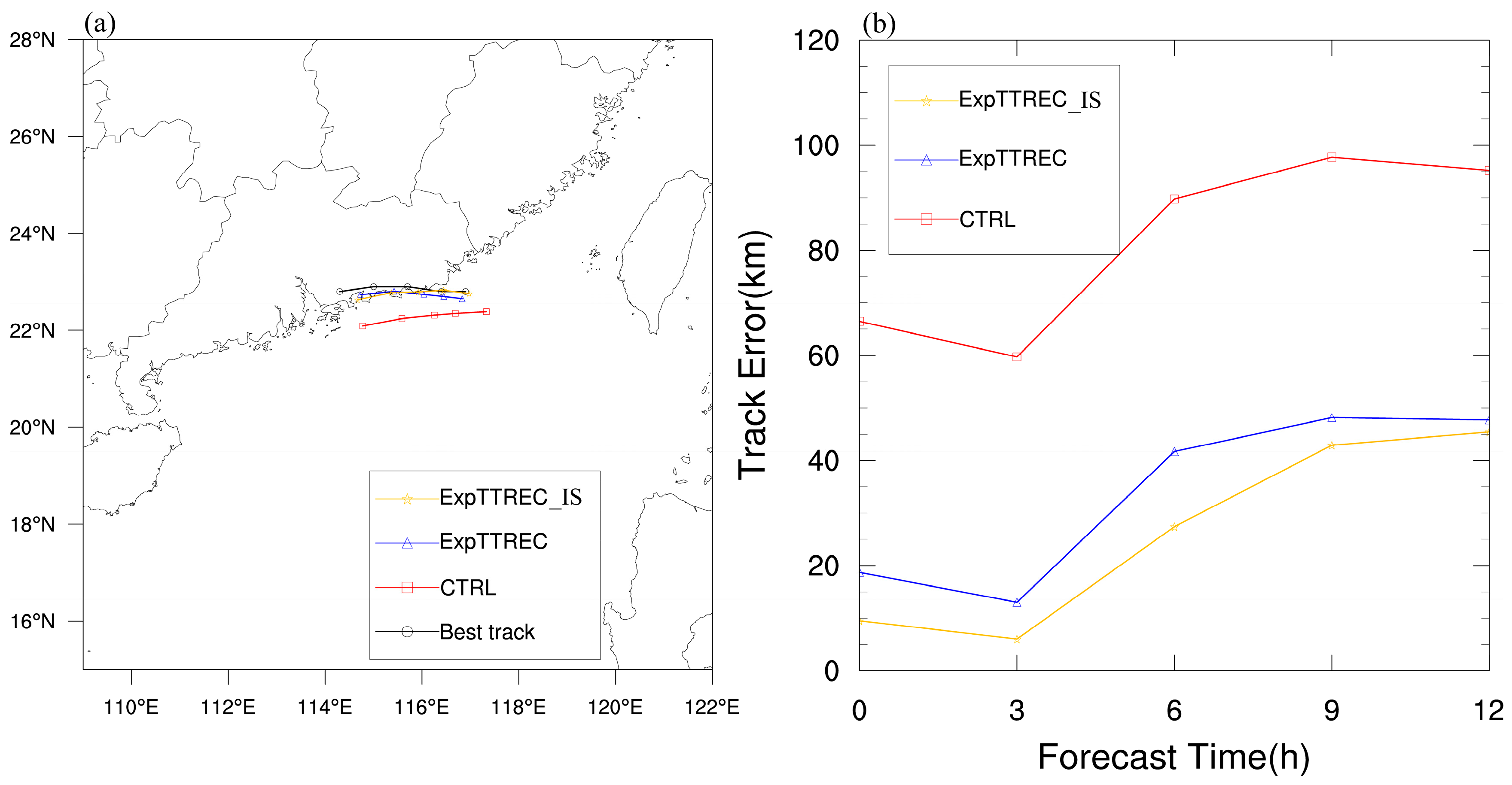
3.3. Impact of Assimilation on the Analysis Field
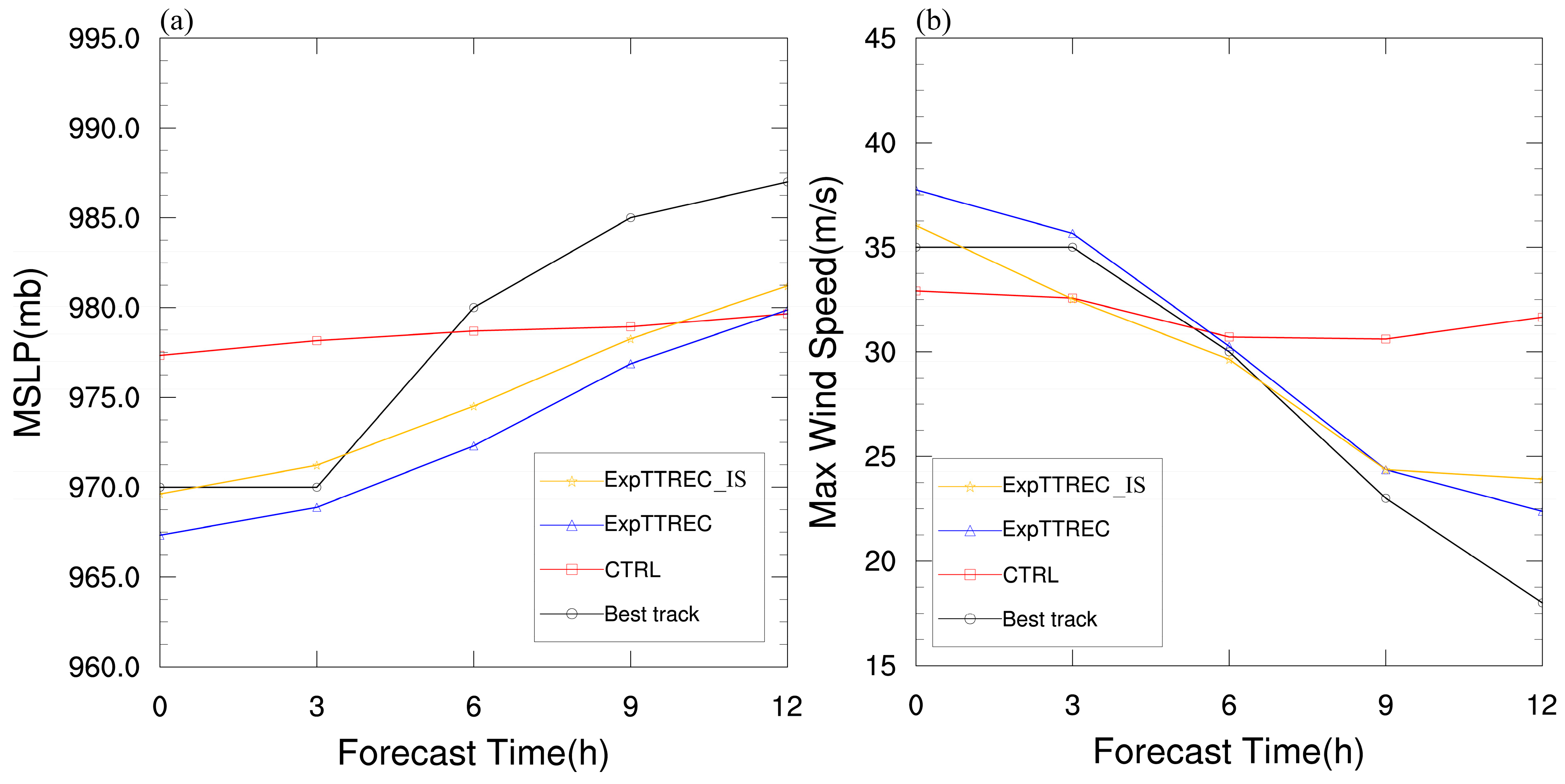
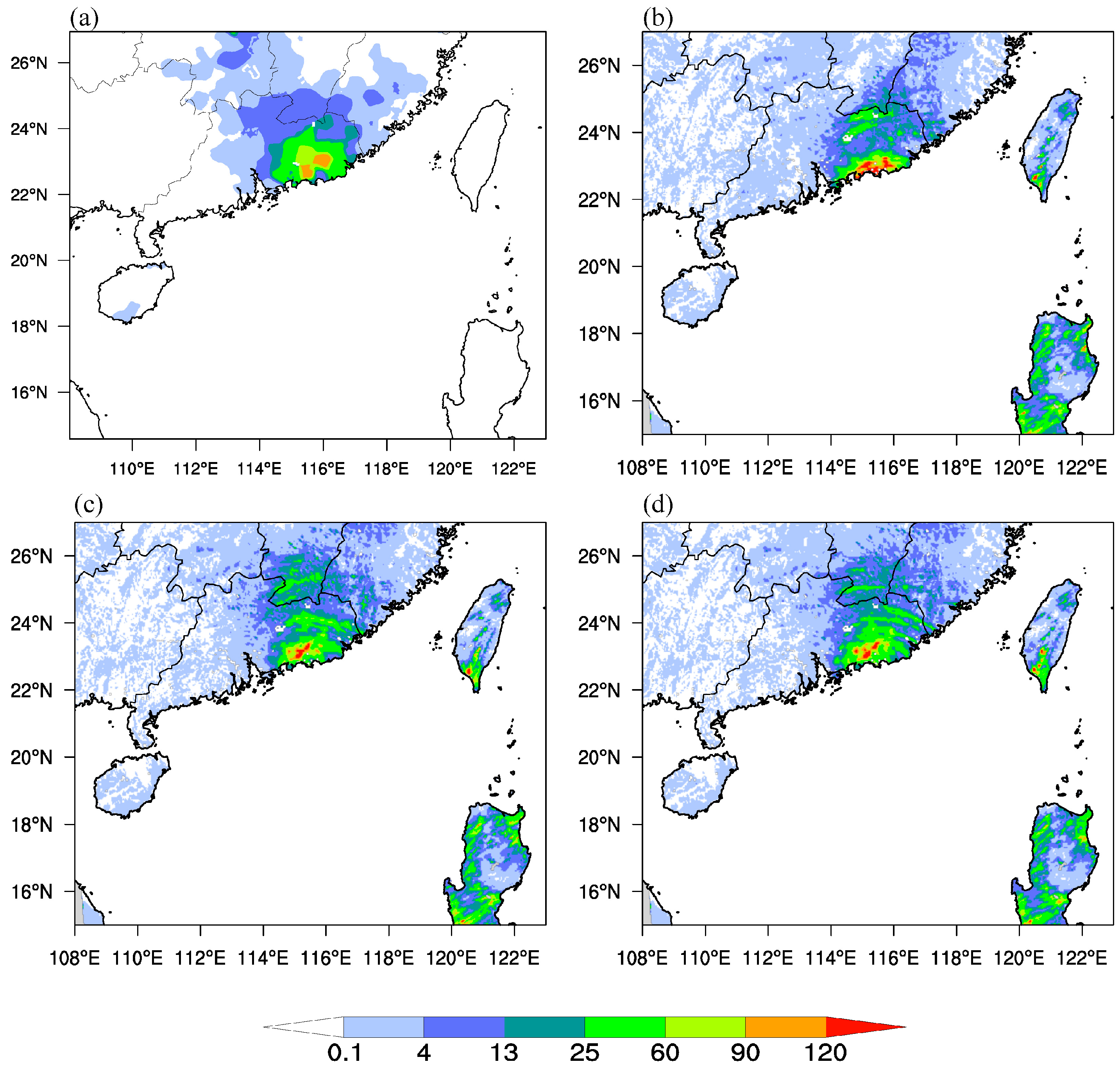
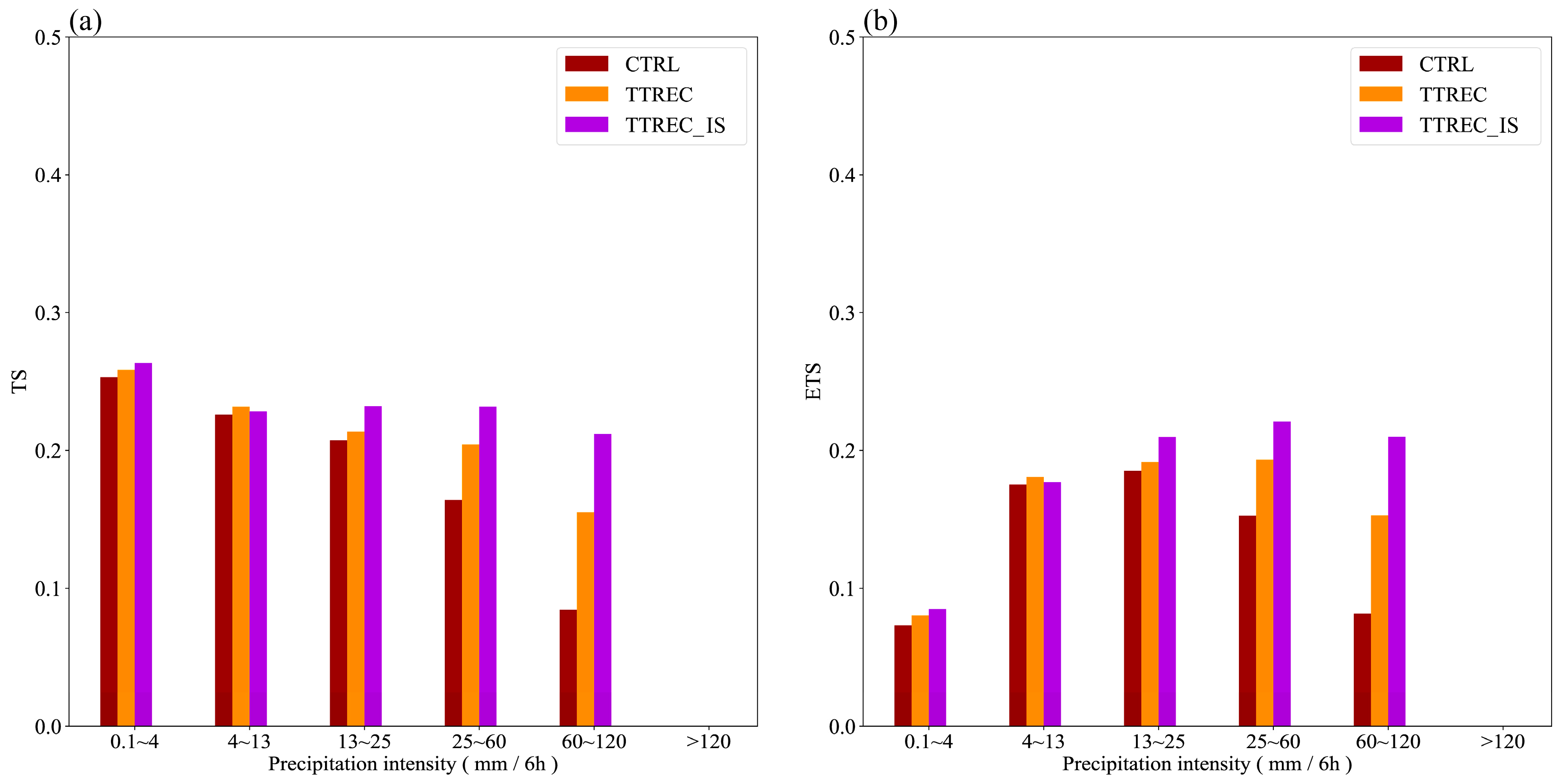
3.4. Impact of Assimilation on Deterministic Forecast
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Meng, Z.; Zhang, F.; Luo, D.; Tan, Z.; Fang, J.; Sun, J.; Shen, X.; Zhang, Y.; Wang, S.; Han, W.; et al. Review of Chinese atmospheric science research over the past 70 years: Synoptic meteorology. Sci. China Earth Sci. 2019, 62, 1946–1991. [Google Scholar] [CrossRef]
- Shu, A.; Shen, F.; Jiang, L.; Zhang, T.; Xu, D. Assimilation of Clear-sky FY-4A AGRI radiances within the WRFDA system for the prediction of a landfalling Typhoon Hagupit (2020). Atmos. Res. 2023, 283, 106556. [Google Scholar] [CrossRef]
- Shen, F.; Min, J. Assimilating AMSU-A radiance data with the WRF Hybrid En3DVAR system for track predictions of Typhoon Megi (2010). Adv. Atmos. Sci. 2015, 32, 1231–1243. [Google Scholar] [CrossRef]
- Schwartz, C.S.; Liu, Z.; Huang, X.-Y.; Kuo, Y.-H.; Fong, C.-T. Comparing Limited-Area 3DVAR and Hybrid Variational-Ensemble Data Assimilation Methods for Typhoon Track Forecasts: Sensitivity to Outer Loops and Vortex Relocation. Mon. Weather Rev. 2013, 141, 4350–4372. [Google Scholar] [CrossRef]
- Lei, L.; Whitaker, J.S.; Bishop, C. Improving Assimilation of Radiance Observations by Implementing Model Space Localization in an Ensemble Kalman Filter. J. Adv. Model. Earth Syst. 2018, 10, 3221–3232. [Google Scholar] [CrossRef]
- Zhang, J.A.; Kalina, E.A.; Biswas, M.K.; Rogers, R.F.; Zhu, P.; Marks, F.D. A Review and Evaluation of Planetary Boundary Layer Parameterizations in Hurricane Weather Research and Forecasting Model Using Idealized Simulations and Observations. Atmosphere 2020, 11, 1091. [Google Scholar] [CrossRef]
- Shu, A.; Shen, F.; Li, H.; Min, J.; Luo, J.; Xu, D.; Chen, J. Impacts of assimilating polarimetric radar KDP observations with an ensemble Kalman filter on analyses and predictions of a rainstorm associated with Typhoon Hato (2017). Q. J. R. Meteorol. Soc. 2025, 151, e4943. [Google Scholar] [CrossRef]
- Song, L.; Shen, F.; Shao, C.; Shu, A.; Zhu, L. Impacts of 3DEnVar-Based FY-3D MWHS-2 Radiance Assimilation on Numerical Simulations of Landfalling Typhoon Ampil (2018). Remote Sens. 2022, 14, 6037. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, X.; Min, J.; Shen, F. Impacts of assimilating all-sky FY-4A AGRI satellite infrared radiances on the prediction of Super Typhoon In-Fa during the period with abnormal changes. J. Geophys. Res. Atmos. 2024, 129, e2024JD040784. [Google Scholar] [CrossRef]
- Christophersen, H.; Sippel, J.; Aksoy, A.; Baker, N.L. Recent advancements for tropical cyclone data assimilation. Ann. N. Y. Acad. Sci. 2022, 1517, 25–43. [Google Scholar] [CrossRef]
- Snyder, C.; Zhang, F. Assimilation of Simulated Doppler Radar Observations with an Ensemble Kalman Filter. Mon. Weather Rev. 2003, 131, 1663–1677. [Google Scholar] [CrossRef]
- Zhang, F.; Weng, Y.; Sippel, J.A.; Meng, Z.; Bishop, C.H. Cloud-Resolving Hurricane Initialization and Prediction through Assimilation of Doppler Radar Observations with an Ensemble Kalman Filter. Mon. Weather Rev. 2009, 137, 2105–2125. [Google Scholar] [CrossRef]
- Shen, F.; Song, L.; Min, J.; He, Z.; Shu, A.; Xu, D.; Chen, J. Impact of Assimilating Pseudo-Observations Derived from the “Z-RH” Relation on Analyses and Forecasts of a Strong Convection Case. Adv. Atmos. Sci. 2025, 42, 1010–1025. [Google Scholar] [CrossRef]
- Fabry, F.; Meunier, V. Why Are Radar Data so Difficult to Assimilate Skillfully? Mon. Weather Rev. 2020, 148, 2819–2836. [Google Scholar] [CrossRef]
- Liang, X.; Xie, Y.; Yin, J.; Luo, Y.; Yao, D.; Li, F. An IVAP-Based Dealiasing Method for Radar Velocity Data Quality Control. J. Atmos. Ocean. Technol. 2019, 36, 2069–2085. [Google Scholar] [CrossRef]
- He, G.; Sun, J.; Ying, Z.; Zhang, L. A Radar Radial Velocity Dealiasing Algorithm for Radar Data Assimilation and its Evaluation with Observations from Multiple Radar Networks. Remote Sens. 2019, 11, 2457. [Google Scholar] [CrossRef]
- Feldmann, M.; James, C.N.; Boscacci, M.; Leuenberger, D.; Gabella, M.; Germann, U.; Wolfensberger, D.; Berne, A. R2D2: A Region-Based Recursive Doppler Dealiasing Algorithm for Operational Weather Radar. J. Atmos. Ocean. Technol. 2020, 37, 2341–2356. [Google Scholar] [CrossRef]
- Zhao, K.; Xue, M. Assimilation of coastal Doppler radar data with the ARPS 3DVAR and cloud analysis for the prediction of Hurricane Ike (2008). Geophys. Res. Lett. 2009, 36, L1280. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Xue, M. Assimilation of Radar Radial Velocity Data with the WRF Hybrid Ensemble–3DVAR System for the Prediction of Hurricane Ike (2008). Mon. Weather Rev. 2012, 140, 3507–3524. [Google Scholar] [CrossRef]
- Dong, J.; Xue, M. Assimilation of radial velocity and reflectivity data from coastal WSR-88D radars using an ensemble Kalman filter for the analysis and forecast of landfalling hurricane Ike (2008). Q. J. R. Meteorol. Soc. 2013, 139, 467–487. [Google Scholar] [CrossRef]
- Xu, D.; Shen, F.; Min, J. Effect of background error tuning on assimilating radar radial velocity observations for the forecast of hurricane tracks and intensities. Meteorol. Appl. 2020, 27, e1820. [Google Scholar] [CrossRef]
- Chen, J.; Xu, D.; Shu, A.; Song, L. The Impact of Radar Radial Velocity Data Assimilation Using WRF-3DVAR System with Different Background Error Length Scales on the Forecast of Super Typhoon Lekima (2019). Remote Sens. 2023, 15, 2592. [Google Scholar] [CrossRef]
- Shen, F.; Xu, D.; Min, J. Effect of momentum control variables on assimilating radar observations for the analysis and forecast for Typhoon Chanthu (2010). Atmos. Res. 2019, 230, 104622. [Google Scholar] [CrossRef]
- Shen, F.; Xue, M.; Min, J. A comparison of limited-area 3DVAR and ETKF-En3DVAR data assimilation using radar observations at convective scale for the prediction of Typhoon Saomai (2006). Meteorol. Appl. 2017, 24, 628–641. [Google Scholar] [CrossRef]
- Zhao, K.; Li, X.; Xue, M.; Jou, B.J.-D.; Lee, W.-C. Short-term forecasting through intermittent assimilation of data from Taiwan and mainland China coastal radars for Typhoon Meranti (2010) at landfall. J. Geophys. Res. Atmos. 2012, 117, D0610. [Google Scholar] [CrossRef]
- Li, X.; Ming, J.; Wang, Y.; Zhao, K.; Xue, M. Assimilation of T-TREC-retrieved wind data with WRF 3DVAR for the short-term forecasting of typhoon Meranti (2010) near landfall. J. Geophys. Res. Atmos. 2013, 118, 10361–10375. [Google Scholar] [CrossRef]
- Xu, D.; Chen, J.; Li, H.; Shen, F.; He, Z. The impact of radar radial velocity data assimilation using variational and EnKF systems on the forecast of Super Typhoon Hato (2017) with Rapid Intensification. Atmos. Res. 2025, 314, 107748. [Google Scholar] [CrossRef]
- Zhao, K.; Lin, Q.; Lee, W.-C.; Qiang Sun, Y.; Zhang, F. Doppler Radar Analysis of Triple Eyewalls in Typhoon Usagi (2013). Bull. Am. Meteorol. Soc. 2016, 97, 25–30. [Google Scholar] [CrossRef]
- Shimada, U.; Kubota, H.; Yamada, H.; Cayanan, E.O.; Hilario, F.D. Intensity and Inner-Core Structure of Typhoon Haiyan (2013) near Landfall: Doppler Radar Analysis. Mon. Weather Rev. 2018, 146, 583–597. [Google Scholar] [CrossRef]
- Liou, Y.-C.; Wang, T.-C.; Lee, W.-C.; Chang, Y.-J. The Retrieval of Asymmetric Tropical Cyclone Structures Using Doppler Radar Simulations and Observations with the Extended GBVTD Technique. Mon. Weather Rev. 2006, 134, 1140–1160. [Google Scholar] [CrossRef]
- Jou, B.J.-D.; Lee, W.-C.; Liu, S.-P.; Kao, Y.-C. Generalized VTD Retrieval of Atmospheric Vortex Kinematic Structure. Part I: Formulation and Error Analysis. Mon. Weather Rev. 2008, 136, 995–1012. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, K.; Lee, W.-C.; Jou, B.J.-D.; Xue, M. The Gradient Velocity Track Display (GrVTD) Technique for Retrieving Tropical Cyclone Primary Circulation from Aliased Velocities Measured by Single-Doppler Radar. J. Atmos. Ocean. Technol. 2012, 29, 1026–1041. [Google Scholar] [CrossRef]
- Rinehart, R.E.; Garvey, E.T. Three-dimensional storm motion detection by conventional weather radar. Nature 1978, 273, 287–289. [Google Scholar] [CrossRef]
- Tuttle, J.; Gall, R. A Single-Radar Technique for Estimating the Winds in Tropical Cyclones. Bull. Am. Meteorol. Soc. 1999, 80, 653–668. [Google Scholar] [CrossRef]
- Harasti, P.R.; McAdie, C.J.; Dodge, P.P.; Lee, W.-C.; Tuttle, J.; Murillo, S.T.; Marks, F.D. Real-Time Implementation of Single-Doppler Radar Analysis Methods for Tropical Cyclones: Algorithm Improvements and Use with WSR-88D Display Data. Weather Forecast. 2004, 19, 219–239. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, K.; Wu, D. The T-TREC technique for retrieving the winds of landfalling typhoon in China. Acta Meteorol. Sin. 2010, 25, 114–124. [Google Scholar] [CrossRef]
- Wang, M.; Xue, M.; Zhao, K.; Dong, J. Assimilation of T-TREC-Retrieved Winds from Single-Doppler Radar with an Ensemble Kalman Filter for the Forecast of Typhoon Jangmi (2008). Mon. Weather Rev. 2014, 142, 1892–1907. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Ming, J.; Mei, H.; Wang, W.; Zhou, J. A combined radar data assimilation strategy of radial velocity and retrieved wind and its impact on the forecasting of tropical cyclone Chanthu (2010). Meteorol. Mon. 2016, 42, 649–663. [Google Scholar]
- Wang, M.; Xue, M.; Zhao, K. The impact of T-TREC-retrieved wind and radial velocity data assimilation using EnKF and effects of assimilation window on the analysis and prediction of Typhoon Jangmi (2008). J. Geophys. Res. Atmos. 2016, 121, 259–277. [Google Scholar] [CrossRef]
- Helmus, J.J.; Collis, S.M. The Python ARM Radar Toolkit (Py-ART), a Library for Working with Weather Radar Data in the Python Programming Language. J. Open Res. Softw. 2016, 4, 25. [Google Scholar] [CrossRef]
- Shen, F.; Min, J.; Xu, D. Assimilation of radar radial velocity data with the WRF Hybrid ETKF–3DVAR system for the prediction of Hurricane Ike (2008). Atmos. Res. 2016, 169, 127–138. [Google Scholar] [CrossRef]
- Chang, P.-L.; Jong-Dao Jou, B.; Zhang, J. An Algorithm for Tracking Eyes of Tropical Cyclones. Weather Forecast. 2009, 24, 245–261. [Google Scholar] [CrossRef]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s Spectral Statistical-Interpolation Analysis System. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Shen, F.; Song, L.; He, Z.; Xu, D.; Chen, J.; Huang, L. Impacts of adding hydrometeor control variables on the radar reflectivity data assimilation for the 6–8 August 2018 mesoscale convective system case. Atmos. Res. 2023, 295, 107012. [Google Scholar] [CrossRef]
- Shen, F.; Song, L.; Li, H.; He, Z.; Xu, D. Effects of different momentum control variables in radar data assimilation on the analysis and forecast of strong convective systems under the background of northeast cold vortex. Atmos. Res. 2022, 280, 106415. [Google Scholar] [CrossRef]
- Bian, H.; Min, J.; Shen, F. Application of Radar Radial Velocity Data Assimilation in the Forecasts of Typhoon Linfa Based on Different Horizontal Length Scale Factors. Atmosphere 2023, 14, 582. [Google Scholar] [CrossRef]



| Number | Name | Schemes |
|---|---|---|
| 1 | CTRL | No data assimilation |
| 2 | ExpTTREC | T-TREC-retrieved wind data assimilation |
| 3 | ExpTTREC_IS | T-TREC-IS-retrieved wind data assimilation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, H.; Fei, H.; Mao, Y.; Li, C.; Shu, A.; Chen, J. Improving the Assimilation of T-TREC-Retrieved Wind Fields with Iterative Smoothing Constraints During Typhoon Linfa. Remote Sens. 2025, 17, 2821. https://doi.org/10.3390/rs17162821
Bian H, Fei H, Mao Y, Li C, Shu A, Chen J. Improving the Assimilation of T-TREC-Retrieved Wind Fields with Iterative Smoothing Constraints During Typhoon Linfa. Remote Sensing. 2025; 17(16):2821. https://doi.org/10.3390/rs17162821
Chicago/Turabian StyleBian, Huimin, Haiyan Fei, Yuqing Mao, Cong Li, Aiqing Shu, and Jiajun Chen. 2025. "Improving the Assimilation of T-TREC-Retrieved Wind Fields with Iterative Smoothing Constraints During Typhoon Linfa" Remote Sensing 17, no. 16: 2821. https://doi.org/10.3390/rs17162821
APA StyleBian, H., Fei, H., Mao, Y., Li, C., Shu, A., & Chen, J. (2025). Improving the Assimilation of T-TREC-Retrieved Wind Fields with Iterative Smoothing Constraints During Typhoon Linfa. Remote Sensing, 17(16), 2821. https://doi.org/10.3390/rs17162821







