Reproduction of Smaller Wildfire Perimeters Observed by Polar-Orbiting Satellites Using ROS Adjustment Factors and Wildfire Spread Simulators
Abstract
1. Introduction
2. Grouping Tree Species into Fuel Models with Similar Fire Behavior
2.1. Fire Behavior Fuel Models
2.2. Fuel Model Classification and Mapping for Major Tree Species in South Korea
3. ROS Adjustment Factor Derivation for Reproducing Wildfire Perimeters Observed by Polar-Orbiting Satellites
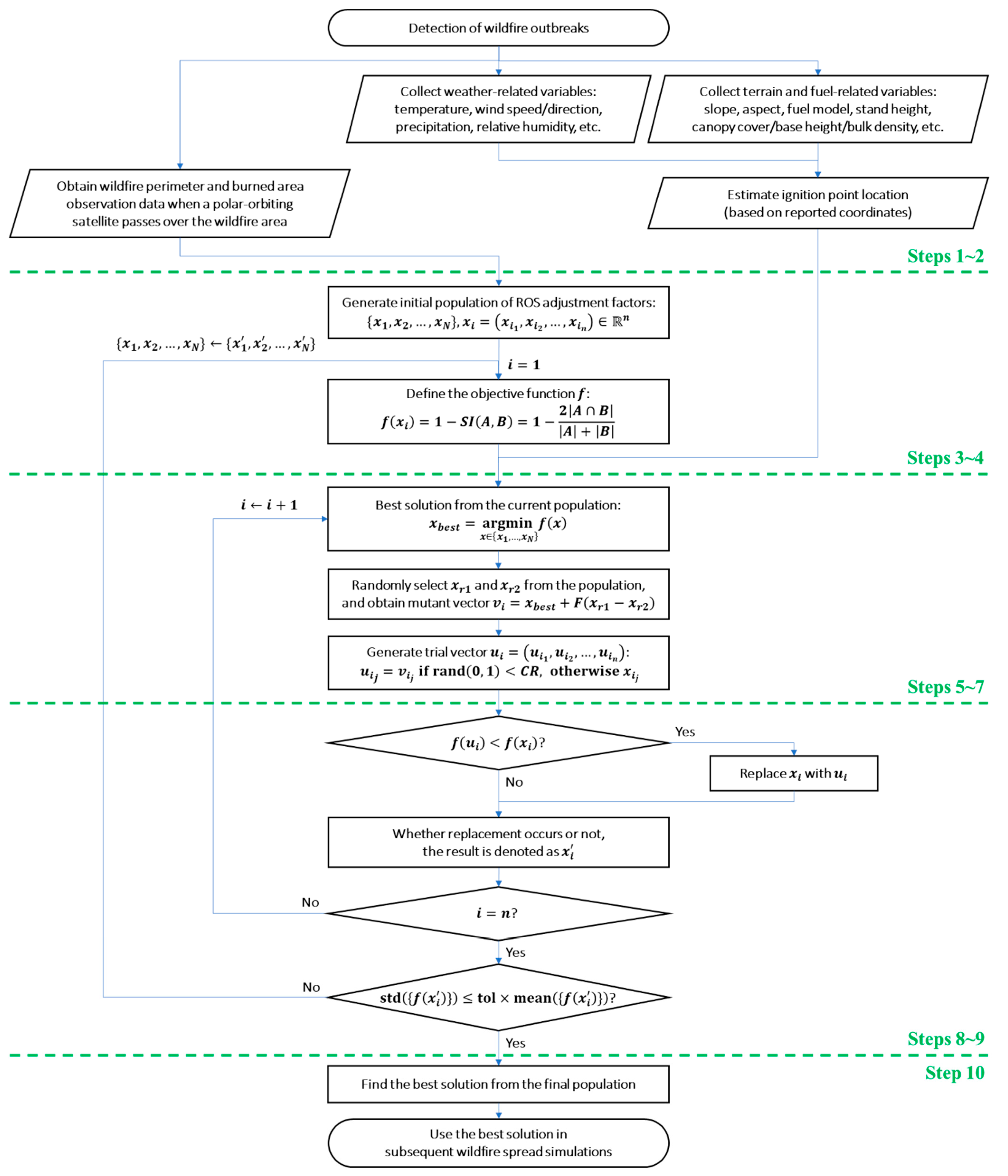
3.1. Differential Evolution-Based ROS Adjustment Factor Derivation Algorithm
- [Step 1]
- Upon wildfire ignition, the following data required for running the wildfire spread simulation are collected in advance:
- ➢
- Terrain and fuel-related variables, including elevation, slope, aspect, fuel model, stand height, canopy cover, canopy base height, canopy bulk density, and foliar moisture content
- ➢
- Weather-related variables consist of temperature, relative humidity, hourly precipitation amount, wind speed and direction, fuel moisture, and cloud cover percentage
- ➢
- Estimated ignition point location (primarily based on the reported location, but terrain, fuel, and weather variables may also inform the estimation)
- [Step 2]
- When a polar-orbiting satellite passes over the wildfire area, obtain wildfire perimeter and burned area observation data.
- [Step 3]
- DE Initialization: An initial population of ROS adjustment factors is generated, consisting of vectors of dimension : . Here, denotes the population size, and is the number of elements in the ROS adjustment factor. A discussion on the appropriate choice of is provided in Section 3.2.
- [Step 4]
- The objective function is defined as:where denotes the Sørensen index, is the burned area observed by the polar-orbiting satellite in Step 2, and is the predicted burned area produced by the wildfire spread simulation using the ROS adjustment factor [35].
- [Step 5]
- The best solution from the current population is selected as . Then, Steps 6 through 8 are applied to each , for .
- [Step 6]
- DE Mutation: Randomly select two individuals and from the population, and compute the mutant vector where is the differential weight. The selection of an appropriate value for is discussed in Section 3.2.
- [Step 7]
- DE Crossover: Given vectors and , a trial vector is generated as follows:This process is independently applied for each index . That is, each element of the trial vector is selected from the mutant vector with probability , or from the original vector with probability . The parameter denotes the crossover probability. A detailed discussion of appropriate values for is provided in Section 3.2.
- [Step 8]
- DE Selection: If the trial vector has a better objective function value than , i.e., if , then is replaced by . Whether replacement occurs or not, the result is denoted as .
- [Step 9]
- If the updated population satisfies the stopping criterion, the algorithm proceeds to Step 10. Otherwise, the updated population is used as the new population, and the process returns to Step 5. The stopping condition is defined as:where is a predefined coefficient used to determine whether the population has sufficiently converged, by evaluating the standard deviation of fitness values relative to their mean. The optimal value of can vary substantially depending on the wildfire spread prediction results, the characteristics of the objective function, and the structure of the solution space. Consequently, it should be selected based on empirical tuning appropriate to the problem context.
- [Step 10]
- Once the stopping criterion is met, the final ROS adjustment factor is selected by applying the same procedure as in Step 5 to the final population. The selected optimal ROS adjustment factor is then used in subsequent wildfire spread simulations.
3.2. Considerations in Implementing the Proposed Algorithm
4. Numerical Investigations
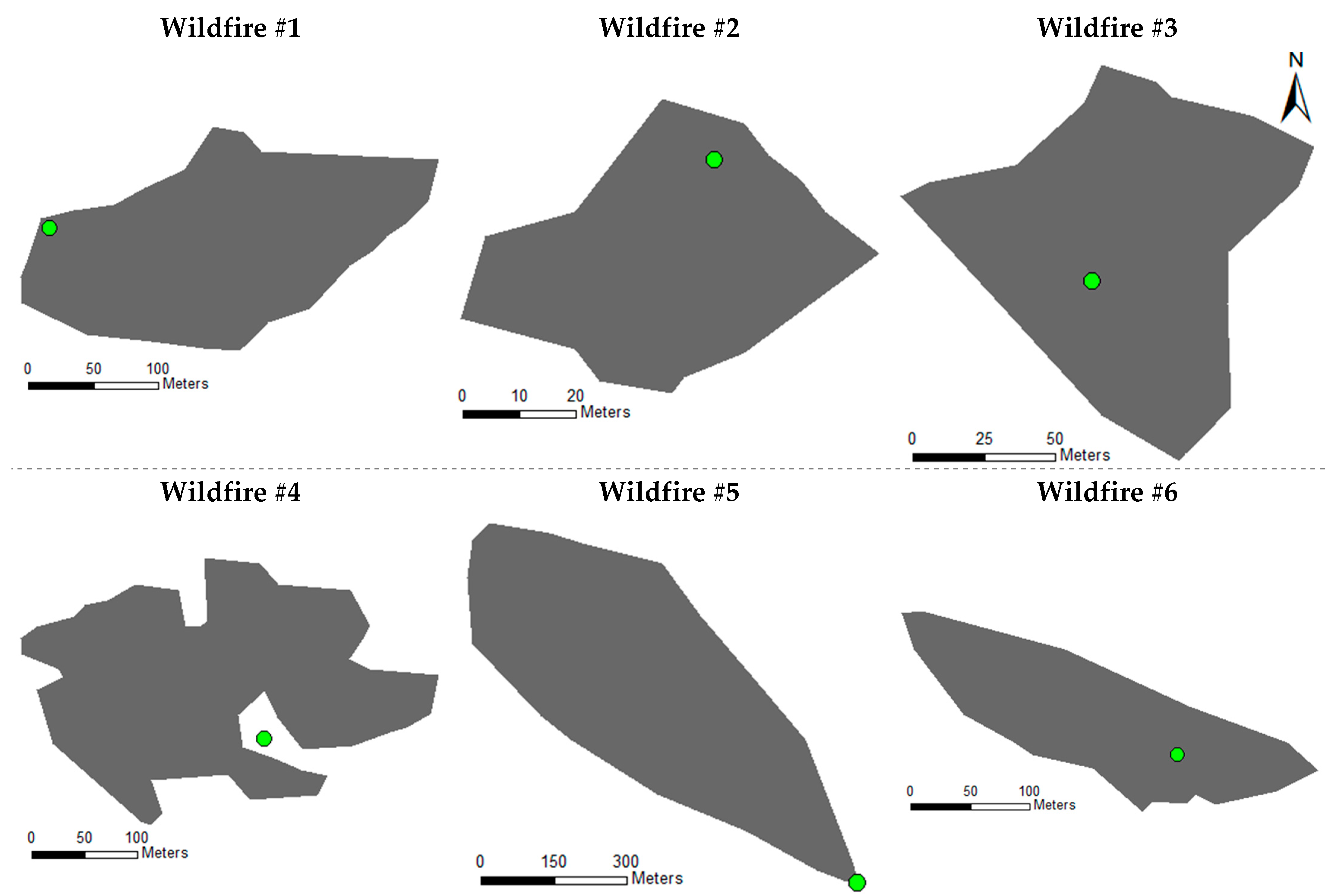
4.1. Description of Observation and Input Data Used for Algorithm Validation
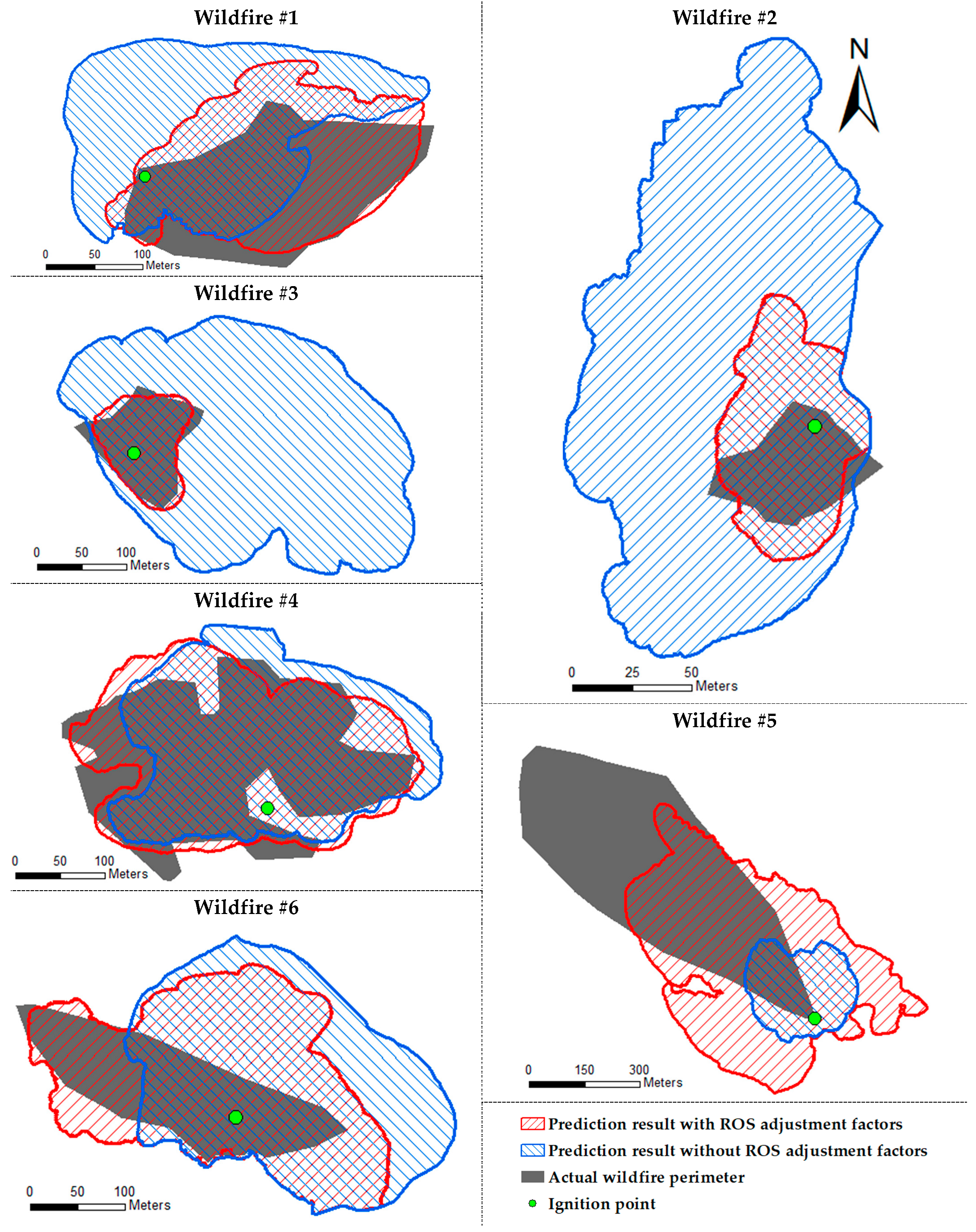
4.2. Derived ROS Adjustment Factors and Accuracy Comparison of Wildfire Spread Predictions
4.3. Limitations and Outlook
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ROS | Rate of Spread |
| FBFM | Fire Behavior Fuel Model |
| EnKF | Ensemble Kalman Filter |
| DE | Differential Evolution |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
References
- CAL FIRE. Top 20 Largest California Wildfires. Available online: https://fire.ca.gov/our-impact/statistics (accessed on 11 March 2025).
- AccuWeather. AccuWeather Estimates More Than $250 Billion in Damages and Economic Loss from LA Wildfires. Available online: https://www.accuweather.com/en/weather-news/accuweather-estimates-more-than-250-billion-in-damages-and-economic-loss-from-la-wildfires/1733821 (accessed on 11 March 2025).
- Chang, D.Y.; Jeong, S.; Park, C.E.; Park, H.; Shin, J.; Bae, Y.; Park, H.; Park, C.R. Unprecedented wildfires in Korea: Historical evidence of increasing wildfire activity due to climate change. Agric. For. Meteorol. 2024, 348, 109920. [Google Scholar] [CrossRef]
- Finney, M.A. FARSITE, Fire Area Simulator—Model Development and Evaluation; No. 4; USDA Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 1998.
- Tymstra, C.; Bryce, R.W.; Wotton, B.M.; Taylor, S.W.; Armitage, O.B. Development and Structure of Prometheus: The Canadian Wildland Fire Growth Simulation Model; Information Report. NOR-X-417; Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre: Edmonton, AB, Canada, 2010.
- Rothermel, R.C.; Rinehart, G.C. Field Procedures for Verification and Adjustment of Fire Behavior Predictions; General Technical Report INT-142; USDA Forest Service: Ogden, UT, USA, 1983.
- Evensen, G. Data Assimilation: The Ensemble Kalman Filter, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Mandel, J.; Bennethum, L.S.; Beezley, J.D.; Coen, J.L.; Douglas, C.C.; Kim, M.; Vodacek, A. A wildland fire model with data assimilation. Math. Comput. Simul. 2008, 79, 584–606. [Google Scholar] [CrossRef]
- Mandel, J.; Beezley, J.D.; Kondratenko, V.Y. Fast Fourier transform ensemble Kalman filter with application to a coupled atmosphere-wildland fire model. In Computational Intelligence in Business and Economics; World Scientific: Singapore, 2010; pp. 777–784. [Google Scholar]
- Rochoux, M.C.; Ricci, S.; Lucor, D.; Cuenot, B.; Trouvé, A. Towards predictive data-driven simulations of wildfire spread–Part I: Reduced-cost Ensemble Kalman Filter based on a Polynomial Chaos surrogate model for parameter estimation. Nat. Hazards Earth Syst. Sci. 2014, 14, 2951–2973. [Google Scholar] [CrossRef]
- Zhou, T.; Ding, L.; Ji, J.; Li, L.; Huang, W. Ensemble transform Kalman filter (ETKF) for large-scale wildland fire spread simulation using FARSITE tool and state estimation method. Fire Saf. J. 2019, 105, 95–106. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, Q.; Zhu, J.; Xu, L.; Zhang, Y. Forest fire spread prediction and assimilation using the deterministic Ensemble Kalman Filter. Fire Technol. 2025, 61, 2467–2492. [Google Scholar] [CrossRef]
- Khanmohammadi, S.; Arashpour, M.; Golafshani, E.M.; Cruz, M.G.; Rajabifard, A.; Bai, Y. Prediction of wildfire rate of spread in grasslands using machine learning methods. Environ. Model. Softw. 2022, 156, 105507. [Google Scholar] [CrossRef]
- Cardil, A.; Tapia, V.M.; Monedero, S.; Quiñones, T.; Little, K.; Stoof, C.R.; Ramirez, J.; de-Miguel, S. Characterizing the rate of spread of large wildfires in emerging fire environments of northwestern Europe using VIIRS active fire data. Nat. Hazards Earth Syst. Sci. 2023, 23, 361–373. [Google Scholar] [CrossRef]
- Pereira, J.; Mendes, J.; Júnior, J.S.; Viegas, C.; Paulo, J.R. A review of genetic algorithm approaches for wildfire spread prediction calibration. Mathematics 2022, 10, 300. [Google Scholar] [CrossRef]
- Pereira, J.; Mendes, J.; Júnior, J.S.; Viegas, C.; Paulo, J.R. Metaheuristic algorithms for calibration of two-dimensional wildfire spread prediction model. Eng. Appl. Artif. Intell. 2024, 136, 108928. [Google Scholar] [CrossRef]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; General Technical Report INT-115; USDA Forest Service: Ogden, UT, USA, 1972.
- Srivas, T.; de Callafon, R.A.; Crawl, D.; Altintas, I. Data assimilation of wildfires with fuel adjustment factors in FARSITE using ensemble Kalman filtering. Procedia Comput. Sci. 2017, 108, 1572–1581. [Google Scholar] [CrossRef]
- Zhou, T.; Ding, L.; Ji, J.; Yu, L.; Wang, Z. Combined estimation of fire perimeters and fuel adjustment factors in FARSITE for forecasting wildland fire propagation. Fire Saf. J. 2020, 116, 103167. [Google Scholar] [CrossRef]
- Yoo, S.; Kang, W.H.; Song, J. Wildfire spread prediction using geostationary satellite observation data and directional ROS adjustment factor. J. Environ. Manag. 2024, 372, 123358. [Google Scholar] [CrossRef] [PubMed]
- Anderson, H.E. Aids to Determining Fuel Models for Estimating Fire Behavior; The Bark Beetles, Fuels, and Fire Bibliography; USDA Forest Service: Ogden, UT, USA, 1982.
- Scott, J.H. Standard Fire Behavior Fuel Models: A Comprehensive Set for Use with Rothermel’s Surface Fire Spread Model; General Technical Report RMRS-GTR-153; USDA Forest Service: Ogden, UT, USA, 2005.
- Mohapatra, A.; Trinh, T. Early wildfire detection technologies in practice—A review. Sustainability 2022, 14, 12270. [Google Scholar] [CrossRef]
- Liu, X.; He, B.; Quan, X.; Yebra, M.; Qiu, S.; Yin, C.; Zhang, H. Near real-time extracting wildfire spread rate from Himawari-8 satellite data. Remote Sens. 2018, 10, 1654. [Google Scholar] [CrossRef]
- Yoo, S.; Song, J. Near-real-time updating of ROS adjustment factors based on geostationary satellite observation data. J. Environ. Manag. 2025, 389, 125857. [Google Scholar] [CrossRef]
- Japan Meteorological Agency. Himawari–8/9 Himawari Standard Data User’s Guide; Version 1.3; Japan Meteorological Agency: Tokyo, Japan, 2017.
- Valenti, J. GOES R Series Product Definition and Users’ Guide; NOAA: Silver Spring, MD, USA, 2018; Volume 4.
- Cardil, A.; Monedero, S.; Silva, C.A.; Ramirez, J. Adjusting the rate of spread of fire simulations in real-time. Ecol. Model. 2019, 395, 39–44. [Google Scholar] [CrossRef]
- Lee, B.; Chung, J.; Lee, S. Development of forest fire growth prediction algorithm for GIS applications. J. Korean For. Soc. 2002, 91, 812–819. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Korea Forest Research Institute. The 5th National Forest Inventory Report; Korea Forest Research Institute: Seoul, Republic of Korea, 2011.
- Korea Forest Service. Natural Hazard Prevention Research. Development of Forest Fire Behavior Prediction and Monitoring Techniques; Korea Forest Service: Daejeon, Republic of Korea, 2003.
- Burgan, R.E.; Rothermel, R.C. Behave: Fire Behavior Prediction and Fuel Modeling System, Fuel Subsystem; USDA Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1984; Volume 167.
- Jacob, P.; Kommuru, P.; Ruchitha, R.; Kuracha, H.; Taruni, T. Comparative study of MODIS, LANDSAT-8, SENTINEL-2B, and LISS-4 images for Precision farming using NDVI approach. E3S Web Conf. 2023, 405, 01004. [Google Scholar] [CrossRef]
- Sørensen, T. A Method of Establishing Groups of Equal Amplitude in Plant Sociology Based on Similarity of Species and Its Application to Analyses of the Vegetation on Danish Commons; Biologiske Skrifter; E. Munksgaard: Copenhagen, Denmark, 1948; Volume 5, pp. 1–34. [Google Scholar]
- Andre, J.; Siarry, P.; Dognon, T. An improvement of thle standard genetic algorithm fighting premature convergence in continuous optimization. Adv. Eng. Softw. 2001, 32, 49–60. [Google Scholar] [CrossRef]
- Vesterstrom, J.; Thomsen, R. A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems. In Proceedings of the 2004 Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; Volume 2, pp. 1980–1987. [Google Scholar]
- Piotrowski, A.P. Review of differential evolution population size. Swarm Evol. Comput. 2017, 32, 1–24. [Google Scholar] [CrossRef]
- Das, S.; Mullick, S.S.; Suganthan, P.N. Recent advances in differential evolution—An updated survey. Swarm Evol. Comput. 2016, 27, 1–30. [Google Scholar] [CrossRef]
- Korea Meteorological Administration. Weather Data Service. Available online: https://data.kma.go.kr/ (accessed on 20 May 2025).
- National Geographic Information Institute. Digital Elevation Model. Available online: https://map.ngii.go.kr/ms/map/NlipMap.do (accessed on 2 March 2025).

| Tools | Advantages | Disadvantages |
|---|---|---|
| Drones | Higher resolution data | Various constraints (weather, battery, range, etc.) |
| Airborne imaging | Higher resolution data; short observation time intervals | Insufficient infrared line scanners: may not be accessible where wildfire occur |
| Polar-orbiting satellite | High resolution data; fewer constraints | Longer observation time intervals |
| Geostationary satellite | Short observation time intervals; fewer constraints | Lower resolution data |
| Group | Model Number | Name |
|---|---|---|
| Grass | 1 | Short Grass |
| 2 | Timber Grass and Understory | |
| 3 | Tall Grass | |
| Shrub | 4 | Chaparral |
| 5 | Brush | |
| 6 | Dormant Brush | |
| 7 | Southern Rough | |
| Timber | 8 | Compact Timber Litter |
| 9 | Hardwood Litter | |
| 10 | Timber Understory | |
| Slash | 11 | Light Slash |
| 12 | Medium Slash | |
| 13 | Heavy Slash |
| Group | Code | Description |
|---|---|---|
| Age Class * | 1 | 1~10-year-old trees |
| 2 | 11~20-year-old trees | |
| 3 | 21~30-year-old trees | |
| 4 | 31~40-year-old trees | |
| 5 | 41~50-year-old trees | |
| 6 | 51-year-old trees | |
| Tree Species | 10~20 | Coniferous forest (Korean Pine, Japanese larch, Pitch pine, Black pine, etc.) |
| 30~49 | Deciduous broadleaf forest (Sawtooth oak, Mongolian oak, East Asian white birch, etc.) | |
| 60~68 | Evergreen broadleaf forest (Bamboo-leaf oak, Camphor tree, etc.) | |
| 77 | Mixed forest | |
| 78 | Bamboo forest | |
| 81~82 | Non-stocked forest land | |
| 91~99 | Non-forest |
| Fuel Model | Tree Species | Age Class Code | Fuel Load (kg/m2) | SV Ratio (m2/m3) | Fuel Depth (m) | |||
|---|---|---|---|---|---|---|---|---|
| 0 | Other Coniferous Trees, Bamboo (Bambusoideae) | 1 | 2 | 0.273 | 0.429 | 200 | 0.026 | 0.045 |
| 3 | 4 | 0.615 | 0.381 | 0.063 | 0.087 | |||
| 5 | 6 | 0.452 | 0.523 | 0.1002 | 0.1187 | |||
| 1 | Korean Red Pine (Pinus densiflora) | 1 | 2 | 0.273 | 0.429 | 200 | 0.026 | 0.045 |
| 3 | 4 | 0.615 | 0.381 | 0.063 | 0.087 | |||
| 5 | 6 | 0.452 | 0.523 | 0.1002 | 0.1187 | |||
| 2 | Korean pine (Pinus koraiensis) | 1 | 2 | 0.44 | 0.79 | 200 | 0.03 | 0.045 |
| 3 | 4 | 0.751 | 0.9713 | 0.045 | 0.055 | |||
| 5 | 6 | 1.1268 | 1.1823 | 0.0625 | 0.07 | |||
| 3 | Japanese larch (Larix kaempferi) | 1 | 2 | 0.257 | 0.678 | 200 | 0.047 | 0.054 |
| 3 | 4 | 0.904 | 1.26 | 0.071 | 0.08 | |||
| 5 | 6 | 1.5835 | 1.907 | 0.09 | 0.1 | |||
| 4 | Pitch Pine (Pinus rigida) | 1 | 2 | 0.321 | 0.764 | 200 | 0.03 | 0.04 |
| 3 | 4 | 0.735 | 1.0207 | 0.05 | 0.06 | |||
| 5 | 6 | 1.2277 | 1.4347 | 0.07 | 0.08 | |||
| 5 | Black Pine (Pinus thunbergii) | 1 | 2 | 0.273 | 0.429 | 200 | 0.026 | 0.045 |
| 3 | 4 | 0.615 | 0.381 | 0.063 | 0.087 | |||
| 5 | 6 | 0.452 | 0.523 | 0.1002 | 0.1187 | |||
| 6 | Other Broadleaf Trees, Maidenhair Tree (Ginkgo biloba) | 1 | 2 | 0.336 | 0.421 | 100 | 0.032 | 0.055 |
| 3 | 4 | 0.515 | 0.603 | 0.059 | 0.0757 | |||
| 5 | 6 | 0.6925 | 0.782 | 0.0892 | 0.1027 | |||
| 7 | Oak (Quercus) | 1 | 2 | 0.336 | 0.421 | 100 | 0.032 | 0.055 |
| 3 | 4 | 0.515 | 0.603 | 0.059 | 0.0757 | |||
| 5 | 6 | 0.6925 | 0.782 | 0.0892 | 0.1027 | |||
| 8 | Mixed forest | 1 | 2 | 0.305 | 0.411 | 150 | 0.3 | 0.05 |
| 3 | 4 | 0.524 | 0.6323 | 0.055 | 0.07 | |||
| 5 | 6 | 0.7418 | 0.8513 | 0.0825 | 0.095 | |||
| Wildfire Number | Ignition Time | Satellite Observation Time | Observed Wildfire Area | Ignition Point Coordinates (Latitude, Longitude) | Fuel Model Types |
|---|---|---|---|---|---|
| 1 | 21 December 2017 21:47 | 21 December 2017 23:50 | 3.3049 ha | 35.89695°N,129.44252°E | 0, 1, 6, 7 |
| 2 | 15 January 2021 23:31 | 16 January 2021 01:40 | 0.2097 ha | 36.92391°N,128.50760°E | 1, 7, 8 |
| 3 | 10 January 2022 17:30 | 10 January 2022 19:45 | 1.0044 ha | 34.91039°N,127.24240°E | 0, 1, 4, 6, 8 |
| 4 | 8 March 2022 20:01 | 8 March 2022 22:55 | 5.5534 ha | 35.56734°N,127.56235°E | 0, 1, 3, 4, 6, 7, 8 |
| 5 | 12 January 2023 12:47 | 12 January 2023 14:32 | 27.2442 ha | 35.88449°N,128.13178°E | 1, 2, 3, 6, 7, 8 |
| 6 | 3 March 2023 14:02 | 3 March 2023 17:56 | 2.5238 ha | 36.49859°N,126.89796°E | 1, 4, 6, 7, 8 |
| Wildfire Number | ROS Adjustment Factor of Each Fuel Model | Sørensen Index | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | w/ Factor | w/o Factor | |
| 1 | 4.918 | 0.106 | 3.366 | 1.413 | 0.786 | 0.366 | |||||
| 2 | 0.106 | 1.844 | 0.106 | 0.551 | 0.162 | ||||||
| 3 | 0.220 | 0.101 | 0.112 | 0.288 | 1.217 | 0.896 | 0.213 | ||||
| 4 | 0.602 | 2.204 | 0.611 | 0.103 | 1.108 | 0.386 | 2.042 | 0.821 | 0.734 | ||
| 5 | 1.869 | 2.862 | 2.402 | 0.178 | 4.988 | 3.612 | 0.471 | 0.145 | |||
| 6 | 2.516 | 1.189 | 0.105 | 0.101 | 1.010 | 0.591 | 0.359 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoo, S.; Kwon, C.; Cha, S. Reproduction of Smaller Wildfire Perimeters Observed by Polar-Orbiting Satellites Using ROS Adjustment Factors and Wildfire Spread Simulators. Remote Sens. 2025, 17, 2824. https://doi.org/10.3390/rs17162824
Yoo S, Kwon C, Cha S. Reproduction of Smaller Wildfire Perimeters Observed by Polar-Orbiting Satellites Using ROS Adjustment Factors and Wildfire Spread Simulators. Remote Sensing. 2025; 17(16):2824. https://doi.org/10.3390/rs17162824
Chicago/Turabian StyleYoo, Seungmin, Chungeun Kwon, and Sungeun Cha. 2025. "Reproduction of Smaller Wildfire Perimeters Observed by Polar-Orbiting Satellites Using ROS Adjustment Factors and Wildfire Spread Simulators" Remote Sensing 17, no. 16: 2824. https://doi.org/10.3390/rs17162824
APA StyleYoo, S., Kwon, C., & Cha, S. (2025). Reproduction of Smaller Wildfire Perimeters Observed by Polar-Orbiting Satellites Using ROS Adjustment Factors and Wildfire Spread Simulators. Remote Sensing, 17(16), 2824. https://doi.org/10.3390/rs17162824






