Modeling Primary Production in Temperate Forests Using Three-Dimensional Canopy Structural Complexity Metrics Derived from Airborne LiDAR Data
Abstract
1. Introduction
- (1)
- Derived a suite of 3D CSC metrics from high-density ALS data acquired by the NEON Airborne Observation Platform (AOP) [24] at seven forested NEON sites, spanning six ecoclimatic domains and three forest types: deciduous, evergreen, and mixed (deciduous and evergreen).
- (2)
- Evaluated how NPP, estimated from field inventories, relates to ALS-derived 3D CSC metrics using a novel modeling framework that combines partial least squares regression with recursive feature elimination.
2. Materials and Methods
2.1. Study Sites and Field Data
- Included greater than or equal to five plots with repeat diameter-at-breast-height (DBH) measurements over a 2–4-year period, overlapping with the year of AOP data collection, for calculating NPP.
- No major disturbances occurred during the NPP measurement window.
2.2. Field-Derived NPP
2.3. Airborne LiDAR Data Collection and Processing
2.4. 3D CSC Metrics for NPP Estimation
2.5. Sensitivity of 3D CSC Metrics to Grid Resolution
2.6. Modeling and Statistical Analyses
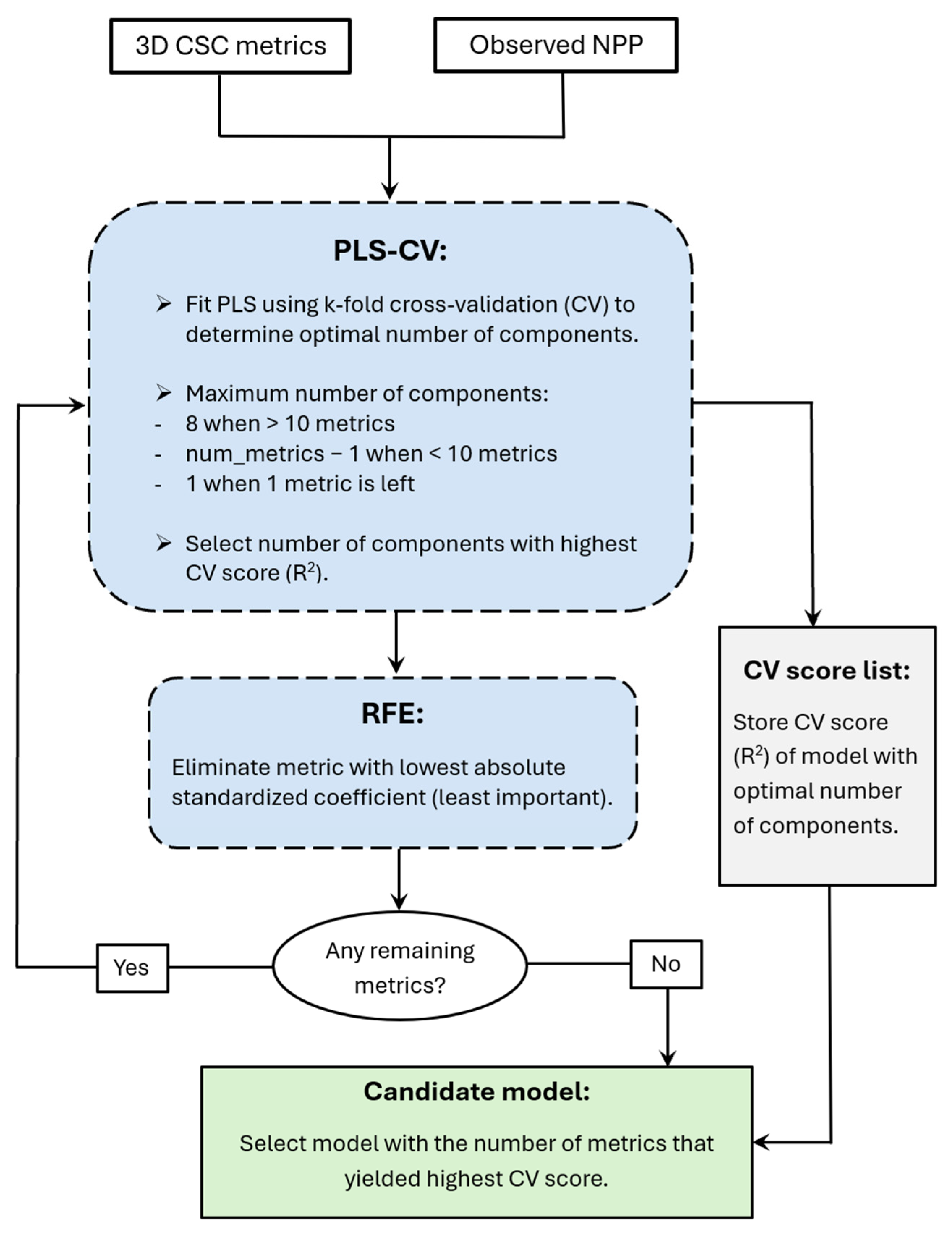
2.6.1. Combining PLS-CV and RFE to Identify Candidate Models
2.6.2. Selecting the Top Candidate Models
2.6.3. Stepwise Elimination of Statistically Insignificant Metrics from the Top Candidate Models
2.6.4. Assessing the Performance of Scale-Sensitive Metrics Selected in the Best Model at Other Highly Correlated Grid Resolutions
3. Results
3.1. NPP Estimation in Deciduous Plots
3.2. NPP Estimation in Evergreen Plots
3.3. NPP Estimation Across All Plots
4. Discussion
4.1. Ecological Significance of Strong CSC Predictors of Deciduous Forest NPP
4.2. Ecological Significance of Strong CSC Predictors of Evergreen Forest NPP
4.3. Explaining the Differences in CSC–NPP Relationships Between Deciduous and Evergreen Forests
4.4. Implications, Limitations, and Future Directions
5. Conclusions
- (1)
- Plot-level NPP in both deciduous and evergreen forests can be reliably estimated using a linear combination of three ALS-derived CSC metrics when modeled separately by forest type.
- (2)
- The best-performing NPP model for deciduous plots outperformed that for evergreen plots, indicating stronger biome-wide CSC-NPP relationships in deciduous forests.
- (3)
- ALS-derived 3D CSC metrics did not yield robust NPP estimation models when the two forest types were combined, suggesting that the structural attributes influencing NPP differ between deciduous and evergreen forests.
- (4)
- The accuracy of NPP predictions was sensitive to the spatial resolution at which some CSC metrics were derived, highlighting the importance of scale when linking canopy structure to primary production.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pretzsch, H. Forest dynamics, growth, and yield: A review, analysis of the present state, and perspective. In Forest Dynamics, Growth and Yield: From Measurement to Model; Spinger: Berlin/Heidelberg, Germany, 2008; pp. 1–39. [Google Scholar]
- Buotte, P.C.; Law, B.E.; Ripple, W.J.; Berner, L.T. Carbon sequestration and biodiversity co-benefits of preserving forests in the western United States. Ecol. Appl. 2020, 30, e02039. [Google Scholar] [CrossRef]
- Forest Owner Carbon and Climate Education (FOCCE). Carbon Accounting in Forest Management. 2023. Available online: https://extension.psu.edu/carbon-accounting-in-forest-management (accessed on 3 July 2024).
- Coops, N.C. Characterizing Forest Growth and Productivity Using Remotely Sensed Data. Curr. For. Rep. 2015, 1, 195–205. [Google Scholar] [CrossRef]
- Gough, C.M.; Atkins, J.W.; Fahey, R.T.; Hardiman, B.S. High Rates of Primary Production in Structurally Complex Forests. Ecology 2019, 100, e02864. [Google Scholar] [CrossRef]
- Hardiman, B.S.; Gough, C.M.; Halperin, A.; Hofmeister, K.L.; Nave, L.E.; Bohrer, G.; Curtis, P.S. Maintaining high rates of carbon storage in old forests: A mechanism linking canopy structure to forest function. For. Ecol. Manag. 2013, 298, 111–119. [Google Scholar] [CrossRef]
- Hardiman, B.S.; Bohrer, G.; Gough, C.M.; Vogel, C.S.; Curtis, P.S. The Role of Canopy Structural Complexity in Wood Net Primary Production of a Maturing Northern Deciduous Forest. Ecology 2011, 92, 1818–1827. [Google Scholar] [CrossRef] [PubMed]
- Atkins, J.W.; Fahey, R.T.; Hardiman, B.S.; Gough, C.M. Forest canopy structural complexity and light absorption relationships at the subcontinental scale. J. Geophys. Res. Biogeosci. 2018, 123, 1387–1405. [Google Scholar] [CrossRef]
- Ahl, D.E.; Gower, S.T.; Mackay, D.S.; Burrows, S.N.; Norman, J.M.; Diak, G.R. Heterogeneity of light use efficiency in a northern Wisconsin forest: Implications for modeling net primary production with remote sensing. Remote Sens. Environ. 2004, 93, 168–178. [Google Scholar] [CrossRef]
- Ishii, H.T.; Tanabe, S.-I.; Hiura, T. Exploring the relationships among canopy structure, stand productivity, and biodiversity of temperate forest ecosystems. For. Sci. 2004, 50, 342–355. [Google Scholar] [CrossRef]
- Duursma, R.A.; Makela, A. Summary models for light interception and light-use efficiency of non-homogeneous canopies. Tree Physiol. 2007, 27, 859–870. [Google Scholar] [CrossRef]
- Niinemets, U. Photosynthesis and resource distribution through plant canopies. Plant Cell Environ. 2007, 30, 1052–1071. [Google Scholar] [CrossRef]
- Walcroft, A.S.; Brown, K.J.; Schuster, W.S.; Tissue, D.T.; Turnbull, M.H.; Griffin, K.L.; Whitehead, D. Radiative transfer and carbon assimilation in relation to canopy architecture, foliage area distribution and clumping in a mature temperate rainforest canopy in New Zealand. Agric. For. Meteorol. 2005, 135, 326–339. [Google Scholar] [CrossRef]
- Niinemets, Ü. Optimization of foliage photosynthetic capacity in tree canopies: Towards identifying missing constraints. Tree Physiol. 2012, 32, 505–509. [Google Scholar] [CrossRef]
- Fahey, R.T.; Atkins, J.W.; Gough, C.M.; Hardiman, B.S.; Nave, L.E.; Tallant, J.M.; Nadehoffer, K.J.; Vogel, C.; Scheuermann, C.M.; Stuart-Haëntjens, E.; et al. Defining a spectrum of integrative trait-based vegetation canopy structural types. Ecol. Lett. 2019, 22, 2049–2059. [Google Scholar] [CrossRef] [PubMed]
- Jarron, L.R.; Coops, N.C.; MacKenzie, W.H.; Tompalski, P.; Dykstra, P. Detection of sub-canopy forest structure using airborne LiDAR. Remote Sens. Environ. 2020, 244, 111770. [Google Scholar] [CrossRef]
- LaRue, E.A.; Hardiman, B.S.; Elliott, J.M.; Fei, S. Structural diversity as a predictor of ecosystem function. Environ. Res. Lett. 2019, 14, 114011. [Google Scholar] [CrossRef]
- Liu, X.; Feng, Y.; Hu, T.; Luo, Y.; Zhao, X.; Wu, J.; Maeda, E.E.; Ju, W.; Liu, L.; Guo, Q.; et al. Enhancing ecosystem productivity and stability with increasing canopy structural complexity in global forests. Sci. Adv. 2024, 10, eadl1947. [Google Scholar] [CrossRef]
- Hayek, M.N.; Wehr, R.; Longo, M.; Hutyra, L.R.; Wiedemann, K.; Munger, J.W.; Bonal, D.; Saleska, S.R.; Fitzjarrald, D.R.; Wofsy, S.C. A novel correction for biases in forest eddy covariance carbon balance. Agric. For. Meteorol. 2018, 250–251, 90–101. [Google Scholar] [CrossRef]
- Skovsgaard, J.P.; Vanclay, J.K. Forest site productivity: A review of the evolution of dendrometric concepts for even-aged stands. Forestry 2008, 81, 13–31. [Google Scholar] [CrossRef]
- Holopainen, M.; Vastaranta, M.; Haapanen, R.; Yu, X.; Hyyppä, J.; Kaartinen, H.; Viitala, R.; Hyyppä, H. Site-type estimation using airborne laser scanning and stand register data. Photogramm. J. Finl. 2010, 22, 16–32. [Google Scholar]
- Maselli, F.; Mari, R.; Chiesi, M. Use of lidar data to simulate forest net primary production. Int. J. Remote Sens. 2012, 34, 2487–2501. [Google Scholar] [CrossRef]
- Tompalski, P.; Coops, N.C.; White, J.C.; Wulder, M.A.; Pickell, P.D. Estimating Forest Site Productivity Using Airborne Laser Scanning Data and Landsat Time Series. Can. J. Remote Sens. 2015, 41, 232–245. [Google Scholar] [CrossRef]
- Kampe, T.U.; Johnson, B.R.; Kuester, M.; Keller, M. NEON: The first continental-scale ecological observatory with airborne remote sensing of vegetation canopy biochemistry and structure. J. Appl. Remote Sens. 2010, 4, 043510. [Google Scholar] [CrossRef]
- Riegl LMS-Q780 Data Sheet, Riegl. 2015. Available online: https://www.rieglusa.com/wp-content/uploads/lms-q780-datasheet.pdf (accessed on 30 October 2024).
- Fotis, A.T.; Morin, T.H.; Fahey, R.T.; Hardiman, B.S.; Bohrer, G.; Curtis, P.S. Forest structure in space and time: Biotic and abiotic determinants of canopy complexity and their effects on net primary productivity. Agric. For. Meteorol. 2018, 250, 181–191. [Google Scholar] [CrossRef]
- Gough, C.M.; Atkins, J.W.; Fahey, R.T.; Curtis, P.S.; Bohrer, G.; Hardiman, B.S.; Hickey, L.J.; Nave, L.E.; Niedermaier, K.M.; Clay, C.; et al. Disturbance has variable effects on the structural complexity of a temperate forest landscape. Ecol. Indic. 2022, 140, 109004. [Google Scholar] [CrossRef]
- NEON (National Ecological Observatory Network). Site Management and Event Reporting (DP1.10111.001), RELEASE-2024. Available online: https://data.neonscience.org/data-products/DP1.10111.001/RELEASE-2024 (accessed on 15 July 2024).
- Correcting Land Cover Maps for NEON Field Sites. Available online: https://www.neonscience.org/impact/observatory-blog/correcting-land-cover-maps-neon-field-sites (accessed on 2 May 2025).
- Swanson, R. TOS Protocol and Procedure: PLT–Plot Establishment and Maintenance; NEON.DOC.001025; NEON (National Ecological Observatory Network): Boulder, CO, USA, 2023. [Google Scholar]
- NEON. Vegetation Structure (DP1.10098.001); RELEASE-2024; National Ecological Observatory Network (NEON): Boulder, CO, USA, 2024. [Google Scholar]
- Chojnacky, D.C.; Heath, L.S.; Jenkins, J.C. Updated generalized biomass equations for North American tree species. Forestry 2014, 87, 129–151. [Google Scholar] [CrossRef]
- Musinsky, J.; Goulden, T.; Wirth, G.; Leisso, N.; Krause, K.; Haynes, M.; Chapman, C. Spanning scales: The airborne spatial and temporal sampling design of the National Ecological Observatory Network. Methods Ecol. Evol. 2022, 13, 1866–1884. [Google Scholar] [CrossRef]
- NEON (National Ecological Observatory Network). Discrete Return LiDAR Point Cloud; DP1.30003.001; RELEASE-2024; NEON (National Ecological Observatory Network): Boulder, CO, USA, 2024; Available online: https://data.neonscience.org/data-products/DP1.30003.001/RELEASE-2024 (accessed on 18 July 2024).
- LAStools. Efficient LiDAR Processing Software, version 230901; Academic; rapidlasso GmbH: Gilching, Germany, 2023; Available online: http://rapidlasso.com/LAStools (accessed on 30 October 2024).
- All_NEON_TOS_Plots_V10. Available online: https://data.neonscience.org/documents/-/document_library_display/kV4WWrbEEM2s/view_file/3411434 (accessed on 28 April 2025).
- Roussel, J.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Meador, A.S.; Bourdon, J.; de Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Roussel, J.; Auty, D. Airborne LiDAR Data Manipulation and Visualization for Forestry Applications; R Package Version 4.1.2. 2024. Available online: https://cran.r-project.org/package=lidR (accessed on 24 October 2024).
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Atkins, J.W.; Bohrer, G.; Fahey, R.T.; Hardiman, B.S.; Morin, T.H.; Stovall, A.E.L.; Gough, C.M. Quantifying vegetation and canopy structural complexity from TLS data using the forestr r package. Methods Ecol. Evol. 2018, 9, 2057–2066. [Google Scholar] [CrossRef]
- Kane, V.R.; Bakker, J.D.; McGaughey, R.J.; Lutz, J.A.; Gersonde, R.F.; Franklin, J.F. Examining conifer canopy structural complexity across forest ages and elevations with LiDAR data. Can. J. For. Res. 2010, 40, 774–787. [Google Scholar] [CrossRef]
- Simonson, W.D.; Allen, H.D.; Coomes, D.A. Applications of airborne lidar for the assessment of animal species diversity. Methods Ecol. Evol. 2014, 5, 719–729. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 24 October 2024).
- Alveshere, B.C.; Siddiqui, T.; Krause, K.; van Aardt, J.A.; Gough, C.M. Hemlock woolly adelgid infestation influences canopy structural complexity and its relationship with primary production in a temperate mixed forest. For. Ecol. Manag. 2025, 586, 122698. [Google Scholar] [CrossRef]
- LaRue, E.A.; Rezendes, K.M.; Choi, D.H.; Wang, J.; Downing, A.G.; Fei, S.; Hardiman, B.S. Gradient surface metrics of ecosystem structural diversity and their relationship with productivity across macrosystems. Ecosphere 2025, 16, e70172. [Google Scholar] [CrossRef]
- Ratner, B. The correlation coefficient: Its values range between +1/−1, or do they? J. Target. Meas. Anal. Mark. 2009, 17, 139–142. [Google Scholar] [CrossRef]
- Wold, H. Soft modeling: The basic design and some extensions. Syst. Under Indirect. Obs. Part II 1982, 2, 36–37. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Abdi, H. Partial least squares regression and projection on latent structure regression (PLS Regression). Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 97–106. [Google Scholar] [CrossRef]
- Kelloway, E.K. Using Mplus for Structural Equation Modeling: A Researcher’s Guide; Sage Publications: Thousand Oaks, CA, USA, 2014. [Google Scholar]
- Hurvich, C.M.; Tsai, C.L. Regression and time series model selection in small samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- Concato, J.; Hartigan, J.A. P values: From suggestion to superstition. J. Investig. Med. 2016, 64, 1166–1171. [Google Scholar] [CrossRef]
- Morin, X.; Toigo, M.; Fahse, L.; Guillemot, J.; Cailleret, M.; Bertrand, R.; Cateau, E.; de Coligny, F.; García-Valdés, R.; Ratcliffe, S.; et al. More species, more trees: The role of tree packing in promoting forest productivity. J. Ecol. 2025, 113, 371–386. [Google Scholar] [CrossRef]
- de Conto, T.; Armston, J.; Dubayah, R. Characterizing the structural complexity of the Earth’s forests with spaceborne lidar. Nat. Commun. 2024, 15, 8116. [Google Scholar] [CrossRef]
- Hickey, L.J.; Atkins, J.; Fahey, R.T.; Kreider, M.R.; Wales, S.B.; Gough, C.M. Contrasting Development of Canopy Structure and Primary Production in Planted and Naturally Regenerated Red Pine Forests. Forests 2019, 10, 566. [Google Scholar] [CrossRef]
- U.S. Forest Service. Wind River Experimental Forest. 2025. Available online: https://research.fs.usda.gov/pnw/forestsandranges/locations/windriver (accessed on 21 February 2025).
- Ishii, H.; Asano, S. The role of crown architecture, leaf phenology and photosynthetic activity in promoting complementary use of light among coexisting species in temperate forests. Ecol. Res. 2010, 25, 715–722. [Google Scholar] [CrossRef]
- Dormann, C.F.; Bagnara, M.; Boch, S.; Hinderling, J.; Janeiro-Otero, A.; Schäfer, D.; Schall, P.; Hartig, F. Plant species richness increases with light availability, but not variability, in temperate forests understorey. BMC Ecol. 2020, 20, 43. [Google Scholar] [CrossRef] [PubMed]
- Tompalski, P.; Coops, N.C.; White, J.C.; Goodbody, T.R.; Hennigar, C.R.; Wulder, M.A.; Socha, J.; Woods, M.E. Estimating Changes in Forest Attributes and Enhancing Growth Projections: A Review of Existing Approaches and Future Directions Using Airborne 3D Point Cloud Data. Curr. For. Rep. 2021, 7, 1–24. [Google Scholar] [CrossRef]
- Yi, X.; Wang, N.; Ren, H.; Yu, J.; Hu, T.; Su, Y.; Mi, X.; Guo, Q.; Ma, K. From canopy complementarity to asymmetric competition: The negative relationship between structural diversity and productivity during succession. J. Ecol. 2021, 110, 457–465. [Google Scholar] [CrossRef]
- Hicke, J.A.; Allen, C.D.; Desai, A.R.; Dietze, M.C.; Hall, R.J.; Hogg, E.H.; Kashian, D.M.; Moore, D.J.; Raffa, K.F.; Sturrock, R.N.; et al. Effects of biotic disturbances on forest carbon cycling in the United States and Canada. Glob. Change Biol. 2012, 18, 7–34. [Google Scholar] [CrossRef]
- Juchheim, J.; Ammer, C.; Schall, P.; Seidel, D. Canopy space filling rather than conventional measures of structural diversity explains productivity of beech stands. For. Ecol. Manag. 2017, 395, 19–26. [Google Scholar] [CrossRef]
- Thorpe, A.S.; Barnett, D.T.; Elmendorf, S.C.; Hinckley, E.L.S.; Hoekman, D.; Jones, K.D.; LeVan, K.E.; Meier, C.L.; Stanish, L.F.; Thibault, K.M. Introduction to the sampling designs of the National Ecological Observatory Network Terrestrial Observation System. Ecosphere 2016, 7, e01627. [Google Scholar] [CrossRef]
- NEON (National Ecological Observatory Network). Field Sites Map. Available online: https://neon.maps.arcgis.com/home/webmap/viewer.html?webmap=6396acd10aab4f0b83299911053dccfc (accessed on 31 October 2024).




| Site | NEON Ecoclimatic Domain | AOP Data Collection Year | NPP Measurement Period | Forest Types (Plot-Level NLCD Classes) | Mean Elevation (m) | Mean Annual Temperature (C) | Mean Annual Precipitation (mm) | Number of Qualifying Plots |
|---|---|---|---|---|---|---|---|---|
| BART | Northeast | 2022 | 2018–2022 | Deciduous, Evergreen, Mixed | 274 | 6.2 | 1325 | 5 (3 deciduous, 2 mixed) |
| GRSM | Appalachians and Cumberland Plateau | 2018 | 2017–2019 | Deciduous, Evergreen | 575 | 13.1 | 1375 | 11 (10 deciduous, 1 mixed) |
| ORNL | Appalachians and Cumberland Plateau | 2018 | 2018–2020 | Deciduous, Evergreen | 344 | 14.4 | 1340 | 5 (all deciduous) |
| RMNP | Southern Rockies and Colorado Plateau | 2020 | 2019–2022 | Evergreen | 2742 | 2.9 | 731 | 5 (all evergreen) |
| TALL | The Ozarks Complex | 2021 | 2018–2021 | Deciduous, Evergreen, Mixed | 166 | 7.2 | 1383 | 13 (7 deciduous, 6 mixed) |
| UNDE | The Great Lakes | 2020 | 2018–2022 | Deciduous, Mixed | 521 | 4.3 | 802 | 13 (7 deciduous, 6 mixed) |
| WREF | The Pacific Northwest | 2019 | 2019–2022 | Evergreen | 351 | 9.2 | 2225 | 5 (all evergreen) |
| CSC Metric | Description | Portion of Canopy | Computational Derivation |
|---|---|---|---|
| Rumple | Area of canopy surface divided by the projected ground surface. | Outer surface | The surface points (highest hit) of DTM-normalized 1 plot point clouds were filtered at 1–10 m resolution 2. The area of the triangulated surface created by the surface points was then divided by the area of the plot DTM using the rumple_index function. |
| Top Rugosity v1 (TopRug_v1) | Overall horizontal variation in maximum height. | Outer surface | The highest hits were gridded at 1–10 m resolution using the zmax function. V1, V2, and Moran’s I 3 [39] were computed from the grid (see footnote). |
| Top Rugosity v (TopRug_v2) | Transect-wise horizontal variation in maximum height. | ||
| Top Rugosity Moran’s I (TopRug_v2) | Spatial autocorrelation of maximum height. | ||
| Upper Rugosity v1 (UpperRug_v1) | Overall horizontal variation in 75th percentile height. | Upper | The 75th percentile heights of column hits were gridded at 1–10 m resolution using the zq75 function. V1, V2, and Moran’s I were computed from the grid (see footnote). |
| Upper Rugosity v2 (UpperRug_v2) | Transect-wise horizontal variation in 75th percentile height. | ||
| Upper Rugosity Moran’s I (UpperRug_MoranI) | Spatial autocorrelation of 75th percentile height. | ||
| Mean Rugosity v1 (MeanRug_v1) | Overall horizontal variation in mean height. | Middle | The mean heights of column hits were gridded at 1–10 m resolution using the mean (Z) function. V1, V2, and Moran’s I were computed from the grid (see footnote). |
| Mean Rugosity v2 (MeanRug_v2) | Transect-wise horizontal variation in mean height. | ||
| Mean Rugosity Moran’s I (MeanRug_MoranI) | Spatial autocorrelation of mean height. | ||
| Lower Rugosity v1 (LowerRug_v1) | Overall horizontal variation in 25th percentile height. | Lower | The 25th percentile heights of column hits were gridded at 1–10 m resolution using the zq25 function. V1, V2, and Moran’s I were computed from the grid (see footnote). |
| Lower Rugosity v2 (LowerRug_v2) | Transect-wise horizontal variation in 25th percentile height. | ||
| Lower Rugosity Moran’s I (LowerRug_MoranI) | Spatial autocorrelation of 25th percentile height. | ||
| Canopy Rugosity v1 (CanRug_v1) | Overall horizontal variation in vertical variation of density adjusted mean vegetation height. | Entire | 1. The ground points were filtered out from the DTM-normalized plot point clouds. 2. The plot point clouds were converted into n × n × 1 m voxels, where n ranged from 1 to 10 m, and the number of hits in each voxel was tallied using the voxel_metrics function. 3. For each n × n m column, the number of hits in each voxel (z-bin) was normalized by the total number of hits in the column to obtain the vegetation area index (VAI) in each z-bin. 4. The standard deviation of density-adjusted mean leaf height (StdBin) was computed for each column by applying the same equations as the PCL derivation in the ForestR package [40]. 5. V1, V2, and Moran’s I were computed from the grid (see footnote). |
| Canopy Rugosity v2 (CanRug_v2) | Transect-wise horizontal variation in vertical variation of density adjusted mean vegetation height. | ||
| Canopy Rugosity Moran’s I (CanRug_MoranI) | Spatial autocorrelation of vertical variation of density adjusted mean vegetation height. | ||
| Canopy Heterogeneity v1 (CanHet_v1) | Overall horizontal variation in standard deviation of column vegetation height. | Entire | The standard deviations of column hits were gridded at 1–10 m resolution using the zsd function. V1, V2, and Moran’s I were computed from the grid (see footnote). |
| Canopy Heterogeneity v2 (CanHet_v2) | Transect-wise horizontal variation in standard deviation of column vegetation height. | ||
| Canopy Heterogeneity Moran’s I (CanHet_MoranI) | Spatial autocorrelation of standard deviation of column vegetation height. | ||
| Entropy variability v1 (EntVar_v1) | Overall horizontal variation in entropy of column height distribution. | Entire | 1. The ground points were filtered out from the plot point clouds. 2. The entropy of column height distribution was gridded at 1–10 m resolution using the zentropy function. 3. V1, V2, and Moran’s I were computed from the grid (see footnote). |
| Entropy variability v2 (EntVar_v2) | Transect-wise horizontal variation in entropy of column height distribution. | ||
| Entropy variability Moran’s I (EntVar_MoranI) | Spatial autocorrelation in entropy of column height distribution. | ||
| Percent Hits Above Mean Height variability v1 (Pz_abovemean_v1) | Overall horizontal variation in percentage of hits above mean column vegetation height. | Upper | 1. The ground points were filtered out from the plot point clouds. 2. The percentage of hits above mean column height was gridded at 1–10 m resolution using the pzabovemean function. 3. V1, V2, and Moran’s I were computed from the grid (see footnote). |
| Percent Hits Above Mean Height variability v2 (Pz_abovemean_v2) | Transect-wise horizontal variation in percentage of hits above mean column vegetation height. | ||
| Percent Hits Above Mean Height Moran’s I (Pz_abovemean_MoranI) | Spatial autocorrelation in percentage of hits above mean column vegetation height. |
| Model Ranking | No. of Metrics; No. of PLS Components | Calibration R2; CV R2 | Top Predictors (Up to Six) Prefixed by Their Standardized Coefficients | AICC |
|---|---|---|---|---|
| 1 | 4; 3 | 0.76; 0.71 | 1.54 CanRug_v1_1m 0.85 Rumple_10m −0.81 EntVar_v2_8m −0.61 EntVar_v1_8m | 18.9 |
| 2 | 8; 5 | 0.80; 0.74 | 1.44 CanRug_v1_1m 1.34 CanRug_v2_1m −0.97 CanHet_v2_9m −0.72 EntVar_v1_10m −0.58 EntVar_v2_10m 0.48 Rumple_10m | 29.1 |
| 3 | 6; 2 | 0.70; 0.61 | 0.79 CanRug_v2_1m 0.79 CanRug_v1_1m −0.58 EntVar_v1_10m −0.55 EntVar_v2_10m 0.49 Rumple_10m 0.47 CanHet_MoranI_9m | 31.5 |
| Forest Type | Calibration R2; CV R2 | No. of PLS Components; RMSE (Mg ha−1 year−1); RMSEr | Model Equation (NPP in Mg ha−1 year−1) | AICC; p-Value |
|---|---|---|---|---|
| Deciduous | 0.77; 0.71 | 2; 1.18; 11% | NPP = 4.69 + 1.56 CanRug_v1_1m − 1.42 EntVar_v2_8m + 0.83 Rumple_10m | 15.5; <0.01 |
| Evergreen | 0.76; 0.54 | 1; 0.85; 13% | NPP = 3.21 − 1.05 EntVar_v2_5m − 0.80 TopRug_v2_1m + 0.52 TopRug_MoranI_7m | 4.13; <0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddiqui, T.; Alveshere, B.; Gough, C.; van Aardt, J.; Krause, K. Modeling Primary Production in Temperate Forests Using Three-Dimensional Canopy Structural Complexity Metrics Derived from Airborne LiDAR Data. Remote Sens. 2025, 17, 2817. https://doi.org/10.3390/rs17162817
Siddiqui T, Alveshere B, Gough C, van Aardt J, Krause K. Modeling Primary Production in Temperate Forests Using Three-Dimensional Canopy Structural Complexity Metrics Derived from Airborne LiDAR Data. Remote Sensing. 2025; 17(16):2817. https://doi.org/10.3390/rs17162817
Chicago/Turabian StyleSiddiqui, Tahrir, Brandon Alveshere, Christopher Gough, Jan van Aardt, and Keith Krause. 2025. "Modeling Primary Production in Temperate Forests Using Three-Dimensional Canopy Structural Complexity Metrics Derived from Airborne LiDAR Data" Remote Sensing 17, no. 16: 2817. https://doi.org/10.3390/rs17162817
APA StyleSiddiqui, T., Alveshere, B., Gough, C., van Aardt, J., & Krause, K. (2025). Modeling Primary Production in Temperate Forests Using Three-Dimensional Canopy Structural Complexity Metrics Derived from Airborne LiDAR Data. Remote Sensing, 17(16), 2817. https://doi.org/10.3390/rs17162817










