A Hybrid RNN-CNN Approach with TPI for High-Precision DEM Reconstruction

Abstract

Digital elevation models (DEMs), as the fundamental unit of terrain morphology, are crucial for understanding surface processes and for land use planning. However, automated classification faces challenges due to inefficient terrain feature extraction from raw LiDAR point clouds and the limitations of traditional methods in capturing fine-scale topographic variations. To address this, we propose a novel hybrid RNN-CNN framework that integrates multi-scale Topographic Position Index (TPI) features to enhance DEM generation. Our approach first models voxelated LiDAR point clouds as spatially ordered sequences, using Recurrent Neural Networks (RNNs) to encode vertical elevation dependencies and Convolutional Neural Networks (CNNs) to extract planar spatial features. By incorporating TPI as a semantic constraint, the model learns to distinguish terrain structures at multiple scales. Residual connections refine feature representations to preserve micro-topographic details during DEM reconstruction. Extensive experiments in the complex terrains of Jiuzhaigou, China, demonstrate that our lightweight hybrid framework not only achieves excellent DEM reconstruction accuracy in complex terrains, but also improves computational efficiency by more than 20% on average compared to traditional interpolation methods, making it highly suitable for resource-constrained applications.

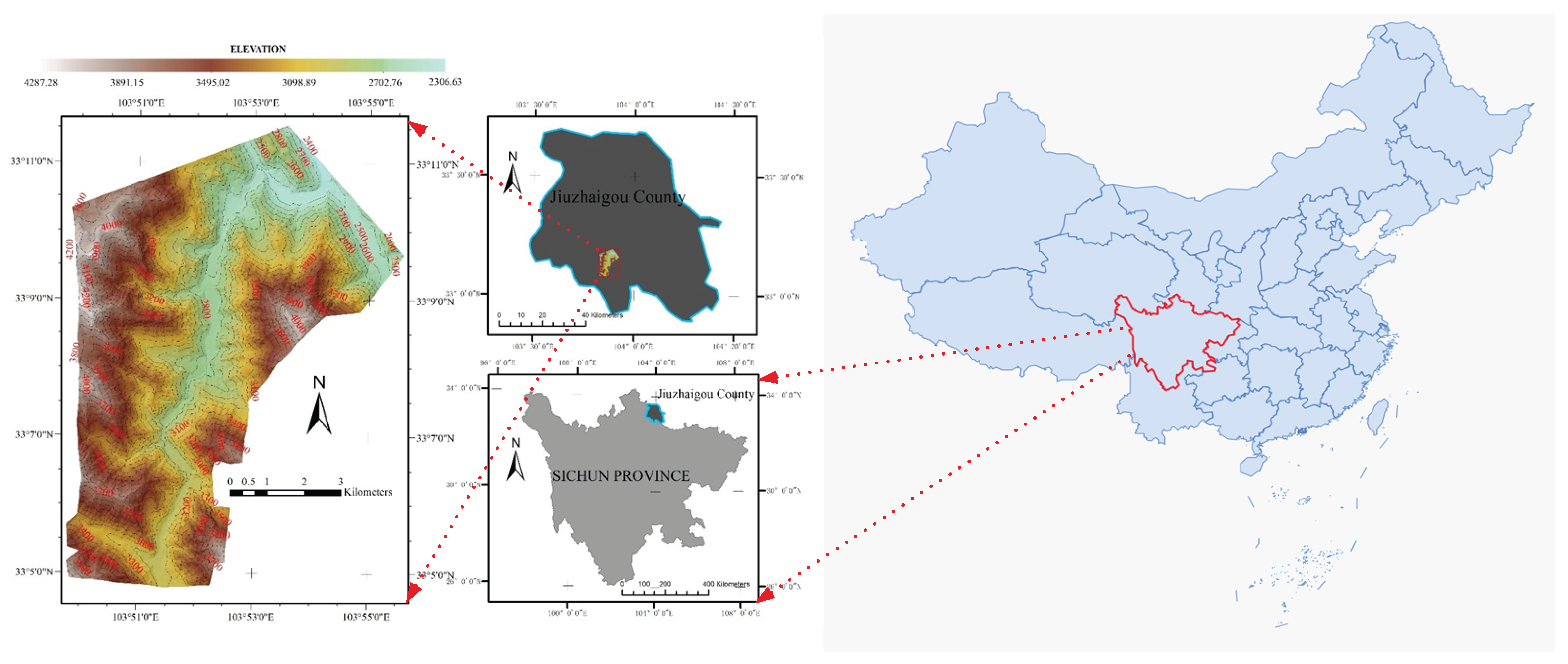
1. Introduction

Digital Elevation Models (DEMs) play a crucial role in various geospatial applications that significantly impact the study of the ecological environment and natural resources [1,2]. The accurate reconstruction of fine-scale DEMs from raw LiDAR point clouds is particularly critical, as these high-precision terrain representations serve as indispensable foundational datasets for a multitude of advanced applications. For instance, in geomorphological analysis [3,4], highly detailed DEMs enable precise landform extraction and classification, as well as the derivation of terrain covariates crucial for understanding geological processes and soil properties. In hydrological modeling [5,6], they are fundamental for accurate surface drainage mapping, water flow simulation, and delineating watersheds, which are vital for water resource management and flood risk assessment. Furthermore, for ecological and environmental studies [7,8], high-fidelity DEMs provide essential topographic context for analyzing fire regimes in forest ecosystems, and for developing robust ground filtering algorithms to process UAV LiDAR data in complex forested environments, facilitating more accurate vegetation and terrain analysis. Consequently, the development of automated algorithms capable of transforming raw point cloud data into high-precision DEMs is essential for improving the efficiency and accuracy of digital terrain modeling workflows [9].

Current methodologies for DEM reconstruction can be comprehensively categorized into three distinct and well-established main types: traditional interpolation methods, machine learning approaches, and deep learning techniques, each representing different philosophical approaches to terrain modeling and data processing. Traditional computational approaches, which include fundamental techniques such as nearest-neighbor interpolation [10] and linear interpolation methods, are characterized by their computational simplicity and operational efficiency. These conventional methods have been widely adopted due to their straightforward implementation and minimal computational overhead. However, despite their practical advantages, they frequently encounter significant difficulties when attempting to capture fine-scale terrain features and topographic details. Furthermore, these traditional methods demonstrate notable inadequacy when confronted with the complex task of handling heterogeneous landscapes that exhibit varying terrain characteristics and spatial complexity [11]. More sophisticated and technically advanced techniques have been developed to address some of these fundamental limitations. These enhanced approaches encompass a range of methodologies including morphological filtering techniques [12], slope-based filtering algorithms [13] that utilize specific threshold criteria for terrain classification, and comprehensive segmentation-based filtering algorithms [14] that partition the landscape into distinct topographic units. While these advanced techniques demonstrate measurably improved performance compared to their traditional counterparts, they continue to exhibit significant sensitivity to data noise and environmental interference. Additionally, these methods typically necessitate extensive manual preprocessing procedures and parameter tuning, which can be both time-consuming and require substantial domain expertise [15]. In response to these persistent limitations and the growing demand for more robust solutions, machine learning-based methodologies have progressively emerged as promising alternatives in the field of DEM generation. These innovative approaches fundamentally reframe the DEM generation process as a sophisticated regression problem that can be solved through statistical learning techniques. Advanced algorithms including decision trees with hierarchical splitting criteria, support vector machines (SVM) with kernel-based transformations [16], and random forests (RF) [17,18] ensemble methods have been successfully implemented to tackle this challenge. These machine learning approaches strategically leverage a diverse array of geospatial features including point density distributions, local slope characteristics, and comprehensive neighborhood statistical measures to inform their predictive models [19,20,21,22,23]. While these machine learning methods demonstrate notable improvements in adaptability to complex and varied terrain conditions, their practical effectiveness continues to be heavily dependent on a fundamental assumption. This critical assumption requires that training datasets and testing datasets maintain similar spatial distributions and geomorphological characteristics. Consequently, this dependency significantly restricts their generalizability across different geographic regions and terrain types. The performance of these methods exhibits considerable variation when applied across different geomorphic regions with distinct topographic signatures. Moreover, maintaining large-scale spatial consistency remains a persistent challenge that compromises the overall reliability of these approaches [24,25,26].

With the unprecedented rapid advancement and maturation of deep learning technologies in recent years, entirely new possibilities and opportunities have emerged for substantially improving model generalization capabilities and enhancing spatial coherence in DEM reconstruction tasks [27,28,29,30]. Convolutional Neural Networks (CNNs) [31,32], which represent a paradigm shift in spatial data processing, possess the remarkable ability to effectively capture complex two-dimensional spatial patterns and hierarchical feature representations. This inherent capability enables these networks to achieve superior learning of intricate topographic features and terrain characteristics [33]. Through this enhanced learning capacity, CNNs successfully overcome many of the fundamental limitations that have historically plagued traditional machine learning approaches in geospatial applications [34]. Although several pioneering research studies have demonstrated successful applications of deep learning methodologies to high-resolution DEM reconstruction tasks [35,36,37,38], most of these studies focus on reconstructing high-accuracy DEMs from low-accuracy DEMs. In contrast, only a few studies have achieved the derivation of highly accurate DEMs from digital surface models (DSMs) through sophisticated neural network architectures [39]. However, despite these encouraging developments and technological advances, the challenge of directly generating high-precision DEMs from raw LiDAR point clouds continues to represent a significant and largely unresolved technical challenge. This particular application requires handling the inherent complexity and irregular nature of point cloud data while maintaining the spatial accuracy and topographic fidelity necessary for high-quality DEM products.

To overcome these challenges, we propose an innovative hybrid RNN-CNN framework, which integrates multi-scale Topographic Position Index (TPI) features to achieve the coordinated optimization of high-precision DEM reconstruction. The TPI method is one of the most widely used techniques for landform classification. By calculating the difference in elevation between a given point and its surrounding area, TPI helps in identifying ridges, valleys, peaks, and other landforms. The approach proposed by Jennes [40] and Weiss [41] utilizes fixed neighborhood sizes to calculate the TPI and classify landforms. In order to obtain a more refined DEM, we introduced TPI. In summary, this study constructed a DEM reconstruction method that takes into account elevation dependency, planar spatial features, and multi-scale terrain semantic constraints by integrating the hybrid framework of RNN and CNN with multi-scale TPI features. It not only retains high-resolution terrain details, but also improves reconstruction accuracy through multi-scale landform structure learning, providing an innovative solution for high-precision DEM reconstruction.

Our method consists of three key contributions. We propose a hybrid RNN-CNN framework for end-to-end high-precision DEM reconstruction directly from raw LiDAR point clouds. This framework uniquely leverages RNNs to model vertical elevation dependencies within voxel columns and CNNs to capture planar spatial features, thereby effectively processing multi-dimensional terrain information. We innovatively integrate multi-scale TPI as a differentiable semantic constraint within the deep learning loss function, guiding the model to generate DEMs with enhanced geomorphometric fidelity and realistic terrain patterns across various scales. Extensive experiments conducted in the complex terrain of Jiuzhaigou demonstrate that our lightweight model achieves high-precision DEM reconstruction accuracy and improved computational efficiency by more than 20% on average compared to traditional interpolation methods, offering a practical solution for resource-constrained applications.

The structure of this paper is as follows:

• Section 2 introduces our data;
• Section 3 details the proposed method and its innovations;
• Section 4 presents the experimental setup and results, highlighting the advantages of our method over traditional approaches;
• Section 5 discusses the implications of our research findings and potential future directions.

2. Data Set

The study area (Figure 1) is located in the northern part of Jiuzhaigou County, Aba Tibetan and Qiang Autonomous Prefecture, in the southern Minshan Mountain Range of northwest Sichuan, China. Situated in the Jiuzhaigou National Nature Reserve, it is part of a transitional zone between the southeastern Tibetan Plateau and the Sichuan Basin. The region lies at the boundary of China’s first topographic step, where diverse geomorphological processes have occurred, including fluvial and glacial erosion, forming the predominant mountainous, hilly, and valley landscapes. The study area (103°50′15″–103°55′15″E, 33°4′45″–33°11′15″N) covers 65.9 km², with elevation varying between 2306 and 4306 m, and a relative elevation difference of 2000 m. Steep high mountains bound the eastern and western sides of the region, while a north–south trending high mountain canyon runs through the middle, creating five small alpine lakes in the northern part.

For our experimental evaluations, specific subsets of this high-resolution LiDAR dataset from Jiuzhaigou were selected to represent distinct terrain characteristics. Experiment 1 focused on data representing steep slope terrain, while Experiment 2 utilized data from undulating terrain. For both experiments, the corresponding ground truth DEMs used for training and evaluation were meticulously prepared from these same high-resolution LiDAR point clouds. These reference DEMs represent the bare-earth terrain, generated through established manual to remove non-ground features such as vegetation and buildings, followed by high-fidelity interpolation to a regular grid. This ensures that our model learns from precise terrain representations during the supervised training phase. The details of the LiDAR point cloud dataset for the Jiuzhaigou study area are presented in

Table 1. The details of the data in Jiuzhaigou.

Properties of the Data	Contents
Altitude of points	2306–4306 (m)
Points density	15 (pts/m2)
LiDAR scanner type	Riegl VG-1560i
Overlap of flight lines	25%
Horizontal accuracy	25–30 (cm)
Vertical accuracy	15 (cm)
Flight platform	Cessna 208B aircraft

.

3. Methodology

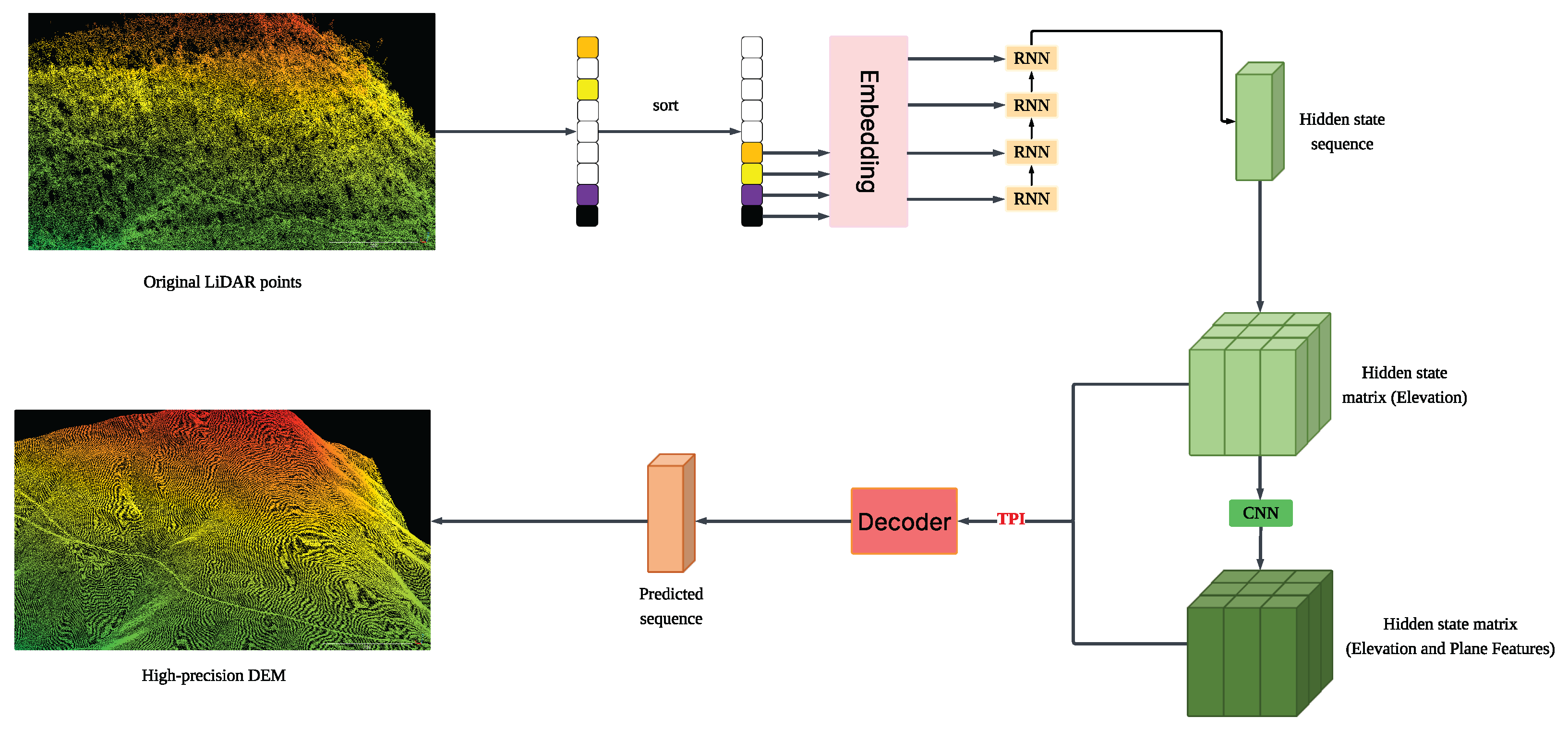
Our methodology is designed to transform raw LiDAR point clouds into high-fidelity DEMs through a lightweight design process. This comprehensive process encompasses voxelization, feature extraction leveraging both RNNs and CNNs, and the application of topographic supervision via TPI constraints. The process commences with denoising and voxelization of the raw input data, followed by ranking and embedding elevation values to capture vertical relationships. An RNN encodes the vertical context, while a CNN extracts planar spatial features, with the resulting representations fused via residual connections. The fused features are then decoded into a DEM under multi-scale TPI constraints, and the output is refined through a threshold-based median filtering post-processing step to enhance topographic fidelity. By integrating the sequential processing strengths of RNNs with the spatial feature extraction capabilities of CNNs, and enhancing the output with TPI-driven geomorphometric coherence. The complete workflow is illustrated in Figure 2.

3.1. Voxelization and Spatially Ordered Sequences

In processing the raw LiDAR point cloud, we first perform preprocessing to eliminate noise and outliers, ensuring a high-quality dataset for subsequent analysis. Following this, the denoised points are systematically mapped onto a regular voxel grid defined by a uniform spatial resolution. Each voxel is uniquely identified by its coordinates within this grid, and for every horizontal position (each $(i,j)$ grid cell on the 2D plane), we aggregate the elevation values of occupied voxels along the vertical dimension (along the k-axis, forming a vertical column of voxels). These elevation values are meticulously ordered to construct a sequence that encapsulates the vertical profile at each location. This spatially ordered sequence representation is particularly advantageous in managing regions with heterogeneous point densities, as it selectively retains valid elevation data, thereby preserving the intricate three-dimensional geometry of the terrain in an efficient and organized manner. Mathematically, the spatial resolution of the voxel grid is defined as $(\Delta x,\Delta y,\Delta z)$, with each voxel $V(i,j,k)$ centered at

$$x_i=x_{min}+i\Delta x,y_j=y_{min}+j\Delta y,z_k=z_{min}+k\Delta z$$

(1)

where $(x_{min},y_{min},z_{min})$ are the minimum coordinates of the point cloud and $i,j,k$ are integer indices. At each horizontal location $(i,j)$, we collect all occupied $z_k$ values and sort them in ascending order to form a variable-length sequence

$$S_{i,j}=\{z_{k_1},z_{k_2},\dots ,z_{k_m}\},k_1<k_2<\dots <k_m$$

(2)

where m is the number of nonempty voxels in that column. This “spatially ordered sequence” representation addresses the issue of empty voxels by only storing valid elevations and provides an efficient and organized way to capture the detailed vertical distribution of points, which is crucial for modeling the terrain’s vertical profile within our network.

3.2. Elevation Index Representation and Encoding

To address the inherent variability and noise in raw elevation measurements, we employ a rank-based transformation strategy. Specifically, each elevation within a sequence is converted into its positional rank relative to other elevations at the same horizontal location. This ordinal representation, denoted as $r_k$, emphasizes the vertical relationships among points, mitigating the influence of absolute elevation fluctuations and noise. Subsequently, these ranks are projected into a high-dimensional vector space through a learnable embedding mechanism, which encodes the structural dependencies and relational attributes of the elevation sequence. The embedding for a rank $r_k$ is denoted as $e_k$. These embedded vectors serve as the foundational input for the sequence encoding phase, enabling robust modeling of vertical patterns across the terrain. For each elevation $z_k$ in $S_{i,j}$, its rank is defined as

$$r_k=\mathrm{Rank}\left(z_k,S_{i,j}\right)$$

(3)

and its embedding ($e_k$) is

$$e_k=\varphi \left(r_k\right),k=1,\dots ,m$$

(4)

where $\varphi$ is a learnable embedding function (inspired by Natural Language Processing (NLP) [42] embedding techniques) that produces d-dimensional vectors capturing semantic relationships among elevation ranks. These embeddings serve as the input to our sequence encoder. Specifically, we utilize 300 distinct elevation rank levels, and the embedding dimension d is set to 32.

3.3. Three-Dimensional Feature Extraction Framework

Given the computational demands of directly applying three-dimensional convolutions across the entire voxel grid, we adopt a hybrid processing paradigm that judiciously separates the extraction of vertical and horizontal features. This dual-strategy approach is designed to optimize computational efficiency while aiming to capture critical three-dimensional spatial information, thereby facilitating the generation of accurate and detailed DEMs.

3.3.1. Sequential Feature Modeling with RNNs

At each horizontal grid position, the sequence of embedded elevation ranks is processed by a Gated Recurrent Unit (GRU)-based Recurrent Neural Network. The GRU architecture is particularly well-suited for this task, as it effectively captures long-range dependencies and local geometric nuances within the elevation sequence. By iteratively processing the sequence, the GRU distills a comprehensive representation of the vertical structure into its final hidden state. This compact encoding retains essential elevation details without requiring aggressive downsampling, thereby preserving the fidelity of the terrain’s vertical characteristics. For each voxel $(i,j,k)$, the hidden state (${\mathbf{h}}_{i,j}$) is obtained through the GRU’s processing of the embedding ($e_k$).

3.3.2. Spatial Feature Enhancement with CNNs

To integrate lateral spatial relationships into the feature set, the hidden states generated by the GRU are organized into a two-dimensional feature map aligned with the horizontal grid layout. This map is subsequently processed by a CNN employing a U-Net-inspired architecture. The CNN applies a series of downsampling and upsampling operations, augmented by residual connections, to extract multi-scale spatial features. These residual connections play a pivotal role in preserving fine-scale details from the RNN outputs across the convolutional layers, ensuring that the resulting feature set captures both broad spatial patterns and localized terrain variations. The CNN output is then fused with the original RNN hidden states through an additional residual linkage, creating a rich feature representation that balances vertical and horizontal terrain information. Mathematically, the fused feature is

$${\mathbf{f}}_{i,j}={\mathbf{h}}_{i,j}+{\mathbf{c}}_{i,j}$$

(5)

where ${\mathbf{c}}_{i,j}$ is the feature extracted by the CNN.

3.4. Decoder Design and Operational Mechanism

The decoder constitutes a pivotal element of our methodology, tasked with synthesizing the final elevation predictions from the integrated features produced by the preceding stages. It leverages the complementary strengths of sequential and spatial processing to generate DEMs that accurately reflect the terrain’s multifaceted characteristics. The decoder employs a GRU-based recurrent neural network, complemented by an embedding layer for input processing and a fully connected layer for output mapping. This configuration enables the generation of elevation class predictions tailored to the quantized elevation space. The decoding process begins with a placeholder input, which is embedded into a high-dimensional space to establish the starting point for sequence generation. Subsequently, this embedded input is combined with the fused features from the encoder and CNN, providing a holistic context for elevation prediction. The GRU processes this integrated input in a single pass, producing an output that encapsulates the synthesized terrain information. This output is then transformed through a fully connected layer into logits representing quantized elevation classes, which are subsequently mapped to continuous elevation values. The residual connection ensures that intricate vertical details from the encoder are effectively incorporated into the decoding process, enhancing the reconstruction of complex terrain features. The predicted elevation (${\widehat{z}}_{i,j}$) is obtained from the class prediction ${\widehat{k}}_{i,j}=arg{max}_k{p}_{i,j}\left(k\right)$, where ($p_{i,j}\left(k\right)$) is the probability of class k.

3.5. Incorporation of TPI Constraints

To ensure that the generated DEMs exhibit realistic topographic characteristics, we introduce supervision based on the TPI during the training phase. TPI serves as a localized metric that quantifies terrain features by comparing a point’s elevation to the average elevation of its surrounding neighborhood. At a given scale (s), TPI is computed as

$${\mathrm{TPI}}_{i,j}^{\left(s\right)}={\widehat{z}}_{i,j}-{\displaystyle \frac{1}{|{\mathcal{N}}_s(i,j)|}}\sum _{(p,q)\in {\mathcal{N}}_s(i,j)}{\widehat{z}}_{p,q}$$

(6)

where ${\mathcal{N}}_s(i,j)$ is the set of neighbors within distance (s). We calculate TPI values for both predicted and ground-truth elevations across multiple scales. The TPI loss, denoted as ${\mathcal{L}}_{\mathrm{TPI}}$, is defined as the mean squared difference between these values, aggregated over all grid cells and scales:

$${\mathcal{L}}_{\mathrm{TPI}}=\sum _{s\in \mathcal{S}}{\displaystyle \frac{1}{N}}\sum _{i,j}{\left({\mathrm{TPI}}_{i,j}^{\left(s\right)}-{\mathrm{TPI}}_{i,j,\mathrm{gt}}^{\left(s\right)}\right)}^2$$

(7)

Here, $\mathcal{S}$ represents the set of scales chosen for TPI calculation. This multi-scale approach allows the model to capture a comprehensive range of terrain features, from localized micro-topography to broader geomorphological structures. For our experiments, we empirically selected three distinct scales: a small scale ($s_1=3\times 3$ grid cells), a medium scale ($s_2=9\times 9$ grid cells), and a large scale ($s_3=27\times 27$ grid cells) to represent local, mesoscale, and regional topographic variations, respectively. Each scale is treated equally in the summation.

This TPI loss is combined with the primary elevation classification objective to form the total loss function. The primary objective, ${\mathcal{L}}_{\mathrm{cls}}$, is based on a masked softmax cross-entropy loss, designed to handle areas with no valid ground truth data. The total loss function (${\mathcal{L}}_{\mathrm{total}}$) is formulated as

$${\mathcal{L}}_{\mathrm{total}}={\mathcal{L}}_{\mathrm{cls}}+\lambda {\mathcal{L}}_{\mathrm{TPI}}$$

(8)

where $\lambda$ is a weighting coefficient that balances the contribution of the TPI loss relative to the classification loss. Through empirical tuning, we set $\lambda =0.1$. This weighting scheme ensures a balance between precise elevation prediction and geomorphometric fidelity, reducing artifacts and enhancing the realism of the DEM. The weight $\lambda$ is kept static throughout the training process.

By enforcing TPI constraints at various scales, the model captures a spectrum of terrain features, from fine-scale details to broader landforms. The weighted TPI loss ensures a balance between elevation accuracy and geomorphometric fidelity, reducing artifacts and enhancing the realism of the DEM.

3.6. Post-Processing Refinement

To polish the predicted DEM and address residual noise, we implement a post-processing phase utilizing a threshold-based median filtering technique. For each grid cell, the median elevation of its immediate neighbors is computed. If the predicted elevation deviates from this median beyond a specified threshold, it is adjusted to the median value. This step mitigates isolated anomalies, such as spikes or depressions, while preserving genuine micro-topographic features by avoiding excessive smoothing. Mathematically, if $|{\widehat{z}}_{i,j}-m_{i,j}|>\tau$, where $m_{i,j}$ is the neighborhood median, then ${\widehat{z}}_{i,j}$ is set to $m_{i,j}$. This refinement ensures that the final DEM is both smooth and detailed, rendering it suitable for advanced terrain analysis and visualization applications.

4. DEM Reconstruction Results and Discussion

4.1. Implementation Details

Our proposed hybrid RNN-CNN framework was implemented using the PyTorch 2.1.0 deep learning library. The model was trained on a laptop system equipped with an Intel Core i7-12700H processor, 32 GB DDR4 RAM, 1 TB SSD storage, and an NVIDIA GeForce RTX 3070Ti Laptop GPU with 8 GB VRAM (NVIDIA Corporation, Santa Clara, CA, USA; Intel Corporation, Santa Clara, CA, USA). Key parameters and configurations are as follows:

• Model Architecture:
  • The hidden state size for the GRU layers in the RNN encoder was set to 32.
  • The number of GRU layers was 2.
  • The CNN component utilized feature channels with dimensions $[128, 256, 512, 1024, 1024]$ across its layers.
• Training Configuration:
  • The model was trained for 50 epochs.
  • The learning rate ($lr$) was initialized to $1\times {10}^{-4}$.
  • The batch size for both training and testing DataLoaders was set to 1.
  • We employed the Adam optimizer with a weight decay of $1\times {10}^{-5}$.

4.2. Baseline DEM Generation for Comparative Analysis

To provide a comprehensive comparative analysis of our proposed end-to-end method, baseline DEMs were generated from the raw LiDAR point clouds using established traditional filtering and interpolation techniques. This conventional process typically involves two main steps: first, robustly identifying and classifying ground points from the raw point cloud, and second, interpolating these identified ground points onto a regular grid to form a continuous DEM.

For the ground point extraction phase, two widely recognized morphological filtering algorithms were employed to process the raw LiDAR point clouds:

• Progressive Morphological Filter (PMF): This algorithm iteratively applies morphological opening operations with increasing window sizes to effectively distinguish and remove non-ground objects, leaving behind bare-earth ground points.
• Simple Morphological Filter (SMRF): This method utilizes a series of basic morphological operations to robustly classify ground and non-ground points based on elevation differences and geometric properties within local neighborhoods.

After ground points were successfully extracted by both PMF and SMRF, these filtered point clouds were then used as input for DEM generation via two standard spatial interpolation methods:

• Linear Interpolation: This technique involves creating a Triangulated Irregular Network (TIN) from the filtered ground points. Elevation values for grid cells are then determined by linear interpolation within the triangles that cover the respective grid locations.
• Nearest-Neighbor Interpolation: This simple method assigns the elevation of the closest ground point in the filtered dataset to each corresponding grid cell within the DEM.

The DEMs derived from these combinations of filtering and interpolation (PMF + Linear, PMF + Nearest Neighbor, SMRF + Linear, SMRF + Nearest Neighbor) served as the primary baselines for quantitative and qualitative comparison against our proposed hybrid RNN-CNN approach. This comparative setup allows us to critically evaluate the performance of our end-to-end framework against established traditional two-step workflows in reconstructing high-precision DEMs from raw LiDAR data.

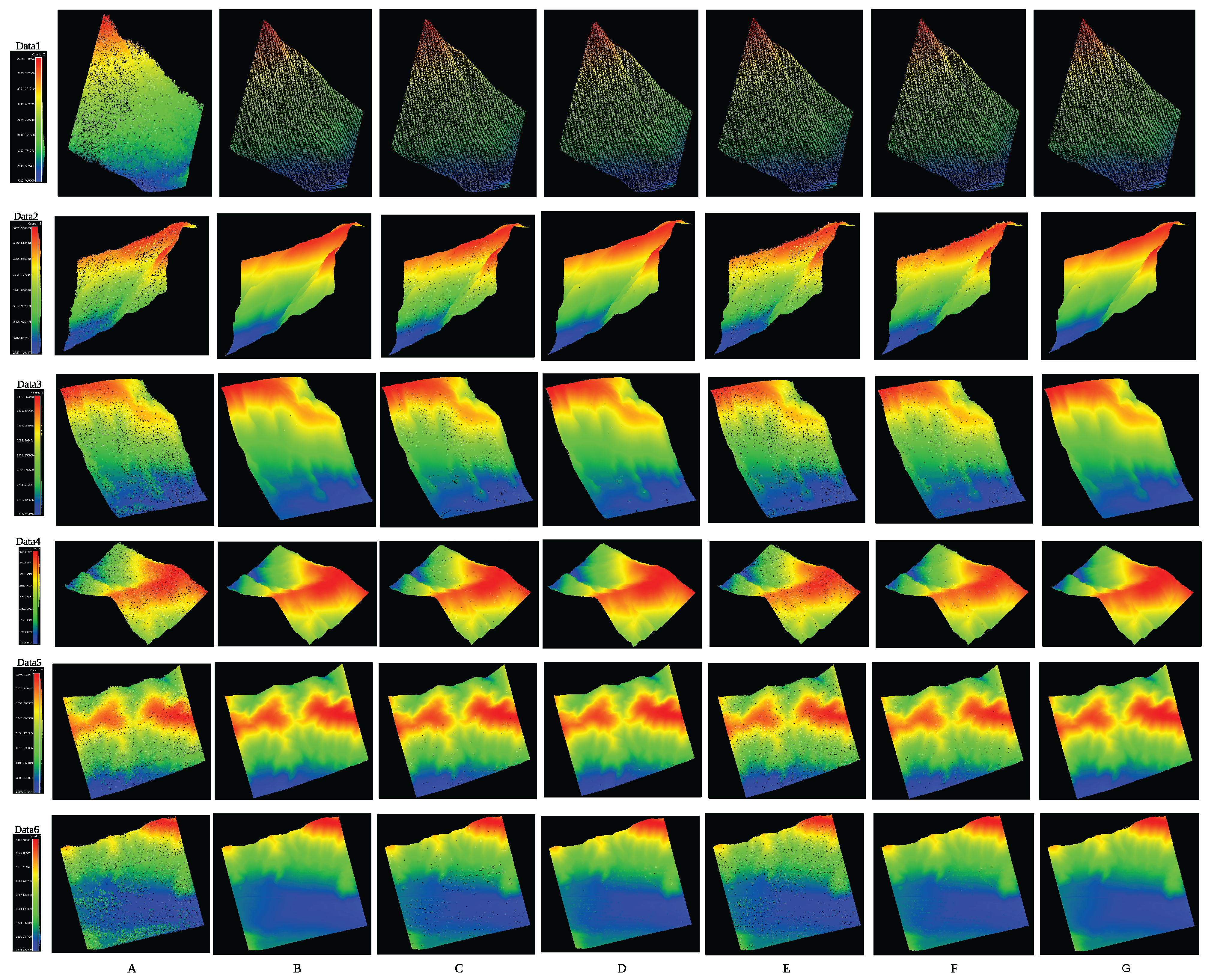
4.3. Visual Comparison Analysis

Figure 3 provides a comprehensive comparative analysis of DEMs produced using various methodological approaches. This visual comparison demonstrates distinct differences in reconstruction quality and spatial accuracy across different techniques. Qualitative assessment reveals significant deficiencies in traditional interpolation approaches, even when preceded by morphological filtering. Both linear and nearest-neighbor interpolation methods yield DEMs with reduced quality.

Specifically, the PMF, while effective at removing many non-ground features, often results in small gaps or voids within the filtered ground point cloud. Subsequent interpolation methods may struggle to accurately fill these fine-scale absences, leading to minor discontinuities. Conversely, the SMRF can incompletely filter out certain non-ground points, such as scattered trees, leading to their erroneous inclusion in the interpolated DEMs and manifesting as artificial elevation variations. Additionally, linear interpolation methods often introduce distinct linear artifacts along the edges of the generated DEMs, particularly noticeable at block boundaries or where data density changes.

In contrast, our proposed hybrid RNN-CNN method addresses these challenges effectively. Its end-to-end learning framework, designed to process raw point clouds and leverage multi-scale TPI constraints, reconstructs terrain surfaces with improved continuity. The method reduces the appearance of gaps or extraneous features and does not introduce the characteristic linear edge artifacts observed with traditional linear interpolation. This results in DEMs that are more consistent and suitable for applications requiring high-fidelity terrain representation.

Furthermore, to provide a more detailed understanding of our method’s performance at a fine scale, Figure 4 presents magnified views comparing DEMs generated by our method against the ground truth. These close-up visualizations reveal that, in the vast majority of cases, our reconstructed DEM closely matches the ground truth, affirming its high fidelity. However, in rare instances, minor imperfections may still be observed, such as extremely small, isolated gaps or occasional points exhibiting minor height discrepancies. These subtle deviations are inherent challenges when processing complex real-world LiDAR data, yet they do not significantly detract from the overall high quality and consistency of the DEMs produced by our framework.

4.4. Quantitative Accuracy Evaluation

In the evaluation of DEM quality, aside from qualitative visual analysis, accuracy is a critical metric. To comprehensively quantify the deviation between the predicted DEM and the ground truth, we adopted the following evaluation metrics: root mean square error (RMSE) and mean absolute error (MAE). Their mathematical formulations are expressed as follows:

• RMSE:

  $$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left({\widehat{z}}_i-z_i\right)}^2}$$

  (9)

  where ${\widehat{z}}_i$ is the predicted elevation, and $z_i$ is the corresponding reference value.
• MAE:

  $$\mathrm{MAE}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left|{\widehat{z}}_i-z_i\right|$$

  (10)

  providing a measure of the average absolute error across the DEM.

Table 2. Quantitative accuracy assessment of DEMs.

Experiment	Data	Metrics	Ours	PMF + Nearest	PMF + Linear	SMRF + Nearest	SMRF + Linear
Experiment 1	Data1	RMSE (m)	1.058	1.091	1.130	1.151	1.019
		MAE (m)	0.706	0.799	0.817	0.844	0.762
	Data2	RMSE (m)	1.306	2.420	1.804	5.985	5.334
		MAE (m)	0.946	1.406	1.252	2.353	2.183
	Data3	RMSE (m)	1.026	2.906	2.746	6.523	6.224
		MAE (m)	0.786	1.434	1.386	2.688	2.680
Experiment 2	Data4	RMSE (m)	2.855	3.214	2.125	9.283	8.275
		MAE (m)	0.978	1.341	1.149	2.981	2.837
	Data5	RMSE (m)	1.640	2.668	2.144	6.057	5.593
		MAE (m)	0.686	1.459	1.358	2.644	2.571
	Data6	RMSE (m)	1.560	3.984	3.626	8.266	7.834
		MAE (m)	0.725	1.477	1.422	3.116	3.087

presents a quantitative accuracy assessment comparing our proposed method against traditional linear and nearest-neighbor interpolation techniques as well as methods combining filtering with interpolation across two distinct experimental scenarios. Accuracy was evaluated by comparing each grid cell of the reconstructed DEMs with the corresponding cell in a high-precision ground truth DEM.

In Experiment 1, which used data from steep slope terrain (Data1, 2, and 3), our proposed method consistently achieved the lowest error metrics. Across these datasets, the RMSE of our method ranged from 1.026 to 1.306 m, and the MAE from 0.706 to 0.946 m. In contrast, after filtering, methods such as PMF+Nearest, PMF+Linear, SMRF+Nearest, and SMRF+Linear produced notably higher errors than our proposed method. For instance, across Experiment 1 datasets, their RMSEs ranged from approximately 1.091 to 6.523 m, and their MAEs from 0.799 to 2.688 m. The RMSEs of our method were approximately 1.5 to 6 times lower, and the MAEs approximately 1.5 to 3.5 times lower, than those of these filtered-interpolation baselines, indicating its superior performance in steep slope environments.

In Experiment 2, which used data from undulating terrain (Data4, 5, and 6), the performance of our method was further validated. Our approach achieved RMSEs ranging from 1.560 to 2.855 m and MAEs from 0.686 to 0.978 m. In contrast, all filtered-interpolation baselines (PMF/SMRF with Linear/Nearest interpolation) consistently exhibited higher error magnitudes. For example, the RMSEs of PMF+Nearest ranged from 2.668 to 3.984 m, while those of SMRF+Nearest were notably higher, ranging from 6.057 to 9.283 m. These results confirm that, although filtering can reduce errors compared to basic interpolation, our end-to-end method maintains significantly higher accuracy across varying terrain complexities, even in relatively smoother undulating areas.

The significant difference in accuracy between our method and traditional interpolation approaches (including those combining PMF and SMRF filtering with linear or nearest-neighbor interpolation) arises from fundamental architectural advantages. Our pipeline directly generates the DEM from raw point clouds through an end-to-end learning process. It is designed to learn to implicitly filter non-ground points and, critically, reconstruct a high-precision DEM under multi-scale TPI supervision. In contrast, these filtering steps can improve ground point identification, the subsequent interpolation step simply connects these filtered points without the benefit of learned topographic patterns or multi-scale semantic constraints. By integrating end-to-end feature learning with TPI supervision, our method simultaneously processes non-ground noise, preserves critical terrain details, and ensures geomorphometric fidelity, resulting in its significantly improved accuracy.

4.5. Computational Efficiency Analysis

Table 3. Processing time analysis for different DEM generation approaches.

Experiment	Data	Ours	PMF + Nearest	PMF + Linear	SMRF + Nearest	SMRF + Linear
Experiment 1	Data1	7.74 s	13.22 s	10.95 s	16.01 s	13.74 s
	Data2	213.81 s	238.61 s	234.83 s	254.85 s	247.63 s
	Data3	113.67 s	142.16 s	125.67 s	148.81 s	142.24 s
Experiment 2	Data4	202.63 s	217.62 s	218.51 s	249.79 s	236.87 s
	Data5	123.47 s	142.85 s	139.21 s	167.06 s	160.66 s
	Data6	160.32 s	177.23 s	177.31 s	197.38 s	192.52 s

Time measurements for the proposed method represent the end-to-end DEM reconstruction duration from raw LiDAR point clouds. For traditional baseline methods (PMF/SMRF + Linear/Nearest Neighbor), time measurements include both the ground filtering process and the subsequent interpolation step. All timings were recorded on the same hardware configuration.

presents a computational performance comparison evaluating the runtime efficiency of our proposed hybrid RNN-CNN framework against established DEM generation approaches across six diverse point cloud datasets. The analysis examines our method’s performance relative to PMF and SMRF variants, each combined with nearest-neighbor and linear interpolation techniques.

Our experimental results show that the proposed framework achieves faster processing times across all tested datasets, with performance improvements ranging from 11.3% to 51.7% compared to conventional approaches. This consistent computational advantage indicates the effectiveness of integrating multi-scale TPI features within the hybrid neural network architecture for point cloud-to-DEM conversion.

The performance patterns provide insights into the method’s computational characteristics. Improvements are more pronounced on smaller datasets, where the hybrid RNN-CNN pipeline can process point cloud data more efficiently. On larger datasets, the improvements remain consistent, suggesting that our approach scales appropriately across different point cloud densities and spatial extents.

Analysis across different baseline methods shows that our approach achieves notable advantages over SMRF-based techniques, with improvements typically exceeding 20%. The performance gains against PMF-based methods are generally more moderate but remain consistent, indicating that our multi-scale TPI feature integration approach addresses computational bottlenecks present in traditional morphological filtering workflows applied to point cloud data.

The computational efficiency stems from our hybrid architecture that processes point cloud data through a streamlined RNN-CNN pipeline, eliminating the need for explicit neighborhood search operations and complex geometric interpolation procedures that characterize traditional point cloud processing methods. The integration of multi-scale TPI features allows the network to capture terrain characteristics directly from the point cloud, reducing the computational overhead associated with iterative filtering and interpolation steps.

These performance improvements have practical implications for operational point cloud processing workflows. In applications requiring processing of large point cloud datasets, the consistent efficiency gains translate to meaningful time savings. The method’s reliable performance across diverse point cloud characteristics makes it suitable for automated DEM generation pipelines where consistent processing times are important for operational deployment.

5. Conclusions

This study introduces a lightweight and efficient framework for high-precision DEM reconstruction directly from LiDAR point clouds, effectively balancing computational demands with robust feature representation. Experimental results on Jiuzhaigou datasets demonstrate that our streamlined approach achieves superior accuracy (in terms of RMSE and MAE) compared to traditional methods. Furthermore, it exhibits superior computational efficiency, with a more than 20% on averageimprovement in processing speed. Our method particularly excels in complex, steep terrain, accurately capturing details such as ridges and valleys. The innovative integration of multi-scale TPI as a semantic constraint during training proved instrumental in ensuring the geomorphometric fidelity and realistic representation of terrain structures.

Despite these strengths, the method is not without limitations. Future work will focus on several improvements:

• In data preprocessing, we plan to further refine noise suppression and outlier removal strategies to enhance reconstruction stability in extremely complex regions.
• In model architecture, we will explore multi-scale fusion mechanisms to enhance feature representation across different spatial extents.
• We will continue to optimize our lightweight network design and develop more efficient parallel computing schemes to further reduce computational complexity and improve large-scale data processing efficiency.
• Crucially, acknowledging the application-driven nature of our research, future work will also involve a more comprehensive quantitative assessment of the usability of our generated DEMs in specific downstream geospatial applications. This includes, but is not limited to, integrating our reconstructed DEMs into hydrological modeling frameworks to evaluate their impact on derived parameters (e.g., flow accumulation, stream networks) and assessing their suitability for advanced landform classification tasks. Such evaluations will provide direct evidence of our method’s utility beyond merely producing accurate elevation surfaces, thereby demonstrating its full potential for real-world environmental and geomorphological analysis.

In summary, this study provides an efficient, robust, and computationally lightweight solution for high-precision DEM reconstruction from LiDAR point clouds, offering significant advantages for resource-constrained environments while maintaining high precision. The proposed framework not only addresses critical challenges in terrain modeling but also outlines clear directions for ongoing research to further enhance its accuracy, scalability, and practical applicability.