Spatiotemporal Super-Resolution of Satellite Sea Surface Salinity Based on a Progressive Transfer Learning-Enhanced Transformer
Abstract
1. Introduction
2. Materials
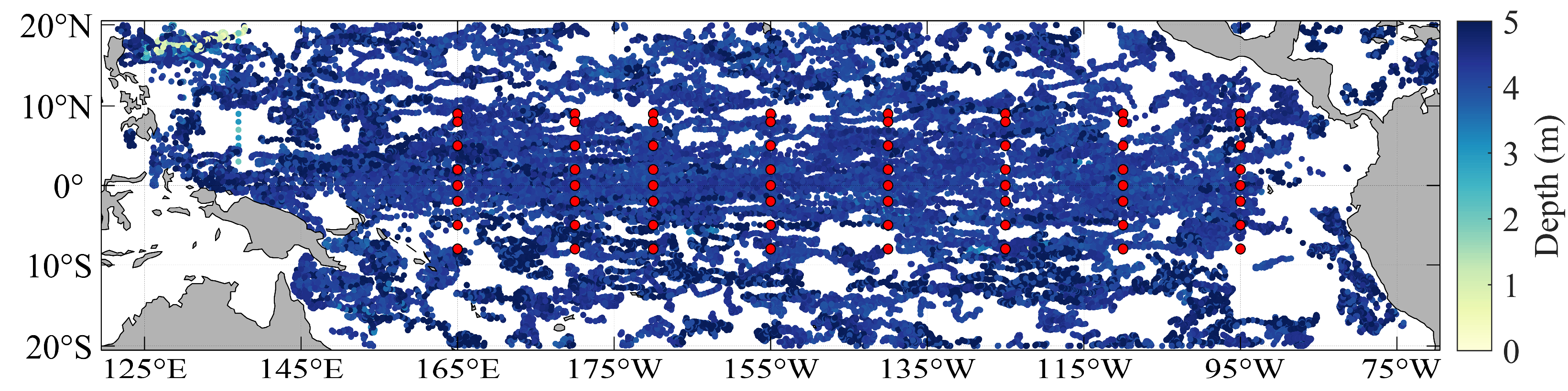
2.1. Study Area
2.2. Data
3. Methods
3.1. TSR
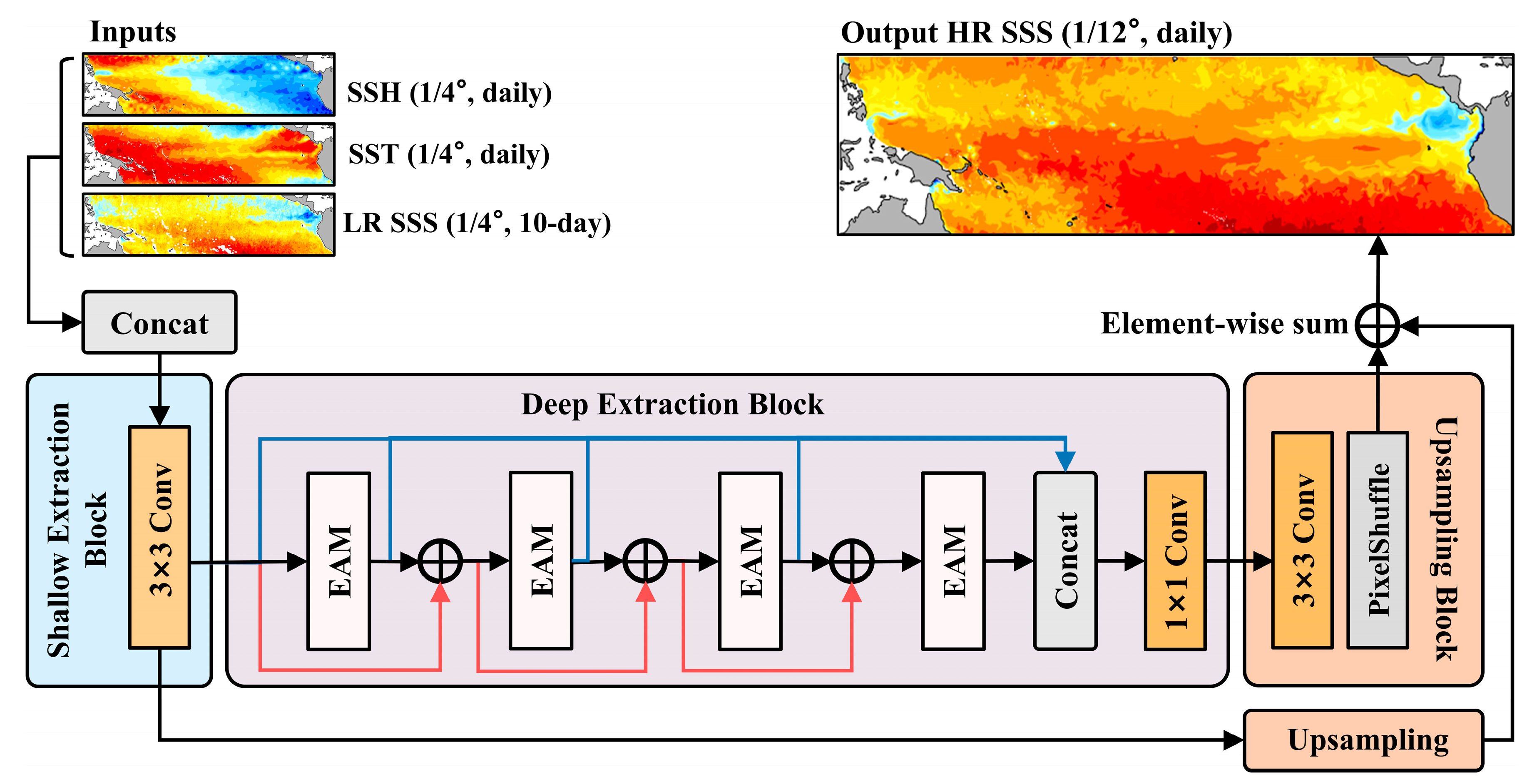
3.1.1. Overall Architecture of TSR
3.1.2. Deep Extraction Block
3.1.3. EAM
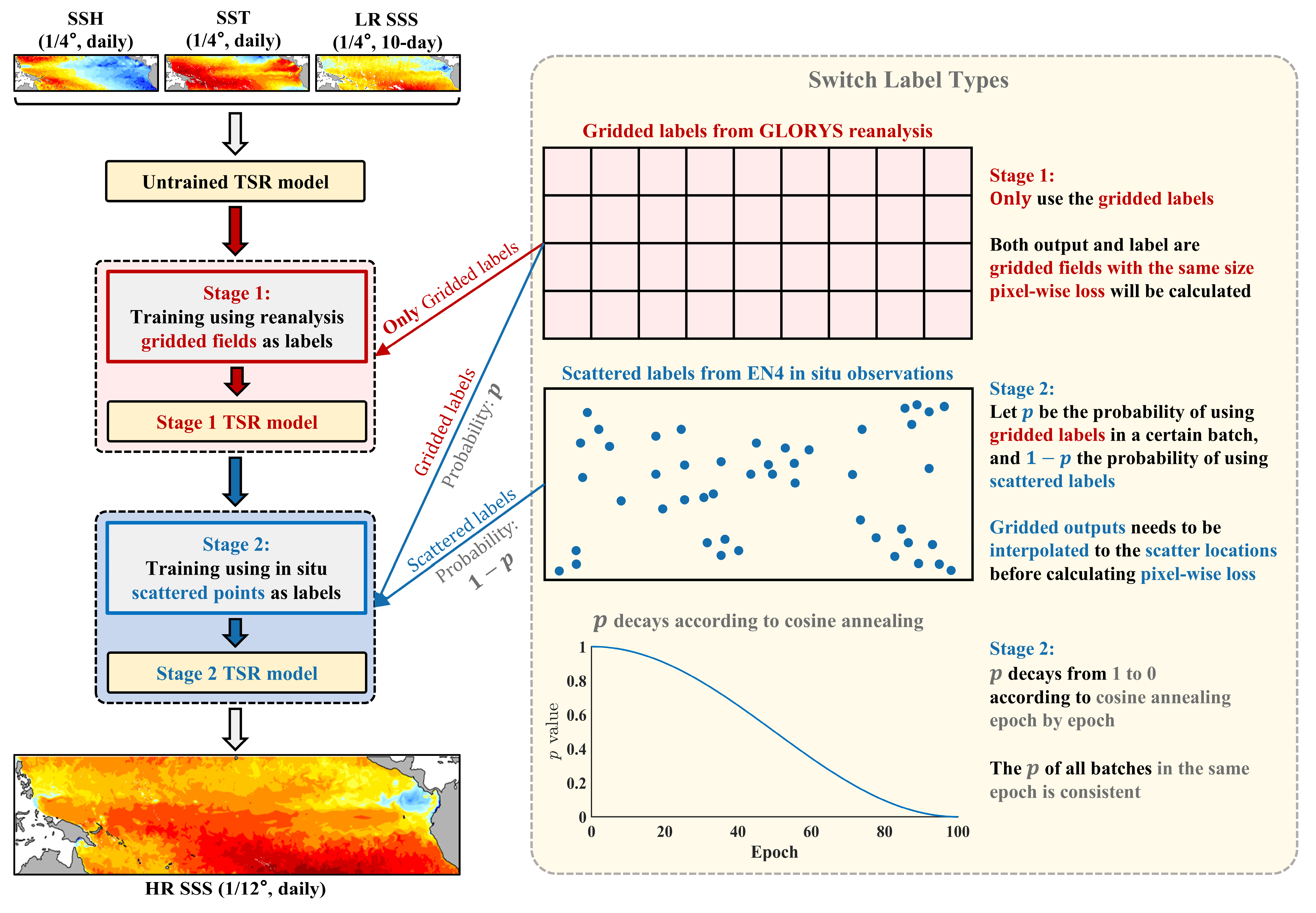
3.2. Progressive Transfer Learning Strategy for TSR
3.3. Implementation Details
4. Results
4.1. Experimental Setup
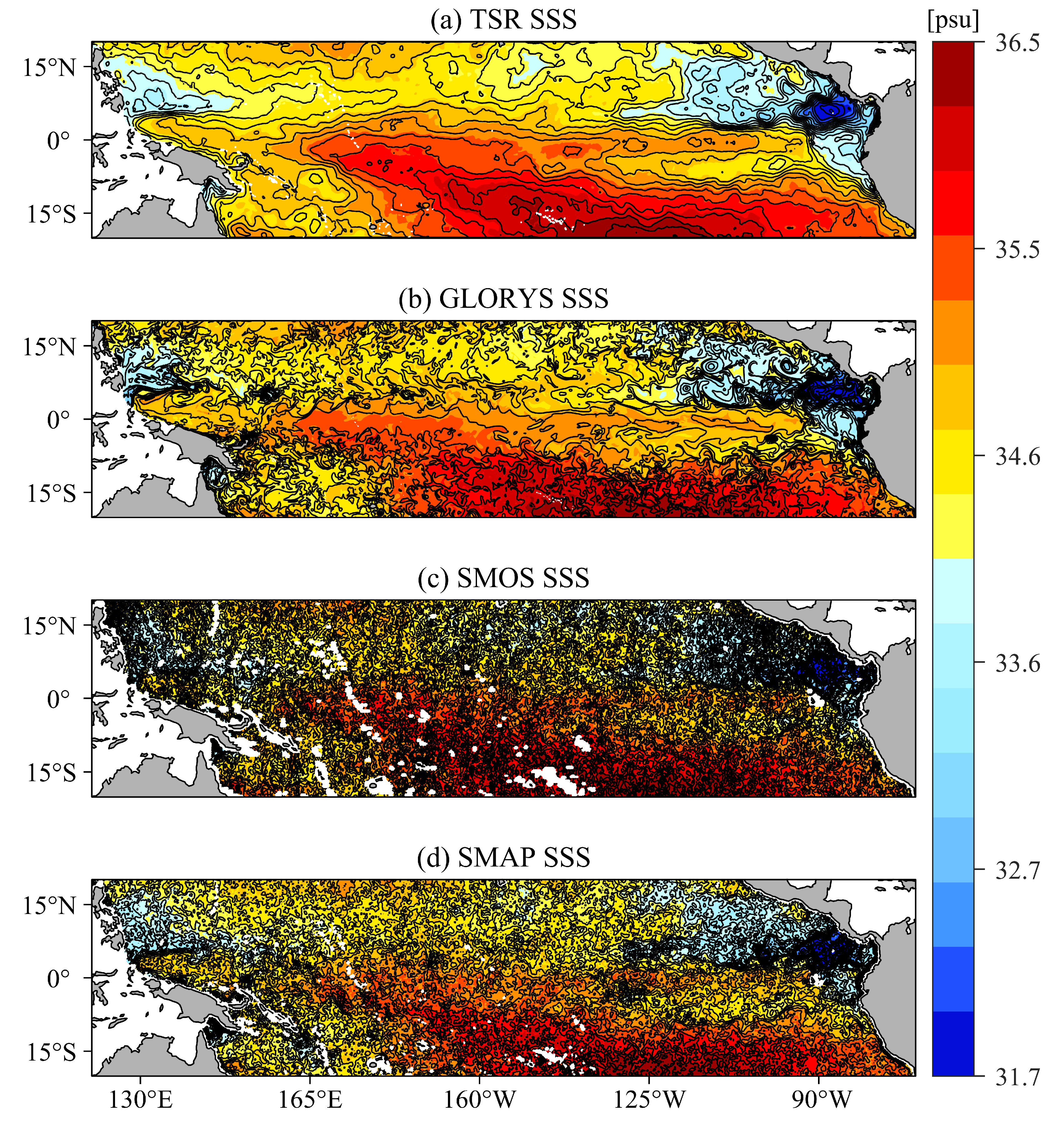
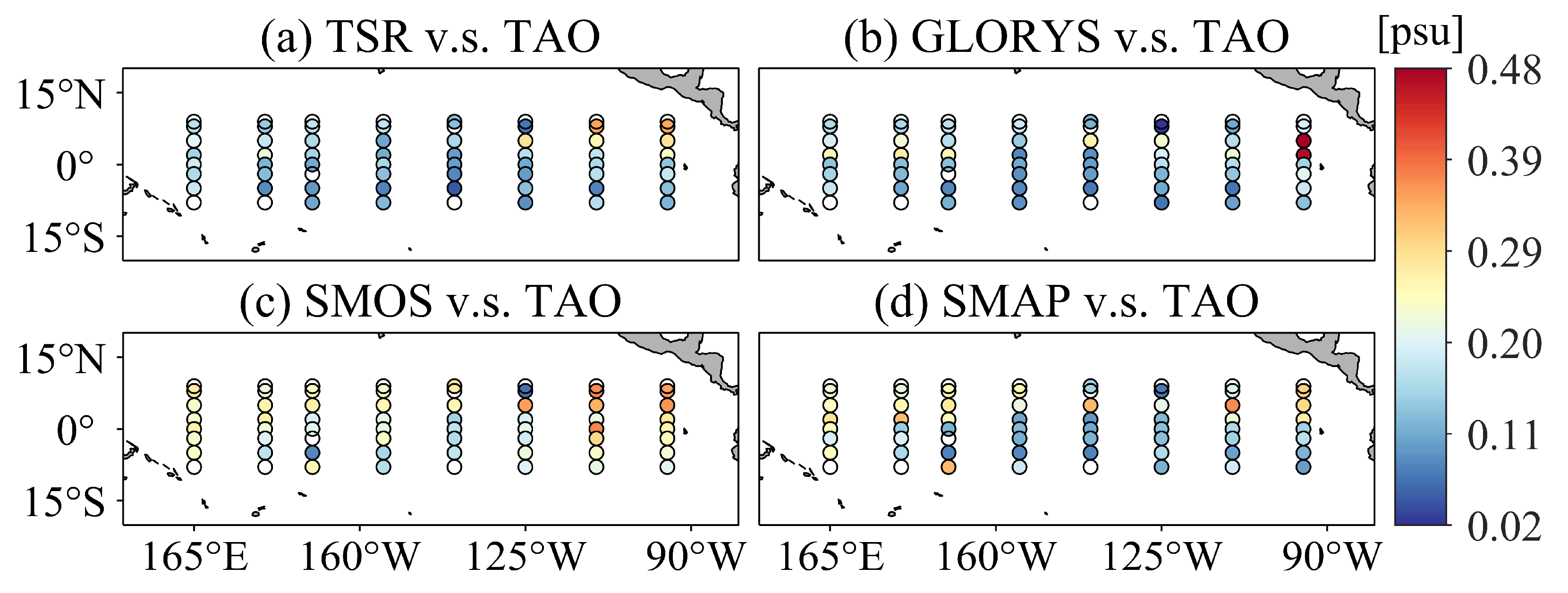
4.2. Spatial Analysis
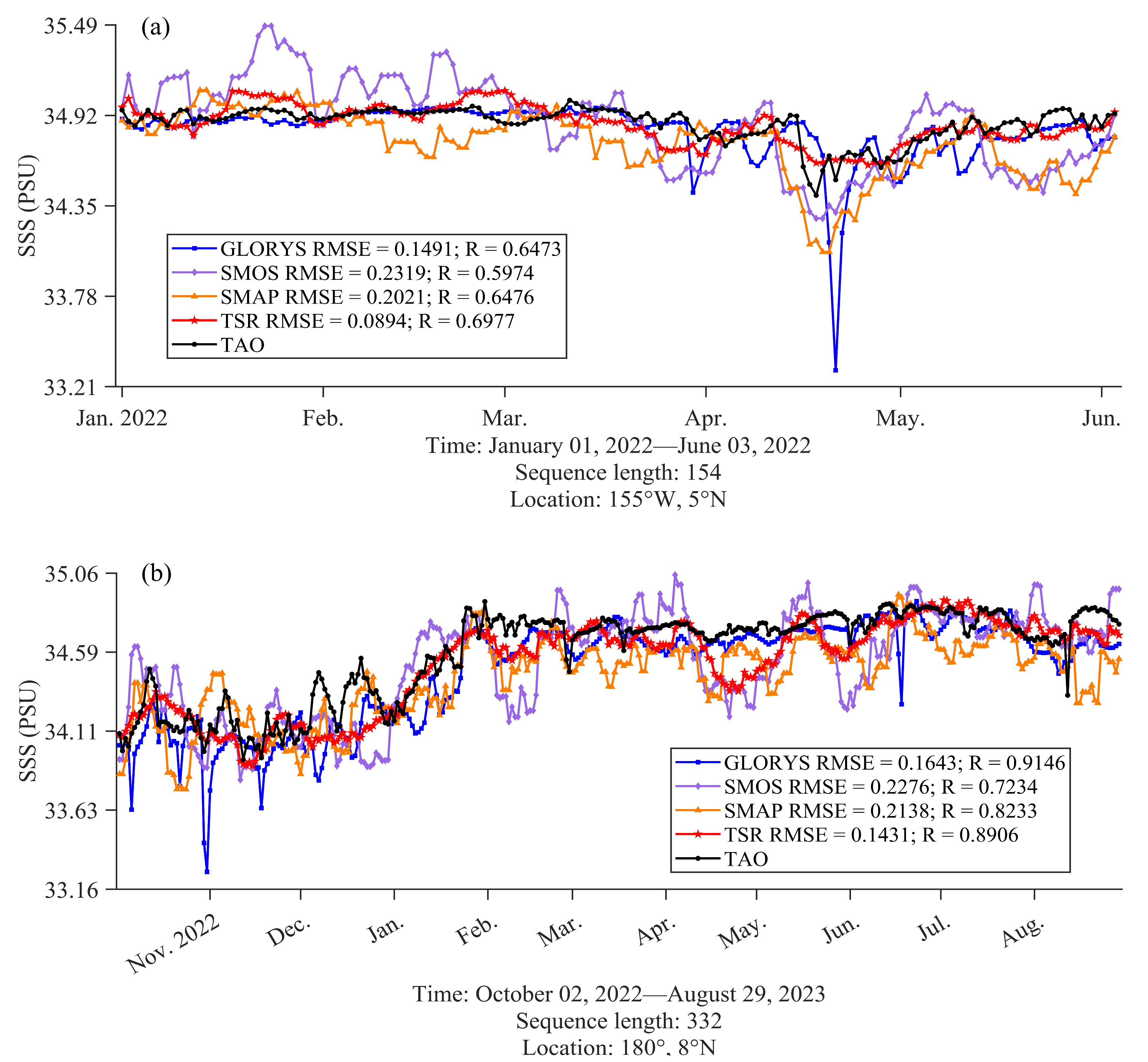
4.3. Temporal Analysis
5. Discussion
5.1. Ablation Experiments
5.2. Comparison of Decay Schemes and Training Strategies
5.3. Comparison of Input Variables
5.4. Comparison of SR Algorithms
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SSS | Sea surface salinity |
| SSSA | Sea surface salinity anomaly |
| SST | Sea surface temperature |
| SSH | Sea surface height |
| SLA | Sea-level anomaly |
| SR | Super-resolution |
| HR | High-resolution |
| LR | Low-resolution |
| TSR | Transformer-based satellite sea surface salinity super-resolution model |
| EAM | Enhanced attention module |
| MHA | Multi-Head Attention |
| SDPA | Scaled dot-product attention |
| CNN | Convolutional Neural Network |
| GAN | Generative Adversarial Network |
| PTL | Progressive transfer learning strategy |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| MB | Mean bias |
| R2 | coefficient of determination |
| SMOS | Soil Moisture and Ocean Salinity mission |
| SMAP | Soil Moisture Active Passive mission |
| TAO | Tropical Atmosphere Ocean |
| CATDS | Centre Aval de Traitement des Données SMOS |
| RSS | Remote Sensing System |
| CMEMS | Copernicus Marine Environment Monitoring Service |
| NRT | Near-real time |
References
- Durack, P.J.; Wijffels, S.E.; Matear, R.J. Ocean Salinities Reveal Strong Global Water Cycle Intensification During 1950 to 2000. Science 2012, 336, 455–458. [Google Scholar] [CrossRef]
- Friedman, A.R.; Reverdin, G.; Khodri, M.; Gastineau, G. A New Record of Atlantic Sea Surface Salinity from 1896 to 2013 Reveals the Signatures of Climate Variability and Long-Term Trends. Geophys. Res. Lett. 2017, 44, 1866–1876. [Google Scholar] [CrossRef]
- Dewey, S.R.; Morison, J.H.; Zhang, J.; Dewey, S.R.; Morison, J.H.; Zhang, J. An Edge-Referenced Surface Fresh Layer in the Beaufort Sea Seasonal Ice Zone. J. Phys. Oceanogr. 2017, 47, 1125–1144. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, W.; Guo, H.; Dong, C.; Zheng, H.; Zhang, Q.; Sun, W.; Guo, H.; Dong, C.; Zheng, H. A Transfer Learning-Enhanced Generative Adversarial Network for Downscaling Sea Surface Height through Heterogeneous Data Fusion. Remote Sens. 2024, 16, 763. [Google Scholar] [CrossRef]
- Kim, J.; Kim, T.; Ryu, J.-G. Multi-Source Deep Data Fusion and Super-Resolution for Downscaling Sea Surface Temperature Guided by Generative Adversarial Network-Based Spatiotemporal Dependency Learning. Int. J. Appl. Earth Obs. Geoinf. 2023, 119, 103312. [Google Scholar] [CrossRef]
- Nardelli, B.B.; Cavaliere, D.; Charles, E.; Ciani, D.; Buongiorno Nardelli, B.; Cavaliere, D.; Charles, E.; Ciani, D. Super-Resolving Ocean Dynamics from Space with Computer Vision Algorithms. Remote Sens. 2022, 14, 1159. [Google Scholar] [CrossRef]
- Reul, N.; Grodsky, S.A.; Arias, M.; Boutin, J.; Catany, R.; Chapron, B.; D’Amico, F.; Dinnat, E.; Donlon, C.; Fore, A.; et al. Sea Surface Salinity Estimates from Spaceborne L-Band Radiometers: An Overview of the First Decade of Observation (2010–2019). Remote Sens. Environ. 2020, 242, 111769. [Google Scholar] [CrossRef]
- Font, J.; Boutin, J.; Reul, N.; Spurgeon, P.; Ballabrera-Poy, J.; Chuprin, A.; Gabarró, C.; Gourrion, J.; Guimbard, S.; Hénocq, C.; et al. Smos First Data Analysis for Sea Surface Salinity Determination. Int. J. Remote Sens. 2012, 34, 3654–3670. [Google Scholar] [CrossRef]
- Vinogradova, N.; Lee, T.; Boutin, J.; Drushka, K.; Fournier, S.; Sabia, R.; Stammer, D.; Bayler, E.; Reul, N.; Gordon, A.; et al. Satellite Salinity Observing System: Recent Discoveries and the Way Forward. Front. Mar. Sci. 2019, 6, 243. [Google Scholar] [CrossRef]
- Shoup, C.G.; Subrahmanyam, B.; Roman-Stork, H.L. Madden-Julian Oscillation-Induced Sea Surface Salinity Variability as Detected in Satellite-Derived Salinity. Geophys. Res. Lett. 2019, 46, 9748–9756. [Google Scholar] [CrossRef]
- Nyadjro, E.S.; Subrahmanyam, B. Smos Mission Reveals the Salinity Structure of the Indian Ocean Dipole. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1564–1568. [Google Scholar] [CrossRef]
- Qu, T.; Yu, J.Y. Enso Indices from Sea Surface Salinity Observed by Aquarius and Argo. J. Oceanogr. 2014, 70, 367–375. [Google Scholar] [CrossRef]
- Yang, G.; Wang, F.; Li, Y.; Lin, P. Mesoscale Eddies in the Northwestern Subtropical Pacific Ocean: Statistical Characteristics and Three-Dimensional Structures. J. Geophys. Res. Ocean. 2013, 118, 1906–1925. [Google Scholar] [CrossRef]
- Xie, H.; Xu, Q.; Zheng, Q.; Xiong, X.; Ye, X.; Cheng, Y.; Xie, H.; Xu, Q.; Zheng, Q.; Xiong, X.; et al. Assessment of Theoretical Approaches to Derivation of Internal Solitary Wave Parameters from Multi-Satellite Images near the Dongsha Atoll of the South China Sea. Acta Oceanol. Sin. 2022, 41, 137–145. [Google Scholar] [CrossRef]
- Wang, M.; Du, Y.; Qiu, B.; Cheng, X.; Luo, Y.; Chen, X.; Feng, M. Mechanism of Seasonal Eddy Kinetic Energy Variability in the Eastern Equatorial Pacific Ocean. J. Geophys. Res. Ocean. 2017, 122, 3240–3252. [Google Scholar] [CrossRef]
- Kao, H.Y.; Lagerloef, G.S. Salinity Fronts in the Tropical Pacific Ocean—Pubmed. J. Geophys. Res. Ocean. 2015, 120, 1096–1106. [Google Scholar] [CrossRef]
- Maes, C.; Reul, N.; Behringer, D.; O’Kane, T.; Maes, C.; Reul, N.; Behringer, D.; O’Kane, T. The Salinity Signature of the Equatorial Pacific Cold Tongue as Revealed by the Satellite Smos Mission. Geosci. Lett. 2014, 1, 17. [Google Scholar] [CrossRef]
- Melnichenko, O.; Amores, A.; Maximenko, N.; Hacker, P.; Potemra, J. Signature of Mesoscale Eddies in Satellite Sea Surface Salinity Data. J. Geophys. Res. Ocean. 2017, 122, 1416–1424. [Google Scholar] [CrossRef]
- Banzon, V.; Smith, T.M.; Chin, T.M.; Liu, C.; Hankins, W. A Long-Term Record of Blended Satellite and in Situ Sea-Surface Temperature for Climate Monitoring, Modeling and Environmental Studies. Earth Syst. Sci. Data 2016, 8, 165–176. [Google Scholar] [CrossRef]
- Mears, C.A.; Scott, J.P.; Wentz, F.J.; Ricciardulli, L.; Leidner, S.M.; Hoffman, R.; Atlas, R. A near-Real-Time Version of the Cross-Calibrated Multiplatform (Ccmp) Ocean Surface Wind Velocity Data Set. J. Geophys. Res. Ocean. 2019, 124, 6997–7010. [Google Scholar] [CrossRef]
- Lepcha, D.C.; Goyal, B.; Dogra, A.; Goyal, V. Image Super-Resolution: A Comprehensive Review, Recent Trends, Challenges and Applications. Inf. Fusion 2023, 91, 230–260. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1646–1654. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar] [CrossRef]
- Vandal, T.; Kodra, E.; Ganguly, S.; Michaelis, A.; Nemani, R.; Ganguly, A. Deepsd: Generating High Resolution Climate Change Projections through Single Image Super-Resolution. In Proceedings of the KDD’17: 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1663–1672. [Google Scholar] [CrossRef]
- Wang, F.; Tian, D.; Carroll, M. Customized Deep Learning for Precipitation Bias Correction and Downscaling. Geosci. Model Dev. 2023, 16, 535–556. [Google Scholar] [CrossRef]
- Ping, B.; Su, F.; Han, X.; Meng, Y. Applications of Deep Learning-Based Super-Resolution for Sea Surface Temperature Reconstruction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 887–896. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014. [Google Scholar] [CrossRef]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual Losses for Real-Time Style Transfer and Super-Resolution. In Proceedings of the ECCV 2018: European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; pp. 694–711. [Google Scholar] [CrossRef]
- Nardelli, B.B.; Droghei, R.; Santoleri, R. Multi-Dimensional Interpolation of Smos Sea Surface Salinity with Surface Temperature and in Situ Salinity Data. Remote Sens. Environ. 2016, 180, 392–402. [Google Scholar] [CrossRef]
- Olmedo, E.; Martínez, J.; Umert, M.; Hoareau, N.; Portabella, M.; Ballabrera-Poy, J.; Turiel, A. Improving Time and Space Resolution of Smos Salinity Maps Using Multifractal Fusion. Remote Sens. Environ. 2016, 180, 246–263. [Google Scholar] [CrossRef]
- McPhaden, M.J.; McPhaden, M.J. The Tropical Atmosphere Ocean Array Is Completed. Bull. Am. Meteorol. Soc. 1995, 76, 739–741. [Google Scholar] [CrossRef]
- Boutin, J.; Vergely, J.; Marchand, S.; D’Amico, F.; Hasson, A.; Kolodziejczyk, N.; Reul, N.; Reverdin, G.; Vialard, J. New Smos Sea Surface Salinity with Reduced Systematic Errors and Improved Variability. Remote Sens. Environ. 2019, 214, 115–134. [Google Scholar] [CrossRef]
- Martin, M.; Dash, P.; Ignatov, A.; Banzon, V.; Beggs, H.; Brasnett, B.; Cayula, J.-F.; Cummings, J.; Donlon, C.; Gentemann, C.; et al. Group for High Resolution Sea Surface Temperature (Ghrsst) Analysis Fields Inter-Comparisons. Part 1: A Ghrsst Multi-Product Ensemble (Gmpe). Deep Sea Res. Part II Top. Stud. Oceanogr. 2012, 77–80, 21–30. [Google Scholar] [CrossRef]
- Taburet, G.; Sanchez-Roman, A.; Ballarotta, M.; Pujol, M.-I.; Legeais, J.-F.; Fournier, F.; Faugere, Y.; Dibarboure, G. Duacs Dt2018: 25 Years of Reprocessed Sea Level Altimetry Products. Ocean Sci. 2019, 15, 1207–1224. [Google Scholar] [CrossRef]
- Fu, H.; Dan, B.; Gao, Z.-g.; Wu, X.; Chao, G.; Zhang, L.; Zhang, Y.; Liu, K.; Zhang, X.; Li, W. Global Ocean Reanalysis Cora2 and Its Inter Comparison with a Set of Other Reanalysis Products. Front. Mar. Sci. 2023, 10, 1084186. [Google Scholar] [CrossRef]
- Jean-Michel, L.; Eric, G.; Romain, B.-B.; Gilles, G.; Angélique, M.; Marie, D.; Clément, B.; Mathieu, H.; Olivier, L.G.; Charly, R.; et al. The Copernicus Global 1/12° Oceanic and Sea Ice Glorys12 Reanalysis. Front. Earth Sci. 2021, 9, 698876. [Google Scholar] [CrossRef]
- Good, S.A.; Martin, M.J.; Rayner, N.A. En4: Quality Controlled Ocean Temperature and Salinity Profiles and Monthly Objective Analyses with Uncertainty Estimates. J. Geophys. Res. Ocean. 2013, 118, 6704–6716. [Google Scholar] [CrossRef]
- Manaster, A.; Meissner, T.; Wentz, F. The Nasa/Rss Smap Salinity Version 5 Release. In AGU Fall Meeting Abstracts; AGU: Washington, DC, USA, 2021. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing System, Long Beach, CA, USA, 4–9 December 2017; Volume 30, pp. 1–11. [Google Scholar] [CrossRef]
- Guo, H.; Li, J.; Dai, T.; Ouyang, Z.; Ren, X.; Xia, S.-T. Mambair: A Simple Baseline for Image Restoration with State-Space Model. Lect. Notes Comput. Sci. 2025, 15076, 222–241. [Google Scholar] [CrossRef]
- Lu, Z.; Li, J.; Liu, H.; Huang, C.; Zhang, L.; Zeng, T. Transformer for Single Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–20 June 2022; pp. 456–465. [Google Scholar] [CrossRef]
- Wang, H.; You, Z.; Guo, H.; Zhang, W.; Xu, P.; Ren, K. Quality Assessment of Sea Surface Salinity from Multiple Ocean Reanalysis Products. J. Mar. Sci. Eng. 2023, 11, 54. [Google Scholar] [CrossRef]
- Abraham, J.P.; Baringer, M.; Bindoff, N.L.; Boyer, T.; Cheng, L.J.; Church, J.A.; Conroy, J.L.; Domingues, C.M.; Fasullo, J.T.; Gilson, J.; et al. A Review of Global Ocean Temperature Observations: Implications for Ocean Heat Content Estimates and Climate Change. Rev. Geophys. 2013, 51, 450–483. [Google Scholar] [CrossRef]
- Zhao, Z.; Alzubaidi, L.; Zhang, J.; Duan, Y.; Gu, Y. A Comparison Review of Transfer Learning and Self-Supervised Learning: Definitions, Applications, Advantages and Limitations. Expert Syst. Appl. 2024, 242, 122807. [Google Scholar] [CrossRef]
- Liu, T.; Yang, Q.; Tao, D. Understanding How Feature Structure Transfers in Transfer Learning. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; AAAI Press: Washington, DC, USA, 2017; pp. 2365–2371. [Google Scholar]
- Argyriou, A.; Evgeniou, T.; Pontil, M. Multi-Task Feature Learning. In Proceedings of the 20th International Conference on Neural Information Processing Systems, San Diego, CA, USA, 2–7 December 2006; MIT Press: Cambridge, MA, USA, 2006; pp. 41–48. [Google Scholar]
- Hendrycks, D.; Lee, K.; Mazeika, M. Using Pre-Training Can Improve Model Robustness and Uncertainty. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 2712–2721. [Google Scholar]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Ling, X.; Huang, Y.; Guo, W.; Wang, Y.; Chen, C.; Qiu, B.; Ge, J.; Qin, K.; Xue, Y.; Peng, J. Comprehensive Evaluation of Satellite-Based and Reanalysis Soil Moisture Products Using in Situ Observations over China. Hydrol. Earth Syst. Sci. 2021, 25, 1–34. [Google Scholar] [CrossRef]
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum Learning. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; Association for Computing Machinery: New York, NY, USA, 2009; pp. 41–48. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]




| Data | Type | Usage | Institution | Resolution (Spatial, Temporal) |
|---|---|---|---|---|
| SMOS SSS | L3 salinity satellite product | Input/comparison | Centre Aval de Traitement des Données SMOS | 1/4°, 10-day |
| REMSS SST | L4 satellite product | Input | Remote Sensing Systems | 1/10°, daily |
| CMEMS SSH | L4 satellite product | Input | Copernicus Marine Environment Monitoring Service | 1/8°, daily |
| GLORYS SSS | Reanalysis product | Label/comparison | Copernicus Marine Environment Monitoring Service | 1/12°, daily |
| SMAP | L3 salinity satellite product | Comparison | Remote Sensing Systems | 1/4°, 8-day |
| EN4 | In situ observations after quality control | Validation | Met Office Hadley Center | —, daily |
| TAO | In situ observations from moored buoys | Validation | National Oceanic and Atmospheric Administration | —, daily |
| Model | MAE (psu) | RMSE (psu) | MB (psu) | |
|---|---|---|---|---|
| TSR | 0.1226 | 0.1647 | −0.0075 | 0.9482 |
| GLORYS | 0.1004 | 0.1615 | −0.0344 | 0.9502 |
| SMOS | 0.1884 | 0.2457 | −0.0394 | 0.8848 |
| SMAP | 0.1609 | 0.2198 | −0.0955 | 0.9078 |
| Model | MAE (psu) | RMSE (psu) | MB (psu) | |
|---|---|---|---|---|
| TSR | 0.1229 | 0.1625 | −0.0101 | 0.9152 |
| GLORYS | 0.1170 | 0.1801 | −0.0470 | 0.8959 |
| SMOS | 0.1931 | 0.2434 | −0.0273 | 0.8099 |
| SMAP | 0.1601 | 0.2096 | −0.1047 | 0.8590 |
| EAM Number | MAE (psu) | RMSE (psu) | MB (psu) | |
|---|---|---|---|---|
| 2 | 0.1321 | 0.1771 | −0.0344 | 0.9401 |
| 4 | 0.1302 | 0.1747 | −0.0358 | 0.9418 |
| 6 | 0.1305 | 0.1747 | −0.0355 | 0.9418 |
| 8 | 0.1296 | 0.1736 | −0.0339 | 0.9425 |
| 10 | 0.1309 | 0.1746 | −0.0397 | 0.9418 |
| Hidden Layers’ Feature Channel Number | MAE (psu) | RMSE (psu) | MB (psu) | |
|---|---|---|---|---|
| 4 | 0.1367 | 0.1820 | −0.0374 | 0.9368 |
| 8 | 0.1348 | 0.1796 | −0.0368 | 0.9385 |
| 16 | 0.1296 | 0.1736 | −0.0339 | 0.9425 |
| 32 | 0.1281 | 0.1718 | −0.0353 | 0.9437 |
| 64 | 0.1313 | 0.1752 | −0.0388 | 0.9414 |
| MHA Head Number | MAE (psu) | RMSE (psu) | MB (psu) | |
|---|---|---|---|---|
| 1 | 0.1299 | 0.1734 | −0.0359 | 0.9426 |
| 2 | 0.1297 | 0.1732 | −0.0371 | 0.9427 |
| 4 | 0.1281 | 0.1718 | −0.0353 | 0.9437 |
| 8 | 0.1291 | 0.1723 | −0.0350 | 0.9433 |
| 16 | 0.1335 | 0.1772 | −0.0505 | 0.9401 |
| Convolutional Kernel Size in EAM | MAE (psu) | RMSE (psu) | MB (psu) | |
|---|---|---|---|---|
| 1 | 0.1349 | 0.1785 | −0.0529 | 0.9392 |
| 3 | 0.1281 | 0.1718 | −0.0353 | 0.9437 |
| 5 | 0.1280 | 0.1716 | −0.0346 | 0.9438 |
| 7 | 0.1280 | 0.1707 | −0.0374 | 0.9444 |
| 9 | 0.1262 | 0.1695 | −0.0277 | 0.9452 |
| 11 | 0.1286 | 0.1722 | −0.0353 | 0.9434 |
| 13 | 0.1290 | 0.1727 | −0.0325 | 0.9431 |
| 15 | 0.1286 | 0.1716 | −0.0371 | 0.9438 |
| 17 | 0.1354 | 0.1803 | −0.0498 | 0.9380 |
| Learning Rate | MAE (psu) | RMSE (psu) | MB (psu) | |
|---|---|---|---|---|
| 0.1 | 0.1617 | 0.2123 | −0.0652 | 0.9140 |
| 0.01 | 0.1559 | 0.2053 | −0.0643 | 0.9196 |
| 0.001 | 0.1262 | 0.1695 | −0.0277 | 0.9452 |
| 0.0001 | 0.1286 | 0.1718 | −0.0314 | 0.9436 |
| 0.00001 | 0.1398 | 0.1856 | −0.0528 | 0.9342 |
| Decay Scheme | MAE (psu) | RMSE (psu) | MB (psu) | |
|---|---|---|---|---|
| Cosine Annealing | 0.1226 | 0.1647 | −0.0075 | 0.9482 |
| Stepped | 0.1235 | 0.1654 | −0.0074 | 0.9478 |
| Linear | 0.1232 | 0.1652 | −0.0113 | 0.9479 |
| Exponential | 0.1230 | 0.1649 | −0.0088 | 0.9481 |
| Model | Configuration | MAE (psu) | RMSE (psu) | MB (psu) | |
|---|---|---|---|---|---|
| TSR | PTL strategy | 0.1226 | 0.1647 | −0.0075 | 0.9482 |
| TSR1 | One-step training and only using gridded labels | 0.1262 | 0.1695 | −0.0277 | 0.9452 |
| TSR2 | One-step training and only using scatter labels | 0.3616 | 0.4783 | −0.0711 | 0.5634 |
| TSR3 | One-step training and using both gridded and scatter labels | 0.1514 | 0.2007 | −0.0346 | 0.9231 |
| TSR4 | Two-step training, but not progressive, using gridded and scatter labels successively | 0.3649 | 0.4939 | −0.0935 | 0.5346 |
| Combination | MAE (psu) | RMSE (psu) | MB (psu) | |
|---|---|---|---|---|
| SSS | 0.1369 | 0.1823 | −0.0407 | 0.9366 |
| SSS SST | 0.1329 | 0.1775 | −0.0314 | 0.9399 |
| SSS SSH | 0.1353 | 0.1806 | −0.0358 | 0.9378 |
| SST SSH | 0.2240 | 0.3292 | −0.0554 | 0.7931 |
| SSS SST SSH | 0.1262 | 0.1695 | −0.0277 | 0.9452 |
| Model | MAE (psu) | RMSE (psu) | MB (psu) | Params | Inference Time (s) | |
|---|---|---|---|---|---|---|
| TSR | 0.1226 | 0.1647 | −0.0075 | 0.9482 | 611 K | 1.0452 |
| Bicubic | 0.1947 | 0.2535 | −0.0395 | 0.8774 | — | — |
| Bilinear | 0.1884 | 0.2457 | −0.0384 | 0.8848 | — | — |
| SRCNN | 0.1457 | 0.1929 | −0.0496 | 0.9290 | 67.6 K | 0.1260 |
| VDSR | 0.1957 | 0.2547 | −0.0460 | 0.8762 | 665 K | 0.6123 |
| EDSR | 0.1383 | 0.1844 | −0.0405 | 0.9351 | 1.6 M | 0.2397 |
| SRResNet | 0.1423 | 0.1884 | −0.0527 | 0.9323 | 1.6 M | 0.2822 |
| SRGAN | 0.1521 | 0.2010 | −0.0673 | 0.9229 | 16.1 M | 0.2808 |
| Model | MAE (psu) (Mean ± SD) | 95% CI | RMSE (psu) (Mean ± SD) | 95% CI |
| TSR | 0.1235 ± 6.8195 × 10−4 | [0.1233, 0.1237] | 0.1657 ± 0.0010 | [0.1654, 0.1660] |
| SRCNN | 0.1468 ± 8.9885 × 10−4 | [0.1466, 0.1471] | 0.1944 ± 0.0012 | [0.1941, 0.1947] |
| VDSR | 0.1970 ± 0.0011 | [0.1967, 0.1973] | 0.2567 ± 0.0017 | [0.2563, 0.2572] |
| EDSR | 0.1395 ± 7.4581 × 10−4 | [0.1393, 0.1397] | 0.1863 ± 0.0010 | [0.1860, 0.1866] |
| SRResNet | 0.1433 ± 8.3597 × 10−4 | [0.1430, 0.1435] | 0.1896 ± 0.0011 | [0.1893, 0.1899] |
| SRGAN | 0.1533 ± 0.0010 | [0.1530, 0.1536] | 0.2027 ± 0.0014 | [0.2023, 0.2031] |
| Model | MB (psu) (Mean ± SD) | 95% CI | (Mean ± SD) | 95% CI |
| TSR | −0.0078 ± 0.0018 | [−0.0083, −0.0073] | 0.9485 ± 7.7903 × 10−4 | [0.9483, 0.9487] |
| SRCNN | −0.0499 ± 0.0020 | [−0.0505, −0.0493] | 0.9291 ± 0.0012 | [0.9288, 0.9294] |
| VDSR | −0.0461 ± 0.0022 | [−0.0467, −0.0454] | 0.8763 ± 0.0022 | [0.8757, 0.8769] |
| EDSR | −0.0414 ± 0.0019 | [−0.0419, −0.0409] | 0.9349 ± 9.7201 × 10−4 | [0.9346, 0.9352] |
| SRResNet | −0.0528 ± 0.0019 | [−0.0533, −0.0522] | 0.9326 ± 0.0011 | [0.9323, 0.9329] |
| SRGAN | −0.0681 ± 0.0020 | [−0.0686, −0.0675] | 0.9229 ± 0.0015 | [0.9225, 0.9233] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Bao, S.; Zhang, W.; Wang, H.; Yan, H.; Dai, J.; Xiao, P. Spatiotemporal Super-Resolution of Satellite Sea Surface Salinity Based on a Progressive Transfer Learning-Enhanced Transformer. Remote Sens. 2025, 17, 2735. https://doi.org/10.3390/rs17152735
Liang Z, Bao S, Zhang W, Wang H, Yan H, Dai J, Xiao P. Spatiotemporal Super-Resolution of Satellite Sea Surface Salinity Based on a Progressive Transfer Learning-Enhanced Transformer. Remote Sensing. 2025; 17(15):2735. https://doi.org/10.3390/rs17152735
Chicago/Turabian StyleLiang, Zhenyu, Senliang Bao, Weimin Zhang, Huizan Wang, Hengqian Yan, Juan Dai, and Peikun Xiao. 2025. "Spatiotemporal Super-Resolution of Satellite Sea Surface Salinity Based on a Progressive Transfer Learning-Enhanced Transformer" Remote Sensing 17, no. 15: 2735. https://doi.org/10.3390/rs17152735
APA StyleLiang, Z., Bao, S., Zhang, W., Wang, H., Yan, H., Dai, J., & Xiao, P. (2025). Spatiotemporal Super-Resolution of Satellite Sea Surface Salinity Based on a Progressive Transfer Learning-Enhanced Transformer. Remote Sensing, 17(15), 2735. https://doi.org/10.3390/rs17152735





