Highlights
What are the main findings?
- Integrating a brightness temperature prediction loss function based on the radiative transfer process enhances the learning of satellite salinity features in traditional neural networks.
- Embedding the radiative transfer process within the loss function enables better capture of complex characteristics in satellite observation data.
What is the implication of the main finding?
- PINN improves the accuracy of salinity bias correction for time-series data.
- PINN enhances the model’s ability to correct data in areas with current disturbances, increasing reliability and accuracy in complex environments.
Abstract
Sea surface salinity (SSS) observations play a crucial role in the study of ocean circulation, climate variability, and marine ecosystems. However, current satellite SSS products suffer from systematic biases due to factors such as radio frequency interference (RFI) and land contamination, resulting in fundamental limitations to their application for SSS monitoring. To address this issue, we propose a physics-informed neural network (PINN) approach that directly integrates radiative transfer physical processes into the neural network architecture for SMAP L2 SSS bias correction. This method ensures oceanographically consistent corrections by embedding physical constraints into the forward propagation model. The results demonstrate that PINN achieved a root mean square error (RMSE) of 0.249 PSU, representing a 5.3% to 8.5% relative performance improvement compared to conventional methods—GBRT, ANN, and XGBoost. Further temporal stability analysis reveals that PINN exhibits significantly reduced RMSE variations over multi-year periods, demonstrating exceptional long-term correction stability. Meanwhile, this method achieves more uniform bias improvement in contaminated nearshore regions, showing distinct advantages over the inconsistent correction patterns of conventional methods. This study establishes a physics-constrained machine learning framework for satellite SSS data correction by integrating oceanographic domain knowledge, providing a novel technical pathway for reliable enhancement of Earth observation data.
1. Introduction
Sea surface salinity (SSS) serves as a critical physical parameter in marine environments, influencing heat transfer and ocean circulation patterns and playing a pivotal role in the global climate system [1]. Traditional SSS monitoring has primarily relied upon sparse in situ observations, which provide limited spatial coverage and temporal resolution. The introduction of satellite remote sensing technology marked a significant advancement, beginning with ESA’s SMOS satellite (2009–present) and continuing with NASA’s Aquarius (2011–2015) and SMAP (2015–present) missions [2]. These L-band passive microwave sensors provide unprecedented global SSS coverage, complementing in situ observations by capturing mesoscale oceanic elements that are difficult to detect through conventional point measurements [3].
Despite these technological advances, significant limitations persist in satellite-derived SSS products. Multiple sources of systematic errors have been identified that compromise Bias Correction accuracy. First, satellite-derived SSS demonstrates elevated uncertainty in coastal regions, principally attributed to radio frequency interference generated by anthropogenic activities and land–sea contamination effects [4]. Second, the sensitivity of brightness temperature to salinity diminishes with decreasing sea surface temperature, leading to error amplification in high-latitude cold environments where effective bias correction becomes increasingly challenging [5]. Third, anomalous mixed-layer conditions resulting from intense precipitation and elevated wind speeds, combined with insufficient multi-source data fusion, render single-variable correlation models inadequate under complex environmental conditions [6]. Most critically, existing satellite SSS products exhibit substantial regional biases and systematic errors that limit their direct application in oceanographic studies and climate modeling [7].
Recognizing these fundamental limitations, advanced computational approaches have been increasingly adopted for bias correction and accuracy enhancement of satellite-derived SSS products. Within empirical modeling frameworks, machine learning methodologies have been demonstrated as effective approaches for improving satellite SSS Bias Correction, as these algorithms can identify and model complex nonlinear relationships between environmental variables and SSS [8]. Fundamental improvements in satellite data processing have also contributed to enhanced SSS accuracy, with Boutin et al. [7] demonstrating systematic error reduction in SMOS SSS retrievals through relaxed filtering in high natural salinity variability regions and correction of seasonally varying latitudinal systematic errors and improved variability representation. Several notable contributions have been made in developing machine learning-based correction schemes for Level-3 SSS products. Jang [9] developed a comprehensive global SSS bias correction utilizing seven machine learning approaches—including k-nearest neighbors, support vector regression, artificial neural network, random forest, and gradient boosting methods—achieving significant enhancement of SMAP Level-3 Bias Correction accuracy with strengthened correlation to in situ data across global oceanic regions. Similarly, precipitation-based correction methodologies have been implemented by Qin et al. [10], who employed precipitation data to correct latitude-dependent biases in SMAP SSS estimates. The superiority of ensemble methods has been further validated by Rajabi-Kiasari and Hasanlou [11], who demonstrated that gradient boosting machines and random forest methods exhibited superior performance compared to conventional approaches in SSS bias correction applications. Recent advances have expanded machine learning applications to region-specific SSS improvements and advanced classification methodologies. Savin et al. [12] achieved substantial accuracy improvements in Arctic Ocean SSS retrieval through ensemble machine learning approaches, while Song et al. [13] developed light gradient boosting models specifically for coastal region SMAP SSS retrieval. Furthermore, contemporary methodologies have evolved beyond conventional supervised frameworks, with Ouyang et al. [14] implementing unsupervised classification algorithms to characterize SMAP Level-3 SSS bias distributions and identify systematic mid-latitude biases. Buongiorno et al. [15] applied support vector machines for regional bias reduction and the development of multi-sensor fusion algorithms combining SMOS and SMAP observations.
However, a critical gap exists in current research approaches, as most existing studies focus exclusively on Level-3 gridded products rather than addressing the fundamental errors present in Level-2 swath data [16]. Furthermore, contemporary methodologies predominantly employ purely data-driven approaches that neglect the underlying physical processes governing microwave radiative transfer and salinity Bias Correction [17]. This separation between physical understanding and statistical correction limits the interpretability and generalizability of existing correction schemes, particularly across diverse oceanographic conditions.
In recent years, physics-informed neural network (PINN) has emerged as a promising methodologies that achieve physics-data dual-driven fusion optimization through embedding physical laws directly within neural network architectures [18]. The integration of physical constraints into machine learning frameworks has demonstrated substantial improvements in various oceanic applications. For instance, Yoon et al. [19] utilized PINN to construct OceanPINN for marine acoustic research, achieving approximately 30% error reduction compared to conventional methods through the incorporation of wave propagation physics. This physics-informed approach addresses the fundamental limitation of traditional neural network that lack physical interpretability while maintaining the flexibility to adapt to complex environmental conditions.
To address these fundamental limitations, A novel bias correction model utilizing physics-informed neural network (PINN) for SMAP Level-2 SSS Data in the Pacific Ocean is presented. The proposed methodology aims to integrate radiative transfer physics directly into neural network architectures through end-to-end differentiable optimization. Furthermore, the framework implements latitude-band-based mechanisms for learning spatially varying physical parameters that accommodate regional oceanographic diversity. Additionally, the approach enables adaptive optimization of wind speed-roughness parameters in the Radiative Transfer Model across diverse environmental conditions. Three key innovations are achieved in this bias correction model: First, a “physics-embedded neural network” approach is developed that channels network-predicted salinity corrections through a complete radiative transfer model, ensuring brightness temperatures align with observations during the optimization process in accordance with the physics-ML integration framework suggested by Willard et al. [20]. Second, a latitude-band-based mechanism for learning spatially varying physical parameters is implemented, enabling zonal characterization of Pacific ocean regions based on their dynamic properties and supporting adaptive optimization across diverse environments. Third, an end-to-end differentiable framework is created that combines the Grossman-West dielectric constant model [21] with differentiable radiative transfer equations, addressing the dual challenges of traditional neural network that lack physical interpretability and conventional physical models that have restricted regional adaptability.
The organization of this paper is structured as follows: Section 2 introduces the datasets and methodology. Section 3 presents the physics-informed neural network model and benchmark models for comparison. Section 4 evaluates model performance across multiple dimensions. Section 5 presents the importance of elements using SHAP.
2. Materials and Methods
2.1. Materials
2.1.1. EN4.2.2 Data
The EN4.2.2 dataset, hereafter referred to as EN4, represents the latest version of the UK Met Office Hadley Centre’s EN series. It provides subsurface temperature and salinity data spanning from 1900 to the present, encompassing both quality-controlled profiles and objective analyses. The database is updated with an approximate half-month delay. EN4 incorporates data from four primary sources: Argo floats, the Arctic Synoptic Basin-wide Oceanography (ASBO) project, the Global Temperature and Salinity Profile Programme (GTSPP), and the World Ocean Database 2018 (WOD18). Argo and GTSPP data are collected monthly from their respective processing centers, while WOD18 data were downloaded as a single batch in October 2020 and remain static until the creation of new EN4 versions.
2.1.2. SMAP Data
SMAP salinity data are produced by Remote Sensing Systems and sponsored by the NASA Ocean Salinity Science Team, available at www.remss.com. The V6 final products maintain a 4-day latency for Level-2C data, distributed on a 0.25° × 0.25° grid with a characteristic resolution of 70 km and approximately 3-day global coverage. In addition to direct SMAP radiometric observations of brightness temperature (Tb) for each polarization (H and V), this study utilizes land fraction data, derived SSS estimates, and auxiliary datasets employed in the CAP/JPL algorithm. The SMAP salinity bias correction algorithm processes Level-2B files to generate calibrated SMAP Level-2C surface ocean brightness temperatures and sea surface salinity values. The auxiliary data sources include NCEP GDAS 0.25° 6-hourly atmospheric fields for atmospheric correction, CCMP V2 wind speed and direction products, the T. Meissner, F. Wentz [22,23] dielectric constant model formulation, HYCOM model data for reference salinity fields, and IMERG precipitation data for rainfall impact correction.
2.1.3. Data Splitting and Preprocessing
The spatial domain encompasses the Pacific Ocean region (60°S–60°N, 110°E–80°W), representing the world’s largest ocean basin. The Pacific Ocean was selected as the study region due to its critical role in global climate regulation through hosting the El Niño-Southern Oscillation (ENSO), which drives significant salinity variability and provides diverse testing conditions for algorithm development [24]. The basin exhibits complex salinity dynamics with distinct variability modes spanning from decadal to global warming-related timescales [25], while its vast spatial extent encompasses diverse oceanographic conditions essential for developing robust SSS bias correction methodologies [26]. Additionally, the Pacific’s dominant influence on ocean-atmosphere interactions and climate variability makes accurate SSS measurements particularly critical for operational forecasting applications [7,25,27].
Data preprocessing involved standardizing SMAP L2 products using 4 polarizations (V, H, S3, and S4-pol) and 2 look angles (look = 1,2), while EN4.2.2 data utilized uppermost profile SSS values.
In situ SSS data were co-located with SMAP L2C products using spatial separation < 50 km and temporal window < ±24 h, prioritizing minimum spatial distance matches [7,15]. This yielded 1,628,851 co-located Pacific Ocean data points (April 2015–December 2022) from global matches. Quality control procedures sequentially removed records with missing key parameters, filtered data based on physically plausible ranges (SSS: 10–40 PSU; SURTEP: 273–308 K;),nd excluded data points where to eliminate anomalous measurements from sensor failure, land contamination, or extreme environmental conditions.
Despite implementing various control measures, validation continues to face challenges from measurement discrepancies. Satellite sensors measure near-surface salinity at centimeter depth, while in situ data are collected from 0 to 10.0475 m. This discrepancy may introduce systematic biases due to salinity variations from precipitation and evaporation. Volkov et al. [28] found that the mean salinity difference between 0.4 m and 5 m is negative (−0.016 ± 0.094 PSU), indicating minimal variation. Comparisons of drifter measurements at 0.4 m with satellite sea surface salinity (SSS) products showed significantly larger discrepancies, often exceeding an order of magnitude. Their study emphasizes that these discrepancies arise more from differences in spatial and temporal sampling scales than from depth variations. Therefore, quality control is necessary when analyzing these data, focusing solely on in situ measurements from 0 to 5 m for detailed comparison.
After quality control, the Pacific dataset size was 1,236,500. The final outlier removal step resulted in a dataset of 1,166,527 points, retaining 94.34% of the quality-controlled Pacific data and representing an overall data reduction of less than 6%. This preprocessing ensures that all subsequent analyses are based on physically sound oceanographic observations.
To ensure a quasi-balanced data distribution for model training, the Pacific Ocean was partitioned into the following latitudinal zones, after partitioning, the distribution of data points in each region is shown in Table 1:

Table 1.
Zonal Partitioning and Data Distribution of the Pacific Ocean Dataset.
After spatial-temporal matching in the Pacific region, 1,166,527 co-located observations were employed for analysis. The geographical distribution of these data points across the four distinct latitudinal zones is illustrated in Figure 1.
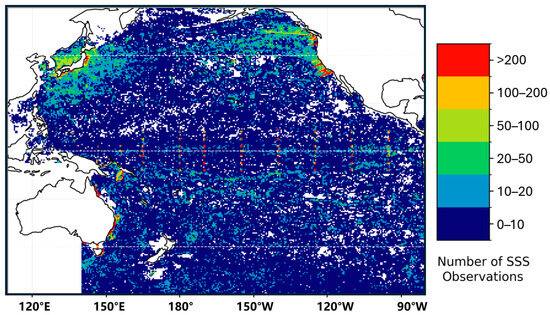
Figure 1.
Spatial Distribution of Quality-Controlled Data Points Across Pacific Ocean Latitudinal Zones.
2.2. Methods
Our physics-informed neural network (PINN) model integrates machine learning with physical oceanographic principles by embedding radiative transfer equations into the neural network loss function. The architecture employs a Multi-Layer Perceptron with 16-dimensional input processed through three hidden layers (64 nodes each) to predict salinity correction values. The fundamental innovation lies in incorporating L-band brightness temperature physics as a constraint mechanism—a forward radiative transfer model predicts brightness temperature from corrected salinity, creating a physics-based loss term alongside traditional data-fitting loss. This dual-constraint system enables the network to learn corrections that are both empirically accurate and physically plausible, addressing limitations of purely data-driven approaches that may violate electromagnetic wave propagation theory.
The process begins with the ANN, which takes seven geophysical parameters as input to generate an initial salinity prediction (). This prediction is then fed into two parallel loss calculations: (1) a direct comparison with measured in situ salinity () to produce the data loss (), and (2) a forward radiative transfer model, which accounts for factors like learnable wind speed factors A and B to produce a predicted brightness temperature (). This is then compared against SMAP observations to generate the physics loss (). The combined, weighted loss () drives the iterative optimization of the ANN. Moreover, because the internal physical relationships within the model remain consistent—satisfying Maxwell’s equations and the laws of radiative transfer—the model maintains its physical plausibility. This allows the forward model to be structured as a loss term, thereby embedding physical information into the neural network.
2.2.1. Input Parameters for the Models
The input parameters include critical observational and geospatial contexts necessary for effectively predicting salinity correction, while also accounting for quantities that exhibit different polarizations in the physical processes. In total, there are 20 input elements utilized in the model. A summary of these input parameters is provided in Table 2.

Table 2.
Summary of Input Parameters.
To validate the intrinsic correlations between the physical variables in our proposed PINN framework, we conducted a Pearson correlation analysis on key ocean remote sensing parameters (Figure 2). This heatmap illustrates the Pearson correlation coefficients (r) for all pairs of input variables.
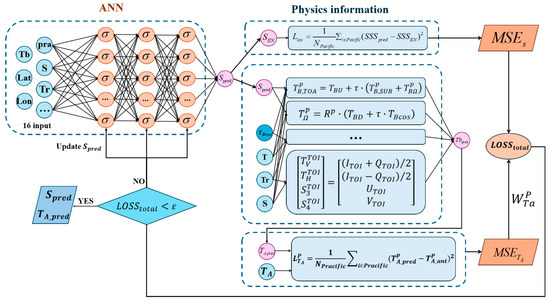
Figure 2.
Workflow of the PINN model, showing how a physics-driven loss function constrains and optimizes the output of an Artificial Neural Network (ANN).
As shown in Figure 3, the strongest positive relationships are between the atmospheric path terms tbup and tbdw (r = 1). Sea surface temperature (surtep) remains strongly coupled with atmospheric transmissivity (tran) (r = 0.797). The dominant negative correlations follow radiative-transfer expectations: tbup and tbdw decrease with increasing tran (r = −0.722 and −0.721, respectively). The reflected Galactic component anticorrelates with the Faraday rotation proxy (pratot_exp) (r = −0.597), and pratot_exp shows a negative correlation with latitude (r = −0.583). Additionally, the correlation between sea surface salinity (smap_sss) and surtep is 0.29, indicating a moderate negative relationship.
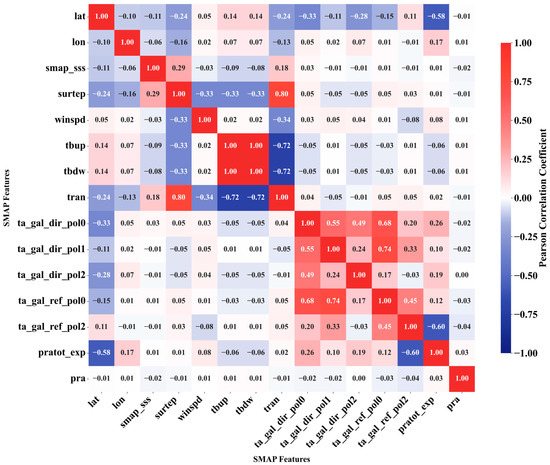
Figure 3.
Pearson Correlation Coefficient Heatmap of the model input parameters. (The element ta_gal_ref_pol1 shows values of 0 across all correlations, indicating no meaningful relationship with other SMAP elements and can therefore be excluded from further analysis.).
2.2.2. Construction of the PINN Model
The PINN model integrates radiative Transfer physics with neural network optimization through a forward physics model that calculates theoretical brightness temperature from salinity values, followed by a multi-component loss function that ensures both physical consistency and data accuracy. The derivation begins with the Radiative Transfer Model (RTM) from Meissner & Wentz [23,29], which combines the formulation of radiative transfer and systematic simplifications needed to accurately represent surface emissivity, including corrections for wind-induced roughness. This foundational framework progresses through the application of a Stokes vector to describe the combined polarization state of the received signal at the Top of Atmosphere (TOA), facilitating a detailed analysis of the signal’s polarization characteristics, while also transitioning the Stokes vector measured at the Earth’s surface to the TOI brightness temperature vector, accounting for specific gain characteristics of the satellite system and contributions from galactic radiation. The process culminates in the optimization of a multi-component loss function, ensuring that the model maintains both physical consistency and accuracy in its salinity predictions. In the equations that follow, the superscript P indicates the polarization state of the respective elements.
- (1)
- Radiative Transfer Model Formulation
Based on the Radiative Transfer Model (RTM) function from Meissner & Wentz [23,29], the general expression for the polarized radiative Transfer model at the Top of Atmosphere (TOA) is formulated in Equation (1):
where represents the upwelling radiation from the ocean surface, is atmospheric Transmittance, is the total sea surface emissivity, and is the sea surface brightness temperature. is the downwelling sky radiation that is scattered off the ocean surface in the direction of the observation. At L-band frequencies, it is a very good approximation to write:
where is the downwelling atmospheric radiation that is incident on the ocean surface, is the Space radiation, which consists of cosmic background (2.73 K). is the ocean surface reflectivity [30].
- (2)
- Emissivity Components and Corrections
The surface emissivity can be simplified to comprise two components in Equation (3), the flat surface emissivity and wind-induced roughness correction.
The emissivity of the specular ocean surface is by far the largest part. It depends on f the frequency band, specifically the L-band for this detection, θ the incidence angle, T the sea surface temperature, and S the sea surface salinity and is related to the complex dielectric constant of sea water ε by means of the Fresnel equations. Following Fresnel reflection theory, the flat surface emissivity for polarization p at the SMAP satellite’s incidence angle of is calculated as
The complex dielectric constant in Equation (5) links electromagnetic properties to oceanographic parameters through the GW model of Zhou et al. [21]:
where and are empirical coefficients, T is sea surface temperature in Celsius, and is sea surface salinity in PSU.
To address the dominant error source in SSS bias correction, wind-induced surface roughness is incorporated through a learnable correction mechanism:
represents wind speed at 10 m height, where A and B are learnable parameters optimized for different latitudinal bands. The Pacific Ocean was divided into four latitudinal bands, each with unique wind speed parameters A and B. Using a PyTorch (version 2.5.1+cu121) implementation, the model minimized RMSE between the forward model-predicted brightness temperature and the SMAP satellite-observed TOA brightness temperature.
- (3)
- Stokes Vector and Polarization Transformation
To describe the combined polarization state of the received signal at the TOA, we represent it using the Stokes vector , which is defined as
where represents the total intensity of the observed brightness temperature, which is derived from the sum of the vertical and horizontal polarized components (, ). The component indicates the difference between these two polarizations, providing insight into the polarization state of the radiation. In this formulation, and correspond to the third and fourth Stokes parameters, which characterize additional aspects of the polarized light.
The rotation angle is the sum of the antenna polarization angle and the Faraday rotation angle , which accounts for the effects of the ionosphere. Here, represents the total polarization rotation angle including the Faraday effect, while denotes the geometric polarization rotation angle. The relation is expressed as
Additionally, the rotation matrix is defined to model the transitions in polarization state, represented as
The Stokes parameters at the Top of Ionosphere (TOI) can be derived through Faraday rotation. The equations encapsulating this transformation are as follows:
Through these transformations, we account for how the polarization state is affected by both the antenna setup and the ionospheric conditions, particularly the effects introduced by Faraday rotation.
Subsequently, the polarized brightness temperatures at the TOI are obtained via an inverse Stokes transformation:
This transformation allows for the extraction of polarized brightness temperatures from the Stokes parameters, enabling a more nuanced understanding of the radiation characteristics at the TOI.
- (4)
- Galactic Radiation Contribution
Furthermore, to transition the Stokes vector measured at the Earth’s surface to the TOI brightness temperature vector , by utilizing a transformation matrix , which encapsulates the specific gain characteristics of the satellite system [31]. This relationship is expressed as
where the elements of matrix A (4-byte real) correspond to the gain coefficients that adjust the Stokes parameters I, Q, S3, and S4.
Moreover, the brightness temperature predictions are influenced by both Earth’s thermal emissions , and aggregated space radiation terms which are critical in [32]. While the direct galactic contribution and the reflected galactic component , which can reach up to 5 K, complicate the measurement process. Accurately accounting for these elements is vital for discerning the true characteristics of the Earth’s radiation. This relationship is expressed as
- (5)
- Loss Function
The PINN optimization leverages this physics model through a multi-component loss function that ensures both physical consistency and data accuracy. The physics-based constraint in Equation (11) ensures that predicted salinity values produce brightness temperatures consistent with satellite observations:
where is calculated using the forward model described in Equations (3)–(10). The data-fitting component in Equation (12) directly optimizes salinity prediction accuracy:
The total loss function combines these objectives through variance-normalized weighting:
where and are the normalized brightness temperature loss and salinity loss, respectively. The coefficient encapsulates the impact of brightness temperature on the overall loss. By reducing this brightness temperature loss, the model aims to extract elements that make predicted salinity values as close as possible to actual measurements. The brightness temperature physical consistency loss also ensures that the salinity predictions output by each hidden layer are constrained, so that salinity correction results not only follow data statistical patterns but also adhere to the physical processes of radiative transfer. This provides dual constraints on salinity correction, making the predicted salinity more accurate than measured salinity while maintaining its physical relationship with brightness temperature. This is an advantage that traditional data-driven methods cannot offer.
2.2.3. Model Training Methodology
To facilitate a fair and dependable comparison, this study employs three well-established machine learning algorithms as baselines: Artificial Neural Network (ANN) [33], Gradient Boosting Regression Trees (GBRT) [34,35,36,37], and Extreme Gradient Boosting (XGBoost) [38,39]. All models examined in this study, including the proposed PINN method and the baseline algorithms for comparison, rely on the same set of seven input parameters to enable a fair comparison. Each model adheres to standardized training protocols under uniform experimental conditions, highlighting reproducibility and comparability through consistent data preprocessing, validation strategies, and evaluation metrics.
The training framework uses a time-based data partitioning method to guarantee reliable performance evaluation and avoid data leakage. The full dataset contains 1,453,838 samples, which are divided along chronological lines: data from 2020 and earlier is used for the training phase (1,453,838 samples), data from 2021 serves as the validation set (81,606 samples), and data from 2022 is set aside as the independent testing period (79,214 samples), enabling an unbiased performance assessment. This sequential time-based division ensures that model development and hyperparameter tuning rely solely on historical training data, while the subsequent year’s validation data guides model optimization, and the future year’s data acts as a completely independent test set to evaluate how well the model generalizes over time and its preparedness for deployment in application situations.
Before the final training, we performed hyperparameter tuning for each model to enhance performance. For the PINN and ANN models, we defined a hyperparameter space suitable for grid search, including batch size, hidden layer size, and learning rate. Similarly, for tree-based methods, such as GBRT and XGB, comprehensive parameter tuning was conducted, optimizing the number of training estimators, maximum tree depth, subsampling ratio, and learning rate, employing cross-validation techniques to ensure the reliability of evaluations.
During this process, we initially conducted Bayesian optimization, performing a total of nine iterations. The results indicated that, for the neural network models, the most crucial hyperparameter was the learning rate, while for the tree models, the two most significant hyperparameters were the subsampling ratio and the learning rate. Building upon these findings, we conducted a 3 × 3 grid search to refine the hyperparameter settings, ensuring the identification of local optimal parameters. This process was complemented by an additional small-scale grid search, based on the results from Bayesian optimization, which allowed us to further fine-tune the hyperparameter configuration. Throughout the training process, an early stopping mechanism was employed to prevent overall overfitting of the model and to maintain the best generalization performance. Specifically, all models were set to stop training before reaching 100 epochs, thus establishing a Training Epochs limit of 100.
Table A1 presents the hyperparameter optimization process, while Table 3 details the final training configurations for each model, highlighting the consistency of training parameters for the neural network and the optimized settings for tree-based methods. This systematic approach to hyperparameter adjustment and optimization not only ensures comparability of model performance but also establishes a solid foundation for subsequent analysis and interpretation of results.

Table 3.
Training Configuration Comparison for Different Models.
The PINN model utilized the same training hyperparameters as the ANN model to assess the effectiveness of physical loss, thereby ensuring that the optimization process could achieve local model optimality and enhance the reliability of the results. The parameter in the PINN model is specifically designed to account for various polarization settings based on the correlation between brightness temperature and sea surface salinity (SSS). It is set to be proportional to the size of the brightness temperature values across different polarizations. This simplification ensures that the model effectively captures the relationship between these parameters, enhancing its ability to accurately predict outputs based on varying polarization conditions.
2.2.4. Evaluation Metrics
The evaluation of satellite salinity data primarily uses several statistical indicators, including bias, Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and coefficient of determination (R2).
Bias represents the systematic error between predicted data and in situ measurements, indicating whether the predicted data demonstrates consistent overestimation or underestimation. RMSE measures the overall error magnitude between predicted and in situ data. Unlike bias, RMSE captures random errors present in the data. MAE offers a robust measure of average prediction error that is less sensitive to outliers compared to RMSE. R2 signifies the proportion of variance in the in situ data explained by the predictions, with values closer to 1 indicating improved model performance.
For regional comparative analysis, we developed an improvement metric to quantify changes in the predictive capability of models across different grid points.
The methodology for calculating bias improvement includes:
- (1)
- spatial aggregation—organizing all prediction points within each 0.5° grid cell for the year 2022;
- (2)
- cumulative bias computation-calculating for original SMAP L2C bias and for algorithm-predicted bias within each grid cell;
- (3)
- , yielding values ranging from −1 to +1, where positive values indicate successful bias reduction and negative values represent performance degradation relative to the original satellite bias correction.
Table 4 presents the corresponding algorithms for these evaluation metrics, where N represents the total number of samples, and refer to the predicted and in situ measured salinity values for the i sample, respectively, and represents the mean value of all in situ measurements.

Table 4.
Statistical Evaluation Metrics for Satellite Salinity Data Assessment.
3. Results
3.1. The Performance of Different Models
Based on the multi-dimensional quantitative evaluation results shown in Table 5, the comprehensive performance ranking of the four sea surface salinity correction algorithms is: PINN > GBRT > XGB > ANN. This ranking is primarily based on RMSE as the dominant indicator, while comprehensively considering the collaborative performance of R2, MAE, and BIAS. The results demonstrate that all machine learning methods significantly outperform the original satellite products, validating the technical advantages of data-driven modeling in the Bias Correction model.

Table 5.
Performance Indicators of Different Models (Pacific Region).
PINN, as the core innovative method of this study, achieves comprehensive performance improvements compared to traditional Artificial Neural Network (ANN). The scatter plot analysis in Figure 4 provides visual evidence of these improvements: precision improvement with RMSE reduced from 1.233 PSU to 0.277 PSU (77.5% improvement), robustness enhancement with MAE decreased from 0.895 PSU to 0.149 PSU (83.3% improvement in error control), and explanatory power enhancement with R2 increased from −0.052 to 0.956 (significant improvement in model fit).
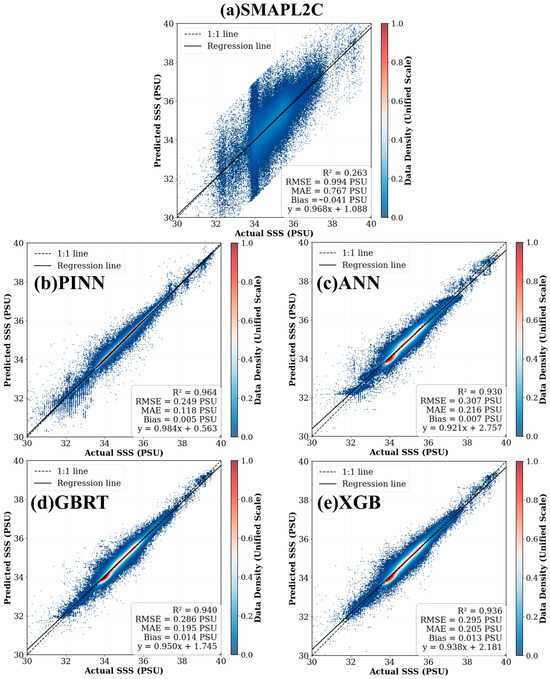
Figure 4.
Scatter Plot Comparison of Predicted Sea Surface Salinity/SMAPL2 Sea Surface Salinity vs. Actual Sea Surface Salinity Values for Different Algorithms. Results from (a) SMAP L2C, (b) PINN, (c) ANN, (d) GBRT, and (e) XGB algorithms. Dashed lines represent perfect agreement (1:1) and solid lines show actual model fits.
The original SMAP L2C product exhibits significant scatter with poor correlation (R2 = 0.263), particularly deviating from the 1:1 line in high salinity ranges, while all machine learning approaches demonstrate substantial improvements with tight clustering around the ideal relationship. PINN shows the most concentrated distribution with the highest correlation (R2 = 0.964), followed by GBRT and XGB, which display strong linear relationships but with slightly more scatter, whereas ANN shows reasonable performance but greater dispersion compared to physics-informed methods.
The analysis of algorithm performance across different salinity ranges shows notable differences in predictive accuracy, particularly highlighting the benefits of the physics-informed neural network (PINN). As shown in Table 6, PINN outperforms the artificial neural network (ANN) model in both low and high salinity ranges. Specifically, PINN achieves a lower Root Mean Square Error (RMSE) of 0.561 in the 30–32 PSU range and 0.259 in the 38–40 PSU range, indicating better accuracy in these salinity levels affected by freshwater inputs and high salinity environments, respectively.

Table 6.
Comparison of Root Mean Square Error (RMSE) for Different Models Across Salinity Ranges.
In comparison to the Gradient Boosted Regression Trees (GBRT) and XGBoost (XGB) models, PINN shows consistent performance across the entire salinity range with RMSE values of 0.238 in the 32–38 PSU range. While GBRT and XGB perform well in moderate salinity ranges (32–38 PSU) with RMSE values of 0.282 and 0.290, respectively, they exhibit less reliability at salinity extremes due to their limited capacity to generalize outside of their trained data. PINN’s ability to leverage physical principles enables it to provide more accurate predictions, especially in data-sparse regions, reinforcing its strengths across all salinity bands.
3.2. Band-Specific Performance Analysis
Latitudinal variations drive distinct oceanographic processes across the Pacific Ocean-from polar regions dominated by sea ice dynamics and freshwater input, to tropical zones characterized by intense evaporation and complex current systems, and mid-latitude regions experiencing strong seasonal variability [7,40]. These environmental differences create varying bias correction challenges that may favor different algorithmic approaches. Therefore, we implemented a latitudinal band stratification approach to examine how physics-informed methods maintain performance consistency across climate zones compared to traditional machine learning approaches, and to identify which algorithms provide the most reliable predictions across the complete latitudinal spectrum.
Figure 5 provides a systematic visual comparison of algorithm performance across four distinct latitudinal bands, demonstrating varying degrees of scatter and correlation patterns that directly correspond to the quantitative metrics presented in Table 7. The multi-panel visualization shows how each method responds to varying oceanic conditions from high-latitude (Band 0) to equatorial environments (Band 3), where dashed lines represent the ideal 1:1 relationship and solid lines show fitted linear regression relationships.
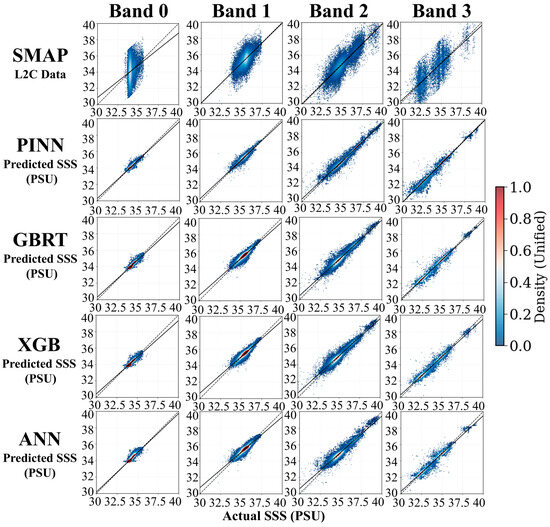
Figure 5.
Band-Stratified Performance Analysis: Scatter Plot Comparison of Algorithm Predictions Across Different Salinity Concentration Ranges. Solid lines represent perfect agreement (1:1) and dashed lines show linear regression fits.

Table 7.
Performance Metrics by Salinity Concentration Bands.
The visual analysis in Figure 5 confirms the quantitative findings in Table 7. In Band 0, the scatter plots reveal that XGB and GBRT exhibit tighter clustering around the 1:1 line with minimal scatter, visually corroborating their superior RMSE values of 0.173 PSU and 0.169 PSU, respectively, compared to PINN’s RMSE of 0.118 PSU and the noticeably more dispersed ANN predictions at 0.192 PSU. The effectiveness of the ensemble methods in polar regions is evident from the concentrated data distribution and strong fit in their respective panels.
Band 0 showcases the initial performance metrics, where PINN exhibits a strong baseline with an RMSE of 0.118 PSU and an R2 value of 0.904. In comparison, XGB and GBRT perform reasonably well with R2 values of 0.816 and 0.825, respectively. However, they show higher RMSEs of 0.173 PSU and 0.169 PSU, indicating a less accurate prediction compared to PINN. The bias for PINN is 0.016 PSU, which further emphasizes its accuracy over the tree-based models.
Band 1 marks a critical transition zone where the visual patterns dramatically shift in favor of PINN. The scatter plot shows PINN achieving a much tighter linear relationship with reduced scatter compared to XGB (R2 = 0.847) and GBRT (R2 = 0.849), which display increased dispersion and systematic deviations from the 1:1 line. This visual improvement directly corresponds to PINN’s correlation (R2 = 0.927), demonstrating how physics-informed constraints become increasingly valuable in transitional oceanic regimes.
Band 2 represents the most striking visual demonstration of PINN’s superiority, where the scatter plot shows an exceptionally tight clustering around the 1:1 line with minimal systematic bias. The visual excellence directly correlates to PINN’s exceptional quantitative performance (R2 = 0.955, RMSE = 0.306 PSU), while XGB and GBRT panels show noticeably increased scatter and deviation patterns that align with their higher RMSE values (0.367 PSU and 0.358 PSU, respectively). This mid-latitude performance advantage visibly confirms the critical importance of incorporating physical constraints in typical open-ocean conditions.
In Band 3, both PINN and GBRT scatter plots demonstrate tight relationships with concentrated data distributions, visually supporting their comparable high R2 values (0.956 for PINN and 0.986 for GBRT). However, PINN’s plot shows more consistent clustering without the subtle systematic deviations visible in other methods, reflecting its superior bias performance (−0.071 PSU) compared to the more variable bias patterns exhibited by tree-based methods.
3.3. Spatio-Temporal Performance Analysis
Understanding the temporal stability of algorithm performance through daily RMSE time series analysis is crucial for operational satellite oceanography, enabling the identification of seasonal variations, systematic biases, and optimal ensemble strategies that leverage complementary algorithm strengths [16,41,42,43].
The temporal stability analysis reveals PINN’s superior consistency across the entire Pacific Ocean, exhibiting the lowest and most stable daily RMSE values throughout 2022. Table 8 presents quantitative performance during four critical periods where algorithm differences were most pronounced, demonstrating PINN’s exceptional robustness during challenging oceanographic conditions.

Table 8.
Model Performance During Critical Periods Identified in Figure 6. Values represent daily RMSE in PSU (Practical Salinity Units). Bold values indicate the best performance for each date. Periods (a), (b), and (c) correspond to the marked critical events in Figure 6, where algorithm performance differences were most pronounced.
Table 8.
Model Performance During Critical Periods Identified in Figure 6. Values represent daily RMSE in PSU (Practical Salinity Units). Bold values indicate the best performance for each date. Periods (a), (b), and (c) correspond to the marked critical events in Figure 6, where algorithm performance differences were most pronounced.
| Period | Date | ANN | PINN | XGBoost | GBRT |
|---|---|---|---|---|---|
| a | 5 June 2022–6 June 2022 | 0.478 | 0.194 | 0.331 | 0.303 |
| b | 16 October 2022–17 October 2022 | 0.505 | 0.301 | 0.392 | 0.407 |
| c | 3 December 2022–4 December 2022 | 0.502 | 0.209 | 0.286 | 0.275 |
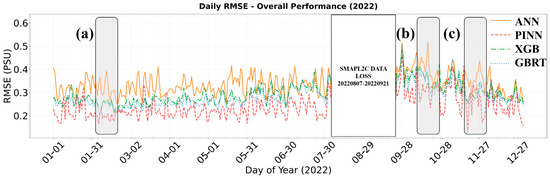
Figure 6.
Temporal Evolution of Daily RMSE for Algorithm Performance Comparison in 2022 (Pacific region). The figure displays the daily root mean square error (RMSE) variations throughout 2022 for four different algorithms (ANN, PINN, XGBoost, and GBRT), with highlighted periods (a–c) corresponding to specific temporal intervals of interest. The data gap period indicates SMAP L2C data loss (20220807–20220921).
During the critical periods marked as (a), (b), and (c), PINN consistently maintained the lowest RMSE values across all timeframes. In Period a (5–6 June 2022), PINN achieved an RMSE of 0.194 PSU compared to ANN’s significantly higher 0.478 PSU. This pattern persisted throughout the year: Period b (16–17 October) showed PINN at 0.301 PSU versus ANN’s 0.505 PSU, and Period c (3–4 December) demonstrated PINN’s 0.209 PSU against ANN’s 0.502 PSU.
The ensemble methods (XGBoost and GBRT) showed intermediate performance, with RMSE values ranging from 0.331 to 0.392 PSU for XGBoost and 0.286 to 0.407 PSU for GBRT, consistently outperforming ANN but falling substantially short of PINN’s stability. Notably, PINN’s RMSE values remained within a narrow range of 0.194, 0.301, and 0.209 PSU across all critical periods, demonstrating remarkable temporal consistency regardless of seasonal variations or challenging oceanographic conditions.
Throughout the temporal analysis, PINN consistently exhibited the most stable performance across all latitudinal bands, with minimal fluctuations and rapid recovery from adverse conditions. GBRT and XGBoost displayed similar performance patterns, with moderate stability and occasional synchronized spikes during extreme conditions. In contrast, ANN exhibited the highest variability, particularly sensitive to seasonal transitions and extreme weather events, underscoring the advantages of physics-informed constraints for temporal consistency.
The spatial analysis reveals that all four algorithms encounter challenges in nearshore and low-latitude regions, where improvement rates frequently fall below zero, indicating that machine learning corrections may inadvertently introduce additional biases in these complex oceanographic environments. These problematic regions likely correspond to areas with complex coastal processes, river discharge influences, and intense air–sea interactions that challenge both satellite bias correction and algorithmic corrections [44,45]
Based on Figure 7, PINN demonstrates superior performance in two critical regions: (1) the northern part of the Kuroshio Current (20°N–50°N, 120°E–180°E) and (2) the South Australian Current region (40°S–0°, 140°E–160°W).
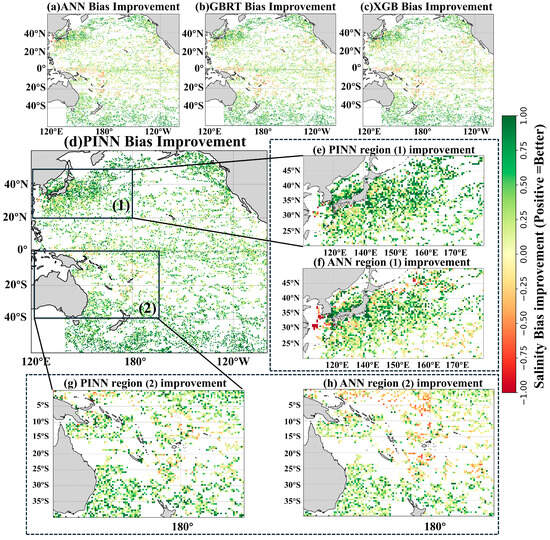
Figure 7.
Spatial Bias Improvement Analysis: Pacific Regional Performance Assessment of Different Algorithms Across the Pacific Ocean. This figure provides a comprehensive spatial comparison of bias improvement across the Pacific Ocean, utilizing a 0.5° × 0.5° grid resolution to evaluate enhancements in algorithm performance relative to the original SMAP L2C bias correction.
In tropical marine environments and offshore areas, satellite-derived sea surface salinity (SSS) products typically align more closely with in situ observations. Consequently, correcting the original satellite salinity measurements poses significant challenges. In our study, Region (1) [46]. Conventional machine learning models often struggle to effectively correct salinity based on the relationships among temperature, salinity, and current velocity, leading to potential fitting errors. In contrast, our PINN model effectively mitigates overfitting in this area, as shown in Table 9.

Table 9.
Regional performance comparison: distribution of salinity bias improvements across different models and geographic regions. Counts of salinity bias improvement across different models, as shown in Figure 7. The table details the number of grid points within the specified improvement range.
Region (2) is located within the South Pacific Convergence Zone (SPCZ), traversed by the South Australian Current (SAC) [47]. The convergence of tropical and subtropical air masses results in frequent rainfall, along with the influence of sea surface evaporation, complicating the interplay between temperature and salinity. Additionally, considering the impacts of global warming (Relationship between sea surface salinity and ocean circulation and climate change), there will be further changes in global hydrological cycles and salinity, posing challenges for machine learning models attempting to fit the elements from previous years in this region. Relatively speaking, the PINN model adheres to physical principles by fitting other relevant parameters, thereby reducing the likelihood of prediction failures.
To further illustrate the predictive results of different models, we have constructed scatter comparison plots (Figure 8 and Figure 9). The distribution of bias across different regions highlights the performance differences among the algorithms in salinity prediction, providing researchers with insights into the effectiveness and applicability of each model. When compared to Figure 7, it becomes evident that the PINN model demonstrates a distinct advantage in the two regions.
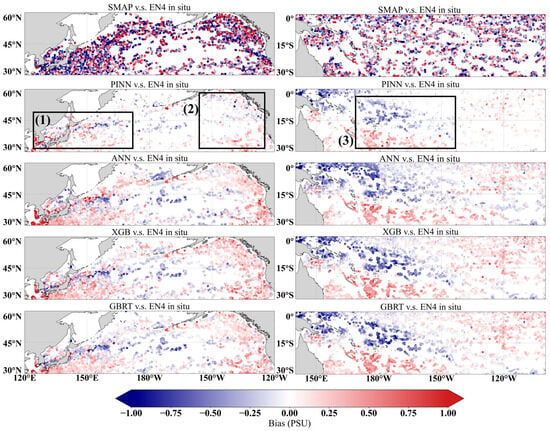
Figure 8.
Comparison of predicted Salinity Bias Scatter Plots Across Different Models. The figure displays the spatial distribution of salinity bias, calculated as the difference between model predictions and actual observations. The left panel covers the North Pacific Ocean (30°N–60°N, 120°E–120°W), while the right panel covers a region of the South Pacific Oceans (30°S–0°, 140°E–100°W). In both plots, dark blue indicates that the model overestimates salinity (positive bias), while dark red indicates underestimation (negative bias). On the color scale, the +1 PSU mark includes all bias values of +1 PSU and higher, and the −1 PSU mark includes all values of −1 PSU and lower. Region (1) represents the confluence area of the Kuroshio and Oyashio currents, region (2) indicates coastal areas influenced by the North Pacific Current, and region (3) denotes areas affected by the East Australian Current and South Equatorial Current.
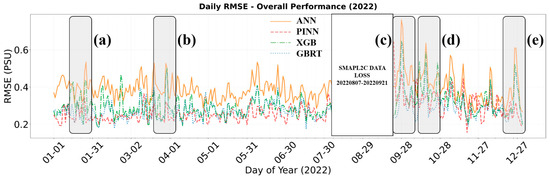
Figure 9.
Temporal Evolution of Daily RMSE for Algorithm Performance Comparison in 2022 (Atlantic region). The figure displays the daily root mean square error (RMSE) variations throughout 2022 for four different algorithms (ANN, PINN, XGBoost, and GBRT), with highlighted periods (a–e) corresponding to specific temporal intervals of interest. The data gap period indicates SMAP L2C data loss (20220807–20220921).
The PINN model demonstrates a significant improvement in predictive accuracy across several dynamically complex oceanic regions. In the North Pacific (left panel), the model substantially mitigates the overestimation of salinity compared to the other three models. This enhancement is particularly pronounced in nearshore areas and at the confluence of the Kuroshio and Oyashio currents-region (1), as well as along the coast and in areas influenced by the North Pacific Current-region (2). Similarly, in the South Pacific (right panel), PINN’s predictions more closely align with in situ observations in the regions influenced by the East Australian Current and the South Equatorial Current-region (3). Collectively, these results underscore the PINN model’s superior adaptive performance and its capability to accurately correct salinity fields in hydrographically complex and current-dominated environments.
4. Discussion
4.1. Analysis of the Generalizability of the Model in the Atlantic Ocean
To validate the generalizability of the model, we conducted tests in the Atlantic region [60°S~60°N, 60°W~20°E], incorporating a comprehensive performance assessment and spatio-temporal performance analysis. Using the same hyperparameters as in the Pacific region, the results demonstrate that the PINN model exhibits strong applicability.
As shown in Table 10, the PINN model outperforms other models across multiple evaluation metrics. Firstly, in terms of root mean square error (RMSE), the PINN achieved an RMSE of 0.282 PSU, significantly lower than SMAP L2C (1.398 PSU) and other models, including the unconstrainted ANN (0.402 PSU), indicating its superior accuracy in salinity predictions. Furthermore, the coefficient of determination (R2) for PINN reached 0.983, reflecting its high fitting capability for observational data, notably surpassing SMAP L2C (0.760) and also exceeding the unconstrained ANN (0.980).

Table 10.
Performance Indicators of Different Models (Atlantic region).
Regarding mean absolute error (MAE), PINN again leads with a value of 0.155 PSU, demonstrating its ability to closely capture true salinity values, while all other models reported MAE exceeding 0.184 PSU, highlighting its distinct advantage. For the prediction bias (BIAS), the PINN model exhibited a BIAS of −0.020 PSU, indicating relatively unbiased predictions, whereas the ANN showed a positive bias of 0.038, which suggests a tendency to overestimate.
In terms of improvement, the PINN model achieved substantial enhancements in RMSE and MAE, with reductions of 79.9% and 84.3%, respectively, further confirming its effectiveness in salinity prediction.
As shown in Table 11, during the periods marked as (a), (b), (c), (d), and (e), PINN consistently maintained the lowest RMSE values across all timeframes. In Period a (24–25 January 2022), PINN achieved an RMSE of 0.194 PSU compared to ANN’s significantly higher 0.616 PSU. This pattern persisted throughout the year: Period b (29–30 March) showed PINN at 0.430 PSU versus ANN’s 0.658 PSU, Period c (27–28 September) demonstrated PINN’s 0.451 PSU against ANN’s 0.668 PSU, Period d (26–27 October) indicated PINN at 0.424 PSU compared to ANN’s 0.643 PSU, and Period e (25–26 December) exhibited PINN achieving an RMSE of 0.360 PSU while ANN remained at 0.790 PSU.

Table 11.
Model Performance During Critical Periods Identified in Figure 9. Values represent daily RMSE in PSU. Bold values indicate the best performance for each date. Periods (a), (b), (c), (d) and (e) correspond to the marked critical events in Figure 9, where algorithm performance differences were most pronounced.
The ensemble methods (XGBoost and GBRT) showed intermediate performance, with RMSE values for XGBoost ranging from 0.634 to 0.718 PSU and 0.543 to 0.711 PSU for GBRT, consistently outperforming ANN but falling substantially short of PINN’s stability. Notably, PINN’s RMSE values remained within a narrow range of 0.194, 0.430, 0.451, 0.424, and 0.360 PSU across all highlighted periods, demonstrating remarkable temporal consistency regardless of seasonal variations or challenging oceanographic conditions.
Throughout the temporal analysis, PINN consistently exhibited the most stable performance across all latitudinal bands, with minimal fluctuations and rapid recovery from adverse conditions. GBRT and XGBoost displayed similar performance patterns, with moderate stability and occasional synchronized spikes during extreme conditions. In contrast, ANN exhibited the highest variability, particularly sensitive to seasonal transitions and extreme weather events, underscoring the advantages of physics-informed constraints for temporal consistency.
In the testing conducted in the Atlantic region, the PINN model demonstrated excellent performance in Region (3), which encompasses the North Equatorial Current and the Guiana Current. This area is characterized by complex hydrological elements and significant temperature-salinity gradients. The North Equatorial Current serves as a crucial connection between tropical and subtropical oceans, profoundly influencing the distribution of salinity and temperature in the region. The intensity and direction of the flow play a key role in mixing and distributing seawater, thereby affecting variations in sea surface salinity. Notably, the salinity changes in the North Equatorial Current are particularly complex due to the interplay between tropical precipitation and evaporation processes.
According to Table 12, the PINN model exhibits a significant advantage in salinity prediction. Specifically, for adjustments within the range of 0.5 to 1, the PINN model recorded a prediction error count of 7585, which is markedly superior to those of XGBoost (6121), GBRT (6165), and ANN (5633). In the smaller error range of −0.5 to 0, the PINN model achieved a prediction error count of 514, while XGBoost and GBRT had errors of 880 and 895, respectively, and ANN’s error reached 1030. This indicates that the PINN model is better equipped to handle salinity variations in complex environments.

Table 12.
Counts of salinity bias improvement across different models, as shown in Figure 10. The table details the number of grid points within specified improvement range.
Table 12.
Counts of salinity bias improvement across different models, as shown in Figure 10. The table details the number of grid points within specified improvement range.
| (20°S~20°N,60°W~20°E), Region (3), 9548 Points | ||||
|---|---|---|---|---|
| Improvement | −1 to −0.5 | −0.5 to 0 | 0 to 0.5 | 0.5 to 1 |
| PINN | 280 | 514 | 1169 | 7585 |
| XGB | 487 | 880 | 2060 | 6121 |
| GBRT | 467 | 895 | 2021 | 6165 |
| ANN | 635 | 1030 | 2250 | 5633 |
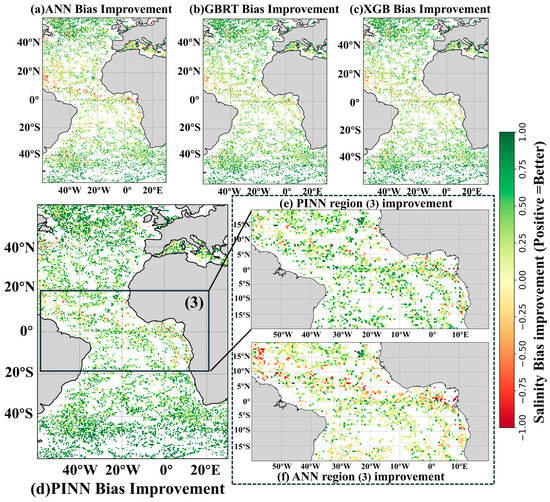
Figure 10.
Spatial Bias Improvement Analysis: Atlantic Regional Performance Assessment of Different Algorithms Across the Atlantic Ocean. This figure provides a comprehensive spatial comparison of bias improvement across the Pacific Ocean, utilizing a 0.5° × 0.5° grid resolution to evaluate enhancements in algorithm performance relative to the original SMAP L2C bias correction.
4.2. SHAP Analysis
Understanding the decision-making mechanisms of machine learning algorithms in oceanographic applications is crucial for establishing trust in model predictions and ensuring robust operational deployment. SHAP (Shapley Additive Explanations) analysis provides a unified framework for quantifying element contributions to model predictions, enabling comprehensive comparison of how different algorithms weight various oceanographic and satellite-derived input parameters [48,49]. This interpretational analysis is particularly valuable for physics-informed approaches, where the integration of physical constraints should theoretically modify element importance patterns compared to purely data-driven methods. SHAP analysis addresses critical questions regarding algorithm Transparency: which environmental variables drive model decisions, how element importance varies across different algorithmic approaches, and whether physics-informed constraints alter the relative significance of input parameters in ways consistent with oceanographic understanding [50,51].
The element importance assessment employs SHAP values to quantify the marginal contribution of each input variable to the final salinity prediction, providing both global element ranking and local prediction explanations. This analysis framework enables systematic comparison of how PINN’s physics-informed architecture influences element utilization patterns compared to conventional machine learning approaches, potentially revealing whether physical constraints guide the model toward more oceanographically meaningful element relationships [2,52].
Figure 11 presents a comprehensive comparison of SHAP values for the six elements with the highest average SHAP values among all input elements across the four machine learning algorithms. The horizontal bar chart format facilitates direct quantitative comparisons of element importance magnitudes, with SHAP values reflecting the average absolute contributions of each element to model predictions.
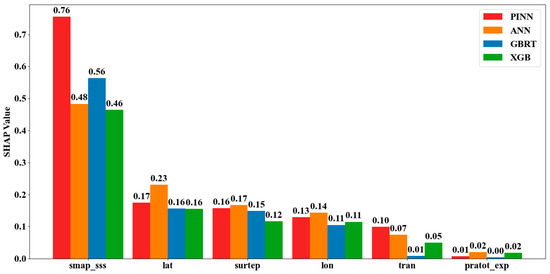
Figure 11.
Comparison of SHAP Values across Models (Top 6 Elements).
The SHAP analysis highlights unique utilization patterns, emphasizing the advantages of PINN’s physics-informed methodology. Among the elements, SMAP Salinity emerges as the most significant, with PINN showing the highest importance (0.755) compared to the baseline methods (ANN: 0.483, GBRT: 0.563, XGB: 0.465). This indicates that the incorporation of physics-informed constraints enhances the contribution of SMAP Salinity to the model, allowing for advanced corrections of auxiliary variables and reflecting the underlying physical processes inherent in the data.
Geographic coordinates (Latitude: 0.175, Longitude: 0.129) demonstrate enhanced sensitivity in PINN relative to traditional algorithms (0.231–0.336), reflecting the integration of spatially dependent oceanographic processes. Meanwhile, environmental variables exhibit specific patterns across algorithms, with surface temperature showing notable importance in PINN (0.157) compared to the other methods (0.166–0.166), suggesting effective utilization of temperature-salinity relationships crucial to ocean thermodynamics.
Figure 12 provides detailed SHAP dependence plots revealing the functional relationships between the top five most important input elements and model predictions, accompanied by a comprehensive summary plot that quantifies the distribution of element impacts. The analysis focuses on the top six-ranked elements to highlight the most critical relationships while maintaining visualization clarity and analytical focus.
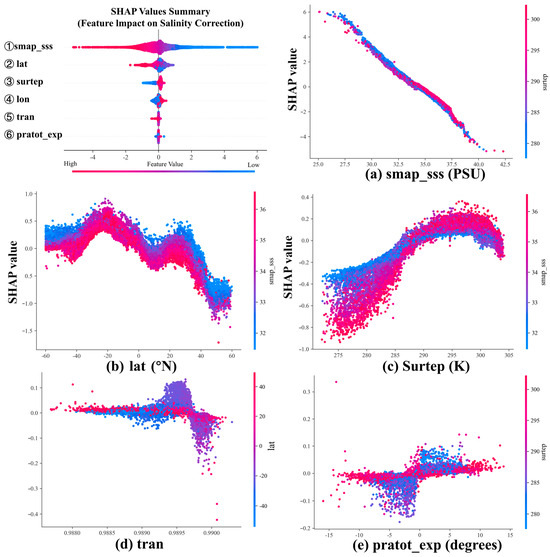
Figure 12.
SHAP Values Summary and Dependence Plots for Element Impact Analysis.
The dependence of SMAP salinity (Panel a) exhibits a pronounced negative correlation, while its SHAP contributions remain stable with variations in sea surface temperature (Panel b). The contribution of latitude to model predictions is positive in the Southern Hemisphere but gradually decreases with increasing latitude in the Northern Hemisphere (Panel c). Above 290 K, the positive contribution of sea surface temperature gradually increases, correlating with higher salinity values. In Panel d, the contributions of Transmission in the equatorial region demonstrate significant variability, while a negative correlation is observed beyond 20 degrees latitude in either hemisphere. Panel e illustrates that at low sea surface temperatures; the Expected Total Polarization Basis Rotation Angle shows a symmetrical positive correlation around the origin.
However, several methodological limitations constrain the applicability of the proposed approach. Due to simplifications in electromagnetic physical processes, the PINN model may not fully exploit the potential of physical loss for effective correction. Additionally, the algorithm’s efficacy diminishes at higher latitudes, necessitating specialized parameterizations and training strategies. Current PINN methods require the integration of fundamental physical constraints to enforce boundaries on outputs in subsequent steps.
5. Conclusions
This study presents a Physics-Informed Neural Network (PINN) framework integrating L-band brightness temperature constraints for SMAP Level-2 SSS Data in the Pacific Ocean. A forward radiative transfer model predicting brightness temperatures from corrected salinity establishes a physics-based loss term operating synergistically with data-fitting loss. This dual-constraint architecture enables physically consistent salinity corrections while maintaining empirical accuracy, resolving fundamental limitations of purely data-driven approaches that yield electromagnetically inconsistent solutions.
Performance evaluation demonstrated PINN’s capabilities across multiple validation metrics. The model consistently outperformed baseline methods (ANN, XGBoost, GBRT) in RMSE, bias, MAE, and R2. Regional analysis revealed strong PINN performance in Bands 2 and 3, with R2 values of 0.955 and 0.956 and RMSE values of 0.306 and 0.361 PSU, respectively, outperforming traditional methods (XGBoost RMSE: 0.367,0.368 PSU; GBRT RMSE: 0.312,0.358 PSU). Temporal analysis confirmed PINN’s stability during critical periods, maintaining RMSE values between 0.194 and 0.301 PSU across challenging conditions, while ANN performance significantly degraded, with RMSE values ranging from 0.478 to 0.505 PSU. Spatial assessment identified two primary areas for improvement: (1) The northern part of the Kuroshio Current (20°N–50°N, 120°E–180°E), where PINN exhibits significantly superior bias correction capabilities compared to the other three algorithms, with improvement rates consistently exceeding 0.5 in many grid cells, while other methods primarily show negative corrections; and (2) The South Australian Current region (40°S–0°, 140°E–160°W), where PINN maintains positive improvement rates and effective bias reduction, while ANN, GBRT, and XGBoost display mixed or negative performance patterns.
The PINN model has demonstrated robust applicability in the validation tests conducted in the Atlantic region (60°S to 60°N, 60°W to 20°E). Experimental results indicate that the PINN model outperforms other models, exhibiting outstanding performance across multiple evaluation metrics, including a root mean square error (RMSE) of 0.282 PSU and a coefficient of determination (R2) of 0.983, highlighting its exceptional capability to fit observational data. In comparison to SMAP L2C (1.398 PSU) and other models such as ANN, XGBoost, and GBRT, the PINN model offers significant advantages in salinity prediction accuracy, particularly within regions characterized by complex hydrological elements and pronounced temperature-salinity gradients, such as the North Equatorial Current and Guiana Current. Consequently, the PINN model demonstrates suitability and robustness in addressing variability across diverse marine environments and seasonal changes, supporting its broader applicability and integration in oceanographic research.
SHAP analysis elucidated these performance advantages through physical constraint mechanisms enhancing element utilization: systematic SMAP salinity correlations compensating for bias correction errors, geographic elements demonstrating spatial dependencies that align with regional advantages, and temperature variables reflecting complex nonlinear relationships indicative of thermodynamic integration. This confirms that incorporating ocean physics facilitates intelligent element interactions and enhances spatiotemporal consistency for operational applications. However, several methodological limitations constrain the proposed approach’s applicability. The PINN model exhibits reduced efficacy due to simplified physical processes that omit critical electromagnetic physics components. Algorithmic efficacy diminishes at high latitudes, necessitating specialized parameterizations and training strategies. Current brightness temperature formulations require additional variables for enhanced precision, while regional disparities suggest ensemble approaches may prove advantageous.
Future developments will focus on refining physics-informed constraints through latitude-specific parameterizations and expanded atmospheric-oceanic variables, while scaling operational applications through multi-sensor integration with missions including SMOS L2. In addition, we plan to integrate regionally dominant algorithms, ultimately transitioning towards a robust integrated prediction algorithm that emphasizes the use of the physical consistency demonstrated by PINN for climate monitoring and forecasting applications.
Author Contributions
Conceptualization, M.W., Z.L. and S.B.; data curation, M.W., Z.L. and S.B.; formal analysis, M.W., Z.L. and S.B.; funding acquisition, S.B. and H.W.; investigation, M.W. and Z.L.; methodology, M.W. and Z.L.; project administration, S.B.; resources, S.B. and H.W.; software, M.W. and Z.L.; supervision, S.B.; validation, M.W., Z.L., Z.Z., Q.X. and Y.L.; visualization, M.W.; writing—original draft, M.W.; Writing—review and editing, S.B., Z.L. and H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China (Grant No. 2021YFC3101502), National Natural Science Foundation of China (Grant Nos. 42406195, 42276205), Hunan Provincial Natural Science Foundation of China (2023JJ10053), and Youth Independent Innovation Science Foundation (Grant No. ZK24-54).
Data Availability Statement
(1) SMAP SSS is obtained from Remote Sensing Systems SMAP L2C SSS V6.0 product, available at https://data.remss.com/smap/SSS/V06.0/ (accessed on 1 September 2025). (2) EN.4.2.2 ocean temperature and salinity profile data were obtained from the Met Office Hadley Centre https://www.metoffice.gov.uk/hadobs/en4/ (accessed on 1 September 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SSS | Sea Surface Salinity |
| ESA | European Space Agency |
| SMOS | Soil Moisture and Ocean Salinity |
| NASA | National Aeronautics and Space Administration |
| SMAP | Soil Moisture Active Passive |
| PINN | Physics-Informed Neural Network |
| GHz | Gigahertz |
| L-band | L-band frequencies |
| ML | Machine Learning |
| SHAP | Shapley Additive Explanations |
| RF | Radio Frequency |
| RTM | Radiative Transfer Model |
| L2 | Level-2 |
| L3 | Level-3 |
| ANN | Artificial Neural Network |
| XGBoost | Extreme Gradient Boosting |
| GBRT | Gradient Boosting Regression Tree |
| PSU | Practical Salinity Unit |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| R2/R2 | Coefficient of Determination |
| SVR | Support Vector Regression |
| RF | Random Forest |
| GBRT | Gradient Boosting Decision Tree |
| OceanPINN | Ocean Physics-Informed Neural Network |
Appendix A
This appendix documents the model tuning experiments referenced in Section 3.3. Table A1 presents the hyperparameter combinations that were input for the ANN, XGB, and GBRT models during the initial Bayesian optimization and subsequent grid search processes, along with the corresponding Root Mean Square Error (RMSE) results for each configuration.

Table A1.
Hyperparameter settings and their corresponding Root Mean Square Error (RMSE) values for different models: ANN, XGB, and GBRT. For ANN, the settings include Batch Size values of [64, 128, 256, 512, 1028], Hidden Layer Sizes of [8, 16, 32, 64, 128], and Learning Rates of [0.01, 0.001, 0.0001]. For XGB and GBRT, the settings comprise Training Estimators of [100, 150, 200], Max Depth values of [10, 15, 20], Subsample ratios of [0.4, 0.6, 0.8, 1.0], and Learning Rates of [0.01, 0.001, 0.0001]. The RMSE indicates the model’s performance, with lower values representing better predictive accuracy.
Table A1.
Hyperparameter settings and their corresponding Root Mean Square Error (RMSE) values for different models: ANN, XGB, and GBRT. For ANN, the settings include Batch Size values of [64, 128, 256, 512, 1028], Hidden Layer Sizes of [8, 16, 32, 64, 128], and Learning Rates of [0.01, 0.001, 0.0001]. For XGB and GBRT, the settings comprise Training Estimators of [100, 150, 200], Max Depth values of [10, 15, 20], Subsample ratios of [0.4, 0.6, 0.8, 1.0], and Learning Rates of [0.01, 0.001, 0.0001]. The RMSE indicates the model’s performance, with lower values representing better predictive accuracy.
| ANN | XBG | GBRT | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bayesian Optimization | Grid Search | Bayesian Optimization | Grid Search | Bayesian Optimization | Grid Search | ||||||
| Setting | RMSE | Setting | RMSE | Setting | RMSE | Setting | RMSE | Setting | RMSE | Setting | RMSE |
| 128, 8, 0.0001 | 0.532 | 128, 64, 0.001 | 0.379 | 150, 10, 0.8,0.0001 | 0.436 | 100, 10, 0.8, 0.001 | 0.477 | 200, 10, 0.4, 0.001 | 0.571 | 100, 10, 0.8, 0.001 | 0.390 |
| 64, 16, 0.01 | 0.508 | 256, 64, 0.001 | 0.308 | 150, 15, 0.6, 0.001 | 0.492 | 100, 15, 0.8, 0.001 | 0.386 | 100, 15, 0.6, 0.0001 | 0.494 | 100, 15, 0.8, 0.001 | 0.402 |
| 512, 16, 0.01 | 0.478 | 512, 64, 0.001 | 0.325 | 100, 10, 0.4, 0.01 | 0.527 | 100, 20, 0.8, 0.001 | 0.363 | 150, 20, 1.0, 0.01 | 0.399 | 100, 20, 0.8, 0.001 | 0.341 |
| 1028, 16, 0.001 | 0.457 | 128, 32, 0.001 | 0.435 | 200, 20, 0.8, 0.0001 | 0.334 | 150, 10, 0.8, 0.001 | 0.325 | 200, 15, 0.6, 0.0001 | 0.439 | 150, 10, 0.8, 0.001 | 0.396 |
| 512, 32, 0.001 | 0.394 | 256, 32, 0.001 | 0.429 | 100, 15, 1.0, 0.01 | 0.410 | 150, 15, 0.8, 0.001 | 0.295 | 100, 10, 0.8, 0.01 | 0.410 | 150, 15, 0.8, 0.001 | 0.379 |
| 512,64, 0.001 | 0.316 | 512, 32, 0.001 | 0.432 | 150, 20, 0.8, 0.001 | 0.297 | 150, 20, 0.8, 0.001 | 0.319 | 150, 15, 0.8, 0.001 | 0.388 | 150, 20, 0.8, 0.001 | 0.302 |
| 256, 64, 0.0001 | 0.307 | 128, 128, 0.001 | 0.409 | 150, 15, 0.8, 0.001 | 0.316 | 200, 10, 0.8, 0.001 | 0.384 | 200, 20, 0.8, 0.001 | 0.286 | 200, 10, 0.8, 0.001 | 0.335 |
References
- Reul, N.; Grodsky, S.; Arias, M.; Boutin, J.; Catany, R.; Chapron, B.; d’Amico, F.; Dinnat, E.; Donlon, C.; Fore, A. Sea surface salinity estimates from spaceborne L-band radiometers: An overview of the first decade of observation (2010–2019). Remote Sens. Environ. 2020, 242, 111769. [Google Scholar] [CrossRef]
- Vinogradova, N.; Lee, T.; Boutin, J.; Drushka, K.; Fournier, S.; Sabia, R.; Stammer, D.; Bayler, E.; Reul, N.; Gordon, A. Satellite salinity observing system: Recent discoveries and the way forward. Front. Mar. Sci. 2019, 6, 243. [Google Scholar] [CrossRef]
- Melnichenko, O.; Amores, A.; Maximenko, N.; Hacker, P.; Potemra, J. Signature of mesoscale eddies in satellite sea surface salinity data. J. Geophys. Res. Ocean. 2017, 122, 1416–1424. [Google Scholar] [CrossRef]
- Olmedo, E.; Taupier-Letage, I.; Turiel, A.; Alvera-Azcárate, A. Improving SMOS sea surface salinity in the Western Mediterranean sea through multivariate and multifractal analysis. Remote Sens. 2018, 10, 485. [Google Scholar] [CrossRef]
- Lang, R.; Zhou, Y.; Utku, C.; Le Vine, D. Accurate measurements of the dielectric constant of seawater at L band. Radio Sci. 2016, 51, 2–24. [Google Scholar] [CrossRef]
- Copernicus, E. Copernicus-Marine Environment Monitoring Service. 2020. Available online: https://marine.copernicus.eu (accessed on 1 September 2025).
- Boutin, J.; Vergely, J.L.; Marchand, S.; D’Amico, F.; Hasson, A.; Kolodziejczyk, N.; Reul, N.; Reverdin, G.; Vialard, J. New SMOS Sea Surface Salinity with reduced systematic errors and improved variability. Remote Sens. Environ. 2018, 214, 115–134. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Jang, E.; Kim, Y.J.; Im, J.; Park, Y.-G. Improvement of SMAP sea surface salinity in river-dominated oceans using machine learning approaches. GIScience Remote Sens. 2021, 58, 138–160. [Google Scholar] [CrossRef]
- Qin, S.; Wang, H.; Zhu, J.; Wan, L.; Zhang, Y.; Wang, H. Validation and correction of sea surface salinity retrieval from SMAP. Acta Oceanol. Sin. 2020, 39, 148–158. [Google Scholar] [CrossRef]
- Rajabi-Kiasari, S.; Hasanlou, M. An efficient model for the prediction of SMAP sea surface salinity using machine learning approaches in the Persian Gulf. Int. J. Remote Sens. 2020, 41, 3221–3242. [Google Scholar] [CrossRef]
- Savin, A.S.; Krinitskiy, M.A.; Osadchiev, A.A. SMAP Sea Surface Salinity Improvement in the Arctic Region Using Machine Learning Approaches. Mosc. Univ. Phys. Bull. 2023, 78, S210–S216. [Google Scholar] [CrossRef]
- Song, H.; Zhang, Y.; Zhang, B.; Lv, Y.; Zhang, L. Coastal Regions Sea Surface Salinity Retrieval of SMAP MISSION Based on Light Gradient Boosting Model. In Proceedings of the 2024 Photonics & Electromagnetics Research Symposium (PIERS), Chengdu, China, 21–25 April 2024; pp. 1–3. [Google Scholar]
- Ouyang, Y.; Zhang, Y.; Feng, M.; Boschetti, F.; Du, Y. Geoclimatic Distribution of Satellite-Observed Salinity Bias Classified by Machine Learning Approach. Remote Sens. 2024, 16, 3084. [Google Scholar] [CrossRef]
- Buongiorno Nardelli, B.; Droghei, R.; Santoleri, R. Multi-dimensional interpolation of SMOS sea surface salinity with surface temperature and in situ salinity data. Remote Sens. Environ. 2016, 180, 392–402. [Google Scholar] [CrossRef]
- Kao, H.-Y.; Lagerloef, G.S.; Lee, T.; Melnichenko, O.; Meissner, T.; Hacker, P. Assessment of aquarius sea surface salinity. Remote Sens. 2018, 10, 1341. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, R.-H.; Moum, J.N.; Wang, F.; Li, X.; Li, D. Physics-informed deep-learning parameterization of ocean vertical mixing improves climate simulations. Natl. Sci. Rev. 2022, 9, nwac044. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Yoon, S.; Park, Y.; Gerstoft, P.; Seong, W. Predicting ocean pressure field with a physics-informed neural network. J. Acoust. Soc. Am. 2024, 155, 2037–2049. [Google Scholar] [CrossRef] [PubMed]
- Willard, J.; Jia, X.; Xu, S.; Steinbach, M.; Kumar, V. Integrating physics-based modeling with machine learning: A survey. arXiv 2020, arXiv:2003.04919. [Google Scholar]
- Zhou, Y.; Lang, R.H.; Dinnat, E.P.; Le Vine, D.M. L-band model function of the dielectric constant of seawater. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6964–6974. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.; Manaster, A.; Lindsley, R. Remote Sensing Systems SMAP Ocean Surface Salinities, Version 2.0 Validated Release; Remote Sensing Systems: Santa Rosa, CA, USA, 2018. [Google Scholar]
- Meissner, T.; Wentz, F.; Manaster, A.; Lindsley, R. NASA/RSS SMAP Salinity: Version 6.0 Validated Release 2024. Available online: https://data.remss.com/smap/SSS/V06.0/documents/Release_V6.0.pdf (accessed on 1 September 2025).
- Bingham, F.M.; Busecke, J.J.M.; Gordon, A.L. Variability of the South Pacific Subtropical Surface Salinity Maximum. J. Geophys. Res. Ocean. 2019, 124, 6050–6066. [Google Scholar] [CrossRef]
- Ouyang, Y.; Zhang, Y.; Chi, J.; Sun, Q.; Du, Y. Regional difference of sea surface salinity variations in the western tropical pacific. J. Oceanogr. 2021, 77, 647–657. [Google Scholar] [CrossRef]
- Maes, C.; Reul, N.; Behringer, D.; O’Kane, T. The salinity signature of the equatorial Pacific cold tongue as revealed by the satellite SMOS mission. Geosci. Lett. 2014, 1, 17. [Google Scholar] [CrossRef]
- Tomczak, M.; Godfrey, J.S. Regional Oceanography: An Introduction. Daya Books. 2003. Available online: https://www.google.com.hk/url?sa=t&source=web&rct=j&opi=89978449&url=https://api.pageplace.de/preview/DT0400.9781483287614_A23884672/preview-9781483287614_A23884672.pdf&ved=2ahUKEwi8nJSs-uGPAxX_6AIHHfMkDRsQFnoECB0QAQ&usg=AOvVaw3-2X9n3M9gLYhPuOfvNw-d (accessed on 1 September 2025).
- Volkov, D.L.; Dong, S.; Foltz, G.R.; Goni, G.; Lumpkin, R. Observations of near-surface salinity and temperature structure with dual-sensor Lagrangian drifters during SPURS-2. Oceanography 2019, 32, 66–75. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.J. The complex dielectric constant of pure and sea water from microwave satellite observations. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1836–1849. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.J. The Emissivity of the Ocean Surface Between 6 and 90 GHz Over a Large Range of Wind Speeds and Earth Incidence Angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3004–3026. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.J.; Le Vine, D.M. The salinity retrieval algorithms for the NASA Aquarius version 5 and SMAP version 3 releases. Remote Sens. 2018, 10, 1121. [Google Scholar] [CrossRef]
- Wentz, F.J.; Le Vine, D.M. Aquarius Salinity Retrieval Algorithm: Final Pre-Launch Version. 2011. Available online: https://ntrs.nasa.gov/api/citations/20110012863/downloads/20110012863.pdf (accessed on 1 September 2025).
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Chen, C.; Liaw, A.; Breiman, L. Using random forest to learn imbalanced data. Univ. Calif. Berkeley 2004, 110, 24. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Mitchell, R.; Frank, E. Accelerating the XGBoost algorithm using GPU computing. PeerJ Comput. Sci. 2017, 3, e127. [Google Scholar] [CrossRef]
- Drushka, K.; Westbrook, E.; Bingham, F.; Gaube, P.; Dickinson, S.; Fournier, S.; Menezes, V.; Misra, S.; Perez, J.; Rainville, E.J. Salinity and Stratification at the Sea Ice Edge (SASSIE): An oceanographic field campaign in the Beaufort Sea. Earth Syst. Sci. Data Discuss. 2024, 2024, 1–56. [Google Scholar] [CrossRef]
- Tian, T.; Cheng, L.; Wang, G.; Abraham, J.; Wei, W.; Ren, S.; Zhu, J.; Song, J.; Leng, H. Reconstructing ocean subsurface salinity at high resolution using a machine learning approach. Earth Syst. Sci. Data 2022, 14, 5037–5060. [Google Scholar] [CrossRef]
- Berry, D.I.; Corlett, G.K.; Embury, O.; Merchant, C.J. Stability Assessment of the (A)ATSR Sea Surface Temperature Climate Dataset from the European Space Agency Climate Change Initiative. Remote Sens. 2018, 10, 126. [Google Scholar] [CrossRef]
- Dash, P.; Saha, K.; DiGiacomo, P.; Miller, S.D.; Zhang, H.-M.; Lazzaro, R.; Son, S. Trends in Satellite-Based Ocean Parameters through Integrated Time Series Decomposition and Spectral Analysis. Part I: Chlorophyll, Sea Surface Temperature, and Sea Level Anomaly. J. Atmos. Ocean. Technol. 2025, 42, 91–123. [Google Scholar] [CrossRef]
- Supply, A.; Boutin, J.; Vergely, J.-L.; Kolodziejczyk, N.; Reverdin, G.; Reul, N.; Tarasenko, A. New insights into SMOS sea surface salinity retrievals in the Arctic Ocean. Remote Sens. Environ. 2020, 249, 112027. [Google Scholar] [CrossRef]
- Vazquez-Cuervo, J.; Gomez-Valdes, J.; Bouali, M.; Miranda, L.E.; Van der Stocken, T.; Tang, W.; Gentemann, C. Using saildrones to validate satellite-derived sea surface salinity and sea surface temperature along the California/Baja Coast. Remote Sens. 2019, 11, 1964. [Google Scholar] [CrossRef]
- Mohammed, A.A.A.; Lee, S.Y. The Trend of SST, SSS, Ocean Current, and Comparison of Kuroshio Strength to Weather Events in Taiwan. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 7103–7106. [Google Scholar]
- Xie, P.; Boyer, T.; Bayler, E.; Xue, Y.; Byrne, D.; Reagan, J.; Locarnini, R.; Sun, F.; Joyce, R.; Kumar, A. An in situ-satellite blended analysis of global sea surface salinity. J. Geophys. Res. Ocean. 2014, 119, 6140–6160. [Google Scholar] [CrossRef]
- Lundberg, S.; Lee, S. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Christoph, M. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable. 2020. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 16 September 2025).
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “ Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Kumar, A.; Liang, P.S.; Ma, T. Verified uncertainty calibration. arXiv 2019. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).