Robust Underwater Vehicle Pose Estimation via Convex Optimization Using Range-Only Remote Sensing Data
Abstract
1. Introduction
1.1. Recent Literature on LBL Localization
1.2. Proposed Method in Context
1.3. Organization
2. Problem Setup
3. Mathematical Formulation
3.1. Optimal Estimation of the Location of the On-Board Receiver
3.1.1. Chebyshev Center of
3.1.2. Maximum Volume Inscribed Ellipsoid of
3.2. Determination of the Sensing Function
3.3. Estimation of the Orientation of the Vehicle from the Location Estimates of the On-Board Receivers
4. Algorithms
4.1. Location Estimation Procedure
4.1.1. Algorithm to Estimate the Chebyshev Center
4.2. Procedure for Orientation Estimation and Correcting the Location Estimates Taking Rigid Body Constraints into Account
5. Computational and Experimental Results
5.1. Simulation of Range Measurements
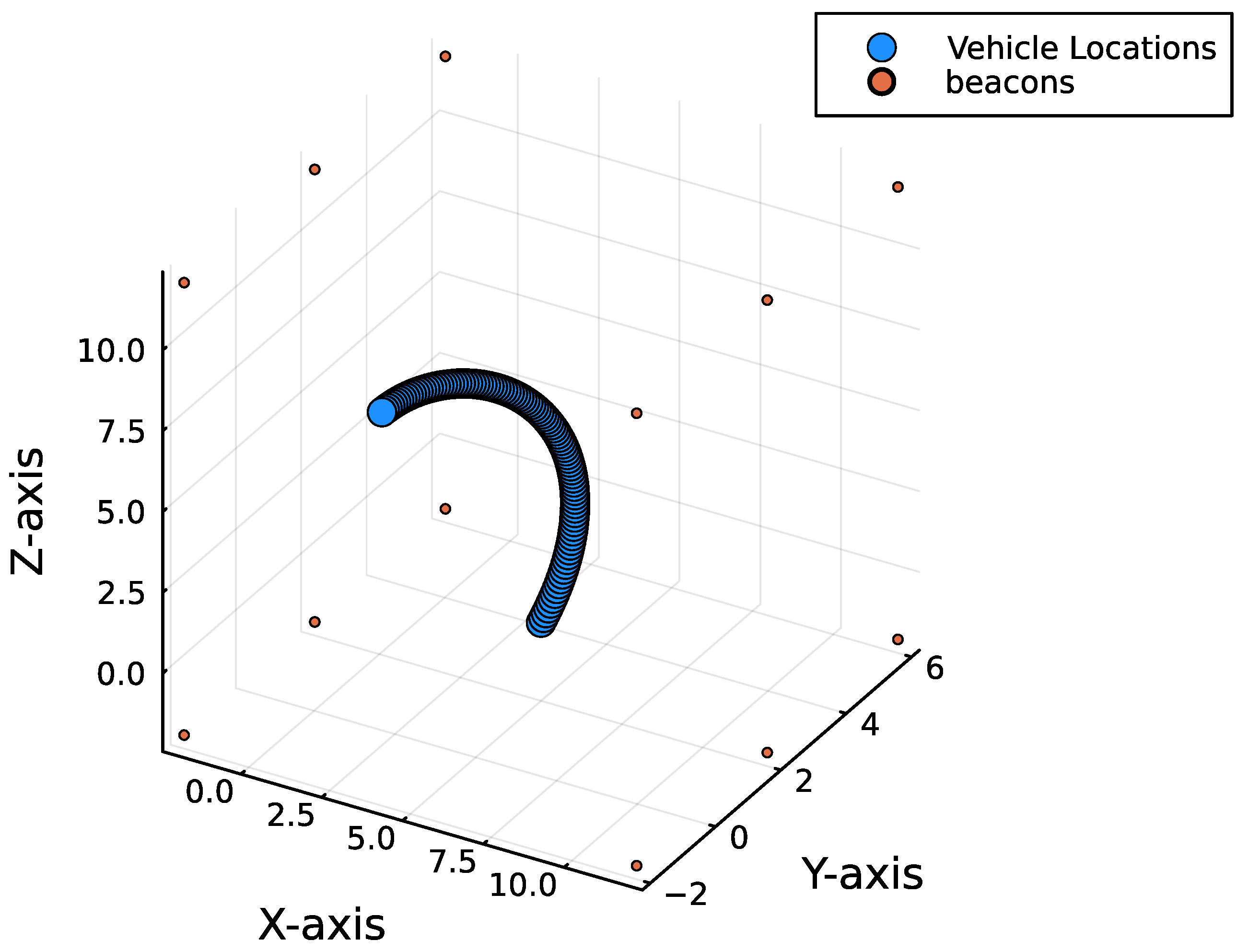
5.2. Position Estimation Algorithm Performance
5.3. Determination of
5.4. Errors in the Orientation Estimates
5.5. Experimental Results
5.5.1. Experimental Setup
5.5.2. Environmental Conditions
5.5.3. Mission Execution and Data Collection
5.5.4. Estimation and Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Proposition 1
Appendix B. Uncertainty in Beacon Locations
References
- Hari, S.K.K.; Rathinam, S.; Darbha, S.; Kalyanam, K.; Manyam, S.G.; Casbeer, D. Optimal UAV route planning for persistent monitoring missions. IEEE Trans. Robot. 2020, 37, 550–566. [Google Scholar] [CrossRef]
- Smith, R.N.; Schwager, M.; Smith, S.L.; Jones, B.H.; Rus, D.; Sukhatme, G.S. Persistent ocean monitoring with underwater gliders: Adapting sampling resolution. J. Field Robot. 2011, 28, 714–741. [Google Scholar] [CrossRef]
- Leonard, J.J.; Bennett, A.A.; Smith, C.M.; Feder, H. Autonomous underwater vehicle navigation. In Proceedings of the IEEE ICRA Workshop on Navigation of Outdoor Autonomous Vehicles, Leuven, Belgium, 16–21 May 1998. [Google Scholar]
- Armstrong, B.; Wolbrecht, E.; Edwards, D. AUV navigation in the presence of a magnetic disturbance with an extended Kalman filter. In Proceedings of the OCEANS 2010 IEEE-Sydney, Sydney, Australia, 24–27 May 2010; pp. 1–6. [Google Scholar]
- Tang, J.; Hu, S.; Ren, Z.; Chen, C.; Xiao, X.; Zhou, C. Analytical Formulas for Underwater and Aerial Object Localization by Gravitational Field and Gravitational Gradient Tensor. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1557–1560. [Google Scholar] [CrossRef]
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV navigation and localization: A review. IEEE J. Ocean. Eng. 2014, 39, 131–149. [Google Scholar] [CrossRef]
- Eustice, R.M.; Singh, H.; Whitcomb, L.L. Synchronous-clock, one-way-travel-time acoustic navigation for underwater vehicles. J. Field Robot. 2011, 28, 121–136. [Google Scholar] [CrossRef]
- Chandrasekhar, V.; Seah, W.K.; Choo, Y.S.; Ee, H.V. Localization in underwater sensor networks: Survey and challenges. In Proceedings of the 1st ACM International Workshop on Underwater Networks, Los Angeles, CA, USA, 25 September 2006; pp. 33–40. [Google Scholar]
- Garcia, J.E. Positioning of sensors in underwater acoustic networks. In Proceedings of the OCEANS, Washington, DC, USA, 17–23 September 2005; Proceedings of MTS/IEEE. pp. 2088–2092. [Google Scholar]
- Yao, X.; Zhangming, H.; Jiongqi, W.; Xuanying, Z.; Yuyun, C.; Xiaogang, P. TOA positioning algorithm of LBL system for underwater target based on PSO. J. Syst. Eng. Electron. 2023, 34, 1319–1332. [Google Scholar] [CrossRef]
- Sun, S.; Liu, T.; Wang, Y.; Zhang, G.; Liu, K.; Wang, Y. High-rate underwater acoustic localization based on the decision tree. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4204912. [Google Scholar] [CrossRef]
- Li, H.; Yang, K.; Duan, R. Robust multipath time-delay estimation of broadband source using a vertical line array in deep water. IEEE Signal Process. Lett. 2019, 27, 51–55. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Qi, B.; Hao, Y. Long baseline acoustic localization based on track-before-detect in complex underwater environments. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4205214. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Qi, B.; Hao, Y. Underwater acoustic localization of the long baseline based on track-before-detect. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1501105. [Google Scholar] [CrossRef]
- Otero, P.; Hernández-Romero, Á.; Luque-Nieto, M.Á.; Ariza, A. Underwater positioning system based on drifting buoys and acoustic modems. J. Mar. Sci. Eng. 2023, 11, 682. [Google Scholar] [CrossRef]
- Vázquez-Mejías, A.I.; Hernández-Romero, Á.; Vidal, J.; Otero, P. Proof of Concept and Accuracy of an LBL Underwater Positioning System. IEEE J. Ocean. Eng. 2024, 50, 1551–1556. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, Y.; Xu, T.; Qin, X.; Liu, Y. Long-range LBL underwater acoustic navigation considering Earth curvature and Doppler effect. Measurement 2025, 240, 115524. [Google Scholar] [CrossRef]
- Kinsey, J.C.; Eustice, R.M.; Whitcomb, L.L. A survey of underwater vehicle navigation: Recent advances and new challenges. In Proceedings of the IFAC Conference of Manoeuvering and Control of Marine Craft, Lisbon, Portugal, 20–22 September 2006; Volume 88, pp. 1–12. [Google Scholar]
- Hari, S.K.K.; Darbha, S. Estimation of Location and Orientation From Range Measurements. In Proceedings of the ASME 2015 Dynamic Systems and Control Conference, Columbus, OH, USA, 28–30 October 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; p. V002T31A005. [Google Scholar]
- Hari, S.K.K.; Sundar, K.; Braga, J.; Teixeira, J.; Darbha, S.; Sousa, J. Adaptive Position Estimation for Vehicles using Range Measurements. IFAC-PapersOnLine 2017, 50, 1145–1150. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Todd, M.J. Minimum-Volume Ellipsoids: Theory and Algorithms; SIAM: Philadelphia, PA, USA, 2016; Volume 23. [Google Scholar]
- Pólya, G.; Szegö, G. Problems and Theorems in Analysis II; Springer: New York, NY, USA, 1976. [Google Scholar]
- Parrilo, P.A. Semidefinite programming relaxations for semialgebraic problems. Math. Program. 2003, 96, 293–320. [Google Scholar] [CrossRef]
- O’Donoghue, B.; Chu, E.; Parikh, N.; Boyd, S. Conic optimization via operator splitting and homogeneous self-dual embedding. arXiv 2013, arXiv:1312.3039. [Google Scholar] [CrossRef]
- Schönemann, P.H. A generalized solution of the orthogonal Procrustes problem. Psychometrika 1966, 31, 1–10. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hari, S.K.K.; Sundar, K.; Braga, J.; Teixeira, J.; Darbha, S.; Sousa, J. Robust Underwater Vehicle Pose Estimation via Convex Optimization Using Range-Only Remote Sensing Data. Remote Sens. 2025, 17, 2637. https://doi.org/10.3390/rs17152637
Hari SKK, Sundar K, Braga J, Teixeira J, Darbha S, Sousa J. Robust Underwater Vehicle Pose Estimation via Convex Optimization Using Range-Only Remote Sensing Data. Remote Sensing. 2025; 17(15):2637. https://doi.org/10.3390/rs17152637
Chicago/Turabian StyleHari, Sai Krishna Kanth, Kaarthik Sundar, José Braga, João Teixeira, Swaroop Darbha, and João Sousa. 2025. "Robust Underwater Vehicle Pose Estimation via Convex Optimization Using Range-Only Remote Sensing Data" Remote Sensing 17, no. 15: 2637. https://doi.org/10.3390/rs17152637
APA StyleHari, S. K. K., Sundar, K., Braga, J., Teixeira, J., Darbha, S., & Sousa, J. (2025). Robust Underwater Vehicle Pose Estimation via Convex Optimization Using Range-Only Remote Sensing Data. Remote Sensing, 17(15), 2637. https://doi.org/10.3390/rs17152637






