Efficient Sampling Schemes for 3D Imaging of Radar Target Scattering Based on Synchronized Linear Scanning and Rotational Motion
Abstract
1. Introduction
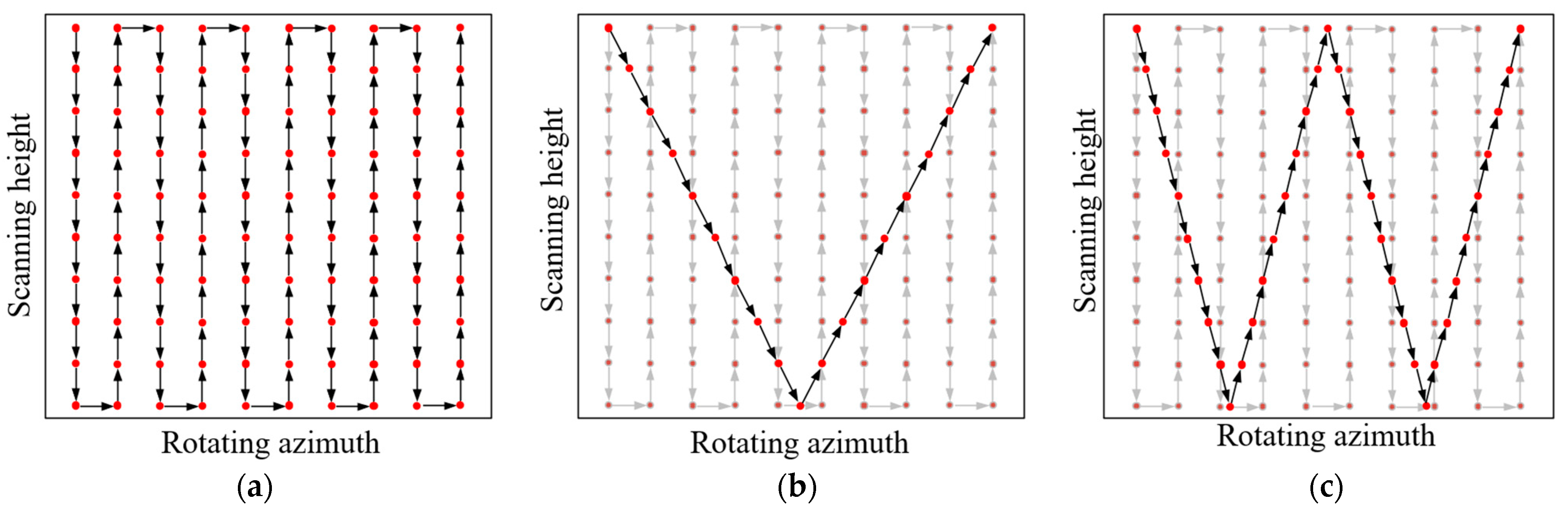
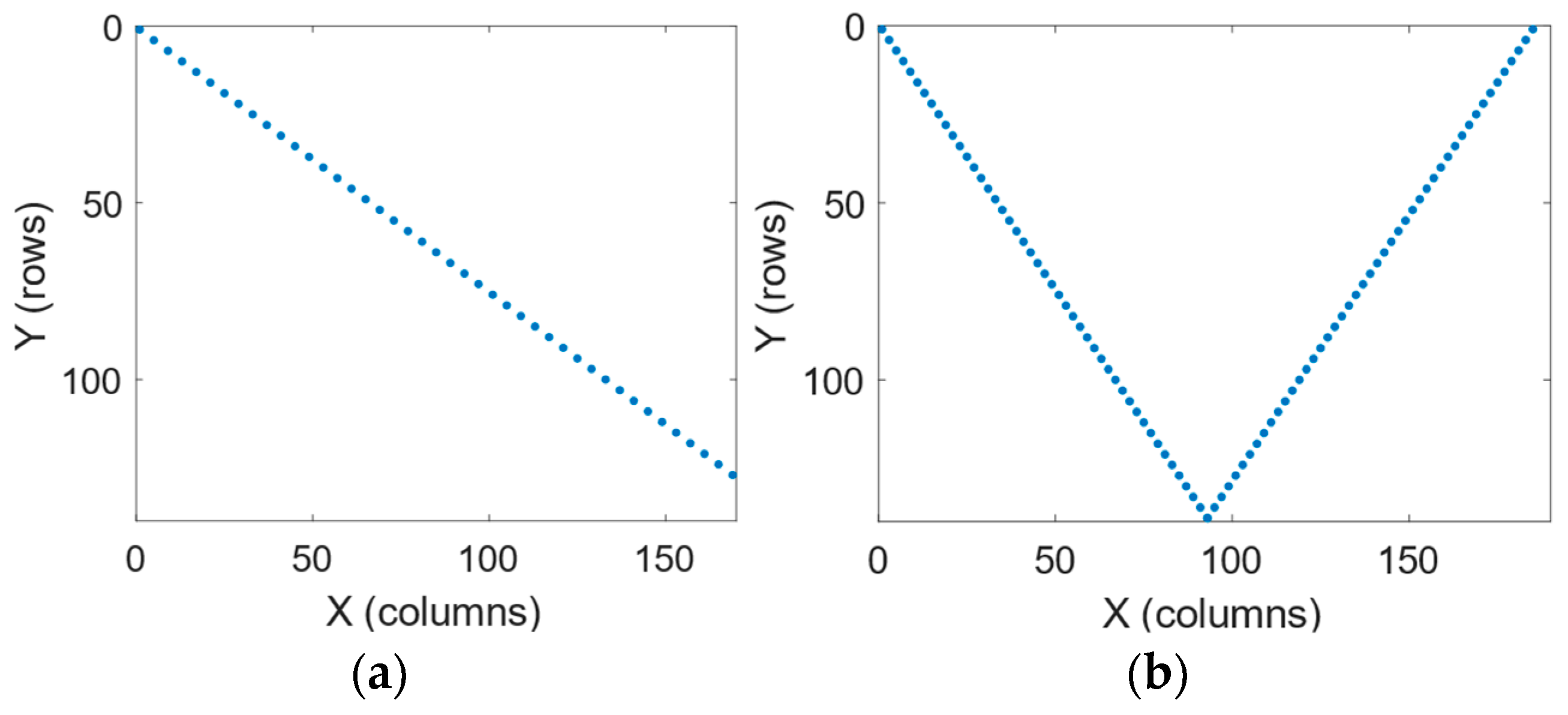
- Development of a “V”-shaped sparse sampling trajectory and introduction of an angular–spatial joint sparse sampling model. This paper presents a “V”-shaped sparse sampling trajectory that attains generalized angular homogeneity and sufficient spatial coverage inside the angular–spatial joint domain, fulfilling the criteria for 3D imaging. A unique angular–spatial joint sparse sampling approach is developed, addressing the constraints of conventional tactics that separately consider the angular and spatial domains. By aligning the target rotation with consistent vertical stepping of the radar sensor, the model generates a non-uniform sparse sampling pattern in the joint domain. The suggested approach effectively maintains the spatial information variety by leveraging the low-rank and sparse characteristics of the target’s scattering field, while substantially decreasing the overall sampling dimension.
- Three-dimensional image reconstruction and analysis of the minimum sampling range for the “V”-shaped sparse trajectory. This study utilizes the back-projection (BP) algorithm to assess the imaging resolution in the horizontal and sagittal planes, facilitating the optimization of parameter settings for 3D reconstruction while maintaining the image quality under diminished sampling conditions. The theoretical minimum sampling range necessary for 3D imaging is determined by the “V”-shaped sparse trajectory, which signifies the bottom limit for effective reconstruction. A comparative analysis of the imaging performance across various sampling trajectories is performed to ascertain the optimal balance among the imaging dynamic range, data volume, and acquisition time, thus offering both theoretical and practical guidance for trajectory design in real-world applications.
2. Methods
2.1. Design of the “V”-Shaped Sparse Sampling Trajectory
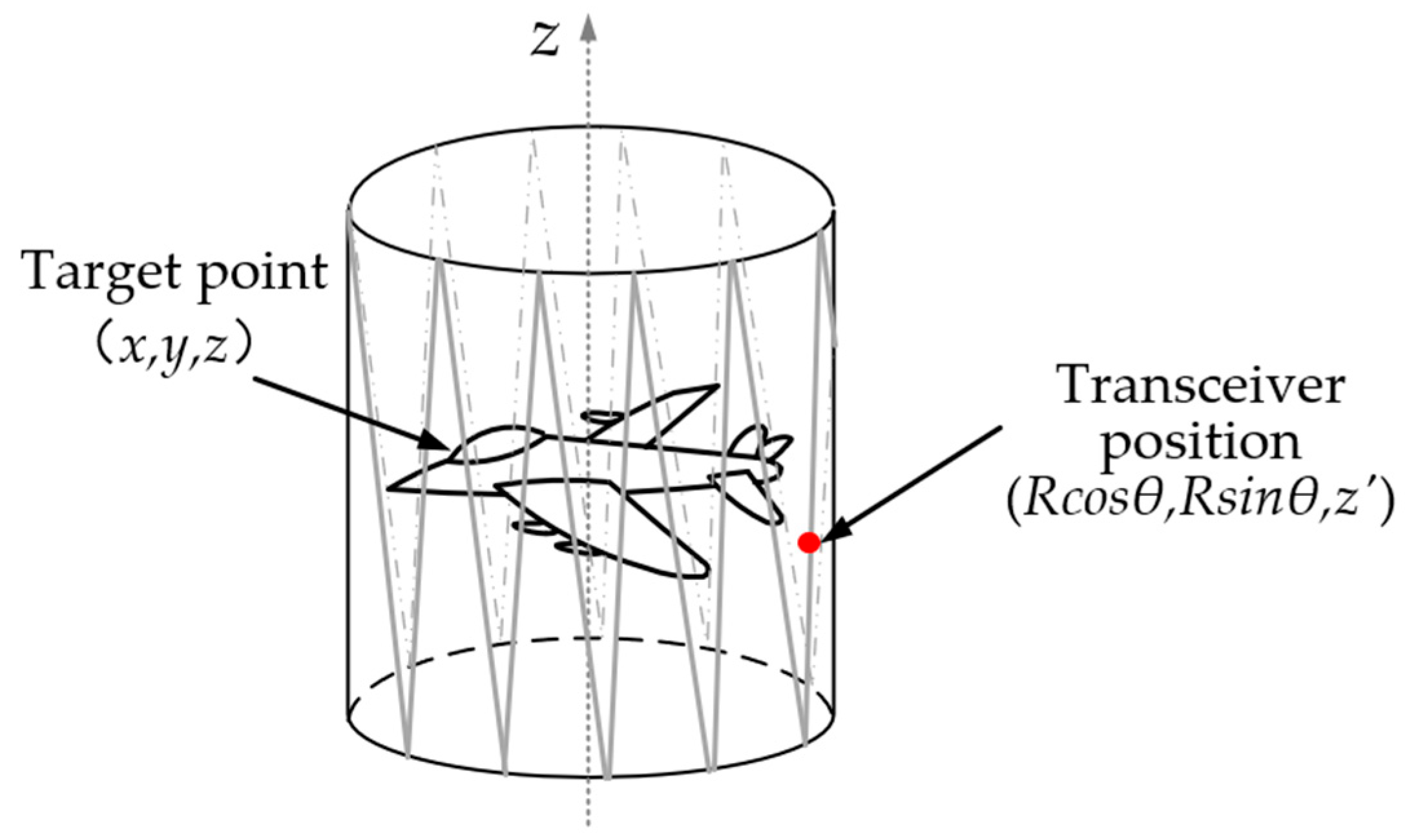
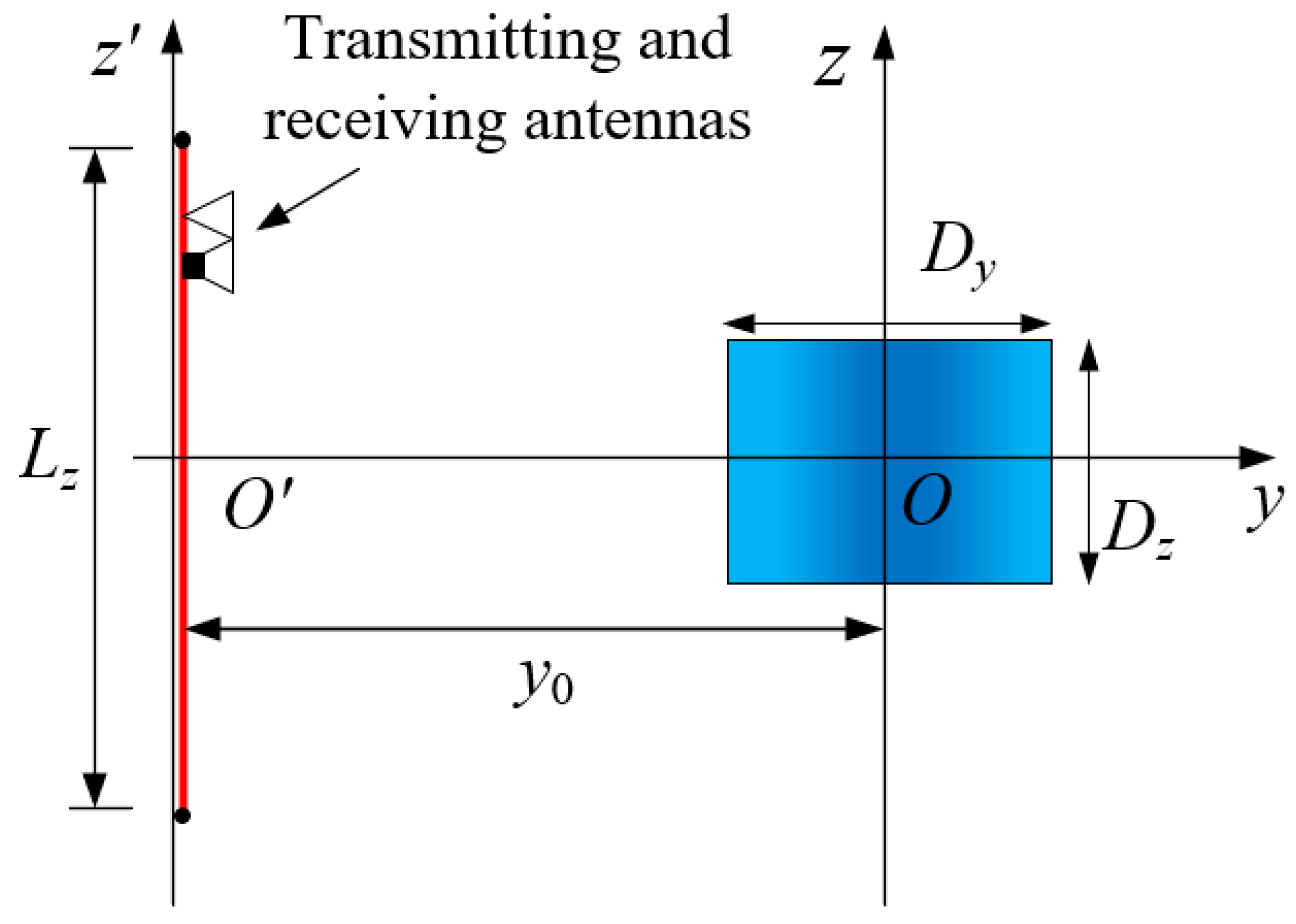
2.2. Construction of the Synchronized Scanning–Rotation Sampling Model
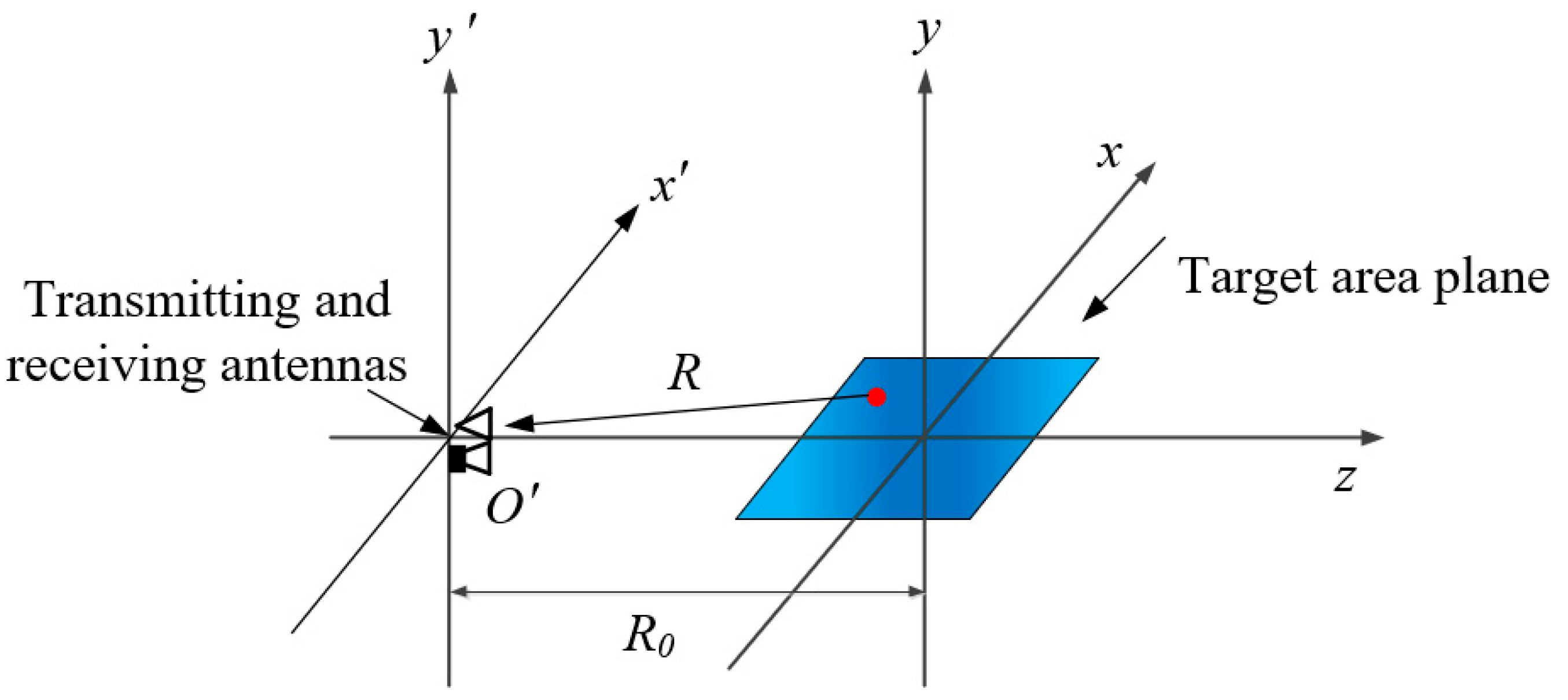
2.3. Computational Modeling for 3D Imaging
2.4. Imaging Resolution
2.4.1. Imaging of Target Rotation in the Horizontal Plane
2.4.2. Imaging of Antenna Scanning in Sagittal Plane
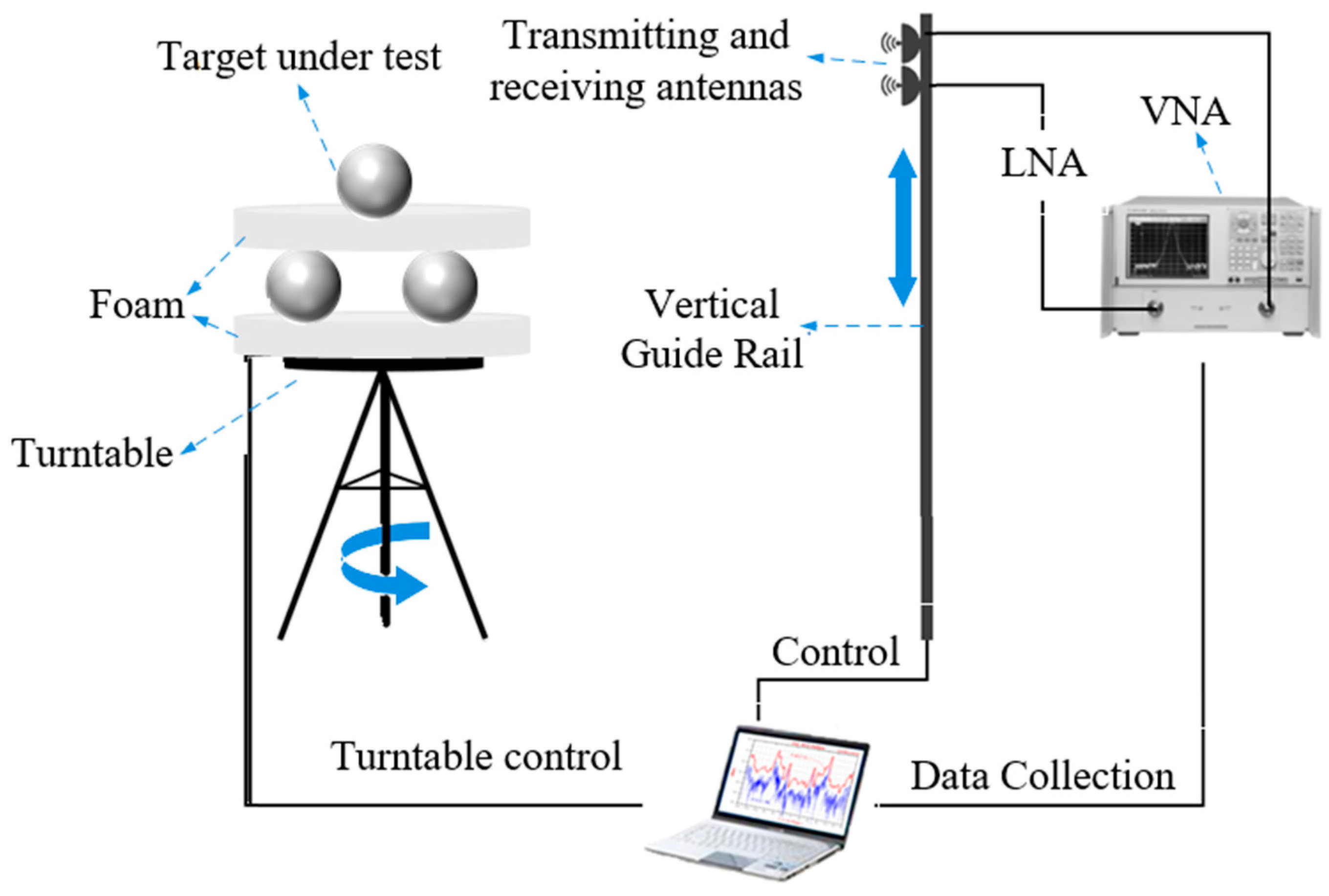
3. Experimental Setup
4. Experimental Results
4.1. Target Selection and Characteristics
4.2. Imaging Results
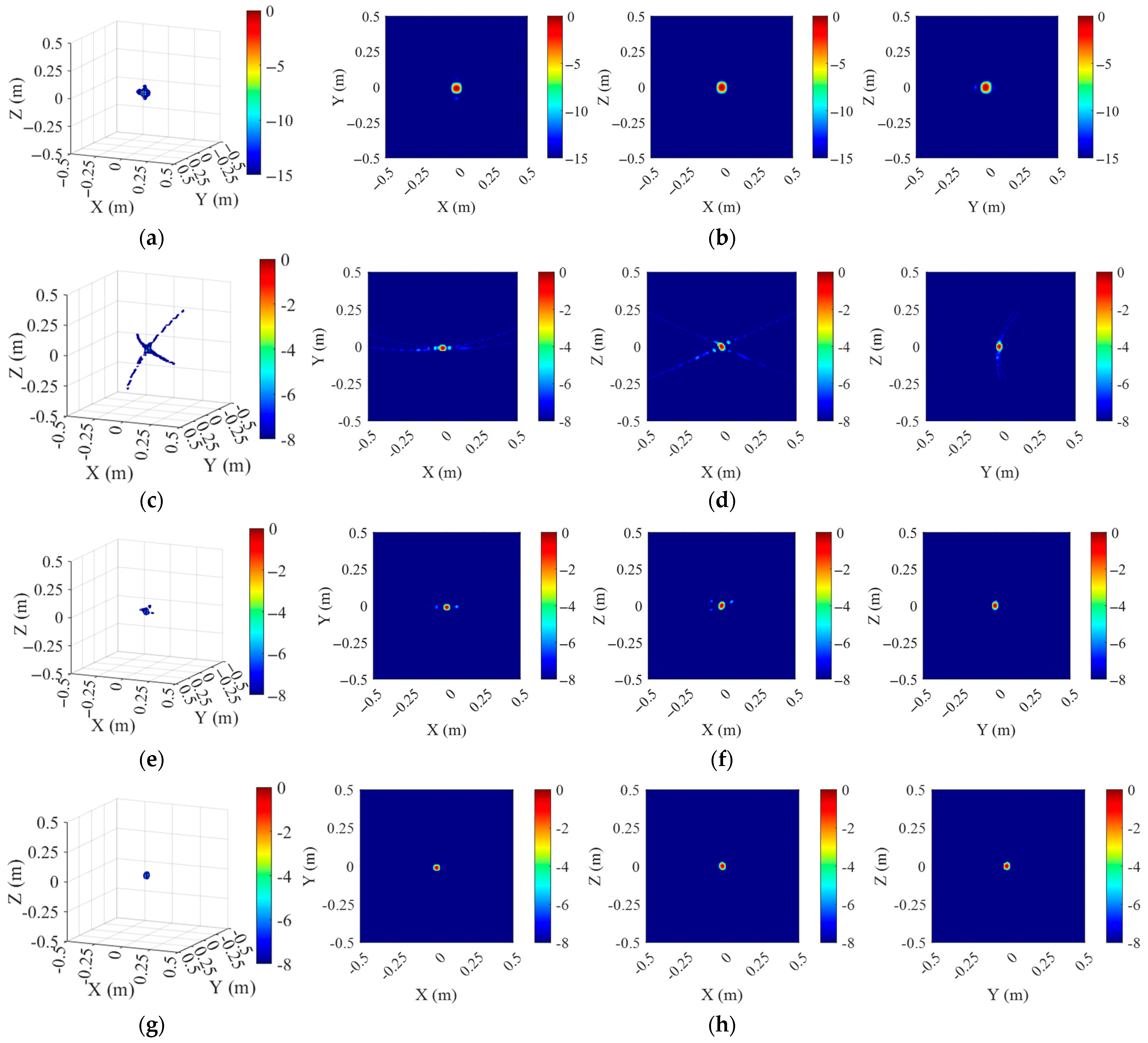
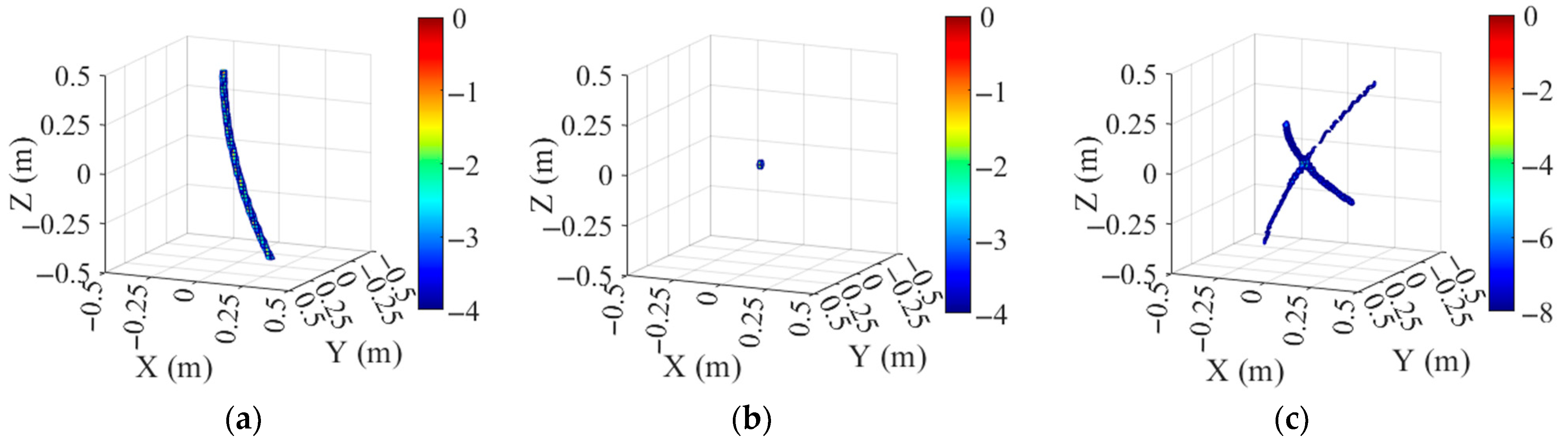
4.2.1. One Sphere
4.2.2. Three Spheres
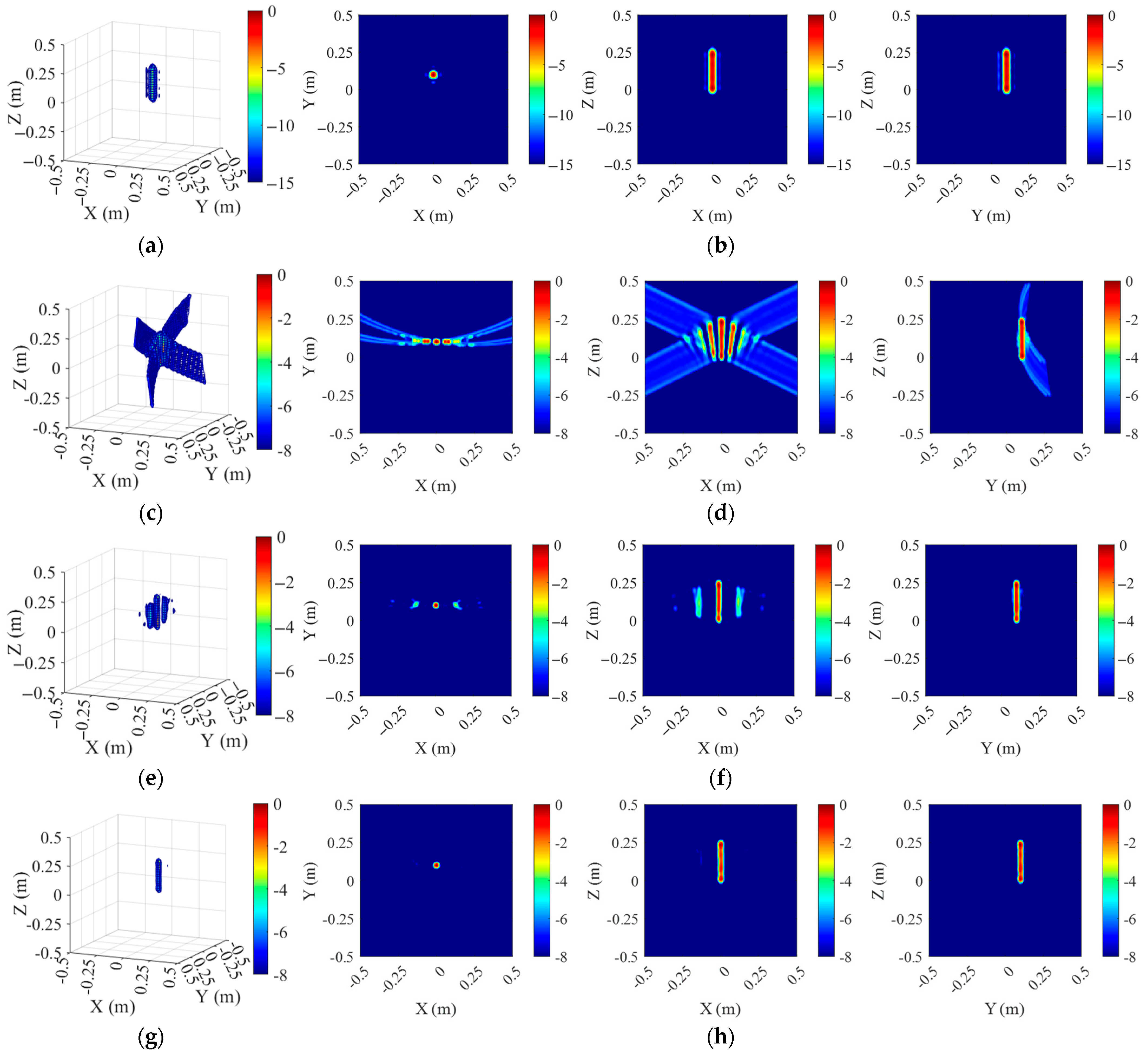
4.2.3. Cylinder
5. Discussion
5.1. Discussion of Imaging Result
5.2. The Minimum Sampling Range
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
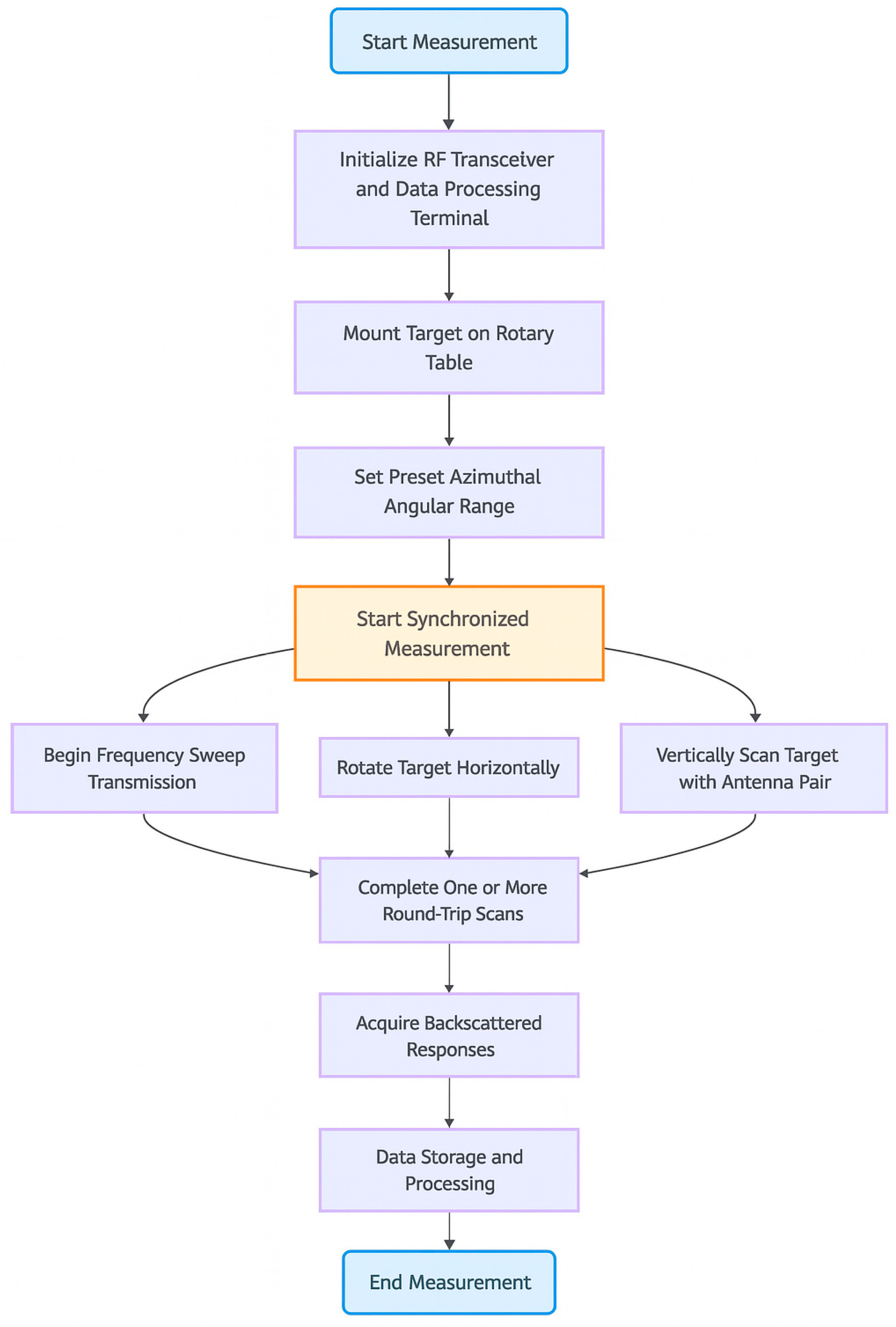
Appendix A. Measurement Process Flowchart
References
- Meng, X.; Xue, M.; Wang, Z. Microwave 3-D imaging echo simulation for discrete targets. Electron. Meas. Technol. 2007, 8, 37–40. [Google Scholar]
- Mensa, D.L. High Resolution Radar Cross-Section Imaging; Artech House: Boston, MA, USA, 1991; Volume 1, p. 280. [Google Scholar]
- Tan, W.; Hong, W.; Wang, Y.; Wu, Y. A novel spherical-wave three-dimensional imaging algorithm for microwave cylindrical scanning geometries. Prog. Electromagn. Res. 2011, 111, 43–70. [Google Scholar] [CrossRef]
- Falconi, M.T.; Comite, D.; Galli, A.; Pastina, D.; Lombardo, P.; Marzano, F.S. Forward Scatter Radar for Air Surveillance: Characterizing the Target-Receiver Transition from Far-Field to Near-Field Regions. Remote Sens. 2017, 9, 50. [Google Scholar] [CrossRef]
- Hu, C.; Li, N.; Chen, W.; Zhang, L. High-precision RCS measurement of aircraft’s weak scattering source. Chin. J. Aeronaut. 2016, 29, 772–778. [Google Scholar] [CrossRef]
- Jain, A.; Patel, I. Dynamic imaging and RCS measurements of aircraft. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 211–226. [Google Scholar] [CrossRef]
- Yang, Z.; Zhao, J.; Si, W.; Lou, C.; Zhao, X.; Miao, J. A Target Near-Field Scattering Measurement Technique Utilizing 3D Near-Field Imaging via Cylindrical Scanning. Remote Sens. 2025, 17, 1575. [Google Scholar] [CrossRef]
- Ding, Z.; Zhang, T.; Li, Y.; Li, G.; Dong, X.; Zeng, T.; Ke, M. A ship ISAR imaging algorithm based on generalized radon-Fourier transform with low SNR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6385–6396. [Google Scholar] [CrossRef]
- Liu, F.; Huang, D.; Guo, X.; Feng, C. Translational motion compensation for maneuvering target echoes with sparse aperture based on dimension compressed optimization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3169275. [Google Scholar] [CrossRef]
- Ren, L.; Mills, J.K.; Sun, D. Trajectory tracking control for a 3-DOF planar parallel manipulator using the convex synchronized control method. IEEE Trans. Control Syst. Technol. 2008, 16, 613–623. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, B.; Yu, H.; Chen, J.; Xing, M.; Hong, W. Sparse synthetic aperture radar imaging from compressed sensing and machine learning: Theories, applications, and trends. IEEE Geosci. Remote Sens. Mag. 2022, 10, 32–69. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Zhan, X.; Zhang, T.; Zhou, L.; Shi, J.; Wei, S. An RCS measurement method using sparse imaging based 3-D SAR complex image. IEEE Antennas Wirel. Propag. Lett. 2021, 21, 24–28. [Google Scholar] [CrossRef]
- He, Y.; Zhang, D.; Chen, Y. 3d radio imaging under low-rank constraint. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 3833–3847. [Google Scholar] [CrossRef]
- Zhang, X.; Lomas, A.; Zhou, M.; Zheng, Y.; Curtis, A. 3-D Bayesian variational full waveform inversion. Geophys. J. Int. 2023, 234, 546–561. [Google Scholar] [CrossRef]
- Park, J.; Raj, R.G.; Martorella, M.; Giusti, E. Multilook polarimetric 3-D interferometric ISAR imaging. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5937–5943. [Google Scholar] [CrossRef]
- Dou, Y.Y.; Wu, Y.M.; Jin, H.Q.; Jin, Y.Q.; Hu, J.; Cheng, J. The efficient norm regularization method applying on the ISAR image with sparse data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3218581. [Google Scholar] [CrossRef]
- Huang, P.; Xia, X.G.; Zhan, M.; Liu, X.; Liao, G.; Jiang, X. ISAR imaging of a maneuvering target based on parameter estimation of multicomponent cubic phase signals. IEEE Trans. Geosci. Remote Sens. 2021, 60, 3091645. [Google Scholar] [CrossRef]
- Shin, H.S.; Lim, J.T. Omega-K algorithm for spaceborne spotlight SAR imaging. IEEE Geosci. Remote Sens. Lett. 2011, 9, 343–347. [Google Scholar] [CrossRef]
- Yan, W.; Xu, J.D.; Li, N.J.; Tan, W. A novel fast near-field electromagnetic imaging method for full rotation problem. Prog. Electromagn. Res. 2011, 120, 387–401. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Zhang, Z.; Liu, L.; Shao, L. Sparse graph based self-supervised hashing for scalable image retrieval. Inf. Sci. 2021, 547, 622–640. [Google Scholar] [CrossRef]
- Li, D.; Zhan, M.; Liu, H.; Liao, Y.; Liao, G. A robust translational motion compensation method for ISAR imaging based on keystone transform and fractional Fourier transform under low SNR environment. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2140–2156. [Google Scholar] [CrossRef]
- Wang, X. DBN-FTLSTM: An Optimized Deep Learning Framework for Speech and Image Recognition. Informatica 2025, 49, 8169. [Google Scholar] [CrossRef]
- Zhang, Q.; Bai, J.; Chang, X. Pioneering Testing and Assessment Framework For AI-Powered SAR ATR Systems. In Proceedings of the 2024 IEEE 7th International Conference on Big Data and Artificial Intelligence (BDAI), Beijing, China, 5–7 July 2024; pp. 230–234. [Google Scholar]
- Gu, T.; Guo, Y.; Zhao, C.; Zhang, J.; Zhang, T.; Liao, G. Thorough Understanding and 3D Super-Resolution Imaging for Forward-Looking Missile-Borne SAR via a Maneuvering Trajectory. Remote Sens. 2024, 16, 3378. [Google Scholar] [CrossRef]
- Xing, S.; Song, S.; Quan, S.; Sun, D.; Wang, J.; Li, Y. Near-field 3D sparse SAR direct imaging with irregular samples. Remote Sens. 2022, 14, 6321. [Google Scholar] [CrossRef]
- Neitz, O.; Mauermayer, R.A.; Eibert, T.F. 3-D monostatic RCS determination from multistatic near-field measurements by plane-wave field synthesis. IEEE Trans. Antennas Propag. 2019, 67, 3387–3396. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X. Improved global range alignment for ISAR. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1070–1075. [Google Scholar] [CrossRef]
- Lv, M.; Chen, W.; Ma, J.; Yang, J.; Ma, X.; Cheng, Q. Joint random stepped frequency ISAR imaging and autofocusing based on 2D alternating direction method of multipliers. Signal Process. 2022, 201, 108684. [Google Scholar] [CrossRef]
- Righero, M.; Giordanengo, G.; Ciorba, L.; Vecchi, G. Fast antenna characterization with numerical expansion functions built with partial knowledge of the antenna and accelerated asymptotic methods. IEEE Trans. Antennas Propag. 2022, 71, 970–983. [Google Scholar] [CrossRef]
- Udupa, J.K. 3D imaging: Principles and approaches. In 3D Imaging in Medicine, 2nd ed; Routledge: New York, NY, USA, 2023; pp. 1–73. [Google Scholar]
- Knaell, K.; Cardillo, G. Radar tomography for the generation of three-dimensional images. IEE Proc. Radar Sonar Navig. 1995, 142, 54–60. [Google Scholar] [CrossRef]
- Tan, W.; Hong, W.; Wang, Y.; Lin, Y.; Wu, Y. Synthetic aperture radar tomography sampling criteria and three-dimensional range migration algorithm with elevation digital spotlighting. Sci. China Ser. F Inf. Sci. 2009, 52, 100–114. [Google Scholar] [CrossRef]





| Symbol | Parameter | Description |
|---|---|---|
| VV | Polarization Mode of the Antenna | |
| 2 m | Distance from the Antenna to the Target Center | |
| 4 GHz | Sweep Bandwidth | |
| 10 GHz | Center Frequency | |
| 23.52° | Angular Sweep Range | |
| 0.828 m | Rail Length | |
| 1 | Number of Round-Trip Samplings on the Turntable | |
| 29 | Number of Round-Trip Samplings Along the Rail | |
| 10 MHz | Frequency Interval | |
| 0.84° | Angular Interval | |
| 0.018 m | Rail Scanning Interval | |
| 401 | Number of Frequency Sampling Points | |
| 29 | Number of Angular Sampling Points | |
| 47 | Number of Rail Sampling Points | |
| 1363 | Total Number of Samples |
| Symbol | Scheme 1 1 | Scheme 2 1 | Scheme 3 1 |
|---|---|---|---|
| 0.14° | 0.14° | 0.14° | |
| 0.012 m | 0.018 m | 0.018 m | |
| 1 | 1 | 2 | |
| 3 | 4 | 8 | |
| 169 | 169 | 338 |
| Target | Dimensions | Pose |
|---|---|---|
| One Sphere | Radius: 5.64 cm | Vertical |
| Three Spheres | Radius: 5.64 cm Radius: 5.64 cm Radius: 5.64 cm | Vertical |
| Cylinder | Radius: 5.2 cm Height: 30.1 cm | Horizontal |
| Symbol | Parameter | Description |
|---|---|---|
| 1363 | Total number of traditional cylindrical samples | |
| 169 or 338 | Total number of “V”-shaped sampling | |
| The data acquisition time with VNA | ||
| Mechanical motion time of traditional cylindrical sampling | ||
| Mechanical motion time of “V”-shaped sampling | ||
| Total sampling time of the traditional cylindrical samples | ||
| Total sampling time of “V”-shaped sampling | ||
| Sampling quantity reduction ratio | ||
| Sampling time reduction ratio |
| Sampling Trajectories | The Traditional Cylindrical Sampling | Scheme 1 | Scheme 2 | Scheme 3 |
|---|---|---|---|---|
| PSLR (dB) | 15 | 6 | 7 | 12 |
| Symbol | The Traditional Cylindrical Sampling | Scheme 1 | Scheme 2 | Scheme 3 |
|---|---|---|---|---|
| The maximum resolvable dynamic range | 15 dB | 6 dB | 7 dB | 12 dB |
| 1 | 1363 | 169 | 169 | 338 |
| 149.9 s | 18.6 s | 18.6 s | 37.2 s | |
| 4802.4 s | 117.6 s | 117.6 s | 235.2 s | |
| 4952.3 s | 136.2 s | 136.2 s | 272.4 s | |
| 0 | 87.6% | 87.6% | 75.2% | |
| 0 | 97.2% | 97.2% | 94.3% |
| Symbol | “\”-Shaped Sampling 1 | “V”-Shaped Sampling 1 |
|---|---|---|
| 0.56° | 0.28° | |
| 0.018 m | 0.018 m | |
| 1 | 1 | |
| 1 | 2 | |
| 43 | 93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lou, C.; Zhao, J.; Wu, X.; Zhang, Y.; Yang, Z.; Li, J.; Miao, J. Efficient Sampling Schemes for 3D Imaging of Radar Target Scattering Based on Synchronized Linear Scanning and Rotational Motion. Remote Sens. 2025, 17, 2636. https://doi.org/10.3390/rs17152636
Lou C, Zhao J, Wu X, Zhang Y, Yang Z, Li J, Miao J. Efficient Sampling Schemes for 3D Imaging of Radar Target Scattering Based on Synchronized Linear Scanning and Rotational Motion. Remote Sensing. 2025; 17(15):2636. https://doi.org/10.3390/rs17152636
Chicago/Turabian StyleLou, Changyu, Jingcheng Zhao, Xingli Wu, Yuchen Zhang, Zongkai Yang, Jiahui Li, and Jungang Miao. 2025. "Efficient Sampling Schemes for 3D Imaging of Radar Target Scattering Based on Synchronized Linear Scanning and Rotational Motion" Remote Sensing 17, no. 15: 2636. https://doi.org/10.3390/rs17152636
APA StyleLou, C., Zhao, J., Wu, X., Zhang, Y., Yang, Z., Li, J., & Miao, J. (2025). Efficient Sampling Schemes for 3D Imaging of Radar Target Scattering Based on Synchronized Linear Scanning and Rotational Motion. Remote Sensing, 17(15), 2636. https://doi.org/10.3390/rs17152636






