Performance Degradation in Monopulse Angle Measurement of Planar Phased-Array Due to Cross-Polarization Component
Abstract
1. Introduction
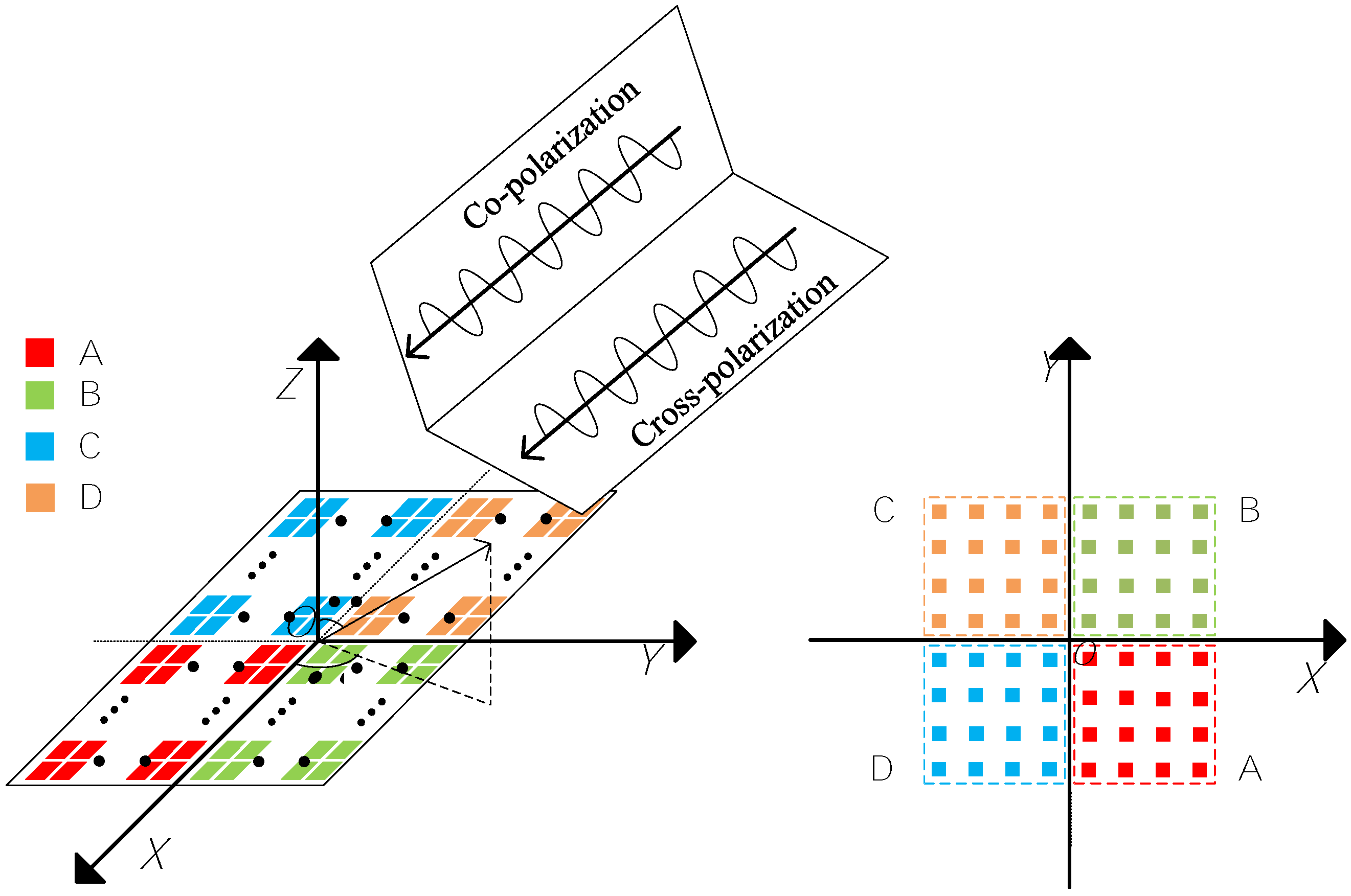
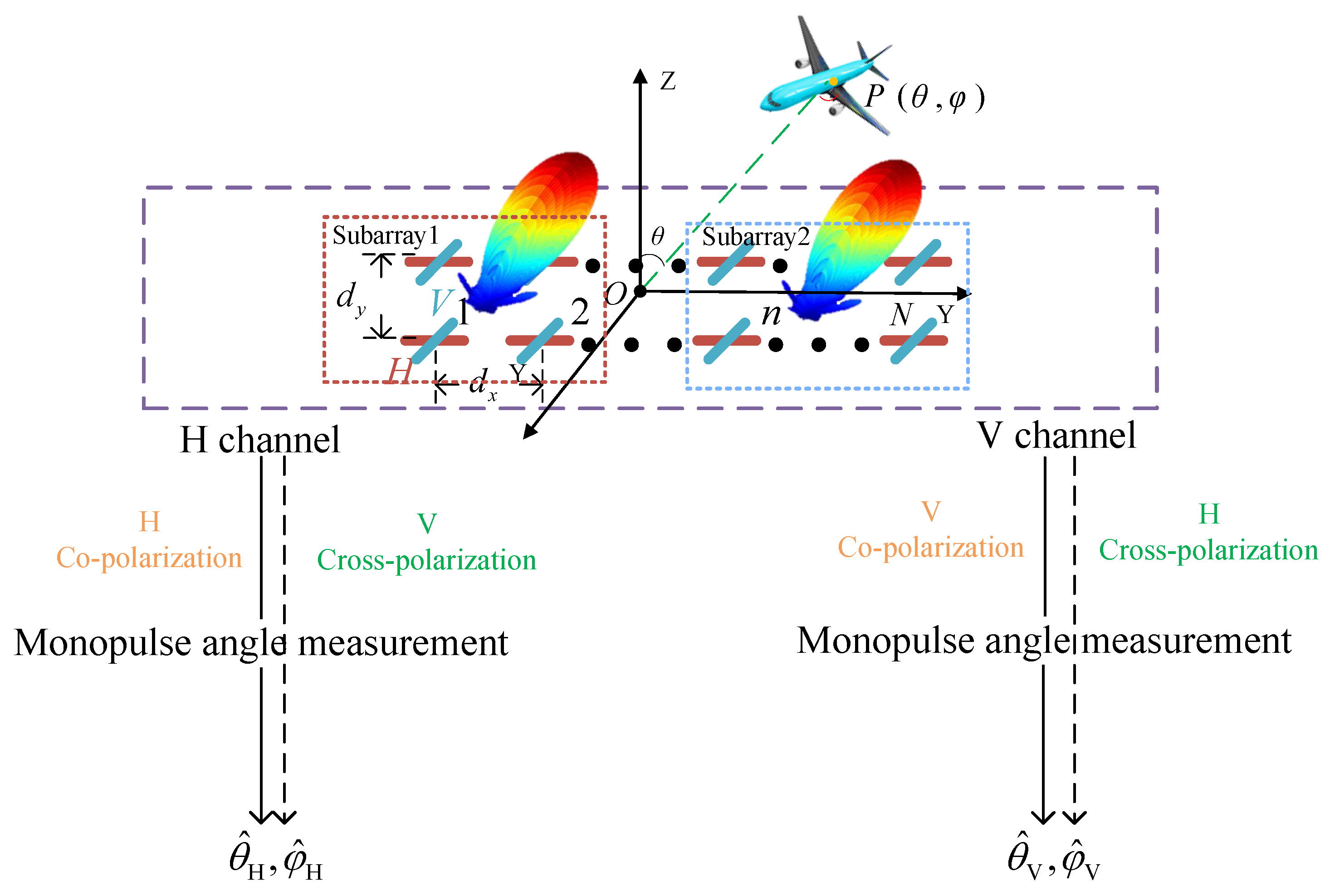
2. Mathematical Model of PA Radar Monopulse 2D-Angle Measurement
2.1. Monopulse Amplitude Comparison
2.2. Monopulse Phase Comparison
3. Monopulse Angle Measurement with Cross-Polarization
3.1. Case 1: Identical Cross-Polarization Patterns
3.2. Case 2: Different Cross-Polarization Patterns
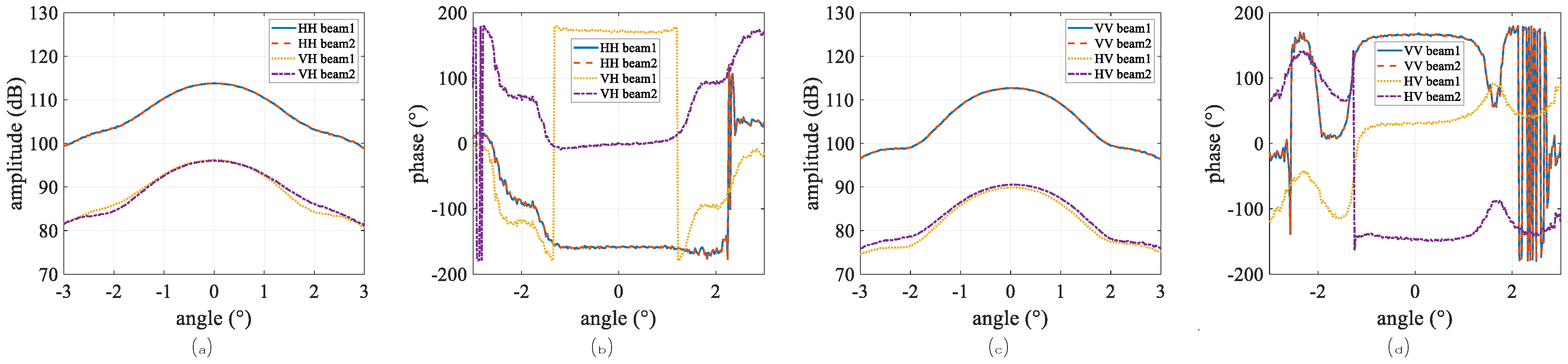
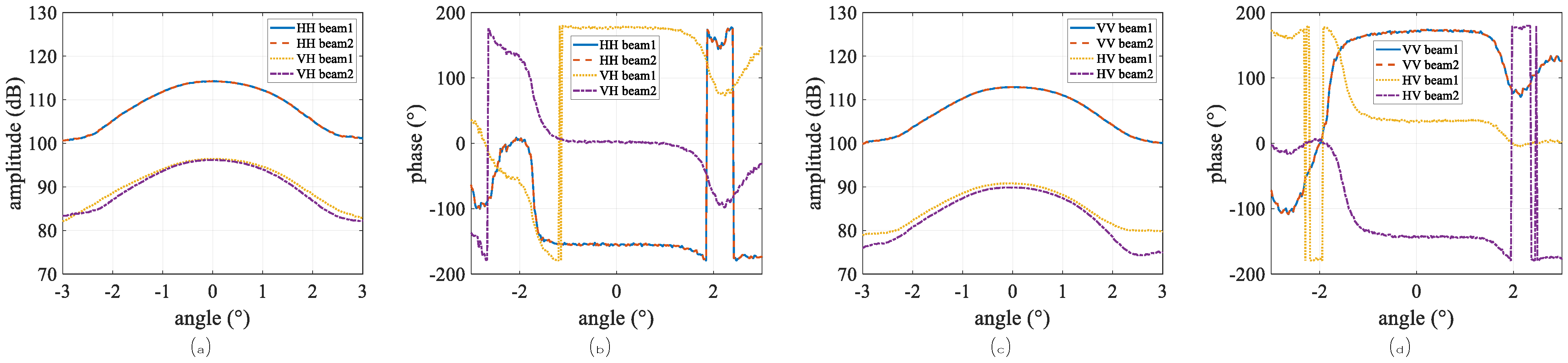
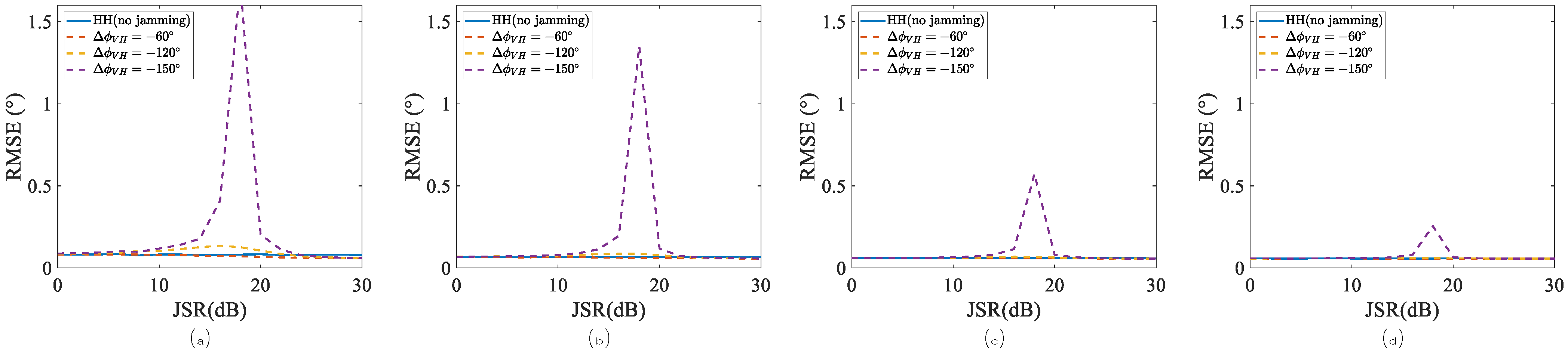
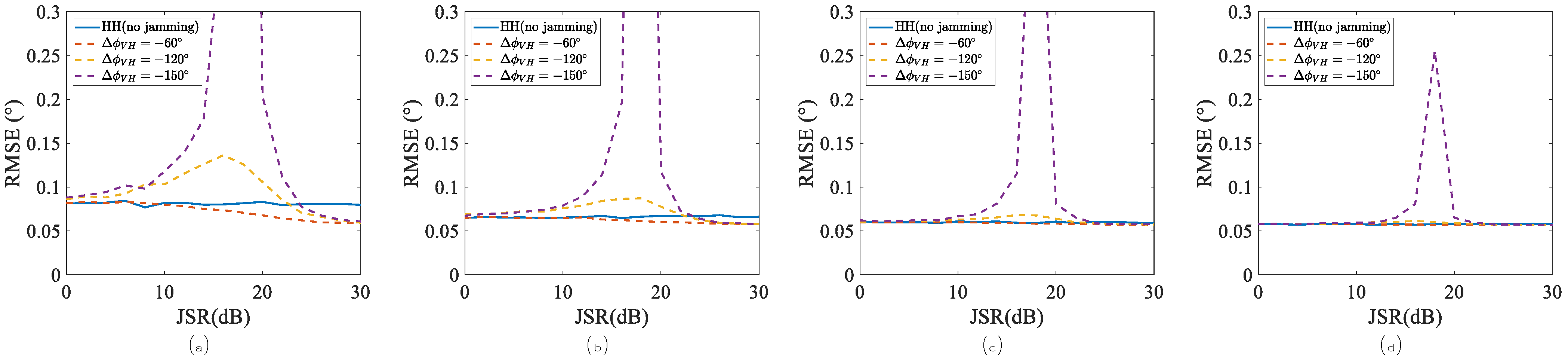
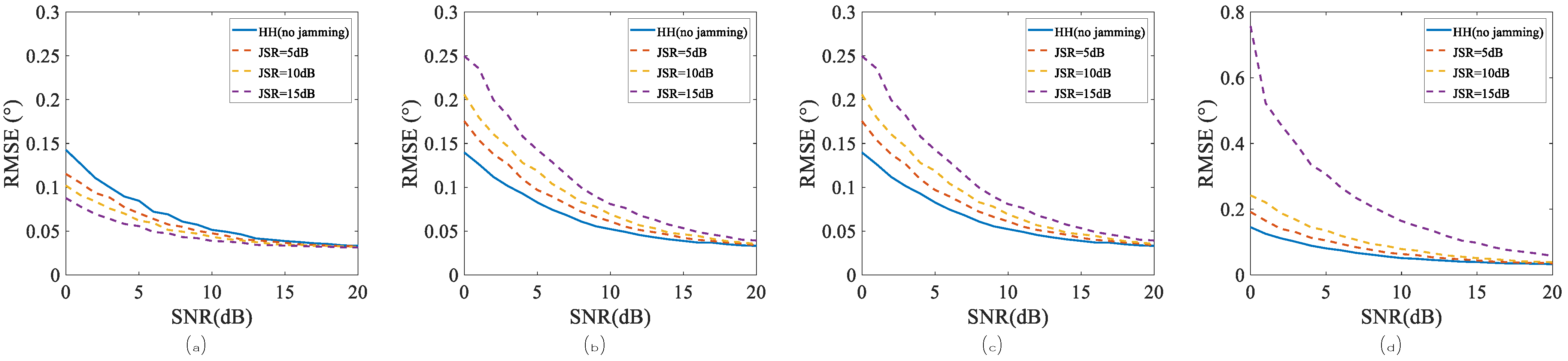
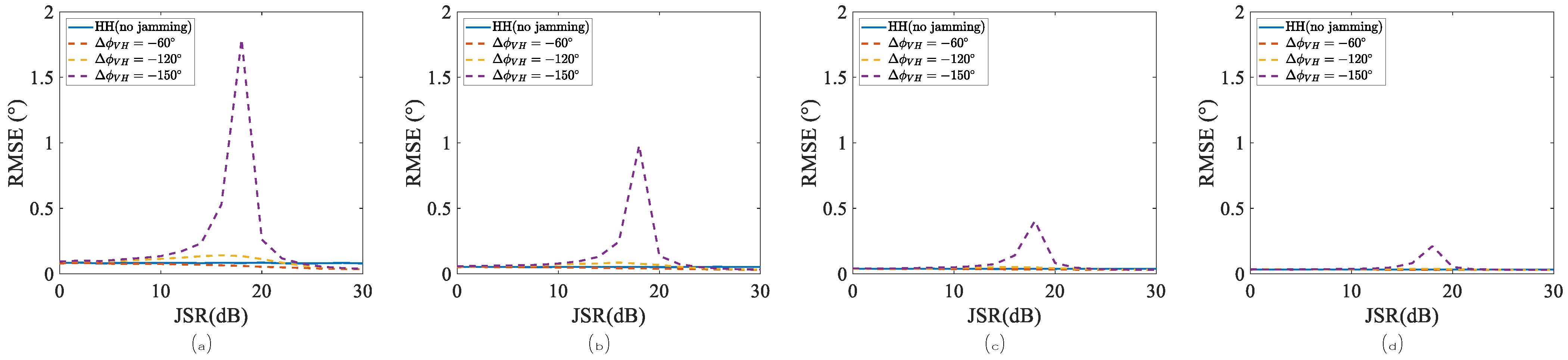
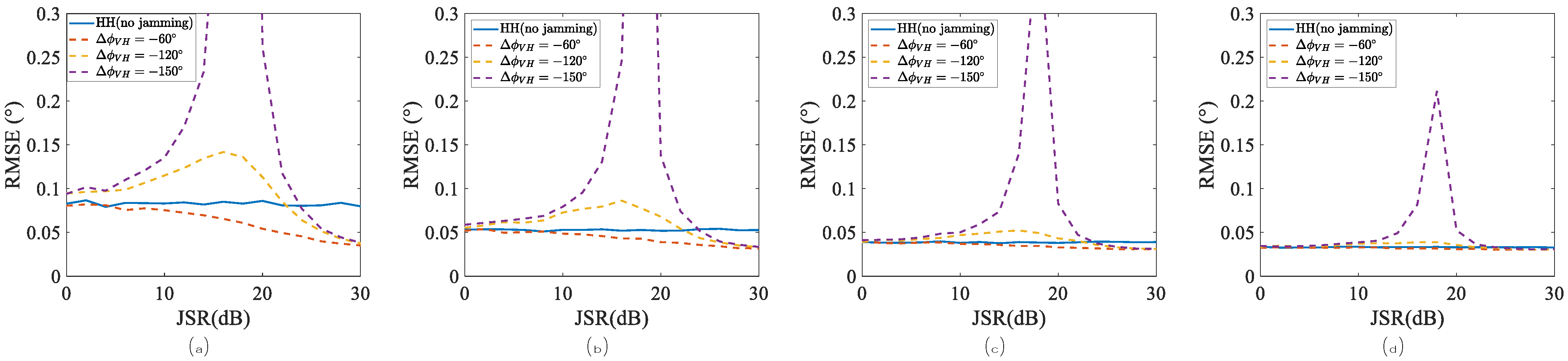
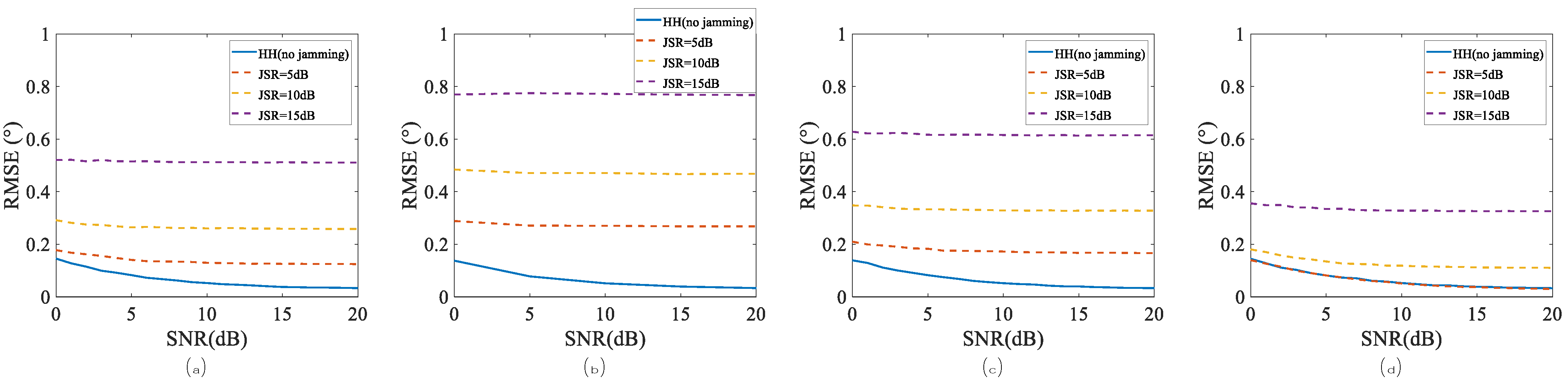
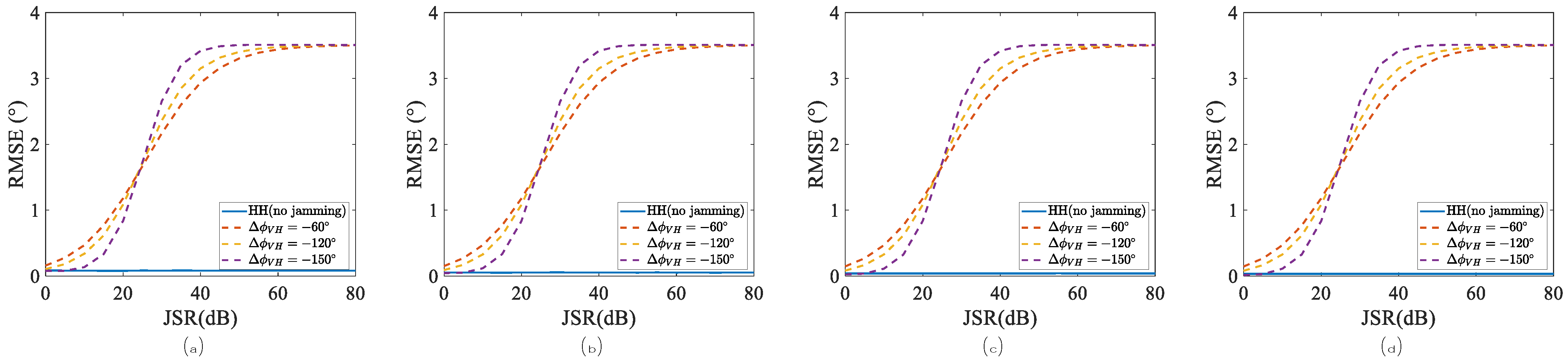
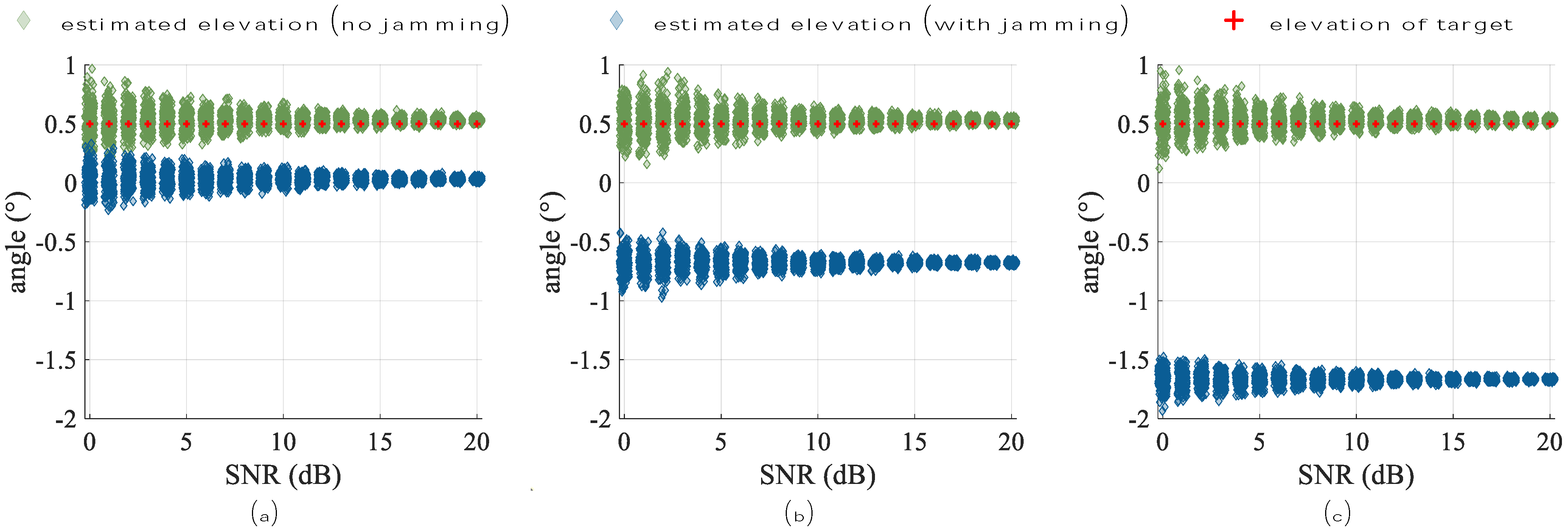
4. Experiments and Simulations
4.1. The Amplitude and Phase Patterns of Measurement
4.2. Performance of Angle Estimations Under Case 1
4.3. Performance of Angle Estimations Under Case 2
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sherman, S.M.; Barton, D.K. Monopulse Principles and Techniques; Artech House: London, UK, 2011. [Google Scholar]
- Liu, Y.; Yu, W.; Li, S.; Zhao, H.; Lin, Q. An Effective Approach for Space-Borne ISAR Receiving Echoes with Variable Sampling Start Based on IMM Method. IEEE Geosci. Remote Sens. Lett. 2025, 22, 1000705. [Google Scholar] [CrossRef]
- Xie, J.; Zhou, W.; Zhou, G.; Yuan, Y.; Li, S. Tracking of Range and Azimuth for Continuous Imaging of Marine Target in Monopulse ISAR with Wideband Echoes. Int. J. Antennas Propag. 2016, 2016, 1865915. [Google Scholar] [CrossRef][Green Version]
- Freeman, A.; Zink, M. An application of the monopulse principle to determining elevation angles in SAR images. IEEE Trans. Geosci. Remote Sens. 1994, 32, 616–625. [Google Scholar] [CrossRef]
- Soumekh, M. Moving target detection in foliage using along track monopulse synthetic aperture radar imaging. IEEE Trans. Image Process. 1997, 6, 1148–1163. [Google Scholar] [CrossRef]
- Sui, R.; Wang, J.; Sun, G.; Xu, Z.; Feng, D. A Dual-Polarimetric High Range Resolution Profile Modulation Method Based on Time-Modulated APCM. IEEE Trans. Antennas Propag. 2025, 73, 1007–1017. [Google Scholar] [CrossRef]
- Ma, J.; Shi, L.; Li, Y.; Xiao, S.; Wang, X. Angle estimation of extended targets in main-lobe interference with polarization filtering. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 169–189. [Google Scholar] [CrossRef]
- Du Plessis, W.P. A Comprehensive Investigation of Retrodirective Cross-Eye Jamming; University of Pretoria (South Africa): Pretoria, South Africa, 2010. [Google Scholar]
- Nickel, U. Overview of generalized monopulse estimation. IEEE Aerosp. Electron. Syst. Mag. 2006, 21, 27–56. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Yang, X.; Zheng, L.; Long, T.; Baker, C.J. A novel monopulse technique for adaptive phased array radar. Sensors 2017, 17, 116. [Google Scholar] [CrossRef] [PubMed]
- Nickel, U. Monopulse estimation with adaptive arrays. In IEE Proceedings F (Radar and Signal Processing); IET: Lucknow, India, 1993; Volume 140, pp. 303–308. [Google Scholar]
- Li, H.L.; Li, M.D.; Cui, X.C.; Chen, S.W. Man-Made Target Structure Recognition with Polarimetric Correlation Pattern and Roll-Invariant Feature Coding. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8024105. [Google Scholar] [CrossRef]
- Li, H.L.; Liu, S.W.; Chen, S.W. PolSAR Ship Characterization and Robust Detection at Different Grazing Angles with Polarimetric Roll-Invariant Features. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5225818. [Google Scholar] [CrossRef]
- Seifer, A.D. Monopulse-radar angle tracking in noise or noise jamming. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 622–638. [Google Scholar] [CrossRef]
- Wang, H.; Xu, L.; Yan, Z.; Gulliver, T.A. Low-Complexity MIMO-FBMC Sparse Channel Parameter Estimation for Industrial Big Data Communications. IEEE Trans. Ind. Inform. 2021, 17, 3422–3430. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, P.; Li, X. Channel Parameter Estimation of mmWave MIMO System in Urban Traffic Scene: A Training Channel-Based Method. IEEE Trans. Intell. Transp. Syst. 2022, 25, 754–762. [Google Scholar] [CrossRef]
- Ludwig, A. The definition of cross polarization. IEEE Trans. Antennas Propag. 1973, 21, 116–119. [Google Scholar] [CrossRef]
- Huang, J.; Yin, J.; An, M.; Li, Y. Azimuth Pointing Calibration for Rotating Phased Array Radar Based on Ground Clutter Correlation. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1000315. [Google Scholar] [CrossRef]
- Abd El-Alim, O.; Agrama, E.; Ezz-El-Arab, M. Second-order discriminant function for amplitude comparison monopulse antenna systems (EW antenna array). IEEE Trans. Instrum. Meas. 1991, 40, 596–600. [Google Scholar] [CrossRef]
- Kırdar, B.; Ayazgök, S. Cross Polarization Jamming and Jammer Antenna Polarization Purity Level Analysis. In Proceedings of the 2022 30th Signal Processing and Communications Applications Conference (SIU), Safranbolu, Turkey, 15–18 May 2022; pp. 1–4. [Google Scholar]
- Kırdar, B.; Uslu, A. Polarization Purity, Jamming Power and Time-Sharing Analysis for Cross Polarization Jamming. In Proceedings of the 2024 32nd Signal Processing and Communications Applications Conference (SIU), Mersin, Turkey, 15–18 May 2024; pp. 1–4. [Google Scholar]
- Du Plessis, W.P.; Mosoma, K. Initial Results for Cross-Polarisation Jamming of Monopulse Radar. In Proceedings of the 2022 International Conference on Electromagnetics in Advanced Applications (ICEAA), Cape Town, South Africa, 5–9 September 2022; pp. 258–263. [Google Scholar]
- Neri, F. Anti-monopulse jamming techniques. In Proceedings of the 2001 SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (Cat. No. 01TH8568), Campina Grande, Brazil, 9–12 November 2001; Volume 2, pp. 45–50. [Google Scholar]
- Han, H.; Xu, X.; Wang, H.; Dai, H. Analysis of cross-polarization jamming for phase comparison monopulse radars. In Proceedings of the 2019 IEEE 2nd International Conference on Electronic Information and Communication Technology (ICEICT), Harbin, China, 20–22 January 2019; pp. 404–407. [Google Scholar]
- Zhong, T.; Tao, H.; Lan, L. Multi-Dimensional Parameter Estimation in Polarimetric ULA with Cross-Distribution Dipole Pairs. Remote Sens. 2022, 14, 3614. [Google Scholar] [CrossRef]
- Deng, Y. The Research on Monopulse Angle Measurement for Digital Phased Array. Ph.D. Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2021. (In Chinese). [Google Scholar]
- Wei, F. Study of Algorithm for Phased Array Monopulse Angle Measurement. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2016. (In Chinese). [Google Scholar]
- Forteza, X.J.; Bhagwat, S.; Kumar, S.; Pani, P. Novel Ringdown Amplitude-Phase Consistency Test. Phys. Rev. Lett. 2023, 130, 021001. [Google Scholar] [CrossRef]
- Kim, J.A.; Lee, J.H. Performance Degradation in Cross-Eye Jamming Due to Amplitude/Phase Instability between Jammer Antennas. Sensors 2021, 21, 5027. [Google Scholar] [CrossRef]
- Liu, T.; Wei, X.; Liu, Z.; Guan, Z. Continuous and Stable Cross-Eye Jamming via a Circular Retrodirective Array. Electronics 2019, 8, 806. [Google Scholar] [CrossRef]
- Zou, R.; Cheng, Y.; Wu, H.; Yang, Z.; Liu, K.; Hua, X. A Two-Step Space-Time Adaptive Matrix Information Geometry Detector for Multi-Channel Radar. IEEE Trans. Aerosp. Electron. Syst. 2025. early access. [Google Scholar] [CrossRef]




| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| number of elements along X-axis | h | orthogonal polarization component | |
| number of elements along Y-axis | E | incident wave field vector | |
| azimuth angle | maximum received power | ||
| elevation angle | polarization match factor | ||
| elements spacing along X-axis | amplitude pattern | ||
| elements spacing along Y-axis | phase pattern | ||
| position vector of element (m,n) | noise | ||
| vector in direction of beam | phase difference between two subarrays | ||
| beam pattern | interval between two subarrays | ||
| slope of angle identification curve | co-polarization component | ||
| V | open-circuit voltage equation | cross-polarization component | |
| sum beam pattern | horizontal polarization component | ||
| elevation difference beam pattern | vertical polarization component | ||
| azimuth difference beam pattern | L | Monte Carlo iterations | |
| s | received signal | phase difference |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Pang, B.; Dai, D.; Chen, B.; Tan, Z. Performance Degradation in Monopulse Angle Measurement of Planar Phased-Array Due to Cross-Polarization Component. Remote Sens. 2025, 17, 2454. https://doi.org/10.3390/rs17142454
Zhang Y, Pang B, Dai D, Chen B, Tan Z. Performance Degradation in Monopulse Angle Measurement of Planar Phased-Array Due to Cross-Polarization Component. Remote Sensing. 2025; 17(14):2454. https://doi.org/10.3390/rs17142454
Chicago/Turabian StyleZhang, Yunhui, Bo Pang, Dahai Dai, Bo Chen, and Zhengkuan Tan. 2025. "Performance Degradation in Monopulse Angle Measurement of Planar Phased-Array Due to Cross-Polarization Component" Remote Sensing 17, no. 14: 2454. https://doi.org/10.3390/rs17142454
APA StyleZhang, Y., Pang, B., Dai, D., Chen, B., & Tan, Z. (2025). Performance Degradation in Monopulse Angle Measurement of Planar Phased-Array Due to Cross-Polarization Component. Remote Sensing, 17(14), 2454. https://doi.org/10.3390/rs17142454






