Abstract
High-resolution mooring observations captured diverse upper-ocean responses during typhoon passage, showing strong agreement with satellite-derived sea surface temperature and salinity. Analysis indicates that significant wind-induced mixing drove pronounced near-surface cooling and salinity increases at the mooring site. This mixing enhancement was predominantly governed by rapid intensification of near-inertial shear in the surface layer, revealed by mooring observations. Unlike shear instability, near-inertial horizontal kinetic energy displays a unique vertical distribution, decreasing with depth before rising again. Interestingly, the subsurface peak in diurnal tidal energy coincides vertically with the minimum in near-inertial energy. While both barotropic tidal forcing and stratification changes negligibly influence diurnal tidal energy emergence, significant energy transfer occurs from near-inertial internal waves to the diurnal tide. This finding highlights a critical tide–wave interaction process and demonstrates energy cascading within the oceanic internal wave spectrum.
1. Introduction
Tropical cyclones (TCs) are low-pressure weather systems, distinguished by strong vertical convection and enclosed wind patterns at lower altitudes. The South China Sea (SCS), recognized as the largest marginal sea in the western North Pacific, experiences an average of approximately 10.2 typhoons annually, either originating from the western North Pacific or developing locally [1]. Previous observations and modeling studies have investigated that TCs induced significant thermal responses in upper-ocean layers, characterized by phenomena such as sea-surface cooling and reduced salinity, as well as variability in temperature and salinity at subsurface levels [2,3,4,5,6,7,8,9]. An analysis of Argo data spanning from 1996 to 2012 revealed that TCs typically induce an average surface cooling of approximately 1.4 °C along their trajectory over a duration of about 20 days within the shallower mixed layer [10]. In the study of typhoon cases, it has been observed that sea surface cooling typically ranges from 1 to 6 °C [5,8,10,11,12,13,14], with coastal areas experiencing even more significant cooling, potentially reaching approximately 11 °C [15,16]. Satellite data (Aquarius/SMOS) show that cyclones like Katia (2011) and Igor (2010) increased sea surface salinity by ~1.5 psu [17,18], while Cyclone Vardah (2016) reduced it by 0.5 psu due to heavy rainfall [19]. Modeling research has indicated that the passage of a typhoon is normally associated with horizontal and vertical advection, mixing, and the air–sea heat exchange, which typically induces deepening of the upper ocean mixed layer, resulting in surface cooling and subsurface warming [2,20]. Additionally, TC-induced water circulation, including upwelling and downwelling, can transport subsurface warm anomalies into deeper oceanic layers [7].
Along with the considerable thermal response, dynamic responses are also triggered by TCs in the upper-ocean layers, one of the most remarkable of which is represented by near-inertial internal waves. The near-inertial currents present in the mixed layer facilitate convergence and divergence within the thermocline, thereby inducing upwelling and downwelling [2]. These upwelling and downwelling events result in the formation of cold and warm anomalies in the upper ocean, respectively [2,3,7,21]. Observational data obtained during TCs, such as Hurricane Frances (2004, category 3) and Hurricane Ivan (2004), have recorded near-inertial oscillation velocities surpassing 1.6 m s−1 [9,22] and 2 m s−1 [23], respectively. The vertical shear associated with these oscillations promotes turbulent mixing through shear instability, which leads to the entrainment of colder thermocline water into the mixed layer [2,14]. Furthermore, TCs significantly contribute to the kinetic energy budget of the upper ocean by generating near-inertial waves (NIWs), which surpass the contributions from other processes [5,8,24].
Within the mixed layer, these waves are characterized by pronounced near-inertial oscillations that can persist for several days, primarily dissipating through downward propagation as internal wave packets into the thermocline and deeper ocean layers. Alford et al. [25] suggested that near-inertial energy reflects multiple times within the pycnocline and dissipates after several inertial periods. This energy is predominantly generated by strong resonant winds at the ocean’s surface, such as those produced by hurricanes, typhoons, and mid-latitude storms [24,26,27,28]. Wind-generated near-inertial waves can penetrate into the ocean’s interior [29]. As they propagate, some NIWs may undergo nonlinear deformation into smaller vertical-scale waves, ultimately breaking and contributing to turbulent mixing in the deep ocean [30,31]. While the impact of TCs on the energy budgets of internal waves remains inadequately characterized, recent developments have highlighted the energy transfer among various wave components. Numerical studies have demonstrated the occurrence of significant energy transfer from NIWs and internal tides (ITs) to higher-mode internal waves through dynamic processes, and the transfer efficiencies are sensitive to background conditions [32,33,34]. An observational study in the northern South China Sea revealed the occurrence of increased energy transfer rates between NIWs and D1 ITs following typhoon occurrences [6]. Near-critical latitudes associated with the M2 and M1 tidal constituents have been shown to enhance the transfer of tidal energy into near-inertial motions, facilitated by resonant frequency relationships [35,36,37,38,39]. Typhoons significantly amplify energy transfer rates to high-frequency internal waves (HFIWs), with storm-induced inertial oscillations altering the kinetic to baroclinic energy transfer budget [40,41,42,43]. This accelerated energy transfer is pivotal in directing internal tidal energy toward small-scale turbulent dissipation, and estimated transfer rates indicate the occurrence of considerable effects on regional mixing budgets [44,45].
Despite extensive research on the oceanic response to tropical cyclones, the specific mechanisms driving upper-ocean dynamics in the SCS—particularly the vertical structure of near-inertial energy and its resultant energy cascading—remain inadequately explored, largely due to a scarcity of high-resolution in situ observations. Typhoon Trami’s (2024) passage over the northwestern South China Sea in October 2024 provided a unique opportunity. Its track over a deep continental slope mooring station (~1360 m; Figure 1a,b) yielded novel, high-resolution observations, complemented by satellite data. This comprehensive dataset enables a valuable investigation into the varied upper-ocean responses. Consequently, this study focuses on analyzing the response characteristics of key ocean parameters (temperature, salinity, currents), examining the vertical distribution of typhoon-excited near-inertial energy, and analyzing the resultant upper-ocean mixing and internal wave energy cascading. The structure of this article is organized as follows: Section 2 outlines the datasets and methodologies employed in the study; Section 3 presents the results; and Section 4 discusses the findings and summarizes the principal conclusions.
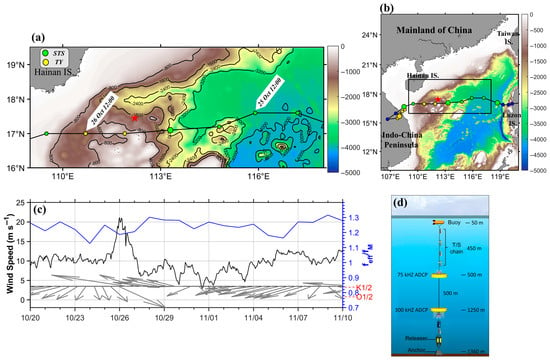
Figure 1.
(a) The mooring position in the southern SCS (red star). The background shaded color and contour lines represent water depth (m). The black line represents the typhoon’s trajectory, and the colored circle represents the location of the typhoon’s center and its intensity (TY: Typhoon; STY: Super Typhoon). (b) is similar to (a) but covers a larger regional scope; the black-line box marks the area corresponding to (a). (c) Time series of 10 m wind speed (black line), wind vector (gray arrows), and feff/fM (blue line) at the mooring location. K1/2 and O1/2 respectively denote the critical values at which the local effective frequency reaches that of the diurnal tides. The wind data and sea surface geostrophic current were obtained from the ERA5 and CMEMS, respectively. (d) Schematic diagrams of self-contained subsurface mooring.
2. Materials and Methods
2.1. Data
2.1.1. Mooring
A high temporal resolution mooring was deployed in the northern South China Sea at coordinates 112.21°E and 17.45°N (the red star in Figure 1a), situated at a bottom depth of 1360 m. The mooring functioned continuously from 20 October 2024 to 15 December 2024. It was outfitted with an upward-looking 75 kHz acoustic Doppler current profiler (ADCP) positioned 500 m below the sea surface, which measured current velocities using vertical bins of 8 m, totaling 74 bins, with a sampling interval of 60 s. Additionally, an instrument chain comprising 21 conductivity-temperature-depth (CTD) or temperature-depth (TD) sensors was deployed at various depths, collecting data at vertical intervals of either 10 m or 20 m, with sampling intervals of 30 s (Figure 1b and Table 1).

Table 1.
Information of Mooring and Detailed Settings of Instruments Used.
2.1.2. TC Best Track and Wind Data
A TC passed through the mooring station location during the observation period (Figure 1). Information on its track and intensities was obtained from the China Meteorological Administration (CMA) [46,47]. All data in this paper are recorded in UTC with a time resolution of 6 h. The near-center maximum wind speed of the TCs in the dataset is considered as the average of the 2 min near-center maximum wind speed. Furthermore, the wind speed at the mooring location was extracted from the ERA5 dataset and interpolated to the specific mooring position. Notably, the wind speed exceeded 20 m s−1 on 26 October, highlighting the influence of the typhoon’s intense winds (Figure 1c).
2.1.3. Satellite
The daily SSH anomalies and geostrophic velocity anomalies were obtained from the Copernicus Marine and Environment Monitoring Service (CMEMS) at a horizontal resolution of 0.25° × 0.25° (Global Ocean Gridded L4 Sea Surface Height and Derived Variables Reprocessed (1993-ongoing)). The daily microwave and infrared optimally interpolated SST (MW_IR OISST) data were provided by Remote Sensing Systems (RSS) at a resolution of nearly 9 km [48]. The daily 8-day running mean level 3 version 4 SSS data were obtained by the soil moisture active passive (SMAP) satellite at a resolution of 0.25° × 0.25° and are available from RSS [49]. Barotropic tidal current data at the mooring location are predicted from the TPXO9 dataset. Detailed availability for data is described in the “Data Availability Statement”.
2.2. Methods
2.2.1. Stability and Energy Estimates
To evaluate the ocean state during the observation period, the square of the buoyancy frequency (), shear squared (), the Richardson number (Ri), and near-inertial horizontal kinetic energy (NIKE) are computed. The buoyancy frequency is calculated following
where g is the gravitational acceleration, is the water density, and is the reference water density of 1023 kg/m3.
The square of velocity shear is calculated following
where u and v are the zonal and meridional velocities, respectively.
To describe the stability of the water column, the Richardson number is calculated based on the buoyancy frequency N2 and the square of vertical velocity shear S2, following the equation:
Generally, Richardson numbers below a critical value of 0.25 are considered a necessary condition for shear-induced turbulent mixing to occur.
To isolate near-inertial frequency variations in the currents, we applied a third-order Butterworth filter to the full observational time series. After removing the barotropic current component from the TPXO9 dataset, the residual current variations were divided into NIWs within the frequency band [(0.85, 1.20) f] using a third-order Butterworth filter, where f denotes the local inertial frequency. Horizontal kinetic energy (HKE) was calculated using the formula . Also, the time-integrated average NIKE is calculated using
where and represent the temporal limits of the time integral.
2.2.2. Energy Transfer Rate
Internal waves within the near-inertial and high-frequency bands constitute significant modes of oceanic variability. Previous studies have investigated the energy transfer mechanisms between these two categories of internal waves [35,41,42]. Notably, internal waves in the low-frequency bands exhibit a considerably smaller vertical-to-horizontal aspect ratio compared to HFIWs. This disparity leads to the predominance of energy transfer occurring as a triple product involving vertical shears in the low-frequency bands and Reynolds stresses in the high-frequency bands [36,41,42,43,50], given by
where , and denote the horizontal and vertical velocities associated with high-frequency internal waves. Here, we set the lower filter cutoff to 0.9 cpd; denotes the vertical shear of NIWs; the angle bracket ⟨ ⟩ represents time averaging; subscript i = 1, 2 stands for the zonal and meridional components; vertical velocity is calculated from the displacement of the isotherms [6]; the symbol Σ signifies the summation over the indices i = 1, 2. This equation has been employed to compute the energy transfer rate. Additionally, to investigate the energy transfer from the near-inertial frequency band to the diurnal tidal frequency band, prior to analyzing the energy transfer rate, the raw velocity data were first subjected to 1.1 cpd low-pass filtering.
3. Results
3.1. Upper Ocean Thermal and Dynamical Response
This section presents an analysis of the upper ocean response characteristics as influenced by Typhoon Trami.
3.1.1. Satellite-Observed Sea Surface Response
Figure 2 illustrates the changes in sea surface temperature as observed by satellite during the passage of Typhoon Trami from 24 to 28 October. Prior to the typhoon’s arrival, the sea surface temperature in the northern region of the South China Sea ranged from approximately 28 to 30 °C (Figure 2a), significantly exceeding the critical threshold of 26 °C, which is normally recognized as the minimum temperature conducive to typhoon formation [51,52]. Consequently, the typhoon exhibited intensification between the 25th and 26th (Figure 2b,c), underscoring the influence of sea surface temperature on the strengthening of typhoons. Following the typhoon’s passage, a marked decrease in sea surface temperature was observed on the right side of the typhoon’s trajectory, with the maximum cooling reaching approximately 2 °C (Figure 2f).
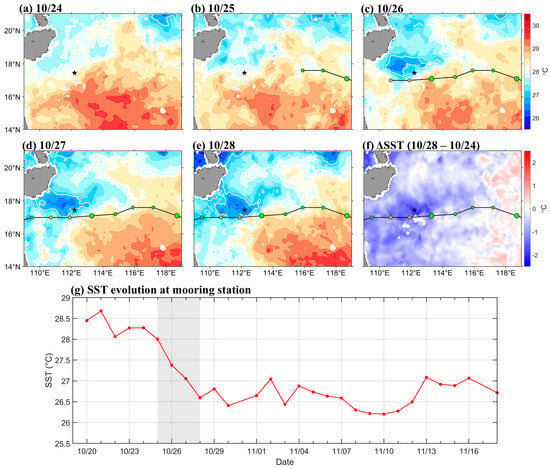
Figure 2.
Daily satellite microwave optimally interpolated sea surface temperature from 24 and 28 October 2024 (a–e) and the difference between 28th and 24th (f), the former minus the latter. The black star indicates the mooring position in the southern SCS. The black line represents the typhoon’s trajectory, and the colored solid circle represents the location of the typhoon’s center and its intensity, as referred to in Figure 1a. The white contour lines in panels (a–e) represent the 26.5 °C isotherm. Daily evolution of SST at the mooring location (g). The grey shaded area represents the period of typhoon impact.
On 26 October, when Trami passed the mooring location, the sea surface temperature in the area to the right of the typhoon’s center diminished to a minimum of around 26 °C (Figure 2c). Within 2 days following Trami’s passage, the sea surface temperature near the mooring station on the right side of the typhoon’s trajectory continued to decline. Satellite observations indicated that the daily average temperature fell to a minimum of approximately 26.5 °C by the 28th, with a substantial area of noticeably cooler seawater surrounding it (Figure 2e).
Figure 2f illustrates the SST cooling induced by Typhoon Trami, calculated as the difference between SST observations on 28 and 24 October at the mooring station. Near the station, a maximum cooling of approximately 2.5 °C was observed. The cooling beneath the typhoon’s trajectory is attributed to vertical upwelling and mixing, while the stronger cooling on the right side primarily results from enhanced vertical mixing [53,54,55].
Similarly, the processes of advection and mixing associated with typhoons also tend to elevate sea surface salinity, whereas precipitation events contribute to a reduction in salinity [56]. Consequently, differently from the variations observed in sea surface temperature, anomalies in sea surface salinity can also be detected on both the left and right sides of the typhoon’s trajectory. Figure 3a–c illustrate the 8-day moving average of the sea surface salinity as measured by the SMAP satellite, encompassing the periods before, during, and after Typhoon Trami. The difference in sea surface salinity attributable to the typhoon is determined by calculating the difference between the 8-day running average salinity values centered on 26 October and 21 October (Figure 3d). Notably, an increase in salinity of approximately 0.5 psu was observed near the mooring station on the right side of the typhoon’s trajectory. Conversely, on 26 October—the center date of its 8-day averaging window—a significant decline in sea surface salinity exceeding 2 psu was observed at the center of the typhoon (Figure 3b). The observed increase in salinity on both sides of the typhoon’s trajectory can primarily be ascribed to the vigorous turbulent mixing induced by the strong winds of the typhoon, which facilitates the upward movement of saltier water from the thermocline into the mixed layer, thereby enhancing surface salinity [57,58]. However, the negative salinity anomalies were likely resulting from the substantial precipitation occurring in that region. Among the five principal factors influencing salinity variations—namely, vertical mixing, entrapment, advection, precipitation, and evaporation—only precipitation is known to decrease sea surface salinity [19,56,59].
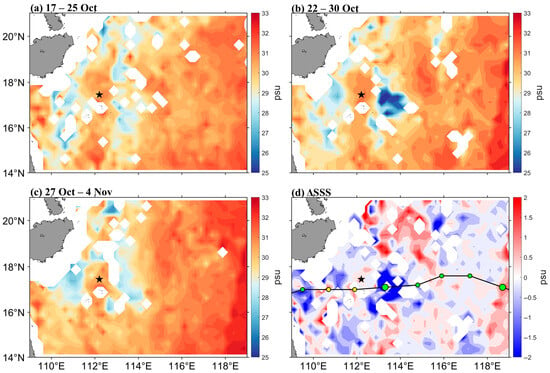
Figure 3.
Daily 8-day running mean Soil Moisture Active Passive (SMAP) satellite sea surface salinity, sea surface salinity before (a), during (b), and after (c) Trami, and the difference between 26 October and 21 October (d), the former minus the latter. The black star indicates the mooring position in the southern SCS. The black line represents the typhoon’s trajectory, and the colored solid circle represents the location of the typhoon’s center and its intensity, as referred to in Figure 1a.
3.1.2. Mooring-Observed Subsurface Response
Typhoons can cause not only a surface response of the ocean but also a subsurface response. Figure 4a shows the temporal evolution of the subsurface temperature response of the upper ocean at depths of 50–300 m as observed by the mooring. The CTD data documented the changes in upper ocean temperature following the passage of Typhoon Trami. Prior to the typhoon’s arrival, the temperature of seawater at a depth of 50 m remained approximately at 26 °C, exhibiting a diurnal period that may be attributed to the interplay of solar radiation variations and tidal dynamics [60,61]. On 27 October at noon, the mooring began recording changes associated with Typhoon Trami, including a temperature drop at 50 m to approximately 22 °C. The upward movement of isotherms and deepening of the mixed layer are primarily attributed to mixing and advection processes caused by the typhoon’s passage (Figure 4). The shoaling in the thermocline and the deepening of the mixed layer are mainly due to mixing and advection processes triggered by the strong wind introduced by the typhoon.
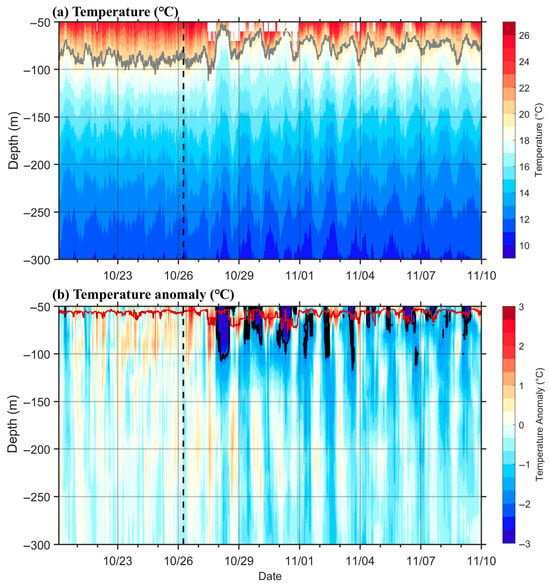
Figure 4.
(a) Depth–time map of the seawater temperature. The solid grey line represents the 20 °C isotherm. (b) Depth–time map of the temperature anomaly with respect to the 20–22 October average. The solid black line represents the −2 °C anomaly contour. The vertical black dashed lines represent the time when the typhoon was closest to the mooring station. The red line denotes the mixed layer depth, defined as the depth at which the temperature is 0.5 °C lower than that at the shallowest observation.
Figure 4b shows the evolution of temperature anomalies over time. It can be observed that the temperature dropped most significantly on 27 October and 28 October. The seawater shallower than 100 m was observed to drop by −2 °C. The cooling oscillation in the upper ocean is seen to continue until around 4 November. The periodicity is still dominated by the inertial period. These findings in terms of temperature underscore the significant impact of near-inertial oscillations, triggered by typhoons, on the periodic changes in seawater temperature.
Figure 5 further shows the velocity changes in the upper ocean recorded by the mooring. Panels a and b represent the eastward current component and northward current component at 50–300 m, respectively. The mooring observed a significant increase in eastward velocity during the passage of Trami, from about 0.1 m s−1 to 0.3 m s−1. In addition to the significant increase in the velocity amplitude, the periodicity of the velocity changes was also affected. Before the passage of Trami, the changes in the velocity basically showed a diurnal cycle, which was consistent with the local tidal cycle in the SCS. After the typhoon passed, the change in velocity showed a near-inertial period of 35 h (Figure 5), which is consistent with the periodic changes in temperature. On 5 November, the inertial oscillation decayed to the state before the typhoon arrived. The variations in temperature and current indicated that the notable near-inertial motion persisted for approximately 9 days, aligning with earlier research that suggests near-inertial oscillations triggered by storms typically persist for about 7 days or more [23]. Stronger velocity signals were observed throughout most of the water column, with a notable enhancement shallower than 250 m (Figure 5). In order to further study the near-inertial oscillation, the velocity of near-inertial waves and energy distribution characteristics are further analyzed in the following section.
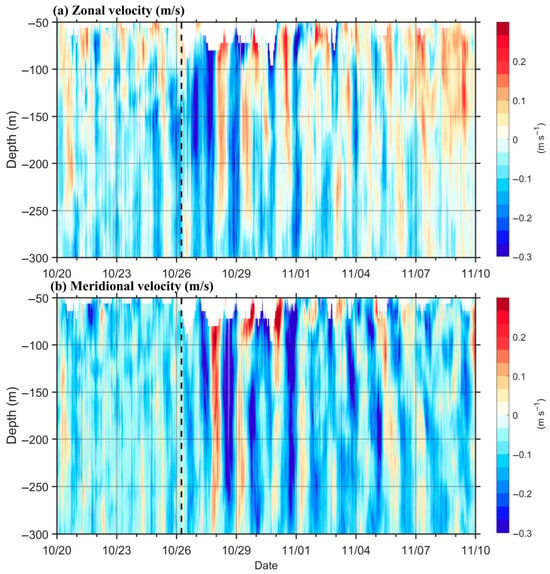
Figure 5.
Raw velocity of zonal (a) and meridional (b) components. The vertical black dashed lines represent the time when the typhoon was closest to the mooring station.
To analyze the characteristics of near-inertial oscillations induced by typhoons, as well as the propagation and distribution patterns of near-inertial energy within the ocean, bandpass filtering was employed to isolate near-inertial velocity. Subsequently, the decomposition and analysis of its clockwise (CW) and counterclockwise (CCW) frequency components were conducted.
Figure 6 reveals a pronounced enhancement of NIWs in the ocean following the passage of Typhoon Trami on 26 October. In terms of vertical structure, the near-inertial velocity within the upper 70 m surface layer exhibited a dramatic increase from approximately 0.05 m s−1 prior to the typhoon’s passage to 0.2 m s−1, representing a 300% increase. Conversely, the velocity within the subsurface layer, specifically at depths ranging from 200 to 260 m, also demonstrated a responsive enhancement; however, this increase was comparatively modest, measuring around 0.07 m s−1, which constitutes only 13% of the surface layer’s increase (Figure 6a,c). Further decomposition of the CW and CCW rotational components revealed that the velocity amplitude of the CW component (>0.15 m s−1) consistently surpassed that of the CCW component (<0.05 m s−1). This finding suggests that the energy associated with near-inertial oscillations exhibits a composite mode of propagation, characterized by both downward (CW) and upward (CCW) movement, with the downward transmission process prevailing. This observation aligns with established theories regarding typhoon-induced near-inertial internal waves, thereby corroborating the notion that the CW-polarized near-inertial energy, generated by wind stress curl through resonance mechanisms, demonstrates significant downward transmission characteristics as influenced by Ekman pumping [53,62].
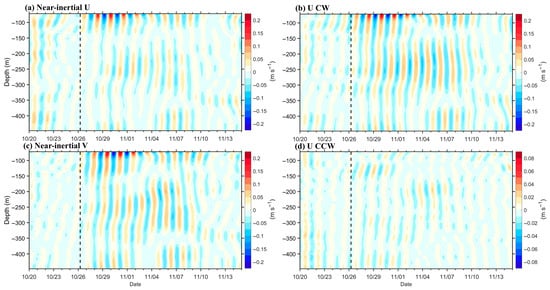
Figure 6.
The depth–time distribution of the near-inertial velocity components for meridional (a) and zonal (c) velocities, along with the depth–time distribution of clockwise (b) and counterclockwise (d) separated near-inertial meridional velocity. The vertical black dashed lines represent the time when the typhoon was closest to the mooring station.
3.2. The Mixing Processes and Driving Factors of the Upper Ocean
The passage of a typhoon is accompanied by strong mixing caused by strong winds, which causes energy to be rapidly dissipated near the surface of the sea. This results in a decrease in sea surface temperature, which facilitates the mixing of both deep and shallow seawater, further lowering the surface temperature and increasing surface salinity [2,63,64].
3.2.1. Enhanced Diapycnal Mixing in the Upper Ocean Following the Typhoon
The analysis of the square of buoyancy frequency (N2), vertical shear squared (), and Richardson number (Ri) during Typhoon Trami, as illustrated in Figure 7, elucidates the significant dynamic responses of the upper ocean to the typhoon. Prior to the typhoon’s approach (indicated by the dashed line in Figure 7), the water column exhibited a pronounced stratified structure, characterized by a buoyancy frequency squared (N2) exceeding 5 × 10−4 s−2 at about 50 m, which established a stable density gradient and effectively suppressed vertical mixing [53,62]. During this period, moderate vertical shear squared ( 2 × 10−5 s−2) predominated the flow field, resulting in Ri values consistently above the critical threshold of 0.25 (Figure 7c), which suggested that no turbulence was present prior to the typhoon.
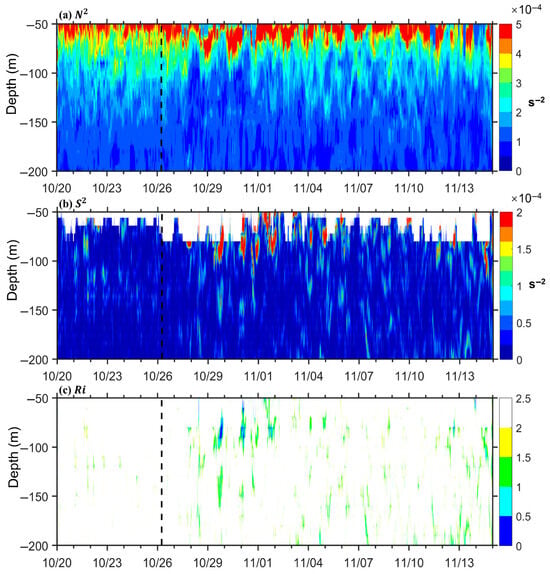
Figure 7.
Time–depth maps of buoyancy frequency ((a), , s−2), vertical current shear squared ((b), , s−2), and Richardson number ((c), Ri). The vertical black dashed lines represent the time when the typhoon was closest to the mooring station.
Following the passage of the typhoon’s center past the mooring location, the dynamic structure of the upper ocean experienced a significant change. Influenced by the typhoon’s strong wind, the intensity of vertical shear in the 50–100 m depth range increased markedly, with peak values of exceeding 2 × 10−4 s−2 (Figure 7b). Concurrently, a substantial decline in buoyancy frequency was recorded in this 50–100 m layer (N2 decreased to 1 × 10−4 s−2, Figure 7a), indicating a rapid reduction in density stratification. This combination of factors led to Ri values in the 50–100 m layer falling below the critical threshold of 0.25 at the mooring location (Figure 7c), thereby fulfilling the dynamically unstable flow condition and promoting vigorous turbulent mixing. In the later stages of the typhoon, although surface density stratification began to reestablish, a residual strong shear persisted in the 50 m depth layer or deeper, indicating a long-lasting effect associated with the subsurface mixing, which was consistent with the continuous weakening of subsurface temperature shown in Figure 4b.
The observational data presented herein demonstrate that typhoon-induced ocean mixing is governed by two primary mechanisms: the current shear instability driven by wind stress, which primarily facilitates mixing, and the convective overturning that disrupts density stratification of the upper water column, while subsurface mixing continues for approximately seven days (Figure 7). This phenomenon of typhoon-induced ocean mixing underscores the interplay between mechanical energy input (as represented by ) and buoyancy suppression (as represented by N2) in influencing turbulent mixing during extreme weather events. Furthermore, the reasons behind the strong shear instability observed in the upper layers can be further investigated by looking into the separate components of the shear.
3.2.2. Contribution of NIWs to the Upper Ocean Shear Instability
To examine the shear contributions from the internal waves, the near-inertial (), diurnal (), and semidiurnal () components of shear squared are calculated as follows. Firstly, the processed ADCP velocity data are decomposed into different frequency bands using a third-order Butterworth filter. Specifically, the velocities within the near-inertial (, ), diurnal (, ), and semidiurnal (, ) bands are bandpass filtering in the ranges [0.85 1.2] f, 1/(26–22 h), and 1/(14–10 h), respectively; secondly, the different components of shear squared are obtained by the corresponding velocities, denoted as , , .
The shear squared of near-surface NIWs exhibited a substantial increase following the passage of the typhoon. Notably, at depths of less than 100 m, the shear squared exceeded 1 × 10−5 s−2 for about 9 days. In comparison, it stayed below 1 × 10−6 s−2 at deeper levels (Figure 8a). Figure 8b shows the temporal evolution of the depth-averaged shear squared of three components at depths shallower than 100 m. Prior to the arrival of the typhoon, the overall change in the three shear squared components was relatively minor, with the relative contributions of each component to the total shear change also being small. During the typhoon, the total shear squared was predominantly influenced by near-inertial shear squared () at depths above 100 m, where the correlation coefficient between and the total shear squared () was 0.32, significantly higher than the correlation coefficients between semi-diurnal shear squared () and (0.16) and between diurnal shear squared () and (0.11). Additionally, the difference in near-inertial shear before and after the typhoon was notably pronounced, measuring 0.8 × 10−3 s−2, while the other two components showed no increase at all.
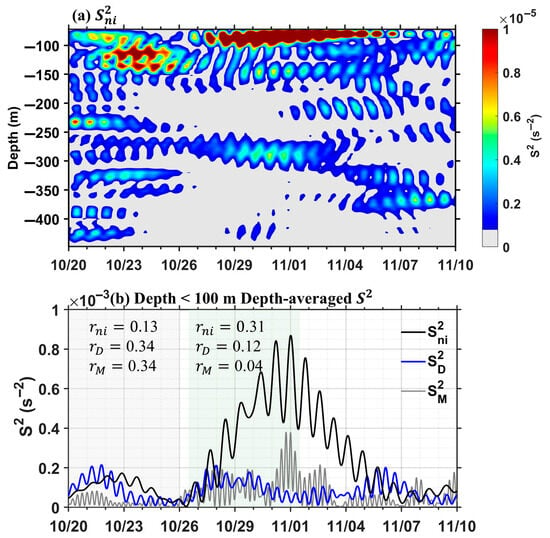
Figure 8.
(a) The vertical distribution of the shear squared components at near-inertial (). (b) The depth integral of the three shear squared components in the layer above 100 m depth. The correlation coefficients of total shear with different shear components in each layer were indicated during the two shaded periods.
In conclusion, the contribution of near-inertial wave dynamics to the enhancement of total shear is greater than that of the diurnal and semi-diurnal components associated with the primary internal tide components. This underscores the strong shear instability induced by near-inertial internal waves in the surface layer and suggests that near-inertial waves generated by typhoons are vital in shaping the primary mixing processes in the ocean’s near-surface layer.
3.3. Characteristics of Internal Wave Energy Distribution
3.3.1. The Temporal Evolution of NIW Kinetic Energy
Under the influence of Trami, the local horizontal kinetic energy of NIWs at the mooring location increased rapidly and propagated to deeper layers over time (Figure 9a). Two peak depths of near-inertial energy were observed; one was concentrated at depths shallower than 90 m (values > 10 J/m3), and the other was at depths of around 240 m (6 J/m3). The deeper high-value center lagged behind the shallower high-value center by approximately 2 days, which indicated the vertical propagation of the near-inertial waves (Figure 9a). In contrast to the abrupt attenuation observed in the near-surface energy occurring around 2 November, the maximum energy level at the 250 m depth remained relatively stable. The kinetic energy maintained a value of 4 J/m3 at the corresponding depth of the subsurface energy peak. These observations indicate that the near-inertial energy at the subsurface layer can be sustained over an extended period, while the near-inertial energy of the near-surface seawater is subject to rapid dissipation.
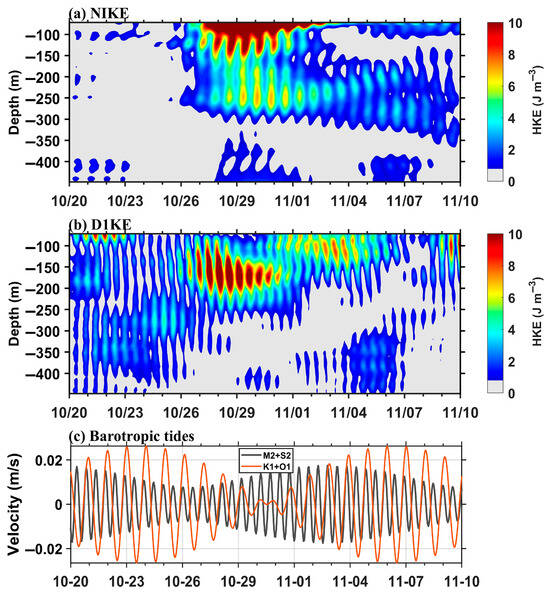
Figure 9.
The vertical distribution of near-inertial energy (a) and diurnal tidal energy (b) at the mooring station. The amplitudes of the semidiurnal (M2 + S2) and diurnal (K1 + O1) barotropic tidal currents at the mooring station as predicted from TPXO9 (c).
Figure 9b illustrates the time–depth evolution of diurnal tidal energy during the typhoon’s passage. The changes in the diurnal internal tide in the northern SCS are linked to variations in the intensity of the barotropic tide. Figure 9c presents the eastward velocity component of the diurnal barotropic tide observed at the mooring station during the typhoon’s passage. The barotropic tide velocity is derived from the TPXO9 model predictions, which primarily include the two main diurnal tidal components, K1 and O1. According to linear theory, the strength of the internal tide generated is proportional to the strength of the barotropic tide [65]. Observational data indicate that the temporal changes in diurnal tidal energy near the sea surface are closely associated with fluctuations in barotropic tide intensity, with two peaks in energy occurring around 22 October and 4 November 2024. However, a notable change was observed in the subsurface waters between 27 October and 2 November, 1 week after the typhoon, during a period of neap tide. This suggests that the increase in diurnal tidal energy within the subsurface layer is a result of the typhoon’s influence.
3.3.2. Decomposition of Near-Inertial Energy
Decomposing the near-inertial currents, the downward-propagating component (CW) of near-inertial energy was stronger than the upward-propagating energy (Figure 10a,b). The downward-propagating energy of near-inertial waves first decreased and then increased with depth, with a weak-value region of CW appearing at approximately 150 m depth (Figure 10a). The downward near-inertial energy is 10 times higher than that of the upward. This preferential downward transmission likely reflects the influence of surface-generated near-inertial motions, which are typically forced by wind stress and subsequently radiate energy into the ocean interior [28,66]. Interestingly, a minimum in CW energy value emerged near 150 m (Figure 10a). This mid-depth energy trough may arise from interactions with mesoscale eddies or background shear, which can disrupt wave coherence [27,40]. The subsequent energy increase at depth suggests either reduced dissipation in stratified layers or the cumulative effects of wave–wave coherence, underscoring the complex interplay between near-inertial waves and the ocean’s thermohaline structure [27,40]. These findings highlight the importance of downward-propagating CW energy in redistributing wind-derived mechanical energy, with implications for abyssal mixing and larger-scale ocean circulation dynamics.
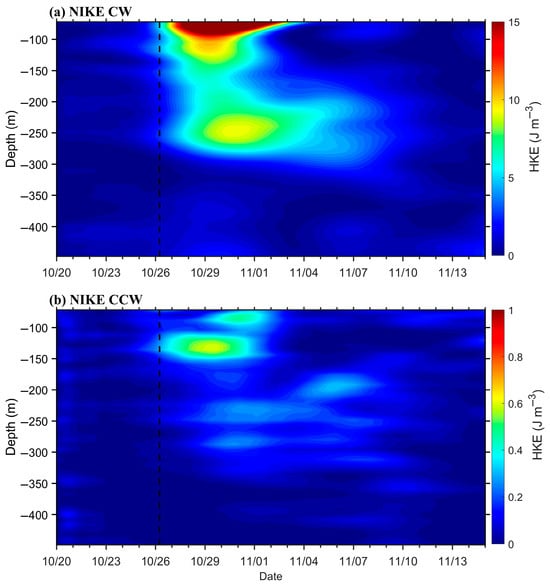
Figure 10.
The vertical distribution of different components of horizontal kinetic energy in near-inertial waves: Clockwise (a), counter-clockwise (b). The vertical black dashed lines represent the time when the typhoon was closest to the mooring station.
3.3.3. Depth Profiles of Time-Averaged Internal Wave Kinetic Energy
Figure 11 presents the time-averaged near-inertial energy and diurnal tidal energy for three distinct time periods, along with the depth-averaged near-inertial energy, diurnal tidal energy, and semidiurnal tidal energy averaged over the entire typhoon period. The three time periods are defined as follows: the pre-typhoon period (20 October 2024, 00:00:00 to 26 October 2024, 00:00:00), the during-typhoon period (27 October 2024, 00:00:00 to 2 November 2024, 00:00:00), and the post-typhoon period (2 November 2024, 00:00:00 to 10 November 2024, 00:00:00).
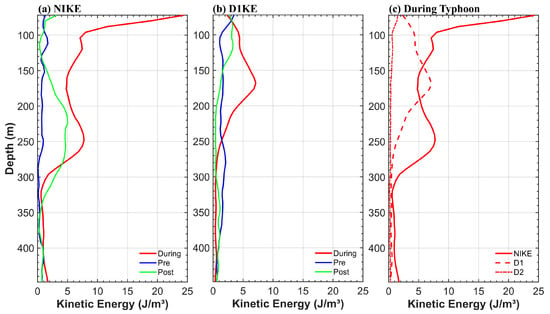
Figure 11.
Time-averaged near-inertial energy (a) and diurnal tidal energy (b) for three distinct time periods. The depth-averaged near-inertial energy, diurnal tidal energy, and semidiurnal tidal energy averaged over the entire typhoon period (c).
The depth profile averaged over the period during the typhoon revealed an unexpected occurrence: the near-inertial energy in subsurface seawater at depths of 120–170 m consistently diminished, whereas the diurnal tidal energy increased with depth, suggesting an inverse correlation between these two components. Below 170 m, the near-inertial energy continued to rise, reaching a second peak at a depth of 250 m, while the diurnal tidal energy returned to normal levels as depth increased (Figure 11).
3.4. Burst of Subsurface-Layer Diurnal Tidal Energy
3.4.1. The Modulation of Stratification Change
Typhoons profoundly impact upper ocean temperature and stratification via upwelling and shear instability-driven mixing [67]. These processes disrupt the upper ocean’s stratification: seawater buoyancy frequency dropped in the top 60 m but rose around 80 m (Figure 12a). Such wind-induced stratification changes reshape near-inertial and internal tidal energy vertical distributions, causing refraction and energy adjustments [68]. Since internal waves are highly sensitive to local stratification, their amplitude and energy continuously adapt during propagation [6,69].
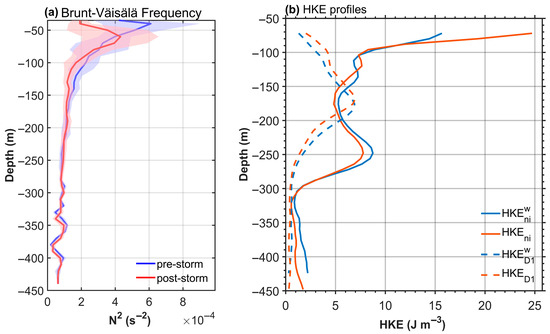
Figure 12.
Depth profiles of buoyancy frequency squared during two periods; the colored shading denotes the standard deviation of the mean of N2 (a). Time-averaged horizontal kinetic energy (HKE) for near-inertial waves (NIWs) and diurnal internal tides (D1 ITs) during typhoon period, compared to Wentzel–Kramers–Brillouin (WKB) scaled theoretical estimates (b).
To minimize the refraction effects caused by internal waves moving through varying stratification, the “Wentzel–Kramers–Brillouin (WKB) scale” and “WKB stretch” are applied to the observed velocities, as described by Leaman and Sanford (1975) [68]. The velocity is adjusted by a factor of , where N(z) represents the local buoyancy frequency obtained from subsurface mooring data, and is the average value. Consequently, the horizontal kinetic energy can be estimated as . Additionally, the depth is modified using the equation . The near-inertial and diurnal tidal energy time-averaged depth distribution before and after the WKB transformation is illustrated in Figure 12b.
Without WKB transformation, there is a notable decrease in the near-inertial energy at the sea surface, which is due to more dissipation of near-inertial energy near the surface brought by the disruption of stratification. However, the distribution of diurnal tidal energy remains consistent before and after the WKB transformation, indicating that the typhoon has minimal impact on subsurface diurnal tidal energy changes caused by alterations in stratification.
In a word, other physical processes contribute to the rise in subsurface diurnal tidal energy. To investigate the source of this increased diurnal tidal energy, the rates of energy transfer from low to high frequencies during the observation period were further calculated.
3.4.2. Energy Transfer from NIWs to D1 ITs
Referring to the previous studies on internal wave energy transfer [41], Equation (5) was applied to investigate the transfer between near-inertial energy and diurnal tidal energy during the typhoon based on the high-resolution mooring observations.
During the typhoon, a notable change in the calculated value was observed, indicating a substantial energy transfer between the two components of the internal waves (Figure 13). A significant positive peak of around 2 × 10–7 W kg–1 was recorded under the typhoon’s influence, especially at depths of approximately 120–170 m, from 27 October to 31 October. This suggests a considerable transfer of energy from NIWs to the diurnal internal tide. This period also aligns closely with the depth and timing of the diurnal tidal energy increase seen in the energy distribution (Figure 4a).
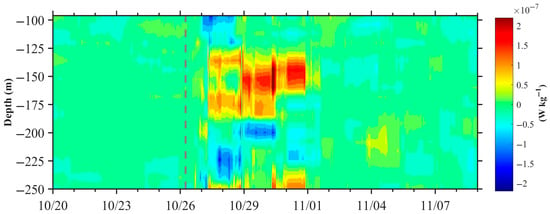
Figure 13.
Energy transfer rate (W kg−1) as given by Equation (5). The vertical grey dashed lines represent the time when the typhoon was closest to the mooring station.
These findings illustrate the energy transfer from near-inertial energy to diurnal tidal energy, highlighting the significant role of the typhoon in redistributing internal wave energy within the ocean’s interior.
4. Discussion and Conclusions
Although numerous prior observational studies have delved into the upper ocean’s response to typhoons, a comprehensive grasp of the specific response traits of the upper ocean in the northwestern SCS to typhoons remains lacking, particularly regarding the characteristics of shear and energy distribution, which have not been thoroughly investigated. From October to November 2024, a high-resolution mooring station deployed in the northern SCS captured upper-ocean responses to Typhoon Trami. This presented a rare opportunity to deepen our understanding of typhoon–ocean interactions. Concurrently, multi-source satellite remote sensing data were employed to conduct a systematic analysis of sea surface parameters during Trami’s passage. Moreover, based on high-resolution observations, this study describes the effect of near-inertial internal waves on mixing and the distribution of their energy at different depths and further analyzes and calculates the transfer of energy to the diurnal tide.
- (1)
- Thermal and dynamical ocean response: Relying on multi-source satellite remote sensing SST and SSS data, it was found that the typhoon generated a “cold wake” with a maximum temperature decline of 2.5 °C and an approximate 0.5 psu increase in salinity to the right of the typhoon’s trajectory near the mooring site. This suggests that turbulent mixing took place in the upper ocean at the mooring location. The mooring data indicate that the maximum temperature drop of 4 °C occurred on 28 October, coinciding with the deepening of the mixed layer and the rise in the thermocline. Also, due to the influence of strong near-inertial oscillations introduced by the typhoon in the upper layer, the temperature changes also showed near-inertial periodicity.
- (2)
- Near-surface mixing process and its driving factors: Intense near-inertial internal waves induced significant near-inertial shear instability in the upper ocean, with peak shear squared persisting for about 9 days in our case. Moreover, the disruption of stratification collectively led to the occurrence of enhanced turbulence dissipation in the upper layer. Further analysis indicates that near-inertial shear was the primary factor responsible for the rapid increase in shear instability in the upper ocean, in contrast to the shear caused by pre-existing diurnal and semidiurnal internal tides.
- (3)
- Subsurface diurnal tidal energy enhancement: The study also investigated the characteristics of internal tidal energy distribution. Interestingly, it was found that near-inertial energy and diurnal tidal energy exhibited an inverse relationship in the subsurface layer between 120 and 170 m. Specifically, near-inertial energy hit a low at 170 m, while diurnal tidal energy peaked unexpectedly at that same depth. We further excluded both the effects of spring-neap tide and the changes in stratification on diurnal tidal energy distribution, and quantitatively assessed the energy transfer rate from near-inertial energy to diurnal tidal energy. The analysis revealed a notable rate of energy transfer from NIWs to D1 ITs within the 120–170 m depth range, peaking at 2 × 10−7 W kg−1. This is consistent with previous observations of energy transfer from low- to high-frequency internal waves. For example, mooring-based observations during Typhoon Fitow (2013) showed that M1 subharmonics and NIWs facilitated energy transfer to high-frequency internal waves (HFIWs) at a rate of 2 × 10−6 W kg−1 [42]. Similar magnitudes of energy transfer have been documented: 2 × 10−7 W kg−1 at the shelf break in the East China Sea [43], while open-ocean measurements indicate weaker transfer rates (3.7 × 10−9 W kg−1) [70].
This study presents a detailed mooring-based analysis in the northern SCS. However, due to a limited sample of observations, the temperature and current data collected are incomplete, especially in terms of the horizontal dimension. Therefore, additional research that includes more comprehensive in situ observations and numerical ocean models is necessary to enhance understanding in this area. Furthermore, this research does not investigate the interactions between mesoscale eddies and typhoons in the SCS, nor does it examine their combined effects with internal tides. The conclusion emphasizes that dynamic processes at multiple scales within the ocean could potentially modify oceanic responses, which may, in turn, affect the development of future typhoons.
Author Contributions
Formal analysis, Investigation, Methodology, Software, Visualization, Writing—original draft, L.C.; Data curation, Methodology, Validation, Writing—review and editing, Conceptualization, software and resources, X.Z.; Funding acquisition, Supervision, Writing—review and editing, Z.Z.; Project administration, Supervision, W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Key R&D Plan Program of China (2021YFC3101500) and the National Natural Science Foundation of China Grants (42305014).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Daily geostrophic current and sea level anomaly data are freely accessible through the Copernicus Marine Service at http://marine.copernicus.eu (accessed on 21 June 2025). Sea Surface Temperature (SST) data were obtained from the Remote Sensing Systems (RSS) repository at https://data.remss.com/SST/daily/ (accessed on 21 June 2025), and Sea Surface Salinity (SSS) data were sourced from the RSS SMAP Level 3 SSS product at https://data.remss.com/smap/SSS/V06.0/ (accessed on 21 June 2025). Typhoon best track data, including storm trajectories and intensity metrics, were provided by the China Meteorological Administration (CMA) and are available at https://tcdata.typhoon.org.cn/zjljsjj.html (accessed on 21 June 2025). The bathymetry data for the northern SCS are from GEBCO at https://www.gebco.net/data-products/gridded-bathymetry-data (accessed on 21 June 2025). Wind data were obtained from the global atmospheric reanalysis dataset ERA5 at https://cds.climate.copernicus.eu/datasets (accessed on 21 June 2025). And the barotropic tidal currents are sourced from TPXO9 https://www.tpxo.net/tpxo-products-and-registration (accessed on 21 June 2025). CTD and ADCP mooring datasets are available at https://doi.org/10.6084/m9.figshare.29276060.
Acknowledgments
We would like to thank Zhao Wei’s research team from Ocean University of China for their help in buoy deployment, recovery and data quality control. We would also like to thank the editor and reviewers for their inspiring comments and valuable contributions to this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, G.; Su, J.; Ding, Y.; Chen, D. Tropical Cyclone Genesis over the South China Sea. J. Mar. Syst. 2007, 68, 318–326. [Google Scholar] [CrossRef]
- Price, J.F. Upper Ocean Response to a Hurricane. J. Phys. Oceanogr. 1981, 11, 153–175. [Google Scholar] [CrossRef]
- Price, J.F.; Weller, R.A.; Pinkel, R. Diurnal Cycling: Observations and Models of the Upper Ocean Response to Diurnal Heating, Cooling, and Wind Mixing. J. Geophys. Res. 1986, 91, 8411–8427. [Google Scholar] [CrossRef]
- Zhu, T.; Zhang, D.-L. The Impact of the Storm-Induced SST Cooling on Hurricane Intensity. Adv. Atmos. Sci. 2006, 23, 14–22. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, X.; Yang, C.; Qi, Y.; Tian, D.; Xu, J.; Cai, S.; Wu, R.; Ma, Y.; Ni, X.; et al. Observed Impact of Typhoon Mangkhut (2018) on a Continental Slope in the South China Sea. J. Geophys. Res. Ocean. 2022, 127, e2022JC018432. [Google Scholar] [CrossRef]
- Guan, S.; Zhao, W.; Huthnance, J.; Tian, J.; Wang, J. Observed Upper Ocean Response to Typhoon Megi (2010) in the Northern South China Sea. J. Geophys. Res. Ocean. 2014, 119, 3134–3157. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, R.; Chen, D.; Liu, X.; He, H.; Tang, Y.; Ke, D.; Shen, Z.; Li, J.; Xie, J.; et al. Net Modulation of Upper Ocean Thermal Structure by Typhoon Kalmaegi (2014). J. Geophys. Res. Ocean. 2018, 123, 7154–7171. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.; Zhou, L.; Liu, X.; Ding, T.; Zhou, B. Upper Ocean Response to Typhoon Kalmaegi (2014). J. Geophys. Res. Ocean. 2016, 121, 6520–6535. [Google Scholar] [CrossRef]
- Sanford, T.B.; Price, J.F.; Girton, J.B. Upper-Ocean Response to Hurricane Frances (2004) Observed by Profiling EM-APEX Floats. J. Phys. Oceanogr. 2011, 41, 1041–1056. [Google Scholar] [CrossRef]
- Wang, G.; Wu, L.; Johnson, N.C.; Ling, Z. Observed Three-dimensional Structure of Ocean Cooling Induced by Pacific Tropical Cyclones. Geophys. Res. Lett. 2016, 43, 7632–7638. [Google Scholar] [CrossRef]
- Lin, I.-I.; Liu, W.T.; Wu, C.-C.; Chiang, J.C.H.; Sui, C.-H. Satellite Observations of Modulation of Surface Winds by Typhoon-Induced Upper Ocean Cooling. Geophys. Res. Lett. 2003, 30, 1311. [Google Scholar] [CrossRef]
- Zhang, H.; He, H.; Zhang, W.-Z.; Tian, D. Upper Ocean Response to Tropical Cyclones: A Review. Geosci. Lett. 2021, 8, 1. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, Y.; Wu, R.; Na, R. Statistical Characteristics of the Response of Sea Surface Temperatures to Westward Typhoons in the South China Sea. Remote Sens. 2021, 13, 916. [Google Scholar] [CrossRef]
- D’Asaro, E.A.; Sanford, T.B.; Niiler, P.P.; Terrill, E.J. Cold Wake of Hurricane Frances. Geophys. Res. Lett. 2007, 34, 2007GL030160. [Google Scholar] [CrossRef]
- Glenn, S.M.; Miles, T.N.; Seroka, G.N.; Xu, Y.; Forney, R.K.; Yu, F.; Roarty, H.; Schofield, O.; Kohut, J. Stratified Coastal Ocean Interactions with Tropical Cyclones. Nat. Commun. 2016, 7, 10887. [Google Scholar] [CrossRef] [PubMed]
- Seroka, G.; Miles, T.; Xu, Y.; Kohut, J.; Schofield, O.; Glenn, S. Rapid Shelf-Wide Cooling Response of a Stratified Coastal Ocean to Hurricanes: Stratified Coastal Ocean Cooling in TCs. J. Geophys. Res. Ocean. 2017, 122, 4845–4867. [Google Scholar] [CrossRef] [PubMed]
- Grodsky, S.A.; Reul, N.; Lagerloef, G.; Reverdin, G.; Carton, J.A.; Chapron, B.; Quilfen, Y.; Kudryavtsev, V.N.; Kao, H. Haline Hurricane Wake in the Amazon/Orinoco Plume: AQUARIUS/SACD and SMOS Observations. Geophys. Res. Lett. 2012, 39, 2012GL053335. [Google Scholar] [CrossRef]
- Neetu, S.; Lengaigne, M.; Vincent, E.M.; Vialard, J.; Madec, G.; Samson, G.; Ramesh Kumar, M.R.; Durand, F. Influence of Upper-ocean Stratification on Tropical Cyclone-induced Surface Cooling in the Bay of Bengal. J. Geophys. Res. 2012, 117, 2012JC008433. [Google Scholar] [CrossRef]
- Chacko, N. Insights into the Haline Variability Induced by Cyclone Vardah in the Bay of Bengal Using SMAP Salinity Observations. Remote Sens. Lett. 2018, 9, 1205–1213. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, G.; Shang, X. Inner-Core Sea Surface Cooling Induced by a Tropical Cyclone. J. Phys. Oceanogr. 2021, 51, 3385–3400. [Google Scholar] [CrossRef]
- Price, J.F.; Sanford, T.B.; Forristall, G.Z. Forced Stage Response to a Moving Hurricane. J. Phys. Oceanogr. 1994, 24, 233–260. [Google Scholar] [CrossRef]
- Sanford, T.B.; Price, J.F.; Girton, J.B.; Webb, D.C. Highly Resolved Observations and Simulations of the Ocean Response to a Hurricane. Geophys. Res. Lett. 2007, 34, L13604. [Google Scholar] [CrossRef]
- Teague, W.J.; Jarosz, E.; Wang, D.W.; Mitchell, D.A. Observed Oceanic Response over the Upper Continental Slope and Outer Shelf during Hurricane Ivan. J. Phys. Oceanogr. 2007, 37, 2181–2206. [Google Scholar] [CrossRef]
- Chen, G.; Xue, H.; Wang, D.; Xie, Q. Observed Near-Inertial Kinetic Energy in the Northwestern South China Sea. J. Geophys. Res. Ocean. 2013, 118, 4965–4977. [Google Scholar] [CrossRef]
- Alford, M.H. Improved Global Maps and 54-Year History of Wind-Work on Ocean Inertial Motions. Geophys. Res. Lett. 2003, 30, 1424. [Google Scholar] [CrossRef]
- D’Asaro, E.A. The Energy Flux from the Wind to Near-Inertial Motions in the Surface Mixed Layer. J. Phys. Ocean. 1985, 15, 1043–1059. [Google Scholar] [CrossRef]
- Jaimes, B.; Shay, L.K. Near-Inertial Wave Wake of Hurricanes Katrina and Rita over Mesoscale Oceanic Eddies. J. Phys. Oceanogr. 2010, 40, 1320–1337. [Google Scholar] [CrossRef]
- Cao, A.; Guo, Z.; Song, J.; Lv, X.; He, H.; Fan, W. Near-Inertial Waves and Their Underlying Mechanisms Based on the South China Sea Internal Wave Experiment (2010–2011). J. Geophys. Res. Ocean. 2018, 123, 5026–5040. [Google Scholar] [CrossRef]
- Gill, A.E. On the Behavior of Internal Waves in the Wakes of Storms. J. Phys. Oceanogr. 1984, 14, 1129–1151. [Google Scholar] [CrossRef]
- Whalen, C.B.; De Lavergne, C.; Naveira Garabato, A.C.; Klymak, J.M.; MacKinnon, J.A.; Sheen, K.L. Internal Wave-Driven Mixing: Governing Processes and Consequences for Climate. Nat. Rev. Earth Environ. 2020, 1, 606–621. [Google Scholar] [CrossRef]
- Alford, M.H. Redistribution of Energy Available for Ocean Mixing by Long-Range Propagation of Internal Waves. Nature 2003, 423, 159–162. [Google Scholar] [CrossRef] [PubMed]
- Simmons, H.L. Spectral Modification and Geographic Redistribution of the Semi-Diurnal Internal Tide. Ocean Model. 2008, 21, 126–138. [Google Scholar] [CrossRef]
- Xing, J.; Davies, A.M. Processes Influencing the Non-Linear Interaction between Inertial Oscillations, near Inertial Internal Waves and Internal Tides. Geophys. Res. Lett. 2002, 29, 11-1–11-14. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, Z.; Wang, H.; Xu, J.; Zhang, Q.; Sun, Y.; Gong, Y.; Cai, S. A Numerical Study on Energy Transfer between Near-Inertial Internal Waves and Super-Inertial Internal Waves in the South China Sea under the Influence of a Typhoon. Cont. Shelf Res. 2024, 276, 105240. [Google Scholar] [CrossRef]
- Hu, Q.; Huang, X.; Xu, Q.; Zhou, C.; Guan, S.; Xu, X.; Zhao, W.; Yang, Q.; Tian, J. Parametric Subharmonic Instability of Diurnal Internal Tides in the Abyssal South China Sea. J. Phys. Oceanogr. 2023, 53, 195–213. [Google Scholar] [CrossRef]
- Jing, Z.; Chang, P.; DiMarco, S.F.; Wu, L. Role of Near-Inertial Internal Waves in Subthermocline Diapycnal Mixing in the Northern Gulf of Mexico. J. Phys. Oceanogr. 2015, 45, 3137–3154. [Google Scholar] [CrossRef]
- Xie, X.-H.; Shang, X.-D.; van Haren, H.; Chen, G.-Y.; Zhang, Y.-Z. Observations of Parametric Subharmonic Instability-Induced near-Inertial Waves Equatorward of the Critical Diurnal Latitude. Geophys. Res. Lett. 2011, 38, L05606. [Google Scholar] [CrossRef]
- Yang, W.; Hibiya, T.; Tanaka, Y.; Zhao, L.; Wei, H. Modification of Parametric Subharmonic Instability in the Presence of Background Geostrophic Currents. Geophys. Res. Lett. 2018, 45, 12957–12962. [Google Scholar] [CrossRef]
- Yang, W.; Wei, H.; Zhao, L. Parametric Subharmonic Instability of the Semidiurnal Internal Tides at the East China Sea Shelf Slope. J. Phys. Oceanogr. 2020, 50, 907–920. [Google Scholar] [CrossRef]
- Jing, Z.; Chang, P. Modulation of Small-Scale Superinertial Internal Waves by Near-Inertial Internal Waves. J. Phys. Oceanogr. 2016, 46, 3529–3548. [Google Scholar] [CrossRef]
- Sun, O.M.; Pinkel, R. Energy Transfer from High-Shear, Low-Frequency Internal Waves to High-Frequency Waves near Kaena Ridge, Hawaii. J. Phys. Oceanogr. 2012, 42, 1524–1547. [Google Scholar] [CrossRef]
- Yang, W.; Wei, H.; Zhao, L. Energy Transfer From PSI-Generated M1 Subharmonic Waves to High-Frequency Internal Waves. Geophys. Res. Lett. 2022, 49, e2021GL095618. [Google Scholar] [CrossRef]
- Yang, W.; Wei, H.; Zhao, L. Near- and Superinertial Internal Wave Responses and the Associated Energy Transfer after the Passage of Tropical Cyclone Fitow at a Midlatitude Shelf Slope. J. Phys. Oceanogr. 2024, 54, 1823–1838. [Google Scholar] [CrossRef]
- MacKinnon, J.A.; Alford, M.H.; Sun, O.; Pinkel, R.; Zhao, Z.; Klymak, J. Parametric Subharmonic Instability of the Internal Tide at 29°N. J. Phys. Oceanogr. 2013, 43, 17–28. [Google Scholar] [CrossRef]
- Sun, O.M.; Pinkel, R. Subharmonic Energy Transfer from the Semidiurnal Internal Tide to Near-Diurnal Motions over Kaena Ridge, Hawaii. J. Phys. Oceanogr. 2013, 43, 766–789. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An Overview of the China Meteorological Administration Tropical Cyclone Database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Lu, X.; Yu, H.; Ying, M.; Zhao, B.; Zhang, S.; Lin, L.; Bai, L.; Wan, R. Western North Pacific Tropical Cyclone Database Created by the China Meteorological Administration. Adv. Atmos. Sci. 2021, 38, 690–699. [Google Scholar] [CrossRef]
- Gentemann, C.L.; Meissner, T.; Wentz, F.J. Accuracy of Satellite Sea Surface Temperatures at 7 and 11 GHz. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1009–1018. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.J.; Le Vine, D.M. The Salinity Retrieval Algorithms for the NASA Aquarius Version 5 and SMAP Version 3 Releases. Remote Sens. 2018, 10, 1121. [Google Scholar] [CrossRef]
- Duda, T.F.; Jacobs, D.C. Stress/Shear Correlation: Internal Wave/Wave Interaction and Energy Flux in the Upper Ocean. Geophys. Res. Lett. 1998, 25, 1919–1922. [Google Scholar] [CrossRef]
- Kanada, S.; Tsujino, S.; Aiki, H.; Yoshioka, M.K.; Miyazawa, Y.; Tsuboki, K.; Takayabu, I. Impacts of SST Patterns on Rapid Intensification of Typhoon Megi (2010). J. Geophys. Res. Atmos. 2017, 122, 13245–13262. [Google Scholar] [CrossRef]
- Emanuel, K.A. Thermodynamic Control of Hurricane Intensity. Nature 1999, 401, 665–669. [Google Scholar] [CrossRef]
- Yuan, S.; Yan, X.; Zhang, L.; Pang, C.; Hu, D. Observation of Near-Inertial Waves Induced by Typhoon Lan in the Northwestern Pacific: Characteristics, Energy Fluxes and Impact on Diapycnal Mixing. J. Geophys. Res. Ocean. 2024, 129, e2023JC020187. [Google Scholar] [CrossRef]
- Yang, Y.J.; Chang, M.-H.; Hsieh, C.-Y.; Chang, H.-I.; Jan, S.; Wei, C.-L. The Role of Enhanced Velocity Shears in Rapid Ocean Cooling during Super Typhoon Nepartak 2016. Nat. Commun. 2019, 10, 1627. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Liu, X.; Wu, R.; Chen, D.; Zhang, D.; Shang, X.; Wang, Y.; Song, X.; Jin, W.; Yu, L.; et al. Sea Surface Current Response Patterns to Tropical Cyclones. J. Mar. Syst. 2020, 208, 103345. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, H.; Ming, J.; Zheng, J.; Tian, D.; Chen, D. Importance of Precipitation on the Upper Ocean Salinity Response to Typhoon Kalmaegi (2014). Water 2020, 12, 614. [Google Scholar] [CrossRef]
- Domingues, R.; Goni, G.; Bringas, F.; Lee, S.; Kim, H.; Halliwell, G.; Dong, J.; Morell, J.; Pomales, L. Upper Ocean Response to Hurricane Gonzalo (2014): Salinity Effects Revealed by Targeted and Sustained Underwater Glider Observations. Geophys. Res. Lett. 2015, 42, 7131–7138. [Google Scholar] [CrossRef]
- Chaudhuri, D.; Sengupta, D.; D’Asaro, E.; Venkatesan, R.; Ravichandran, M. Response of the Salinity-Stratified Bay of Bengal to Cyclone Phailin. J. Phys. Oceanogr. 2019, 49, 1121–1140. [Google Scholar] [CrossRef]
- Perigaud, C.; McCreary Jr, J.P.; Zhang, K.Q. Impact of Interannual Rainfall Anomalies on Indian Ocean Salinity and Temperature Variability. J. Geophys. Res. Ocean. 2003, 108, 3319. [Google Scholar] [CrossRef]
- Wang, H.; Li, J.; Song, J.; Leng, H.; Zhang, H.; Chen, X.; Ke, D.; Zhao, C. Ocean Response Offshore of Taiwan to Super Typhoon Nepartak (2016) Based on Multiple Satellite and Buoy Observations. Front. Mar. Sci. 2023, 10, 1132714. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, H. Near-Surface Ocean Temperature and Air-Sea Heat Flux Observed by a Buoy Array during Summer to Autumn in Year 2014 in the Northern South China Sea. Front. Mar. Sci. 2024, 11, 1457829. [Google Scholar] [CrossRef]
- Liu, K.; Chen, X.; Zhan, P.; Da, L.; Wang, H.; Guo, W.; Liu, J.; Chen, L.; Liu, B.; Gao, G.; et al. Observations of Near-Inertial Internal Wave Amplification and Enhanced Mixing after Surface Reflection. Prog. Oceanogr. 2024, 220, 103177. [Google Scholar] [CrossRef]
- Wang, H.; Li, J.; Song, J.; Leng, H.; Wang, H.; Zhang, Z.; Zhang, H.; Zheng, M.; Yang, X.; Wang, C. The Abnormal Track of Super Typhoon Hinnamnor (2022) and Its Interaction with the Upper Ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 2023, 201, 104160. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Wang, G.; Cheng, H.; Sun, L. Enhanced Oceanic Environmental Responses and Feedbacks to Super Typhoon Nida (2009) during the Sudden-Turning Stage. Remote Sens. 2021, 13, 2648. [Google Scholar] [CrossRef]
- Vlasenko, V.; Stashchuk, N.; Hutter, K. (Eds.) Baroclinic Tides: Theoretical Modeling and Observational Evidence; Cambridge University Press: Cambridge, UK, 2005; p. 372. ISBN 0521843952. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Z.; Yu, F.; Qiang, R.; Liu, X.; Nan, F.; Wang, J.; Si, G.; Hu, Y. Deep Propagation of Wind-Generated near-Inertial Waves in the Northern South China Sea. Deep Sea Res. Part I Oceanogr. Res. Pap. 2024, 204, 104226. [Google Scholar] [CrossRef]
- Hall, P.; Davies, A.M. Internal Tide Modelling and the Influence of Wind Effects. Cont. Shelf Res. 2007, 27, 1357–1377. [Google Scholar] [CrossRef]
- Leaman, K.D.; Sanford, T.B. Vertical Energy Propagation of Inertial Waves: A Vector Spectral Analysis of Velocity Profiles. J. Geophys. Res. (1896–1977) 1975, 80, 1975–1978. [Google Scholar] [CrossRef]
- Xu, Z.; Yin, B.; Hou, Y.; Xu, Y. Variability of Internal Tides and Near-inertial Waves on the Continental Slope of the Northwestern South China Sea. J. Geophys. Res. Ocean. 2013, 118, 197–211. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, F.; Chen, Z.; Wang, J.; Nan, F.; Ren, Q.; Hu, Y.; Cao, A.; Zheng, T. Downward Propagation and Trapping of Near-Inertial Waves by a Westward-Moving Anticyclonic Eddy in the Subtropical Northwestern Pacific Ocean. J. Phys. Oceanogr. 2023, 53, 2105–2120. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).