A Directional Wave Spectrum Inversion Algorithm with HF Surface Wave Radar Network
Abstract
1. Introduction
2. Materials and Methods
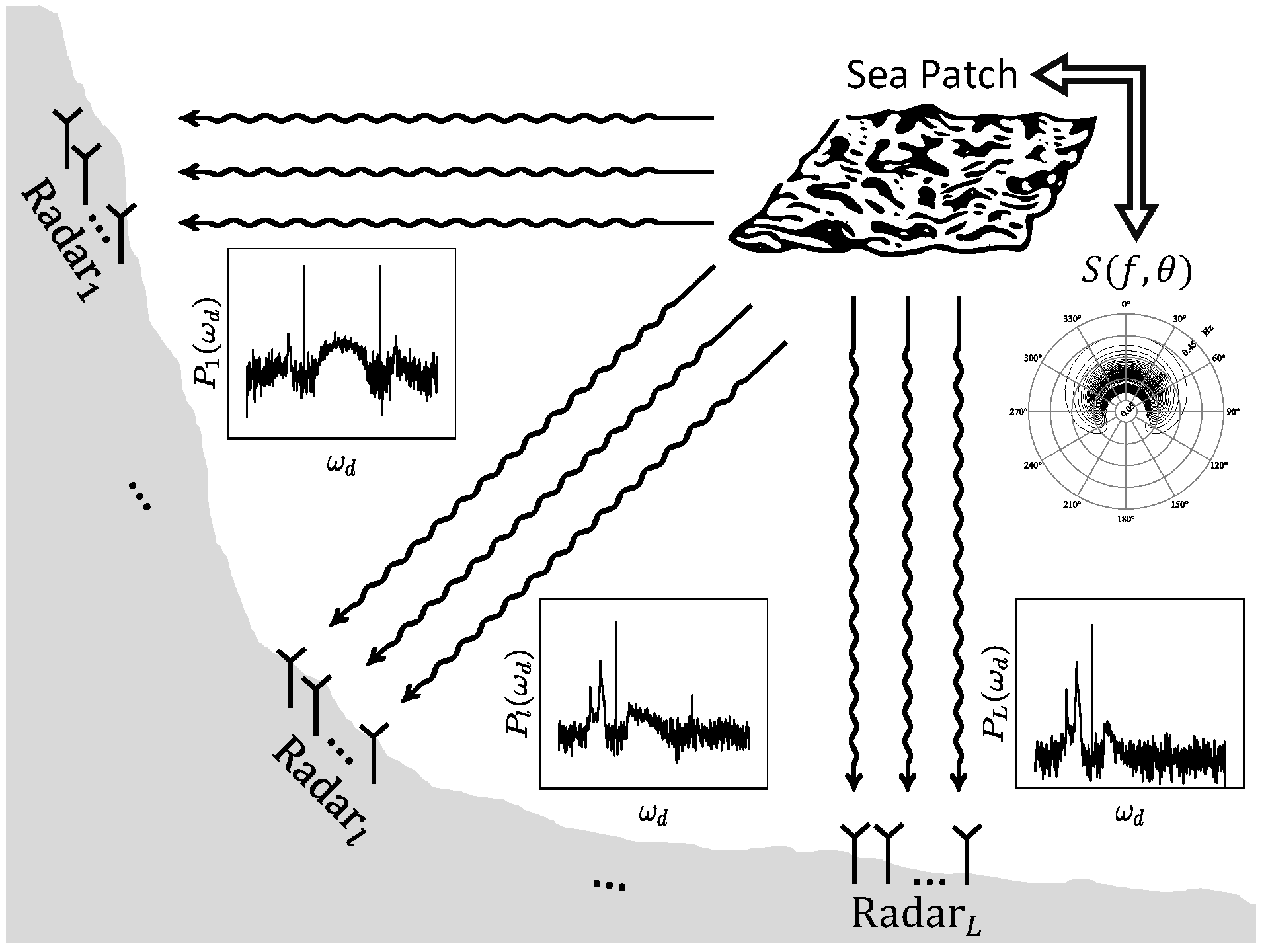
2.1. Problem Formulation and System Model
2.2. AMR Radar System
2.3. Radar Cross-Section Equations
2.4. Linearization of the Second-Order Equation
2.5. Functional Representation and Matrixing
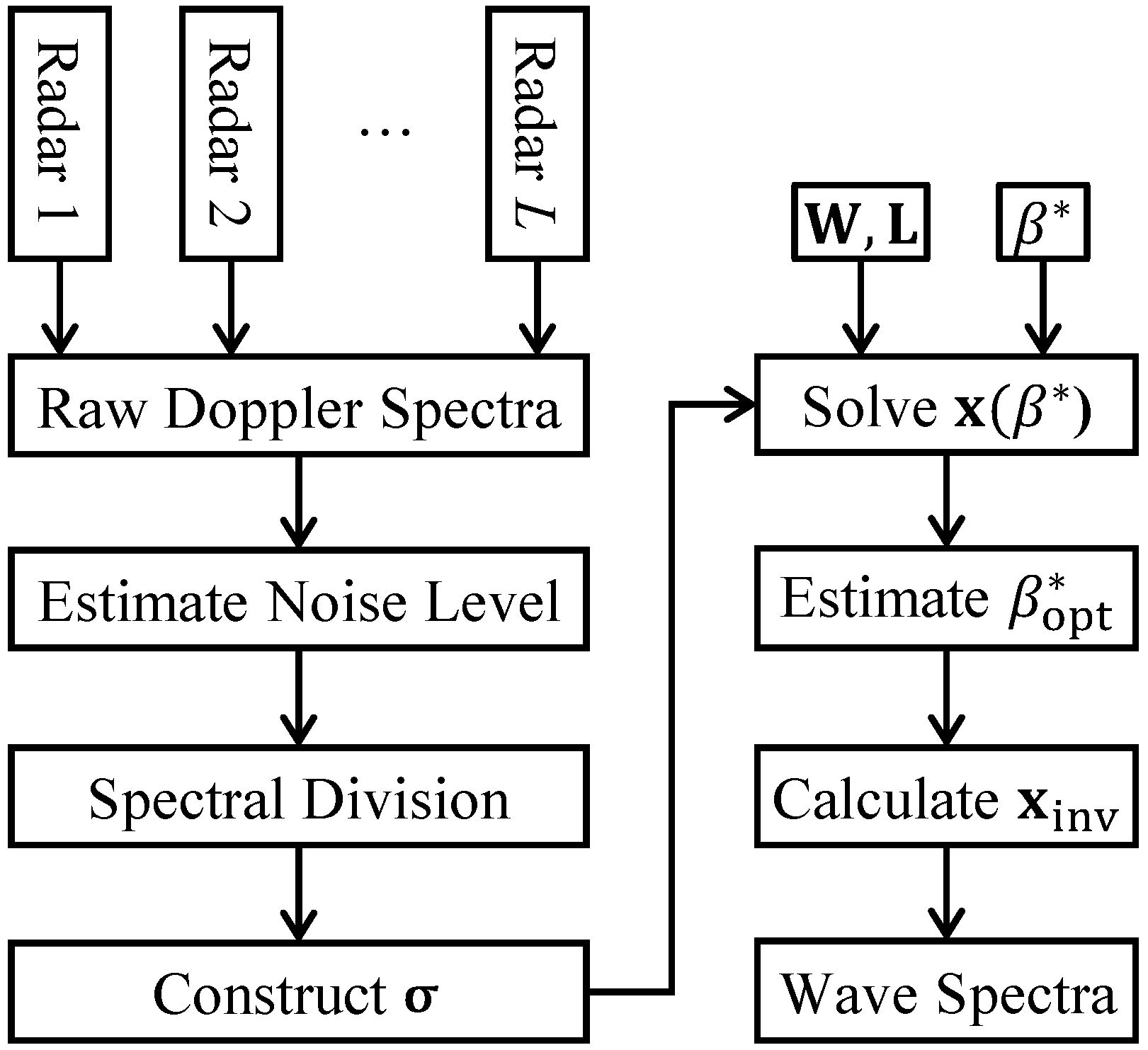
2.6. Inversion with Two or More Radars
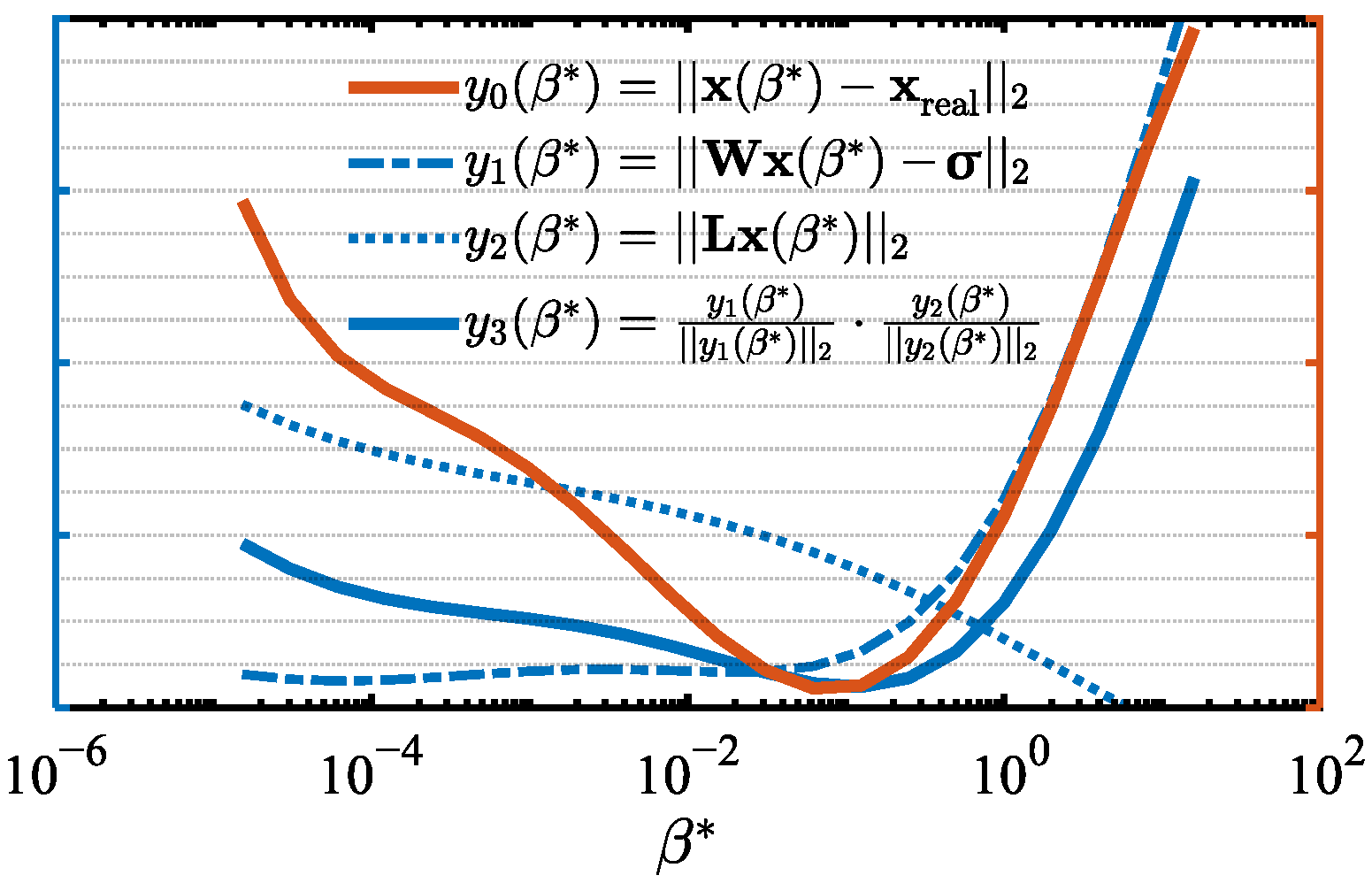
2.7. Equation Constraints and Solution
3. Results
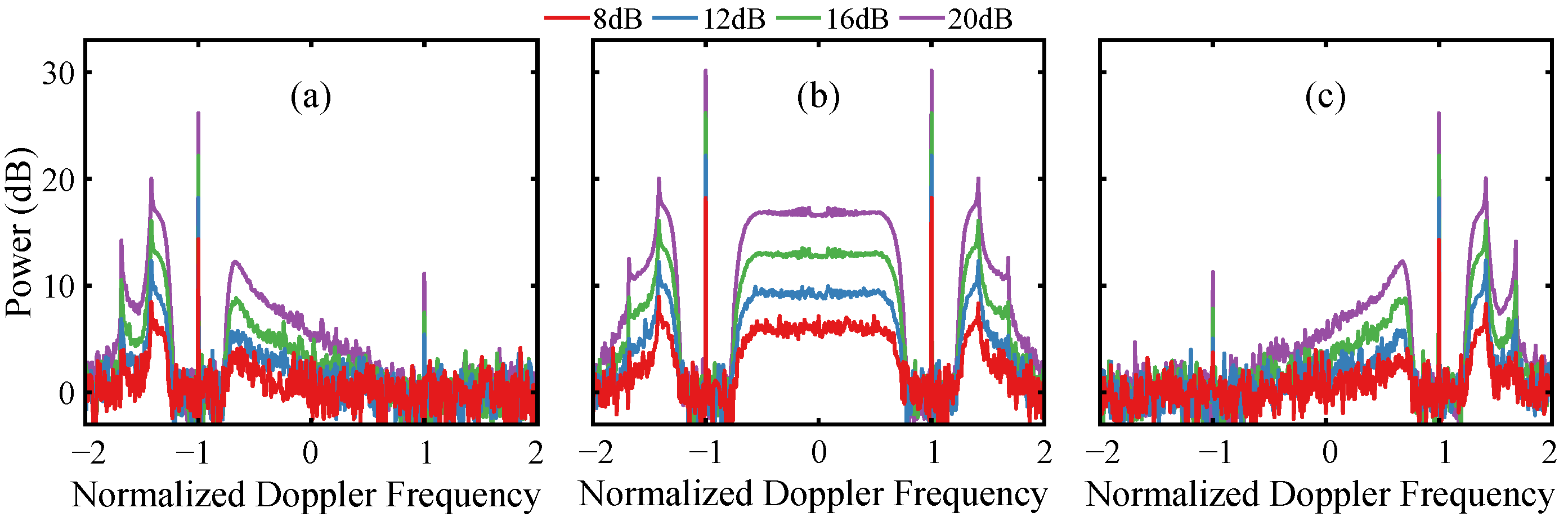
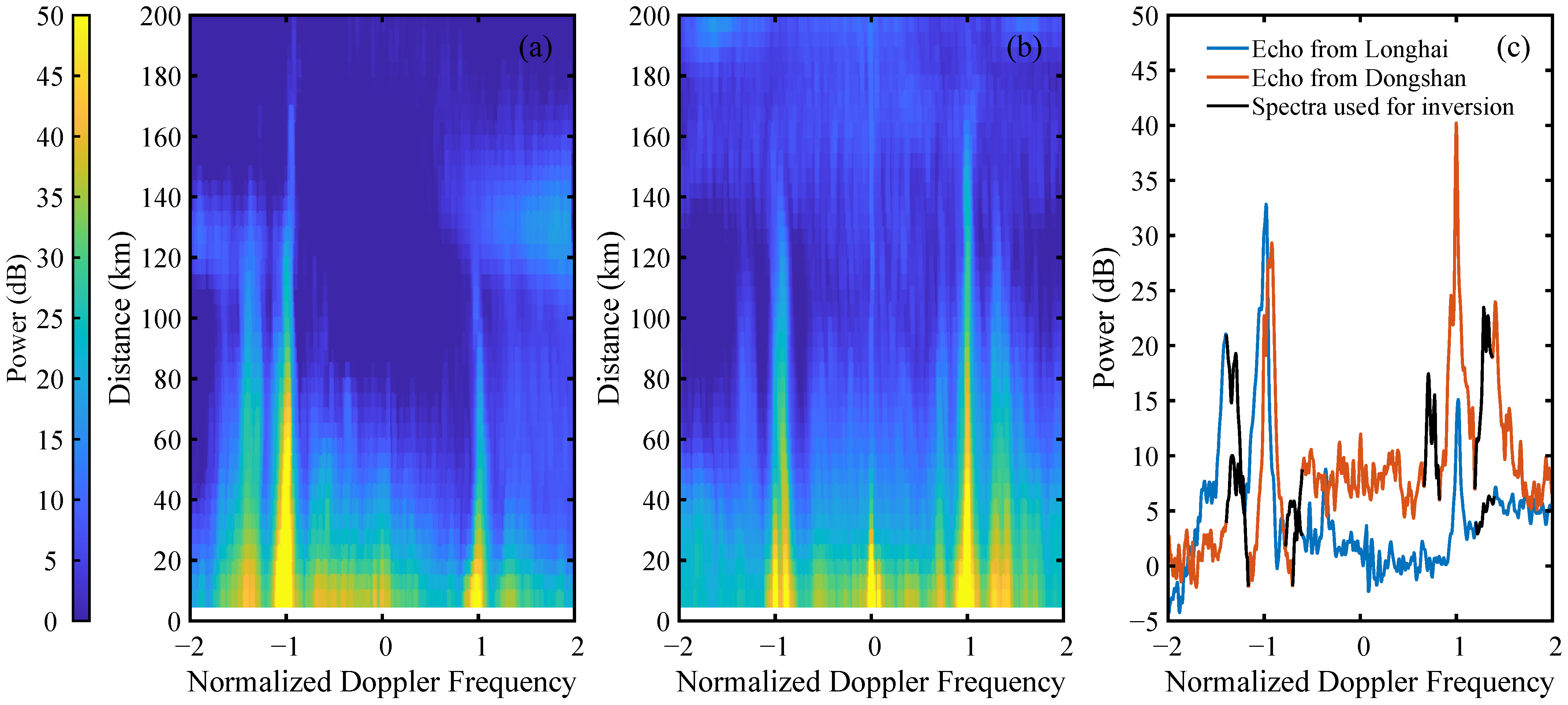
3.1. Radar Doppler Spectrum Simulation and Noise
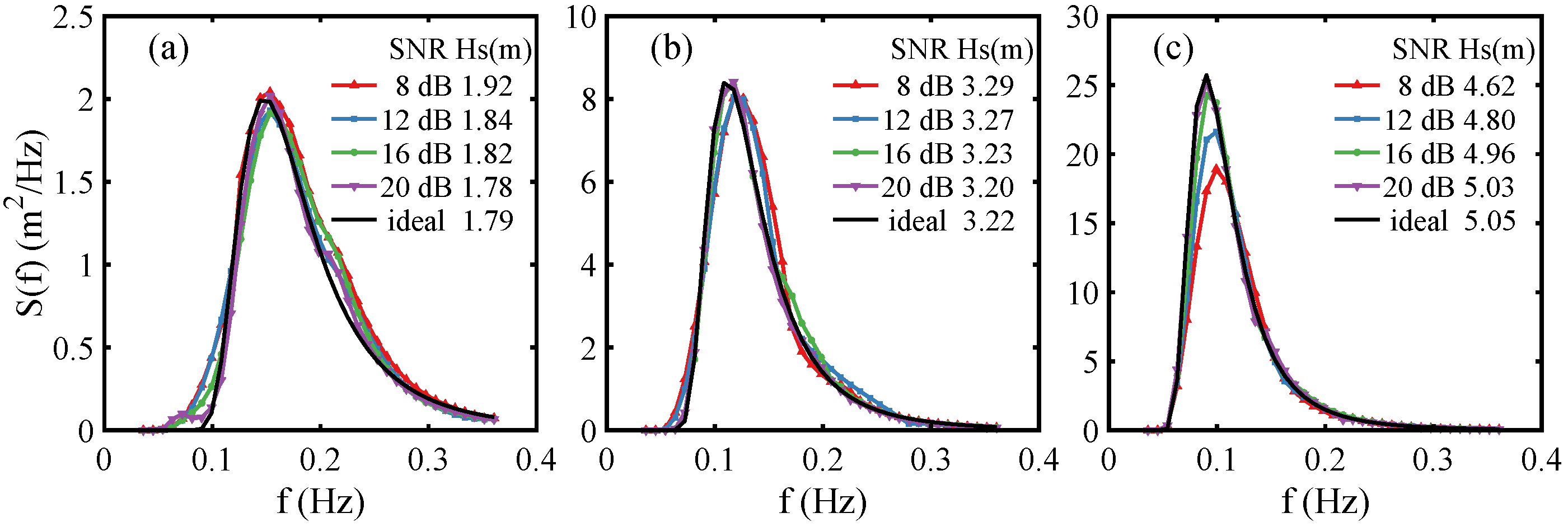
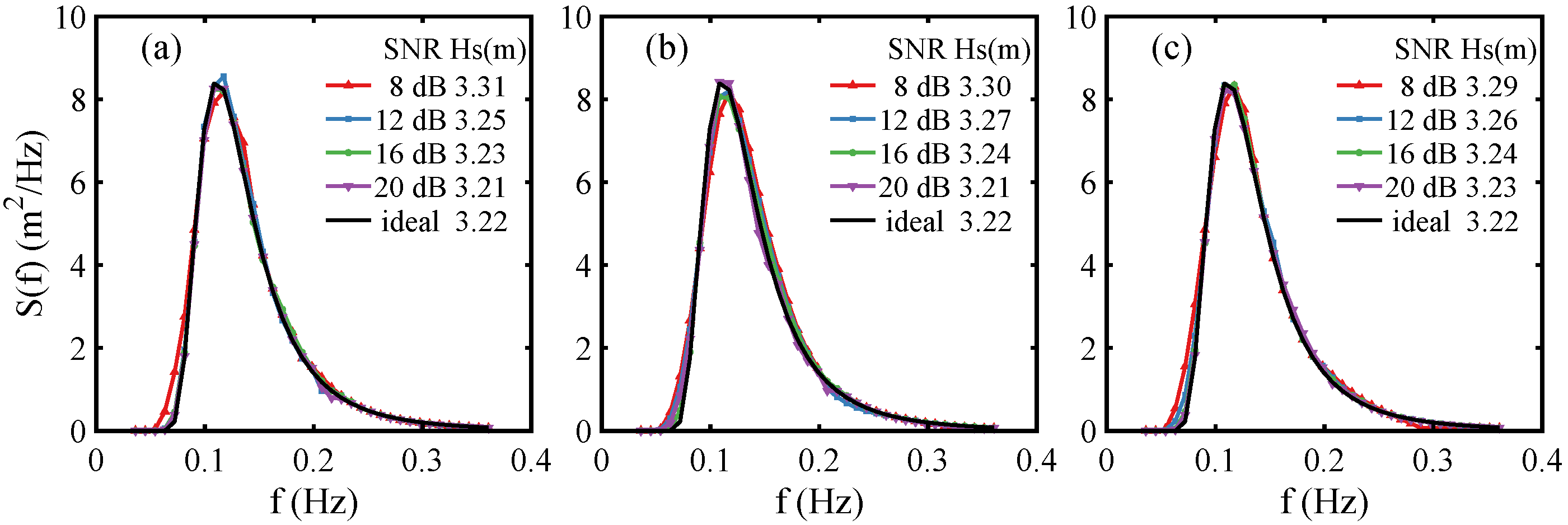
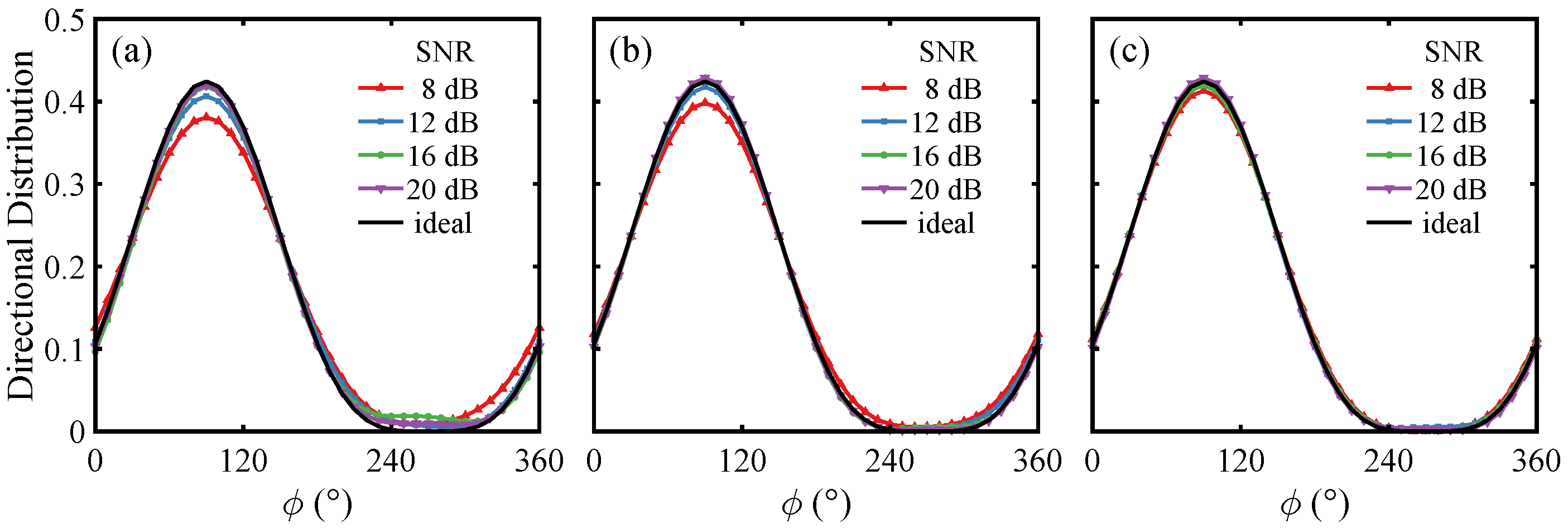
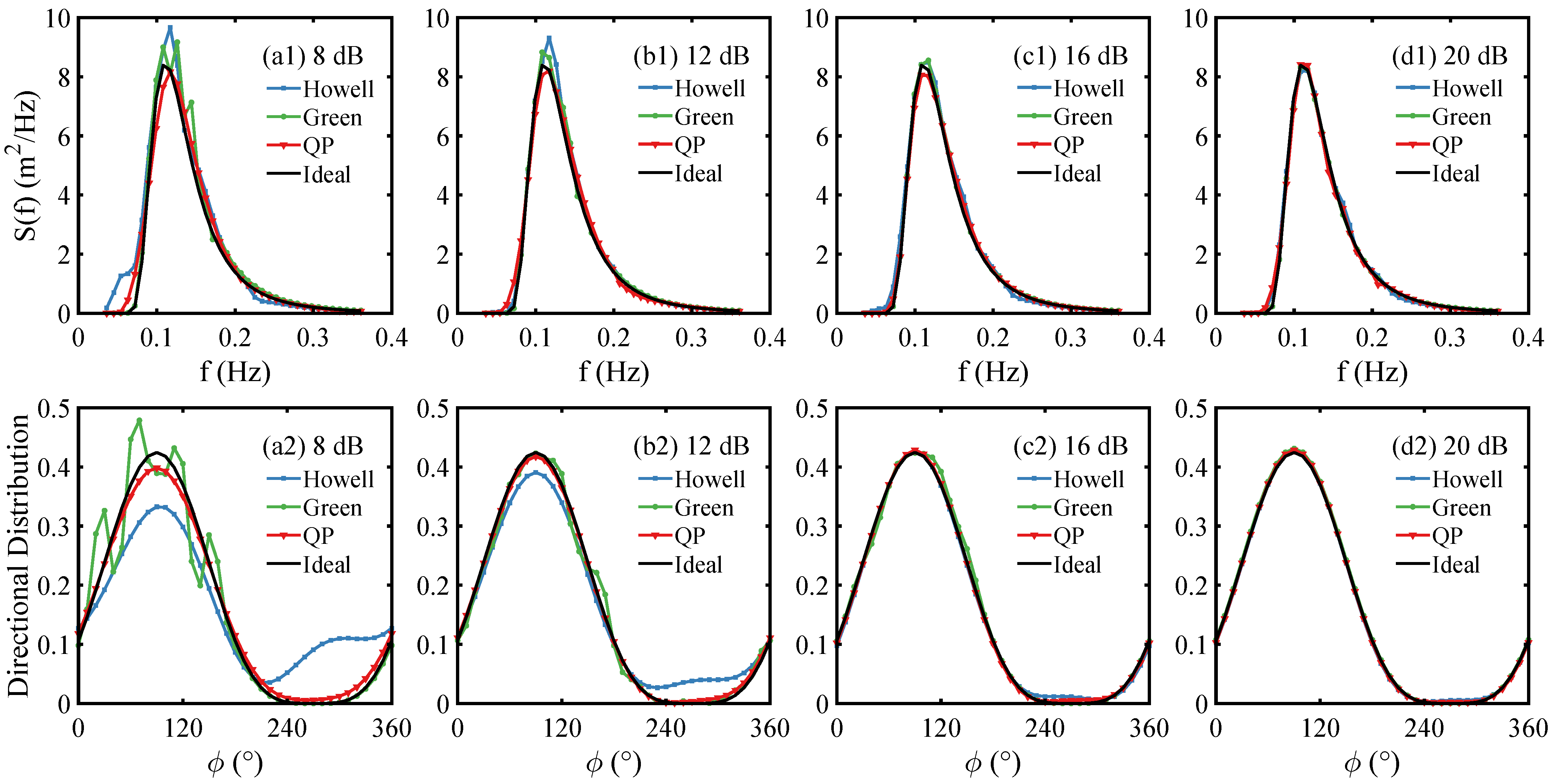
3.2. Single-Radar Inversion Simulation
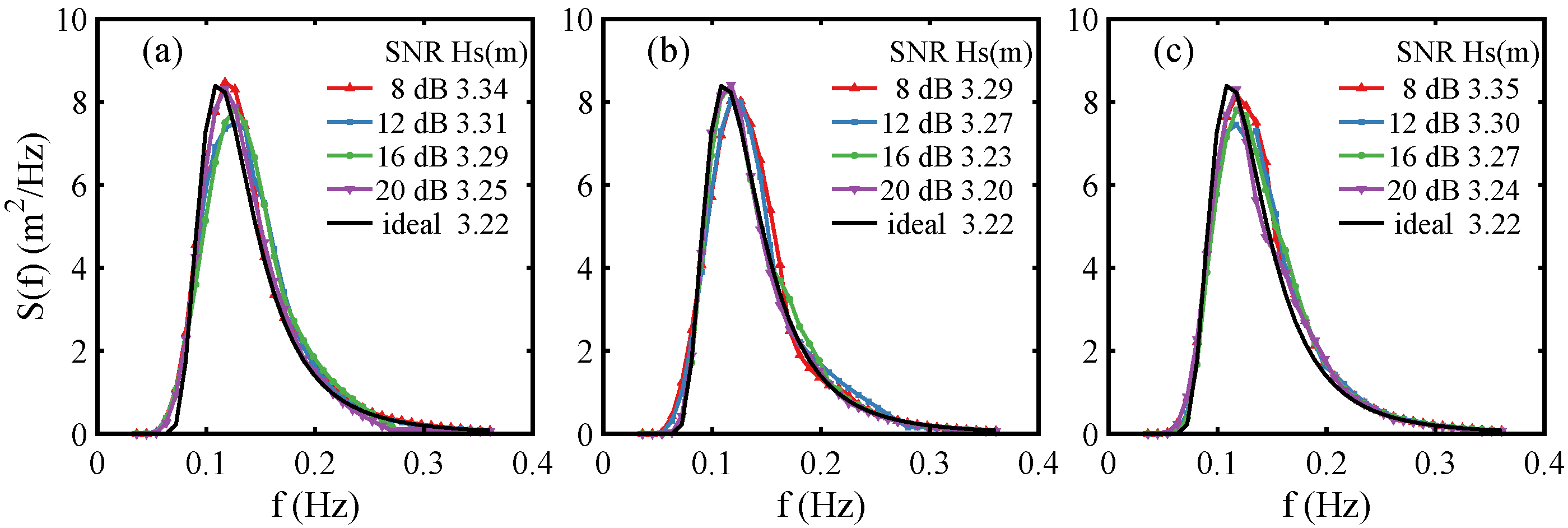
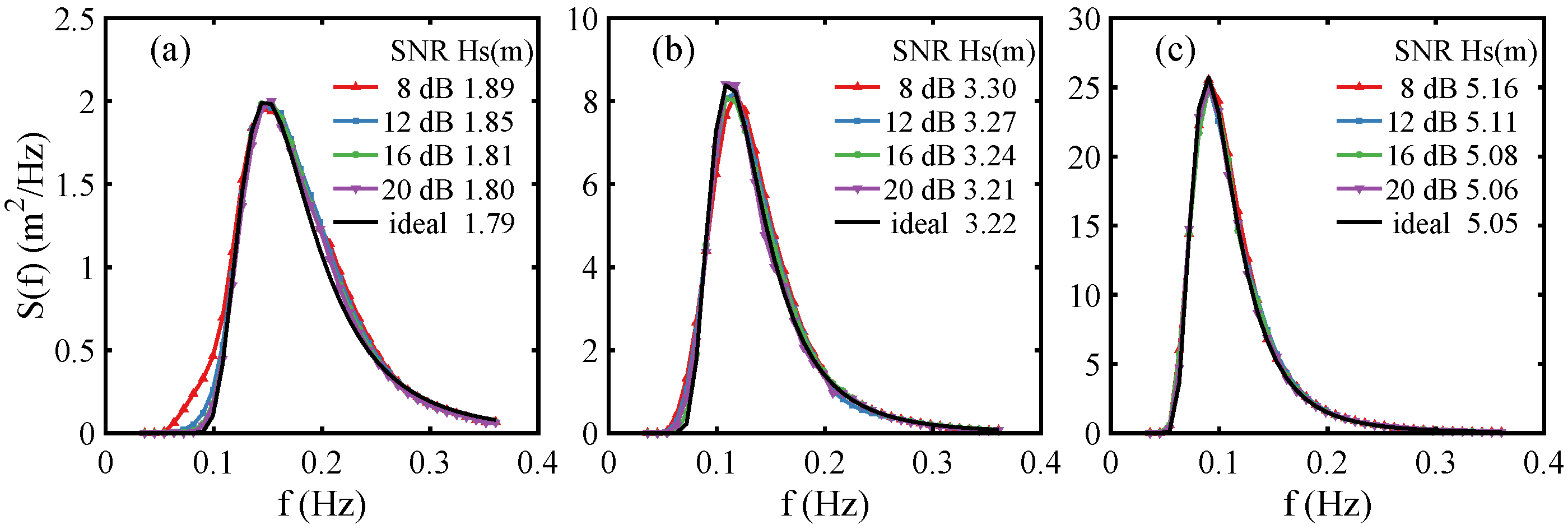
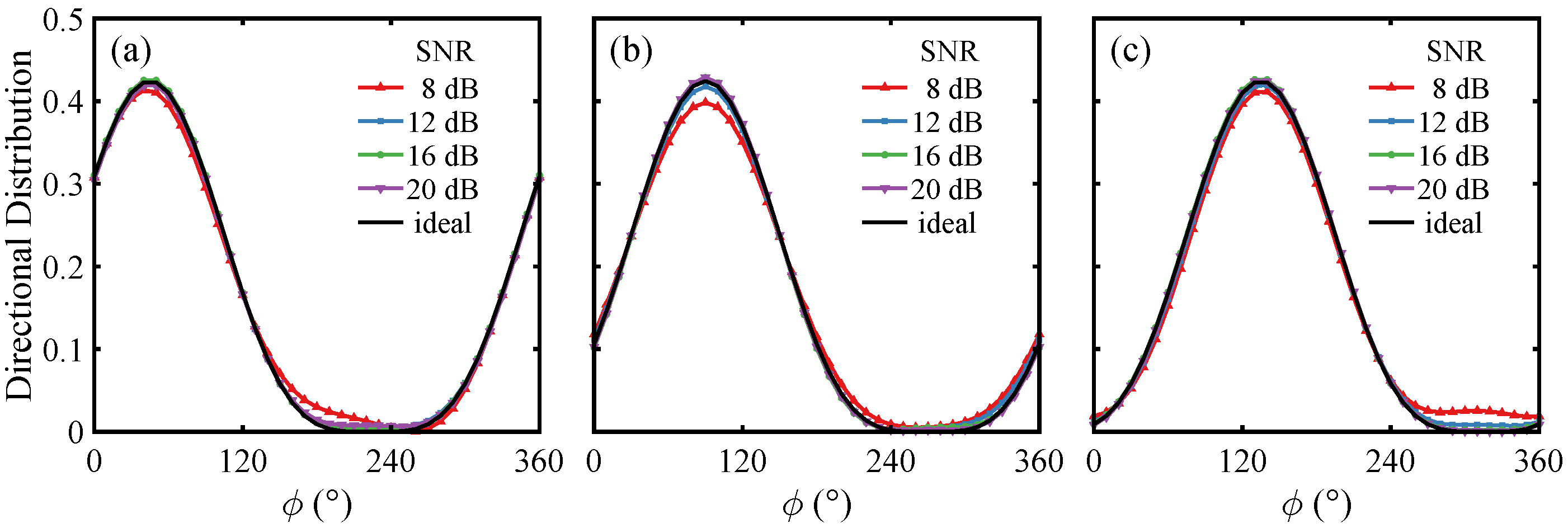
3.3. Dual-Radar Inversion Simulation
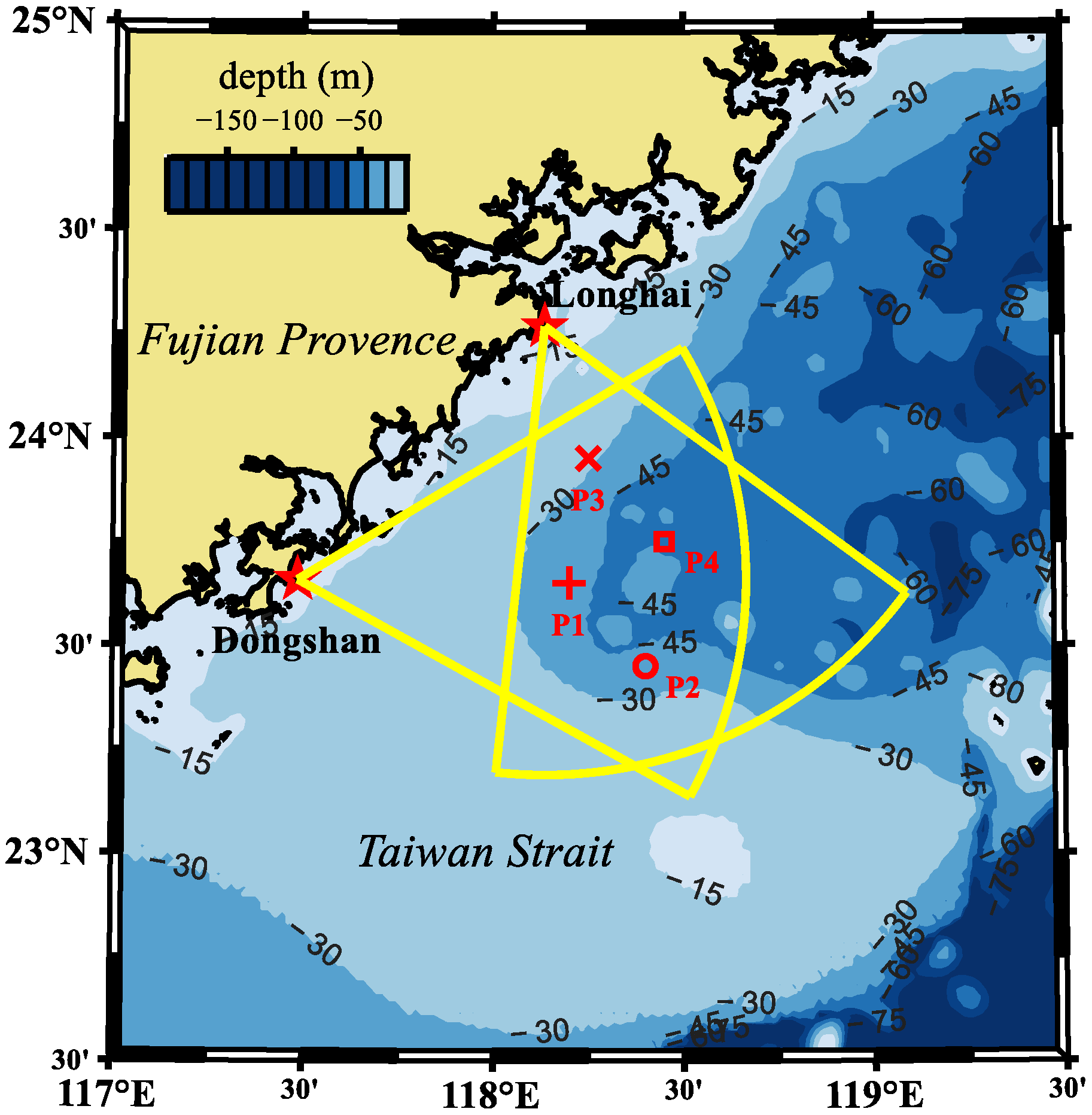
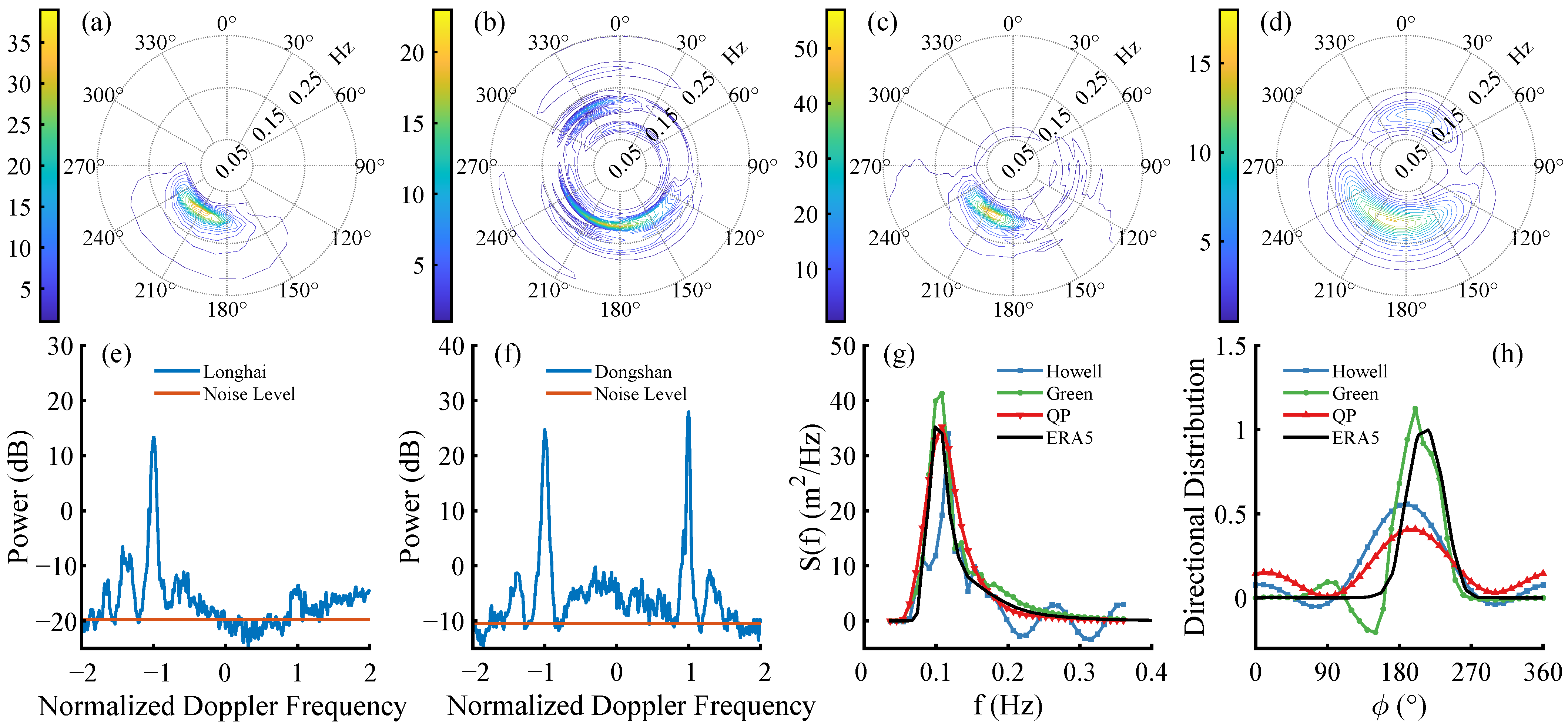
3.4. Directional Wave Spectrum Results
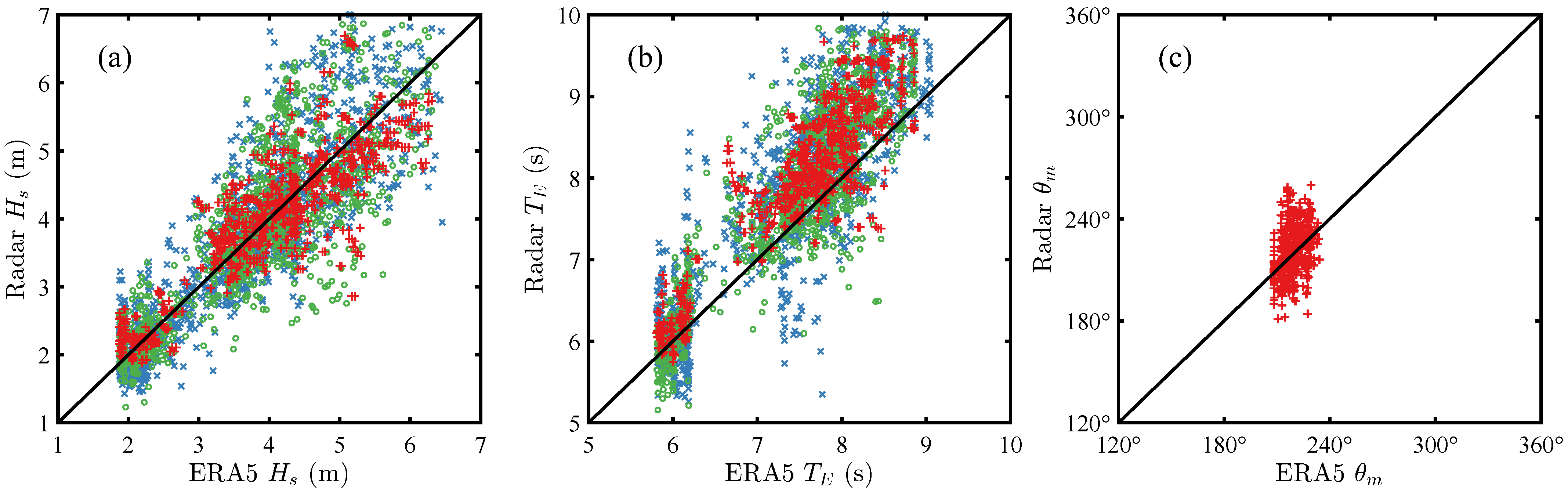
3.5. Wave Parameter Comparison
3.6. Method Comparison and Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crombie, D.D. Doppler spectrum of sea echo at 13.56 Mc./s. Nature 1955, 175, 681–682. [Google Scholar] [CrossRef]
- Barrick, D.E. Remote sensing of sea state by radar. In Proceedings of the Ocean 72—IEEE International Conference on Engineering in the Ocean Environment, Newport, RI, USA, 13–15 September 1972; pp. 186–192. [Google Scholar]
- Gurgel, K.W.; Antonischki, G.; Essen, H.H.; Schlick, T. Wellen radar (WERA): A new ground-wave HF radar for ocean remote sensing. Coast. Eng. 1999, 37, 219–234. [Google Scholar] [CrossRef]
- Barrick, D.E.; Weber, B.L. On the nonlinear theory for gravity waves on the ocean’s surface. Part II: Interpretation and applications. J. Phys. Oceanogr. 1977, 7, 11–21. [Google Scholar] [CrossRef]
- Fujii, S.; Heron, M.L.; Kim, K.; Lai, J.W.; Lee, S.H.; Wu, X.; Wu, X.; Wyatt, L.R.; Yang, W.c. An overview of developments and applications of oceanographic radar networks in Asia and Oceania countries. Ocean Sci. J. 2013, 48, 69–97. [Google Scholar] [CrossRef]
- Barrick, D.E. The ocean waveheight nondirectional spectrum from inversion of the HF sea-echo Doppler spectrum. Remote Sens. Environ. 1977, 6, 201–227. [Google Scholar] [CrossRef]
- Lipa, B. Derivation of directional ocean-wave spectra by integral inversion of second-order radar echoes. Radio Sci. 1977, 12, 425–434. [Google Scholar] [CrossRef]
- Lipa, B. Inversion of second-order radar echoes from the Sea. J. Geophys. Res.-Oceans 1978, 83, 959–962. [Google Scholar] [CrossRef]
- Wyatt, L.R. The measurement of the ocean wave directional spectrum from HF radar Doppler spectra. Radio Sci. 1986, 21, 473–485. [Google Scholar] [CrossRef]
- Wyatt, L.R. A relaxation method for integral inversion applied to HF radar measurement of the ocean wave directional spectrum. Int. J. Remote Sens. 1990, 11, 1481–1494. [Google Scholar] [CrossRef]
- Gill, E.W.; Walsh, J. Extraction of ocean wave parameters from HF backscatter received by a four-element array: Analysis and application. IEEE J. Ocean. Eng. 1992, 17, 376–386. [Google Scholar] [CrossRef]
- Howell, R.; Walsh, J. Measurement of ocean wave spectra using narrow-beam HF radar. IEEE J. Ocean. Eng. 1993, 18, 296–305. [Google Scholar] [CrossRef]
- Hisaki, Y. Nonlinear inversion of the integral equation to estimate ocean wave spectra from HF radar. Radio Sci. 1996, 31, 25–39. [Google Scholar] [CrossRef]
- Li, L.; Wu, X.; Long, C.; Liu, B. Regularization inversion method for extracting ocean wave spectra from HFSWR sea echo. Chinese J. Geophys. 2013, 56, 219–229. [Google Scholar]
- Hisaki, Y. Ocean wave parameters and spectrum estimated from single and dual high-frequency radar systems. Ocean Dyn. 2016, 66, 1065–1085. [Google Scholar] [CrossRef]
- Lopez, G.; Conley, D.C.; Greaves, D. Calibration, validation, and analysis of an empirical algorithm for the retrieval of wave spectra from HF radar sea echo. J. Atmos. Ocean. Technol. 2016, 33, 245–261. [Google Scholar] [CrossRef]
- Lopez, G.; Conley, D.C. Comparison of HF radar fields of directional wave spectra against in situ measurements at multiple locations. J. Mar. Sci. Eng. 2019, 7, 271. [Google Scholar] [CrossRef]
- Silva, M.T.; Shahidi, R.; Gill, E.W.; Huang, W. Nonlinear extraction of directional ocean wave spectrum from synthetic bistatic high-frequency surface wave radar data. IEEE J. Ocean. Eng. 2020, 45, 1004–1021. [Google Scholar] [CrossRef]
- Shahidi, R.; Gill, E.W. A new automatic nonlinear optimization-based method for directional ocean wave spectrum extraction from monostatic HF-radar data. IEEE J. Ocean. Eng. 2021, 46, 900–918. [Google Scholar] [CrossRef]
- Zhao, C.; Deng, M.; Chen, Z.; Ding, F.; Huang, W. Ocean wave parameters and nondirectional spectrum measurements using multifrequency HF radar. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Wyatt, L.R.; Green, J.J. Developments in scope and availability of HF radar wave measurements and robust evaluation of their accuracy. Remote Sens. 2023, 15, 5536. [Google Scholar] [CrossRef]
- Hardman, R.L.; Wyatt, L.R. Inversion of HF radar Doppler spectra using a neural network. J. Mar. Sci. Eng. 2019, 7, 255–272. [Google Scholar] [CrossRef]
- Lewitt, R.M. Multidimensional digital image representations using generalized Kaiser–Bessel window functions. J. Opt. Soc. Am. A 1990, 7, 1834–1846. [Google Scholar] [CrossRef] [PubMed]
- Green, J.J.; Wyatt, L.R. Row-action inversion of the Barrick-Weber equations. J. Atmos. Ocean. Technol. 2006, 23, 501–510. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Cartwright, D.E.; Smith, N.D. Observation of the directional spectrum of sea waves using the motions of a floating buoy. In Proceedings of the Ocean Wave Spectra, Easton, MD, USA, 1–4 May 1963; pp. 111–132. [Google Scholar]
- Xie, X.; Zhang, L.; Chen, Z.; Wu, X.; Yue, X. MIMO ground wave radar radio frequency monitoring. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, M.; Wu, X.; Zhang, L.; Yue, X.; Yi, X.; Xie, X.; Yu, L. Measurement and analysis of antenna pattern for MIMO HF surface wave radar. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 1788–1792. [Google Scholar] [CrossRef]
- Bliss, D.W.; Forsythe, K.W. Multiple-input multiple-output (MIMO) radar and imaging: Degrees of freedom and resolution. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, 2003, Pacific Grove, CA, USA, 9–12 November 2003; Volume 1, pp. 54–59. [Google Scholar]
- Lesturgie, M. Improvement of high-frequency surface waves radar performances by use of multiple-input multiple-output configurations. IET Radar Sonar Navig. 2009, 3, 49–61. [Google Scholar] [CrossRef]
- Barrick, D.E.; Snider, J.B. The statistics of HF sea-echo Doppler spectra. IEEE Trans. Antennas Propag. 1977, 25, 19–28. [Google Scholar] [CrossRef]
- Wyatt, L.R.; Green, J.J.; Middleditch, A. Signal sampling impacts on HF radar wave measurement. J. Atmos. Ocean. Technol. 2009, 26, 793–805. [Google Scholar] [CrossRef]
- Barrick, D.E. First-order theory and analysis of MF/HF/VHF scatter from the sea. IEEE Trans. Antennas Propag. 1972, 20, 2–10. [Google Scholar] [CrossRef]
- Rice, S.O. Reflection of electromagnetic waves from slightly rough surfaces. Commun. Pure Appl. Math. 1951, 4, 351–378. [Google Scholar] [CrossRef]
- Barrick, D.E.; Lipa, B.J. The second-order shallow-water hydrodynamic coupling coefficient in interpretation of HF radar sea echo. IEEE J. Ocean. Eng. 1986, 11, 310–315. [Google Scholar] [CrossRef]
- Howell, R.K. An Algorithm for the Extraction of Ocean Wave Spectra from Narrow Beam HF Radar Backscatter. Master’s Thesis, Memorial University of Newfoundland, St. John’s, NF, Canada, 1990. [Google Scholar]
- Hasselmann, K. Determination of ocean wave spectra from Doppler radio return from the sea surface. Nature Phys. Sci. 1971, 229, 16–17. [Google Scholar] [CrossRef]
- Phillips, O.M. The Dynamics of the Upper Ocean; Cambridge University Press: London, UK, 1966. [Google Scholar]
- Moskowitz, L. Estimates of the power spectrums for fully developed seas for wind speeds of 20 to 40 knots. J. Geophys. Res. 1964, 69, 5161–5179. [Google Scholar] [CrossRef]
- Wyatt, L.R. High order nonlinearities in HF radar backscatter from the ocean surface. IEE Proc.-Radar Sonar Navig. 1995, 142, 293–300. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Operating frequency range (MHz) | 8∼13.5 |
| Average transmitting power (W) | 200 |
| Maximum range (km) | 200 |
| Range resolution (km) | 5 |
| Doppler sampling interval (s) | 0.25 |
| FFT length for Doppler spectra | 2048 |
| Wave measurement period (min) | 10 |
| SNR (dB) | 9 m/s | 12 m/s | 15 m/s | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 0.18 | 0.13 | 0.15 | 0.12 | 0.07 | 0.13 | 0.52 | 0.43 | 0.46 | |
| 0.13 | 0.05 | 0.11 | 0.09 | 0.11 | 0.15 | 0.36 | 0.25 | 0.39 | ||
| 12 | 0.09 | 0.05 | 0.10 | 0.09 | 0.05 | 0.08 | 0.41 | 0.25 | 0.39 | |
| 0.08 | 0.06 | 0.12 | 0.16 | 0.10 | 0.15 | 0.23 | 0.13 | 0.27 | ||
| 16 | 0.08 | 0.03 | 0.09 | 0.07 | 0.01 | 0.05 | 0.24 | 0.09 | 0.36 | |
| 0.10 | 0.04 | 0.06 | 0.18 | 0.03 | 0.13 | 0.15 | 0.07 | 0.13 | ||
| 20 | 0.03 | 0.01 | 0.05 | 0.03 | 0.02 | 0.02 | 0.07 | 0.02 | 0.05 | |
| 0.05 | 0.03 | 0.03 | 0.06 | 0.02 | 0.07 | 0.05 | 0.02 | 0.09 | ||
| SNR (dB) | 9 m/s | 12 m/s | 15 m/s | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 0.13 | 0.10 | 0.11 | 0.09 | 0.08 | 0.07 | 0.15 | 0.11 | 0.12 | |
| 0.07 | 0.05 | 0.03 | 0.05 | 0.06 | 0.03 | 0.03 | 0.02 | 0.06 | ||
| 2.31 | 3.78 | 3.27 | 4.21 | 2.68 | 2.32 | 1.62 | 1.97 | 2.23 | ||
| 12 | 0.05 | 0.06 | 0.04 | 0.03 | 0.05 | 0.04 | 0.08 | 0.06 | 0.05 | |
| 0.02 | 0.03 | 0.05 | 0.03 | 0.03 | 0.02 | 0.02 | 0.01 | 0.04 | ||
| 1.45 | 2.13 | 1.77 | 1.18 | 1.89 | 1.22 | 1.10 | 0.85 | 1.26 | ||
| 16 | 0.01 | 0.02 | 0.02 | 0.01 | 0.02 | 0.02 | 0.01 | 0.03 | 0.02 | |
| 0.06 | 0.03 | 0.04 | 0.02 | 0.02 | 0.02 | 0.05 | 0.02 | 0.03 | ||
| 2.10 | 1.76 | 1.19 | 1.09 | 1.16 | 0.98 | 1.05 | 1.08 | 1.13 | ||
| 20 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | |
| 0.02 | 0.02 | 0.03 | 0.01 | 0.02 | 0.01 | 0.03 | 0.01 | 0.02 | ||
| 0.86 | 1.55 | 1.12 | 1.21 | 0.73 | 0.87 | 1.13 | 0.52 | 0.96 | ||
| Location | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE (m) | CC | No. | RMSE (s) | CC | No. | RMSE(°) | CC | No. | |
| P1 | 0.60 | 0.88 | 382 | 0.62 | 0.87 | 382 | - | - | - |
| 0.67 | 0.79 | 294 | 0.54 | 0.83 | 294 | - | - | - | |
| 0.46 | 0.90 | 258 | 0.52 | 0.89 | 258 | 10 | 0.24 | 258 | |
| P2 | 0.62 | 0.89 | 325 | 0.72 | 0.81 | 325 | - | - | - |
| 0.87 | 0.79 | 171 | 0.69 | 0.86 | 171 | - | - | - | |
| 0.56 | 0.91 | 106 | 0.68 | 0.90 | 106 | 13 | 0.31 | 106 | |
| P3 | 0.67 | 0.86 | 328 | 0.78 | 0.92 | 328 | - | - | - |
| 0.76 | 0.90 | 273 | 0.69 | 0.89 | 273 | - | - | - | |
| 0.63 | 0.89 | 197 | 0.72 | 0.91 | 197 | 15 | 0.15 | 197 | |
| P4 | 0.62 | 0.90 | 289 | 0.58 | 0.92 | 289 | - | - | - |
| 0.65 | 0.86 | 280 | 0.66 | 0.92 | 280 | - | - | - | |
| 0.51 | 0.92 | 236 | 0.59 | 0.93 | 236 | 15 | 0.25 | 236 | |
| SNR (dB) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE (m) | CC | No. | RMSE (s) | CC | No. | RMSE(°) | CC | No. | |
| 8 | 0.63 | 0.87 | 165 | 0.69 | 0.76 | 165 | - | - | - |
| 0.75 | 0.84 | 223 | 0.62 | 0.88 | 223 | - | - | - | |
| 0.55 | 0.89 | 165 | 0.58 | 0.91 | 165 | 12 | 0.42 | 165 | |
| 12 | 0.61 | 0.89 | 329 | 0.68 | 0.88 | 329 | - | - | - |
| 0.68 | 0.86 | 284 | 0.72 | 0.85 | 284 | - | - | - | |
| 0.56 | 0.90 | 296 | 0.64 | 0.93 | 296 | 15 | 0.47 | 296 | |
| 16 | 0.62 | 0.87 | 363 | 0.65 | 0.87 | 363 | - | - | - |
| 0.59 | 0.83 | 266 | 0.68 | 0.86 | 266 | - | - | - | |
| 0.51 | 0.86 | 237 | 0.60 | 0.85 | 237 | 15 | 0.32 | 237 | |
| 20 | 0.68 | 0.75 | 390 | 0.70 | 0.77 | 390 | - | - | - |
| 0.75 | 0.69 | 209 | 0.66 | 0.83 | 209 | - | - | - | |
| 0.47 | 0.81 | 118 | 0.53 | 0.80 | 118 | 13 | 0.19 | 118 | |
| SNR (dB) | Howell | Green | QP | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (m) | (s) | (°) | (m) | (s) | (°) | (m) | (s) | (°) | |
| 8 | 0.54 | 0.53 | - | 0.38 | 0.20 | - | 0.07 | 0.11 | - |
| 0.27 | 0.42 | 9.60 | 0.19 | 0.04 | 5.64 | 0.08 | 0.06 | 2.68 | |
| 12 | 0.32 | 0.37 | - | 0.17 | 0.06 | - | 0.05 | 0.10 | - |
| 0.11 | 0.23 | 5.30 | 0.08 | 0.02 | 3.40 | 0.05 | 0.03 | 1.89 | |
| 16 | 0.13 | 0.21 | - | 0.05 | 0.02 | - | 0.01 | 0.03 | - |
| 0.08 | 0.15 | 1.54 | 0.05 | 0.03 | 2.37 | 0.02 | 0.02 | 1.16 | |
| 20 | 0.05 | 0.12 | - | 0.03 | 0.03 | - | 0.02 | 0.02 | - |
| 0.02 | 0.10 | 0.86 | 0.02 | 0.02 | 0.84 | 0.01 | 0.02 | 0.73 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, F.; Wu, X.; Li, X.; Yu, L.; Zhou, H. A Directional Wave Spectrum Inversion Algorithm with HF Surface Wave Radar Network. Remote Sens. 2025, 17, 2573. https://doi.org/10.3390/rs17152573
Mo F, Wu X, Li X, Yu L, Zhou H. A Directional Wave Spectrum Inversion Algorithm with HF Surface Wave Radar Network. Remote Sensing. 2025; 17(15):2573. https://doi.org/10.3390/rs17152573
Chicago/Turabian StyleMo, Fuqi, Xiongbin Wu, Xiaoyan Li, Liang Yu, and Heng Zhou. 2025. "A Directional Wave Spectrum Inversion Algorithm with HF Surface Wave Radar Network" Remote Sensing 17, no. 15: 2573. https://doi.org/10.3390/rs17152573
APA StyleMo, F., Wu, X., Li, X., Yu, L., & Zhou, H. (2025). A Directional Wave Spectrum Inversion Algorithm with HF Surface Wave Radar Network. Remote Sensing, 17(15), 2573. https://doi.org/10.3390/rs17152573








