Modeling Multivariable Associations and Inter-Eddy Interactions: A Dual-Graph Learning Framework for Mesoscale Eddy Trajectory Forecasting
Abstract
1. Introduction
- 1.
- We propose EddyGnet, a framework for mesoscale eddy trajectory forecasting that combines dynamic multivariable and spatiotemporal associations.
- 2.
- We designed a dynamic multivariable association graph (MAG) module that captures associations between mesoscale eddy variables by storing and propagating historical information.
- 3.
- We developed a spatiotemporal eddy association graph (STEAG) module to model the interactions and temporal dependencies of mesoscale eddy trajectories.
2. Data and Methods
2.1. Data
- Absolute Dynamic Topography (ADT): the sea surface height above the geoid, reflecting the ocean’s dynamic state;
- Absolute Geostrophic Velocity at the Sea Surface: including both the zonal (Ugos) and meridional (Vgos) components.
2.2. Methods
2.2.1. Overall Framework
2.2.2. Embedding
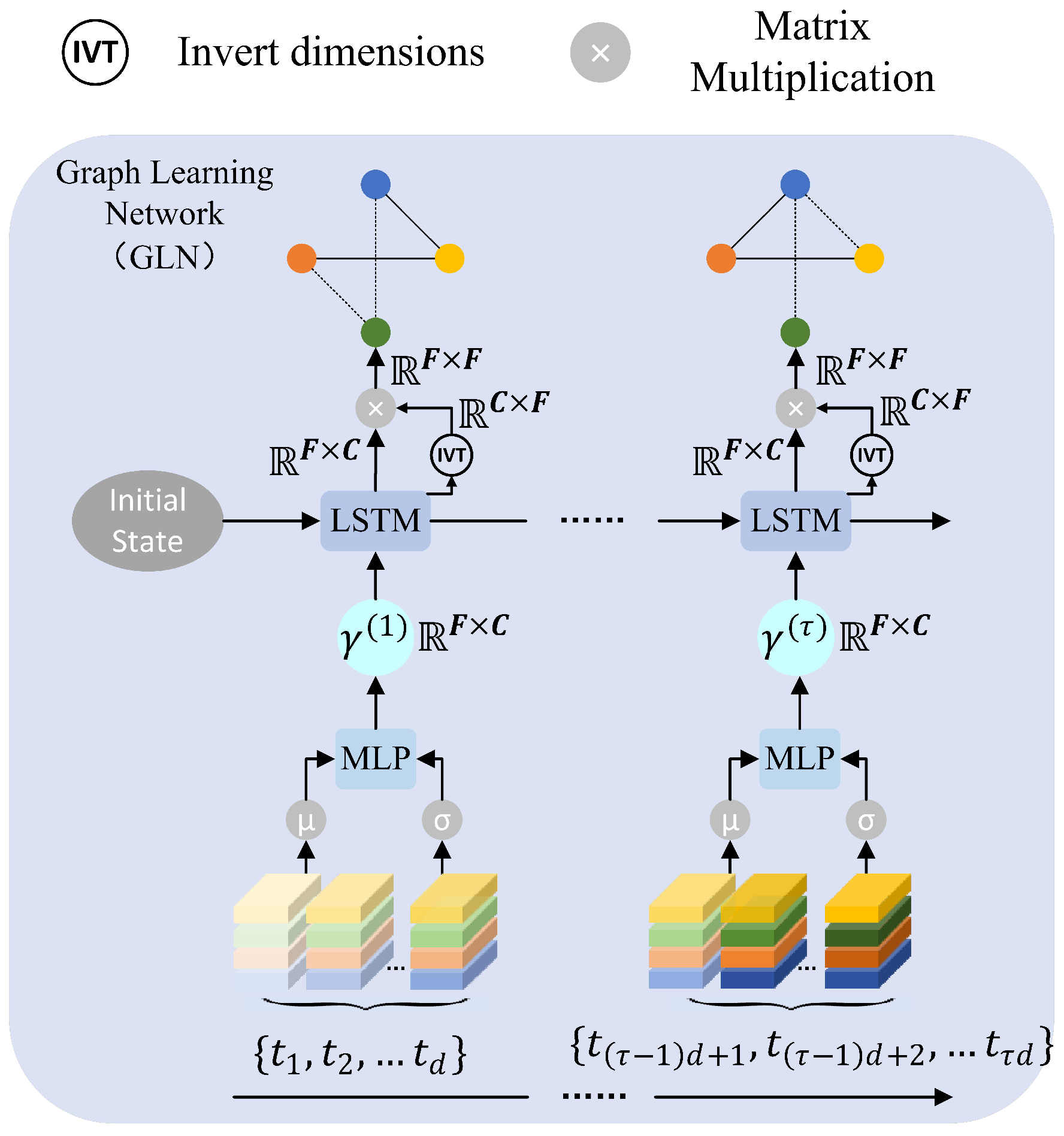
2.2.3. Dynamic Multivariable Association Graph Learning
2.2.4. Spatiotemporal Eddy Association Graph Learning
Temporal Dependency Learning
Eddy–Eddy Interaction Learning
- Since each eddy exists independently, it does not need to embed positional encoding for each eddy.
- The predefined graph structure is a complete square matrix rather than an upper triangular matrix. Moreover, the predefined interaction scores are independent of the eddy numbering and are instead potentially related to the proximity of their geographical locations. On the Earth’s surface, spherical trigonometry can be employed to calculate the distance between two coordinates defined by latitude and longitude. The most commonly used method is the Haversine formula, which calculates the great-circle distance on a sphere, representing the shortest arc length between two points.
Spatiotemporal Fusion
2.2.5. Forecasting and Loss Function
2.3. Experimental Setup
2.3.1. Evaluation Metrics
- MAE and MSE: MAE and MSE are traditional evaluation metrics in regression tasks within machine learning, commonly used to quantitatively analyze the errors between forecastings and ground truth.
- ADE and FDE: ADE measures the average distance between all predicted trajectory points and their corresponding ground truth future trajectory points, while FDE measures the distance between the final predicted destination and the final ground truth destination.
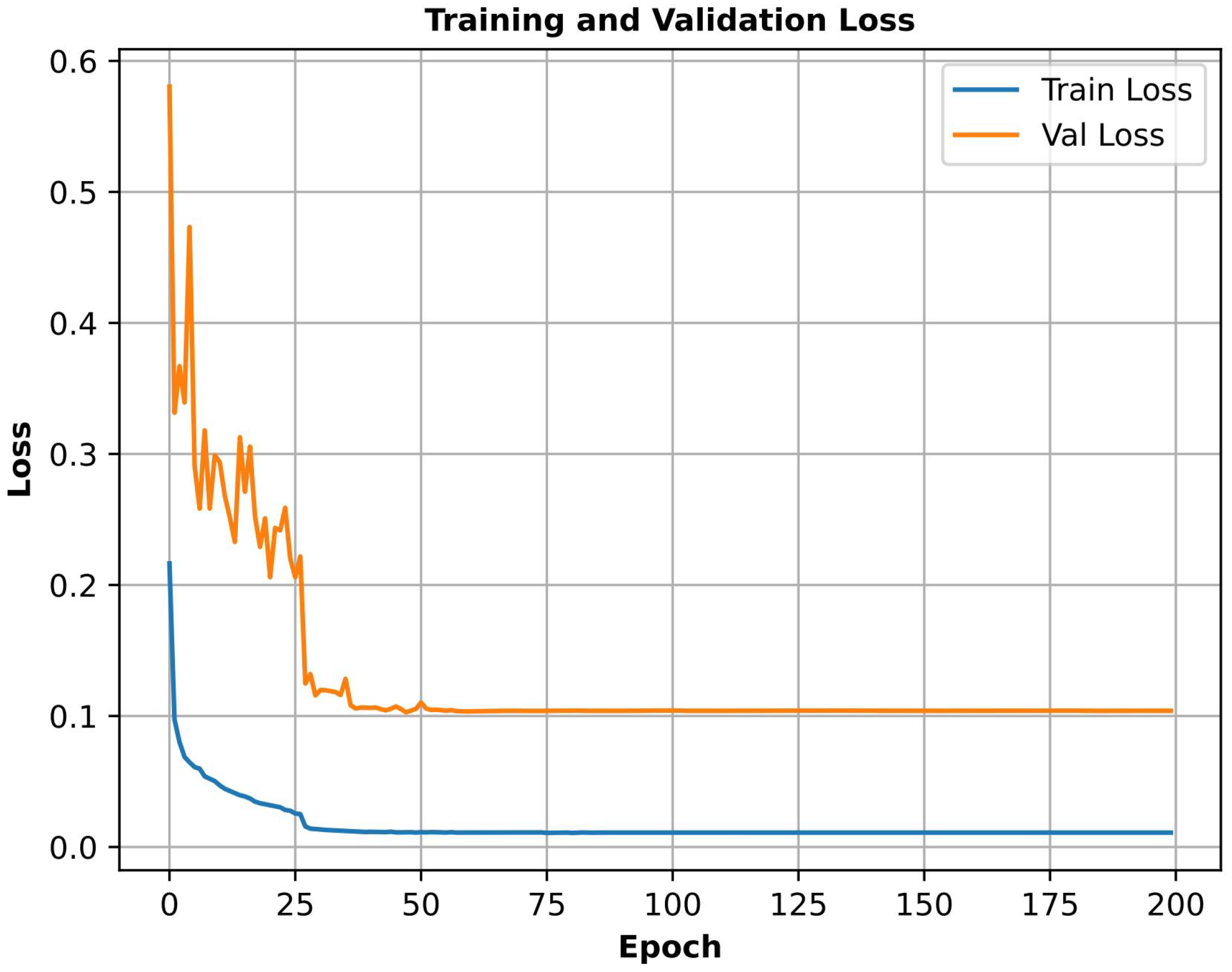
2.3.2. Experiment Configuration
3. Results
- LSTM and Transformer are classic methods for time-series forecasting. LSTM enhances long-term memory ability through the gating mechanism. Transformer, which is based on the attention mechanism, can directly model dependencies and allows for greater parallelization.
- STGCN, ASTGNN, and SGCN are advanced spatiotemporal forecasting methods that integrate both spatial and temporal information. STGCN employs a 1D CNN for temporal modeling and a GCN for spatial modeling, with a fixed graph structure. ASTGNN utilizes a Transformer for temporal modeling and a graph attention convolutional network (GAN) for spatial modeling, dynamically constructing the graph structure based on node information. SGCN leverages GANs for both spatial and temporal modeling, capturing sparse and directional interactions between nodes.
- EGRU and ETPNet are designed for mesoscale eddy trajectory forecasting. EGRU utilizes the GRU framework from MesoGRU [15], with data processing aligned to the approach presented in this study, and is referred to as EGRU. ETPNet incorporates ocean current data into the LSTM gating units as the “physical constraint”. In the experiment, the dataset described in Section 2.1 is uniformly used.
4. Discussion
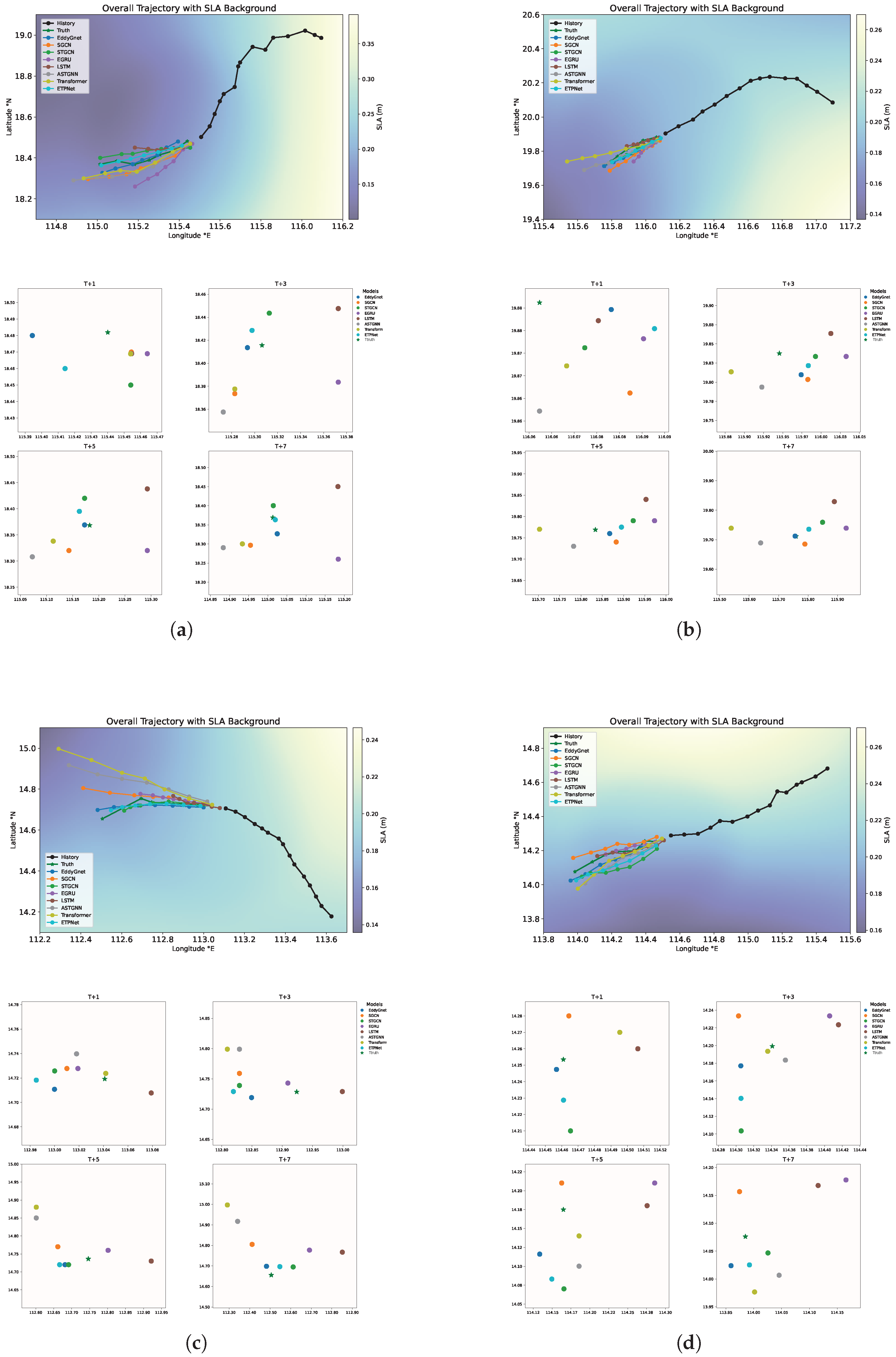
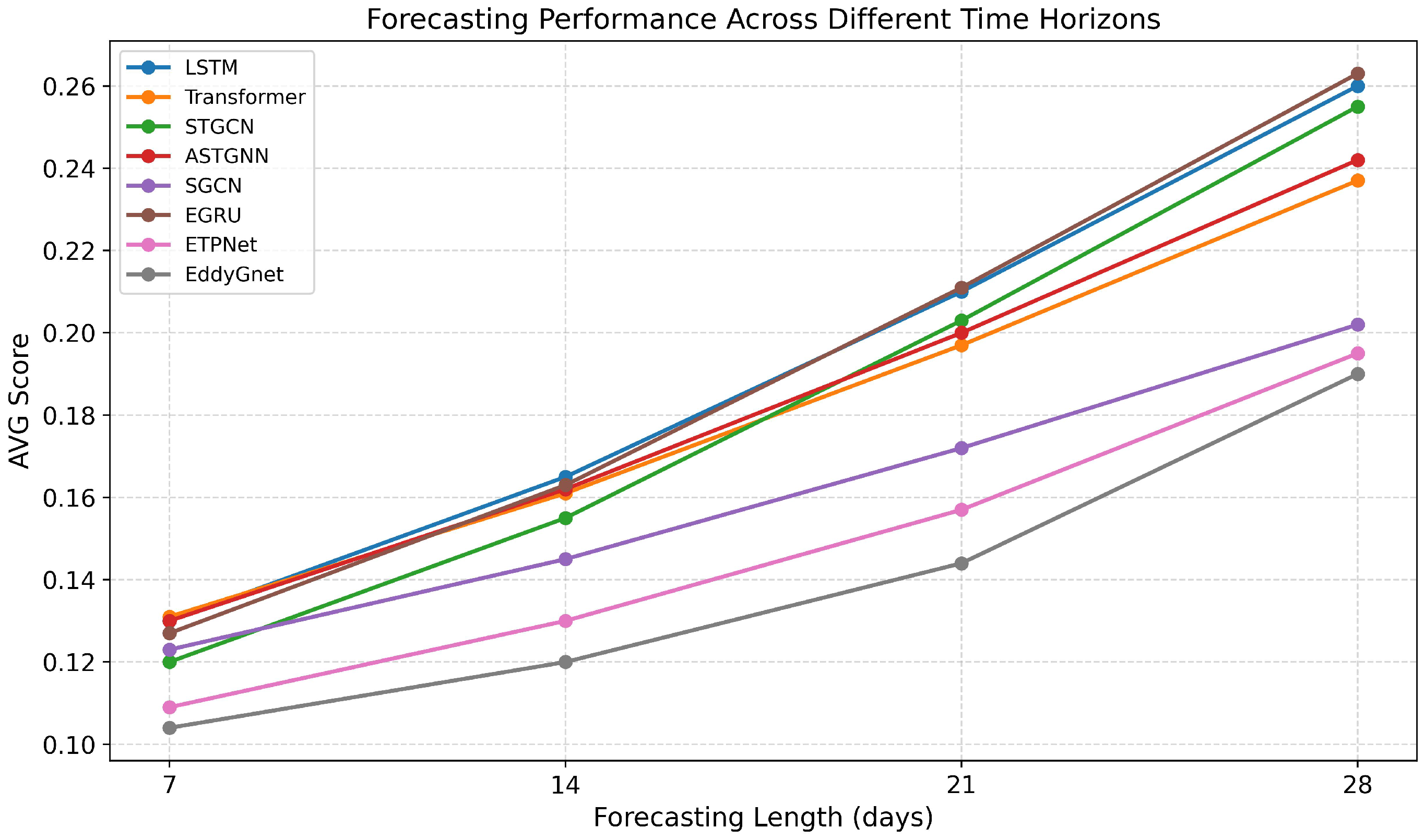
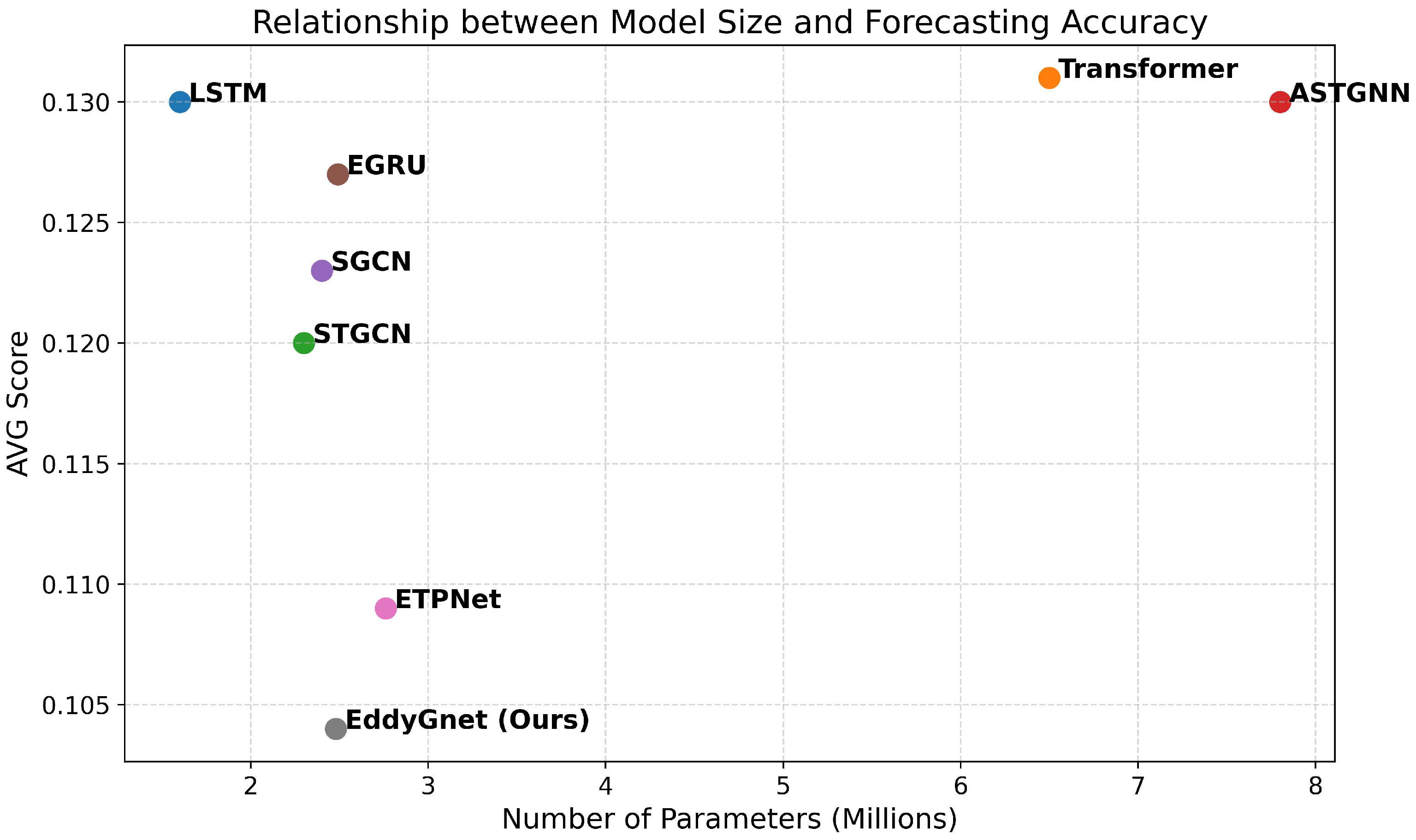
4.1. Performance Analysis
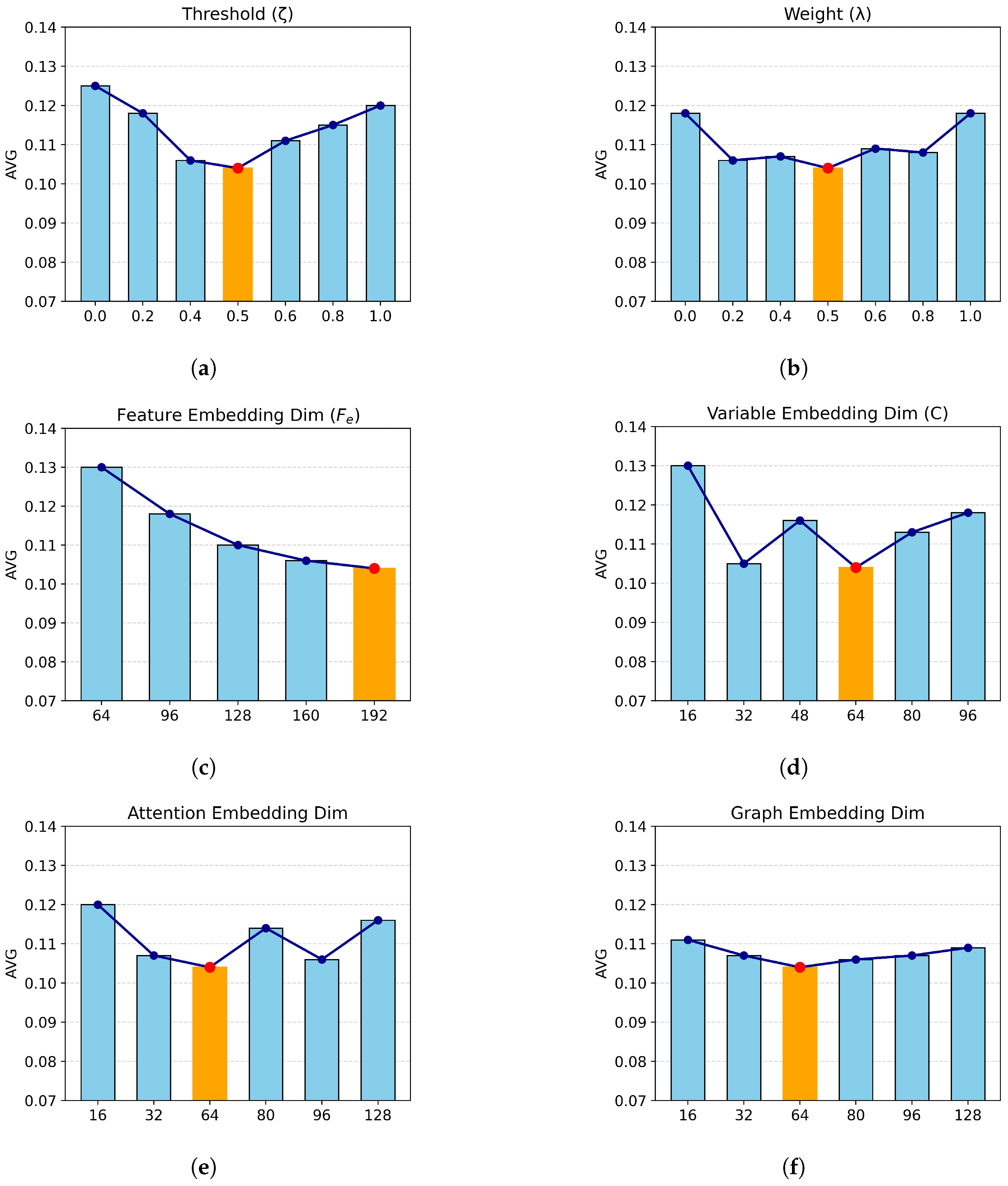
4.2. Parameter Sensitivity Analysis
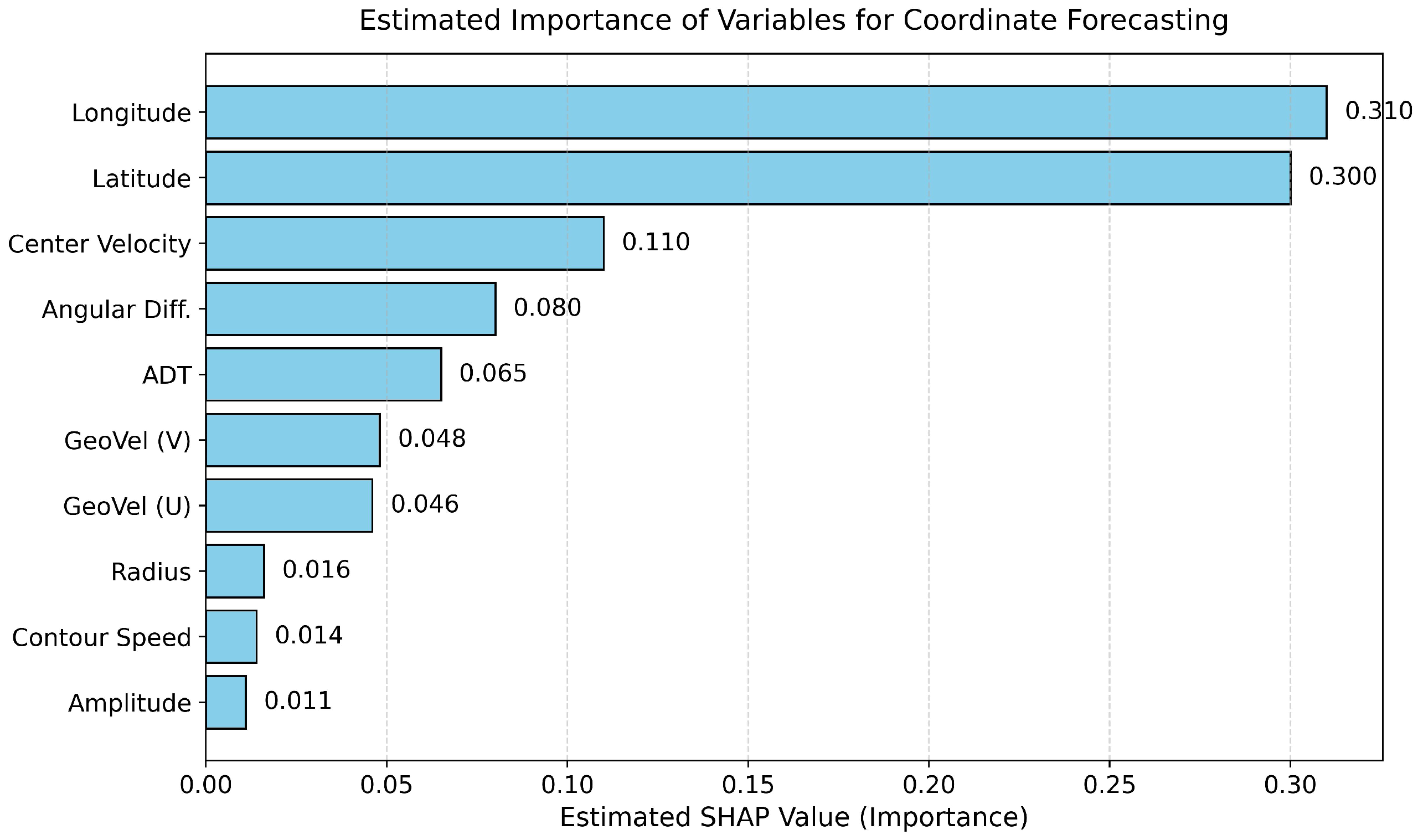
4.3. Ablation Study
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MAG | multivariable association graph |
| STEAG | spatiotemporal eddy association graph |
| GLN | Graph Learning Network |
| DVLoss | decayed volatility loss function |
References
- Morrow, R.; Church, J.; Coleman, R.; Chelton, D.; White, N. Eddy momentum flux and its contribution to the Southern Ocean momentum balance. Nature 1992, 357, 482–484. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, G. The effects of eddy size on the sea surface heat flux. Geophys. Res. Lett. 2021, 48, e2021GL095687. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Qiu, B. Oceanic mass transport by mesoscale eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Han, G. Contrasting short-lived with long-lived mesoscale eddies in the global ocean. J. Geophys. Res. Oceans 2019, 124, 3149–3167. [Google Scholar] [CrossRef]
- Martínez-Moreno, J.; Hogg, A.M.; England, M.H.; Constantinou, N.C.; Kiss, A.E.; Morrison, A.K. Global changes in oceanic mesoscale currents over the satellite altimetry record. Nat. Clim. Change 2021, 11, 397–403. [Google Scholar] [CrossRef]
- van Westen, R.M.; Dijkstra, H.A. Ocean eddies strongly affect global mean sea-level projections. Sci. Adv. 2021, 7, eabf1674. [Google Scholar] [CrossRef] [PubMed]
- Beech, N.; Rackow, T.; Semmler, T.; Danilov, S.; Wang, Q.; Jung, T. Long-term evolution of ocean eddy activity in a warming world. Nat. Clim. Change 2022, 12, 910–917. [Google Scholar] [CrossRef]
- Horvat, C.; Tziperman, E.; Campin, J.M. Interaction of sea ice floe size, ocean eddies, and sea ice melting. Geophys. Res. Lett. 2016, 43, 8083–8090. [Google Scholar] [CrossRef]
- Goldstein, E.D.; Pirtle, J.L.; Duffy-Anderson, J.T.; Stockhausen, W.T.; Zimmermann, M.; Wilson, M.T.; Mordy, C.W. Eddy retention and seafloor terrain facilitate cross-shelf transport and delivery of fish larvae to suitable nursery habitats. Limnol. Oceanogr. 2020, 65, 2800–2818. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; de Szoeke, R.A. Global observations of large oceanic eddies. Geophys. Res. Lett. 2007, 34, L15606. [Google Scholar] [CrossRef]
- Shriver, J.; Hurlburt, H.E.; Smedstad, O.M.; Wallcraft, A.J.; Rhodes, R.C. 1/32 real-time global ocean prediction and value-added over 1/16 resolution. J. Mar. Syst. 2007, 65, 3–26. [Google Scholar] [CrossRef]
- Masina, S.; Pinardi, N. Mesoscale data assimilation studies in the Middle Adriatic Sea. Cont. Shelf Res. 1994, 14, 1293–1310. [Google Scholar] [CrossRef]
- Ma, C.; Li, S.; Wang, A.; Yang, J.; Chen, G. Altimeter observation-based eddy nowcasting using an improved Conv-LSTM network. Remote Sens. 2019, 11, 783. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Liu, D.; Wang, W. The prediction of oceanic mesoscale eddy properties and propagation trajectories based on machine learning. Water 2020, 12, 2521. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Yu, M.; Li, C.; Song, D.; Ren, P.; Wu, J. MesoGRU: Deep learning framework for mesoscale eddy trajectory prediction. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Nian, R.; Cai, Y.; Zhang, Z.; He, H.; Wu, J.; Yuan, Q.; Geng, X.; Qian, Y.; Yang, H.; He, B. The identification and prediction of mesoscale eddy variation via memory in memory with scheduled sampling for sea level anomaly. Front. Mar. Sci. 2021, 8, 753942. [Google Scholar] [CrossRef]
- Wang, X.; Li, C.; Wang, X.; Tan, L.; Wu, J. Spatio–temporal attention-based deep learning framework for mesoscale eddy trajectory prediction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3853–3867. [Google Scholar] [CrossRef]
- Ge, L.; Huang, B.; Chen, X.; Chen, G. Medium-range trajectory prediction network compliant to physical constraint for oceanic eddy. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4206514. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, B.; Chen, G.; Ge, L.; Radenkovic, M.; Hou, G. Global oceanic mesoscale eddies trajectories prediction with knowledge-fused neural network. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4205214. [Google Scholar] [CrossRef]
- Tang, H.; Lin, J.; Ma, D. Direct prediction for oceanic mesoscale eddy geospatial distribution through prior statistical deep learning. Expert Syst. Appl. 2024, 249, 123737. [Google Scholar] [CrossRef]
- Long, S.; Tian, F.; Ma, Y.; Cao, C.; Chen, G. “Gear-like” process between asymmetric dipole eddies from satellite altimetry. Remote Sens. Environ. 2024, 314, 114372. [Google Scholar] [CrossRef]
- Graves, A.; Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Raksincharoensak, P.; Hasegawa, T.; Nagai, M. Motion planning and control of autonomous driving intelligence system based on risk potential optimization framework. Int. J. Automot. Eng. 2016, 7, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social lstm: Human trajectory prediction in crowded spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 961–971. [Google Scholar]
- Vaswani, A. Attention is all you need. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. arXiv 2017, arXiv:1709.04875. [Google Scholar]
- Guo, S.; Lin, Y.; Wan, H.; Li, X.; Cong, G. Learning dynamics and heterogeneity of spatial-temporal graph data for traffic forecasting. IEEE Trans. Knowl. Data Eng. 2021, 34, 5415–5428. [Google Scholar] [CrossRef]
- Shi, L.; Wang, L.; Long, C.; Zhou, S.; Zhou, M.; Niu, Z.; Hua, G. SGCN: Sparse graph convolution network for pedestrian trajectory prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8994–9003. [Google Scholar]
- Shen, L.; Wei, Y.; Wang, Y. GBT: Two-stage transformer framework for non-stationary time series forecasting. Neural Netw. 2023, 165, 953–970. [Google Scholar] [CrossRef] [PubMed]
- Chlorophyll, O. The Influence of Nonlinear Mesoscale Eddies on Near-Surface. Science 2011, 1208897, 334. [Google Scholar]
- Faghmous, J.H.; Frenger, I.; Yao, Y.; Warmka, R.; Lindell, A.; Kumar, V. A daily global mesoscale ocean eddy dataset from satellite altimetry. Sci. Data 2015, 2, 150028. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Abernathey, R. A global Lagrangian eddy dataset based on satellite altimetry. Earth Syst. Sci. Data Discuss. 2023, 15, 1765–1778. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2017; Volume 30, pp. 4768–4777. [Google Scholar]





| Model | MAE | MSE | ADE | FDE | AVG |
|---|---|---|---|---|---|
| LSTM [22] | 0.120 | 0.058 | 0.150 | 0.192 | 0.130 |
| Transformer [26] | 0.124 | 0.047 | 0.149 | 0.204 | 0.131 |
| STGCN [27] | 0.121 | 0.044 | 0.139 | 0.177 | 0.120 |
| ASTGNN [28] | 0.123 | 0.047 | 0.147 | 0.203 | 0.130 |
| SGCN [29] | 0.113 | 0.038 | 0.145 | 0.196 | 0.123 |
| EGRU [15] | 0.119 | 0.049 | 0.147 | 0.191 | 0.127 |
| ETPNet [18] | 0.095 | 0.039 | 0.125 | 0.179 | 0.109 |
| EddyGnet (Ours) | 0.093 | 0.021 | 0.124 | 0.179 | 0.104 |
| Model | 8 km | 9 km | 10 km | 11 km | 12 km | 13 km | 14 km | 15 km |
|---|---|---|---|---|---|---|---|---|
| LSTM | 0 | 1 | 2 | 3 | 3 | 3 | 3 | 4 |
| Transformer | 0 | 0 | 1 | 1 | 2 | 3 | 3 | 3 |
| STGCN | 0 | 0 | 1 | 2 | 2 | 5 | 6 | 7 |
| ASTGNN | 0 | 0 | 2 | 3 | 3 | 3 | 3 | 4 |
| SGCN | 0 | 0 | 2 | 3 | 4 | 4 | 4 | 4 |
| EGRU | 1 | 1 | 2 | 3 | 3 | 3 | 4 | 4 |
| ETPNet | 0 | 1 | 2 | 3 | 4 | 4 | 5 | 6 |
| EddyGnet | 1 | 1 | 2 | 3 | 4 | 4 | 6 | 7 |
| Model | Params (M) | Train Time (s/Epoch) | Inference Time (ms/Sample) | AVG Score | Train Time × AVG |
|---|---|---|---|---|---|
| LSTM | 1.6 | 28 | 84 | 0.13 | 3.64 |
| Transformer | 6.5 | 61 | 87 | 0.131 | 7.99 |
| STGCN | 2.3 | 35 | 32 | 0.12 | 4.2 |
| ASTGNN | 7.8 | 72 | 89 | 0.13 | 9.36 |
| SGCN | 2.4 | 62 | 41 | 0.123 | 7.63 |
| EGRU | 2.49 | 85 | 79 | 0.127 | 10.8 |
| ETPNet | 2.76 | 82 | 91 | 0.109 | 8.94 |
| EddyGnet (Ours) | 2.48 | 68 | 85 | 0.104 | 7.07 |
| Variants | MAE | MSE | ADE | FDE | AVG |
|---|---|---|---|---|---|
| wo/MAG Learning | 0.110 | 0.034 | 0.139 | 0.189 | 0.118 |
| wo/Embedding | 0.094 | 0.025 | 0.126 | 0.184 | 0.107 |
| wo/TGL | 0.100 | 0.025 | 0.130 | 0.182 | 0.109 |
| wo/EGL | 0.095 | 0.022 | 0.125 | 0.179 | 0.105 |
| w/L2 | 0.099 | 0.030 | 0.131 | 0.189 | 0.112 |
| EddyGnet (Ours) | 0.093 | 0.021 | 0.124 | 0.179 | 0.104 |
| Variants | MAE | MSE | ADE | FDE | AVG | Train Time (s/Epoch) | Inference Time (ms) |
|---|---|---|---|---|---|---|---|
| w/TCN | 0.096 | 0.025 | 0.125 | 0.180 | 0.107 | 55 | 32 |
| w/Informer | 0.115 | 0.042 | 0.139 | 0.182 | 0.120 | 61 | 47 |
| w/LSTM + TCN | 0.094 | 0.024 | 0.124 | 0.180 | 0.106 | 64 | 58 |
| EddyGnet (Ours) | 0.093 | 0.021 | 0.124 | 0.179 | 0.104 | 68 | 85 |
| Variant | MAE | MSE | ADE | FDE | AVG |
|---|---|---|---|---|---|
| w/o ADT | 0.096 | 0.025 | 0.129 | 0.184 | 0.109 |
| w/o GeoVel (u/v) | 0.097 | 0.026 | 0.130 | 0.185 | 0.110 |
| w/o All Physics | 0.099 | 0.028 | 0.132 | 0.189 | 0.112 |
| EddyGnet (Ours) | 0.093 | 0.021 | 0.124 | 0.179 | 0.104 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Y.; Zhang, B.; Wang, J.; Qian, Z.; Song, W. Modeling Multivariable Associations and Inter-Eddy Interactions: A Dual-Graph Learning Framework for Mesoscale Eddy Trajectory Forecasting. Remote Sens. 2025, 17, 2524. https://doi.org/10.3390/rs17142524
Du Y, Zhang B, Wang J, Qian Z, Song W. Modeling Multivariable Associations and Inter-Eddy Interactions: A Dual-Graph Learning Framework for Mesoscale Eddy Trajectory Forecasting. Remote Sensing. 2025; 17(14):2524. https://doi.org/10.3390/rs17142524
Chicago/Turabian StyleDu, Yanling, Bin Zhang, Jian Wang, Zhenli Qian, and Wei Song. 2025. "Modeling Multivariable Associations and Inter-Eddy Interactions: A Dual-Graph Learning Framework for Mesoscale Eddy Trajectory Forecasting" Remote Sensing 17, no. 14: 2524. https://doi.org/10.3390/rs17142524
APA StyleDu, Y., Zhang, B., Wang, J., Qian, Z., & Song, W. (2025). Modeling Multivariable Associations and Inter-Eddy Interactions: A Dual-Graph Learning Framework for Mesoscale Eddy Trajectory Forecasting. Remote Sensing, 17(14), 2524. https://doi.org/10.3390/rs17142524






