Abstract
To address the persistent computational bottlenecks in point cloud registration, this paper proposes a hierarchical grouping strategy named HiGoReg. This method incrementally updates the pose of the source point cloud via a hierarchical mechanism, while adopting a grouping strategy to efficiently conduct recursive parameter estimation. Instead of operating on high-dimensional matrices, HiGoReg leverages previous group estimates and current observations to achieve precise alignment with reduced computational overhead. The method’s effectiveness was validated using both simulated and real-world datasets. The results demonstrate that HiGoReg attains comparable accuracy to traditional batch solutions while significantly improving efficiency, achieving up to 99.79% speedup. Furthermore, extensive experiments confirmed that optimal performance is achieved when each group contains approximately 100 observations. In contrast, excessive grouping could undermine computational efficiency.
1. Introduction
Owing to its exceptional efficiency and precision in data acquisition, point cloud data obtained through three-dimensional (3D) laser scanners has found widespread application across various domains, including autonomous driving [1], deformation monitoring [2], industrial inspection [3], and 3D reconstruction [4]. Despite notable progress in acquisition techniques, the massive volume of collected data presents ongoing challenges for point cloud registration (PCR), particularly in terms of computational efficiency and parameter estimation accuracy [5,6,7,8,9].
PCR arises from the inherent limitation whereby a single scan typically fails to capture complete information about a target object or scene. To obtain a comprehensive representation, multiple point clouds acquired from different viewpoints, at different times, or using different sensors may be integrated. The primary goal of PCR is to spatially align these datasets by estimating a six-degree-of-freedom (6-DOF) transformation between the source and target point clouds.
Considerable efforts have been devoted to designing PCR approaches that jointly address efficiency, reliability, and structural integrity [10,11]. One fundamental approach to this problem is the reduction of data volume while retaining essential geometric and structural features. Recently, adaptive downsampling strategies have been investigated in this regard. For instance, Xu et al. [12] introduced the Box Improved Moving Average (BIMA) method, which dynamically adjusts the downsampling window size based on local point density variations, enabling efficient and adaptive data simplification. Complementing this, Lyu et al. [13] proposed a dynamic voxel-filtering algorithm that integrates edge-aware mechanisms to preserve salient structural details during the downsampling process, thereby maintaining the fidelity of critical geometric features.
In addition to data simplification, efficient and robust feature extraction methods are paramount for reducing the computational burden during registration. Contemporary advances in feature extraction for PCR fall into two main strategies. The first leverages geometric projections to utilize structural regularities within 3D data. For example, Tao et al. [14] projected point clouds onto a horizontal plane, extracting precise feature points at structural line intersections. This reduced the problem to 2D transformation estimation, which was later combined with vertical displacement to restore full 3D alignment, effectively lowering computational complexity while maintaining accuracy. The second strategy emphasizes robust descriptor design to capture salient, scale-invariant features in 3D space. Yang et al. [15] applied 3D Scale-Invariant Feature Transform (3D-SIFT) descriptors, which ensured scale robustness and reduced the number of points involved in registration without sacrificing precision.
To accelerate feature-matching, histogram-based descriptors have gained widespread adoption. Dong et al. [16] presented a novel 3D Binary Shape Context (BSC) descriptor that encodes local surface geometry through binary spatial histograms, optimizing parameter settings to balance descriptiveness and efficiency. The Fast Point Feature Histogram (FPFH) method introduced by Rusu et al. [17] significantly reduces computational complexity by computing Simplified Point Feature Histograms (SPFHs) within local neighborhoods and applying weighted fusion, bringing the complexity down to . Building on this foundation, Lim et al. [18] enhanced the approach by employing k-kernel based graph-theoretic pruning techniques to efficiently reject outlier correspondences, thereby improving both robustness and speed. Furthermore, Yan et al. [19] applied a graph-based correspondence optimization strategy that assessed the reliability of correspondence graphs by integrating both loose and compact constraint functions. This combined framework streamlines computation, enabling fast and robust PCR even in challenging conditions.
While many efforts focus on algorithmic enhancements, hardware-based acceleration techniques have likewise contributed significantly to runtime performance. Chang et al. [20] demonstrated the effectiveness of graphics processing unit (GPU) parallel processing to accelerate nearest neighbor searches, a key bottleneck in many registration pipelines, enabling substantial runtime reductions, especially for large-scale point clouds.
Once a set of (relatively) accurate point correspondences has been established—either through handcrafted features, learning-based matching, or geometric constraints—the next critical step is to estimate the transformation parameters that best align the source and target point clouds. This parameter estimation process lies at the core of most PCR pipelines and directly affects the final alignment accuracy.
Conventionally, PCR is formulated as an optimization problem. To achieve more accurate alignment, Besl and McKay [21] introduced the Iterative Closest Point (ICP) algorithm, which minimizes the sum of squared Euclidean distances between corresponding closest points. The rigid transformation parameters—rotation and translation—are typically estimated using the Singular Value Decomposition (SVD) method [22], which offers a closed-form solution with favorable numerical stability and computational efficiency. Despite its simplicity and widespread use, ICP is sensitive to initial alignment conditions and the efficiency of the nearest neighbor search process [23]. To address these limitations, numerous improvements have been proposed to enhance its robustness, accuracy, and convergence characteristics [24,25,26].
In parallel with optimization-based approaches, more rigorous mathematical model-based techniques, such as Least Squares Matching (LSM) based on the Gauss–Markov (GM) model, can further optimize parameter estimation [27,28,29]. Originating from the problem of image patch-matching in photogrammetry, Gruen et al. [30] expanded LSM to handle 3D point cloud data, called LS3D. Akca [31] highlighted the ability of LS3D to handle the surface matching of diverse qualities and resolutions by contending with surface modeling errors to ensure model flexibility and accuracy. The mathematical model of LS3D only allows for the random errors in the target point cloud but omits the error factors in the source point cloud. This one-sided error sensitivity approach is incapable of comprehensively capturing and dealing with all possible potential error sources affecting the adjustment accuracy.
The Errors-In-Variables (EIV) model can account for random errors in both source and target point clouds [32] and is typically solved via the Total Least Squares (TLS) method. While offering improved parameter accuracy, its applications are always limited by repeated variables or fixed elements, which can lead to a singular variance–covariance matrix [9]. With the advancement of research, the nonlinear Gauss–Helmert (GH) model emerged as a prevailing framework that uniformly considers all errors in the observation space, regardless of whether they stem from the observations or the design matrices [33]. Wang et al. [34,35] proposed a point cloud fitting approach grounded in the Gauss–Helmert model, yielding highly accurate parameter estimates. Vogel et al. [36] applied the recursive GH model (RGH) to the system calibration of scanners. In the context of PCR, Ge and Wunderlich [37] introduced the GH-LS3D method, which demonstrated superior estimation accuracy compared to the traditional ICP algorithm. Zhao et al. [9] adopted quaternions to represent rotational parameters and utilized sensitivity analysis to construct test statistics, enabling the effective identification of outliers and thus improving registration accuracy. Furthermore, some methods enhanced registration accuracy by imposing constraint conditions based on known prior information of parameters based on the GH model [38]. Beyond the aforementioned efforts, researchers have further investigated the enhancement of parameter estimation accuracy through diverse approaches, such as feature extraction [39,40], geometric representation [41,42], matching strategies [43,44,45], and the integration of physical attributes [46,47].
Invariably, the above methods adopt a batch estimation framework that incorporates all features simultaneously into the mathematical model. This results in a computational complexity of , limiting scalability in large-scale scenarios. For the specific details, refer to the contents in Table 1. High-performance computing platforms can partially alleviate this burden [48,49], but they come with trade-offs such as higher deployment costs, increased energy consumption, and greater system complexity. More importantly, such hardware-based solutions do not reduce the algorithm’s intrinsic complexity, they merely offset it through brute-force computation. Therefore, beyond optimizing peripheral components, it is essential to rethink the core structure of registration algorithms to achieve true scalability.

Table 1.
A comparison of 3D point cloud registration function models covering mathematical formulations, time complexity, and application constraints.
Recently, deep learning-based PCR methods have gained considerable attention due to their high accuracy in parameter estimation and strong inference capabilities [3,11,55,56,57]. Despite these advantages, several challenges remain. These methods often exhibit sensitivity to hyperparameter tuning, require large volumes of labeled data, and struggle to generalize effectively to unseen scenarios. Moreover, they typically involve substantial computational costs and prolonged training times.
Thus, while many studies boost early-stage computational efficiency, the adjustment process for registration parameter estimation stays slow, failing to break the core computational bottleneck in algorithm design. Hence, under the premise of ensuring stable and reliable results, further reducing PCR parameter estimation time remains a pressing issue.
In this paper, a novel PCR methodology rooted in the hierarchical grouping framework is presented with the designation HiGoReg. Here, “hierarchical” emphasizes the iterative parameter estimation used to refine the progress of the source point cloud pose tuning, whereas “grouping” involves the systematic division of observations into groups within a single layer. Drawing inspiration from the effectiveness of Recursive Least Squares (RLS) in filtering contexts [58,59,60,61,62] and the solid performance of the GH model, our objective is to harmoniously blend their respective strengths. The proposed method not only guarantees the accuracy of the results, which is consistent with the batch solution (BS), but also significantly improves the computational time cost. Specifically, the filtered point pairs are first divided into groups by slicing. For the first group, a linearized version of the GH model is used to estimate the parameters. Subsequently, the parameter estimates and parameter cofactor matrices of the previous group, as well as the observations of the current group, are modeled together to predict new parameter values, facilitating a seamless association between groups. Since the amount of data involved in the computation of each group is significantly reduced, large dimensional matrix operations are avoided. But do more groups yield more benefits? By investigating different grouping sizes, we explored the mystery of “moderate grouping” and endeavored to find the optimal spot for balancing accuracy and efficiency. In summary, our main contributions include the following:
- 1.
- The random errors present in all measurements are taken into account in the functional model, resulting in a more rigorous treatment of the observations with higher robustness.
- 2.
- Compared with the batch solution, the proposed PCR method based on the hierarchical grouping strategy substantially improves the efficiency of parameter estimation while ensuring consistent parameter estimation results.
- 3.
- The effects of two commonly used stochastic models on parameter estimation accuracy and computational efficiency are explored.
- 4.
- We introduce the concept of optimal grouping, and give the value of the number of groups under the minimum computation time through plentiful experiments.
This paper is structured as follows: Section 2 introduces HiGoReg, detailing its mathematical foundations, key formulas, and computational process. Section 3 presents experiments of the algorithm using simulated and measured data. In Section 4, we present the computational results of the proposed method in comparison with existing approaches. Section 5 further analyzes these results to explore underlying patterns and method characteristics, while Section 6 summarizes findings and addresses limitations.
2. Methodology
Compared to the traditional batch solution, which incorporates all qualified observations into the mathematical model for parameter estimation, HiGoReg updates the parameters by relying solely on the parameter estimates of the previous group and combining them with the observation data (and random information) of the current group. If the convergence fails, the updated parameter estimates are taken as the initial values for the first group, and the iteration continues until convergence is achieved or the maximum number of iterations is reached. The whole pipeline is presented in Figure 1.

Figure 1.
The pipeline of the proposed methodology.
2.1. Batch Solution
Random errors arising from sensor noise and environmental variations affect both the target surface and the search surface , represented by and , respectively. With the aid of the transformation parameters, the registration function model for the ith surface element based on the GH model can be formulated as
where is the translation parameter vector, ; is the rotation matrix, .
To perform the TLS estimation, suitable initial values are introduced of the transformation parameter vector () and the random error vectors (, ), indicated by the superscript 0, namely, (). Equation (1) is then linearized by Taylor series:
where , , , , and .
Then, Equation (2) can be rewritten as
where , , .
Further, for all n point pairs, we have
where , , , ⊗ denotes the Kronecker inner product, , and .
For the error vector ,
where and signify the cofactor matrix and the weight matrix, respectively, and is the unit weight variance.
Based on the principle of least squares and the linearized observation equation, the Lagrangian objective function is formulated. By applying the necessary conditions for optimality, the parameter estimates can be obtained:
where , and the predicted values of the respective random errors are
The above solution process needs to be carried out iteratively to gradually approach the optimal estimate [35,63]. In Equations (6)–(8), the vector has a dimension of , with being a matrix of size , a vector of size , the coefficient matrix having dimensions , the global covariance factor matrix with dimensions , a matrix of size , and the final calculated result being a vector of dimension . This underscores the inherent high-dimensional nature of the matrices involved. Given that n can potentially scale to hundreds of thousands, tens of millions, or even more, the computational demands for parameter estimation tasks are significantly heightened. To mitigate this challenge, the following section introduces our novel and efficient PCR method.
2.2. Hierarchical Grouping Solution
Assuming that the data are divided into m groups of different observation vectors, each containing at least 3 pairs of points, the grouping of these vectors and the corresponding stochastic model are described below:
where v, u denote numerical values and satisfy .
Concerning Equations (4) and (9) as our theoretical backbone, for two adjacent groups, labeled as the k − 1 and k, we have
The corresponding stochastic models are
Based on Section 2.1, the batch solution for both sets of data can thus be stated as
where
Then, for group k − 1, its solution follows:
The cofactor matrix of the batch solution for the two sets of data is
Consequently, Equation (12) can be reorganized as
By substituting from Equation (17) into Equation (16),
and subsequently incorporating the resulting expression into Equation (15), we can derive the fundamental solution of the HiGoReg method:
Upon scrutinizing the preceding equation, it becomes evident that the batch solution for two sequential datasets can be efficiently attained by leveraging the computational outcomes of the current dataset in conjunction with those from the preceding one. Nevertheless, a hindrance arises in the form of the elusive matrix present in Equation (19). To circumvent this obstacle and establish a recursive linkage for the covariance matrices associated with the parameter vectors across adjacent groups, we meticulously multiply both sides of Equation (17) by from the left and from the right. Consequently, the recursive relationship for the covariance matrices of the parameter vectors spanning the (k−1)th and kth groups is elegantly formulated as follows:
According to the Woodbury matrix transformation formula [64], where is an invertible matrix, is an invertible matrix, , and are matrices with dimensions that ensure the operations within the formula are well-defined, the subsequent equation is valid:
Given and , and rewriting Equation (19), the final form of HiGoReg can thus be obtained:
here, , so that for the first group of data, one still needs to perform the computation using the batch solution, cf. Section 2.1. Then the a posterior unit-weight median error is
Based on the above derivation process, the systematic computational steps of HiGoReg are outlined in Algorithm A1 in Appendix B.
In practical applications, an insufficient number of observations within a group may result in rank deficiency. To avoid this, the minimum number of observations per group is typically determined by the number of parameters to be estimated. If rank deficiency still arises, additional point pairs can be randomly selected from other groups to supplement the deficient set. This is feasible because all point pairs share the same parameter structure. More commonly, observations within a group may exhibit strong linearity or planarity. This leads to an ill-conditioned coefficient matrix, compromising solution stability and accuracy. To address this, regularization methods such as ridge estimation [65] or Tikhonov regularization [66] could be introduced.
From Equations (12) and (24), the batch solution incurs a time complexity of approximately and a space complexity of [67,68], where n denotes the total number of points in the cloud. This high cost stems from the need to simultaneously process all pairwise correspondences by constructing and solving a large-scale matrix equation. In contrast, the HiGoReg alleviates computational burden through a grouping strategy combined with recursive estimation. The point cloud is divided into m groups, each containing a subset of the data, and processed in sequence. This reduces the time complexity to , indicating that a larger number of groups leads to smaller per-iteration data volumes and, thus, lower time costs. The space complexity is similarly reduced to , reflecting decreased memory usage per group. However, an excessively large m results in too few points per group, causing instability in matrix operations and potentially increasing the total computation time. Moreover, a greater number of iterations may raise memory demands due to intermediate result storage. Therefore, in practice, it is critical to select an appropriate number of groups. A well-balanced m can optimize the trade-off between per-iteration complexity and the total number of iterations, thereby maximizing the computational efficiency of HiGoReg.
3. Experiments
In this section, the proposed method is rigorously tested on both synthetic and real-world datasets. Its computational efficiency and parameter estimation accuracy are benchmarked against batch solution, with particular emphasis on diverse group configuration scenarios.
3.1. Simulation Experiment
To rigorously assess the efficacy of our method, we selected Bunny, Monkey, and Dragon point clouds from Stanford University’s publicly available point cloud dataset (http://graphics.stanford.edu/data/3Dscanrep/, accessed on 17 March 2025), as depicted in Figure 2. The target point cloud (in green) was realized by slight rotation and translation from the source point cloud (in red). Before solving for the transformation parameters, keypoints were first detected using the intrinsic shape signature (ISS) method [69]. This step significantly reduced the number of coordinates involved in the registration of the Bunny, Monkey, and Dragon point clouds from 35,947, 125,952, and 437,645 to a more manageable 330, 233, and 936, respectively. Subsequently, point correspondences were established and selected for parameter estimation. Following the picky ICP algorithm [70], only point pairs whose Euclidean distances were less than the mean value with median error were retained.
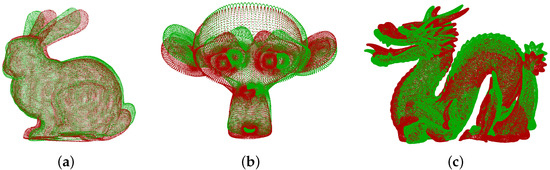
Figure 2.
Stanford point cloud dataset, where red indicates the source point cloud and green stands for the target point cloud. (a) Bunny; (b) Monkey; (c) Dragon.
Considering the limited number of points in the Stanford dataset and the dimensionality reduction resulting from ISS keypoint extraction, two additional synthetic point clouds were generated to simulate large-scale registration scenarios. Each synthetic point cloud contained 7000 corresponding keypoints. The source point cloud consisted of randomly distributed coordinates within the ranges , , and . The target point cloud was obtained by applying a rigid transformation to the source, characterized by Euler angles , , and and a translation vector . The simulated point clouds are illustrated in Figure 3.
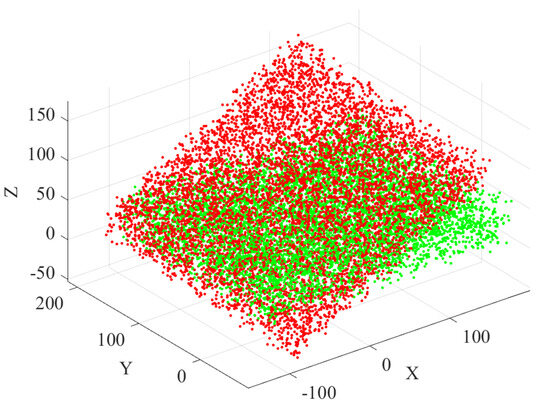
Figure 3.
Simulated large−scale point cloud dataset, where red indicates the source point cloud and green stands for the target point cloud.
Given the superior performance of GH, the GM model was excluded from further analysis (see [62] for details), and the comparison was focused on the following two approaches:
- Batch solution.
- HiGoReg method.
Due to the absence of instrument-specific details, all point cloud observations were equally weighted. Within the HiGoReg scheme, the point clouds from the Stanford dataset were segmented into 2, 3, 4, 5, and 6 groups, while the large-scale synthetic dataset was divided into 10, 20, 50, 100, and 200 groups, aiming for a balanced distribution of points across groups. As an illustrative example, dividing 330 points into four groups would yield an approximately uniform distribution of 83, 83, 83, and 81 points, respectively. During the registration phase, the number of iterations was conservatively set with a minimum of 5 and a maximum of 20. The hierarchical iteration process was terminated early if the difference between two successive Root Mean Squared Error (RMSE) values fell below a threshold of , as defined in Equation (28). Within each iteration, to solve for the nonlinear rotation and translation parameters, convergence was determined based on the thresholds and , respectively.
where is the abbreviation of point pairs.
All experiments and operations were executed on Matlab R2022a, hosted on a Windows 10 operating system, leveraging the Intel Core i9-10900K central processing unit (CPU) and 32 GB of random access memory (RAM). The visualized outcomes of the registration are presented in Figure 4, in which the registered source point clouds are depicted in blue. Each scheme with distinct groups was replicated 10 times, and the resulting efficiency statistics are displayed in Table 2 and Table 3 as well as Figure 5 and Figure 6. Additionally, in Table 2, we also compare the ground-truth values and the estimated transformation parameters through Equations (29) and (30) to get the rotation error and the translation error [71]. For all figures below, the label “BS” represents the batch solution results; “G2”∼“G200” represents group segments from 2 to 200, respectively.
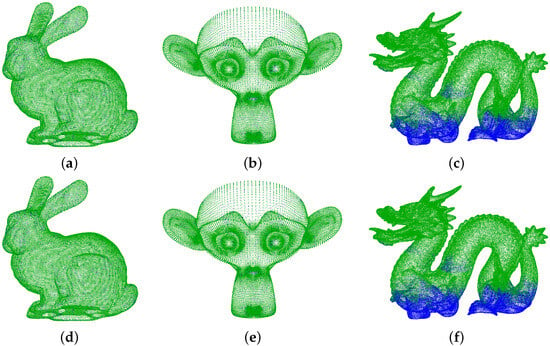
Figure 4.
Stanford point cloud dataset visualized registration results. (a) Bunny based on Batch solution; (b) Monkey based on Batch solution; (c) Dragon based on Batch solution; (d) Bunny based on HiGoReg method; (e) Monkey based on HiGoReg method; (f) Dragon based on HiGoReg method.

Table 2.
Simulated point cloud dataset registration results.

Table 3.
Time consumption of simulated dataset registration under their respective optimal group.
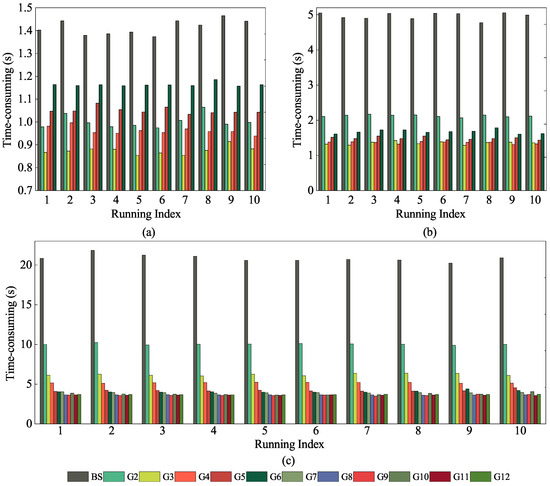
Figure 5.
Statistics on computing time cost of Stanford point cloud datasets under equal weighting. (a) Bunny; (b) Monkey; (c) Dragon. “Running index” denotes the index of execution counts, where each execution sequentially completed the batch solving process and HiGoReg algorithm workflows under different groups, with a total of 10 executions.
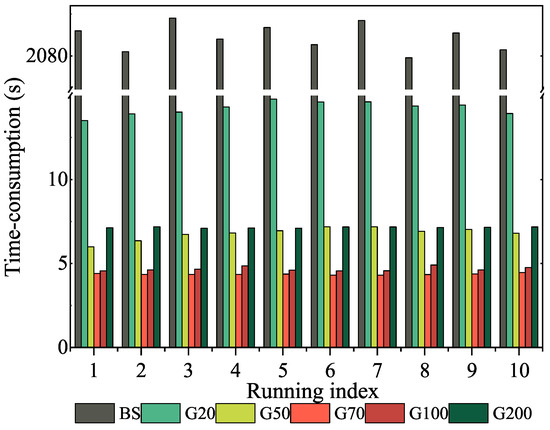
Figure 6.
Statistics on computing time cost of simulated large-scale dataset under equal weighting. “Running index” denotes the index of execution counts, where each execution sequentially completes the batch solving process and HiGoReg algorithm workflows under different groups, with a total of 10 executions.
3.2. Real-World Data Experiment
Under real conditions, the first experiment was implemented using the open-source dataset WHU-TLS proposed by [72]. We selected the subway station TLS data (https://github.com/WHU-USI3DV/WHU-TLS, accessed on 20 March 2025) as the registration object, which covers a scene with dimensions of 20 m in length and 11 m in width. In this case, as displayed in Figure 7, the source and target point clouds contained 5,092,812 and 6,094,880 points, respectively.

Figure 7.
Subway station point clouds from WHU-TLS. (a) Source point cloud; (b) target point cloud.
Another demonstration study was conducted using the self-collected point cloud data of a statue. For this work, a Faro Focus 3D X330 scanner (FARO Technologies Inc., Lake Mary, FL, USA) was engaged to acquire data from two different angles at a distance of about 7 m from the target. The scanner achieved excellent accuracy, with a distance accuracy of 0.4 mm and an angular resolution of 0.009°, ensuring high fidelity of the captured data. The source point cloud and target point cloud consisted of 32,546 and 27,894 points, respectively, as depicted in Figure 8.

Figure 8.
Point clouds of the statue. (a) Source point cloud; (b) target point cloud.
Before the experiment, meticulous preparations were performed: Considering the requirements of the Matlab platform for matrix dimensions, we first grid-sampled the original data; then, three points were carefully selected using the open-source CloudCompare software (version: 2.13.1, https://www.danielgm.net/cc/, accessed on 20 March 2024) to establish a quality initial pose for subsequent iterations. After ISS processing, the source and target point clouds in the subway station scene contained 3818 and 3943 feature points, respectively. In comparison, the statue scene yielded 344 and 367 feature points. Following the feature-matching process, the subway scene yielded 3698 and 1665 correspondences at voxel grid sizes of 0.03 m and 0.05 m, respectively. In contrast, the statue scene produced only 244 correspondences at a voxel size of 0.001 m.
As WHU-TLS did not provide the accuracy information of the scanner, only equal weighting for the stochastic model was carried out. On the other side, as for the statue, we introduced two commonly used stochastic models, namely, identity matrix (equal weighting) and nominal accuracy weighting, to evaluate their impacts on the HiGoReg registration results. After successful registration, for WHU-TLS, which supplied the ground-truth of parameters, we evaluated the parameters’ precision through Equations (29) and (30) similarly. The results of the visualized registration and efficiency statistics are illustrated in Table 4 and Figure 9 and Figure 10. The advanced 3D comparison module in Geomagic Studio 2012 software was then introduced to strictly analyze the overlapping area between the two point clouds of the statue, as shown in Figure 11. To validate efficiency, the above two registrations were repeated 10 times to ensure consistency and reliability, and the statistical results are shown in Table 5 and Figure 12.

Table 4.
Statistics on the results of the subway station point cloud registration.

Figure 9.
Registered subway station point clouds. (a) Batch solution; (b) HiGoReg.
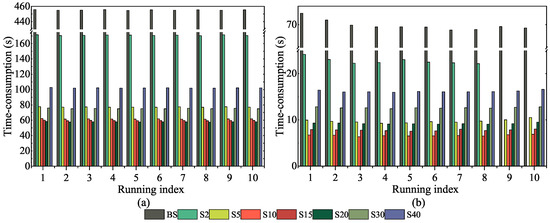
Figure 10.
Time cost of subway station point cloud registration. (a) Voxel size = 0.03 m; (b) voxel size = 0.05 m. “Running index” denotes the index of execution counts, where each execution sequentially completed the batch solving process and HiGoReg algorithm workflows under different groups, with a total of 10 executions.
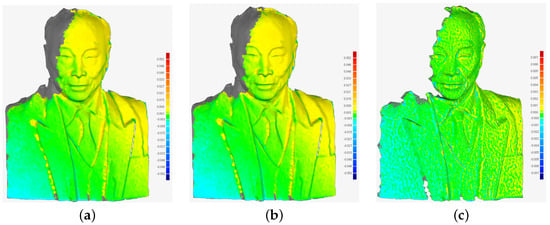
Figure 11.
Registration errors of HiGoReg under different stochastic models. (a) Equal weighting result against the target point cloud; (b) nominal accuracy result against the target point cloud; (c) equal weighting result against nominal accuracy result.

Table 5.
Statue point cloud registration results under different stochastic models.
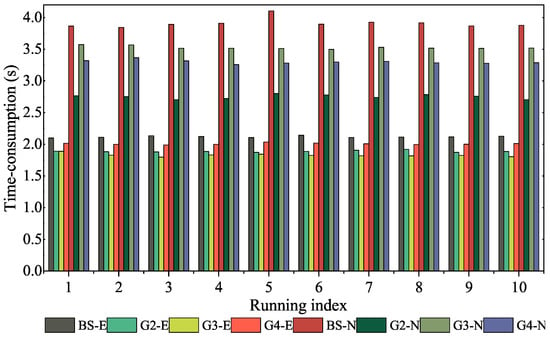
Figure 12.
Comparison of calculating efficiency of two schemes for statue point cloud data under different stochastic models. “Running index” denotes the index of execution counts, where each execution sequentially completed the batch solving process and HiGoReg algorithm workflows under different groups, with a total of 10 executions. The suffixes “E” and “N” indicate equal weighting and nominal accuracy weighting methods.
4. Results
The performance of the HiGoReg method was systematically evaluated through simulation and real-world experiments, focusing on verifying the effects of its registration accuracy, computational efficiency, and grouping configuration on the performance.
4.1. Simulated Datasets
4.1.1. Registration Accuracy Metrics
As visually illustrated in Figure 4, the registration results of HiGoReg and the batch solution were in agreement for the Stanford datasets. Table 2 presents a detailed comparison of accuracy metrics between the two methods across all simulated datasets. For the Bunny dataset, both methods yielded identical results, with an RMSE of , a posterior unit-weight standard deviation () of , a rotation error () of , and a translation error () of . Similarly, for the Monkey dataset, both approaches reported an RMSE of , of , of , and of . For the Dragon dataset, both methods also produced consistent results, with an RMSE of , of , of , and of . The large-scale synthetic dataset further confirmed this consistency: both methods achieved an RMSE of , of , of , and of . These results demonstrate that HiGoReg maintained accuracy comparable to the batch solution, even as the number of points in the point cloud increased.
4.1.2. Computational Efficiency
Table 3 illustrates that HiGoReg consistently delivered substantial speedups across all tested simulated datasets. Specifically, for the Bunny dataset, HiGoReg reduced the average runtime from 1.4151 s (using the batch method) down to 0.08748 s, which corresponded to an improvement of 38.18%. For the Monkey dataset, the runtime decreased from 4.9710 s to 1.3517 s, achieving a notable 72.81% acceleration. When processing the Dragon dataset, HiGoReg completed the task in 3.6131 s compared to the 20.8628 s required by the batch approach, resulting in a speedup of 82.68%. The largest gain was observed on the large-scale synthetic dataset: HiGoReg finished in just 4.3611 s, whereas the batch method took an overwhelming 2081.1157 s, yielding an exceptional 99.79% boost in efficiency. These results underscore HiGoReg’s pronounced advantage, especially when handling large-scale data. Besides the improvements in average values, similar enhancements were also observed in terms of maximum and minimum values.
As shown in Figure 5 and Figure 6, grouping observations significantly reduced computation time compared to the batch solution. However, as the number of groups increased, the runtime exhibited a U-shaped trend—initially decreasing and then increasing—due to the trade-off between per-group computation and recursive update overhead. This behavior allowed the optimal number of groups, corresponding to the highest computational efficiency, to be easily identified. The optimal group configuration varied across datasets. For the Bunny dataset, the best balance was achieved with three groups, while the Monkey dataset performed similarly with three or four groups. The Dragon dataset, which contained substantially more data, reached peak efficiency with nine groups. In the case of the large-scale synthetic dataset, the lowest runtime was observed when the number of groups was set to 70. Clearly, these represent their optimal numbers of groups.
4.2. Real-World Datasets
4.2.1. Registration Accuracy Metrics
As summarized in Table 4, HiGoReg and the batch method achieved identical registration accuracy on the WHU-TLS subway station dataset across varying voxel sizes, demonstrating the reliability of HiGoReg. At a voxel size of 0.03 m, both methods reached an RMSE of 0.0240 m, with a posterior unit-weight standard deviation of 0.0078 m, a rotation error of rad, and a translation error of 0.0041 m, confirming consistent and precise alignment. When the voxel size increased to 0.05 m, a marginal increase in RMSE (0.0243 m) and translation error (0.0044 m) was observed, along with a rise in the number of iterations from 5 to 6. This slight performance degradation was attributed to reduced feature quality due to the coarser voxel grid.
For the statue dataset, Table 5 further confirms the agreement between the two approaches under two different stochastic modeling strategies. Under equal weighting, both methods yielded identical accuracy metrics. When nominal accuracy weighting was applied to reflect scanner precision, a slight improvement in RMSE and posterior variance was observed (with only a 1% difference in RMSE, see Figure 11); nevertheless, the results remained consistent across methods. This similarity stemmed from the close proximity of the TLS to the target and the inherently high precision of the point cloud data, which diminished the influence of the weighting strategy on registration accuracy. These findings reinforce the robustness of HiGoReg under varying real-world noise and data conditions.
Compared with the simulation experiments, the registration error in the real-world dataset was relatively higher. This was primarily due to the presence of noise and occlusion in the real-world data, which could lead to missing regions and mismatched feature point pairs, thereby introducing additional errors into the matching process.
4.2.2. Computational Efficiency
In terms of computational efficiency, for the WHU-TLS subway dataset under a voxel size of 0.03 m, the batch solution required 454.66 s, whereas HiGoReg completed the registration in just 19.08 s under optimal grouping, approximately 4% of the batch runtime. At a voxel size of 0.05 m, the batch method took 71.93 s, while HiGoReg reduced this to 6.61 s, representing less than 10% of the original time. These results highlight the significant impact of high-dimensional matrix operations on computational cost in large-scale point cloud processing. As illustrated in Figure 10, similar to the simulation experiments, runtime was strongly influenced by the number of groups. When the data was divided into two groups, a noticeable improvement in efficiency was observed. Runtime continued to decrease until it reached a minimum at the optimal grouping configuration: 20 groups for the 0.03 m voxel case and 10 groups for the 0.05 m case. Beyond these points, increasing the number of groups led to longer runtimes due to overhead from excessive partitioning.
For the statue dataset (Table 5 and Figure 12), HiGoReg also demonstrated superior efficiency under optimal grouping. Compared to the average runtime of the batch solution, HiGoReg achieved a reduction of 13.69% under equal weighting and 29.65% under nominal accuracy weighting. Regarding the stochastic models, the equal weighting approach was significantly faster, primarily because inverting the identity matrix was computationally trivial. In contrast, nominal accuracy weighting required the inversion of a non-trivial covariance matrix, which incurred additional computational overhead.
5. Discussions
An in-depth interpretation of the experimental findings is here provided, with a focus on the influence of grouping strategies, weighting schemes, and inherent dataset characteristics on registration performance. The analysis aims to elucidate the underlying mechanisms responsible for the observed trends and offer practical insights into the scalability and applicability of the proposed method across diverse scenarios.
5.1. Impact of Grouping Strategy
The number of groups in the HiGoReg framework plays a critical role in balancing computational efficiency. By partitioning the dataset into smaller groups, the algorithm operates on lower-dimensional matrices, significantly reducing the computational cost associated with matrix inversion. However, this benefit does not scale indefinitely with increased group numbers. As the number of groups becomes excessively large, two key issues emerge. First, more frequent matrix operations—such as inversions and updates—accumulate computational overhead, offsetting the gains from operating on smaller matrices. Second, overly fine grouping results in fewer observations per group, which can degrade the robustness of parameter estimation and slow down convergence due to instability in iterative optimization. Empirical evidence from both simulated and real-world datasets supports this trade-off. As shown in Table 6, maintaining approximately 100 observations per group consistently provides an effective balance, yielding high computational efficiency without sacrificing registration accuracy.

Table 6.
Statistics of optimal groups across different scenes.
5.2. Effect of Dataset Characteristics
Each dataset exhibited unique geometric and distributional properties that influenced registration outcomes. For example, the Monkey dataset featured scattered ISS keypoints distributed across a clearly defined structure. This allowed for the use of fewer points per group (approximately 74) while still achieving reliable convergence. Conversely, the Subway Station dataset was characterized by planar and repetitive structures, which necessitated a larger number of observations per group (about 166) to maintain numerical stability during optimization. In general, sparse structures could be handled with fewer points per group, while dense or repetitive structures required more points to ensure robustness and stability. These findings emphasize the importance of adapting grouping strategies to the specific topology and distribution of the data. Moreover, introducing randomness in the point order prior to grouping further ensures statistical homogeneity within each group, enhancing estimation robustness.
Apart from geometric structure and point distribution, the inherent noise level of a dataset also plays a crucial role in determining the optimal grouping strategy. For example, in the subway station dataset, which exhibited a relatively high level of measurement noise due to environmental interference and large-scale acquisition, the optimal performance was achieved when each group contained approximately 166–185 observations. In contrast, the statue dataset, collected under controlled conditions with high-precision equipment and minimal ambient noise, achieved optimal results with fewer observations per group (81–122 points).
This contrast suggests that higher noise levels may necessitate more observations per group to stabilize the estimation process and mitigate the influence of random errors. With fewer points, highly noisy groups may suffer from poor conditioning or unstable convergence during iterative optimization. Therefore, datasets with greater noise benefit from coarser grouping—with each group containing more observations—to ensure numerical robustness. Conversely, in low-noise contexts, finer grouping becomes feasible without sacrificing stability, allowing for greater computational efficiency.
5.3. Weighting Schemes in Stochastic Models
Two distinct weighting schemes were examined: equal weighting and nominal accuracy weighting. Equal weighting offers the advantage of faster computation and demonstrates stable performance. In contrast, nominal accuracy weighting, which adapts weights based on estimated variance, tends to yield improved estimates in real-world data contexts. Notably, the nominal weighting scheme required fewer groups to achieve optimal performance—exemplified by the Statue dataset—suggesting that weighting observations allows larger group sizes without sacrificing accuracy. This adaptability helps enhance robustness and potentially reduces computational overhead by minimizing the need for excessive partitioning.
5.4. Scalability and Real-World Performance
Compared to traditional batch processing methods, the HiGoReg algorithm demonstrates significant advantages in scalability. The experimental results show that as the data size and number of groups increase, the efficiency gains of HiGoReg become increasingly pronounced, particularly when handling large-scale point cloud datasets. Moreover, the consistent and stable registration accuracy observed in both synthetic and real-world datasets further validates the robustness and broad applicability of the proposed framework, highlighting its reliable performance across diverse scenarios. However, HiGoReg currently does not incorporate an outlier rejection mechanism during adjustment. Consequently, the presence of erroneous point correspondences may lead to registration failures or degraded results. Addressing this potential limitation, future work should focus on enhancing the identification and removal of outliers to improve the stability and accuracy of the algorithm, ensuring its effectiveness in more complex and noisy real-world environments.
6. Conclusions
This study presented HiGoReg, a point cloud registration framework that integrates the Gauss–Helmert model with a hierarchical grouping strategy. By dividing observations into manageable subsets, the method avoids the high-dimensional matrix computations characteristic of traditional batch approaches. Experimental results on both synthetic and real-world datasets demonstrate that HiGoReg not only maintains the accuracy of batch solutions but also significantly reduces computation time, particularly for large-scale point clouds. This study also explored the impact of stochastic models and group sizes on performance. It was found that grouping around 100 observations per segment generally offers an optimal trade-off between accuracy and efficiency.
Despite these advantages, HiGoReg currently depends on accurately matched correspondences, which may reduce its robustness in noisy or low-overlap scenarios. Future improvements will focus on integrating robust feature-matching techniques and accommodating correlated data. While the current implementation runs on CPUs, migrating to GPU platforms is expected to significantly enhance runtime performance. Leveraging parallel computing architectures will be crucial to unlocking HiGoReg’s full potential for real-time, high-throughput 3D processing. Future work will also explore extensions in the areas of multi-view registration and multi-source data fusion.
Author Contributions
Conceptualization, T.Z. and Z.D.; methodology, T.Z., J.G., and Z.D.; software, T.Z.; validation, T.Z., J.G., and Z.D.; formal analysis, T.Z. and Z.D.; investigation, T.Z.; resources, T.Z., J.G., and Z.D.; data curation, T.Z., J.G., and Z.D.; writing—original draft preparation, T.Z. and Z.D.; writing—review and editing, T.Z., J.G., and Z.D.; visualization, T.Z. and Z.D.; supervision, J.G. and Z.D.; project administration, Z.D.; funding acquisition, Z.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China, grant number 2023YFF0725200.
Data Availability Statement
The data that support the findings of this study are openly available at http://graphics.stanford.edu/data/3Dscanrep/ (accessed on 17 March 2025) and https://github.com/WHU-USI3DV/WHU-TLS (accessed on 20 March 2025), and additional data related to this study are available upon reasonable request to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Derivation of the Woodbury Matrix Identity
In the context of matrix analysis, the Woodbury identity provides a crucial method for efficiently computing the inverse of a matrix sum. Consider the matrix expression
where the matrices are defined in Section 2.2, Equation (21).
To simplify the expression, both sides are right-multiplied by , yielding
Then, multiplying both sides on the right by leads to
Assuming that is invertible, both sides can be right-multiplied by , and then can be added:
Subsequently, left-multiplying both sides by yields
Finally, right-multiplying both sides by leads to the Woodbury matrix identity:
Appendix B. Algorithm of Hierarchical Grouping Strategy
Based on the theoretical development in Section 2.2, we present the HiGoReg algorithm in pseudocode to clarify its computational flow. This formal representation highlights the algorithmic structure, including initialization, iterative refinement, and convergence criteria, and serves as a reference for implementation and analysis.
| Algorithm A1: HiGoReg |
 |
References
- Wu, D.; Han, W.; Liu, Y.; Wang, T.; Xu, C.Z.; Zhang, X.; Shen, J. Language prompt for autonomous driving. In Proceedings of the 39th AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 9, pp. 8359–8367. [Google Scholar] [CrossRef]
- Hao, D.; Li, Y.; Liu, H.; Xu, Z.; Zhang, J.; Ren, J.; Wu, J. Deformation monitoring of large steel structure based on terrestrial laser scanning technology. Measurement 2025, 116962. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, C.; Dong, X.; Ning, J. Point Cloud-Based Deep Learning in Industrial Production: A Survey. ACM Comput. Surv. 2025, 57, 1–36. [Google Scholar] [CrossRef]
- Zhou, Y.; Ye, D.; Zhang, H.; Xu, X.; Sun, H.; Xu, Y.; Liu, X.; Zhou, Y. Recurrent diffusion for 3d point cloud generation from a single image. IEEE Trans. Image Process. 2025, 34, 1753–1765. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.; Li, H.; Peng, L.; Liu, Y.; Liu, Y.H. Efficient and robust point cloud registration via heuristics-guided parameter search. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 6966–6984. [Google Scholar] [CrossRef]
- Li, R.; Yuan, X.; Gan, S.; Bi, R.; Gao, S.; Luo, W.; Chen, C. An effective point cloud registration method based on robust removal of outliers. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5701316. [Google Scholar] [CrossRef]
- Jia, S.; Liu, C.; Wu, H.; Huan, W.; Wang, S. Incremental registration towards large-scale heterogeneous point clouds by hierarchical graph matching. ISPRS J. Photogramm. Remote Sens. 2024, 213, 87–106. [Google Scholar] [CrossRef]
- Tang, Z.; Meng, K. Efficient multi-scale 3D point cloud registration. Computing 2025, 107, 48. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Z.; Wang, B.; Wang, Y.; Shao, K. A Novel 3-D Point Cloud Registration Method with Quaternions Optimization and Data Snooping. IEEE Trans. Instrum. Meas. 2025, 74, 1005215. [Google Scholar] [CrossRef]
- Li, B.L.; Fan, J.S.; Li, J.H.; Liu, Y.F. Semirigid optimal step iterative algorithm for point cloud registration and segmentation in grid structure deformation detection. Autom. Constr. 2025, 171, 105981. [Google Scholar] [CrossRef]
- Lyu, M.; Yang, J.; Qi, Z.; Xu, R.; Liu, J. Rigid pairwise 3D point cloud registration: A survey. Pattern Recognit. 2024, 110408. [Google Scholar] [CrossRef]
- Xu, Y.; Ma, S.; Yao, X.; Zhang, Z.; Yan, Q.; Chen, J. Tunnel full-space deformation measurement based on improved downsampling and registration approach by point clouds. Measurement 2025, 242, 116026. [Google Scholar] [CrossRef]
- Lyu, W.; Ke, W.; Sheng, H.; Ma, X.; Zhang, H. Dynamic Downsampling Algorithm for 3D Point Cloud Map Based on Voxel Filtering. Appl. Sci. 2024, 14, 3160. [Google Scholar] [CrossRef]
- Tao, W.; Xiao, Y.; Wang, R.; Lu, T.; Xu, S. A Fast Registration Method for Building Point Clouds Obtained by Terrestrial Laser Scanner via 2-D Feature Points. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 9324–9336. [Google Scholar] [CrossRef]
- Yang, L.; Xu, S.; Yang, Z.; He, J.; Gong, L.; Wang, W.; Li, Y.; Wang, L.; Chen, Z. Fast Registration Algorithm for Laser Point Cloud Based on 3D-SIFT Features. Sensors 2025, 25, 628. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, B.; Liu, Y.; Liang, F.; Li, B.; Zang, Y. A novel binary shape context for 3D local surface description. ISPRS J. Photogramm. Remote Sens. 2017, 130, 431–452. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar] [CrossRef]
- Lim, H.; Kim, D.; Shin, G.; Shi, J.; Vizzo, I.; Myung, H.; Park, J.; Carlone, L. KISS-Matcher: Fast and Robust Point Cloud Registration Revisited. arXiv 2024, arXiv:2409.15615. [Google Scholar]
- Yan, L.; Wei, P.; Xie, H.; Dai, J.; Wu, H.; Huang, M. A new outlier removal strategy based on reliability of correspondence graph for fast point cloud registration. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 7986–8002. [Google Scholar] [CrossRef]
- Chang, Q.; Wang, W.; Miyazaki, J. Accelerating Nearest Neighbor Search in 3D Point Cloud Registration on GPUs. ACM Trans. Archit. Code Optim. 2025, 22, 1–24. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Lan, F.; Castellani, M.; Zheng, S.; Wang, Y. The SVD-enhanced bees algorithm, a novel procedure for point cloud registration. Swarm Evol. Comput. 2024, 88, 101590. [Google Scholar] [CrossRef]
- Fu, S.; Ma, C.; Li, K.; Xie, C.; Fan, Q.; Huang, H.; Xie, J.; Zhang, G.; Yu, M. Modified LSHADE-SPACMA with new mutation strategy and external archive mechanism for numerical optimization and point cloud registration. Artif. Intell. Rev. 2025, 58, 72. [Google Scholar] [CrossRef]
- Koide, K. small_gicp: Efficient and parallel algorithms for point cloud registration. J. Open Source Softw. 2024, 9, 6948. [Google Scholar] [CrossRef]
- Vizzo, I.; Guadagnino, T.; Mersch, B.; Wiesmann, L.; Behley, J.; Stachniss, C. Kiss-icp: In defense of point-to-point icp–simple, accurate, and robust registration if done the right way. IEEE Robot. Autom. Lett. 2023, 8, 1029–1036. [Google Scholar] [CrossRef]
- Lyu, F.; Song, X.; Shi, Y.; Li, G.; Wang, H. Different-scale dense point cloud registration algorithm for drone based on VCDEI-SCHO-ICP. Surv. Rev. 2025, 1–13. [Google Scholar] [CrossRef]
- Gruen, A. Adaptive least squares correlation: A powerful image matching technique. S. Afr. J. Photogramm. Remote Sens. Cartogr. 1985, 14, 175–187. [Google Scholar]
- Brockett, R.W. Least squares matching problems. Linear Algebra Its Appl. 1989, 122, 761–777. [Google Scholar] [CrossRef]
- Bethmann, F.; Luhmann, T. Least-squares matching with advanced geometric transformation models. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 86–91. [Google Scholar]
- Gruen, A.; Akca, D. Least squares 3D surface and curve matching. ISPRS J. Photogramm. Remote Sens. 2005, 59, 151–174. [Google Scholar] [CrossRef]
- Akca, D. Co-registration of surfaces by 3D least squares matching. Photogramm. Eng. Remote Sens. 2010, 76, 307–318. [Google Scholar] [CrossRef]
- Guo, F.; Liu, K.; Huang, B. Laplace Distribution Based Robust Identification of Errors-in-Variables Systems with Outliers. IEEE Trans. Ind. Electron. 2025, 1–10. [Google Scholar] [CrossRef]
- Hu, Y.; Fang, X. Linear estimation under the Gauss–Helmert model: Geometrical interpretation and general solution. J. Geod. 2023, 97, 44. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, Z.; Wang, S.; Yu, J.; Chen, Y. Robust LS-VCE for the nonlinear Gauss-Helmert model: Case studies for point cloud fitting and geodetic symmetric transformation. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4701413. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, Z.; Chen, Y.; Yu, J. A novel robust point cloud fitting algorithm based on nonlinear Gauss-Helmert model. IEEE Trans. Instrum. Meas. 2023, 72, 1002012. [Google Scholar] [CrossRef]
- Vogel, S.; Ernst, D.; Neumann, I.; Alkhatib, H. Recursive Gauss-Helmert model with equality constraints applied to the efficient system calibration of a 3D laser scanner. J. Appl. Geod. 2022, 16, 37–57. [Google Scholar] [CrossRef]
- Ge, X.M.; Wunderlich, T. Surface-based matching of 3D point clouds with variable coordinates in source and target system. ISPRS J. Photogramm. Remote Sens. 2016, 111, 1–12. [Google Scholar] [CrossRef]
- Hu, Y.; Fang, X.; Zeng, W. Nonlinear least-squares solutions to the TLS multi-station registration adjustment problem. ISPRS J. Photogramm. Remote Sens. 2024, 218, 220–231. [Google Scholar] [CrossRef]
- Lee, E.; Kwon, Y.; Kim, C.; Choi, W.; Sohn, H.G. Multi-source point cloud registration for urban areas using a coarse-to-fine approach. Giscience Remote Sens. 2024, 61, 2341557. [Google Scholar] [CrossRef]
- Ghorbani, F.; Chen, Y.C.; Hollaus, M.; Pfeifer, N. A Robust and Automatic Algorithm for TLS–ALS Point Cloud Registration in Forest Environments Based on Tree Locations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 4015–4035. [Google Scholar] [CrossRef]
- Wu, Y.; Sheng, J.; Ding, H.; Gong, P.; Li, H.; Gong, M.; Ma, W.; Miao, Q. Evolutionary Multitasking Descriptor Optimization for Point Cloud Registration. IEEE Trans. Evol. Comput. 2024, 2024, 1. [Google Scholar] [CrossRef]
- Wang, Z.; Li, P.; Zhang, Q.; Zhu, L.; Tian, W. A LiDAR-depth camera information fusion method for human robot collaboration environment. Inf. Fusion 2025, 114, 102717. [Google Scholar] [CrossRef]
- Wimmer, T.; Wonka, P.; Ovsjanikov, M. Back to 3D: Few-Shot 3D Keypoint Detection with Back-Projected 2D Features. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 4154–4164. [Google Scholar] [CrossRef]
- Liu, Q.; Zhu, H.; Wang, Z.; Zhou, Y.; Chang, S.; Guo, M. Extend your own correspondences: Unsupervised distant point cloud registration by progressive distance extension. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 20816–20826. [Google Scholar]
- Xing, X.; Lu, Z.; Wang, Y.; Xiao, J. Efficient Single Correspondence Voting for Point Cloud Registration. IEEE Trans. Image Process. 2024, 33, 2116–2130. [Google Scholar] [CrossRef] [PubMed]
- Mu, J.; Bie, L.; Du, S.; Gao, Y. Colorpcr: Color point cloud registration with multi-stage geometric-color fusion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 21061–21070. [Google Scholar]
- Zhou, W.; Ren, L.; Yu, J.; Qu, N.; Dai, G. Boosting RGB-D Point Cloud Registration via Explicit Position-Aware Geometric Embedding. IEEE Robot. Autom. Lett. 2024, 9, 5839–5846. [Google Scholar] [CrossRef]
- Brockmann, J.M.; Schuh, W.D. Computational Aspects of High-resolution Global Gravity Field Determination–Numbering Schemes and Reordering. In Proceedings of the NIC Symposium 2016, Jülich, Germany, 1–12 February 2016; John von Neumann-Institut für Computing: Jülich, Germany, 2016; pp. 309–317. [Google Scholar]
- Klees, R.; Ditmar, P.; Kusche, J. Numerical techniques for large least-squares problems with applications to GOCE. In Proceedings of the V Hotine-Marussi Symposium on Mathematical Geodesy, Matera, Italy, 17–21 June 2003; Springer: Berlin/Heidelberg, Germany, 2004; pp. 12–21. [Google Scholar] [CrossRef]
- Zhang, Z. Iterative point matching for registration of free-form curves and surfaces. Int. J. Comput. Vis. 1994, 13, 119–152. [Google Scholar] [CrossRef]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings of the 3rd International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar] [CrossRef]
- Mahboub, V.; Saadatseresht, M.; Ardalan, A.A. A solution to dynamic errors-in-variables within system equations. Acta Geod. Geophys. 2018, 53, 31–44. [Google Scholar] [CrossRef]
- Zeng, W.; Liu, J.; Yao, Y. On partial errors-in-variables models with inequality constraints of parameters and variables. J. Geod. 2015, 89, 111–119. [Google Scholar] [CrossRef]
- Xu, P.; Liu, J.; Shi, C. Total least squares adjustment in partial errors-in-variables models: Algorithm and statistical analysis. J. Geod. 2012, 86, 661–675. [Google Scholar] [CrossRef]
- Wang, J.; Lu, X.; Bennamoun, M.; Sheng, B. Non-rigid Point Cloud Registration via Anisotropic Hybrid Field Harmonization. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 1–18. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Gui, J.; Cong, X.; Gong, X.; Tao, W. A comprehensive survey and taxonomy on point cloud registration based on deep learning. arXiv 2024, arXiv:2404.13830. [Google Scholar]
- Zhao, Y.; Zhang, J.; Xu, S.; Ma, J. Deep learning-based low overlap point cloud registration for complex scenario: The review. Inf. Fusion 2024, 107, 102305. [Google Scholar] [CrossRef]
- Hou, P.; Zhang, B. A generalized least-squares filter designed for GNSS data processing. J. Geod. 2025, 99, 3. [Google Scholar] [CrossRef]
- Teunissen, P.J. Dynamic Data Processing: Recursive Least-Squares; TU Delft OPEN Publishing: Delft, The Netherlands, 2024. [Google Scholar] [CrossRef]
- Zhao, J.; Qian, X.; Jiang, B. Lithium battery state of charge estimation based on improved variable forgetting factor recursive least squares method and adaptive Kalman filter joint algorithm. J. Energy Storage 2024, 100, 113392. [Google Scholar] [CrossRef]
- Koide, H.; Vayssettes, J.; Mercère, G. A Robust and Regularized Algorithm for Recursive Total Least Squares Estimation. IEEE Control. Syst. Lett. 2024, 8, 1006–1011. [Google Scholar] [CrossRef]
- Zhou, T.; Lin, P.; Zhang, S.; Zhang, J.; Fang, J. A novel sequential solution for multi-period observations based on the Gauss-Helmert model. Measurement 2022, 193, 110916. [Google Scholar] [CrossRef]
- Shen, Y.; Li, B.; Chen, Y. An iterative solution of weighted total least-squares adjustment. J. Geod. 2011, 85, 229–238. [Google Scholar] [CrossRef]
- Hager, W.W. Updating the inverse of a matrix. SIAM Rev. 1989, 31, 221–239. [Google Scholar] [CrossRef]
- Lu, T.; Wu, G.; Zhou, S. Ridge estimation algorithm to ill-posed uncertainty adjustment model. Acta Geod. Cartogr. Sin. 2019, 48, 403. [Google Scholar] [CrossRef]
- Golub, G.H.; Hansen, P.C.; O’Leary, D.P. Tikhonov regularization and total least squares. SIAM J. Matrix Anal. Appl. 1999, 21, 185–194. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, Q.; Jiao, J.; Chen, J. InSAR Time Series Analysis Technique Combined with Sequential Adjustment Method for Monitoring of Surface Deformation. Acta Sci. Nat. Univ. Pekin. 2021, 57, 241–249. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, X.; Xia, Y.; Zhao, Z. Monitoring and Analysis of Surface Deformation in Beijing Plain Using Progressive SBAS-InSAR. J. Geod. Geodyn. 2023, 43, 239–245. [Google Scholar] [CrossRef]
- Zhong, Y. Intrinsic shape signatures: A shape descriptor for 3D object recognition. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; pp. 689–696. [Google Scholar] [CrossRef]
- Zinßer, T.; Schmidt, J.; Niemann, H. A refined ICP algorithm for robust 3-D correspondence estimation. In Proceedings of the 2003 International Conference on Image Processing (Cat. No. 03CH37429), Barcelona, Spain, 14–17 September 2003; Volume 2, p. II-695. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Z.; Cheng, X.; Stoter, J.; Xu, W.; Wu, Z.; Nan, L. GlobalMatch: Registration of forest terrestrial point clouds by global matching of relative stem positions. ISPRS J. Photogramm. Remote Sens. 2023, 197, 71–86. [Google Scholar] [CrossRef]
- Dong, Z.; Liang, F.; Yang, B.; Xu, Y.; Zang, Y.; Li, J.; Wang, Y.; Dai, W.; Fan, H.; Hyyppä, J.; et al. Registration of large-scale terrestrial laser scanner point clouds: A review and benchmark. ISPRS J. Photogramm. Remote Sens. 2020, 163, 327–342. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).