Seasonal and Long-Term Water Regime Trends of Cheremsky Wetland: Analysis Based on Sentinel-2 Spectral Indices and Composite Indicator Development
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Region
2.2. Datasets
2.3. Methodology
2.3.1. Water Indexes
- Vegetation: High reflectance in the NIR band and low reflectance in the RED band, resulting in high NDVI values.
- Water: Low reflectance in both NIR and RED bands, leading to low NDVI and high NDWI values.
- MNDWI1: uses SWIR1 (shortwave infrared 1).
- MNDWI2: uses SWIR2 (shortwave infrared 2).
- Suppress non-water classes like vegetation and built-up surfaces more effectively;
- Enhance the separability of spectrally similar water types (e.g., saline or polluted waters);
- Reduce misclassification due to urban shadow or subpixel heterogeneity.
2.3.2. Correlation Analysis
2.3.3. Principal Component Analysis (PCA)
2.3.4. Composite Index
3. Results
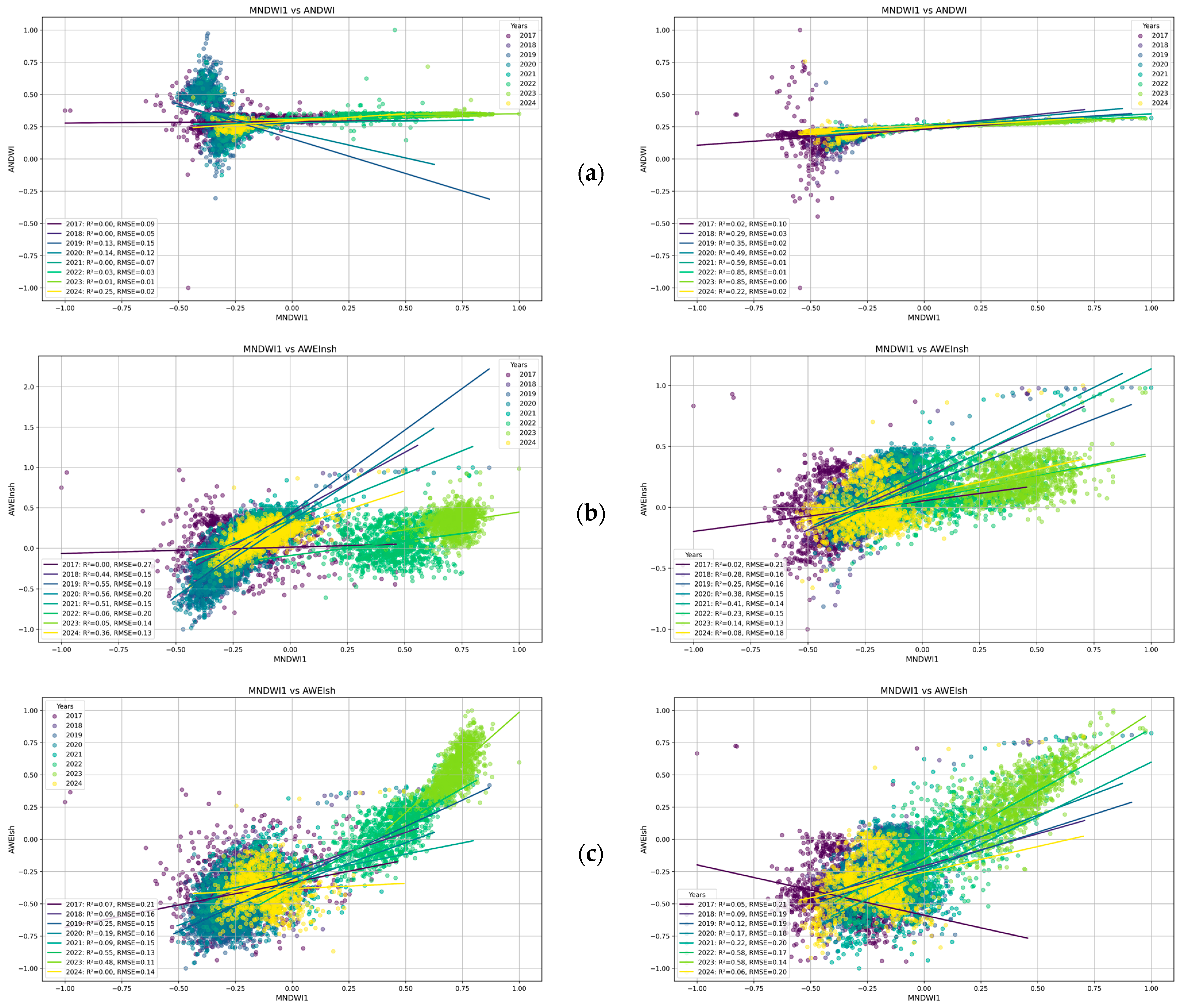
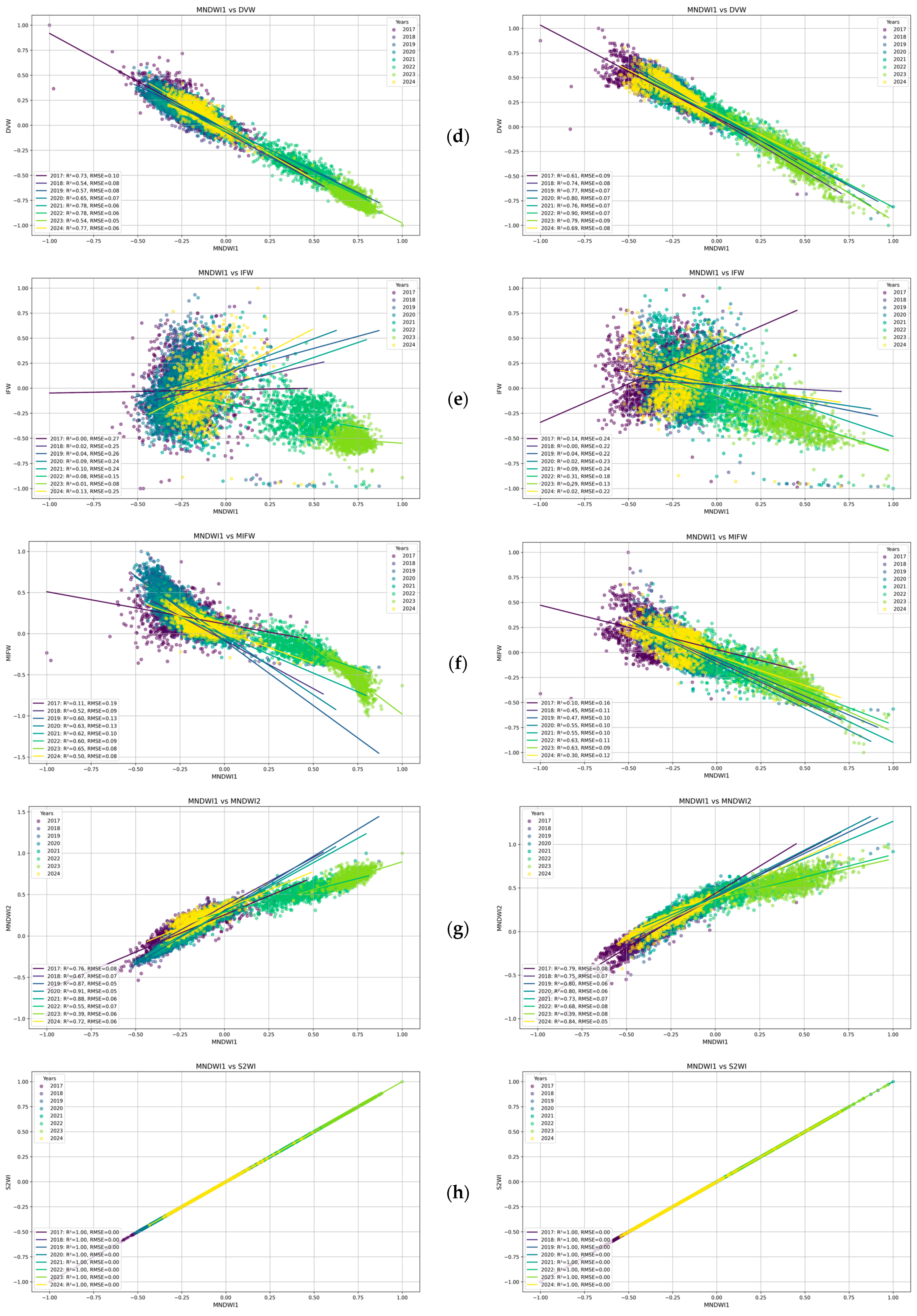
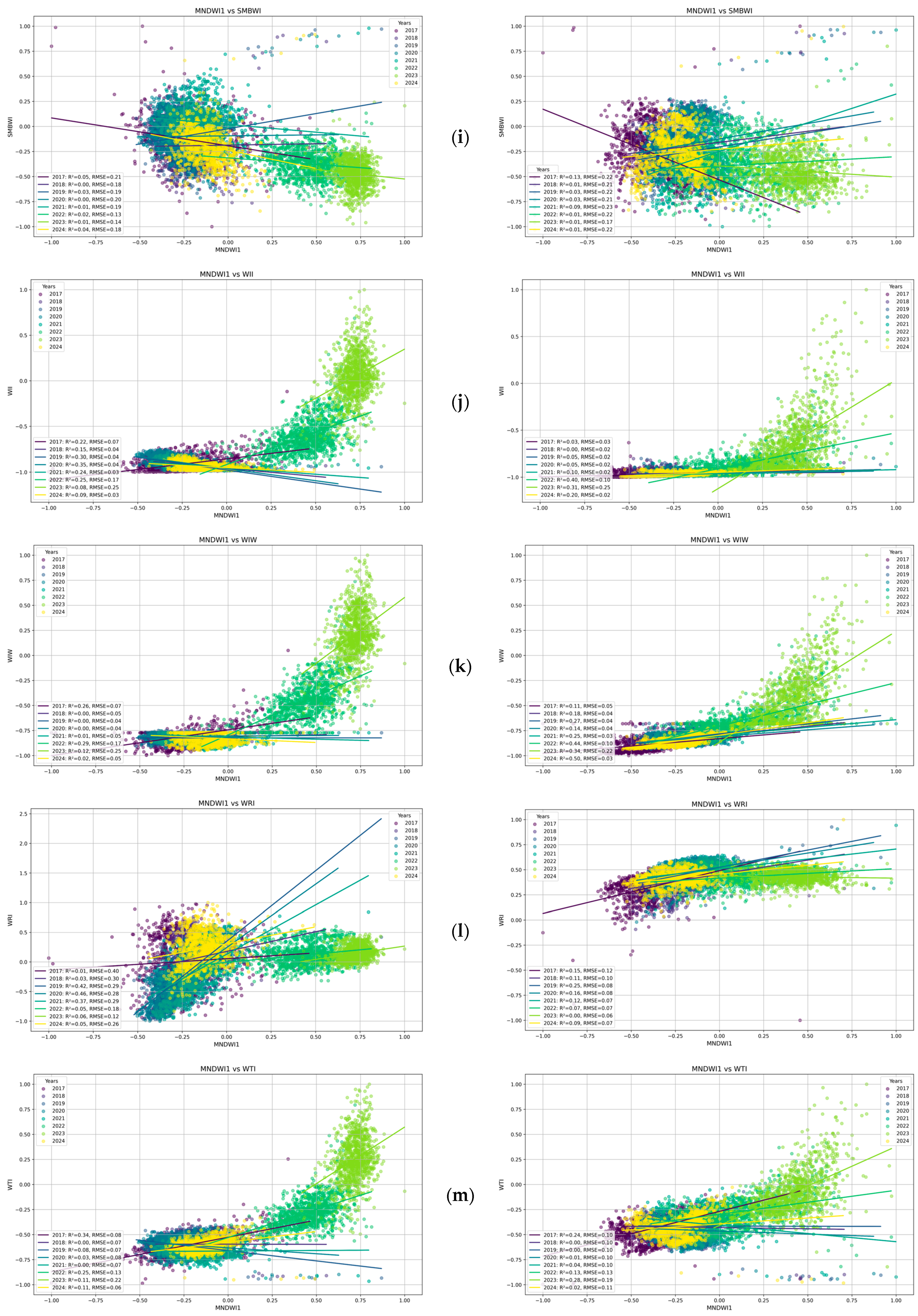
3.1. Trend Analysis and Correlation Relationship
3.2. Principal Component Analysis (PCA)
3.3. Composite Index
4. Discussion
5. Conclusions
- The creation of a composite index combining water and vegetation data is presented. The development of a CI that simultaneously considers trends in both water surfaces and vegetation condition (e.g., health, density, ferrology) can provide a more comprehensive understanding of ecological changes in bogs. This is of particular pertinence in regions where hydrological processes are inextricably linked to vegetation dynamics, a phenomenon that is exemplified by the Cheremsky Reserve. A range of studies have adopted an approach that combines water and vegetation metrics in order to assess droughts or ecosystem health (for example, Kogan, 1995—VHI [60]; AghaKouchak et al., 2015—MWDI [61]).
- The investigation of the correlations and time lags between changes in water indices and vegetation indices can facilitate the identification of cause-and-effect relationships. For instance, it can be determined how changes in water levels affect vegetation productivity, or conversely, how vegetation succession affects water regimes.
- The utilization of commercial satellite data (e.g., PlanetScope, WorldView) with very high resolution, or radar sensor data (e.g., Sentinel-1), which are insensitive to cloud cover and can penetrate vegetation, has the potential to enhance the precision and reliability of monitoring, particularly in the context of detecting water beneath vegetation [7,62].
- In addition to linear trends, breakpoint analysis methods (e.g., BFAST) should be considered in order to identify abrupt changes in water index dynamics. Such changes may be associated with extreme events or land use changes.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Solovey, T. Wetlands of the Volhynian Polissia (Western Ukraine): Classification, Natural Conditions of Distribution and Spatial Difference. Geol. Q. 2019, 63, 139–149. [Google Scholar] [CrossRef]
- Convention on Wetlands Global. Guidelines for Peatland Rewetting and Restoration; Convention on Wetlands Global: Gland, Switzerland, 2021. [Google Scholar]
- Ramsar Convention Secretariat. The Ramsar Convention Manual: A Guide to the Convention on Wetlands (Ramsar, Iran, 1971), 6th ed.; Ramsar Convention Secretariat: Gland, Switzerland, 2007. [Google Scholar]
- Zhang, S.; Na, X.; Kong, B.; Wang, Z.; Jiang, H.; Yu, H.; Zhao, Z.; Li, X.; Liu, C.; Dale, P. Identifying Wetland Change in China’s Sanjiang Plain Using Remote Sensing. Wetlands 2009, 29, 302–313. [Google Scholar] [CrossRef]
- Frohn, R.C.; Reif, M.; Lane, C.; Autrey, B. Satellite Remote Sensing of Isolated Wetlands Using Object-Oriented Classification of Landsat-7 Data. Wetlands 2009, 29, 931–941. [Google Scholar] [CrossRef]
- Ozesmi, S.L.; Bauer, M.E. Satellite Remote Sensing of Wetlands. Wetl. Ecol. Manag. 2002, 10, 381–402. [Google Scholar] [CrossRef]
- Kaplan, G.; Avdan, U. Monthly Analysis of Wetlands Dynamics Using Remote Sensing Data. ISPRS Int. J. Geo-Inf. 2018, 7, 411. [Google Scholar] [CrossRef]
- Sentinel-2—Sentinel Online. Available online: https://sentinels.copernicus.eu/copernicus/sentinel-2 (accessed on 13 March 2025).
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Belloli, T.F.; Guasselli, L.A.; Kuplich, T.M.; Fernando, L.; Ruiz, C.; Carvalho De Arruda, D.; Balsamo Etchelar, C.; Simioni, J.D. Estimation of Aboveground Biomass and Carbon in Palustrine Wetland Using Bands and Multispectral Indices Derived from Optical Satellite Imageries PlanetScope and Sentinel-2A. J. Appl. Remote Sens. 2022, 16, 034516. [Google Scholar] [CrossRef]
- Ade, C.; Khanna, S.; Lay, M.; Ustin, S.L.; Hestir, E.L. Genus-Level Mapping of Invasive Floating Aquatic Vegetation Using Sentinel-2 Satellite Remote Sensing. Remote Sens. 2022, 14, 3013. [Google Scholar] [CrossRef]
- Yu, H.; Li, S.; Liang, Z.; Xu, S.; Yang, X.; Li, X. Multi-Source Remote Sensing Data for Wetland Information Extraction: A Case Study of the Nanweng River National Wetland Reserve. Sensors 2024, 24, 6664. [Google Scholar] [CrossRef]
- Salas, E.A.L.; Kumaran, S.S.; Bennett, R.; Willis, L.P.; Mitchell, K. Machine Learning-Based Classification of Small-Sized Wetlands Using Sentinel-2 Images. AIMS Geosci. 2024, 10, 62–79. [Google Scholar] [CrossRef]
- Usman, M.; Chua, L.H.; Irvine, K.N.; Teang, L. Estimating Water Surface Elevation for a Wetland Using Integrated Multi-Sourced Remote Sensing Data. Wetl. Ecol. Manag. 2025, 33, 20. [Google Scholar] [CrossRef]
- Jamali, A.; Mahdianpari, M.; Mohammadimanesh, F.; Brisco, B.; Salehi, B. A Synergic Use of Sentinel-1 and Sentinel-2 Imagery for Complex Wetland Classification Using Generative Adversarial Network (GAN) Scheme. Water 2021, 13, 3601. [Google Scholar] [CrossRef]
- Solovey, T. Flooded Wetlands Mapping from Sentinel-2 Imagery with Spectral Water Index: A Case Study of Kampinos National Park in Central Poland. Geol. Q. 2020, 64, 492–505. [Google Scholar] [CrossRef]
- Tajadod, M.J.; Haghighi Khomami, M.; Modaberi, H.; Panahandeh, M. Integrating Sentinel 1 and 2 Satellite Data with Spectral Indices to Improve Classification Methods (Anzali Wetland). Environ. Sci. 2024, 22, 389–406. [Google Scholar] [CrossRef]
- Chaudhary, R.K.; Puri, L.; Acharya, A.K.; Aryal, R. Wetland Mapping and Monitoring with Sentinel-1 and Sentinel-2 Data on the Google Earth Engine. J. For. Nat. Resour. Manag. 2023, 3, 1–21. [Google Scholar] [CrossRef]
- Li, L.; Vrieling, A.; Skidmore, A.; Wang, T.; Muñoz, A.R.; Turak, E. Evaluation of MODIS Spectral Indices for Monitoring Hydrological Dynamics of a Small, Seasonally-Flooded Wetland in Southern Spain. Wetlands 2015, 35, 851–864. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Brisco, B. Spectral Analysis of Wetlands Using Multi-Source Optical Satellite Imagery. ISPRS J. Photogramm. Remote Sens. 2018, 144, 119–136. [Google Scholar] [CrossRef]
- Lyalko, V.; Zholobak, G.; Dugin, S.; Sybirtseva, O.; Golubov, S.; Dorofey, Y.; Polishchuk, O. Experimental Research of the Carbon Circle Features in “Atmosphere–Vegetation” System over the Wetland Area within the Forest–Steppe Zone in Ukraine Using Remote Spectro- and Gasometry under the Global Climate Changes. Ukr. J. Remote Sens. 2020, 24, 15–23. [Google Scholar] [CrossRef]
- Azimov, O.; Tomchenko, O.; Shevchenko, O.; Dorofey, Y. Satellite Monitoring of the Natural and Technogenic Events on the Left-Bank Pripyat Reclamation System of the Chornobyl Exclusion Zone. In Proceedings of the XVI International Scientific Conference “Monitoring of Geological Processes and Ecological Condition of the Environment”, Kyiv, Ukraine, 15–18 November 2022; pp. 1–6. [Google Scholar]
- Lyalko, V.I.; Shportiuk, Z.M.; Sibirtseva, O.M.; Dugin, S.S. Research of Hyperspectral Red Edge Indices for Vegetation Cover Change Detection over the Oil Field Using Spectrometric Survey Data. Geol. Zhurnal 2014, 3, 95–103. [Google Scholar]
- Lyalko, V.I.; Popov, M.O. (Eds.) Multispectral Methods of Earth Remote Sensing in Land Use Tasks; Naukova Dumka: Kyiv, Ukraine, 2006. [Google Scholar]
- Trofymchuk, O.M.; Trisyuk, V.M.; Anpilova, E.S.; Butenko, O.S.; Vishnyakov, V.Y.; Zagorodnia, S.A.; Klymenko, V.I.; Klochko, T.O.; Krasovska, I.G.; Kreta, D.L.; et al. Geoinformation Studies of Water Ecosystems in Ukraine: Monitoring and Forecasting; Suprun V.P.: Ivano-Frankivsk, Ukraine, 2022; ISBN 978-617-8128-10-4. [Google Scholar]
- Konishchuk, V.V. Estimation of Difersity Ecosystems Cheremskyi Natural Reserve on the Basis of Cartographical Modelling, A Manuscript. Ph.D. Dissertation, National Taras Shevchenko University, Kyiv, Ukraine, 2006. Available online: https://uacademic.info/ua/document/0406U000865 (accessed on 13 March 2025).
- Martyniuk, V.; Korbutiak, V.; Hopchak, I.; Kovalchuk, I.; Zubkovych, I. Methodology for Assessing the Geoecological State of Landscape-Lake Systems and Their Cartographic Modelling (Case Study of Lake Bile, Rivne Nature Reserve, Ukraine). Baltica 2023, 36, 13–29. [Google Scholar] [CrossRef]
- Kovalchuk, I.P.; Martyniuk, V.A. Methodology and Experience of Landscape-Limnological Research into Lake-Basin Systems of Ukraine. Geogr. Nat. Resour. 2015, 36, 305–312. [Google Scholar] [CrossRef]
- Pavlovska, T.S.; Kovalchuk, I.P. Geomorphology: Textbook for Students of Higher Education Institutions; VezhaDruk: Lutsk, Ukraine, 2022. [Google Scholar]
- Cheremske Bog|Ramsar Sites Information Service. Available online: https://rsis.ramsar.org/ris/2272 (accessed on 10 March 2025).
- Harmonized Sentinel-2 MSI: MultiSpectral Instrument, Level-2A (SR)|Earth Engine Data Catalog|Google for Developers. Available online: https://developers.google.com/earth-engine/datasets/catalog/COPERNICUS_S2_SR_HARMONIZED#terms-of-use (accessed on 13 March 2025).
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A New Technique for Surface Water Mapping Using Landsat Imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Acharya, T.D.; Subedi, A.; Lee, D.H. Evaluation of Water Indices for Surface Water Extraction in a Landsat 8 Scene of Nepal. Sensors 2018, 18, 2580. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Feng, M.; Zhu, Y.; Lu, N.; Huang, J.; Xiao, T. An Automated Method for Extracting Rivers and Lakes from Landsat Imagery. Remote Sens. 2014, 6, 5067–5089. [Google Scholar] [CrossRef]
- Gond, V.; Bartholomé, E.; Ouattara, F.; Nonguierma, A.; Bado, L. Surveillance et Cartographie Des Plans d’eau et Des Zones Humides et Inondables En Régions Arides Avec l’instrument VEGETATION Embarqué Sur SPOT-4. Int. J. Remote Sens. 2004, 25, 987–1004. [Google Scholar] [CrossRef]
- Crippen, R.E. Calculating the Vegetation Index Faster. Remote Sens. Environ. 1990, 34, 71–73. [Google Scholar] [CrossRef]
- McFeeters, S.K. The Use of the Normalized Difference Water Index (NDWI) in the Delineation of Open Water Features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Adell, C.; Puech, C. Will the Spatial Analysis of Water Maps Extracted by Remote Satellite Detection Allow Locating the Footprints of Hunting Activity in the Camargue? Bull.—Soc. Fr. Photogramm. Teledetect. 2003, 171, 76–86. [Google Scholar]
- Davranche, A.; Poulin, B.; Lefebvre, G. Mapping Flooding Regimes in Camargue Wetlands Using Seasonal Multispectral Data. Remote Sens. Environ. 2013, 138, 165–171. [Google Scholar] [CrossRef]
- Xu, H. Modification of Normalised Difference Water Index (NDWI) to Enhance Open Water Features in Remotely Sensed Imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Jones, S.K.; Fremier, A.K.; DeClerck, F.A.; Smedley, D.; Pieck, A.O.; Mulligan, M. Big Data and Multiple Methods for Mapping Small Reservoirs: Comparing Accuracies for Applications in Agricultural Landscapes. Remote Sens. 2017, 9, 1307. [Google Scholar] [CrossRef]
- Sawetwong, C.; Reungsang, P. Comparison of NDWI, MNDWI1 and MNDWI2 Indices from Sentinel-2 Satellite Images for Extracting Urban Surface Water Bodies in Khon Kaen. J. Appl. Informatics Technol. 2022, 4, 1–12. [Google Scholar] [CrossRef]
- Feng, M.; Sexton, J.O.; Channan, S.; Townshend, J.R. A Global, High-Resolution (30-m) Inland Water Body Dataset for 2000: First Results of a Topographic–Spectral Classification Algorithm. Int. J. Digit. Earth 2016, 9, 113–133. [Google Scholar] [CrossRef]
- Potapov, P.V.; Turubanova, S.A.; Tyukavina, A.; Krylov, A.M.; McCarty, J.L.; Radeloff, V.C.; Hansen, M.C. Eastern Europe’s Forest Cover Dynamics from 1985 to 2012 Quantified from the Full Landsat Archive. Remote Sens. Environ. 2015, 159, 28–43. [Google Scholar] [CrossRef]
- Sharma, R.C.; Durga Rao, K.H.V.; Jagarlapudi, A. Effect of Spatial Resolution on Classification of Wetlands. Asian-Pac. Remote Sens. J. 1996, 8, 47–51. [Google Scholar]
- Rokni, K.; Ahmad, A.; Selamat, A.; Hazini, S. Water Feature Extraction and Change Detection Using Multitemporal Landsat Imagery. Remote Sens. 2014, 6, 4173–4189. [Google Scholar] [CrossRef]
- Kameyama, S.; Yamagata, Y.; Nakamura, F.; Kaneko, M. Development of WTI and Turbidity Estimation Model Using SMA—Application to Kushiro Mire, Eastern Hokkaido, Japan. Remote Sens. Environ. 2001, 77, 1–9. [Google Scholar] [CrossRef]
- Rad, A.M.; Kreitler, J.; Sadegh, M. Augmented Normalized Difference Water Index for Improved Surface Water Monitoring. Environ. Model. Softw. 2021, 140, 105030. [Google Scholar] [CrossRef]
- Su, Z.; Xiang, L.; Steffen, H.; Jia, L.; Deng, F.; Wang, W.; Hu, K.; Guo, J.; Nong, A.; Cui, H.; et al. A New and Robust Index for Water Body Extraction from Sentinel-2 Imagery. Remote Sens. 2024, 16, 2749. [Google Scholar] [CrossRef]
- Lefebvre, G.; Davranche, A.; Willm, L.; Campagna, J.; Redmond, L.; Merle, C.; Guelmami, A.; Poulin, B. Introducing WIW for Detecting the Presence of Water in Wetlands with Landsat and Sentinel Satellites. Remote Sens. 2019, 11, 2210. [Google Scholar] [CrossRef]
- Jiang, W.; Ni, Y.; Pang, Z.; Li, X.; Ju, H.; He, G.; Lv, J.; Yang, K.; Fu, J.; Qin, X. An Effective Water Body Extraction Method with New Water Index for Sentinel-2 Imagery. Water 2021, 13, 1647. [Google Scholar] [CrossRef]
- Kevin Sinisterra-Solís, N.; Sanjuán, N.; Ribal, J.; Estruch, V.; Clemente, G.; Rozakis, S. Developing a Composite Indicator to Assess Agricultural Sustainability: Influence of Some Critical Choices. Ecol. Indic. 2024, 161, 111934. [Google Scholar] [CrossRef]
- Melo-Aguilar, C.; Agulles, M.; Jordà, G. Introducing Uncertainties in Composite Indicators. The Case of the Impact Chain Risk Assessment Framework. Front. Clim. 2022, 4, 1019888. [Google Scholar] [CrossRef]
- Melnyk, O.; Brunn, A. Analysis of Spectral Index Interrelationships for Vegetation Condition Assessment on the Example of Wetlands in Volyn Polissya, Ukraine. Earth 2025, 6, 28. [Google Scholar] [CrossRef]
- Yang, W.; Zhong, J.; Xia, Y.; Hu, Q.; Fang, C.; Cong, M.; Yao, B.; You, Q. A Comprehensive Multi-Metric Index for Health Assessment of the Poyang Lake Wetland. Remote Sens. 2023, 15, 4061. [Google Scholar] [CrossRef]
- Medland, S.J.; Shaker, R.R.; Forsythe, K.W.; Mackay, B.R.; Rybarczyk, G. A Multi-Criteria Wetland Suitability Index for Restoration across Ontario’s Mixedwood Plains. Sustain. 2020, 12, 9953. [Google Scholar] [CrossRef]
- Munyati, C. Use of Principal Component Analysis (PCA) of Remote Sensing Images in Wetland Change Detection on the Kafue Flats, Zambia. Geocarto Int. 2004, 19, 11–22. [Google Scholar] [CrossRef]
- Deng, J.S.; Wang, K.; Deng, Y.H.; Qi, G.J. PCA-Based Land-Use Change Detection and Analysis Using Multitemporal and Multisensor Satellite Data. Int. J. Remote Sens. 2008, 29, 4823–4838. [Google Scholar] [CrossRef]
- Liu, X.; Yang, X.; Zhang, T.; Wang, Z.; Zhang, J.; Liu, Y.; Liu, B. Remote Sensing Based Conservation Effectiveness Evaluation of Mangrove Reserves in China. Remote Sens. 2022, 14, 1386. [Google Scholar] [CrossRef]
- Kogan, F.N. Application of Vegetation Index and Brightness Temperature for Drought Detection. Adv. Sp. Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Feldman, D.; Hoerling, M.; Huxman, T.; Lund, J. Water and Climate: Recognize Anthropogenic Drought. Nature 2015, 524, 409–411. [Google Scholar] [CrossRef] [PubMed]
- Uddin, M.P.; Mamun, M.A.; Hossain, M.A. PCA-Based Feature Reduction for Hyperspectral Remote Sensing Image Classification. IETE Tech. Rev. (Institution Electron. Telecommun. Eng. India) 2021, 38, 377–396. [Google Scholar] [CrossRef]
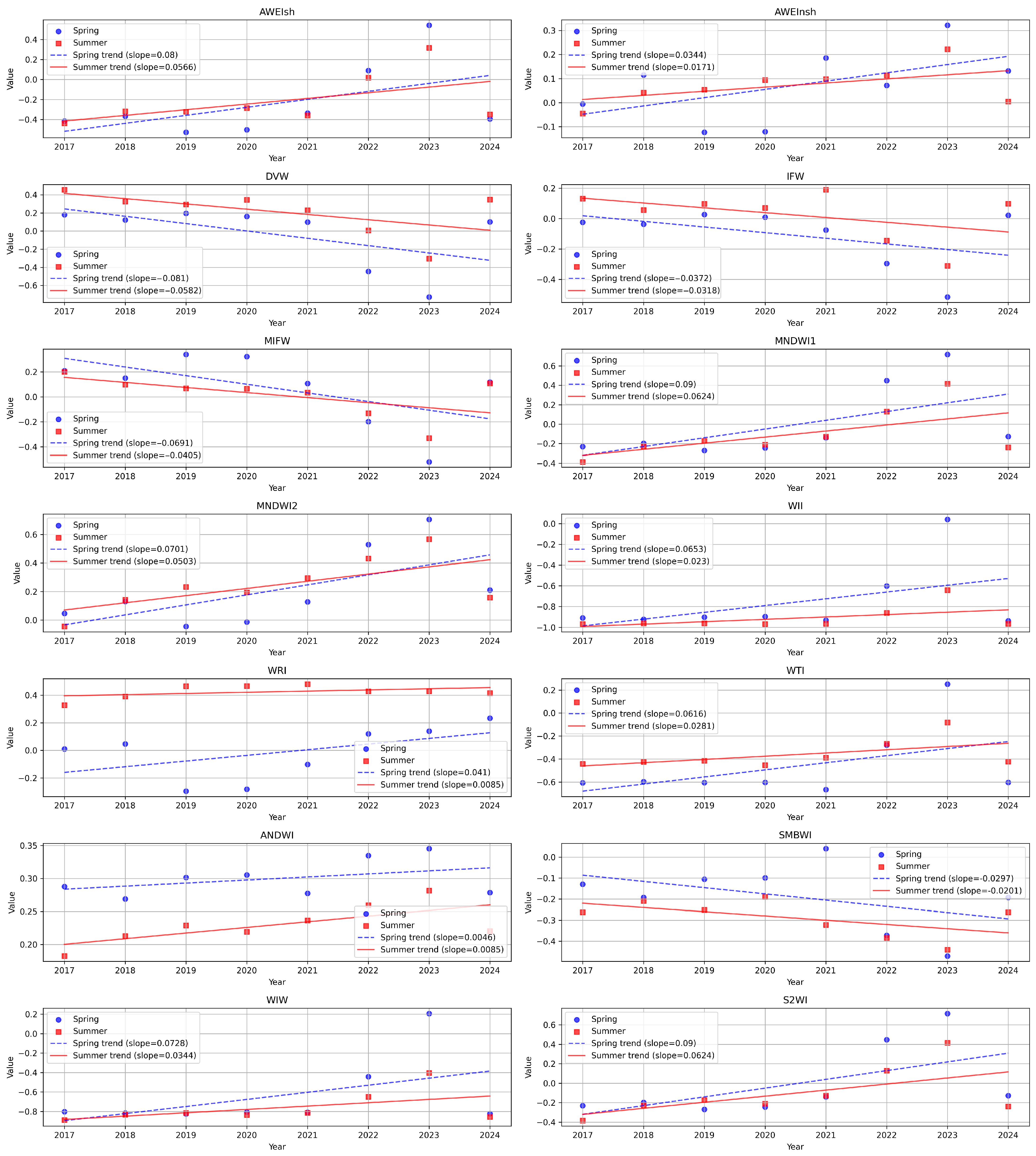
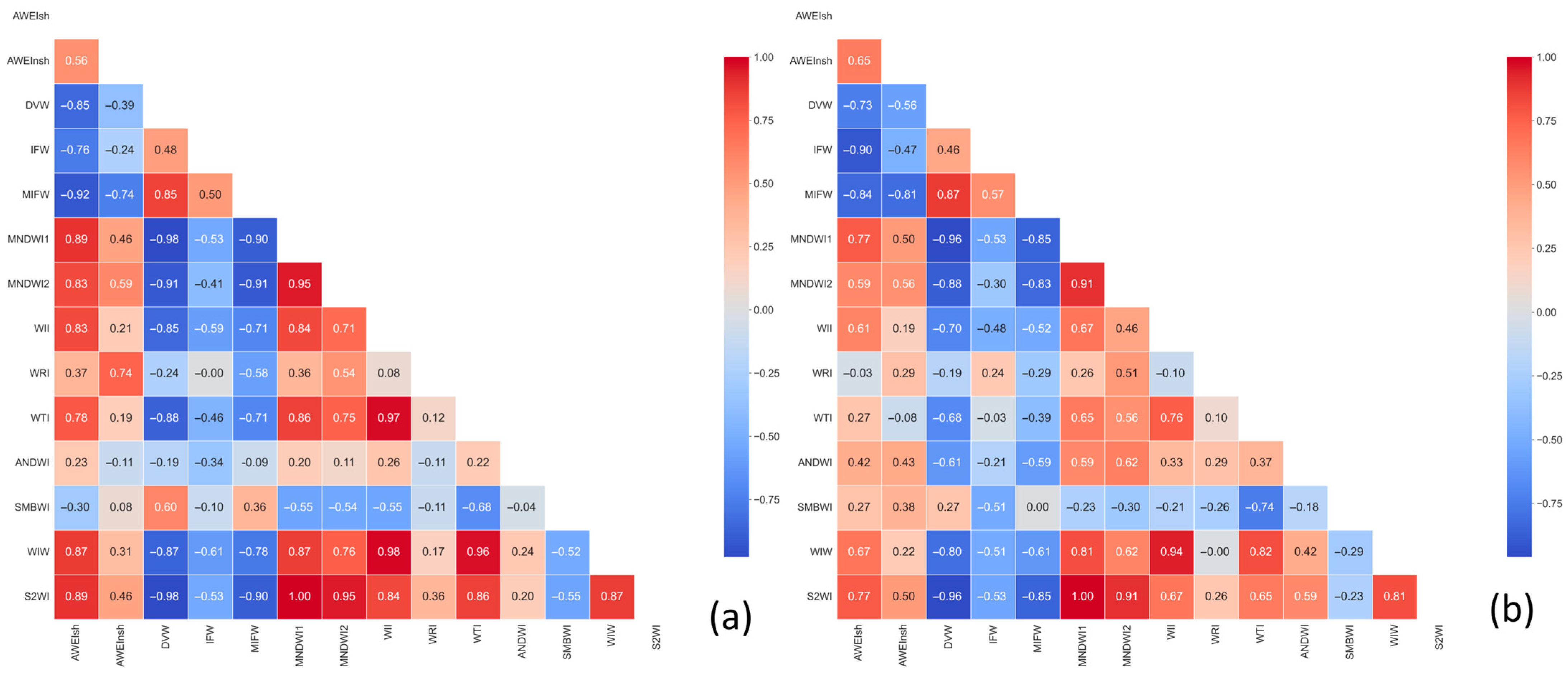


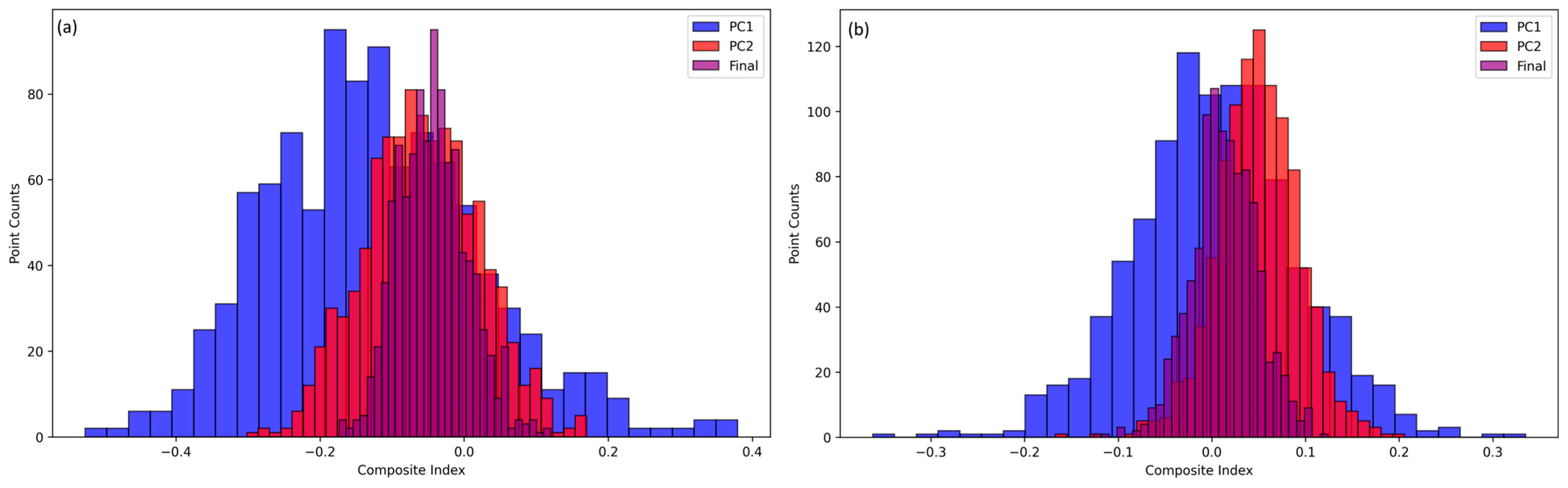
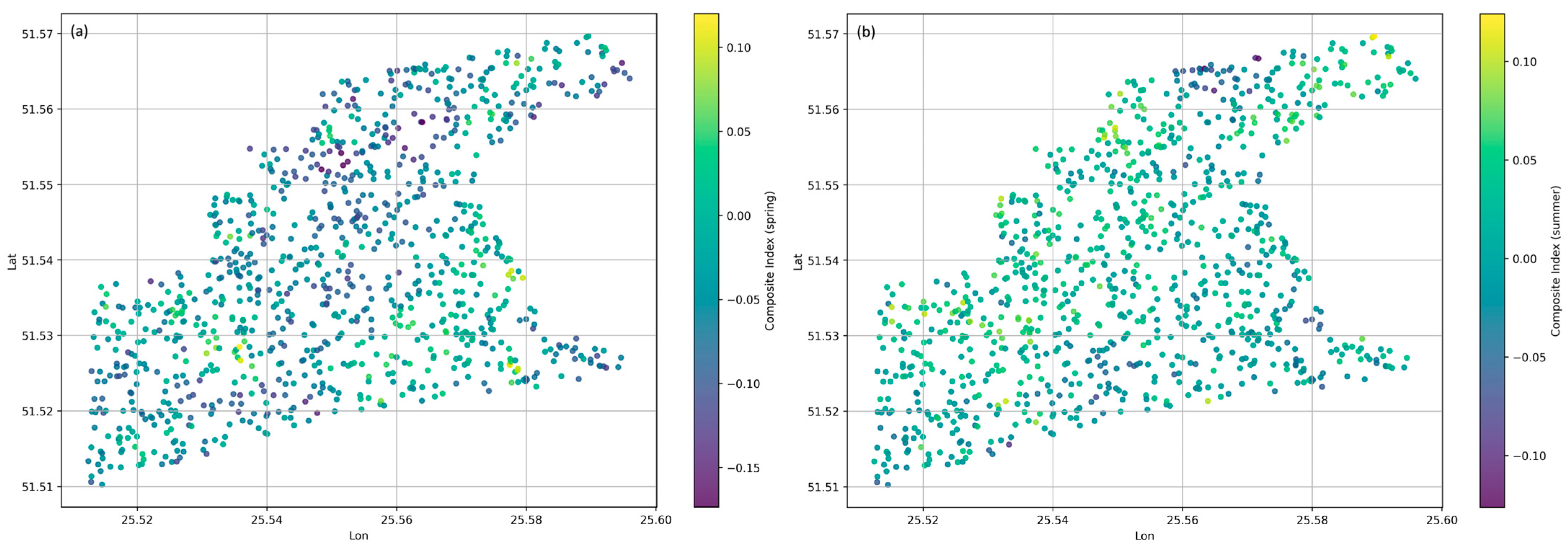
| Year | Number of Images (Spring/Summer) | Year | Number of Images (Spring/Summer) |
|---|---|---|---|
| 2017 | 22/29 | 2021 | 74/74 |
| 2018 | 68/64 | 2022 | 74/72 |
| 2019 | 72/74 | 2023 | 74/72 |
| 2020 | 74/72 | 2024 | 73/74 |
| № | Index | Formula | Bands | Central Wavelength (nm) 2A/2B | Bandwidth (nm) 2A/2B |
|---|---|---|---|---|---|
| 1 | AWEIsh | B2, B3, B4, B8, B11, B12 | 490, 560, 665, 842, 1610, 2190 | 65, 35, 30, 115, 90, 180 | |
| 2 | AWEInsh | B3, B8, B11, B12 | 560, 842, 1610, 2190 | 35, 115, 90, 180 | |
| 3 | DVW | B3, B4, B8 | 560, 665, 842 | 35, 30, 115 | |
| 4 | IFW | B3, B8 | 560, 842 | 35, 115 | |
| 5 | MIFW | B3, B11 | 560, 1610 | 35, 90 | |
| 6 | MNDWI1 | B3, B11 | 560, 1610 | 35, 90 | |
| 7 | MNDWI2 | B3, B12 | 560, 2190 | 35, 180 | |
| 8 | WII | B4, B8 | 665, 842 | 30, 115 | |
| 9 | WRI | B3, B4, B8, B11 | 560, 665, 842, 1610 | 35, 30, 115, 90 | |
| 10 | WTI | B4, B8 | 665, 842 | 30, 115 | |
| 11 | ANDWI | B2, B3, B4, B8, B11, B12 | 490, 560, 665, 842, 1610, 2190 | 65, 35, 30, 115, 90, 180 | |
| 12 | SMBWI | B2, B3, B4, B8, B8a, B9, B11, B12 | 490, 560, 665, 842, 865, 945, 1610, 2190 | 65, 35, 30, 115, 20, 20, 90, 180 | |
| 13 | WIW | B8, B12 | 842, 2190 | 115, 180 | |
| 14 | S2WI | B5, B12 | 705, 2190 | 15, 180 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melnyk, O.; Brunn, A. Seasonal and Long-Term Water Regime Trends of Cheremsky Wetland: Analysis Based on Sentinel-2 Spectral Indices and Composite Indicator Development. Remote Sens. 2025, 17, 2363. https://doi.org/10.3390/rs17142363
Melnyk O, Brunn A. Seasonal and Long-Term Water Regime Trends of Cheremsky Wetland: Analysis Based on Sentinel-2 Spectral Indices and Composite Indicator Development. Remote Sensing. 2025; 17(14):2363. https://doi.org/10.3390/rs17142363
Chicago/Turabian StyleMelnyk, Oleksandr, and Ansgar Brunn. 2025. "Seasonal and Long-Term Water Regime Trends of Cheremsky Wetland: Analysis Based on Sentinel-2 Spectral Indices and Composite Indicator Development" Remote Sensing 17, no. 14: 2363. https://doi.org/10.3390/rs17142363
APA StyleMelnyk, O., & Brunn, A. (2025). Seasonal and Long-Term Water Regime Trends of Cheremsky Wetland: Analysis Based on Sentinel-2 Spectral Indices and Composite Indicator Development. Remote Sensing, 17(14), 2363. https://doi.org/10.3390/rs17142363






