Remotely Sensing Phytoplankton Size Structure in the Mediterranean Sea: Insights from In Situ Data and Temperature-Corrected Abundance-Based Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
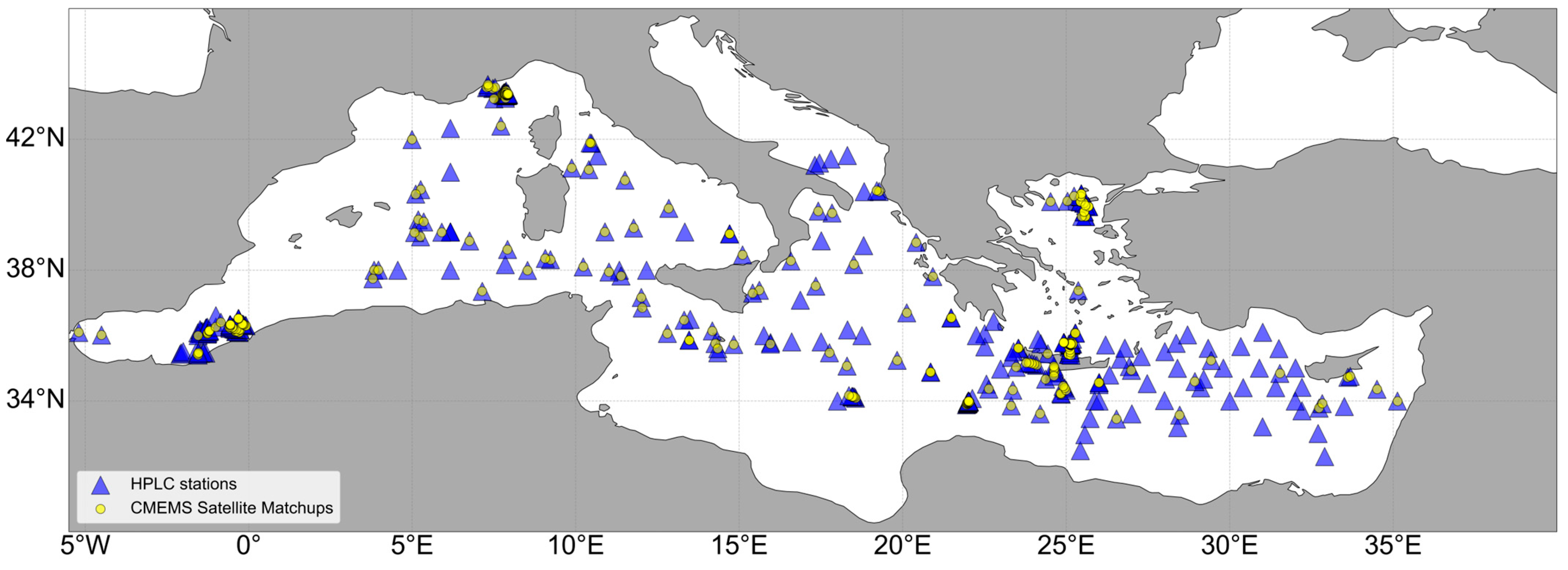
2.1.1. High-Performance Liquid Chromatography (HPLC) Pigment Datasets
2.1.2. Auxiliary Size-Fractionated Chlorophyll-a and Phytoplankton Cell Abundance Datasets
2.1.3. Satellite Ocean Color Data and Data Partitioning for Model Training and Validation
2.1.4. Satellite-Derived Sea Surface Temperature Datasets
2.2. Methods
2.2.1. Diagnostic Pigment Approach
2.2.2. SST-Independent Three-Component Phytoplankton Size Class Model
2.2.3. SST-Dependent Three-Component Phytoplankton Size Class Model
2.2.4. Statistical Performance Metrics
3. Results and Discussion
3.1. Three-Component Model Re-Parameterization
3.2. Incorporation of Temperature Dependency into the Three-Component Model
3.3. Independent Model Validation
3.4. Satellite Validation
3.5. Application of the Re-Parameterized Model to Satellite Ocean Color Data
3.6. Re-Evaluating In Situ Estimates of Phytoplankton Size Structure from Diagnostic Pigment Approaches
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bethoux, J.P.; Gentili, B.; Morin, P.; Nicolas, E.; Pierre, C.; Ruiz-Pino, D. The Mediterranean Sea: A Miniature Ocean for Climatic and Environmental Studies and a Key for the Climatic Functioning of the North Atlantic. Prog. Oceanogr. 1999, 44, 131–146. [Google Scholar] [CrossRef]
- D’Ortenzio, F.; D’Alcalà, M.R. On the Trophic Regimes of the Mediterranean Sea: A Satellite Analysis. Biogeosciences 2009, 6, 139–148. [Google Scholar] [CrossRef]
- Skliris, N. Past, Present and Future Patterns of the Thermohaline Circulation and Characteristic Water Masses of the Mediterranean Sea. In The Mediterranean Sea: Its History and Present Challenges; Springer: Dordrecht, The Netherlands, 2014; pp. 29–48. [Google Scholar] [CrossRef]
- Berland, B.; Bonin, D.; Maestrini, S.Y. Azote ou phosphore? Considérations sur le paradoxe nutritionnel de la mer Méditerranée. Oceanol. Acta 1980, 3, 135–141. [Google Scholar]
- Krom, M.D.; Kress, N.; Brenner, S.; Gordon, L.I. Phosphorus Limitation of Primary Productivity in the Eastern Mediterranean Sea. Limnol. Oceanogr. 1991, 36, 424–432. [Google Scholar] [CrossRef]
- Antoine, D.; Morel, A.; Andre, J.M. Algal Pigment Distribution and Primary Production in the Eastern Mediterranean as Derived from Coastal Zone Color Scanner Observations. J. Geophys. Res. Oceans 1995, 100, 16193–16209. [Google Scholar] [CrossRef]
- Lazzari, P.; Solidoro, C.; Salon, S.; Bolzon, G. Spatial Variability of Phosphate and Nitrate in the Mediterranean Sea: A Modeling Approach. Deep Sea Res. I Oceanogr. Res. Pap. 2016, 108, 39–52. [Google Scholar] [CrossRef]
- Siokou-Frangou, I.; Christaki, U.; Mazzocchi, M.G.; Montresor, M.; Ribera D’Alcala, M.; Vaque, D.; Zingone, A. Plankton in the Open Mediterranean Sea: A Review. Biogeosciences 2010, 7, 1543–1586. [Google Scholar] [CrossRef]
- Macias, D.; Garcia-Gorriz, E.; Stips, A. Major Fertilization Sources and Mechanisms for Mediterranean Sea Coastal Ecosystems. Limnol. Oceanogr. 2018, 63, 897–914. [Google Scholar] [CrossRef]
- Kalloniati, K.; Christou, E.D.; Kournopoulou, A.; Gittings, J.A.; Theodorou, I.; Zervoudaki, S.; Raitsos, D.E. Long-Term Warming and Human-Induced Plankton Shifts at a Coastal Eastern Mediterranean Site. Sci. Rep. 2023, 13, 21068. [Google Scholar] [CrossRef]
- Estrada, M. Primary production in the Northwestern Mediterranean. Eur. Anchovy Environ. 1996, 60, 55–64. [Google Scholar]
- Sabatés, A.; Olivar, M.P.; Salat, J.; Palomera, I.; Alemany, F. Physical and Biological Processes Controlling the Distribution of Fish Larvae in the NW Mediterranean. Prog. Oceanogr. 2007, 74, 355–376. [Google Scholar] [CrossRef]
- Lejeusne, C.; Chevaldonné, P.; Pergent-Martini, C.; Boudouresque, C.F.; Pérez, T. Climate Change Effects on a Miniature Ocean: The Highly Diverse, Highly Impacted Mediterranean Sea. Trends Ecol. Evol. 2010, 25, 250–260. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, R.G.A.; Haarer, J.; Ibm, H.J.; Bethoux, J.; Gentili, B.; Raunet, J.; Tailliez, D. Warming Trend in the Western Mediterranean Deep Water. Nature 1990, 347, 660–662. [Google Scholar] [CrossRef]
- Nykjaer, L. Mediterranean Sea Surface Warming 1985–2006. Clim. Res. 2009, 39, 11–17. [Google Scholar] [CrossRef]
- Raitsos, D.E.; Beaugrand, G.; Georgopoulos, D.; Zenetos, A.; Pancucci-Papadopoulou, A.M.; Theocharis, A.; Papathanassiou, E. Global Climate Change Amplifies the Entry of Tropical Species into the Eastern Mediterranean Sea. Limnol. Oceanogr. 2010, 55, 1478–1484. [Google Scholar] [CrossRef]
- Mohamed, B.; Abdallah, A.M.; Alam El-Din, K.; Nagy, H.; Shaltout, M. Inter-Annual Variability and Trends of Sea Level and Sea Surface Temperature in the Mediterranean Sea over the Last 25 Years. Pure Appl. Geophys. 2019, 176, 3787–3810. [Google Scholar] [CrossRef]
- Pastor, F.; Valiente, J.A.; Khodayar, S. A Warming Mediterranean: 38 Years of Increasing Sea Surface Temperature. Remote Sens. 2020, 12, 2687. [Google Scholar] [CrossRef]
- Pisano, A.; Marullo, S.; Artale, V.; Falcini, F.; Yang, C.; Leonelli, F.E.; Santoleri, R.; Nardelli, B.B. New Evidence of Mediterranean Climate Change and Variability from Sea Surface Temperature Observations. Remote Sens. 2020, 12, 132. [Google Scholar] [CrossRef]
- Giorgi, F. Climate Change Hot-Spots. Geophys. Res. Lett. 2006, 33, 8707. [Google Scholar] [CrossRef]
- Tuel, A.; Eltahir, E.A.B. Why Is the Mediterranean a Climate Change Hot Spot? J. Clim. 2020, 33, 5829–5843. [Google Scholar] [CrossRef]
- El Hourany, R.; Mejia, C.; Faour, G.; Crépon, M.; Thiria, S. Evidencing the Impact of Climate Change on the Phytoplankton Community of the Mediterranean Sea Through a Bioregionalization Approach. J. Geophys. Res. Oceans 2021, 126, e2020JC016808. [Google Scholar] [CrossRef]
- Cabrerizo, M.J.; Medina-Sánchez, J.M.; González-Olalla, J.M.; Sánchez-Gómez, D.; Carrillo, P. Microbial plankton responses to multiple environmental drivers in marine ecosystems with different phosphorus limitation degrees. Sci. Total Environ. 2022, 816, 151491. [Google Scholar] [CrossRef] [PubMed]
- Soulié, T.; Vidussi, F.; Courboulès, J.; Mas, S.; Mostajir, B. Metabolic Responses of Plankton to Warming during Different Productive Seasons in Coastal Mediterranean Waters Revealed by In Situ Mesocosm Experiments. Sci. Rep. 2022, 12, 9001. [Google Scholar] [CrossRef]
- Soulié, T.; Vidussi, F.; Mas, S.; Mostajir, B. Functional and Structural Responses of Plankton Communities toward Consecutive Experimental Heatwaves in Mediterranean Coastal Waters. Sci. Rep. 2023, 13, 8050. [Google Scholar] [CrossRef]
- Deserti, M.; Cacciamani, C.; Chiggiato, J.; Rinaldi, A.; Ferrari, C.R. Relationships between Northern Adriatic Sea Mucilage Events and Climate Variability. Sci. Total Environ. 2005, 353, 82–88. [Google Scholar] [CrossRef]
- Molinero, J.C.; Ibanez, F.; Souissi, S.; Buecher, E.; Dallot, S.; Nival, P. Climate Control on the Long-Term Anomalous Changes of Zooplankton Communities in the Northwestern Mediterranean. Glob. Change Biol. 2008, 14, 11–26. [Google Scholar] [CrossRef]
- Vergés, A.; Tomas, F.; Cebrian, E.; Ballesteros, E.; Kizilkaya, Z.; Dendrinos, P.; Karamanlidis, A.A.; Spiegel, D.; Sala, E. Tropical rabbitfish and the deforestation of a warming temperate sea. J. Ecol. 2014, 102, 1518–1527. [Google Scholar] [CrossRef]
- Vasilakopoulos, P.; Raitsos, D.E.; Tzanatos, E.; Maravelias, C.D. Resilience and Regime Shifts in a Marine Biodiversity Hotspot. Sci. Rep. 2017, 7, 13647. [Google Scholar] [CrossRef]
- Christidis, G.; Mandalakis, M.; Anastasiou, T.I.; Tserpes, G.; Peristeraki, P.; Somarakis, S. Keeping Lagocephalus Sceleratus off the Table: Sources of Variation in the Quantity of Ttx, Ttx Analogues, and Risk of Tetrodotoxication. Toxins 2021, 13, 896. [Google Scholar] [CrossRef]
- Coll, M.; Albo-Puigserver, M.; Navarro, J.; Palomera, I.; Dambacher, J.M. Who Is to Blame? Plausible Pressures on Small Pelagic Fish Population Changes in the Northwestern Mediterranean Sea. Mar. Ecol. Prog. Ser. 2019, 617–618, 277–294. [Google Scholar] [CrossRef]
- Maynou, F.; Sabatés, A.; Salat, J. Clues from the Recent Past to Assess Recruitment of Mediterranean Small Pelagic Fishes under Sea Warming Scenarios. Clim. Change 2014, 126, 175–188. [Google Scholar] [CrossRef]
- Moltó, V.; Palmer, M.; Ospina-Álvarez, A.; Pérez-Mayol, S.; Benseddik, A.B.; Gatt, M.; Morales-Nin, B.; Alemany, F.; Catalán, I.A. Projected Effects of Ocean Warming on an Iconic Pelagic Fish and Its Fishery. Sci. Rep. 2021, 11, 8803. [Google Scholar] [CrossRef]
- Tzanatos, E.; Raitsos, D.E.; Triantafyllou, G.; Somarakis, S.; Tsonis, A.A. Indications of a Climate Effect on Mediterranean Fisheries. Clim. Change 2014, 122, 41–54. [Google Scholar] [CrossRef]
- Darmaraki, S.; Denaxa, D.; Theodorou, I.; Livanou, E.; Rigatou, D.; Raitsos, D.E.; Stavrakidis-Zachou, O.; Dimarchopoulou, D.; Bonino, G.; McAdam, R.; et al. Marine Heatwaves in the Mediterranean Sea: A Literature Review. Mediterr. Mar. Sci. 2024, 25, 586–620. [Google Scholar] [CrossRef]
- Longhurst, A.; Sathyendranath, S.; Platt, T.; Caverhill, C. An Estimate of Global Primary Production in the Ocean from Satellite Radiometer Data. J. Plankton Res. 1995, 17, 1245–1271. [Google Scholar] [CrossRef]
- Field, C.B.; Behrenfeld, M.J.; Randerson, J.T.; Falkowski, P. Primary Production of the Biosphere: Integrating Terrestrial and Oceanic Components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Sathyendranath, S.; Platt, T.; Bouman, H.; Ciavatta, S.; Dall’Olmo, G.; Dingle, J.; Groom, S.; Jönsson, B.; Kostadinov, T.S.; et al. Sensing the Ocean Biological Carbon Pump from Space: A Review of Capabilities, Concepts, Research Gaps and Future Developments. Earth Sci. Rev. 2021, 217, 103604. [Google Scholar] [CrossRef]
- Niemi, G.J.; McDonald, M.E. Application of Ecological Indicators. Annu. Rev. Ecol. Evol. Syst. 2004, 35, 89–111. [Google Scholar] [CrossRef]
- Racault, M.F.; Platt, T.; Sathyendranath, S.; Aǧirbaş, E.; Martinez Vicente, V.; Brewin, R. Plankton Indicators and Ocean Observing Systems: Support to the Marine Ecosystem State Assessment. J. Plankton Res. 2014, 36, 621–629. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S. Ecological Indicators for the Pelagic Zone of the Ocean from Remote Sensing. Remote Sens. Environ. 2008, 112, 3426–3436. [Google Scholar] [CrossRef]
- Chisholm, S.W. Phytoplankton size. In Primary Productivity and Biogeochemical Cycles in the Sea; Platt, T., Li, W.K.W., Eds.; Springer: New York, NY, USA, 1992; pp. 213–237. [Google Scholar] [CrossRef]
- McCave, I.N. Vertical Flux of Particles in the Ocean. Deep Sea Res. Oceanogr. Abstr. 1975, 22, 491–502. [Google Scholar] [CrossRef]
- Eppley, R.W.; Peterson, B.J. Particulate Organic Matter Flux and Planktonic New Production in the Deep Ocean. Nature 1979, 282, 677–680. [Google Scholar] [CrossRef]
- Briggs, N.; Perry, M.J.; Cetinić, I.; Lee, C.; D’Asaro, E.; Gray, A.M.; Rehm, E. High-Resolution Observations of Aggregate Flux during a Sub-Polar North Atlantic Spring Bloom. Deep Sea Res. Part I Oceanogr. Res. Pap. 2011, 58, 1031–1039. [Google Scholar] [CrossRef]
- Mouw, C.B.; Barnett, A.; McKinley, G.A.; Gloege, L.; Pilcher, D. Phytoplankton Size Impact on Export Flux in the Global Ocean. Global Biogeochem. Cycles 2016, 30, 1542–1562. [Google Scholar] [CrossRef]
- Henson, S.A.; Laufkötter, C.; Leung, S.; Giering, S.L.C.; Palevsky, H.I.; Cavan, E.L. Uncertain Response of Ocean Biological Carbon Export in a Changing World. Nat. Geosci. 2022, 15, 248–254. [Google Scholar] [CrossRef]
- Legendre, L.; Le Fèvre, J. From Individual Plankton Cells to Pelagic Marine Ecosystems and to Global Biogeochemical Cycles. In Particle Analysis in Oceanography; Springer: Berlin/Heidelberg, Germany, 1991; pp. 261–300. [Google Scholar] [CrossRef]
- Moloney, C.L.; Field, J.G. The Size-Based Dynamics of Plankton Food Webs. I. A Simulation Model of Carbon and Nitrogen Flows. J. Plankton Res. 1991, 13, 1003–1038. [Google Scholar] [CrossRef]
- Finkel, Z.V. Does Phytoplankton Cell Size Matter? The Evolution of Modern Marine Food Webs. In Evolution of Primary Producers in the Sea; Falkowski, P.G., Knoll, A.H., Eds.; Academic Press: Cambridge, MA, USA, 2007; pp. 333–350. [Google Scholar] [CrossRef]
- Sathyendranath, S. (Ed.) Phytoplankton Functional Types from Space; IOCCG Report 15; International Ocean Colour Coordinating Group: Dartmouth, NS, Canada, 2014; p. 156. [Google Scholar]
- Navarro, G.; Alvain, S.; Vantrepotte, V.; Huertas, I.E. Identification of Dominant Phytoplankton Functional Types in the Mediterranean Sea Based on a Regionalized Remote Sensing Approach. Remote Sens. Environ. 2014, 152, 557–575. [Google Scholar] [CrossRef]
- Navarro, G.; Almaraz, P.; Caballero, I.; Vázquez, Á.; Huertas, I.E. Reproduction of Spatio-Temporal Patterns of Major Mediterranean Phytoplankton Groups from Remote Sensing OC-CCI Data. Front. Mar. Sci. 2017, 4, 266825. [Google Scholar] [CrossRef]
- Alvain, S.; Moulin, C.; Dandonneau, Y.; Bréon, F.M. Remote Sensing of Phytoplankton Groups in Case 1 Waters from Global SeaWiFS Imagery. Deep Sea Res. Part I Oceanogr. Res. Pap. 2005, 52, 1989–2004. [Google Scholar] [CrossRef]
- Alvain, S.; Moulin, C.; Dandonneau, Y.; Loisel, H. Seasonal Distribution and Succession of Dominant Phytoplankton Groups in the Global Ocean: A Satellite View. Global Biogeochem. Cycles 2008, 22, GB3001. [Google Scholar] [CrossRef]
- Sammartino, M.; Di Cicco, A.; Marullo, S.; Santoleri, R. Spatio-Temporal Variability of Micro-, Nano- and Pico-Phytoplankton in the Mediterranean Sea from Satellite Ocean Colour Data of SeaWiFS. Ocean Sci. 2015, 11, 759–778. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Devred, E.; Sathyendranath, S.; Lavender, S.J.; Hardman-Mountford, N.J. Model of Phytoplankton Absorption Based on Three Size Classes. Appl. Opt. 2011, 50, 4535–4549. [Google Scholar] [CrossRef] [PubMed]
- Brewin, R.J.W.; Sathyendranath, S.; Hirata, T.; Lavender, S.J.; Barciela, R.M.; Hardman-Mountford, N.J. A Three-Component Model of Phytoplankton Size Class for the Atlantic Ocean. Ecol. Modell. 2010, 221, 1472–1483. [Google Scholar] [CrossRef]
- Di Cicco, A.; Sammartino, M.; Marullo, S.; Santoleri, R. Regional Empirical Algorithms for an Improved Identification of Phytoplankton Functional Types and Size Classes in the Mediterranean Sea Using Satellite Data. Front. Mar. Sci. 2017, 4, 254855. [Google Scholar] [CrossRef]
- Brando, V.E.; Santoleri, R.; Colella, S.; Volpe, G.; Di Cicco, A.; Sammartino, M.; González Vilas, L.; Lapucci, C.; Böhm, E.; Zoffoli, M.L.; et al. Overview of Operational Global and Regional Ocean Colour Essential Ocean Variables Within the Copernicus Marine Service. Remote Sens. 2024, 16, 4588. [Google Scholar] [CrossRef]
- Colella, S.; Brando, V.E.; Di Cicco, A.; D’Alimonte, D.; Forneris, V.; Bracaglia, M. Quality Information Document for Ocean Colour Mediterranean and Black Sea Observation Product Release 4.0; Mercator Ocean International: Toulouse, France, 2024. [Google Scholar] [CrossRef]
- El Hourany, R.; Abboud-Abi Saab, M.; Faour, G.; Mejia, C.; Crépon, M.; Thiria, S. Phytoplankton Diversity in the Mediterranean Sea From Satellite Data Using Self-Organizing Maps. J. Geophys. Res. Oceans 2019, 124, 5827–5843. [Google Scholar] [CrossRef]
- Bracher, A.; Bouman, H.A.; Brewin, R.J.W.; Bricaud, A.; Brotas, V.; Ciotti, A.M.; Clementson, L.; Devred, E.; Di Cicco, A.; Dutkiewicz, S.; et al. Obtaining Phytoplankton Diversity from Ocean Color: A Scientific Roadmap for Future Development. Front. Mar. Sci. 2017, 4, 245888. [Google Scholar] [CrossRef]
- Morel, A.; Prieur, L. Analysis of Variations in Ocean Color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Brewin, R.J.W.; Jackson, T.; Mélin, F.; Platt, T. Ocean-Colour Products for Climate-Change Studies: What Are Their Ideal Characteristics? Remote Sens. Environ. 2017, 203, 125–138. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Morán, X.A.G.; Raitsos, D.E.; Gittings, J.A.; Calleja, M.L.; Viegas, M.; Ansari, M.I.; Al-Otaibi, N.; Huete-Stauffer, T.M.; Hoteit, I. Factors Regulating the Relationship Between Total and Size-Fractionated Chlorophyll-a in Coastal Waters of the Red Sea. Front. Microbiol. 2019, 10, 472071. [Google Scholar] [CrossRef]
- Sun, X.; Brewin, R.J.W.; Sathyendranath, S.; Dall’Olmo, G.; Airs, R.; Barlow, R.; Bracher, A.; Brotas, V.; Kheireddine, M.; Lamont, T.; et al. Coupling Ecological Concepts with an Ocean-Colour Model: Phytoplankton Size Structure. Remote Sens. Environ. 2023, 285, 113415. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Hardman-Mountford, N.J.; Lavender, S.J.; Raitsos, D.E.; Hirata, T.; Uitz, J.; Devred, E.; Bricaud, A.; Ciotti, A.; Gentili, B. An Intercomparison of Bio-Optical Techniques for Detecting Dominant Phytoplankton Size Class from Satellite Remote Sensing. Remote Sens. Environ. 2011, 115, 325–339. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Sathyendranath, S.; Tilstone, G.; Lange, P.K.; Platt, T. A Multicomponent Model of Phytoplankton Size Structure. J. Geophys. Res. Oceans 2014, 119, 3478–3496. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Sathyendranath, S.; Jackson, T.; Barlow, R.; Brotas, V.; Airs, R.; Lamont, T. Influence of Light in the Mixed-Layer on the Parameters of a Three-Component Model of Phytoplankton Size Class. Remote Sens. Environ. 2015, 168, 437–450. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Ciavatta, S.; Sathyendranath, S.; Jackson, T.; Tilstone, G.; Curran, K.; Airs, R.L.; Cummings, D.; Brotas, V.; Organelli, E.; et al. Uncertainty in Ocean-Color Estimates of Chlorophyll for Phytoplankton Groups. Front. Mar. Sci. 2017, 4, 254350. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Tilstone, G.H.; Jackson, T.; Cain, T.; Miller, P.I.; Lange, P.K.; Misra, A.; Airs, R.L. Modelling Size-Fractionated Primary Production in the Atlantic Ocean from Remote Sensing. Prog. Oceanogr. 2017, 158, 130–149. [Google Scholar] [CrossRef]
- Brotas, V.; Brewin, R.J.W.; Sá, C.; Brito, A.C.; Silva, A.; Mendes, C.R.; Diniz, T.; Kaufmann, M.; Tarran, G.; Groom, S.B.; et al. Deriving Phytoplankton Size Classes from Satellite Data: Validation along a Trophic Gradient in the Eastern Atlantic Ocean. Remote Sens. Environ. 2013, 134, 66–77. [Google Scholar] [CrossRef]
- Corredor-Acosta, A.; Morales, C.E.; Brewin, R.J.W.; Auger, P.A.; Pizarro, O.; Hormazabal, S.; Anabalón, V. Phytoplankton Size Structure in Association with Mesoscale Eddies off Central-Southern Chile: The Satellite Application of a Phytoplankton Size-Class Model. Remote Sens. 2018, 10, 834. [Google Scholar] [CrossRef]
- Lamont, T.; Barlow, R.G.; Brewin, R.J.W. Variations in Remotely-Sensed Phytoplankton Size Structure of a Cyclonic Eddy in the Southwest Indian Ocean. Remote Sens. 2018, 10, 1143. [Google Scholar] [CrossRef]
- Lin, J.; Cao, W.; Wang, G.; Hu, S. Satellite-Observed Variability of Phytoplankton Size Classes Associated with a Cold Eddy in the South China Sea. Mar. Pollut. Bull. 2014, 83, 190–197. [Google Scholar]
- Sahay, A.; Ali, S.M.; Gupta, A.; Goes, J.I. Ocean Color Satellite Determinations of Phytoplankton Size Class in the Arabian Sea during the Winter Monsoon. Remote Sens. Environ. 2017, 198, 286–296. [Google Scholar] [CrossRef]
- Liu, X.; Devred, E.; Johnson, C. Remote Sensing of Phytoplankton Size Class in Northwest Atlantic from 1998 to 2016: Bio-Optical Algorithms Comparison and Application. Remote Sens. 2018, 10, 1028. [Google Scholar] [CrossRef]
- Sun, X.; Shen, F.; Brewin, R.J.W.; Liu, D.; Tang, R. Twenty-Year Variations in Satellite-Derived Chlorophyll-a and Phytoplankton Size in the Bohai Sea and Yellow Sea. J. Geophys. Res. Oceans 2019, 124, 8887–8912. [Google Scholar] [CrossRef]
- Sun, X.; Shen, F.; Liu, D.; Bellerby, R.G.J.; Liu, Y.; Tang, R. In Situ and Satellite Observations of Phytoplankton Size Classes in the Entire Continental Shelf Sea, China. J. Geophys. Res. Oceans 2018, 123, 3523–3544. [Google Scholar] [CrossRef]
- Gittings, J.A.; Brewin, R.J.W.; Raitsos, D.E.; Kheireddine, M.; Ouhssain, M.; Jones, B.H.; Hoteit, I. Remotely Sensing Phytoplankton Size Structure in the Red Sea. Remote Sens. Environ. 2019, 234, 111387. [Google Scholar] [CrossRef]
- Gittings, J.A.; Raitsos, D.E.; Brewin, R.J.; Hoteit, I. Links between Phenology of Large Phytoplankton and Fisheries in the Northern and Central Red Sea. Remote Sens. 2021, 13, 231. [Google Scholar] [CrossRef]
- Turner, K.J.; Mouw, C.B.; Hyde, K.J.W.; Morse, R.; Ciochetto, A.B. Optimization and Assessment of Phytoplankton Size Class Algorithms for Ocean Color Data on the Northeast U.S. Continental Shelf. Remote Sens. Environ. 2021, 267, 112729. [Google Scholar] [CrossRef]
- Werdell, P.J.; Bailey, S.; Fargion, G.; Pietras, C.; Knobelspiesse, K.; Feidman, G.; McClain, C. Unique Data Repository Facilitates Ocean Color Satellite Validation. Eos, Trans. Am. Geophys. Union 2003, 84, 377–387. [Google Scholar] [CrossRef]
- Claustre, H.; Antoine, D.; Babin, M.; Belviso, S.; Begovic, M.; Bianchi, M.; Birdwhistell, S.; Blanchot, J.; Bricaud, A.; Bruyant, F.; et al. BIOGEOCHEMICAL Dataset Collected During the PROSOPE Cruise. Available online: https://www.seanoe.org/data/00605/71723/ (accessed on 1 December 2024).
- Antoine, D.; Chami, M.; Claustre, H.; d’Ortenzio, F.; Morel, A.; Becu, G.; Gentili, B.; Louis, F.; Ras, J.; Roussier, E.; et al. BOUSSOLE: A Joint CNRS-INSU, ESA, CNES, and NASA Ocean Color Calibration and Validation Activity; Goddard Space Flight Center: Greenbelt, MD, USA, 2006. [Google Scholar]
- Behrenfeld, M.; Dall’Olmo, G. BOUM08 HLPC Dataset. 2021. Available online: https://seabass.gsfc.nasa.gov/archive/OSU/VF/archive (accessed on 1 December 2024).
- Peloquin, J.; Swan, C.; Gruber, N.; Vogt, M.; Claustre, H.; Ras, J.; Uitz, J.; Barlow, R.; Behrenfeld, M.; Bidigare, R.; et al. The MAREDAT Global Database of High Performance Liquid Chromatography Marine Pigment Measurements. Earth Syst. Sci. Data 2013, 5, 109–123. [Google Scholar] [CrossRef]
- Prieur, L. ALMOFRONT 2—LEG 2 Cruise, RV L’Atalante. 1997. Available online: https://campagnes.flotteoceanographique.fr/campagnes/97010132/. (accessed on 1 December 2024).
- Prieur, L. ALMOFRONT.LEG2 Cruise, RV L’Atalante. 1991. Available online: https://campagnes.flotteoceanographique.fr/campagnes/91004212/ (accessed on 1 December 2024).
- Raimbault, P. MTPII-MATER/MINOS MAY96 Cruise, RV Le Suroît. 1996. Available online: https://campagnes.flotteoceanographique.fr/campagnes/96020030/ (accessed on 1 December 2024).
- Vidussi, F.; Claustre, H.; Manca, B.B.; Luchetta, A.; Marty, J.C. Phytoplankton Pigment Distribution in Relation to Upper Thermocline Circulation in the Eastern Mediterranean Sea during Winter. J. Geophys. Res. Oceans 2001, 106, 19939–19956. [Google Scholar] [CrossRef]
- Chiaverini, J. DYFAMED. 1987. Available online: https://campagnes.flotteoceanographique.fr/series/89/ (accessed on 1 December 2024).
- Taillandier, V.; Wagener, T.; D’Ortenzio, F.; Mayot, N.; Legoff, H.; Ras, J.; Coppola, L.; Pasqueron de Fommervault, O.; Bittig, H.; Lefevre, D.; et al. Oceanographic Dataset in the Mediterranean Sea Collected During the Cruise BioArgoMed. 2021. Available online: https://www.seanoe.org/data/00405/51678/ (accessed on 1 December 2024).
- Livanou, E.; Sauzède, R.; Psarra, S.; Mandalakis, M.; Dall’Olmo, G.; Brewin, R.J.W.; Raitsos, D.E. Evaluating MULTIOBS Chlorophyll-a with Ground-Truth Observations in the Eastern Mediterranean Sea. Remote Sens. 2024, 16, 4705. [Google Scholar] [CrossRef]
- Livanou, E.; Lagaria, A.; Santi, I.; Mandalakis, M.; Pavlidou, A.; Lika, K.; Psarra, S. Pigmented and Heterotrophic Nanoflagellates: Abundance and Grazing on Prokaryotic Picoplankton in the Ultra-Oligotrophic Eastern Mediterranean Sea. Deep Sea Res. Part II Top. Stud. Oceanogr. 2019, 164, 100–111. [Google Scholar] [CrossRef]
- Lagaria, A.; Mandalakis, M.; Mara, P.; Frangoulis, C.; Karatsolis, B.T.; Pitta, P.; Triantaphyllou, M.; Tsiola, A.; Psarra, S. Phytoplankton Variability and Community Structure in Relation to Hydrographic Features in the NE Aegean Frontal Area (NE Mediterranean Sea). Cont. Shelf Res. 2017, 149, 124–137. [Google Scholar] [CrossRef]
- Petihakis, G.; Perivoliotis, L.; Korres, G.; Ballas, D.; Frangoulis, C.; Pagonis, P.; Ntoumas, M.; Pettas, M.; Chalkiopoulos, A.; Sotiropoulou, M.; et al. An Integrated Open-Coastal Biogeochemistry, Ecosystem and Biodiversity Observatory of the Eastern Mediterranean—The Cretan Sea Component of the POSEIDON System. Ocean Sci. 2018, 14, 1223–1245. [Google Scholar] [CrossRef]
- Ntoumas, M.; Perivoliotis, L.; Petihakis, G.; Korres, G.; Frangoulis, C.; Ballas, D.; Pagonis, P.; Sotiropoulou, M.; Pettas, M.; Bourma, E.; et al. The POSEIDON Ocean Observing System: Technological Development and Challenges. J. Mar. Sci. Eng. 2022, 10, 1932. [Google Scholar] [CrossRef]
- Kournopoulou, A.; Kikaki, K.; Varkitzi, I.; Psarra, S.; Assimakopoulou, G.; Karantzalos, K.; Raitsos, D.E. Atlas of Phytoplankton Phenology Indices in Selected Eastern Mediterranean Marine Ecosystems. Sci. Rep. 2024, 14, 9975. [Google Scholar] [CrossRef]
- Aiken, J.; Pradhan, Y.; Barlow, R.; Lavender, S.; Poulton, A.; Holligan, P.; Hardman-Mountford, N. Phytoplankton Pigments and Functional Types in the Atlantic Ocean: A Decadal Assessment, 1995–2005. Deep Sea Res. Part II Topical Stud. Oceanogr. 2009, 56, 899–917. [Google Scholar] [CrossRef]
- Psarra, S.; Livanou, E.; Varkitzi, I.; Lagaria, A.; Assimakopoulou, G.; Pagou, K.; Ignatiades, L. Phytoplankton Dynamics in the Aegean Sea. Handb. Environ. Chem. 2022, 129, 89–114. [Google Scholar] [CrossRef]
- García, C.; Pruzzo, M.; Rodríguez-Unda, N.; Contreras, C.; Lagos, N. Zur Vervollkommung Der Quantitativen Phytoplankton-Methodik. Mitt Int. Ver Limnol. 1958, 9, 38. [Google Scholar] [CrossRef]
- Psarra, S.; Tselepides, A.; Ignatiades, L. Primary Productivity in the Oligotrophic Cretan Sea (NE Mediterranean): Seasonal and Interannual Variability. Prog. Oceanogr. 2000, 46, 187–204. [Google Scholar] [CrossRef]
- Galgani, L.; Tsapakis, M.; Pitta, P.; Tsiola, A.; Tzempelikou, E.; Kalantzi, I.; Esposito, C.; Loiselle, A.; Tsotskou, A.; Zivanovic, S.; et al. Microplastics Increase the Marine Production of Particulate Forms of Organic Matter. Environ. Res. Lett. 2019, 14, 124085. [Google Scholar] [CrossRef]
- Oikonomou, A.; Livanou, E.; Mandalakis, M.; Lagaria, A.; Psarra, S. Grazing Effect of Flagellates on Bacteria in Response to Phosphate Addition in the Oligotrophic Cretan Sea, NE Mediterranean. FEMS Microbiol. Ecol. 2020, 96, 86. [Google Scholar] [CrossRef]
- Ktistaki, G.; Magiopoulos, I.; Corno, G.; Courboulès, J.; Eckert, E.M.; González, J.; Kalantzi, I.; Middelboe, M.; Symiakaki, K.; Tsapakis, M.; et al. Brownification in the Eastern Mediterranean Sea: Effect of Simulated Terrestrial Input on the Planktonic Microbial Food Web in an Oligotrophic Sea. Front. Mar. Sci. 2024, 11, 1343415. [Google Scholar] [CrossRef]
- Berthon, J.-F.; Zibordi, G.; Ois Berthon, J.-F.; Zibordi, G. Bio-Optical Relationships for the Northern Adriatic Sea. Int. J. Remote Sens. 2004, 25, 1527–1532. [Google Scholar] [CrossRef]
- Volpe, G.; Colella, S.; Brando, V.E.; Forneris, V.; La Padula, F.; Di Cicco, A.; Sammartino, M.; Bracaglia, M.; Artuso, F.; Santoleri, R. Mediterranean Ocean Colour Level 3 Operational Multi-Sensor Processing. Ocean Sci. 2019, 15, 127–146. [Google Scholar] [CrossRef]
- Concha, J.A.; Bracaglia, M.; Brando, V.E. Assessing the Influence of Different Validation Protocols on Ocean Colour Match-up Analyses. Remote Sens. Environ. 2021, 259, 112415. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Brewin, R.J.W.; Brockmann, C.; Brotas, V.; Calton, B.; Chuprin, A.; Cipollini, P.; Couto, A.B.; Dingle, J.; Doerffer, R. An Ocean-Colour Time Series for Use in Climate Studies: The Experience of the Ocean-Colour Climate Change Initiative (OC-CCI). Sensors 2019, 19, 4285. [Google Scholar]
- Pisano, A.; Buongiorno Nardelli, B.; Tronconi, C.; Santoleri, R. The New Mediterranean Optimally Interpolated Pathfinder AVHRR SST Dataset (1982–2012). Remote Sens. Environ. 2016, 176, 107–116. [Google Scholar] [CrossRef]
- Claustre, H. The Trophic Status of Various Oceanic Provinces as Revealed by Phytoplankton Pigment Signatures. Limnol. Oceanogr. 1994, 39, 1206–1210. [Google Scholar]
- Uitz, J.; Claustre, H.; Morel, A.; Hooker, S.B. Vertical Distribution of Phytoplankton Communities in Open Ocean: An Assessment Based on Surface Chlorophyll. J. Geophys. Res. Oceans 2006, 111, C08005. [Google Scholar] [CrossRef]
- Devred, E.; Sathyendranath, S.; Stuart, V.; Platt, T. Remote Sensing of Environment A Three Component Classification of Phytoplankton Absorption Spectra: Application to Ocean-Color Data. Remote Sens. Environ. 2011, 115, 2255–2266. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Cota, G.; Stuart, V.; Maass, H.; Platt, T. Remote Sensing of Phytoplankton Pigments: A Comparison of Empirical and Theoretical Approaches. Int. J. Remote Sens. 2001, 22, 249–273. [Google Scholar] [CrossRef]
- Raimbault, P. Size Fractionation of Phytoplankton in the Ligurian Sea and the Algerian Basin (Mediterranean Sea): Size Distribution versus Total Concentration. Mar. Microb. Food Webs 1988, 3, 1–7. [Google Scholar]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 569–593. [Google Scholar]
- Brewin, R.J.; Hirata, T.; Hardman-Mountford, N.J.; Lavender, S.J.; Sathyendranath, S.; Barlow, R. The influence of the Indian Ocean Dipole on interannual variations in phytoplankton size structure as revealed by Earth Observation. Deep Sea Res. Part II Top. Stud. Oceanogr. 2012, 77, 117–127. [Google Scholar] [CrossRef]
- Seegers, B.N.; Stumpf, R.P.; Schaeffer, B.A.; Loftin, K.A.; Werdell, P.J. Performance Metrics for the Assessment of Satellite Data Products: An Ocean Color Case Study. Opt. Express 2018, 26, 7404–7422. [Google Scholar] [CrossRef]
- Stramski, D.; Joshi, I.; Reynolds, R.A. Ocean Color Algorithms to Estimate the Concentration of Particulate Organic Carbon in Surface Waters of the Global Ocean in Support of a Long-Term Data Record from Multiple Satellite Missions. Remote Sens. Environ. 2022, 269, 112776. [Google Scholar] [CrossRef]
- Kong, C.E.; Sathyendranath, S.; Jackson, T.; Stramski, D.; Brewin, R.J.W.; Kulk, G.; Jönsson, B.F.; Loisel, H.; Galí, M.; Le, C. Comparison of Ocean-Colour Algorithms for Particulate Organic Carbon in Global Ocean. Front. Mar. Sci. 2024, 11, 1309050. [Google Scholar] [CrossRef]
- Broomell, S.B.; Budescu, D.V.; Por, H.H. Pair-Wise Comparisons of Multiple Models. Judgm. Decis. Mak. 2011, 6, 821–831. [Google Scholar] [CrossRef]
- Ward, B.A. Temperature-Correlated Changes in Phytoplankton Community Structure Are Restricted to Polar Waters. PLoS ONE 2015, 10, e0135581. [Google Scholar] [CrossRef]
- Marty, J.C.; Chiavérini, J.; Pizay, M.D.; Avril, B. Seasonal and Interannual Dynamics of Nutrients and Phytoplankton Pigments in the Western Mediterranean Sea at the DYFAMED Time-Series Station (1991–1999). Deep Sea Res. Part II Topical Stud. Oceanogr. 2002, 49, 1965–1985. [Google Scholar] [CrossRef]
- Arin, L.; Morán, X.A.G.; Estrada, M. Phytoplankton Size Distribution and Growth Rates in the Alboran Sea (SW Mediterranean): Short Term Variability Related to Mesoscale Hydrodynamics. J. Plankton Res. 2002, 24, 1019–1033. [Google Scholar] [CrossRef]
- Ignatiades, L.; Psarra, S.; Zervakis, V.; Pagou, K.; Souvermezoglou, E.; Assimakopoulou, G.; Gotsis-Skretas, O. Phytoplankton Size-Based Dynamics in the Aegean Sea (Eastern Mediterranean). J. Mar. Syst. 2002, 36, 11–28. [Google Scholar] [CrossRef]
- Psarra, S.; Zohary, T.; Krom, M.D.; Mantoura, R.F.C.; Polychronaki, T.; Stambler, N.; Tanaka, T.; Tselepides, A.; Thingstad, F. Phytoplankton Response to a Lagrangian Phosphate Addition in the Levantine Sea (Eastern Mediterranean). Deep Sea Res. Part II Top. Stud. Oceanogr. 2005, 52, 2944–2960. [Google Scholar] [CrossRef]
- Uitz, J.; Stramski, D.; Gentili, B.; D’Ortenzio, F.; Claustre, H. Estimates of Phytoplankton Class-Specific and Total Primary Production in the Mediterranean Sea from Satellite Ocean Color Observations. Global Biogeochem. Cycles 2012, 26. [Google Scholar] [CrossRef]
- Varkitzi, I.; Psarra, S.; Assimakopoulou, G.; Pavlidou, A.; Krasakopoulou, E.; Velaoras, D.; Papathanassiou, E.; Pagou, K. Phytoplankton Dynamics and Bloom Formation in the Oligotrophic Eastern Mediterranean: Field Studies in the Aegean, Levantine and Ionian Seas. Deep Sea Res. Part II Top. Stud. Oceanogr. 2020, 171, 104662. [Google Scholar] [CrossRef]
- Jacquet, S.; Lennon, J.F.; Marie, D.; Vaulot, D. Picoplankton Population Dynamics in Coastal Waters of the Northwestern Mediterranean Sea. Limnol. Oceanogr. 1998, 43, 1916–1931. [Google Scholar] [CrossRef]
- Agawin, N.S.R.; Duarte, C.M.; Agustí, S. Nutrient and Temperature Control of the Contribution of Picoplankton to Phytoplankton Biomass and Production. Limnol. Oceanogr. 2000, 45, 591–600. [Google Scholar] [CrossRef]
- Cerino, F.; Bernardi Aubry, F.; Coppola, J.; La Ferla, R.; Maimone, G.; Socal, G.; Totti, C. Spatial and Temporal Variability of Pico-, Nano- and Microphytoplankton in the Offshore Waters of the Southern Adriatic Sea (Mediterranean Sea). Cont. Shelf Res. 2012, 44, 94–105. [Google Scholar] [CrossRef]
- van de Poll, W.H.; Boute, P.G.; Rozema, P.D.; Buma, A.G.J.; Kulk, G.; Rijkenberg, M.J.A. Sea Surface Temperature Control of Taxon Specific Phytoplankton Production along an Oligotrophic Gradient in the Mediterranean Sea. Mar. Chem. 2015, 177, 536–544. [Google Scholar] [CrossRef]
- Pulina, S.; Brutemark, A.; Suikkanen, S.; Padedda, B.M.; Grubisic, L.M.; Satta, C.T.; Caddeo, T.; Farina, P.; Sechi, N.; Lugliè, A. Effects of Warming on a Mediterranean Phytoplankton Community. Web Ecol. 2016, 16, 89–92. [Google Scholar] [CrossRef]
- Raven, J.A. The Twelfth Tansley Lecture. Small Is Beautiful: The Picophytoplankton. New Phytol. 1998, 140, 9–13. [Google Scholar]
- Morán, X.A.G.; López-Urrutia, Á.; Calvo-Díaz, A.; LI, W.K.W. Increasing Importance of Small Phytoplankton in a Warmer Ocean. Glob. Change Biol. 2010, 16, 1137–1144. [Google Scholar] [CrossRef]
- Marañón, E.; Cermeño, P.; Latasa, M.; Tadonléké, R.D. Temperature, Resources, and Phytoplankton Size Structure in the Ocean. Limnol. Oceanogr. 2012, 57, 1266–1278. [Google Scholar] [CrossRef]
- Ramírez-Romero, E.; Molinero, J.C.; Sommer, U.; Salhi, N.; Kéfi-Daly Yahia, O.; Daly Yahia, M.N. Phytoplankton Size Changes and Diversity Loss in the Southwestern Mediterranean Sea in Relation to Long-Term Hydrographic Variability. Estuar. Coast. Shelf Sci. 2020, 235, 106574. [Google Scholar] [CrossRef]
- Hillebrand, H.; Acevedo-Trejos, E.; Moorthi, S.D.; Ryabov, A.; Striebel, M.; Thomas, P.K.; Schneider, M.L. Cell Size as Driver and Sentinel of Phytoplankton Community Structure and Functioning. Funct. Ecol. 2022, 36, 276–293. [Google Scholar] [CrossRef]
- Marañón, E.; Holligan, P.; Barciela, R.; González, N.; Mouriño, B.; Pazó, M.; Varela, M. Patterns of Phytoplankton Size Structure and Productivity in Contrasting Open-Ocean Environments. Mar. Ecol. Prog. Ser. 2001, 216, 43–56. [Google Scholar] [CrossRef]
- Leblanc, K.; Quéguiner, B.; Diaz, F.; Cornet, V.; Michel-Rodriguez, M.; Durrieu De Madron, X.; Bowler, C.; Malviya, S.; Thyssen, M.; Grégori, G.; et al. Nanoplanktonic Diatoms Are Globally Overlooked but Play a Role in Spring Blooms and Carbon Export. Nat. Commun. 2018, 9, 953. [Google Scholar] [CrossRef]
- Marty, J.C.; Chiavérini, J. Hydrological Changes in the Ligurian Sea (NW Mediterranean, DYFAMED Site) during 1995-2007 and Biogeochemical Consequences. Biogeosciences 2010, 7, 2117–2128. [Google Scholar] [CrossRef]
- Ciavatta, S.; Kay, S.; Brewin, R.J.W.; Cox, R.; Di Cicco, A.; Nencioli, F.; Polimene, L.; Sammartino, M.; Santoleri, R.; Skákala, J.; et al. Ecoregions in the Mediterranean Sea Through the Reanalysis of Phytoplankton Functional Types and Carbon Fluxes. J. Geophys. Res. Oceans 2019, 124, 6737–6759. [Google Scholar] [CrossRef]
- Pan, X.; Wong, G.T.F.; Ho, T.Y.; Shiah, F.K.; Liu, H. Remote Sensing of Picophytoplankton Distribution in the Northern South China Sea. Remote Sens. Environ. 2013, 128, 162–175. [Google Scholar] [CrossRef]
- Mozetič, P.; Francé, J.; Kogovšek, T.Š.; Talaber, I.; Malej, A. Plankton Trends and Community Changes in a Coastal Sea (Northern Adriatic): Bottom-up vs. Top-down Control in Relation to Environmental Drivers. Estuar. Coast. Shelf Sci. 2012, 115, 138–148. [Google Scholar] [CrossRef]
- Maugendre, L.; Gattuso, J.P.; Louis, J.; De Kluijver, A.; Marro, S.; Soetaert, K.; Gazeau, F. Effect of Ocean Warming and Acidification on a Plankton Community in the NW Mediterranean Sea. ICES J. Mar. Sci. 2015, 72, 1744–1755. [Google Scholar] [CrossRef]
- Li, M.; Organelli, E.; Serva, F.; Bellacicco, M.; Landolfi, A.; Pisano, A.; Marullo, S.; Shen, F.; Mignot, A.; van Gennip, S.; et al. Phytoplankton spring bloom inhibited by marine heatwaves in the North-Western Mediterranean Sea. Geophys. Res. Lett. 2024, 51, e2024GL109141. [Google Scholar] [CrossRef]
- Neri, F.; Garzia, A.; Ubaldi, M.; Romagnoli, T.; Accoroni, S.; Coluccelli, A.; Di Cicco, A.; Memmola, F.; Falco, P.; Totti, C. Ocean Warming, Marine Heatwaves and Phytoplankton Biomass: Long-Term Trends in the Northern Adriatic Sea. Estuar. Coast. Shelf Sci. 2025, 322, 109282. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; O’Malley, R.T.; Siegel, D.A.; McClain, C.R.; Sarmiento, J.L.; Feldman, G.C.; Milligan, A.J.; Falkowski, P.G.; Letelier, R.M.; Boss, E.S. Climate-Driven Trends in Contemporary Ocean Productivity. Nature 2006, 444, 752–755. [Google Scholar] [CrossRef]
- Bopp, L.; Aumont, O.; Cadule, P.; Alvain, S.; Gehlen, M. Response of Diatoms Distribution to Global Warming and Potential Implications: A Global Model Study. Geophys. Res. Lett. 2005, 32, L19606. [Google Scholar] [CrossRef]
- Hirata, T.; Aiken, J.; Hardman-Mountford, N.; Smyth, T.J.; Barlow, R.G. An Absorption Model to Determine Phytoplankton Size Classes from Satellite Ocean Colour. Remote Sens. Environ. 2008, 112, 3153–3159. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Sathyendranath, S.; Lange, P.K.; Tilstone, G. Comparison of Two Methods to Derive the Size-Structure of Natural Populations of Phytoplankton. Deep Sea Res. I Oceanogr. Res. Pap. 2014, 85, 72–79. [Google Scholar] [CrossRef]
- Worden, A.Z.; Nolan, J.K.; Palenik, B. Assessing the Dynamics and Ecology of Marine Picophytoplankton: The Importance of the Eukaryotic Component. Limnol. Oceanogr. 2004, 49, 168–179. [Google Scholar] [CrossRef]
- Shi, X.L.; Lepère, C.; Scanlan, D.J.; Vaulot, D. Plastid 16S RRNA Gene Diversity among Eukaryotic Picophytoplankton Sorted by Flow Cytometry from the South Pacific Ocean. PLoS ONE 2011, 6, e18979. [Google Scholar] [CrossRef]
- Rii, Y.M.; Duhamel, S.; Bidigare, R.R.; Karl, D.M.; Repeta, D.J.; Church, M.J. Diversity and Productivity of Photosynthetic Picoeukaryotes in Biogeochemically Distinct Regions of the South East Pacific Ocean. Limnol. Oceanogr. 2016, 61, 806–824. [Google Scholar] [CrossRef]
- Shi, X.L.; Marie, D.; Jardillier, L.; Scanlan, D.J.; Vaulot, D. Groups without Cultured Representatives Dominate Eukaryotic Picophytoplankton in the Oligotrophic South East Pacific Ocean. PLoS ONE 2009, 4, e7657. [Google Scholar] [CrossRef]
- Lagaria, A.; Mandalakis, M.; Mara, P.; Papageorgiou, N.; Pitta, P.; Tsiola, A.; Kagiorgi, M.; Psarra, S. Phytoplankton Response to Saharan Dust Depositions in the Eastern Mediterranean Sea: A Mesocosm Study. Front. Mar. Sci. 2017, 3, 230802. [Google Scholar] [CrossRef]
- Man-Aharonovich, D.; Philosof, A.; Kirkup, B.C.; Le Gall, F.; Yogev, T.; Berman-Frank, I.; Polz, M.F.; Vaulot, D.; Béjà, O. Diversity of Active Marine Picoeukaryotes in the Eastern Mediterranean Sea Unveiled Using Photosystem-II PsbA Transcripts. ISME J. 2010, 4, 1044–1052. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Guo, C.; Pitta, P.; Liu, H. Response of Active Picoeukaryotes to the Deposition of Saharan Dust and European Aerosols in the Eastern Mediterranean Sea. Aquat. Microb. Ecol. 2018, 82, 31–42. [Google Scholar] [CrossRef]
- Chase, A.P.; Kramer, S.J.; Haëntjens, N.; Boss, E.S.; Karp-Boss, L.; Edmondson, M.; Graff, J.R. Evaluation of Diagnostic Pigments to Estimate Phytoplankton Size Classes. Limnol. Oceanogr. Methods 2020, 18, 570–584. [Google Scholar] [CrossRef]
- Hirata, T.; Hardman-Mountford, N.J.; Brewin, R.J.W.; Aiken, J.; Barlow, R.; Suzuki, K.; Isada, T.; Howell, E.; Hashioka, T.; Noguchi-Aita, M.; et al. Synoptic Relationships between Surface Chlorophyll-a and Diagnostic Pigments Specific to Phytoplankton Functional Types. Biogeosciences 2011, 8, 311–327. [Google Scholar] [CrossRef]
- Specchia, V.; Zangaro, F.; Tzafesta, E.; Saccomanno, B.; Vadrucci, M.R.; Pinna, M. Environmental DNA Detects Biodiversity and Ecological Features of Phytoplankton Communities in Mediterranean Transitional Waters. Sci. Rep. 2023, 13, 15192. [Google Scholar] [CrossRef]






| Model | SST-Independent Model | SST-Dependent Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Study | This study | [58] | [119] | [70] | [71] | [73] | [67] | This study | [71] | [67] | |
| Region | Mediterranean Sea | Atlantic Ocean | Indian Ocean | Global | North Atlantic Ocean | Northeast Atlantic Ocean | Global | Mediterranean Sea | North Atlantic Ocean | Global | |
| N | 1294 | 1935 | 686 | 5841 | 2239 | 1100 | 30,579 | ||||
| Cp,nm (mg m−3) | 2.15 (1.71–2.63) | 1.06 | 0.94 | 0.77 (0.72–0.84) | 0.82 (0.76–0.88) | 0.28 | 0.95 (0.927–0.968) | ||||
| G1 | −1.57 (−2.18–−1.45) | −1.51 (−1.57–−1.43) | −0.56 (−0.562–−0.549) | ||||||||
| G2 | −3.51 (−4.21–−2.45) | −1.25 (−1.41–−1.25) | −3.79 (−4.053–−3.549) | ||||||||
| G3 | 12.83 (12.59–12.87) | 14.95 (14.87–15.05) | 1.92 (1.888–1.944) | ||||||||
| G4 | −0.14 (−0.16–−0.11) | 0.25 (0.23–0.26) | −0.14 (−0.142–−0.137) | ||||||||
| Cpm (mg m−3) | 0.10 (0.09–0.12) | 0.11 | 0.17 | 0.13 (0.12–0.14) | 0.13 (0.12–0.13) | 0.06 | 0.17 (0.167–0.174) | ||||
| H1 | 0.24 (0.16–0.26) | 0.29 (0.28–0.30) | −0.28 (−0.279–−0.272) | ||||||||
| H2 | 0.58 (0.47–0.77) | 3.05 (2.87–3.26) | 1.13 (1.070–1.187) | ||||||||
| H3 | 12.00 (12.00–12.90) | 16.24 (16.19–16.29) | 5.03 (4.957–5.103) | ||||||||
| H4 | 0.69 (0.68–0.75) | 0.56 (0.55−0.57) | 0.89 (0.892–0.898) | ||||||||
| Dp,n | 0.87 (0.86–0.88) | 0.9 | 0.97 | 0.94 (0.93–0.95) | 0.87 (0.86–0.89) | 0.96 | 0.87 (0.868–0.878) | ||||
| J1 | 0.048 (0.046–0.070) | 0.37 (0.367–0.373) | 0.39 (0.390–0.392) | ||||||||
| J2 | 5.20 (−14.41–5.76) | 1.13 (1.10–1.16) | 0.33 (0.330–0.333) | ||||||||
| J3 | 12.91 (12.89–17.99) | 14.89 (14.87–14.91) | 8.02 (8.000–8.047) | ||||||||
| J4 | 0.853 (0.821–0.854) | 0.569 (0.566–0.571) | 0.55 (0.546–0.547) | ||||||||
| Dp | 0.60 (0.56–0.64) | 0.73 | 0.82 | 0.80 (0.78–0.82) | 0.73 (0.71–0.76) | 0.99 | 0.67 (0.658–0.675) | ||||
| O1 | 0.66 (0.52–1.10) | 0.503 (0.501–0.505) | 0.65 (0.647–0.650) | ||||||||
| O2 | 0.35 (−2.30–0.49) | 1.33 (1.31–1.37) | 0.22 (0.222–0.224) | ||||||||
| O3 | 12.00 (12.00–12.54) | 17.31 (17.28–17.32) | 12.79 (12.772–12.800) | ||||||||
| O4 | 0.09 (0–0.52) | 0.258 (0.256–0.259) | 0.09 (0.085–0.087) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gittings, J.A.; Livanou, E.; Sun, X.; Brewin, R.J.W.; Psarra, S.; Mandalakis, M.; Peltekis, A.; Di Cicco, A.; Brando, V.E.; Raitsos, D.E. Remotely Sensing Phytoplankton Size Structure in the Mediterranean Sea: Insights from In Situ Data and Temperature-Corrected Abundance-Based Models. Remote Sens. 2025, 17, 2362. https://doi.org/10.3390/rs17142362
Gittings JA, Livanou E, Sun X, Brewin RJW, Psarra S, Mandalakis M, Peltekis A, Di Cicco A, Brando VE, Raitsos DE. Remotely Sensing Phytoplankton Size Structure in the Mediterranean Sea: Insights from In Situ Data and Temperature-Corrected Abundance-Based Models. Remote Sensing. 2025; 17(14):2362. https://doi.org/10.3390/rs17142362
Chicago/Turabian StyleGittings, John A., Eleni Livanou, Xuerong Sun, Robert J. W. Brewin, Stella Psarra, Manolis Mandalakis, Alexandra Peltekis, Annalisa Di Cicco, Vittorio E. Brando, and Dionysios E. Raitsos. 2025. "Remotely Sensing Phytoplankton Size Structure in the Mediterranean Sea: Insights from In Situ Data and Temperature-Corrected Abundance-Based Models" Remote Sensing 17, no. 14: 2362. https://doi.org/10.3390/rs17142362
APA StyleGittings, J. A., Livanou, E., Sun, X., Brewin, R. J. W., Psarra, S., Mandalakis, M., Peltekis, A., Di Cicco, A., Brando, V. E., & Raitsos, D. E. (2025). Remotely Sensing Phytoplankton Size Structure in the Mediterranean Sea: Insights from In Situ Data and Temperature-Corrected Abundance-Based Models. Remote Sensing, 17(14), 2362. https://doi.org/10.3390/rs17142362








