Abstract
Short-term precipitation forecasting is a core task in meteorological science, aiming to achieve accurate predictions by modeling the spatiotemporal evolution of radar echo sequences, thereby supporting meteorological services and disaster warning systems. However, existing spatiotemporal sequence prediction methods still struggle to disentangle complex spatiotemporal dependencies effectively and fail to capture the nonlinear chaotic characteristics of precipitation systems. This often results in ambiguous predictions, attenuation of echo intensity, and spatial localization errors. To address these challenges, this paper proposes a unified spatiotemporal sequence prediction framework based on spatiotemporal masking, which comprises two stages: self-supervised pre-training and task-oriented fine-tuning. During pre-training, the model learns global structural features of meteorological systems from sparse contexts by randomly masking local spatiotemporal regions of radar images. In the fine-tuning stage, considering the importance of the temporal dimension in short-term precipitation forecasting and the complex long-range dependencies in spatiotemporal evolution of precipitation systems, we design an RNN-based cyclic temporal mask self-encoder model (MAE-RNN) and a transformer-based spatiotemporal attention model (STMT). The former focuses on capturing short-term temporal dynamics, while the latter simultaneously models long-range dependencies across space and time via a self-attention mechanism, thereby avoiding the smoothing effects on high-frequency details that are typical of conventional convolutional or recurrent structures. The experimental results show that STMT improves 3.73% and 2.39% in CSI and HSS key indexes compared with the existing advanced models, and generates radar echo sequences that are closer to the real data in terms of air mass morphology evolution and reflection intensity grading.
1. Introduction
Short-range precipitation forecasting aims to provide short-duration, high temporal and spatial resolution precipitation forecasts, which is the core link between meteorological services and disaster warning, and its accuracy directly affects the efficiency of decision-making in the fields of urban flood control, transportation scheduling and agricultural production [1,2,3]. The core of this task is to predict the radar echo sequence of future moments based on current observations. In essence, the task is a spatiotemporal sequence prediction problem, but there are some significant features.
In traditional video or spatiotemporal prediction tasks [4,5], models usually focus on accurate modeling of deterministic motion paths of rigid objects. However, the spatiotemporal evolution of the precipitation system is significantly different: it is essentially a nonlinear chaotic system governed by multi-scale physical mechanisms. Specifically, the evolution of the precipitation field not only reflects the deterministic advection characteristics of large-scale meteorological systems (e.g., frontal movement [6] and vortex propagation [7]) but also includes local stochastic generation or dissipation behaviors triggered by microphysical processes, such as particle phase transitions and turbulent mixing. Especially critical is the dynamic correlation between global dynamical processes and local stochastic upwelling through multi-physics field coupling. Taking the persistent precipitation triggered by frontal systems as an example [8], its spatiotemporal distribution is characterized not exclusively by spatial advection of the precipitation area, but is mainly driven by nonlinear interactions of physical processes such as convective activity triggered by frontal forcing, particle touch-and-go growth, and evaporative attenuation. For example, even if the large-scale circulation model is accurately captured, small initial errors in the boundary layer water vapor or wind field may be rapidly amplified by nonlinear processes within the short-range forecast timeframe, resulting in significant deviations of the forecast heavy precipitation fallout area and intensity from the actual conditions. This intrinsic interaction between macro and micro scales makes precipitation prediction require modeling the complex equilibrium between deterministic trends and stochastic perturbations simultaneously.
However, most of the previous spatiotemporal prediction methods are designed for traditional tasks, and their theoretical frameworks are difficult to effectively characterize the nonlinear chaotic properties of precipitation systems. Existing methods can be categorized into two types: global trend-driven and local fluctuation capture, but both of them have significant limitations. Global trend-driven (e.g., ConvRNN [9], Swin-Transformer [10]) optimizes the model parameters by minimizing the pixel-by-pixel difference between the predicted sequence and the real observation (e.g., MSE and SSIM). While such methods are effective in capturing large-scale advective features, their ability to characterize the high-frequency details of the precipitation field declines significantly with the extension of the prediction time horizon, leading to a systematic underestimation of the echo strength [11]. For example, Ravuri et al. [12] pointed out that the main reason for the large error in the maximum echo intensity of the ConvLSTM-based deterministic model in strong convective scenarios is that its implicit smoothing prior suppresses the stochastic up-and-down modeling of microphysical processes. Local fluctuation capture methods (e.g., GAN [13], diffusion models [14]) generate diverse prediction samples by implicitly learning data distributions, which theoretically mitigates the ambiguity effect of deterministic models. However, experiments by Leinonen, J. et al. [15] show that despite the realistic details of precipitation textures generated by diffusion models, their spatial location errors rise compared to deterministic models, attributed to the global randomness of the generation process that destroys the dynamical consistency constraints of the meteorological system. Recent related studies have attempted to improve the positional accuracy of GANs by physically constraining the loss function, but the prediction stability is still constrained by the pattern collapse problem [16]. The above shortcomings are rooted in the failure of traditional methods to synergistically model the multi-scale coupling mechanism between the deterministic dynamical evolution of precipitation systems and stochastic microphysical processes. Constructing a hybrid framework that balances physical interpretability and generative accuracy has become a central challenge in the field of short-range precipitation prediction.
Inspired by the MAE [17] method in CV, this paper proposes a unified spatiotemporal sequence prediction framework based on spatiotemporal masking, aiming at effectively solving the spatiotemporal modeling problem in the task of short-range precipitation prediction, which is divided into two phases: the first phase is the self-supervised pre-training phase, and the second phase is the task-oriented fine-tuning phase. In the pre-training phase, a spatiotemporal masking strategy is proposed to force the model to learn the implicit physical constraints (e.g., mass conservation, vorticity advection) of the precipitation field by randomly masking the local spatiotemporal blocks of the input sequence. In the fine-tuning stage, different backbone networks are selected according to different tasks to fine-tune the parameters of the model weights in the pre-training stage. In order to effectively model the spatiotemporal dependencies in short-range precipitation prediction, two different fine-tuning models are proposed in this paper: a temporal modeling approach based on RNN for the temporal dimension of radar image sequences, and a spatiotemporal modeling approach based on the Transformer architecture for complex long-range dependencies in the spatiotemporal evolution of precipitation systems. While both models share the same spatiotemporal representation in the pre-training phase, the respective design architectures are optimized for different spatiotemporal features in the fine-tuning phase.
Experiments show that the framework proposed in this paper has three distinctive features; first, unlike the usual end-to-end single-stage trained models, our framework explicitly decouples generic spatiotemporal feature learning from task-oriented prediction optimization, allowing the model to learn the inherent structure and implicit physical constraints of radar echo data before adapting to the prediction task. Second, the spatiotemporal masking strategy is applied to both spatiotemporal dimensions of the input sequence, and the reconstruction targets the entire original sequence, forcing the model to learn long-range contextual dependencies. Finally, the spatiotemporal representations obtained from pre-training are independent of the specific prediction architecture, allowing us to integrate different backbone networks in the fine-tuning phase. In terms of evaluation metrics and prediction details, our framework significantly improves the prediction performance of the backbone network, and experiments on a dataset with a temporal resolution of 6 min and a spatial resolution of 1 km show that the STMT model improves the CSI and HSS key metrics by 3.73% and 2.39% compared to the existing state-of-the-art models, which proves the model’s effectiveness in the task of predicting precipitation over a short period of time, and brings a higher accuracy and better performance to the meteorological prediction field with higher accuracy, more real-time and more detailed precipitation forecasting capability, which has a wide range of practical application value.
2. Related Work
2.1. Spatiotemporal Sequence Prediction
Existing spatiotemporal sequence prediction methods for precipitation forecasting can be broadly categorized into two paradigms: global trend-driven models and local fluctuation capture models, each with distinct characteristics and limitations.
2.1.1. Global Trend-Driven Models
Global trend-driven models focus on capturing long-term evolutionary trends in data from a global perspective. They usually rely on recursive updates of historical data to predict future states by learning past evolutionary patterns. For example, Shi et al. [9] enhanced the capture of spatiotemporal correlation in precipitation forecasting by extending fully connected LSTM (FC-LSTM) to convolutional LSTM (ConvLSTM). Tian et al. [18] improved image clarity and diversity of intensity distributions in precipitation forecasting by combining Generative Adversarial Networks (GANs) and convolutionally gated recurrent units (ConvGRUs). Han et al. [19] achieved efficient radar echogram prediction by transforming the precipitation forecasting problem into an image-to-image transformation task using a U-Net model with a CNN architecture. Gao et al. [20] achieved efficient radar echogram prediction by proposing a spatial-temporal based Transformer model called Earthformer, utilizing the Cuboid Attention to improve the efficiency of capturing spatiotemporal dependence. These models can effectively capture the global time series trend; however, the global trend-driven models all suffer from prediction ambiguity and local smoothing problems due to the neglect of local stochasticity.
2.1.2. Local Fluctuation Capture Models
Local fluctuation capture models focus on modeling randomness and local variation in the data. These models not only focus on global trends but also try to capture fluctuations and uncertainties in local details, and are able to generate multiple possible predictions for future states. For example, Luo et al. [21] solved the ambiguity problem in precipitation forecasting by using Wasserstein Generative Adversarial Network (WGAN) for adversarial regularization of ConvRNN. Chen et al. [22] proposed Temporal and Spatial GAN (TSGAN) methods to improve the accuracy and spatial detail representation of extreme precipitation forecasts. Philipp Hess et al. [16] improved both the temporal distribution and spatial structure of precipitation by combining a physically constraint-based GAN with the CM2Mc-LPJmL model, to address spatial intermittency and bias in the precipitation field in particular. However, these methods introduce uncontrollable stochasticity that affects the accuracy of forecasts. In addition, these methods often suffer from pattern collapse and are difficult to train.
2.2. Pre-Training and Fine-Tuning
The pre-training [23] and fine-tuning [24] paradigms have shown significant advantages in the field of deep learning due to their strong knowledge transfer capabilities and task adaptation properties. Current research mainly focuses on knowledge encoding in the pre-training phase and domain adaptation in the fine-tuning phase. For example, Ko et al. [25] proposed to optimize the classification accuracy and numerical estimation stability of heavy precipitation events using the U-Net architecture by introducing a pre-training scheme with meteorological a priori and a hybrid loss function for extreme events, which significantly improves the reliability of the short-term heavy precipitation prediction. Zeng et al. [26] designed a three-stage training framework for Tri-Train. By inserting a pre-finetuning transition phase between traditional pre-training and fine-tuning, the semantic fragments related to named entities of scientific literature are automatically filtered using self-supervised comparative learning, which effectively mitigates the semantic gap problem of domain migration in the scientific named entity recognition (SciNER) task. However, existing methods usually assume that the knowledge representations in the pre-training phase are perfectly aligned with the downstream task requirements, and this idealized setting may lead to an implicit bias in the optimization objectives of the two phases. Especially in application scenarios with large differences in data distributions, direct fine-tuning is likely to cause the model to fall into a local optimum, and the domain fitness of the generated results still needs to be further improved.
3. Methods
In this section, a unified spatiotemporal sequence prediction framework based on spatiotemporal masks is proposed with the aim of applying it to the task of short-range precipitation prediction. With the introduction of this unified framework, it is expected to provide a flexible and efficient solution for spatiotemporal sequence prediction tasks.
3.1. Model Structure
This spatiotemporal sequence prediction framework consists of two main phases: the first phase is self-supervised pre-training, and the second phase is task-oriented fine-tuning.
In the self-supervised pre-training phase, the model partially masks the input spatiotemporal sequences through a Masked Modeling strategy, which forces the model to reconstruct the masked region based on the known information to learn the structured features in the spatiotemporal sequences. At this stage, the architecture of the model consists of a mask encoder, an embedded representation layer and a mask decoder. The Mask Encoder is responsible for extracting valid contextual information from unmasked spatiotemporal chunks and generating high-level semantic representations, and the Embedding Layer further maps these semantic features to adapt them to specific spatial and temporal dimensions. The mask decoder then reconstructs the original spatiotemporal sequence based on the semantic representation output by the encoder and the supplementary mask information. The core task of this phase is to drive the model to learn the intrinsic structure of the spatiotemporal data through the reconstruction of the mask image.
In the second stage, the main framework of the model consists of a mask encoder, an embedding layer, a body network, and a mask decoder, and the model is optimized for task-specific prediction capability through a fine-tuning strategy. The spatiotemporal representation obtained in the pre-training phase is adapted for the prediction task using the fine-tuning strategy to ensure that the model can adequately capture the spatiotemporal dependence properties in the precipitation prediction task. The end-to-end optimization of the spatiotemporal sequences through the fine-tuning process enhances the performance of the model in the precipitation prediction task.
Based on this framework, two models are proposed, the first one is based on the propagation structure of temporal information and employs typical temporal models (e.g., RNN-like models) to model temporal dependencies in spatiotemporal sequences. The model relies on a recursive structure in the time dimension to propagate temporal information. However, considering the complexity of spatial dependence and temporal dependence in spatiotemporal sequences, the second model introduces a more efficient attentional mechanism using a Transformer-based architecture that is able to model spatiotemporal features in a unified manner, thus overcoming the limitations of traditional temporal models in modeling long time dependence and further improving the model’s perceptual ability in both spatial and temporal dimensions.
3.2. Self-Supervised Pre-Training Stage
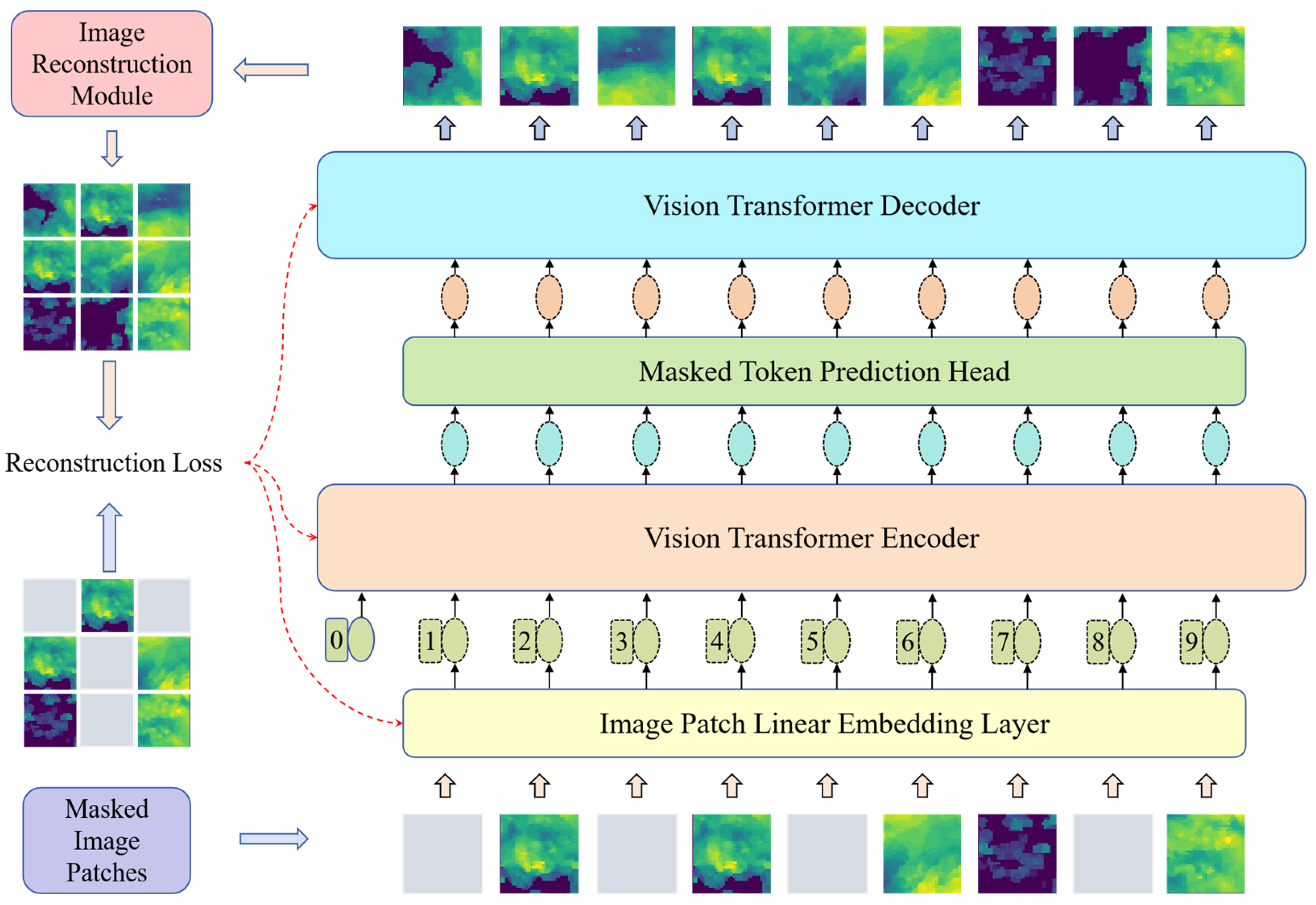
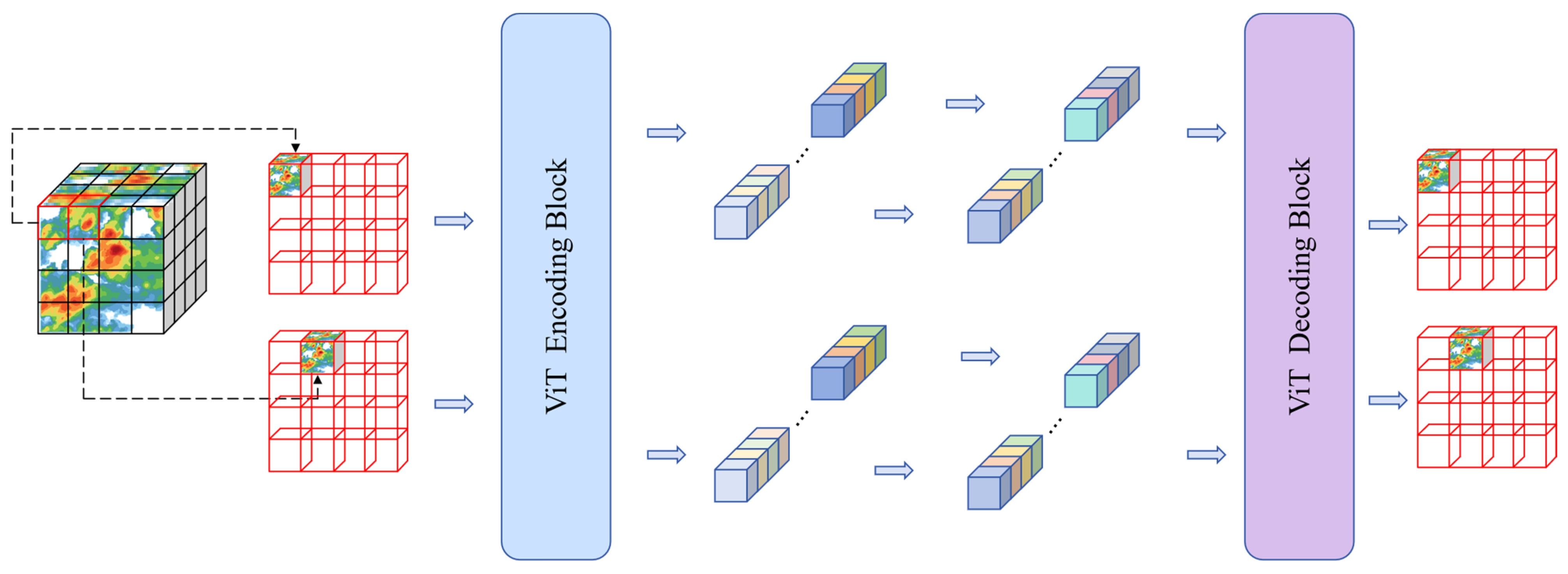
In this stage, the radar echo image is pre-trained by a masked auto-encoder (MAE). The radar image is randomly masked, and the masked portion is reconstructed through the encoding-decoding structure of the self-encoder. The purpose of this process is to learn the underlying patterns and structures in the spatiotemporal sequence, enabling the model to effectively model the spatiotemporal sequence data in subsequent stages. In this way, the model is able to extract useful information from the context of localized image chunks, thus providing an initial spatiotemporal representation in the spatiotemporal sequence prediction task. The structure of the pre-training process model is shown in Figure 1.
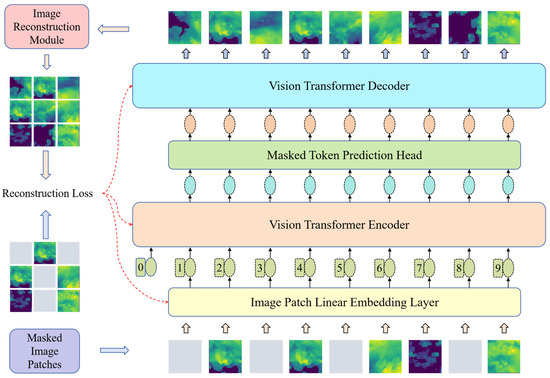
Figure 1.
Model structure of the pre-training phase.
The model architecture is broadly consistent with the MAE model. The MAE combines a masked pre-training technique for sequence data and the spatial structure of the image to enable the model to learn contextual information in the image space. The asymmetric encoding-decoding structure distinguishes the learning tasks of the encoder and decoder. The encoder is responsible for extracting structured information from unmasked image chunks and generating high-level semantic representations of image structures. Note that the masked regions are not input to the encoder but are directly added to the high-level semantic feature tensor output by the encoder. The decoder takes the output of the encoder with the complementary masked image block as input, decodes the high-level semantic features into low-level semantic features, and finally realizes the reconstruction of the masked image.
The operational steps include (1) randomly masking the original radar echo image; (2) inputting the unmasked image block into a linear mapping layer, extracting abstract features, and appending positional encoding; (3) inputting the image block into the encoder as a contextual sequence of tokens for obtaining a high-level semantic feature representation; (4) supplementing the masked tokens at the corresponding positions of the high-level semantic feature tensor; and (5) inputting the supplemented high-level semantic features into the decoder to map to the low-level semantic features.
Ultimately, the model reconstructs the radar echo image. End-to-end training of the model was achieved using pixel-level reconstruction loss as the loss function. The training parameters include the encoder and decoder, as well as the MLP layer that linearly maps the initial image blocks.
3.3. Task-Oriented Fine-Tuning Stage
In the task-oriented fine-tuning phase, for the problem of approaching precipitation forecasting, we propose two models: a temporal modeling approach based on RNN, which is more focused on modeling temporal dependencies and is suitable for capturing short-term variations in the precipitation process, and a spatiotemporal modeling approach based on the Transformer architecture. Modeling spatiotemporal dependence through a global self-attention mechanism, it is capable of handling long-range spatiotemporal evolution. The independent design of the two provides flexibility to choose the most appropriate model for different task requirements.
3.3.1. Radar Echo Sequence Prediction Based on Time Series Information
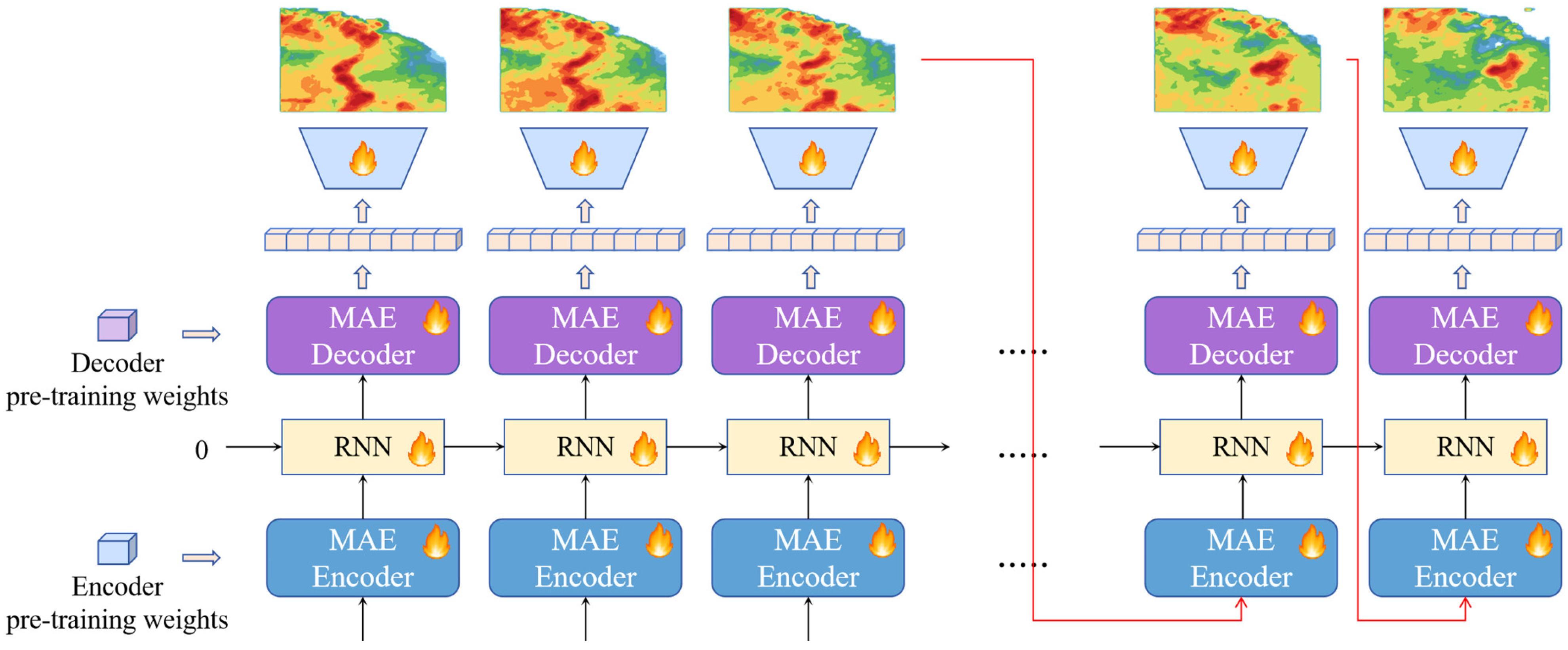
The temporal dimension of radar image sequences is particularly critical in short-range precipitation forecasting, and RNNs [27] are uniquely suited to capture temporal dependencies and are especially suitable for handling tasks with strong temporal correlations. Therefore, this section proposes an RNN-based cyclic temporal mask self-encoder model (MAE-RNN). The model uses the spatiotemporal features learned in the pre-training phase, combined with the temporal propagation capability of RNN networks, to predict spatiotemporal sequences in the temporal dimension. Through the information propagation in the RNN layer, the model is able to capture the short-term dependencies in the precipitation evolution and perform effective time series prediction. The sketch of its network structure is shown in Figure 2.
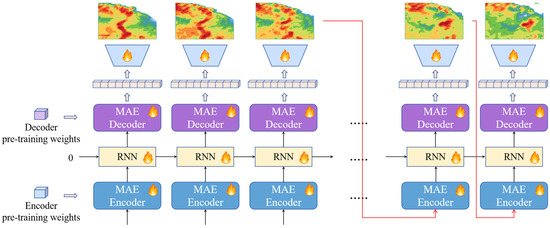
Figure 2.
Cyclic Timing Mask Self-Encoder Model Structure.
The encoder and decoder are pre-trained ViT models whose parameters have been pre-trained on radar echo mask images done through the MAE framework. The recurrent network is the RNN model for propagating the information flow in the time dimension. Due to the domain differences between the reconstruction task of the radar echo mask image and the spatiotemporal sequence prediction problem, the learnable parameters in the encoder, decoder, and recurrent network need to be fine-tuned. The modules marked with a flame icon in Figure 2 are the modules that need to be fine-tuned.
In the generation phase, the model predicts the future radar echo sequence frame by frame in an autoregressive manner, as shown by the red curved arrow in Figure 2. Taking the radar echo image generation process at time t as an example, the operation flow is shown in the following formula:
The MAE encoder takes the output image of the model at moment as the current input. The encoder extracts the structured information in the radar echo image at time to generate a feature tensor with high-level semantics . Subsequently, it is passed into the RNN module and fused with the high-level semantic feature of the antecedent sequence to obtain the spatiotemporal feature with both spatial structural information and temporal correlation. Finally, the spatiotemporal features are transformed from high-level semantic features to low-level semantic features using MAE decoder . In order to alleviate the difference between the masking task and the sequence generation task, an additional simple CNN model is set up. Its role is to transform the low-level semantic features into the pixel space and output the radar echo image at moment .
The cyclic temporal mask self-encoder is a temporal separation model. Encoder can only perceive the radar echo history image of the previous moment and lacks the ability to perceive the sequence context information. The RNN module is responsible for modeling the temporal dependency between the high-level semantic features at each moment output by encoder . The state transfer process inside the RNN module is implemented through the MLP layer, and the semantic features of the image are in the form of a 1D tensor to perform various operations in the network. The role of this model is to integrate the semantic features of historical sequences and express the spatiotemporal relationships of sequence contexts, but it does not have the ability to understand the spatial structure of images. The decoder transforms the spatiotemporal representation of the sequence context by the RNN module into a low-level semantic representation of the radar echo image at the current moment with some spatiotemporal awareness.
3.3.2. Predictive Modeling of Mask Sequences Based on Spatiotemporal Dependence
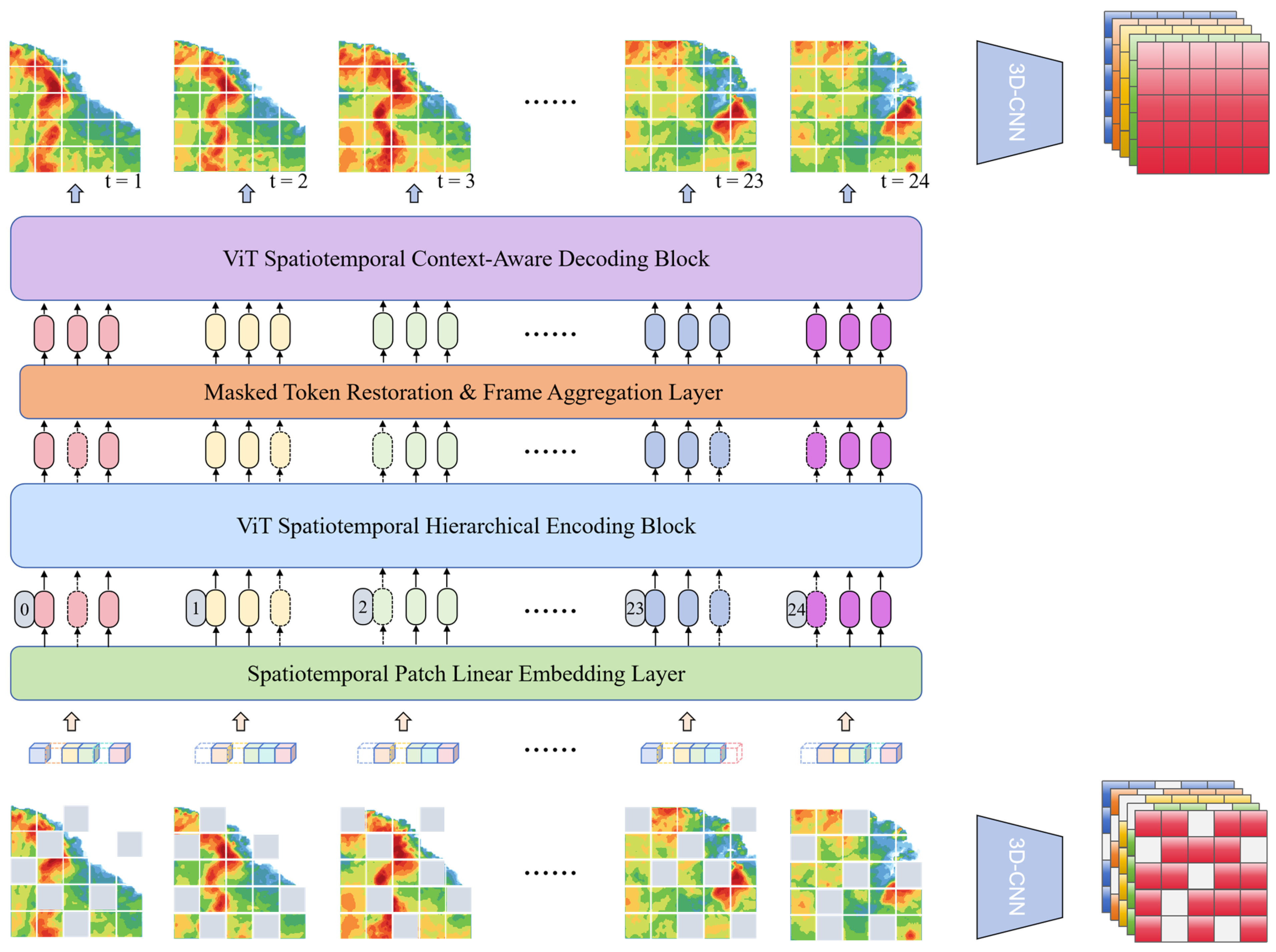
Considering that the spatiotemporal evolution of precipitation systems has complex long-range dependencies, Transformer can capture the long-range dependencies in both spatial and temporal dimensions through the self-attention mechanism, which is crucial for dealing with the inter-temporal evolution in the short-advance precipitation task. Therefore, a spatiotemporal mask sequence prediction model (STMT) based on the Transformer architecture is proposed. The STMT model uses pre-trained spatiotemporal features to efficiently model long-range spatiotemporal dependencies in the fine-tuning stage using the self-attention mechanism. Compared with RNN models, the Transformer architecture is able to focus on global information in both temporal and spatial dimensions, which is especially suitable for dealing with complex spatiotemporal evolutionary processes. Its network structure diagram is shown in Figure 3.
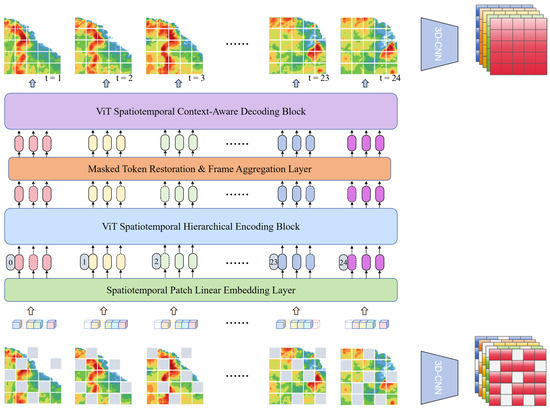
Figure 3.
Structure of Spatiotemporal Mask Sequence Prediction Model (STMT) based on Transformer architecture.
The operational steps include (1) performing a masking operation, i.e., spatiotemporal masking, on the radar echo sequence; (2) stacking the masked sequence into a tensor and inputting it into the 3D-CNN module to extract the spatiotemporal features; (3) inputting unmasked spatiotemporal blocks into the linear mapping layer to obtain the abstract features and adding positional encoding to them; (4) inputting the spatiotemporal blocks into the STMT model using them as a token for the context of the sequence; (5) Finally, the features output from the STMT model are fed into a 3D-CNN-based generative module to recover the unmasked radar echo sequence.
The model processes spatiotemporal data through spatial location embedding, temporal location embedding and Transformer blocks. Spatial location embedding is used to represent the encoding of each spatial location in the image. The dimensions of the input image are set as HxW, where H and W are the height and width of the image, respectively, and temporal embedding is used to encode each time step in the input image sequence. The temporal and spatial embedding can be represented as:
where d is the dimension of the embedding, is the total number of spatial locations in each image, and T is the temporal dimension. For each patch, the spatial and temporal position embeddings are added to the corresponding patches, respectively, by which the model is able to process both spatial and temporal information.
To simulate missing data, the model uses a temporal masking technique. For each sample, a portion of the image and time frame is randomly masked. For each input patch sequence , where N is the batch size, L is the length of the sequence (including spatial location and time step), and d is the dimension of each patch, a random masking operation is performed, setting the masking rate to m and randomly selecting the masking location:
where Xmasked is the masked input, M is the binary matrix of the mask, and R and K are the recovered and preserved mask position indices, respectively.
The pre-training method of spatiotemporal masking is different from the single-image-based masking approach described in the previous section. Spatiotemporal masking takes the spatiotemporal sequence as the masking object, and generates mask blocks randomly according to a set masking rate, which are distributed in the sequence, instead of concentrating all the mask blocks on a particular image. Thus, the goal of the mask reconstruction task for spatiotemporal sequences is to recover the entire original sequence. This approach helps the model to learn structural information about the data in both spatial and temporal dimensions, which enhances the model’s ability to perceive and learn about the spatiotemporal dependencies of the sequence. To accommodate the improvement of the masking mechanism, we design a predictive network based on spatiotemporal mask pre-training STMT. Since the spatiotemporal mask pre-training technique empowers the STMT with spatiotemporal modeling capabilities, we improve the network structure by replacing all functional modules with a Transformer-based architecture that captures both temporal and long-range dependencies in the spatial dimension. Overall, STMT is an improved version of the previously mentioned masked self-encoder based on radar echo data, which realizes a model capable of masking and reconstructing spatiotemporal sequences directly by introducing a spatiotemporal masking mechanism. The model enhances the spatiotemporal modeling capability in the pre-training phase.
3.4. Evaluation Metrics
In order to further validate the superior performance of STMT in the radar echo sequence prediction task, we convert the pixel values in its output radar echo sequence into precipitation metrics, aiming to quantitatively evaluate the performance of STMT with other advanced models in the short-term precipitation prediction task. We selected CSI (Critical Success Index) [28] and HSS (Heidke Skill Score) [29] as the evaluation criteria for model performance, and their formulas are shown below:
where , , , and denote true positive, true negative, false positive and false negative, respectively. Take true positive as an example to illustrate the meaning of the above parameters: when the radar echo intensity (unit: dBZ) of a point in the image is greater than the set threshold and its corresponding true echo intensity is greater than the set threshold, it is a true positive, and the meaning of other parameters is similar. The meanings of the other parameters are similar. The thresholds of CSI and HSS are set to 5, 20, and 40. Short-term precipitation forecasting is an important task for natural disaster reduction, and the CSI metric directly quantifies the accuracy of event detection, which is a major operational concern, reflecting the real cost of underreporting in emergency response. The HSS metric measures the skill of the model relative to random probabilities, considering both positive and negative scenarios, and is widely used by meteorological agencies to evaluate precipitation forecasting systems because it imposes the same penalties for forecasting too high or too low, ensuring robustness to unbalanced rainfall scenarios. A threshold of 5 focuses on the testing of minor precipitation events, while thresholds of 20 and 40 assess the ability of the model to predict heavy and widespread precipitation.
4. Experiments
This section describes the experimental setup, model training process and parameter fine-tuning method. First, we pre-trained the proposed STMT model to optimize the model parameters using the CIKM2017 radar echo sequence data. The dataset contains radargrams with different time spans and height levels, each of which represents the total amount of precipitation at the target site for the next 1 to 2 h, covers an area of 101 × 101 km2, and provides data for 15 time periods at 6-min intervals. Subsequently, a fine-tuning strategy is employed to further enhance the model’s performance with a short-term precipitation forecasting task. In our experiments, we use quantitative metrics such as CSI and HSS to evaluate the model’s performance in real-world applications and compare it with other state-of-the-art models to validate the advantages of the STMT model in the radar echo sequence prediction task.
4.1. Fine-Tuning of Model Parameters
In the pre-training stage, we use the sequence training set of CIKM2017 as the pre-training sample, and the sequence length is 15 frames. The pre-training process is as follows: (1) randomly mask the pixels of the sequence in spatial and temporal dimensions; (2) input the masked spatiotemporal sequence into the model for sequence reconstruction; (3) calculate the error between the reconstructed sequence and the original sequence output by the model at the pixel level, and back-propagate the error to the encoder, the decoder, and the MLP layer, which is responsible for linear mapping of the sequence blocks, in the model to optimize its parameters. Afterward, we keep the parameters of the trained model and perform a fine-tuning operation. The fine-tuning is achieved by performing a prediction task of the radar echo sequence to align the knowledge of the model with the domain knowledge of the spatiotemporal sequence task. The fine-tuning dataset is still selected as the sequence training set of CIKM2017. The process of the fine-tuning operation is as follows: (1) loading the pre-training weights (parameters) of the model; (2) adjusting the parameters of the last layer of the MLP in the decoder to realize the extrapolation function to the radar echo sequence; (3) inputting the historical five-frame radar echo sequence into the model to obtain its output of 15 frames of radar echo sequences (including 10 frames of the future radar echo sequences); and (4) calculating the radar echo sequences outputted by the model with the real radar echo sequence at the pixel level, propagate the error backward to the internal model, and fine-tune the parameters therein. The key component parameters are shown in Table 1.

Table 1.
The key component parameters.
4.2. Visualization of the Effect of Mask Pretraining Reconstruction
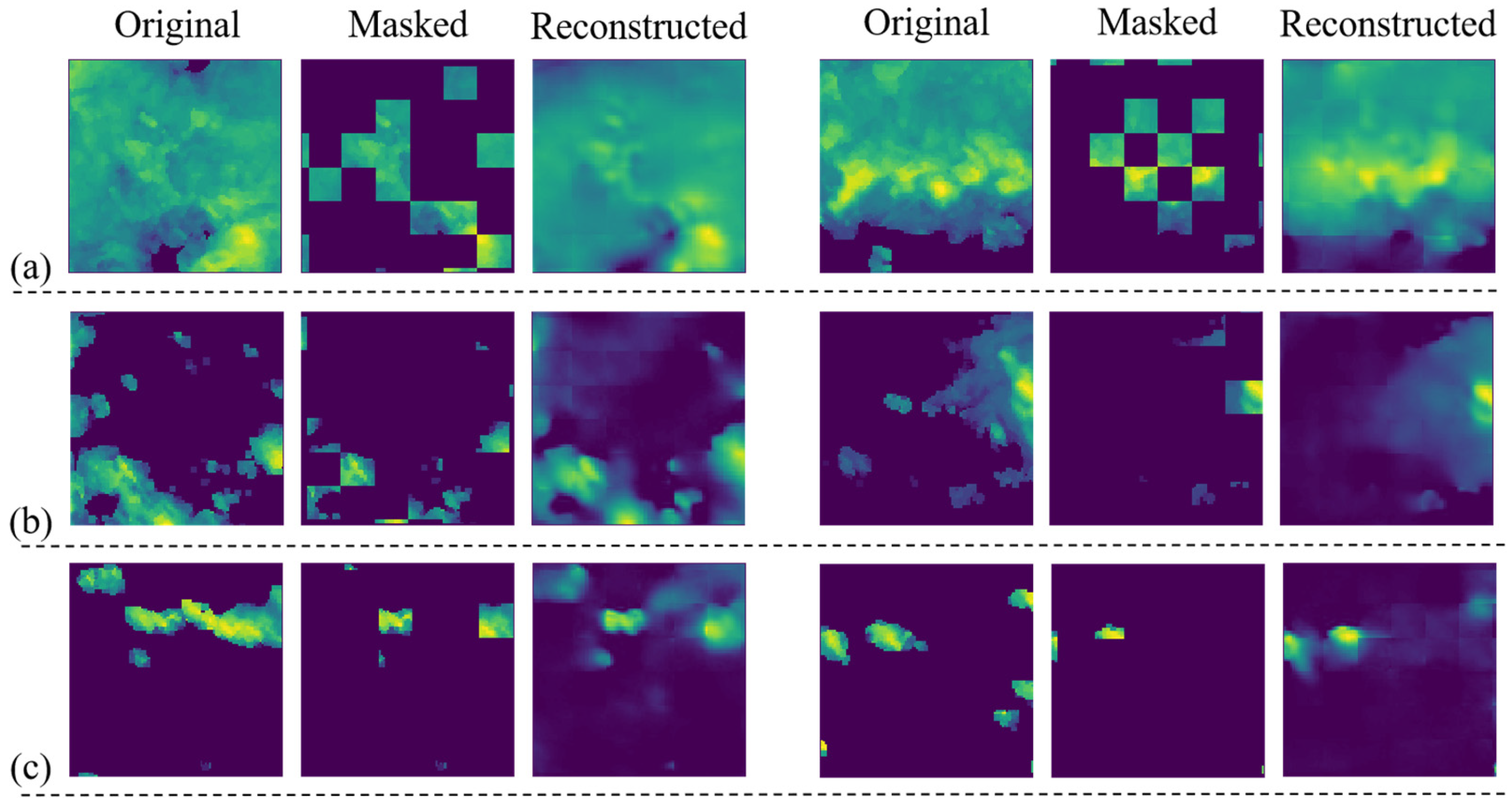
The ViT-Base model is selected for both encoder and decoder, and the radar echo training data is obtained from the CIKM2017 dataset, with the mask rate set to 70%. Figure 4 demonstrates the mask reconstruction effect of the MAE model on the radar echo image.

Figure 4.
Visualization of the effect of masked pre-training reconstruction of radar echo data (70% masking). (a) Large radar echo coverage area; (b) Small radar echo coverage area; (c) Extremely small radar echo coverage area.
Figure 4a shows two example images with larger echo coverage. From the reconstruction results, the model successfully recovers the coverage of the echoes in the region and their reflected intensities. There is a clear difference between the two original radar echo images: in the first sample, all regions have radar reflection intensity, while the lower region of the second sample lacks radar reflection intensity. However, the mask images of the two are similar and fail to reflect these differences in the original images. The model’s mask reconstruction results for these two samples accurately reflect the differences in radar echoes over the regions. This indicates that the model has learned the physical structure of the air mass and related physics to some extent. The model’s ability in mask image reconstruction comes from understanding the structure of the data rather than from mere image interpolation calculations.
Further, Figure 4b shows two example images with smaller echo coverage. From the reconstruction results, the model’s reconstruction of the masked image is similar to the original image in general, but there are slight differences in details. This phenomenon indicates that the model has learned the potential structural knowledge in the radar echo image dataset. The reason for this is that the available information in the masked images of both samples is spatially sparse, which increases the difficulty of image reconstruction. Although the model is different from the original image in details, the distribution of air masses in space and the shape and structure are basically the same as the original image. This shows that the model is not only able to understand the underlying structure of meteorological data, but also has a strong ability to reconstruct mask images.
Since the image masks are randomly generated, the radar echo image after the two masks illustrated in Figure 4c retains only very little usable information. This is an extreme case where the masked image contains almost no structured air mass profile. In this case, it can be viewed as the model generating the radar echo image from a zero initial field. By observing the results of the model’s reconstruction, the distribution and shape of the air mass are consistent with common sense in appearance, even though the reconstruction differs significantly from the original image.
In addition, observing the results of the model’s reconstruction of the first sample, the model generates a localized radar reflection in the lower left region. However, there is no radar reflection in this region in both the original and masked images of this sample. This suggests that the model has the ability to perceive spatial correlation during the reconstruction of the masked image, and is able to infer information about the air mass that may be physically relevant to it based on the initial distribution of the air mass, including the location of its occurrence, its shape, and the intensity of its radar reflections. It is worth noting that the model’s reconstructed images of these two samples do not appear in the dataset. This verifies that the strong reconstruction capability demonstrated by the model in the first two cases does not stem from overfitting the training data, but rather indicates that the model is truly capable of generating radar echo images.
In summary, it can be confirmed that the ViT model can successfully reconstruct the masked radar echo images and that the MAE-based training method can motivate the model to learn the underlying data structures and physical knowledge in the radar echo images. This finding motivates us to use the MAE pre-training model to build a spatiotemporal sequence prediction model for radar echo sequence prediction.
4.3. Numerical Experiment: Short-Range Precipitation Forecasting Based on Radar Echo Sequences
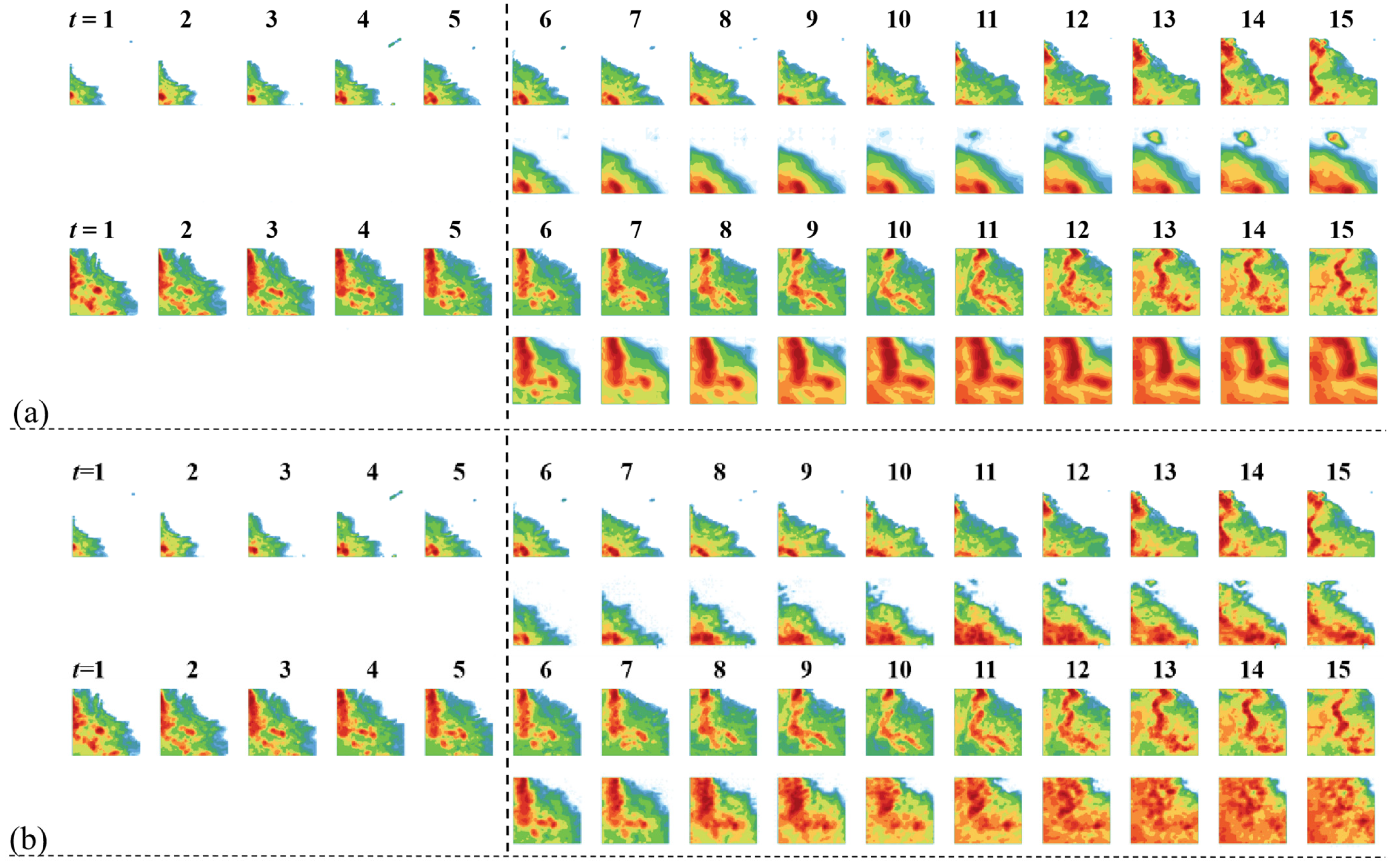
To further validate the effectiveness of the proposed framework in short-term precipitation forecasting tasks, this experiment evaluates its performance in radar echo sequence prediction through numerical experiments. The generated result cases of cyclic timing mask self-encoder and STMT on the CIKM2017 sequence test set are shown in Figure 5.
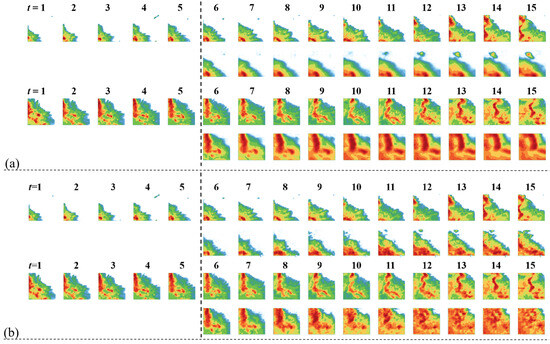
Figure 5.
Examples of short-range precipitation forecast generation results: (a) MAE-RNN generation results; (b) STMT generation results.
As can be seen in Figure 5, the future sequence generated by STMT is highly consistent with the original sequence in terms of details such as air mass deformation and radar echo strength. As far as the subjective human visualization is concerned, the spatiotemporal prediction of STMT is significantly better than that of the cyclic time-sequence mask self-encoder.
The results of the numerical experiments are shown in Table 2. It can be seen that STMT outperforms all comparison models in both CSI and HSS indicators. Among them, the CSI40 indicator reflects the strong rainfall weather in the region, and its prediction accuracy is of great practical significance for effective prevention of strong convective weather. Compared with the state-of-the-art model PredRANN, the accuracy of STMT on this indicator is significantly improved by 3.14%. This result verifies the superiority of STMT in the task of spatiotemporal sequence prediction and its practical application value.

Table 2.
Performance comparison between STMT and comparison models in the CIKM2017 short-term precipitation forecasting task. 5/20/40—threshold settings. Average—average value of the metric under the 5/20/40 thresholds. Bolded values indicate the optimal results, while underlined values indicate the second-best results.
4.4. Predicting the Visual Quality of Sequence Images
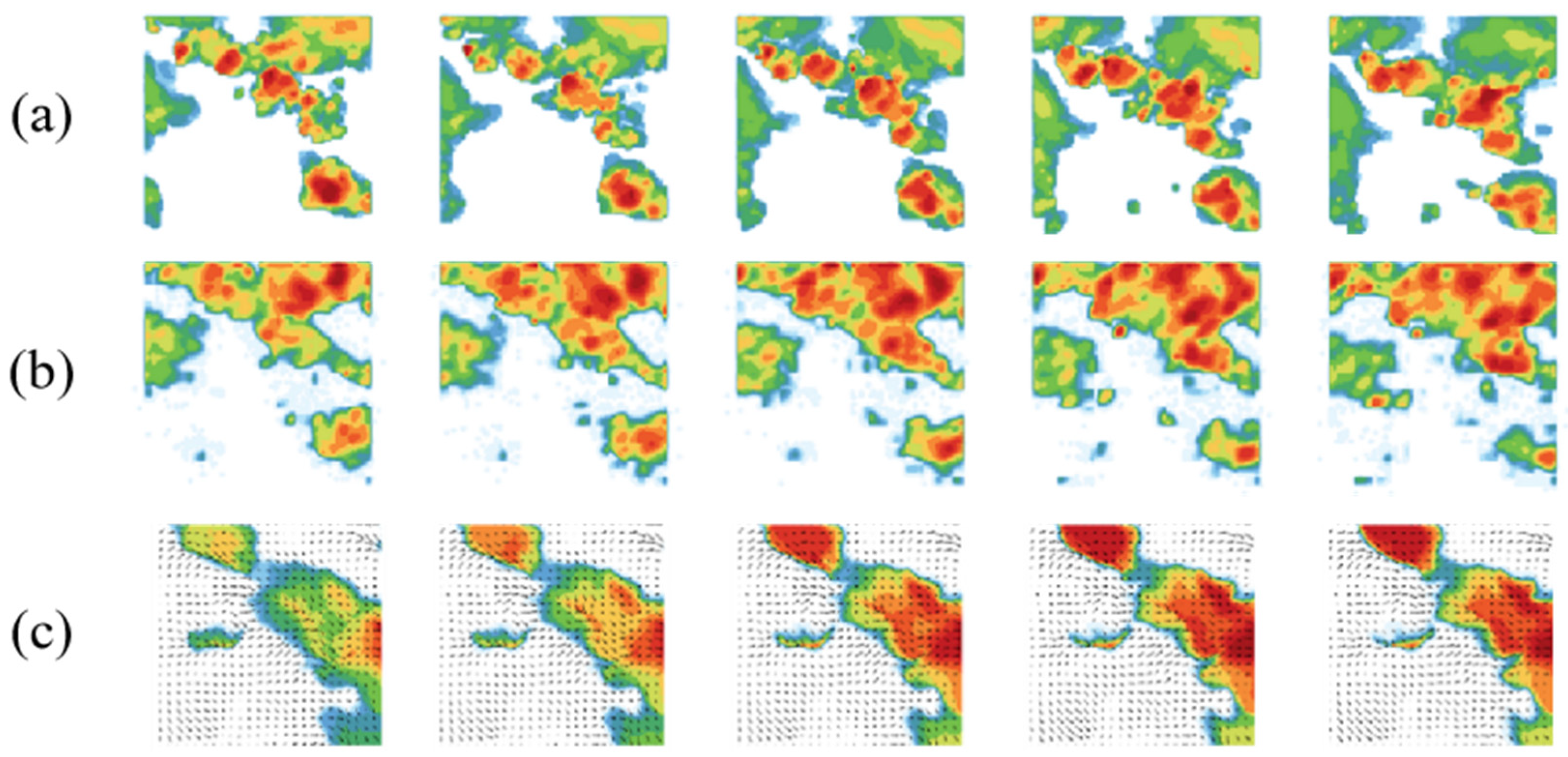
In order to comprehensively assess the performance of the STMT model in the radar echo sequence prediction task, in addition to the traditional quantitative metrics, the visual quality of the model-generated images needs to be further verified. Since radar echo images contain rich spatial and temporal information, the image quality directly affects the accuracy and reliability of short-term precipitation forecasts. Therefore, this experiment analyzes the prediction performance of the STMT model and the optical flow-based prediction model [41] by comparing their retention of details in generating radar echo images. Figure 6 shows five frames of real radar echo sequences and the corresponding sequence prediction results given by the STMT model and the optical flow-based prediction model.
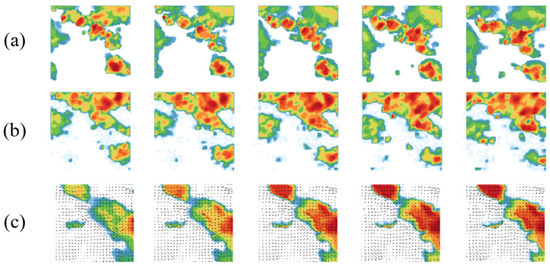
Figure 6.
Comparison of visual quality of generated images: (a) Ground Truth; (b) STMT; (c) Optical Flow.
It can be clearly observed that there is a significant difference between the predicted image quality of the STMT model and the predicted image quality based on optical flow. The future image predicted by the former contains rich detail information, and the radar echo intensity levels in the local area in the figure show obvious hierarchical phenomenon, i.e., there are multiple radar echo intensity levels in the local area (the intensity levels are indicated by the colors in the figure, with the redder representing the higher intensity, the greener representing the lower intensity, and the white representing the intensity of 0). The latter predicted future image lacks the detailed information of radar echo intensity, and the radar echo intensity levels in the local area are closer. Globally, the radar echo intensity level decreases from the center of the maximum intensity to the surrounding space, and the image shows the aggregation of large color blocks. Due to the lack of details, the similarity between the radar echo prediction image and the real image is significantly reduced.
4.5. Ablation Experiment
An ablation experiment was conducted to evaluate the performance improvement of each proposed component within the framework. The first rows of Table 3 show that as the pre-training strategy is removed, the model performance decreases significantly, which proves the effectiveness of the pre-training strategy. Additionally, the performance results under different masking rates (rows 2–4 of Table 2) indicate that the model performs best when the masking rate is set around 70%, effectively learning the inherent structure and implicit physical constraints in radar echo data. This confirms the rationality of the masking rate selection.

Table 3.
Ablation experiment (for STMT). 5/20/40—Threshold values for calculating CSI and HSS indicators. Average—Average values of the CSI and HSS indicators at the 5/20/40 threshold values. Bold numbers indicate the best results.
5. Discussion
In this section, the experimental results are analyzed and discussed in depth, focusing on comparing the performance differences between the STMT model and other spatiotemporal sequence prediction models. The advantages of the STMT model in detail preservation and global air mass evolution modeling are verified through the pixel distribution analysis of the prediction images generated by different models. In addition, from the perspective of model structure, we analyze the differences between the STMT model based on the self-attention mechanism and the models based on convolutional or cyclic structures in dealing with the detail generation of radar echoes, which further elucidates the superiority of the STMT model and its potential for application in spatiotemporal sequence prediction tasks.
5.1. Comparative Analysis of Pixel Distribution of Prediction Results
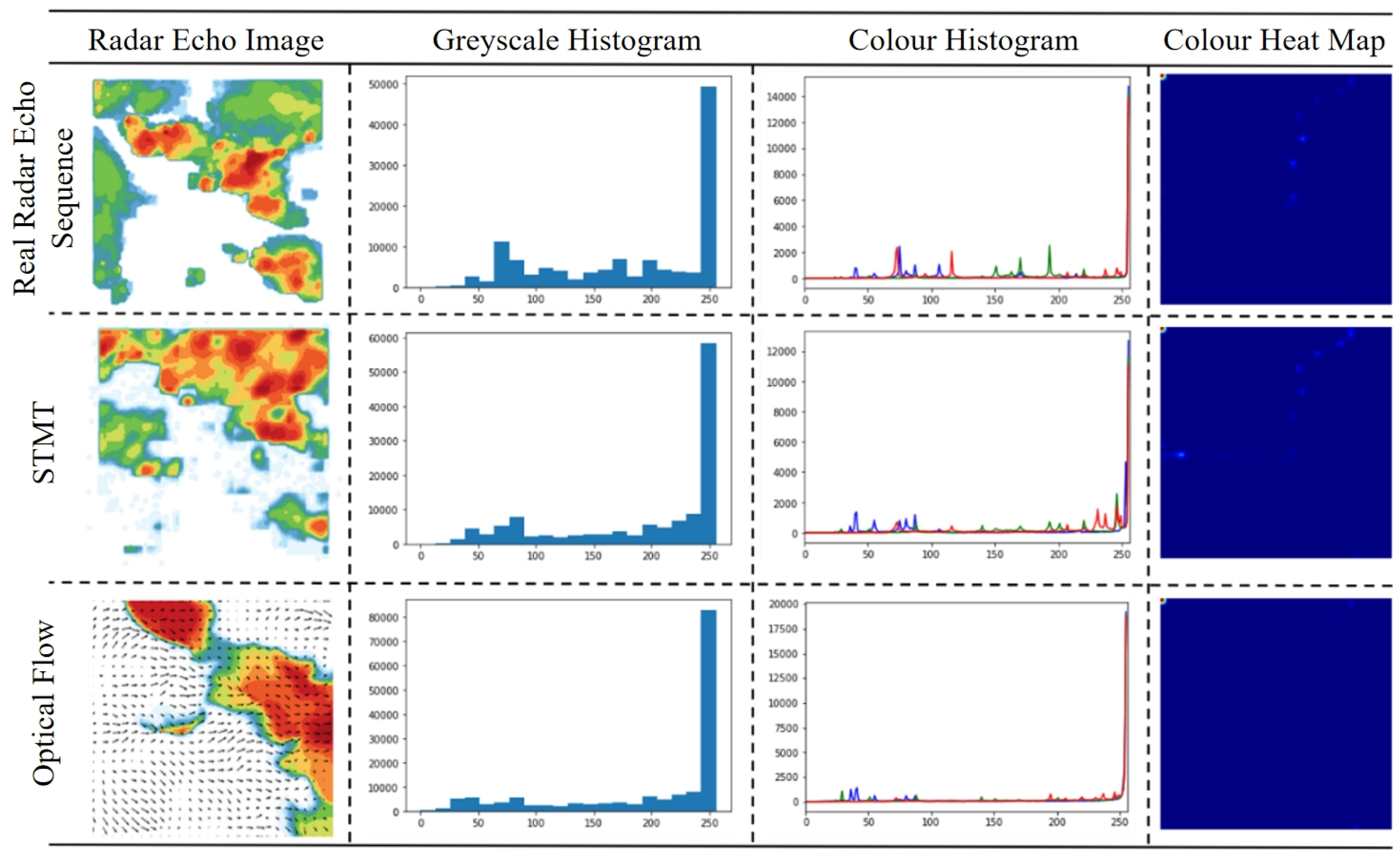
In order to evaluate the detail retention ability and global air mass evolution modeling performance of different models in generating radar echo images, the pixel distribution analysis maps of the last frame of the radar echo sequence image output by different models in Figure 6 are given in Figure 7.
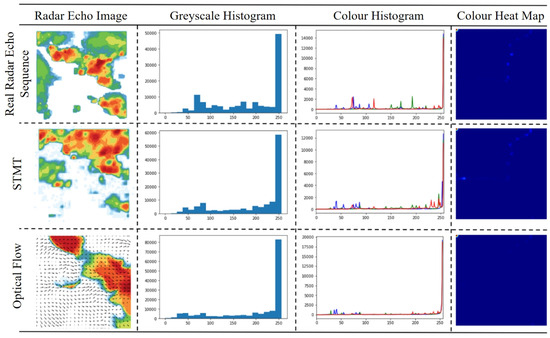
Figure 7.
Pixel distribution analysis of radar echo sequences (last frame) output by different models.
It can be found that the predicted images output by the STMT model are closer to the original images than those output by the optical flow-based prediction model, both in terms of the pixel statistics of the grayscale histogram and the color histogram. We attribute the advantage of the STMT model in predicting the image quality to the strong global and local modeling capability of the model, which enables it not only to generate rich echo intensity detail information, but also to maintain the global air mass evolution pattern (including the shape and motion trend) consistent with the real radar echo sequence.
5.2. Analysis of Differences in Predictive Model Network Structure
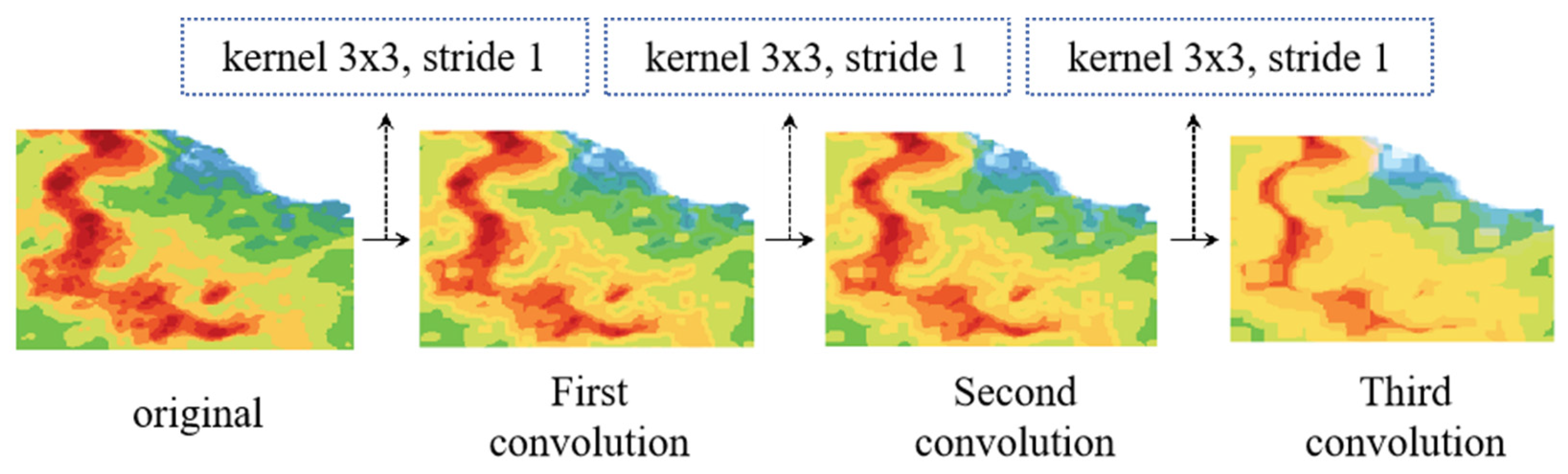
Analyzing from the perspective of model structure, the STMT model is capable of generating detail-rich radar echo images, whereas the radar echo prediction images generated by the optical flow-based or cyclic structure-based prediction models lack the detail-generating capability. We believe that the fundamental reason lies in the different structure of the feature operation operators of these two types of models. The feature operation process of the STMT model is based on the MLP layer and the self-attention mechanism, whereas the optical flow-based or cyclic structure-based prediction models employ the convolution operator. The convolution operator is a learnable local filter. In the convolution operation with multiple stacked layers, the details of the radar echoes, especially the information about the changing edges of the radar echo intensity, are filtered out. Figure 8 visualizes the effect of the convolution operator on the generated results.
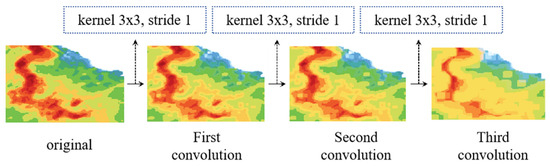
Figure 8.
Impact of convolutional operations on generated results.
We chose three successive size-invariant operations with a convolution kernel size of a certain value, a step size of 1, and an expansion factor of 1. It can be observed that after three convolution operations, the edge information and the details of the radar reflection intensity of the original image are smoothed, and the image as a whole becomes smoother. Therefore, we can conclude that the filtering property of the convolution operation removes the high-frequency information in the radar echo image, which is detrimental to the model’s output of accurate radar echo images, thus affecting the accuracy of the short-term precipitation forecast.
The feature operations of the STMT model are based on the self-attention mechanism of the image/sequence patch as the unit of operation, and a sketch of this process is visualized in Figure 9.
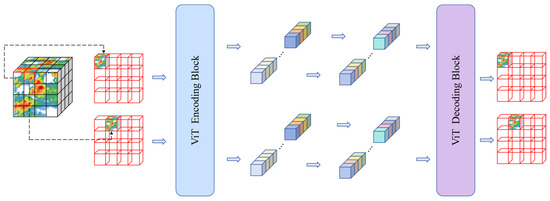
Figure 9.
Sketch of STMT feature operation flow.
We believe that the ability of the STMT model to accurately portray the details of radar echoes comes from the local and global spatiotemporal sensing capability brought about by the self-attention operation. First, the operation process based on patches as computational units avoids high-frequency information from being filtered out by the sliding convolution window. The computational process of each patch is kept independent, and the correlation between multiple patches is modeled by the attention mechanism, thus giving the model the ability to model spatiotemporal correlations in spatiotemporal sequence data while keeping the information of each patch independent. From this, we infer that the prediction model based on the attention operator is more suitable for application scenarios that require rich details of radar echoes, such as short-term precipitation forecasting tasks.
5.3. Exploration of the Effect of Spatiotemporal Resolution on the Modeling of Physical Processes
The STMT framework proposed in this paper demonstrates excellent performance on the CIKM2017 dataset (with a spatial resolution of about 1 km and a temporal resolution of 6 min). However, it needs to be recognized that the physical and microphysical processes of the precipitation system are significantly scale-dependent, and their dominant mechanisms change with spatial and temporal resolution.
High spatial and temporal resolution (e.g., 100 m scale, minute scale): At this scale, local convective activity, microphysical processes (e.g., particle collision growth and evaporative decay), and turbulent mixing effects become dominant. Models need to accurately capture these rapidly evolving, relatively small-scale nonlinear processes and their interactions. The self-attention mechanism in the STMT framework theoretically has the ability to model arbitrary distance dependencies, and its Patch-based operation (especially with smaller Patch sizes) helps to resolve the fine structure. However, at high resolution, data noise may be more significant and randomness is enhanced, placing higher demands on the model’s ability to distinguish real physical signals from noise. Our spatiotemporal mask pre-training strategy, by forcing the model to learn the global structure and physical constraints (e.g., mass conservation and vorticity advection) from sparse contexts, may enhance the robustness of the model to complex, non-smooth features at high resolution to some extent.
Low to medium spatial and temporal resolution (e.g., kilometers, 10 min to hours): At this scale, large-scale dynamical processes (e.g., frontal movement, vortex propagation) become dominant, and the evolution of the precipitation field is characterized more by advection. The collective effects of microphysical processes are smoothed or parameterized. Although the global attention of STMT can effectively capture the large-scale advective trends, too fine a Patch delineation may introduce unnecessary computational overheads, and larger Patch sizes may lose part of the mesoscale information. At this point, the accuracy of the model prediction relies more on the accurate learning of the large-scale dynamical constraints, which is one of the key points emphasized in our mask pre-training phase.
The core strength of this framework lies in the generalized spatiotemporal characterization capability obtained by mask pre-training and the flexibility of the Transformer architecture. The effective spatiotemporal resolution is determined by both the input data granularity and the model patch size: the input resolution limits the scale of the resolvable physical processes; smaller patch size retains the high-resolution details (which is good for capturing the microphysical processes) but is computationally expensive; and larger patch size improves the efficiency and focuses on large-scale dynamical characterization but may lose the small- and medium-scaled information. Physical constraints (e.g., continuity, conservation) learned from mask pre-training have some cross-resolution generalization, but the feature scales are limited by the training data. Future work will focus on exploring the generalizability of the framework at different resolutions and improving its cross-scale physical process modeling capability and business applicability by optimizing the Patch strategy, attention mechanism, or introducing explicit multi-scale modules (e.g., adapting to the high-resolution requirements of urban flood warning or the low-resolution scenarios of climate model post-processing).
5.4. Limitations of the Framework
Although STMT has demonstrated strong long-range spatial and temporal modeling capabilities in short-range precipitation forecasting, it still has some limitations. First, the computational cost of the global self-attention mechanism is high, and its complexity constrains real-time operational deployment, especially with high-resolution data. Second, the model implicitly learns physical laws through masked pre-training, but lacks explicit fusion of atmospheric dynamics equations, limiting its extrapolation capability under extreme weather (e.g., rapidly enhanced convection) that relies on first principles. In addition, the inherent error amplification effect of the precipitation system may lead to degradation of forecast quality if forecast length and refinement are enhanced, and performance in radar-sparse or terrain-complex regions is susceptible to artifacts such as beam masking. In the future, there is a need to explore efficient attention variants or to construct hybrid frameworks combining physically driven numerical models to enhance robustness.
6. Conclusions
In this paper, a unified spatiotemporal sequence prediction framework based on spatiotemporal masks is proposed. The framework innovatively decouples the spatiotemporal sequence data prediction process into two synergistic phases of self-supervised pre-training and task-oriented fine-tuning. This decoupled design enables the model to first learn the underlying structural features and implicit physical constraints inherent in the radar echo data, and subsequently optimize for specific prediction tasks. Based on this framework, we further propose two core models: an RNN-based temporal modeling approach that focuses on capturing the short-term temporal dependence of the precipitation process, and a spatiotemporal modeling approach based on the Transformer architecture, which efficiently models the long-range spatiotemporal evolutionary relationships using its global self-attention mechanism. The experimental results validate the flexibility of the proposed framework: the generic spatiotemporal representations obtained from pre-training are independent of the downstream prediction architectures, thus allowing the flexibility of integrating different backbone networks (e.g., RNN or Transformer) during the fine-tuning stage to meet specific needs, generating more accurate and physically sound prediction results. Inspired by the intrinsic evolution mechanism of meteorological elements, we introduce a spatiotemporal mask pre-training strategy to effectively drive the model to learn the implicit physical constraints of the meteorological field, and the experiments fully validate the necessity and effectiveness of the strategy.
Extensive experiments on the CIMK2017 dataset show that the present framework significantly improves the prediction performance of the backbone network and provides a competitive solution for short-range precipitation forecasting. Specifically, our spatiotemporal mask Transformer model (STMT) achieves an absolute improvement of 3.73% and 2.39% in the key evaluation metrics, CSI and HSS, respectively, compared to the existing optimal model. Meanwhile, the predicted sequences generated by STMT show significant advantages in terms of echo detail retention and air mass motion continuity. These results strongly validate the effectiveness and application potential of the present framework in spatiotemporal sequence prediction tasks. The framework can provide more reliable decision support for urban flood prevention and agricultural disaster prevention, and can generate forecast content that is closer to the real situation, helping the meteorological part to issue refined warning information and improve the response speed of public services.
Author Contributions
Conceptualization, Z.Y. and P.M.; Data curation, Z.Y.; Formal analysis, Z.Y. and C.L.; Funding acquisition, C.L.; Investigation, Z.Y. and L.W.; Methodology, Z.Y., C.L., and P.M.; Project administration, Z.Y.; Resources, C.L.; Software, Z.Y.; Supervision, Z.Y. and P.M.; Validation, Z.Y.; Visualization, Z.Y.; Writing—original draft, Z.Y.; Writing—review and editing, Z.Y. and P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Joint Research Project for Meteorological Capacity Improvement, grant number No. 24NLTSZ007 and the China Meteorological Administration (CMA) Youth Innovation Team, grant number CMA2024QN06. Both of the above grants were provided by the China Meteorological Administration.
Data Availability Statement
The data used in this study are publicly available and can be accessed through the following link: https://tianchi.aliyun.com/dataset/dataDetail?dataId=1085 (accessed on 6 October 2024). This dataset is the CIKM AnalytiCup 2017 Short-Term Quantitative Precipitation Forecasting dataset, released by Tianchi in 2018. The dataset is freely available for academic research purposes.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MAE | Masked Auto-Encoder |
| MAE-RNN | Masked Auto-Encoder Recurrent Neural Network |
| STMT | Spatiotemporal Mask Transformer |
| RNN | Recurrent Neural Network |
| ConvRNN | Convolutional Recurrent Neural Network |
| ConvLSTM | Convolutional Long Short-Term Memory |
| Swin-Transformer | Shifted Window Transformer |
| GAN | Generative Adversarial Network |
| ConvGRU | Convolutional Gated Recurrent Unit |
| CDNA | Conditional Dynamic Neural Advection |
| DFN | Dynamic Filter Network |
| PhyDNet | Physics-inspired Dynamic Network |
| PredRANN | Spatiotemporal Attention Convolutional Recurrent Neural Network |
| MIM | Memory in Memory |
| E3D-LSTM | Eidetic 3D LSTM |
| SA-ConvLSTM | Self-Attention ConvLSTM |
| PFST-LSTM | Pseudoflow SpatioTemporal LSTM |
| ViT | Vision Transformer |
| 3D-CNN | Three-Dimensional Convolutional Neural Network |
| TrajGRU | Trajectory Gated Recurrent Unit |
References
- Gao, Z.; Shi, X.; Wang, H.; Yeung, D.Y.; Woo, W.C.; Wong, W.K. Deep learning and the weather forecasting problem: Precipitation nowcasting. In Deep Learning for the Earth Sciences: A Comprehensive Approach to Remote Sensing, Climate Science, and Geosciences; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2021; pp. 218–239. [Google Scholar]
- Wilson, J.W.; Feng, Y.; Chen, M.; Roberts, R.D. Nowcasting Challenges during the Beijing Olympics: Successes, Failures, and Implications for Future Nowcasting Systems. Weather Forecast. 2010, 25, 1691–1714. [Google Scholar] [CrossRef]
- Yuan, H.; Lu, C.; McGinley, J.A.; Schultz, P.J.; Jamison, B.D.; Wharton, L.; Anderson, C.J. Evaluation of Short-Range Quantitative Precipitation Forecasts from a Time-Lagged Multimodel Ensemble. Weather Forecast. 2009, 24, 18–38. [Google Scholar] [CrossRef]
- Gao, Z.; Tan, C.; Wu, L.; Li, S.Z. Simvp: Simpler yet better video prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 3170–3180. [Google Scholar]
- Lee, A.X.; Zhang, R.; Ebert, F.; Abbeel, P.; Finn, C.; Levine, S. Stochastic adversarial video prediction. arXiv 2018, arXiv:1804.01523. [Google Scholar]
- Takahashi, H.; Naud, C.M.; Posselt, D.J.; Duffy, G.A. Systematic Differences between the Northern and Southern Hemispheres: Warm-Frontal Ice Water Path Linked to the Origin of Extratropical Cyclones. J. Clim. 2024, 37, 2491–2504. [Google Scholar] [CrossRef]
- Peng, L.; Chen, G.; Guan, L.; Tian, F. Contrasting Westward and Eastward Propagating Mesoscale Eddies in the Global Ocean. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4504710. [Google Scholar] [CrossRef]
- Solari, F.I.; Blázquez, J.; Solman, S. Relationship between frontal systems and extreme precipitation over southern South America. Int. J. Climatol. 2022, 42, 7535–7549. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Trebing, K.; Staǹczyk, T.; Mehrkanoon, S. SmaAt-UNet: Precipitation nowcasting using a small attention-UNet architecture. Pattern Recognit. Lett. 2021, 145, 178–186. [Google Scholar] [CrossRef]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S.; et al. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef]
- Kim, Y.; Hong, S. Very short-term rainfall prediction using ground radar observations and conditional generative adversarial networks. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–8. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Leinonen, J.; Hamann, U.; Nerini, D.; Germann, U.; Franch, G. Latent diffusion models for generative precipitation nowcasting with accurate uncertainty quantification. arXiv 2023, arXiv:2304.12891. [Google Scholar]
- Hess, P.; Drüke, M.; Petri, S.; Strnad, F.M.; Boers, N. Physically constrained generative adversarial networks for improving precipitation fields from Earth system models. Nat. Mach. Intell. 2022, 4, 828–839. [Google Scholar] [CrossRef]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked autoencoders are scalable vision learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16000–16009. [Google Scholar]
- Tian, L.; Li, X.; Ye, Y.; Xie, P.; Li, Y. A generative adversarial gated recurrent unit model for precipitation nowcasting. IEEE Geosci. Remote Sens. Lett. 2019, 17, 601–605. [Google Scholar] [CrossRef]
- Han, L.; Liang, H.; Chen, H.; Zhang, W.; Ge, Y. Convective precipitation nowcasting using U-Net model. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–8. [Google Scholar] [CrossRef]
- Gao, Z.; Shi, X.; Wang, H.; Zhu, Y.; Wang, Y.B.; Li, M.; Yeung, D.Y. Earthformer: Exploring space-time transformers for earth system forecasting. Adv. Neural Inf. Process. Syst. 2022, 35, 25390–25403. [Google Scholar]
- Luo, C.; Li, X.; Ye, Y.; Feng, S.; Ng, M.K. Experimental study on generative adversarial network for precipitation nowcasting. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–20. [Google Scholar] [CrossRef]
- Chen, X.; Wang, M.; Wang, S.; Chen, Y.; Wang, R.; Zhao, C.; Hu, X. Weather radar nowcasting for extreme precipitation prediction based on the temporal and spatial generative adversarial network. Atmosphere 2022, 13, 1291. [Google Scholar] [CrossRef]
- Erhan, D.; Bengio, Y.; Courville, A.; Manzagol, P.-A.; Vincent, P.; Bengio, S. Why Does Unsupervised Pre-training Help Deep Learning? J. Mach. Learn. Res. 2010, 11, 625–660. [Google Scholar]
- Tajbakhsh, N.; Shin, J.Y.; Gurudu, S.R.; Hurst, R.T.; Kendall, C.B.; Gotway, M.B.; Liang, J. Convolutional Neural Networks for Medical Image Analysis: Full Training or Fine Tuning? IEEE Trans. Med. Imaging 2016, 35, 1299–1312. [Google Scholar] [CrossRef]
- Ko, J.; Lee, K.; Hwang, H.; Oh, S.G.; Son, S.W.; Shin, K. Effective training strategies for deep-learning-based precipitation nowcasting and estimation. Comput. Geosci. 2022, 161, 105072. [Google Scholar] [CrossRef]
- Zeng, Q.; Yu, W.; Yu, M.; Jiang, T.; Weninger, T.; Jiang, M. Tri-train: Automatic pre-fine tuning between pre-training and fine-tuning for SciNER. In Proceedings of the Findings of the Association for Computational Linguistics: EMNLP 2020, Online Event, 16–20 November 2020; pp. 4778–4787. [Google Scholar]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent neural network regularization. arXiv 2014, arXiv:1409.2329. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Deep learning for precipitation nowcasting: A benchmark and a new model. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Hogan, R.J.; Ferro, C.A.; Jolliffe, I.T.; Stephenson, D.B. Equitability revisited: Why the “equitable threat score” is not equitable. Weather Forecast. 2010, 25, 710–726. [Google Scholar] [CrossRef]
- Grecu, M.; Krajewski, W.F. A large-sample investigation of statistical procedures for radar-based short-term quantitative precipitation forecasting. J. Hydrol. 2000, 239, 69–84. [Google Scholar] [CrossRef]
- Finn, C.; Goodfellow, I.; Levine, S. Unsupervised learning for physical interaction through video prediction. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Jia, X.; De Brabandere, B.; Tuytelaars, T.; Gool, L.V. Dynamic filter networks. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. Adv. Neural Inf. Process. Syst. 2017, 30, 879–888. [Google Scholar]
- Wang, Y.; Gao, Z.; Long, M.; Wang, J.; Yu, P.S. Predrnn++: Towards a resolution of the deep-in-time dilemma in spatiotemporal predictive learning. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 5123–5132. [Google Scholar]
- Wang, Y.; Zhang, J.; Zhu, H.; Long, M.; Wang, J.; Yu, P.S. Memory in memory: A predictive neural network for learning higher-order non-stationarity from spatiotemporal dynamics. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9154–9162. [Google Scholar]
- Wang, Y.; Jiang, L.; Yang, M.-H.; Li, L.-J.; Long, M.; Fei-Fei, L. Eidetic 3D LSTM: A Model for Video Prediction and Beyond. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Lin, Z.; Li, M.; Zheng, Z.; Cheng, Y.; Yuan, C. Self-Attention ConvLSTM for Spatiotemporal Prediction. In Proceedings of the 34th AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Le Guen, V.; Thome, N. Disentangling physical dynamics from unknown factors for unsupervised video prediction. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Luo, C.; Li, X.; Ye, Y. PFST-LSTM: A SpatioTemporal LSTM Model With Pseudoflow Prediction for Precipitation Nowcasting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 843–857. [Google Scholar] [CrossRef]
- Luo, C.; Zhao, X.; Sun, Y.; Li, X.; Ye, Y. PredRANN: The spatiotemporal attention Convolution Recurrent Neural Network for precipitation nowcasting. Knowl.-Based Syst. 2022, 239, 107900. [Google Scholar] [CrossRef]
- Walker, J.; Gupta, A.; Hebert, M. Dense optical flow prediction from a static image. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2443–2451. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).