Image Characteristic-Guided Learning Method for Remote-Sensing Image Inpainting
Abstract
1. Introduction
2. Related Work
2.1. CNN-Based Methods
2.2. Transformer-Based and Diffusion-Based Methods
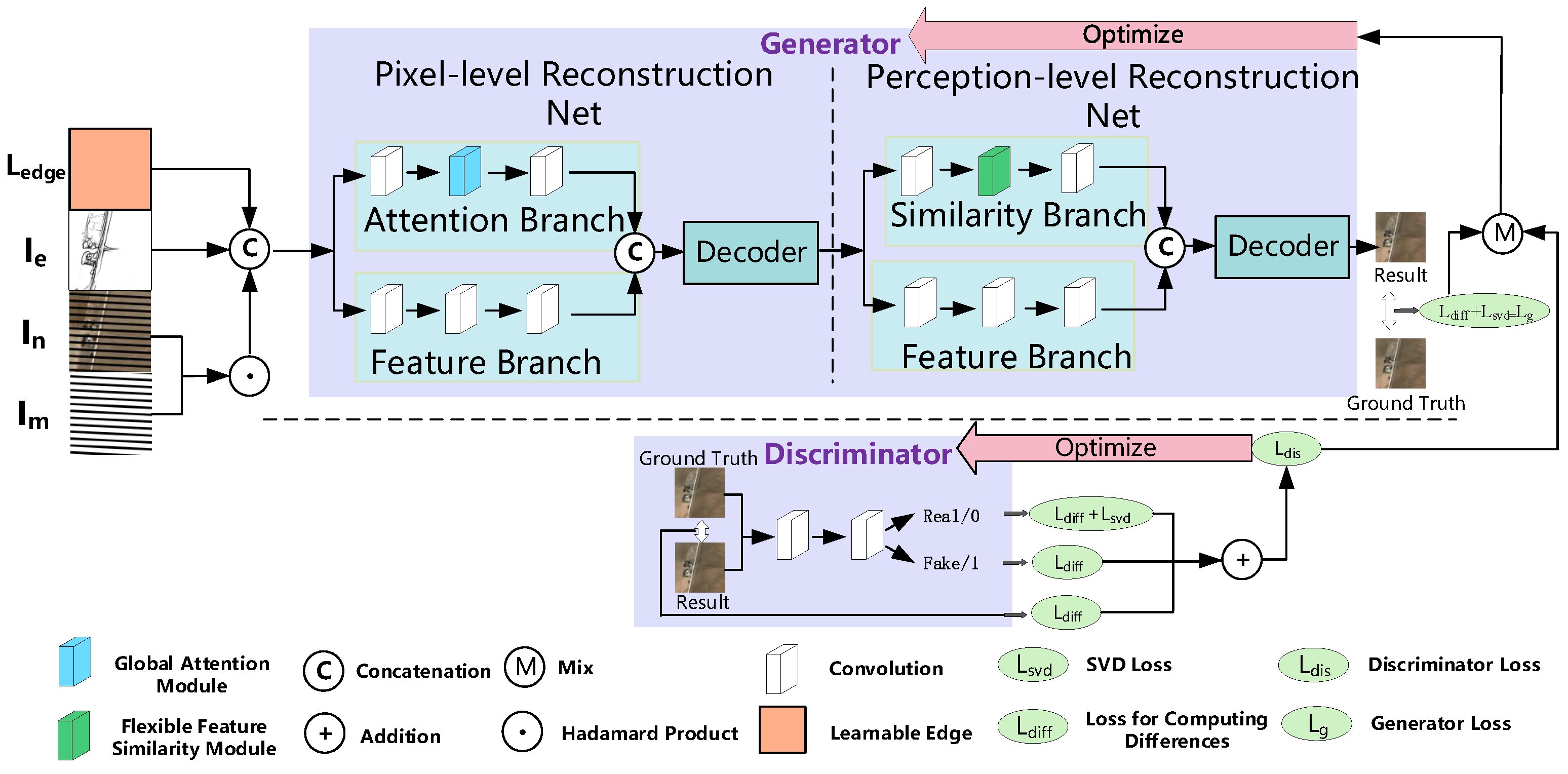
3. Methodology
3.1. The Preliminaries of Low-Rankness and Local-Smoothness
3.2. Network Architecture
3.3. Mechanisms Designed for Low-Rankness and Local-Smoothness
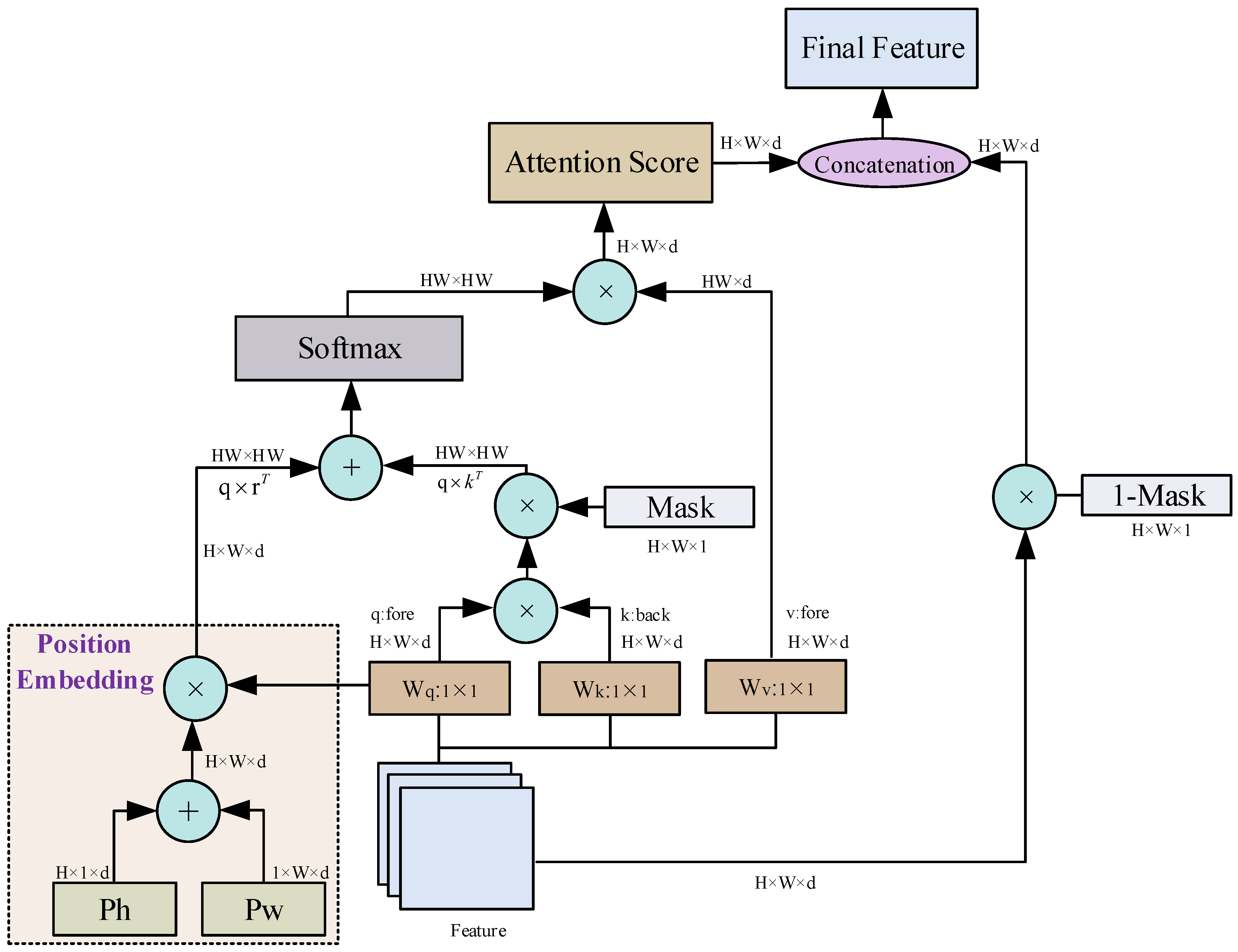
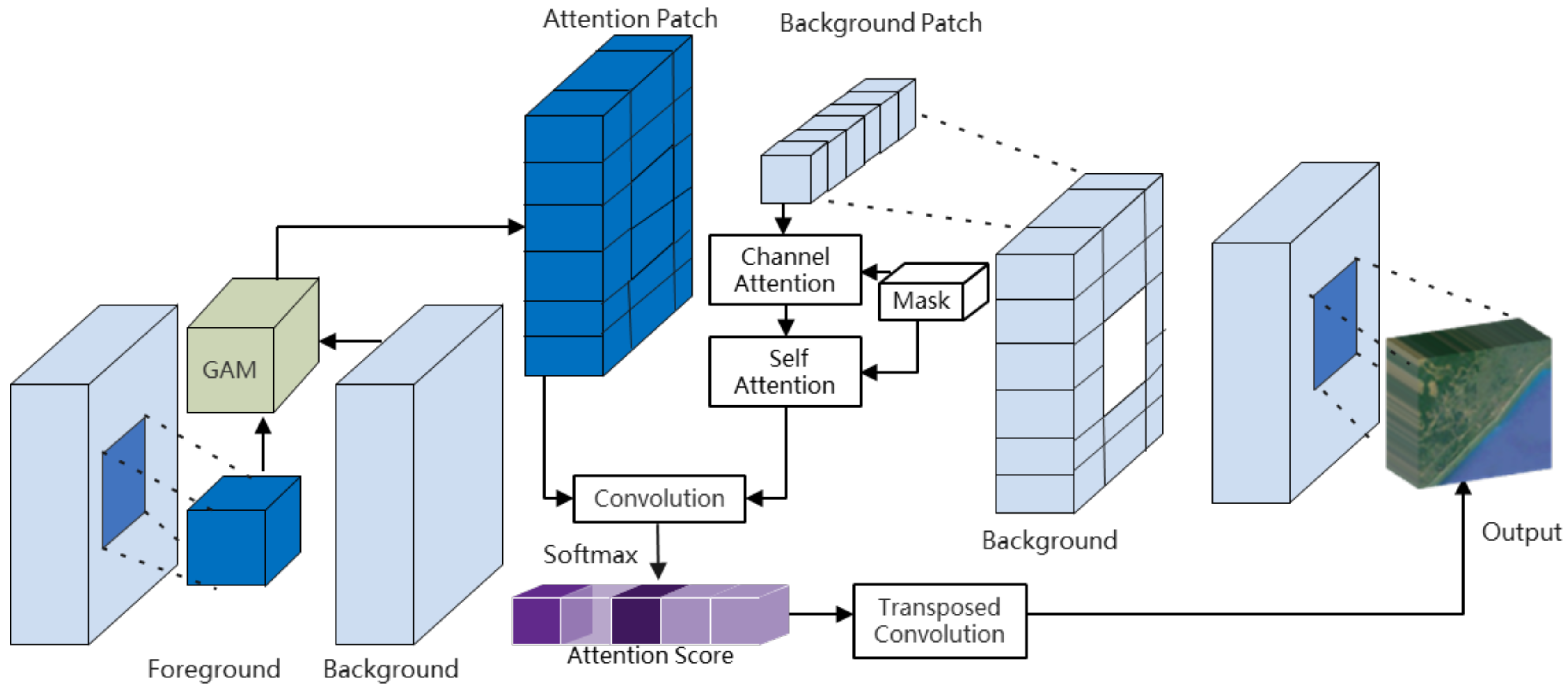
3.4. Global Attention Module
3.5. Flexible Feature Similarity Module
3.6. Loss Function
4. Experiments and Result Analysis
4.1. Datasets
4.2. Experimental Details
4.3. Inpainting Experiments
4.4. Ablation Study
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Rossow, W.B.; Lacis, A.A.; Oinas, V.; Mishchenko, M.I. Calculation of radiative fluxes from the surface to top of atmosphere based on ISCCP and other global data sets: Refinements of the radiative transfer model and the input data. J. Geophys. Res. Atmos. 2004, 109, D19105. [Google Scholar] [CrossRef]
- Wang, Y. DMDiff: A Dual-Branch Multimodal Conditional Guided Diffusion Model for Cloud Removal Through SAR-Optical Data Fusion. Remote Sens. 2025, 17, 965. [Google Scholar]
- Du, Y.; He, J.; Huang, Q.; Sheng, Q.; Tian, G. A Coarse-to-Fine Deep Generative Model with Spatial Semantic Attention for High-Resolution Remote Sensing Image Inpainting. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5621913. [Google Scholar] [CrossRef]
- Palejwala, S.K.; Skoch, J.; Lemole, G.M., Jr. Removal of symptomatic craniofacial titanium hardware following craniotomy: Case series and review. Interdiscip. Neurosurg. 2015, 2, 115–119. [Google Scholar] [CrossRef]
- Sun, H.; Ma, J.; Guo, Q.; Zou, Q.; Song, S.; Lin, Y.; Yu, H. Coarse-to-fine task-driven inpainting for geoscience images. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 7170–7182. [Google Scholar] [CrossRef]
- Karwowska, K.; Wierzbicki, D.; Kedzierski, M. Image Inpainting and Digital Camouflage: Methods, Applications, and Perspectives for Remote Sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 8215–8247. [Google Scholar] [CrossRef]
- Zhang, Y.; Tu, Z.; Lu, J.; Xu, C.; Shen, L. Fusion of low-rankness and smoothness under learnable nonlinear transformation for tensor completion. Knowl.-Based Syst. 2024, 296, 111917. [Google Scholar] [CrossRef]
- Wang, H.; Peng, J.; Qin, W.; Wang, J.; Meng, D. Guaranteed tensor recovery fused low-rankness and smoothness. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10990–11007. [Google Scholar] [CrossRef]
- Zha, Z.; Wen, B.; Yuan, X.; Zhou, J.; Zhu, C.; Kot, A.C. Low-rankness guided group sparse representation for image restoration. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 7593–7607. [Google Scholar] [CrossRef]
- Kohler, M.; Langer, S. Statistical theory for image classification using deep convolutional neural network with cross-entropy loss under the hierarchical max-pooling model. J. Stat. Plan. Inference 2025, 234, 106188. [Google Scholar] [CrossRef]
- Ružić, T.; Pižurica, A. Context-aware patch-based image inpainting using Markov random field modeling. IEEE Trans. Image Process. 2014, 24, 444–456. [Google Scholar] [CrossRef]
- Cao, R.; Chen, Y.; Chen, J.; Zhu, X.; Shen, M. Thick cloud removal in Landsat images based on autoregression of Landsat time-series data. Remote Sens. Environ. 2020, 249, 112001. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, X.; Vogelmann, J.E.; Gao, F.; Jin, S. A simple and effective method for filling gaps in Landsat ETM+ SLC-off images. Remote Sens. Environ. 2011, 115, 1053–1064. [Google Scholar] [CrossRef]
- Wong, R.; Zhang, Z.; Wang, Y.; Chen, F.; Zeng, D. HSI-IPNet: Hyperspectral imagery inpainting by deep learning with adaptive spectral extraction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4369–4380. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, J.; Chen, D.; Liao, J. High-fidelity pluralistic image completion with transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 4692–4701. [Google Scholar]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context encoders: Feature learning by inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2536–2544. [Google Scholar]
- Dong, Q.; Cao, C.; Fu, Y. Incremental transformer structure enhanced image inpainting with masking positional encoding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11358–11368. [Google Scholar]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked autoencoders are scalable vision learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16000–16009. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Chen, S.; Atapour-Abarghouei, A.; Shum, H.P. HINT: High-quality INpainting Transformer with Mask-Aware Encoding and Enhanced Attention. IEEE Trans. Multimed. 2024, 26, 7649–7660. [Google Scholar] [CrossRef]
- Zeng, Y.; Fu, J.; Chao, H.; Guo, B. Aggregated contextual transformations for high-resolution image inpainting. IEEE Trans. Vis. Comput. Graph. 2023, 29, 3266–3280. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Lin, Z.; Zhou, K.; Qi, L.; Wang, Y.; Jia, J. Mat: Mask-aware transformer for large hole image inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10758–10768. [Google Scholar]
- Panboonyuen, T.; Charoenphon, C.; Satirapod, C. SatDiff: A Stable Diffusion Framework for Inpainting Very High-Resolution Satellite Imagery. IEEE Access 2025, 13, 51617–51631. [Google Scholar] [CrossRef]
- Khanna, S.; Liu, P.; Zhou, L.; Meng, C.; Rombach, R.; Burke, M.; Lobell, D.; Ermon, S. Diffusionsat: A generative foundation model for satellite imagery. arXiv 2023, arXiv:2312.03606. [Google Scholar]
- Dong, J.; Yin, R.; Sun, X.; Li, Q.; Yang, Y.; Qin, X. Inpainting of remote sensing SST images with deep convolutional generative adversarial network. IEEE Geosci. Remote. Sens. Lett. 2019, 16, 173–177. [Google Scholar] [CrossRef]
- Hui, Z.; Li, J.; Wang, X.; Gao, X. Image fine-grained inpainting. arXiv 2020, arXiv:2002.02609. [Google Scholar]
- Yi, Z.; Tang, Q.; Azizi, S.; Jang, D.; Xu, Z. Contextual residual aggregation for ultra high-resolution image inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7505–7517. [Google Scholar]
- Wang, N.; Zhang, Y.; Zhang, L. Dynamic selection network for image inpainting. IEEE Trans. Image Process. 2021, 30, 1784–1798. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Hui, S.; Meng, R.; Zhou, S.; Wang, J. Hourglass Attention Network for Image Inpainting. In Computer Vision—ECCV 2022, Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 483–501. [Google Scholar]
- Wang, N.; Ma, S.; Li, J.; Zhang, Y.; Zhang, L. Multistage attention network for image inpainting. Pattern Recognit. 2020, 106, 107448. [Google Scholar] [CrossRef]
- Song, J.; Meng, C.; Ermon, S. Denoising diffusion implicit models. arXiv 2020, arXiv:2010.02502. [Google Scholar]
- Song, Y.; Ermon, S. Improved techniques for training score-based generative models. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 October 2020; Volume 33, pp. 12438–12448. [Google Scholar]
- Ettari, A.; Nappa, A.; Quartulli, M.; Azpiroz, I.; Longo, G. Adaptation of Diffusion Models for Remote Sensing Imagery. In Proceedings of the IGARSS 2024-2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 7240–7243. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar]
- Su, Z.; Liu, W.; Yu, Z.; Hu, D.; Liao, Q.; Tian, Q.; Pietikäinen, M.; Liu, L. Pixel difference networks for efficient edge detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 5117–5127. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, vol. 6. long and short papers: Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL HLT 2019), Minneapolis, MN, USA, 2–7 June 2019. [Google Scholar]
- Gatys, L.A.; Ecker, A.S.; Bethge, M. Image style transfer using convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2414–2423. [Google Scholar]
- Gatys, L.A.; Ecker, A.S.; Bethge, M. A neural algorithm of artistic style. arXiv 2015, arXiv:1508.06576. [Google Scholar] [CrossRef]
- Wang, C.; Xu, C.; Wang, C.; Tao, D. Perceptual adversarial networks for image-to-image transformation. IEEE Trans. Image Process. 2018, 27, 4066–4079. [Google Scholar] [CrossRef]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Change Loy, C. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Kilmer, M.E.; Martin, C.D. Factorization strategies for third-order tensors. Linear Algebra Its Appl. 2011, 435, 641–658. [Google Scholar] [CrossRef]
- Struski, L.; Morkisz, P.; Trzcinski, B.T. Efficient GPU implementation of randomized SVD and its applications. Expert Syst. Appl. 2024, 248, 123462. [Google Scholar] [CrossRef]
- Farnia, F.; Ozdaglar, A. Do GANs always have Nash equilibria? In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 3029–3039. [Google Scholar]
- Lin, D.; Xu, G.; Wang, X.; Wang, Y.; Sun, X.; Fu, K. A remote sensing image dataset for cloud removal. arXiv 2019, arXiv:1901.00600. [Google Scholar]
- Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A benchmark data set for performance evaluation of aerial scene classification. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Baweja, T. Clear-view: A dataset for missing data in remote sensing images. In Proceedings of the 2021 IEEE 19th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 21–23 January 2021; pp. 000077–000082. [Google Scholar]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar]
- Eskicioglu, A.M.; Fisher, P.S. Image quality measures and their performance. IEEE Trans. Commun. 1995, 43, 2959–2965. [Google Scholar] [CrossRef]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar]
- Sun, S.; Zhao, B.; Mateen, M.; Chen, X.; Wen, J. Mask guided diverse face image synthesis. Front. Comput. Sci. 2022, 16, 163311. [Google Scholar] [CrossRef]
- Fang, Z.; Lin, H.; Xu, X. Mask-guided model for seismic data denoising. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 8026705. [Google Scholar] [CrossRef]









| Dataset | Type | Spectrum | Resolution | Image Size | Source | Quantity |
|---|---|---|---|---|---|---|
| RICE [45] | RGB | 3 | 30 m | 512 × 512 | Google Earth | 500 |
| AID [46] | RGB | 3 | (8–0.5) m | 600 × 600 | Google Earth | 10,000 |
| Clear-View [47] | RGB | 3 | 0.3 m and 0.5 m | 1024 × 1024 | Landsat | 21,080 |
| Method | Mask Rate | DMFN [26] | HiFIll [27] | HAN [29] | HINT [20] | Our | |
|---|---|---|---|---|---|---|---|
| MS-SSIM ↑ | 10% | AID | 0.916 | 0.928 | 0.937 | 0.304 | 0.948 |
| RICE | 0.922 | 0.931 | 0.951 | 0.310 | 0.952 | ||
| Clear-View | 0.900 | 0.905 | 0.912 | 0.300 | 0.933 | ||
| 25% | AID | 0.811 | 0.830 | 0.839 | 0.311 | 0.865 | |
| RICE | 0.821 | 0.832 | 0.850 | 0.312 | 0.875 | ||
| Clear-View | 0.772 | 0.805 | 0.779 | 0.301 | 0.814 | ||
| 77% | AID | 0.711 | 0.734 | 0.750 | 0.324 | 0.757 | |
| RICE | 0.736 | 0.758 | 0.760 | 0.330 | 0.764 | ||
| Clear-View | 0.654 | 0.664 | 0.722 | 0.322 | 0.710 | ||
| PSNR ↑ | 10% | AID | 27.253 | 28.330 | 29.190 | 16.276 | 31.621 |
| RICE | 27.359 | 28.456 | 29.890 | 16.290 | 31.892 | ||
| Clear-View | 25.890 | 26.573 | 27.518 | 16.001 | 30.875 | ||
| 25% | AID | 23.003 | 23.835 | 24.224 | 16.409 | 27.282 | |
| RICE | 23.362 | 23.973 | 24.633 | 17.103 | 31.621 | ||
| Clear-View | 21.971 | 22.361 | 22.258 | 16.074 | 27.282 | ||
| 77% | AID | 20.241 | 21.552 | 22.031 | 16.591 | 21.848 | |
| RICE | 21.004 | 22.217 | 22.307 | 16.701 | 22.925 | ||
| Clear-View | 20.050 | 20.383 | 21.812 | 16.286 | 21.578 | ||
| FID ↓ | 10% | AID | 17.078 | 18.906 | 11.911 | 16.045 | 6.573 |
| RICE | 16.630 | 16.758 | 10.395 | 16.008 | 5.298 | ||
| Clear-View | 18.354 | 20.083 | 12.257 | 16.232 | 8.252 | ||
| 25% | AID | 58.343 | 59.951 | 43.333 | 28.600 | 19.554 | |
| RICE | 56.247 | 58.231 | 42.58 | 27.560 | 18.603 | ||
| Clear-View | 60.000 | 60.058 | 45.087 | 28.973 | 21.257 | ||
| 77% | AID | 79.092 | 77.502 | 77.502 | 39.343 | 30.118 | |
| RICE | 78.352 | 77.255 | 76.281 | 39.060 | 29.222 | ||
| Clear-View | 80.257 | 79.271 | 79.354 | 38.640 | 33.581 | ||
| LPIPS ↓ | 10% | AID | 0.088 | 0.084 | 0.066 | 0.445 | 0.035 |
| RICE | 0.076 | 0.077 | 0.051 | 0.438 | 0.024 | ||
| Clear-View | 0.099 | 0.092 | 0.089 | 0.450 | 0.039 | ||
| 25% | AID | 0.231 | 0.228 | 0.178 | 0.456 | 0.134 | |
| RICE | 0.217 | 0.199 | 0.155 | 0.446 | 0.126 | ||
| Clear-View | 0.359 | 0.282 | 0.194 | 0.483 | 0.136 | ||
| 77% | AID | 0.327 | 0.323 | 0.286 | 0.470 | 0.177 | |
| RICE | 0.259 | 0.258 | 0.251 | 0.379 | 0.169 | ||
| Clear-View | 0.389 | 0.381 | 0.354 | 0.493 | 0.179 |
| Method | Param (M) ↓ | Gflops (GB) ↓ |
|---|---|---|
| DMFN [26] | 13.036 | 128.765 |
| HiFIll [27] | 9.853 | 80.307 |
| HAN [29] | 19.446 | 114.737 |
| HINT [20] | 21.167 | 72.940 |
| IGLL | 4.458 | 42.613 |
| Method | MS-SSIM ↑ | PSNR ↑ | FID ↓ | LPIPS ↓ |
|---|---|---|---|---|
| w/o GAM | 0.8463 | 25.2109 | 25.3540 | 0.1333 |
| w/o FFSM | 0.8453 | 25.0450 | 26.5767 | 0.1403 |
| w/o structure prior | 0.8076 | 22.2340 | 92.201 | 0.2564 |
| w/o position information | 0.8453 | 24.9933 | 28.8948 | 0.1435 |
| w/multi-head attention | 0.8241 | 23.4782 | 67.3224 | 0.2190 |
| w/o SVD loss | 0.8462 | 25.8886 | 21.1133 | 0.1256 |
| IGLL | 0.8653 | 27.2821 | 19.5542 | 0.1305 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Gao, X.; Wu, X.; Wang, F.; Jing, W.; Hu, X. Image Characteristic-Guided Learning Method for Remote-Sensing Image Inpainting. Remote Sens. 2025, 17, 2132. https://doi.org/10.3390/rs17132132
Zhou Y, Gao X, Wu X, Wang F, Jing W, Hu X. Image Characteristic-Guided Learning Method for Remote-Sensing Image Inpainting. Remote Sensing. 2025; 17(13):2132. https://doi.org/10.3390/rs17132132
Chicago/Turabian StyleZhou, Ying, Xiang Gao, Xinrong Wu, Fan Wang, Weipeng Jing, and Xiaopeng Hu. 2025. "Image Characteristic-Guided Learning Method for Remote-Sensing Image Inpainting" Remote Sensing 17, no. 13: 2132. https://doi.org/10.3390/rs17132132
APA StyleZhou, Y., Gao, X., Wu, X., Wang, F., Jing, W., & Hu, X. (2025). Image Characteristic-Guided Learning Method for Remote-Sensing Image Inpainting. Remote Sensing, 17(13), 2132. https://doi.org/10.3390/rs17132132







