Interpreting Global Terrestrial Water Storage Dynamics and Drivers with Explainable Deep Learning
Abstract
1. Introduction
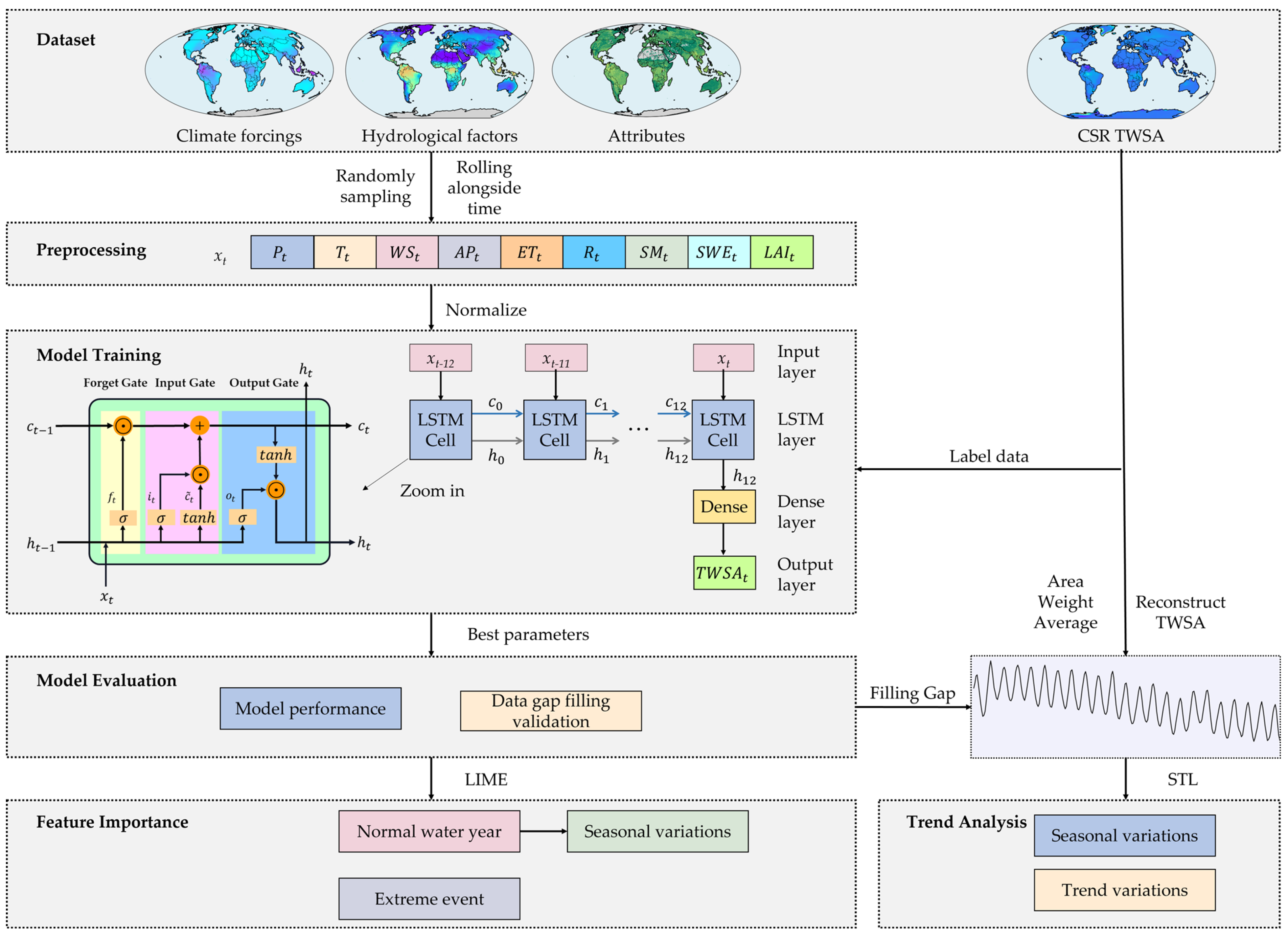
2. Methodology
2.1. Data Sources
2.1.1. GRACE Data
2.1.2. Auxiliary Data
2.2. LSTM Model
2.3. LIME
2.4. Temporal Variation Analysis
3. Results
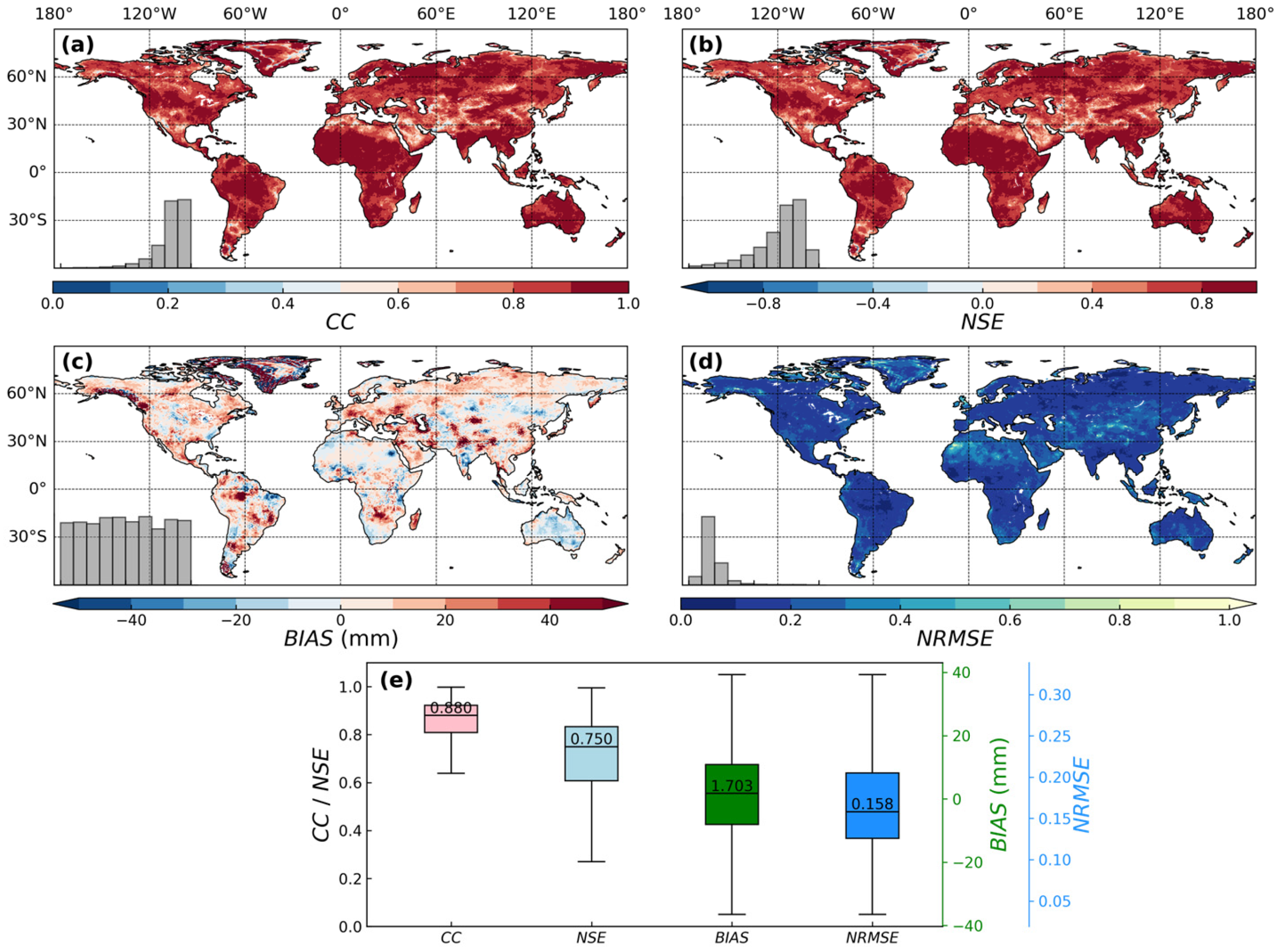
3.1. Model Performance
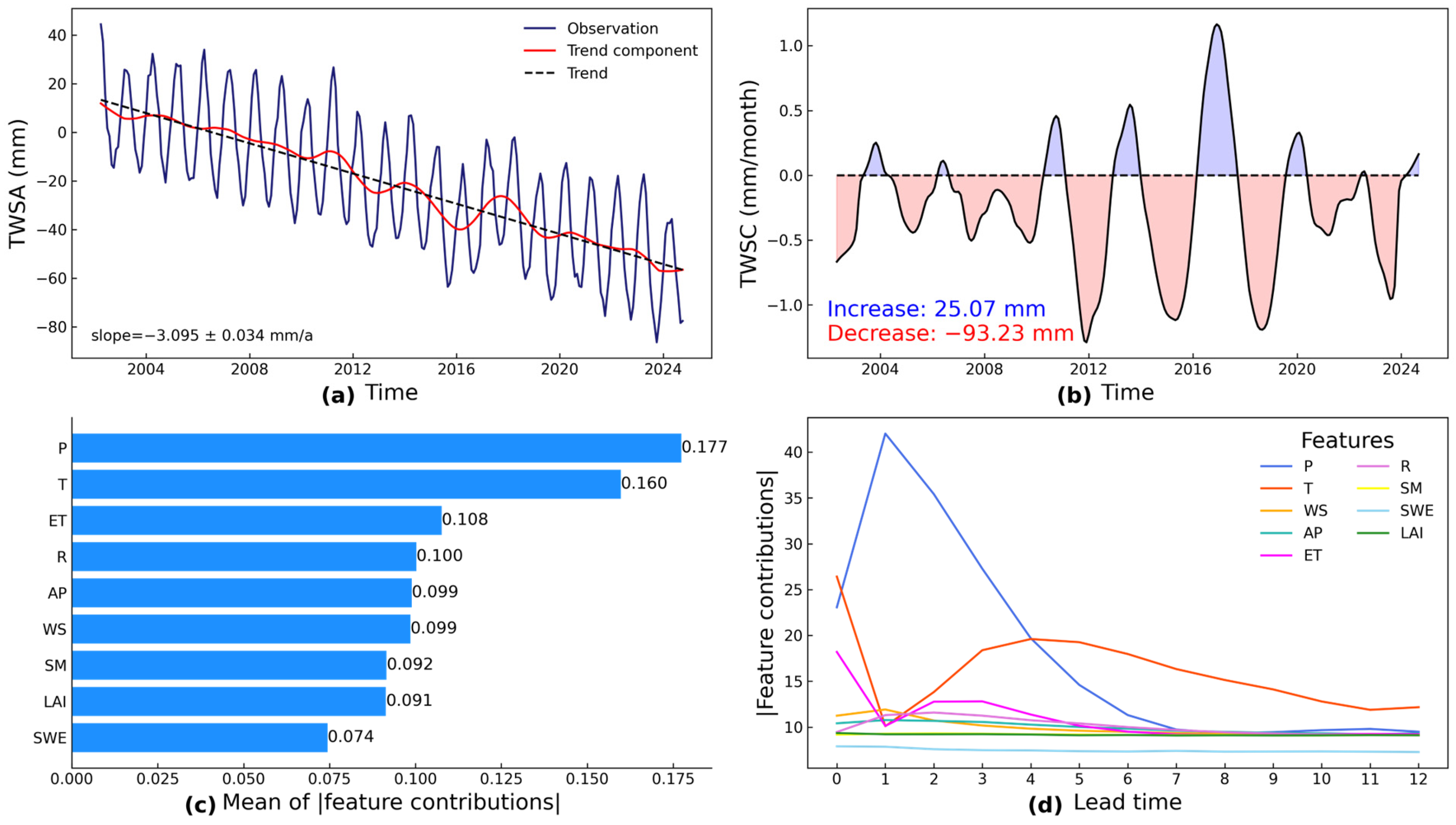
3.2. Trend Analysis and Seasonal Variations
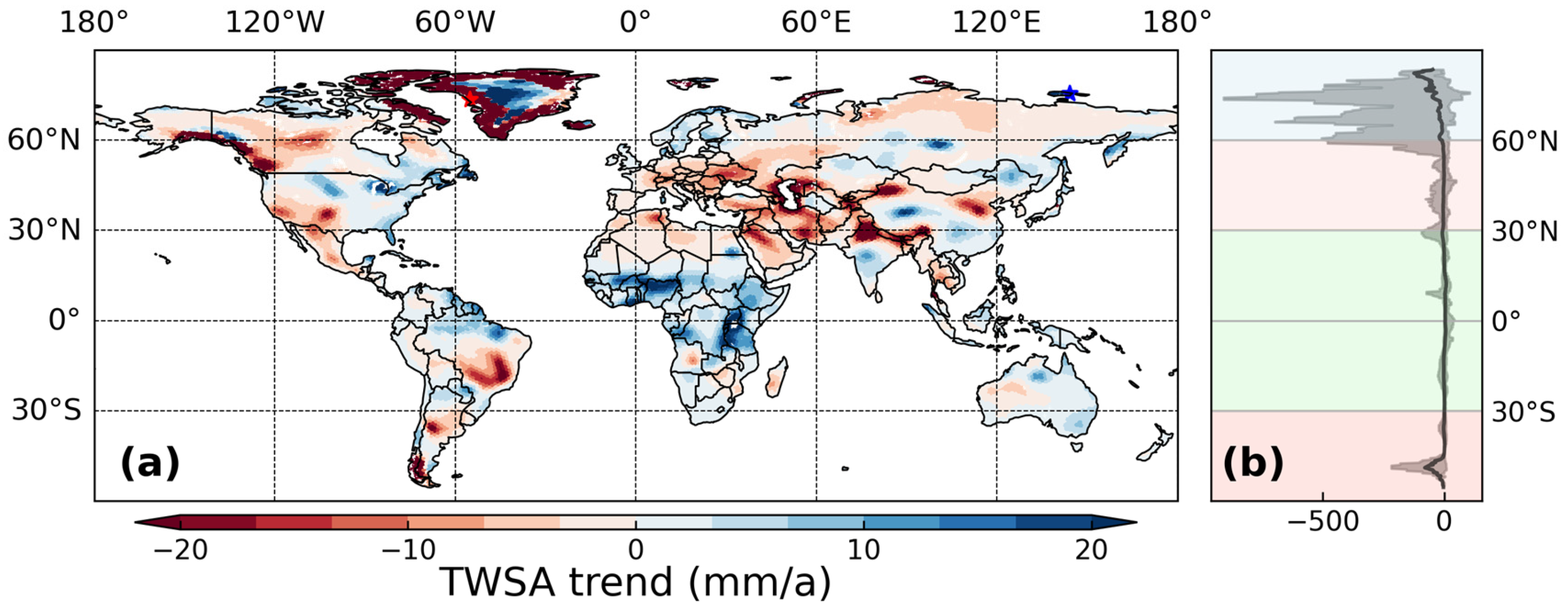
3.3. Spatial Patterns of TWSA Trends and Drivers
4. Discussion
4.1. Impact of Driving Factors on TWS
4.2. Limitations and Future Prospects
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rodell, M.; Famiglietti, J.S. An Analysis of Terrestrial Water Storage Variations in Illinois with Implications for the Gravity Recovery and Climate Experiment (Grace). Water Resour. Res. 2001, 37, 1327–1339. [Google Scholar] [CrossRef]
- Deng, H.; Pepin, N.C.; Liu, Q.; Chen, Y. Understanding the Spatial Differences in Terrestrial Water Storage Variations in the Tibetan Plateau from 2002 to 2016. Clim. Change 2018, 151, 379–393. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved Methods for Observing Earth’s Time Variable Mass Distribution with Grace Using Spherical Cap Mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, H.; Steffen, H.; Wu, P.; Jia, L.; Jiang, L.; Shen, Q. Groundwater Storage Changes in the Tibetan Plateau and Adjacent Areas Revealed from Grace Satellite Gravity Data. Earth Planet. Sci. Lett. 2016, 449, 228–239. [Google Scholar] [CrossRef]
- Pokhrel, Y.N.; Hanasaki, N.; Yeh, P.J.F.; Yamada, T.J.; Kanae, S.; Oki, T. Model Estimates of Sea-Level Change Due To anthropogenic Impacts on Terrestrial Water storage. Nat. Geosci. 2012, 5, 389–392. [Google Scholar] [CrossRef]
- Felfelani, F.; Wada, Y.; Longuevergne, L.; Pokhrel, Y.N. Natural and Human-Induced Terrestrial Water Storage Change: A Global Analysis Using Hydrological Models and Grace. J. Hydrol. 2017, 553, 105–118. [Google Scholar] [CrossRef]
- Lin, W.; Yuan, H.; Dong, W.; Zhang, S.; Liu, S.; Wei, N.; Lu, X.; Wei, Z.; Hu, Y.; Dai, Y. Reprocessed Modis Version 6.1 Leaf Area Index Dataset and Its Evaluation for Land Surface and Climate Modeling. Remote Sens. 2023, 15, 1780. [Google Scholar] [CrossRef]
- Wu, W.-Y.; Lo, M.-H.; Wada, Y.; Famiglietti, J.S.; Reager, J.T.; Yeh, P.J.F.; Ducharne, A.; Yang, Z.-L. Divergent Effects of Climate Change on Future Groundwater Availability in Key Mid-Latitude Aquifers. Nat. Commun. 2020, 11, 3710. [Google Scholar] [CrossRef]
- Abhishek; Kinouchi, T. Synergetic Application of Grace Gravity Data, Global Hydrological Model, and in-Situ Observations to Quantify Water Storage Dynamics over Peninsular India during 2002–2017. J. Hydrol. 2021, 596, 126069. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S. Accuracy of Scaled Grace Terrestrial Water Storage Estimates. Water Resour. Res. 2012, 48, W04531. [Google Scholar] [CrossRef]
- Feng, W.; Zhong, M.; Lemoine, J.-M.; Biancale, R.; Hsu, H.-T.; Xia, J. Evaluation of Groundwater Depletion in North China Using the Gravity Recovery and Climate Experiment (Grace) Data and Ground-Based Measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Huang, Z.; Pan, Y.; Gong, H.; Yeh, P.J.-F.; Li, X.; Zhou, D.; Zhao, W. Subregional-Scale Groundwater Depletion Detected by Grace for Both Shallow and Deep Aquifers in North China Plain. Geophys. Res. Lett. 2015, 42, 1791–1799. [Google Scholar] [CrossRef]
- Tiwari, V.M.; Wahr, J.; Swenson, S. Dwindling Groundwater Resources in Northern India, from Satellite Gravity Observations. Geophys. Res. Lett. 2009, 36, L18401. [Google Scholar] [CrossRef]
- Amiri, V.; Ali, S.; Sohrabi, N. Estimating the Spatio-Temporal Assessment of Grace/Grace-Fo Derived Groundwater Storage Depletion and Validation with in-Situ Water Quality Data (Yazd Province, Central Iran). J. Hydrol. 2023, 620, 129416. [Google Scholar] [CrossRef]
- Joodaki, G.; Wahr, J.; Swenson, S. Estimating the Human Contribution to Groundwater Depletion in the Middle East, from Grace Data, Land Surface Models, and Well Observations. Water Resour. Res. 2014, 50, 2679–2692. [Google Scholar] [CrossRef]
- Peltier, W.R. Global Glacial Isostasy and the Surface of the Ice-Age Earth: The Ice-5g (Vm2) Model and Grace. Annu. Rev. Earth Planet. Sci. 2004, 32, 111–149. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Sabaka, T.J.; Loomis, B.D.; Arendt, A.A.; McCarthy, J.J.; Camp, J. Antarctica, Greenland and Gulf of Alaska Land-Ice Evolution from an Iterated Grace Global Mascon Solution. J. Glaciol. 2013, 59, 613–631. [Google Scholar] [CrossRef]
- Li, X.; Long, D.; Scanlon, B.R.; Mann, M.E.; Li, X.; Tian, F.; Sun, Z.; Wang, G. Climate Change Threatens Terrestrial Water Storage over the Tibetan Plateau. Nat. Clim. Change 2022, 12, 801–807. [Google Scholar] [CrossRef]
- Zhao, F.; Long, D.; Li, X.; Huang, Q.; Han, P. Rapid Glacier Mass Loss in the Southeastern Tibetan Plateau since the Year 2000 from Satellite Observations. Remote Sens. Environ. 2022, 270, 112853. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Blankenship, D.D.; Ivins, E.R. Patagonia Icefield Melting Observed by Gravity Recovery and Climate Experiment (Grace). Geophys. Res. Lett. 2007, 34, L22501. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of Grace to Understanding Climate Change. Nat. Clim. Change 2019, 9, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Ran, J.; Ditmar, P.; Liu, L.; Xiao, Y.; Klees, R.; Tang, X. Analysis and Mitigation of Biases in Greenland Ice Sheet Mass Balance Trend Estimates from Grace Mascon Products. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020880. [Google Scholar] [CrossRef]
- Velicogna, I.; Mohajerani, Y.; Geruo, A.; Landerer, F.; Mouginot, J.; Noel, B.; Rignot, E.; Sutterley, T.; van den Broeke, M.; van Wessem, M.; et al. Continuity of Ice Sheet Mass Loss in Greenland and Antarctica from the Grace and Grace Follow-on Missions. Geophys. Res. Lett. 2020, 47, e2020GL087291. [Google Scholar] [CrossRef]
- Boergens, E.; Güntner, A.; Dobslaw, H.; Dahle, C. Quantifying the Central European Droughts in 2018 and 2019 with Grace Follow-On. Geophys. Res. Lett. 2020, 47, e2020GL087285. [Google Scholar] [CrossRef]
- Shen, C. A Transdisciplinary Review of Deep Learning Research and Its Relevance for Water Resources Scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Sun, A.Y.; Scanlon, B.R. How Can Big Data and Machine Learning Benefit Environment and Water Management: A Survey of Methods, Applications, and Future Directions. Environ. Res. Lett. 2019, 14, 073001. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep Learning and Process Understanding for Data-Driven Earth System Science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A Comprehensive Review of Deep Learning Applications in Hydrology and Water Resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and Flood Monitoring for a Large Karst Plateau in Southwest China Using Extended Grace Data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Huang, X.; Gao, L.; Crosbie, R.S.; Zhang, N.; Fu, G.; Doble, R.C. Groundwater Recharge Prediction Using Linear Regression, Multi-Layer Perception Network, and Deep Learning. Water 2019, 11, 1879. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–Runoff Modelling Using Long Short-Term Memory (Lstm) Networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Huang, H.J.; Feng, G.B.; Cao, Y.R.; Feng, G.N.; Dai, Z.K.; Tian, P.Z.; Wei, J.C.; Cai, X.T. Simulation and Driving Factor Analysis of Satellite-Observed Terrestrial Water Storage Anomaly in the Pearl River Basin Using Deep Learning. Remote Sens. 2023, 15, 3983. [Google Scholar] [CrossRef]
- Yu, Q.T.; Wang, S.S.; He, H.J.; Yang, K.; Ma, L.F.; Li, J. Reconstructing Grace-Like Tws Anomalies for the Canadian Landmass Using Deep Learning and Land Surface Model. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102404. [Google Scholar] [CrossRef]
- Humphrey, V.; Gudmundsson, L. Grace-Rec: A Reconstruction of Climate-Driven Water Storage Changes over the Last Century. Earth Syst. Sci. Data 2019, 11, 1153–1170. [Google Scholar] [CrossRef]
- Gerdener, H.; Schulze, K.; Kusche, J. Glws 2.0: A Global Product That Provides Total Water Storage Anomalies, Groundwater, Soil Moisture and Surface Water with a Spatial Resolution of 0.5° from 2003 to 2019. J. Geod. 2023, 97, 73. [Google Scholar] [CrossRef]
- Yin, J.; Slater, L.J.; Khouakhi, A.; Yu, L.; Liu, P.; Li, F.; Pokhrel, Y.; Gentine, P. Gtws-Mlrec: Global Terrestrial Water Storage Reconstruction by Machine Learning from 1940 to Present. Earth Syst. Sci. Data 2023, 15, 5597–5615. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, T.; Yin, W.; Bateni, S.M.; Jun, C.; Kim, D.; Liu, S.; Xu, Z.; Ming, W.; Wang, J. A Machine Learning Downscaling Framework Based on a Physically Constrained Sliding Window Technique for Improving Resolution of Global Water Storage Anomaly. Remote Sens. Environ. 2024, 313, 114359. [Google Scholar] [CrossRef]
- Mo, S.; Zhong, Y.; Forootan, E.; Mehrnegar, N.; Yin, X.; Wu, J.; Feng, W.; Shi, X. Bayesian Convolutional Neural Networks for Predicting the Terrestrial Water Storage Anomalies during Grace and Grace-Fo Gap. J. Hydrol. 2022, 604, 127244. [Google Scholar] [CrossRef]
- Gyawali, B.; Ahmed, M.; Murgulet, D.; Wiese, D.N. Filling Temporal Gaps within and between Grace and Grace-Fo Terrestrial Water Storage Records: An Innovative Approach. Remote Sens. 2022, 14, 1565. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y. Filling Grace Data Gap Using an Innovative Transformer-Based Deep Learning Approach. Remote Sens. Environ. 2024, 315, 114465. [Google Scholar] [CrossRef]
- Palazzoli, I.; Ceola, S.; Gentine, P. Graice: Reconstructing Terrestrial Water Storage Anomalies with Recurrent Neural Networks. Sci. Data 2025, 12, 146. [Google Scholar] [CrossRef] [PubMed]
- Tulio Ribeiro, M.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. arXiv 2016, arXiv:1602.04938. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Wen, Y.; Zhao, J.; Zhu, G.; Xu, R.; Yang, J. Evaluation of the Rf-Based Downscaled Smap and Smos Products Using Multi-Source Data over an Alpine Mountains Basin, Northwest China. Water 2021, 13, 2875. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B. Interpretable and Explainable Ai (Xai) Model for Spatial Drought Prediction. Sci. Total Environ. 2021, 801, 149797. [Google Scholar] [CrossRef]
- Yang, B.B.; Li, Y.X.; Tao, C.X.; Cui, C.L.; Hu, F.M.; Cui, Q.; Meng, L.K.; Zhang, W. Variations and Drivers of Terrestrial Water Storage in Ten Basins of China. J. Hydrol. Reg. Stud. 2023, 45, 101286. [Google Scholar] [CrossRef]
- Jing, W.; Yao, L.; Zhao, X.; Zhang, P.; Liu, Y.; Xia, X.; Song, J.; Yang, J.; Li, Y.; Zhou, C. Understanding Terrestrial Water Storage Declining Trends in the Yellow River Basin. J. Geophys. Res. Atmos. 2019, 124, 12963–12984. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-Resolution Csr Grace Rl05 Mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Himanshu, S. Csr Grace and Grace-Fo Rl06 Mascon Solutions V02; University of Texas at Austin: Austin, TX, USA, 2020. [Google Scholar]
- Beaudoing, H.; Rodell, M. NASA/GSFC/HSL. Gldas Noah Land Surface Model L4 3 Hourly 0.25 X 0.25 Degree V2.1; Goddard Earth Sciences Data and Information Services Center (Ges Disc): Greenbelt, MD, USA, 2020. [Google Scholar]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.; Yang, H.; Di, D.; Zhao, Y.; Liang, Q. Utilizing Grace-Based Groundwater Drought Index for Drought Characterization and Teleconnection Factors Analysis in the North China Plain. J. Hydrol. 2020, 585, 124849. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, F. Cycling Comfort Evaluation with Instrumented Probe Bicycle. Transp. Res. Part A Policy Pract. 2019, 129, 217–231. [Google Scholar] [CrossRef]
- Mudryk, L.; Mortimer, C.; Derksen, C.; Elias Chereque, A.; Kushner, P. Benchmarking of Snow Water Equivalent (Swe) Products Based on Outcomes of the Snowpex+ Intercomparison Project. Cryosphere 2025, 19, 201–218. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. Stl: A Seasonal-Trend Decomposition. J. Off. Stat 1990, 6, 3–73. [Google Scholar]
- Humphrey, V.; Gudmundsson, L.; Seneviratne, S.I. Assessing Global Water Storage Variability from Grace: Trends, Seasonal Cycle, Subseasonal Anomalies and Extremes. Surv. Geophys. 2016, 37, 357–395. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend Detection in Hydrologic Data: The Mann–Kendall Trend Test under the Scaling Hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: Chicago, IL, USA, 1948. [Google Scholar]
- Hussain, M.; Mahmud, I. Pymannkendall: A Python Package for Non Parametric Mann Kendall Family of Trend Tests. J. Open Source Softw. 2019, 4, 1556. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Rodell, M.; Chen, J.; Wilson, C.R. Analysis of Terrestrial Water Storage Changes from Grace and Gldas. Water Resour. Res. 2008, 44, W02433. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in Evapotranspiration from Land Surface Modeling, Remote Sensing, and Grace Satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging Trends in Global Freshwater Availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef]
- Long, D.; Yang, Y.; Wada, Y.; Hong, Y.; Liang, W.; Chen, Y.; Yong, B.; Hou, A.; Wei, J.; Chen, L. Deriving Scaling Factors Using a Global Hydrological Model to Restore Grace Total Water Storage Changes for China’s Yangtze River Basin. Remote Sens. Environ. 2015, 168, 177–193. [Google Scholar] [CrossRef]
- Ndehedehe, C.; Awange, J.; Agutu, N.; Kuhn, M.; Heck, B. Understanding Changes in Terrestrial Water Storage over West Africa between 2002 and 2014. Adv. Water Resour. 2016, 88, 211–230. [Google Scholar] [CrossRef]
- Xu, M.; Kang, S.; Chen, X.; Wu, H.; Wang, X.; Su, Z. Detection of Hydrological Variations and Their Impacts on Vegetation from Multiple Satellite Observations in the Three-River Source Region of the Tibetan Plateau. Sci. Total Environ. 2018, 639, 1220–1232. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; He, B.; Guo, L.; Liu, D. Differences in Response of Terrestrial Water Storage Components to Precipitation over 168 Global River Basins. J. Hydrometeorol. 2019, 20, 1981–1999. [Google Scholar] [CrossRef]
- Huang, Z.; Hejazi, M.; Li, X.; Tang, Q.; Vernon, C.; Leng, G.; Liu, Y.; Döll, P.; Eisner, S.; Gerten, D.; et al. Reconstruction of Global Gridded Monthly Sectoral Water Withdrawals for 1971–2010 and Analysis of Their Spatiotemporal Patterns. Hydrol. Earth Syst. Sci. 2018, 22, 2117–2133. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M. Terrestrial Water Storage in 2023. Nat. Rev. Earth Environ. 2024, 5, 247–249. [Google Scholar] [CrossRef]


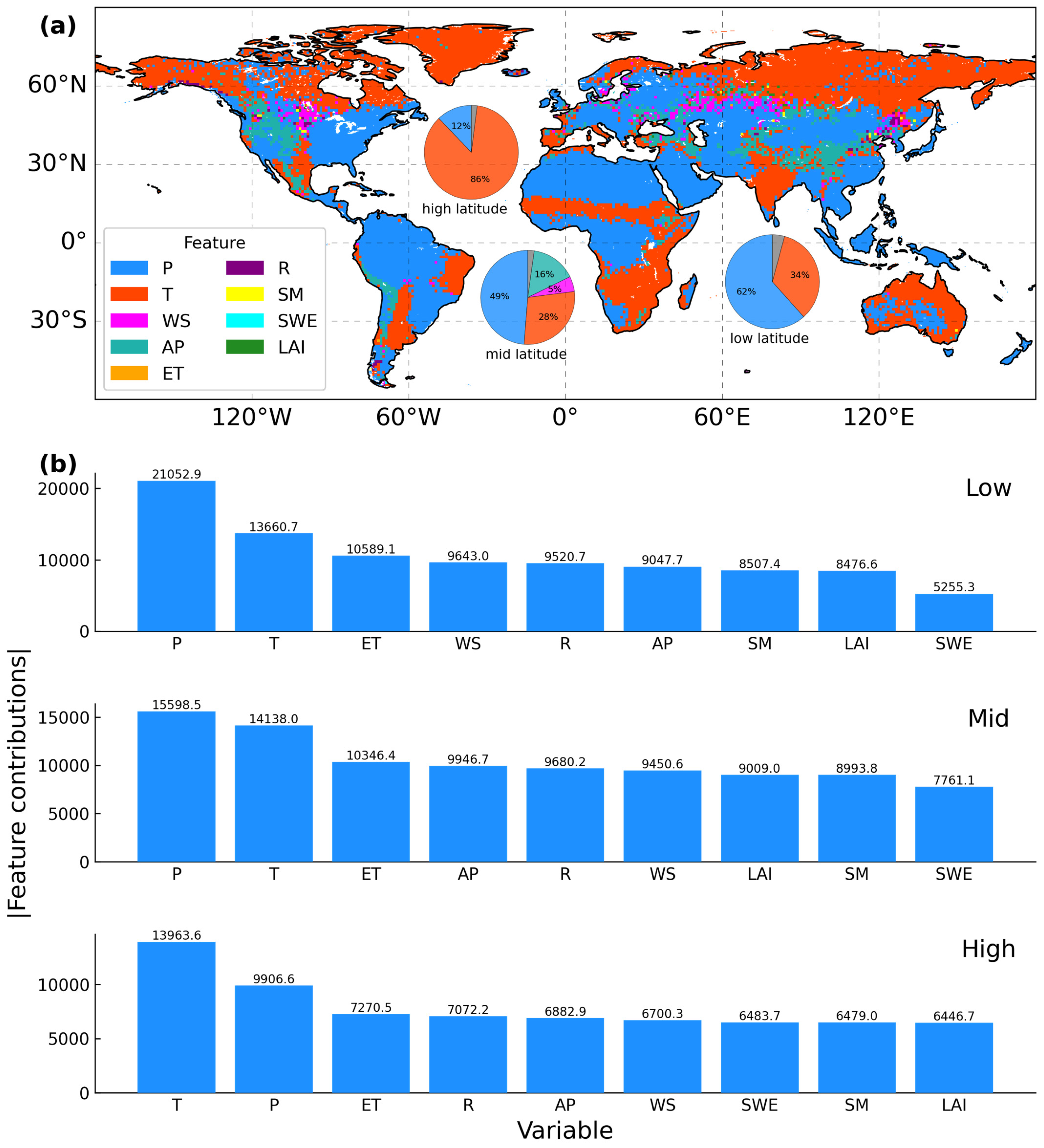
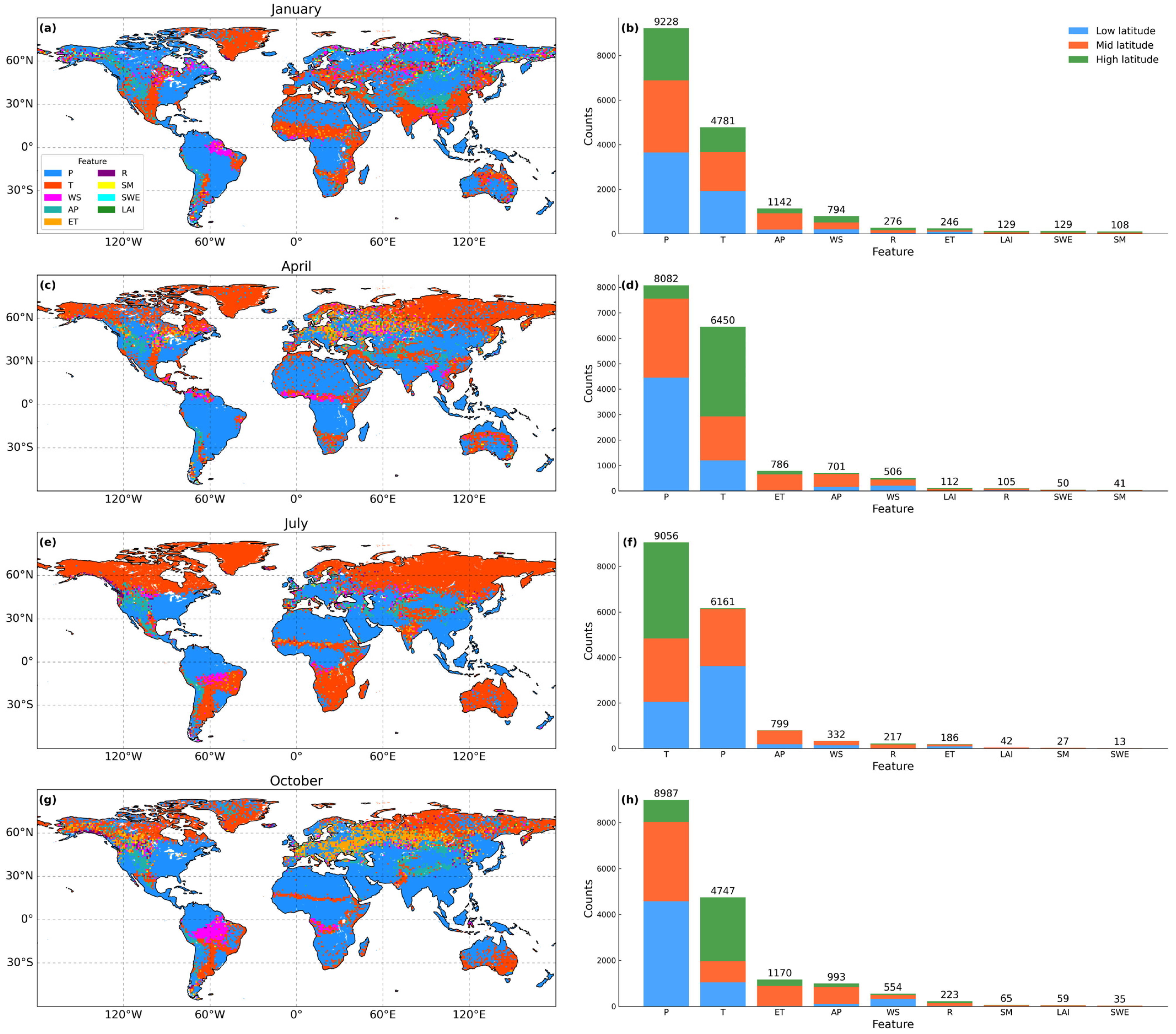

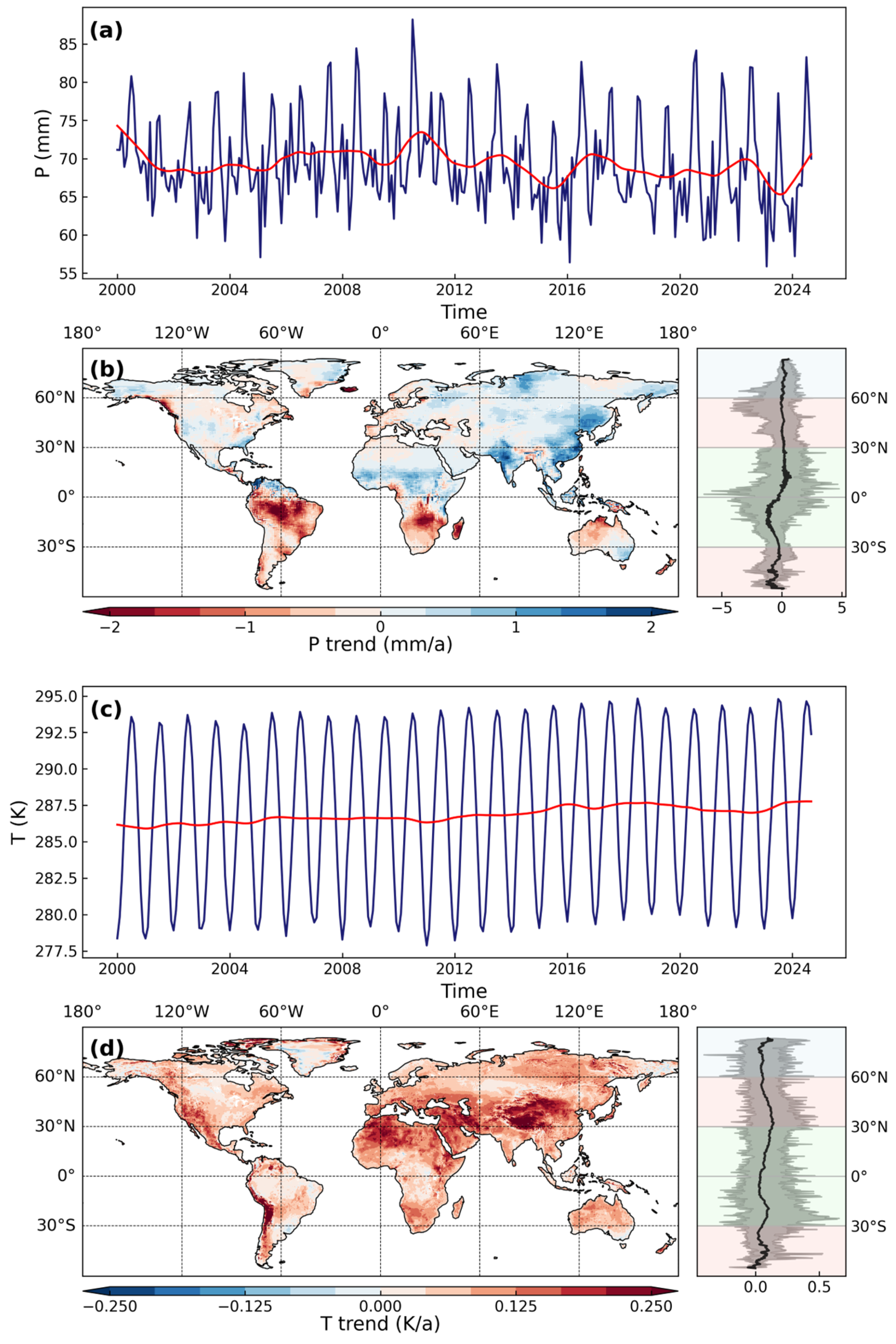
| Type | Variable | Acronym | Spatial Resolution | Temporal Resolution | Unit | Data Source |
|---|---|---|---|---|---|---|
| climate forcings | precipitation | P | 0.25° (60°S–90°N) | monthly | mm | GLDAS-2.1 |
| air temperature | T | K | ||||
| wind speed | WS | m/s | ||||
| surface air pressure | AP | Pa | ||||
| hydrological factors | evapotranspiration | ET | 0.25° (60°S–90°N) | monthly | mm | GLDAS Noah LSM 2.1 |
| runoff | R | mm | ||||
| soil moisture | SM | mm | ||||
| snow water equivalent | SWE | 0.1° | monthly | mm | ERA5-Land | |
| attributes | leaf area index | LAI | 0.1° | monthly | \ | ERA5-Land |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Cai, X.; Li, L.; Wu, X.; Zhao, Z.; Tan, X. Interpreting Global Terrestrial Water Storage Dynamics and Drivers with Explainable Deep Learning. Remote Sens. 2025, 17, 2118. https://doi.org/10.3390/rs17132118
Huang H, Cai X, Li L, Wu X, Zhao Z, Tan X. Interpreting Global Terrestrial Water Storage Dynamics and Drivers with Explainable Deep Learning. Remote Sensing. 2025; 17(13):2118. https://doi.org/10.3390/rs17132118
Chicago/Turabian StyleHuang, Haijun, Xitian Cai, Lu Li, Xiaolu Wu, Zichun Zhao, and Xuezhi Tan. 2025. "Interpreting Global Terrestrial Water Storage Dynamics and Drivers with Explainable Deep Learning" Remote Sensing 17, no. 13: 2118. https://doi.org/10.3390/rs17132118
APA StyleHuang, H., Cai, X., Li, L., Wu, X., Zhao, Z., & Tan, X. (2025). Interpreting Global Terrestrial Water Storage Dynamics and Drivers with Explainable Deep Learning. Remote Sensing, 17(13), 2118. https://doi.org/10.3390/rs17132118






