Landslide Risk Assessment as a Reference for Disaster Prevention and Mitigation: A Case Study of the Renhe District, Panzhihua City, China
Abstract
1. Introduction
- (1)
- This study methodically contrasts the TabPFN model with two conventional reinforcement learning models: random forest (RF) and eXtreme Gradient Boosting tree (XGBoost). We assess the predictive performance, generalization capability, and adaptability of the TabPFN model under limited sample conditions by training and testing on the same dataset, while also investigating its feasibility and potential applications as a rapid and lightweight alternative in geological disaster modelling.
- (2)
- A multi-factor landslide risk-assessment system is developed to furnish data support and a decision-making foundation for local government agencies in disaster prevention and mitigation, thereby enhancing local landslide management.
2. Materials and Methods
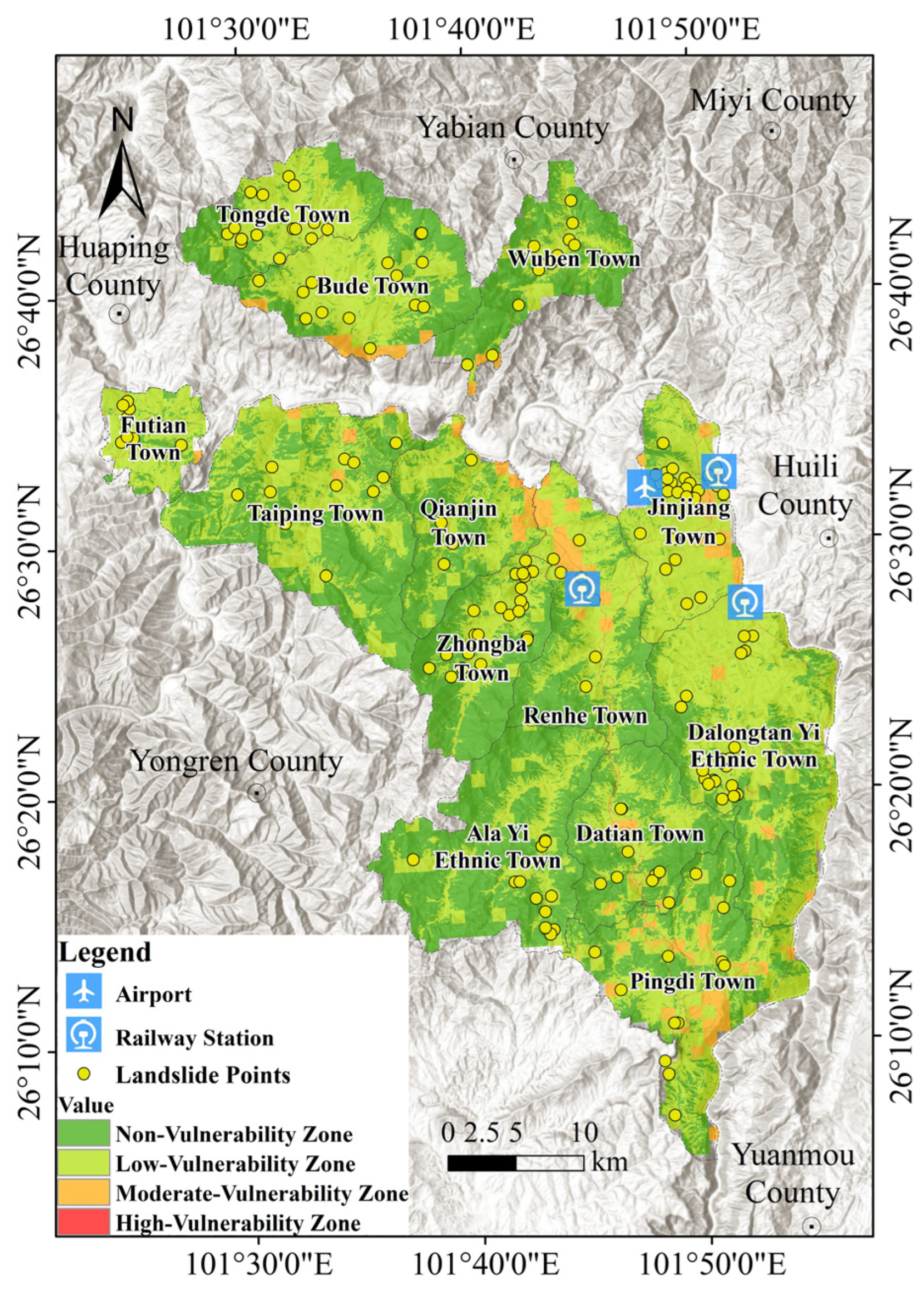
2.1. Study Area
2.2. Data Sources
3. Methodology
- (1)
- Systematically gather multi-source data, including topography, geology, meteorological, and remote sensing, for evaluation factor selection. Select suitable assessment criteria based on study goals and the attributes of each data type, categorizing them into groups such as geographical and environmental elements to create a cohesive geographic information database.
- (2)
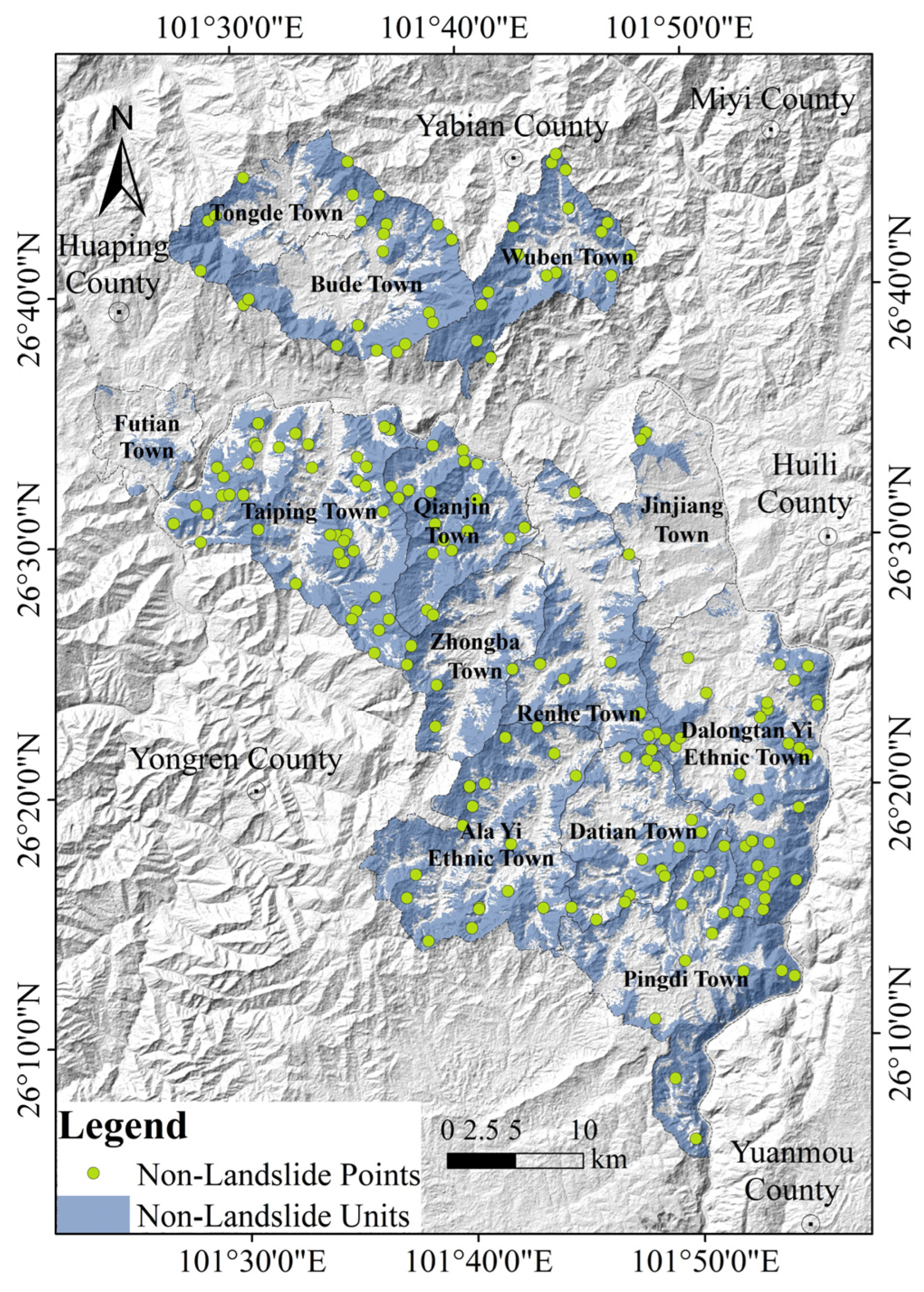
- Utilize the information content model (IV) to identify non-landslide units within the study area and randomly select a quantity of non-landslide points equivalent to the number of landslide points inside these units. Integrate the landslide points with the non-landslide points to provide the training sample set necessary for the model.
- (3)
- Conduct a hazard assessment by partitioning the sample set into a training set and a test set in a 7:3 ratio. Employ the RF, XGBoost, and TabPFN algorithms to model the training set, evaluate the fitting capability and predictive accuracy of the three models, and identify the optimal model to compute the landslide occurrence probability for each grid cell within the study area. Utilize this probability as the landslide hazard index to finalize the hazard assessment.
- (4)
- Select representative disaster-prone carriers based on population density, GDP, road type, and land-use type, and develop a vulnerability assessment indicator system. Calculate the weights of each disaster-bearing body utilizing the Analytic Hierarchy Process (AHP) and do a sensitivity analysis. Amend the judgment matrix in accordance with the analysis results. Compute the vulnerability index utilizing the adjusted weights and derive the spatial grading outcomes of vulnerability.
- (5)
- Combine the landslide hazard index with the vulnerability grade outcomes to produce a landslide hazard risk zoning map, thereby finalizing the regional landslide risk assessment.
3.1. Landslide Hazard Assessment Method
- (1)
- Data processing of pertinent evaluation criteria was conducted utilizing QGIS 3.34. Non-landslide units were delineated utilizing the information volume model (IV), and non-landslide points were collected from these units as negative samples. The negative samples were combined with landslide unit samples to create a sample set for the model data.
- (2)
- Three models were trained based on Python 3.11.11. Both RF and XGBoost employed the grid_search function to explore various hyperparameter combinations in order to identify the ideal parameters and then trained the sample set to derive the final model.
- (3)
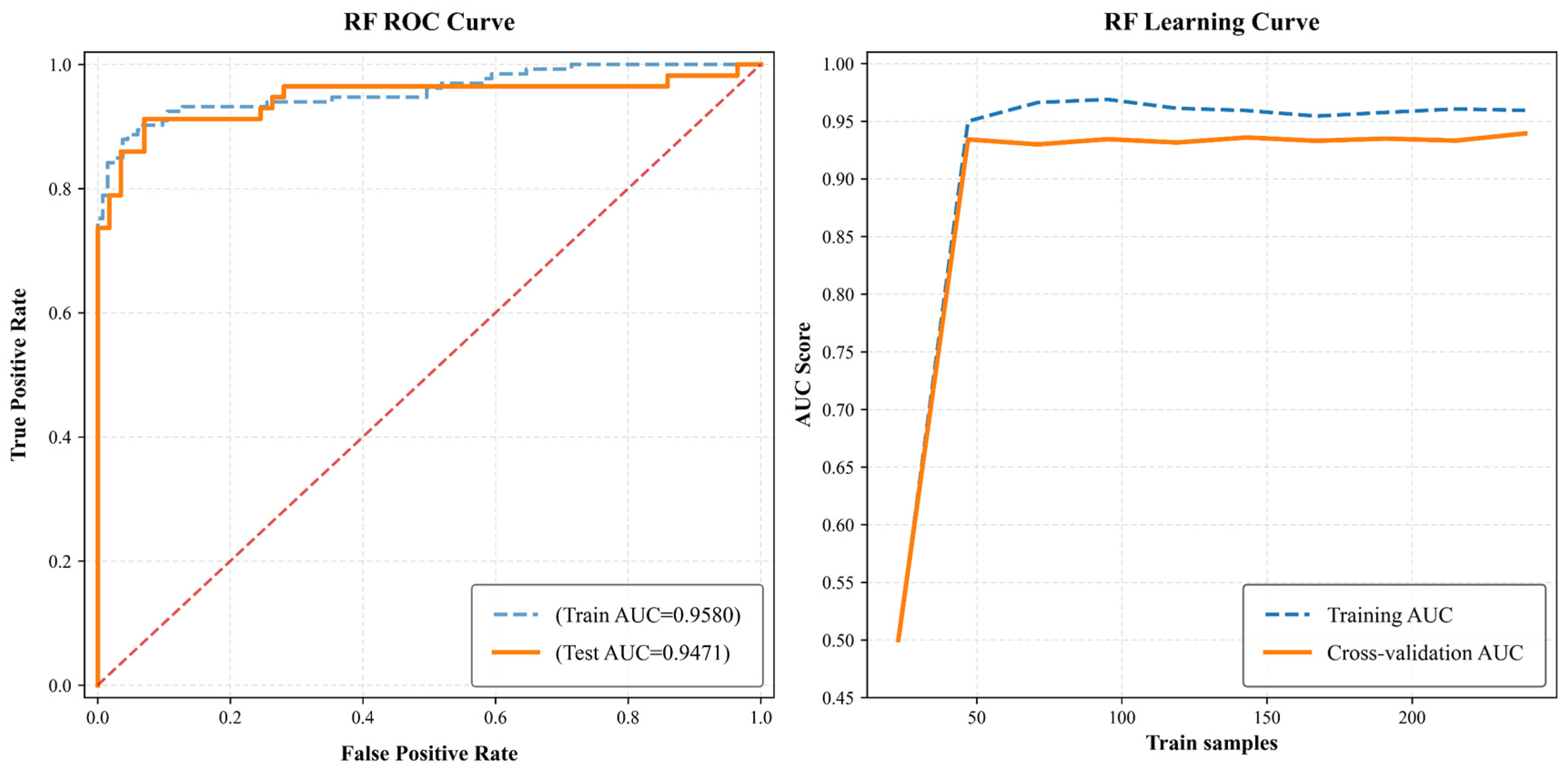
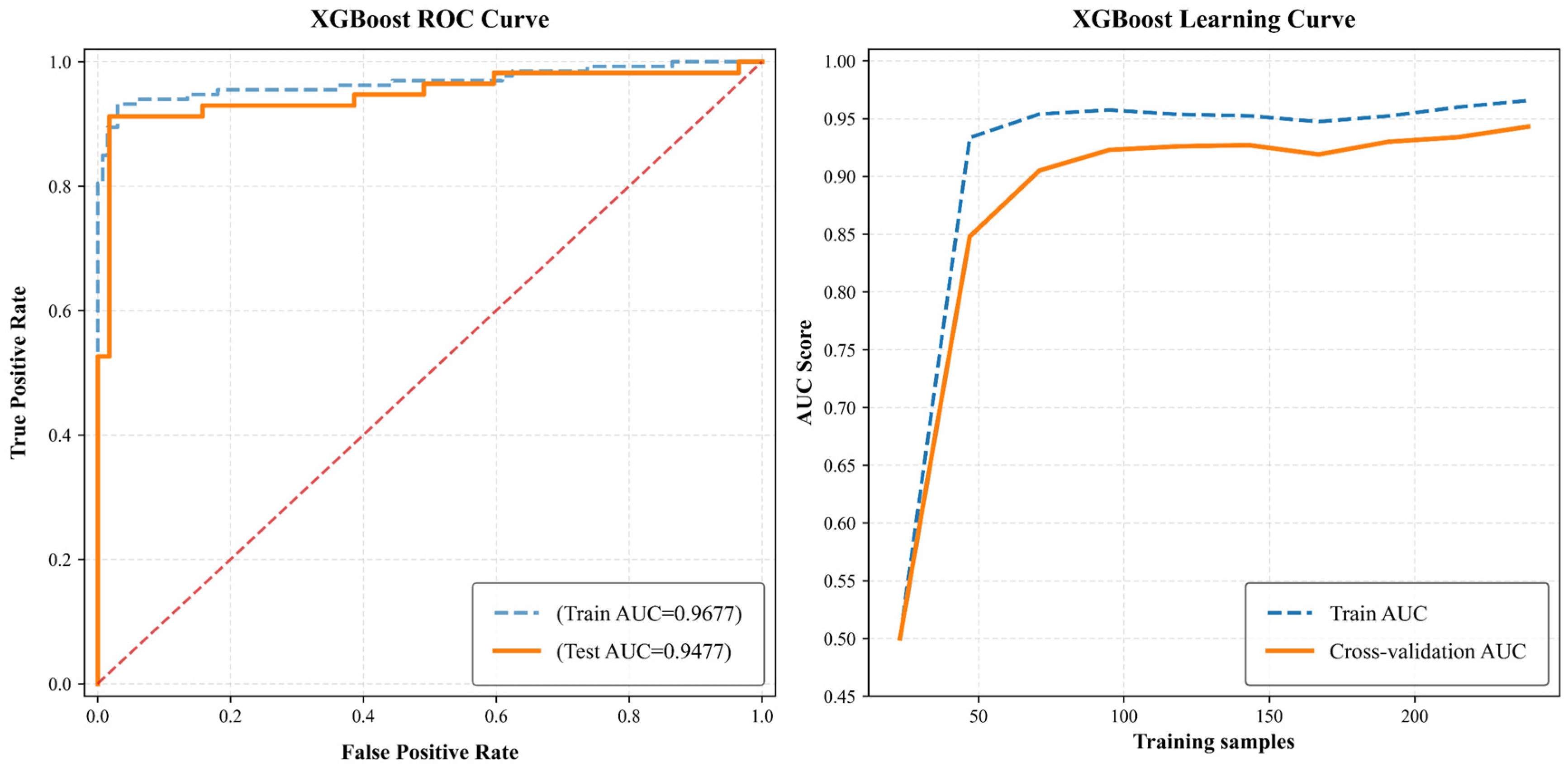
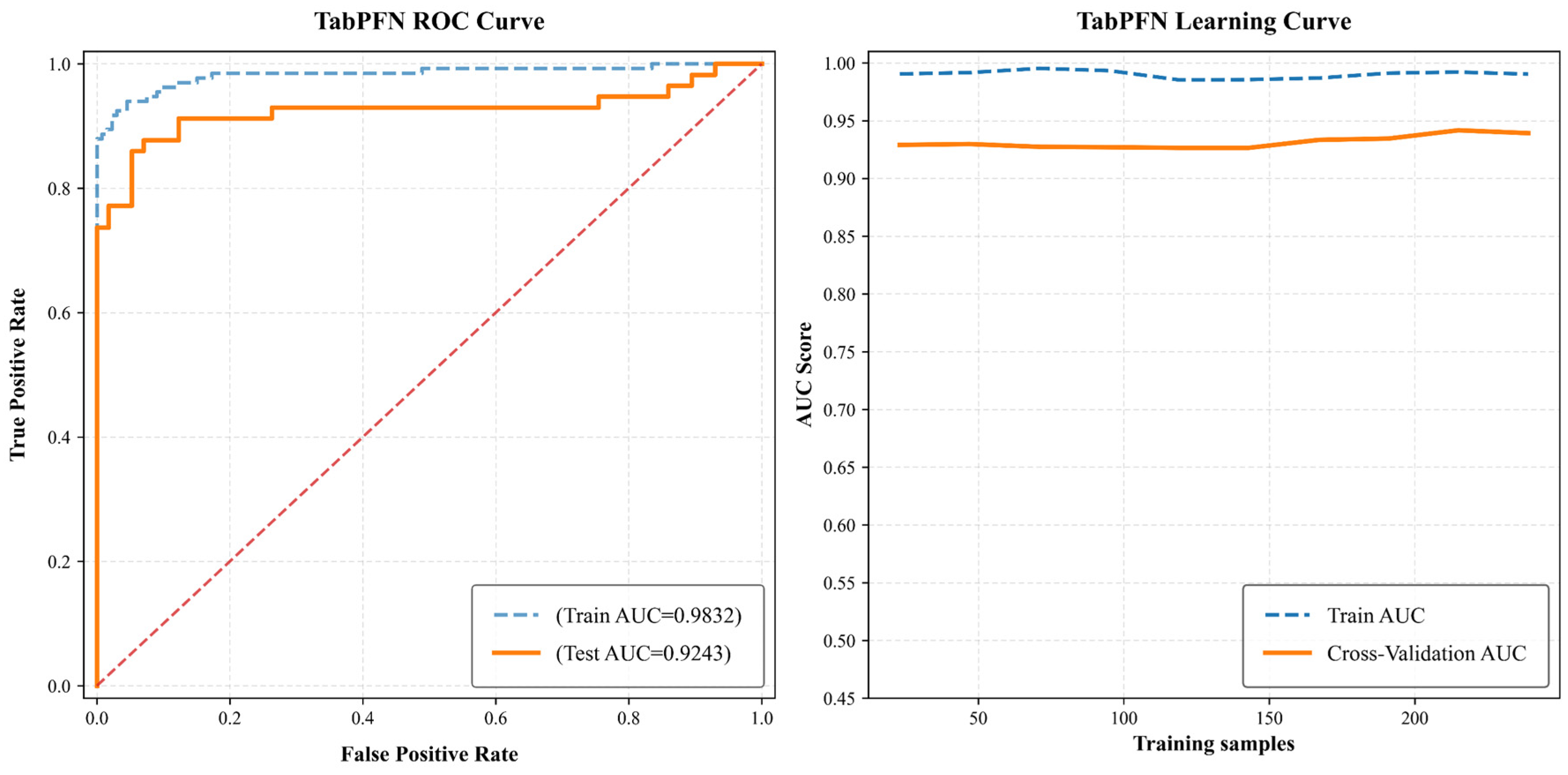
- The data from the research region was input into the optimal model developed to forecast landslide hazard probability, and the outcomes were assessed by generating ROC curves and learning curves.
3.1.1. Information Value (IV) Model
3.1.2. Random Forest (RF) Model
3.1.3. The eXtreme Gradient Boosting (XGBoost) Model
3.1.4. The Tabular Prior-Data Fitted Network (TabPFN) Model
3.1.5. Evaluation of Model
3.2. Landslide Vulnerability Assessment Method
3.2.1. The Analytic Hierarchy Process (AHP)
3.2.2. Sensitivity Analysis (SA)
3.3. Landslide Risk-Assessment Method
4. Results
4.1. Results of Landslide Hazard Assessment
4.1.1. Selection and Grading of Evaluation Factors
4.1.2. Determination of Non-Landslide Units
4.1.3. Model Training
4.1.4. Evaluation of the Accuracy and Analysis of the Results
4.2. Results of Landslide Vulnerability Assessment
4.3. Results of Landslide Risk Assessment
5. Discussion
5.1. Model Selection
5.2. Vulnerability Assessment Methods
5.3. Contributions and Shortcomings
6. Conclusions
- (1)
- This research analyzes 190 landslide locations, selecting 10 factors such as elevation, slope gradient, and aspect. Three models—random forest (RF), eXtreme Gradient Boosting Tree (XGBoost), and Tabular Prior-data Fitted Network (TabPFN)—are utilized to assess landslide hazard. Random forest and XGBoost exhibited exceptional generalization and precision. RF attained an area-under-the-curve (AUC) value of 0.9471, demonstrating superior generalization performance, and was recognized as the ideal model for hazard mapping. TabPFN attained an AUC value of 0.9243, indicating substantial accuracy, although it also presented a potential risk of overfitting. As a pre-trained model designed for rapid responses, it demonstrates potential for small-scale datasets and situations necessitating prompt decision-making.
- (2)
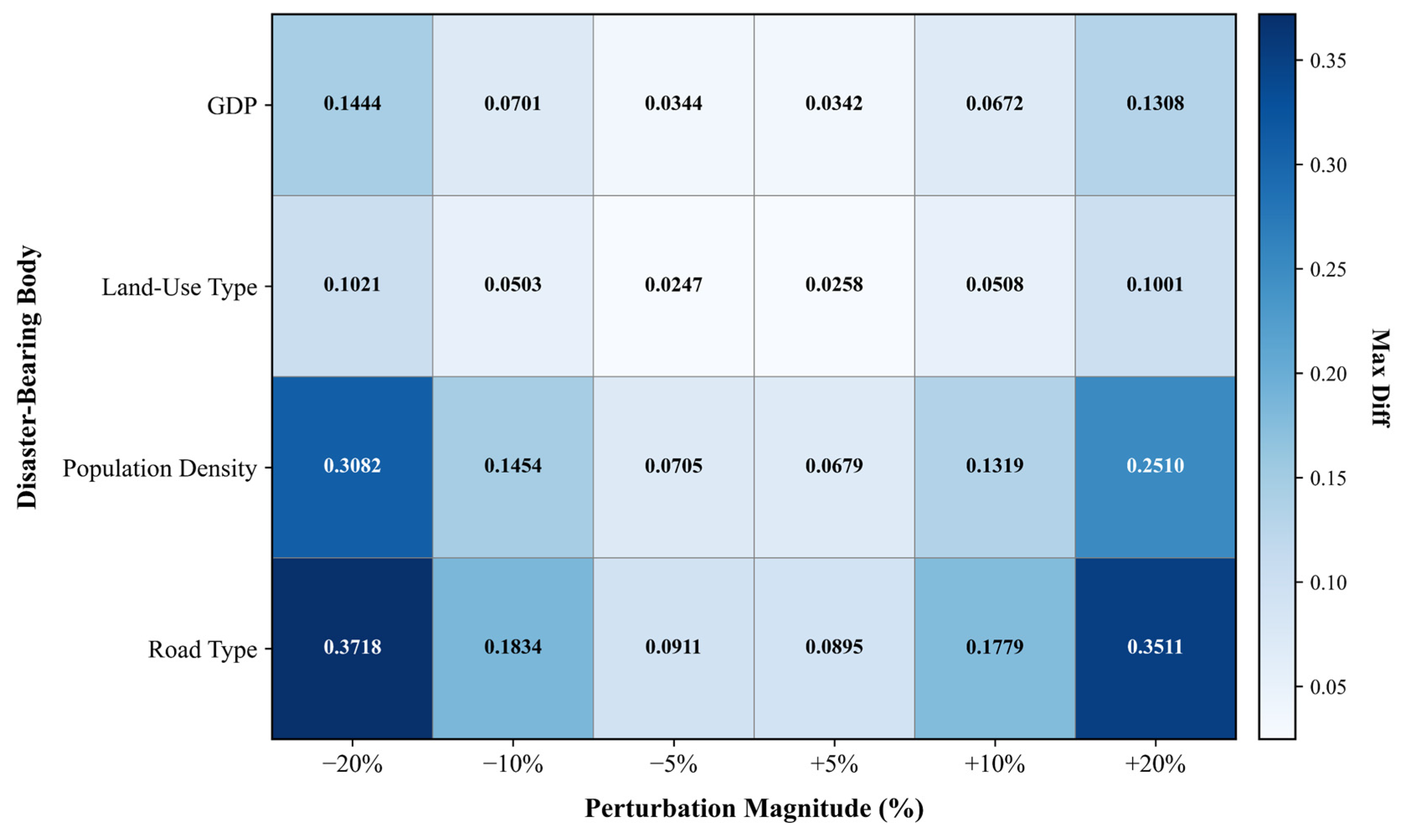
- The Analytic Hierarchy Process (AHP) was employed to ascertain the weights of the four disaster-bearing bodies: land-use type, Gross Domestic Product (GDP), road type, and population density. The expert scoring technique was found to be highly subjective through sensitivity analysis. The lagging nature of economic indicators was not completely considered, and the initial weights calculated using AHP underestimated the impact of engineering and overestimated the contribution of population indicators. The most sensitive vulnerability factor was determined to be road type, followed by population density. GDP and land-use type were relatively less sensitive.
- (3)
- The vulnerability assessment map and the landslide hazard assessment map were combined to produce the landslide hazard assessment map of the Renhe District. The findings suggest that the high-risk area comprises 2.08% of the studied area, with all three railway stations situated within this zone. Consequently, it is necessary to implement more stringent protective measures. These consist of the optimization of drainage systems, the enhancement of geological disaster monitoring systems, and reinforcement engineering. A relatively large area, 34.23%, is covered by the medium-risk zone, which is widely distributed throughout the district, particularly in the vicinity of main transportation routes, residential areas, and significant economic zones. The establishment of a comprehensive landslide early warning system and the enhancement of landslide early warning measures are necessary in this region. The regular installation of real-time monitoring apparatus and the improvement of public emergency response capabilities are examples of specific measures. The aforementioned conclusions offer significant support for the safe operation of public transportation infrastructure, including train stations and airports, and provide a scientific foundation for landslide prevention in the Renhe District, Panzhihua City.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Varnes, D.J. Slope Movement Types and Processes, Special Report 176. In Landslides: Analysis and Control; Schuster, R., Krizek, R., Eds.; Transportation Research Board, National Research Council: Washington, DC, USA, 1978; pp. 11–33. [Google Scholar]
- Wang, D.; Hao, M.; Chen, S.; Meng, Z.; Jiang, D.; Ding, F. Assessment of Landslide Susceptibility and Risk Factors in China. Nat. Hazard. 2021, 108, 3045–3059. [Google Scholar] [CrossRef]
- Dai, F.C.; Lee, C.F.; Ngai, Y.Y. Landslide Risk Assessment and Management: An Overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar] [CrossRef]
- Huang, R. Some Catastrophic Landslides since the Twentieth Century in the Southwest of China. Landslides 2009, 6, 69–81. [Google Scholar] [CrossRef]
- Xu, Q. Remote Sensing for Landslide Investigations: A Progress Report from China. Eng. Geol. 2023, 321, 107156. [Google Scholar] [CrossRef]
- Dai, X.; Gao, Y.; He, X.; Liu, T.; Jiang, B.; Shao, H.; Yao, Y. Spatial-Temporal Pattern Evolution and Driving Force Analysis of Ecological Environment Vulnerability in Panzhihua City. Environ. Sci. Pollut. Res. 2021, 28, 7151–7166. [Google Scholar] [CrossRef]
- Peng, L.; Xu, S.; Hou, J.; Peng, J. Quantitative Risk Analysis for Landslides: The Case of the Three Gorges Area, China. Landslides 2015, 12, 943–960. [Google Scholar] [CrossRef]
- Wang, W.-D.; Li, J.; Han, Z. Comprehensive Assessment of Geological Hazard Safety along Railway Engineering Using a Novel Method: A Case Study of the Sichuan-Tibet Railway, China. Geomat. Nat. Hazards Risk 2020, 11, 1–21. [Google Scholar] [CrossRef]
- Lin, J.; Chen, W.; Qi, X.; Hou, H. Risk Assessment and Its Influencing Factors Analysis of Geological Hazards in Typical Mountain Environment. J. Clean. Prod. 2021, 309, 127077. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Y.; Liang, Y.; Sun, P.; Li, Y.; Su, X.; Wang, A.; Meng, X. Landslide Risk Assessment Using a Combined Approach Based on InSAR and Random Forest. Remote Sens. 2022, 14, 2131. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, W.; Pun, M.-O.; Shi, W. Cross-Domain Landslide Mapping from Large-Scale Remote Sensing Images Using Prototype-Guided Domain-Aware Progressive Representation Learning. ISPRS J. Photogramm. Remote Sens. 2023, 197, 1–17. [Google Scholar] [CrossRef]
- Dai, X.; Chen, J.; Zhang, T.; Xue, C. Integrated Landslide Risk Assessment via a Landslide Susceptibility Model Based on Intelligent Optimization Algorithms. Remote Sens. 2025, 17, 545. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, R.; Wang, T.; Liu, A.; He, Y.; Lv, J.; He, X.; Mao, W.; Xiang, W.; Zhang, B. An Information Quantity and Machine Learning Integrated Model for Landslide Susceptibility Mapping in Jiuzhaigou, China. Nat. Hazard. 2024, 120, 10185–10217. [Google Scholar] [CrossRef]
- Li, R.; Tan, S.; Zhang, M.; Zhang, S.; Wang, H.; Zhu, L. Geological Disaster Susceptibility Evaluation Using a Random Forest Empowerment Information Quantity Model. Sustainability 2024, 16, 765. [Google Scholar] [CrossRef]
- He, W.; Chen, G.; Zhao, J.; Lin, Y.; Qin, B.; Yao, W.; Cao, Q. Landslide Susceptibility Evaluation of Machine Learning Based on Information Volume and Frequency Ratio: A Case Study of Weixin County, China. Sensors 2023, 23, 2549. [Google Scholar] [CrossRef]
- Ohlmacher, G.C.; Davis, J.C. Using Multiple Logistic Regression and GIS Technology to Predict Landslide Hazard in Northeast Kansas, USA. Eng. Geol. 2003, 69, 331–343. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Landslide Hazard Mapping at Selangor, Malaysia Using Frequency Ratio and Logistic Regression Models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Dong, J.-J.; Tung, Y.-H.; Chen, C.-C.; Liao, J.-J.; Pan, Y.-W. Logistic Regression Model for Predicting the Failure Probability of a Landslide Dam. Eng. Geol. 2011, 117, 52–61. [Google Scholar] [CrossRef]
- Budimir, M.E.A.; Atkinson, P.M.; Lewis, H.G. A Systematic Review of Landslide Probability Mapping Using Logistic Regression. Landslides 2015, 12, 419–436. [Google Scholar] [CrossRef]
- Carrara, A.; Cardinali, M.; Detti, R.; Guzzetti, F.; Pasqui, V.; Reichenbach, P. GIS Techniques and Statistical Models in Evaluating Landslide Hazard. Earth Surf. Process. Landf. 1991, 16, 427–445. [Google Scholar] [CrossRef]
- Wang, G.; Chen, X.; Chen, W. Spatial Prediction of Landslide Susceptibility Based on GIS and Discriminant Functions. ISPRS Int. J. Geo-Inf. 2020, 9, 144. [Google Scholar] [CrossRef]
- Lo, C.-M.; Feng, Z.-Y.; Chang, K.-T. Landslide Hazard Zoning Based on Numerical Simulation and Hazard Assessment. Geomat. Nat. Hazards Risk 2018, 9, 368–388. [Google Scholar] [CrossRef]
- Jia, L.; Wang, J.; Gao, S.; Fang, L.; Wang, D. Landslide Risk Evaluation Method of Open-Pit Mine Based on Numerical Simulation of Large Deformation of Landslide. Sci. Rep. 2023, 13, 15410. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Dai, F.; Xu, X.; Lee, Y.H. GIS-Based Support Vector Machine Modeling of Earthquake-Triggered Landslide Susceptibility in the Jianjiang River Watershed, China. Geomorphology 2012, 145–146, 70–80. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Han, Z.; Pham, B.T. Improved Landslide Assessment Using Support Vector Machine with Bagging, Boosting, and Stacking Ensemble Machine Learning Framework in a Mountainous Watershed, Japan. Landslides 2020, 17, 641–658. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Tien Bui, D. Spatial Prediction of Landslide Hazard at the Yihuang Area (China) Using Two-Class Kernel Logistic Regression, Alternating Decision Tree and Support Vector Machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Krkač, M.; Špoljarić, D.; Bernat, S.; Arbanas, S.M. Method for Prediction of Landslide Movements Based on Random Forests. Landslides 2017, 14, 947–960. [Google Scholar] [CrossRef]
- Zhao, L.; Wu, X.; Niu, R.; Wang, Y.; Zhang, K. Using the Rotation and Random Forest Models of Ensemble Learning to Predict Landslide Susceptibility. Geomatics Nat. Hazards Risk 2020, 11, 1542–1564. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Zhang, Z.; Xu, Q.; Li, W. Risk Factor Detection and Landslide Susceptibility Mapping Using Geo-Detector and Random Forest Models: The 2018 Hokkaido Eastern Iburi Earthquake. Remote Sens. 2021, 13, 1157. [Google Scholar] [CrossRef]
- Tanyu, B.F.; Abbaspour, A.; Alimohammadlou, Y.; Tecuci, G. Landslide Susceptibility Analyses Using Random Forest, C4.5, and C5.0 with Balanced and Unbalanced Datasets. Catena 2021, 203, 105355. [Google Scholar] [CrossRef]
- Wang, Y.; Wen, H.; Sun, D.; Li, Y. Quantitative Assessment of Landslide Risk Based on Susceptibility Mapping Using Random Forest and GeoDetector. Remote Sens. 2021, 13, 2625. [Google Scholar] [CrossRef]
- Guo, W.; Ye, J.; Liu, C.; Lv, Y.; Zeng, Q.; Huang, X. An Approach for Predicting Landslide Susceptibility and Evaluating Predisposing Factors. Int. J. Appl. Earth Obs. Geoinf. 2024, 135, 104217. [Google Scholar] [CrossRef]
- Wang, L.; Yang, K.; Wu, C.; Zhou, Y.; Liu, J.; Hu, H. Novel Approach to Quantitative Risk Assessment of Reservoir Landslides Using a Hybrid CNN-LSTM Model. Landslides 2024, 22, 943–956. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, C.; Cao, Y.; Meena, S.R.; Feng, Y.; Wang, Y. Utilizing Deep Learning Approach to Develop Landslide Susceptibility Mapping Considering Landslide Types. Bull. Eng. Geol. Environ. 2024, 83, 430. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; Zhang, L. Transfer Learning Improves Landslide Susceptibility Assessment. Gondwana Res. 2023, 123, 238–254. [Google Scholar] [CrossRef]
- Wang, Z.; Brenning, A. Unsupervised Active–Transfer Learning for Automated Landslide Mapping. Comput. Geosci. 2023, 181, 105457. [Google Scholar] [CrossRef]
- Huang, F.; Mao, D.; Jiang, S.-H.; Zhou, C.; Fan, X.; Zeng, Z.; Catani, F.; Yu, C.; Chang, Z.; Huang, J.; et al. Uncertainties in Landslide Susceptibility Prediction Modeling: A Review on the Incompleteness of Landslide Inventory and Its Influence Rules. Geosci. Front. 2024, 15, 101886. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Zhang, W.; He, Y.; Pijush, S. A Comprehensive Review of Machine Learning-based Methods in Landslide Susceptibility Mapping. Geol. J. 2023, 58, 2283–2301. [Google Scholar] [CrossRef]
- Song, J.; Wang, Y.; Fang, Z.; Peng, L.; Hong, H. Potential of Ensemble Learning to Improve Tree-Based Classifiers for Landslide Susceptibility Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4642–4662. [Google Scholar] [CrossRef]
- Kumar, C.; Walton, G.; Santi, P.; Luza, C. An Ensemble Approach of Feature Selection and Machine Learning Models for Regional Landslide Susceptibility Mapping in the Arid Mountainous Terrain of Southern Peru. Remote Sens. 2023, 15, 1376. [Google Scholar] [CrossRef]
- Liu, B.; Guo, H.; Li, J.; Ke, X.; He, X. Application and Interpretability of Ensemble Learning for Landslide Susceptibility Mapping along the Three Gorges Reservoir Area, China. Nat. Hazard. 2024, 120, 4601–4632. [Google Scholar] [CrossRef]
- Sahin, E.K. Implementation of Free and Open-Source Semi-Automatic Feature Engineering Tool in Landslide Susceptibility Mapping Using the Machine-Learning Algorithms RF, SVM, and XGBoost. Stoch. Environ. Res. Risk Assess. 2022, 37, 1067–1092. [Google Scholar] [CrossRef]
- Lv, J.; Zhang, R.; Shama, A.; Hong, R.; He, X.; Wu, R.; Bao, X.; Liu, G. Exploring the Spatial Patterns of Landslide Susceptibility Assessment Using Interpretable Shapley Method: Mechanisms of Landslide Formation in the Sichuan-Tibet Region. J. Environ. Manag. 2024, 366, 121921. [Google Scholar] [CrossRef] [PubMed]
- Lv, L.; Chen, T.; Liu, G.; Dou, J.; Plaza, A. A Comparative Study of Model Interpretability Considering the Decision Differentiation of Landslide Susceptibility Models. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–18. [Google Scholar] [CrossRef]
- Das, R.; Chattoraj, S.L.; Singh, M.; Bisht, A. Synergetic Use of Geospatial and Machine Learning Techniques in Modelling Landslide Susceptibility in Parts of Shimla to Kinnaur National Highway, Himachal Pradesh. Model. Earth Syst. Environ. 2024, 10, 4163–4183. [Google Scholar] [CrossRef]
- Hollmann, N.; Müller, S.; Eggensperger, K.; Hutter, F. Tabpfn: A Transformer That Solves Small Tabular Classification Problems in a Second. arXiv 2023, arXiv:2207.01848. [Google Scholar]
- Hollmann, N.; Müller, S.; Purucker, L.; Krishnakumar, A.; Körfer, M.; Hoo, S.B.; Schirrmeister, R.T.; Hutter, F. Accurate Predictions on Small Data with a Tabular Foundation Model. Nature 2025, 637, 319–326. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Y.; Tan, S. Evaluation of Mine Geological Hazard Susceptibility of Coupling CF with Information Model Based on GIS in Panzhihua City. J. Yunnan Univ. Nat. Sci. Ed. 2022, 44, 754–764. [Google Scholar]
- Dai, X.; Li, W.; Liu, Z.; Tong, C.; Li, C.; Zeng, J.; Ye, Y.; Li, W.; Shan, Y.; Zhou, J.; et al. Effects of Mining on Urban Environmental Change: A Case Study of Panzhihua. Remote Sens. 2022, 14, 6004. [Google Scholar] [CrossRef]
- GB 18306-2015; Seismic Ground Motion Parameter Zonation Map of China. Standards Press of China: Beijing, China, 2015.
- Xu, X. China Population Spatial Distribution Kilometer Grid Dataset. Resource and Environmental Science Data Center 2017. Available online: https://www.resdc.cn/DOI/doi.aspx?DOIid=32 (accessed on 24 July 2024). [CrossRef]
- Xu, X. China GDP Spatial Distribution Kilometer Grid Dataset. Resource and Environmental Science Data Center 2017. Available online: https://www.resdc.cn/DOI/doi.aspx?DOIid=33 (accessed on 24 July 2024). [CrossRef]
- Corominas, J.; Van Westen, C.; Frattini, P.; Cascini, L.; Malet, J.-P.; Fotopoulou, S.; Catani, F.; Van Den Eeckhaut, M.; Mavrouli, O.; Agliardi, F.; et al. Recommendations for the Quantitative Analysis of Landslide Risk. Bull. Eng. Geol. Environ. 2013, 73, 209–263. [Google Scholar] [CrossRef]
- Varnes, D. Landslide Hazard Zonation: A Review of Principles and Practice; United Nations: Paris, France, 1984. [Google Scholar]
- United Nations Department of Humanitarian Affairs. International Decade for Disaster Reduction. Internationally Agreed Glossary of Basic Terms Related to Disaster Management; United Nations Department of Humanitarian Affairs (DHA): Geneva, Switzerland, 1992; Volume 81. [Google Scholar]
- Sharma, L.P.; Patel, N.; Ghose, M.K.; Debnath, P. Development and Application of Shannon’s Entropy Integrated Information Value Model for Landslide Susceptibility Assessment and Zonation in Sikkim Himalayas in India. Nat. Hazard. 2015, 75, 1555–1576. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I.; Hong, H.; Chen, W.; Xu, C. Applying Information Theory and GIS-Based Quantitative Methods to Produce Landslide Susceptibility Maps in Nancheng County, China. Landslides 2017, 14, 1091–1111. [Google Scholar] [CrossRef]
- Karir, D.; Ray, A.; Kumar Bharati, A.; Chaturvedi, U.; Rai, R.; Khandelwal, M. Stability Prediction of a Natural and Man-Made Slope Using Various Machine Learning Algorithms. Transp. Geotech. 2022, 34, 100745. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- El Gana, E.M.; Ouallali, A.; Taleb, A. Scour Depth Prediction around Bridge Piers of Various Geometries Using Advanced Machine Learning and Data Augmentation Techniques. Transp. Geotech. 2025, 51, 101537. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Zeng, T.; Wu, L.; Peduto, D.; Glade, T.; Hayakawa, Y.S.; Yin, K. Ensemble Learning Framework for Landslide Susceptibility Mapping: Different Basic Classifier and Ensemble Strategy. Geosci. Front. 2023, 14, 101645. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Han, L.; Chen, L.; Wang, L. Slope Stability Prediction Using Ensemble Learning Techniques: A Case Study in Yunyang County, Chongqing, China. J. Rock Mech. Geotech. Eng. 2022, 14, 1089–1099. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Teke, A. Advanced Hyperparameter Optimization for Improved Spatial Prediction of Shallow Landslides Using Extreme Gradient Boosting (XGBoost). Bull. Eng. Geol. Environ. 2022, 81, 201. [Google Scholar] [CrossRef]
- Carter, J.V.; Pan, J.; Rai, S.N.; Galandiuk, S. ROC-Ing along: Evaluation and Interpretation of Receiver Operating Characteristic Curves. Surgery 2016, 159, 1638–1645. [Google Scholar] [CrossRef]
- Thammaboribal, P.; Triapthti, N.K.; Lipiloet, S. Using of Analytical Hierarchy Process (AHP) in Disaster Management: A Review of Flooding and Landslide Susceptibility Mapping. Int. J. Geoinformatics 2025, 21, 177–196. [Google Scholar] [CrossRef]
- Ilia, I.; Tsangaratos, P. Applying Weight of Evidence Method and Sensitivity Analysis to Produce a Landslide Susceptibility Map. Landslides 2016, 13, 379–397. [Google Scholar] [CrossRef]
- DZ/T 0438-2023; Specification of Geological Hazard Risk Survey and Assessment (1:50000). Ministry of Natural Resources: Beijing, China, 2023.
- Samia, J.; Temme, A.; Bregt, A.; Wallinga, J.; Guzzetti, F.; Ardizzone, F.; Rossi, M. Do Landslides Follow Landslides? Insights in Path Dependency from a Multi-Temporal Landslide Inventory. Landslides 2017, 14, 547–558. [Google Scholar] [CrossRef]
- Silalahi, F.E.S.; Pamela; Arifianti, Y.; Hidayat, F. Landslide Susceptibility Assessment Using Frequency Ratio Model in Bogor, West Java, Indonesia. Geosci. Lett. 2019, 6, 10. [Google Scholar] [CrossRef]
- Li, B.; Liu, K.; Wang, M.; He, Q.; Jiang, Z.; Zhu, W.; Qiao, N. Global Dynamic Rainfall-Induced Landslide Susceptibility Mapping Using Machine Learning. Remote Sens. 2022, 14, 5795. [Google Scholar] [CrossRef]
- Dou, J.; Tien Bui, D.; Yunus, A.P.; Jia, K.; Song, X.; Revhaug, I.; Xia, H.; Zhu, Z. Optimization of Causative Factors for Landslide Susceptibility Evaluation Using Remote Sensing and GIS Data in Parts of Niigata, Japan. PLoS ONE 2015, 10, e0133262. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Peng, J.; Wang, J.; Duan, Z.; Hong, H. GIS-Based Landslide Susceptibility Modelling: A Comparative Assessment of Kernel Logistic Regression, Naïve-Bayes Tree, and Alternating Decision Tree Models. Geomat. Nat. Hazards Risk 2017, 8, 950–973. [Google Scholar] [CrossRef]
- Kalantar, B.; Ueda, N.; Saeidi, V.; Ahmadi, K.; Halin, A.A.; Shabani, F. Landslide Susceptibility Mapping: Machine and Ensemble Learning Based on Remote Sensing Big Data. Remote Sens. 2020, 12, 1737. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Merghadi, A.; Shirzadi, A.; Nguyen, H.; Hussain, Y.; Avtar, R.; Chen, Y.; Pham, B.T.; Yamagishi, H. Different Sampling Strategies for Predicting Landslide Susceptibilities Are Deemed Less Consequential with Deep Learning. Sci. Total Environ. 2020, 720, 137320. [Google Scholar] [CrossRef]
- Kornejady, A.; Ownegh, M.; Bahremand, A. Landslide Susceptibility Assessment Using Maximum Entropy Model with Two Different Data Sampling Methods. Catena 2017, 152, 144–162. [Google Scholar] [CrossRef]
- Liu, Y.; Meng, Z.; Zhu, L.; Hu, D.; He, H. Optimizing the Sample Selection of Machine Learning Models for Landslide Susceptibility Prediction Using Information Value Models in the Dabie Mountain Area of Anhui, China. Sustainability 2023, 15, 1971. [Google Scholar] [CrossRef]
- Qin, Z.; Zhou, X.; Li, M.; Tong, Y.; Luo, H. Landslide Susceptibility Mapping Based on Resampling Method and FR-CNN: A Case Study of Changdu. Land 2023, 12, 1213. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, Y.; Xie, Y.; Uddin, M.G.; Xu, Z.; Chang, X.; Zhang, Y. Landslide Susceptibility Assessment Using Information Quantity and Machine Learning Integrated Models: A Case Study of Sichuan Province, Southwestern China. Earth Sci. Inform. 2025, 18, 190. [Google Scholar] [CrossRef]
- Ramampiandra, E.C.; Scheidegger, A.; Wydler, J.; Schuwirth, N. A Comparison of Machine Learning and Statistical Species Distribution Models: Quantifying Overfitting Supports Model Interpretation. Ecol. Modell. 2023, 481, 110353. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Overfitting, Model Tuning, and Evaluation of Prediction Performance. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer International Publishing: Cham, Switzerland, 2022; pp. 109–139. ISBN 978-3-030-89009-4. [Google Scholar]
- Frédéric, L.; Asté, J.; Leroi, E. Vulnerability Assessment of Elements Exposed to Mass-Movement: Working toward a Better Risk Perception. Landslides 1996, 1, 263–269. [Google Scholar]
- Froude, M.J.; Petley, D.N. Global Fatal Landslide Occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Zeng, T.; Guo, Z.; Wang, L.; Jin, B.; Wu, F.; Guo, R. Tempo-Spatial Landslide Susceptibility Assessment from the Perspective of Human Engineering Activity. Remote Sens. 2023, 15, 4111. [Google Scholar] [CrossRef]
- Zhao, G.; Lan, H.; Yin, H.; Li, L.; Strom, A.; Sun, W.; Tian, C. Deformation, Structure and Potential Hazard of a Landslide Based on InSAR in Banbar County, Xizang (Tibet). China Geol. 2024, 7, 203–221. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A Review of Statistically-Based Landslide Susceptibility Models. Earth Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]



| H4 | H3 | H2 | H1 | |
|---|---|---|---|---|
| V4 | HR | HR | MR | LR |
| V3 | HR | MR | LR | LR |
| V2 | MR | MR | LR | NR |
| V1 | MR | LR | NR | NR |
| Evaluation Factors | Classification | Grading | Nij/Count | Nij/N/% | Sij/Count | Sij/S/% | Information Values |
|---|---|---|---|---|---|---|---|
| Elevation (m) | 1 | <1200 | 32 | 16.84% | 196,693 | 10.25% | 0.4966 |
| 2 | 1200–1400 | 37 | 19.47% | 350,275 | 18.25% | 0.0649 | |
| 3 | 1400–1600 | 56 | 29.47% | 398,589 | 20.77% | 0.3500 | |
| 4 | 1600–1800 | 34 | 17.89% | 366,142 | 19.08% | −0.0641 | |
| 5 | 1800–2000 | 25 | 13.16% | 323,517 | 16.86% | −0.2479 | |
| 6 | >2000 | 6 | 3.16% | 160,301 | 8.35% | −0.9724 | |
| Slope (°) | 1 | <5 | 23 | 12.11% | 228,885 | 11.95% | 0.0129 |
| 2 | 5–10 | 27 | 14.21% | 125,319 | 6.54% | 0.7760 | |
| 3 | 10–15 | 46 | 24.21% | 198,756 | 10.38% | 0.8469 | |
| 4 | 15–20 | 34 | 17.89% | 273,378 | 14.28% | 0.2256 | |
| 5 | 20–25 | 26 | 13.68% | 333,737 | 17.43% | −0.2420 | |
| 6 | 25–30 | 17 | 8.95% | 310,359 | 16.21% | −0.5943 | |
| 7 | 30–40 | 15 | 7.89% | 347,619 | 18.15% | −0.8325 | |
| 8 | 40–50 | 2 | 1.05% | 85,089 | 4.44% | −1.4394 | |
| 9 | >50 | 0 | 0.00% | 11,794 | 0.62% | — | |
| Aspect (°) | 1 | Plane | 0 | 0.00% | 24,760 | 1.30% | — |
| 2 | 0–45 | 33 | 17.37% | 246,929 | 12.95% | 0.2936 | |
| 3 | 45–90 | 21 | 11.05% | 270,879 | 14.20% | −0.2506 | |
| 4 | 90–135 | 41 | 21.58% | 292,268 | 15.33% | 0.3419 | |
| 5 | 135–180 | 24 | 12.63% | 239,793 | 12.57% | 0.0049 | |
| 6 | 180–225 | 11 | 5.79% | 196,315 | 10.29% | −0.5751 | |
| 7 | 225–270 | 11 | 5.79% | 217,184 | 10.23% | −0.5693 | |
| 8 | 270–315 | 23 | 12.11% | 217,184 | 11.39% | 0.0609 | |
| 9 | 315–360 | 26 | 13.68% | 223,765 | 11.73% | 0.1541 | |
| Lithology | 1 | Hard Limestone–Dolomite | 2 | 1.05% | 122,377 | 6.38% | −1.8019 |
| 2 | Igneous Rock | 92 | 48.42% | 919,305 | 47.91% | 0.0106 | |
| 3 | Weak Interlayer Gneiss | 2 | 1.05% | 11,755 | 0.61% | 0.5456 | |
| 4 | Sandy Shale | 55 | 28.95% | 697,800 | 36.36% | −0.2280 | |
| 5 | Interbedded Shale and Siltstone | 36 | 18.95% | 157,592 | 8.21% | 0.8363 | |
| 6 | Loose Sand, Gravel, and Cobbles | 3 | 1.58% | 10,104 | 0.53% | 1.0916 | |
| Distance To Fault (m) | 1 | <50 | 4 | 2.11% | 16,062 | 0.84% | 0.9230 |
| 2 | 50–100 | 4 | 2.11% | 16,427 | 0.86% | 0.9006 | |
| 3 | 100–200 | 4 | 2.11% | 32,621 | 1.70% | 0.2145 | |
| 4 | 200–400 | 11 | 5.79% | 65,202 | 3.40% | 0.5336 | |
| 5 | 400–800 | 13 | 6.84% | 126,714 | 6.60% | 0.0362 | |
| 6 | 800–1600 | 32 | 16.84% | 239,639 | 12.48% | 0.2998 | |
| 7 | 1600–3200 | 40 | 21.05% | 416,424 | 21.69% | −0.0296 | |
| 8 | 3200–6400 | 51 | 26.84% | 605,797 | 31.55% | −0.1615 | |
| 9 | >64000 | 31 | 16.32% | 401,379 | 20.90% | −0.2477 | |
| Distance to River System (m) | 1 | <50 | 28 | 14.74% | 182,370 | 9.50% | 0.4394 |
| 2 | 50–100 | 36 | 18.95% | 167,564 | 8.73% | 0.7753 | |
| 3 | 100–150 | 30 | 15.79% | 153,952 | 8.02% | 0.6778 | |
| 4 | 150–200 | 20 | 10.53% | 142,182 | 7.40% | 0.3518 | |
| 5 | 200–400 | 47 | 24.74% | 464,563 | 24.19% | 0.0222 | |
| 6 | 400–600 | 18 | 9.47% | 322,264 | 16.78% | −0.5718 | |
| 7 | 600–800 | 5 | 2.63% | 207,669 | 10.81% | −1.4133 | |
| 8 | 800–1600 | 5 | 2.63% | 241,564 | 12.58% | −1.5645 | |
| 9 | >1600 | 1 | 0.53% | 38,137 | 1.99% | −1.3280 | |
| NDVI | 1 | <0.1 | 4 | 2.11% | 46,011 | 2.40% | −0.1302 |
| 2 | 0.1–0.15 | 13 | 6.84% | 84,934 | 4.43% | 0.4355 | |
| 3 | 0.15–0.2 | 30 | 15.79% | 184,460 | 9.61% | 0.4962 | |
| 4 | 0.2–0.25 | 44 | 23.16% | 300,109 | 15.64% | 0.3925 | |
| 5 | 0.25–0.3 | 34 | 17.89% | 387,685 | 20.20% | −0.1214 | |
| 6 | 0.3–0.35 | 23 | 12.11% | 406,862 | 21.20% | −0.5606 | |
| 7 | 0.35–0.4 | 22 | 11.58% | 277,016 | 14.44% | −0.2206 | |
| 8 | 0.4–0.45 | 15 | 7.89% | 150,139 | 7.82% | 0.0089 | |
| 9 | >0.45 | 5 | 2.63% | 81,544 | 4.25% | −0.4793 | |
| Topographic Relief (m) | 1 | <60 | 49 | 25.79% | 240,497 | 12.53% | 0.7216 |
| 2 | 60–100 | 73 | 38.42% | 501,638 | 26.14% | 0.3851 | |
| 3 | 100–130 | 45 | 23.68% | 398,977 | 20.79% | 0.1303 | |
| 4 | 130–160 | 13 | 6.84% | 346,357 | 18.05% | −0.9700 | |
| 5 | 160–190 | 6 | 3.16% | 211,072 | 11.00% | −1.2479 | |
| 6 | 190–220 | 2 | 1.05% | 113,033 | 5.89% | −1.7220 | |
| 7 | 220–260 | 1 | 0.53% | 67,941 | 3.54% | −1.9061 | |
| 8 | >260 | 1 | 0.53% | 31,727 | 1.65% | −1.1447 | |
| 24 h Maximum Precipitation (mm) | 1 | <40 | 4 | 2.11% | 111,060 | 5.78% | −1.0100 |
| 2 | 40–60 | 53 | 27.89% | 519,640 | 27.06% | 0.0304 | |
| 3 | 60–80 | 23 | 12.11% | 111,551 | 5.81% | 0.7341 | |
| 4 | 80–100 | 45 | 23.68% | 450,222 | 23.45% | 0.0099 | |
| 5 | 100–120 | 22 | 11.58% | 249,080 | 12.97% | −0.1135 | |
| 6 | >120 | 43 | 22.63% | 478712 | 24.93% | −0.0967 | |
| PGA | 1 | 0.1 | 17 | 8.95% | 102,200 | 5.32% | 0.5199 |
| 2 | 0.15 | 151 | 79.47% | 1,568,985 | 81.71% | −0.0278 | |
| 3 | 0.2 | 22 | 11.58% | 249,080 | 12.97% | −0.1135 |
| Parameter | Setting |
|---|---|
| n_estimators | 300 |
| max_depth | 8 |
| max_features | 0.25 |
| max_samples | 0.7 |
| min_samples_split | 10 |
| min_samples_leaf | 8 |
| ccp_alpha | 0.005 |
| Parameter | Setting |
|---|---|
| n_estimators | 500 |
| max_depth | 2 |
| colsample_bytree | 0.6 |
| learning_rate | 0.05 |
| min_child_weight | 5 |
| reg_alpha | 0.1 |
| reg_lambda | 5 |
| subsample | 0.8 |
| Disaster-Bearing Body | Grading Value | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Population Density/persons·km−2 | <100 | 100~200 | 200~500 | 500~1000 | >1000 | —— |
| GDP/10,000 yuan·km−2 | <5000 | 5000~10,000 | 10,000~15,000 | 15,000~20,000 | 20,000~250,000 | >25,000 |
| Road Type | Country Road | County Road | Provincial Road | Railway | National Road | Expressway |
| Land-Use Type | Cropland | Forest | Grassland | Water | Barren | Construction Land |
| Disaster-Bearing Body | Population Density | GDP | Road Type | Land-Use Type | Weight |
|---|---|---|---|---|---|
| Population Density | 1 | 2 | 4 | 6 | 0.5195 |
| GDP | 1/2 | 1 | 2 | 3 | 0.2598 |
| Road Type | 1/4 | 1/2 | 1 | 2 | 0.1400 |
| Land-Use Type | 1/6 | 1/3 | 1/2 | 1 | 0.0808 |
| Disaster-Bearing Body | Population Density | GDP | Road Type | Land-Use Type | Weight |
|---|---|---|---|---|---|
| Population Density | 1 | 4 | 2/3 | 5 | 0.3518 |
| GDP | 1/4 | 1 | 1/5 | 2 | 0.1042 |
| Road Type | 3/2 | 5 | 1 | 6 | 0.4777 |
| Land-Use Type | 1/5 | 1/2 | 1/6 | 1 | 0.0665 |
| Risk Zoning | Area (km) | Percentage (%) |
|---|---|---|
| High-Risk Zone | 35.1297 | 2.08% |
| Medium-Risk Zone | 577.1313 | 34.23% |
| Low-Risk Zone | 358.9749 | 21.29% |
| Non-Risk Zone | 714.8448 | 42.40% |
| Disaster-Bearing Bodies | Expert Weight Ranking | Sensitivity Ranking | Reason for Deviation |
|---|---|---|---|
| Road Types | 3 | 1 | Underestimating the impact of human engineering |
| Population Density | 1 | 2 | Overestimating the contribution of the indicator |
| GDP | 2 | 3 | Ignoring the lag effect of economic indicators |
| Land-Use Types | 4 | 4 | -- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Xue, L.; Ding, H.; Wang, H.; Huang, K.; Li, L.; Li, Z. Landslide Risk Assessment as a Reference for Disaster Prevention and Mitigation: A Case Study of the Renhe District, Panzhihua City, China. Remote Sens. 2025, 17, 2120. https://doi.org/10.3390/rs17132120
Zhou Y, Xue L, Ding H, Wang H, Huang K, Li L, Li Z. Landslide Risk Assessment as a Reference for Disaster Prevention and Mitigation: A Case Study of the Renhe District, Panzhihua City, China. Remote Sensing. 2025; 17(13):2120. https://doi.org/10.3390/rs17132120
Chicago/Turabian StyleZhou, Yimeng, Lei Xue, Hao Ding, Haoyu Wang, Kun Huang, Longfei Li, and Zhuan Li. 2025. "Landslide Risk Assessment as a Reference for Disaster Prevention and Mitigation: A Case Study of the Renhe District, Panzhihua City, China" Remote Sensing 17, no. 13: 2120. https://doi.org/10.3390/rs17132120
APA StyleZhou, Y., Xue, L., Ding, H., Wang, H., Huang, K., Li, L., & Li, Z. (2025). Landslide Risk Assessment as a Reference for Disaster Prevention and Mitigation: A Case Study of the Renhe District, Panzhihua City, China. Remote Sensing, 17(13), 2120. https://doi.org/10.3390/rs17132120






