Incremental SAR Automatic Target Recognition with Divergence-Constrained Class-Specific Dictionary Learning
Abstract
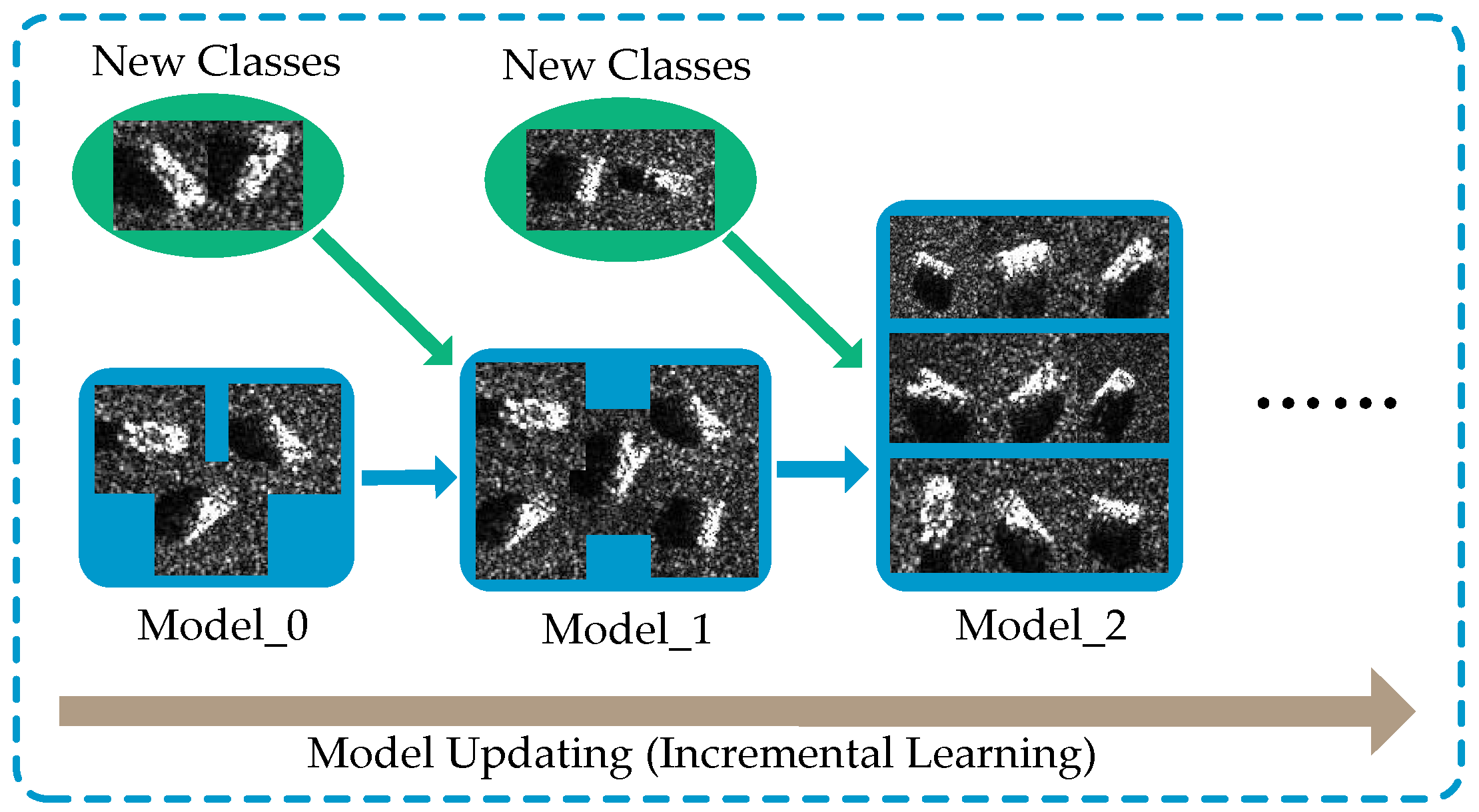
1. Introduction
2. Related Works
2.1. Incremental Learning
2.2. Sparse Representation Classifier
3. Methods
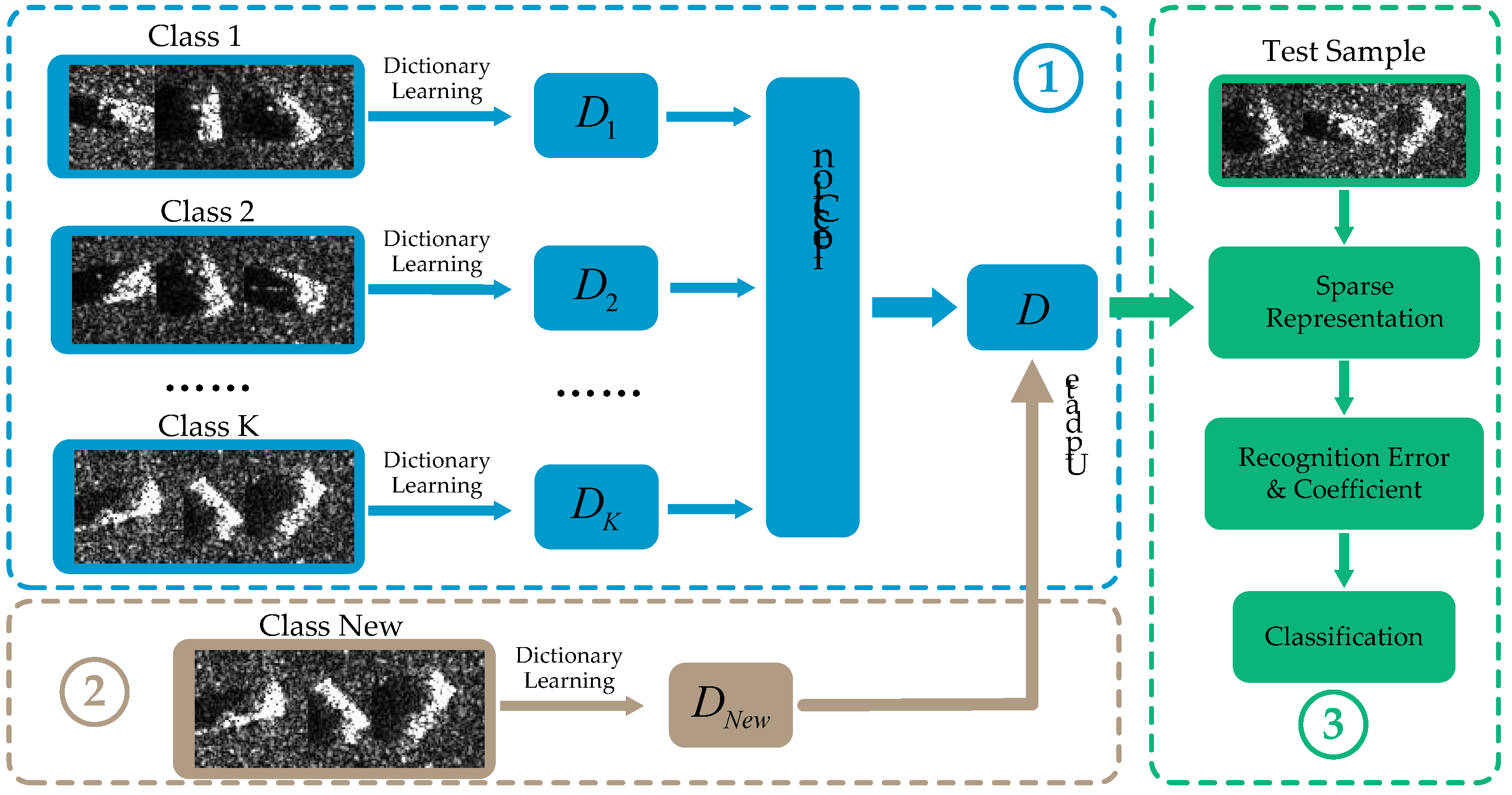
3.1. Class-Specific Dictionary Learning
| Algorithm 1: Fix and optimize |
| Input: //Initialized class-specific dictionary |
| Input: //Training data of class |
| Input: //Sparse coefficient matrix |
| 1: For do |
| 2: It’s known that (). Let , then Equation (9) can be represented as . |
| 3: Solve by least square method. |
| 4: Normalize , and . |
| 5: end for |
| Output: //The updated class-specific dictionary |
3.2. Target Classification Scheme
3.3. Incremental Dictionary Learning
4. Experiments and Results
4.1. Inplementations
4.1.1. Dataset
4.1.2. Evaluation Protocol
- Replay: Replay retains a small amount of old category data as an instance set. Then, the instance set is used for training in the process of updating new data to review old knowledge.
- iCaRL: iCaRL builds and manages an exemplar set, which is a representative sample set of old data. After the representation learning of these data, iCaRL classifies the sample with the nearest-mean-of-exemplars rule.
- Wa: Wa is an improvement of iCaRL. On the basis of iCaRL, Wa normalized the classifier amplitude. This operation could eliminate the deviation in the model updating process.
- Podnet: Inspired by the representation learning, Podnet improves the distillation loss with pooled outputs distillation (POD). In addition, it represents every class with several proxy vectors, so it has better performance in incremental learning.
- ICAC: ICAC adaptively adds new anchored class centers for new classes, and the features of new class will be clustered around the corresponding center. For old classes, ICA retains key samples for each class. In addition, ICAC proposes an SL (Separable Learning) strategy to address the class imbalance between new and old classes.
- CBesIL: To reduce data storage pressure, CBesIL proposes a class boundary selection method to build the exemplar set. When performing incremental learning, CBesIL employs a boundary-based reconstruction method to rebuild the key data to avoid catastrophic forgetting.
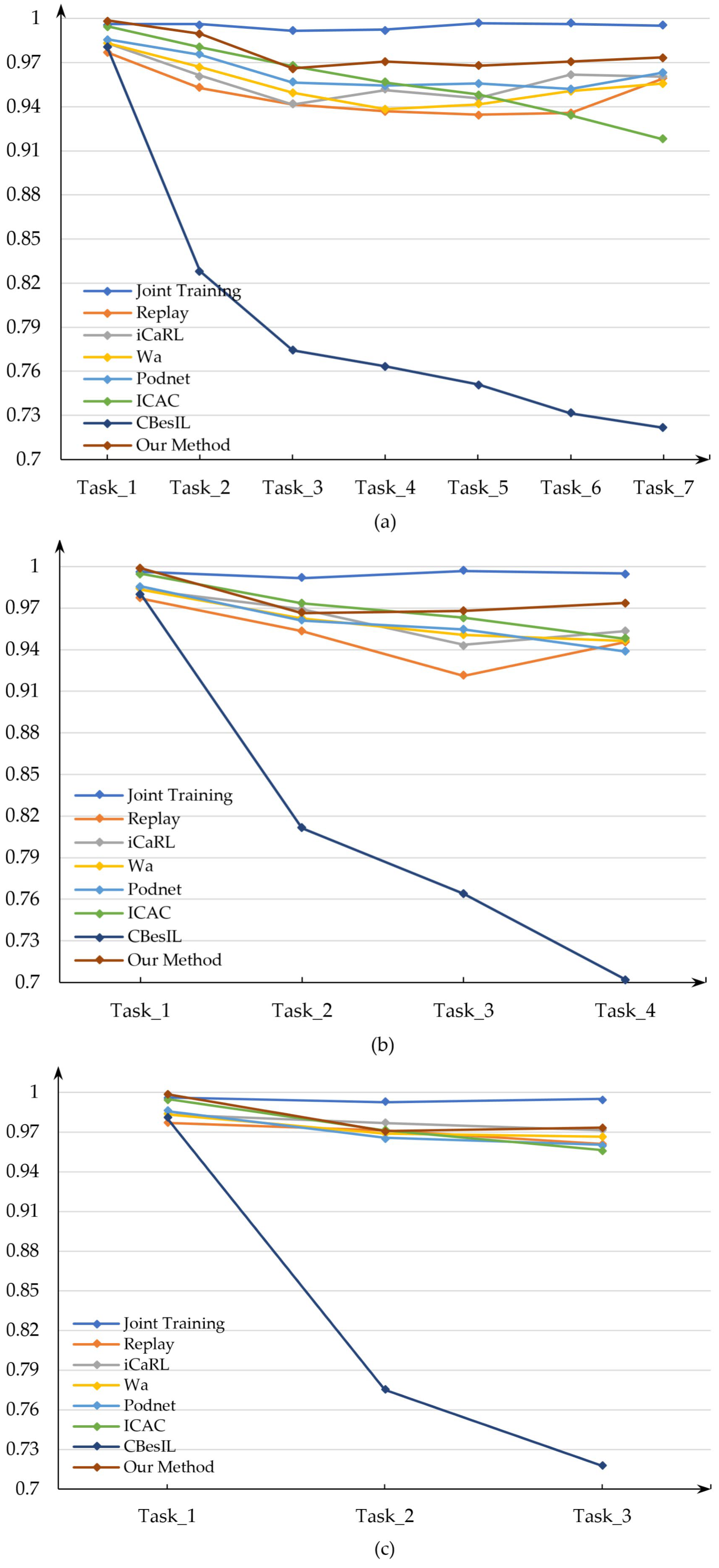
4.2. Incremental Recognition Performance
4.3. Parametric Analysis
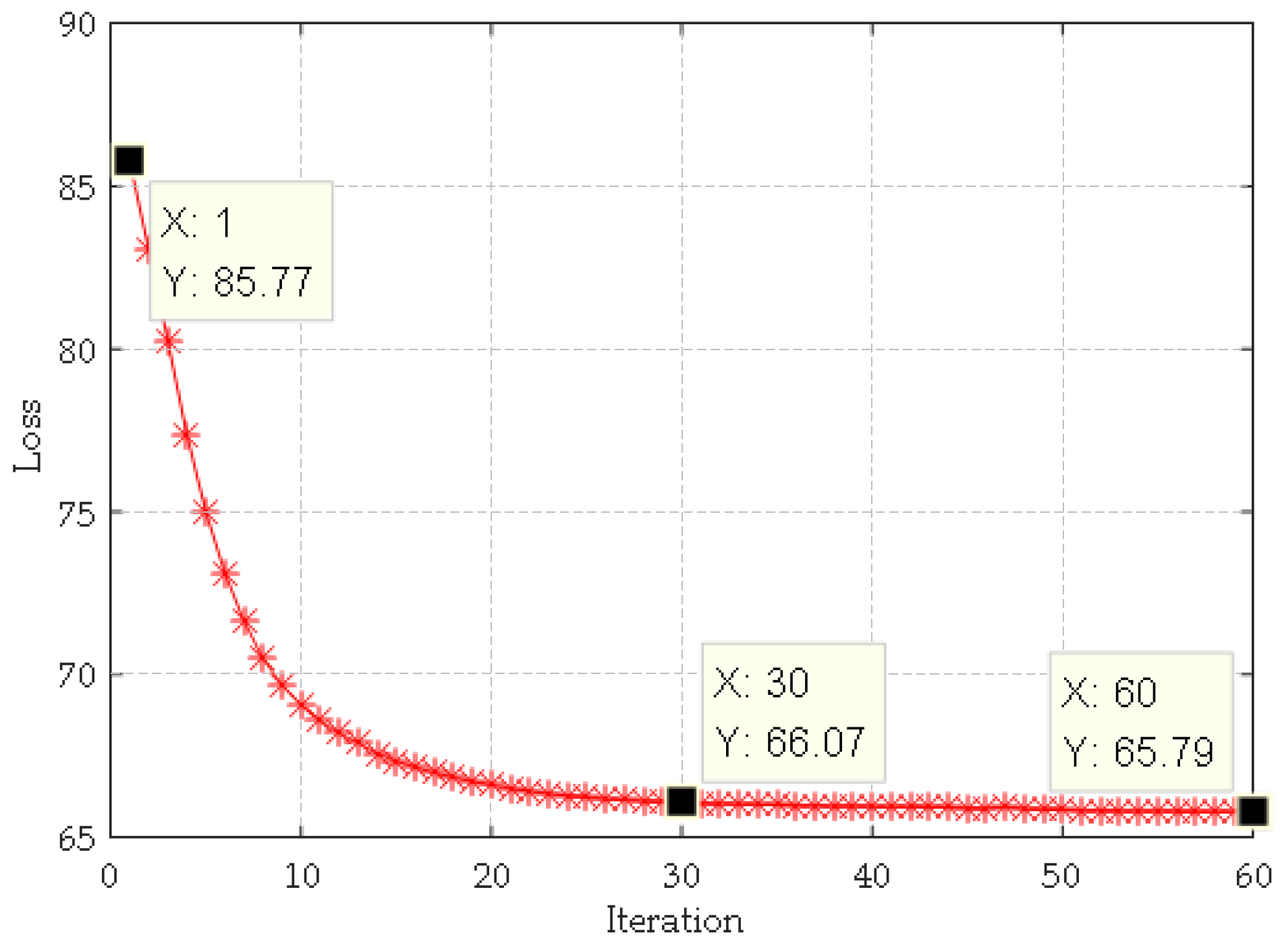
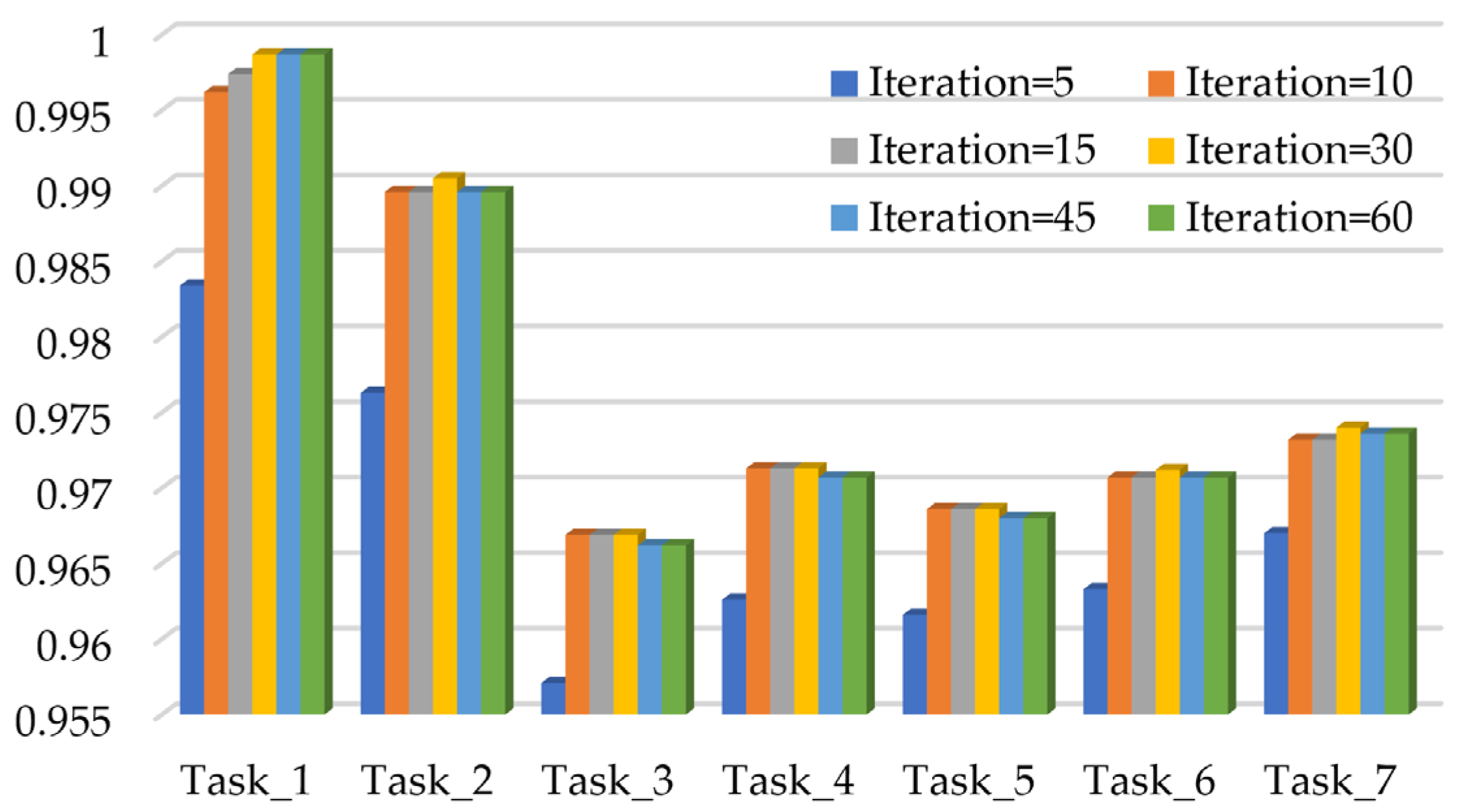
4.3.1. The Effect of Iterations
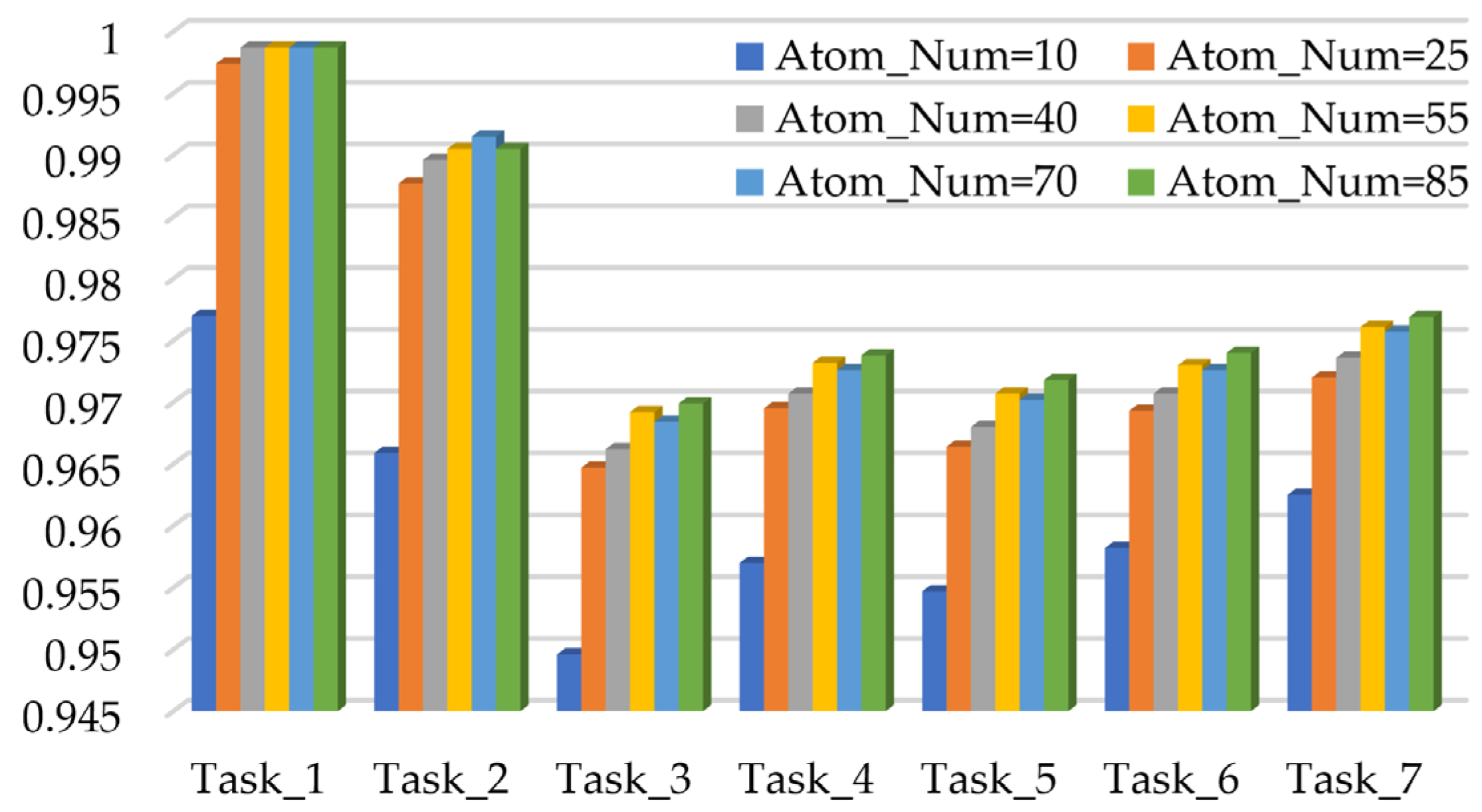
4.3.2. The Effect of Atom Number
4.3.3. The Effect of Weight Factors and
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kechagias-Stamatis, O.; Aouf, N. Automatic Target Recognition on Synthetic Aperture Radar Imagery: A Survey. IEEE Aerosp. Electron. Syst. Mag. 2021, 36, 56–81. [Google Scholar] [CrossRef]
- Sun, Z.; Leng, X.; Zhang, X.; Zhou, Z.; Xiong, B.; Ji, K. Arbitrary-Direction SAR Ship Detection Method for Multi-Scale Imbalance. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5208921. [Google Scholar] [CrossRef]
- Guan, T.; Chang, S.; Wang, C.; Jia, X. SAR Small Ship Detection Based on Enhanced YOLO Network. Remote Sens. 2025, 17, 839. [Google Scholar] [CrossRef]
- Deng, Y.; Tang, S.; Chang, S.; Zhang, H.; Liu, D.; Wang, W. A Novel Scheme for Range Ambiguity Suppression of Spaceborne SAR Based on Underdetermined Blind Source Separation. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5207915. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, S.; Sun, Z.; Liu, C.; Sun, Y.; Ji, K. Cross-Sensor SAR Image Target Detection Based on Dynamic Feature Discrimination and Center-Aware Calibration. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5209417. [Google Scholar] [CrossRef]
- Dong, G.; Liu, H.; Chanussot, J. Keypoint-Based Local Descriptors for Target Recognition in SAR Images: A Comparative Analysis. IEEE Geosci. Remote Sens. Mag. 2021, 9, 139–166. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, G.; Xu, Y.; Leung, H. SAR Target Recognition Based on Probabilistic Meta-Learning. IEEE Geosci. Remote Sens. Lett. 2021, 18, 682–686. [Google Scholar] [CrossRef]
- Pei, J.; Huang, Y.; Huo, W.; Zhang, Y.; Yang, J.; Yeo, T. SAR Automatic Target Recognition Based on Multi-view Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2196–2210. [Google Scholar] [CrossRef]
- Chen, S.; Wang, H.; Xu, F.; Jin, Y. Target Classification Using the Deep Convolutional Networks for SAR Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4806–4817. [Google Scholar] [CrossRef]
- Feng, S.; Ji, K.; Zhang, L.; Ma, X.; Kuang, G. SAR Target Classification Based on Integration of ASC Parts Model and Deep Learning Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10213–10225. [Google Scholar] [CrossRef]
- Coppock, W.; Freund, E. All-or-none versus incremental learning of errorless shock escapes by the rat. Science 1962, 135, 318–319. [Google Scholar] [CrossRef] [PubMed]
- Asthana, A.; Zafeiriou, S.; Cheng, S.; Pantic, M. Incremental Face Alignment in the Wild. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Pratama, M.; Anavatti, S.; Angelov, P.; Lughofer, E. Panfis: A novel incremental learning machine. IEEE Trans. Neural Netw. Learn. Syst. 2013, 25, 55–68. [Google Scholar] [CrossRef] [PubMed]
- Ayoobi, H.; Cao, M.; Verbrugge, R.; Verheij, B. Argumentation-Based Online Incremental Learning. IEEE Trans. Autom. Sci. Eng. 2022, 19, 3419–3433. [Google Scholar] [CrossRef]
- Dang, S.; Cao, Z.; Cui, Z.; Pi, Y.; Liu, N. Class Boundary Exemplar Selection Based Incremental Learning for Automatic Target Recognition. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5782–5792. [Google Scholar] [CrossRef]
- Dang, S.; Cui, Z.; Cao, Z.; Liu, N. SAR Target Recognition via Incremental Nonnegative Matrix Factorization. Remote Sens. 2018, 10, 374. [Google Scholar] [CrossRef]
- Tang, J.; Xiang, D.; Zhang, F.; Ma, F.; Zhou, Y.; Li, H. Incremental SAR Automatic Target Recognition with Error Correction and High Plasticity. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1327–1339. [Google Scholar] [CrossRef]
- De Lange, M.; Aljundi, R.; Masana, M.; Parisot, S.; Jia, X.; Leonardis, A.; Slabaugh, G.; Tuytelaars, T. A Continual Learning Survey: Defying Forgetting in Classification Tasks. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3366–3385. [Google Scholar]
- Liu, Y.; Zhang, F.; Ma, F.; Yin, Q.; Zhou, Y. Incremental Multitask SAR Target Recognition with Dominant Neuron Preservation. In Proceedings of the 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 754–757. [Google Scholar]
- Guo, C.; Qiu, Z.; Sun, R. Synthetic Aperture Radar Target Recognition Based on Incremental Learning Algorithm. Electron. Opt. Control. 2019, 26, 31–34. [Google Scholar]
- Tao, L.; Jiang, X.; Li, Z.; Liu, X.; Zhou, Z. Multiscale Incremental Dictionary Learning with Label Constraint for SAR Object Recognition. IEEE Geosci. Remote Sens. Lett. 2019, 16, 80–84. [Google Scholar] [CrossRef]
- Pan, Q.; Liao, K.; He, X.; Bu, Z.; Huang, J. A Class-Incremental Learning Method for SAR Images Based on Self-Sustainment Guidance Representation. Remote Sens. 2023, 15, 2631. [Google Scholar] [CrossRef]
- Zhang, Y.; Xing, M.; Zhang, J.; Vitale, S. SCF-CIL: A Multi-Stage Regularization-Based SAR Class-Incremental Learning Method Fused with Electromagnetic Scattering Features. Remote Sens. 2025, 17, 1586. [Google Scholar] [CrossRef]
- Cao, C.; Chou, R.; Zhang, H.; Li, X.; Luo, T.; Liu, B. L2,1-Constrained Deep Incremental NMF Approach for SAR Automatic Target Recognition. IEEE Geosci. Remote Sens. Lett. 2024, 21, 4003905. [Google Scholar] [CrossRef]
- Gao, F.; Kong, L.; Lang, R.; Sun, J.; Wang, J.; Hussain, A.; Zhou, H. SAR Target Incremental Recognition Based on Features with Strong Separability. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5202813. [Google Scholar] [CrossRef]
- Yu, X.; Dong, F.; Ren, H.; Zhang, C.; Zou, L.; Zhou, Y. Multilevel Adaptive Knowledge Distillation Network for Incremental SAR Target Recognition. IEEE Geosci. Remote Sens. Lett. 2023, 20, 4004405. [Google Scholar] [CrossRef]
- He, Z.; Xiao, H.; Tian, Z. Multi-View Tensor Sparse Representation Model for SAR Target Recognition. IEEE Access 2019, 7, 48256–48265. [Google Scholar] [CrossRef]
- Dong, G.; Kuang, G.; Wang, N.; Wang, W. Classification via Sparse Representation of Steerable Wavelet Frames on Grassmann Manifold: Application to Target Recognition in SAR Image. IEEE Trans. Image Process 2017, 26, 2892–2904. [Google Scholar] [CrossRef]
- He, Z.; Xiao, H.; Gao, C.; Tian, Z.; Chen, S. Fusion of Sparse Model Based on Randomly Erased Image for SAR Occluded Target Recognition. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7829–7844. [Google Scholar] [CrossRef]
- Pan, F.; Zhang, Z.; Liu, B.; Xie, J. Class-Specific Sparse Principal Component Analysis for Visual Classification. IEEE Access 2020, 8, 110033–110047. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, L.; Feng, X.; Zhang, D. Sparse Representation Based Fisher Discrimination Dictionary Learning for Image Classification. Int. J. Comput. Vis. 2014, 109, 209–232. [Google Scholar] [CrossRef]
- Mai, Z.; Li, R.; Jeong, J.; Quispe, D.; Kim, H.; Sanner, S. Online Continual Learning in Image Classification: An Empirical Survey. Neurocomputing 2022, 469, 28–51. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Z. Broad Learning System: An Effective and Efficient Incremental Learning System Without the Need for Deep Architecture. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 10–24. [Google Scholar] [CrossRef] [PubMed]
- Dvgm, V.; Tolias, A. Three scenarios for continual learning. arXiv 2019, arXiv:1904.07734v1. [Google Scholar]
- Masana, M.; Liu, X.; Twardowski, B.; Menta, M.; Bagdanov, A.; van de Weijer, J. Class-Incremental Learning: Survey and Performance Evaluation on Image Classification. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 5513–5533. [Google Scholar] [CrossRef]
- Tahir, G.; Loo, C. An Open-Ended Continual Learning for Food Recognition Using Class Incremental Extreme Learning Machines. IEEE Access 2020, 8, 82328–82346. [Google Scholar] [CrossRef]
- Singh, P.; Mazumder, P.; Rai, P.; Namboodiri, V. Rectification-based Knowledge Retention for Continual Learning. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 15282–15291. [Google Scholar]
- Lee, K.; Kim, D.; Lee, K.; Lee, D. Density-induced support vector data description. IEEE Trans. Neural Netw. Learn. Syst. 2007, 18, 284–289. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, H.; Xu, W. Parameter selection of Gaussian kernel for one-class SVM. IEEE Trans. Cybern. 2015, 45, 927–939. [Google Scholar]
- Li, B.; Cui, Z.; Cao, Z.; Yang, J. Incremental Learning Based on Anchored Class Centers for SAR Automatic Target Recognition. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5235313. [Google Scholar] [CrossRef]
- Rebuffi, S.; Kolesnikov, A.; Sperl, G.; Lampert, C. iCaRL: Incremental Classifier and Representation Learning. In Proceedings of the 2017 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5533–5542. [Google Scholar]
- Rudd, E.; Jain, L.; Scheirer, W.; Boult, T. The Extreme Value Machine. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 762–768. [Google Scholar] [CrossRef]
- Wright, J.; Yang, A.; Ganesh, A.; Sastry, S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 21–27. [Google Scholar] [CrossRef]
- The Air Force Moving and Stationary Target Recognition Database. Available online: https://www.sdms.afrl.af.mil/index.php?coll-ection=mstar (accessed on 4 June 2025).
- Ross, T.; Worrell, S.; Velten, V.; Mossing, J.; Bryant, M. Standard SAR ATR evaluation experiments using the MSTAR public release data set. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery V, Proceedings of the Aerospace/Defense Sensing and Controls, Orlando, FL, USA, 13–17 April 1998; Volume 3370, pp. 566–573. [Google Scholar]
- Keydel, E.; Lee, S.; Moore, J. MSTAR extended operating conditions: A tutorial. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery III, Proceedings of the Aerospace/Defense Sensing and Controls, Orlando, FL, USA, 8–12 April 1996; Volume 2757, pp. 228–242. [Google Scholar]
- Rakshit, S.; Mohanty, A.; Chavhan, R.; Banerjee, B.; Roig, G.; Chaudhuri, S. FRIDA—Generative feature replay for incremental domain adaptation. Comput. Vis. Image Underst. 2022, 217, 103367. [Google Scholar] [CrossRef]
- Zhao, B.; Xiao, X.; Gan, G.; Zhang, B.; Xia, S. Maintaining discrimination and fairness in class incremental learning. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 13208–13217. [Google Scholar]
- Douillard, A.; Cord, M.; Ollion, C.; Robert, T.; Valle, E. PODNet: Pooled Outputs Distillation for Small-Tasks Incremental Learning. In Proceedings of the 2020 European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 86–102. [Google Scholar]
- Sang, B.; Chen, H.; Yang, L.; Li, T.; Xu, W. Incremental Feature Selection Using a Conditional Entropy Based on Fuzzy Dominance Neighborhood Rough Sets. IEEE Trans. Fuzzy Syst. 2022, 30, 1683–1697. [Google Scholar] [CrossRef]
- Choi, Y.; Ozawa, S.; Lee, M. Incremental two-dimensional kernel principal component analysis. Neurocomputing 2014, 134, 280–288. [Google Scholar] [CrossRef]
- Bendale, A.; Boult, T. Towards Open World Recognition. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1893–1902. [Google Scholar]
- Koch, T.; Liebezeit, F.; Riess, C.; Christlein, V.; Köhler, T. Exploring the Open World Using Incremental Extreme Value Machines. In Proceedings of the 2022 IEEE International Conference on Pattern Recognition, Montreal, QC, Canada, 21–25 August 2022; pp. 2792–2799. [Google Scholar]
- Ma, X.; Ji, K.; Zhang, L.; Feng, S.; Xiong, B.; Kuang, G. An Open Set Recognition Method for SAR Targets Based on Multitask Learning. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4014005. [Google Scholar] [CrossRef]
- Geng, X.; Dong, G.; Xia, Z.; Liu, H. SAR Target Recognition via Random Sampling Combination in Open-World Environments. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 331–343. [Google Scholar] [CrossRef]


| Target | Training | Test | ||
|---|---|---|---|---|
| Num | Angle | Num | Angle | |
| BMP2 | 233 | 17 | 195 | 15 |
| BTR70 | 233 | 17 | 196 | 15 |
| T72 | 233 | 17 | 196 | 15 |
| BTR60 | 256 | 17 | 195 | 15 |
| 2S1 | 299 | 17 | 274 | 15 |
| BRDM2 | 298 | 17 | 274 | 15 |
| D7 | 299 | 17 | 274 | 15 |
| T62 | 299 | 17 | 273 | 15 |
| ZIL131 | 299 | 17 | 274 | 15 |
| ZSU234 | 299 | 17 | 274 | 15 |
| Scenario | BMP2 | BTR70 | T72 | BTR60 | 2S1 | BRDM2 | D7 | T62 | ZIL131 | ZSU234 |
|---|---|---|---|---|---|---|---|---|---|---|
| A | Task_1 | Task_2 | Task_3 | Task_4 | Task_5 | Task_6 | Task_7 | |||
| B | Task_1 | Task_2 | Task_3 | Task_4 | ||||||
| C | Task_1 | Task_2 | Task_3 | |||||||
| Method | Scenario_A | Scenario_B | Scenario_C | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Task_1 | Task_2 | Task_3 | Task_4 | Task_5 | Task_6 | Task_7 | Task_1 | Task_2 | Task_3 | Task_4 | Task_1 | Task_2 | Task_3 | |
| Replay | 0.9770 | 0.9527 | 0.9414 | 0.9370 | 0.9345 | 0.9358 | 0.9592 | 0.9770 | 0.9534 | 0.9212 | 0.9456 | 0.9770 | 0.9713 | 0.9612 |
| iCaRL | 0.9834 | 0.9612 | 0.9414 | 0.9514 | 0.9457 | 0.9619 | 0.9604 | 0.9834 | 0.9692 | 0.9435 | 0.9534 | 0.9834 | 0.9769 | 0.9715 |
| Wa | 0.9834 | 0.9669 | 0.9496 | 0.9383 | 0.9414 | 0.9507 | 0.9559 | 0.9834 | 0.9624 | 0.9505 | 0.9464 | 0.9834 | 0.9688 | 0.9666 |
| Podnet | 0.9859 | 0.9754 | 0.9564 | 0.9545 | 0.9558 | 0.9521 | 0.9633 | 0.9859 | 0.9609 | 0.9547 | 0.9386 | 0.9859 | 0.9657 | 0.9604 |
| ICAC | 0.9949 | 0.9804 | 0.9676 | 0.9565 | 0.9483 | 0.9342 | 0.9176 | 0.9949 | 0.9735 | 0.963 | 0.9477 | 0.9949 | 0.9713 | 0.9564 |
| CBesIL | 0.9806 | 0.828 | 0.7744 | 0.7633 | 0.7511 | 0.7313 | 0.7215 | 0.9806 | 0.8113 | 0.7639 | 0.7021 | 0.9806 | 0.7749 | 0.7175 |
| Our Method | 0.9987 | 0.9896 | 0.9662 | 0.9707 | 0.9680 | 0.9707 | 0.9736 | 0.9987 | 0.9662 | 0.9680 | 0.9736 | 0.9987 | 0.9707 | 0.9736 |
| Joint Training | 0.9962 | 0.9962 | 0.9917 | 0.9925 | 0.9968 | 0.9963 | 0.9951 | 0.9962 | 0.9917 | 0.9968 | 0.9951 | 0.9962 | 0.9925 | 0.9951 |
| Method | BMP2 | BTR70 | T72 | BTR60 | 2S1 | BRDM2 | D7 | T62 | ZIL131 | ZSU234 | Overall |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Joint Training | 0.9897 | 1.0000 | 1.0000 | 1.0000 | 0.9818 | 0.9891 | 1.0000 | 0.9963 | 0.9964 | 1.0000 | 0.9951 |
| Replay | 0.8821 | 0.9694 | 0.9592 | 0.9436 | 0.9891 | 0.8650 | 0.9891 | 0.9817 | 0.9891 | 1.0000 | 0.9592 |
| iCaRL | 0.9282 | 0.9694 | 0.9796 | 0.8462 | 0.9635 | 0.9124 | 0.9781 | 0.9963 | 0.9964 | 1.0000 | 0.9604 |
| Wa | 0.9641 | 0.9694 | 0.9643 | 0.9026 | 0.9343 | 0.8942 | 0.9380 | 0.9853 | 1.0000 | 1.0000 | 0.9559 |
| Podnet | 0.9744 | 0.9694 | 0.9898 | 0.9538 | 0.9489 | 0.9088 | 0.9270 | 0.9707 | 1.0000 | 1.0000 | 0.9633 |
| Our Method | 1.0000 | 1.0000 | 1.0000 | 0.9949 | 0.9635 | 0.8759 | 0.9927 | 0.9524 | 0.9891 | 0.9964 | 0.9736 |
| Method | Replay | iCaRL | Wa | Podnet | Our Method |
|---|---|---|---|---|---|
| Time (s) | 310 | 485 | 524 | 929 | 457 |
| Case | Case_A | Case_B | Case_C | Case_D |
|---|---|---|---|---|
| 0.1 | 0.1 | 0.1 | 0.1 | |
| 0 | 0.1 | 0.02 | 0.01 | |
| - | 1 | 5 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Bu, X.; Zhang, D.; Wang, Z.; Li, J. Incremental SAR Automatic Target Recognition with Divergence-Constrained Class-Specific Dictionary Learning. Remote Sens. 2025, 17, 2090. https://doi.org/10.3390/rs17122090
Ma X, Bu X, Zhang D, Wang Z, Li J. Incremental SAR Automatic Target Recognition with Divergence-Constrained Class-Specific Dictionary Learning. Remote Sensing. 2025; 17(12):2090. https://doi.org/10.3390/rs17122090
Chicago/Turabian StyleMa, Xiaojie, Xusong Bu, Dezhao Zhang, Zhaohui Wang, and Jing Li. 2025. "Incremental SAR Automatic Target Recognition with Divergence-Constrained Class-Specific Dictionary Learning" Remote Sensing 17, no. 12: 2090. https://doi.org/10.3390/rs17122090
APA StyleMa, X., Bu, X., Zhang, D., Wang, Z., & Li, J. (2025). Incremental SAR Automatic Target Recognition with Divergence-Constrained Class-Specific Dictionary Learning. Remote Sensing, 17(12), 2090. https://doi.org/10.3390/rs17122090







