Abstract
Arc scanning synthetic aperture radar (ArcSAR) can achieve high-resolution panoramic imaging and retrieve submillimeter-level deformation information. To monitor buildings in a city scenario, ArcSAR must be lightweight; have a high resolution, a mid-range (around a hundred meters), and low power consumption; and be cost-effective. In this study, a novel high-resolution wide-beam single-chip millimeter-wave (mmwave) ArcSAR system, together with an imaging algorithm, is presented. First, to handle the non-uniform azimuth sampling caused by motor motion, a high-accuracy angular coder is used in the system design. The coder can send the radar a hardware trigger signal when rotated to a specific angle so that uniform angular sampling can be achieved under the unstable rotation of the motor. Second, the ArcSAR’s maximum azimuth sampling angle that can avoid aliasing is deducted based on the Nyquist theorem. The mathematical relation supports the proposed ArcSAR system in acquiring data by setting the sampling angle interval. Third, the range cell migration (RCM) phenomenon is severe because mmwave radar has a wide azimuth beamwidth and a high frequency, and ArcSAR has a curved synthetic aperture. Therefore, the fourth-order RCM model based on the range-Doppler (RD) algorithm is interpreted with a uniform azimuth angle to suit the system and implemented. The proposed system uses the TI 6843 module as the radar sensor, and its azimuth beamwidth is 64°. The performance of the system and the corresponding imaging algorithm are thoroughly analyzed and validated via simulations and real data experiments. The output image covers a 360° and 180 m area at an azimuth resolution of 0.2°. The results show that the proposed system has good application prospects, and the design principles can support the improvement of current ArcSARs.
1. Introduction
Synthetic aperture radar (SAR) is a high-resolution imaging system that has all-weather and all-day capabilities, and it has been widely applied in remote sensing domains such as Earth surface high-resolution imaging and target detection and recognition [1,2,3]. It has been installed on various platforms, such as satellites, planes, cars, and railways [4,5,6,7,8]. Arc scanning synthetic aperture radar (ArcSAR) is a type of ground-based SAR (GBSAR) system, with a rotating arm installed on the radar to illuminate the outside area. The circular synthetic aperture enables the system to obtain high-resolution 360° images [9,10]. Compared with traditional linear rail-based GBSAR, it has the advantages of a smaller size and weight, a wider coverage, and the same azimuth angular resolution in all directions [11,12]. Because the radar is mounted on an arm rotated by a motor, its trajectory is fixed, and it can revisit a scene within minutes [13]. Due to the above advantages, it is widely used to retrieve deformation information on mine slopes, dams, and key urban infrastructure.
Urban infrastructure monitoring includes the use of a camera, an infrared sensor, a mmwave radar, and other sensors to determine the status of infrastructure such as buildings, bridges, and gas pipes [14,15,16,17,18,19,20,21,22]. ArcSAR’s panorama imaging and submillimeter deformation information retrieval capabilities make it suitable for monitoring the health and integrity of structures. However, most typical commercial ArcSAR systems are designed for open spaces without obstacles, such as mine fields. Additionally, they have a relatively large volume, a large weight, and a high power consumption to meet the long-range, large-coverage, and steady installation demands, allowing one piece of equipment to be sufficient for a large observation scene. However, when using an ArcSAR system in a city scenario to monitor complex buildings, several challenges are encountered that must be addressed. In a city scenario, buildings are situated close together, with a relatively high density, and nearby buildings also block transmitted signals; thus, a long range and high power consumption are not needed. Although one ArcSAR may not be sufficient for monitoring tasks, placing too many current commercial systems would be costly. In addition, the system’s large volume and weight make it difficult to move during installation and transportation to, for example, a rooftop. Last but most importantly, a high resolution is required to meet the needs of imaging complex shapes and the 3D structure of buildings. In summary, to monitor buildings in urban scenarios, the system must be lightweight; have a high resolution, a mid-range (around a hundred meters), and low power consumption; and be cost-effective. Thus, a single-chip millimeter-wave (mmwave) radar-based ArcSAR may be the solution.
Few studies have been conducted on single-chip millimeter-wave (mmwave) radar-based ArcSAR systems. The concept of ArcSAR was first proposed in [23], inspired by the circular SAR mode [24]. Later, Hoonyol Lee et. al., developed a track-mounted X-band ArcSAR system [25], together with stripmap and spotlight imaging modes and their imaging algorithms. Representative commercial ArcSAR systems are the IBIS-ArcSAR system [26]; the ArcFMCW-SAR system from the Institute of Electronics, Chinese Academy of Sciences [27]; and the Risk Radar system [10]. These systems work at around 17 GHz, and the imaging algorithms include time and frequency domain methods, such as BP, RD, and PFA [25,28,29,30,31,32]. These systems typically have a large size and a long-range capability for deformation monitoring in mine fields and dams, where they encounter the problems previously mentioned. Recently, Bing Sun et. al., proposed an improved fourth-order RD algorithm [33], and they validated it via their experimental single-chip millimeter-wave ArcSAR system, which can achieve high-resolution panoramic imaging; however, this system is a prototype and is not fully developed.
To develop a single-chip millimeter-wave ArcSAR system, several system and signal processing issues must be solved. First, typical imaging algorithms assume a constant rotation to obtain uniform angular samples. However, such an assumption cannot hold because the motor accelerates and decelerates and has an unstable rotation state, thus resulting in the degradation of focusing performance. Moreover, the maximum angular sampling interval that avoids aliasing is not reported. Such criteria can support the design of the system, for example, in controlling the size of the echo data so that accuracy and processing time can be balanced. Third, a single-chip mmwave radar usually has a wide azimuth beamwidth [34] and works at a higher frequency; additionally, ArcSAR has a nonlinear trajectory. These factors make the range cell migration phenomenon of targets much more severe. Thus, these three issues need to be solved when designing a mature mmwave ArcSAR system.
To address these problems, the main contributions of this study include the following:
- First, in this study, a mmwave ArcSAR system is proposed, and it uses the TI 6843 module as a radar sensor. To handle the non-uniform azimuth sampling caused by motor motion, a high-accuracy angular coder is used in the system design. The coder can send the radar a hardware trigger signal to indicate when to rotate to a specific angle so that uniform angular sampling can be achieved under the unstable rotation of the motor. The time delay of the hardware trigger signal and its influence on focusing are analyzed.
- Second, the ArcSAR’s maximum azimuth sampling angle that can avoid aliasing is deducted based on the Nyquist theorem. The mathematical relation supports the proposed ArcSAR system in acquiring data by setting the sampling angle interval. The relation is validated via simulations and real data experiments.
- Third, the range cell migration (RCM) phenomenon is severe because mmwave radar has a wide azimuth beamwidth and a high frequency, and ArcSAR has a curved synthetic aperture. The second-order approximation based on Taylor expansion is typically used for modeling. One viable solution is increasing the approximation order. Considering that the odd-order term in Taylor expansion is zero when in side-looking mode, the first- and third-order terms do not exist. Therefore, a forth-order expansion approximation formula for RCM would be enough in most cases, and this is shown in the following section. Hence, the fourth-order RCM model based on the range-Doppler (RD) algorithm is interpreted with a uniform azimuth angle to suit the system and implemented. The focusing performance of the imaging algorithm is thoroughly analyzed and validated using both simulation and real data.
The subsequent sections of this paper are arranged as follows: Section 2 presents the method, and it consists of four parts. In the first subsection, the proposed mmwave ArcSAR system is introduced in detail. In the second and third subsections, the signal model of ArcSAR is presented, and the improved RD algorithm is derived using uniform angular sampling. In the last subsection, the maximum azimuth angular sampling interval is derived, and the influence of residual sampling errors on the system due to the coder delay is analyzed. Section 3 presents the data and experimental results, which are used to validate the improved algorithm and proposed system via simulations and real data experiments. Before coming to a conclusion, a discussion is presented in Section 4. This section presents a comparative experiment with the current 17 GHz ArcSAR system in a more complex urban scenario, and it presents a discussion on the system performance, limitations, and future work. In Section 5, the last section, the entire study is summarized.
2. Method
2.1. Design of the ArcSAR System
The system consists of three main components: (1) a mmWave radar module, (2) a motion platform module, and (3) a power supply module. The radar module transmits and receives signals and uploads the echo signals to a PC. The motion platform contains a turntable, which rotates the radar module with an arm to form a synthetic aperture. When the arm rotates, the angular coder, which is installed in the turntable, generates a hardware trigger and sends it to the radar. The signal processing and full system control are carried out on a PC linked to the two modules.
The overall workflow of the ArcSAR system is shown in Figure 1. After the system is powered on and initialized, the motor starts to rotate, and the microcontroller unit (MCU) counts the pulses from the angular coder. The rotation angle between every two consecutive pulses is constant. During the process of counting the output pulses from the angular coder, a trigger signal is sent to the radar when the counted number meets a threshold. The external pin reserved in the mmwave radar data module is used to receive the trigger signal. Upon receiving the signal, the radar works once to ensure uniform sampling of the radar data in the spatial angular domain. Finally, the collected data are uploaded to the PC. Each part is discussed in detail below.
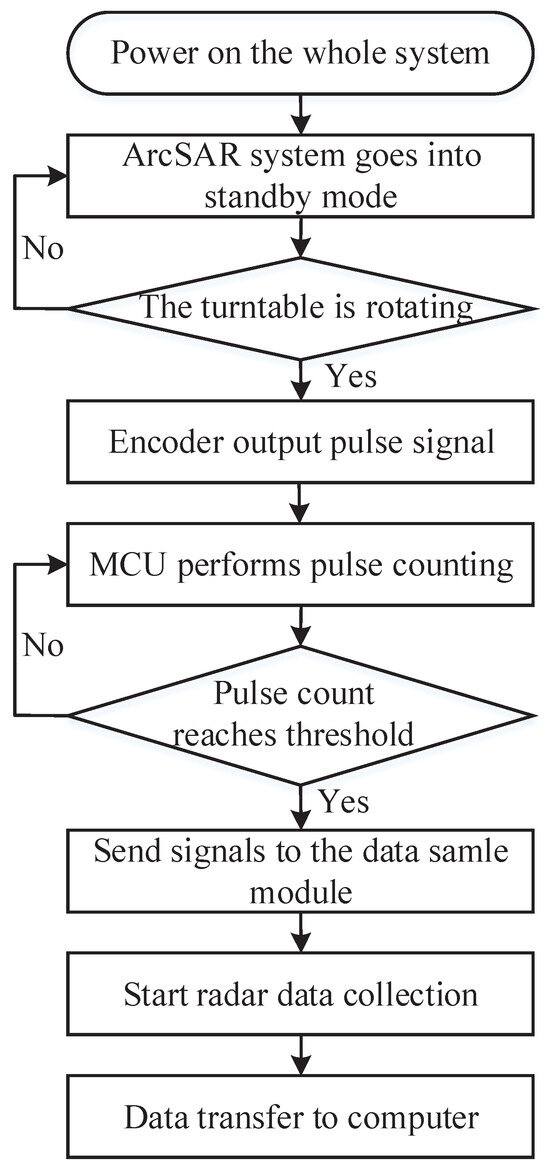
Figure 1.
ArcSAR system workflow.
2.1.1. Mmwave Radar Module
The mmwave radar module utilizes the IWR6843 millimeter-wave radar from Texas Instruments (TI) as the radar sensor, operating in the 60 GHz band, with a maximum signal bandwidth of 4 GHz. A schematic diagram of the basic composition of the mmwave radar module is shown in Figure 2a. The radar system employs a power amplifier (PA) and a low-noise amplifier (LNA) to amplify the transmitted and received signals, respectively. A mixer performs a conjugate multiplication of the signals from the transmission and reception antennas, producing an intermediate frequency (IF) signal, which is then converted to a digital signal by an analog-to-digital converter (ADC) unit. The MCU is programmed using the Keil5 development environment, which enables it to issue commands to start or stop the radar via a serial port to the digital signal processor (DSP). If the radar is activated, the DSP’s data transmission port sends the radar data to the field-programmable gate array (FPGA). After receiving the data, the FPGA transmits them in real time to the PC via an Ethernet interface for analysis and processing, enabling SAR imaging. An external trigger capability has been developed for the millimeter-wave radar sensor, with a dedicated external trigger pin that allows it to receive trigger signals from an external source. The data acquisition module is depicted in Figure 2b. The module is compact in size, has low power consumption, and offers stable operational performance, making it well suited for application in building monitoring in a city scenario.
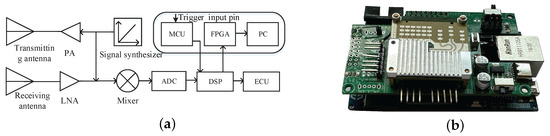
Figure 2.
Diagram (a) and photo (b) of the mmwave radar.
2.1.2. Motion Platform Module
The ArcSAR motion platform consists of several components, including a turntable, a rotating arm, an MCU, a high-accuracy angular coder, and a differential-to-single-ended signal conversion module. The rotating arm is placed on the surface of the turntable. Inside the turntable is a stepper motor that drives the turntable to rotate. The turntable is connected to a computer via an RS485 communication interface, enabling functions such as forward rotation, reverse rotation, stopping, speed setting, and the setting of cyclic work modes. The radar module is positioned at the front of the rotating arm, which is far from the rotation center. A diagram of the basic composition of the ArcSAR motion platform is shown in Figure 3.
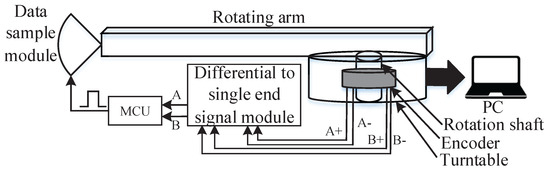
Figure 3.
ArcSAR platform structure.
When attempting to obtain a well-focused ArcSAR image, the platform’s rotation speed can affect the uniform sampling in the spatial angular domain, leading to defocus in the SAR image. To address this, we integrated a high-precision angular encoder into the system. This encoder provides feedback on the position, allowing us to overcome the influence of the platform’s motion speed, and it is able to provide a hardware trigger signal to the radar when rotating to a specific angle, thus improving the quality of the SAR image and reducing the difficulty of signal acquisition. This advantage is not only good for SAR image formation but also makes interferometry much easier because the sampled positions at each repeated pass are the same. The angular encoder is mounted on the same axis as the motor inside the turntable. As the turntable rotates, the angular encoder generates pulse signals. After a full rotation of 360 degrees, the encoder outputs a fixed number of pulses ; thus, the resolution of this encoder is .
The angular encoder generates two sets of differential signals during rotation: A+ and A−, and B+ and B−. A differential-to-single-ended signal conversion module is used to invert the A− and B− signals and superimpose them onto the A+ and B+ phases, thereby enhancing the stability of the signal. The two output single-ended signals are denoted as A and B. The A and B signals are phase-shifted by 90 degrees relative to each other. By comparing whether the A phase is ahead of the B phase, it is able to determine whether the turntable is rotating clockwise or counterclockwise. The A and B signals are fed into the MCU microcontroller’s quadrature encoder pins to decode the signals. Using timers, interrupts, and other methods, the MCU can count the input pulses and identify the rotation direction, thereby sending the trigger signal to the radar when the turntable rotates to every angular position.
2.1.3. Power Supply Module
The power module is relatively simple, consisting of an AC-to-DC power adapter that converts 220 V AC into multiple power outputs, including 24 V and 5 V. The 24 V output supplies power to the turntable motor and high-precision angular encoder, while the 5 V output powers the radar module and the hardware trigger signal conversion module of the motion platform.
2.2. Signal Model
Figure 4 shows the geometry of the ArcSAR. The rotation center is O, the rotation radius is r, the radar is located at the end of the arm, and the synthetic aperture is circular in shape. The rotation speed is , the azimuth slow time is , and the coordinates of the point target P are . The point is set to P due to the rotation invariant feature of the ArcSAR. The distance from the point target P to the rotation center is . The range equation is expressed as follows:
where represents the azimuthal pulse number, and denotes the angular sampling interval. is equal to , as the system can achieve uniform azimuth angular sampling.
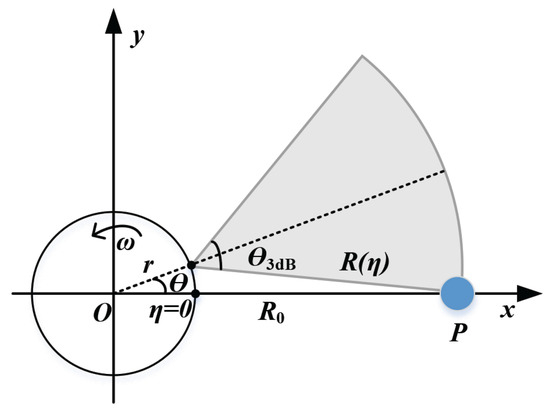
Figure 4.
Geometric model of ArcSAR.
The radar module uses frequency-modulated continuous-wave (FMCW) signals; therefore, the transmitted signal is
where is the window function in the range dimension, represents the fast time, is the pulse width, is the center frequency, and is the frequency modulation rate. The returned echo is given as
where is the azimuthal window function, and is the width of the radar beam. The pulse compression in the FMCW radar uses a reference signal to conduct the dechirp [35] process.
where represents the time delay, C is the light speed, and is the reference range. The signal after dechirp is an IF signal, which can be written as
The imaging algorithm conducts a process on the IF signal to remove the range cell migration and azimuth compression so that a high-resolution SAR image can be obtained. The range resolution is determined by the signal bandwidth , which is given by
The azimuth bandwidth is formed via the rotation of the radar. The instantaneous Doppler frequency is given by
When the target is illuminated by the entire radar beam, which has a 3 dB beamwidth, the azimuth bandwidth is
The azimuth resolution can, therefore, be expressed as
The azimuth resolution is an angular resolution with a unit of (rad). The formula matches the related azimuth resolution reported in other studies [25]. From a qualitative point of view, the nominator is the wavelength, and the denominator can be interpreted as the length of the arc-shaped synthetic aperture. If is replaced with the length of the rail, then the structure of this formula will be similar to the azimuth resolution of the linear rail GBSAR. Aside from deduction via the Doppler point of view, another method of combining the usual azimuth resolution and sin theorem is given in [10].
2.3. Fourth-Order RD Algorithm
The single-chip mmwave ArcSAR system works at a frequency of 60 GHz or even higher, together with a nonlinear aperture and a wide azimuth beamwidth. These features cause the current second-order range equation model to obtain errors in range cell migration correction (RCMC) [36,37] and azimuth compression, thereby degrading the imaging performance of traditional RD. Increasing the order of approximation when calculating the range model can solve this problem, and series inversion can help obtain the analytic formula, as in [33]. This method is implemented in the system and interpreted with a uniform azimuth angle to suit the system.
The overall flowchart of the algorithm is shown in Figure 5.
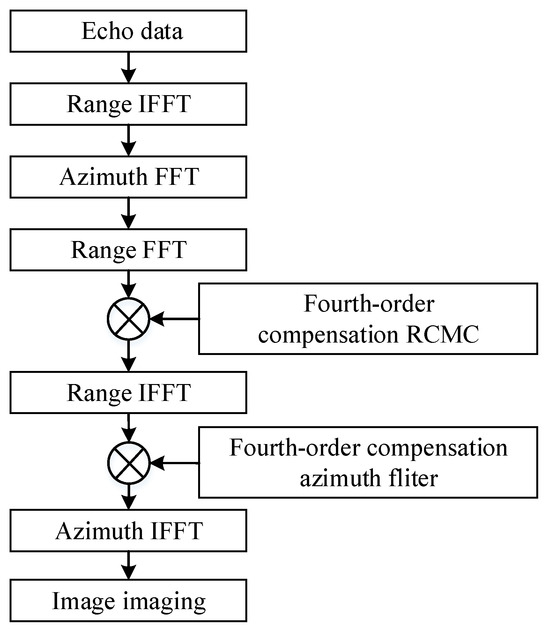
Figure 5.
Flowchart of the proposed algorithm.
The specific steps of the improved RD algorithm are as follows: The last term in (10) is the residual video phase (RVP) [38,39] term, which is usually neglected. Inverse fast Fourier transform (IFFT) is performed on the IF signal to achieve pulse compression in the range direction, which is
Subsequently, azimuth fast Fourier transform (FFT) is applied, and the azimuth window function is neglected to obtain the signal in the range-Doppler domain:
where is a variable in the frequency domain of . By examining the aforementioned equation, it is found that the phase of the signal in the range-Doppler domain is
A fourth-order Taylor expansion is applied to the signal model (1) at , and the resulting expression is as follows:
where a and b are the values obtained after taking the second- and fourth-order derivatives of , respectively. It follows that
By substituting into (13) and then replacing (13) with the term (1), the phase is obtained as follows:
Using the principle of the stationary phase (POSP), (15) is derived and set to equal 0:
Thus, the time–frequency relationship in the azimuth direction can be derived as
By using the series inversion [40,41] method, the following can be obtained:
Comparing both sides of the equation yields
The final result is obtained as follows:
The specific expression for the time–frequency relationship is
Therefore, in the range-Doppler domain, the range cell migration is
Equation (23) indicates that the range migration momentum is a function of . To achieve RCMC, inverse fast Fourier transform (IFFT) and linear phase multiplication [42] are used. The expression for the phase multiplier is
Applying fast Fourier transform (FFT) to in the range domain, followed by multiplication with and subsequently IFFT, results in a second pulse compression in the range direction. The expression of the signal after this correction is as follows:
Next, azimuth compression is performed to focus the data. The azimuth matched filter in the range-Doppler domain is represented as follows:
It compensates for the azimuth phase associated with . To perform azimuth pulse compression on , it is multiplied by the azimuth matched filter , and then IFFT is applied. This process results in the final two-dimensional focused image [43], and the expression of the final imaging model is as follows:
2.4. System Performance Analysis
In this section, the following four aspects of the proposed system’s performance are analyzed:
First, as the system has a hardware trigger to initiate uniform angular sampling, the maximum angular sampling interval for the system is deduced using the Nyquist sampling theorem. Second, the imaging error caused by the approximation of the range equation is analyzed. Third, the imaging error caused by imperfect angular sampling is also analyzed. Because the hardware trigger signal transmission still needs time, the sampling error may influence the imaging accuracy. Thus, the aim of this analysis is to determine the sampling error tolerated by the system via a theoretical simulation. Fourth, the actual sampling error caused by the hardware trigger signal transmission delay is estimated.
2.4.1. Maximum Angular Sampling Interval
According to the Nyquist sampling theorem, it follows that
where is the pulse repetition frequency, which must be greater than the azimuth bandwidth to avoid aliasing. If the angular gap between two triggers is , then
Within the beam coverage area, can be at most . It can be derived that
Equation (31) determines the maximum angular sampling interval. The right side of Equation (31) is identical to (9), meaning that the value of must be less than the azimuthal resolution . Moreover, the angular sampling interval depends on the wavelength , the rotation radius r, and the radar beamwidth .
When the rotation radius is m and is set to X, Ku, K, and other bands, the maximum angular sampling interval versus azimuth beam width is as depicted in Figure 6. Qualitatively, it can be observed that, across different bands, as the radar beamwidth increases, a smaller should be set. Equation (31) is applicable to radars operating in various frequency bands.
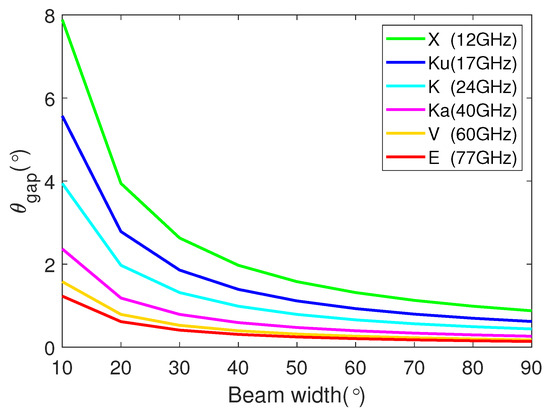
Figure 6.
of different bands varying with beam width when r = 0.52 m.
2.4.2. Imaging Error Analysis Based on Order of Range Equation
The current method holds a uniform angular sampling assumption. This subsection presents an analysis of the imaging error caused by the approximation order of the range equation. The expression of is as follows:
For a typical imaging algorithm, it is necessary for the error associated with the slant range to meet [33]:
The ArcSAR system presented in this study employs a TI IWR6843 mmwave radar. As a reference, its parameters are shown in Table 1.

Table 1.
ArcSAR system parameters.
With a carrier frequency of 60 GHz, a beamwidth of 64°, and a rotating radius of m, the maximum angular sampling interval is calculated to be . Next, the range error versus the target range and azimuth beamwidth can be analyzed using the second- and fourth-order range equations, respectively. The range errors of the second- and fourth-order range models, which vary with the range and azimuth angles, are shown in Figure 7 and Figure 8, represented by a gradient surface, where the red plane represents the threshold value of . It can be observed that, under the fourth-order model, the applicable space of the range and beamwidth is larger. The second- and fourth-order range model curves, with beamwidths of 64° and 50°, are selected, as shown in Figure 9. It is evident that the second-order range model does not meet the accuracy requirements of the slant range error when the beamwidth is 64° and that the improved fourth-order RD algorithm meets the slant range error condition when the target distance is larger than 12.7771 m. Assuming a beamwidth of 50°, the improved fourth-order RD algorithm remains unaffected when the distance from the point target to the rotation center is m. Therefore, it can be concluded that the algorithm is affected by the wide beam, and, as the beamwidth increases, the applicable range of the distance decreases.
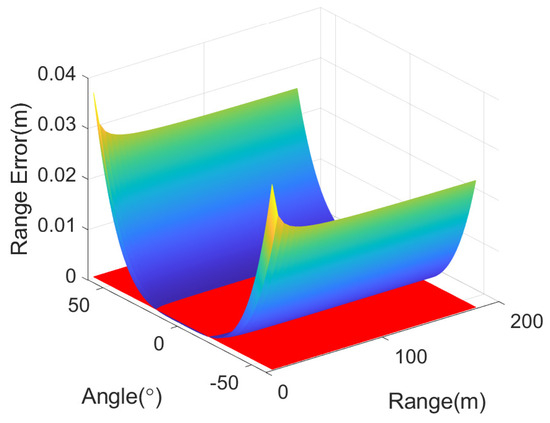
Figure 7.
The range error of the second-order range model varying with the range and azimuth angles. The red plane is the threshold of the required range error.
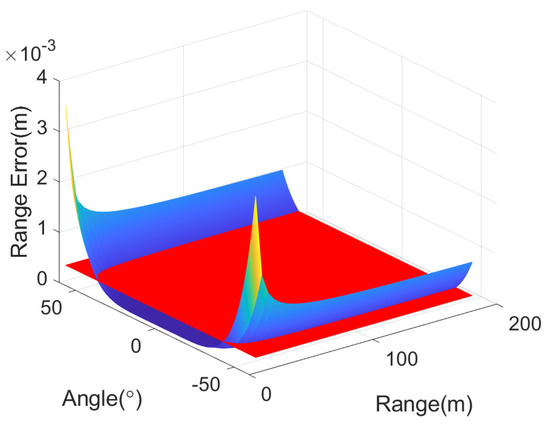
Figure 8.
The range error of the fourth-order range model varying with the range and azimuth angles. The red plane is the threshold of the required range error.
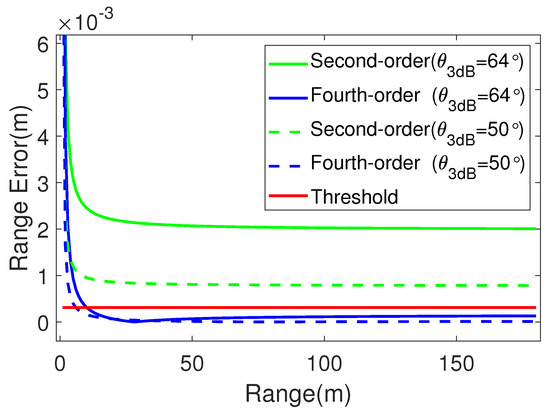
Figure 9.
The range error of the two range models varying with the range when = 64° and = 50°.
Next, the second- and fourth-order distance error curves, which vary with the azimuth angles, with m, are extracted, as shown in Figure 10. It can be observed that the applicable beamwidth range for the traditional second-order RD algorithm is approximately , whereas that for the improved RD algorithm is approximately . Hence, the improved fourth-order RD algorithm is suitable for ArcSAR systems operating under near-range, wide-beam conditions.
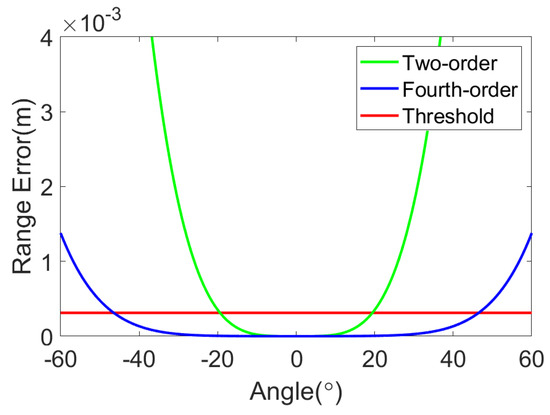
Figure 10.
The range error of the two range models varying with the azimuth angle when 20 m.
2.4.3. Imaging Error Analysis Based on Angular Sampling Error
This subsection presents an analysis aiming to identify the sampling error tolerated by the system using a theoretical simulation. This analysis can help determine whether the encoder can help improve the uniform sampling condition.
The following analysis focuses on the allowable error range introduced by the encoder. Using a uniform angular interval as a baseline, random position errors are generated at the angular sampling positions. Then, the imaging accuracy can be analyzed quantitatively. There are two types of errors: constant and random deviation errors. If the angular deviation is a constant error, meaning that the radar is triggered at a fixed angular deviation each time, then the data remain uniformly sampled. Therefore, this case is not specifically analyzed or discussed. The main discussion focuses on random errors. As the radar system on board is triggered externally to start working, that is, as it is a causal system, the generated random errors are positive.
When random angular errors with ranges of , , and are introduced at each radar trigger position during the rotation process, with a beamwidth of 64°, the curve showing the variation in the slant range error with distance is as shown in Figure 11. The variation in the slant range error with the beamwidth is shown in Figure 12. It can be observed in Figure 11 that, if the angular error is within the range, then the imaging algorithm discussed in this study is applicable when m. Figure 12 shows that the applicable range of the beamwidth narrows down from to . Within the range, the imaging algorithm discussed in this study is applicable when m. Figure 12 shows that the applicable range of the beamwidth narrows down from to . Therefore, this angular error range has a minimal impact on both the distance and beamwidth applicability of the algorithm. Within the range, it is clear that an angular error within the range barely alters the distance range suitable for the imaging algorithm in this study, keeping it nearly identical to that in an undisturbed scenario. Moreover, this level of angular error also has a negligible effect on the wider beamwidths that can be effectively used.
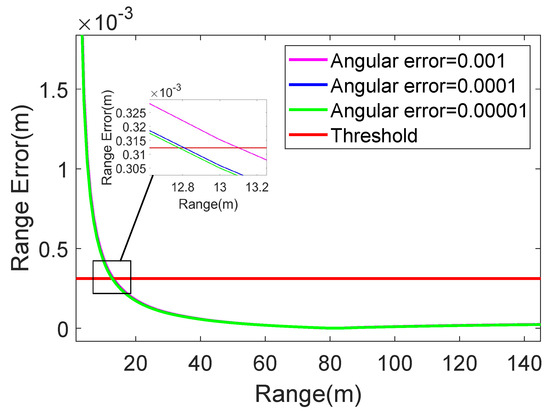
Figure 11.
The range error of the improved RD algorithm varying with the range when adding angular errors with ranges of , , and .
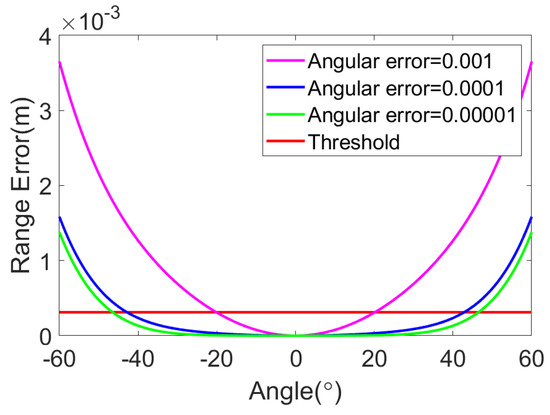
Figure 12.
The range error of the improved RD algorithm varying with the azimuth angle when adding angular errors with ranges of , , and .
2.4.4. Angular Sampling Error Analysis of Proposed System
This subsection presents a test conducted on the proposed system to observe the trigger signal delay of the encoder in order to obtain quantitative data on the system’s uniform sampling performance.
First, an error analysis is conducted on the system without using an angular encoder. The motor is operated at velocities ranging from to in each test. The radar works periodically at a PRF of 200 Hz. The encoder’s pulse is not used as the trigger, but its data are collected as truth data to identify the position of the radar at each pulse. Turntable tests are conducted several times on each of the set speeds. A logic analyzer is used to receive the pulse signal. Diagrams of the angle versus time when the speed is set to range from to are shown in Figure 13. The blue line represents the estimated data, and the red line represents the theoretical uniform rotation angle between two chirps. Figure 13a–f reveal that, in practical situations, due to the acceleration and deceleration of the motor, the angle intervals are not uniform, and there is a large deviation at the beginning and end of the rotation. When the motor reaches the set speed, it becomes relatively stable but with a small deviation.
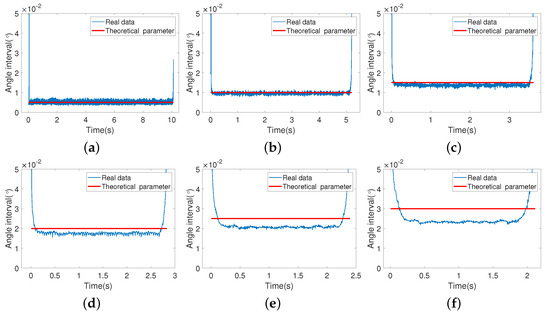
Figure 13.
Angle interval versus time in theoretical and actual situations without an angular encoder. (a) . (b) . (c) . (d) . (e) . (f) .
Next, an analysis of the system’s error with the addition of an angular encoder is conducted. When the pulse counter reaches the preset threshold, the radar is triggered to start once at that position. As before, a logic analyzer is used to capture the trigger signal from the angular encoder. The encoder’s signal is first sent to the counter, and, when it meets the set threshold, a hardware trigger is sent to the radar. Therefore, the main angular sampling error is caused by the delay of the counter and the signal transmission circuits. The logic analyzer captures the time delay between the moment that the pulse sent to the counter reaches the threshold and the moment that the radar receives the command to start working, as shown in Figure 14. The red and blue lines are used to denote the instances when the encoder’s signal reaches the threshold and the radar receives the trigger signal, respectively. There is a difference in the delay time; the rotation is , and the maximum delay obtained after several repeat tests is 15.6 μs. Hence, the maximum error in the position of each radar trigger can be calculated as . According to the previous analysis, it is determined that this error has a minimal impact on the improved fourth-order RD algorithm, and, thus, the system is capable of achieving high-quality SAR imaging.
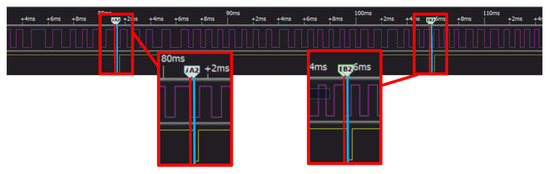
Figure 14.
Diagram of delay waveform of system.
3. Data and Experimental Results
3.1. Simulation Experiment
To examine performance, a simulation experiment was conducted. The improved RD algorithm was compared with the traditional RD algorithm and the BP algorithm under the uniform sampling condition. The simulation parameters were the same as those in Table 1 in Section 2. The point target was 17 m away from the rotation center.
Figure 15a–c present the imaging results of a point target using the improved RD algorithm, the BP algorithm, and the traditional RD algorithm. Figure 15d–f show the azimuth profiles of a point target using three algorithms. The BP algorithm range model makes no approximations, and its imaging results and integral sidelobe ratio (ISLR) are used as references. By observing Figure 15a–c, it can be noted that the focusing effect of the second-order RD algorithm in Figure 15c is the poorest. A quality assessment of the three algorithms is shown in the table below. In Table 2, it can be observed that the improved RD algorithm has significantly advanced the azimuth angle ISLR compared to the traditional RD algorithm, and it is almost equivalent to the BP algorithm.
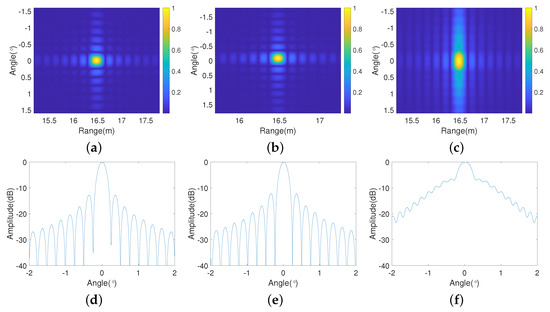
Figure 15.
Imaging results of point target with (a–c) Image of improved RD algorithm, BP algorithm, and traditional algorithm when the point target is at (17 m, 0°). (d–f) Azimuth profiles of the three algorithms.

Table 2.
Imaging criteria of point target simulation.
3.2. Real Experiment 1: Corner Reflector
To validate the applicability of the improved RD algorithm, a real data experiment on a corner reflector was conducted. A corner reflector was placed for testing. Figure 16 shows an image of the experimental scene and the setup of the corner reflector.

Figure 16.
Experimental scene.
Figure 17a–c show the imaging results after processing the data collected by a system with an encoder using the improved RD algorithm, BP algorithm, and traditional RD algorithm. Figure 17d–f are the azimuth profiles of the three algorithms with an encoder, and the quality assessment results are provided in Table 3. By comparing these results with those of the improved RD algorithm, it can be observed that the traditional algorithm does not achieve good performance.
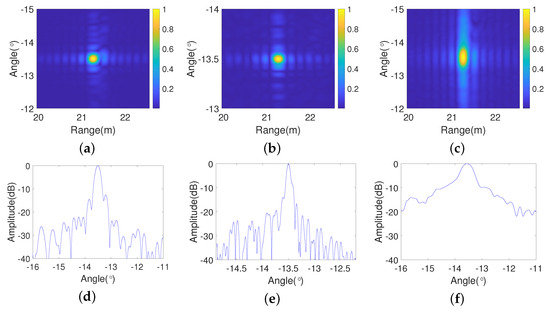
Figure 17.
Imaging results of the corner reflector with (a–c) Images of improved RD algorithm, BP algorithm, and traditional algorithm when the point target is 21.85 m with an encoder. (d–f) Azimuth profiles of the three algorithms with an encoder.

Table 3.
Imaging criteria of the corner reflector experiment (with an encoder).
Furthermore, to validate the advantages of the ArcSAR system with an encoder, data without an angular encoder were collected and processed. Figure 18 presents the imaging result and azimuth profile of the corner reflector obtained by the improved algorithm without an encoder. By comparison, it can be observed that the imaging quality with the encoder is superior to that without the encoder.
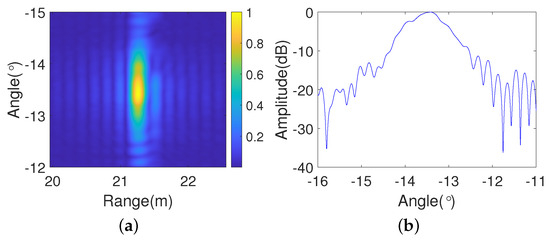
Figure 18.
Imaging results of the corner reflector with (a) Image of improved RD algorithm without an encoder. (b) Azimuth profile of the improved RD algorithm without an encoder.
Finally, to validate the maximum angular sampling interval, experiments were conducted using different angular sampling intervals. Figure 19a–c show the frequency domains of the different angular sampling intervals, where it can be observed that the sampling interval increases, and Figure 19c presents the maximum sampling interval, with the two yellow lines labeling the spectral width. Figure 19d,e show the corresponding imaging results for the different angular sampling intervals. It can be observed in Figure 19a–c that the signal spectra broaden as the angular sampling interval increases, which validates the deduced Equation (31).
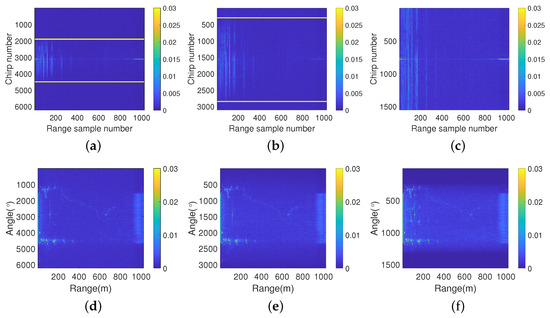
Figure 19.
(a–c) Spectrum diagrams of different angular sampling intervals. (d–f) Imaging diagrams with different angular sampling intervals.
3.3. Real Experiment 2: Full-Aspect Imaging
To verify the large-scene imaging performance of the ArcSAR system with an angle encoder, two full-aspect imaging experiments (scene 1 and scene 2) were conducted.
The first imaging scenario (scene 1) is shown in Figure 20. The Cartesian coordinate imaging results obtained with the traditional RD, improved RD, and BP algorithms are shown in Figure 21a–c, respectively. It can be clearly observed that the corner reflector area in (a) is wider than that in (b) and (c), which means that the second-order model-based RD cannot output good results in widebeam 60 GHz ArcSAR. However, it can be observed that the imaging result of the improved RD algorithm is consistent with that of the BP algorithm, which means that they have nearly the same level of good focusing results.

Figure 20.
Experimental scene.

Figure 21.
First scene imaging. (a) Traditional RD algorithm. (b) Improved RD algorithm. (c) BP algorithm.
The second imaging scenario (scene 2) is shown in Figure 22. Panels (a)–(d) show the optical image and results of the traditional RD, improved RD, and BP algorithms. Similar to scene 1, by examining the structures of the left circles, it can be observed that the azimuth focusing performance of the traditional RD algorithm is worse than that of the improved RD and BP algorithms. The Cartesian coordinate image results obtained after processing with the improved RD and BP algorithms are shown in Figure 22c,d. The experimental scene corresponds to the processed image, and the imaging results of the two algorithms are both consistent and good.
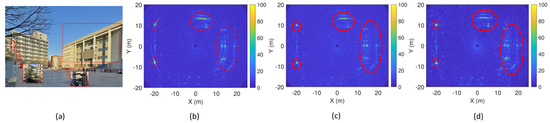
Figure 22.
Second scene imaging. (a) Optical image of scene. (b) Traditional RD algorithm. (c) Improved RD algorithm. (d) BP algorithm.
4. Discussion
This section presents the results obtained when applying the proposed system to a more complex urban scenario (scene 3). Additionally, a comparative experiment with the current 17 GHz ArcSAR is conducted. The processing time, imaging entropy, and imaging contrast criteria of the traditional RD, improved RD, and BP algorithms for all three scenes are summarized. Furthermore, the advantages, performance, limitations, and future research directions are discussed.
Figure 23 shows the results of a complex urban scene with dense buildings. The upper image is the optical picture. The reader can see that it contains a shopping mall on the left, a small square in the middle, and several buildings on the right. The middle image shows the ArcSAR full-scene imaging results, and the three areas match the three positions in the upper image.
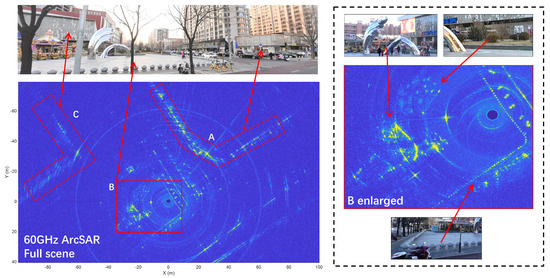
Figure 23.
Imaging results of the improved RD algorithm for a complex urban scene with dense buildings.
Areas A and C represent the right-side buildings and the shopping mall, respectively, and the edge of the bottom of these buildings can be seen clearly. Their vertical planes are not very clear, which is because the radar is on the ground. To obtain the vertical plane of tall buildings, the data observation geometry needs to be optimized when installing the ArcSAR system. As the current ArcSAR is a 2D imaging system, to image 3D buildings, a new ArcSAR with 3D imaging capabilities needs to be developed. This can be achieved by installing the radar module vertically so that multi-baseline data alongside height can be acquired to form a 3D image.
Area B represents the little square in the middle, which is enlarged and labeled in the bottom image. The area is well focused. The upper part is the bushes and trees, the lower left is the metal statue, and the L-shaped structures are the fences made with stone balls. The details of the small structures can be seen vividly, demonstrating the system’s good performance. Another phenomenon is the circular-shaped signature stretched at the strong point. This is because the polar-to-Cartesian interpolation transforms the straight sidelobe in the polar image into a circle. Hence, a sidelobe suppressing method is needed for ArcSAR.
Figure 24 shows the scene 3 imaging results of the BP (a) and traditional RD algorithms (b). Compared with Figure 23, the BP and improved RD algorithms have a similar imaging quality, determined by looking at the mainlobe of the building’s edge in area A. Conversely, the traditional RD still does not output good imaging results, thus demonstrating the proposed method’s effectiveness.

Figure 24.
Imaging results of the BP (a) and traditional RD algorithms (b) for a complex urban scene with dense buildings.
Table 4 shows the processing time of the three methods for the three scenes. The machine used to collect the processing time has an Intel(R) Core(TM) i5-7300HQ CPU @ 2.50 GHz, 16G RAM, and an NVIDIA GeForce GTX 1050 GPU. The BP algorithm runs on the GPU to save time. It is clear that, for all three scenes, the two RD methods require the same amount of time for processing, which is only several seconds. This is because the RD method is a frequency-domain method that can fully utilize FFT and phase multiplications to save time. The BP method, however, needs much more time for imaging, even with a GPU device, due to it being a time-domain method. The focusing performance metrics of all three methods for all scenarios are listed in Table 5. The metrics are image contrast (IC) [44] and image entropy (IE) [45]. Both can be used to evaluate the focus performance of an image. The greater the image contrast value, the better the focus effect, and the smaller the image entropy, the better the focus effect. Thus, it can be observed that the improved RD and BP methods have similar performance, and they perform better than the traditional RD method. Thus, the proposed method can achieve similar quality to the BP method while having a short processing time. This demonstrates the method’s effectiveness.

Table 4.
Imaging time of the three methods for the three scenes.

Table 5.
Imaging metrics of the three methods for the three scenes.
To further illustrate the advantage of the proposed system, a comparative experiment with the 17 GHz ArcSAR system is conducted in the same area. A photo of the system is shown in Figure 25. It is developed by our team, and it is a RiskRadar-360-type system. The system works in the Ku band (17 GHz), with a maximum bandwidth of 1 GHz and a maximum imaging range of 5 km. The rotation arm’s length is 0.75 m, and the azimuth beamwidth is . To obtain images under similar conditions, the bandwidth is set to 800 MHz, and the maximum range is set to 200 m. The obtained image is shown in Figure 26.

Figure 25.
Photo of 17 GHz ArcSAR system.
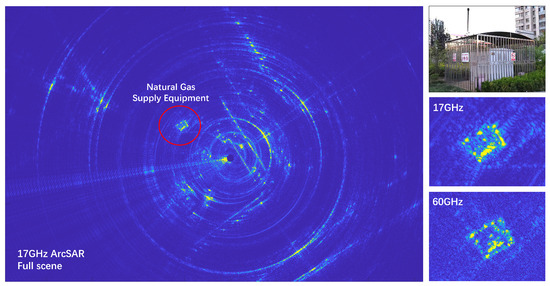
Figure 26.
The left side shows the full scene of the 17 GHz ArcSAR image. The right side shows enlarged images of the natural gas supply equipment obtained by the two systems.
By making a comparison with Figure 23, it can be observed that most structures are similar in areas A to C. However, the building’s details are not as clear as with the 60 GHz system. This is because, although the range resolution is the same, the azimuth resolution is lower than that of the 60 GHz system. Hence, the building’s resolution at a far range drops a lot when projecting to Cartesian coordinates. According to the system parameters, the theoretical azimuth resolution of the 17 GHz system is , which is three times that of the proposed 60 GHz system. The main reason for this is that the 60 GHz system has a much smaller wavelength and a wide beamwidth. To further illustrate the advantages, an image of natural gas supply equipment is extracted and enlarged, as shown on the right side of the figure. The top image is the optical image, which shows that the equipment is locked in a cage surrounded by a fence. The bottom two images are obtained with the 17 GHz and 60 GHz systems. It can be seen that the rectangular-shaped fences are much clearer in the 60 GHz image, while only a coarse shape can be seen in the 17 GHz image. It should also be noted that the gap between the equipment and the fence is only discriminated in the 60 GHz image. Thus, the results show that the proposed system can achieve a higher resolution than the 17 GHz system with a shorter arm length and a lighter weight, thereby demonstrating its advantages.
Based on the above analysis, in future work, the radar module’s multiple channels will be used to form 3D images, and the observation geometry will be optimized. Additionally, a sidelobe suppressing method will be designed for ArcSAR to enhance image quality.
5. Conclusions
In this study, a ground-based ArcSAR system based on millimeter-wave radar is introduced, with a high-precision encoder integrated to address the issue of image defocusing in SAR imaging caused by platform motion. Additionally, the existing RD algorithm is optimized to better suit high-frequency, wide-beam millimeter-wave radar systems.
First, a lightweight and compact ArcSAR system suitable for urban buildings was designed. In terms of system design, according to the Nyquist theorem, the maximum azimuth sampling angle was calculated to avoid aliasing, providing theoretical support for radar data sampling.
Then, the imaging algorithm was improved. To verify the effectiveness of the improved RD algorithm, a series of simulation experiments were conducted, and the improved algorithm was analyzed and compared with traditional algorithms and the BP algorithm. The experimental results show that the improved algorithm performs similarly to the BP algorithm.
Real-scene experiments were conducted using the system, and the collected data were processed using the improved algorithm. The experimental results confirm the performance of the system, with the imaging scene achieving clear focusing, validating the accuracy of the system and the effectiveness of the algorithm. The presented results indicate the potential of the proposed system for building monitoring in urban environments.
Author Contributions
W.S. and W.L. performed the experiments and implemented the methods; W.S. and W.L. wrote the manuscript; W.S. and W.L. contributed equally to this work; Y.L. (Yang Li) and Y.L. (Yun Lin) obtained the resources; Y.W. supervised; Y.W. administered the project; W.S. and Y.W. acquired funding; Y.W., Y.L. (Yang Li), Y.L. (Yun Lin), Z.B., and K.Y. gave valuable advice on manuscript writing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (grant Nos. 62201011 and 62131001), the Yuxiu Innovation Project of NCUT (grant Nos. 2024NCUTYXCX210 and 2024NCUTYXCX119), and the Young Scientists Project of the National Key Research and Development Program of China (grant No. 2023YFB3905200).
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. (Publicly unavailable data due to privacy or ethical restrictions.).
Acknowledgments
We thank the anonymous reviewers for their good advice and comments, which helped improve the quality of this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liang, D.; Zhang, H.; Fang, T.; Deng, Y.; Yu, W.; Zhang, L.; Fan, H. Processing of Very High Resolution GF-3 SAR Spotlight Data with Non-Start-Stop Model and Correction of Curved Orbit. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2112–2122. [Google Scholar] [CrossRef]
- Werninghaus, R.; Buckreuss, S. The TerraSAR-X Mission and System Design. IEEE Trans. Geosci. Remote Sens. 2010, 48, 606–614. [Google Scholar] [CrossRef]
- Martorella, M.; Pastina, D.; Berizzi, F.; Lombardo, P. Spaceborne Radar Imaging of Maritime Moving Targets With the Cosmo-SkyMed SAR System. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2797–2810. [Google Scholar] [CrossRef]
- Shen, W.; Lin, Y.; Li, Y.; Hong, W.; Wang, Y. Moving Targets Artifacts Removal in Multiaspect SAR Imagery Based on Logarithm Background Subtraction. IEEE J. Miniatur. Air Space Syst. 2023, 4, 62–69. [Google Scholar] [CrossRef]
- Hao, J.; Li, J.; Pi, Y.; Fang, X. A Drone Fleet-Borne SAR Model and Three-Dimensional Imaging Algorithm. IEEE Sens. J. 2019, 19, 9178–9186. [Google Scholar] [CrossRef]
- Appleby, R.; Anderton, R.N. Millimeter-Wave and Submillimeter-Wave Imaging for Security and Surveillance. Proc. IEEE 2007, 95, 1683–1690. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, W.; Zhang, Y.; Lin, Y.; Li, Y.; Bai, Z.; Zhang, Q.; Lv, S.; Liu, H.; Song, Y. Ground-Based Differential Interferometry SAR: A Review. IEEE Geosci. Remote Sens. Mag. 2020, 8, 43–70. [Google Scholar] [CrossRef]
- Vu, V.T.; Sjogren, T.K.; Pettersson, M.I.; Gustavsson, A.; Ulander, L.M. Detection of moving targets by focusing in UWB SAR-Theory and experimental results. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3799–3815. [Google Scholar] [CrossRef]
- Pieraccini, M.; Miccinesi, L. ArcSAR: Theory, Simulations, and Experimental Verification. IEEE Trans. Microw. Theory Tech. 2017, 65, 293–301. [Google Scholar] [CrossRef]
- Lin, Y.; Liu, Y.T.; Wang, Y.P.; Ye, S.B.; Zhang, Y.; Li, Y.; Li, W.; Qu, H.Q.; Hong, W. Frequency Domain Panoramic Imaging Algorithm for Ground-Based ArcSAR. Sensors 2020, 20, 7027. [Google Scholar] [CrossRef]
- Hua, Y.; Yang, Y.; Lu, B.; Cui, S.; Jiang, Z. Quantitative Analysis of Motion Effects on ArcSAR Panoramic Imaging Quality. In Proceedings of the 2024 9th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 12–14 July 2024; pp. 644–648. [Google Scholar] [CrossRef]
- Gao, Z.Y.; Jia, Y.; Liu, S.Y.; Zhang, X.K. Development of Ground-Based SFCW-ArcSAR System and Investigation on Point Target Response. Prog. Electromagn. Res. 2022, 109, 137–148. [Google Scholar] [CrossRef]
- Gao, Z.Y.; Jia, Y.; Liu, S.Y.; Zhang, X.K. A 2-D Frequency-Domain Imaging Algorithm for Ground-Based SFCW-ArcSAR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 61660. [Google Scholar] [CrossRef]
- Fuentes, S.; Tongson, E.; Gonzalez Viejo, C. Urban Green Infrastructure Monitoring Using Remote Sensing from Integrated Visible and Thermal Infrared Cameras Mounted on a Moving Vehicle. Sensors 2021, 21, 295. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, M.R.; Lyons, T. Transforming CCTV cameras into NO2 sensors at city scale for adaptive policymaking. Sci. Rep. 2025, 15, 86532. [Google Scholar] [CrossRef]
- Schuetze, C.; Sauer, U. Challenges associated with the atmospheric monitoring of areal emission sources and the need for optical remote sensing techniques-an open-path Fourier transform infrared (OP-FTIR) spectroscopy experience report. Environ. Earth Sci. 2016, 75, 5482. [Google Scholar] [CrossRef]
- Tsuno, K.; Akahori, Y.; Yui, T.; Furukawa, H.; Watanabe, A.; Fujimaki, M.; Oto, M.; Katsuyama, T.; Iguchi, Y.; Inada, H.; et al. Highly-Sensitive Near-Infrared Spectroscopy System for Remote Monitoring of Concrete Structures. J. Disaster Res. 2017, 12, 536–545. [Google Scholar] [CrossRef]
- Wu, Y.C.; Noh, S.J.; Ham, S. Identification of Inundation Using Low-Resolution Images from Traffic-Monitoring Cameras: Bayes Shrink and Bayesian Segmentation. Water 2020, 12, 1725. [Google Scholar] [CrossRef]
- Xu, J.; Yu, X. The Immune Depth Presentation Convolutional Neural Network Used for Oil and Gas Pipeline Fault Diagnosis. IEEE Access 2024, 12, 163739–163751. [Google Scholar] [CrossRef]
- Yu, X.; Liang, X.; Zhou, Z.; Zhang, B.; Xue, H. Deep soft threshold feature separation network for infrared handprint identity recognition and time estimation. Infrared Phys. Technol. 2024, 138, 105223. [Google Scholar] [CrossRef]
- Yu, X.; Liang, X.J.; Zhou, Z.J.; Zhang, B.F. Multi-task learning for hand heat trace time estimation and identity recognition. Expert Syst. Appl. 2024, 255, 124551. [Google Scholar] [CrossRef]
- Wang, Y.; Sasamura, T.; Mustafa, A.; Morita, T. Real-time torque prediction for ultrasonic motors using an attention-based BiLSTM model and improved differential evolution algorithm. Measurement 2025, 251, 117266. [Google Scholar] [CrossRef]
- Broquetas, A.; De Porrata, R. Circular synthetic aperture radar (C-SAR) system for ground-based applications. Electron. Lett. 2002, 33, 988–989. [Google Scholar] [CrossRef]
- Yu, L.; Lin, Y.; Li, Y.; Wang, J.; Hong, W. Height Profile Estimation of Power Lines Based on Two-Dimensional CSAR Imagery. IEEE Geosci. Remote Sens. Lett. 2016, 13, 339–343. [Google Scholar] [CrossRef]
- Lee, H.; Lee, J.H.; Kim, K.E.; Sung, N.H.; Cho, S.J. Development of a Truck-Mounted Arc-Scanning Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2773–2779. [Google Scholar] [CrossRef]
- Viviani, F.; Michelini, A.; Mayer, L.; Conni, F. IBIS-ArcSAR: An Innovative Ground-Based SAR System for Slope Monitoring. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1348–1351. [Google Scholar] [CrossRef]
- Luo, Y.; Song, H.; Wang, R.; Deng, Y.; Zhao, F.; Xu, Z. Arc FMCW SAR and Applications in Ground Monitoring. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5989–5998. [Google Scholar] [CrossRef]
- Ponce, O.; Prats, P.; Scheiber, R.; Reigber, A.; Moreira, A. Study of the 3-D Impulse Response Function of Holographic SAR Tomography with Multicircular Acquisitions. In Proceedings of the EUSAR 2014—0th European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014; pp. 1–4. [Google Scholar]
- Cao, N.; Lee, H.; Zaugg, E.; Shrestha, R.; Carter, W.; Glennie, C.; Wang, G.; Lu, Z.; Fernandez-Diaz, J.C. Airborne DInSAR Results Using Time-Domain Backprojection Algorithm: A Case Study Over the Slumgullion Landslide in Colorado With Validation Using Spaceborne SAR, Airborne LiDAR, and Ground-Based Observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4987–5000. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Liu, Q.H. Frequency-Domain Backprojection Algorithm for Synthetic Aperture Radar Imaging. IEEE Geosci. Remote Sens. Lett. 2015, 12, 905–909. [Google Scholar] [CrossRef]
- Ash, J.N. An Autofocus Method for Backprojection Imagery in Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Lett. 2012, 9, 104–108. [Google Scholar] [CrossRef]
- Gui, S.; Li, J.; Hao, J.; Zuo, F.; Pi, Y. Extension of Polar Format Algorithm to CSAR Imaging for Arbitrary Region of Interest. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 2579–2582. [Google Scholar] [CrossRef]
- Wang, H.; Sun, B.; Li, C.; Jiang, Y.; Yang, W. An Improved Range-Doppler Imaging Algorithm Based on High-Order Range Model for Near-Field Panoramic Millimeter-Wave ArcSAR. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5211016. [Google Scholar] [CrossRef]
- Ding, M.; Wang, X.; Wang, Y.; Dong, Q.; Tang, L.; Qu, J.; Liu, L.; Song, C.; Wang, B. First Demonstration of Metamaterial-Modulated Tag Localization and Imaging Based on K-Band FMCW Mini-SAR System. IEEE Trans. Microw. Theory Tech. 2024, 72, 6072–6082. [Google Scholar] [CrossRef]
- Jia, G.; Buchroithner, M.; Chang, W.; Li, X. Simplified Real-Time Imaging Flow for High-Resolution FMCW SAR. IEEE Geosci. Remote Sens. Lett. 2015, 12, 973–977. [Google Scholar] [CrossRef]
- Xu, L.; Lien, J.; Li, J. Doppler–Range Processing for Enhanced High-Speed Moving Target Detection Using LFMCW Automotive Radar. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 568–580. [Google Scholar] [CrossRef]
- Wang, S.; Guo, L.X.; Yu, Z.F.; Wang, J.; Chen, J. Method of 2-D Range-Doppler Imaging for Plasma Wake Based on Range Walk Correction. IEEE Trans. Plasma Sci. 2023, 51, 1076–1084. [Google Scholar] [CrossRef]
- Meta, A.; Hoogeboom, P.; Ligthart, L.P. Signal Processing for FMCW SAR. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3519–3532. [Google Scholar] [CrossRef]
- Mittermayer, J.; Moreira, A.; Loffeld, O. Spotlight SAR data processing using the frequency scaling algorithm. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2198–2214. [Google Scholar] [CrossRef]
- Neo, Y.L.; Wong, F.; Cumming, I.G. A Two-Dimensional Spectrum for Bistatic SAR Processing Using Series Reversion. IEEE Geosci. Remote Sens. Lett. 2007, 4, 93–96. [Google Scholar] [CrossRef]
- Neo, Y.L.; Wong, F.H.; Cumming, I.G. A Comparison of Point Target Spectra Derived for Bistatic SAR Processing. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2481–2492. [Google Scholar] [CrossRef]
- de Wit, J.; Meta, A.; Hoogeboom, P. Modified range-Doppler processing for FM-CW synthetic aperture radar. IEEE Geosci. Remote Sens. Lett. 2006, 3, 83–87. [Google Scholar] [CrossRef]
- Huang, L.; Qiu, X.; Hu, D.; Han, B.; Ding, C. Medium-Earth-Orbit SAR Focusing Using Range Doppler Algorithm With Integrated Two-Step Azimuth Perturbation. IEEE Geosci. Remote Sens. Lett. 2015, 12, 626–630. [Google Scholar] [CrossRef]
- Berizzi, F.; Corsini, G. Autofocusing of inverse synthetic aperture radar images using contrast optimization. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1185–1191. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X. SAR Minimum-Entropy Autofocus Using an Adaptive-Order Polynomial Model. IEEE Geosci. Remote Sens. Lett. 2006, 3, 512–516. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).