Abstract
Multi-object tracking (MOT) in satellite videos presents significant challenges, including small target sizes, dense distributions, and complex motion patterns. To address these issues, we propose OITrack, an improved tracking framework that integrates a Trajectory Completion Module (TCM), an Adaptive Kalman Filter (AKF), and an Iterative Expansion Intersection over Union Strategy (I-EIoU) strategy. Specifically, TCM enhances temporal continuity by compensating for missing trajectories, AKF improves tracking robustness by dynamically adjusting observation noise, and I-EIoU optimizes target association, leading to more accurate small-object matching. Experimental evaluations on the VIdeo Satellite Objects (VISO) dataset demonstrated that OITrack outperforms existing MOT methods across multiple key metrics, achieving a Multiple Object Tracking Accuracy (MOTA) of 57.0%, an Identity F1 Score (IDF1) of 67.5%, a reduction in False Negatives (FN) to 29,170, and a decrease in Identity Switches (ID switches) to 889. These results indicate that our method effectively improves tracking accuracy while minimizing identity mismatches, enhancing overall robustness.
1. Introduction
Multi-object tracking (MOT) in satellite videos is a crucial research topic in remote sensing, with applications in military surveillance [1], disaster response [2], environmental monitoring, and more [3]. Due to the low resolution, small target size, complex background, and dynamic motion of objects in satellite videos [4], traditional MOT methods often struggle to achieve high tracking accuracy. In this study, we define small targets as objects that occupy fewer than 50 pixels in area, and dense distributions as scenarios where more than 200 targets may appear in a single frame. This corresponds to an average spatial density of at least one target per 50 × 50 pixel region. This definition is consistent with prior research in satellite video analysis, where object instances are typically small in size and numerous in count due to the inherent low resolution and wide-area coverage of satellite sensors. Small target detection is particularly problematic due to their low contrast and small size, leading to frequent missed detections, which significantly degrades the accuracy and stability of tracking. Additionally, issues such as identity switches (ID switches) and track fragmentation further complicate the problem. Figure 1 illustrates the challenges in MOT within satellite video. Therefore, improving the tracking accuracy of small targets, especially addressing missed detections, has become one of the key challenges in MOT research for satellite videos. Figure 1 describes a typical scenario in satellite video where objects, such as vehicles, are small in size, densely distributed, and often appear visually similar to the background. These characteristics lead to challenges such as occlusion, trajectory fragmentation, and difficulty in distinguishing targets from the background, especially under low contrast conditions.

Figure 1.
Challenges in satellite video object tracking. (a) Similar background: the objects and background share similar textures, making discrimination difficult. (b) Target congestion: multiple objects densely distributed in proximity, increasing association ambiguity. (c) Occlusion: moving objects are partially or completely covered by other objects or background elements, causing interruptions in tracking. (d) Small object: objects occupy very few pixels, resulting in limited spatial features and making detection and tracking more challenging.
Currently, there are two main paradigms in multi-object tracking: Detection-Based Tracking (DBT) and Joint Detection and Tracking (JDT) [5]. These paradigms have distinct advantages and disadvantages and impact the tracking accuracy in satellite videos differently.
DBT separates detection and tracking, relying heavily on the detector. In satellite videos, small targets in complex backgrounds are easily missed by the detector, and once undetected, the tracking system cannot make up for it, leading to a sharp decline in tracking accuracy. Fast-moving and complexly interacting targets in satellite videos also exacerbate detection failures and ID switches.
The JDT paradigm, although it jointly optimizes detection and tracking, is not a perfect solution for small target tracking in satellite videos either. In complex scenarios, the dynamic adjustments in JDT may introduce computational instability, affecting the system’s robustness and overall performance.
To overcome the limitations of both the DBT and JDT paradigms in satellite video MOT, we propose a novel algorithm that combines trajectory completion, adaptive Kalman filtering, and iterative extended IOU strategies to achieve more efficient and accurate multi-object tracking.
- Trajectory Completion Module (TCM): We propose a novel trajectory completion method based on Long Short-Term Memory (LSTM) networks and an adaptive Kalman Filter. This module effectively compensates for missed detections, reducing target loss caused by detector failures and improving tracking continuity.
- Adaptive Kalman Filter (AKF): Unlike the traditional Kalman Filter, which assumes a fixed observation noise, our method dynamically adjusts observation noise based on detection confidence, enhancing tracking robustness.
- Iterative Extended Intersection over Union (I-EIoU) Strategy: We propose an enhanced target matching strategy that significantly reduces identity switches and false negatives in small-object tracking.
2. Related Work
MOT has been a long-standing challenge in the field of computer vision, especially in applications such as satellite video analysis, where targets often exhibit weak features and motion patterns that are different from those in conventional video scenes. In recent years, several tracking paradigms have been proposed to address these challenges, each with its strengths and limitations. Among them, traditional methods such as DBT and JDT have emerged as some of the most widely explored approaches in both research and practice. This section reviews and compares these methodologies, highlighting their respective advantages and shortcomings in the context of satellite video tracking.
2.1. Traditional Multi-Object Tracking Methods
Classic measurement-driven target generation methods typically approximate the target generation intensity using Random Finite Set (RFS) filters [6]. For example, in reference [7], low correlation measurements from the previous frame were used to initialize new targets, which helped avoid missing the initial few detections of new targets. However, this approach might fail to detect the target in its early frames and is robust to clutter measurements. Paper [8] combined Cardinalized Probability Hypothesis Density (CPHD) [9] and Generalized Labelled Multi-Bernoulli (GLMB) [10] models for adaptive clutter rate estimation, but they still relied on pre-coded parameters and did not leverage historical trajectory information. Methods like the one proposed by Fu et al. [11], which utilized online dictionary learning to distinguish targets from clutter measurements, are less effective for satellite images, where target features are often weak due to small object sizes (over 90% are smaller than 50 pixels), low contrast with complex backgrounds, and limited texture information.
2.2. DBT Method
The DBT paradigm is a key classic method used in Multi-Object Tracking (MOT). Its basic workflow involves first obtaining detection results from a detector and then using an independent model to generate the corresponding features for inter-frame association analyses. In the context of computer vision-based MOT, various methods emphasize different aspects:
Motion-Based Methods: For example, SORT [12] predicts the motion state of a target using Kalman filters [13] and computes the Intersection over Union (IoU) between detection results and predicted bounding boxes, constructing a cost matrix for subsequent association. ByteTrack [14] innovates on this by processing detections based on their scores, leveraging motion similarity to filter out false positives and focusing on high-confidence detections to significantly improve tracking performance in occlusion scenarios. OC-SORT [15] further addresses the shortcomings of SORT in handling occlusions and nonlinear motion by proposing an observation-centered tracking method, improving tracking performance through smoothing filters, enhanced association cost functions, and re-associating lost tracks to reduce accumulated errors. BoT-SORT [16] takes it further by incorporating both motion and appearance information, as well as more accurate Kalman filter state vectors to refine the tracking results. CKDNet-SMTNet [17] designs a cross-frame module to assist in keypoint detection and improves tracking through LSTM networks [18].
Re-identification (ReID)-Based Methods: DeepSORT [19] integrates ReID features with SORT, effectively reducing ID switching errors caused by target occlusion. Tang et al. [20] utilized human mesh and appearance recovery techniques to associate targets using transformer models. StrongSORT [21] introduces an independent ReID model to extract appearance features from detection boxes and improves trajectory association with global matching algorithms and Gaussian smoothing interpolation.
When DBT is applied to MOT tasks in satellite videos, a variety of exploration paths have emerged:
Improving the Detector: MMB stands out by introducing advanced motion features and detector modules that not only generate proposals for regions of interest but also incorporate low-rank matrix completion to reduce false positives while recovering missed targets. DSFNet [22] develops a dual-stream detection network, effectively integrating static and dynamic information, which enhances detection accuracy for small moving objects.
Improving Association Accuracy: The bi-level K-shortest [23] method introduces a probabilistic two-step global data association approach, effectively mitigating detection inconsistencies caused by low resolution in satellite videos. The DSORT-PT [24] method effectively addresses the challenge of detecting objects with weak visual features. However, it involves substantial computational complexity. BMTC [4] cleverly integrates single-object tracking techniques into a bi-directional MOT framework, allowing efficient localization of both new and existing targets. In recent years, unsupervised methods and computationally efficient networks have attracted increasing attention. Wu et al. [25] proposed a highly efficient unsupervised framework for moving object detection in satellite videos, utilizing a pseudo-label evolution mechanism and a sparse spatio-temporal representation to reduce background redundancy, achieving 98.8 FPS on 1024 × 1024 images. Similarly, Xiao et al. [26] introduced a sparsity-aware global channel pruning (SAGCP) method for infrared small-target detection, which reduces computation while preserving key target features, leading to a more compact and accurate model.
Cooperative Improvement of Detector and Tracking: CKDNet [17], proposed by Feng et al., utilizes inter-frame information to assist in keypoint detection and combines LSTM-based SMTNet to regress the virtual vehicle’s location, ultimately merging with real detections to improve overall performance. SFMFMOT [27] uses slow feature analysis to better separate background moving objects during detection and develops optimization strategies that incorporate motion features and accumulated time information to enhance tracking performance.
However, the DBT paradigm still has limitations, particularly with small-sized targets. It is prone to miss detections, detect false positives, and track interruptions.
2.3. JDT Method
The JDT paradigm integrates the detector and feature model into a unified architecture, aiming to improve the efficiency and coherence of multi-object tracking. For example, FairMOT [28] strikes a balance between detection and ReID tasks by optimizing the model at the architecture level. It integrates a center-point-based detection network into the detection branch, eliminating the need for an additional feature extraction network and allowing simultaneous learning of detection and ReID embeddings with faster computation. CenterTrack [29] builds an integrated detection and tracking network based on keypoints, predicting offset and the distance from the center points of the previous frame to complete associations. By using the center point distribution of the current frame and the previous frame’s object center heatmaps as input, the system outputs the current frame’s center point heatmap, seamlessly accomplishing both detection and association within the same architecture.
In satellite video research, many novel approaches have emerged. TGraM [30] proposes a graph-based modeling approach, using spatiotemporal reasoning modules to capture inter-frame correlations and enhance tracking accuracy with multi-task gradient adversarial learning. CFTracker [31] introduces an end-to-end JDT network, incorporating cross-frame feature update modules and corresponding training strategies to optimize overall performance. Moreover, CSTracker [32] introduces reciprocal networks and SAAN methods, taking a novel approach to feature extraction.
Although JDT methods have achieved significant success in certain applications, motion-based DBT methods offer greater advantages for multi-object tracking tasks in satellite videos. The performance of DBT methods is influenced by the quality of the front-end detector. Some scholars [33,34,35] have studied on-board and ground detection algorithms for remote sensing images, yielding promising results. This paper aimed to further explore valuable information, such as trajectory and motion features, to enhance overall tracking performance. Targets in satellite videos typically exhibit simple, linear motion patterns, with minimal background dynamics, which makes motion-based DBT methods particularly effective for such tasks. Compared to JDT methods, DBT methods are better at leveraging target motion information and mitigating the negative impact of missing appearance features, making them more suitable for satellite video applications. Therefore, this study adopted a motion model-based DBT framework to more effectively address the challenges of multi-object tracking in satellite videos.
3. Methods
In the process of small object tracking in satellite videos, several challenges arise, such as detection omissions and trajectory fragmentation. To address these issues, this paper proposed a lightweight online Trajectory Completion Module, which integrates adaptive Kalman filtering and iterative Expansion IoU matching strategies to enhance trajectory completion and matching performance for small targets. These three innovations are consolidated into a unified tracking framework, which is based on a detection-based multi-object tracking paradigm. Figure 2 illustrates the overall framework of the proposed method.
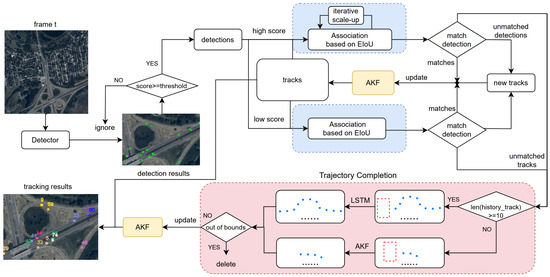
Figure 2.
The framework of the proposed method.
The proposed method employs the DSFNet detector, which excels in small object detection, to generate detection boxes for each frame. These boxes are classified into high- and low-confidence detections based on confidence scores. Data association is carried out using I-EIoU for high-confidence detections and standard ExpansionIoU for low-confidence ones. Unmatched detections are assigned new trackers, while unmatched trackers are supplemented via the trajectory completion module. Depending on the available historical trajectory data, either LSTM or AKF is used for trajectory completion, with the completed trajectory updating the position and state in the AKF.
3.1. Trajectory Completion Module
To address the challenge of missed detections in small objects tracking within satellite video, we designed a Trajectory Completion Module that integrates the LSTM network with a Kalman Filter for real-time trajectory inference. The module compensates for detection failures by predicting and updating target motion states based on both short-term and long-term temporal context.
Specifically, detection outputs in the format of bounding box coordinates are converted to the center-point representation and object size , forming a compact motion state vector. These vectors are sequentially accumulated into trajectory histories and serve as the input to the TCM. Considering that the dataset has a frame rate of 10 fps, we set the historical window to 10 frames, corresponding to a 1 s temporal span. This 1 s window is selected as it provides a meaningful duration to observe the motion trajectory of small targets, allowing the model to effectively learn movement patterns while avoiding the inclusion of outdated or noisy data. When the available historical trajectory length is less than 10 frames, we employ a conventional Kalman Filter to propagate motion estimates based on linear dynamics. However, for trajectories with ≥10 frames, an LSTM-based prediction model is activated.
The LSTM model receives as input the motion state deltas—i.e., inter-frame differences such as extracted from the past 10 frames. These temporal derivatives serve as a compact representation of motion patterns, allowing the model to capture acceleration, direction change, or deformation trends that may not be apparent in raw coordinate sequences. This feature transformation helps enhance robustness against abrupt motion and noise, which are common in small-object detection.
A sliding window strategy is employed to generate fixed-length input sequences, which are then fed into a stacked LSTM network. The model leverages its memory gates to preserve temporal dependencies and filter out irrelevant fluctuations. The final hidden state is passed to a fully connected layer to regress the predicted motion state at the current time step t. The output includes both positional estimates and inferred motion trends, enabling the system to anticipate the likely location of missed targets.
To further refine the predicted trajectory, the LSTM output is used as the observation input to the Kalman Filter. This step allows the system to account for detection uncertainty and correct the predicted state using statistical motion modeling. A boundary checking mechanism is integrated to ensure that targets outside the frame are excluded from further updates, avoiding erroneous propagation.
The implementation logic is formalized in the pseudocode provided in Algorithm 1. A visual illustration of the LSTM-based temporal modeling process is presented in Figure 3. To handle frames where detections may be missing due to occlusion, low resolution, or dense clutter, the TCM uses temporal information to supplement the association data, which helps maintain continuity in object trajectories.
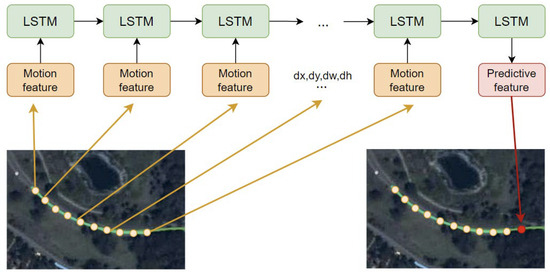
Figure 3.
The LSTM model enables effective prediction of the target’s future motion state through feature transformation and inverse transformation.
Algorithm 1: The pseudocode related to the TCM.
| Algorithm 1: Trajectory Completion Module |
| Input: Detection results format: , convert to center and size: ; Historical trajectory of the target: ; Detection result of the current frame; Output: Completed trajectory information: ; Data: Initialize Kalman Filter and LSTM model ; Initialize the completed trajectory set ; Initialize Kalman filter state ; for to do if Historical trajectory is less than 10 frames then Use Kalman filter to update trajectory: Complete the current state of the target; end else Use LSTM model for trajectory completion; Input historical trajectory ; LSTM predicts the current trajectory ; Feed LSTM-completed trajectory into Kalman filter: end Perform boundary check for the target; ; if Target is out of bounds then Delete historical trajectory information for the target, stop updating it; end else Add the completed trajectory to the completed trajectory set: ; end end return Updated completed trajectory ; |
Figure 4 illustrates the internal structure of the LSTM network, which consists of several key components, including the forget gate, input gate, output gate, and cell state. The formulae are as follows:
where , and are the activation values of the input gate, forget gate, and output gate, respectively, controlling information flow into, retention within, and output from the cell state; , , and are the weight matrices corresponding to the input gate, forget gate, output gate, and candidate cell state, respectively; , , and are their associated bias terms; is the previous hidden state; is the current input; is the sigmoid activation function; is the hyperbolic tangent function; is the current cell state; is the previous cell state; denotes the candidate cell state generated through a hyperbolic tangent activation ; and is the current hidden state, the model’s final output.
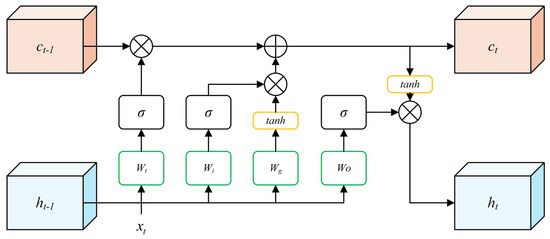
Figure 4.
The structure of the LSTM.
All weight matrices and bias terms in the LSTM module are initialized using a uniform distribution, following the default initialization strategy in PyTorch 1.10.0. During training, these parameters are optimized using the Adam optimizer. The LSTM takes as input the positions of a target over the past 10 frames, represented as center coordinates and bounding box sizes. It outputs the predicted position in the next frame. The training objective is to minimize the mean squared error (MSE) between the predicted and ground-truth positions in the frame.
3.2. Adaptive Kalman Filter
In traditional KF methods, the measurement noise covariance matrix for all targets is typically set to be the same, which assumes that all targets have the same level of observation noise. However, in practical applications, especially in scenarios with complex background noise (such as satellite video), this assumption does not hold. The background noise in satellite video is often significant, and the quality of target detection can be influenced by various factors, including complex background environments, low-resolution images, and differences in detector performance. As a result, traditional Kalman filtering methods struggle to effectively handle the uncertainty in target detection quality, making them susceptible to low-quality detection results, which in turn affects the accuracy of trajectory tracking.
To address this issue, we used an AKF method [36]. This method dynamically adjusts the observation noise covariance matrix based on the detector’s confidence. In the target detection process, the confidence of the detector reflects the reliability of the detection result, which usually changes over time. We define detections as the set of bounding boxes output by the object detector for each frame, each associated with a confidence score. Specifically, detections with confidence scores ≥ 0.4 are defined as high-confidence detections, as they represent the upper percentile of the distribution and are more reliable. Detections with scores < 0.4 are considered low-confidence detections, as they are more prone to false positives and uncertainty.
When the detector’s confidence is low, this indicates that the detection result may contain large errors, so the observation noise covariance needs to be increased, reducing the trust in the measurement data, thus minimizing the impact of low-quality observations on state estimation. Conversely, when the detector’s confidence is high, the observation noise covariance can be appropriately reduced, increasing trust in the observation data. This dynamic adjustment mechanism allows KF to more flexibly adapt to variations in the outputs of different detectors, thereby improving the accuracy of target state estimation. This is particularly effective in satellite video, where the motion state estimation of small targets can be significantly enhanced.
Within the framework of Kalman filtering, the state of a target is typically represented by a state vector. In traditional multi-target tracking, the state vector of a target usually includes basic information such as position and velocity. For small targets in satellite videos, this study proposes a more refined state vector representation method to better accommodate the motion and size variations of small targets.
The traditional KF state vector is generally defined as follows:
where represent the horizontal and vertical coordinates of the target’s center point, typically in pixel coordinates in the image; represents the area of the target’s bounding box; r represents the aspect ratio (width-to-height ratio) of the target’s bounding box; and represent the rate of change of the target’s center coordinates and area.
This state vector formulation is suitable for tracking the motion of general targets and enables Kalman filtering to predict and update the state of the target. However, the state of small targets in satellite videos may be more complex, especially since such targets exhibit subtle and often difficult-to-detect variations in scale, orientation, and position. Consequently, a more refined definition of the state vector is required to accommodate these complexities.
To better adapt to small targets in satellite videos, this study extends and refines the target state vector. The new state vector is defined as:
where u, v represent the horizontal and vertical coordinates of the target’s center point, in pixels, indicating the target’s position on the image plane; and w, h represent the width and height of the target, respectively, providing the target’s size information. Unlike the traditional state vector’s size s, the width and height are listed separately to more precisely account for size changes, especially since size variations are often more significant in satellite video data. represent the rate of change of the target’s position and size. These rates of change help the model capture the dynamic features of the target over time.
This refined state vector provides a more accurate representation of the target’s dynamics, especially for small targets in satellite video, where precise modeling of position, scale, and motion is essential for robust tracking.
In KF, the prediction and update of the target state are performed through two main steps: the prediction step and the update step. The prediction step is based on the state estimate from the previous time step and the motion model, while the update step incorporates new observation data to correct the target’s state estimate.
In KF, the state prediction of the target is based on the system’s state transition equation:
where is the predicted state at time k; is the previous state; A is the state transition matrix, which defines the state transition process from the previous time step to the current time step; B is the control input matrix; and is the control input at time k.
At each time step, KF predicts the change in the covariance matrix based on process noise:
where is the predicted covariance at time k; A is the state transition matrix; is the state covariance from the previous time step; and Q is the process noise covariance matrix.
The goal of the update step is to refine the target state estimation based on the actual observation data, thereby improving the accuracy of the estimate. This step is accomplished through the following equations:
where is the Kalman gain, H is the observation matrix, is the measurement noise covariance matrix, is the updated state estimate, is the actual observation at time k, is the identity matrix, and is the updated state covariance.
By updating the covariance, Kalman filtering can adaptively adjust the uncertainty of the state estimate, thereby improving the accuracy and robustness of tracking.
In complex environments such as satellite videos, background noise and fluctuations in detector performance may lead to variations in the quality of observation data, thereby affecting the accuracy of Kalman filtering. To address this issue, inspired by the work of Du et al. [36], we introduced an adjustment factor , which dynamically adjusts the measurement noise covariance matrix based on the confidence of the target detection. Specifically, the relationship between the updated measurement noise covariance and the detection confidence is as follows:
When the confidence is low, the noise covariance is increased, thereby reducing the impact of the observation data on the state update. Conversely, when the confidence is high, the noise covariance is decreased, enhancing the influence of the observation data.
Through this adaptive noise update strategy, the AKF adjusts the measurement noise based on the real-time confidence of the detector, avoiding the impact of low-confidence observations on the target state estimation. In satellite video applications, the quality of target detection often fluctuates, particularly when targets are in regions with complex backgrounds or low resolution, where detection accuracy is typically poor. The adaptive measurement noise update strategy effectively addresses this uncertainty, improving the trajectory tracking accuracy for small targets.
3.3. Iterative Extension IoU
In multi-object tracking, a commonly used object matching method is based on the traditional IoU to compute the cost matrix, which typically calculates the IoU between each detection box and predicted box in the current frame. However, for small targets in satellite videos, whose sizes are generally smaller than 9 × 9 pixels, continuing to use the traditional IoU may result in very small or even zero IoU values between the detection and predicted boxes, even when the predicted box undergoes slight displacement. This can lead to failures in target association. Since this paper introduced an online trajectory completion module, a failure to associate the predicted box with the detection box in time would result in the continuous accumulation of errors in the AKF and LSTM, thereby increasing the likelihood of false positives and ID switches. Therefore, to expand the association range between detection and predicted boxes and avoid matching with zero or extremely small IoU values, we used an extended IoU method, which enhances target association by expanding the boundaries of the boxes. Figure 5 illustrates the concept of bounding box expansion.
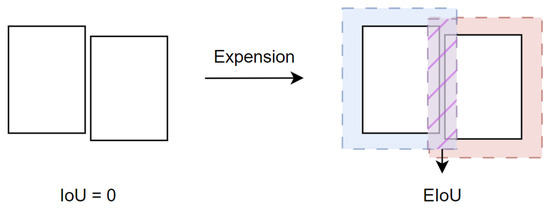
Figure 5.
After applying the Expansion IoU, two originally non-overlapping detection boxes may have a non-zero IoU.
Specifically, the height and width of the extended detection and predicted boxes are calculated using the following formulas:
where h and w represent the original height and width of the detection and predicted boxes and E is the extension factor. By increasing the size of the box, the success rate of matching is effectively improved.
However, the extension factor E is a critical hyperparameter whose value significantly impacts tracking results. Since it is not feasible to find a universal extension factor that can accommodate all scenarios and motion states, this paper proposes a novel iterative extension IoU method, inspired by Huang et al. [37]. In this method, detection boxes are first divided into high-confidence and low-confidence detections based on a predefined confidence threshold. During the matching phase, high-confidence detections are associated using the I-EIoU, with the extension factor updated according to the following formula:
where is the initial extension factor, λ is the growth factor for during each iteration, and t is the current iteration round. As the iterations progress, the extension factor increases, expanding the search space. Each successfully associated detection box is removed from the pool until the maximum number of iterations is reached. The iterative process terminates after three rounds, as further increasing the number of iterations yields limited improvement and may even degrade the overall performance due to false associations and accumulated noise.
For low-confidence detections, some may originate from false positives. We avoid using an excessive extension factor for these cases, as it may lead to incorrect associations between predicted boxes and unreliable detections. Therefore, we apply the standard extended IoU strategy for association. This approach helps reduce mis-associations.
4. Experiments
4.1. Datasets and Evaluation Metrics
This study evaluated the proposed method on the VIdeo Satellite Objects (VISO) dataset [38]. Figure 6 presents several representative examples from the VISO dataset. The VISO dataset was selected for evaluation because it provides high-resolution satellite video sequences with detailed annotations for multiple moving targets across diverse environments. It specifically includes small objects with dense distributions and complex motion patterns, which align well with the main challenges addressed by our proposed tracking method. Moreover, the availability of frame-by-frame object annotations enables rigorous quantitative evaluation of tracking accuracy, identity preservation, and trajectory continuity under real-world satellite imaging conditions.

Figure 6.
Examples from the VISO dataset. The images illustrate annotated moving objects with unique IDs under various complex scenes, including highways, overpasses, and urban residential areas. Objects are densely distributed and labeled with different colors.
The SAT-MTB dataset [39] was also selected because it complements VISO by providing more diverse object categories, including vehicles, ships, and aircraft, captured under complex satellite video scenarios. This diversity enables the evaluation of the proposed method across different target types, motion patterns, and scene complexities. Moreover, the dataset covers high-density environments, large-scale object movements, and dynamic occlusions, allowing for a comprehensive assessment of the robustness and adaptability of the tracking framework. Figure 7 provides example scenes from the SAT-MTB dataset.

Figure 7.
Examples from the SAT-MTB dataset. The dataset contains diverse object categories captured in satellite videos, including (a) cars in urban traffic scenes, (b) airplanes flying over open areas, and (c) ships navigating across the ocean. The SAT-MTB dataset offers a wide range of target types, motion patterns, and scene complexities, providing a comprehensive benchmark for evaluating tracking robustness and adaptability.
To quantitatively evaluate the effectiveness of the proposed method, we used the widely adopted Comprehensive Evaluation for Object Tracking (CLEAR-MOT) framework, which is commonly applied in the field of MOT [40]. This framework consists of seven key metrics: Multiple Object Tracking Accuracy (MOTA), Identity F1 Score (IDF1), Mostly Tracked (MT), Mostly Lost (ML), False Positives (FP), False Negatives (FN), and IDs (Identity Switches). These metrics are used to assess tracking accuracy, identity consistency, the number of successfully tracked targets, missed targets, false positives, false negatives, and identity switches.
MOTA is a core metric for evaluating multi-object tracking accuracy, considering the combined effects of FN, FP, and IDs. Its formula is as follows:
Here, FN refers to the number of missed targets, FP indicates the number of false positives, IDs represents the number of identity switches, and GT denotes the total number of ground truth targets. A higher MOTA indicates better overall tracking performance.
IDF1 measures the consistency of target identities across frames, reflecting the system’s ability to maintain consistent identity labeling over time. It is the harmonic mean of precision and recall for identity matching, computed as follows:
where IDTP represents correctly matched identities and IDFP and IDFN indicate the number of false matches and missed identities, respectively. A higher IDF1 value reflects better identity consistency during tracking.
Additionally, MT represents the percentage of successfully tracked targets, ML indicates the percentage of lost targets, and IDs quantifies the number of identity switches. These metrics collectively offer a comprehensive evaluation of the tracking performance and provide insights for optimization.
4.2. Experimental Setup
The experiments were conducted on an NVIDIA RTX 3090 GPU, with the experimental environment consisting of Ubuntu 20.04, PyTorch 1.10.0, and CUDA 11.3. For the object detection network, the batch size was set to four, with data augmentation techniques such as random flipping and color jitter applied. The training was performed using the Adam optimizer [41] for 55 epochs, with an initial learning rate of 1.25 × 10−4, which was reduced at the 30th and 45th epochs. For the trajectory completion module utilizing LSTM, we trained the model for 40 epochs using the Adam optimizer, with a batch size of 64 and an initial learning rate of 5 × 10−4. The learning rate was adjusted using a cosine annealing strategy.
4.3. Comparison with Existing Methods
We conducted a comprehensive comparative analysis between the proposed method and several existing multi-object tracking approaches, including ByteTrack [14], OCSORT [15], StrongSORT [21], FairMOT [28], DSFNet [22], SMTNet [17], CFTracker [31] and TGraM [30]. The experimental results are presented in Table 1. As illustrated in Table 1, the proposed method demonstrated significant superiority across multiple key performance metrics.

Table 1.
A comparison of existing state-of-the-art methods using the VISO test set. “↓” indicates that lower values are preferred, while “↑” indicates that higher values are preferred. The red color indicates the best performance for the metric, while the green color represents the second-best performance.
The experimental results demonstrated that although our method exhibited a higher number of false positives, it achieved the best performance in key metrics such as MOTA and IDF1. Specifically, our method achieved a MOTA score of 51.7%, demonstrating its competitive overall performance in complex tracking scenarios involving small and dense targets. When handling small targets in complex scenes, our method stabilizes target tracking through precise trajectory completion, reducing the fragmentation and target loss commonly observed in traditional methods. Our method achieved an IDF1 score of 67.5% and an MT count of 296. The second-best IDF1 score was 66.3% (OC-SORT), and the second-best MT count was 190 (DSFNet). Compared to these, OITrack improved the IDF1 by 1.2 percentage points and increased the number of mostly tracked targets by 106, highlighting its superior capability in preserving target identity and achieving longer-term trajectory tracking.
Furthermore, while our method does not have an advantage in terms of FPS, all compared methods, including ours, operate below the real-time multi-object tracking requirement of 30 FPS. Therefore, the reduction in FPS remains within an acceptable range given the improvements in tracking accuracy and robustness.
A negative MOTA indicates that the sum of tracking errors exceeds the number of ground-truth objects, meaning the tracker introduces more errors than correct detections. In Table 1, FairMOT [28] and TGraM [30] exhibit negative MOTA values, primarily due to a high number of FP and false negatives FN. Trackers with poor detection precision tend to generate excessive FP, incorrectly identifying background noise as targets. Additionally, significant FN values suggest that many actual objects are not detected, leading to substantial tracking failures.
The experimental results on the SAT-MTB test set, presented in Table 2, demonstrate the performance of various state-of-the-art tracking methods under complex satellite video scenarios. Compared to the VISO dataset, SAT-MTB introduces additional challenges due to its high-density target environments and large-scale motion variations.

Table 2.
A comparison of existing state-of-the-art methods using the SAT-MTB test set. “↓” indicates that lower values are preferred, while “↑” indicates that higher values are preferred. The red color indicates the best performance for the metric, while the green color represents the second-best performance.
Compared to other methods, OITrack achieved a substantial improvement in the MT metric, reaching 1853 targets, which was 65.3% higher than the second-best result of 1121 from DSFNet. This improvement demonstrates its effectiveness in maintaining complete target trajectories. The ML metric was also reduced, indicating fewer targets are lost over time due to more robust association and motion prediction strategies. Although there was an increase in the number of FP, this is primarily due to the trajectory completion module generating supplementary trajectories for low-confidence detections. However, the increase was effectively controlled by AKF and improved matching strategies. Moreover, the number of FN substantially decreased, highlighting the effectiveness of our method in recovering missed targets and enhancing the tracking completeness in complex environments.
Although OITrack had a slightly higher FP, its trajectory completion strategy significantly reduced missed detections and improved tracking consistency. Compared to other methods, it maintains a better balance between detection accuracy and trajectory stability, making it a strong choice for satellite-based multi-object tracking.
Figure 8 presents the tracking results of OITrack, along with those from other comparative models. As observed, the visualized trajectories of other algorithms exhibited frequent interruptions and identity switches of the same target, leading to significant trajectory fragmentation. In contrast, OITrack demonstrated a clear advantage in terms of trajectory completeness, with an increased number of successfully tracked trajectories.

Figure 8.
Visualization of tracking results on the VISO test set 008 for OITrack and other methods. Trajectories with the same color indicate they belong to the same target. (a) Ground Truth (GT), (b) FairMOT, (c) CFTrack, (d) TraM, (e) DSFNet, (f) OITrack.
To evaluate the frame-by-frame tracking performance of the proposed method across different urban scenarios, Figure 9 presents tracking results in three representative environments: a highway traffic scene, a bridge with both land and maritime transportation, and an urban road network with intersections. Even in cases where targets are densely distributed, frequently occluded, or moving in multiple directions, the model maintains stable tracking performance. In the three sequences shown in Figure 9, the recall rates reached 0.92, 0.91, and 0.88, respectively, as measured through experimental evaluation.
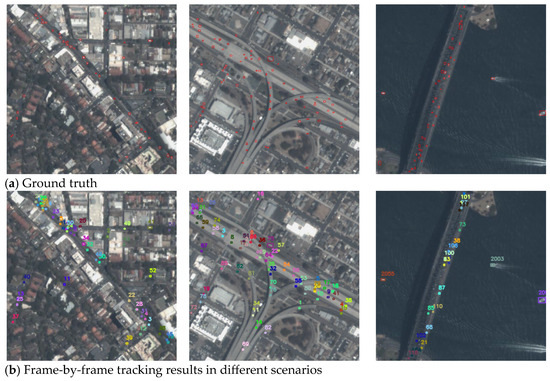
Figure 9.
Examples of comparisons between the ground truth and frame-by-frame tracking results.
4.4. Ablation Experiments
In this experiment, we conducted an ablation study to investigate the contribution of different modules to the overall performance of the proposed multi-object tracking algorithm. Specifically, we analyzed the impact of three key modules: TCM, AKF, and I-EIOU through various combinations, and the results are shown in Table 3.

Table 3.
The effectiveness of each proposed module on the VISO test set. “↓” indicates that lower values are preferred, while “↑” indicates that higher values are preferred. The best performance for each metric is highlighted in red.
4.4.1. Effectiveness of the TCM
When TCM was added, MOTA increased to 50.5%, IDF1 improved to 65.1%, and MT increased from 190 to 289 (an increase of over 52%), while ML decreased from 248 to 163. These results indicate that the trajectory completion module effectively enhances tracking continuity by compensating for missed detections and improving the completeness of target trajectories. However, there was an increase in FP (from 6353 to 15,553) due to TCM generating additional trajectory points for previously undetected targets. Additionally, FN dropped significantly from 41,996 to 29,644, demonstrating the module’s effectiveness in mitigating missed detections. The trajectory completion module significantly improved tracking accuracy for small targets by filling in missing target trajectory information, thus reducing target loss and tracking fragmentation. However, there was an increase in false positives and missed targets.
To further evaluate the impact of LSTM architecture within TCM, we conducted an ablation study by varying the LSTM hidden size from 64 to 128 while keeping all other components unchanged. The results, as shown in Table 4, indicated that increasing the hidden size had a minor effect on tracking performance but a significant impact on FPS.

Table 4.
Impact of LSTM hidden size on tracking performance and computational efficiency. “↓” indicates that lower values are preferred, while “↑” indicates that higher values are preferred.
The results indicated that increasing the LSTM hidden size within the TCM module yielded negligible improvements in tracking accuracy while significantly reducing FPS. Given the computational constraints in multi-object tracking for satellite video, using LSTM-64 provides a better trade-off between accuracy and efficiency.
To investigate the impact of different motion modeling strategies on tracking performance, we conducted an ablation study using the DLA-34 backbone. As shown in Table 5, replacing the GRU-based motion modeling with an LSTM network resulted in a noticeable improvement in both MOTA and IDF1, demonstrating the LSTM’s superior ability to capture long-term motion dependencies. Furthermore, integrating the LSTM predictions with a Kalman filter (LSTM + KF) further enhanced tracking performance, yielding the highest MOTA and IDF1 scores among the compared approaches. These results validate the effectiveness of the proposed motion modeling and prediction framework for improving the continuity and accuracy of small objects tracking.

Table 5.
Ablation study on different motion modeling strategies based on the DLA-34 backbone. “↓” indicates that lower values are preferred, while “↑” indicates that higher values are preferred.
Figure 10 shows the visualization of motion information extracted by the TCM module, where highlighted regions represent moving objects. As shown in the figure, the highlighted areas in the feature maps correspond well to the actual positions of small moving targets in the original video frames, indicating that the TCM module captures the motion cues of small targets.

Figure 10.
Motion features extracted by the TCM module.
4.4.2. Effectiveness of the AKF
With the addition of the AKF, MOTA further improved to 50.80%, IDF1 reached 65.3%, and MT slightly increased to 292. The AKF dynamically adjusts the observation noise based on the confidence of the detector, making the tracking more robust to variations in the satellite video’s noisy background. While false positives and missed targets are still relatively high, the performance improvement in tracking accuracy is evident.
To further evaluate the impact of KF and AKF on tracking performance, we conducted an ablation study comparing these two approaches. The experimental results, presented in Table 6, demonstrated that AKF provides a moderate improvement over standard KF, particularly in reducing IDs and improving tracking completeness.

Table 6.
Comparison of KF and AKF on tracking performance. “↓” indicates that lower values are preferred, while “↑” indicates that higher values are preferred.
AKF adaptively modifies noise parameters based on detection confidence, helping to better handle variations in target motion and observation uncertainty.
4.4.3. Effectiveness of the I-EIoU
With the addition of the I-EIoU, MOTA increased from 50.8% to 51.7% (a relative improvement of 1.8%), IDF1 improved from 65.3% to 67.5% (a relative improvement of 3.4%), and IDs decreased from 1094 to 889 (a relative reduction of 18.7%). These results demonstrated that I-EIoU effectively enhances overall tracking performance, especially by improving identity consistency and reducing ID mismatches.
Figure 11 presents a comparison between the proposed method and the baseline. In this scenario, where the target is occluded by trees and reappears later, the baseline fails to associate the reappeared target with its previous trajectory, resulting in identity switching. In contrast, the proposed method effectively maintains trajectory completeness and successfully avoids identity switching in this case.
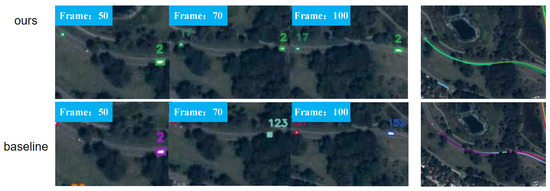
Figure 11.
Comparison visualization between OITrack and the baseline on Test Set 002. Colors are used to distinguish targets; the same color indicates the same target.
5. Conclusions
In this paper, we proposed OITrack, a novel MOT framework designed specifically for small target tracking in satellite videos. OITrack integrates an LSTM-based TCM, an AKF, and an I-EIoU strategy to address key challenges such as missed detections, ID switches, and trajectory fragmentation.
Experimental evaluations on the VISO dataset demonstrated that OITrack outperforms existing tracking methods across multiple key metrics. Specifically, it achieved a MOTA of 57.0%, reflecting an improvement in overall tracking accuracy. The IDF1 reached 67.5%, indicating better identity preservation throughout the tracking sequence. Additionally, OITrack successfully tracked 296 targets, surpassing competing methods in maintaining object trajectories over extended sequences, while also reducing FN to 29,170, which enhances detection robustness in complex environments.
Despite these improvements, our approach has certain limitations. While the TCM module effectively compensates for missed detections, it can introduce a higher false positive rate, potentially affecting tracking precision in densely populated target scenarios. Furthermore, the computational cost of the framework remains relatively high, which may pose challenges for deployment in real-time or resource-constrained settings.
Future research directions include: (1) Optimizing TCM to achieve a more lightweight design, balancing accuracy and computational efficiency; (2) Enhancing false positive suppression mechanisms to improve tracking precision, particularly in dense target environments; and (3) Exploring multi-task learning frameworks to jointly optimize detection and tracking, thereby enhancing system robustness in complex tracking scenarios.
Author Contributions
Conceptualization, W.L. and X.W.; investigation, W.L., X.W., W.A. and C.X.; methodology, W.L. and X.W.; project administration, W.A.; software, W.L. and C.X.; supervision, X.W.; validation, W.L.; visualization, W.L., W.A. and C.X.; writing—original draft, W.L., X.W. and W.A.; writing—review and editing, X.W., W.A., C.X., G.Z. and Q.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (NSFC) (No. 62207030).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bauk, S.; Kapidani, N.; Lukšić, Ž.; Rodrigues, F.; Sousa, L. Review of Unmanned Aerial Systems for the Use as Maritime Surveillance Assets. In Proceedings of the 2020 24th International Conference on Information Technology (IT), Zabljak, Montenegro, 18–22 February 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Yuan, C.; Liu, Z.; Zhang, Y. UAV-based forest fire detection and tracking using image processing techniques. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 639–643. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, Y.; Lin, C.; Yang, X.; Jia, Y.; Liu, Y. Object Tracking in Satellite Videos Based on Correlation Filter with Multi-Feature Fusion and Motion Trajectory Compensation. Remote Sens. 2022, 14, 777. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Huang, Z.; Cheng, X.; Feng, J.; Jiao, L. Bidirectional Multiple Object Tracking Based on Trajectory Criteria in Satellite Videos. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5603714. [Google Scholar] [CrossRef]
- Li, Y.; Liao, X.; Yuan, Q.; Jin, X.; Liu, Y.; He, J. Advancing Multi-object Tracking for Small Vehicles in Satellite Videos: A More Focused and Continuous Approach. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5631519. [Google Scholar] [CrossRef]
- Mahler, R. Statistical Multisource Multitarget Information Fusion; Artech House: Boston, MA, USA, 2007; pp. 1255–1259. [Google Scholar]
- Lin, S.; Vo, B.; Nordholm, S. Measurement driven birth model for the generalized labeled multi-Bernoulli filter. In Proceedings of the 2016 International Conference on Control, Automation and Information Sciences (ICCAIS), Ansan, Republic of Korea, 27–29 October 2016; pp. 94–99. [Google Scholar] [CrossRef]
- Reuter, S.; Meissner, D.; Wilking, B.; Dietmayer, K. Cardinality balanced multi-target multi-Bernoulli filtering using adaptive birth distributions. In Proceedings of the 16th International Conference on Information Fusion, Istanbul, Turkey, 9–12 July 2013; pp. 1608–1615. [Google Scholar]
- Vo, B.; Vo, B.; Cantoni, A. The Cardinalized Probability Hypothesis Density Filter for Linear Gaussian Multi-Target Models. In Proceedings of the 2006 40th Annual Conference on Information Sciences and Systems, Ansan, Republic of Korea, 22–24 March 2006; pp. 681–686. [Google Scholar] [CrossRef]
- Vo, B.; Vo, B.; Hoang, H. An Efficient Implementation of the Generalized Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2017, 65, 1975–1987. [Google Scholar] [CrossRef]
- Fu, Z.; Feng, P.; Angelini, F.; Chambers, J.; Naqvi, S. Particle PHD Filter Based Multiple Human Tracking Using Online Group-Structured Dictionary Learning. IEEE Access 2018, 6, 14764–14778. [Google Scholar] [CrossRef]
- Bewley, A.; Ge, Z.; Ott, L.; Ramos, F.; Upcroft, B. Simple online and realtime tracking. In Proceedings of the 2016 IEEE international conference on image processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 3464–3468. [Google Scholar] [CrossRef]
- Kalman, R. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, P.; Jiang, Y.; Yu, D.; Weng, F.; Yuan, Z.; Luo, P.; Liu, W.; Wang, X. Bytetrack: Multi-object tracking by associating every detection box. In Proceedings of the Computer Visio—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–21. [Google Scholar] [CrossRef]
- Cao, J.; Pang, J.; Weng, X.; Khirodkar, R.; Kitani, K. Observation-Centric SORT: Rethinking SORT for Robust Multi-Object Tracking. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 9686–9696. [Google Scholar] [CrossRef]
- Aharon, N.; Orfaig, R.; Bobrovsky, B. Bot-sort: Robust associations multi-pedestrain tracking. arXiv 2022, arXiv:2206.14651. [Google Scholar]
- Feng, J.; Zeng, D.; Jia, X.; Zhang, X.; Li, J.; Liang, Y.; Jiao, L. Cross-frame keypoint-based and spatial motion information-guided networks for moving vehicle detection and tracking in satellite videos. ISPRS J. Photogramm. 2021, 177, 116–130. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Wojke, N.; Bewley, A.; Paulus, D. Simple online and realtime tracking with a deep association. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3645–3649. [Google Scholar] [CrossRef]
- Tang, S.; Andriluka, M.; Andres, B.; Schiele, B. Multiple People Tracking by Lifted Multicut and Person Re-identification. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3701–3710. [Google Scholar] [CrossRef]
- Du, Y.; Zhao, Z.; Song, Y.; Zhao, Y.; Su, F.; Gong, T.; Meng, H. StrongSORT: Make DeepSORT Great Again. IEEE Trans. Multimed. 2023, 25, 8725–8737. [Google Scholar] [CrossRef]
- Xiao, C.; Yin, Q.; Ying, X.; Li, R.; Wu, S.; Li, M.; Liu, L.; An, W.; Chen, Z. DSFNet: Dynamic and Static Fusion Network for Moving Object Detection in Satellite Videos. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3510405. [Google Scholar] [CrossRef]
- Zhang, J.; Jia, X.; Hu, J.; Tan, K. Satellite Multi-Vehicle Tracking under Inconsistent Detection Conditions by Bilevel K-Shortest Paths Optimization. In Proceedings of the 2018 Digital Image Computing: Techniques and Applications (DICTA), Canberra, ACT, Australia, 10–13 December 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Sommer, L.; Krüger, W.; Teutsch, M. Appearance and Motion Based Persistent Multiple Object Tracking in Wide Area Motion Imagery. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Montreal, BC, Canada, 11–17 October 2021; pp. 3871–3881. [Google Scholar] [CrossRef]
- Wu, S.; Xiao, C.; Wang, Y.; Yang, J.; An, W. Sparsity-Aware Global Channel Pruning for Infrared Small-target Detection Networks. IEEE Trans. Geosci. Remote. Sens. 2025, 63, 5615011. [Google Scholar] [CrossRef]
- Xiao, C.; An, W.; Zhang, Y.; Su, Z.; Li, M.; Sheng, W.; Pietikäinen, M.; Liu, L. Highly Efficient and Unsupervised Framework for Moving Object Detection in Satellite Videos. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 11532–11539. [Google Scholar] [CrossRef]
- Wu, J.; Su, X.; Yuan, Q.; Shen, H.; Zhang, L. Multivehicle Object Tracking in Satellite Video Enhanced by Slow Features and Motion Features. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5616426. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.; Wang, X.; Zeng, W.; Liu, W. FairMOT: On the fairness of detection and re-identification in multiple object tracking. Int. J. Comput. Vis. 2021, 129, 3069–3087. [Google Scholar] [CrossRef]
- Zhou, X.; Koltun, V. Tracking objects as points. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2016; pp. 474–490. [Google Scholar] [CrossRef]
- He, Q.; Sun, X.; Yan, Z.; Li, B.; Fu, K. Multi-object tracking in satellite videos with graph-based multitask modeling. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5619513. [Google Scholar] [CrossRef]
- Kong, L.; Yan, Z.; Zhang, Y.; Diao, W.; Zhu, Z.; Wang, L. CFTracker: Multi-object tracking with cross-frame connections in satellite videos. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5611214. [Google Scholar] [CrossRef]
- Liang, C.; Zhang, Z.; Zhou, X.; Li, B.; Zhu, S.; Hu, W. Rethinking the competition between detection and ReID in multi-object tracking. IEEE Trans. Image Process. 2022, 31, 3182–3196. [Google Scholar] [CrossRef]
- Zhang, H.; Wen, S.; Wei, Z.; Chen, Z. High-Resolution Feature Generator for Small-Ship Detection in Optical Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5617011. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, M.; Zhu, G.; Liu, Y.; Guo, P.; Yan, J. FFCA-YOLO for Small Object Detection in Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5611215. [Google Scholar] [CrossRef]
- Hou, Q.; Wang, Z.; Tan, F.; Zhao, Y.; Zheng, H.; Zhang, W. RISTDnet: Robust Infrared Small Target Detection Network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7000805. [Google Scholar] [CrossRef]
- Du, Y.; Wan, J.; Zhao, Y.; Zhang, B.; Tong, Z.; Dong, J. GIAOTracker: A comprehensive framework for MCMOT with global information and optimizing strategies in VisDrone. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Montreal, BC, Canada, 11–17 October 2021; pp. 2809–2819. [Google Scholar] [CrossRef]
- Huang, H.; Yang, C.; Sun, J.; Kim, P.; Kim, K.; Lee, K.; Huang, C.; Hwang, J. Iterative Scale-Up ExpansionIoU and Deep Features Association for Multi-Object Tracking in Sports. In Proceedings of the 2024 IEEE/CVF Winter Conference on Applications of Computer Vision Workshops (WACVW), Waikoloa, HI, USA, 1–6 January 2024; pp. 163–172. [Google Scholar] [CrossRef]
- Yin, Q.; Hu, Q.; Liu, H.; Zhang, F.; Wang, Y.; Lin, Z.; An, W.; Guo, Y. Detecting and Tracking Small and Dense Moving Objects in Satellite Videos: A Benchmark. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5612518. [Google Scholar] [CrossRef]
- Li, S.; Zhou, Z.; Zhao, M.; Yang, J.; Guo, W.; Lv, Y.; Kou, L.; Wang, H.; Gu, Y. A Multitask Benchmark Dataset for Satellite Video: Object Detection, Tracking, and Segmentation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5611021. [Google Scholar] [CrossRef]
- Bernardin, K.; Stiefelhagen, R. Evaluating Multiple Object Tracking Performance: The CLEAR MOT Metrics. EURASIP J. Image Video Process. 2008, 2008, 246309. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).