Remote Sensing of Seismic Signals via Enhanced Moiré-Based Apparatus Integrated with Active Convolved Illumination
Abstract
1. Introduction
2. Background
2.1. State-of-the-Art Seismic Remote Sensing Methods
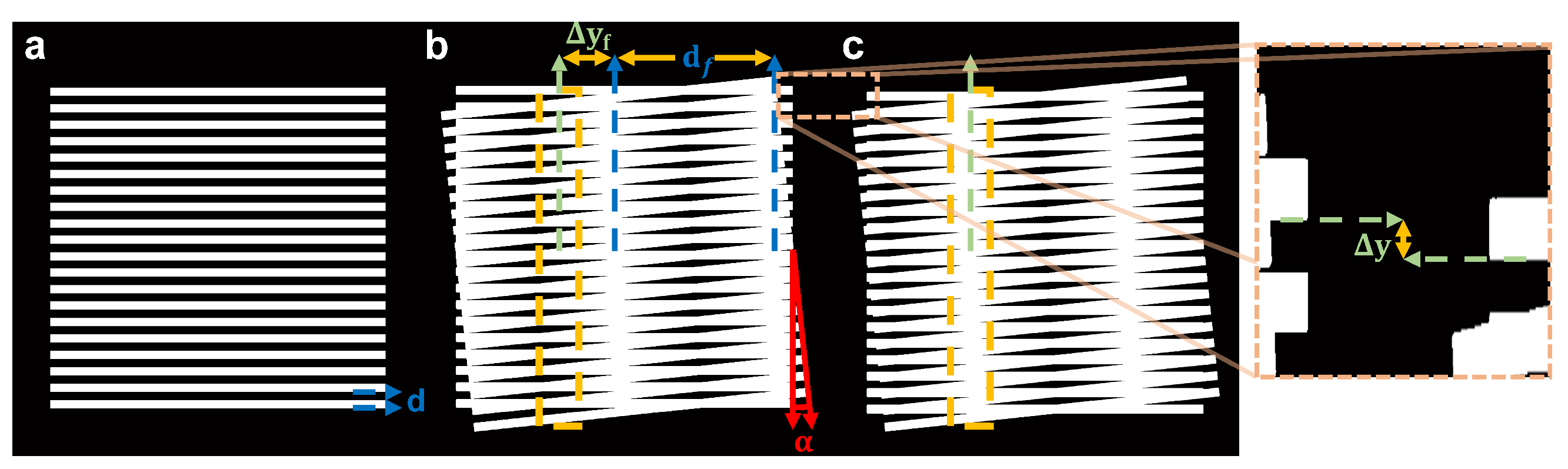
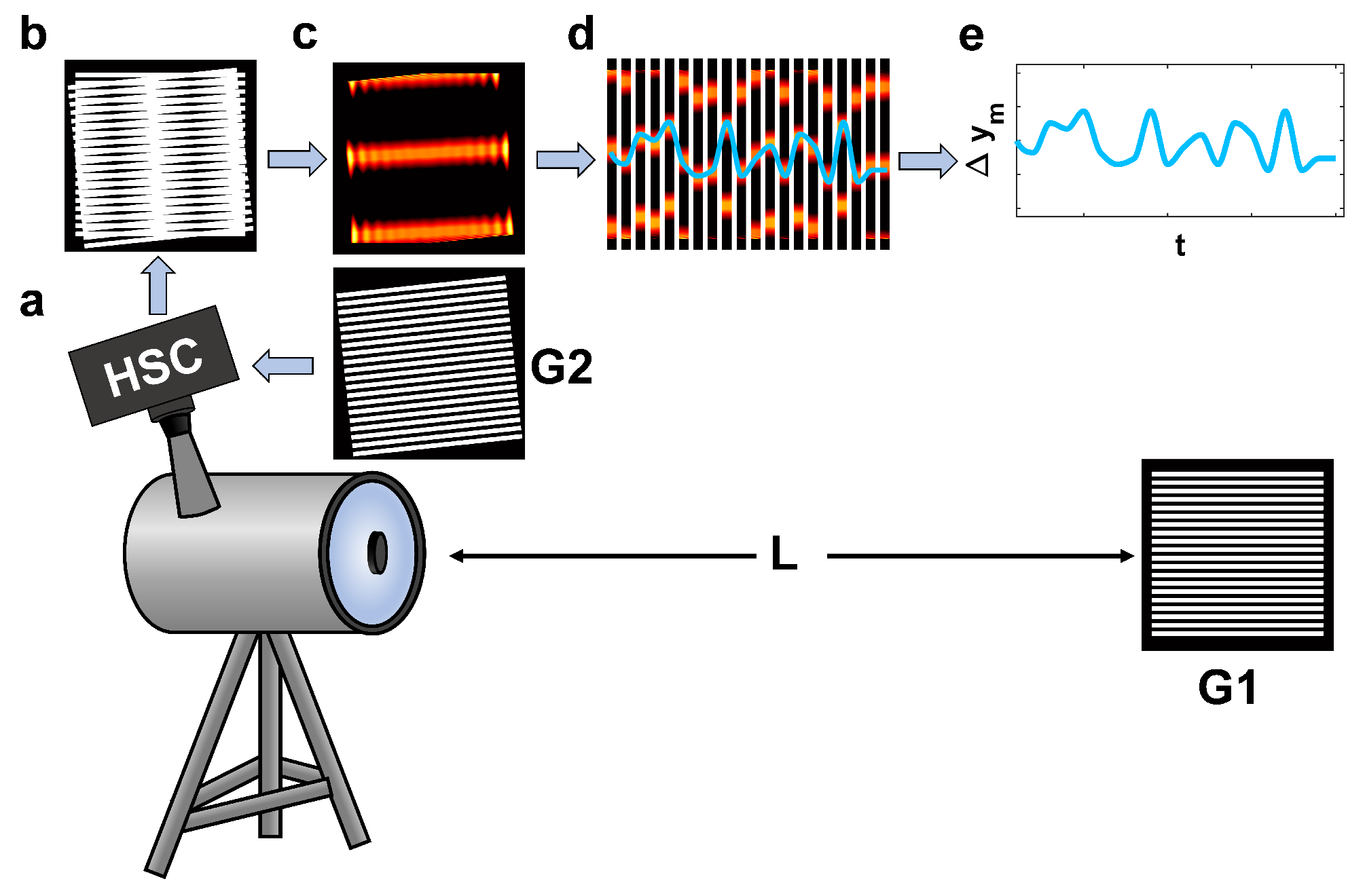
2.2. Moiré-Based Apparatus
2.3. Active Convolved Illumination to Improve Wave Propagation in a Turbulent Volume
3. Data Simulation Framework
4. Results
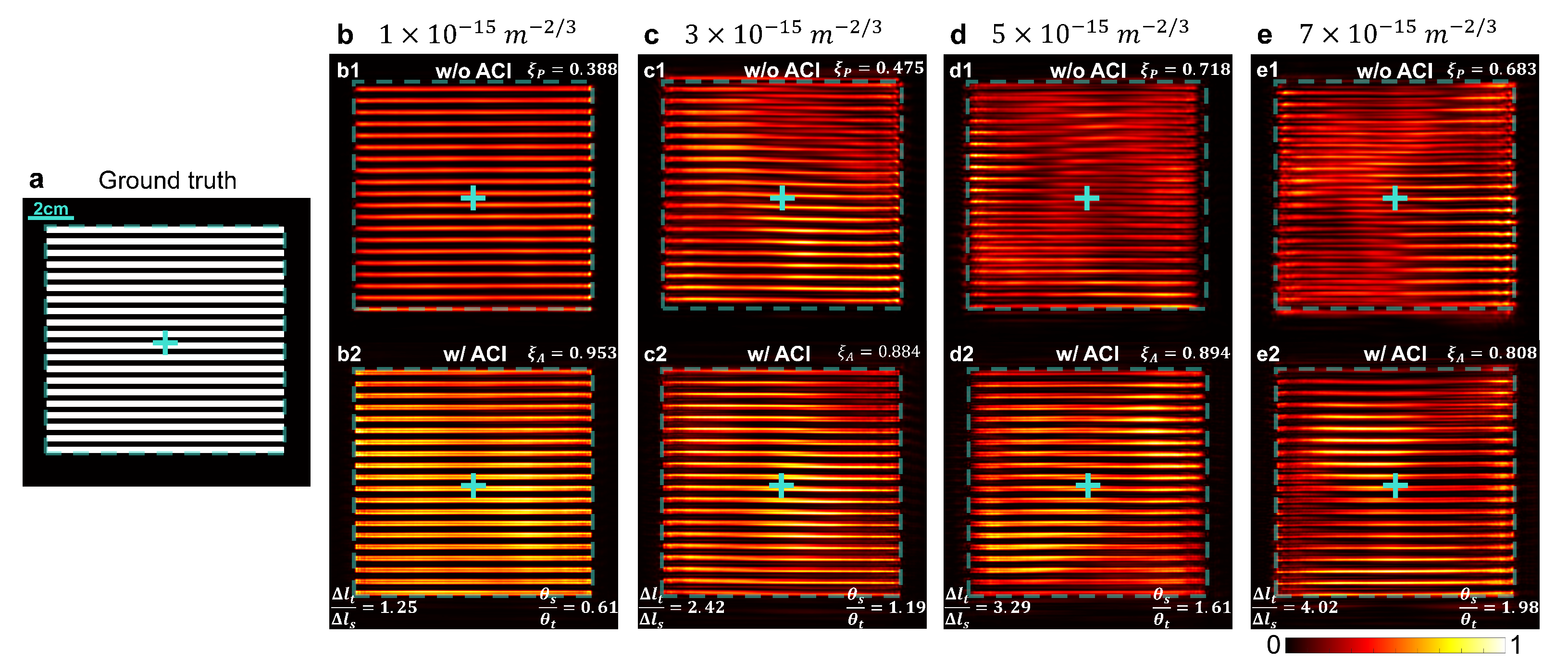
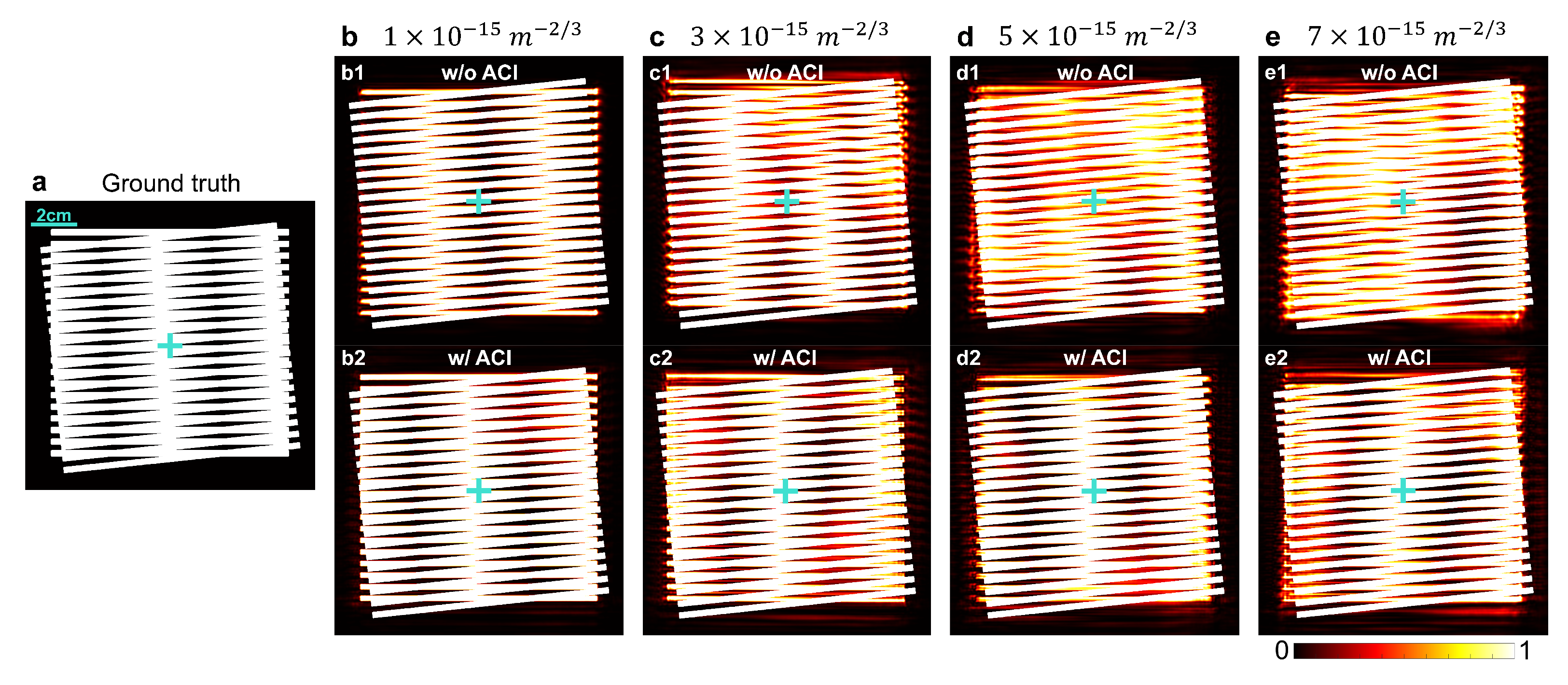
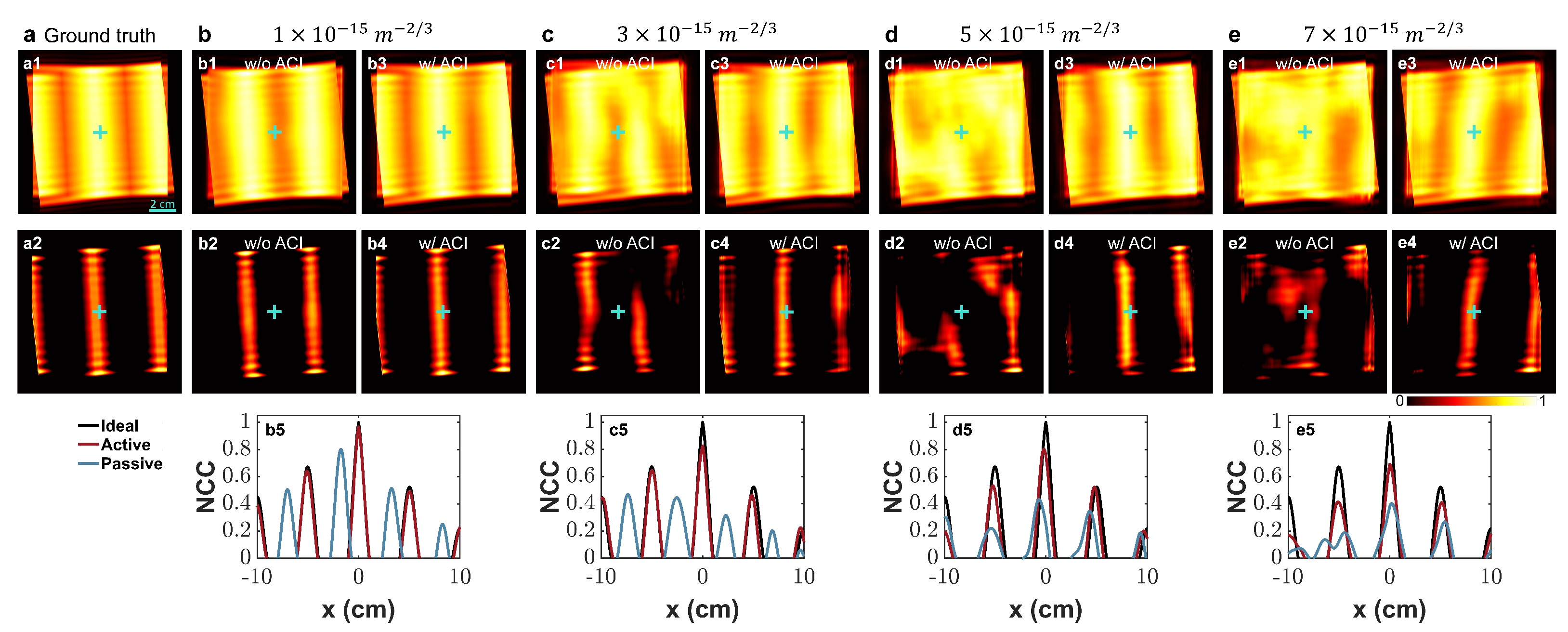
4.1. Performance Across Turbulence Levels
4.2. Filtering and Post-Processing for Fringe Extraction
4.3. Influence of Turbulence on Measurement Accuracy and Displacement Detection
5. Discussion
5.1. Field Deployment and Monitoring
5.2. Atmospheric Distortion and ACI Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oster, G.; Nishijima, Y. Moiré patterns. Sci. Am. 1963, 208, 54–63. [Google Scholar] [CrossRef]
- Shao, J.; Ding, Y.; Tian, H.; Li, X.; Li, X.; Liu, H. Digital moiré fringe measurement method for alignment in imprint lithography. Opt. Laser Technol. 2012, 44, 446–451. [Google Scholar] [CrossRef]
- Xiao, X.; Kang, Y.; Hou, Z.; Qiu, W.; Li, X.; Li, X. Displacement and strain measurement by circular and radial gratings moiré method. Exp. Mech. 2010, 50, 239–244. [Google Scholar] [CrossRef]
- Khurana, R.K. Moiré patterns in nanomaterials. Mater. Sci. Semicond. Process. 2022, 140, 106406. [Google Scholar] [CrossRef]
- Tang, H.; Ni, X.; Du, F.; Srikrishna, V.; Mazur, E. On-chip light trapping in bilayer moiré photonic crystal slabs. Appl. Phys. Lett. 2022, 121, 231101. [Google Scholar] [CrossRef]
- Alagappan, G.; Png, C.E. Dense and sharp resonance peaks in stretched moiré waveguides. Phys. Rev. A 2024, 110, 033516. [Google Scholar] [CrossRef]
- Bezryadina, A.; Zhao, J.; Xia, Y.; Zhang, X.; Liu, Z. High spatiotemporal resolution imaging with localized plasmonic structured illumination microscopy. ACS Nano 2018, 12, 8248–8254. [Google Scholar] [CrossRef]
- Schirripa Spagnolo, G.; Ambrosini, D.; Paoletti, D. Liquid diffusion coefficients by digital moiré. Opt. Eng. 2004, 43, 798–805. [Google Scholar]
- Huyeh, M.R.; Goudarzi, P.; Rasouli, S. Study of thermal conductivity of nano-fluids containing gold nanoparticles using moiré deflectometry. Int. J. Green Nanotechnol. 2012, 4, 385–388. [Google Scholar] [CrossRef]
- Zhao, J.; Hou, Y.; Liu, Z.; Xie, H.; Liu, S. Modified color CCD moiré method and its application in optical distortion correction. Precis. Eng. 2020, 65, 279–286. [Google Scholar] [CrossRef]
- Bryngdahl, O. Moiré: Formation and interpretation. J. Opt. Soc. Am. 1974, 64, 1287–1294. [Google Scholar] [CrossRef]
- Post, D.; Han, B.; Ifju, P. High Sensitivity Moiré: Experimental Analysis for Mechanics and Materials; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Amidror, I. The Theory of the Moiré Phenomenon: Volume I: Periodic Layers; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 38. [Google Scholar]
- Pan, B.; Xie, H.; Kishimoto, S.; Xing, Y. Experimental study of moiré method in laser scanning confocal microscopy. Rev. Sci. Instruments 2006, 77, 045101. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.; Xie, H.; Wu, D. Novel 3D SEM moiré method for micro height measurement. Opt. Express 2013, 21, 15734–15746. [Google Scholar] [CrossRef]
- Tang, S.; Wang, H.; Wang, H.S.; Sun, Q.; Zhang, X.; Cong, C.; Xie, H.; Liu, X.; Zhou, X.; Huang, F.; et al. Silane-catalysed fast growth of large single-crystalline graphene on hexagonal boron nitride. Nat. Commun. 2015, 6, 6499. [Google Scholar] [CrossRef] [PubMed]
- Takasaki, H. Moiré topography. Appl. Opt. 1970, 9, 1467–1472. [Google Scholar] [CrossRef]
- Adler, N.S.; Csongradi, J.; Bleck, E.E. School screening for scoliosis—one experience in California using clinical examination and moiré photography. West. J. Med. 1984, 141, 631. [Google Scholar]
- Rossler, T.; Hrabovsky, M.; Pochmon, M. Moiré methods for measurement of displacement and topography. Czechoslov. J. Phys. 2006, 56, 101–124. [Google Scholar] [CrossRef]
- Porto, F.; Gurgel, J.L.; Russomano, T.; Farinatti, P.D.T.V. Moiré topography: Characteristics and clinical application. Gait Posture 2010, 32, 422–424. [Google Scholar] [CrossRef]
- Breque, C.; Dupre, J.C.; Bremand, F. Calibration of a system of projection moiré for relief measuring: Biomechanical applications. Opt. Lasers Eng. 2004, 41, 241–260. [Google Scholar] [CrossRef]
- Yilan, K.; Hua, L. Investigation of near-tip displacement fields of a crack normal to and terminating at a bimaterial interface under mixed-mode loading. Eng. Fract. Mech. 2002, 69, 2199–2208. [Google Scholar] [CrossRef]
- Savalia, P.C.; Tippur, H.V. A study of crack–inclusion interactions and matrix–inclusion debonding using moiré interferometry and finite element method. Exp. Mech. 2007, 47, 533–547. [Google Scholar] [CrossRef]
- Mollenhauer, D.; Iarve, E.V.; Kim, R.; Langley, B. Examination of ply cracking in composite laminates with open holes: A moiré interferometric and numerical study. Compos. Part A Appl. Sci. Manuf. 2006, 37, 282–294. [Google Scholar] [CrossRef]
- Shrotriya, P.; Sottos, N.R. Local time—Temperature-dependent deformation of a woven composite. Exp. Mech. 2004, 44, 336–353. [Google Scholar]
- Chen, K.; Rajeeva, B.B.; Wu, Z.; Rukavina, M.; Dao, T.D.; Ishii, S.; Aono, M.; Nagao, T.; Zheng, Y. Moiré nanosphere lithography. ACS Nano 2015, 9, 6031–6040. [Google Scholar] [CrossRef] [PubMed]
- Cadarso, V.J.; Chosson, S.; Sidler, K.; Hersch, R.D.; Brugger, J. High-resolution 1D moirés as counterfeit security features. Light. Sci. Appl. 2013, 2, e86. [Google Scholar] [CrossRef]
- Ragulskis, K.; Maskeliunas, R.; Zubavičius, L. Analysis of structural vibrations using time averaged shadow moiré. J. Vibroeng. 2006, 8, 267–275. [Google Scholar]
- Ezazshahabi, N.; Latifi, M.; Madanipour, K. Surface roughness assessment of woven fabrics using fringe projection moiré techniques. Fibres Text. East. Eur. 2015, 23, 76–84. [Google Scholar] [CrossRef]
- Khanna, S.K.; He, C.; Agrawal, H.N. Residual stress measurement in spot welds and the effect of fatigue loading on redistribution of stresses using high sensitivity moiré interferometry. J. Eng. Mater. Technol. 2001, 123, 132–138. [Google Scholar] [CrossRef]
- Prabhakara, V.; Jannis, D.; Béché, A.; Bender, H.; Verbeeck, J. Strain measurement in semiconductor FinFET devices using a novel moiré demodulation technique. Semicond. Sci. Technol. 2020, 35, 034002. [Google Scholar] [CrossRef]
- Kishimoto, S.; Egashira, M.; Shinya, N. Microcreep deformation measurements by a moiré method using electron beam lithography and electron beam scan. Opt. Eng. 1993, 32, 522–526. [Google Scholar] [CrossRef]
- Ri, S.; Fujigaki, M.; Morimoto, Y. Sampling moiré method for accurate small deformation distribution measurement. Exp. Mech. 2010, 50, 501–508. [Google Scholar] [CrossRef]
- Han, B. Micromechanical deformation analysis of beta alloy titanium in elastic and elastic/plastic tension. Exp. Mech. 1996, 36, 120–126. [Google Scholar] [CrossRef]
- Bastawros, A.F.; Kim, K.S. Experimental analysis of near-crack-tip plastic flow and deformation characteristics (I): Polycrystalline aluminum. J. Mech. Phys. Solids 2000, 48, 67–98. [Google Scholar] [CrossRef]
- Meadows, D.M.; Johnson, W.O.; Allen, J.B. Generation of surface contours by moiré patterns. Appl. Opt. 1970, 9, 942–947. [Google Scholar] [CrossRef]
- Tsuruta, T.; Itoh, Y.; Anzai, S. Moiré topography for the measurement of film flatness. Appl. Opt. 1970, 9, 2802–2804. [Google Scholar] [CrossRef]
- Bian, Y.; Zhang, P.; Wang, J.; Wang, C.; Pu, S. Learning multiple explainable and generalizable cues for face anti-spoofing. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 2310–2314. [Google Scholar]
- Wu, J.; Zhou, T.T.; Yuan, B.; Wang, L.Q. A digital moiré fringe method for displacement sensors. Front. Inf. Technol. Electron. Eng. 2016, 17, 946–953. [Google Scholar] [CrossRef]
- Rasouli, S.; Esmaeili, S.; Sobouti, F. Design and construction of a seismometer based on the moiré technique: Detailed theoretical analysis, experimental apparatus, and primary results. Int. J. Opt. Photonics 2016, 10, 3–10. [Google Scholar]
- Bemelmans, M.J.W.; Biggs, J.; Poland, M.; Wookey, J.; Ebmeier, S.K.; Diefenbach, A.K.; Syahbana, D. High-resolution InSAR reveals localized pre-eruptive deformation inside the crater of Agung Volcano, Indonesia. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025669. [Google Scholar] [CrossRef]
- Salzer, J.T.; Nikkhoo, M.; Walter, T.R.; Sudhaus, H.; Reyes-Dávila, G.; Bretón, M.; Arámbula, R. Satellite radar data reveal short-term pre-explosive displacements and a complex conduit system at Volcán de Colima, Mexico. Front. Earth Sci. 2014, 2, 12. [Google Scholar] [CrossRef]
- Daigle, J.F.; Kamali, Y.; Châteauneuf, M.; Tremblay, G.; Thérèbe, F.; Dubois, J.; Roy, G.; Chin, S.L. Remote sensing with intense filaments enhanced by adaptive optics. Appl. Phys. B 2009, 97, 701–713. [Google Scholar] [CrossRef]
- Shen, H.; Du, L.; Zhang, L.; Gong, W. A blind restoration method for remote sensing images. IEEE Geosci. Remote Sens. Lett. 2012, 9, 1137–1141. [Google Scholar] [CrossRef]
- Wang, J.; Gong, Z.; Liu, X.; Guo, H.; Yu, D.; Ding, L. Object detection based on adaptive feature-aware method in optical remote sensing images. Remote Sens. 2022, 14, 3616. [Google Scholar] [CrossRef]
- Sadatgol, M.; Özdemir, Ş.K.; Yang, L.; Güney, D.Ö. Plasmon injection to compensate and control losses in negative index metamaterials. Phys. Rev. Lett. 2015, 115, 035502. [Google Scholar] [CrossRef] [PubMed]
- Ghoshroy, A.; Özdemir, Ş.K.; Güney, D.Ö. Loss compensation in metamaterials and plasmonics with virtual gain. Opt. Mater. Express 2020, 10, 1862–1880. [Google Scholar] [CrossRef]
- Adams, W.; Sadatgol, M.; Güney, D.Ö. Review of near-field optics and superlenses for sub-diffraction-limited nano-imaging. AIP Adv. 2016, 6, 105123. [Google Scholar] [CrossRef]
- Adams, W.; Sadatgol, M.; Zhang, X.; Güney, D.Ö. Bringing the ‘perfect lens’ into focus by near-perfect compensation of losses without gain media. New J. Phys. 2016, 18, 125004. [Google Scholar] [CrossRef]
- Zhang, X.; Adams, W.; Sadatgol, M.; Güney, D.Ö. Enhancing the resolution of hyperlens by the compensation of losses without gain media. arXiv 2016, arXiv:1607.07466. [Google Scholar] [CrossRef]
- Zhang, X.; Adams, W.; Güney, D.Ö. Analytical description of inverse filter emulating the plasmon injection loss compensation scheme and implementation for ultrahigh-resolution hyperlens. J. Opt. Soc. Am. B Opt. Phys. 2017, 34, 1310–1318. [Google Scholar] [CrossRef]
- Adams, W.; Ghoshroy, A.; Güney, D.Ö. Plasmonic superlens image reconstruction using intensity data and equivalence to structured light illumination for compensation of losses. J. Opt. Soc. Am. B Opt. Phys. 2017, 34, 2161–2168. [Google Scholar] [CrossRef]
- Adams, W.; Ghoshroy, A.; Güney, D.Ö. Plasmonic superlens imaging enhanced by incoherent active convolved illumination. ACS Photonics 2018, 5, 1294–1302. [Google Scholar] [CrossRef]
- Adams, W.; Ghoshroy, A.; Güney, D.Ö. Incoherent active convolved illumination enhances the signal-to-noise ratio for shot noise: Experimental evidence. Phys. Rev. Appl. 2022, 18, 064080. [Google Scholar] [CrossRef]
- Ghoshroy, A.; Adams, W.; Güney, D.Ö. Theory of coherent active convolved illumination for superresolution enhancement. J. Opt. Soc. Am. B Opt. Phys. 2020, 37, 2452–2463. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation Through Random Media; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]
- Ghoshroy, A.; Davis, J.; Moazzam, A.A.; Askari, R.; Güney, D.Ö. Enhancing complex light beam propagation in turbulent atmosphere with active convolved illumination. ACS Photonics 2024, 11, 4541–4558. [Google Scholar] [CrossRef]
- Moazzam, A.A.; Ghoshroy, A.; Askari, R.; Güney, D.Ö. Active convolved illumination towards enhanced remote sensing through a turbulent atmosphere. In Proceedings of the AGU 2023, San Francisco, CA, USA, 11–15 December 2023; p. S11F-0322. [Google Scholar]
- Burlini, L.; Vinciguerra, S.; Di Toro, G.; De Natale, G.; Meredith, P.; Burg, J.P. Seismicity preceding volcanic eruptions: New experimental insights. Geology 2007, 35, 183–186. [Google Scholar] [CrossRef]
- Rodean, H.C. Inelastic processes in seismic wave generation by underground explosions. In Identification of Seismic Sources—Earthquake or Underground Explosion: Proceedings of the NATO Advance Study Institute Held at Voksenåsen, Oslo, Norway, 8–18 September 1980; Springer: Berlin/Heidelberg, Germany, 1981; pp. 97–189. [Google Scholar]
- Gudmundsson, A. Toughness and failure of volcanic edifices. Tectonophysics 2009, 471, 27–35. [Google Scholar] [CrossRef]
- Coughlin, M.; Harms, J. Seismic topographic scattering in the context of GW detector site selection. Class. Quantum Gravity 2012, 29, 075004. [Google Scholar] [CrossRef]
- Berni, A.J. Remote sensing of seismic vibrations by laser Doppler interferometry. Geophysics 1994, 59, 1856–1867. [Google Scholar] [CrossRef]
- Meyer-Arendt, J.R. Introduction to Classical and Modern Optics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Stanbridge, A.B.; Ewins, D.J.; Khan, A.Z. Modal testing using impact excitation and a scanning LDV. Shock Vib. 2000, 7, 91–100. [Google Scholar] [CrossRef]
- Rapstine, T.; Sava, P.; Arias, E. Airborne seismic data acquisition using stereo vision. J. Unmanned Veh. Syst. 2017, 6, 31–42. [Google Scholar] [CrossRef]
- Rapstine, T.D. Towards Airborne Measurements of Ground Displacement; Colorado School of Mines: Golden, CO, USA, 2020. [Google Scholar]
- Bock, Y.; Nikolaidis, R.M.; de Jonge, P.J.; Bevis, M. Instantaneous geodetic positioning at medium distances with the Global Positioning System. J. Geophys. Res. Solid Earth 2000, 105, 28223–28253. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Kouba, J. Measuring seismic waves induced by large earthquakes with GPS. Stud. Geophys. Et Geod. 2003, 47, 741–755. [Google Scholar] [CrossRef]
- Geng, T.; Xie, X.; Fang, R.; Su, X.; Zhao, Q.; Liu, G.; Li, H.; Shi, C.; Liu, J. Real-time capture of seismic waves using high-rate multi-GNSS observations: Application to the 2015 Mw 7.8 Nepal earthquake. Geophys. Res. Lett. 2016, 43, 161–167. [Google Scholar] [CrossRef]
- Garthwaite, M.C.; Miller, V.L.; Saunders, S.; Parks, M.M.; Hu, G.; Parker, A.L. A simplified approach to operational InSAR monitoring of volcano deformation in low-and middle-income countries: Case study of Rabaul Caldera, Papua New Guinea. Front. Earth Sci. 2019, 6, 240. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D.; Lu, Z. Remote sensing of volcanic processes and risk. Remote Sens. 2020, 12, 2567. [Google Scholar] [CrossRef]
- Di Traglia, F.; Calvari, S.; D’Auria, L.; Nolesini, T.; Bonaccorso, A.; Fornaciai, A.; Esposito, A.; Cristaldi, A.; Favalli, M.; Casagli, N. The 2014 effusive eruption at Stromboli: New insights from in situ and remote-sensing measurements. Remote Sens. 2018, 10, 2035. [Google Scholar] [CrossRef]
- Kuraoka, S.; Nakashima, Y.; Doke, R.; Mannen, K. Monitoring ground deformation of eruption center by ground-based interferometric synthetic aperture radar (GB-InSAR): A case study during the 2015 phreatic eruption of Hakone volcano. Earth Planets Space 2018, 70, 1–9. [Google Scholar] [CrossRef]
- Huebner, C.S. A profiling scheme for algorithms and applications to enable a methodological evaluation of turbulence mitigation methods. In Proceedings of the Environmental Effects on Light Propagation and Adaptive Systems III; SPIE: Bellingham, WA, USA, 2020; Volume 11532, pp. 107–117. [Google Scholar]
- Xu, F.; Chang, S.; Zhao, Y.; Li, W.; Xia, H. High-precision moiré alignment method using centrosymmetric grating for 3D interlayer interconnect. Opt. Lasers Eng. 2023, 171, 107815. [Google Scholar] [CrossRef]
- Cox, M.A.; Mphuthi, N.; Nape, I.; Mashaba, N.; Cheng, L.; Forbes, A. Structured light in turbulence. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 1–21. [Google Scholar] [CrossRef]
- Deledalle, C.A.; Gilles, J. Blind atmospheric turbulence deconvolution. IET Image Process. 2020, 14, 3422–3432. [Google Scholar] [CrossRef]
- Chen, G.; Gao, Z.; Wang, Q.; Luo, Q. Blind de-convolution of images degraded by atmospheric turbulence. Appl. Soft Comput. 2020, 89, 106131. [Google Scholar] [CrossRef]
- Mao, Z.; Jaiswal, A.; Wang, Z.; Chan, S.H. Single frame atmospheric turbulence mitigation: A benchmark study and a new physics-inspired transformer model. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 430–446. [Google Scholar]
- Jin, D.; Chen, Y.; Lu, Y.; Chen, J.; Wang, P.; Liu, Z.; Guo, S.; Bai, X. Neutralizing the impact of atmospheric turbulence on complex scene imaging via deep learning. Nat. Mach. Intell. 2021, 3, 876–884. [Google Scholar] [CrossRef]
- Schmidt, J.D. Numerical Simulation of Optical Wave Propagation with Examples in Matlab; SPIE Press: Bellingham, WA, USA, 2010. [Google Scholar]
- Ke, X.; Wang, J. Generation, Transmission, Detection, and Application of Vortex Beams; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Chen, J.; Kong, L.; Zhan, Q. Demonstration of a vectorial optical field generator with adaptive close loop control. Rev. Sci. Instruments 2017, 88, 125101. [Google Scholar] [CrossRef]
- Liu, J.; Wang, P.; Zhang, X.; He, Y.; Zhou, X.; Ye, H.; Li, Y.; Xu, S.; Chen, S.; Fan, D. Deep learning based atmospheric turbulence compensation for orbital angular momentum beam distortion and communication. Opt. Express 2019, 27, 16671–16688. [Google Scholar] [CrossRef]
- Hua, X.; Pan, C.; Shi, Y.; Liu, J.; Hong, H. Removing atmospheric turbulence effects via geometric distortion and blur representation. IEEE Trans. Geosci. Remote Sens. 2020, 60, 1–13. [Google Scholar] [CrossRef]
- Maulik, R.; San, O. A neural network approach for the blind deconvolution of turbulent flows. J. Fluid Mech. 2017, 831, 151–181. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Soltani, S.; Wong, A.K. A survey of thresholding techniques. Comput. Vision Graph. Image Process. 1988, 41, 233–260. [Google Scholar] [CrossRef]
- Moufti, M.R.; Németh, K.; Moufti, M.R.; Németh, K. Harrat Rahat: The geoheritage value of the youngest long-lived volcanic field in the Kingdom of Saudi Arabia. In Geoheritage of Volcanic Harrats in Saudi Arabia; Springer: Berlin/Heidelberg, Germany, 2016; pp. 33–120. [Google Scholar]
- Tunick, A.; Tikhonov, N.; Vorontsov, M.; Carhart, G. Characterization of Optical Turbulence (Cn2) Data Measured at the ARL A_LOT Facility; US Army Research Laboratory: Adelphi, MD, USA, 2005. [Google Scholar]
- Walters, D.; Kunkel, K. Atmospheric modulation transfer function for desert and mountain locations: The atmospheric effects on r 0. J. Opt. Soc. Am. 1981, 71, 397–405. [Google Scholar] [CrossRef]
- Liu, H.; Yuan, R.; Mei, J.; Sun, J.; Liu, Q.; Wang, Y. Scale properties of anisotropic and isotropic turbulence in the urban surface layer. Bound.-Layer Meteorol. 2017, 165, 277–294. [Google Scholar] [CrossRef]
- Serafin, S.; Adler, B.; Cuxart, J.; De Wekker, S.F.; Gohm, A.; Grisogono, B.; Kalthoff, N.; Kirshbaum, D.J.; Rotach, M.W.; Schmidli, J.; et al. Exchange processes in the atmospheric boundary layer over mountainous terrain. Atmosphere 2018, 9, 102. [Google Scholar] [CrossRef]
- Finnigan, J. Turbulence in plant canopies. Annu. Rev. Fluid Mech. 2000, 32, 519–571. [Google Scholar] [CrossRef]
- Cherubini, T.; Businger, S.; Lyman, R.; Chun, M. Modeling optical turbulence and seeing over Mauna Kea. J. Appl. Meteorol. Climatol. 2008, 47, 1140–1155. [Google Scholar] [CrossRef]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H. Restormer: Efficient transformer for high-resolution image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5728–5739. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moazzam, A.A.; Ghoshroy, A.; Güney, D.Ö.; Askari, R. Remote Sensing of Seismic Signals via Enhanced Moiré-Based Apparatus Integrated with Active Convolved Illumination. Remote Sens. 2025, 17, 2032. https://doi.org/10.3390/rs17122032
Moazzam AA, Ghoshroy A, Güney DÖ, Askari R. Remote Sensing of Seismic Signals via Enhanced Moiré-Based Apparatus Integrated with Active Convolved Illumination. Remote Sensing. 2025; 17(12):2032. https://doi.org/10.3390/rs17122032
Chicago/Turabian StyleMoazzam, Adrian A., Anindya Ghoshroy, Durdu Ö. Güney, and Roohollah Askari. 2025. "Remote Sensing of Seismic Signals via Enhanced Moiré-Based Apparatus Integrated with Active Convolved Illumination" Remote Sensing 17, no. 12: 2032. https://doi.org/10.3390/rs17122032
APA StyleMoazzam, A. A., Ghoshroy, A., Güney, D. Ö., & Askari, R. (2025). Remote Sensing of Seismic Signals via Enhanced Moiré-Based Apparatus Integrated with Active Convolved Illumination. Remote Sensing, 17(12), 2032. https://doi.org/10.3390/rs17122032





