Abstract
Intrinsic parameter estimation by self-calibration is commonly used in Unmanned aerial vehicle (UAV)-based photogrammetry with Structure from Motion (SfM). However, obtaining stable estimates of these parameters from image-based SfM—which relies solely on images, without auxiliary data such as ground control points (GCPs)—remains challenging. Aerial imagery acquired with the constant-pitch (CP) flight pattern often exhibits non-linear deformations, highly unstable intrinsic parameters, and even alignment failures. We hypothesize that CP flights form a “critical configuration” that renders certain intrinsic parameters indeterminate. Through numerical experiments, we confirm that a CP flight configuration does not provide sufficient constraints to estimate focal length (f) and the principal point coordinate (cy) in image-based SfM. Real-world CP datasets further demonstrate the pronounced instability of these parameters. As a remedy, we show that by introducing intermediate strips into the CP flight plan—what we call a CP-Plus flight—can effectively mitigate the indeterminacy of f and cy in simulations and markedly improve their stability in all tested cases. This approach enables more effective image-only SfM workflows without auxiliary data, simplifies data acquisition, and improves three-dimensional reconstruction accuracy.
1. Introduction
Unmanned aerial vehicle (UAV)-based photogrammetry has emerged recently as an effective technique to generate high-resolution three-dimensional (3D) models across multiple fields including infrastructure inspection [1,2,3], mining surveying [4,5,6], hazard modeling [7,8,9], and environmental condition monitoring [10,11]. Structure from Motion (SfM) underpins this technique, estimating intrinsic and extrinsic camera parameters. These parameters are then exploited in the Multi-View Stereo (MVS) to produce dense point clouds, enabling the generation of high-resolution deliverables, such as meshes, digital elevation models (DEMs), and orthophotos. Therefore, the precision of camera parameter estimation in SfM has a direct effect on the accuracy and precision of reconstructed models. While the accurate estimation of these parameters relies hardly on the number and distribution of auxiliary information such as Ground Control Points (GCPs), it is cost-intensive and time-consuming. Ensuring accurate parameter estimation without a heavy reliance on GCPs remains a primary concern for UAV-based photogrammetry.
Intrinsic parameters—such as focal length (f), principal point coordinates (cx, cy), radial distortion, and tangential distortion—can be estimated during the bundle adjustment (BA) stage in a typical SfM pipeline (self-calibration), or alternatively, calculated using imagery captured specially for calibration purposes (pre-calibration). However, in UAV-based photogrammetry, where lightweight and compact drones with small cameras are commonly used, pre-calibrated intrinsic parameters are often considered unstable [12,13,14,15]. This instability can arise from mechanical effects during camera shooting, changes in image sensor temperature [16,17,18], or ambient temperature [19] during drone operations, potentially affecting the sensor geometry. Therefore, self-calibration has become the preferred approach for estimating these intrinsic parameters. By eliminating GCP surveys and dedicated calibration processes, self-calibration using image-based SfM significantly reduces fieldwork time and cost, enabling rapid, cost-effective surveys even in remote or hazardous areas.
A widely employed image acquisition method in UAV-based photogrammetry is the constant-pitch (CP) flight [18,20,21,22,23,24], where the optical axes of images within the same strip are parallel. In this flight design (Figure 1), the camera is tilted at a fixed pitch angle along the flight lines, and when drones fly in the opposing direction, the local convergence is achieved, thereby facilitating 3D reconstruction.
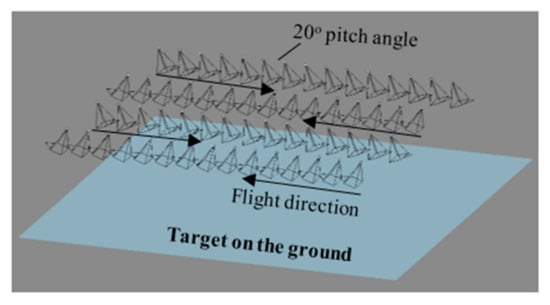
Figure 1.
Constant-pitch flight at 20° pitch angle.
SfM using CP-based images has been reported to perform well when the camera positions measured by RTK-GNSS are incorporated in BA [21,23]. However, when camera position measurements are unavailable, referred to as image-based SfM, the performance of SfM becomes notably unstable. Sanz-Ablanedo et al. [18] reported poor image-based SfM performance using CP flight images captured at a 25° pitch angle, highlighting non-linear deformation (the dome effect). Their study also noted large mean vertical errors at validation points located at the four corners of the model, which can be caused by inaccuracy in the estimation of focal length (f). Similarly, Kon et al. [25] reported dome errors accompanied with large root mean square (RMS) errors of all validation points, and in some cases, alignment failures across various SfM analysis settings (1500 trials) for images captured by CP flights at a 20° pitch angle. For these 1500 SfM trials, the standard deviation of f and cy were notably large: 209 pixels and 84 pixels for the Phantom 4 RTK drone camera, and 53 pixels and 36 pixels for the SONY α7 III drone camera, respectively (unpublished). Observations of large mean vertical errors at validation points and alignment failures, coupled with the instability in estimations of f and cy, suggest that factors beyond the dome effect may contribute to the poor performance of image-based SfM. Despite these observations, the root causes of this instability have not been thoroughly investigated.
It has been mathematically shown that certain combinations of camera motion and scene geometry, known as critical configurations, can introduce indeterminacy into the bundle adjustment with self-calibration [26]. We suspected that the instability of camera parameters observed in image-based SfM under CP flights [21,23,27] stems from such critical configurations, leading to inaccurate or even incorrect model reconstructions.
Therefore, the objectives of this study are:
- (a)
- To investigate the indeterminacy of two basic intrinsic parameters f and cy, which showed significant instabilities in the previous experiment as described above [25].
- (b)
- To validate these numerical findings using real datasets acquired at three different ground sampling distances (GSDs).
- (c)
- To discuss a practical mitigation strategy to stabilize intrinsic parameter estimation.
By bridging the theoretical–practical gap, we aim to provide a reliable UAV-SfM workflow without auxiliary information.
2. Materials and Methods
2.1. Fundamental of Self-Calibration in SfM
Suppose three 3D ground points P, T, and U that are visible in multiple images captured from different viewpoints (cameras A, B, and C), as shown in Figure 2. For the camera considered in this study, the geometric relationship between a 3D point and its 2D projection on each image is described by collinearity equations as follows:
where:
- (x, y): image coordinates of the projection of ground point.
- (X, Y, Z): object space coordinates of the ground point.
- (X0, Y0, Z0): object space coordinates of the camera projection center.
- cy: y-coordinate of the principal point in the image.
- f: camera focal length.
- α1i, α2i, α3i (i = 1, 2, 3): elements of the rotation matrix formed by three rotation angles.
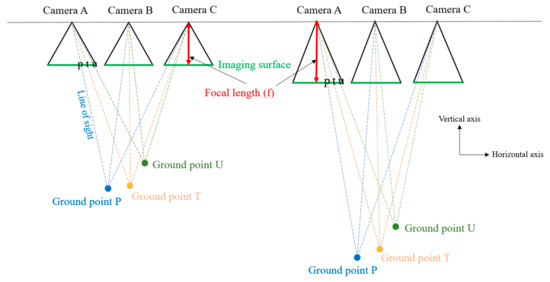
Figure 2.
Example of a critical configuration where the focal length f cannot be determined from parallel shooting images. In this situation, multiple values of f can be estimated, making it impossible to uniquely determine the correct value.
The collinearity equations contain three categories of unknowns:
- Extrinsic parameters: parameters representing relative position and the orientation of each camera.
- Intrinsic parameters: parameters representing the geometric characteristics of the camera, such as focal length and principal points. Note that only two parameters f and cy are considered in this study and in Equation (1).
- Three-dimensional point coordinates: relative coordinates of scene points in object space.
These parameters are estimated simultaneously in the bundle adjustment (BA) of SfM by minimizing the overall reprojection error. The reprojection error of point i onto image j can be expressed as follows:
where (xp, yp) are the 2D projected coordinates computed via the collinearity equations and (xd, yd) are the 2D observed image coordinates of the point.
In SfM, for successful camera estimation, the objective function - root mean square (RMS) reprojection error - must have a unique global minimum. If multiple minima exist, the optimization becomes ambiguous, and SfM fails to produce reliable camera parameters. Parameters with multiple minimizing values are considered indeterminate. In such cases, a specific combination of camera motion and scene geometry that generates images impossible to unique estimation of certain intrinsic parameters is referred to as critical configuration (Figure 2).
2.2. Numerical Experiments
The indeterminacy of f and cy was investigated by analyzing RMS reprojection error, which is the objective function to be minimized at the BA stage in SfM. This was achieved by fixing either f or cy to incorrect values in BA and estimating the other parameters along with extrinsic parameters and tie points. If RMS reprojection error remains nearly unchanged regardless of the input values of f or cy, it indicates that these parameters do not influence the objective function, thereby demonstrating their indeterminacy in SfM.
- (a)
- Synthetic Image Acquisition
We used Blender version 2.79b [28], an open-source computer graphic (CG) software program, to generate a flat plane with the dimensions of 400 m × 400 m and randomly place multiple rectangular parallelepiped objects of various sizes on it. Various random textures with a resolution of 5940 × 8410 pixels were applied to the plane and objects. These textures included local features suitable for matching in SfM, as shown in Figure 3. The details of the associated textures and the Blender project file are provided in the Supplementary Materials.
Figure 3.
Two views of the target used for image acquisition in the numerical experiments: (a) side view; (b) front view.
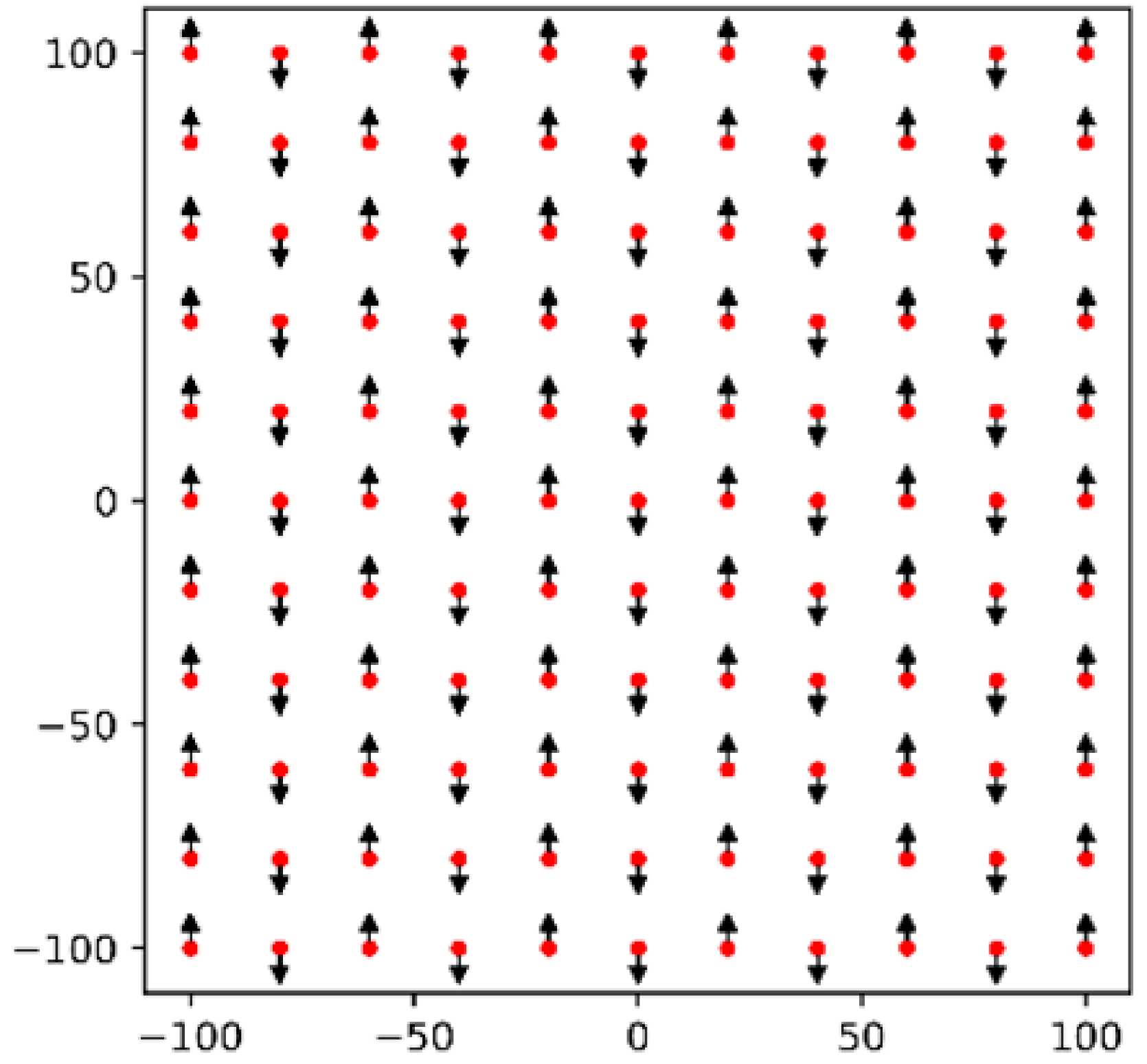
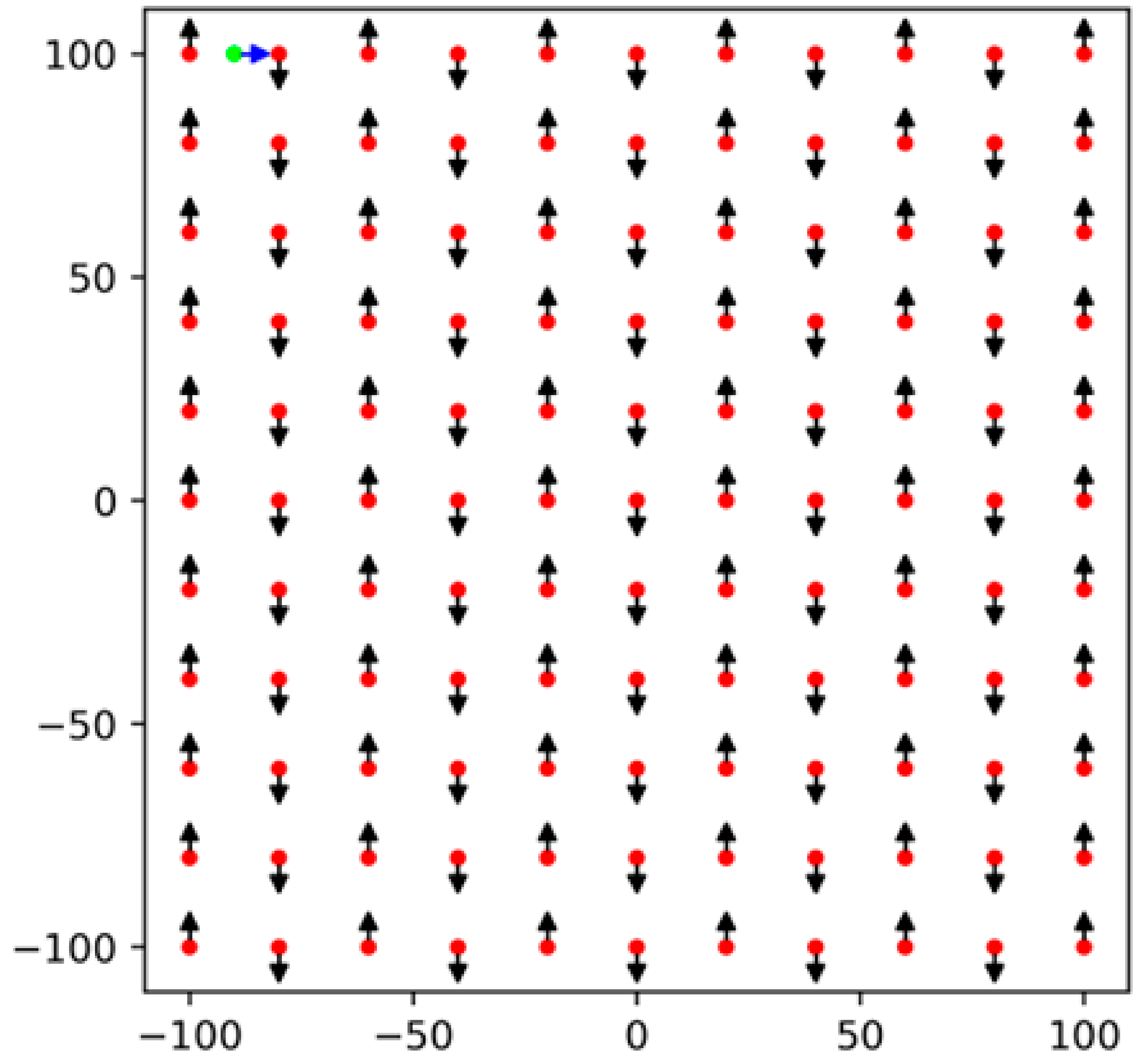
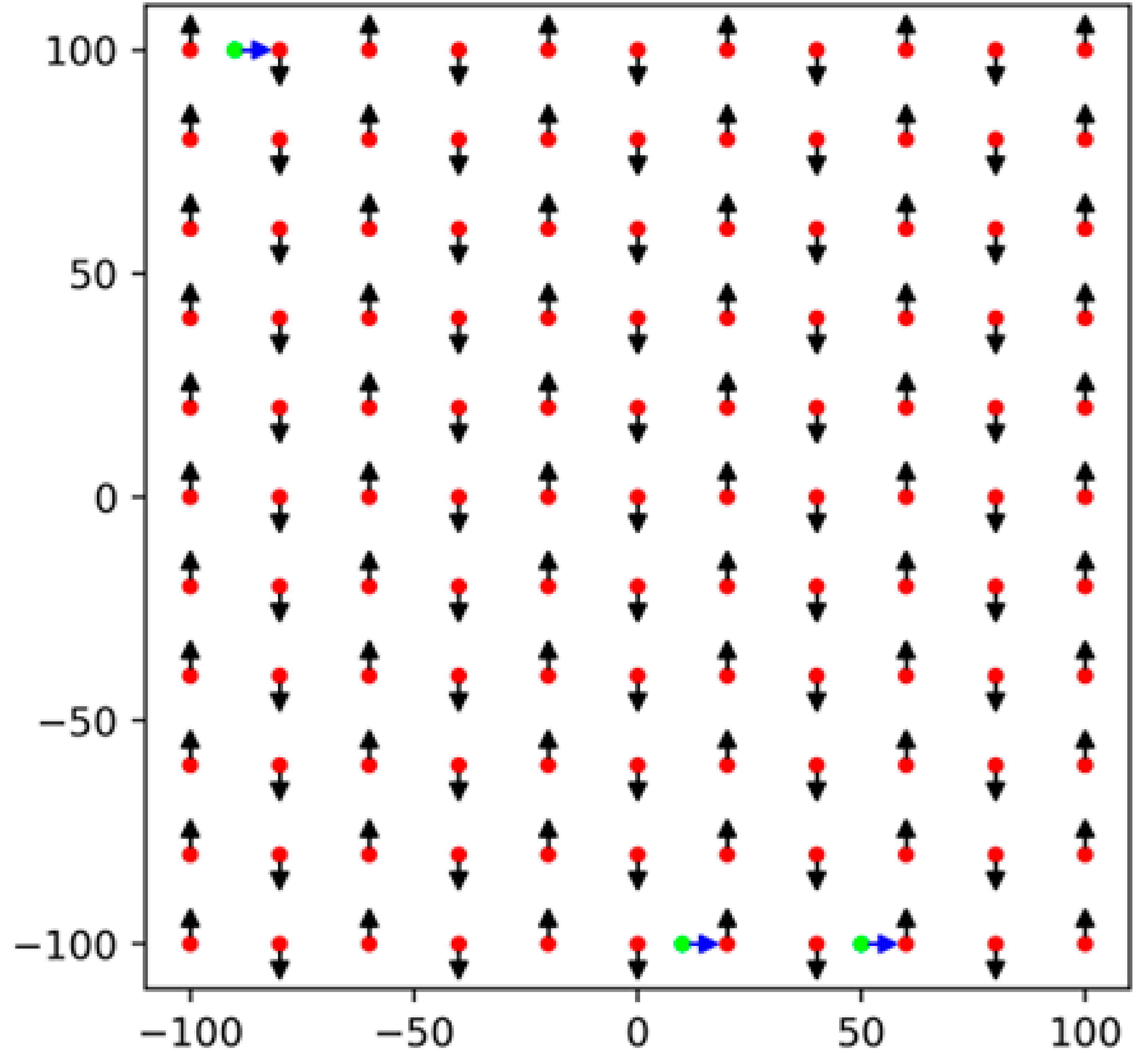
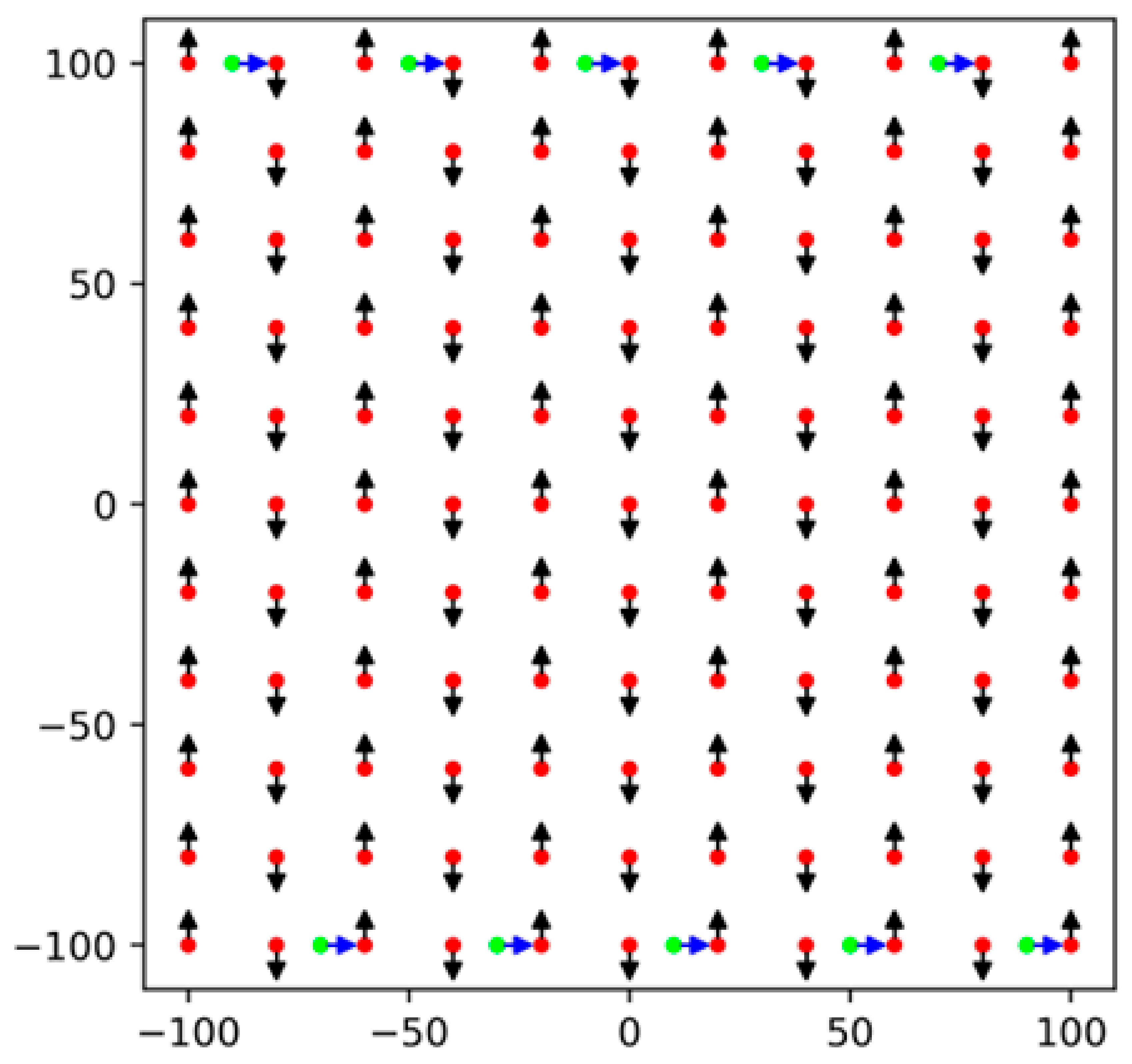
The synthetic image acquisition of the target was performed using the image and camera specifications described in Table 1. In CG space, six image-sets were generated using six different flight designs, divided into two groups: (1) flight designs without an intermediate strip, including CP and CP random, and (2) flight designs with an intermediate strip such as CP flight plus one image in the intermediate strip, the CP flight plus three images randomly placed in the intermediate strip, CP-Plus flight, and CP random plus one image in the intermediate strip. The intermediate strip refers to a short flight path positioned between two primary strips, illustrated as green-blue arrows in Table 2. The pitch angle was set to 20° for all six flight designs, and the flight altitude was fixed at 73 m to achieve a Ground Sample Distance (GSD) of 40 mm. The details of flight designs are provided in Table 2. In this study, a 20° pitch angle was selected based on its proven effectiveness in enhancing UAV-SfM calibration from previous studies [18,24,29,30,31] and its confirmed robustness in SfM accuracy and precision across various analysis settings [21,25]. The indeterminacy of f and cy was examined with this best performing pitch angle, which serves as a representative case for indeterminacy under other pitch angles.

Table 1.
Camera specifications used in CG space.

Table 2.
Descriptions of six image-sets taken by six flight designs in numerical experiments. Black-red arrows indicate image positions along the main flight strips, while green-blue arrows indicate those in the intermediate strips. The arrow size corresponds to the camera pitch angle. In this study, all CP flight designs used a fixed pitch angle of 20 degrees.
- (b)
- SfM Processing
For each simulated image-set created in CG space, SfM was performed using the commercial software Agisoft Metashape version 1.5.5. The SfM workflow (Figure 4) began with “align photos”, followed by bundle adjustment (BA) with the camera parameters effectively fixed to their true values to generate an accurate set of tie points. The settings used are detailed in Table 3.
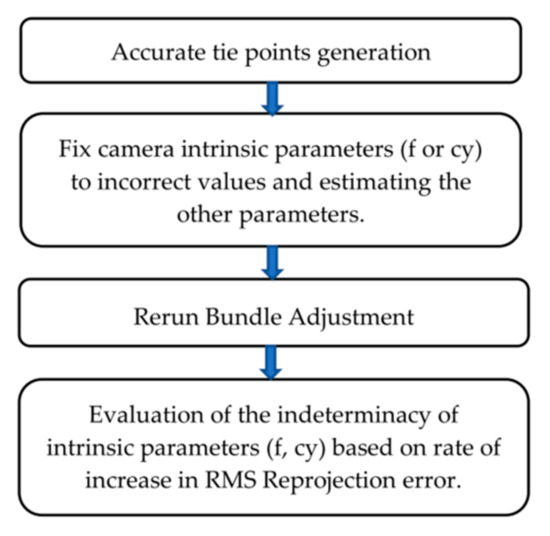
Figure 4.
SfM flow in numerical experiments to evaluate the indeterminacy of each intrinsic parameter (f or cy).

Table 3.
Settings for “Alignment” used to generate accurate tie points.
Based on these tie points, an intrinsic camera parameter (either f or cy) was fixed to values higher than true value (v+) and values lower than true values (v−), while the other parameter (cy or f) was not fixed. Then, BA was rerun. In this process, BA was performed using the previously generated accurate tie points. This approach allowed us to observe the behavior of RMS reprojection error in relation to the fixed intrinsic parameters (f or cy).
- (c)
- Evaluation of The Indeterminacy of Intrinsic Camera Parameters in SfM
To evaluate the indeterminacy of camera intrinsic parameters in SfM, we analyzed the variation in RMS reprojection error between two BA conditions: (1) BA with the intrinsic parameters (f and cy) fixed to their true values and (2) BA with f or cy fixed to incorrect values. The degree of variation was quantified by the rate of increase in RMS reprojection error, which serves as an indicator of how inaccurate intrinsic parameters influence the SfM and helps identify occurrences of their indeterminacy. In principle, the objective function minimized during BA - RMS reprojection error - must have a unique global minimum. The presence of multiple local minima, dependent on different fixed intrinsic parameter values, indicates that the SfM process is unable to uniquely determine these parameters. In such cases, the corresponding intrinsic parameters are considered as indeterminate.
Additionally, fixing either f or cy to incorrect values while estimating the remaining parameter (cy or f, respectively) provides insight into the correlation between f and cy.
The rate of increase in RMS reprojection error is calculated as follows:
where: Rincrease is the rate of increase in RMS reprojection error.
Eincorrect (pixels) is RMS reprojection error when fixing either f or cy to the incorrect values and estimating the remaining parameter in BA.
Etrue (pixels) is RMS reprojection error when fixing both f and cy to true values (1824 and 0 pixels, respectively) in BA.
2.3. Real-Data Analysis
- (a)
- Study Site
The in situ data in this study utilized the data from Truc et al. [23]. These images captured an area of around 100 × 100 m2, located in Tsukubamirai city, Ibaraki prefecture, Japan. This area was constructed for housing purposes. Figure 5 shows the ground condition of the target terrain, mostly bare land covered with short vegetation.

Figure 5.
Distribution of camera positions and validation points at the study site overlaid with orthophotos generated by GSD10 (a), GSD15 (b), GSD20 (c). At each validation point, world coordinates were measured by Aerobo markers (d) with a built-in GNSS receiver.
- (b)
- Image Acquisition
Aerial photos were collected using a high-precision 1-inch 20 MP CMOS camera sensor attached to a lightweight quad-copter UAV (DJI Phantom 4 RTK, hereafter named P4RTK) [32]. The Phantom 4 RTK used for image acquisition was manufactured by DJI, Shenzhen, Guangdong, China. The assembled camera lens has an approximate focal length of 8.8 mm and a mechanical shutter feature that avoids typical rolling shutter problems. This UAV can measure the camera position at the time of exposure by RTK-GNSS (real-time kinematic global navigation satellite system) positioning. A set of nine validation points evenly distributed across the study area (Figure 5) was employed to evaluate the accuracy of the SfM performance using the Aerobo marker [33]. The Aerobo markers used for ground validation were manufactured by Aerobo, Inc., Tokyo, Japan. Each Aerobo marker is equipped with an integrated GNSS receiver, enabling it to record the coordinates at the center of a 24 cm diameter circular target with sub-centimeter accuracy. The red-and-black reflective pattern of the marker is designed to enhance automatic detection by SfM processing software, such as Agisoft Metashape version 1.5.5, which was used in this study.
A flight design similar to the CP-Plus flight design was adopted for data acquisition. This flight pattern was generated using the 3D photogrammetry preset feature in the P4RTK system to capture images at two-second intervals and record camera coordinates via RTK-GNSS during image capture. In these CP-Plus flights, the camera was tilted at a fixed pitch angle of 20° along the flight lines, and the consecutive images with yaw angle deviation over 10° from the main flight line, taken during the drone rotation, were referred to as the intermediate strips. They were removed to simulate three CP flights (Figure 6).
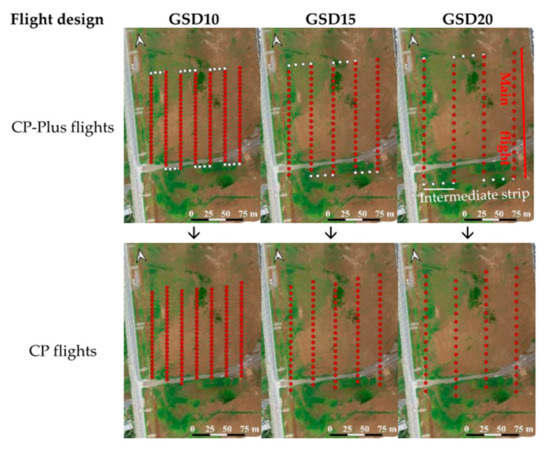
Figure 6.
Generation of CP flights from CP-Plus flights used in real-data analysis (Red dots indicate image positions in the main flight strips, while white dots represent image positions in the intermediate strips.).
In this study, P4RTK was flown at three altitudes of 73, 55, and 36 m above ground level (at the drone’s home point), which yielded three GSDs of 20, 15, and 10 mm, respectively. All photographs were captured along parallel flight lines with an overlap ratio of 80% forward and 60% side lap when the camera’s optical axis was oriented toward nadir. The details of the image-sets used in the real-data analysis are described in Table 4.

Table 4.
Summary of three CP-Plus flights acquired by P4RTK and three generated CP flights in real-data analysis.
- (c)
- SfM Processing
For each image-set, SfM was performed following the “align photos” in Agisoft Metashape version 1.5.5 software. In this process, camera parameters were estimated by using images only, then the point clouds were georeferenced using projection centers recorded by an RTK-GNSS receiver embedded in the images taken by P4RTK. The absolute coordinates of the validation points evaluated by multi-view triangulation using camera parameters estimated in SfM were used to validate the accuracy of the SfM-derived model, in accordance with the nine validation points. It is worth noting that in this study, self-calibration was performed using images only, without additional information.
SfM was tested through a combination of SfM analysis settings summarized in Table 5, resulting in 30 settings with 50 trials for each image-set listed in Table 4. This analysis was conducted to observe the variation in the estimation of intrinsic parameters under different SfM settings.

Table 5.
Summary of the analysis settings tested in this study.
In order to evaluate the variation of intrinsic parameters estimated in one SfM setting, we used a standard SfM setting repeated 50 times (trials), with the following parameters:
- Size of input images for feature detection: High
- Key point limit: a half (½) of the average number of detectable key points for the input images (35,643).
- Intrinsic parameters considered in Brown models: f, cx, cy, k1–k3, p1–p2.
- (d)
- Intrinsic Parameters Estimation and Error Evaluation.
In this study, we quantified the variation of intrinsic parameter estimation (f and cy), in accordance with the accuracy and precision of SfM for each image-set. The accuracy and precision of SfM were evaluated using the RMS error of all nine validation points for each analysis setting, as recommended by James et al. [34]. The validation point error represents the difference between the estimated 3D coordinates of the validation points (calculated through triangulation using camera parameters estimated during the SfM process) and those obtained through static GNSS positioning by Aerobo markers. Additionally, statistical analyses were conducted on the total RMS error (Val_RMSE_T) and the vertical RMS error (Val_RMSE_Z) computed from all validation points for both a standard setting (with 50 trials) and 30 settings such as the maximum value, 75th percentile (Q3), 50th percentile (Q2), and interquartile range (IQR). For each of the 30 settings, the mean values of the estimated f, cy, Val_RMSE_T, and Val_RMSE_Z of all the validation points were first calculated over 50 repeated trials. These mean values were subsequently used to derive the statistical indicators (maximum, Q3, Q2, and IQR), thereby enabling a comparative assessment of SfM accuracy and precision across different settings. Moreover, we evaluated the mean vertical error of all nine validation points (MEZ) for each analysis setting. The mean vertical error is defined as the average difference between the estimated elevation of the validation points (derived using camera parameters estimated by SfM) and the measured elevation of corresponding validation points obtained by Aerobo markers.
3. Results
The results are divided into two main sections: numerical experiments and real-data analysis. In the numerical experiments, we present the verification of the indeterminacy of intrinsic parameters in image-based SfM for six flight designs. The real data analysis focuses on three points: the estimates of camera intrinsic parameters (f, cy) across multiple repetitions of a single SfM setting and in various SfM settings, and the correlation between the estimates of f and the mean vertical error (MEZ) for all validation points.
3.1. Numerical Experiments
This section verifies the indeterminacy of intrinsic parameters in image-based SfM by analyzing six different flight designs. The RMS reprojection error and its rate of increase were analyzed to evaluate the sensitivity of SfM when the intrinsic parameters were fixed to inaccurate values relative to their true values (Figure 7 and Figure 8).
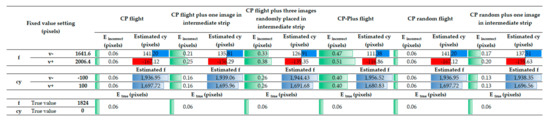
Figure 7.
RMS Reprojection Error and Estimated Parameter Values When Fixing Parameter f or cy to Incorrect Values for Six Flight Designs. Eincorrect: RMS reprojection error when fixing either f or cy to the incorrect values and estimating the remaining parameter in BA. Etrue: RMS reprojection error when fixing both f and cy to true values (1824 and 0 pixels, respectively) in BA. Red and blue indicate the estimated intrinsic parameters (f and cy), while green represents the RMS reprojection error (in pixels). The bar length is scaled relative to the maximum value within each group.

Figure 8.
Rate of Increase in RMS Reprojection Error When Fixing Parameter f or cy to Incorrect Values for Six Flight Designs. Green represents the rate of increase in RMS reprojection error (Rincrease). The bar length is scaled relative to the maximum value in the table.
As shown in Figure 8, the rate of increase in RMS reprojection error was zero for images captured by flight designs without image in the intermediate strip including the CP flight and CP random flight. In contrast, for flight designs with images in the intermediate trip, including the CP flight plus one image in intermediate strip, CP flight plus three images randomly placed in intermediate strip, CP-Plus flight, and CP random plus one image in intermediate strip, the rate of increase in RMS reprojection error ranged from 1.1 to 7.6.
In CP and CP random flight, the RMS reprojection error remained unchanged regardless of whether the intrinsic parameters f or cy were fixed to true or incorrect values in BA. However, in flight designs with images in the intermediate strip, the addition of one image between two flight lines resulted in a noticeable increase in RMS reprojection error. Moreover, when f was fixed to incorrect values, the estimates of cy derived from BA were strongly inaccurate compared to the true value (0), and vice versa (Figure 7).
These results demonstrate that both f and cy are indeterminate in image-based SfM. In CP random flights, where camera positions were randomly distributed compared to CP flights, and the camera orientation remained fixed at 20° forward and backward, the RMS reprojection error remained unchanged regardless of whether the intrinsic parameters were fixed to incorrect or true values. This indicates that altering the shooting positions alone does not resolve the indeterminacy.
In contrast, for flight patterns with at least one image in the intermediate trip, the values of f or cy had a substantial impact on RMS reprojection error, with rates of increase in RMS reprojection error exceeding 7.6 for f and 5.8 for cy (Figure 8). This demonstrates that f and cy become determinable in image-based SfM when at least one image is added to the intermediate strip.
In summary, the numerical experiments showed that the intrinsic parameters f and cy are indeterminate in image-based SfM when using aerial images captured by flight designs without an intermediate strip such as the CP flight design. Adding images to the intermediate short strips effectively resolves the indeterminacy of f and cy.
In the next section, we will evaluate the estimation of intrinsic parameters in image-based SfM using in situ data captured by CP and CP-Plus flights.
3.2. Real-Data Analysis
3.2.1. Estimates of Intrinsic Camera Parameters (f, cy) Across 50 Trials of a Single SfM Setting
Figure 9 presents the results of a standard SfM setting for six image-sets captured at three different GSDs using two flight designs: the CP and CP-Plus. Across 50 repeated trials of a standard SfM setting, the standard deviation in the estimates of intrinsic parameters f and cy was zero for the image-sets taken by the CP-Plus flight design, indicating a highly stable estimation. In contrast, image-sets from the CP flight showed substantial variability with a standard deviation of 0.32 pixels for f and 0.08 pixels for cy. This instability also resulted in a 0.008 m and 0.009 m deviation in the interquartile range (IQR) of total RMS error (Val_RMSE_T) and vertical RMS error (Val_RMSE_Z), respectively.
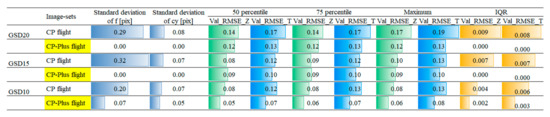
Figure 9.
Intrinsic Parameter Estimation and Statistics of Total RMS Error (Val_RMSE_T) and Vertical RMS Error (Val_RMSE_Z) of All Validation Points for Each Image-Set (One SfM Analysis Setting with 50 Trials). Dark blue represents the standard deviation of the estimated intrinsic parameters (f and cy) in pixels, calculated from 50 trials of one SfM analysis settings. Green and bright blue represent Val_RMSE_Z and Val_RMSE_T, respectively, at the 50th, 75th, and maximum values, calculated from 50 trials of one SfM analysis settings. Orange indicates the interquartile range (IQR) of Val_RMSE_Z and Val_RMSE_T. In all cases, the bar length is scaled relative to the maximum value within each group.
These results demonstrate that the estimation of f and cy is unstable in image-based SfM when using images from the CP flight. However, in the CP-Plus flight, where images were added to the intermediate strips of the CP flight, the estimates of the intrinsic parameters f and cy became more stable, even within a single SfM setting.
3.2.2. Estimates of Intrinsic Camera Parameters (f and cy) Across 30 SfM Settings
The estimates of f and cy in image-based SfM obtained from 30 different SfM settings, each repeated 50 times, exhibited instability (Figure 10). The standard deviation of f ranged from over 1 pixel to 7.3 pixels, while the standard deviation of cy ranged from 0.6 to 3.1 pixels. This instability was particularly pronounced when using images from the CP flight, where the standard deviation was about six times higher for f and five times higher for cy (GSD20 image-sets) compared to those taken by the CP-Plus flight.
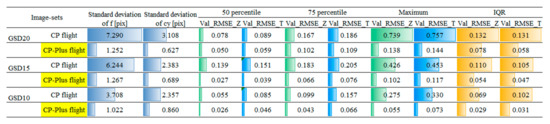
Figure 10.
Intrinsic Parameter Estimation and Statistics of Total RMS Error (Val_RMSE_T) and Vertical RMS Error (Val_RMSE_Z) of All Validation Points for Each Image-Set (30 Analysis Settings). Dark blue represents the standard deviation of the estimated intrinsic parameters (f and cy) in pixels, calculated from 30 SfM analysis settings. Green and bright blue represent Val_RMSE_Z and Val_RMSE_T, respectively, at the 50th, 75th, and maximum values, calculated from 30 SfM analysis settings. Orange indicates the interquartile range (IQR) of Val_RMSE_Z and Val_RMSE_T. In all cases, the bar length is scaled relative to the maximum value within each group.
As shown in Figure 10, the RMS error of all the validation points was substantially higher for image-sets from the CP flight compared to those from the CP-Plus flight. For instance, in GSD15 image-set, the median RMS error of all the validation points (Val_RMSE_T) was 0.151 m, nearly four times greater than the 0.039 m observed for the CP-Plus flight. Similarly, the median vertical RMS error (Val_RMSE_Z) was approximately five times larger for the CP flight (0.139 m) compared to that for the CP-Plus flight (0.027 m). Furthermore, the accuracy and precision of SfM varied considerably across the 30 SfM settings for the CP flight image-sets. The interquartile range (IQR) of the RMS error of all validation points was 0.105 m for CP flights, compared to 0.047 m for CP-Plus flights (GSD15). Similar patterns were observed for image-sets from GSD10 and GSD20.
Overall, the estimates of f and cy were significantly less stable for images captured by CP flights than CP-Plus flights, both across multiple trials of a single setting and across different settings.
3.2.3. Correlation Between the Estimates of f and the Mean Vertical Error for All Validation Points
Theoretically, incorrect estimates of f lead to mean vertical error (MEZ) for all validation points in model reconstruction. As illustrated in Figure 11, a negative correlation was observed between the estimates of f and MEZ across 30 different SfM settings. This relationship can be explained by a simple pin hole camera model: as the estimated f increases, the triangulated ground point moves farther from the camera, causing its estimated vertical coordinate to decrease.
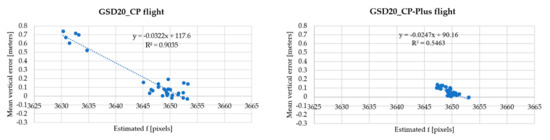
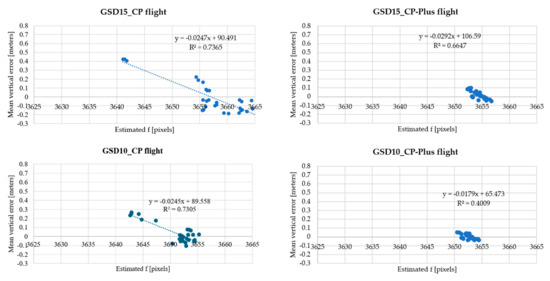
Figure 11.
The correlation between estimated f and mean vertical error (MEZ).
To assess the contribution of vertical error due to incorrect f estimation to the total vertical error, the vertical error ratio was calculated as the proportion of the absolute mean vertical error (MEZ) to the total vertical error of all validation points (Val_RMSE_Z). As shown in Table 6, the average vertical error ratio for each image-set exceeded 80%, indicating that vertical error resulting from incorrect f estimation served as the primary contributor to the total vertical error, regardless of flight design.

Table 6.
Average of Vertical Error Ratio for Each Image-Set (30 SfM Analysis Settings).
In summary, the indeterminacy of intrinsic parameters, especially f and cy, in image-based SfM has been demonstrated using six flight designs in numerical experiments, and its effect has been demonstrated in a real-data analysis using six image-sets. In the next section, we will discuss the implications of these findings on existing studies and suggestions for practical application.
4. Discussion
4.1. Indeterminacy of Intrinsic Camera Parameters in Image-Based SfM
To our knowledge, this study provides the first combined numerical and in situ analysis of the indeterminacy of intrinsic parameters in image-based SfM for CP flights. The numerical experiments show that when images are captured under a CP flight design, f and cy are indeterminable in image-based SfM.
Critical configurations - specific combinations of camera motion and scene geometry - are known to induce intrinsic parameter indeterminacy. Previous studies have extensively documented critical configurations related to linear images (images captured by a pin hole camera without lens distortion) [26,35]. For example, planar motion over general terrain, in which the camera moves on a plane while rotating around an axis normal to that plane, prevents the estimation of a single intrinsic parameter [26].
CP flight represents a restrictive form of planar motion in which the camera’s movement is constrained into a plane, and rotation is limited to only two orientations (pitch and yaw) rather than allowing free rotation around the roll axis. Therefore, it is possible that these additional constraints cause more than one intrinsic parameter to become indeterminate, and in fact, our study confirmed that two parameters (f and cy) became indeterminate for CP flights.
In real CP flight datasets acquired at three different GSDs, we observed significant variations in f and cy across 30 distinct SfM analysis settings and across 50 repeat trials of a single setting. These results demonstrated that the theoretical indeterminacy of intrinsic parameters observed in numerical experiments under ideal conditions manifested in real-world scenarios as pronounced instability.
Our findings suggest that the previously reported poor performance of image-based SfM using CP flight images [18,25] - commonly attributed to the dome effect - is also influenced by the inaccurate estimation of f, which causes large mean vertical errors. Images acquired under CP flight, as confirmed in our study, significantly compromise the accuracy and precision of image-based SfM and can even lead to an incorrect model reconstruction in MVS. Therefore, practical surveys should avoid employing CP flight design or apply appropriate countermeasures such as augmenting camera coordinates measured by RTK-GNSS or adding many GCPs to ensure stable SfM results when using CP flights.
4.2. Remedy for Indeterminacy of Intrinsic Parameters in Image-Based SfM
Our numerical experiments demonstrate that adjustments to the shooting positions of CP flights, such as a CP random flight, do not resolve the indeterminacy of intrinsic parameters (f and cy). However, introducing intermediate short strips between primary CP lines, as in the CP-Plus flight, effectively eliminated this indeterminacy in numerical experiments and substantially reduced f and cy instability in the real-data analysis. This result aligns with the known fact in aerial triangulation that introducing “cross strips” to a block can improve the accuracy of block adjustment [36,37].
Our finding suggests that practitioners can largely mitigate concerns regarding the significant instability of intrinsic parameters estimated by image-based SfM by incorporating intermediate short strips into CP flights. Some built-in flight missions in flight planning software packages automatically include intermediate strips. Such strips can be achieved using timed-interval or distance-interval shot modes, as seen in the 3D photogrammetry function of the DJI P4RTK drone or the “area route” option of the DJI Mavic 3E drone, for example.
In contrast, there are other flight missions that do not include intermediate strips, such as “waypoint” flight, where the camera shutter is triggered at specific predefined points. Additionally, some flight planning software packages, such as Pix4D Capture [18,24,29,38] or Pix4D Capture Pro, do not generate intermediate strips by default. These choices preserve the CP critical configuration and risk that the intrinsic parameter estimation will be unstable. Overall, embedding short cross-strips within CP flight plans prevents theoretical indeterminacy of intrinsic parameters, delivering more stable and accurate SfM reconstructions in practice without a reliance on camera coordinates measured by RTK-GNSS or extensive GCP networks.
4.3. Implications for Common Flight Configurations
The commonly used nadir-viewing flight represents a special case of critical configuration, where the pitch angle is zero. Therefore, our findings suggest that nadir-viewing flights are also unable to determine f and cy.
Although not explicitly analyzed in this study, the results of the CP-Plus flight imply that images captured by a “double grid” flight—commonly generated by many flight planning software packages and built-in drone missions—are expected to support the determination of f and cy. In this “double grid” flight, the images captured in the reverse direction function as intermediate strips, thereby mitigating the indeterminacy of f and cy.
5. Conclusions
In this study, we investigated how certain intrinsic camera parameters in image-based SfM become indeterminate using aerial photos from CP flights. Our numerical experiments (Section 3.1) confirmed that the CP flight is a critical configuration that causes the indeterminacy of intrinsic parameters, particularly focal length (f) and principal point coordinate (cy), under idealized conditions in CG simulations. Further analyses with real data (Section 3.2), involving three image-sets over 30 different SfM settings, demonstrated that estimates of f and cy are highly unstable when using CP flight imagery.
As a countermeasure, we found that integrating intermediate short strips into the CP flight design eliminates the indeterminacy of intrinsic parameters (f and cy) in numerical experiments and markedly improves the stability of these parameters in real-data analyses.
Our study reveals the potential to improve the accuracy of self-calibration using only aerial images in SfM, without the need for GCPs or RTK-GNSS data. This advancement not only simplifies the data acquisition process but also makes it more accessible and cost-effective for practitioners. By stabilizing SfM calibration, all the subsequent stages—such as MVS and dense point cloud generation—can be effectively enhanced, leading to more accurate 3D reconstructions.
This study initiated the investigation of the indeterminacy from two basic intrinsic parameters, f and cy. Investigations of other intrinsic parameters, including the principal point in the x-direction (cx) and nonlinear distortion coefficients, need to be considered in future research. Additionally, beyond CP flight designs, various other combinations of camera motion and scene geometry may form critical configurations and highlight the need for further exploration.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs17122030/s1.
Author Contributions
Conceptualization: A.K.; methodology and software: T.T.H. and R.S.; formal analysis: T.T.H. and R.S.; writing—original draft preparation: T.T.H.; writing—review and editing: A.K.; T.I.; K.Y. and T.H.; visualization: T.T.H.; supervision: A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by JSPS KAKENHI Grant Number 22K04333.
Data Availability Statement
The original contributions presented in this study are included in the article and Supplementary Materials. Further inquiries can be directed to the corresponding author.
Acknowledgments
The in situ data (photos and ground surveying data) was obtained by Fujita Corporation, Japan.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BA | Bundle Adjustment |
| CP | Constant Pitch |
| DEM | Digital Elevation Model |
| GCP | Ground Control Point |
| GNSS | Global Navigation Satellite System |
| MEZ | Mean vertical error of all validation points |
| MVS | Multi-View Stereo |
| RMS Error | Root Mean Square Error |
| RTK-GNSS | Real-Time Kinematic Global Navigation Satellite System |
| SfM | Structure from Motion |
| UAV | Unmanned Aerial Vehicle |
| Val_RMSE_T | Total RMS error of all validation points |
| Val_RMSE_Z | Vertical RMS error of all validation points |
References
- Xu, Y.; Zhang, J. UAV-Based Bridge Geometric Shape Measurement Using Automatic Bridge Component Detection and Distributed Multi-View Reconstruction. Autom. Constr. 2022, 104376. [Google Scholar] [CrossRef]
- Wang, F.; Zou, Y.; del Rey Castillo, E.; Ding, Y.; Xu, Z.; Zhao, H.; Lim, J.B.P. Automated UAV Path-Planning for High-Quality Photogrammetric 3D Bridge Reconstruction. Struct. Infrastruct. Eng. 2024, 20, 1595–1614. [Google Scholar] [CrossRef]
- Khaloo, A.; Lattanzi, D.; Cunningham, K.; Dell’Andrea, R.; Riley, M. Unmanned Aerial Vehicle Inspection of the Placer River Trail Bridge through Image-Based 3D Modelling. Struct. Infrastruct. Eng. 2018, 14, 124–136. [Google Scholar] [CrossRef]
- Siqueira, H.L.; Marcato, J.; Matsubara, E.T.; Eltner, A.; Colares, R.A.; Santos, F.M. The Impact of Ground Control Point Quantity on Area and Volume Measurements with UAV SFM Photogrammetry Applied in Open Pit Mines. In Proceedings of the IGARSS 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July 2019; pp. 9093–9096. [Google Scholar]
- Hao, J.; Zhang, X.; Wang, C.; Wang, H.; Wang, H. Application of UAV Digital Photogrammetry in Geological Investigation and Stability Evaluation of High-Steep Mine Rock Slope. Drones 2023, 7, 198. [Google Scholar] [CrossRef]
- Dawei, Z.; Lizhuang, Q.; Demin, Z.; Baohui, Z.; Lianglin, G. Unmanned Aerial Vehicle (UAV) Photogrammetry Technology for Dynamic Mining Subsidence Monitoring and Parameter Inversion: A Case Study in China. IEEE Access 2020, 8, 16372–16386. [Google Scholar] [CrossRef]
- Bonali, F.L.; Corti, N.; Russo, E.; Marchese, F.; Fallati, L.; Pasquaré Mariotto, F.; Tibaldi, A. Commercial-UAV-Based Structure from Motion for Geological and Geohazard Studies. In Building Knowledge for Geohazard Assessment and Management in the Caucasus and Other Orogenic Regions; Springer: Dordrecht, The Netherlands, 2021; pp. 389–427. [Google Scholar]
- Yakar, M.; Ulvi, A.; Yiğit, A.Y.; Alptekin, A. Discontinuity Set Extraction from 3D Point Clouds Obtained by UAV Photogrammetry in a Rockfall Site. Surv. Rev. 2023, 55, 416–428. [Google Scholar] [CrossRef]
- Butcher, B.; Walton, G.; Kromer, R.; Gonzales, E.; Ticona, J.; Minaya, A. High-Temporal-Resolution Rock Slope Monitoring Using Terrestrial Structure-from-Motion Photogrammetry in an Application with Spatial Resolution Limitations. Remote Sens. 2023, 16, 66. [Google Scholar] [CrossRef]
- Saito, T.; Kawai, T.; Takahara, Y.; Nagamatsu, D.; Inosako, K. Sand Movement Analysis of the Tottori Sand Dunes Using Aerial Photogrammetry by UAVs. J. Arid. Land Stud. 2024, 34, 87–91. [Google Scholar] [CrossRef]
- Laporte-Fauret, Q.; Marieu, V.; Castelle, B.; Michalet, R.; Bujan, S.; Rosebery, D. Low-Cost UAV for High-Resolution and Large-Scale Coastal Dune Change Monitoring Using Photogrammetry. J. Mar. Sci. Eng. 2019, 7, 63. [Google Scholar] [CrossRef]
- Fraser, C.S.; Al-Ajlouni, S. Zoom-Dependent Camera Calibration in Digital Close-Range Photogrammetry. Photogramm. Eng. Remote Sens. 2006, 72, 1017–1026. [Google Scholar] [CrossRef]
- Fraser, C.S. Photogrammetry and Remote Sensing Digital Camera Self-Calibration. ISPRS J. Photogramm. Remote Sens. 1997, 52, 149–159. [Google Scholar] [CrossRef]
- Abeho, D.R.; Shoko, M.; Odera, P.A. Effects of Camera Calibration on the Accuracy of Unmanned Aerial Vehicle Sensor Products. Int. J. Eng. Geosci. 2024, 9, 314–323. [Google Scholar] [CrossRef]
- Senn, J.A.; Mills, J.; Walsh, C.L.; Addy, S.; Peppa, M. On-site Geometric Calibration of RPAS Mounted Sensors for SfM Photogrammetric Geomorphological Surveys. Earth Surf. Process Landf. 2022, 47, 1615–1634. [Google Scholar] [CrossRef]
- Daakir, M.; Zhou, Y.; Pierrot Deseilligny, M.; Thom, C.; Martin, O.; Rupnik, E. Improvement of Photogrammetric Accuracy by Modeling and Correcting the Thermal Effect on Camera Calibration. ISPRS J. Photogramm. Remote Sens. 2019, 148, 142–155. [Google Scholar] [CrossRef]
- Elias, M.; Eltner, A.; Liebold, F.; Maas, H.-G. Assessing the Influence of Temperature Changes on the Geometric Stability of Smartphone- and Raspberry Pi Cameras. Sensors 2020, 20, 643. [Google Scholar] [CrossRef]
- Sanz-Ablanedo, E.; Chandler, J.H.; Ballesteros-Pérez, P.; Rodríguez-Pérez, J.R. Reducing Systematic Dome Errors in Digital Elevation Models through Better UAV Flight Design. Earth Surf. Process Landf. 2020, 45, 2134–2147. [Google Scholar] [CrossRef]
- Smith, M.J.; Cope, E. The Effects of Temperature Variation on Single-Lens-Reflex Digital Camera Calibration Parameters. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Commission V Symposium, Part 5, Newcastle upon Tyne, UK, 21–24 June 2010; Volume 38, pp. 554–559. [Google Scholar]
- Luo, W.; Shao, M.; Che, X.; Hesp, P.A.; Bryant, R.G.; Yan, C.; Xing, Z. Optimization of UAVs-SfM Data Collection in Aeolian Landform Morphodynamics: A Case Study from the Gonghe Basin, China. Earth Surf. Process Landf. 2020, 45, 3293–3312. [Google Scholar] [CrossRef]
- Kanno, A.; Yuji, M.; Otsu, Y.; Sugimoto, K.; Takada, M. Effect of Constant Pitch Meandering Flight Method and Analysis Settings in SfM without GCPs. In Proceedings of the Annual Conference of the Japan Society of Photogrammetry and Remote Sensing, 20–21 May 2021; pp. 49–52. Available online: https://ds.cc.yamaguchi-u.ac.jp/~kanno/pdf/JSPRS_2021_1/paper_JSPRS_2021_1.pdf (accessed on 7 June 2025). (In Japanese).
- Ariyo, K.; Junnosuke, K.; Truc, T.H.; Masaki, H.; Tatsuji, F.; Kyouhei, K. Accuracy Verification Experiment of UAV Photogrammetry Using Optical Axis Optimization Shooting with Airpeak S1 + A7Ⅲ. In Proceedings of the Fall Conference of the Japan Society of Photogrammetry and Remote Sensing, 10–11 November 2022; pp. 41–42. Available online: https://ds.cc.yamaguchi-u.ac.jp/~kanno/pdf/JSPRS_2022_2/proceedings_JSPRS22_C-5.pdf (accessed on 7 June 2025). (In Japanese).
- Truc, T.H.; Ariyo, K.; Yuji, M.; Masahiko, S.; Tsuyoshi, I.; Koichi, Y.; Takaya, H. Robustness of Structure from Motion Accuracy/Precision against the Non-Optimality in Analysis Settings: Case Study in Constant-Pitch Flight Design. Int. J. Autom. Technol. 2024, 18, 621–631. [Google Scholar]
- Nesbit, P.R.; Hugenholtz, C.H. Enhancing UAV-SfM 3D Model Accuracy in High-Relief Landscapes by Incorporating Oblique Images. Remote Sens. 2019, 11, 239. [Google Scholar] [CrossRef]
- Kon, J.; Kanno, A.; Haruna, M.; Fujii, T.; Kurita, K. The Robustness of SfM Settings and Vulnerability to Dome-Shaped Deformation in Four Types of UAV Oblique Photography Methods. In Proceedings of the Annual Conference of the Japan Society of Photogrammetry and Remote Sensing, 18–19 May 2023; pp. 37–38. Available online: https://jglobal.jst.go.jp/detail?JGLOBAL_ID=202302237161111141 (accessed on 7 June 2025). (In Japanese).
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; ISBN 9780521540513. [Google Scholar]
- Štroner, M.; Urban, R.; Seidl, J.; Reindl, T.; Brouček, J. Photogrammetry Using UAV-Mounted GNSS RTK: Georeferencing Strategies without GCPs. Remote Sens. 2021, 13, 1336. [Google Scholar] [CrossRef]
- Blender Foundation Blender 2.79 Release Notes. Available online: https://developer.blender.org/docs/release_notes/2.79/ (accessed on 7 June 2025).
- Ahmed, S.; El-Shazly, A.; Abed, F.; Ahmed, W. The Influence of Flight Direction and Camera Orientation on the Quality Products of UAV-Based SfM-Photogrammetry. Appl. Sci. 2022, 12, 10492. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating Systematic Error in Topographic Models Derived from UAV and Ground-Based Image Networks. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Dai, W.; Zheng, G.; Antoniazza, G.; Zhao, F.; Chen, K.; Lu, W.; Lane, S.N. Improving UAV-SfM Photogrammetry for Modelling High-relief Terrain: Image Collection Strategies and Ground Control Quantity. Earth Surf. Process. Landf. 2023, 48, 2884–2899. [Google Scholar] [CrossRef]
- DJI Enterprise Phantom 4 RTK. Available online: https://www.dji.com/jp/support/product/phantom-4-rtk (accessed on 19 November 2024).
- Aerosense Inc. Aerobo Marker. Available online: https://aerosense.co.jp/en/products/equipment_systems/ (accessed on 19 November 2024).
- James, M.R.; Chandler, J.H.; Eltner, A.; Fraser, C.; Miller, P.E.; Mills, J.P.; Noble, T.; Robson, S.; Lane, S.N. Guidelines on the Use of Structure-from-Motion Photogrammetry in Geomorphic Research. Earth Surf. Process. Landf. 2019, 44, 2081–2084. [Google Scholar] [CrossRef]
- Kahl, F.; Triggs, B.; Åström, K. Critical Motions for Auto-Calibration When Some Intrinsic Parameters Can Vary. J. Math. Imaging. Vis. 2000, 13, 131–146. [Google Scholar] [CrossRef]
- Ackermann, F.; Schade, H. Application of GPS for Aerial Triangulation. Photogramm. Eng. Remote Sens. 1993, 59, 1625–1632. [Google Scholar]
- Forstner, W. The Reliability of Block Triangulation. Photogramm. Eng. Remote Sens. 1985, 51, 1137–1149. [Google Scholar]
- Iheaturu, C.; Okolie, C.; Ayodele, E.; Stanley, E.A.; Musa, S.; Ifejika Speranza, C.I. A Simplified Structure-from-Motion Photogrammetry Approach for Urban Development Analysis. Remote Sens. Appl. 2022, 28, 100850. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).