A Holistic Solution for Supporting the Diagnosis of Historic Constructions from 3D Point Clouds
Abstract
1. Introduction
- The application of both unsupervised and supervised ML methods for constructive system and damage detection.
- The ability to segment 3D point clouds using a Point Transformer Neural Network (PTNN).
- The computation of geometric-based and statistics-based features, as well as the capability to compute several colour spaces within the same 3D point cloud.
- The implementation of algorithms for analysing deflections in beams and slabs, inclinations in columns and out-of-plane deformations in arches and vaults.
- The integration of a voxel discretisation method, a noise reduction filter and a web-based viewer for large 3D point clouds.
2. Background
2.1. The 3D Point Cloud
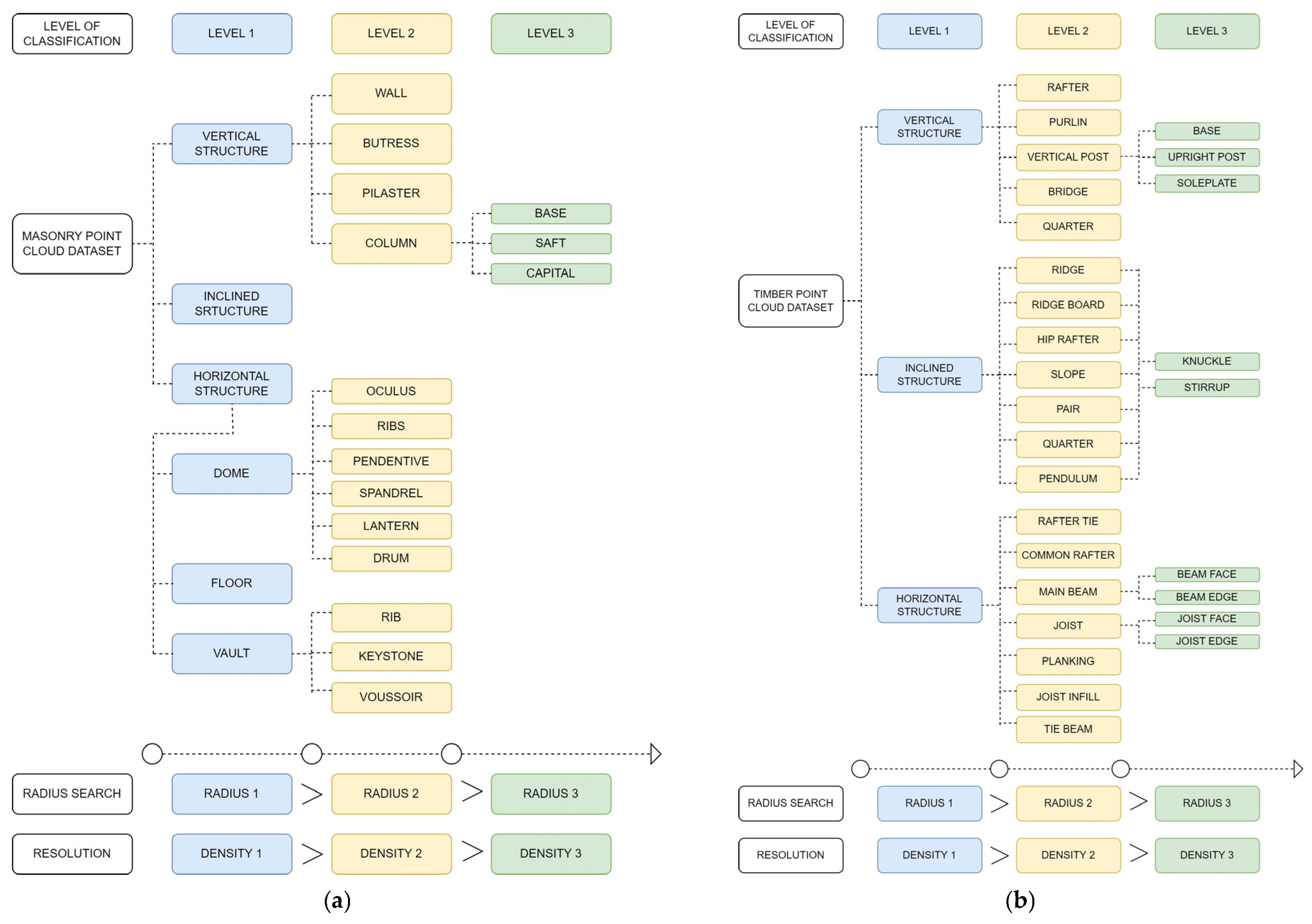
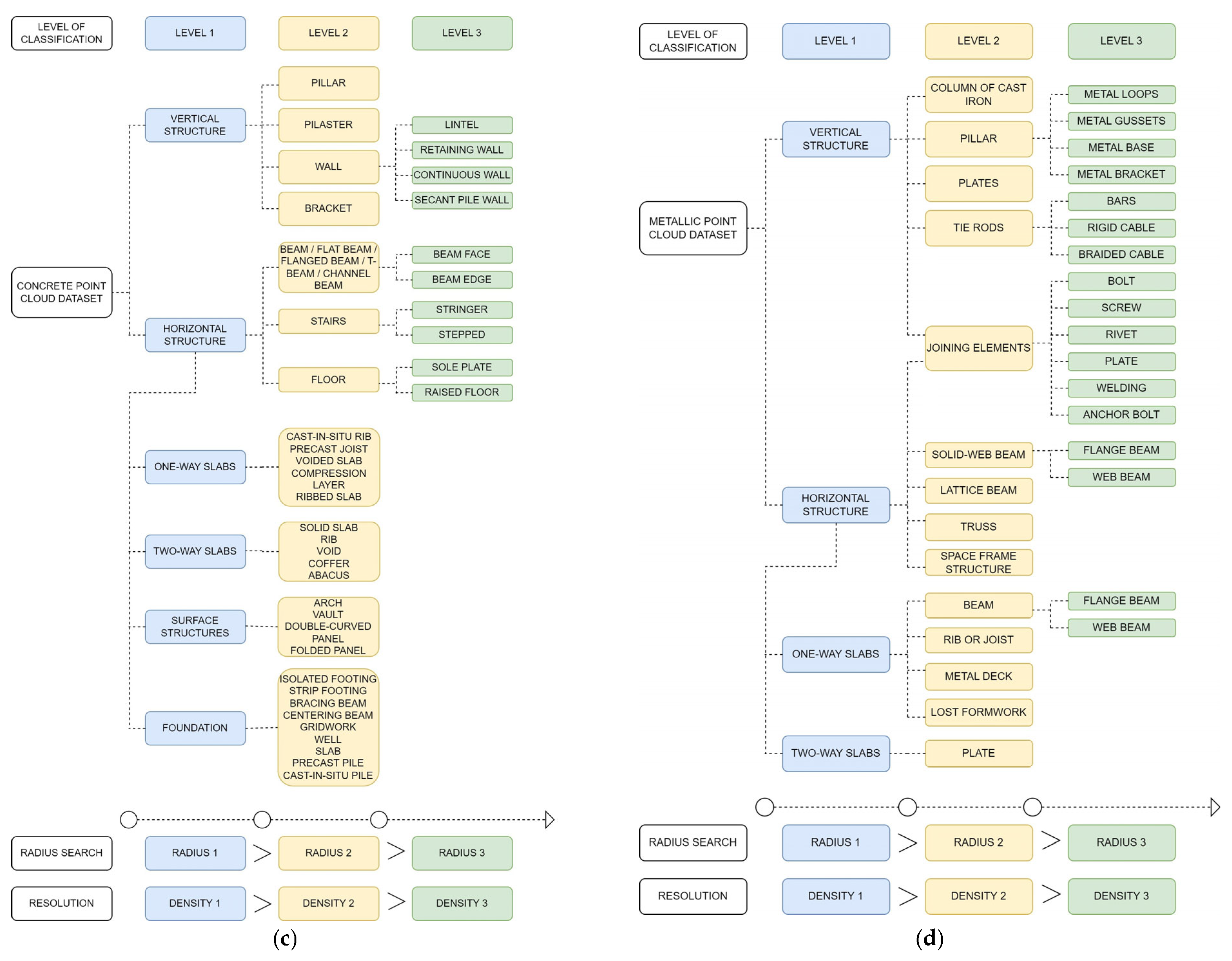
2.2. Segmentation of Constructive Elements Using 3D Point Clouds
2.3. Damage Detection Based on 3D Point Clouds
3. Materials and Methods
- M3C2 (Multiscale Model-to-Model Cloud Comparison) [45]: This technique estimates discrepancies between two-point clouds using a modified cloud-to-cloud distance calculation that considers the normal vector and local roughness of the point cloud. The algorithm can estimate the uncertainty in the distance calculation and identify significant changes. Thanks to this, it is possible to monitor geometrical changes between different epochs, evaluating material losses or even structural movements, as demonstrated by Costamagna et al. [46] and Dominici et al. [47].
- RANSAC Shape Detector (Random Sample Consensus Shape Detector): This is a modified version of the well-known RANSAC approach, designed to estimate the best-fit parametric shape (plane, sphere, toroid or cone) from a set of points while dealing with outliers. This method is commonly used in heritage for estimating the inclination of walls [12] or the segmentation of point clouds into constructive systems [48].
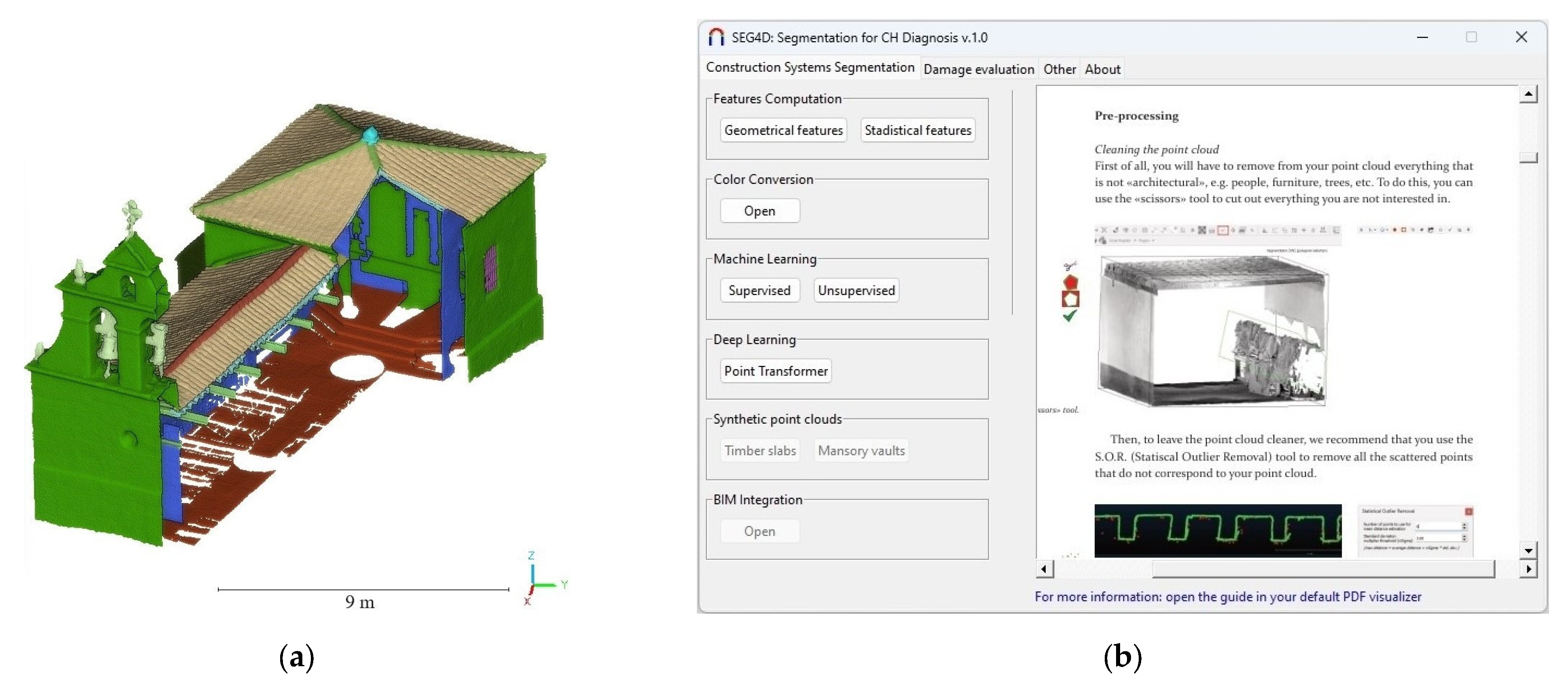
- Tab for construction system detection: This tab provides all strategies that allow users to segment the constructive systems of the 3D point cloud.
- Tab for damage detection: When the user clicks on this tab, the plugin displays all strategies devoted to detecting damage. Since damage detection is mainly performed on construction systems, it is highly recommended to previously segment the 3D point cloud into constructive systems.
- Tab for other methods: This tab includes additional algorithms that may be useful for the post-processing of 3D point clouds (e.g., noise reduction or voxelisation of the 3D point cloud).
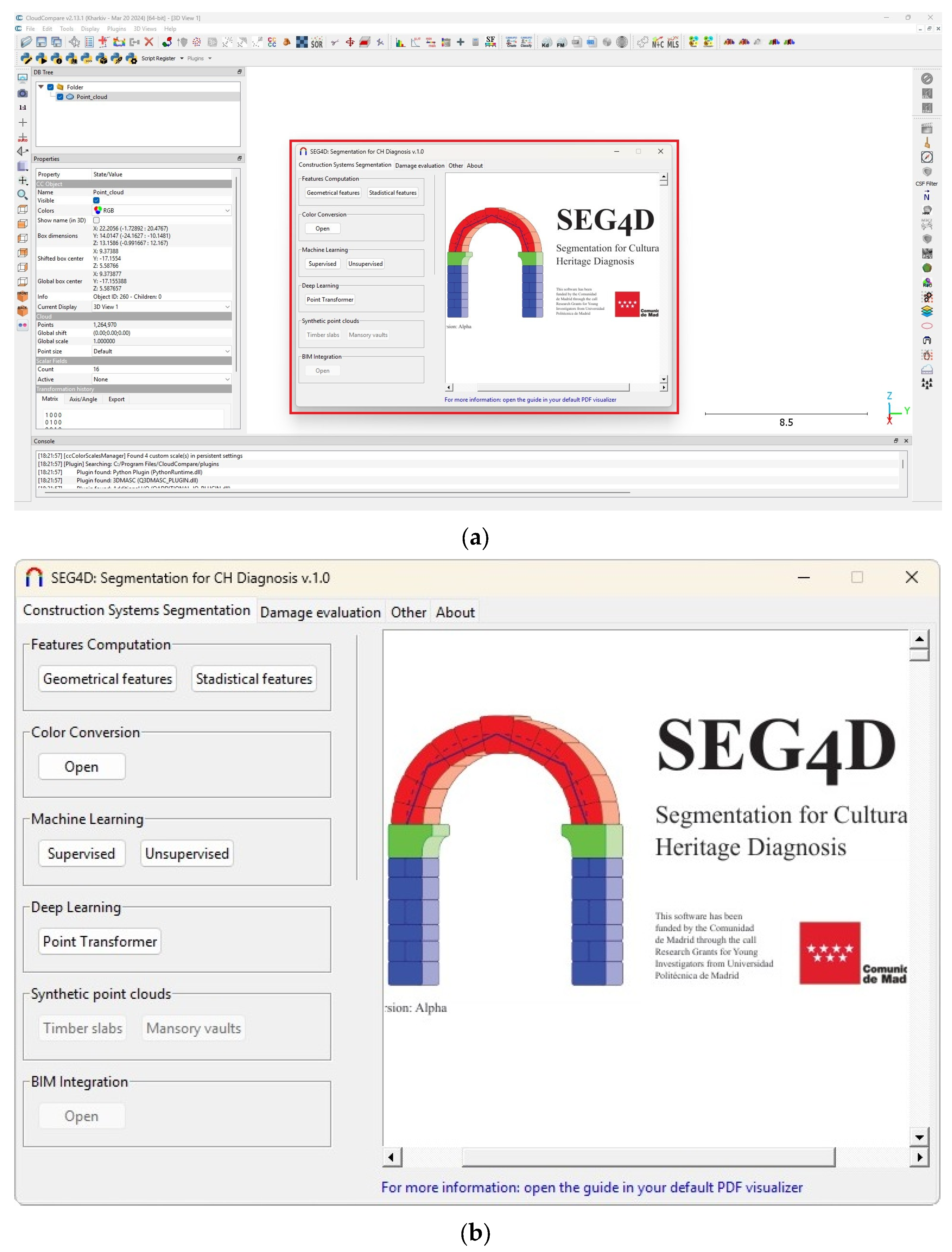
- Pre-processing the point cloud: Removal of irrelevant parts using the Segment tool, and reduction of noise using the Noise Reduction tool available under the Other tab.
- Construction system segmentation: Use the ML and DL methods available in the Construction Systems Segmentation tab to classify points based on the construction systems present in the building.
- Selection of construction system: Choose the specific construction system or construction element for which the user intends to evaluate damage.
- Damage extraction: Apply one of the strategies provided in the Damage Evaluation tab to identify and assess damage in the selected system.
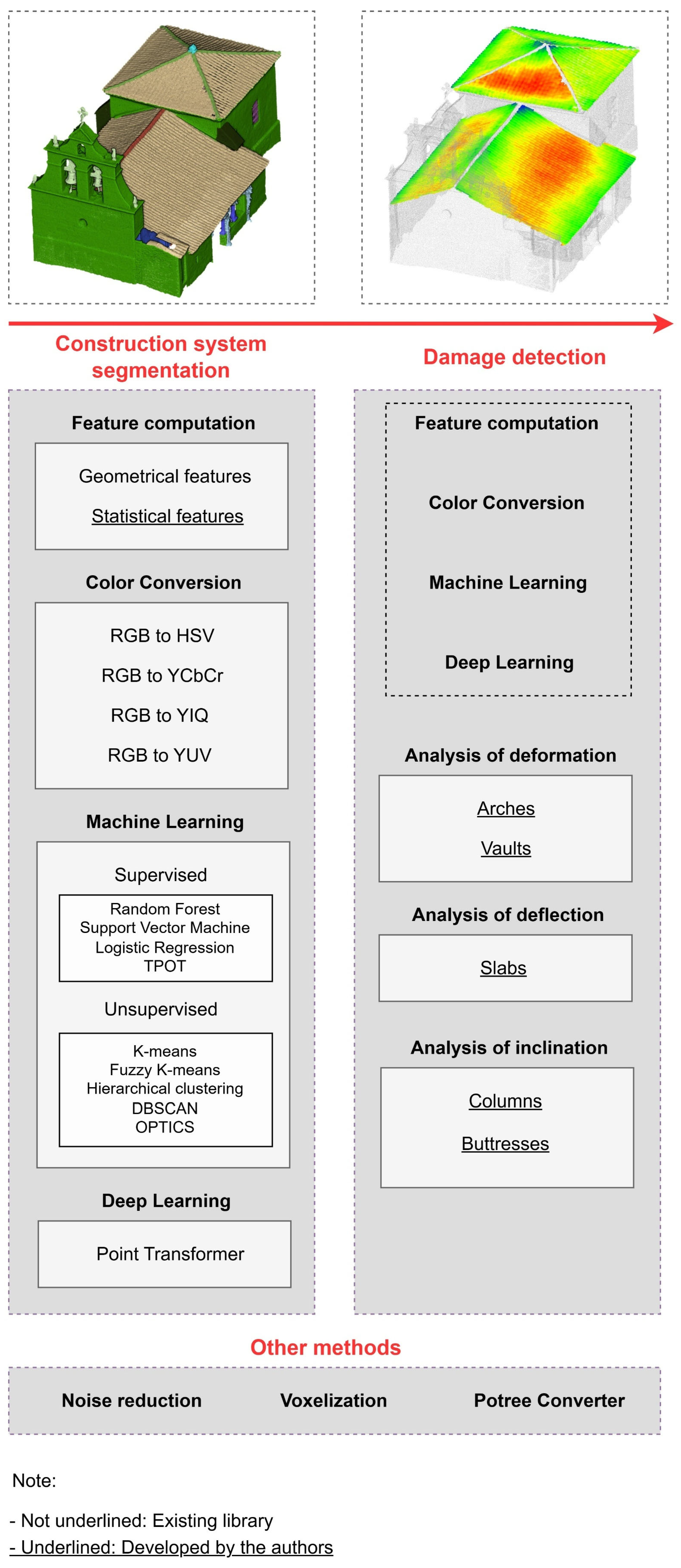
3.1. Constructive System Detection Tab
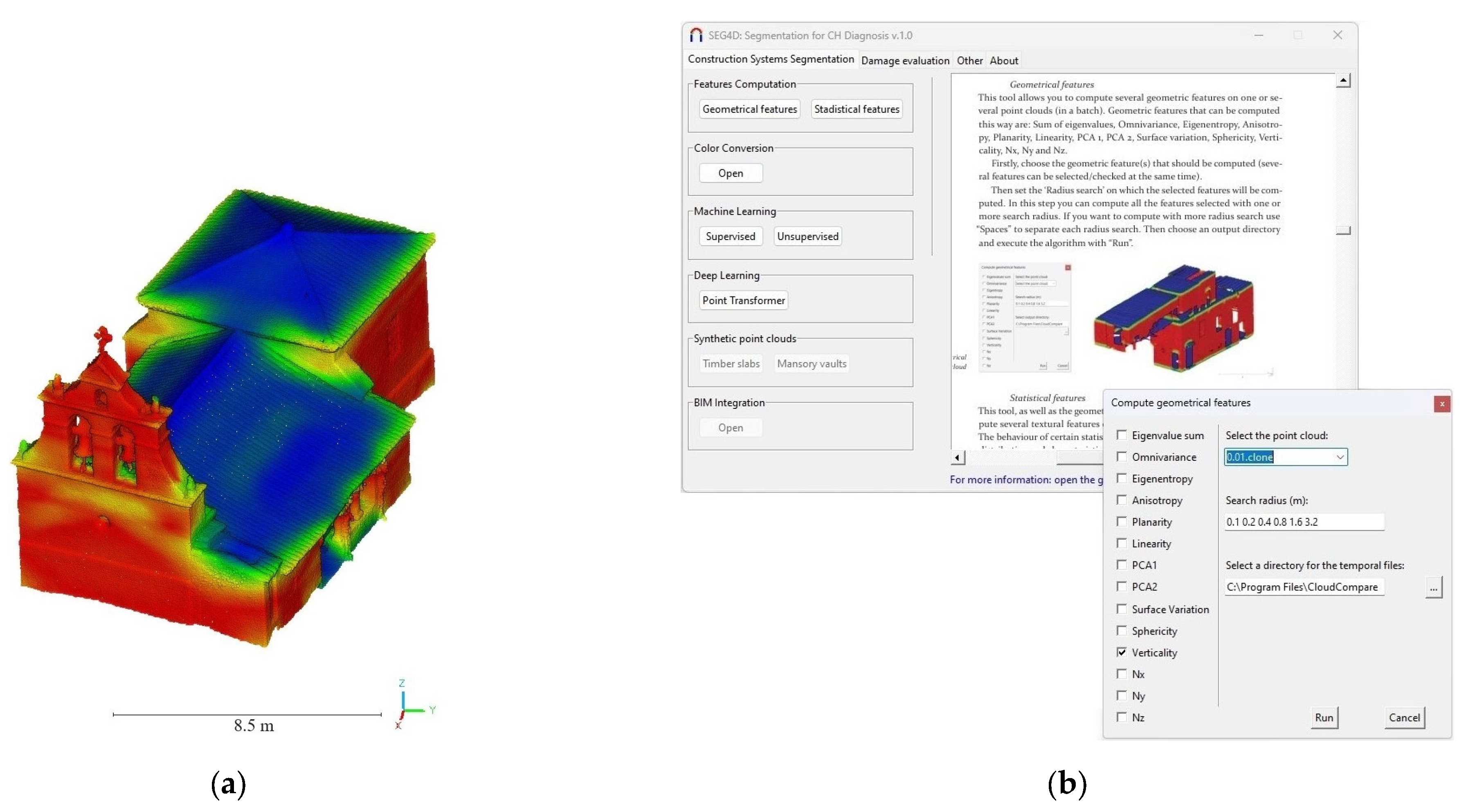
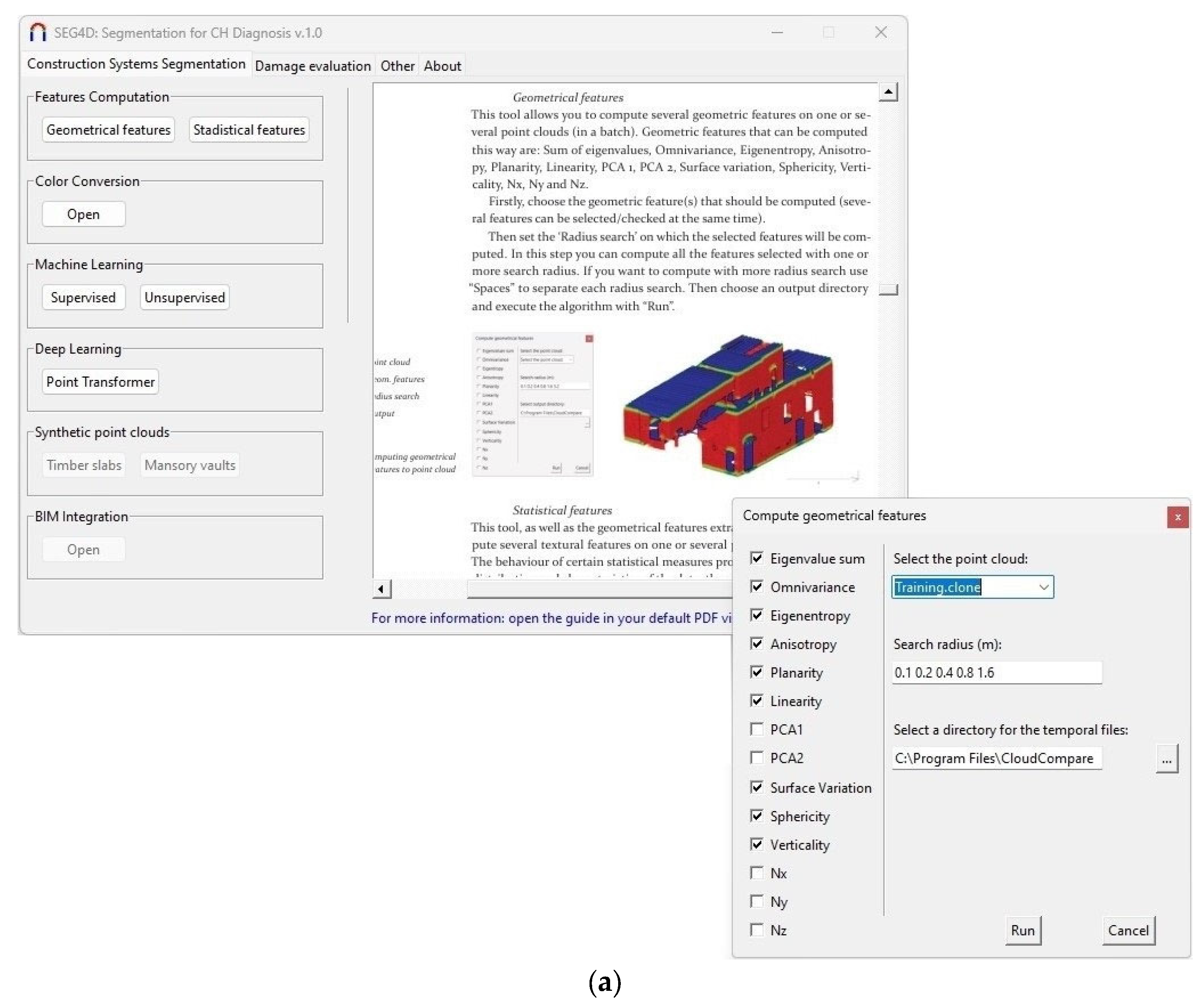
3.1.1. Feature Computation Module
- Geometrical features: This button allows users to compute the geometric features of the 3D point cloud by using the data extracted from the Principal Component Analysis (PCA) of each point. The current version of the software includes the geometric features defined by Weinmann et al. [49]. The Python library Jakteristics (https://jakteristics.readthedocs.io/en/latest (accessed on 7 February 2025)) was used for this purpose. A geometric feature is a variable that characterises the geometry surrounding a point within the point cloud. For instance, a high value of the geometric feature known as ‘planarity’ indicates that the region surrounding a given point is predominantly planar.
- Statistical features: In addition to geometric features, the software can compute several statistical features related to the statistical indices between each point and its neighbours. The statistical features implemented in the current version include Mean value, Standard deviation, Range, Energy, Entropy, Kurtosis, and Skewness. These features allow for the evaluation of similarity between the neighbourhoods at different levels.
3.1.2. Colour Conversion Module
- HSV: This colour system refers to the layers Hue, Saturation, Value.
- YCbCr: Y represents the luma component, and the Cb and Cr signals are the blue difference and red difference chrominance components, respectively.
- YIQ: Y represents the luminance information; I and Q represent the chrominance information and the orange–blue and purple–green range, respectively.
- YUV: Y represents the luminance information; U and V represent the chrominance information and the red and blue range, respectively.
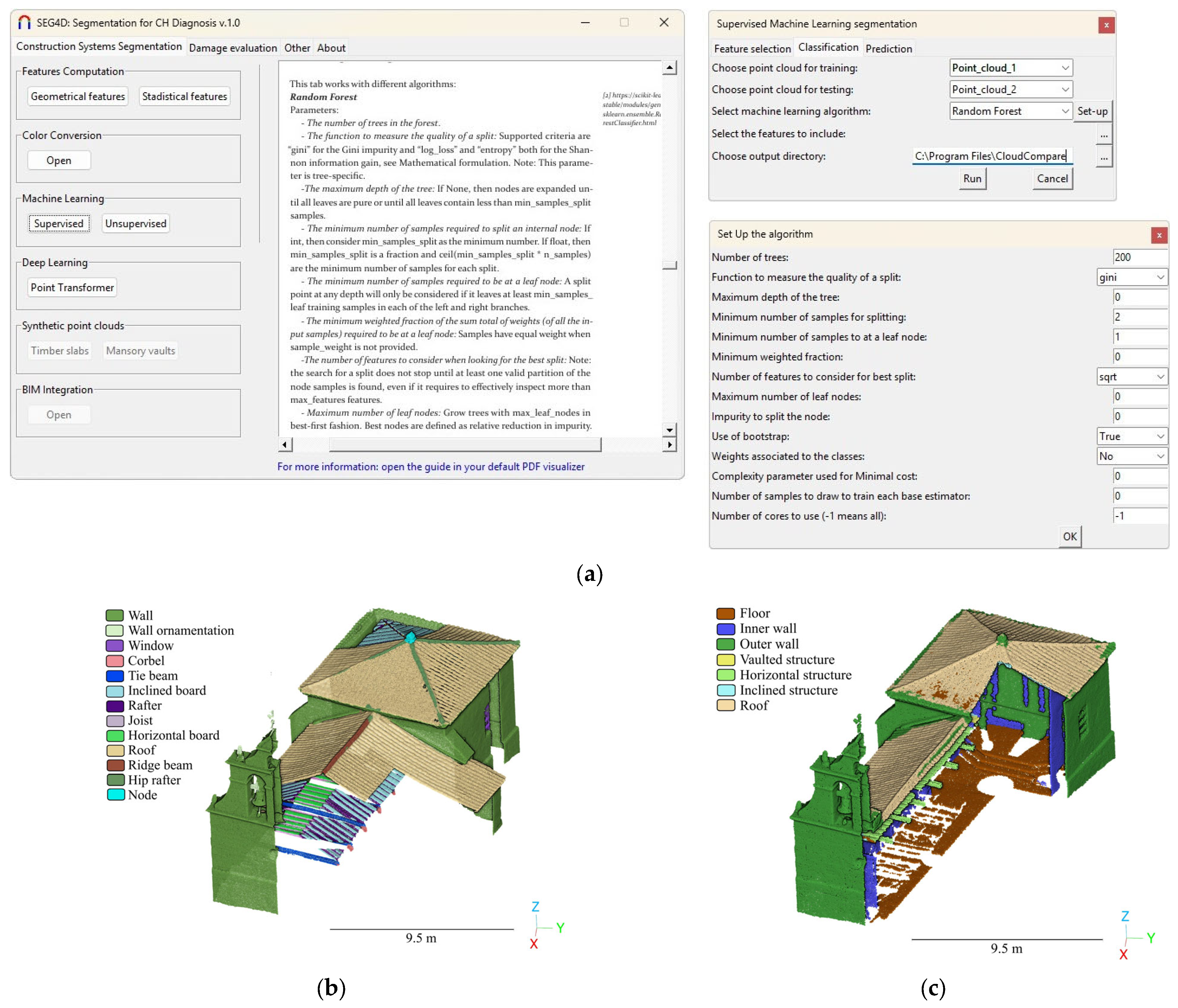
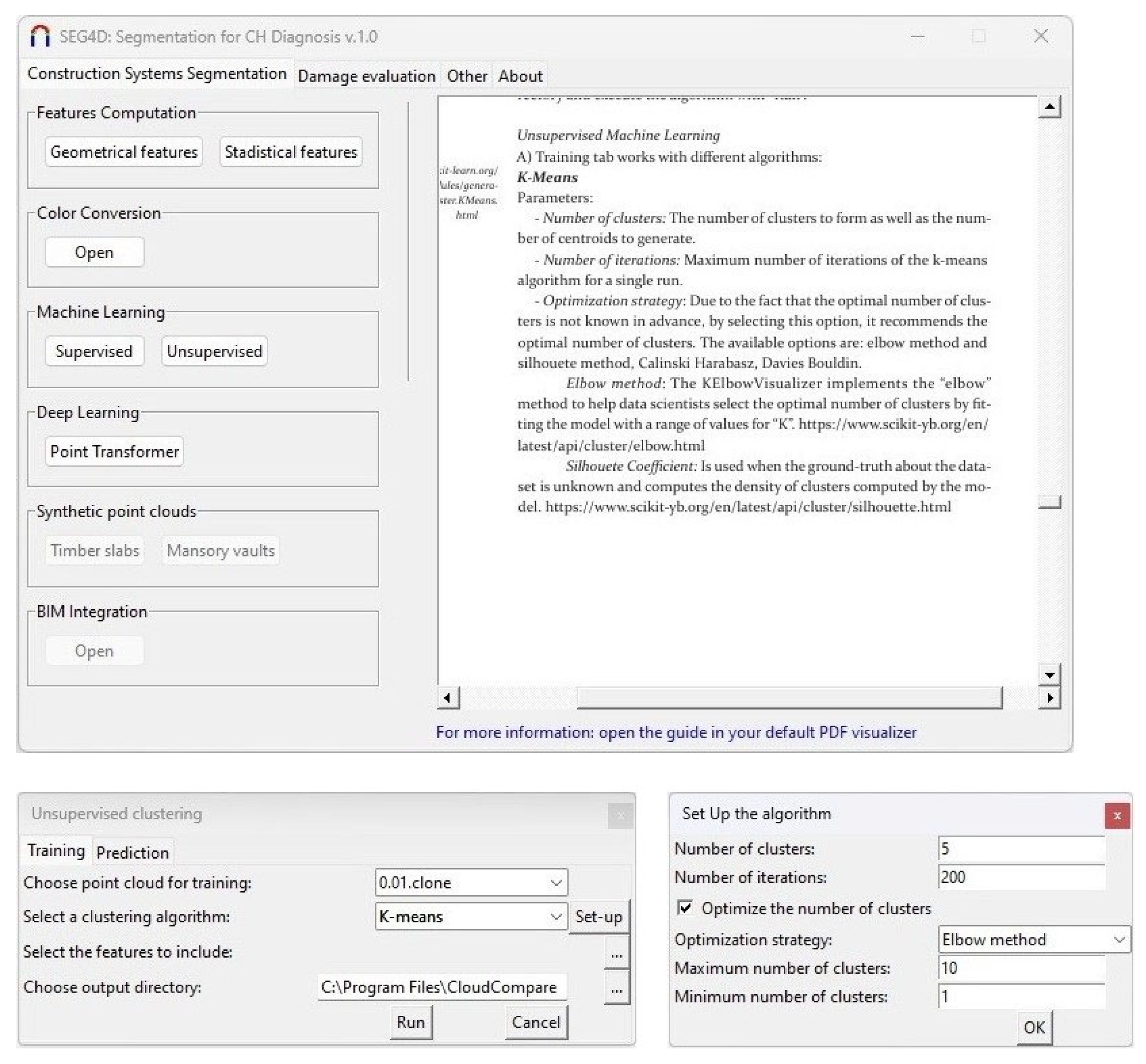
3.1.3. Machine and Deep Learning Modules
- Feature selection: This option allows the evaluation of the relevance of the different features contained in the 3D point cloud to reduce the complexity of the ML models. Within this context, the current version of Seg4D includes the library Optimal-Flow [52]. The current version is 0.1.11 (https://optimal-flow.readthedocs.io/en/latest/ (accessed on 7 February 2025)). This library integrates several approaches to select the most relevant features for the ML model, as detailed in the user manual.
- Classification: This option allows the setup of supervised ML algorithms. The current version of the software includes the common supervised ML algorithms used in the literature (Random Forest, Support Vector Machine and Linear Regression) [10] as well as an Auto-Machine Learning method. Automated machine learning refers to the process of automating the end-to-end workflow of applying ML algorithms. It involves automating tasks such as feature selection, selection of algorithms and hyperparameter tuning. To this end, the solution integrates the scikit-learn library (https://scikit-learn.org/stable/ (accessed on 7 February 2025)) for the supervised methods and the Tree-based Pipeline Optimization Tool library (https://epistasislab.github.io/tpot/ (accessed on 7 February 2025)) for automated machine learning. This library includes the most relevant ML algorithms and feature selection methods. The process iterates through multiple solutions until it reaches a predefined time limit or the desired level of accuracy. To this end, the approach uses an optimisation method that attempts to maximise a metric of accuracy (i.e., accuracy, precision, f1, etc.) by using a genetic algorithm. The user only needs to define the maximum number of iterations (or a time limit) for the genetic algorithm as well as the metric of accuracy that will be maximised.
- Prediction: This option enables the application of a previously trained algorithm to an unclassified 3D point cloud. The user needs to select the 3D point cloud to be used and the file containing the parameters of the trained ML algorithm (in .pkl format).
3.2. Damage Detection Tab
3.2.1. Feature Computation, Colour Conversion, Machine Learning and Deep Learning Modules
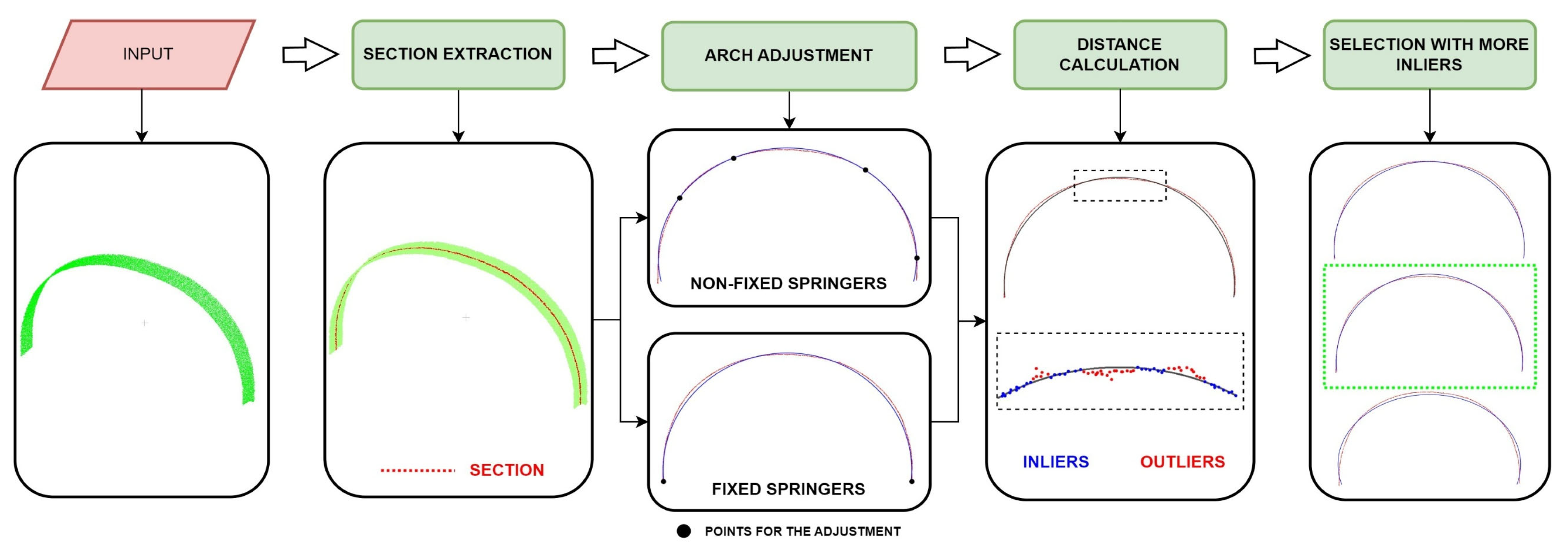
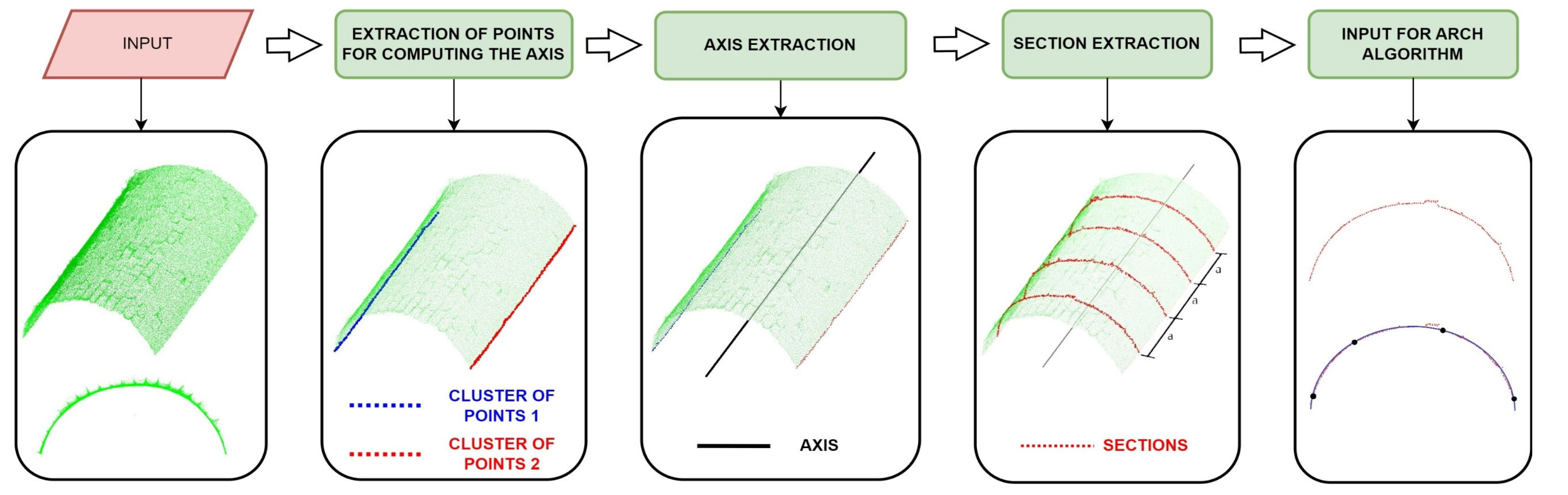
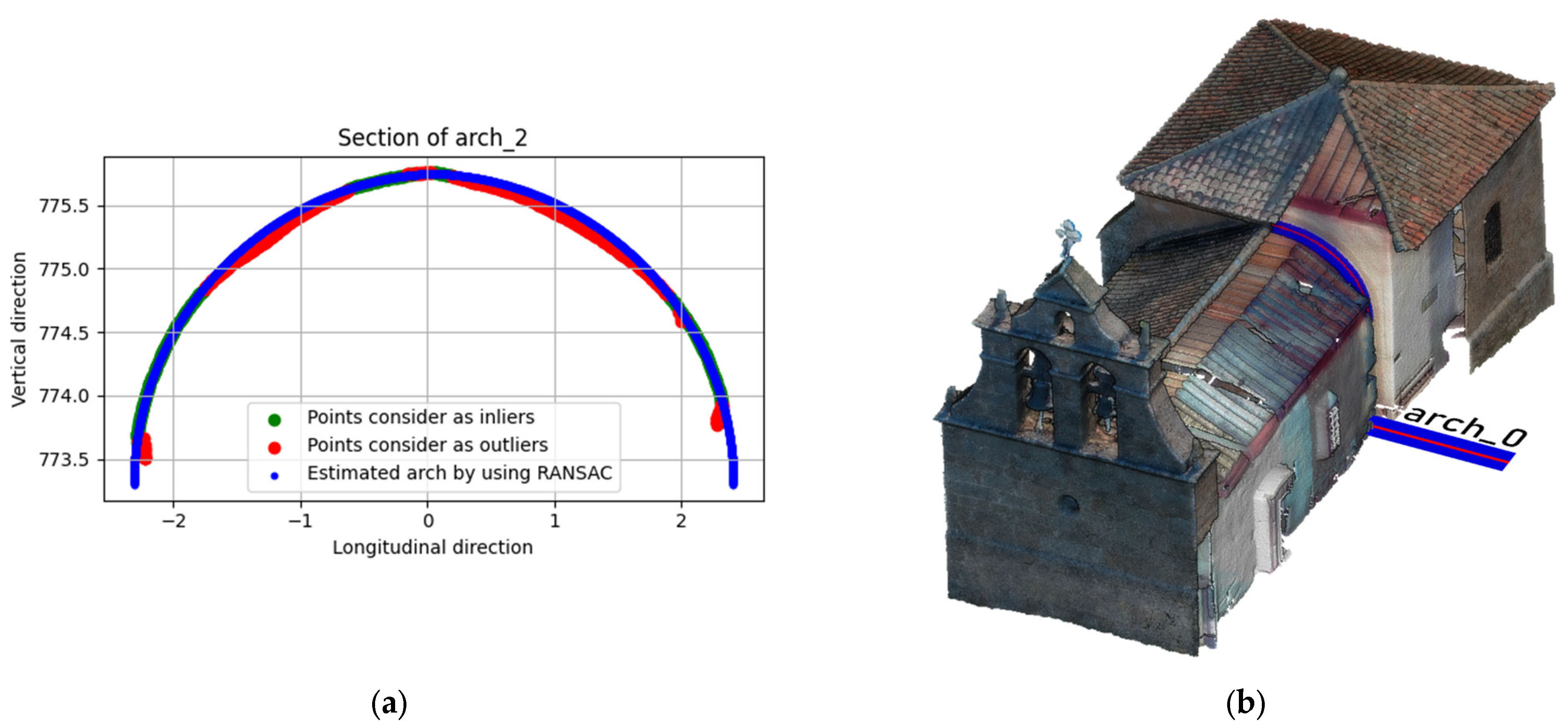
3.2.2. Module for Analysing the Deformation in Arches and Vaults
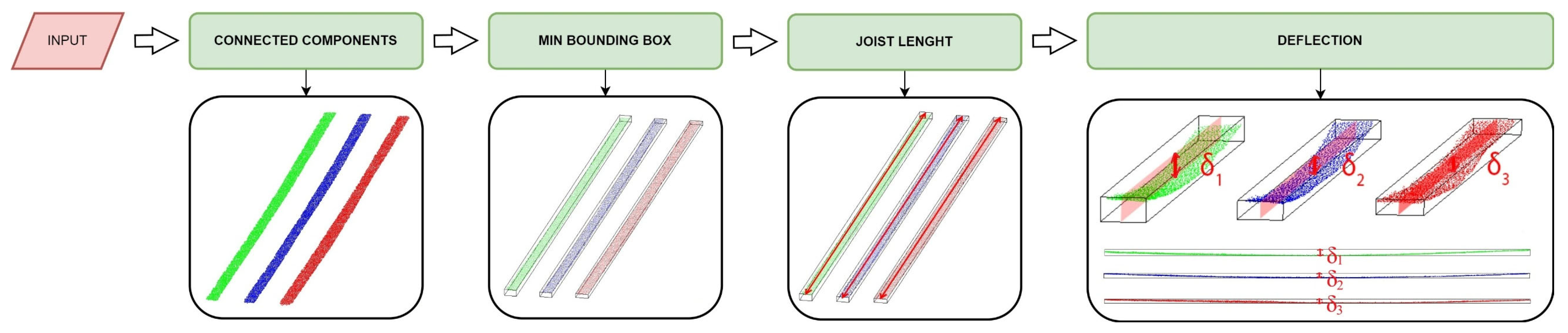
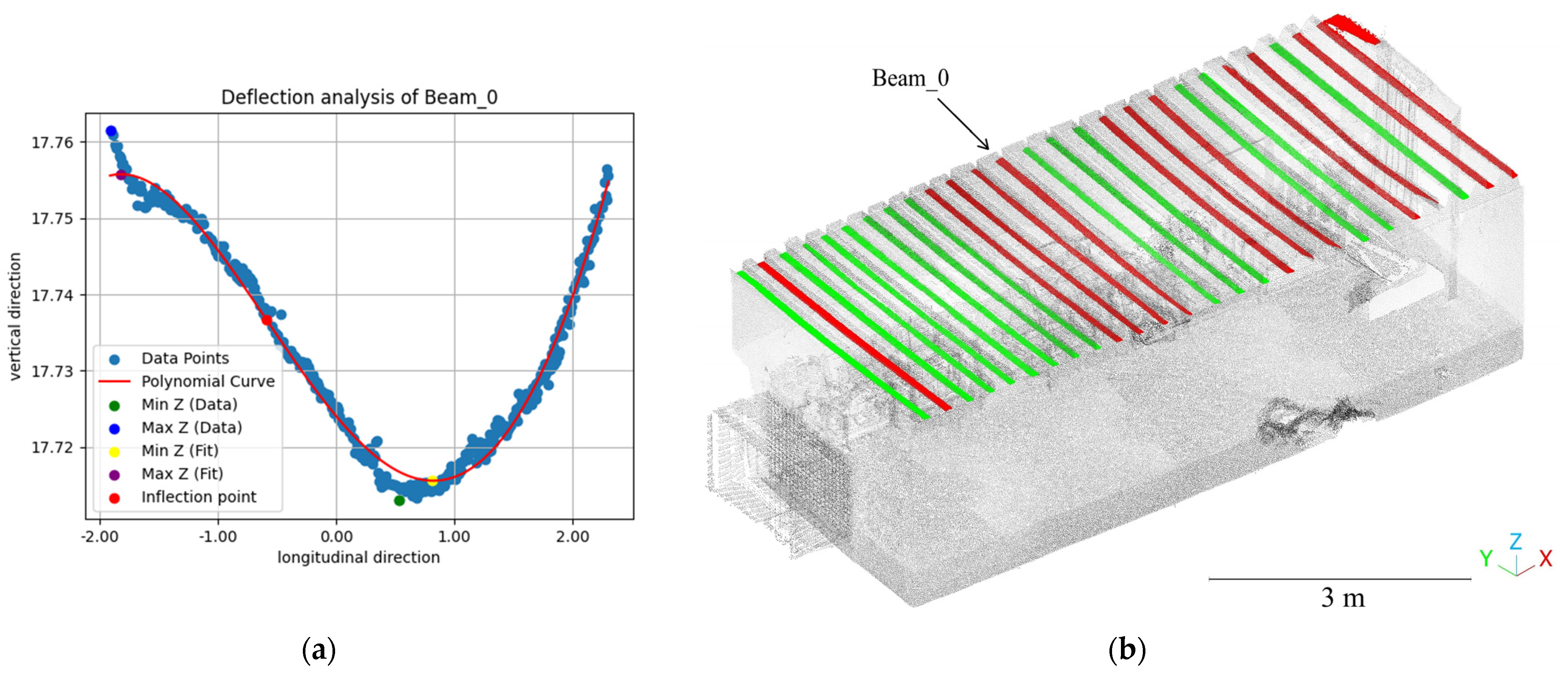
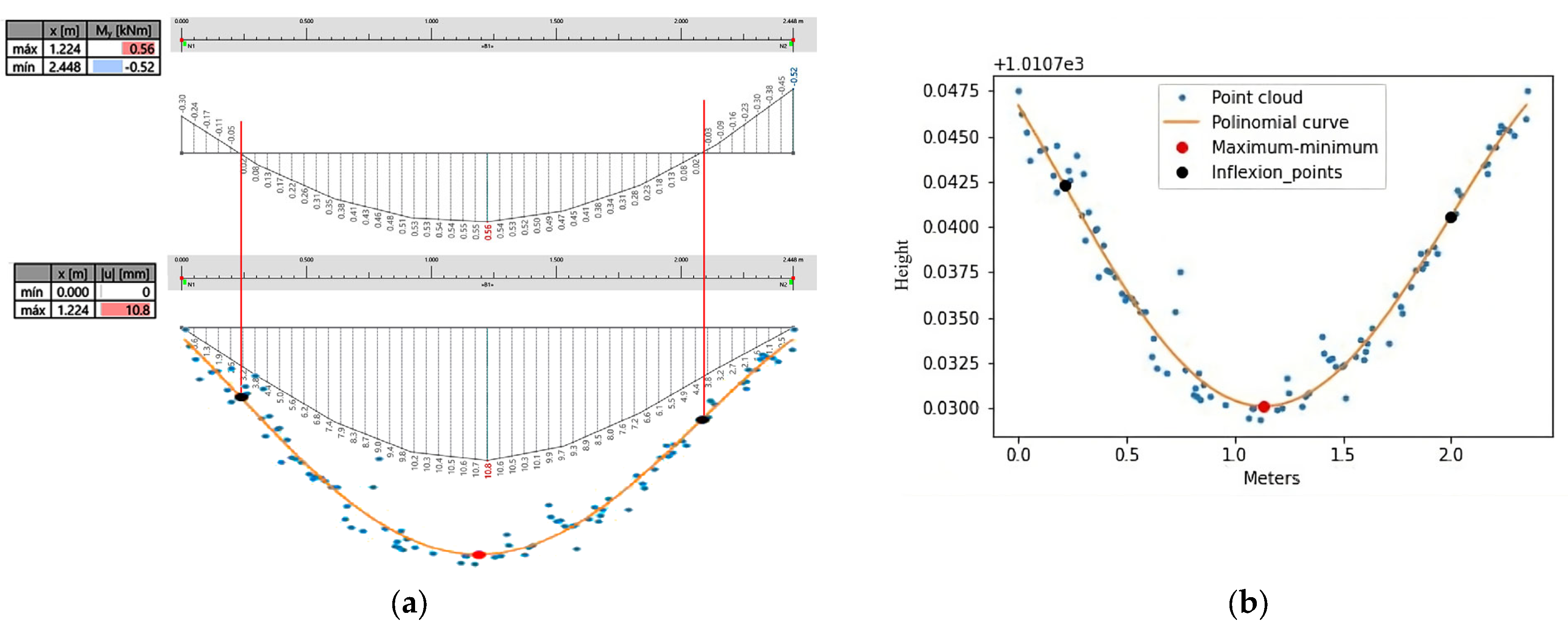
3.2.3. Module for Analysis of the Deflection in Slabs
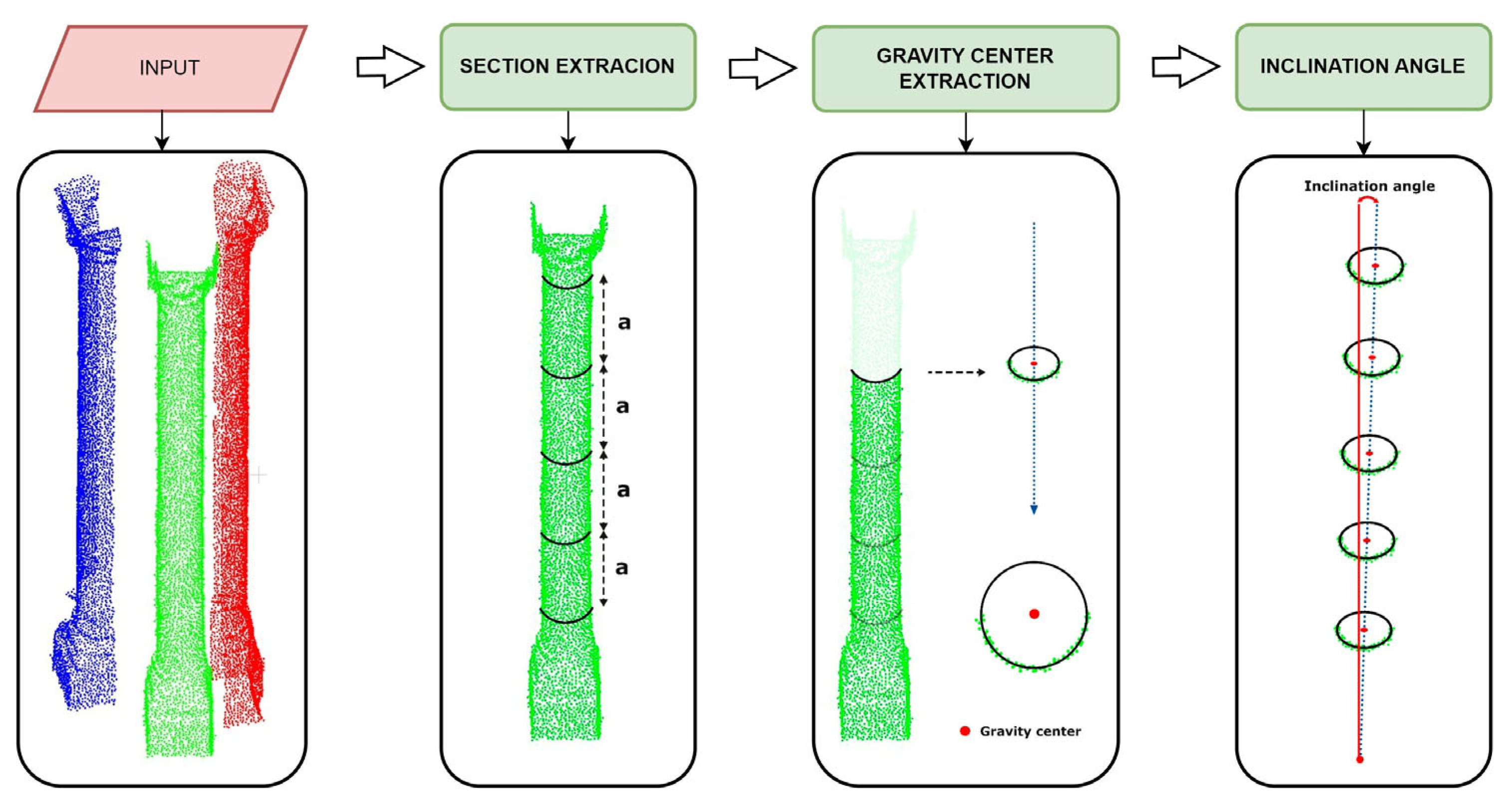
3.2.4. Module for Analysis of the Inclination in Columns and Buttresses
3.3. Other Algorithms Tab
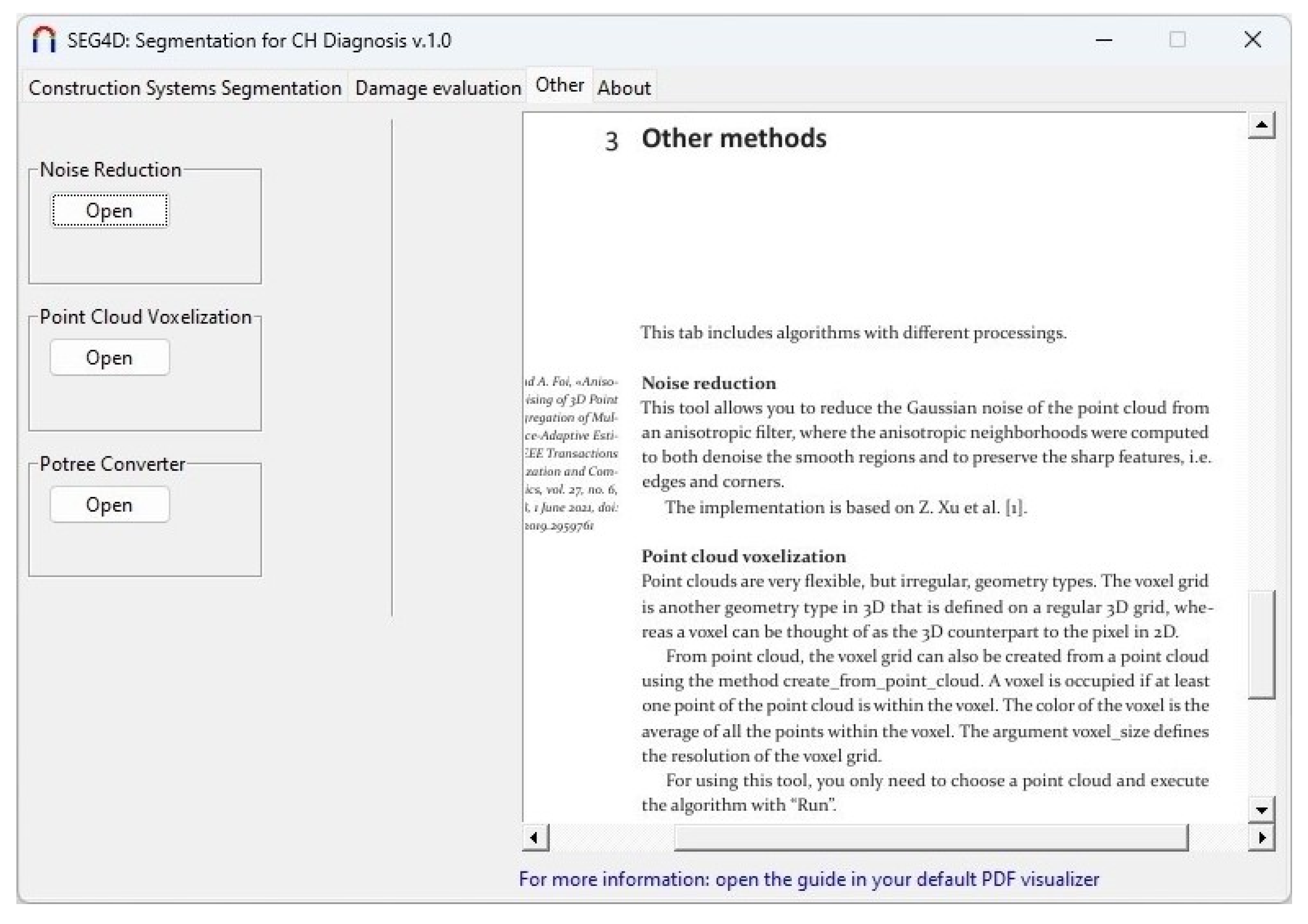
3.3.1. Noise Reduction Module
3.3.2. Point Cloud Voxelisation Module
3.3.3. Potree Converter Module
4. Experimental Results
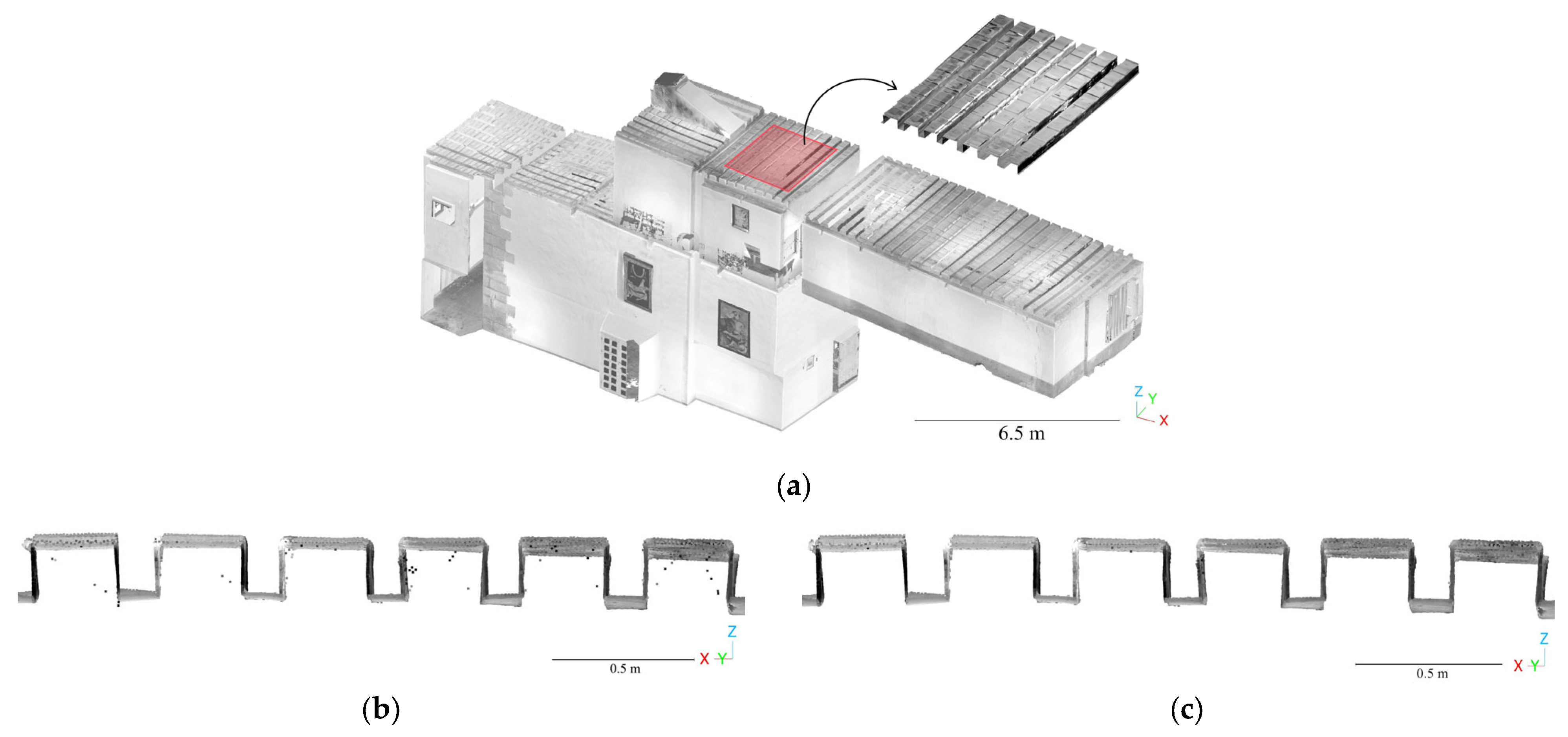
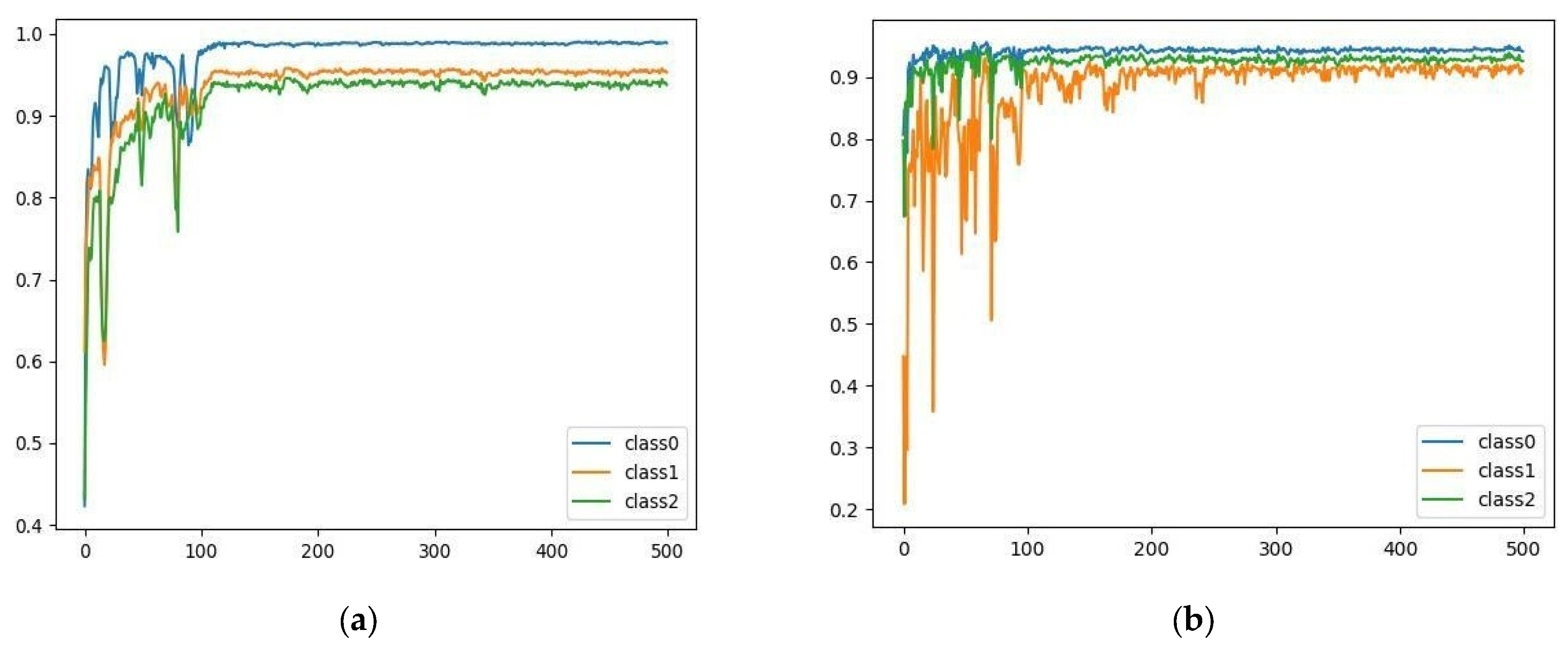
4.1. Evaluation of Deflection in Timber Slabs—Nuestra Señora de Gracia Convent
4.2. Three-Dimensional Mapping of Biological Colonies, Salts, Soiling and Material Loss—Saint Francisco Master Gate
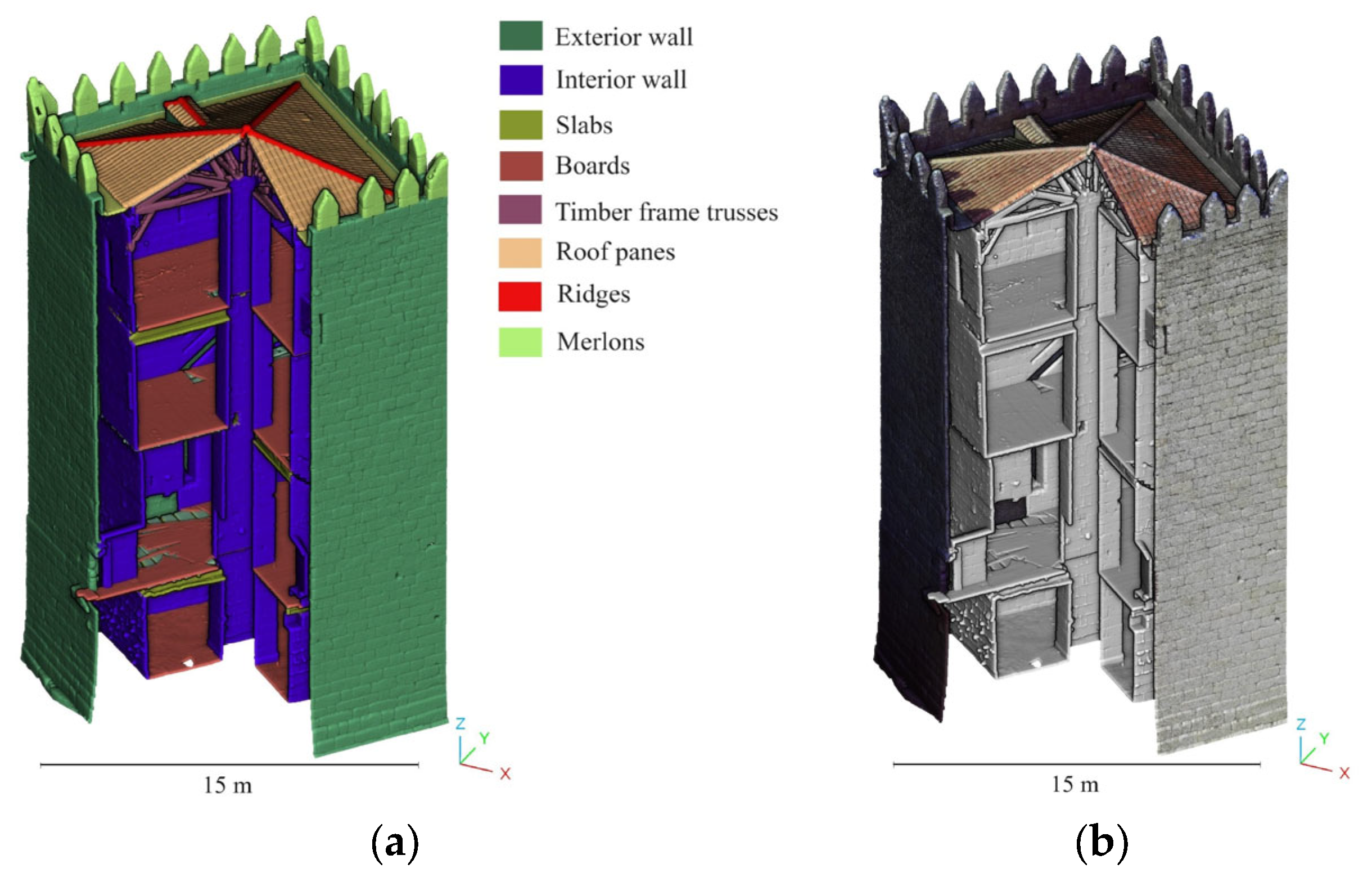
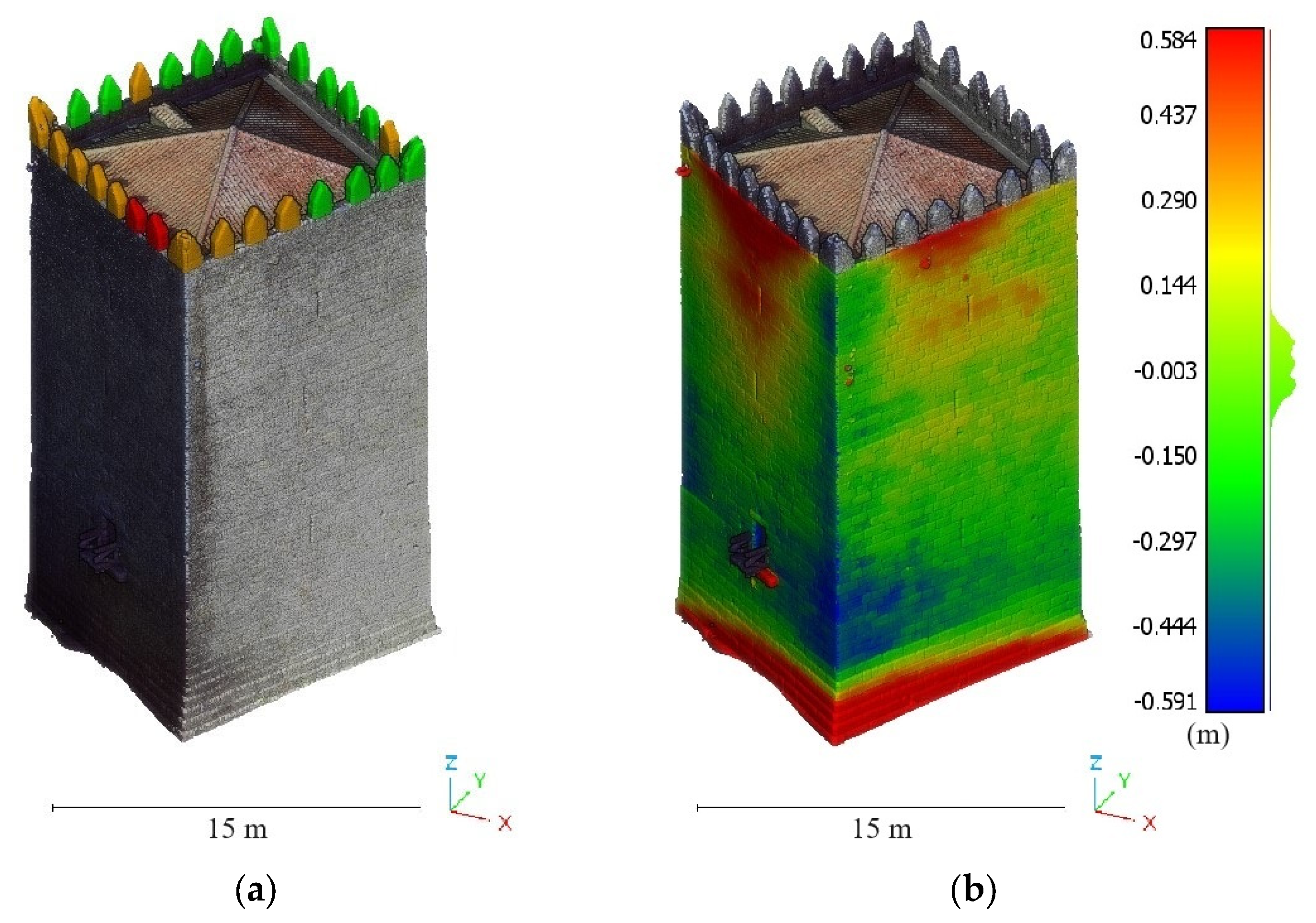
4.3. Analysis of Out-of-Plane Deformations in Masonry Walls and Timber Floors—Keep Tower of Guimaraes Castle
- A geometric-based method with a point-to-primitive distance strategy for evaluating the out-of-plane deformations of walls and floorboards.
- A geometric-based method based on the extraction of vertical sections.
5. Discussion and Conclusions
- The capability to segment constructive systems by using ML and DL strategies.
- The capability of applying Auto-Machine Learning methods to reduce the complexity of training ML algorithms.
- The possibility of computing geometric and textural features for training artificial intelligence models.
- The ability to implement all damage detection strategies identified in the recent systematic review performed by Sánchez-Aparicio et al. [8].
- The proposal of several classification trees for constructive segmentation and damage detection.
- The integration of novel strategies for evaluating deformations in arches and vaults, deflections in slabs, or inclinations in vertical elements.
- The capacity to reduce the noise of the 3D point cloud, voxelise the 3D point cloud, or generate a web-viewer.
- Training DL algorithms requires a large dataset, which could limit the application of these methods.
- Both ML and DL methods show excellent performance. However, the results are not perfect and require the revision of the 3D point cloud by an expert user. The outcomes and performance in different situations were evaluated through a series of case studies on historical building diagnosis, presented in Section 4. In some cases, the process could not be fully automated, and minor manual adjustments were required. However, these adjustments demanded significantly less time compared to a fully manual segmentation.
- The module devoted to the analysis of inclinations in vertical elements requires a point cloud with no shadows or that is mostly complete. This is because otherwise the fitting strategies could lead to a sub-optimal result.
- The results cannot be translated directly to Building Information Modelling (BIM). It is necessary to develop ad hoc scripts.
- Future works will focus on including new functionalities to the plugin, namely
- Integration of synthetic 3D point clouds. This will enable the training of DL methods by following a similar strategy to that employed by Jing et al. [73].
- Improvement of the module for analysing deformations in arches and vaults by adding more typologies.
- Improvement of the module for analysing inclination in vertical elements in situations where there is a large portion of shadows by approximating the element to common shapes (e.g., IPE section for steel, rectangular sections, etc.).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Morel, H.; Megarry, W.; Potts, A.; Hosagrahar, J.; Roberts, D.; Arikan, Y.; Brondizio, E.; Cassar, M.; Flato, G.; Forgesson, S.; et al. Global Research and Action Agenda on Culture, Heritage and Climate Change; Project Report; ICOMOS & ISCM CHC: Charenton-le-Pont, France, 2022; pp. 1–69. [Google Scholar]
- Pritchard, D.; Rigauts, T.; Ripanti, F.; Ioannides, M.; Brumana, R.; Davies, R.; Avouri, E.; Cliffen, H.; Joncic, N.; Osti, G.; et al. Study on Quality in 3D Digitisation of Tangible Cultural Heritage. In Proceedings of the Arqueológica 2.0—9th International Congress & 3rd GEORES—Geomatics and Preservation, Virtual Event, 26–28 April 2021. [Google Scholar] [CrossRef]
- Román, A. Reconstruction—From the Venice Charter to the Charter of Cracow 2000. 2002. Available online: https://openarchive.icomos.org/id/eprint/555/ (accessed on 1 March 2025).
- Xiao, W.; Mills, J.; Guidi, G.; Rodríguez-Gonzálvez, P.; Gonizzi Barsanti, S.; González-Aguilera, D. Geoinformatics for the Conservation and Promotion of Cultural Heritage in Support of the UN Sustainable Development Goals. ISPRS J. Photogramm. Remote Sens. 2018, 142, 389–406. [Google Scholar] [CrossRef]
- Yang, X.; Grussenmeyer, P.; Koehl, M.; Macher, H.; Murtiyoso, A.; Landes, T. Review of Built Heritage Modelling: Integration of HBIM and Other Information Techniques. J. Cult. Herit. 2020, 46, 350–360. [Google Scholar] [CrossRef]
- Moyano, J.; León, J.; Nieto-Julián, J.E.; Bruno, S. Semantic Interpretation of Architectural and Archaeological Geometries: Point Cloud Segmentation for HBIM Parameterisation. Autom. Constr. 2021, 130, 103856. [Google Scholar] [CrossRef]
- Yang, S.; Hou, M.; Li, S. Three-Dimensional Point Cloud Semantic Segmentation for Cultural Heritage: A Comprehensive Review. Remote Sens. 2023, 15, 548. [Google Scholar] [CrossRef]
- Sánchez-Aparicio, L.J.; Blanco-García, F.L.; Mencías-Carrizosa, D.; Villanueva-Llauradó, P.; Aira-Zunzunegui, J.R.; Sanz-Arauz, D.; Pierdicca, R.; Pinilla-Melo, J.; Garcia-Gago, J. Detection of Damage in Heritage Constructions Based on 3D Point Clouds. A Systematic Review. J. Build. Eng. 2023, 77, 107440. [Google Scholar] [CrossRef]
- González-Aguilera, D.; Soilán, M.; Morcillo, A.; del Pozo, S.; Courtenay, L.A.; Rodríguez-Gonzálvez, P.; Hernández-López, D. Intelligent Recording of Cultural Heritage: From Point Clouds to Semantic Enriched Models. In Diagnosis of Heritage Buildings by Non-Destructive Techniques; Woodhead Publishing: Cambridge, UK, 2024; pp. 183–218. [Google Scholar] [CrossRef]
- Teruggi, S.; Grilli, E.; Russo, M.; Fassi, F.; Remondino, F. A Hierarchical Machine Learning Approach for Multi-Level and Multi-Resolution 3D Point Cloud Classification. Remote Sens. 2020, 12, 2598. [Google Scholar] [CrossRef]
- Del Pozo, S.; Herrero-Pascual, J.; Felipe-García, B.; Hernández-López, D.; Rodríguez-Gonzálvez, P.; González-Aguilera, D. Multispectral Radiometric Analysis of Façades to Detect Pathologies from Active and Passive Remote Sensing. Remote Sens. 2016, 8, 80. [Google Scholar] [CrossRef]
- Sánchez-Aparicio, L.J.; Del Pozo, S.; Ramos, L.F.; Arce, A.; Fernandes, F.M. Heritage Site Preservation with Combined Radiometric and Geometric Analysis of TLS Data. Autom. Constr. 2018, 85, 24–39. [Google Scholar] [CrossRef]
- Valero, E.; Bosché, F.; Forster, A. Automatic Segmentation of 3D Point Clouds of Rubble Masonry Walls, and Its Application to Building Surveying, Repair and Maintenance. Autom. Constr. 2018, 96, 29–39. [Google Scholar] [CrossRef]
- Historic England. Photogrammetric Applications for Cultural Heritage; Historic England: London, UK, 2017. [Google Scholar]
- Historic England. 3D Laser Scanning for Heritage: Advice and Guidance on the Use of Laser Scanning in Archaeology and Architecture; Historic England: London, UK, 2018. [Google Scholar]
- Gonizzi Barsanti, S.; Marini, M.R.; Malatesta, S.G.; Rossi, A. Evaluation of Denoising and Voxelization Algorithms on 3D Point Clouds. Remote Sens. 2024, 16, 2632. [Google Scholar] [CrossRef]
- Sánchez-Aparicio, L.J.; Villanueva-Llauradó, P.; Sanz-Honrado, P.; Aira-Zunzunegui, J.R.; Pinilla Melo, J.; González-Aguilera, D.; Oliveira, D.V. Evaluation of a Slam-Based Point Cloud for Deflection Analysis in Historic Timber Floors. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, XLVIII-M-2–2023, 1411–1418. [Google Scholar] [CrossRef]
- Yue, H.; Wang, Q.; Zhao, H.; Zeng, N.; Tan, Y. Deep Learning Applications for Point Clouds in the Construction Industry. Autom. Constr. 2024, 168, 105769. [Google Scholar] [CrossRef]
- Xiao, X.; Wang, K.; Zhong, Z.; Qu, W.; Wu, W.; Cui, Z.; Su, Y.; Li, A.; Gong, J.; Li, D. A Novel Data-Driven Based High-Precision Building Roof Contour Full-Automatic Extraction and Structured 3D Reconstruction Method Combining Stereo Images and LiDAR Points. Int. J. Digit. Earth 2025, 18, 2484668. [Google Scholar] [CrossRef]
- Poux, F.; Mattes, C.; Selman, Z.; Kobbelt, L. Automatic Region-Growing System for the Segmentation of Large Point Clouds. Autom. Constr. 2022, 138, 104250. [Google Scholar] [CrossRef]
- Ochmann, S.; Vock, R.; Klein, R. Automatic Reconstruction of Fully Volumetric 3D Building Models from Oriented Point Clouds. ISPRS J. Photogramm. Remote Sens. 2019, 151, 251–262. [Google Scholar] [CrossRef]
- Rauch, L.; Braml, T. Semantic Point Cloud Segmentation with Deep-Learning-Based Approaches for the Construction Industry: A Survey. Appl. Sci. 2023, 13, 9146. [Google Scholar] [CrossRef]
- Mirzaei, K.; Arashpour, M.; Asadi, E.; Masoumi, H.; Bai, Y.; Behnood, A. 3D Point Cloud Data Processing with Machine Learning for Construction and Infrastructure Applications: A Comprehensive Review. Adv. Eng. Inform. 2022, 51, 101501. [Google Scholar] [CrossRef]
- Bagate, A.; Shah, M. Human Activity Recognition Using RGB-D Sensors. In Proceedings of the 2019 International Conference on Intelligent Computing and Control Systems, ICCS 2019, Madurai, India, 15–17 May 2019; pp. 902–905. [Google Scholar] [CrossRef]
- Pushkar, A.; Senthilvel, M.; Varghese, K. Automated Progress Monitoring of Masonry Activity Using Photogrammetric Point Cloud. In Proceedings of the ISARC 2018—35th International Symposium on Automation and Robotics in Construction and International AEC/FM Hackathon: The Future of Building Things, Berlin, Germany, 20–25 July 2018. [Google Scholar] [CrossRef]
- Mohammadi, M.E.; Wood, R.L.; Wittich, C.E. Non-Temporal Point Cloud Analysis for Surface Damage in Civil Structures. ISPRS Int. J. Geo-Inf. 2019, 8, 527. [Google Scholar] [CrossRef]
- Galantucci, R.A.; Musicco, A.; Verdoscia, C.; Fatiguso, F. Machine Learning for the Semi-Automatic 3D Decay Segmentation and Mapping of Heritage Assets. Int. J. Archit. Herit. 2023, 19, 389–407. [Google Scholar] [CrossRef]
- Matrone, F.; Grilli, E.; Martini, M.; Paolanti, M.; Pierdicca, R.; Remondino, F. Comparing Machine and Deep Learning Methods for Large 3D Heritage Semantic Segmentation. ISPRS Int. J. Geo-Inf. 2020, 9, 535. [Google Scholar] [CrossRef]
- Grilli, E.; Özdemir, E.; Remondino, F. Application of Machine and Deep Learning Strategies for the Classification of Heritage Point Clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-4-W18, 447–454. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, L.; Wang, P.S.; Liu, Z.; Liu, X.; Qiao, Y.; Ouyang, W.; He, T.; Zhao, H. Point Transformer V3: Simpler, Faster, Stronger. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 4840–4851. [Google Scholar] [CrossRef]
- Kim, Y.; Nguyen, C.H.P.; Choi, Y. Automatic Pipe and Elbow Recognition from Three-Dimensional Point Cloud Model of Industrial Plant Piping System Using Convolutional Neural Network-Based Primitive Classification. Autom. Constr. 2020, 116, 103236. [Google Scholar] [CrossRef]
- Braun, A.; Tuttas, S.; Borrmann, A.; Stilla, U. Improving Progress Monitoring by Fusing Point Clouds, Semantic Data and Computer Vision. Autom. Constr. 2020, 116, 103210. [Google Scholar] [CrossRef]
- Tang, S.; Li, X.; Zheng, X.; Wu, B.; Wang, W.; Zhang, Y. BIM Generation from 3D Point Clouds by Combining 3D Deep Learning and Improved Morphological Approach. Autom. Constr. 2022, 141, 104422. [Google Scholar] [CrossRef]
- Pierdicca, R.; Paolanti, M.; Matrone, F.; Martini, M.; Morbidoni, C.; Malinverni, E.S.; Frontoni, E.; Lingua, A.M. Point Cloud Semantic Segmentation Using a Deep Learning Framework for Cultural Heritage. Remote Sens. 2020, 12, 1005. [Google Scholar] [CrossRef]
- Lou, Y.; Meng, S.; Zhou, Y. Deep Learning-Based Three-Dimensional Crack Damage Detection Method Using Point Clouds without Color Information. Struct. Health Monit. 2024, 24, 657–675. [Google Scholar] [CrossRef]
- Zhao, S.; Kang, F.; Li, J.; Ma, C. Structural Health Monitoring and Inspection of Dams Based on UAV Photogrammetry with Image 3D Reconstruction. Autom. Constr. 2021, 130, 103832. [Google Scholar] [CrossRef]
- Raushan, R.; Singhal, V.; Jha, R.K. Damage Detection in Concrete Structures with Multi-Feature Backgrounds Using the YOLO Network Family. Autom. Constr. 2025, 170, 105887. [Google Scholar] [CrossRef]
- Jiang, Y.; Pang, D.; Li, C.; Wang, J. A Method of Concrete Damage Detection and Localization Based on Weakly Supervised Learning. Comput.-Aided Civ. Infrastruct. Eng. 2024, 39, 1042–1060. [Google Scholar] [CrossRef]
- Zhang, W.J.; Wan, H.P.; Todd, M.D. An Efficient 2D-3D Fusion Method for Bridge Damage Detection Under Complex Backgrounds with Imbalanced Training Data. Adv. Eng. Inform. 2025, 65, 103373. [Google Scholar] [CrossRef]
- Yamane, T.; Chun, P.-j.; Honda, R. Detecting and Localising Damage Based on Image Recognition and Structure from Motion, and Reflecting It in a 3D Bridge Model. Struct. Infrastruct. Eng. 2024, 20, 594–606. [Google Scholar] [CrossRef]
- Shibano, K.; Morozova, N.; Ito, Y.; Shimamoto, Y.; Tachibana, Y.; Suematsu, K.; Chiyoda, A.; Ito, H.; Suzuki, T. Evaluation of Surface Damage for In-Service Deteriorated Agricultural Concrete Headworks Using 3D Point Clouds by Laser Scanning Method. Paddy Water Environ. 2024, 22, 257–269. [Google Scholar] [CrossRef]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS. ACM SIGMOD Record 1999, 28, 49–60. [Google Scholar] [CrossRef]
- Brodu, N.; Lague, D. 3D Terrestrial Lidar Data Classification of Complex Natural Scenes Using a Multi-Scale Dimensionality Criterion: Applications in Geomorphology. ISPRS J. Photogramm. Remote Sens. 2012, 68, 121–134. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D Comparison of Complex Topography with Terrestrial Laser Scanner: Application to the Rangitikei Canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Costamagna, E.; Santana Quintero, M.; Bianchini, N.; Mendes, N.; Lourenço, P.B.; Su, S.; Paik, Y.M.; Min, A. Advanced Non-Destructive Techniques for the Diagnosis of Historic Buildings: The Loka-Hteik-Pan Temple in Bagan. J. Cult. Herit. 2020, 43, 108–117. [Google Scholar] [CrossRef]
- Dominici, D.; Alicandro, M.; Rosciano, E.; Massimi, V. Multiscale Documentation and Monitoring of l’aquila Historical Centre Using Uav Photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2017, 42, 365–371. [Google Scholar] [CrossRef]
- Croce, V.; Caroti, G.; De Luca, L.; Jacquot, K.; Piemonte, A.; Véron, P. From the Semantic Point Cloud to Heritage-Building Information Modeling: A Semiautomatic Approach Exploiting Machine Learning. Remote Sens. 2021, 13, 461. [Google Scholar] [CrossRef]
- Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic Point Cloud Interpretation Based on Optimal Neighborhoods, Relevant Features and Efficient Classifiers. ISPRS J. Photogramm. Remote Sens. 2015, 105, 286–304. [Google Scholar] [CrossRef]
- Valero, E.; Forster, A.; Bosché, F.; Hyslop, E.; Wilson, L.; Turmel, A. Automated Defect Detection and Classification in Ashlar Masonry Walls Using Machine Learning. Autom. Constr. 2019, 106, 102846. [Google Scholar] [CrossRef]
- Grilli, E.; Farella, E.M.; Torresani, A.; Remondino, F. Geometric Features Analysis for the Classification of Cultural Heritage Point Clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2-W15, 541–548. [Google Scholar] [CrossRef]
- Dong, L.; Syed, K. OptimalFlow. 2020. Available online: https://github.com/tonyleidong/OptimalFlow.git (accessed on 1 February 2025).
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.; Koltun, V. Point Transformer. In Proceedings of the IEEE International Conference on Computer Vision, Seattle, WA, USA, 13–19 June 2020; pp. 16239–16248. [Google Scholar] [CrossRef]
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3D Semantic Parsing of Large-Scale Indoor Spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1534–1543. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D ShapeNets: A Deep Representation for Volumetric Shapes. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar] [CrossRef]
- Yi, L.; Kim, V.G.; Ceylan, D.; Shen, I.C.; Yan, M.; Su, H.; Lu, C.; Huang, Q.; Sheffer, A.; Guibas, L. A Scalable Active Framework for Region Annotation in 3D Shape Collections. ACM Trans. Graph. 2016, 35, 210. [Google Scholar] [CrossRef]
- Matrone, F.; Lingua, A.; Pierdicca, R.; Malinverni, E.S.; Paolanti, M.; Grilli, E.; Remondino, F.; Murtiyoso, A.; Landes, T. A Benchmark For Large-Scale Heritage Point Cloud Semantic Segmentation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B2-2020, 1419–1426. [Google Scholar] [CrossRef]
- Dong, Z.; Liang, F.; Yang, B.; Xu, Y.; Zang, Y.; Li, J.; Wang, Y.; Dai, W.; Fan, H.; Hyyppäb, J.; et al. Registration of Large-Scale Terrestrial Laser Scanner Point Clouds: A Review and Benchmark. ISPRS J. Photogramm. Remote Sens. 2020, 163, 327–342. [Google Scholar] [CrossRef]
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.D.; Schindler, K.; Pollefeys, M. Semantic3D.Net: A New Large-Scale Point Cloud Classification Benchmark. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 91–98. [Google Scholar] [CrossRef]
- ICOMOS Illustrated Glossary on Stone Deterioration Patterns. Monum. Sitios XV 2008, 1, 82.
- Ye, C.; Acikgoz, S.; Pendrigh, S.; Riley, E.; DeJong, M.J. Mapping Deformations and Inferring Movements of Masonry Arch Bridges Using Point Cloud Data. Eng. Struct. 2018, 173, 530–545. [Google Scholar] [CrossRef]
- Sacco, G.L.S.; Battini, C.; Calderini, C. Damage Detection in Heritage Vaults Through Geometric Deformation Analysis. Lect. Notes Civ. Eng. 2024, 437, 171–179. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for Point-Cloud Shape Detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Huerta Fernández, S. Mechanics of Masonry Vaults: The Equilibrium Approach. In Mechanics of Masonry Vaults: The Equilibrium Approach|En: Historical Constructions. Possibilities of Numerical and Experimental Techniques; Universidade do Minho: Braga, Portugal, 2001; pp. 47–70. [Google Scholar]
- Xu, Z.; Foi, A. Anisotropic Denoising of 3D Point Clouds by Aggregation of Multiple Surface-Adaptive Estimates. IEEE Trans. Vis. Comput. Graph. 2021, 27, 2851–2868. [Google Scholar] [CrossRef]
- Sánchez-Aparicio, L.J.; Mora, R.; Conde, B.; Maté-González, M.Á.; Sánchez-Aparicio, M.; González-Aguilera, D. Integration of a Wearable Mobile Mapping Solution and Advance Numerical Simulations for the Structural Analysis of Historical Constructions: A Case of Study in San Pedro Church (Palencia, Spain). Remote Sens 2021, 13, 1252. [Google Scholar] [CrossRef]
- Gaspari, F.; Barbieri, F.; Fascia, R.; Ioli, F.; Pinto, L. An Open-Source Web Platform for 3D Documentation and Storytelling of Hidden Cultural Heritage. Heritage 2024, 7, 517–536. [Google Scholar] [CrossRef]
- Villanueva Llauradó, P.; Maté González, M.Á.; Sánchez Aparicio, L.J.; Benito Pradillo, M.Á.; González Aguilera, D.; García Palomo, L.C. A Comparative Study Between a Static and a Mobile Laser Scanner for the Digitalization of Inner Spaces in Historical Constructions. In Proceedings of the Construction Pathology, Rehabilitation Technology and Heritage Management, Granada, Spain, 13–16 September 2022; pp. 2492–2498. [Google Scholar]
- Sánchez-Aparicio, L.J.; Masciotta, M.G.; Pellegrini, D.; Conde, B.; Girardi, M.; Padovani, C.; Ramos, L.F.; Riveiro, B. A Multidisciplinary Approach Integrating Geomatics, Dynamic Field Testing and Finite Element Modelling to Evaluate the Conservation State of the Guimarães Castle’s Tower Keep. In Proceedings of the International Conference on Structural Dynamic, EURODYN, Athens, Greece, 23–26 November 2020; Volume 1, pp. 2310–2322. [Google Scholar] [CrossRef]
- Garcia-Gago, J.; Sánchez-Aparicio, L.J.; Soilán, M.; González-Aguilera, D. HBIM for Supporting the Diagnosis of Historical Buildings: Case Study of the Master Gate of San Francisco in Portugal. Autom. Constr. 2022, 141, 104453. [Google Scholar] [CrossRef]
- Viana Da Fonseca, A.; Karam, K.; Ribeiro E Sousa, O.L. Studies and Investigations on Forts with Portuguese Legacy. In Proceedings of the 4th Central Asia Geotechnical Symposium on Geo-Engineering for Construction and Conservation of Cultural Heritage and Historical Site, Samarkand, Uzbekistan, 21–23 September 2012; pp. 67–72. [Google Scholar]
- Heyman, J. The Stone Skeleton. Int J Solids Struct 1966, 2, 249–279. [Google Scholar] [CrossRef]
- Jing, Y.; Sheil, B.; Acikgoz, S. Segmentation of Large-Scale Masonry Arch Bridge Point Clouds with a Synthetic Simulator and the BridgeNet Neural Network. Autom. Constr. 2022, 142, 104459. [Google Scholar] [CrossRef]
- Barontini, A.; Alarcon, C.; Sousa, H.S.; Oliveira, D.V.; Masciotta, M.G.; Azenha, M. Development and Demonstration of an HBIM Framework for the Preventive Conservation of Cultural Heritage. Int. J. Archit. Herit. 2022, 16, 1451–1473. [Google Scholar] [CrossRef]
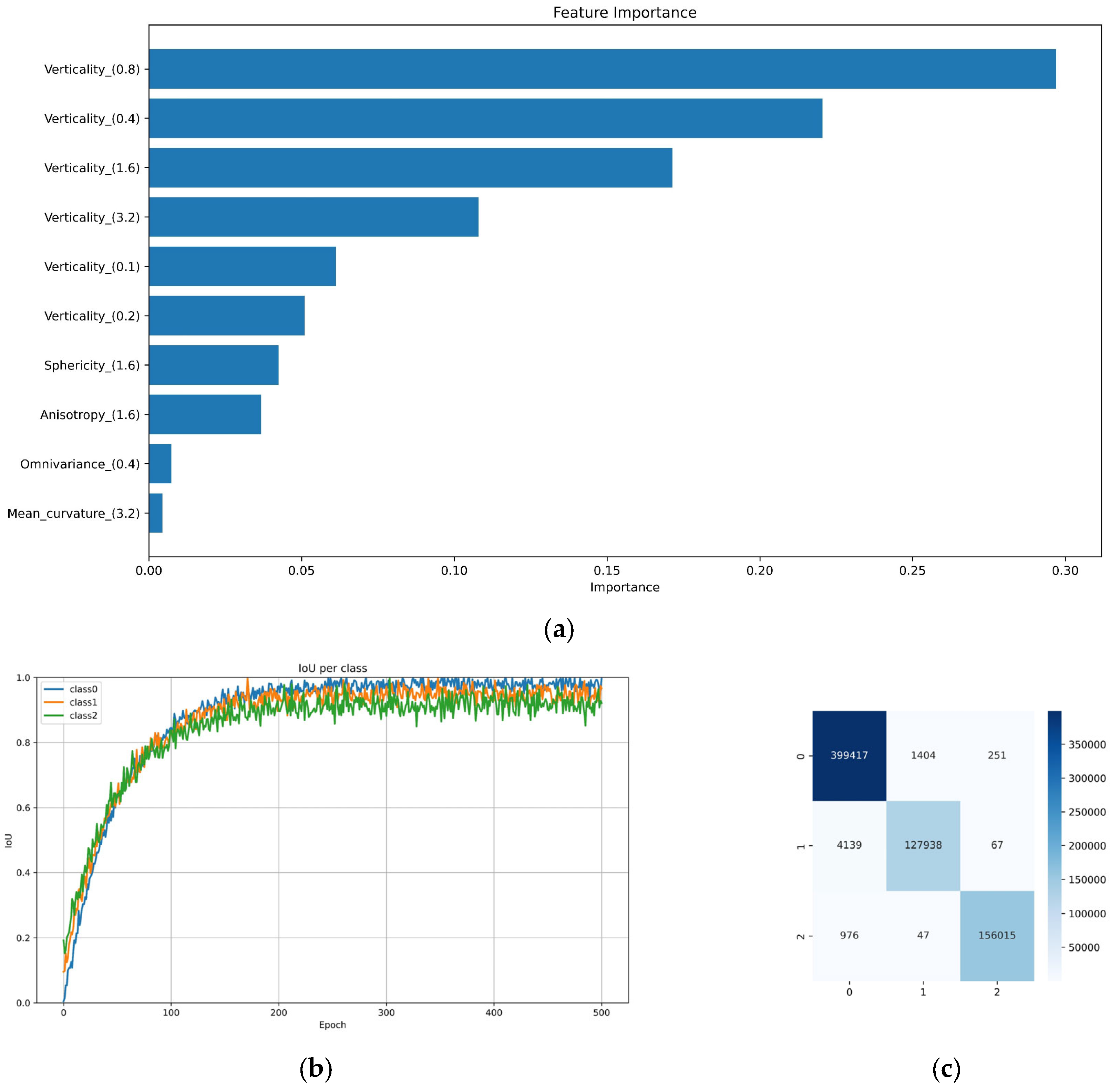
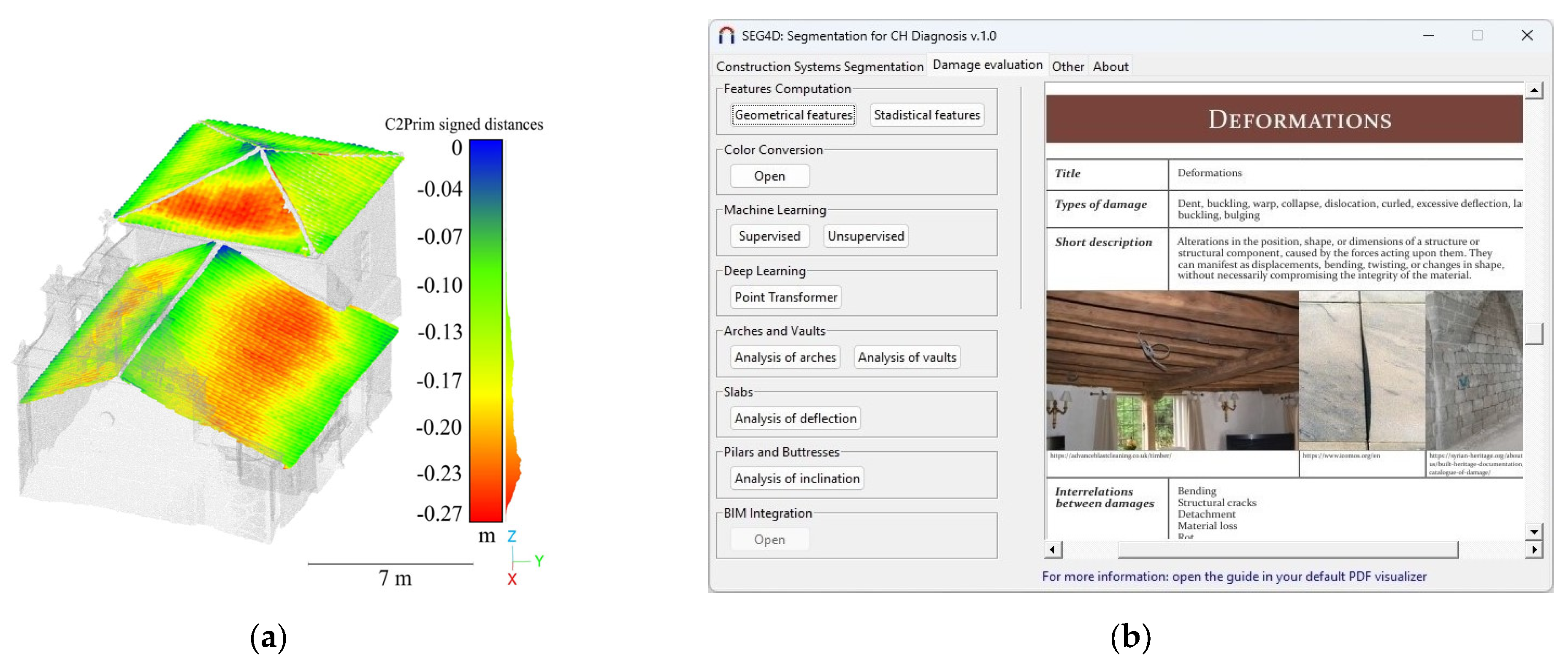
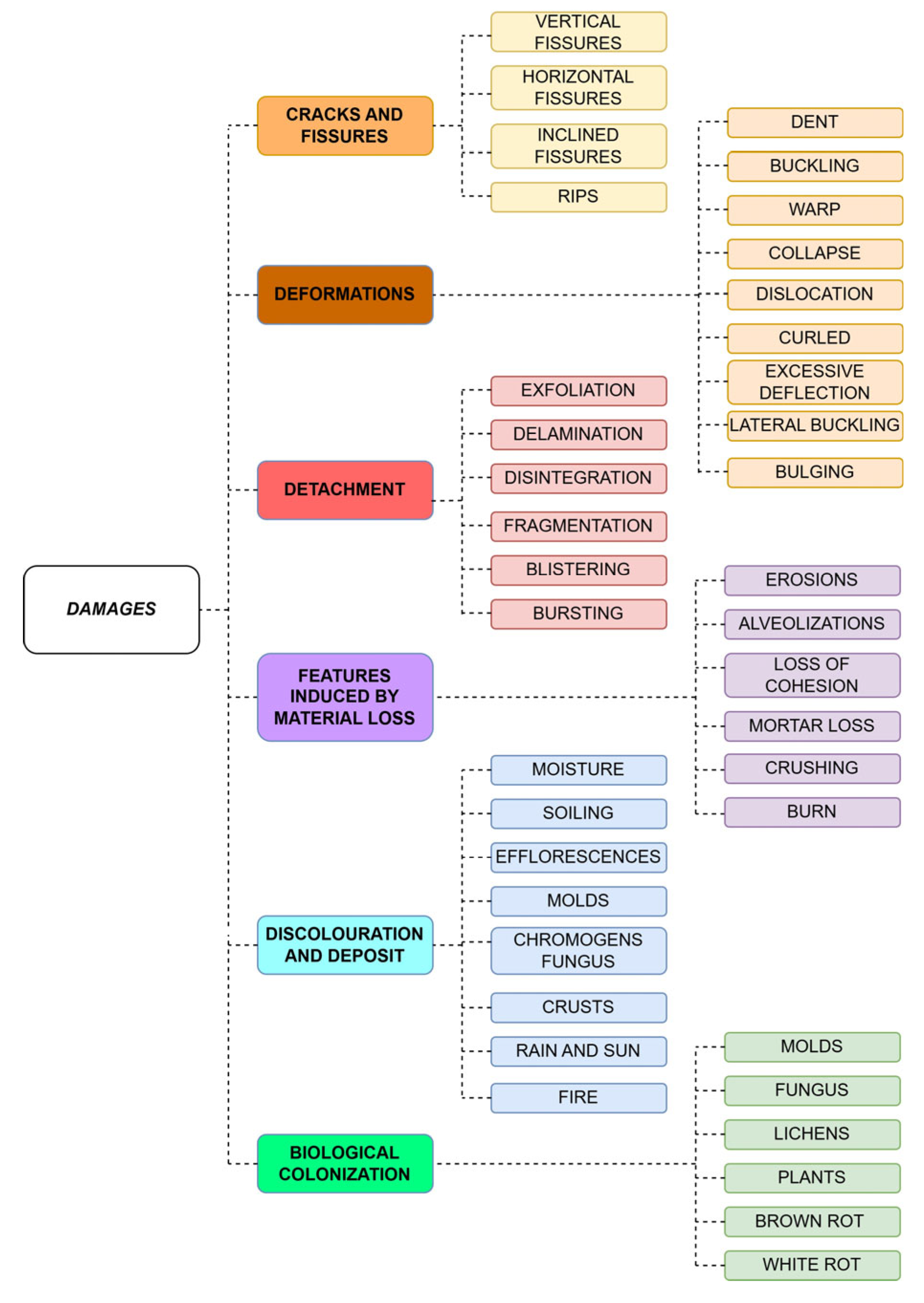


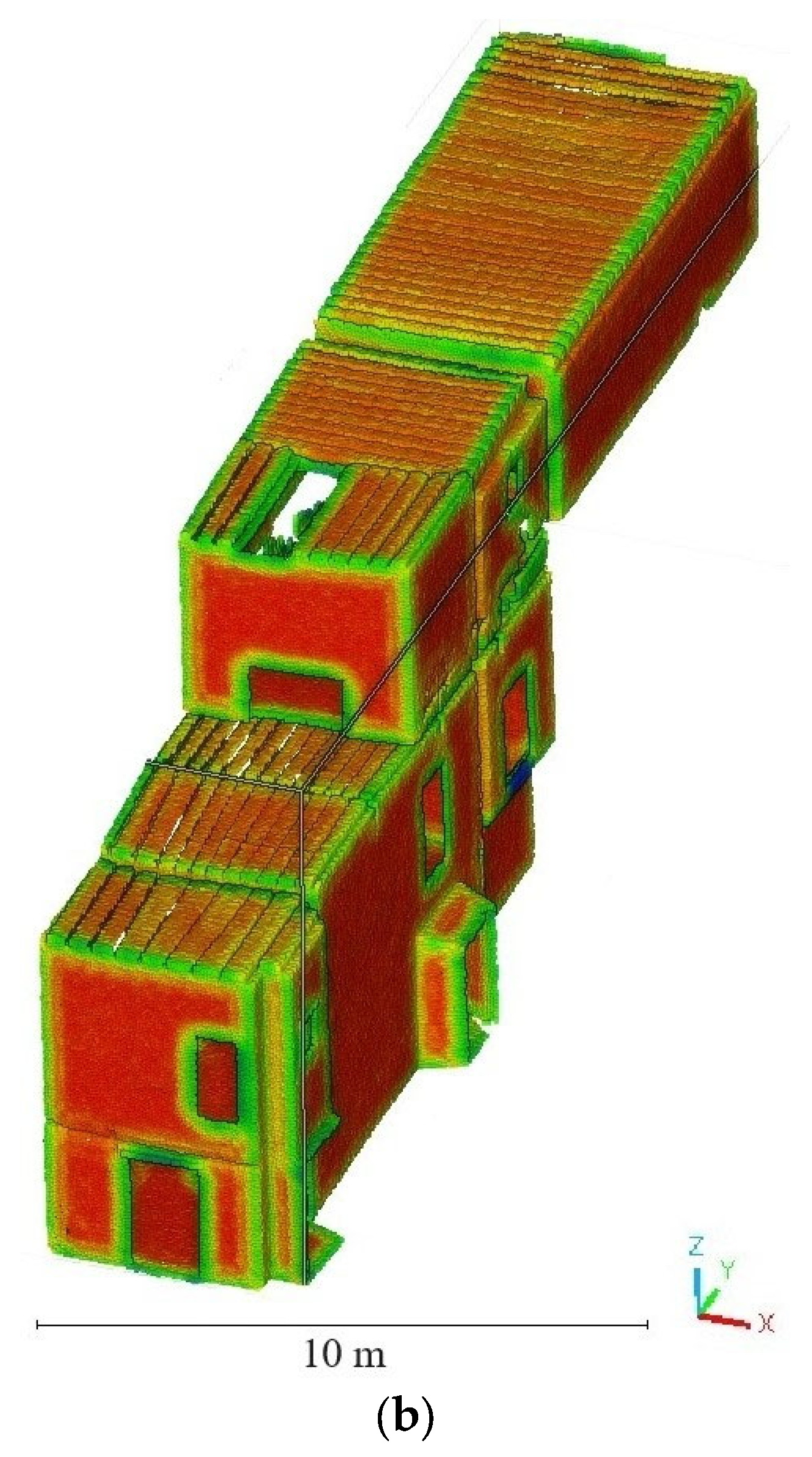


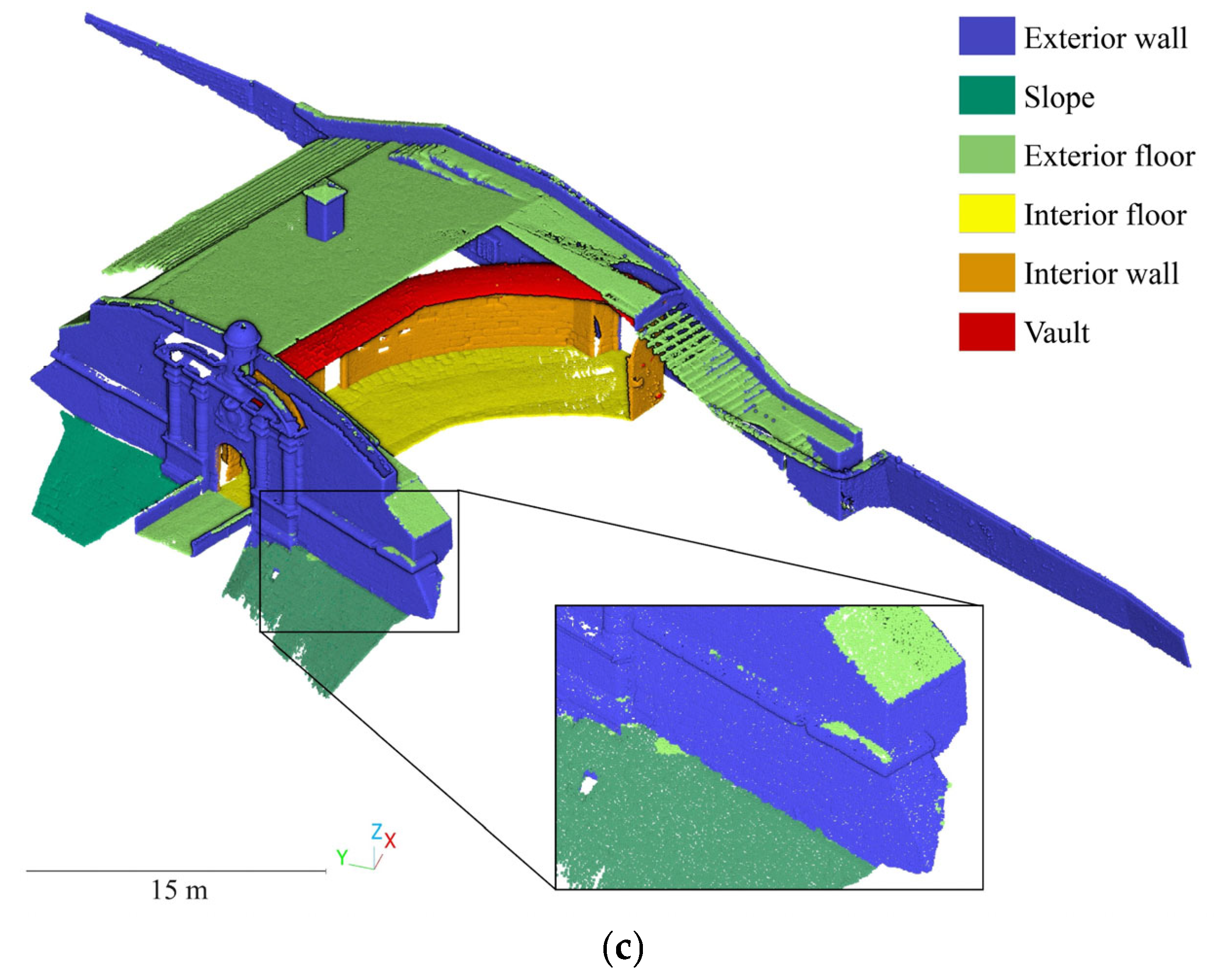
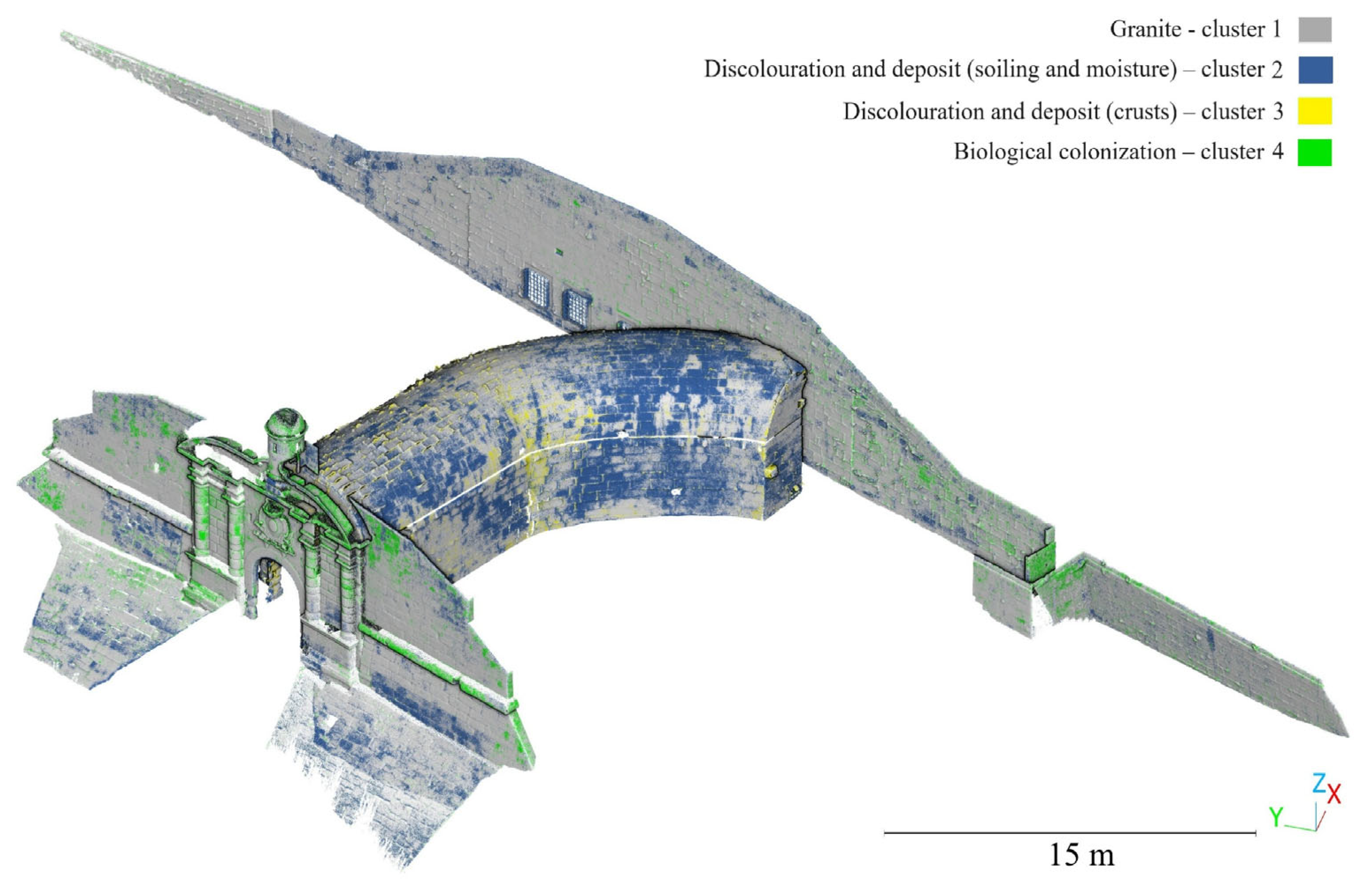
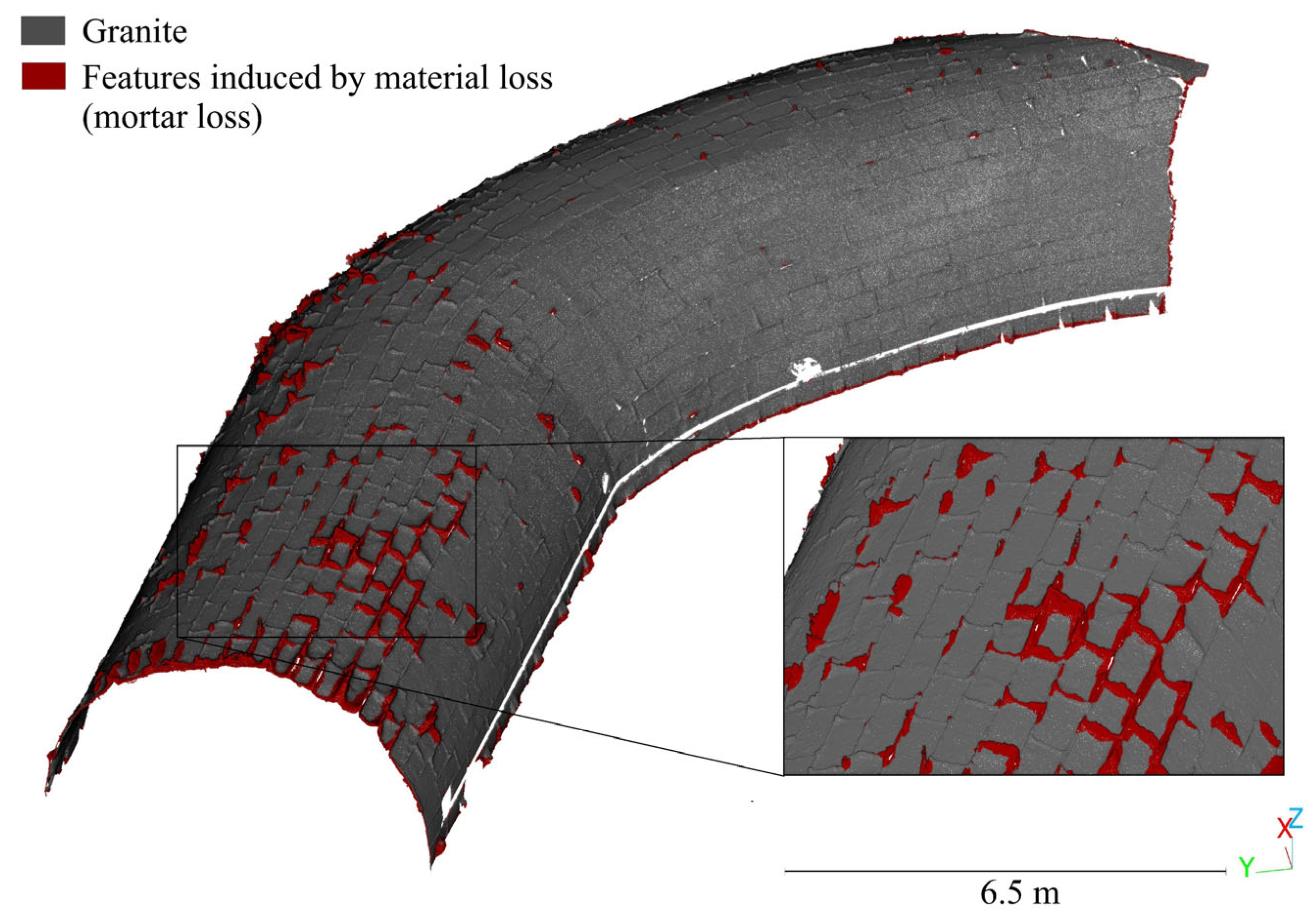

| Approaches that Could Be Used | Damage Class |
|---|---|
| Sections and curve fitting strategies Point-to-point distance Point to primitive Geometrical features. Possible use of statistical features* Threshold by using scalar fields. Possible use of statistical features * Supervised machine learning * Unsupervised machine learning * | Cracks and fissures |
| Sections and curve fitting strategies. Possible in-depth evaluation of deflection in slabs, inclination in pillars/columns/buttresses or deformation in arches and vaults * Point-to-point distance Point to primitive Point to 3D model Geometrical features. Possible use of statistical features * | Deformations |
| Geometrical features. Possible use of statistical features * Threshold by using scalar fields. Possible use of statistical features * Supervised machine learning * Unsupervised machine learning * | Detachment |
| Sections and curve fitting strategies Threshold by using scalar fields. Possible use of statistical features * Supervised machine learning * Unsupervised machine learning * | Features induced by material loss |
| Geometrical features. Possible use of statistical features * Threshold by using scalar fields. Possible use of statistical features * Supervised machine learning * Unsupervised machine learning * | Discolouration and deposits |
| Threshold by using scalar fields. Possible use of statistical features* Supervised machine learning * Unsupervised machine learning * | Biological colonisation |
| F1 Score (%) | Recall (%) | Precision (%) | |
|---|---|---|---|
| Level 1 | |||
| 99.7 | 99.9 | 99.5 | Floor |
| 98.5 | 98.0 | 99.0 | Wall |
| 97.8 | 98.4 | 97.1 | Slab |
| 98.7 | 98.8 | 98.5 | Macro average |
| 98.5 | 98.5 | 98.5 | Weighted average |
| Level 2 | |||
| 97.8 | 98.1 | 97.5 | Timber joist |
| 97.3 | 97.0 | 97.7 | Timber deck |
| 97.6 | 97.6 | 97.6 | Macro average |
| 97.6 | 97.6 | 97.6 | Weighted average |
| Level 3 | |||
| 99.1 | 99.1 | 99.2 | Joist edge |
| 99.4 | 99.4 | 99.4 | Joist face |
| 99.3 | 99.3 | 99.3 | Macro average |
| 99.3 | 99.3 | 99.3 | Weighted average |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Aparicio, L.J.; Santamaría-Maestro, R.; Sanz-Honrado, P.; Villanueva-Llauradó, P.; Aira-Zunzunegui, J.R.; González-Aguilera, D. A Holistic Solution for Supporting the Diagnosis of Historic Constructions from 3D Point Clouds. Remote Sens. 2025, 17, 2018. https://doi.org/10.3390/rs17122018
Sánchez-Aparicio LJ, Santamaría-Maestro R, Sanz-Honrado P, Villanueva-Llauradó P, Aira-Zunzunegui JR, González-Aguilera D. A Holistic Solution for Supporting the Diagnosis of Historic Constructions from 3D Point Clouds. Remote Sensing. 2025; 17(12):2018. https://doi.org/10.3390/rs17122018
Chicago/Turabian StyleSánchez-Aparicio, Luis Javier, Rubén Santamaría-Maestro, Pablo Sanz-Honrado, Paula Villanueva-Llauradó, Jose Ramón Aira-Zunzunegui, and Diego González-Aguilera. 2025. "A Holistic Solution for Supporting the Diagnosis of Historic Constructions from 3D Point Clouds" Remote Sensing 17, no. 12: 2018. https://doi.org/10.3390/rs17122018
APA StyleSánchez-Aparicio, L. J., Santamaría-Maestro, R., Sanz-Honrado, P., Villanueva-Llauradó, P., Aira-Zunzunegui, J. R., & González-Aguilera, D. (2025). A Holistic Solution for Supporting the Diagnosis of Historic Constructions from 3D Point Clouds. Remote Sensing, 17(12), 2018. https://doi.org/10.3390/rs17122018











