Performance Assessment of Undifferenced GPS/Galileo Precise Time Transfer with a Refined Clock Model
Abstract
1. Introduction
2. Methodology
2.1. GPS/Galileo Combined PPP Time Transfer Model
2.2. Refined Clock Model with the Characteristics of an Atomic Clock
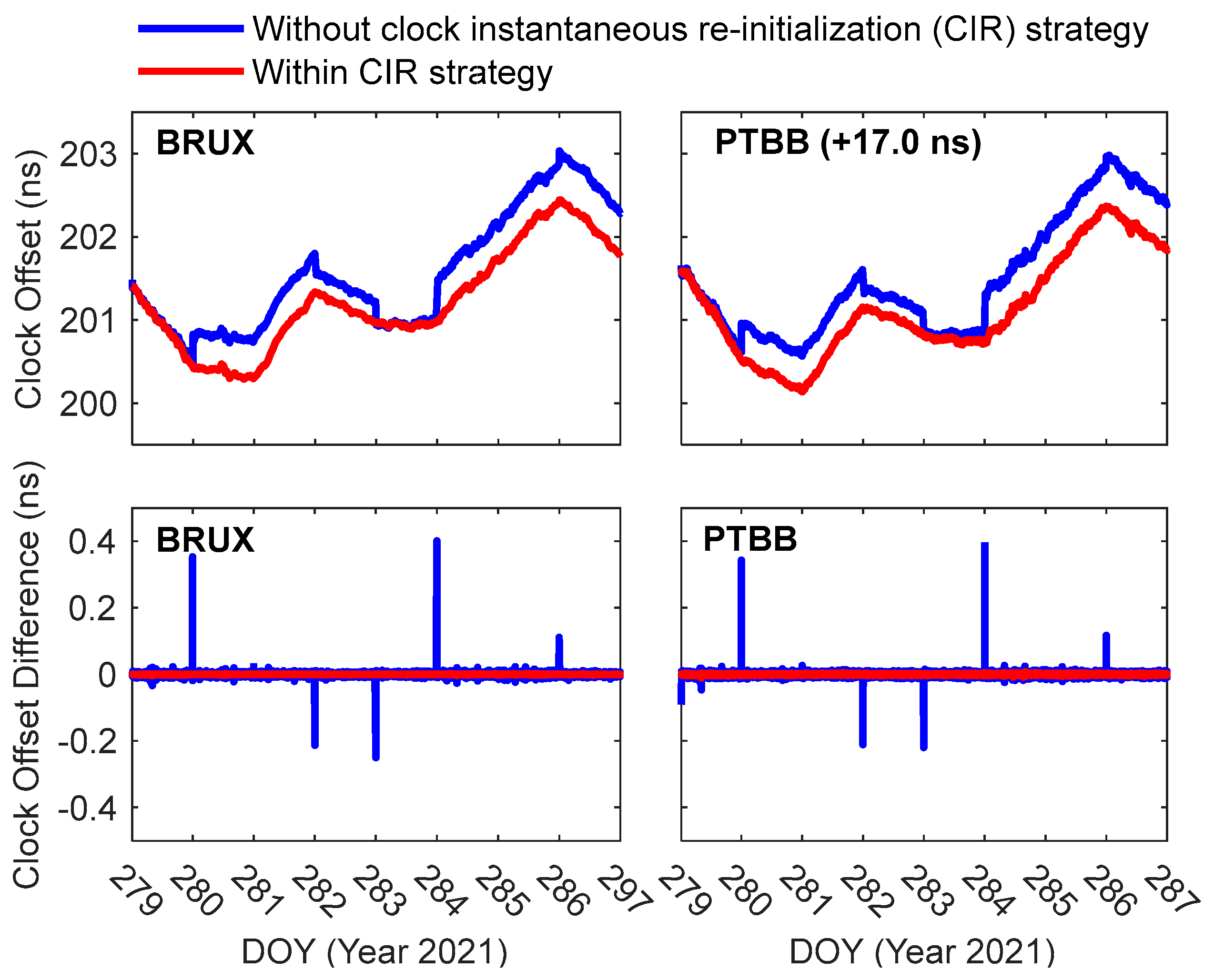
2.3. Clock Instantaneous Re-Initialization Strategy
3. Data Selection and Processing Strategies
4. Results
4.1. Quality Assessment of Observation
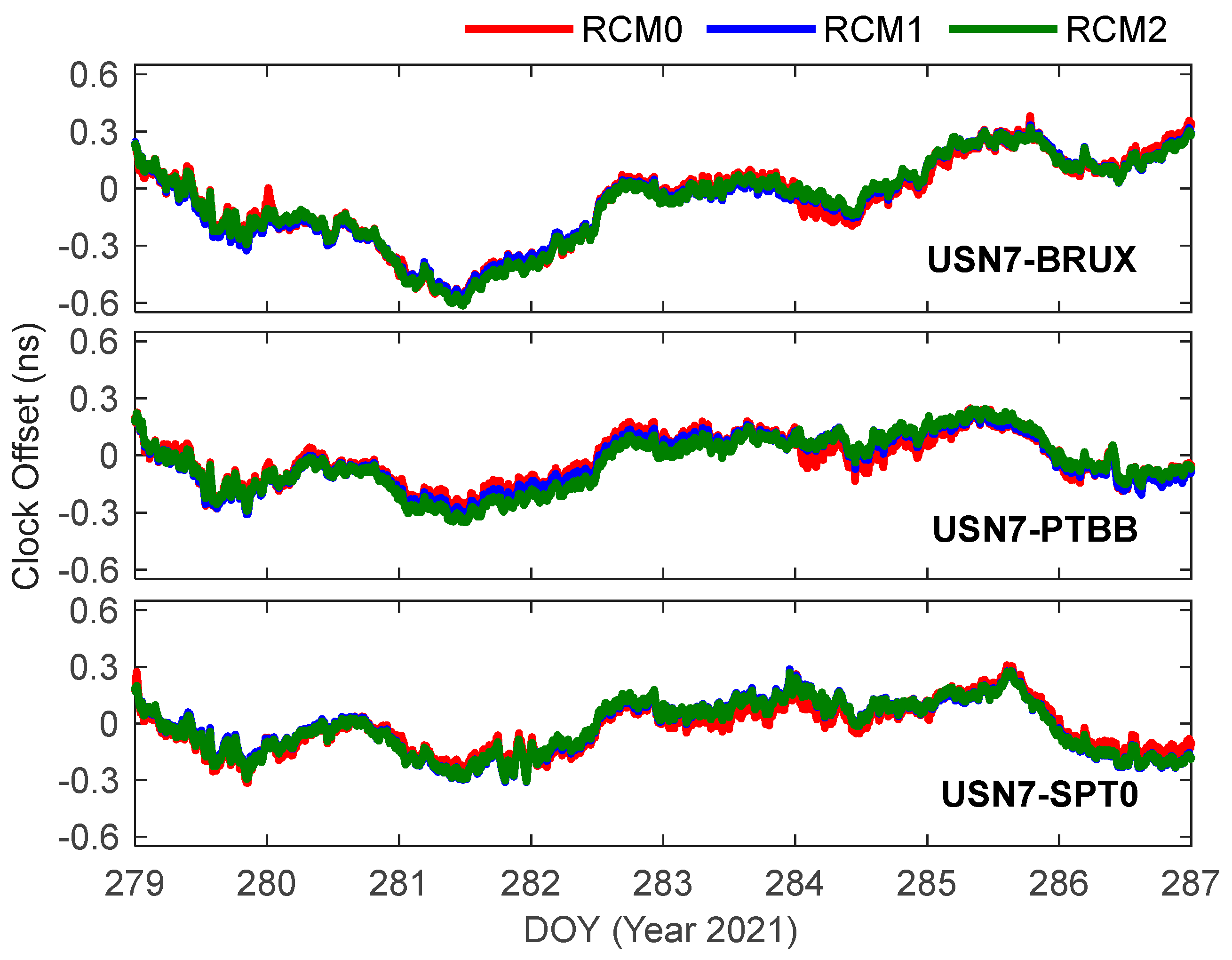
4.2. PPP Time Transfer with Refined Clock Model
4.3. PPP Time Transfer with Refined Clock Model and Ambiguity Resolution
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allan, D.W.; Weiss, M.A. Accurate time and frequency transfer during common-view of a GPS satellite. In Proceedings of the 34th Annual Symposium on Frequency Control, Philadelphia, PA, USA, 28–30 May 1980; pp. 334–346. [Google Scholar]
- Zhang, M.; Lü, J.; Bai, Z.; Jiang, Z.; Chen, B. An overview on GNSS carrier-phase time transfer research. Sci. China-Tech. Sci. 2020, 63, 589–596. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res.-Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Ray, J.; Senior, K. IGS/BIPM pilot project: GPS carrier phase for time/frequency transfer and timescale formation. Metrologia 2003, 40, S270. [Google Scholar] [CrossRef]
- Dow, J.M.; Neilan, R.E.; Rizos, C. The international GNSS service in a changing landscape of global navigation satellite systems. J. Geod. 2009, 83, 191–198. [Google Scholar] [CrossRef]
- Defraigne, P.; Baire, Q. Combining GPS and GLONASS for time and frequency transfer. Adv. Space Res. 2011, 47, 265–275. [Google Scholar] [CrossRef]
- Zhang, P.; Tu, R.; Zhang, R.; Gao, Y.; Cai, H. Combining GPS, BeiDou, and Galileo satellite systems for time and frequency transfer based on carrier phase observations. Remote Sens. 2018, 10, 324. [Google Scholar] [CrossRef]
- Zhang, P.; Tu, R.; Han, J.; Gao, Y.; Zhang, R.; Lu, X. Characterization of biases between BDS-3 and BDS-2, GPS, Galileo and GLONASS observations and their effect on precise time and frequency transfer. Meas. Sci. Technol. 2020, 32, 035006. [Google Scholar] [CrossRef]
- Tu, R.; Hong, J.; Zhang, P.; Zhang, R.; Fan, L.; Liu, J.; Lu, X. Multiple GNSS inter-system biases in precise time transfer. Meas. Sci. Technol. 2019, 30, 115003. [Google Scholar] [CrossRef]
- Lyu, D.; Zeng, F.; Ouyang, X. Time transfer algorithm using multi-GNSS PPP with ambiguity resolution. Chin. Astron. Astrophys. 2020, 44, 371–382. [Google Scholar]
- Ge, Y.; Ding, S.; Dai, P.; Qin, W.; Yang, X. Modeling and assessment of real-time precise point positioning timing with multi-GNSS observations. Meas. Sci. Technol. 2020, 31, 065016. [Google Scholar] [CrossRef]
- Lyu, D.; Zeng, F.; Ouyang, X.; Zhang, H. Real-time clock comparison and monitoring with multi-GNSS precise point positioning: GPS, GLONASS and Galileo. Adv. Space Res. 2020, 65, 560–571. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, X.; Ge, Y.; Yang, X. Investigation of real-time carrier phase time transfer using current multi-constellations. Measurement 2020, 166, 108237. [Google Scholar] [CrossRef]
- Xu, W.; Yan, C.; Zhang, P.; Chen, J.; Qiu, D.; Liang, L.; Tao, J. Real-ime undifferenced precision time transfer of multi-GNSS and multi-frequency. Meas. Sci. Technol. 2025, 36, 025005. [Google Scholar] [CrossRef]
- Shi, J.; Gao, Y. A comparison of three PPP integer ambiguity resolution methods. GPS Solut. 2014, 18, 519–528. [Google Scholar] [CrossRef]
- Banville, S.; Geng, J.; Loyer, S.; Schaer, S.; Springer, T.; Strasser, S. On the interoperability of IGS products for precise point positioning with ambiguity resolution. J. Geod. 2020, 94, 10. [Google Scholar] [CrossRef]
- Mi, X.; Zhang, B.; El-Mowafy, A.; Wang, K.; Yuan, Y. Undifferenced and uncombined GNSS time and frequency transfer with integer ambiguity resolution. J. Geod. 2023, 97, 13. [Google Scholar] [CrossRef]
- Baudiquez, A.; Defraigne, P.; Gertsvolf, M.; Guo, J.; Jian, B.; Meynadier, F.; Tagliaferro, G. Comparison between four integer ambiguity resolved PPP GNSS time transfer software solutions. Metrologia 2025, 62, 025009. [Google Scholar] [CrossRef]
- Petit, G.; Kanj, A.; Loyer, S.; Delporte, J.; Mercier, F.; Perosanz, F. 1 × 10−16 frequency transfer by GPS PPP with integer ambiguity resolution. Metrologia 2015, 52, 301. [Google Scholar] [CrossRef]
- Petit, G.; Kanj, A.; Harmegnies, A.; Loyer, S.; Delporte, J.; Mercier, F.; Perosanz, F. GPS frequency transfer with IPPP. In Proceedings of the 2014 European Frequency and Time Forum (EFTF), Budapest, Hungary, 12–16 April 2014; pp. 451–454. [Google Scholar]
- Petit, G. Sub-10−16 accuracy GNSS frequency transfer with IPPP. GPS Solut. 2021, 25, 22. [Google Scholar] [CrossRef]
- Petit, G.; Defraigne, P. Calibration of GNSS stations for UTC. Metrologia 2023, 60, 025009. [Google Scholar] [CrossRef]
- Xu, W.; Shen, W.; Cai, C.; Li, L.; Wang, L.; Ning, A.; Shen, Z. Comparison and evaluation of carrier phase PPP and single difference time transfer with multi-GNSS ambiguity resolution. GPS Solut. 2022, 26, 58. [Google Scholar] [CrossRef]
- Ren, Z.; Lyu, D.; Gong, H.; Peng, J.; Huang, X.; Sun, G. Continuous time and frequency transfer using robust GPS PPP integer ambiguity resolution method. GPS Solut. 2023, 27, 82. [Google Scholar] [CrossRef]
- Qin, W.; Yang, H.; Zhang, Z.; Wei, P.; Yang, X. The analysis on time transfer of GPS/Galileo/BDS PPP with integer ambiguity resolution. Phys. Scr. 2024, 99, 025011. [Google Scholar] [CrossRef]
- Zhang, R.; Tu, R.; Ge, Y.; Wang, S.; Lu, X. An investigation into multi-frequency ambiguity resolution for real-time PPP time and frequency transfer. Meas. Sci. Technol. 2025, 36, 045003. [Google Scholar] [CrossRef]
- Su, K.; Jin, S. Triple-frequency carrier phase precise time and frequency transfer models for BDS-3. GPS Solut. 2019, 23, 86. [Google Scholar] [CrossRef]
- Zhang, P.; Tu, R.; Gao, Y.; Zhang, R.; Han, J. Performance of Galileo precise time and frequency transfer models using quad-frequency carrier phase observations. GPS Solut. 2020, 24, 40. [Google Scholar] [CrossRef]
- Ge, Y.; Cao, X.; Shen, F.; Yang, X.; Wang, S. BDS-3/Galileo time and frequency transfer with quad-frequency precise point positioning. Remote Sens. 2021, 13, 2704. [Google Scholar] [CrossRef]
- Xu, W.; Yan, C.; Chen, J. Performance evaluation of BDS-2/BDS-3 combined precise time transfer with B1I/B2I/B3I/B1C/B2a five-frequency observations. GPS Solut. 2022, 26, 80. [Google Scholar] [CrossRef]
- Ge, Y.; Zhou, F.; Liu, T.; Qin, W.; Wang, S.; Yang, X. Enhancing real-time precise point positioning time and frequency transfer with receiver clock modeling. GPS Solut. 2019, 23, 20. [Google Scholar] [CrossRef]
- Ge, Y.; Dai, P.; Qin, W.; Yang, X.; Zhou, F.; Wang, S.; Zhao, X. Performance of multi-GNSS precise point positioning time and frequency transfer with clock modeling. Remote Sens. 2019, 11, 347. [Google Scholar] [CrossRef]
- Ge, Y.; Wang, Q.; Wang, Y.; Lyu, D.; Cao, X.; Shen, F.; Meng, X. A new receiver clock model to enhance BDS-3 real-time PPP time transfer with the PPP-B2b service. Satell. Navig. 2023, 4, 8. [Google Scholar] [CrossRef]
- Lyu, D.; Zeng, F.; Ouyang, X.; Yu, H. Enhancing multi-GNSS time and frequency transfer using a refined stochastic model of a receiver clock. Meas. Sci. Technol. 2019, 30, 125016. [Google Scholar] [CrossRef]
- Qin, W.; Ge, Y.; Wei, P.; Yang, X. An approach to a clock offsets model for real-time PPP time and frequency transfer during data discontinuity. Appl. Sci. 2019, 9, 1405. [Google Scholar] [CrossRef]
- Qin, W.; Ge, Y.; Wang, W.; Yang, X. An approach for mitigating PPP day boundary with clock stochastic model. In Proceedings of the 2020 Joint Conference of the IEEE International Frequency Control Symposium and International Symposium on Applications of Ferroelectrics (IFCS-ISAF), New Orleans, LA, USA, 19–23 July 2020; pp. 1–5. [Google Scholar]
- Mikoś, M.; Kazmierski, K.; Hadas, T.; Sośnica, K. Stochastic modeling of the receiver clock parameter in Galileo-only and multi-GNSS PPP solutions. GPS Solut. 2024, 28, 14. [Google Scholar] [CrossRef]
- Han, J.; Zhang, J.; Zhong, S.; Lu, R.; Peng, B. PPP time transfer using an adaptive clock constraint model. Geo-Spatial Inf. Sci. 2024, 1–13. [Google Scholar] [CrossRef]
- Ai, Q.; Yuan, Y.; Xu, T.; Zhang, B. Time and frequency characterization of GLONASS and Galileo on-board clocks. Meas. Sci. Technol. 2020, 31, 065003. [Google Scholar] [CrossRef]
- Zucca, C.; Tavella, P. The clock model and its relationship with the Allan and related variances. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2005, 52, 289–296. [Google Scholar] [CrossRef]
- Zucca, C.; Tavella, P. A mathematical model for the atomic clock error in case of jumps. Metrologia 2015, 52, 514. [Google Scholar] [CrossRef]
- Huang, G.; Zhang, Q. Real-time estimation of satellite clock offset using adaptively robust Kalman filter with classified adaptive factors. GPS Solut. 2012, 16, 531–539. [Google Scholar] [CrossRef]
- Hutsell, S.T. Relating the Hadamard variance to MCS Kalman filter clock estimation. In Proceedings of the 27th Annual Precise Time and Time Interval Systems and Applications Meeting, Bethesda, MD, USA, 29 November–1 December 1995; pp. 291–302. [Google Scholar]
- Yang, Y.; Yue, X.; Yuan, J.; Rizos, C. Enhancing the kinematic precise orbit determination of low earth orbiters using GPS receiver clock modelling. Adv. Space Res. 2014, 54, 1901–1912. [Google Scholar] [CrossRef]
- Wang, K.; Rothacher, M. Stochastic modeling of high-stability ground clocks in GPS analysis. J. Geod. 2013, 87, 427–437. [Google Scholar] [CrossRef]
- Stein, S.R.; Filler, R.L. Kalman filter analysis for real time applications of clocks and oscillators. In Proceedings of the 42nd Annual Frequency Control Symposium, Philadelphia, PA, USA, 1–3 June 1988; IEEE: Piscataway, NJ, USA, 1988; pp. 447–452. [Google Scholar]
- Wang, N.; Yuan, Y.; Li, Z.; Montenbruck, O.; Tan, B. Determination of differential code biases with multi-GNSS observations. J. Geod. 2016, 90, 209–228. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions (2010). In IERS Technical Note 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main/Berlin, Germany, 2010. [Google Scholar]
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products IGS Central Bureau; Jet Propulsion Laboratory: Pasadena, CA, USA, 2009; p. 34.
- Mudrak, A.; De Simone, P.; Lisi, M. Relativistic corrections in the European GNSS Galileo. Aerotec. Missili Spaz. 2015, 94, 139–144. [Google Scholar] [CrossRef]
- Wu, J.-T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. Astron. Astrophys. Trans. 1991, 18, 1647–1660. [Google Scholar] [CrossRef]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géod. 1972, 105, 279–298. [Google Scholar] [CrossRef]
- Böhm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global mapping function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L03304. [Google Scholar] [CrossRef]
- Müller, J.; Dirkx, D.; Kopeikin, S.M.; Lion, G.; Panet, I.; Petit, G.; Visser, P.N. High performance clocks and gravity field determination. Space Sci. Rev. 2018, 214, 5. [Google Scholar] [CrossRef]
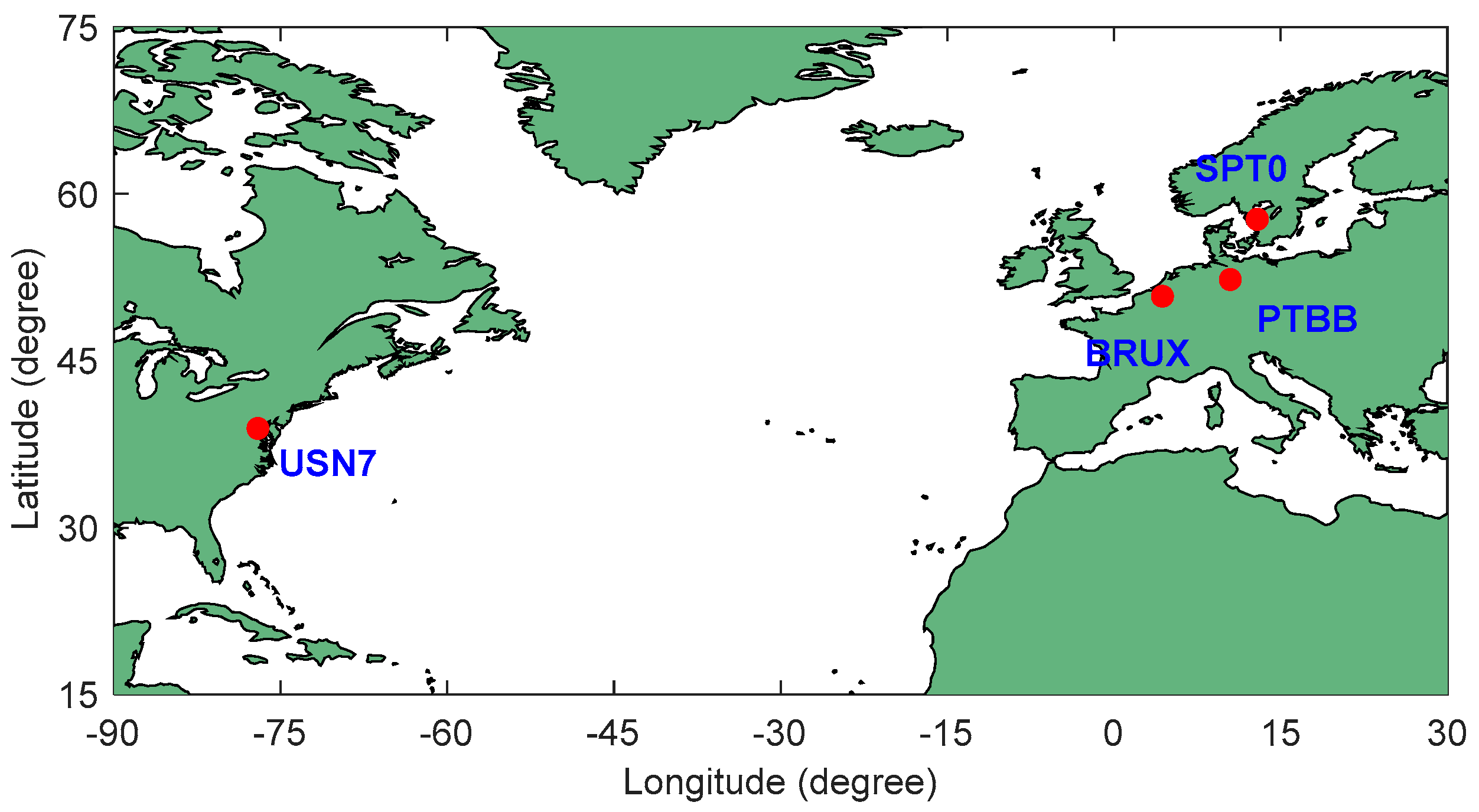

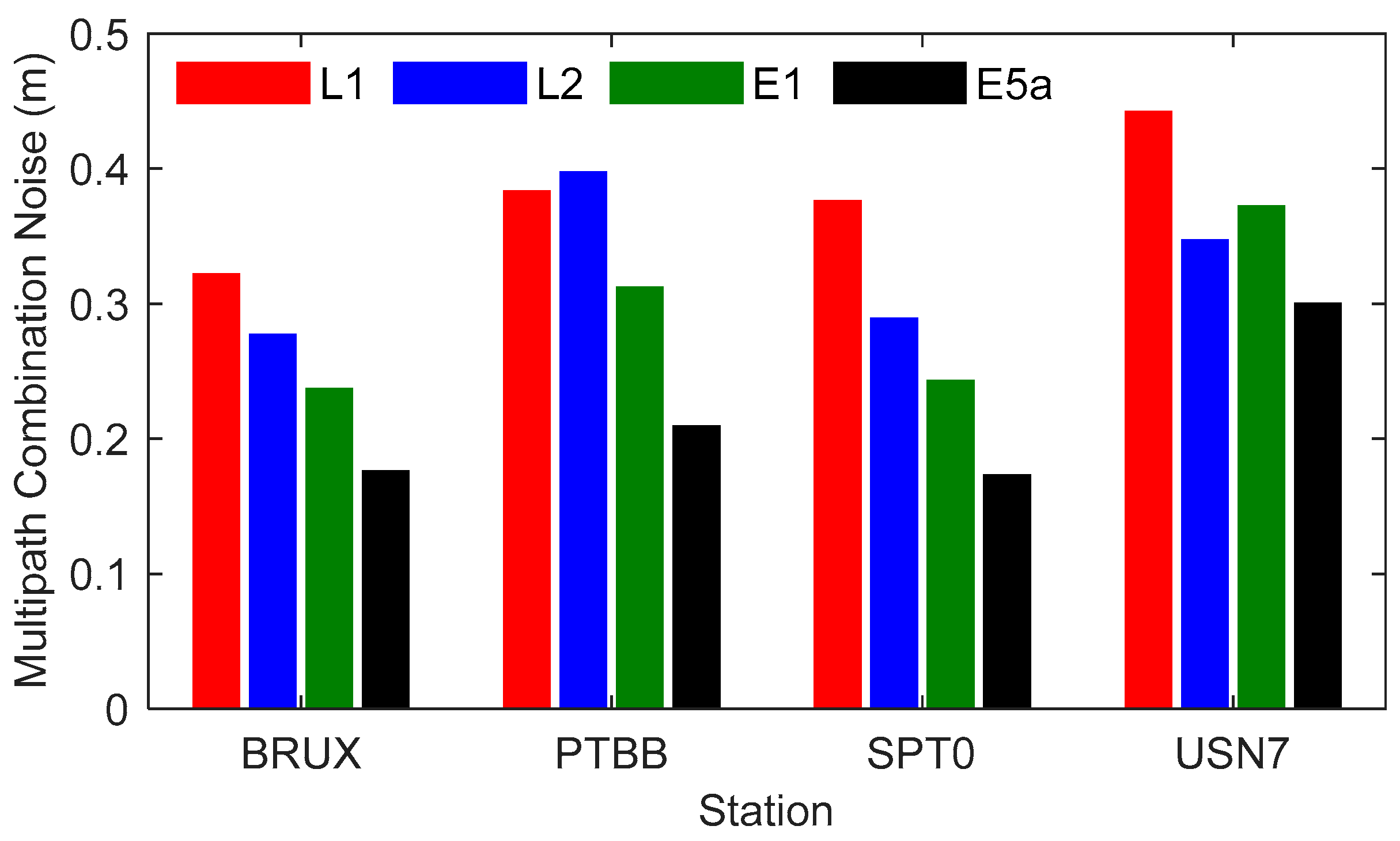


| Station | Receiver | Antenna | Country |
|---|---|---|---|
| BRUX | SEPT POLARX5TR | JAVRINGANT_DM | Belgium |
| PTBB | SEPT POLARX5TR | LEIAR25.R4 | Germany |
| SPT0 | SEPT POLARX5TR | JNSCR_C145-22-1 | Sweden |
| USN7 | SEPT POLARX5TR | TPSCR.G5 | America |
| Station | q0 | q1 | q2 | ADEV |
|---|---|---|---|---|
| BRUX | 1.67 × 10−24 | 2.37 × 10−25 | 6.96 × 10−35 | 1.16 × 10−13 |
| PTBB | 1.59 × 10−24 | 2.97 × 10−25 | 1.16 × 10−35 | 1.23 × 10−13 |
| SPT0 | 1.01 × 10−23 | 1.77 × 10−25 | 9.32 × 10−35 | 2.06 × 10−13 |
| USN7 | 9.50 × 10−23 | 6.33 × 10−25 | 1.03 × 10−33 | 2.30 × 10−13 |
| Item | Strategy |
|---|---|
| Observations | GPS/Galileo combination; GPS: L1/L2; Galileo: E1/E5a |
| Elevation cutoff | 7° |
| Satellite orbit & clock | CNES GRG final precise products |
| Satellite DCB | Corrected by Chinese Academy of Sciences product [47] |
| Earth’s rotation | International Earth Rotation Service (IERS) convention [48] |
| Relativistic effect | Corrected: elliptical orbit and Shapiro effect [49,50] |
| Phase windup effect | Corrected by model [51] |
| Tide effect | Corrected [48,52] |
| Antenna PCO and PCV | Corrected igs14.atx file |
| Inter-system bias | Estimated as white noise (104 m2/s2) |
| Inter-frequency bias | Estimated as constants |
| Station coordinate | Static, estimated as constant |
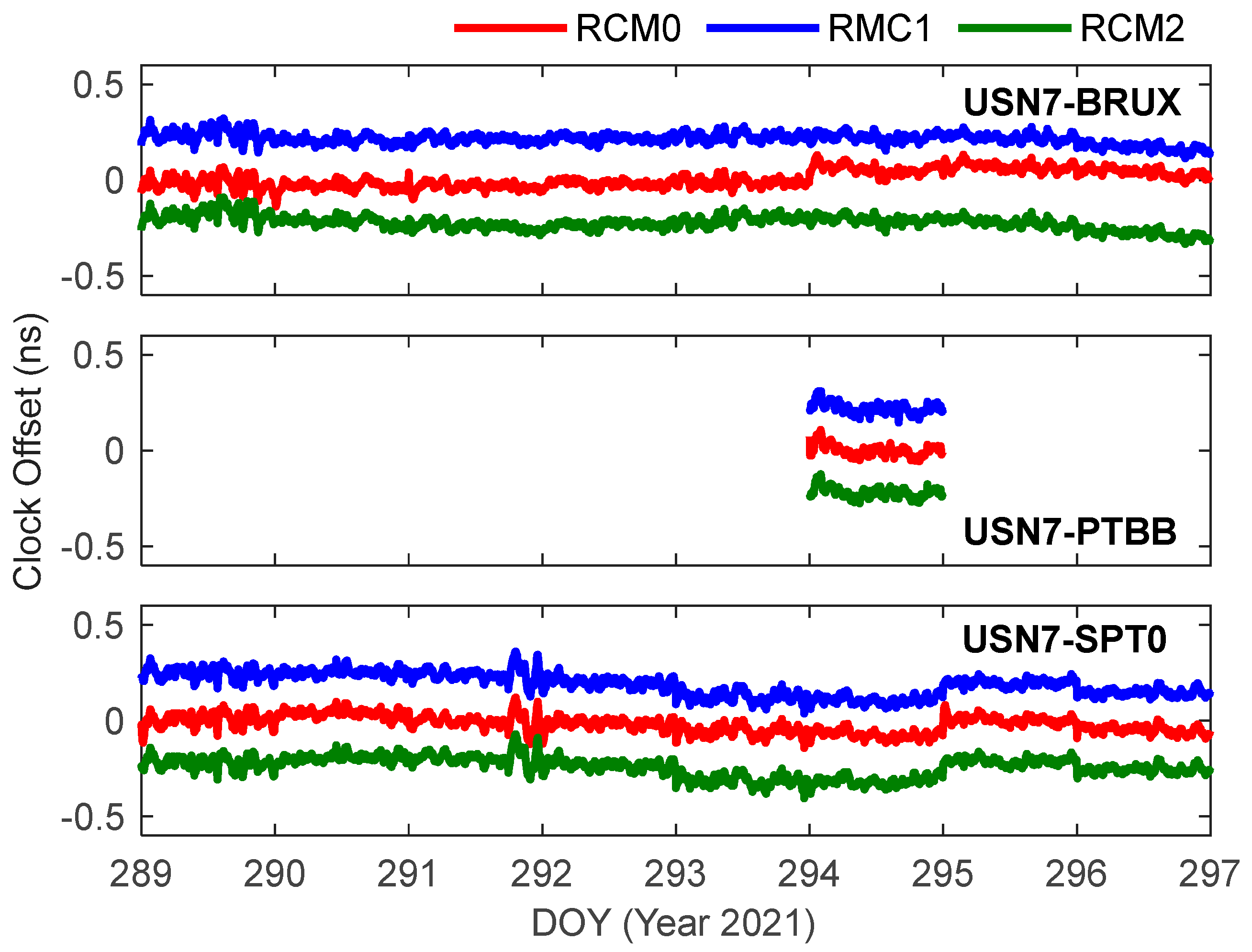
| Receiver clock | RCM0 (estimated as white noise), RCM1 (refined one-state clock model), and RCM2 (refined two-state clock model) |
| Ionospheric delay | First-order eliminated by IF combination |
| Tropospheric delay | Saastamoinen model [53] and estimated as a random walk (10−8 m2/s2), global mapping function (GMF) [54] |
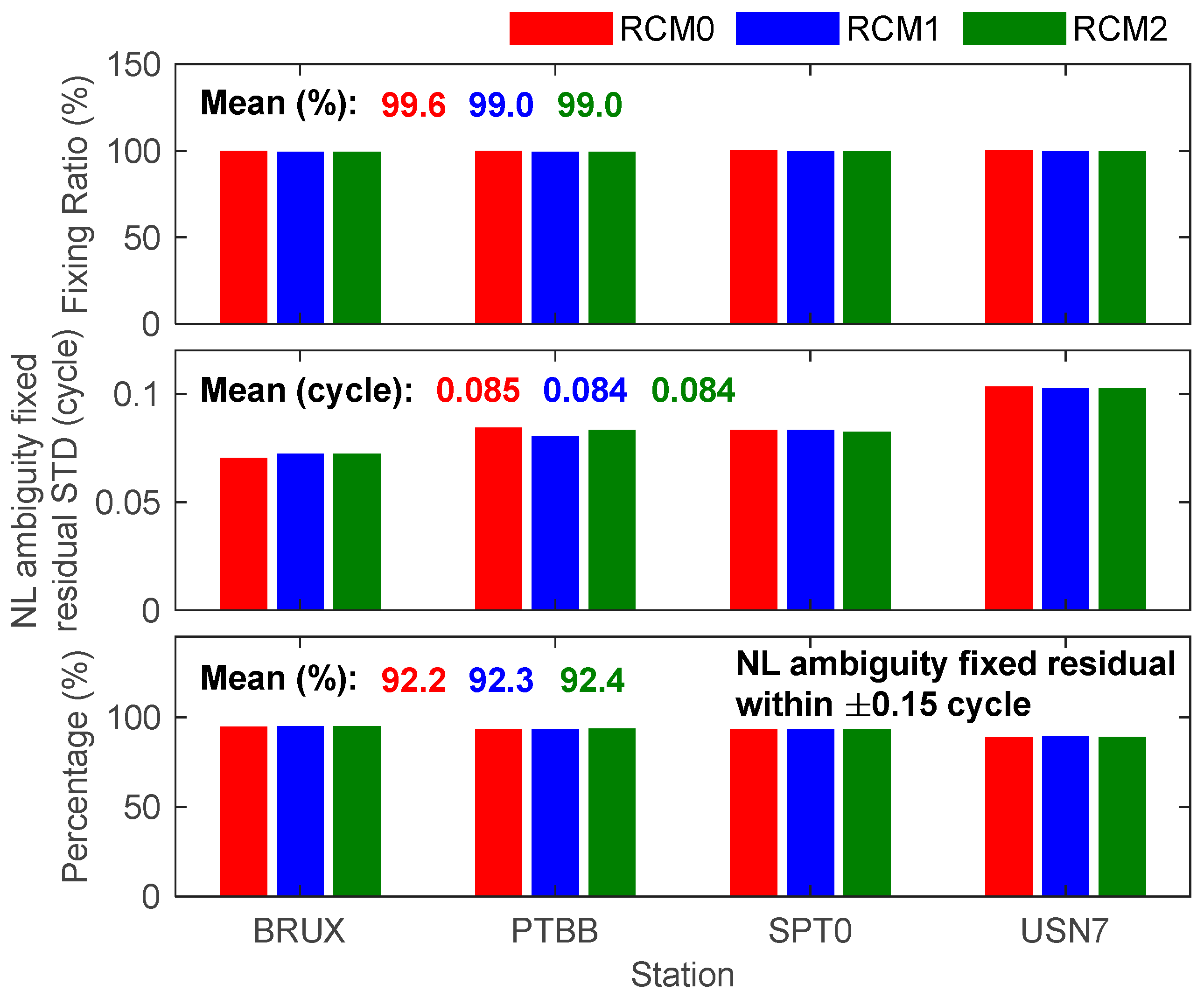
| Ambiguity | Estimated as constant, float, and fixed solutions |
| Link | RCM0 | RCM1 | RCM2 |
|---|---|---|---|
| USN7-BRUX | 32.04 | 30.72 | 29.80 |
| USN7-PTBB | 36.27 | 31.21 | 30.36 |
| USN7-SPT0 | 34.13 | 32.92 | 31.69 |
| Mean | 34.14 | 31.62 | 30.62 |
| Link | RCM0 | RCM1 | RCM2 |
|---|---|---|---|
| USN7-BRUX | 22.32 | 21.59 | 20.67 |
| USN7-PTBB | 30.52 | 28.17 | 29.29 |
| USN7-SPT0 | 24.47 | 23.87 | 23.53 |
| Mean | 25.77 | 24.54 | 24.49 |
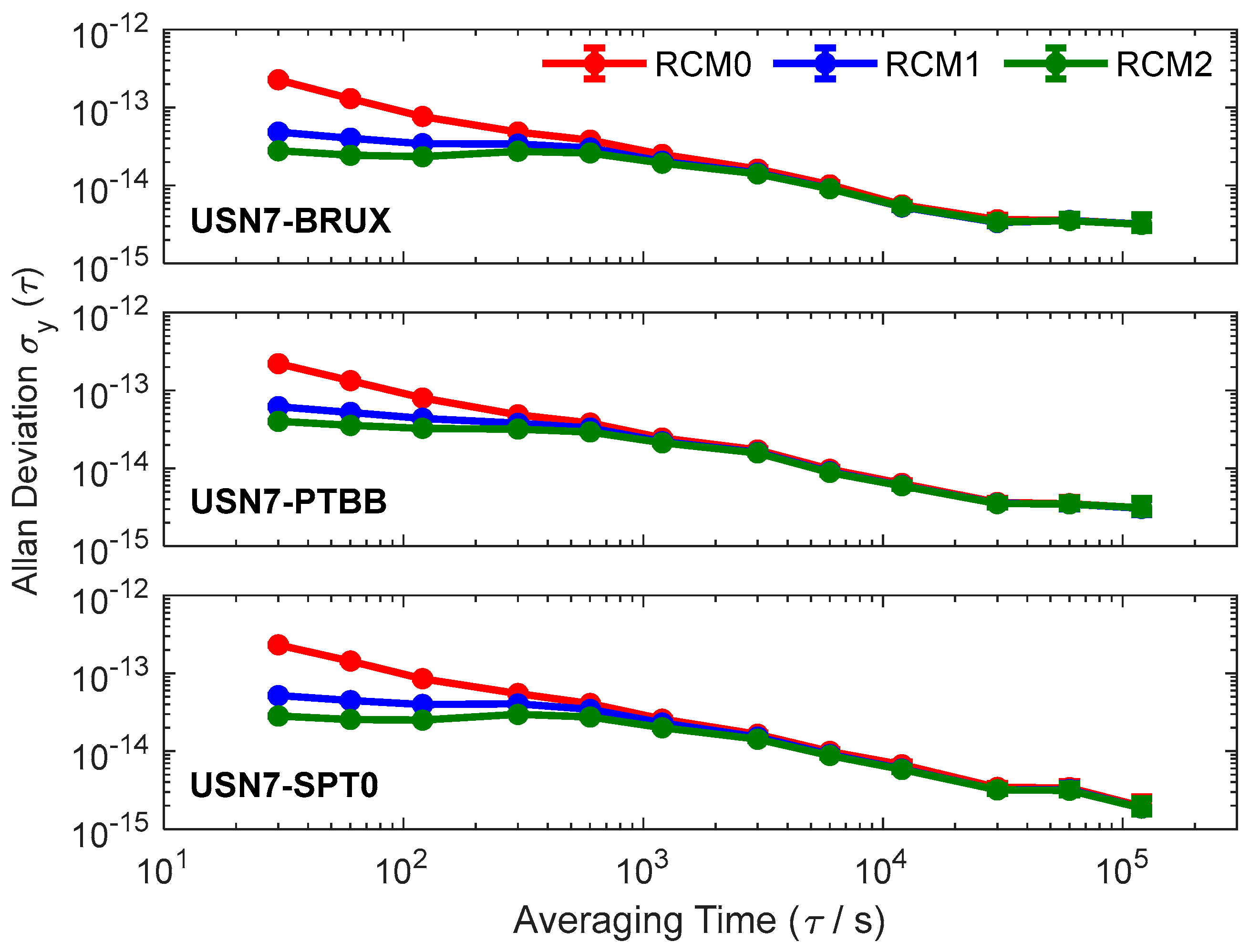
| Tau/s | RCM0 | RCM1 | RMC2 |
|---|---|---|---|
| 30 | 229.513 | 64.346 | 47.524 |
| 60 | 137.617 | 51.783 | 37.202 |
| 120 | 82.093 | 42.716 | 31.649 |
| 300 | 51.495 | 38.429 | 31.080 |
| 600 | 39.307 | 32.808 | 27.977 |
| 1200 | 25.264 | 22.068 | 20.465 |
| 3000 | 16.210 | 15.003 | 14.503 |
| 6000 | 9.554 | 8.980 | 8.801 |
| 12,000 | 5.695 | 5.370 | 5.359 |
| 30,000 | 3.250 | 3.133 | 3.118 |
| 60,000 | 3.339 | 3.337 | 3.323 |
| 120,000 | 2.697 | 2.672 | 2.682 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Zhang, P.; Wang, L.; Yan, C.; Chen, J. Performance Assessment of Undifferenced GPS/Galileo Precise Time Transfer with a Refined Clock Model. Remote Sens. 2025, 17, 1910. https://doi.org/10.3390/rs17111910
Xu W, Zhang P, Wang L, Yan C, Chen J. Performance Assessment of Undifferenced GPS/Galileo Precise Time Transfer with a Refined Clock Model. Remote Sensing. 2025; 17(11):1910. https://doi.org/10.3390/rs17111910
Chicago/Turabian StyleXu, Wei, Pengfei Zhang, Lei Wang, Chao Yan, and Jian Chen. 2025. "Performance Assessment of Undifferenced GPS/Galileo Precise Time Transfer with a Refined Clock Model" Remote Sensing 17, no. 11: 1910. https://doi.org/10.3390/rs17111910
APA StyleXu, W., Zhang, P., Wang, L., Yan, C., & Chen, J. (2025). Performance Assessment of Undifferenced GPS/Galileo Precise Time Transfer with a Refined Clock Model. Remote Sensing, 17(11), 1910. https://doi.org/10.3390/rs17111910






