A New Quasi-Linear Integral Transform Between Ocean Wave Spectrum and Phase Spectrum of an XTI-SAR
Abstract
1. Introduction
2. Methods
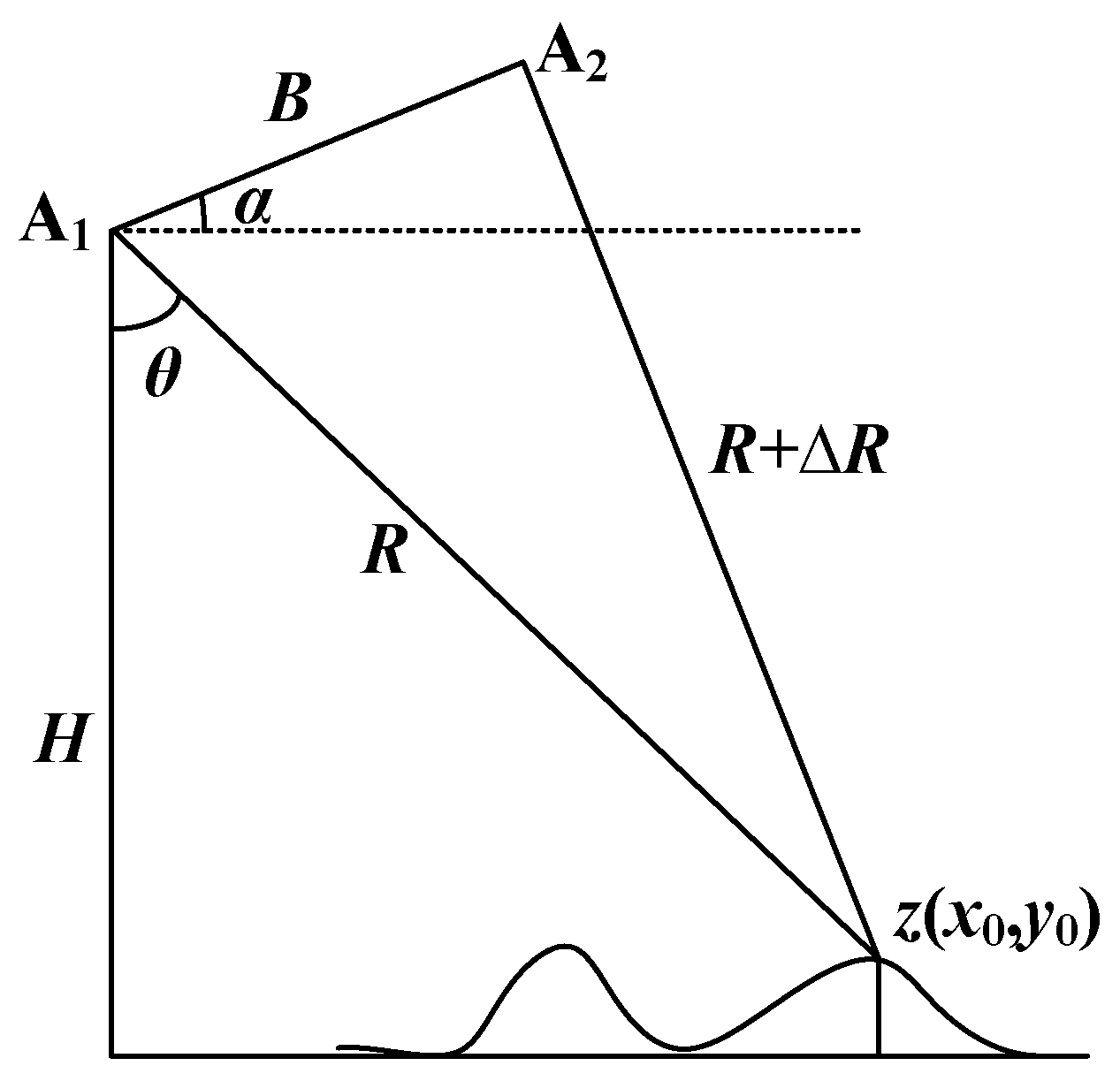
2.1. The Nonlinear Integral Transform Model
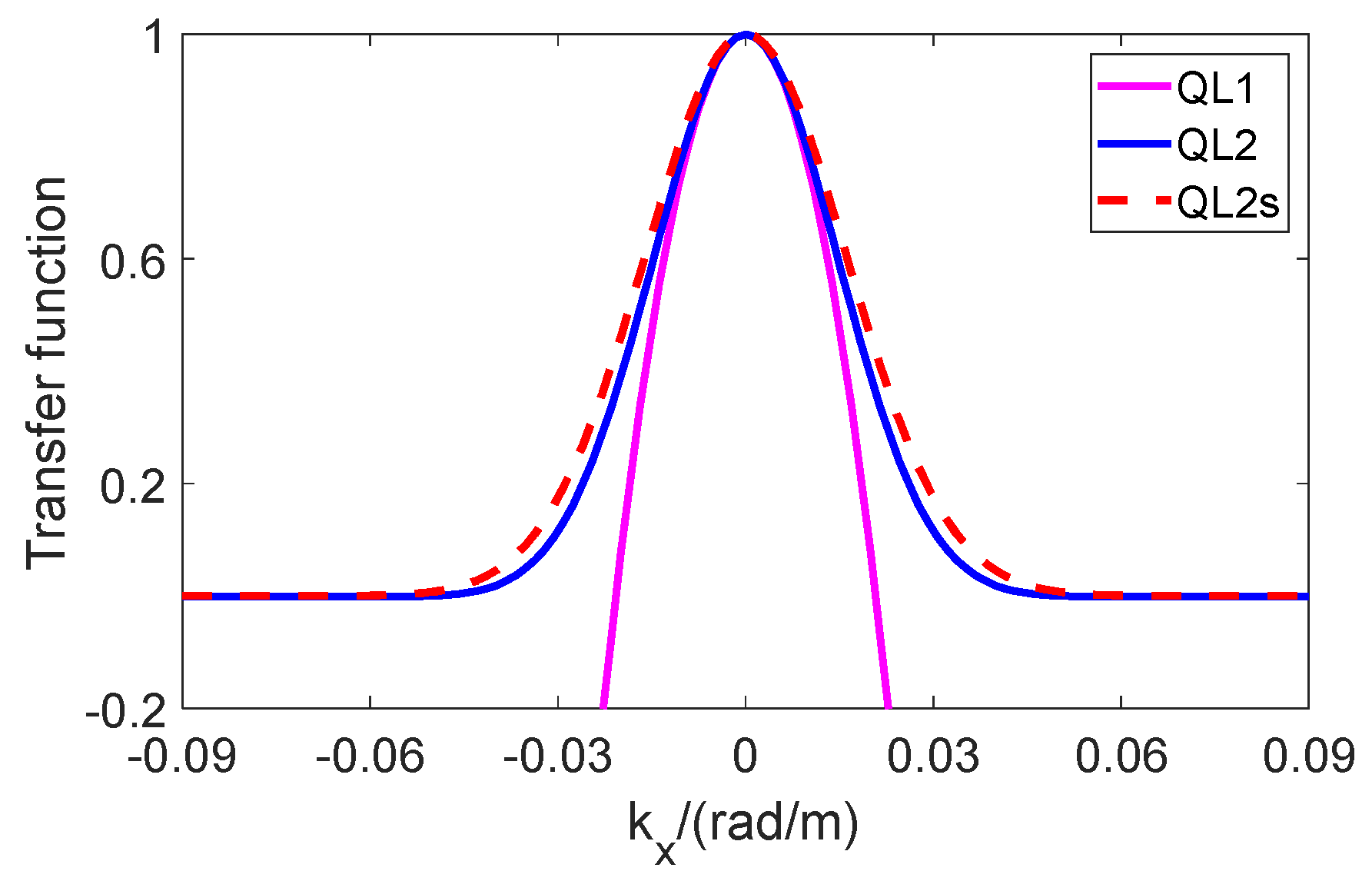
2.2. The First Quasi-Linear Integral Transform Model (QL1)
2.3. The Second Quasi-Linear Integral Transform Model (QL2)
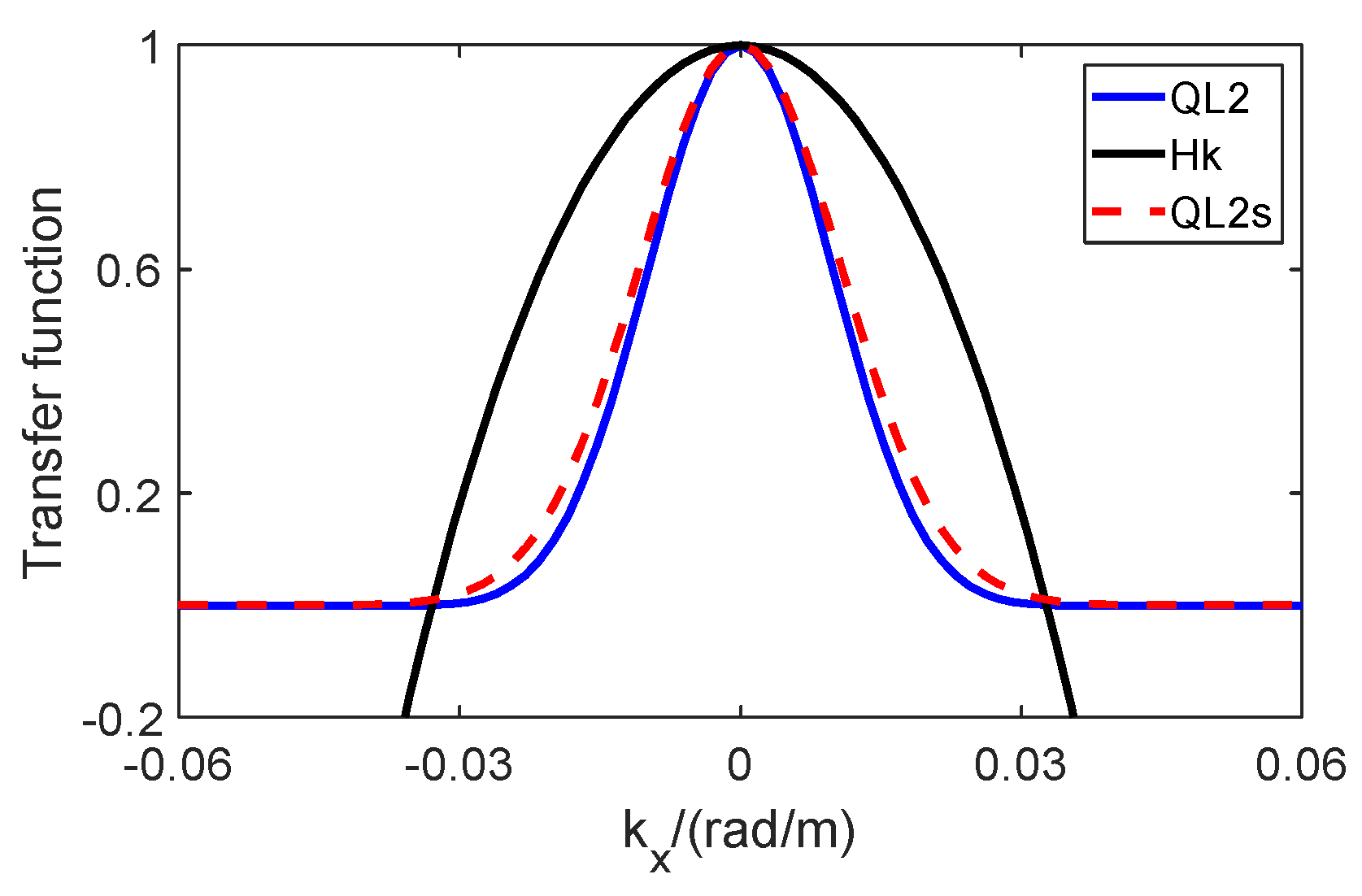
2.4. Optimization of the Second Quasi-Linear Integral Transform Model (QL2s)
2.5. Discussions
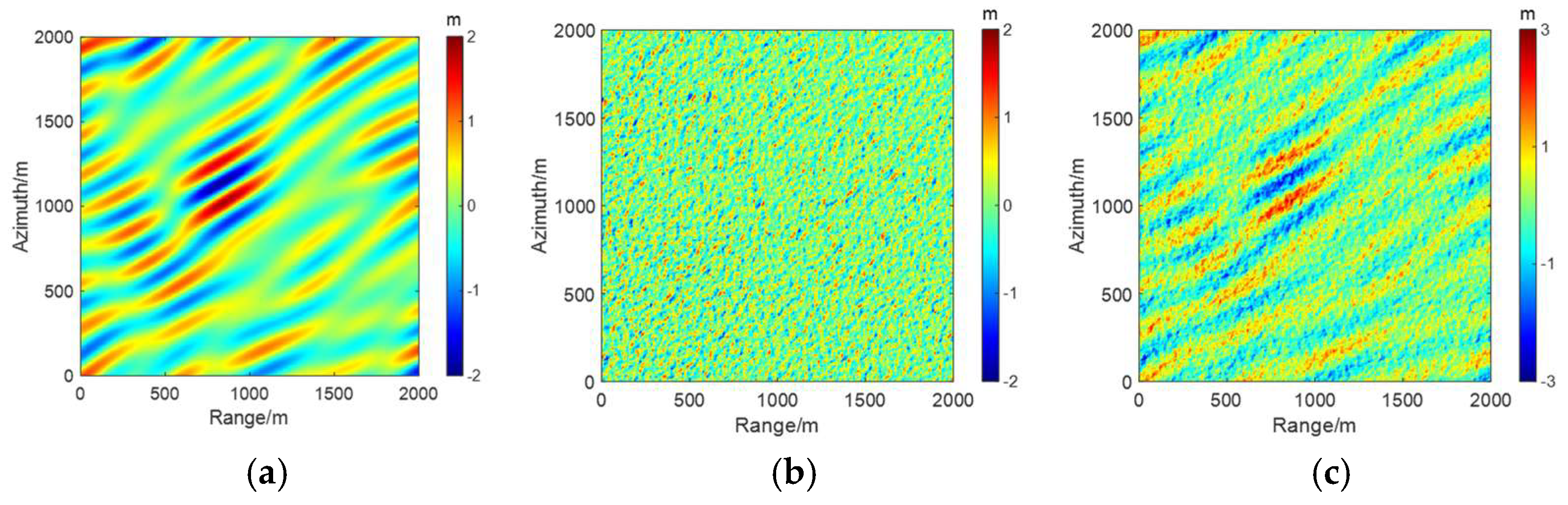
2.6. Methods of Difference Analysis
3. Results
3.1. The Influence of Wind Speed on the Difference
3.2. The Influence of Wind Direction on the Difference
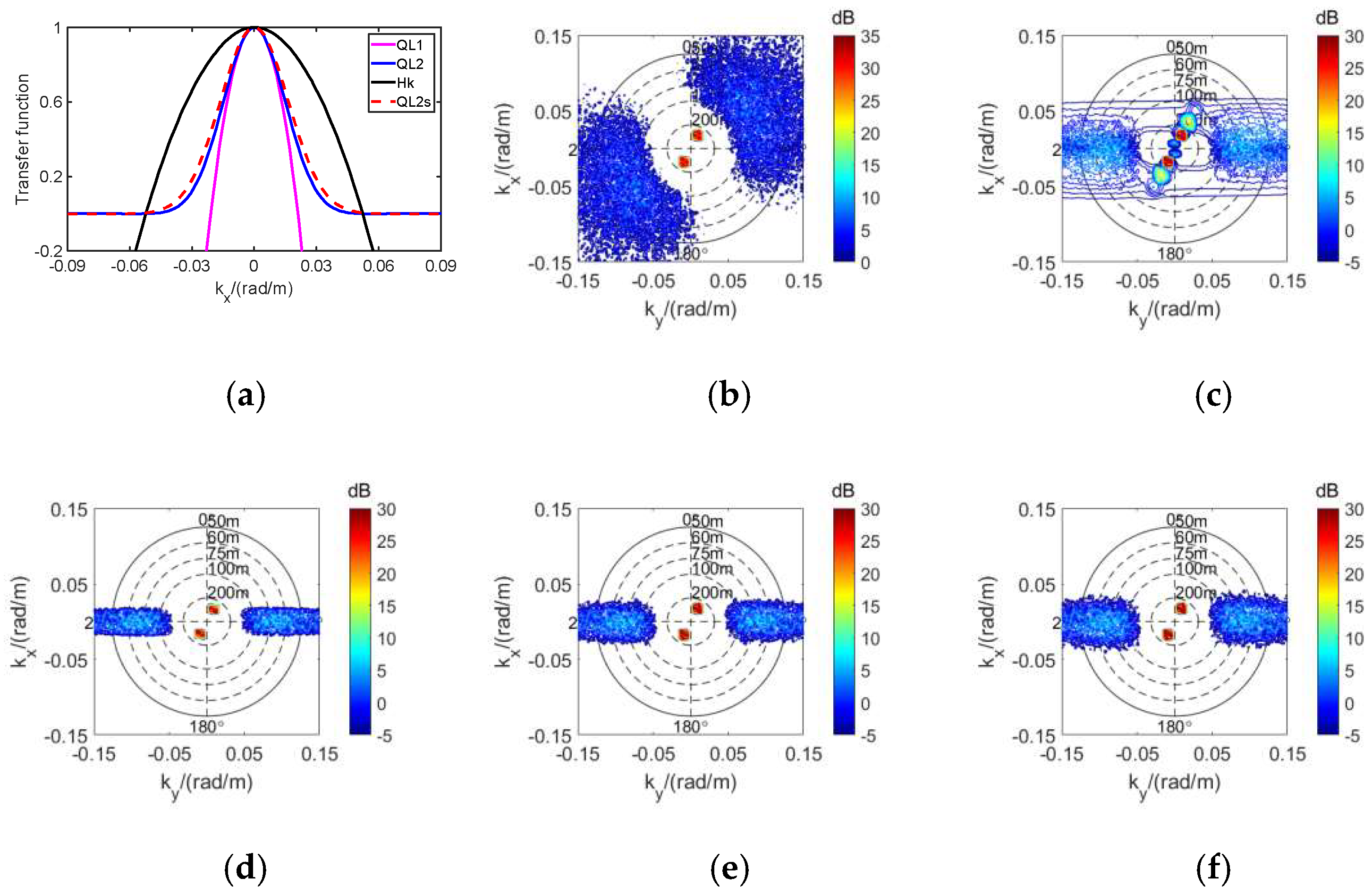
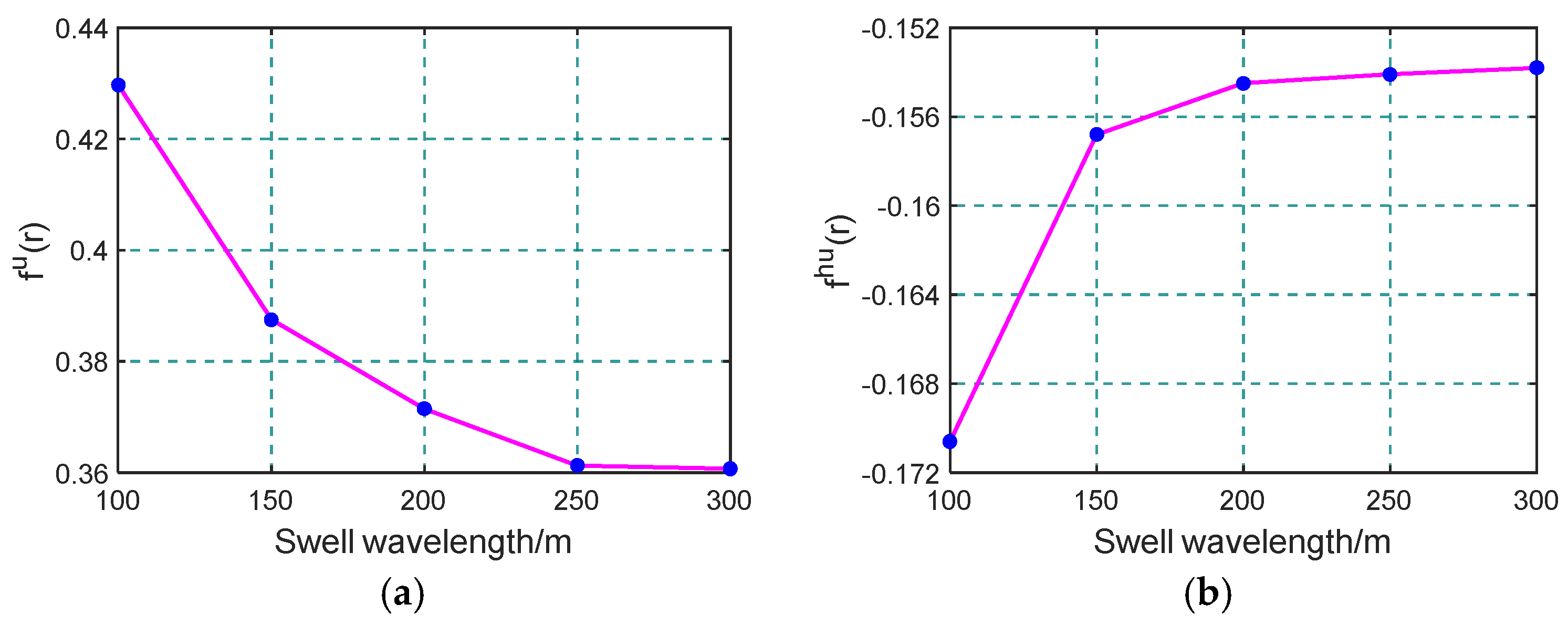
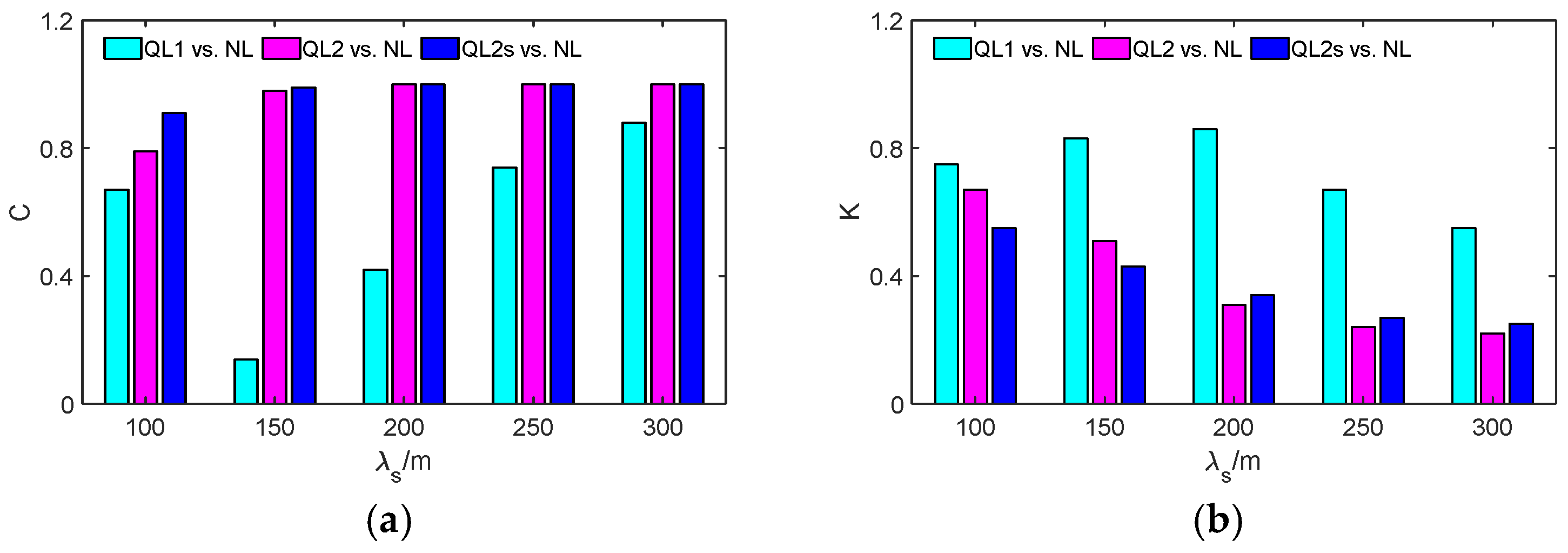
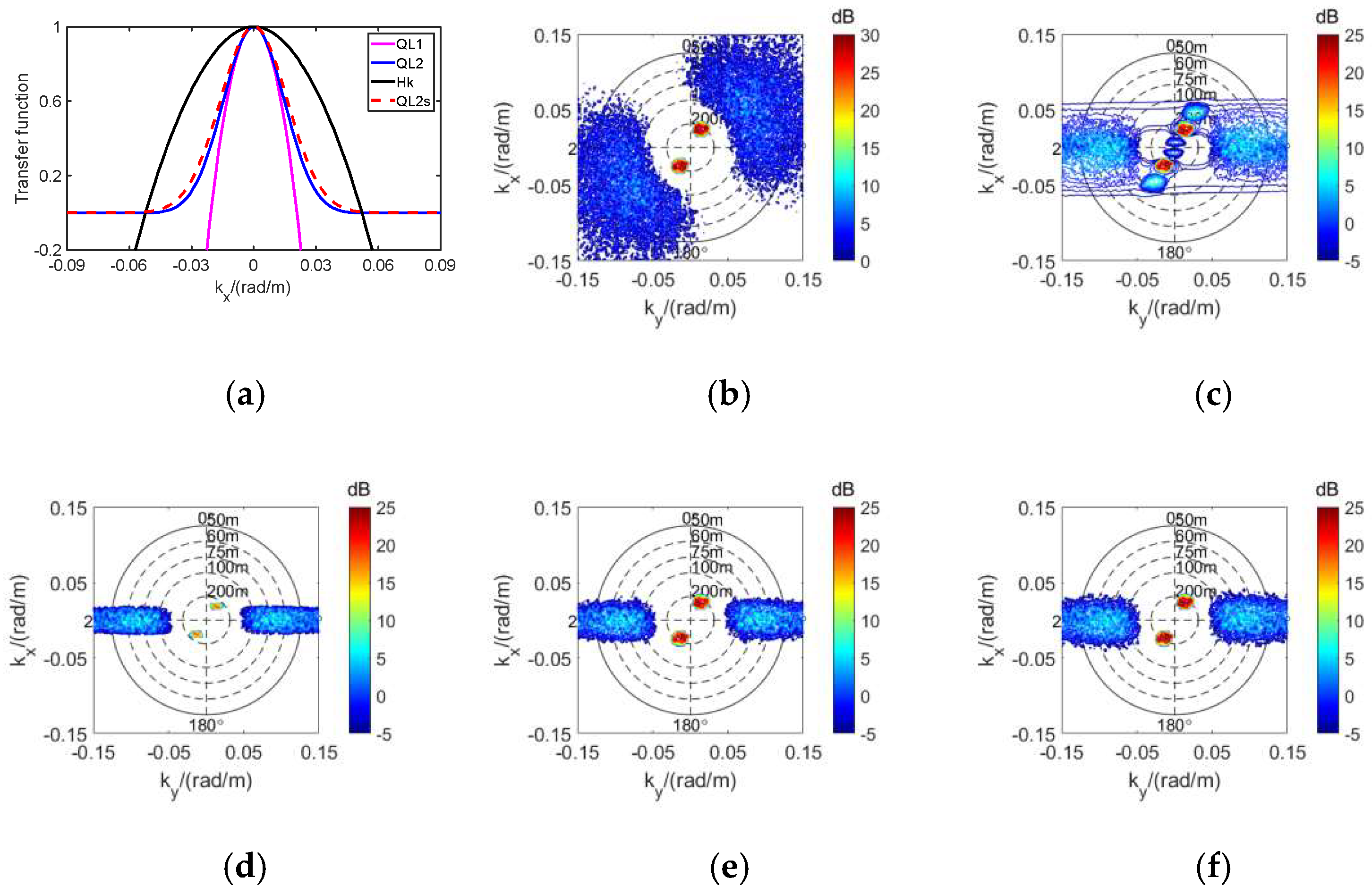
3.3. The Influence of Swell Wavelength on the Difference
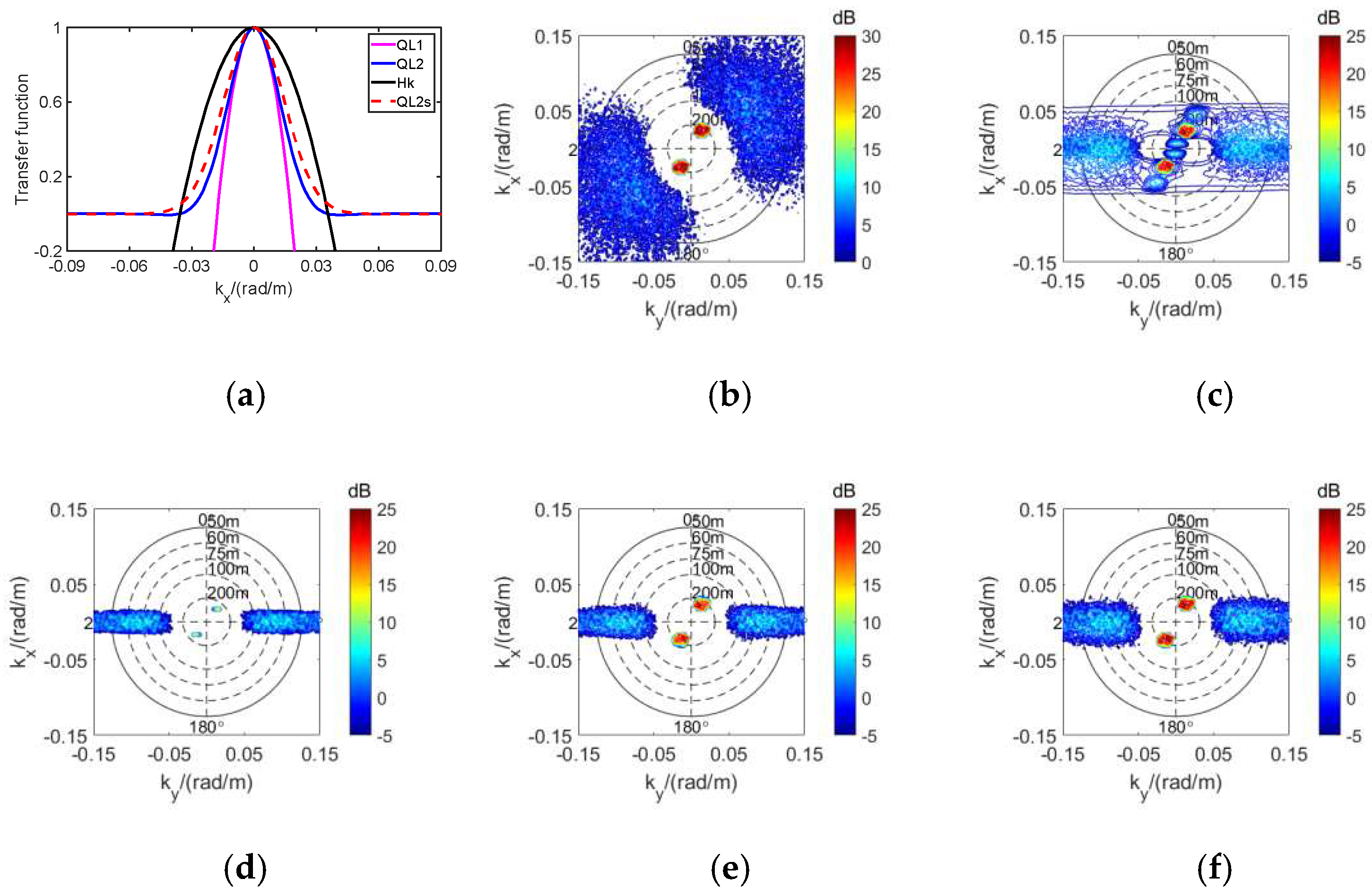
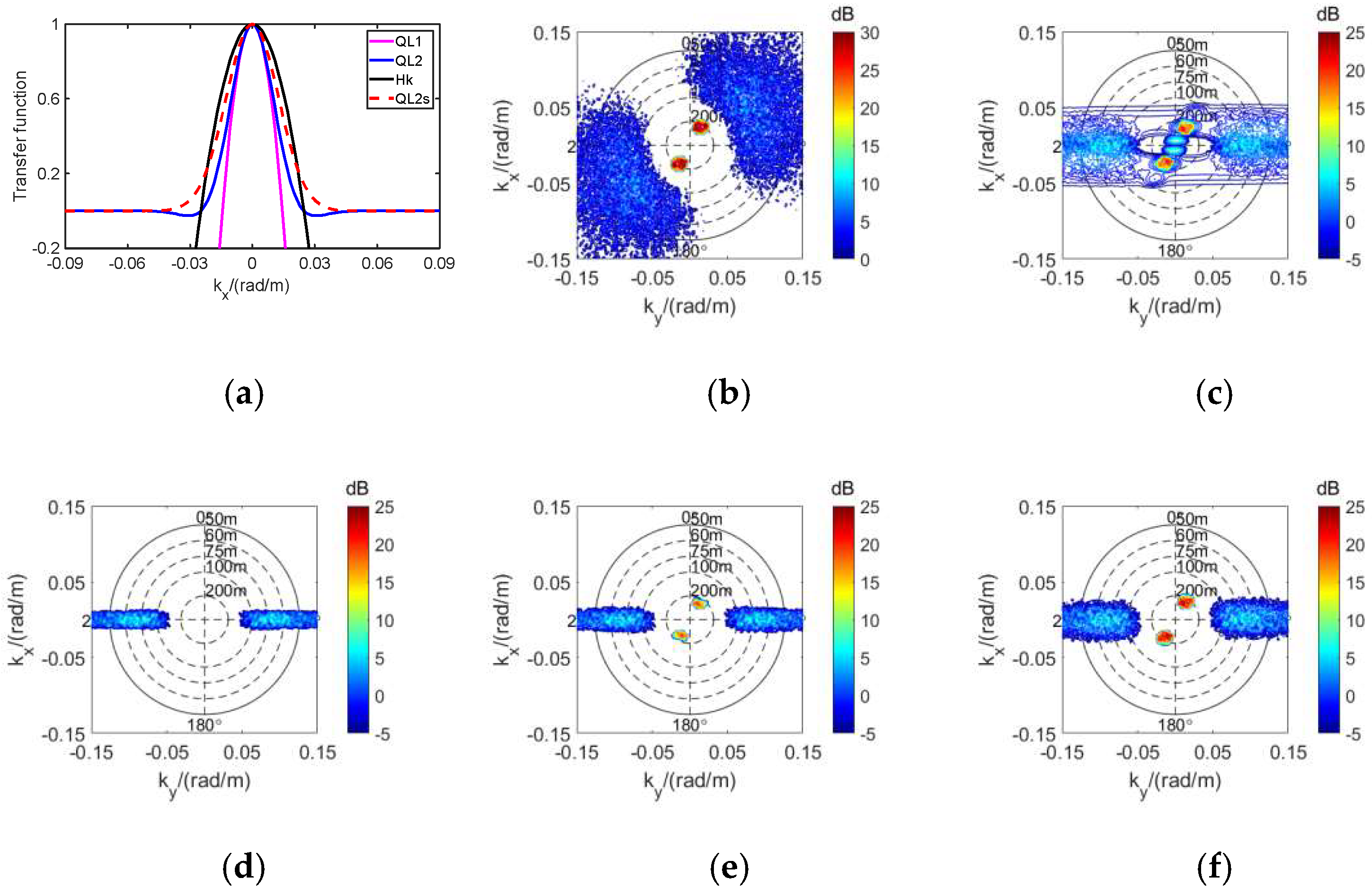
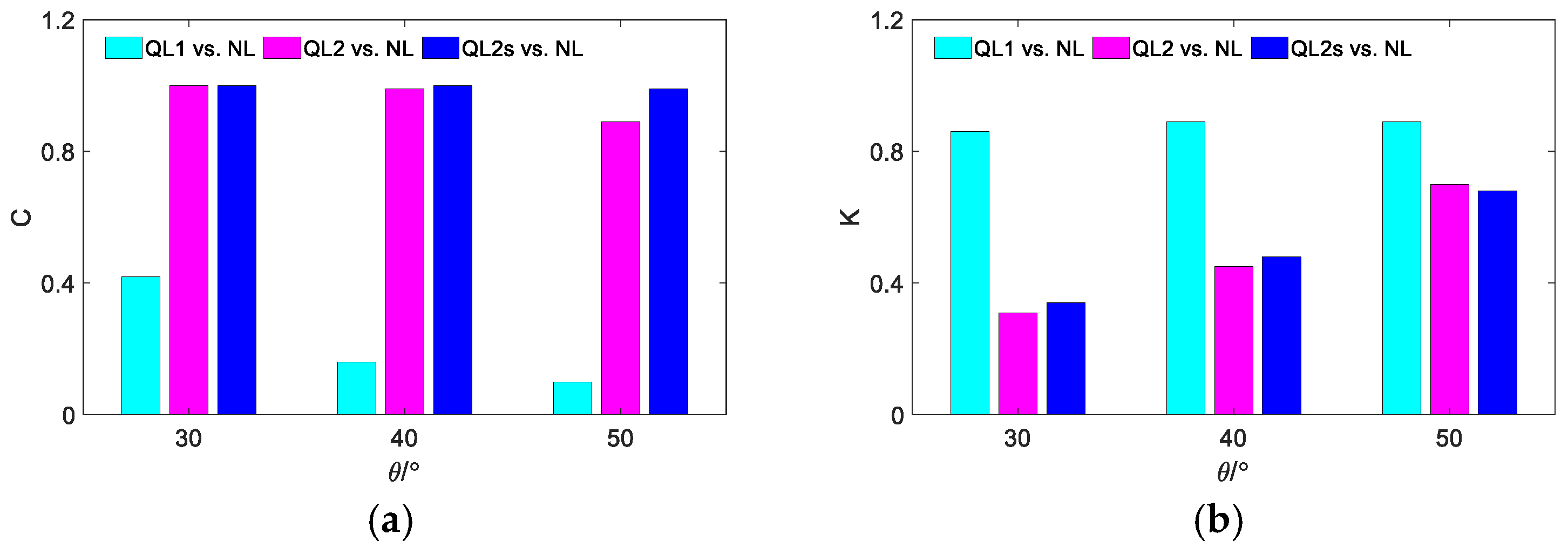
3.4. The Influence of Incidence Angle on the Difference
3.5. Applicability Analysis of the Quasi-Linear Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiang, C.; Zhang, K.; Li, M.; Yang, F.; Xu, S. Three-Dimensional Modeling for Ocean Electromagnetic Environment. In Proceedings of the 2020 IEEE International Symposium on Antennas and Propagation and North American Radio Science Meeting, Montreal, QC, Canada, 5–10 July 2020. [Google Scholar]
- Gao, H.; Liang, B.; Shao, Z. A global climate analysis of wave parameters with a focus on wave period from 1979 to 2018. Appl. Ocean Res. 2021, 111, 102652. [Google Scholar] [CrossRef]
- Gao, Y.; Kamenkovich, I.; Perlin, N.; Kirtman, B. Oceanic Advection Controls Mesoscale Mixed Layer Heat Budget and Air–Sea Heat Exchange in the Southern Ocean. J. Phys. Oceanogr. 2022, 52, 537–555. [Google Scholar] [CrossRef]
- Li, S.; Yu, H.; Wu, K.; Yin, X.; Lang, S.; Ye, J. Validation of the Ocean Wave Spectrum from the Remote Sensing Data of the Chinese–French Oceanography Satellite. Remote Sens. 2023, 15, 3918. [Google Scholar] [CrossRef]
- Zhang, X.; Su, X.; Liu, L.; Wu, Z. Experimental Investigation of Meter-Level Resolution Radar Measurement at Ka Band in Yellow Sea. Remote Sens. 2024, 16, 3835. [Google Scholar] [CrossRef]
- Matos, T.; Rocha, J.L.; Martins, M.S.; Gonçalves, L.M. Enhancing Sea Wave Monitoring Through Integrated Pressure Sensors in Smart Marine Cables. J. Mar. Sci. Eng. 2025, 13, 766. [Google Scholar] [CrossRef]
- Martínez-Rodrigo, R.; Águeda, B.; Lopez-Sanchez, J.M.; Altelarrea, J.M.; Alejandro, P.; Gómez, C. Exploring the Relationship Between Time Series of Sentinel-1 Interferometric Coherence Data and Wild Edible Mushroom Yields in Mediterranean Forests. J. Geovis. Spat. Anal. 2024, 8, 38. [Google Scholar] [CrossRef]
- Elyouncha, A.; Eriksson, L.E.B.; Romeiser, R.; Ulander, L.M.H. Measurements of Sea Surface Currents in the Baltic Sea Region Using Spaceborne Along-Track InSAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8584–8599. [Google Scholar] [CrossRef]
- An, S.; Han, S.; Kim, D.J. Enhancing SAR ATR Accuracy for Military Targets: A Novel Approach Using XTI and Amplitude Data Integration. IEEE Geosci. Remote Sens. Lett. 2024, 22, 4001705. [Google Scholar] [CrossRef]
- Zhang, J.B.; Duan, W.; Fu, X.K. The Stepwise Multi-Temporal Interferometric Synthetic Aperture Radar with Partially Coherent Scatterers for Long-Time Series Deformation Monitoring. Remote Sens. 2025, 17, 1374. [Google Scholar] [CrossRef]
- Marom, M.; Goldstein, R.M.; Thornton, E.B.; Shemer, L. Remote Sensing of Ocean Wave Spectra by Interferometric Synthetic Aperture Radar. Nature 1990, 345, 793–795. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, M.; Zhang, Y.; Wang, C.; Duan, T. An Analytical Method for Dynamic Wave—Related Errors of Interferometric SAR Ocean Altimetry under Multiple Sea States. Remote Sens. 2021, 13, 986. [Google Scholar] [CrossRef]
- Shemer, L. Interferometric SAR imagery of a monochromatic ocean wave in the presence of the real aperture radar modulation. Int. J. Remote Sens. 1993, 14, 3005–3019. [Google Scholar] [CrossRef]
- Zhang, B.; He, Y.J. A Parametric Algorithm to Retrieve Ocean Wave Spectra from Interferometric Synthetic Aperture Radar. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; pp. 424–427. [Google Scholar]
- Bao, M. A nonlinear integral transform between ocean wave spectra and phase image spectra of a cross-track interferometric SAR. In Proceedings of the 1999 IEEE International Geoscience and Remote Sensing Symposium, Hamburg, Germany, 28 June–2 July 1999; Volume 5, pp. 2619–2621. [Google Scholar]
- Schulz-Stellenfleth, J.; Lehner, S. Ocean wave imaging using an airborne single pass across-track interferometric synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2001, 39, 38–45. [Google Scholar] [CrossRef]
- Schulz-Stellenfleth, J.; Horstmann, J.; Lehner, S.; Rosenthal, W. Sea surface imaging with an across track interferometric synthetic aperture radar---The SINEWAVE experiment. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2017–2028. [Google Scholar] [CrossRef]
- Zhang, B.; He, Y.J. Interferometric phase model and numerical simulations of swell for across-track interferometric SAR. Chin. J. Radio Sci. 2007, 22, 1014–1028. [Google Scholar]
- Vaze, P.; Kaki, S.; Limonadi, D.; Esteban-Fernandez, D.; Zohar, G. The Surface Water and Ocean Topography Mission. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018. [Google Scholar]
- Yao, J.; Xu, N.; Wang, M.; Liu, T.; Lu, H.; Cao, Y.; Tang, X.; Mo, F.; Chang, H.; Gong, H.; et al. SWOT satellite for global hydrological applications: Accuracy assessment and insights into surface water dynamics. Int. J. Digit. Earth 2025, 18, 2472924. [Google Scholar] [CrossRef]
- Rodriguez, E.; Esteban-Fernandez, D. The Surface Water and Ocean Topography Mission (SWOT): The Ka-band Radar Interferometer (KaRIn) for water level measurements at all scales. In Proceedings of the SPIE Remote Sensing, Toulouse, France, 20–23 September 2010; Volume 7826, pp. 1–8. [Google Scholar]
- Neeck, S.P.; Lindstrom, E.J.; Vaze, P.V.; Fu, L.L. Surface Water and Ocean Topography (SWOT) mission. In Proceedings of the SPIE Remote Sensing, Edinburgh, UK, 24–27 September 2012. [Google Scholar]
- Chen, G.; Tang, J.; Zhao, C.; Wu, S.; Yu, F.; Ma, C.; Xu, Y.; Chen, W.; Zhang, Y.; Liu, J.; et al. Concept Design of the “Guanlan” Science Mission: China’s Novel Contribution to Space Oceanography. Front. Mar. Sci. 2019, 6, 194. [Google Scholar] [CrossRef]
- Yang, L.; Xu, Y.; Zhou, X.; Zhu, L.; Jiang, Q.; Sun, H.; Chen, G.; Wang, P.; Mertikas, S.P.; Fu, Y.; et al. Calibration of an Airborne Interferometric Radar Altimeter over the Qingdao Coast Sea, China. Remote Sens. 2020, 12, 1651. [Google Scholar] [CrossRef]
- Jiang, Q.; Xu, Y.; Sun, H.; Wei, L.; Yang, L.; Zheng, Q.; Jiang, H.; Zhang, X.; Qian, C. Wind-generated gravity waves retrieval from high-resolution 2-D maps of sea surface elevation by airborne interferometric altimeter. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Ma, C.; Pan, L.; Qiu, Z.; Liang, D.; Chen, G.; Yu, F.; Sun, H.; Sun, D.; Wu, W. Ocean Wave Inversion Based on a Ku/Ka Dual-Band Airborne Interferometric Imaging Radar Altimeter. Remote Sens. 2022, 14, 3578. [Google Scholar] [CrossRef]
- Qiu, Z.; Ma, C.; Wang, Y.; Yu, F.; Zhao, C.; Sun, H.; Zhao, S.; Yang, L.; Tang, J.; Chen, G. Improving Sea Surface Height Reconstruction by Simultaneous Ku- and Ka-Band Near-Nadir Single-Pass Interferometric SAR Altimeter. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5209614. [Google Scholar] [CrossRef]
- Sun, D.; Zhang, Y.; Wang, Y.; Chen, G.; Sun, H.; Yang, L.; Bai, Y.; Yu, F.; Zhao, C. Ocean Wave Inversion Based on Airborne IRA Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1001013. [Google Scholar] [CrossRef]
- Sun, D.; Wang, Y.; Xu, Z.; Zhang, Y.; Zhang, Y.; Meng, J.; Sun, H.; Yang, L. Ocean wave inversion based on hybrid along- and crosstrack interferometry. Remote Sens. 2022, 14, 2793. [Google Scholar] [CrossRef]
- Stoffelen, A.; Anderson, D. Scatterometer data interpretation: Estimation and validation of the transfer function CMOD4. J. Geophys. Res. Ocean. 1997, 102, 5767–5780. [Google Scholar] [CrossRef]
- Raney, R. Synthetic aperture imaging radar and moving targets. IEEE Trans. Aerosp. Electron. Syst. 1971, AES-7, 499–505. [Google Scholar]
- Sun, D.; Wang, Y.; Zhang, Y.; Sun, H.; Yang, L.; Yu, F. Wind wave and wind speed inversion based on azimuth cutoff of airborne IRA images. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4201914. [Google Scholar] [CrossRef]
- Bao, M.Q.; Alpers, W. A new nonlinear integral transform relating ocean wave spectra to phase image spectra of an along-track interferometric synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 1999, 37, 461–466. [Google Scholar]
- Krogstad, H.E. A simple derivation of Hasselmann’s nonlinear ocean-synthetic aperture radar transform. J. Geophys. Res. Ocean. 1992, 97, 873–885. [Google Scholar] [CrossRef]
- Parzen, E. Stochastic Processes; Holden-Day: San Francisco, CA, USA, 1962; Volume 324. [Google Scholar]
- Hasselmann, K.; Hasselmann, S. On the nonlinear mapping of an ocean wave spectrum into a synthetic aperture radar image spectrum and its inversion. J. Geophys. Res. 1991, 96, 10713–10729. [Google Scholar] [CrossRef]
- Pierson, W.J.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of SA Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Chapron, B.; Katsaros, K.; Vandemark, D. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. Ocean. 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Alpers, W.R. Monte Carlo simulations for studying the relationship between ocean wave and synthetic aperture radar image spectra. J. Geophys. Res. 1983, 88, 1745–1759. [Google Scholar] [CrossRef]
- Bruning, C.; Alpers, W.R.; Hasselmann, K. Monte-Carlo simulation studies of the nonlinear imaging of a two dimensional surface wave field by a synthetic aperture radar. Int. J. Remote Sens. 1990, 11, 1695–1727. [Google Scholar] [CrossRef]
- He, Y.J.; Alpers, W. On the nonlinear integral transform of an ocean wave spectrum into an along-track interferometric synthetic aperture radar image spectrum. J. Geophys. Res. Atmos. 2003, 108, 3205. [Google Scholar] [CrossRef]
- Vachon, P.W.; Campbell, J.W.; Gray, A.L.; Dobson, F.W. Validation of along-track interferometric SAR measurements of ocean surface waves. IEEE Trans. Geosci. Remote Sens. 1999, 37, 150–162. [Google Scholar] [CrossRef]
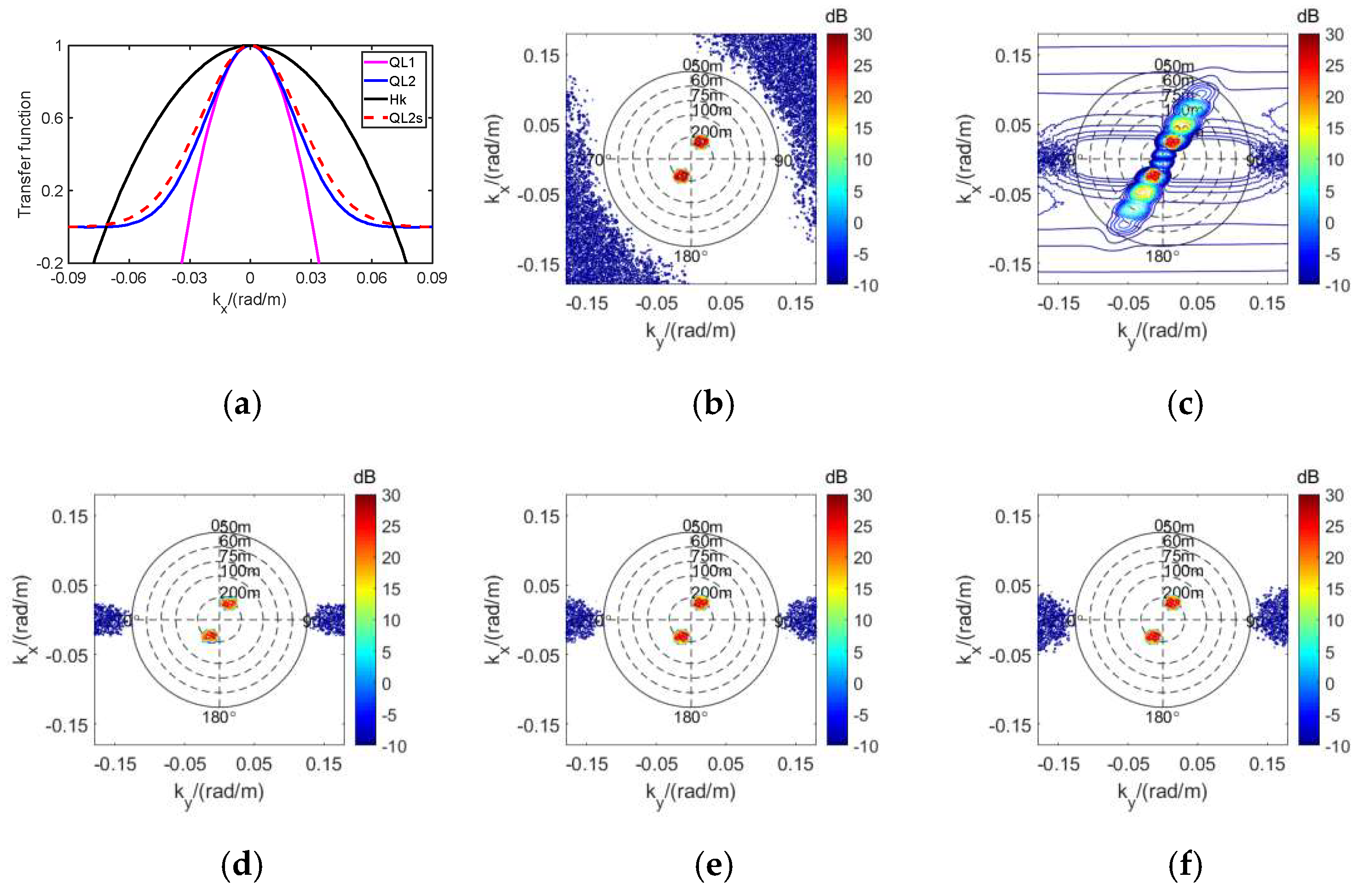

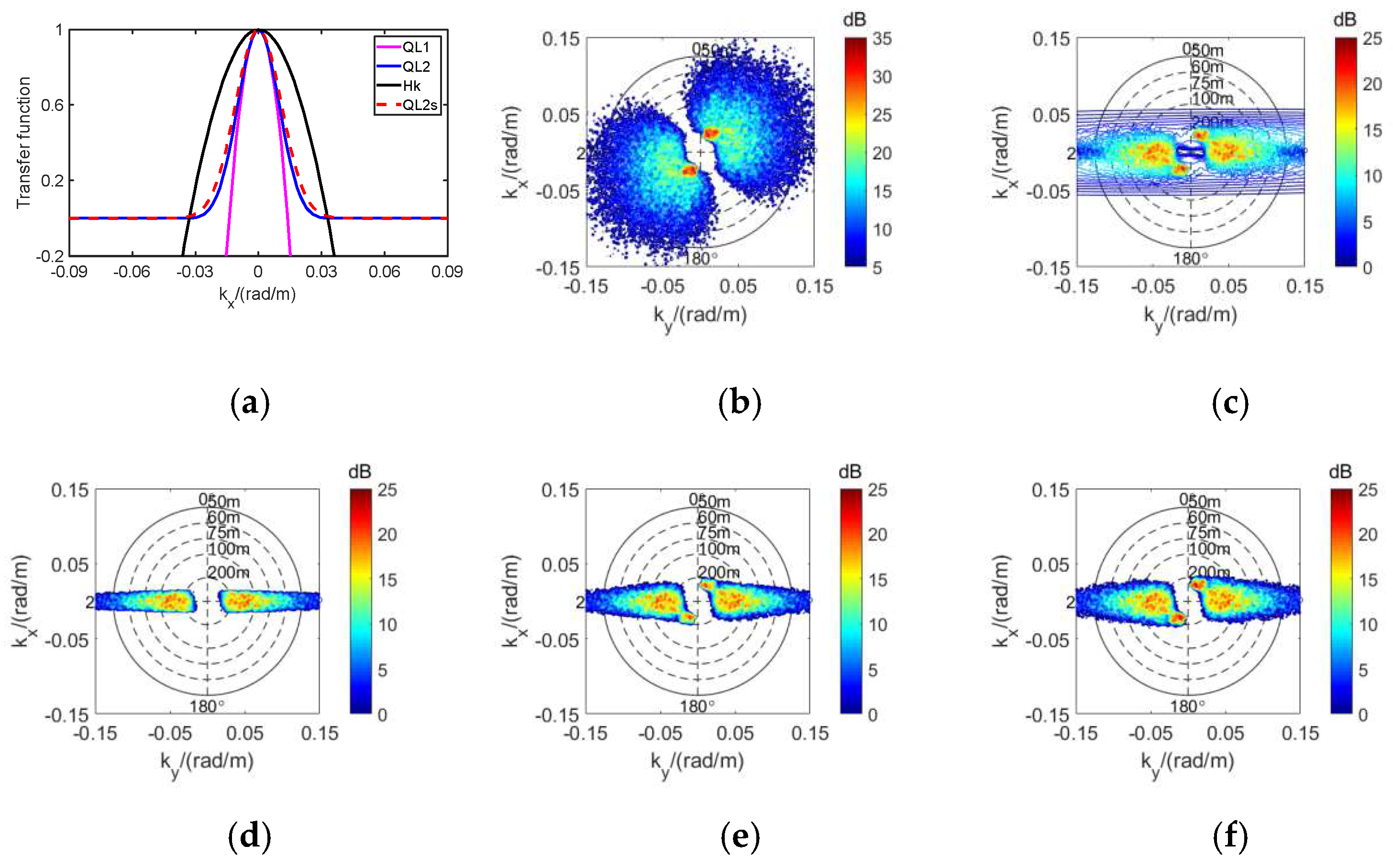
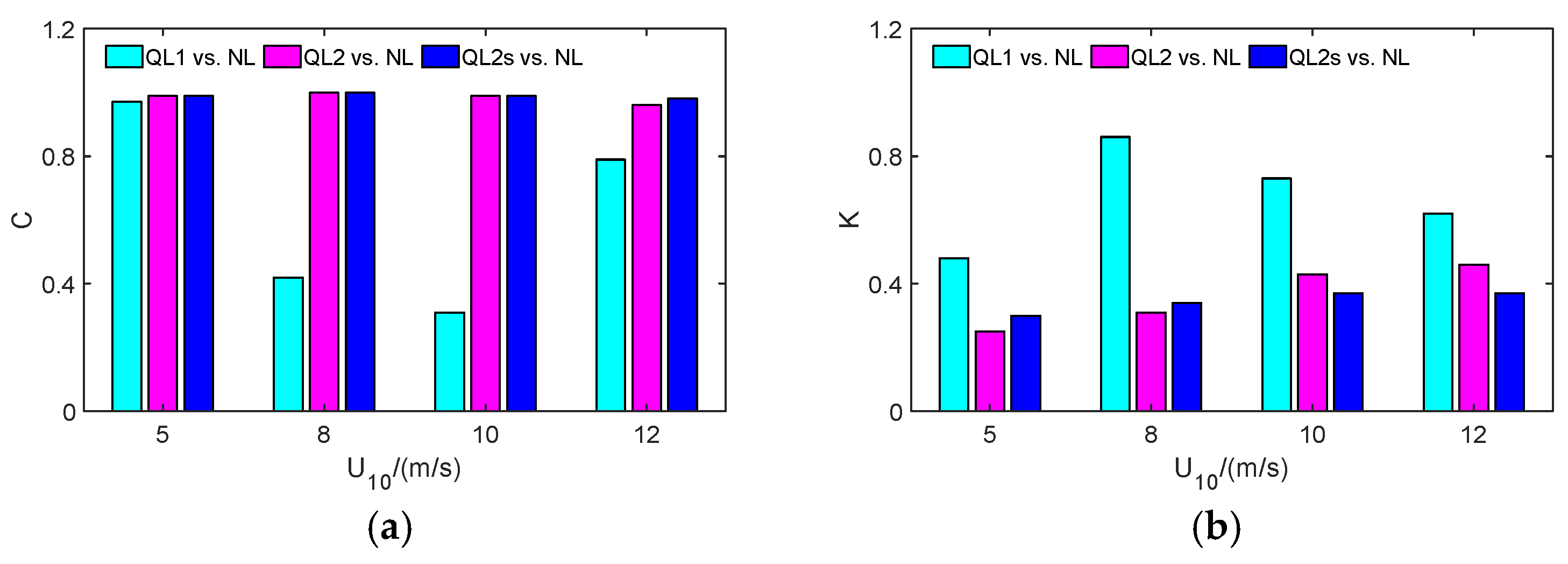
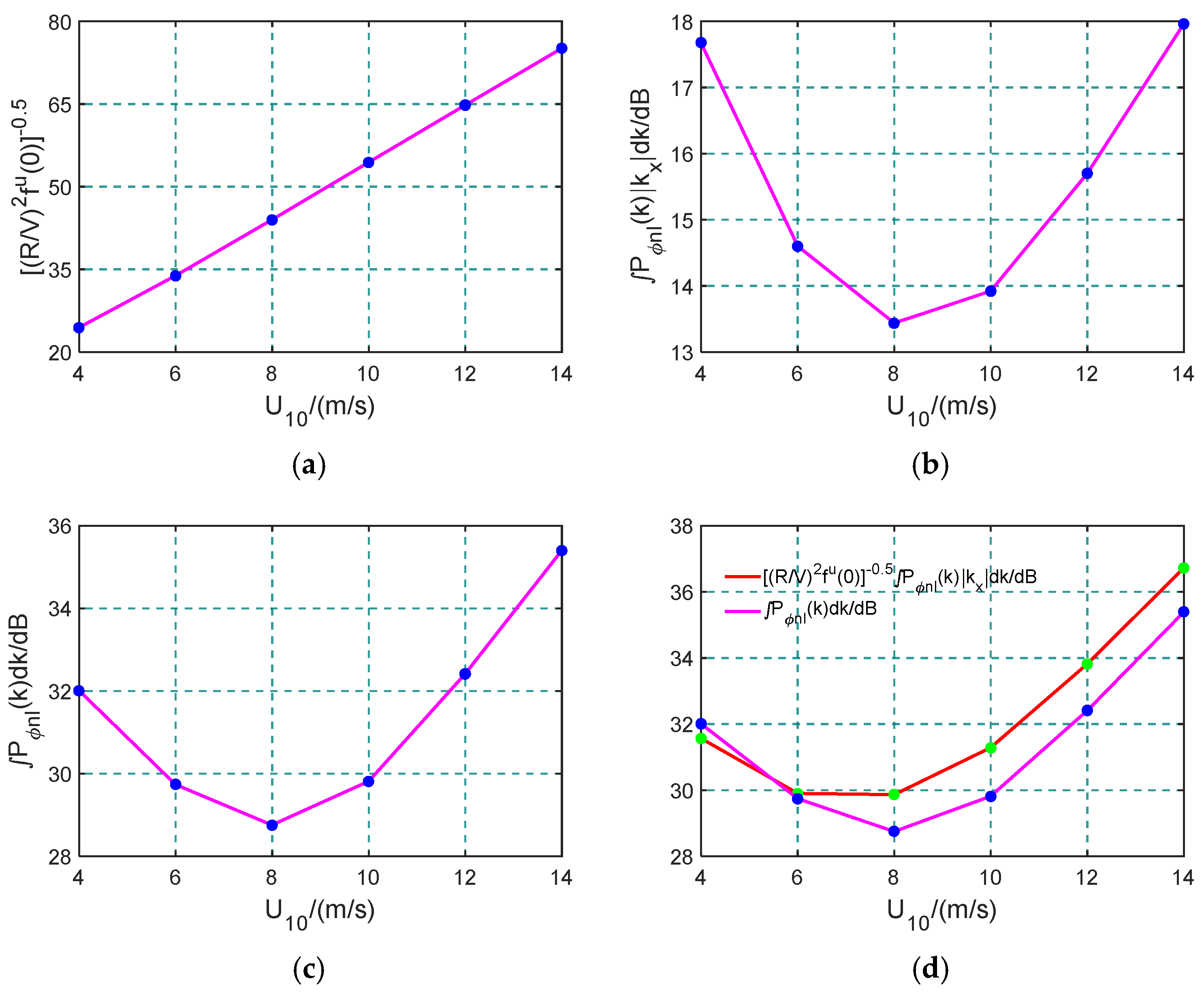
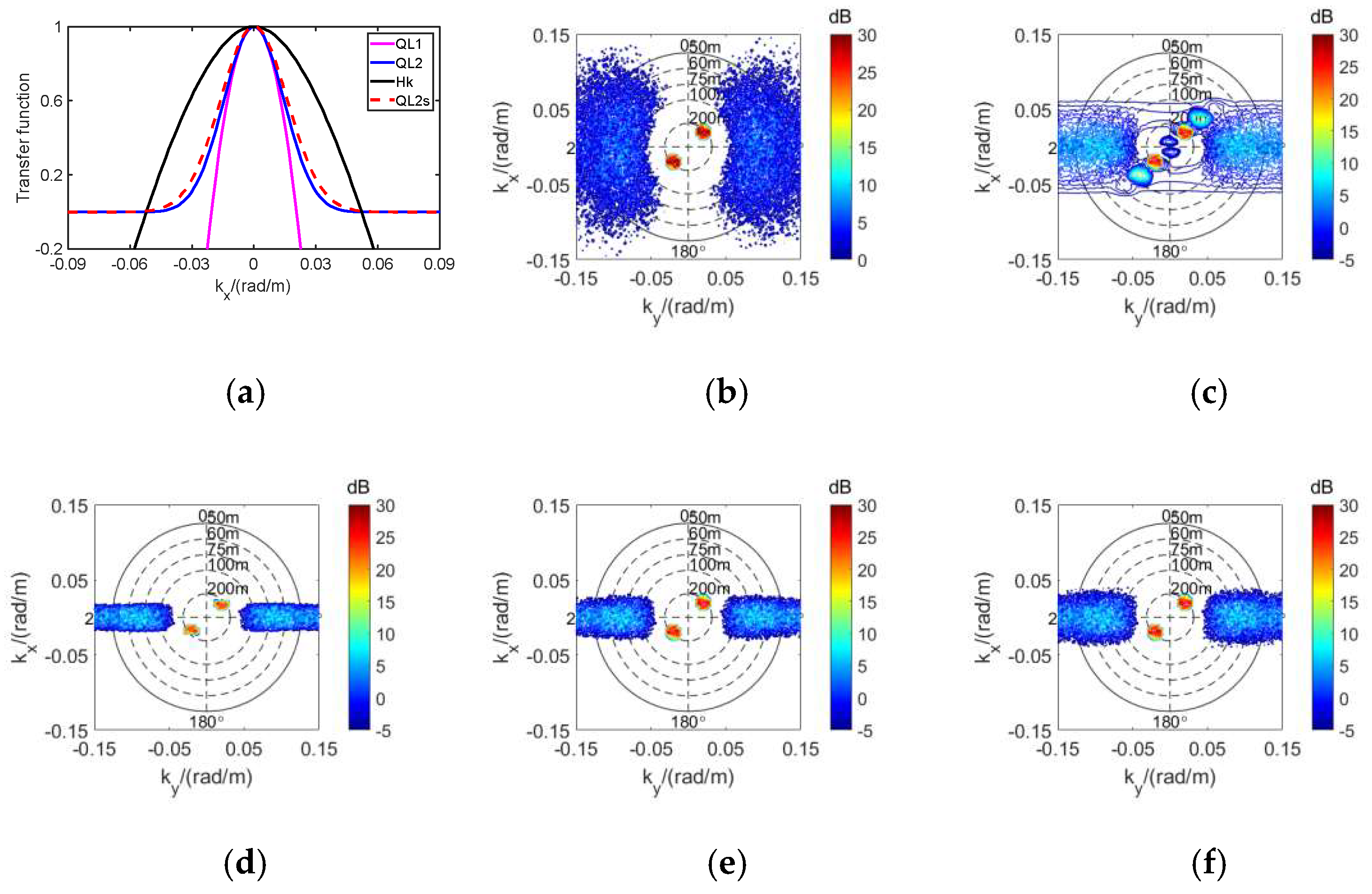

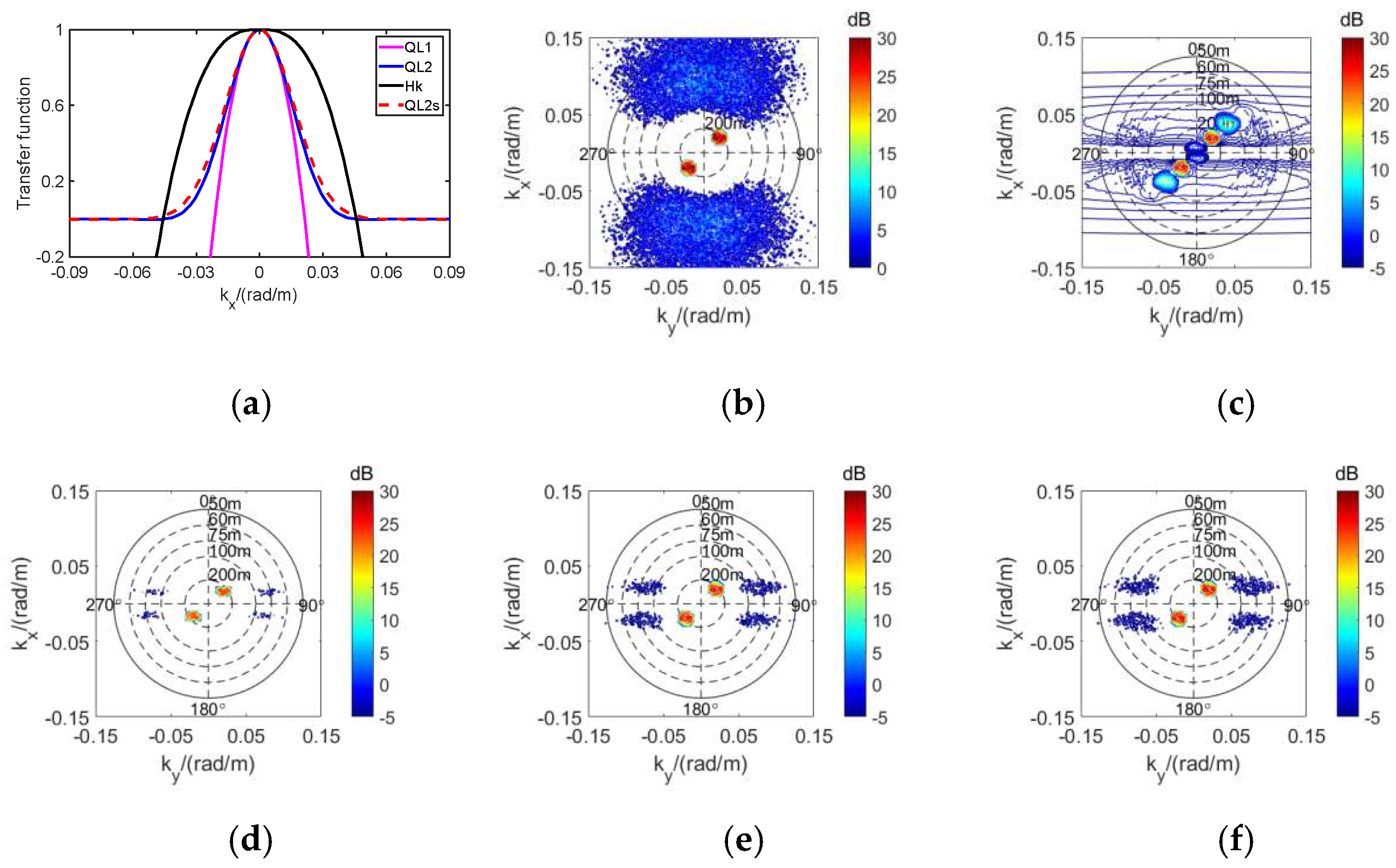
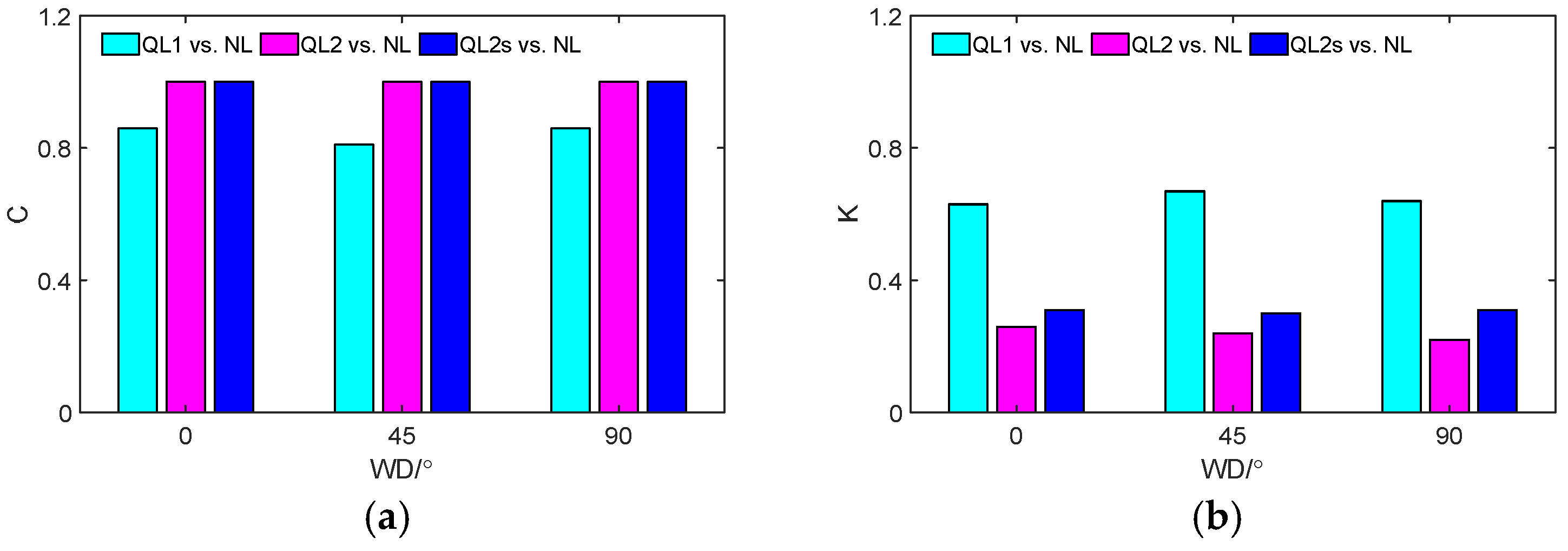

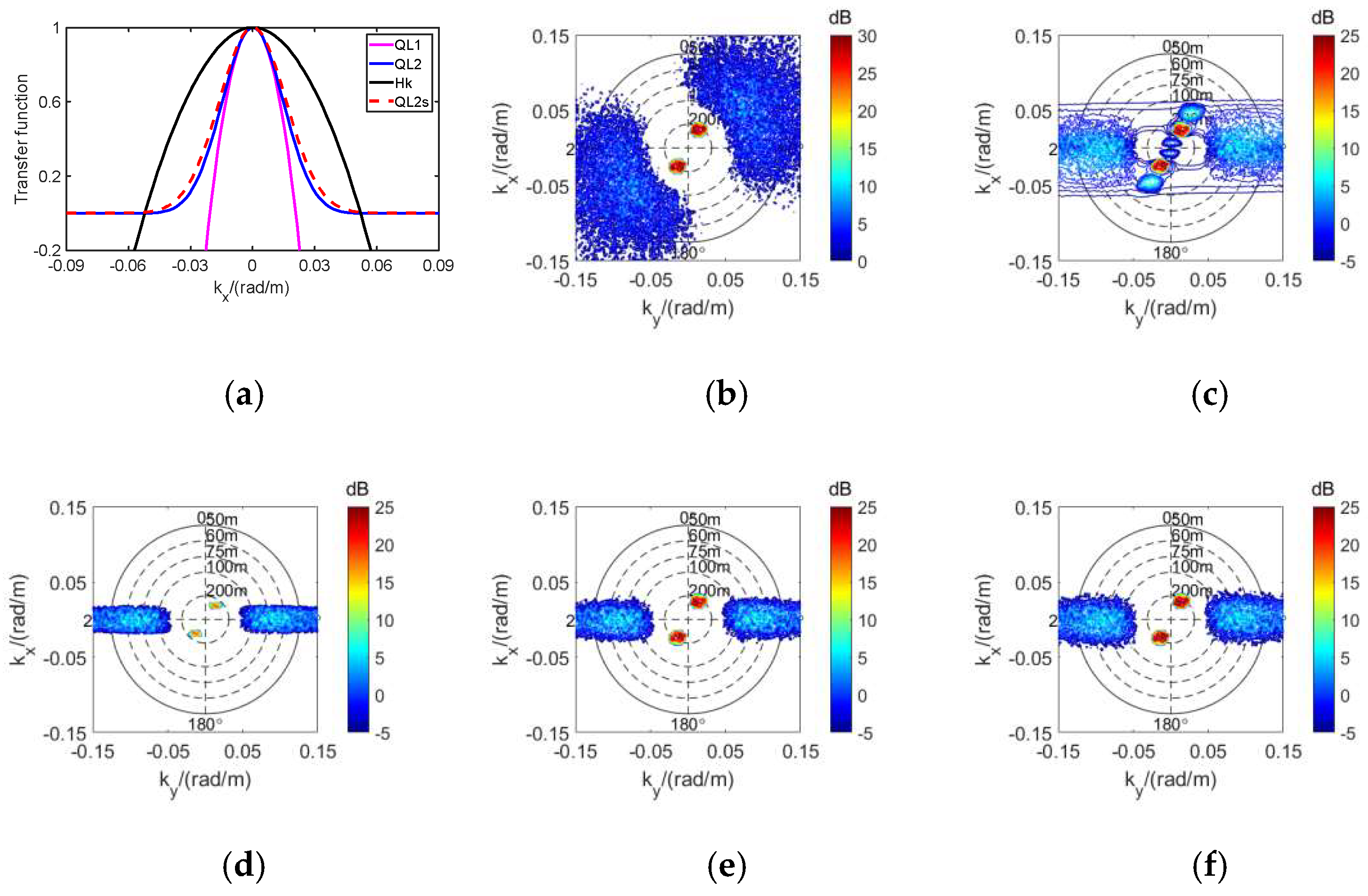
| U10/(m/s) | WD/° | λs/m | SD/° | SWH/m | H/km | θ/° | — |
|---|---|---|---|---|---|---|---|
| 30 | 200 | 60 | 2 | 500 | 30 | — | |
| Cql1 | Cql2 | Cql2s | Kql1 | Kql2 | Kql2s | NLP | |
| 5 | 0.97 | 0.99 | 0.99 | 0.48 | 0.25 | 0.30 | 0.94 |
| 8 | 0.42 | 1 | 1 | 0.86 | 0.31 | 0.34 | 1.29 |
| 10 | 0.31 | 0.99 | 0.99 | 0.73 | 0.43 | 0.37 | 1.40 |
| 12 | 0.79 | 0.96 | 0.98 | 0.62 | 0.46 | 0.37 | 1.38 |
| WD/° | U10/(m/s) | λs/m | SD/° | SWH/m | H/km | θ/° | — |
|---|---|---|---|---|---|---|---|
| 8 | 200 | 45 | 2 | 500 | 30 | — | |
| Cql1 | Cql2 | Cql2s | Kql1 | Kql2 | Kql2s | NLP | |
| 0 | 0.86 | 1.00 | 1.00 | 0.63 | 0.26 | 0.31 | 1.09 |
| 45 | 0.81 | 1.00 | 1.00 | 0.67 | 0.24 | 0.30 | 1.12 |
| 90 | 0.86 | 1.00 | 1.00 | 0.64 | 0.22 | 0.31 | 1.18 |
| λs/m | U10/(m/s) | WD/° | SD/° | SWH/m | H/km | θ/° | — |
|---|---|---|---|---|---|---|---|
| 8 | 30 | 60 | 2 | 500 | 30 | — | |
| Cql1 | Cql2 | Cql2s | Kql1 | Kql2 | Kql2s | NLP | |
| 100 | 0.67 | 0.79 | 0.91 | 0.75 | 0.67 | 0.55 | 1.76 |
| 150 | 0.14 | 0.98 | 0.99 | 0.83 | 0.51 | 0.43 | 1.55 |
| 200 | 0.42 | 1 | 1 | 0.86 | 0.31 | 0.34 | 1.29 |
| 250 | 0.74 | 1 | 1 | 0.67 | 0.24 | 0.27 | 1.09 |
| 300 | 0.88 | 1 | 1 | 0.55 | 0.22 | 0.25 | 1.01 |
| θ/° | U10/(m/s) | WD/° | λs/m | SD/° | SWH/m | H/km | — |
|---|---|---|---|---|---|---|---|
| 8 | 30 | 200 | 60 | 2 | 500 | — | |
| Cql1 | Cql2 | Cql2s | Kql1 | Kql2 | Kql2s | NLP | |
| 30 | 0.42 | 1.00 | 1.00 | 85.88 | 31.12 | 33.71 | 1.29 |
| 40 | 0.16 | 0.99 | 1.00 | 89.22 | 45.08 | 48.04 | 1.44 |
| 50 | 0.10 | 0.89 | 0.99 | 88.54 | 69.74 | 68.32 | 1.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, D.; Wang, Y.; Luo, F.; Luo, X. A New Quasi-Linear Integral Transform Between Ocean Wave Spectrum and Phase Spectrum of an XTI-SAR. Remote Sens. 2025, 17, 1790. https://doi.org/10.3390/rs17101790
Sun D, Wang Y, Luo F, Luo X. A New Quasi-Linear Integral Transform Between Ocean Wave Spectrum and Phase Spectrum of an XTI-SAR. Remote Sensing. 2025; 17(10):1790. https://doi.org/10.3390/rs17101790
Chicago/Turabian StyleSun, Daozhong, Yunhua Wang, Feng Luo, and Xianxian Luo. 2025. "A New Quasi-Linear Integral Transform Between Ocean Wave Spectrum and Phase Spectrum of an XTI-SAR" Remote Sensing 17, no. 10: 1790. https://doi.org/10.3390/rs17101790
APA StyleSun, D., Wang, Y., Luo, F., & Luo, X. (2025). A New Quasi-Linear Integral Transform Between Ocean Wave Spectrum and Phase Spectrum of an XTI-SAR. Remote Sensing, 17(10), 1790. https://doi.org/10.3390/rs17101790








