Abstract
Leaf biochemical traits are crucial for understanding plant physiological status and ecological dynamics. Partial least squares regression (PLSR) models have been widely used to estimate leaf biochemical traits from spectral reflectance information. However, variations in sun–sensor geometry, the sensor field of view, and the random orientation of leaves can introduce multi-angular reflection properties that differ between leaf sides. In this context, the transferability of PLSR models across different leaf sides and viewing zenith angles (VZAs) remains unclear. This study investigated the potential of multi-angular spectral reflection from dorsiventral leaves to improve the transferability of PLSR models for estimating the leaf chlorophyll content (LCC) and equivalent water thickness (EWT). We compared models trained using multi-angular data from both leaf sides with models trained using nadir data (from the adaxial side, abaxial side, or their combination). The results show that the PLSR models trained with multi-angular data from both leaf sides outperformed the models trained with nadir data, achieving the highest accuracy in estimating biochemical traits (LCC: R2 = 0.87, RMSE = 7.17 μg/cm2, NRMSE = 10.71%; EWT: R2 = 0.86, RMSE = 0.0015 g/cm2, NRMSE = 10.00%). In contrast, the PLSR models trained using single-angle reflection from either the adaxial or abaxial side showed a lower estimation accuracy and greater variability across leaf sides and VZAs. The superior performance across datasets obtained under different measurement conditions (e.g., integrating spheres and leaf clips) further confirmed the improved generalizability of the PLSR model trained with multi-angular data from dorsiventral leaves. These findings highlight the potential of the multi-angular spectral reflection of dorsiventral leaves to enhance the estimation of biochemical traits across various leaf sides, viewing angles, and measurement conditions. They also underscore the importance of incorporating spectral diversity into model training for improved transferability.
1. Introduction
Leaf biochemical traits are critical indicators of plant physiological status, photosynthetic activity, and functional processes, and therefore provide valuable insights for interpreting and predicting the impacts of environmental change on terrestrial ecosystems [1,2,3,4,5]. Leaf chlorophyll content (LCC), as one of the major plant pigments, plays a key role in light absorption and photosynthetically active radiation [6,7], which serves as a measure of plant stress physiology and nutrient status [8,9,10]. Leaf water content, expressed as equivalent water thickness (EWT), is a useful indicator of drought stress and plant productivity [11,12], and is related to forest fire drought and risk assessment and net ecosystem exchange [13,14]. Quantifying these leaf biochemical traits could improve our understanding of the ecosystem functioning and contribute to ecological, forestry, and agricultural management endeavors [15,16,17].
Optical remote sensing provides a non-destructive and effective approach for estimating leaf biochemical traits [18,19,20]. Leaf spectral characteristics, such as the absorption of LCC in the blue and red wavelength [21,22,23,24], as well as the absorption of EWT in the near-infrared (such as 970 nm) and shortwave infrared regions [25,26,27], enable the quantification of leaf biochemical traits based on reflected light [1,28]. Two main approaches have been used to estimate leaf biochemical traits from reflectance spectra: physics-based models and data-driven models [29,30,31]. Physics-based models, such as leaf radiative transfer models, rely on predefined physical mechanisms describing the interactions between electromagnetic radiation and leaf biochemical traits, which are considered robust across different conditions [32,33,34,35,36]. However, their implementation is complex, computationally expensive, and their inversion may suffer from the “ill-posed” problem [37], as different parameter combinations may generate similar reflectance spectra [38,39,40,41]. In contrast, data-driven models have been widely applied due to their simplicity and efficiency in estimating leaf biochemical traits [42]. These methods range from simple regression based on spectral indices [8,43,44] to more advanced statistical approaches, such as stepwise linear regression, partial least squares regression (PLSR), and machine learning algorithms [45,46,47,48,49]. While stepwise linear regression struggles with high-dimensional data due to its reliance on sequential variable selection [50,51], machine learning models are often considered ‘black-box’ methods because of their complexity and lack of interpretability [31,52]. PLSR, an advanced form of multivariate linear regression, has been extensively applied to predict plant traits from hyperspectral data due to its high accuracy, explainability, and ability to handle high-dimensional spectral data [30,53,54,55,56,57,58]. It should be noted that PLSR methods rely heavily on training data [31,59,60]. Thus, the selection of representative and diverse training samples is crucial for improving model performance and generalizability.
Most PLSR models are primarily trained using the adaxial reflection near the nadir direction measured by spectrometers equipped with an integrating sphere or leaf clip [30,61,62], while their transferability to the abaxial reflection at the off-nadir direction remains uncertain. In reality, most broadleaf species exhibit dorsiventral asymmetry, where differentiation in internal leaf structures (e.g., palisade and spongy mesophyll) leads to uneven biochemical distributions [63,64]. Additionally, differences in surface properties such as roughness, trichomes, and wax layers contribute to the structural asymmetry between the adaxial and abaxial sides [65,66]. The asymmetry of the internal and surface structure results in distinct reflection distributions between the two sides. The adaxial leaf sides do not always face the sensor as plants adjust leaf orientation in response to growth stages and environmental conditions (e.g., heat and drought stress) to optimize photosynthesis and water use efficiency [67,68]. Apart from this, factors such as varying solar geometry [69,70], sensor field of view [71,72], random leaf orientation, and wind movement [3,73] lead to a mixed signal comprising reflection from two leaf sides under different angular geometries. The reflection from the leaf surface exhibits anisotropy, which varies with the viewing zenith angle [74,75]. Therefore, developing a robust and generalized PLSR model requires accounting for both the spectral and angular properties of the adaxial and abaxial leaf sides.
Previous studies have attempted to mitigate the angular effects and dorsiventral asymmetry on biochemical trait estimation [24,76,77,78,79,80]. Spectral preprocessing techniques, such as first- and second-order derivatives and continuous wavelet transforms, have been integrated with physical models and spectral indices to improve retrieval accuracy [81,82,83,84]. However, these methods have not yet been fully explored within the context of PLSR models to address the multi-angular effect of dorsiventral leaves. Therefore, the potential of incorporating these preprocessing methods into PLSR models to enhance biochemical trait estimation remains to be further investigated.
This study attempts to develop a generalized PLSR model by incorporating diverse spectral variability from both leaf sides across multiple viewing angles. We evaluated the transferability of PLSR models trained using nadir and multi-angular reflection spectra by testing their performance in estimating the LCC and EWT across different leaf sides, viewing angles, and datasets. The overall goal is to improve the transferability and applicability of PLSR models for accurately estimating the biochemical traits of dorsiventral leaves under diverse observation scenarios.
2. Materials and Methods
2.1. Description of Datasets
This study utilized four datasets of various plant species acquired for different studies [33,78,80,85], which were collected in diverse environments using different measurement equipment (Table 1).

Table 1.
Description of datasets used in this study. BRFad indicates bidirectional reflectance factor from the adaxial side, BRFab from the abaxial side, and DHRad indicates directional hemispherical reflectance from the adaxial side.
The DATAMA dataset contains multi-angular reflection spectra from both the adaxial and abaxial leaf sides, along with the corresponding LCC and EWT [80]. It was collected between October 2019 and October 2022 and includes 176 leaf samples from seven tree species (Populus alba L., Morus alba L., Quercus mongolica Fisch. ex Ledeb., Fraxinus mandshurica Rupr., Juglans, Schefflera microphylla Merr., Pachira aquatica, Catalpa ovata G.Don), two shrubs (Swida alba Opiz, Syzygium aromaticum (L.) Merr. & L.M.Perry), and one liana (Parthenocissus quinquefolia (L.) Planch.). These species exhibit substantial variation in adaxial and abaxial surface properties. For example, Populus alba (Po) has a smooth, glossy, and dark green adaxial surface, while its abaxial surface is densely covered with trichomes and appears silvery. In contrast, Syzygium aromaticum (Sy) has a rough, dark green adaxial surface with fine trichomes, while its abaxial surface is smoother and lighter in color [80].
Leaf spectral measurements were performed using the Northeast Normal University Laboratory Goniospectrometer System (NENULGS) across the 400–2500 nm range under various observation geometries [86]. The source zenith angle was set to 40°, and each leaf side was measured at 12 viewing zenith angles (VZAs) in the principal plane (−60°, −50°, −40°, −30°, −20°, −10°, 0°, 10°, 20°, 30°, 50°, and 60°). “−” angles correspond to the forward scattering directions.
The MPRLDLCC and MPRLDEWT datasets contain the bidirectional reflectance factor (BRF) for dorsiventral leaves measured using an ASD FieldSpec spectrometer (Analytical Spectral Devices Inc., Boulder, CO, USA) equipped with a leaf clip. MPRLDLCC, collected between October 2013 and June 2014, consists of 115 leaf samples from two broadleaf species with distinct adaxial and abaxial surface structures, together with LCC measurements [78]. MPRLDEWT, collected in 2016, consists of 300 leaf samples from five species with corresponding EWT measurements [85]. The two datasets were measured at the Multi-angular Polarized Remote Laboratory (MPRL) in Changchun, China.
The ANGERS dataset, collected in 2003 at the National Institute for Agricultural Research (INRA), Angers, France, has been widely used by the remote sensing community for biochemical trait estimation. It includes 276 leaf samples from 43 plant species [33]. The directional hemispherical reflectance (DHR) was measured from the adaxial leaf sides in the 400–2500 nm range using an ASD FieldSpec spectrometer with an integrating sphere. LCC and EWT were measured for each sample.
Basic statistics of the biochemical traits for the four datasets are shown in Figure 1. These datasets encompass a wide range of plant functional types, leaf surface structures, and biochemical traits, allowing for a comprehensive assessment of the transferability and generalizability of PLSR models.
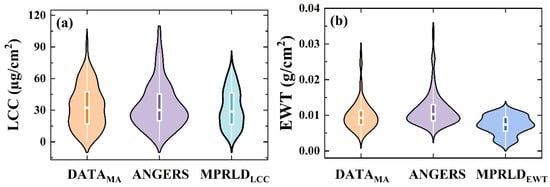
Figure 1.
Violin plots of leaf biochemical traits across all datasets listed in Table 1. (a) Leaf chlorophyll content (LCC); (b) equivalent water thickness (EWT). The boxes represent the first, mean, and third quartiles.
2.2. Estimation of Leaf Biochemical Traits Using PLSR
PLSR is a linear non-parametric method that identifies latent variables by iteratively transforming the predictor and response variables to generate calibration factors and linear models. By maximizing the covariance between predictors and responses while maintaining orthogonality with previous factors, PLSR efficiently handles high-dimensional, collinear spectral data, projecting spectra onto latent components that maximize covariance with the biochemical trait of interest.
Following methods similar to previous studies [30,57,87], we used PLSR modeling integrated with the repeated double cross-validation (rdCV) method, which uses two cross-validation loops (inner and outer). This approach significantly reduces model bias caused by data partitioning and produces stable models [88]. In the outer cross-validation loop, the entire dataset is split into k folds. The model is trained using k−1 folds as the calibration set, and the remaining fold is used as the validation set. Within each calibration set, the data are further split into 70% for training and 30% for testing. This process is repeated 100 times for model training (inner CV loop). For each outer CV iteration, the average coefficients were calculated from the 100 models generated in the inner loop [89]. Model performance and uncertainty were then evaluated on the validation set. At the end of the rdCV, we generated k models and averaged their outputs to derive the final model. In this study, 5-fold cross-validation was used for the inner loop, and 10-fold cross-validation for the outer loop. The optimal number of PLSR components for the final model was determined by minimizing the prediction residual error sum of squares [30].
To evaluate the performance of PLSR models trained on nadir (VZA = 0°) and multi-angular (VZA = −60° to 60°) reflection spectra, we compared the estimation performance of models across different leaf sides and VZAs. Four training strategies were investigated as follows:
- (1)
- Strategy 1: training with adaxial reflection spectra measured at the nadir.
- (2)
- Strategy 2: training with abaxial reflection spectra measured at the nadir.
- (3)
- Strategy 3: training with both adaxial and abaxial reflection spectra measured at the nadir.
- (4)
- Strategy 4: training with multi-angular reflection spectra from both the adaxial and abaxial sides.
For each strategy, we developed separate models using both original and preprocessed spectral data as predictive factors. The preprocessing methods included first derivative (FD), second derivative (SD), and continuous wavelet transform (CWT). Spectral derivatives enhance local spectral features and reduce small spectral variations, helping to mitigate differences in reflectance from different viewing angles [90,91]. The CWT decomposes leaf reflectance spectra into multiple scale components, capturing absorption features at different scales [92]. These components can improve the prediction of leaf biochemical traits [93]. Lower scales extract fine spectral features (such as spectral noise and subtle absorption peaks), while higher scales capture overall spectral features (such as spectral continuities or broad absorption features) [81,94]. The second derivative of the Gaussian function was chosen as the mother wavelet due to its similarity to the shape of leaf absorption features [95]. Given the large range of leaf biochemical traits, we selected wavelet scales 23 (CWT3), 24 (CWT4), and the larger scale 25 (CWT5) for this study [82,95,96]. Additionally, PLSR models were trained using adaxial, abaxial, and combined original reflection spectra measured at 12 VZAs in the principal plane. The 400–1000 nm spectral range was used for LCC estimation, which includes the chlorophyll absorption bands, as the LCC has negligible influence on the SWIR reflection. The full spectral range of leaf reflection was used for EWT estimation.
For cross-dataset modeling, we investigated the transferability of the PLSR models in estimating the LCC and EWT using three datasets for each trait (LCC: DATAMA, MPRLDLCC, and ANGERS; EWT: DATAMA, MPRLDEWT, and ANGERS). We iteratively used one dataset as the calibration set and the remaining datasets for validation. This approach allowed us to assess the robustness and generalizability of PLSR models across different measurement conditions.
2.3. Statistical Analysis
The performance of the PLSR models in estimating leaf biochemical traits was evaluated using standard statistical metrics, including the coefficient of determination (R2), root mean square error (RMSE), and normalized RMSE (NRMSE), which was calculated by dividing the RMSE by the range of the estimated trait values.
To assess the spectral variability across datasets, we calculated the mean and coefficient of variation (CV, defined as the standard deviation divided by the mean) of leaf reflection for each dataset. This analysis provides insight into the differences in spectral characteristics among datasets, which may influence model transferability and generalization.
3. Results
3.1. Spectral Variations Across Leaf Sides, VZAs, and Datasets
The spectral variations across leaf sides and VZAs were investigated using the DATAMA dataset. Figure 2 shows the mean, standard deviation, and range of the BRF spectra from the adaxial and abaxial leaf sides at the nadir (VZA = 0°) and across all VZAs in the principal plane, as well as the mean BRF spectra at different VZAs. Due to the asymmetry of the leaf’s internal and surface structure [35,80], the BRF spectra of the adaxial and abaxial sides exhibit different ranges (Figure 2a–d), with the abaxial side displaying a broader spectral range. Moreover, notable differences are observed between the nadir and multi-angular BRF spectra, with the spectral range across all VZAs being significantly wider than that at the nadir. As shown in Figure 2e,f, similar magnitudes are found for the mean BRF spectra at the nadir and in the backward scattering directions (VZA = 10° to 60°). However, the BRF values in the forward scattering directions (VZA = −10° to −60°) are notably higher. This is primarily due to specular reflection, which mainly occurs in the forward scattering directions and acts as an additive component to the overall leaf reflectance. The different angular distribution of the BRF is due to the varying magnitude of the specular reflection. In contrast, the contribution of specular reflection at the nadir and in the backward scattering directions is relatively small, and the majority of the total reflection is the diffuse reflection [74,75,97].
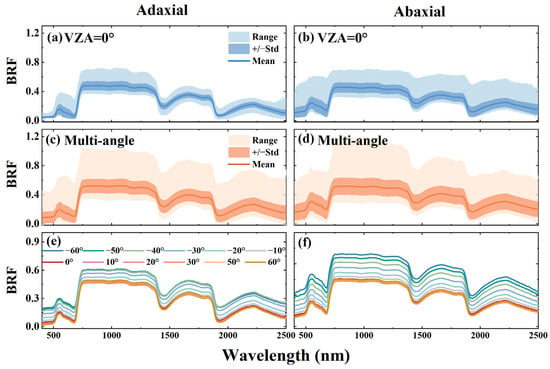
Figure 2.
Mean, standard deviation (Std), and range of BRF spectra from adaxial and abaxial leaf sides at the nadir (a,b) and across all VZAs (c,d), along with the mean BRF spectra at different VZAs for both leaf sides (e,f). “−” represents the forward scattering directions.
Figure 3 shows the multi-angular reflectance factors and angular BRF distribution at 560 nm, 670 nm, 865 nm, and 1590 nm for two plant species with distinct surface structures between the adaxial and abaxial sides. These wavelengths were selected as they correspond directly or approximately to spectral bands on satellite-mounted sensors, including the Multi-angle Imaging SpectroRadiometer (MISR) [98], Polarization and Directionality of Earth’s Reflectances (POLDER) [99], and the Research Scanning Polarimeter (RSP) [100]. The BRFs of the adaxial and abaxial leaf sides varied significantly with the VZA, particularly in the forward scattering direction. For example, the adaxial side of Po (Figure 3a,e) and the abaxial side of Sy (Figure 3d,h), which have relatively smooth surfaces, exhibit strong reflection peaks, with maximum reflection occurring near the specular direction. In contrast, the abaxial side of Po (Figure 3b,f) and the adaxial side of Sy (Figure 3c,g), which have relatively rough surfaces, exhibit weak anisotropic reflection, with maximum reflection occurring at very high VZAs. These differences arise from variations in the leaf surface structure, which affect the angular distribution of specular reflection; the smoother leaf surfaces result in stronger anisotropic reflection [74,79,101]. Overall, the substantial variability in leaf reflection across leaf sides and VZAs highlights the importance of incorporating these spectral variations into PLSR model training to improve the robustness and generalizability of biochemical trait estimation.
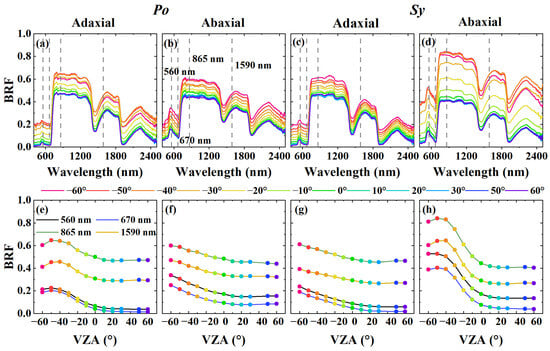
Figure 3.
Multi-angular reflectance factor (a–d) and angular BRF distribution at 560 nm, 670 nm, 865 nm, and 1590 nm (e–h) for adaxial and abaxial leaf sides of two plant species (the first two columns: Populus alba L. (Po); the last two columns: Syzygium aromaticum (L.) Merr. & L.M.Perry (Sy)).
In addition, the spectral range of leaf reflection varies significantly across datasets at different wavelengths (Figure 4). Compared with the MPRLDLCC and MPRLDEWT datasets (Figure 4b,c, obtained using a leaf clip equipment) and the ANGERS dataset (Figure 4d, obtained using an integrating sphere equipment), the DATAMA dataset (measured using a goniospectrometer system) exhibits the widest reflection range (Figure 4a). It also shows a high coefficient of variation at the wavelengths with strong absorption features. Moreover, the DATAMA dataset showed the typical shape of the leaf spectra, including a sharp increase in reflection at the red edge and prominent water absorption features in the shortwave infrared region.
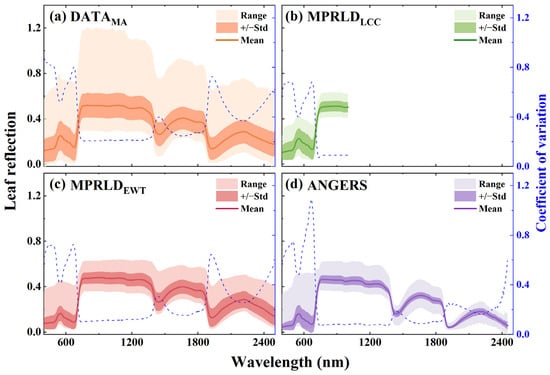
Figure 4.
Mean, standard deviation, range, and coefficient of variation of leaf reflection spectra from the four datasets (DATAMA, MPRLDLCC, MPRLDEWT, and ANGERS) used in this study.
3.2. The Transferability of the PLSR Model to Different VZAs
To evaluate the transferability of PLSR models across different VZAs, models were developed using four strategies (see Section 2.2) based on both the original and preprocessed spectra. Figure 5 shows the estimation performance of the PLSR models trained using these strategies across varying VZAs. The estimation accuracies of the PLSR models trained using original spectra at the nadir from either the adaxial (Strategy 1) or abaxial (Strategy 2) leaf sides are strongly dependent on the VZAs (Figure 5a,g), as evidenced by the sharp increase in NRMSE values in the forward scattering direction (dominated by the specular reflection). Strategy 3, which combined both adaxial and abaxial spectra at the nadir for training, improved the estimation performance of the PLSR model compared to Strategies 1 and 2. Nevertheless, its estimation accuracy remained sensitive to VZA variations, especially for the EWT estimation (Figure 5g). In contrast, the PLSR model trained with multi-angular spectra from both leaf sides (Strategy 4) achieved the highest accuracy and was largely insensitive to the VZA in the principal plane, as indicated by its stable and consistent performance across different VZAs. Additionally, while spectral preprocessing methods, such as first-derivative transformation (Figure 5b,h), slightly improved the performance of the PLSR models trained on the spectra measured at the nadir (Strategies 1, 2, and 3), these models still underperformed compared to Strategy 4. Notably, applying preprocessing methods to the PLSR model trained using Strategy 4 did not yield significant accuracy improvements. This may be because multi-angular spectra from both leaf sides inherently integrate information across three dimensions (leaf side, viewing angle, and spectral properties), providing a more comprehensive dataset for model training.
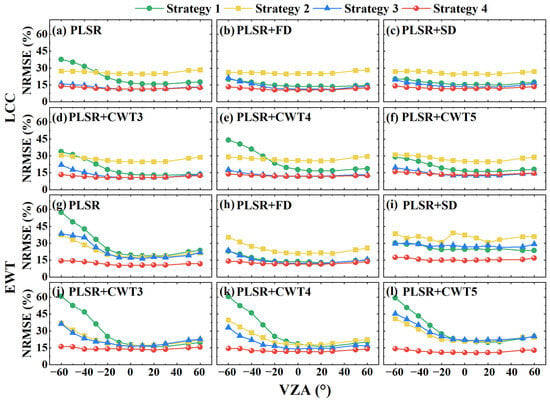
Figure 5.
NRMSE for estimating LCC (a–f) and EWT (g–l) using PLSR models trained on different VZAs based on the DATAMA dataset under four training strategies incorporating original spectra (PLSR), first-derivative spectra (PLSR+FD), second-derivative spectra (PLSR+SD), and continuous wavelet transform spectra at scale 23 (PLSR+CWT3), scale 24 (PLSR+CWT4), and scale 25 (PLSR+CWT5). Strategy 1: trained with adaxial reflection spectra at the nadir; Strategy 2: trained with abaxial reflection spectra at the nadir; Strategy 3: trained with both adaxial and abaxial reflection spectra at the nadir; Strategy 4: trained with multi-angular reflection spectra from both the adaxial and abaxial sides.
Furthermore, we compared the transferability of the PLSR models trained with reflection spectra from a single VZA, either from the adaxial, abaxial, or both leaf sides, with models trained with multi-angular spectra from both leaf sides (Figure 6). The PLSR model trained with multi-angular spectra from both the adaxial and abaxial sides achieved the best estimation performance, with a lower NRMSE% compared to the models trained with spectra from a single VZA or a single leaf side. These findings highlight the advantage of incorporating multi-angular reflection spectra from dorsiventral leaves in improving the transferability of PLSR models across different observation geometries.
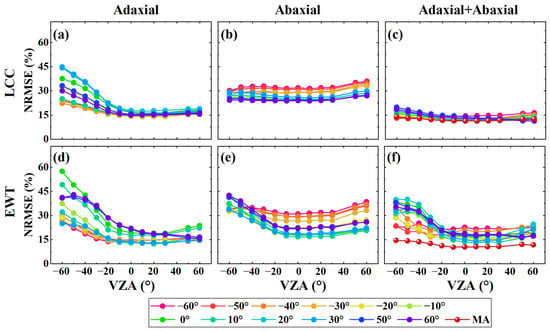
Figure 6.
Comparison of the estimation performance of PLSR models trained using single VZA spectra from the adaxial (a,d), abaxial (b,e), and combined leaf sides (c,f) in the principal plane, and models trained with multi-angular (MA) spectra from both leaf sides.
3.3. The Transferability of the PLSR Model to Different Leaf Sides
To assess the transferability of the PLSR models across different leaf sides, we compared the estimation performance of the models trained on original and preprocessed reflection spectra from the adaxial, abaxial, and combined leaf sides for the LCC (Table 2) and EWT (Table 3). When a PLSR model trained on one leaf side was applied to the opposite side, its performance decreased significantly, with the estimation accuracy differing by up to 24.97% for the LCC (Strategy 2, PLSR) and 21.47% for the EWT (Strategy 1, PLSR). Moreover, spectral preprocessing did not improve the transferability of the PLSR models trained on a single leaf side. In contrast, the PLSR models trained on spectra from both leaf sides exhibited a more stable estimation accuracy across leaf sides, with the differences in the estimation accuracy between the adaxial and abaxial sides reduced to within 2.69% for the LCC (Strategy 3, PLSR) and 1.28% for the EWT (Strategy 3, PLSR). Furthermore, models trained on multi-angular spectra from both leaf sides outperformed models trained on spectra from both sides measured at the nadir direction. Scatterplots of measured versus estimated biochemical content using the PLSR models trained with four strategies, incorporating both original and preprocessed spectra, are shown in Figure 7 and Figure 8. It was found that the estimated values of the PLSR models trained with the multi-angular spectra of dorsiventral leaves (Strategy 4) were closely distributed around the 1:1 line, with greater consistency between the adaxial and abaxial sides (fourth columns in Figure 7 and Figure 8). In contrast, models trained with other strategies exhibited more deviation from the 1:1 line (first three columns in Figure 7 and Figure 8). Overall, the PLSR models trained with multi-angular spectra from both leaf sides demonstrated strong transferability and the highest estimation accuracy (LCC: R2 = 0.84, RMSE = 7.76 μg/cm2, NRMSE = 11.55%; EWT: R2 = 0.84, RMSE = 0.0016 g/cm2, NRMSE = 10.91%).

Table 2.
The R2, RMSE, and NRMSE for LCC (μg/cm2) estimation using PLSR models trained on different leaf sides (AD: adaxial; AB: abaxial) from the DATAMA dataset under four training strategies, incorporating original spectra and five preprocessing methods.

Table 3.
The R2, RMSE, and NRMSE for EWT (g/cm2) estimation using PLSR models trained on different leaf sides from the DATAMA dataset under four training strategies, incorporating original spectra and five preprocessing methods.
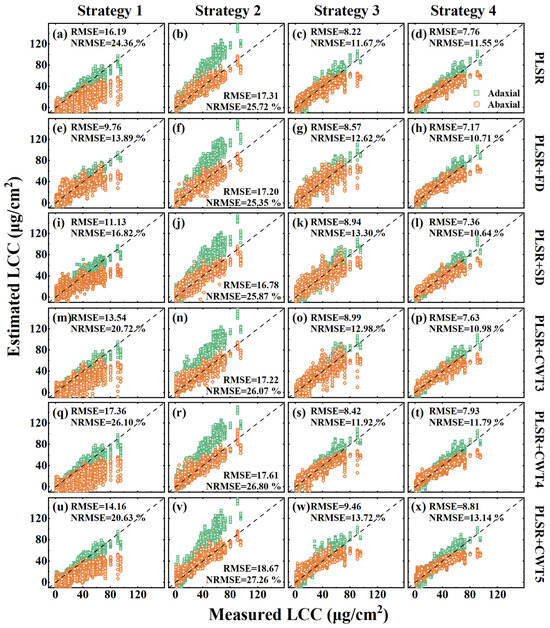
Figure 7.
Scatterplots of measured and estimated LCC from the adaxial and abaxial sides in the DATAMA dataset using PLSR models trained under four strategies, incorporating original spectra and five preprocessed methods.
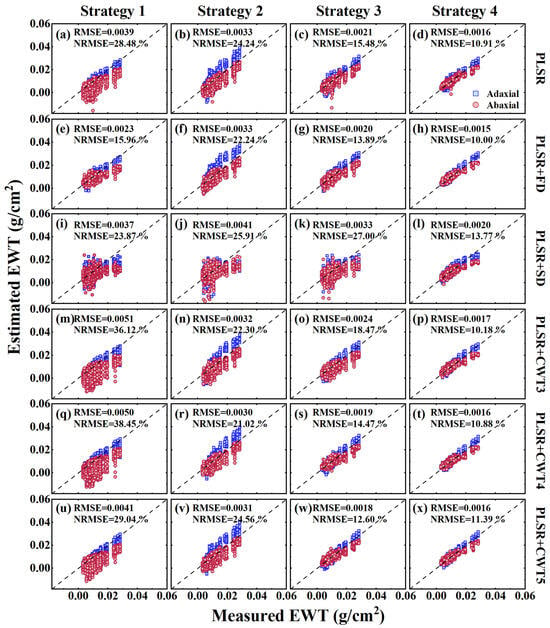
Figure 8.
Scatterplots of measured and estimated EWT from the adaxial and abaxial sides in the DATAMA dataset using PLSR models trained under four strategies, incorporating original spectra and five preprocessed methods.
3.4. The Transferability of the PLSR Model to Different Datasets
To evaluate the transferability of the PLSR models under different measurement conditions, the models were trained on one dataset and validated on the remaining two datasets (Table 4). As shown in Table 4, the PLSR models calibrated using the DATAMA dataset achieved the highest validation accuracy, with the highest R2 values (LCC: 0.76; EWT: 0.88) and the lowest RMSE (LCC: 10.39 μg/cm2; EWT: 0.0018 g/cm2) and NRMSE (LCC: 9.81%; EWT: 5.55%). In comparison, the models calibrated on the ANGERS dataset, obtained with spectrometers equipped with an integrating sphere, exhibited moderate accuracy. Meanwhile, the models trained on the MPRLDLCC and MPRLDEWT datasets, obtained using spectrometers with a leaf clip, showed the lowest estimation accuracy when validated on other datasets. This may be attributed to the lower spectral variability within these datasets (Figure 4). These results highlight the advantage of the DATAMA dataset, which incorporates a broader range of measurement geometries and conditions, enhancing its representativeness as a training dataset. As a result, the PLSR models trained on the DATAMA dataset demonstrate greater transferability and stability across datasets with varying measurement conditions.

Table 4.
Results of calibration and validation of the PLSR models using different datasets to estimate LCC (μg/cm2) and EWT (g/cm2). The models were trained on one dataset and validated using the remaining two datasets.
4. Discussion
4.1. The Importance of Considering Leaf Reflection Spectral Variations Across Leaf Sides and VZAs for PLSR Modeling
Leaf reflection spectra exhibit significant variations across different leaf sides and VZAs (Figure 3 and Figure 4) due to differences in internal structure, surface properties, and biochemical composition [35,56,66,80,102]. In PLSR analysis, the best practice is to use the estimation model to be applied strictly within the range of measurement conditions that were used during model training [30]. For leaf biochemical trait estimation based on spectral data, the quality and diversity of the training dataset are critical for ensuring model transferability [31]. To minimize bias in model validation, the training dataset should encompass a broader range of confounding factors [103], such as measurement geometry and leaf surface structural characteristics, than the independent datasets used for model application.
Most existing biochemical trait estimation models rely on spectral measurements from the adaxial leaf side, often neglecting the effects of angular variations and dorsiventral asymmetry [29,54,77]. However, in high spatial resolution remote sensing, reflectance factors can be detected from a small portion of an individual leaf, either from the adaxial or abaxial side. When estimating leaf biochemical traits from spectral data, it is essential to account for the multiple effects of leaf orientation, inclination distribution, and varying observation geometries [73,104,105]. Moreover, under drought stress, leaf curling can expose the abaxial side to the sensor, further emphasizing the need to consider dorsiventral differences [68,106,107]. The rapid development of UAV-based remote sensing has facilitated the acquisition of high spatial resolution hyperspectral data over large areas in a short time [108,109]. Hyperspectral cameras mounted on UAVs are now more accessible and can be used in specially designed flight paths to collect multi-angular observations by capturing reflectance from different positions and directions [70]. Therefore, the comprehensive consideration of the variations in leaf reflection spectra across leaf sides and VZAs is essential for improving the generalizability of PLSR models.
4.2. Implications of Using Multi-Angular Reflection Spectra of Dorsiventral Leaves to Improve PLSR Model Transferability
Unlike previous studies that primarily focused on reducing the dorsiventral asymmetry or angular effects on biochemical trait estimation through spectral preprocessing methods such as wavelet transforms and spectral derivatives [77,83,84], this study provides interesting insights by explicitly incorporating reflection information from both leaf sides and multiple viewing angles to improve the estimation accuracy. Integrating spectral data from both the adaxial and abaxial leaf sides across multiple VZAs significantly improved the performance of the PLSR models in this study (Figure 5, Figure 6, Figure 7 and Figure 8), which highlights the importance of incorporating the leaf side, angle, and spectral dimensions to enhance the accuracy of leaf trait estimation. In contrast, the models trained on spectra from a single VZA or single leaf side exhibited limited transferability, with significant decreases in estimation accuracy when applied to different measurement geometries and leaf sides. Moreover, the estimation accuracy of the PLSR models combined with spectral preprocessing methods remains lower than that of the PLSR models trained using multi-angular reflection spectra of dorsiventral leaves. A generalizable PLSR model for estimating leaf biochemical traits should be developed using reflectance factors from both the adaxial and abaxial leaf sides, which differ in surface structure, across various VZAs. In the principal plane, strong specular reflection is typically observed in forward scattering directions, while the lowest reflectance factor occurs near the nadir and in backward scattering directions [74,101]. Thus, the multi-angular reflectance spectra of dorsiventral leaves collected in this study can effectively capture the reflection properties observed under different measurement setups (i.e., integrating spheres, leaf clips, and goniometers), including specular reflection with different magnitudes from both leaf sides [110]. This also explains the superior estimation performance of the PLSR models trained on the DATAMA dataset across different datasets (Table 4). Despite incorporating multi-angular reflection spectra from dorsiventral leaves measured in the principal plane, the accuracy of the PLSR model has yet to reach its maximum potential. Further studies are needed to collect extensive reflection spectra of leaf surfaces across a wider range of illumination–observation geometries, plant species, and biochemical traits (e.g., carotenoid content and leaf mass per area) to enhance model performance and assess the transferability and applicability of the multi-angular PLSR model across a broader spectrum of leaf characteristics. Additionally, with the future incorporation of interpretable methods, investigating spectral band selection and exploring alternative regression algorithms, such as support vector machine [111,112], random forests [113,114], and Gaussian process regression [46,115], may provide valuable insights into model transferability and performance. Our results imply that incorporating reflection spectra measured from multiple VZAs for both leaf sides into PLSR modeling can improve model transferability, which provides a robust framework for accurately estimating biochemical traits in high spatial and spectral resolution remote sensing applications.
5. Conclusions
This study investigated the transferability of PLSR models for estimating the LCC and EWT across different leaf sides, VZAs, and datasets with different measurement conditions. Significant spectral variations were observed across leaf sides and VZAs, which resulted in poor transferability when the PLSR models were trained using data from a single leaf side or VZA. In contrast, the PLSR models trained using multi-angular reflection spectra from both the adaxial and abaxial leaf sides achieved higher accuracy and greater stability across different leaf sides, VZAs, and datasets. The superior performance of the PLSR models trained on the DATAMA dataset highlights the advantages of combining spectral information from multiple VZAs and leaf sides to better capture spectral variability.
Our results emphasize the necessity of incorporating multi-angular reflection spectral data from dorsiventral leaves into PLSR modeling, which may provide a robust approach for effective and reliable biochemical trait estimation in high spatial resolution remote sensing. Multi-angular optical observations offer complementary information to characterize plant traits in a more robust and accurate way, with great potential to achieve the required accuracy for the remote sensing of biochemical traits. Future work will therefore be dedicated to testing these models for high spatial resolution multi-angular remote sensing observations using UAVs with embedded hyperspectral cameras flying along concentric circles at different altitudes.
Author Contributions
Conceptualization, D.R., Z.S. and S.L.; methodology, D.R.; validation, D.R. and S.L.; formal analysis, D.R. and Z.S.; investigation, D.R.; resources, Z.S. and S.L.; data curation, Z.S. and S.L.; writing—original draft preparation, D.R.; writing—review and editing, D.R., Z.S. and S.L.; visualization, D.R.; supervision, Z.S. and S.L.; project administration, Z.S. and S.L.; funding acquisition, Z.S. and S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (Grant No. 2022YFB3902904), National Natural Science Foundation of China (Grant No. 42471377), and the Jilin Provincial Scientific and Technological Development Program (Grant Nos. 20240402034GH and 20240101047JC).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We would like to thank the scientists who collected and shared the leaf datasets.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Féret, J.-B.; François, C.; Gitelson, A.; Asner, G.P.; Barry, K.M.; Panigada, C.; Richardson, A.D.; Jacquemoud, S. Optimizing spectral indices and chemometric analysis of leaf chemical properties using radiative transfer modeling. Remote Sens. Environ. 2011, 115, 2742–2750. [Google Scholar] [CrossRef]
- Kattge, J.; Diaz, S.; Lavorel, S.; Prentice, I.C.; Leadley, P.; Bönisch, G.; Garnier, E.; Westoby, M.; Reich, P.B.; Wright, I.J. TRY–A global database of plant traits. Glob. Change Biol. 2011, 17, 2905–2935. [Google Scholar] [CrossRef]
- Ollinger, S.V. Sources of variability in canopy reflectance and the convergent properties of plants. New Phytol. 2011, 189, 375–394. [Google Scholar] [CrossRef]
- Schimel, D.; Pavlick, R.; Fisher, J.B.; Asner, G.P.; Saatchi, S.; Townsend, P.; Miller, C.; Frankenberg, C.; Hibbard, K.; Cox, P. Observing terrestrial ecosystems and the carbon cycle from space. Glob. Change Biol. 2015, 21, 1762–1776. [Google Scholar] [CrossRef]
- Schweiger, A.K.; Cavender-Bares, J.; Townsend, P.A.; Hobbie, S.E.; Madritch, M.D.; Wang, R.; Tilman, D.; Gamon, J.A. Plant spectral diversity integrates functional and phylogenetic components of biodiversity and predicts ecosystem function. Nat. Ecol. Evol. 2018, 2, 976–982. [Google Scholar] [CrossRef] [PubMed]
- Croft, H.; Chen, J.M.; Luo, X.; Bartlett, P.; Chen, B.; Staebler, R.M. Leaf chlorophyll content as a proxy for leaf photosynthetic capacity. Glob. Change Biol. 2017, 23, 3513–3524. [Google Scholar] [CrossRef]
- Gamon, J.A.; Huemmrich, K.F.; Wong, C.Y.; Ensminger, I.; Garrity, S.; Hollinger, D.Y.; Noormets, A.; Penuelas, J. A remotely sensed pigment index reveals photosynthetic phenology in evergreen conifers. Proc. Natl. Acad. Sci. USA 2016, 113, 13087–13092. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F.; Cescatti, A.; Gitelson, A.A. Leaf chlorophyll constraint on model simulated gross primary productivity in agricultural systems. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 160–176. [Google Scholar] [CrossRef]
- Van Bodegom, P.M.; Douma, J.C.; Verheijen, L.M. A fully traits-based approach to modeling global vegetation distribution. Proc. Natl. Acad. Sci. USA 2014, 111, 13733–13738. [Google Scholar] [CrossRef]
- Galmés, J.; Medrano, H.; Flexas, J. Photosynthetic limitations in response to water stress and recovery in Mediterranean plants with different growth forms. New Phytol. 2007, 175, 81–93. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Estimation of vegetation water content and photosynthetic tissue area from spectral reflectance: A comparison of indices based on liquid water and chlorophyll absorption features. Remote Sens. Environ. 2003, 84, 526–537. [Google Scholar] [CrossRef]
- Humphrey, V.; Zscheischler, J.; Ciais, P.; Gudmundsson, L.; Sitch, S.; Seneviratne, S.I. Sensitivity of atmospheric CO2 growth rate to observed changes in terrestrial water storage. Nature 2018, 560, 628–631. [Google Scholar] [CrossRef]
- Maki, M.; Ishiahra, M.; Tamura, M. Estimation of leaf water status to monitor the risk of forest fires by using remotely sensed data. Remote Sens. Environ. 2004, 90, 441–450. [Google Scholar] [CrossRef]
- Houborg, R.; Fisher, J.B.; Skidmore, A.K. Advances in remote sensing of vegetation function and traits. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 1–6. [Google Scholar] [CrossRef]
- Luo, X.; Croft, H.; Chen, J.M.; He, L.; Keenan, T.F. Improved estimates of global terrestrial photosynthesis using information on leaf chlorophyll content. Glob. Change Biol. 2019, 25, 2499–2514. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Gamon, J.A. Remote sensing of terrestrial plant biodiversity. Remote Sens. Environ. 2019, 231, 111218. [Google Scholar] [CrossRef]
- Asner, G.P.; Martin, R.E. Spectral and chemical analysis of tropical forests: Scaling from leaf to canopy levels. Remote Sens. Environ. 2008, 112, 3958–3970. [Google Scholar] [CrossRef]
- Carter, G.A.; Knapp, A.K. Leaf optical properties in higher plants: Linking spectral characteristics to stress and chlorophyll concentration. Am. J. Bot. 2001, 88, 677–684. [Google Scholar] [CrossRef]
- Hill, J.; Buddenbaum, H.; Townsend, P.A. Imaging spectroscopy of forest ecosystems: Perspectives for the use of space-borne hyperspectral earth observation systems. Surv. Geophys. 2019, 40, 553–588. [Google Scholar] [CrossRef]
- Curran, P.J.; Dungan, J.L.; Peterson, D.L. Estimating the foliar biochemical concentration of leaves with reflectance spectrometry: Testing the Kokaly and Clark methodologies. Remote Sens. Environ. 2001, 76, 349–359. [Google Scholar] [CrossRef]
- Datt, B. A new reflectance index for remote sensing of chlorophyll content in higher plants: Tests using Eucalyptus leaves. J. Plant Physiol. 1999, 154, 30–36. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Quantitative estimation of chlorophyll-a using reflectance spectra: Experiments with autumn chestnut and maple leaves. J. Photochem. Photobiol. B Biol. 1994, 22, 247–252. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Ceccato, P.; Flasse, S.; Tarantola, S.; Jacquemoud, S.; Grégoire, J.-M. Detecting vegetation leaf water content using reflectance in the optical domain. Remote Sens. Environ. 2001, 77, 22–33. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Peñuelas, J.; Pinol, J.; Ogaya, R.; Filella, I. Estimation of plant water concentration by the reflectance water index WI (R900/R970). Int. J. Remote Sens. 1997, 18, 2869–2875. [Google Scholar] [CrossRef]
- Asner, G.P.; Martin, R.E.; Anderson, C.B.; Knapp, D.E. Quantifying forest canopy traits: Imaging spectroscopy versus field survey. Remote Sens. Environ. 2015, 158, 15–27. [Google Scholar] [CrossRef]
- Féret, J.B.; le Maire, G.; Jay, S.; Berveiller, D.; Bendoula, R.; Hmimina, G.; Cheraiet, A.; Oliveira, J.C.; Ponzoni, F.J.; Solanki, T.; et al. Estimating leaf mass per area and equivalent water thickness based on leaf optical properties: Potential and limitations of physical modeling and machine learning. Remote Sens. Environ. 2019, 231, 110959. [Google Scholar] [CrossRef]
- Ji, F.; Li, F.; Hao, D.; Shiklomanov, A.N.; Yang, X.; Townsend, P.A.; Dashti, H.; Nakaji, T.; Kovach, K.R.; Liu, H.; et al. Unveiling the transferability of PLSR models for leaf trait estimation: Lessons from a comprehensive analysis with a novel global dataset. New Phytol. 2024, 243, 111–131. [Google Scholar] [CrossRef]
- Verrelst, J.; Malenovský, Z.; Van der Tol, C.; Camps-Valls, G.; Gastellu-Etchegorry, J.-P.; Lewis, P.; North, P.; Moreno, J. Quantifying vegetation biophysical variables from imaging spectroscopy data: A review on retrieval methods. Surv. Geophys. 2019, 40, 589–629. [Google Scholar] [CrossRef] [PubMed]
- Féret, J.-B.; Berger, K.; de Boissieu, F.; Malenovský, Z. PROSPECT-PRO for estimating content of nitrogen-containing leaf proteins and other carbon-based constituents. Remote Sens. Environ. 2021, 252, 112173. [Google Scholar] [CrossRef]
- Feret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Stuckens, J.; Verstraeten, W.W.; Delalieux, S.; Swennen, R.; Coppin, P. A dorsiventral leaf radiative transfer model: Development, validation and improved model inversion techniques. Remote Sens. Environ. 2009, 113, 2560–2573. [Google Scholar] [CrossRef]
- Jiang, J.; Comar, A.; Weiss, M.; Baret, F. FASPECT: A model of leaf optical properties accounting for the differences between upper and lower faces. Remote Sens. Environ. 2021, 253. [Google Scholar] [CrossRef]
- Combal, B.; Baret, F.; Weiss, M.; Trubuil, A.; Mace, D.; Pragnere, A.; Myneni, R.; Knyazikhin, Y.; Wang, L. Retrieval of canopy biophysical variables from bidirectional reflectance: Using prior information to solve the ill-posed inverse problem. Remote Sens. Environ. 2003, 84, 1–15. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; D’Urso, G.; Mauser, W.; Vuolo, F.; Hank, T. Evaluation of the PROSAIL model capabilities for future hyperspectral model environments: A review study. Remote Sens. 2018, 10, 85. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F.; Andrieu, B.; Danson, F.M.; Jaggard, K. Extraction of vegetation biophysical parameters by inversion of the PROSPECT + SAIL models on sugar beet canopy reflectance data. Application to TM and AVIRIS sensors. Remote Sens. Environ. 1995, 52, 163–172. [Google Scholar] [CrossRef]
- Kimes, D.S.; Knyazikhin, Y.; Privette, J.L.; Abuelgasim, A.A.; Gao, F. Inversion methods for physically-based models. Remote Sens. Rev. 2000, 18, 381–439. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F. Evaluation of canopy biophysical variable retrieval performances from the accumulation of large swath satellite data. Remote Sens. Environ. 1999, 70, 293–306. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Cao, Z.X.; Wang, Q.; Zheng, C.L. Best hyperspectral indices for tracing leaf water status as determined from leaf dehydration experiments. Ecol. Indic. 2015, 54, 96–107. [Google Scholar] [CrossRef]
- Main, R.; Cho, M.A.; Mathieu, R.; O’Kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS J. Photogramm. Remote Sens. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Sun, J.; Yang, J.; Shi, S.; Chen, B.; Du, L.; Gong, W.; Song, S. Estimating rice leaf nitrogen concentration: Influence of regression algorithms based on passive and active leaf reflectance. Remote Sens. 2017, 9, 951. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Gitelson, A.; Delegido, J.; Moreno, J.; Camps-Valls, G. Spectral band selection for vegetation properties retrieval using Gaussian processes regression. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 554–567. [Google Scholar] [CrossRef]
- Wan, L.; Zhou, W.; He, Y.; Wanger, T.C.; Cen, H. Combining transfer learning and hyperspectral reflectance analysis to assess leaf nitrogen concentration across different plant species datasets. Remote Sens. Environ. 2022, 269, 112826. [Google Scholar] [CrossRef]
- García-Soria, J.L.; Morata, M.; Berger, K.; Pascual-Venteo, A.B.; Rivera-Caicedo, J.P.; Verrelst, J. Evaluating epistemic uncertainty estimation strategies in vegetation trait retrieval using hybrid models and imaging spectroscopy data. Remote Sens. Environ. 2024, 310, 114228. [Google Scholar] [CrossRef]
- Cherif, E.; Feilhauer, H.; Berger, K.; Dao, P.D.; Ewald, M.; Hank, T.B.; He, Y.; Kovach, K.R.; Lu, B.; Townsend, P.A.; et al. From spectra to plant functional traits: Transferable multi-trait models from heterogeneous and sparse data. Remote Sens. Environ. 2023, 292, 113580. [Google Scholar] [CrossRef]
- Hwang, J.-S.; and Hu, T.-H. A stepwise regression algorithm for high-dimensional variable selection. J. Stat. Comput. Simul. 2015, 85, 1793–1806. [Google Scholar] [CrossRef]
- Atzberger, C.; Guérif, M.; Baret, F.; Werner, W. Comparative analysis of three chemometric techniques for the spectroradiometric assessment of canopy chlorophyll content in winter wheat. Comput. Electron. Agric. 2010, 73, 165–173. [Google Scholar] [CrossRef]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Guzman, Q.J.A.; Sanchez-Azofeifa, G.A. Prediction of leaf traits of lianas and trees via the integration of wavelet spectra in the visible-near infrared and thermal infrared domains. Remote Sens. Environ. 2021, 259, 112406. [Google Scholar] [CrossRef]
- Kothari, S.; Beauchamp-Rioux, R.; Blanchard, F.; Crofts, A.L.; Girard, A.; Guilbeault-Mayers, X.; Hacker, P.W.; Pardo, J.; Schweiger, A.K.; Demers-Thibeault, S.; et al. Predicting leaf traits across functional groups using reflectance spectroscopy. New Phytol. 2023, 238, 549–566. [Google Scholar] [CrossRef]
- Nakaji, T.; Oguma, H.; Nakamura, M.; Kachina, P.; Asanok, L.; Marod, D.; Aiba, M.; Kurokawa, H.; Kosugi, Y.; Kassim, A.R.; et al. Estimation of six leaf traits of East Asian forest tree species by leaf spectroscopy and partial least square regression. Remote Sens. Environ. 2019, 233, 111381. [Google Scholar] [CrossRef]
- Neuwirthová, E.; Lhotáková, Z.; Červená, L.; Lukeš, P.; Campbell, P.; Albrechtová, J. Asymmetry of leaf internal structure affects PLSR modelling of anatomical traits using VIS-NIR leaf level spectra. Eur. J. Remote Sens. 2024, 57, 2292154. [Google Scholar] [CrossRef]
- Yan, Z.; Guo, Z.; Serbin, S.P.; Song, G.; Zhao, Y.; Chen, Y.; Wu, S.; Wang, J.; Wang, X.; Li, J.; et al. Spectroscopy outperforms leaf trait relationships for predicting photosynthetic capacity across different forest types. New Phytol. 2021, 232, 134–147. [Google Scholar] [CrossRef]
- Wang, Z.; Féret, J.-B.; Liu, N.; Sun, Z.; Yang, L.; Geng, S.; Zhang, H.; Chlus, A.; Kruger, E.L.; Townsend, P.A. Generality of leaf spectroscopic models for predicting key foliar functional traits across continents: A comparison between physically-and empirically-based approaches. Remote Sens. Environ. 2023, 293, 113614. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Nunes, M.H.; Stoddart, J.; Khoury, S.; Chan, A.H.Y.; Coomes, D.A. Predicting leaf traits of temperate broadleaf deciduous trees from hyperspectral reflectance: Can a general model be applied across a growing season? Remote Sens. Environ. 2022, 269, 112767. [Google Scholar] [CrossRef]
- Wu, J.; Chavana-Bryant, C.; Prohaska, N.; Serbin, S.P.; Guan, K.; Albert, L.P.; Yang, X.; van Leeuwen, W.J.D.; Garnello, A.J.; Martins, G.; et al. Convergence in relationships between leaf traits, spectra and age across diverse canopy environments and two contrasting tropical forests. New Phytol. 2017, 214, 1033–1048. [Google Scholar] [CrossRef]
- Wang, S.; Guan, K.; Wang, Z.; Ainsworth, E.A.; Zheng, T.; Townsend, P.A.; Li, K.; Moller, C.; Wu, G.; Jiang, C. Unique contributions of chlorophyll and nitrogen to predict crop photosynthetic capacity from leaf spectroscopy. J. Exp. Bot. 2020, 72, 341–354. [Google Scholar] [CrossRef]
- Yang, X.; Tang, J.; Mustard, J.F.; Wu, J.; Zhao, K.; Serbin, S.; Lee, J.-E. Seasonal variability of multiple leaf traits captured by leaf spectroscopy at two temperate deciduous forests. Remote Sens. Environ. 2016, 179, 1–12. [Google Scholar] [CrossRef]
- Borsuk, A.M.; Roddy, A.B.; Théroux-Rancourt, G.; Brodersen, C.R. Structural organization of the spongy mesophyll. New Phytol. 2022, 234, 946–960. [Google Scholar] [CrossRef] [PubMed]
- Wall, S.; Vialet-Chabrand, S.; Davey, P.; Van Rie, J.; Galle, A.; Cockram, J.; Lawson, T. Stomata on the abaxial and adaxial leaf surfaces contribute differently to leaf gas exchange and photosynthesis in wheat. New Phytol. 2022, 235, 1743–1756. [Google Scholar] [CrossRef]
- Nakata, M.; Okada, K. The leaf adaxial-abaxial boundary and lamina growth. Plants 2013, 2, 174–202. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, T.; Nukazuka, A.; Tsukaya, H. Leaf adaxial–abaxial polarity specification and lamina outgrowth: Evolution and development. Plant Cell Physiol. 2012, 53, 1180–1194. [Google Scholar] [CrossRef]
- Drake, P.L.; de Boer, H.J.; Schymanski, S.J.; Veneklaas, E.J. Two sides to every leaf: Water and CO2 transport in hypostomatous and amphistomatous leaves. New Phytol. 2019, 222, 1179–1187. [Google Scholar] [CrossRef]
- Wieneke, S.; Pacheco-Labrador, J.; Mahecha, M.D.; Poblador, S.; Vicca, S.; Janssens, I.A. Comparing the quantum use efficiency of red and far-red sun-induced fluorescence at leaf and canopy under heat-drought stress. Remote Sens. Environ. 2024, 311, 114294. [Google Scholar] [CrossRef]
- Sagan, V.; Maimaitijiang, M.; Paheding, S.; Bhadra, S.; Gosselin, N.; Burnette, M.; Demieville, J.; Hartling, S.; LeBauer, D.; Newcomb, M.; et al. Data-driven artificial intelligence for calibration of hyperspectral big data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5510320. [Google Scholar] [CrossRef]
- Li, W.; Jiang, J.; Weiss, M.; Madec, S.; Tison, F.; Philippe, B.; Comar, A.; Baret, F. Impact of the reproductive organs on crop BRDF as observed from a UAV. Remote Sens. Environ. 2021, 259, 112433. [Google Scholar] [CrossRef]
- Schläpfer, D.; Richter, R.; Feingersh, T. Operational BRDF effects correction for wide-field-of-view optical scanners (BREFCOR). IEEE Trans. Geosci. Remote Sens. 2015, 53, 1855–1864. [Google Scholar] [CrossRef]
- Zhao, F.; Li, Y.; Dai, X.; Verhoef, W.; Guo, Y.; Shang, H.; Gu, X.; Huang, Y.; Yu, T.; Huang, J. Simulated impact of sensor field of view and distance on field measurements of bidirectional reflectance factors for row crops. Remote Sens. Environ. 2015, 156, 129–142. [Google Scholar] [CrossRef]
- Lukeš, P.; Neuwirthová, E.; Lhotáková, Z.; Janoutová, R.; Albrechtová, J. Upscaling seasonal phenological course of leaf dorsiventral reflectance in radiative transfer model. Remote Sens. Environ. 2020, 246, 111862. [Google Scholar] [CrossRef]
- Bousquet, L.; Lachérade, S.; Jacquemoud, S.; Moya, I. Leaf BRDF measurements and model for specular and diffuse components differentiation. Remote Sens. Environ. 2005, 98, 201–211. [Google Scholar] [CrossRef]
- Comar, A.; Baret, F.; Vienot, F.; Yan, L.; De Solan, B. Wheat leaf bidirectional reflectance measurements: Description and quantification of the volume, specular and hot-spot scattering features. Remote Sens. Environ. 2012, 121, 26–35. [Google Scholar] [CrossRef]
- Jay, S.; Bendoula, R.; Hadoux, X.; Feret, J.B.; Gorretta, N. A physically-based model for retrieving foliar biochemistry and leaf orientation using close-range imaging spectroscopy. Remote Sens. Environ. 2016, 177, 220–236. [Google Scholar] [CrossRef]
- Li, D.; Tian, L.; Wan, Z.; Jia, M.; Yao, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cheng, T. Assessment of unified models for estimating leaf chlorophyll content across directional-hemispherical reflectance and bidirectional reflectance spectra. Remote Sens. Environ. 2019, 231, 111240. [Google Scholar] [CrossRef]
- Lu, S.; Lu, X.; Zhao, W.; Liu, Y.; Wang, Z.; Omasa, K. Comparing vegetation indices for remote chlorophyll measurement of white poplar and Chinese elm leaves with different adaxial and abaxial surfaces. J. Exp. Bot. 2015, 66, 5625–5637. [Google Scholar] [CrossRef]
- Ran, D.; Sun, Z.; Lu, S.; Omasa, K. Optimizing angular resistant spectral indices to estimate leaf biochemical parameters from multi-angular spectral reflection. Agric. For. Meteorol. 2024, 348, 109916. [Google Scholar] [CrossRef]
- Ran, D.; Sun, Z.; Lu, S.; Omasa, K. An advanced dorsiventral leaf radiative transfer model for simulating multi-angular and spectral reflection: Considering asymmetry of leaf internal and surface structure. Remote Sens. Environ. 2025, 318, 114531. [Google Scholar] [CrossRef]
- Cheng, T.; Rivard, B.; Sánchez-Azofeifa, A.G.; Féret, J.-B.; Jacquemoud, S.; Ustin, S.L. Predicting leaf gravimetric water content from foliar reflectance across a range of plant species using continuous wavelet analysis. J. Plant Physiol. 2012, 169, 1134–1142. [Google Scholar] [CrossRef]
- Li, D.; Cheng, T.; Jia, M.; Zhou, K.; Lu, N.; Yao, X.; Tian, Y.C.; Zhu, Y.; Cao, W.X. PROCWT: Coupling PROSPECT with continuous wavelet transform to improve the retrieval of foliar chemistry from leaf bidirectional reflectance spectra. Remote Sens. Environ. 2018, 206, 1–14. [Google Scholar] [CrossRef]
- Wan, L.; Zhang, J.; Xu, Y.; Huang, Y.; Zhou, W.; Jiang, L.; He, Y.; Cen, H. PROSDM: Applicability of PROSPECT model coupled with spectral derivatives and similarity metrics to retrieve leaf biochemical traits from bidirectional reflectance. Remote Sens. Environ. 2021, 267, 112761. [Google Scholar] [CrossRef]
- Yao, C.; Sun, Z.; Lu, S. Evaluation of PROSPECT inversion approaches using multiangular spectral reflectance factor of leaves. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–16. [Google Scholar] [CrossRef]
- You, W. Methods for Estimating Water Content of Bifacial Leaf Plants. Master’s Thesis, Northeast Normal University, Changchun, China, 2018. [Google Scholar]
- Sun, Z.; Wu, Z.F.; Zhao, Y.S. Semi-automatic laboratory goniospectrometer system for performing multi-angular reflectance and polarization measurements for natural surfaces. Rev. Sci. Instrum. 2014, 85, 014503. [Google Scholar] [CrossRef]
- Dechant, B.; Cuntz, M.; Vohland, M.; Schulz, E.; Doktor, D. Estimation of photosynthesis traits from leaf reflectance spectra: Correlation to nitrogen content as the dominant mechanism. Remote Sens. Environ. 2017, 196, 279–292. [Google Scholar] [CrossRef]
- Filzmoser, P.; Liebmann, B.; Varmuza, K. Repeated double cross validation. J. Chemom. A J. Chemom. Soc. 2009, 23, 160–171. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Demetriades-Shah, T.H.; Steven, M.D.; Clark, J.A. High resolution derivative spectra in remote sensing. Remote Sens. Environ. 1990, 33, 55–64. [Google Scholar] [CrossRef]
- Tsai, F.; Philpot, W. Derivative analysis of hyperspectral data. Remote Sens. Environ. 1998, 66, 41–51. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Rivard, B.; Feng, J.; Gallie, A.; Sanchez-Azofeifa, A. Continuous wavelets for the improved use of spectral libraries and hyperspectral data. Remote Sens. Environ. 2008, 112, 2850–2862. [Google Scholar] [CrossRef]
- Feng, J.; Rogge, D.; Rivard, B. Comparison of lithological mapping results from airborne hyperspectral VNIR-SWIR, LWIR and combined data. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 340–353. [Google Scholar] [CrossRef]
- Cheng, T.; Rivard, B.; Sánchez-Azofeifa, A.G.; Féret, J.-B.; Jacquemoud, S.; Ustin, S.L. Deriving leaf mass per area (LMA) from foliar reflectance across a variety of plant species using continuous wavelet analysis. ISPRS J. Photogramm. Remote Sens. 2014, 87, 28–38. [Google Scholar] [CrossRef]
- Li, D.; Cheng, T.; Yao, X.; Zhang, Z.; Tian, Y.; Zhu, Y.; Cao, W. Wavelet-based PROSPECT inversion for retrieving leaf mass per area (LMA) and equivalent water thickness (EWT) from leaf reflectance. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 6910–6913. [Google Scholar]
- Sun, Z.; Wu, D.; Lv, Y.; Lu, S. Optical properties of reflected light from leaves: A case study from one species. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4388–4406. [Google Scholar] [CrossRef]
- Diner, D.J.; Beckert, J.C.; Reilly, T.H.; Bruegge, C.J.; Conel, J.E.; Kahn, R.A.; Martonchik, J.V.; Ackerman, T.P.; Davies, R.; Gerstl, S.A.W.; et al. Multi-angle Imaging SpectroRadiometer (MISR) instrument description and experiment overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1072–1087. [Google Scholar] [CrossRef]
- Deschamps, P.-Y.; Bréon, F.-M.; Leroy, M.; Podaire, A.; Bricaud, A.; Buriez, J.-C.; Seze, G. The POLDER mission: Instrument characteristics and scientific objectives. IEEE Trans. Geosci. Remote Sens. 1994, 32, 598–615. [Google Scholar] [CrossRef]
- Cairns, B.; Russell, E.E.; Travis, L.D. Research scanning polarimeter: Calibration and ground-based measurements. In Proceedings of the Polarization: Measurement, Analysis, and Remote Sensing II, Denver, CO, USA, 19–21 July 1999; pp. 186–196. [Google Scholar]
- Roth, B.D.; Saunders, M.G.; Bachmann, C.M.; van Aardt, J.A. On leaf BRDF estimates and their fit to microfacet models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1761–1771. [Google Scholar] [CrossRef]
- Woolley, J.T. Reflectance and transmittance of light by leaves. Plant Physiol. 1971, 47, 656–662. [Google Scholar] [CrossRef]
- Meyer, H.; Pebesma, E. Predicting into unknown space? Estimating the area of applicability of spatial prediction models. Methods Ecol. Evol. 2021, 12, 1620–1633. [Google Scholar] [CrossRef]
- Jay, S.; Gorretta, N.; Morel, J.; Maupas, F.; Bendoula, R.; Rabatel, G.; Dutartre, D.; Comar, A.; Baret, F. Estimating leaf chlorophyll content in sugar beet canopies using millimeter- to centimeter-scale reflectance imagery. Remote Sens. Environ. 2017, 198, 173–186. [Google Scholar] [CrossRef]
- Stuckens, J.; Somers, B.; Delalieux, S.; Verstraeten, W.W.; Coppin, P. The impact of common assumptions on canopy radiative transfer simulations: A case study in Citrus orchards. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 1–21. [Google Scholar] [CrossRef]
- Chávez, R.O.; Clevers, J.G.; Verbesselt, J.; Naulin, P.I.; Herold, M. Detecting leaf pulvinar movements on NDVI time series of desert trees: A new approach for water stress detection. PLoS ONE 2014, 9, e106613. [Google Scholar] [CrossRef] [PubMed]
- Pastenes, C.; Pimentel, P.; Lillo, J. Leaf movements and photoinhibition in relation to water stress in field-grown beans. J. Exp. Bot. 2005, 56, 425–433. [Google Scholar] [CrossRef]
- Zhang, Y.; Hui, J.; Qin, Q.; Sun, Y.; Zhang, T.; Sun, H.; Li, M. Transfer-learning-based approach for leaf chlorophyll content estimation of winter wheat from hyperspectral data. Remote Sens. Environ. 2021, 267, 112724. [Google Scholar] [CrossRef]
- Chen, A.; Xu, C.; Zhang, M.; Guo, J.; Xing, X.; Yang, D.; Xu, B.; Yang, X. Cross-scale mapping of above-ground biomass and shrub dominance by integrating UAV and satellite data in temperate grassland. Remote Sens. Environ. 2024, 304, 114024. [Google Scholar] [CrossRef]
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing-definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Moreno-Martínez, Á.; Camps-Valls, G.; Kattge, J.; Robinson, N.; Reichstein, M.; van Bodegom, P.; Kramer, K.; Cornelissen, J.H.C.; Reich, P.; Bahn, M. A methodology to derive global maps of leaf traits using remote sensing and climate data. Remote Sens. Environ. 2018, 218, 69–88. [Google Scholar] [CrossRef]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Efficient RTM-based training of machine learning regression algorithms to quantify biophysical & biochemical traits of agricultural crops. ISPRS J. Photogramm. Remote Sens. 2021, 173, 278–296. [Google Scholar]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving soybean leaf area index from unmanned aerial vehicle hyperspectral remote sensing: Analysis of RF, ANN, and SVM regression models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Jiao, Q.; Sun, Q.; Zhang, B.; Huang, W.; Ye, H.; Zhang, Z.; Zhang, X.; Qian, B. A random forest algorithm for retrieving canopy chlorophyll content of wheat and soybean trained with PROSAIL simulations using adjusted average leaf angle. Remote Sens. 2021, 14, 98. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian processes in machine learning. In Summer School on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2003; pp. 63–71. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).