Rapid Probabilistic Inundation Mapping Using Local Thresholds and Sentinel-1 SAR Data on Google Earth Engine
Abstract
1. Introduction
2. Materials and Methods
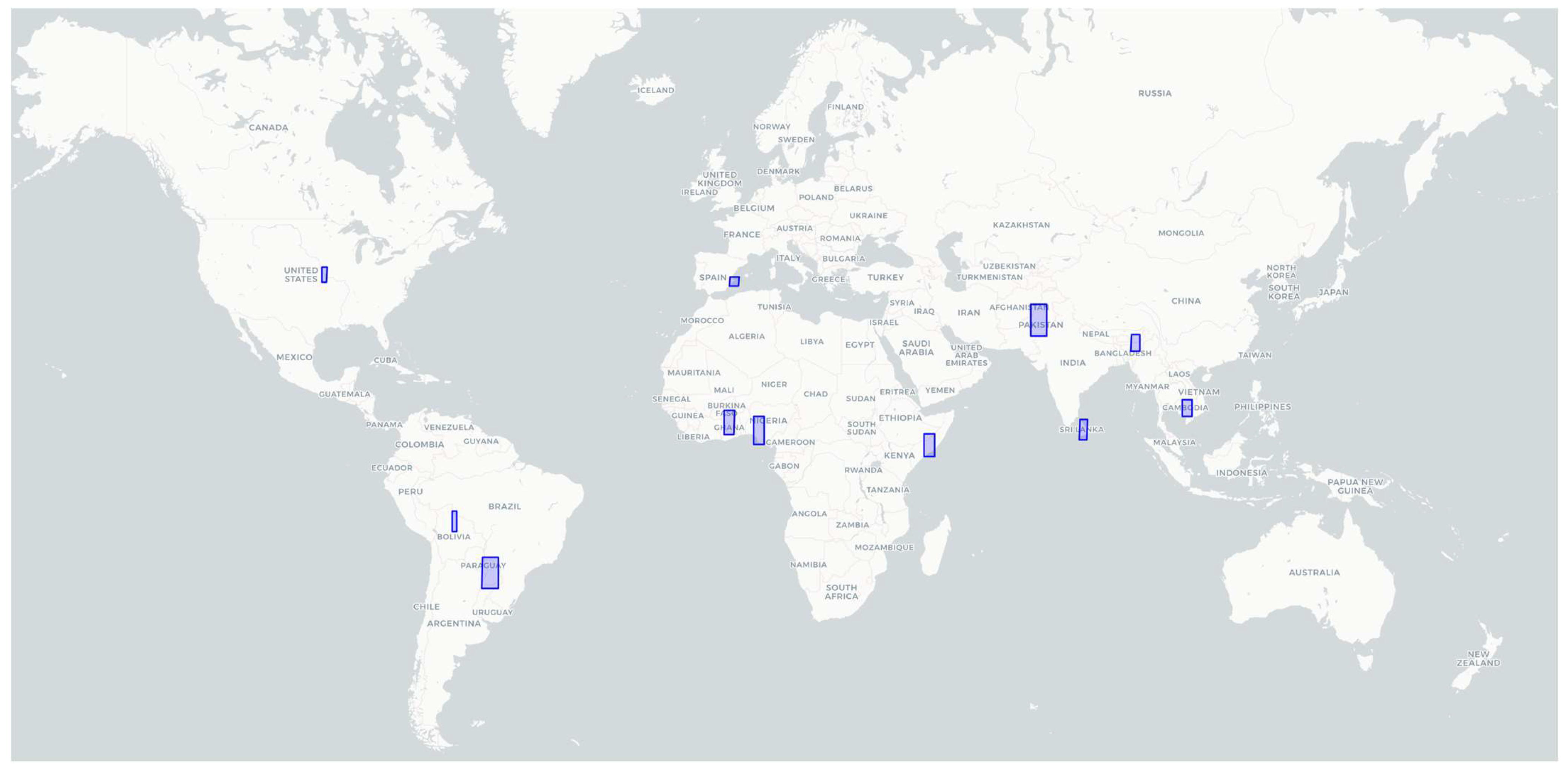
2.1. Data
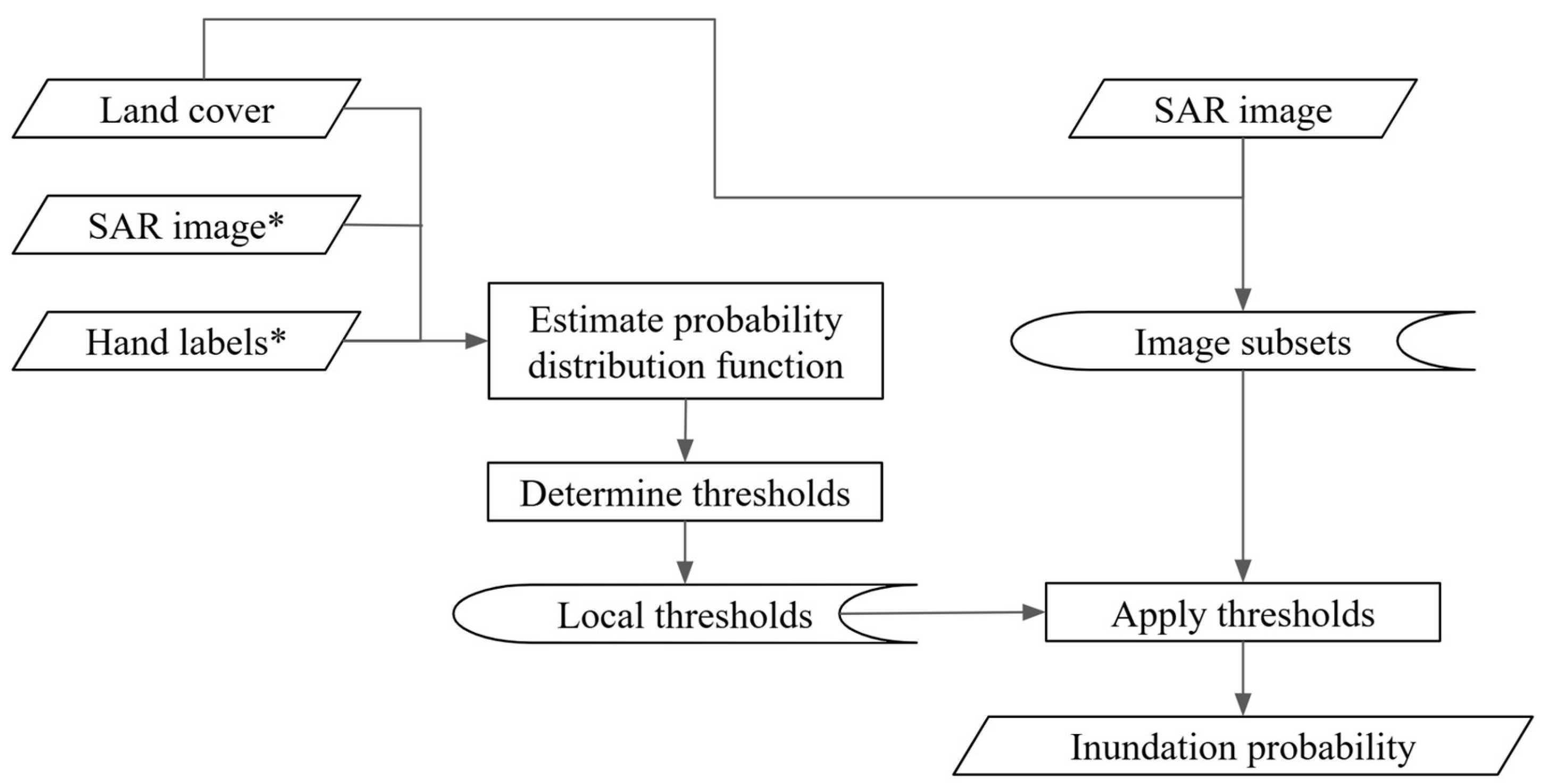
2.2. Method
2.2.1. Extract Samples
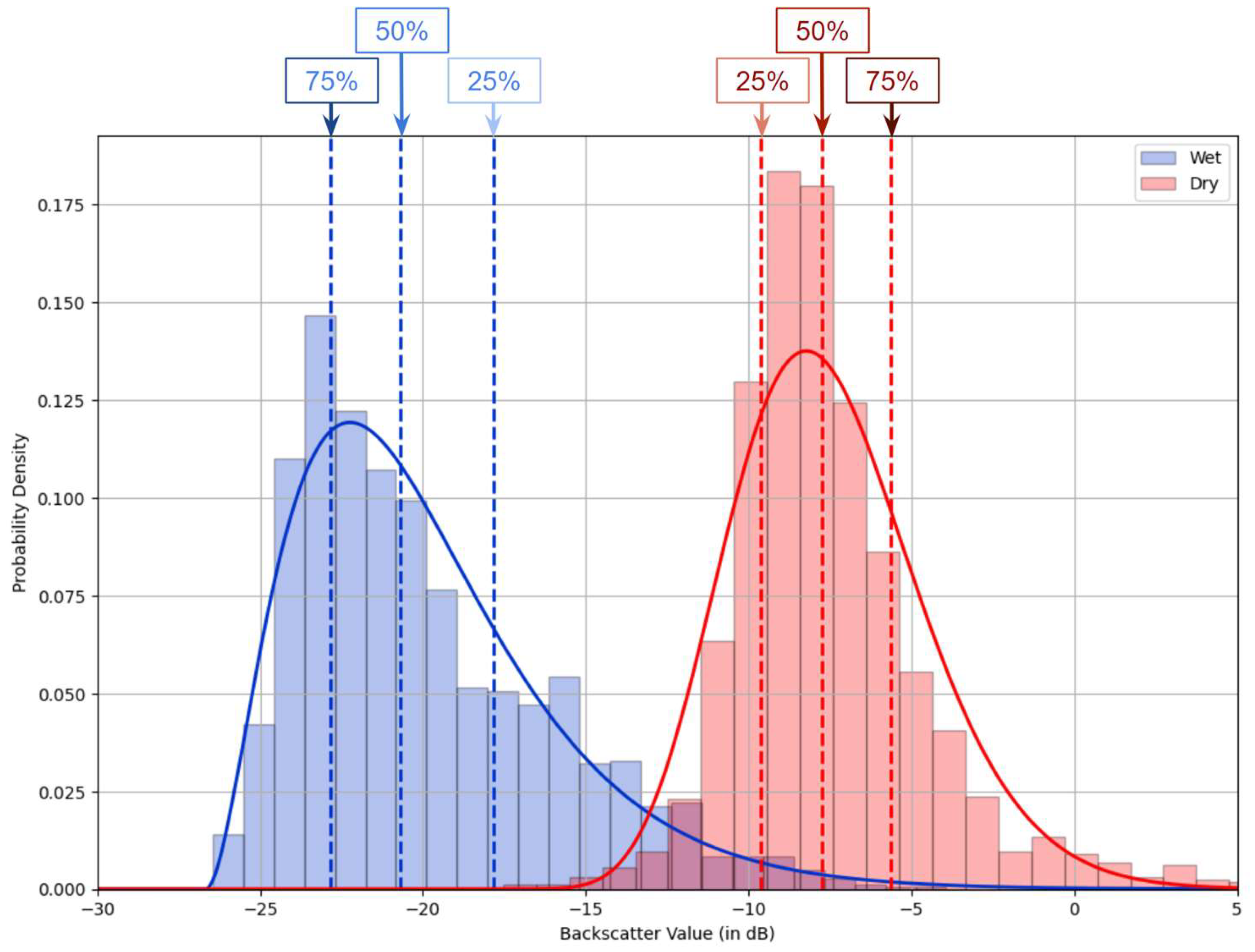
2.2.2. Fit Gamma Distributions
2.2.3. Calculate Local Thresholds
2.2.4. Apply Local Thresholds on GEE
2.2.5. Accuracy Metrics
3. Results
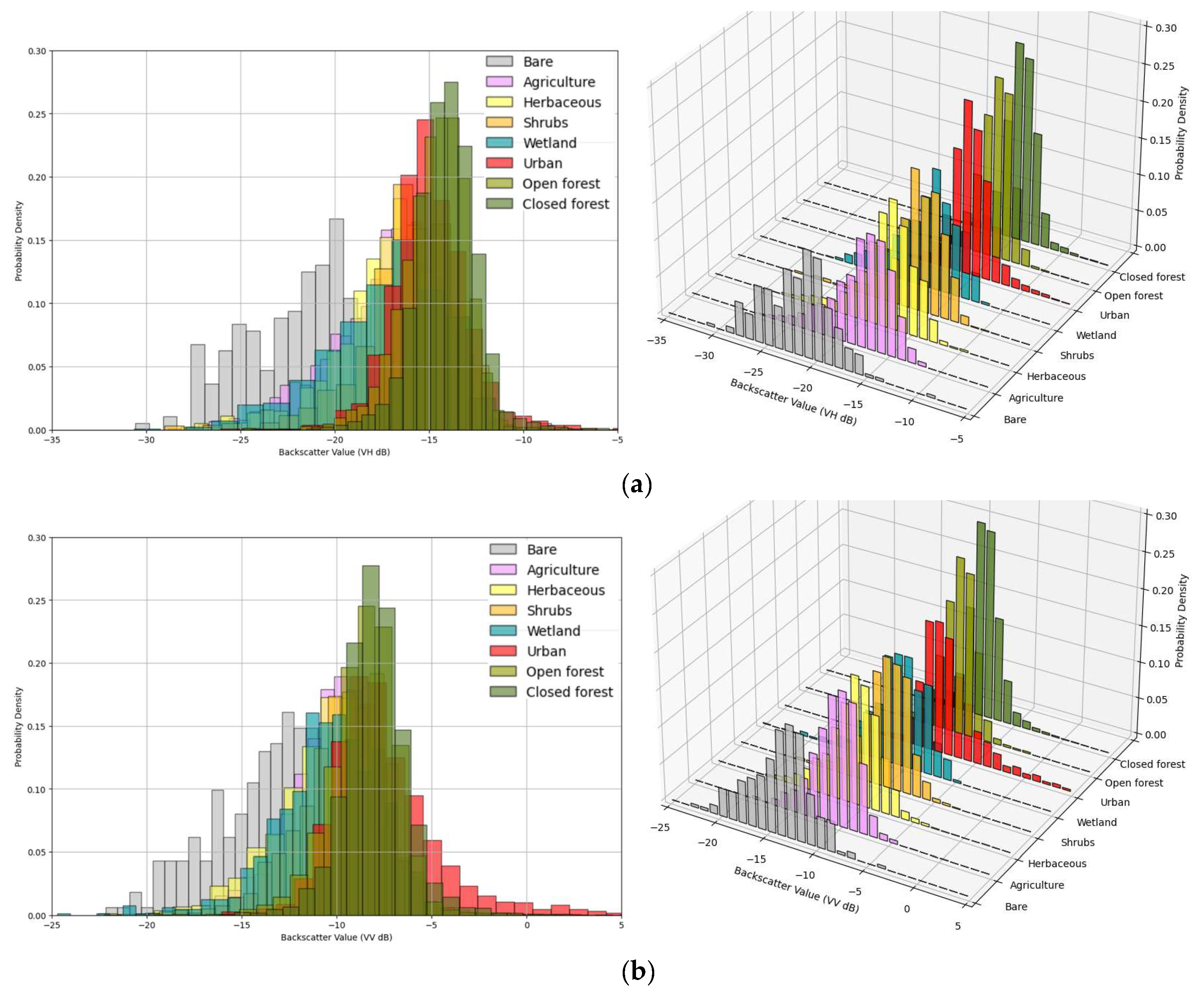
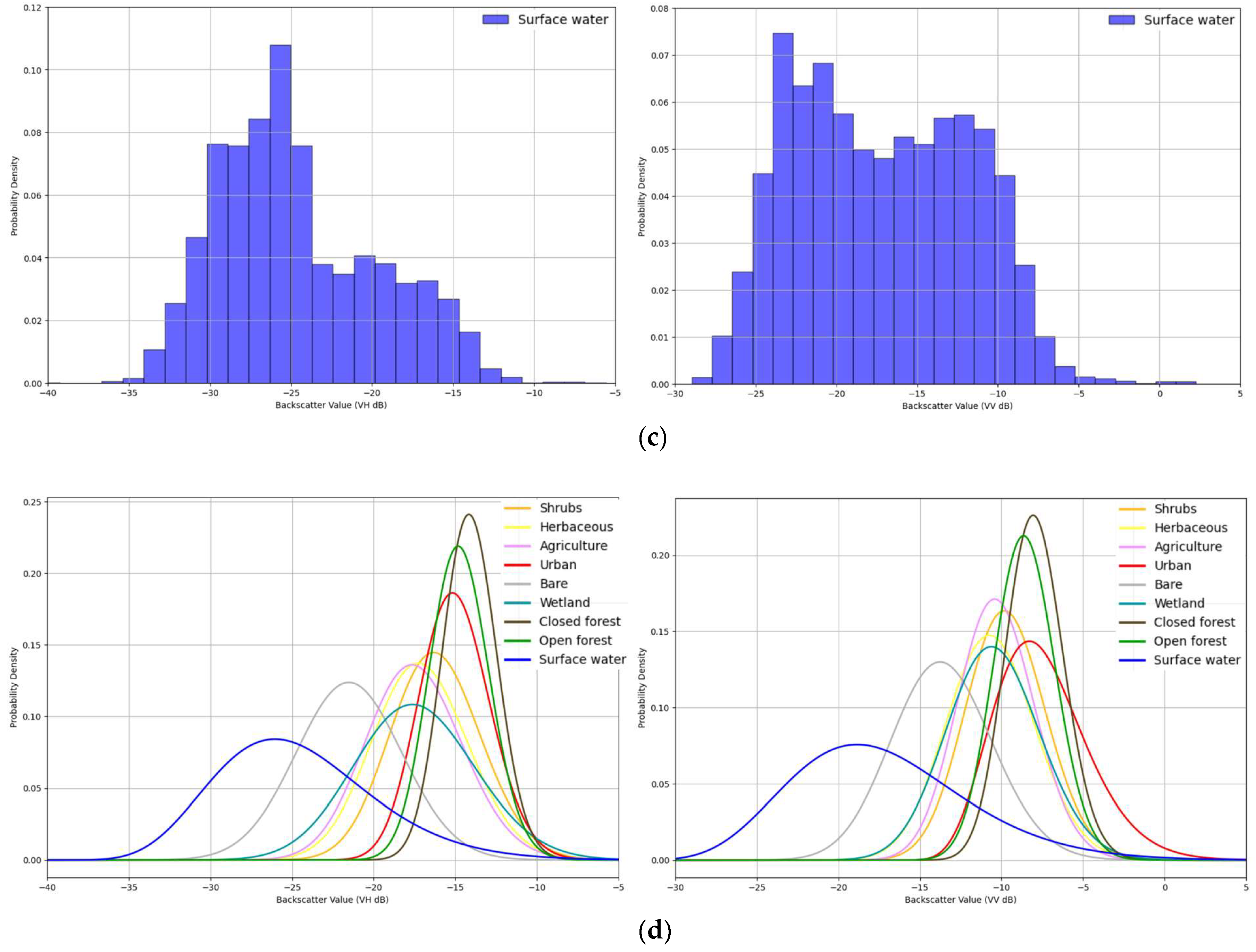
3.1. SAR Backscatter Distribution
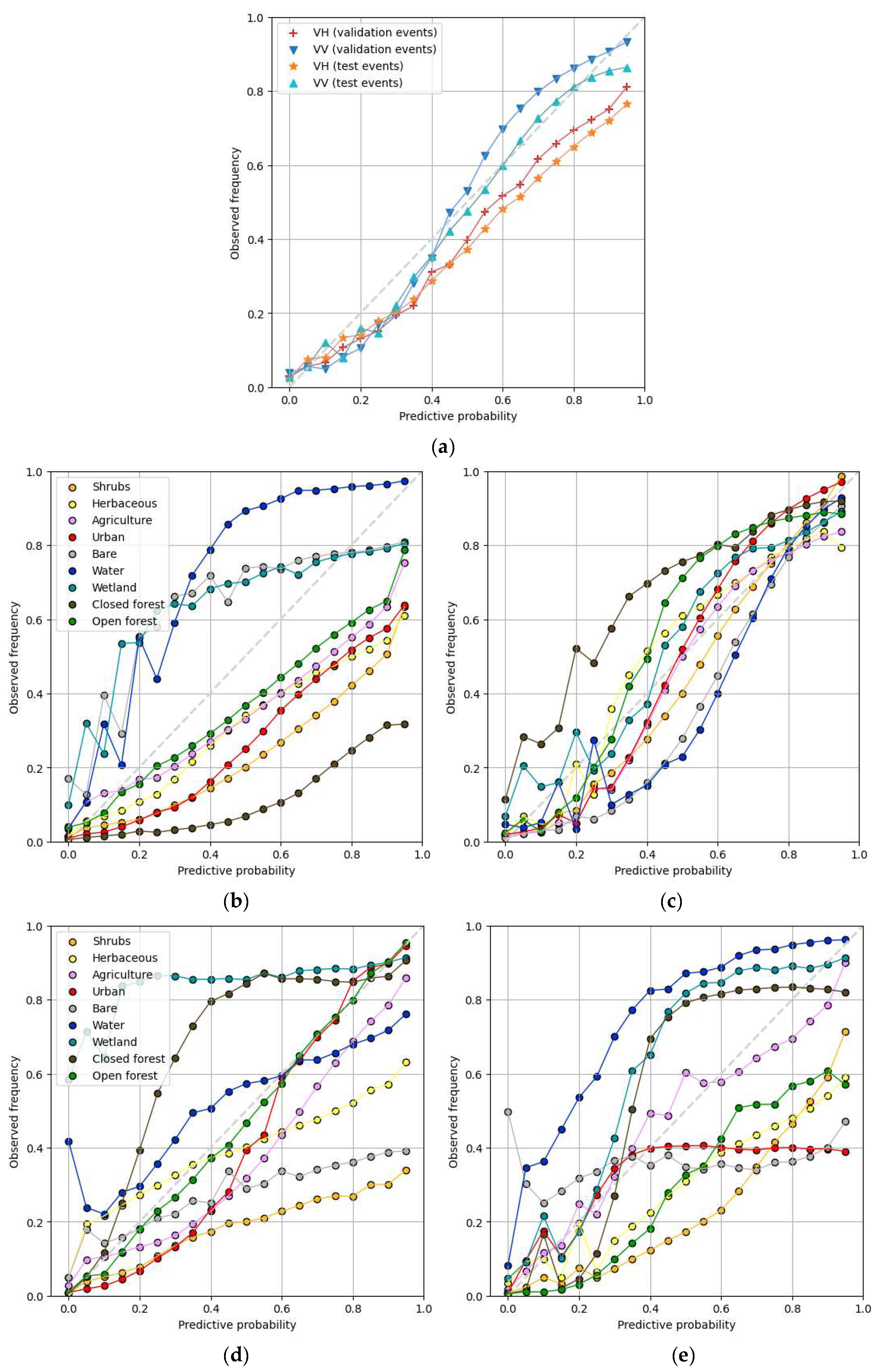
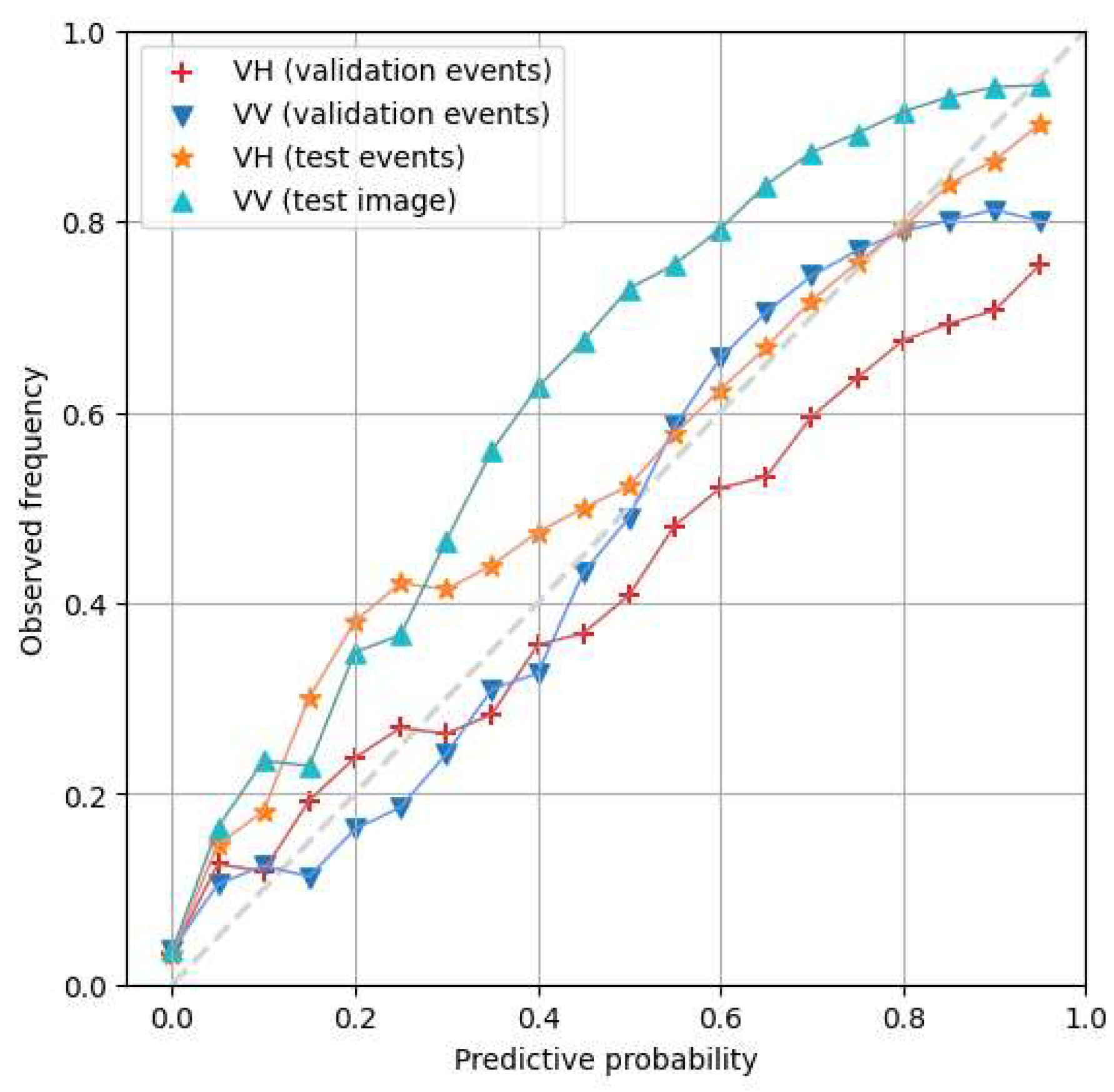
3.2. Accuracy Assessment
3.3. Flood Event Image
4. Discussion
4.1. Flood Detection
4.2. Limitation and Future Direction
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rentschler, J.; Salhab, M.; Jafino, B.A. Flood exposure and poverty in 188 countries. Nat. Commun. 2022, 13, 3527. [Google Scholar] [CrossRef] [PubMed]
- Tellman, B.; Sullivan, J.A.; Kuhn, C.; Kettner, A.J.; Doyle, C.S.; Brakenridge, G.R.; Erickson, T.A.; Slayback, D.A. Satellite imaging reveals increased proportion of population exposed to floods. Nature 2021, 596, 80–86. [Google Scholar] [CrossRef]
- Tiggeloven, T.; de Moel, H.; Winsemius, H.C.; Eilander, D.; Erkens, G.; Gebremedhin, E.; Loaiza, A.D.; Kuzma, S.; Luo, T.Y.; Iceland, C.; et al. Global-scale benefit-cost analysis of coastal flood adaptation to different flood risk drivers using structural measures. Nat. Hazards Earth Syst. Sci. 2020, 20, 1025–1044. [Google Scholar] [CrossRef]
- Tebaldi, C.; Ranasinghe, R.; Vousdoukas, M.; Rasmussen, D.J.; Vega-Westhoff, B.; Kirezci, E.; Kopp, R.E.; Sriver, R.; Mentaschi, L. Extreme sea levels at different global warming levels. Nat. Clim. Change 2021, 11, 746–751. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Wing, O.E.J.; Colven, E.; Gleason, C.J.; Bates, P.D.; Brown, C.M. Urbanizing the floodplain: Global changes of imperviousness in flood-prone areas. Environ. Res. Lett. 2022, 17, 104024. [Google Scholar] [CrossRef]
- Paprotny, D.; Mengel, M. Population, land use and economic exposure estimates for Europe at 100 m resolution from 1870 to 2020. Sci. Data 2023, 10, 372. [Google Scholar] [CrossRef]
- Rajib, A.; Zheng, Q.J.; Lane, C.R.; Golden, H.E.; Christensen, J.R.; Isibor, I.I.; Johnson, K. Human alterations of the global floodplains 1992–2019. Sci. Data 2023, 10, 499. [Google Scholar] [CrossRef] [PubMed]
- Kulp, S.A.; Strauss, B.H. New elevation data triple estimates of global vulnerability to sea-level rise and coastal flooding. Nat. Commun. 2019, 10, 4844. [Google Scholar] [CrossRef]
- Strauss, B.H.; Kulp, S.A.; Rasmussen, D.J.; Levermann, A. Unprecedented threats to cities from multi-century sea level rise. Environ. Res. Lett. 2021, 16, 114015. [Google Scholar] [CrossRef]
- Hirabayashi, Y.; Tanoue, M.; Sasaki, O.; Zhou, X.D.; Yamazaki, D. Global exposure to flooding from the new CMIP6 climate model projections. Sci. Rep. 2021, 11, 3740. [Google Scholar] [CrossRef]
- Trigg, M.A.; Birch, C.E.; Neal, J.C.; Bates, P.D.; Smith, A.; Sampson, C.C.; Yamazaki, D.; Hirabayashi, Y.; Pappenberger, F.; Dutra, E.; et al. The credibility challenge for global fluvial flood risk analysis. Environ. Res. Lett. 2016, 11, 094014. [Google Scholar] [CrossRef]
- CRED. 2021 Disasters in Numbers; Centre for Research on the Epidemiology of Disasters (CRED): Brussels, Belgium, 2022. [Google Scholar]
- Hemmati, M.; Mahmoud, H.N.; Ellingwood, B.R.; Crooks, A.T. Shaping urbanization to achieve communities resilient to floods. Environ. Res. Lett. 2021, 16, 094033. [Google Scholar] [CrossRef]
- Jones, R.L.; Guha-Sapir, D.; Tubeuf, S. Human and economic impacts of natural disasters: Can we trust the global data? Sci. Data 2022, 9, 572. [Google Scholar] [CrossRef]
- Malenovsky, Z.; Rott, H.; Cihlar, J.; Schaepman, M.E.; García-Santos, G.; Fernandes, R.; Berger, M. Sentinels for science: Potential of Sentinel-1, -2, and -3 missions for scientific observations of ocean, cryosphere, and land. Remote Sens. Environ. 2012, 120, 91–101. [Google Scholar] [CrossRef]
- Voigt, S.; Giulio-Tonolo, F.; Lyons, J.; Kucera, J.; Jones, B.; Schneiderhan, T.; Platzeck, G.; Kaku, K.; Hazarika, M.K.; Czaran, L.; et al. Global trends in satellite-based emergency mapping. Science 2016, 353, 247–252. [Google Scholar] [CrossRef] [PubMed]
- Manavalan, R. SAR image analysis techniques for flood area mapping—Literature survey. Earth Sci. Inform. 2017, 10, 1–14. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- D'Addabbo, A.; Refice, A.; Pasquariello, G.; Lovergine, F.P.; Capolongo, D.; Manfreda, S. A Bayesian Network for Flood Detection Combining SAR Imagery and Ancillary Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3612–3625. [Google Scholar] [CrossRef]
- Nico, G.; Pappalepore, M.; Pasquariello, G.; Refice, A.; Samarelli, S. Comparison of SAR amplitude vs. coherence flood detection methods—A GIS application. Int. J. Remote Sens. 2000, 21, 1619–1631. [Google Scholar] [CrossRef]
- Plank, S.; Jüssi, M.; Martinis, S.; Twele, A. Mapping of flooded vegetation by means of polarimetric Sentinel-1 and ALOS-2/PALSAR-2 imagery. Int. J. Remote Sens. 2017, 38, 3831–3850. [Google Scholar] [CrossRef]
- Refice, A.; Capolongo, D.; Lepera, A.; Pasquariello, G.; Pietranera, L.; Volpec, F. SAR and InSAR for Flood Monitoring: Examples With COSMO-SkyMed Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2711–2722. [Google Scholar] [CrossRef]
- Zhang, X.; Jones, C.E.; Oliver-Cabrera, T.; Simard, M.; Fagherazzi, S. Using rapid repeat SAR interferometry to improve hydrodynamic models of flood propagation in coastal wetlands. Adv. Water Resour. 2022, 159, 104088. [Google Scholar] [CrossRef]
- Bauer-Marschallinger, B.; Cao, S.M.; Navacchi, C.; Freeman, V.; Reuss, F.; Geudtner, D.; Rommen, B.; Vega, F.C.; Snoeij, P.; Attema, E.; et al. The normalised Sentinel-1 Global Backscatter Model, mapping Earth’s land surface with C-band microwaves. Sci. Data 2021, 8, 277. [Google Scholar] [CrossRef]
- Chini, M.; Hostache, R.; Giustarini, L.; Matgen, P. A Hierarchical Split-Based Approach for Parametric Thresholding of SAR Images: Flood Inundation as a Test Case. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6975–6988. [Google Scholar] [CrossRef]
- Cian, F.; Marconcini, M.; Ceccato, P. Normalized Difference Flood Index for rapid flood mapping: Taking advantage of EO big data. Remote Sens. Environ. 2018, 209, 712–730. [Google Scholar] [CrossRef]
- Ety, N.J.; Chu, Z.; Masum, S.M. Monitoring of flood water propagation based on microwave and optical imagery. Quatern. Int. 2021, 574, 137–145. [Google Scholar] [CrossRef]
- Kuenzer, C.; Guo, H.D.; Huth, J.; Leinenkugel, P.; Li, X.W.; Dech, S. Flood Mapping and Flood Dynamics of the Mekong Delta: ENVISAT-ASAR-WSM Based Time Series Analyses. Remote Sens. 2013, 5, 687–715. [Google Scholar] [CrossRef]
- Long, S.; Fatoyinbo, T.E.; Policelli, F. Flood extent mapping for Namibia using change detection and thresholding with SAR. Environ. Res. Lett. 2014, 9, 035002. [Google Scholar] [CrossRef]
- Manjusree, P.; Kumar, L.P.; Bhatt, C.M.; Rao, G.S.; Bhanumurthy, V. Optimization of Threshold Ranges for Rapid Flood Inundation Mapping by Evaluating Backscatter Profiles of High Incidence Angle SAR Images. Int. J. Disaster Risk Sci. 2012, 3, 113–122. [Google Scholar] [CrossRef]
- Markert, K.N.; Chishtie, F.; Anderson, E.R.; Saah, D.; Griffin, R.E. On the merging of optical and SAR satellite imagery for surface water mapping applications. Results Phys. 2018, 9, 275–277. [Google Scholar] [CrossRef]
- Moser, G.; Serpico, S.B. Generalized minimum-error thresholding for unsupervised change detection from SAR amplitude imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2972–2982. [Google Scholar] [CrossRef]
- Schlaffer, S.; Matgen, P.; Hollaus, M.; Wagner, W. Flood detection from multi-temporal SAR data using harmonic analysis and change detection. Int. J. Appl. Earth Obs. 2015, 38, 15–24. [Google Scholar] [CrossRef]
- Tong, X.H.; Luo, X.; Liu, S.G.; Xie, H.; Chao, W.; Liu, S.; Liu, S.J.; Makhinov, A.N.; Makhinova, A.F.; Jiang, Y.Y. An approach for flood monitoring by the combined use of Landsat 8 optical imagery and COSMO-SkyMed radar imagery. ISPRS J. Photogramm. Remote. Sens. Remote. Sens. 2018, 136, 144–153. [Google Scholar] [CrossRef]
- Twele, A.; Cao, W.X.; Plank, S.; Martinis, S. Sentinel-1-based flood mapping: A fully automated processing chain. Int. J. Remote Sens. 2016, 37, 2990–3004. [Google Scholar] [CrossRef]
- White, L.; Brisco, B.; Dabboor, M.; Schmitt, A.; Pratt, A. A Collection of SAR Methodologies for Monitoring Wetlands. Remote Sens. 2015, 7, 7615–7645. [Google Scholar] [CrossRef]
- Huang, W.L.; DeVries, B.; Huang, C.Q.; Lang, M.W.; Jones, J.W.; Creed, I.F.; Carroll, M.L. Automated Extraction of Surface Water Extent from Sentinel-1 Data. Remote Sens. 2018, 10, 797. [Google Scholar] [CrossRef]
- Martinis, S.; Kersten, J.; Twele, A. A fully automated TerraSAR-X based flood service. ISPRS J. Photogramm. Remote. Sens. Remote. Sens. 2015, 104, 203–212. [Google Scholar] [CrossRef]
- Pulvirenti, L.; Pierdicca, N.; Chini, M.; Guerriero, L. An algorithm for operational flood mapping from Synthetic Aperture Radar (SAR) data using fuzzy logic. Nat. Hazards Earth Syst. Sci. 2011, 11, 529–540. [Google Scholar] [CrossRef]
- Singha, M.; Dong, J.W.; Sarmah, S.; You, N.S.; Zhou, Y.; Zhang, G.L.; Doughty, R.; Xiao, X.M. Identifying floods and flood-affected paddy rice fields in Bangladesh based on Sentinel-1 imagery and Google Earth Engine. ISPRS J. Photogramm. Remote. Sens. 2020, 166, 278–293. [Google Scholar] [CrossRef]
- Amitrano, D.; Di Martino, G.; Iodice, A.; Riccio, D.; Ruello, G. Unsupervised Rapid Flood Mapping Using Sentinel-1 GRD SAR Images. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 3290–3299. [Google Scholar] [CrossRef]
- Clement, M.A.; Kilsby, C.G.; Moore, P. Multi-temporal synthetic aperture radar flood mapping using change detection. J. Flood Risk Manag. 2018, 11, 152–168. [Google Scholar] [CrossRef]
- Hostache, R.; Matgen, P.; Wagner, W. Change detection approaches for flood extent mapping: How to select the most adequate reference image from online archives? Int. J. Appl. Earth Obs. 2012, 19, 205–213. [Google Scholar] [CrossRef]
- Lu, J.; Li, J.; Chen, G.; Zhao, L.J.; Xiong, B.L.; Kuang, G.Y. Improving Pixel-Based Change Detection Accuracy Using an Object-Based Approach in Multitemporal SAR Flood Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2015, 8, 3486–3496. [Google Scholar] [CrossRef]
- Mason, D.C.; Giustarini, L.; Garcia-Pintado, J.; Cloke, H.L. Detection of flooded urban areas in high resolution Synthetic Aperture Radar images using double scattering. Int. J. Appl. Earth Obs. 2014, 28, 150–159. [Google Scholar] [CrossRef]
- Debusscher, B.; Van Coillie, F. Object-Based Flood Analysis Using a Graph-Based Representation. Remote Sens. 2019, 11, 1883. [Google Scholar] [CrossRef]
- Mason, D.C.; Speck, R.; Devereux, B.; Schumann, G.J.P.; Neal, J.C.; Bates, P.D. Flood Detection in Urban Areas Using TerraSAR-X. IEEE Trans. Geosci. Remote. Sens. 2010, 48, 882–894. [Google Scholar] [CrossRef]
- Bonafilia, D.; Tellman, B.; Anderson, T.; Issenberg, E. Sen1Floods11: A georeferenced dataset to train and test deep learning flood algorithms for Sentinel-1. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020; pp. 835–845. [Google Scholar] [CrossRef]
- Liu, B.; Li, X.F.; Zheng, G. Coastal Inundation Mapping From Bitemporal and Dual-Polarization SAR Imagery Based on Deep Convolutional Neural Networks. J. Geophys. Res. Oceans 2019, 124, 9101–9113. [Google Scholar] [CrossRef]
- Muñoz, D.F.; Muñoz, P.; Moftakhari, H.; Moradkhani, H. From local to regional compound flood mapping with deep learning and data fusion techniques. Sci. Total Environ. 2021, 782, 146927. [Google Scholar] [CrossRef]
- Otsu, N. Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Liang, J.Y.; Liu, D.S. A local thresholding approach to flood water delineation using Sentinel-1 SAR imagery. ISPRS J. Photogramm. Remote. Sens. 2020, 159, 53–62. [Google Scholar] [CrossRef]
- Jafarzadegan, K.; Abbaszadeh, P.; Moradkhani, H. Sequential data assimilation for real-time probabilistic flood inundation mapping. Hydrol. Earth Syst. Sci. 2021, 25, 4995–5011. [Google Scholar] [CrossRef]
- Westerhoff, R.S.; Kleuskens, M.P.H.; Winsemius, H.C.; Huizinga, H.J.; Brakenridge, G.R.; Bishop, C. Automated global water mapping based on wide-swath orbital synthetic-aperture radar. Hydrol. Earth Syst. Sci. 2013, 17, 651–663. [Google Scholar] [CrossRef]
- Schlaffer, S.; Chini, M.; Giustarini, L.; Matgen, P. Probabilistic mapping of flood-induced backscatter changes in SAR time series. Int. J. Appl. Earth Obs. 2017, 56, 77–87. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- DeVries, B.; Huang, C.Q.; Armston, J.; Huang, W.L.; Jones, J.W.; Lang, M.W. Rapid and robust monitoring of flood events using Sentinel-1 and Landsat data on the Google Earth Engine. Remote Sens. Environ. 2020, 240, 111664. [Google Scholar] [CrossRef]
- Hamidi, E.; Peter, B.G.; Muñoz, D.F.; Moftakhari, H.; Moradkhani, H. Fast Flood Extent Monitoring with SAR Change Detection Using Google Earth Engine. IEEE Trans. Geosci. Remote. Sens. 2023, 61, 4201419. [Google Scholar] [CrossRef]
- Buchhorn, M.; Bertels, L.; Smets, B.; De Roo, B.; Lesiv, M.; Tsendbazar, N.E.; Masiliunas, D.; Linlin, L. Copernicus Global Land Service: Land Cover 100 m: Version 3 Globe 2015–2019: Algorithm Theoretical Basis Document; Zenodo: Geneve, Switzerland, 2020. [Google Scholar] [CrossRef]
- Tsendbazar, N.E.; Tarko, A.; Linlin, L.; Herold, M.; Lesiv, M.; Fritz, S.; Maus, V. Copernicus Global Land Service: Land Cover 100 m: Version 3 Globe 2015–2019: Validation Report; Zenodo: Geneve, Switzerland, 2020. [Google Scholar] [CrossRef]
- Brier, G.W. Verification of forecasts expressed in terms of probability. Mon. Weather. Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Good, I.J. Rational decisions. J. R. Stat. Soc. Ser. B (Methodol.) 1952, 14, 107–114. [Google Scholar] [CrossRef]
- Morris, H.; DeGroot, S.E.F. The comparison and evaluation of forecasters. J. R. Stat. Soc. Ser. D (Stat.) 1983, 32, 12–22. [Google Scholar]
- Nicolas Posocco, A.B. Estimating Expected Calibration Errors. In Proceedings of the Artificial Neural Networks and Machine Learning—ICANN 2021, Bratislava, Slovakia, 14–17 September 2021; Farkaš, I., Masulli, P., Otte, S., Wermter, S., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Dimitriadis, T.; Gneiting, T.; Jordan, A.I. Stable reliability diagrams for probabilistic classifiers. Proc. Natl. Acad. Sci. USA 2021, 118, e2016191118. [Google Scholar] [CrossRef]
- Huang, C.; Nguyen, B.D.; Zhang, S.Q.; Cao, S.M.; Wagner, W. A Comparison of Terrain Indices toward Their Ability in Assisting Surface Water Mapping from Sentinel-1 Data. ISPRS Int. J. Geo-Inf. 2017, 6, 140. [Google Scholar] [CrossRef]
- Jafarzadegan, K.; Muñoz, D.F.; Moftakhari, H.; Gutenson, J.L.; Savant, G.; Moradkhani, H. Real-time coastal flood hazard assessment using DEM-based hydrogeomorphic classifiers. Nat. Hazards Earth Syst. Sci. 2022, 22, 1419–1435. [Google Scholar] [CrossRef]
- Johnson, J.M.; Munasinghe, D.; Eyelade, D.; Cohen, S. An integrated evaluation of the National Water Model (NWM)-Height Above Nearest Drainage (HAND) flood mapping methodology. Nat. Hazards Earth Syst. Sci. 2019, 19, 2405–2420. [Google Scholar] [CrossRef]
- Small, D. Flattening Gamma: Radiometric Terrain Correction for SAR Imagery. IEEE Trans. Geosci. Remote. Sens. 2011, 49, 3081–3093. [Google Scholar] [CrossRef]
- Ali, I.; Cao, S.; Naeimi, V.; Paulik, C.; Wagner, W. Methods to Remove the Border Noise From Sentinel-1 Synthetic Aperture Radar Data: Implications and Importance For Time-Series Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 777–786. [Google Scholar] [CrossRef]
- Malgwi, M.B.; Fuchs, S.; Keiler, M. A generic physical vulnerability model for floods: Review and concept for data-scarce regions. Nat. Hazards Earth Syst. Sci. 2020, 20, 2067–2090. [Google Scholar] [CrossRef]
- Tanoue, M.; Taguchi, R.; Nakata, S.; Watanabe, S.; Fujimori, S.; Hirabayashi, Y. Estimation of Direct and Indirect Economic Losses Caused by a Flood with Long-Lasting Inundation: Application to the 2011 Thailand Flood. Water Resour. Res. 2020, 56, e2019WR026092. [Google Scholar] [CrossRef]
- Peter, B.G.; Cohen, S.; Lucey, R.; Munasinghe, D.; Raney, A.; Brakenridge, G.R. Google Earth Engine Implementation of the Floodwater Depth Estimation Tool (FwDET-GEE) for Rapid and Large Scale Flood Analysis. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 1501005. [Google Scholar] [CrossRef]
- Giustarini, L.; Matgen, P.; Hostache, R.; Montanari, M.; Plaza, D.; Pauwels, V.R.N.; De Lannoy, G.J.M.; De Keyser, R.; Pfister, L.; Hoffmann, L.; et al. Assimilating SAR-derived water level data into a hydraulic model: A case study. Hydrol. Earth Syst. Sci. 2011, 15, 2349–2365. [Google Scholar] [CrossRef]
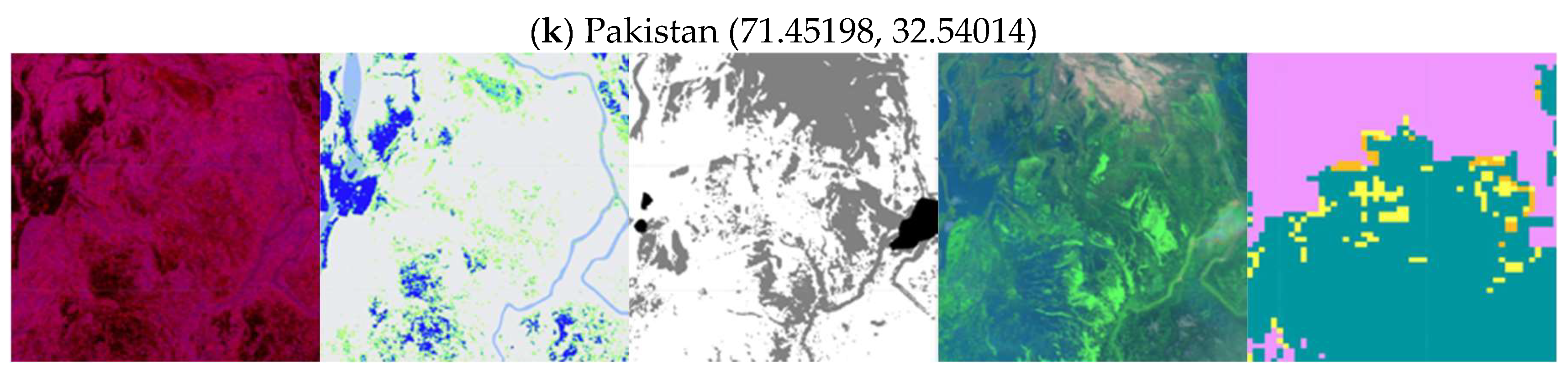
 blue—high probability), the hand-labeled classification from Sen1floods11 (third column, white—surface water, gray—land, black—cloud or shadows), Sentinel-2 image (fourth column), and the land use and land cover map (fifth column, color as per CGLS-LC100).
blue—high probability), the hand-labeled classification from Sen1floods11 (third column, white—surface water, gray—land, black—cloud or shadows), Sentinel-2 image (fourth column), and the land use and land cover map (fifth column, color as per CGLS-LC100).
 blue—high probability), the hand-labeled classification from Sen1floods11 (third column, white—surface water, gray—land, black—cloud or shadows), Sentinel-2 image (fourth column), and the land use and land cover map (fifth column, color as per CGLS-LC100).
blue—high probability), the hand-labeled classification from Sen1floods11 (third column, white—surface water, gray—land, black—cloud or shadows), Sentinel-2 image (fourth column), and the land use and land cover map (fifth column, color as per CGLS-LC100).

| Polarization | Brier Score | Log Loss | ECE | |
|---|---|---|---|---|
| Validation | VH | 0.0533 | 0.1029 | 0.0402 |
| VV | 0.0585 | 0.1054 | 0.0428 | |
| Test | VH | 0.0702 | 0.2030 | 0.0379 |
| VV | 0.0574 | 0.1303 | 0.0301 |
| Validation | Test | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VH | VV | VH | VV | |||||||||
| Land Cover | Brier Score | Log Loss | ECE | Brier Score | Log Loss | ECE | Brier Score | Log Loss | ECE | Brier Score | Log Loss | ECE |
| Shrubs | 0.0664 | 0.1895 | 0.0502 | 0.0646 | 0.1998 | 0.0342 | 0.0706 | 0.3087 | 0.0174 | 0.0581 | 0.2281 | 0.0267 |
| Herbaceous | 0.0828 | 0.1766 | 0.0411 | 0.0757 | 0.1846 | 0.0291 | 0.1503 | 0.5212 | 0.0641 | 0.1484 | 0.3516 | 0.0567 |
| Agriculture | 0.0705 | 0.1811 | 0.0519 | 0.0599 | 0.1616 | 0.0346 | 0.0484 | 0.1432 | 0.0453 | 0.0389 | 0.0905 | 0.0197 |
| Urban | 0.0229 | 0.0479 | 0.0440 | 0.0234 | 0.0528 | 0.0369 | 0.0187 | 0.0716 | 0.0273 | 0.0179 | 0.0677 | 0.1248 |
| Bare | 0.2132 | 1.3844 | 0.1688 | 0.2022 | 1.5499 | 0.0410 | 0.1828 | 0.8448 | 0.1940 | 0.1238 | 0.6172 | 0.3482 |
| Wetland | 0.1996 | 0.5402 | 0.1236 | 0.2074 | 0.5769 | 0.0654 | 0.3102 | 0.5320 | 0.4642 | 0.2936 | 0.4736 | 0.0614 |
| Closed forest | 0.0200 | 0.0352 | 0.0455 | 0.0217 | 0.0504 | 0.1199 | 0.0445 | 0.0277 | 0.0143 | 0.0425 | 0.0393 | 0.0515 |
| Open forest | 0.0301 | 0.0680 | 0.0448 | 0.0324 | 0.0901 | 0.0370 | 0.0269 | 0.0291 | 0.0129 | 0.0291 | 0.0464 | 0.0281 |
| Low Probability | Median Probability | High Probability | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Label | Prediction | Ratio | Label | Prediction | Ratio | Label | Prediction | Ratio | |
| DeVries et al. (2020) [57] | 216,316 | 530,769 | 0.4076 | 348,350 | 995,115 | 0.3501 | 699,942 | 782,448 | 0.8946 |
| Local thresholding with VH | 890,364 | 25,614,406 | 0.0348 | 466,832 | 1,283,697 | 0.3637 | 729,054 | 1,138,800 | 0.6402 |
| Local thresholding with VV | 868,864 | 25,980,653 | 0.0334 | 544,226 | 1,235,856 | 0.4404 | 1,100,726 | 1,402,275 | 0.7850 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Liu, D.; Feng, L.; Huang, K. Rapid Probabilistic Inundation Mapping Using Local Thresholds and Sentinel-1 SAR Data on Google Earth Engine. Remote Sens. 2025, 17, 1747. https://doi.org/10.3390/rs17101747
Liang J, Liu D, Feng L, Huang K. Rapid Probabilistic Inundation Mapping Using Local Thresholds and Sentinel-1 SAR Data on Google Earth Engine. Remote Sensing. 2025; 17(10):1747. https://doi.org/10.3390/rs17101747
Chicago/Turabian StyleLiang, Jiayong, Desheng Liu, Lihan Feng, and Kangning Huang. 2025. "Rapid Probabilistic Inundation Mapping Using Local Thresholds and Sentinel-1 SAR Data on Google Earth Engine" Remote Sensing 17, no. 10: 1747. https://doi.org/10.3390/rs17101747
APA StyleLiang, J., Liu, D., Feng, L., & Huang, K. (2025). Rapid Probabilistic Inundation Mapping Using Local Thresholds and Sentinel-1 SAR Data on Google Earth Engine. Remote Sensing, 17(10), 1747. https://doi.org/10.3390/rs17101747








