Probabilistic Site Adaptation for High-Accuracy Solar Radiation Datasets in the Western Sichuan Plateau
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Area
2.2. Gridded DSR Data and Surface Measurement
2.2.1. Satellite Remote Sensing Data
2.2.2. Reanalysis Data
2.2.3. Ground-Based Data
2.2.4. Data Processing
2.3. Method
2.3.1. Three Benchmarking Methods
2.3.2. Five Stand-Alone Methods
2.3.3. Four Quantile Combination Methods
2.4. Model Validation Methods
3. Results
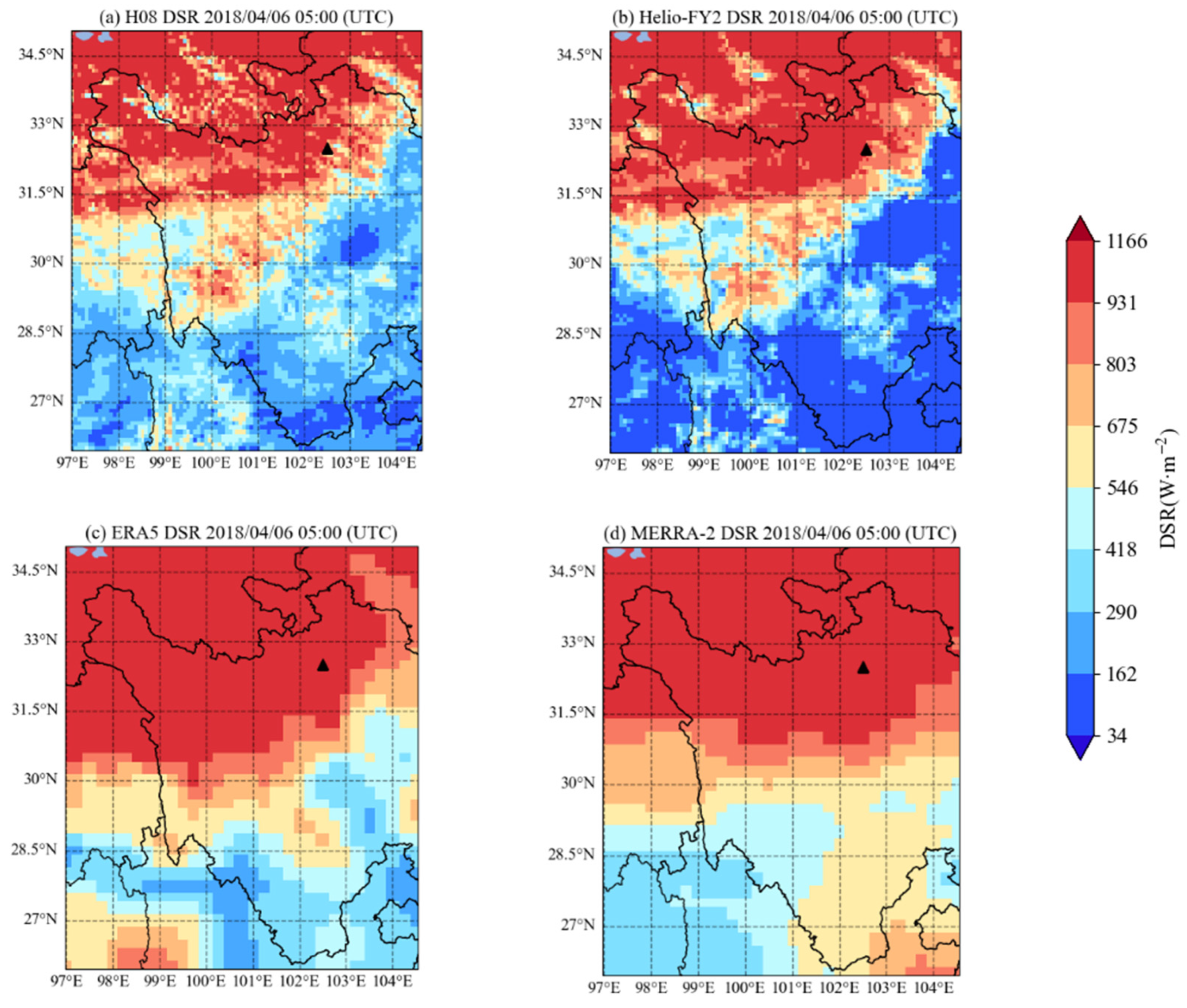
3.1. Validation of Gridded DSR Product
3.2. Model Validation
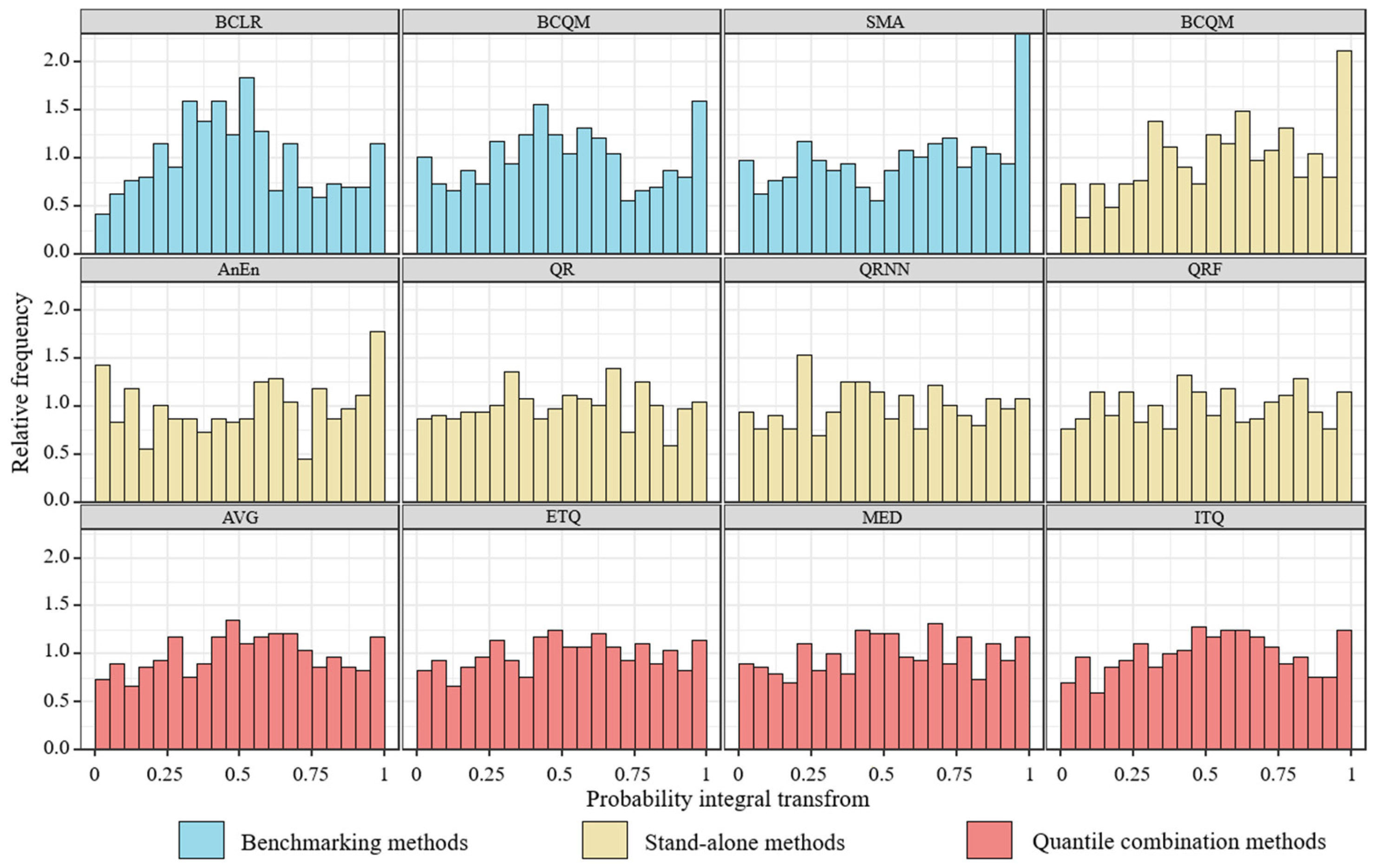
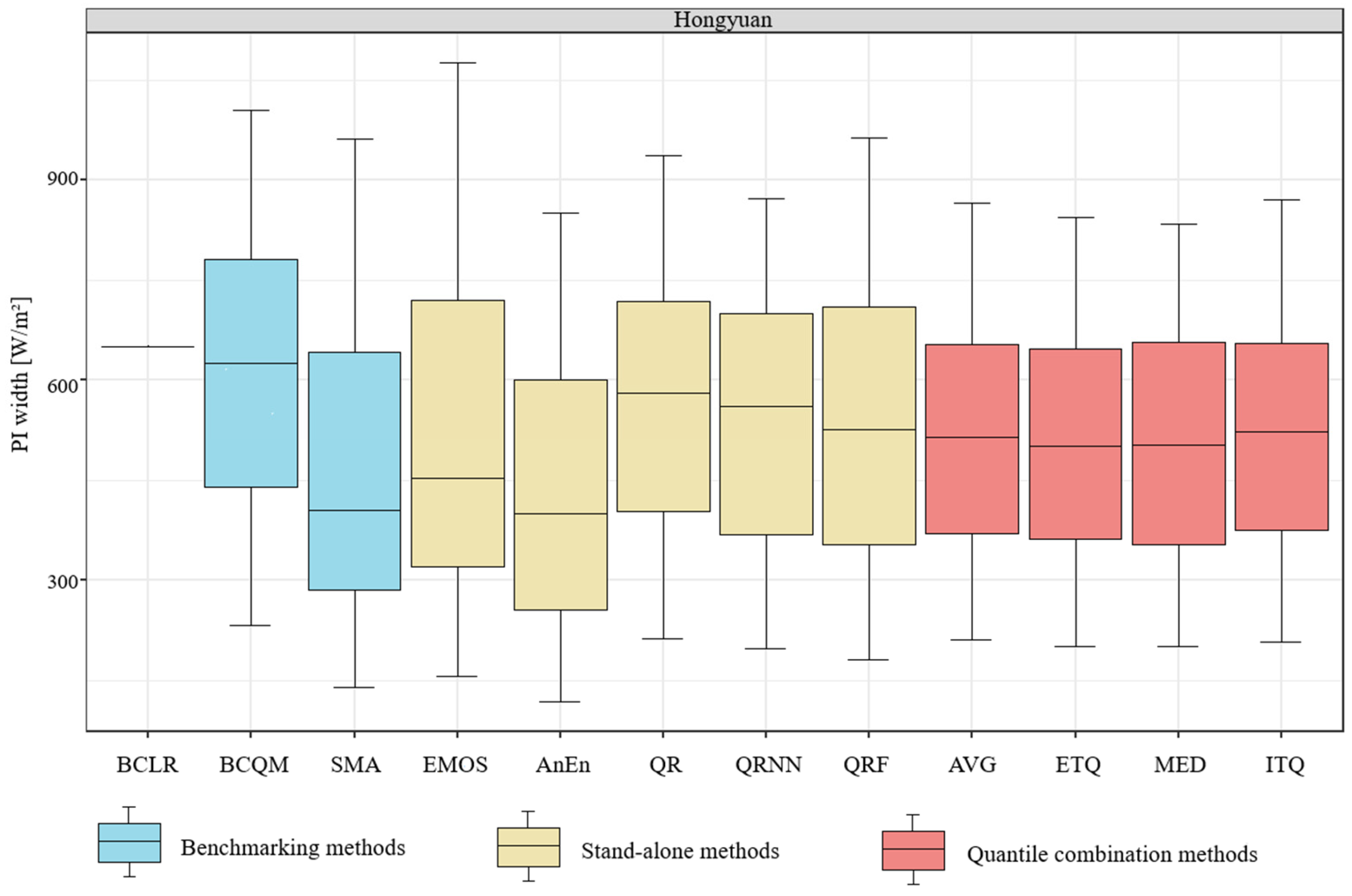
3.3. Probabilistic Forecasting Performance
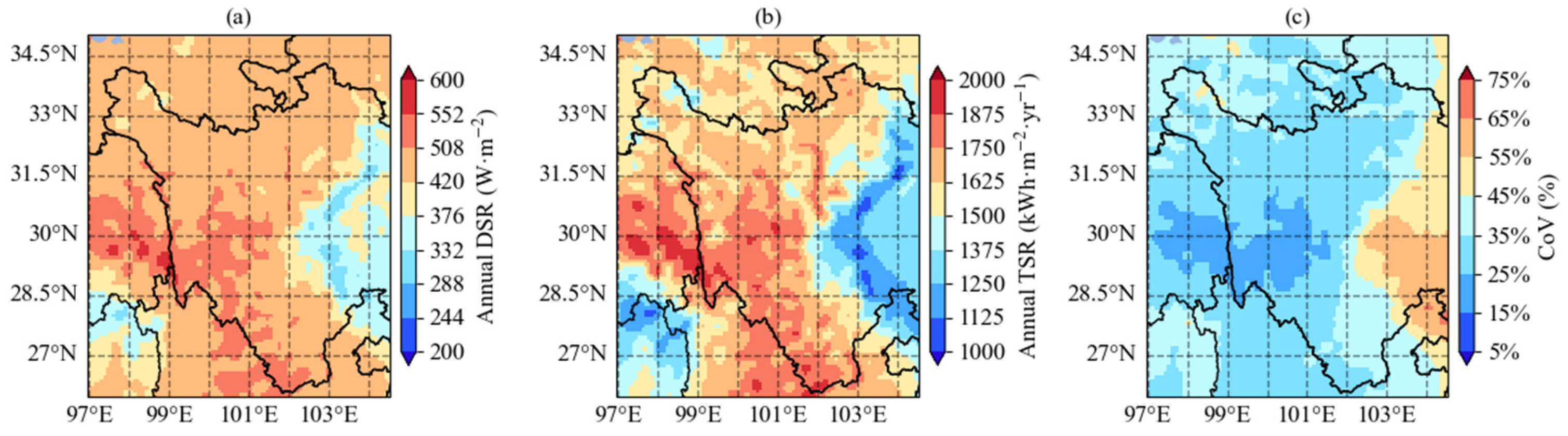
3.4. Solar Resource Analysis
4. Discussion
5. Conclusions
- (1)
- The validation results show that satellite products (H08 and Helio-FY2) underestimate the hourly DSR, while reanalysis products (ERA5 and MERRA-2) overestimate it. All four datasets exhibit high RMSE (>200 W/m2).
- (2)
- Compared to the four products, all PSA methods show lower RMSEs. The quantile combination methods perform best, with each method achieving a lower RMSE (<165 W/m2) and CRPS (<85 W/m2). The MED had the lowest RMSE (nRMSE) of 163.97 W/m2 (34.43%) and CRPS of 83.40 W/m2.
- (3)
- The optimal dataset is developed using the MED method, with the spatial resolution of 0.05° × 0.05° and temporal resolution of 1 h. The mean DSR and TSR in the WSP are 455.41 W/m2 and 1593.10 kWh/m2/yr, and there is a negative correlation between TSR and CoV. In other words, the WSP exhibits a high annual TSR and low radiation variability, indicating that the solar resources have significant potential for utilization.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AHI | Advanced Himawari Imager |
| AnEn | Analogue Ensemble |
| AOD | Aerosol optical depth |
| AVG | Quantile averaging |
| BSRN | Baseline Solar Radiation Network |
| BCLR | Best Component Linear Regression |
| BCQM | Best Component Quantile Mapping |
| CDF | Cumulative distribution function |
| CERES | The Clouds and the Earth’s Radiant Energy System |
| CERN | Chinese Ecosystem Research Network |
| CMA | China Meteorological Administration |
| CoV | Coefficient of Variation |
| CRPS | Continuous rank probability score |
| DSR | Downward shortwave radiation |
| ECMWF | The European Centre for Medium-Range Weather Forecasts |
| EMOS | Ensemble Model Output Statistics |
| ETQ | Quantile averaging, external trimmed |
| FY-4 | Fengyun-4 |
| GOES-R | The Geostationary Operational Environmental Satellite-R series |
| H08 | Himawari-8 |
| Helio-FY2 | Helio-Fengyun 2G |
| ITQ | Quantile averaging, internal trimmed |
| MED | Quantile averaging, median |
| MERRA | The Modern-Era Retrospective analysis for Research and Applications |
| NWP | Numerical weather prediction |
| nRMSE | Normalized root mean square error |
| PI | Prediction interval |
| PIT | Probability integral transform |
| PSA | Probabilistic site adaptation |
| PV | Photovoltaic |
| QR | Quantile Regression |
| QRF | Quantile Regression Forest |
| QRNN | Quantile Regression Neural Network |
| R2 | Coefficient of determination |
| RMSE | Root mean square error |
| SMA | Simple Model Averaging |
| SSRD | Surface solar radiation downwards |
| TSR | Total solar radiation |
| VISSR-II | Stretched Visible and Infrared Spin Scan Radiometer-II |
| WSP | Western Sichuan Plateau |
References
- Nielsen, A.H.; Iosifidis, A.; Karstoft, H. IrradianceNet: Spatiotemporal deep learning model for satellite-derived solar irradiance short-term forecasting. Sol. Energy 2021, 228, 659–669. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, L.; Deng, S.; Xu, W.; Zhang, Y. A critical review of the models used to estimate solar radiation. Renew. Sustain. Energy Rev. 2017, 70, 314–329. [Google Scholar] [CrossRef]
- Huang, G.; Li, Z.; Li, X.; Liang, S.; Yang, K.; Wang, D.; Zhang, Y. Estimating surface solar irradiance from satellites: Past, present, and future perspectives. Remote Sens. Environ. 2019, 233, 111371–111386. [Google Scholar] [CrossRef]
- Yang, D.; Wang, W.; Xia, X.A. A concise overview on solar resource assessment and forecasting. Adv. Atmos. Sci. 2022, 39, 1239–1251. [Google Scholar] [CrossRef]
- Huang, C.; Shi, H.; Yang, D.; Gao, L.; Zhang, P.; Fu, D.; Xia, X.; Chen, Q.; Yuan, Y.; Liu, M.; et al. Retrieval of sub-kilometer resolution solar irradiance from Fengyun-4A satellite using a region-adapted Heliosat-2 method. Sol. Energy 2023, 264, 112038. [Google Scholar] [CrossRef]
- Choi, Y.; Suh, J.; Kim, S.M. GIS-based solar radiation mapping, site evaluation, and potential assessment: A review. Appl. Sci. 2019, 9, 1960. [Google Scholar] [CrossRef]
- Xia, X.A.; Wang, P.C.; Chen, H.B.; Liang, F. Analysis of downwelling surface solar radiation in China from National Centers for Environmental Prediction reanalysis, satellite estimates, and surface observations. J. Geophys. Res. Atmos. 2006, 111, D09103. [Google Scholar] [CrossRef]
- Liang, S.; Wang, D.; He, T.; Yu, Y. Remote sensing of earth’s energy budget: Synthesis and review. Int. J. Digit. Earth 2019, 12, 737–780. [Google Scholar] [CrossRef]
- Yang, D.; Gueymard, C.A. Probabilistic post-processing of gridded atmospheric variables and its application to site adaptation of shortwave solar radiation. Sol. Energy 2021, 225, 427–443. [Google Scholar] [CrossRef]
- Letu, H.; Nakajima, T.Y.; Wang, T.; Shang, H.; Ma, R.; Yang, K.; Baran, A.J.; Riedi, J.; Ishimoto, H.; Yoshida, M.; et al. A new benchmark for surface radiation products over the East Asia-Pacific region retrieved from the Himawari-8/AHI next-generation geostationary satellite. Bull. Am. Meteorol. Soc. 2022, 103, E873–E888. [Google Scholar] [CrossRef]
- Xian, D.; Zhang, P.; Gao, L.; Sun, R.; Zhang, H.; Jia, X. Fengyun meteorological satellite products for earth system science applications. Adv. Atmos. Sci. 2021, 38, 1267–1284. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Olson, J.G. An evaluation and intercomparison of global analyses from the National Meteorological Center and the European Centre for Medium Range Weather Forecasts. Bull. Am. Meteorol. Soc. 1988, 69, 1047–1057. [Google Scholar] [CrossRef]
- Yang, D.; Bright, J.M. Worldwide validation of 8 satellite-derived and reanalysis solar radiation products: A preliminary evaluation and overall metrics for hourly data over 27 years. Sol. Energy 2020, 210, 3–19. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERAInterim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Cao, Q.; Liu, Y.; Sun, X.; Yang, L. Country-level evaluation of solar radiation data sets using ground measurements in China. Energy 2022, 241, 122938. [Google Scholar] [CrossRef]
- Bright, J.M. Solcast: Validation of a satellite-derived solar irradiance dataset. Sol. Energy 2019, 189, 435–449. [Google Scholar] [CrossRef]
- Babar, B.; Graversen, R.; Boström, T. Solar radiation estimation at high latitudes: Assessment of the CMSAF databases, ASR and ERA5. Sol. Energy 2019, 182, 397–411. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, S.; Wang, G.; Yao, Y.; Jiang, B.; Cheng, J. Evaluation of the reanalysis surface incident shortwave radiation products from NCEP, ECMWF, GSFC, and JMA using satellite and surface observations. Remote Sens. 2016, 8, 225. [Google Scholar] [CrossRef]
- Qian, P.Z.; Wu, C.J. Bayesian hierarchical modeling for integrating low-accuracy and high-accuracy experiments. Technometrics 2008, 50, 192–204. [Google Scholar] [CrossRef]
- Xiong, S.; Qian, P.Z.; Wu, C.J. Sequential design and analysis of high-accuracy and low-accuracy computer codes. Technometrics 2013, 55, 37–46. [Google Scholar] [CrossRef]
- Yang, D.; Gueymard, C.A. Producing high-quality solar resource maps by integrating high-and low-accuracy measurements using Gaussian processes. Renew. Sustain. Energy Rev. 2019, 113, 109260. [Google Scholar] [CrossRef]
- Weiss, A.; Hays, C.J. Simulation of daily solar irradiance. Agric. For. Meteorol. 2004, 123, 187–199. [Google Scholar] [CrossRef]
- Abraha, M.G.; Savage, M.J. Comparison of estimates of daily solar radiation from air temperature range for application in crop simulations. Agric. For. Meteorol. 2008, 148, 401–416. [Google Scholar] [CrossRef]
- Liu, J.; Pan, T.; Chen, D.; Zhou, X.; Yu, Q.; Flerchinger, G.N.; Shen, Y. An improved Ångström-type model for estimating solar radiation over the Tibetan Plateau. Energies 2017, 10, 892. [Google Scholar] [CrossRef]
- Suri, M.; Cebecauer, T. Requirements and standards for bankable DNI data products in CSP projects. In Proceedings of the SolarPACES Conference, Granada, Spain, 20−23 September 2011. [Google Scholar]
- Polo, J.; Wilbert, S.; Ruiz-Arias, J.; Meyer, R.; Gueymard, C.; Súri, M.; Martín, L.; Mieslinger, T.; Blanc, P.; Grant, I.; et al. Preliminary survey on site-adaptation techniques for satellite derived and reanalysis solar radiation datasets. Sol. Energy 2016, 132, 25–37. [Google Scholar] [CrossRef]
- Polo, J.; Fernandez-Peruchena, C.; Salamalikis, V.; Mazorra-Aguiar, L.; Turpin, M.; Martin-Pomares, L.; Kazantzidis, A.; Blanc, P.; Remund, J. Benchmarking on improvement and site-adaptation techniques for modeled solar radiation datasets. Sol. Energy 2020, 201, 469–479. [Google Scholar] [CrossRef]
- Yang, D.; Liu, L. Solar project financing, bankability, and resource assessment. In Sustainable Energy Solutions for Remote Areas in the Tropics; Springer: Cham, Switzerland, 2020; pp. 179–211. [Google Scholar] [CrossRef]
- Feng, Q.; Niu, B.; Ren, Y.; Su, S.; Wang, J.; Shi, H.; Yang, J.; Han, M. A 10-m national-scale map of ground-mounted photovoltaic power stations in China of 2020. Sci. Data 2024, 11, 198. [Google Scholar] [CrossRef]
- Hu, Y.; Huang, W.; Wang, J.; Chen, S.; Zhang, J. Current status, challenges, and perspectives of Sichuan’s renewable energy development in Southwest China. Renew. Sustain. Energy Rev. 2016, 57, 1373–1385. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, B.; Ren, S.; Han, W.; Ding, Y.; Peng, S. A 4 km daily gridded meteorological dataset for China from 2000 to 2020. Sci. Data 2024, 11, 1230. [Google Scholar] [CrossRef]
- Tang, L.; Liu, Y.; Pan, Y.; Ren, Y.; Yao, L.; Li, X. Optimizing solar photovoltaic plant siting in Liangshan Prefecture, China: A policy-integrated, multi-criteria spatial planning framework. Sol. Energy 2024, 283, 113012. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Yoshida, R. An introduction to Himawari-8/9—Japan’s new-generation geostationary meteorological satellites. J. Meteorol. Soc. Jpn. 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Wang, K.; Ma, Q.; Li, Z.; Wang, J. Decadal variability of surface incident solar radiation over China: Observations, satellite retrievals, and reanalyses. J. Geophys. Res. Atmos. 2015, 120, 6500–6514. [Google Scholar] [CrossRef]
- Feng, F.; Wang, K. Merging ground-based sunshine duration observations with satellite cloud and aerosol retrievals to produce high-resolution long-term surface solar radiation over China. Earth Syst. Sci. Data 2021, 13, 907–922. [Google Scholar] [CrossRef]
- Maulud, D.; Abdulazeez, A.M. A review on linear regression comprehensive in machine learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
- Maraun, D. Bias correction, quantile mapping, and downscaling: Revisiting the inflation issue. J. Clim. 2013, 26, 2137–2143. [Google Scholar] [CrossRef]
- Wasserman, L. All of nonparametric statistics. Technometrics 2007, 49, 103. [Google Scholar] [CrossRef]
- Yang, D.; Alessandrini, S. An ultra-fast way of searching weather analogs for renewable energy forecasting. Sol. Energy 2019, 185, 255–261. [Google Scholar] [CrossRef]
- Yang, D.; van der Meer, D.; Munkhammar, J. Probabilistic solar forecasting benchmarks on a standardized dataset at Folsom, California. Sol. Energy 2020, 206, 628–639. [Google Scholar] [CrossRef]
- Junk, C.; Delle Monache, L.; Alessandrini, S.; Cervone, G.; Von Bremen, L. Predictor-weighting strategies for probabilistic wind power forecasting with an analog ensemble. Meteorol. Z 2015, 24, 361–379. [Google Scholar] [CrossRef]
- Junk, C.; Delle Monache, L.; Alessandrini, S. Analog-based ensemble model output statistics. Mon. Weather Rev. 2015, 143, 2909–2917. [Google Scholar] [CrossRef]
- Meinshausen, N.; Ridgeway, G. Quantile regression forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Koenker, R. Quantile regression. In Econometric Society Monographs; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G. Regression quantiles. Econom. J. Econom. Soc. 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Cannon, A.J. Quantile regression neural networks: Implementation in R and application to precipitation downscaling. Comput. Geosci. 2011, 37, 1277–1284. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Gneiting, T.; Katzfuss, M. Probabilistic forecasting. Annu. Rev. Stat. Its Appl. 2014, 1, 125–151. [Google Scholar] [CrossRef]
- Gneiting, T.; Balabdaoui, F.; Raftery, A.E. Probabilistic forecasts, calibration and sharpness. J. R. Stat. Soc. Ser. B Stat. Methodol. 2007, 69, 243–268. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Laiti, L.; Andreis, D.; Zottele, F.; Giovannini, L.; Panziera, L.; Toller, G.; Zardi, D. A solar atlas for the Trentino region in the Alps: Quality control of surface radiation data. Energy Procedia 2014, 59, 336–343. [Google Scholar] [CrossRef]
- Du, Y.; Shi, H.; Zhang, J.; Xia, X.; Yao, Z.; Fu, D.; Bo, H.; Huang, C. Evaluation of MERRA-2 hourly surface solar radiation across China. Sol. Energy 2022, 234, 103–110. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y. Evaluation of the Accuracy and Trend Consistency of Hourly Surface Solar Radiation Datasets of ERA5, MERRA-2, SARAH-E, CERES, and Solcast over China. Remote Sens. 2025, 17, 1317. [Google Scholar] [CrossRef]
- Li, T.; Xin, X.; Zhang, H.; Yu, S.; Li, L.; Ye, Z.; Liu, Q.; Cai, H. Evaluation of Six Data Products of Surface Downward Shortwave Radiation in Tibetan Plateau Region. Remote Sens. 2024, 16, 791. [Google Scholar] [CrossRef]
- Filonchyk, M.; Yan, H.; Zhang, Z.; Yang, S.; Li, W.; Li, Y. Combined use of satellite and surface observations to study aerosol optical depth in different regions of China. Sci. Rep. 2019, 9, 6174. [Google Scholar] [CrossRef]
- Boilley, A.; Wald, L. Comparison between meteorological re-analyses from ERA-Interim and MERRA and measurements of daily solar irradiation at surface. Renew. Energy 2015, 75, 135–143. [Google Scholar] [CrossRef]
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Lecué, G.; Lerasle, M. Robust machine learning by median-of-means: Theory and practice. Ann. Statist. 2020, 48, 906–931. [Google Scholar] [CrossRef]
- Wang, X.; Fang, Z. Robust recursive estimation for the errors-in-variables nonlinear systems with impulsive noise. Sci. Rep. 2025, 15, 6031. [Google Scholar] [CrossRef]




| Satellite | Instrument | Product | Spatial Resolution | Temporal Resolution |
|---|---|---|---|---|
| FY-2G | VISSR | SSI | 5 km × 5 km | 15 min |
| H08 | AHI | SWR | 5 km × 5 km | 10 min |
| - | - | ERA5 | 0.25° × 0.25° | 1 h |
| - | - | MERRA-2 | 0.5° × 0.625° | 1 h |
| Category | Method | Description | Advantage | Disadvantage | Parametric/ Non-Parametric |
|---|---|---|---|---|---|
| Benchmarking | BCLR | Linear regression was applied to the optimal grid dataset. | Simplicity, computational efficiency and suitability for modeling data with linear relationships. | Sensitivity to outlier. | Parametric |
| BCQM | Based on the conditional error sampling method, the empirical cumulative distribution function and the conditional variable are used to adjust the prediction error. | High accuracy of prediction; high discrimination ability; high calculation efficiency. | Limitations in the selection of conditioning variables and sample representativeness. | Parametric | |
| SMA | Integrated learning method that averages the prediction results from multiple models. | Easy to implement and versatile; high stability; independent of observations. | Limitations of the model assumptions; result in an underestimation of the variance; poor adaptability. | Parametric | |
| Stand-alone | EMOS | Model the expectation and variance of the predictions. | Model expectations and variances to improve the accuracy of probabilistic predictions; provide quantification of uncertainty; adapt to multiple models and data types; use CRPS metrics to improve model credibility. | May perform poorly when lacking a priori knowledge. | Parametric |
| AnEn | A weather forecasting technique based on similarity search that predicts future weather by analyzing historical weather patterns. | AnEn is a simpler implementation than dynamic integration; no need to build complex numerical models, just use historical data directly. | Limited by historical data; the choice and calculation of similarity may affect the prediction result. | Parametric | |
| QR | A regression method for non-parametric probability prediction that allows modeling different quantiles of the conditional distribution, not just the mean. | Capture data heterogeneity; compared to least squares regression, QR is less affected by outliers; it does not depend on specific assumptions about the distribution of response variables and is applicable to various types of data. | High degree of complexity in calculation; parametric estimation is not unique; high sample size requirements. | Non-parametric | |
| QRNN | A regression method that combines the properties of quantile regression and neural networks is used to model the conditional distribution of the response variable. | Combines the advantages of quantile regression and neural networks to analyze conditional distributions and predict asymmetry. | The training process is more complex than traditional regression methods, with high computational and resource requirements and the potential for over-fitting. | Non-parametric | |
| QRF | An extension of random forests, which estimates conditional quantiles using a collection of multiple trees generated by random forests. | Provides a variety of predictive information; It can effectively process data with high-dimensional feature spaces and is suitable for complex datasets. | High computational complexity and high storage requirements; the predicted result may appear discontinuous or in steps. | Non-parametric | |
| Quantile combination | AVG | The final quantile for event t is obtained by averaging the quantiles produced by the 5 stand-alone site adaptation methods. | Simple to understand and achieve. | May be affected by extreme values, causing predicted results to deviate from the actual values. | Non-parametric |
| ETQ | The exterior quantile is trimmed from both sides. | Reduces the impact of extreme predictions on the result; predictions are generally better when there are outliers. | When the data are not evenly distributed, removing quantiles may result in the loss of useful information. | Non-parametric | |
| MED | Removing two outer quantiles from both samples results in a median quantile. | Not sensitive to extreme values, providing a more robust estimate; relatively simple to operate and easy to calculate. | The median may be insufficiently representative. | Non-parametric | |
| ITQ | Once the median quantile has been trimmed, the average quantile of the internal pruning is derived. | Reduced influence of noise and outliers. | The operation is relatively complicated; the trimming process may result in the loss of valuable information. | Non-parametric |
| Methods | BIAS (W/m2) | RMSE (W/m2) | nRMSE (%) | CRPS (W/m2) | |
|---|---|---|---|---|---|
| Benchmarking | BCLR | −7.25 | 180.79 | 37.96 | 100.25 |
| BCQM | −12.32 | 194.12 | 40.76 | 104.63 | |
| SMA | −19.64 | 169.68 | 35.62 | 91.11 | |
| Stand-alone | EMOS | −33.71 | 169.25 | 35.53 | 91.20 |
| AnEn | −9.00 | 172.78 | 36.27 | 86.69 | |
| QR | −21.93 | 166.00 | 34.85 | 85.94 | |
| QRNN | −11.85 | 166.24 | 34.91 | 84.43 | |
| QRF | −8.48 | 167.30 | 35.12 | 84.90 | |
| Quantile combination | AVG | −16.99 | 164.50 | 34.54 | 83.83 |
| ETQ | −17.22 | 164.33 | 34.50 | 83.49 | |
| MED | −17.46 | 163.97 | 34.43 | 83.44 | |
| ITQ | −16.88 | 164.82 | 34.61 | 84.06 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, L.; Liu, M.; Fu, D.; Wu, H.; Shi, H.; Huang, C. Probabilistic Site Adaptation for High-Accuracy Solar Radiation Datasets in the Western Sichuan Plateau. Remote Sens. 2025, 17, 1720. https://doi.org/10.3390/rs17101720
Ye L, Liu M, Fu D, Wu H, Shi H, Huang C. Probabilistic Site Adaptation for High-Accuracy Solar Radiation Datasets in the Western Sichuan Plateau. Remote Sensing. 2025; 17(10):1720. https://doi.org/10.3390/rs17101720
Chicago/Turabian StyleYe, Lianlian, Mengqi Liu, Disong Fu, Hao Wu, Hongrong Shi, and Chunlin Huang. 2025. "Probabilistic Site Adaptation for High-Accuracy Solar Radiation Datasets in the Western Sichuan Plateau" Remote Sensing 17, no. 10: 1720. https://doi.org/10.3390/rs17101720
APA StyleYe, L., Liu, M., Fu, D., Wu, H., Shi, H., & Huang, C. (2025). Probabilistic Site Adaptation for High-Accuracy Solar Radiation Datasets in the Western Sichuan Plateau. Remote Sensing, 17(10), 1720. https://doi.org/10.3390/rs17101720









