Detection of Small-Scale Subsurface Echoes Using Lunar Radar Sounder and Surface Scattering Simulations with a DEM Generated Using a Generative Adversarial Network
Abstract
1. Introduction
2. Materials and Methods
2.1. Generation of a High-Resolution DEM Using a GAN
2.2. Surface Scattering Simulation
2.3. SELENE LRS Data
2.4. Detection of Subsurface Echoes
2.5. Estimation of Subsurface Echo Intensity Using the Radar Equation
2.6. Geological Characteristics of the Analyzed Region

3. Results
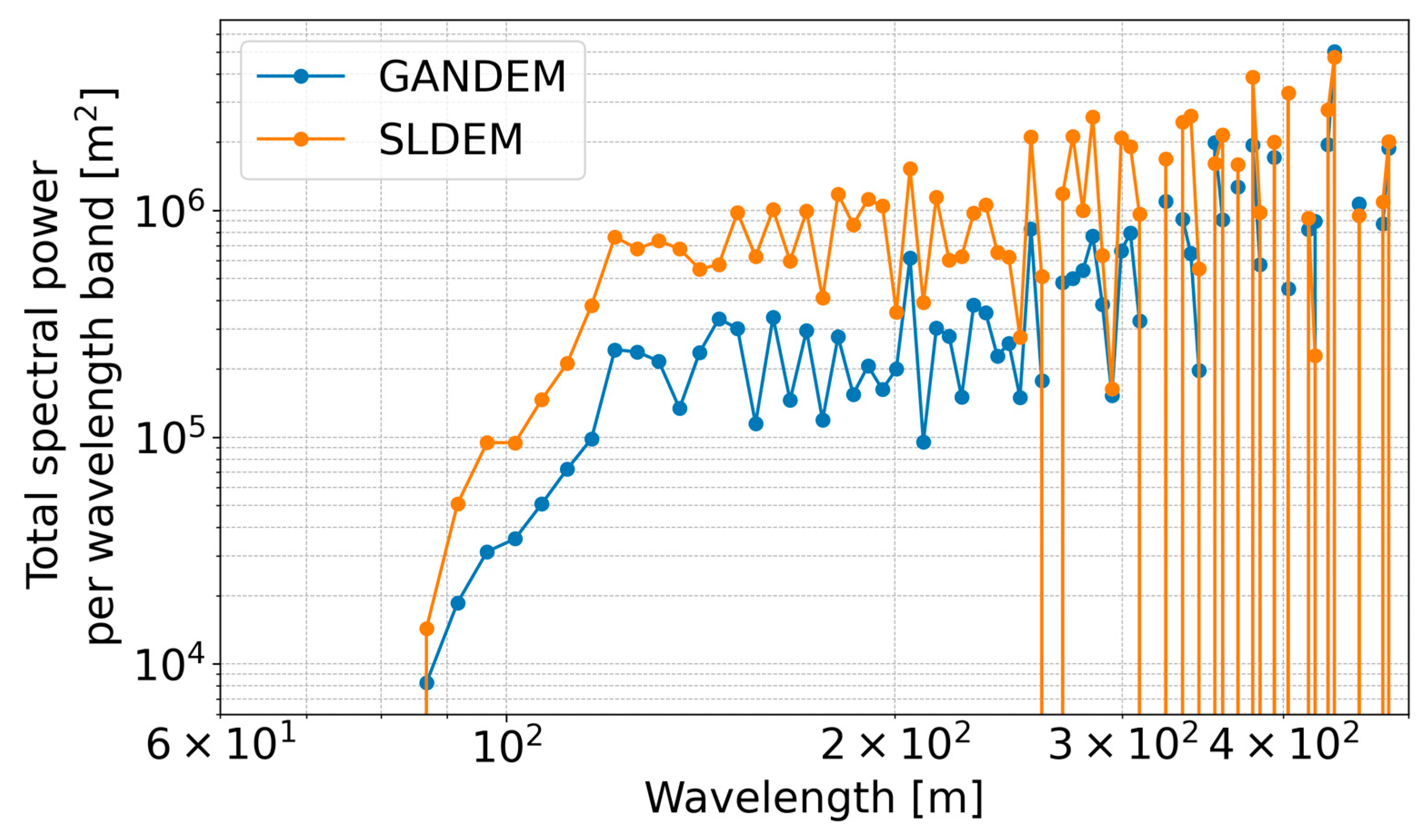
3.1. Generation Result of a High-Resolution DEM
3.2. Determination of Roughness Parameters at Scales Smaller than the DEM Resolution
3.3. Results of Surface Scattering Simulations Using GANDEM
3.4. Detection Results of Subsurface Echoes from LRS Data
3.5. Estimation of Subsurface Structure Indicated by SEC Using the Radar Equation
4. Discussion
4.1. Factors Improving Surface Scattering Simulation
4.2. Detection Validity of Subsurface Echo Candidates
4.3. Subsurface Structures Indicated by SECs
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Plaut, J.J.; Picardi, G.; Safaeinili, A.; Ivanov, A.B.; Milkovich, S.M.; Cicchetti, A.; Kofman, W.; Mouginot, J.; Farrell, W.M.; Phillips, R.J.; et al. Subsurface Radar Sounding of the South Polar Layered Deposits of Mars. Science 2007, 316, 92–95. [Google Scholar] [CrossRef]
- Holt, J.W.; Safaeinili, A.; Plaut, J.J.; Head, J.W.; Phillips, R.J.; Seu, R.; Kempf, S.D.; Choudhary, P.; Young, D.A.; Putzig, N.E.; et al. Radar Sounding Evidence for Buried Glaciers in the Southern Mid-Latitudes of Mars. Science 2008, 322, 1235–1238. [Google Scholar] [CrossRef] [PubMed]
- Orosei, R.; Lauro, S.E.; Pettinelli, E.; Cicchetti, A.; Coradini, M.; Cosciotti, B.; Di Paolo, F.; Flamini, E.; Mattei, E.; Pajola, M.; et al. Radar Evidence of Subglacial Liquid Water on Mars. Science 2018, 361, 490–493. [Google Scholar] [CrossRef]
- Ono, T.; Kumamoto, A.; Nakagawa, H.; Yamaguchi, Y.; Oshigami, S.; Yamaji, A.; Kobayashi, T.; Kasahara, Y.; Oya, H. Lunar Radar Sounder Observations of Subsurface Layers under the Nearside Maria of the Moon. Science 2009, 323, 909–912. [Google Scholar] [CrossRef] [PubMed]
- Oshigami, S.; Okuno, S.; Yamaguchi, Y.; Ohtake, M.; Haruyama, J.; Kobayashi, T.; Kumamoto, A.; Ono, T. The Layered Structure of Lunar Maria: Identification of the HF-Radar Reflector in Mare Serenitatis Using Multiband Optical Images. Icarus 2012, 218, 506–512. [Google Scholar] [CrossRef]
- Oshigami, S.; Watanabe, S.; Yamaguchi, Y.; Yamaji, A.; Kobayashi, T.; Kumamoto, A.; Ishiyama, K.; Ono, T. Mare Volcanism: Reinterpretation Based on Kaguya Lunar Radar Sounder Data. J. Geophys. Res. Planets 2014, 119, 1037–1045. [Google Scholar] [CrossRef]
- Ishiyama, K.; Kumamoto, A. Volcanic History in the Smythii Basin Based on SELENE Radar Observation. Sci. Rep. 2019, 9, 14502. [Google Scholar] [CrossRef] [PubMed]
- Ishiyama, K.; Kumamoto, A.; Ono, T.; Yamaguchi, Y.; Haruyama, J.; Ohtake, M.; Katoh, Y.; Terada, N.; Oshigami, S. Estimation of the Permittivity and Porosity of the Lunar Uppermost Basalt Layer Based on Observations of Impact Craters by SELENE. J. Geophys. Res. Planets 2013, 118, 1453–1467. [Google Scholar] [CrossRef]
- Hongo, K.; Toh, H.; Kumamoto, A. Estimation of Bulk Permittivity of the Moon’s Surface Using Lunar Radar Sounder on-Board Selenological and Engineering Explorer. Earth Planets Space 2020, 72, 1–15. [Google Scholar] [CrossRef]
- Kobayashi, T.; Kim, J.H.; Lee, S.R.; Araki, H.; Ono, T. Simultaneous Observation of Lunar Radar Sounder and Laser Altimeter of Kaguya for Lunar Regolith Layer Thickness Estimate. IEEE Geosci. Remote Sens. Lett. 2010, 7, 435–439. [Google Scholar] [CrossRef]
- Head, J.W.; Wilson, L. Generation, Ascent and Eruption of Magma on the Moon: New Insights into Source Depths, Magma Supply, Intrusions and Effusive/Explosive Eruptions (Part 2: Predicted Emplacement Processes and Observations). Icarus 2017, 283, 176–223. [Google Scholar] [CrossRef]
- Wilson, L.; Head, J.W. Eruption of Magmatic Foams on the Moon: Formation in the Waning Stages of Dike Emplacement Events as an Explanation of “Irregular Mare Patches”. J. Volcanol. Geotherm. Res. 2017, 335, 113–127. [Google Scholar] [CrossRef]
- Head, J.W.; Ivanov, B. Impact Cratering at the Lunar Ina Irregular Mare Patch (IMP): Experimental Evidence for the Nature of Impacts into Porous Basaltic Substrate and Outstanding Questions. Planet. Space Sci. 2024, 250, 105954. [Google Scholar] [CrossRef]
- Haruyama, J.; Hioki, K.; Shirao, M.; Morota, T.; Hiesinger, H.; van der Bogert, C.H.; Miyamoto, H.; Iwasaki, A.; Yokota, Y.; Ohtake, M.; et al. Possible Lunar Lava Tube Skylight Observed by SELENE Cameras. Geophys. Res. Lett. 2009, 36, L21206. [Google Scholar] [CrossRef]
- Kaku, T.; Haruyama, J.; Miyake, W.; Kumamoto, A.; Ishiyama, K.; Nishibori, T.; Yamamoto, K.; Crites, S.T.; Michikami, T.; Yokota, Y.; et al. Detection of Intact Lava Tubes at Marius Hills on the Moon by SELENE (Kaguya) Lunar Radar Sounder. Geophys. Res. Lett. 2017, 44, 10–155. [Google Scholar] [CrossRef]
- Chappaz, L.; Sood, R.; Melosh, H.J.; Howell, K.C.; Blair, D.M.; Milbury, C.; Zuber, M.T. Evidence of Large Empty Lava Tubes on the Moon Using GRAIL Gravity. Geophys. Res. Lett. 2017, 44, 105–112. [Google Scholar] [CrossRef]
- Zhu, K.; Yang, M.; Yan, X.Y.; Li, W.K.; Feng, W.; Zhong, M. GRAIL Gravity Gradients Evidence for a Potential Lava Tube at Marius Hills on the Moon. Icarus 2024, 408, 115814. [Google Scholar] [CrossRef]
- Kobayashi, T.; Kim, J.-H.; Lee, S.R.; Song, K.-Y. Nadir Detection of Lunar Lava Tube by Kaguya Lunar Radar Sounder. IEEE Trans. Geosci. Remote Sens. 2020, 59, 7395–7418. [Google Scholar] [CrossRef]
- Donini, E.; Carrer, L.; Gerekos, C.; Bruzzone, L.; Bovolo, F. An Unsupervised Fuzzy System for the Automatic Detection of Candidate Lava Tubes in Radar Sounder Data. Geosci. Remote Sens. 2022, 60, 1–19. [Google Scholar] [CrossRef]
- Barker, M.K.; Mazarico, E.; Neumann, G.A.; Zuber, M.T.; Haruyama, J.; Smith, D.E. A New Lunar Digital Elevation Model from the Lunar Orbiter Laser Altimeter and SELENE Terrain Camera. Icarus 2016, 273, 346–355. [Google Scholar] [CrossRef]
- Wu, B.; Liu, W.C.; Grumpe, A.; Wöhler, C. Construction of Pixel-Level Resolution DEMs from Monocular Images by Shape and Albedo from Shading Constrained with Low-Resolution DEM. ISPRS J. Photogramm. Remote Sens. 2018, 140, 3–19. [Google Scholar] [CrossRef]
- Tao, Y.; Muller, J.P.; Conway, S.J.; Xiong, S. Large Area High-Resolution 3d Mapping of Oxia Planum: The Landing Site for the Exomars Rosalind Franklin Rover. Remote Sens. 2021, 13, 3270. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Hu, X.; Oberst, J. Pixel-Resolution Dtm Generation for the Lunar Surface Based on a Combined Deep Learning and Shape-from-Shading (Sfs) Approach. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 3, 511–516. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Di, K.; Peng, M.; Wan, W.; Liu, Z. A Generative Adversarial Network for Pixel-Scale Lunar DEM Generation from High-Resolution Monocular Imagery and Low-Resolution DEM. Remote Sens. 2022, 14, 5420. [Google Scholar] [CrossRef]
- Gerekos, C.; Haynes, M.S.; Schroeder, D.M.; Blankenship, D.D. The Phase Response of a Rough Rectangular Facet for Radar Sounder Simulations of Both Coherent and Incoherent Scattering. Radio Sci. 2023, 58, 1–30. [Google Scholar] [CrossRef]
- Berquin, Y.; Herique, A.; Kofman, W.; Heggy, E. Computing Low-Frequency Radar Surface Echoes for Planetary Radar Using Huygens-Fresnel’s Principle. Radio. Sci. 2015, 50, 1097–1109. [Google Scholar] [CrossRef]
- Ono, T.; Kumamoto, A.; Kasahara, Y.; Yamaguchi, Y.; Yamaji, A.; Kobayashi, T.; Oshigami, S.; Nakagawa, H.; Goto, Y.; Hashimoto, K.; et al. The Lunar Radar Sounder (LRS) Onboard TheáKAGUYA (SELENE) Spacecraft. Space Sci. Rev. 2010, 154, 145–192. [Google Scholar] [CrossRef]
- Kobayashi, T.; Kim, J.H.; Lee, S.R.; Kumamoto, A.; Nakagawa, H.; Oshigami, S.; Oya, H.; Yamaguchi, Y.; Yamaji, A.; Ono, T. Synthetic Aperture Radar Processing of Kaguya Lunar Radar Sounder Data for Lunar Subsurface Imaging. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2161–2174. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Goossens, S.; Matsumoto, K.; Rowlands, D.D.; Lemoine, F.G.; Noda, H.; Araki, H. Orbit Determination of the SELENE Satellites Using Multi-Satellite Data Types and Evaluation of SELENE Gravity Field Models. J. Geod. 2011, 85, 487–504. [Google Scholar] [CrossRef]
- Carrier, W.D., III; Olhoeft, G.R.; Mendell, W. Physical properties of the lunar surface. In Lunar Sourcebook, a User’s Guide to the Moon; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Olhoeft, G.R.; Strangway, D.W. Dielectric Properties of the First 100 Meters of the Moon. Earth Planet. Sci. Lett. 1975, 24, 394–404. [Google Scholar] [CrossRef]
- Chyba, C.F.; Ostro, S.J.; Edwards, B.C. Radar Detectability of a Subsurface Ocean on Europa. Icarus 1998, 134, 292–302. [Google Scholar] [CrossRef]
- Ishihara, Y.; Goossens, S.; Matsumoto, K.; Noda, H.; Araki, H.; Namiki, N.; Hanada, H.; Iwata, T.; Tazawa, S.; Sasaki, S. Crustal Thickness of the Moon: Implications for Farside Basin Structures. Geophys. Res. Lett. 2009, 36, L19202. [Google Scholar] [CrossRef]
- Wieczorek, M.A.; Neumann, G.A.; Nimmo, F.; Kiefer, W.S.; Taylor, G.J.; Melosh, H.J.; Phillips, R.J.; Solomon, S.C.; Andrews-Hanna, J.C.; Asmar, S.W.; et al. The Crust of the Moon as Seen by GRAIL. Science 2013, 339, 671–675. [Google Scholar] [CrossRef]
- Kobayashi, S.; Karouji, Y.; Morota, T.; Takeda, H.; Hasebe, N.; Hareyama, M.; Kobayashi, M.; Shibamura, E.; Yamashita, N.; d’Uston, C.; et al. Lunar Farside Th Distribution Measured by Kaguya Gamma-Ray Spectrometer. Earth Planet. Sci. Lett. 2012, 337, 10–16. [Google Scholar] [CrossRef]
- Lawrence, D.J.; Puetter, R.C.; Elphic, R.C.; Feldman, W.C.; Hagerty, J.J.; Prettyman, T.H.; Spudis, P.D. Global Spatial Deconvolution of Lunar Prospector Th Abundances—Lawrence—2007—Geophysical Resea. Geophys. Res. Lett. 2007, 34, L03201. [Google Scholar] [CrossRef]
- Head, J.W.; Wilson, L. Lunar Graben Formation Due to Near-Surface Deformation Accompanying Dike Emplacement Introduction and Background. Planet. Space Sci. 1993, 41, 719–727. [Google Scholar] [CrossRef]
- Haruyama, J.; Matsunaga, T.; Ohtake, M.; Morota, T.; Honda, C.; Yokota, Y.; Torii, M.; Ogawa, Y. Global Lunar-Surface Mapping Experiment Using the Lunar Imager/Spectrometer on SELENE. Earth Planets Space 2008, 60, 243–255. [Google Scholar] [CrossRef]
- Robinson, M.S.; Ashley, J.W.; Boyd, A.K.; Wagner, R.V.; Speyerer, E.J.; Ray Hawke, B.; Hiesinger, H.; Van Der Bogert, C.H. Confirmation of Sublunarean Voids and Thin Layering in Mare Deposits. Planet. Space Sci. 2012, 69, 18–27. [Google Scholar] [CrossRef]
- Otake, H.; Ohtake, M.; Hirata, N. Lunar Iron and Titanium Abundance Algorithms Based on SELENE (Kaguya) Multiband Imager Data. In Proceedings of the 43rd Annual Lunar and Planetary Science Conference, Woodlands, TX, USA, 19–23 March 2012; p. 1905. [Google Scholar]
- Kiefer, W.S.; MacKe, R.J.; Britt, D.T.; Irving, A.J.; Consolmagno, G.J. The Density and Porosity of Lunar Rocks. Geophys. Res. Lett. 2012, 39, L07201. [Google Scholar] [CrossRef]
- Golombek, M.P. Structural Analysis of Lunar Grabens and the Shallow Crustal Structure of the Moon. J. Geophys. Res. Solid. Earth 1979, 84, 4657–4666. [Google Scholar] [CrossRef]
- Wilson, L.; Head, J.W. Controls on Lunar Basaltic Volcanic Eruption Structure and Morphology: Gas Release Patterns in Sequential Eruption Phases. Geophys. Res. Lett. 2018, 45, 5852–5859. [Google Scholar] [CrossRef]
- Wilson, L.; Head, J.W., III. Deep Generation of Magmatic Gas on the Moon and Implications for Pyroclastic Eruptions. Geophys. Res. Lett. 2003, 30, 1605. [Google Scholar] [CrossRef]
- Head, J.W.; Wilson, L.; Hiesinger, H.; van der Bogert, C.; Chen, Y.; Dickson, J.L.; Gaddis, L.R.; Haruyama, J.; Jawin, E.R.; Jozwiak, L.M.; et al. Lunar Mare Basaltic Volcanism: Volcanic Features and Emplacement Processes. Rev. Mineral. Geochem. 2023, 89, 453–507. [Google Scholar] [CrossRef]
- Rutherford, M.J.; Head, J.W.; Saal, A.E.; Hauri, E.; Wilson, L. Model for the Origin, Ascent, and Eruption of Lunar Picritic Magmas. Am. Mineral. 2017, 102, 2045–2053. [Google Scholar] [CrossRef]














| Area | Data Name | Center Position Latitude (°N), Longitude (°E) |
|---|---|---|
| Apollo 11 | NAC_DTM_APOLLO11_E008N0234.IMG | 0.77, 23.44 |
| Tranquillitatis pit | NAC_DTM_TRANQPIT1_E084N0332.IMG | 8.39, 33.19 |
| ID | Data Name | Solar Altitude Angle (°) (LE, RE) | ID | Data Name | Solar Altitude Angle (°) (LE, RE) |
|---|---|---|---|---|---|
| 1 | M1111656414 | 18.35, 18.2 | 7 | M1197661005 | 58.69, 57.98 |
| 2 | M150361817 | 27.46, 27.39 | 8 | M1302291967 | 59.44, 59.29 |
| 3 | M104362199 | 36.22, 36.03 | 9 | M106719774 | 62.77, 62.57 |
| 4 | M1159956344 | 43.17, 43.01 | 10 | M188071231 | 72.51, 72.29 |
| 5 | M1121074527 | 49.08, 48.91 | 11 | M1116379787 | 73.36, 73.17 |
| 6 | M1121088726 | 51.02, 50.85 | 12 | M188099822 | 76.22, 75.99 |
| ID | Data Name | Solar Altitude Angle (°) (LE, RE) | ID | Data Name | Solar Altitude Angle (°) (LE, RE) |
|---|---|---|---|---|---|
| 1 | M1230505012 | 22.67, 22.54 | 8 | M1458346403 | 50.49, 50.29 |
| 2 | M1319855669 | 28.79, 28.66 | 9 | M152655237 | 54.2, 54.13 |
| 3 | M1279892111 | 32.09, 31.94 | 10 | M1478239463 | 56.00, 55.77 |
| 4 | M1421980119 | 38.65, 38.42 | 11 | M1286947293 | 63.81, 63.68 |
| 5 | M1221115717 | 43.88, 43.53 | 12 | M1445448984 | 69.59, 69.47 |
| 6 | M1113950638 | 45.38, 45.22 | 13 | M1223457806 | 70.89, 70.72 |
| 7 | M190380271 | 47.56, 47.38 | 14 | M188021351 | 73.46, 73.3 |
| Region | MAE (m) | RMSE (m) | Maximum Error (m) |
|---|---|---|---|
| Apollo 11 | 2.36 | 3.16 | 27.0 |
| Tranquillitatis pit | 2.93 | 4.09 | 29.4 |
| Region | MAE (m) | RMSE (m) | Maximum Error (m) |
|---|---|---|---|
| Apollo 11 | 2.04 | 2.64 | 17.6 |
| Tranquillitatis pit | 2.25 | 3.31 | 23.7 |
| No. | Data Name | No. | Data Name |
|---|---|---|---|
| 1 | LRS_SW_WF_05N_032145E.tbl | 9 | LRS_SW_WF_05N_033232E.tbl |
| 2 | LRS_SW_WF_05N_032278E.tbl | 10 | LRS_SW_WF_05N_033344E.tbl |
| 3 | LRS_SW_WF_05N_032336E.tbl | 11 | LRS_SW_WF_05N_033405E.tbl |
| 4 | LRS_SW_WF_05N_032444E.tbl | 12 | LRS_SW_WF_05N_033510E.tbl |
| 5 | LRS_SW_WF_05N_032617E.tbl | 13 | LRS_SW_WF_05N_033686E.tbl |
| 6 | LRS_SW_WF_05N_032804E.tbl | 14 | LRS_SW_WF_05N_033873E.tbl |
| 7 | LRS_SW_WF_05N_032835E.tbl | 15 | LRS_SW_WF_05N_033905E.tbl |
| 8 | LRS_SW_WF_05N_033101E.tbl |
| Simulation No. | Normal Distribution 1 (Mean, Standard Derivation) | Normal Distribution 2 (Mean, Standard Derivation) | Threshold |
|---|---|---|---|
| 1 | 0.449, 1.09 | 4.39, 1.49 | 3.70 |
| 2 | 0.439, 1.01 | 4.33, 1.67 | 3.46 |
| 3 | 0.474, 1.12 | 4.67, 1.56 | 3.84 |
| 4 | 0.478, 1.03 | 4.44, 1.64 | 3.56 |
| 5 | 0.373, 1.02 | 4.54, 1.59 | 3.44 |
| 6 | 0.431, 1.02 | 4.22, 1.50 | 3.49 |
| 7 | 0.516, 1.09 | 4.61, 1.58 | 3.78 |
| 8 | 0.482, 1.09 | 4.50, 1.49 | 3.76 |
| 9 | 0.357, 1.07 | 4.28, 1.56 | 3.43 |
| 10 | 0.476, 1.07 | 4.37, 1.53 | 3.67 |
| NACDEM–SLDEM MAE (m) | NACDEM–GANDEM MAE (m) | |
|---|---|---|
| Apollo 11 site Low-frequency topography | 1.43 | 1.41 |
| Apollo 11 site High-frequency topography | 2.00 | 1.34 |
| Tranquillitatis pit site Low-frequency topography | 1.64 | 1.49 |
| Tranquillitatis pit site High-frequency topography | 2.47 | 1.77 |
| NACDEM–SLDEM RMSE (m) | NACDEM–GANDEM RMSE (m) | |
|---|---|---|
| Apollo 11 site Low-frequency topography | 1.74 | 1.72 |
| Apollo 11 site High-frequency topography | 2.82 | 1.90 |
| Tranquillitatis pit site Low-frequency topography | 2.21 | 2.10 |
| Tranquillitatis pit site High-frequency topography | 3.39 | 2.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nozawa, H.; Haruyama, J.; Kumamoto, A.; Iwata, T.; Toyokawa, K.; Head, J.W.; Orosei, R. Detection of Small-Scale Subsurface Echoes Using Lunar Radar Sounder and Surface Scattering Simulations with a DEM Generated Using a Generative Adversarial Network. Remote Sens. 2025, 17, 1710. https://doi.org/10.3390/rs17101710
Nozawa H, Haruyama J, Kumamoto A, Iwata T, Toyokawa K, Head JW, Orosei R. Detection of Small-Scale Subsurface Echoes Using Lunar Radar Sounder and Surface Scattering Simulations with a DEM Generated Using a Generative Adversarial Network. Remote Sensing. 2025; 17(10):1710. https://doi.org/10.3390/rs17101710
Chicago/Turabian StyleNozawa, Hitoshi, Junichi Haruyama, Atsushi Kumamoto, Takahiro Iwata, Kosei Toyokawa, James W. Head, and Roberto Orosei. 2025. "Detection of Small-Scale Subsurface Echoes Using Lunar Radar Sounder and Surface Scattering Simulations with a DEM Generated Using a Generative Adversarial Network" Remote Sensing 17, no. 10: 1710. https://doi.org/10.3390/rs17101710
APA StyleNozawa, H., Haruyama, J., Kumamoto, A., Iwata, T., Toyokawa, K., Head, J. W., & Orosei, R. (2025). Detection of Small-Scale Subsurface Echoes Using Lunar Radar Sounder and Surface Scattering Simulations with a DEM Generated Using a Generative Adversarial Network. Remote Sensing, 17(10), 1710. https://doi.org/10.3390/rs17101710











