Abstract
Near-surface air temperature (Ta) is a key variable in global climate studies. Global climate models such as ERA5 and CMIP6 predict various parameters at coarse spatial resolution (>9 km). As a result, local phenomena such as the urban heat islands are not reflected in the model’s outputs. In this study, we address this limitation by downscaling the resolution of ERA5 (9 km) and CMIP6 (27 km) Ta to 1 km, employing two different machine learning algorithms (XGBoost and Deep Learning). Our models leverage a diverse set of features, including data from satellites (land surface temperature and normalized difference vegetation index), from ERA5 and CMIP6 climate models (e.g., solar and thermal radiation, wind), and from digital elevation models to develop accurate machine learning prediction models. These models were rigorously validated against observations from 98 meteorological stations in the East Mediterranean (Israel) using a standard cross-validation technique as well as a leave-one-group-out on the station ID evaluation methodology to avoid overfitting and dependence on geographic location. We demonstrate the sensitivity of the downscaled Ta to local land cover and topography, which is missing in the climate models. Our results demonstrate impressive accuracy with the Deep Learning-based models, obtaining Root Mean Squared Error (RMSE) values of 0.98 °C (ERA5) and 1.86 °C (CMIP6) for daily Ta and 2.20 °C (ERA5) for hourly Ta. Additionally, we explore the impact of the various input features and offer an extended application for future climate predictions. Finally, we propose an enhanced evaluation framework, which addresses the problem of model overfitting. This work provides practical tools and insights for building and evaluating Ta downscaling models. The code and data are publicly shared online.
1. Introduction
Near-surface air temperature at 2 m height (Ta) is a key variable of critical importance and plays a significant role in various fields, including agriculture ([1,2,3]), epidemiology ([4]), health ([5]), and urban planning. Additionally, predicting climate trends at a high resolution is essential for developing climate change adaptation decision-support tools (climate services). However, obtaining accurate high-resolution Ta data can be challenging.
Meteorological stations do provide continuous measurements of Ta; however, their spatial distribution is irregular and coarse. To address this limitation, reanalysis data, a process that standardizes weather models using ground-based observation data ([6]), can be used. The European Centre for Medium-Range Weather Forecasts (ECMWF) ERA5 reanalysis provides hourly Ta data at a spatial resolution of 9 km. Additionally, ensemble forecasting uses a set (or ensemble) of forecasts to indicate the range of possible future states of the atmosphere. It runs multiple climate models with different initial conditions and selects the scenario with the highest probability. The Coupled Model Intercomparison Project Phase 6 (CMIP6) [7] is an ensemble of multiple climate models and re-analyses, offering climate change scenarios at a spatial resolution of 27 km. Despite these advances, the spatial resolution of ERA5 Ta data is too coarse and remains inadequate for many climate services. For example, local terrain effects are often missed in regions with rugged topography, and in agricultural areas characterized by small field sizes, the coarse resolution hinders precise climate analysis. Consequently, there is a growing need to enhance the spatial resolution of ERA5 (and CMIP6) data. Sharpening climate models’ Ta data to 1 km would contribute to the development of improved climate services and other applications.
Downscaling Ta can be performed by modeling the effect of different influencing parameters. Specifically, vegetation cover impacts Ta through evapotranspiration where the Normalized Difference Vegetation Index (NDVI) is often used to account for the impact of vegetation ([4]). Land Surface Temperature (LST) impacts Ta through sensible and latent heat fluxes ([8]), solar radiation through surface heating, and winds through vertical mixing. Wind direction can influence Ta through temperature advection ([9]). For example, in the Eastern Mediterranean, winds with a northern component often advect cold air, while southeastern winds, which are common during transitional seasons, advect warm air. Additionally, topographic height significantly affects Ta through adiabatic air vertical motion ([10]). Topography in the Eastern Mediterranean varies significantly within short distances, leading to drastic changes in the local temperature. For example, Mount Naftali, at 436 m above sea level, experiences maximum summer temperatures around 30 °C, while just about 2 km away in the Hula Valley, at 70 m above sea level, temperatures can reach 37 °C.
Multiple studies have undertaken the task of downscaling Ta using various methodologies, including statistical and classical (not neural-based) machine learning (ML) techniques ([4,11,12,13,14,15,16]). These studies exhibit diversity in terms of geographical coverage, choice of algorithms (ranging from statistical and classical ML to Deep Learning), and the features utilized in model training. While some investigations focused on daily downscaling resolutions, either in terms of mean or min/max values, others delved into hourly downscaling predictions. A prevalent trend emerged in recent research, highlighting the efficacy of ML algorithms such as XGboost (XGB) and Random Forest (RF) in the Ta downscaling task. Furthermore, there is a growing body of work introducing Deep Learning (DL) models, including Artificial Neural Networks (ANNs) and Convolutional Neural Networks (CNNs), demonstrating their potential and versatility in this context. These studies span various regions worldwide, each presenting unique challenges and opportunities. To assess model performance, these studies typically employed cross-validation techniques, involving random data splitting for training and testing. The evaluation metrics commonly employed to gauge the quality of downscaling predictions are Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and the R2 coefficient of determination. Table 1 summarizes the RMSE values reported in these studies. As can be seen from the comparison table, RMSE values for downscaling daily Ta range between 0.85 and 2.14 and 1.58 and 1.77 for hourly predictions.

Table 1.
Comparison of recent studies on Ta downscaling.
Though previous research efforts have made valuable contributions to the field of downscaling Ta, there are notable gaps in the existing body of work. There is a need to compare the performance of different downscaling methods at both daily and hourly resolutions and to consider additional features for model training, such as satellite data and topographic information. Furthermore, while much attention has been given to downscaling historical temperature data, there is a growing demand for downscaling future climate predictions. Finally, there is room for improvement in the evaluation methodology to avoid model overfitting and verifying the generalization of Ta downscaling models.
This study aims to address these challenges by comparing various downscaling methods, exploring the impact of additional features, extending the application to enable future climate predictions, and enhancing the evaluation framework. Through this research, we aspire to contribute to the advancement of downscaling techniques, ultimately providing more accurate and reliable climate data for a wide range of applications.
The following sections of this paper detail our methodology, experiments, results, and discussions, presenting a significant step forward in the field of downscaling air temperature using machine and Deep Learning algorithms.
2. Data and Methods
In this section, we present the data and methods employed in our study, which aims to compare machine-learning based methods for downscaling Ta. We compare the performance of 6 different ML implementations consisting of two different ML algorithms (XGBoost and Deep Learning) and two different time resolutions (hourly and daily) and based on input data obtained from two different climate models (ERA5 and CMIP6). The “ground truth” data target labels for training and testing the supervised ML models consists of Ta observations from meteorological stations. Input features for the ML models consist of climate (ERA5 and CMIP6), satellite, and topography data obtained from publicly available resources. We compared the performance of the 6 different ML implementations using two different evaluation methodologies. To extend the application of the various downscaling models to future climate predictions of CMIP6, we used historical CMIP6 data and adjusted the features appropriately. The overall flow chart describing the various implementations’ flow and architecture can be seen in Figure 1.
2.1. Study Area
The study area, located in the Eastern Mediterranean (Figure 2a), is characterized by high spatial variability of climatic conditions ([17]) due to the region’s complex orography (elevation: −430 up to 2814 m) and the spatial heterogeneity of land covers.
2.2. Data
The data for the supervised ML models consist of Ta observations as target values (“ground truth”) and climate (ERA5 and CMIP6), satellite, and topography data used as model input features. The grids were projected on the same coordinate system (CRS) EPSG:4326.
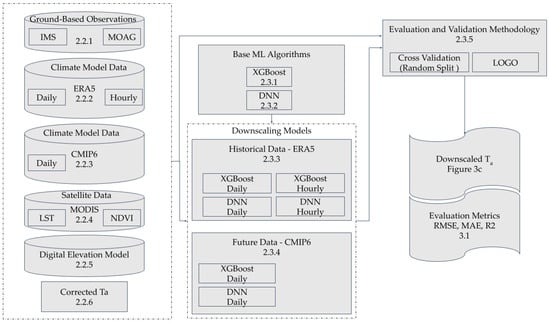
Figure 1.
System flow chart describing the various data sources, the base underlying ML algorithms, the 6 corresponding Ta downscaling models, the evaluation methodologies, and the resulting outcomes of our proposed system. References to the corresponding sections appear in each component.
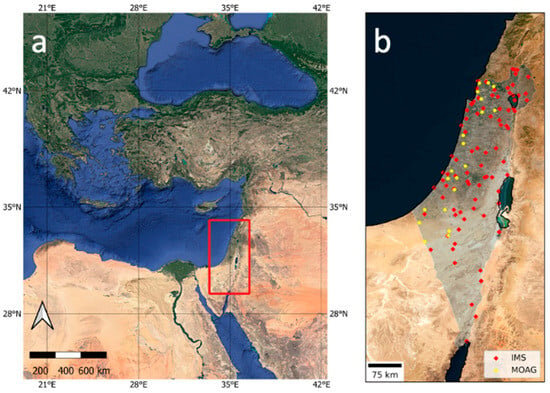
Figure 2.
(a) The study area (red rectangle) in the Eastern Mediterranean. (b) Locations of the IMS (red) and MOAG (yellow) meteorological stations.
2.2.1. Ground-Based Observations
We used Ta observations from the Israel Meteorological Service (IMS) and Ministry of Agriculture (MOAG) meteorological stations. The IMS data were obtained via an API [18] in 10 min temporal resolution and were resampled to hourly and daily temporal resolutions. The MOAG hourly data were provided by the Ministry of Agriculture as a CSV file. Figure 2b shows the geographical location of the 98 meteorological stations used in this study. The station data include 12 years (2008–2019) of hourly Ta measurements with a total of 10.3 million hourly samples from all stations. A total of 3.42 million hourly samples were used for the historical (ERA5) model and 6.87 million for the future (CMIP6) model. We used a different number of stations for each model with respect to the quality and availability of the data from the stations and the climate models. Ta measurement errors (i.e., values above 50 °C or below −20 °C) were excluded from the datasets. On top of that, we excluded stations with less than a minimum threshold (70%) of acceptable data samples.
2.2.2. ERA5 Climate Model Data
ERA5 is the fifth generation ECMWF atmospheric reanalysis of the global climate covering the period from January 1940 to the present. ERA5 is produced by the Copernicus Climate Change Service (C3S) at ECMWF. ERA5 provides hourly estimates of a large number of atmospheric, land, and oceanic climate variables on a 9 km grid. It combines observational data from diverse sources, such as weather stations, satellites, and buoys, with a numerical weather prediction model to generate a comprehensive and consistent analysis of historical weather and climate conditions. With its high spatiotemporal resolution and global coverage, ERA5 provides a valuable resource for downscaling Ta and capturing detailed atmospheric information for machine and Deep Learning algorithms. ERA5 data containing Ta, U&V wind components, downward surface solar and thermal radiation, and net radiation were retrieved from the Climate Data Store (CDS) as netCDF files. Figure 3a illustrates the outcome of the ERA5 daily Ta values for 9 September 2015.
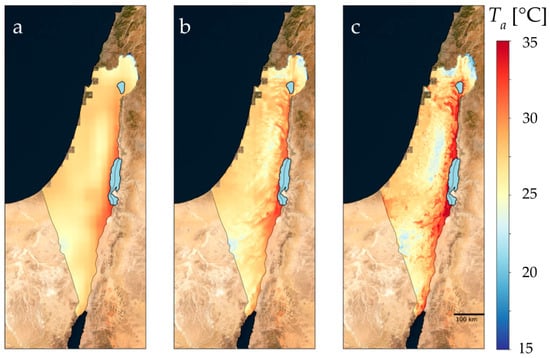
Figure 3.
Ta daily values for 1 September 2015. (a) 9 × 9 resolution ERA5 Ta smoothed to 1 × 1 km resolution. (b) Smoothed ERA5 Ta values corrected based on topography and dry adiabatic lapse rate. (c) Ta NN ERA5 daily model predictions—1 × 1 km resolution.
2.2.3. CMIP6 Climate Model Data
The Coupled Model Intercomparison Project (CMIP) is a project of the World Climate Research Programme (WCRP) that provides climate projections to understand past, present, and future climate changes ([19]). The CMIP and its associated data infrastructure have become essential to the Intergovernmental Panel on Climate Change (IPCC) and other international and national climate assessments. CMIP6 historical data are available till the end of 2014, and future data till the end of the 21st century under different Representative Concentration Pathway greenhouse gas concentration (not emissions) trajectories are adopted by the IPCC. The data were obtained utilizing the Google Earth Engine (GEE) platform.
2.2.4. MODIS Satellite Data
The spatial resolution and coverage of the Moderate Resolution Imaging Spectroradiometer (MODIS) onboard the AQUA satellite, launched in 2002 as part of NASA’s Earth Observing System, makes it a valuable resource for downscaling. We used the Shiff et al. ([20]) gap-filled MODIS LST dataset, which was found as the most suitable gap-filling method for MODIS LST data ([21]). We added MODIS daily 1 km LST and 250 m NDVI to the hourly dataset after up-sampling to hourly resolution using linear interpolation.
2.2.5. Digital Elevation Model Data
As Ta is highly influenced by elevation, we obtained Digital Elevation Model (DEM) data for the study area. We downloaded the Shuttle Radar Topography Mission (SRTM) 90 m resolution DEM from the GEE platform ([22]). These data were used to calculate the mean elevation of all ERA5 (9 km) and CMIP6 (27 km) low-resolution (LR) grid cells in the study area. Similarly, we calculated the mean elevation of all 1 km high-resolution (HR) grid cells in the study area.
2.2.6. Corrected Ta Based on Height Difference and Adiabatic Lapse Rate
As the Ta values obtained from the climate models (ERA5 and CMIP6) are at a low resolution (9 and 27 km), we included a naïve correction of the Ta values based on the height difference between the mean height (h[LR]) of the low-resolution (LR) ERA5 or CMIP6 grid and the mean height (h[HR]) of the high-resolution (HR) 1 km grid. The corrected Ta [HR] value was calculated by using a vertical temperature gradient (dry adiabatic lapse rate) of 9.8 °C/1000 m as follows:
Ta [HR] = Ta [LR] − 9.8 × (h[HR] − h[LR])
The corrected values were used as an additional input feature to the supervised machine learning models. Figure 3b illustrates the outcome of the ERA5 Ta correction for 9 September 2015.
2.3. Methods
In the following section, we describe the two chosen ML algorithms, the implementation details for the past and future models based on the corresponding climate data, as well as the two evaluation methodologies that were used.
2.3.1. XGBoost Algorithm
One of the two algorithms employed in this study was XGBoost (Extreme Gradient Boosting), a powerful ensemble learning algorithm widely recognized for its robust predictive capabilities. For our XGBoost model, we configured specific hyperparameters to optimize its performance. We set the learning rate to 0.5 to control the step size at each iteration, ensuring a balance between model convergence and accuracy. A maximum depth of 6 branches was imposed on individual decision trees within the ensemble, regulating model complexity. A gamma rate of 0.1 was applied to specify the minimum reduction in loss required to make a new split, contributing to the overall model’s ability to generalize. We employed 500 estimators, which represent the number of boosting rounds, allowing the model to progressively learn and adapt. This customized configuration of XGBoost was based on trial-and-error experimentation on our training data, enabling us to construct a predictive model tailored to our specific research data and task.
2.3.2. Deep Neural Network
In our study, we employed a Deep Neural Network (DNN) as one of the two modeling approaches. This Deep Learning (DL) algorithm was implemented using Keras and TensorFlow, known for their effectiveness in developing intricate neural architectures. The Neural Network (NN) structured architecture consists of four fully connected layers, each with a varying number of neurons, configured in the following order: 200, 200, 100, and 50 neurons. To introduce non-linearity and enhance the model’s expressive power, the Leaky-ReLu activation function was applied to each of these hidden layers. For the final dense layer, we used a single neuron, which aligns with our regression problem setting.
To initialize the weights in the NN layers, we employed a seeded Keras Glorot initializer, ensuring stability during training. Model performance was assessed using the Root Mean Square Error (RMSE) metric, which is suitable for regression tasks. To optimize the model’s weights, we selected the Adam Optimizer, a popular choice for its ability to efficiently handle large datasets and complex architectures.
During training, a batch size of 2000 was employed to balance computational efficiency and convergence. To prevent overfitting and streamline model training, we incorporated early stopping callbacks, which halted training when performance on a validation set ceased to improve, thus preventing unnecessary iterations. This customized NN configuration, with careful consideration of the architecture, activation functions, and optimization techniques, was integral to our research methodology, enabling us to effectively tackle the research questions at hand.
2.3.3. Models for Downscaling Historical Data
We used the ERA5 dataset as the historical climate model data. The training data of the historical model refer to a period of five years (2015–2019). For each of the historic ground observations, we collected ERA5, terrain, remote sensing, and temporal data to be used as input features for the supervised regression model. LST and NDVI daily values were up-sampled to hourly resolution using mean interpolation. Overall, the raw historical data used to train the regression models include 3.2 million samples, each with 15 different features (Table 2). Temporal features include the Day of Year (DOY, 0:364) and the Time of Day (TOD, 0:23), both of which were subjected to a sin and cos based trigonometric transformation [23], mapping each of them into two features in the range of [0, 1]. This transformation aids in accounting for the cyclic nature of temporal variables. As a means for the learning process to generalize to unseen stations, we excluded features that contain station-specific information such as geographical coordinates or station ID.

Table 2.
The features used to train the various models. The first 13 features were used in training the models for downscaling historical data (ERA5); DOY and HOD were used in all models, and the 10 remaining features were used to train the models for downscaling future data (CMIP6).
RMSE was chosen to estimate the models’ performance. We applied both the XGBoost and the DNN algorithms for both daily and hourly temporal resolutions—a total of 4 models. The hourly dataset included 3.3 M samples and the daily dataset included 140 K samples. The various ML algorithms were trained separately on hourly and daily data. Grid search was executed for each model to minimize loss rates.
2.3.4. Models for Downscaling Future Data
To develop models suitable for the downscaling of CMIP6 climate scenario predictions, we followed a methodology akin to the historical model training process outlined above (Section 2.3.3). However, this necessitated specific adaptations to accommodate the characteristics of future data predictions. Consequently, we tailored the input features for the model, ensuring their alignment with the variables available in the CMIP6 climate scenario data, while omitting features, such as NDVI observations, that do not apply in this context. In this setting, we only run daily prediction models as the future climate predictions of CMIP6 are not available at an hourly resolution.
The CMIP6 historical climate data, characterized by a spatial resolution of 27 km and a daily temporal resolution, served as the foundation for our model training. We harnessed a seven-year dataset spanning from 2008 to 2014, which encompassed 13 essential features. The feature set comprised daily mean near-surface wind speed, surface downwelling shortwave radiation, surface downwelling longwave radiation, near-surface specific humidity, near-surface relative humidity, as well as daily Ta and daily minimum and maximum Ta.
In a similar manner to our approach for the ERA5-based models used in historical data downscaling, we employed both XGBoost and DNN algorithms to assess the downscaling of CMIP6 data.
2.3.5. Evaluation and Validation Methodology
As stated above, RMSE was chosen to estimate the models’ performance. To test our models, we applied two different validation techniques. In alignment with previous studies (see Table 1), we randomly split the data to a training set (80%) and a test set (20%) for Cross Validation (CV). The training set was used to train the machine learning model, while the performance was evaluated on the test set. It is important to note that in this setting, observations from the same station (though from a different day and/or time) appear in both the train and test set, and although we excluded features that contain station-specific information such as geographical coordinates or station ID, the learning models may be partially station-specific, and the learning process may not generalize properly to unseen stations. Thus, we also implemented a more rigorous evaluation technique consisting of K-fold cross-validation while leaving-one-group-out (LOGO) on the station ID. These measures were instrumental in meticulously validating the model’s proficiency in downscaling Ta data.
3. Results
Following the demonstration of the ERA5 Ta data for 1 September 2015 (Figure 3a) and the downscaled Ta only with the topography (Figure 3b), Figure 3c demonstrated the downscaled Ta of the ERA5 Daily NN model. Figure 4 is a zoomed-in view of the area of Tel Aviv.
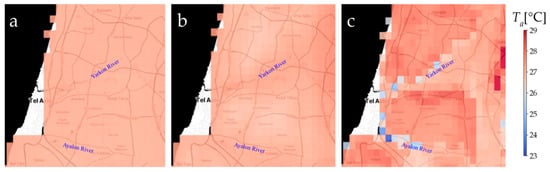
Figure 4.
Ta daily values for 01 Sep 2015 for the Tel Aviv area. (a) 9 × 9 resolution ERA5 Ta smoothed to 1 × 1 km resolution. (b) Smoothed ERA5 Ta values corrected based on topography and dry adiabatic lapse rate. (c) Ta NN ERA5 daily model predictions—1 × 1 km resolution.
3.1. Historical (ERA5) and Future (CMIP6) Data Models
Table 3 summarizes the evaluation baseline results along with the results of the various ML algorithms on the data from the two climate models on both daily and hourly temporal resolution. Table 3a presents the baseline results obtained by running no downscaling (original Ta) and downscaling by simply using the corrected Ta. For the historical data models hourly dataset, the best-performing models on the test set obtained RMSE values of 1.33 for the NN and 1.39 for the XGB model. The corresponding results when evaluating using the LOGO procedure were higher (i.e., lower prediction accuracy)—2.10 for the NN and 2.65 for the XGB model.

Table 3.
(a). Baseline result metrics are included also for simply using the climate model original resolution Ta and corrected Ta as predictions. (b). Random split Cross Validation (CV) and leave-one-group-out based on station ID (LOGO) RMSE, MAE, and R2 values for XGboost and Neural Network, for daily and hourly ERA5 (9 km, 2015–2019) datasets and daily CMIP6 (27 km, 2008–2014) datasets.
As with the historic hourly dataset, the daily RMSE values were, as expected, lower (better) than the hourly RMSE values. The best-performing models obtained RMSE values of 0.79 for the NN and 0.82 for the XGB model. The corresponding results when evaluating using the LOGO procedure were higher—0.90 for the NN and 1.44 for the XGB model.
RMSE results for the future daily models (CMIP6) were slightly higher—1.27 and 1.32 for the NN and XGB models and 1.56 and 2.05 when applying LOGO.
To gain deeper insights into the model’s performance, we computed the average RMSE across different diurnal (Time of Day, TOD) and seasonal (Day of Year, DOY) cycles for the observations in the test dataset. In Figure 5a, the RMSE values for the hourly historical (ERA5) NN model with LOGO are displayed over the course of the day, revealing a fluctuating pattern with peaks occurring between 4 and 9 a.m. and from 3 to 6 p.m. In Figure 5b, the corresponding RMSE values for this model are displayed over the course of the year, revealing a peak in the spring in which RMSE values are comparatively high. Figure 6a shows RMSE values over the DOY for the daily historic model. As can be seen from the figure, higher RMSE values are obtained during spring and especially in autumn. Figure 6b shows RMSE values over the DOY for the daily future CMIP6 model showing high values at the end of winter.

Figure 5.
RMSE values (°C) for leave-one-group-out (on Station ID) using Neural Network, resulting from the hourly dataset at (a) diurnal (TOD) and (b) seasonal (DOY) cycles.

Figure 6.
RMSE values (°C) per Day of Year (DOY) for leave-one-group-out (on Station ID) using Neural Network on the (a) ERA5 and (b) CMIP6 daily dataset.
3.2. Feature Importance
Investigating the feature importance across the diverse models employed in our study reveals valuable insights into their predictive capabilities and their contribution to the model performance. Figure 7 shows the feature weights for the XGboost daily CMIP6 model. The feature with the highest importance was near-surface relative humidity, followed by surface downwelling shortwave radiation. For the historical hourly XGB model, the mean height difference had the highest importance, followed by NDVI and LST (Figure 8b). While Ta from reanalysis (T2M) and wind U component (U_comp) were the prominent features for the historical daily XGB model (Figure 8a).
To further test the impact of the various types of features, we run the NN ERA5 Models with LOGO evaluation with and without satellite and topography. Results without the satellite features (LST and NDVI) were slightly worse with an RMSE of 2.24 (up from 2.20) and an MAE of 1.47 (up from 1.50) for the hourly model and an RMSE of 1.06 (up from 0.99) and an MAE of 0.70 (up from 0.67) for the daily model. Removing the topography-related features had a stronger effect with an hourly RMSE of 2.45 (up from 2.20) and an MAE of 1.75 (up from 1.50) and a daily RMSE of 1.12 (up from 0.99) and an MAE of 0.85 (up from 0.67).
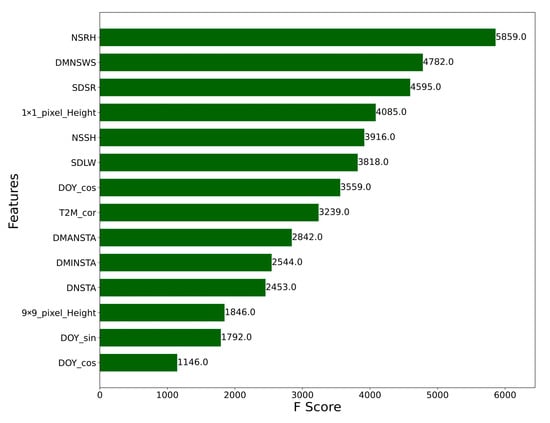
Figure 7.
Feature weights for XGboost daily CMIP6 dataset.
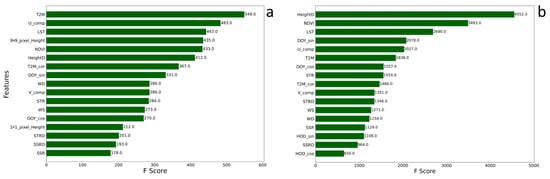
Figure 8.
XGBoost feature weights for historic ERA5 (a) daily and (b) hourly model.
4. Discussion
4.1. Results—Qualitative
Figure 3c shows the Ta NN ERA5 daily model predictions at 1 × 1 km resolution for 1 September 2015. A closer look at the effects of the land cover as captured by the MODIS land surface temperature and NDVI features on the Ta predictions are presented in Figure 4. Figure 4a presents the 9 × 9 resolution ERA5 Ta for the Tel Aviv area, showing uniform Ta values; in Figure 4b, the ERA5 Ta values are corrected based only on the topography and dry adiabatic lapse rate, showing higher Ta values in lower altitudes (Yarkon and Ayalon rivers). Figure 4c presents the Ta NN ERA5 daily model predictions at 1 × 1 km resolution revealing the urban heat island of Tel Aviv and the surrounding cities (higher Ta) and especially in the densely populated city of Bnei Brak, with very low vegetation cover. On the other hand, lower Ta can be seen along the Yarkon River and Yarkon Park and along the Ayalon River and Ariel Sharon Park, the two main green corridors of the Tel Aviv metropolitan. Note that the effects of the land cover (MODIS LST and NDVI) are more dominant than the topography (as manifested in Figure 4b). This is a major contribution of our suggested Ta downscaling.
4.2. Results—Quantitative
Overall, the quantitative results indicate that both the XGB and the NN-based models downscaled Ta to 1 km at hourly and daily temporal resolution with high accuracy improving over RMSE results reported in similar Ta-downscaling studies. This implies the strength of our models and approach. It is important to note that given that the various studies reported in Table 1 applied their models to different geographical areas and time points, one cannot make an exact one-to-one comparison of the results. To facilitate such future work, we share our models and data and are making them available to the academic community.
When comparing the two machine learning models NN and XGB, both models obtained comparable results though the Deep Learning models consistently outperformed the XGBoost-based ones. This is possibly due to the large amount of training data and the strong capacity of NN to learn complex non-linear patterns and memorize information from the training data. It is important to note that the NN models required significantly more time to train.
The future (CMIP6) model’s performance was inferior to the ERA5 as expected due to fewer input features and coarser resolution. However, this model still obtains good results and can be used to be applied on future data.
Atmospheric processes’ spatial and temporal scales are related. This is manifested in the feature importance that differs for the daily vs. hourly models. ERA5 coarse temporal resolution (daily) Ta values are influenced by 9 km resolution ERA5 features, i.e., temperature and wind U (east–west) component (Figure 8a), while the fine temporal resolution (hourly, Figure 8b) Ta values are influenced by fine spatial resolution features that capture the local conditions, i.e., topography and NDVI. LST is the third feature of importance in both models.
The diurnal variations of RMSE over TOD (Figure 5a) show a peak at sunrise (6 a.m.) when the maximal effect of nocturnal radiative cooling occurs. It is related to the spatial distribution of the meteorological stations where stations in rural areas are strongly affected, while most other stations (in proximity to urban areas) are less prone to this effect due to the urban heat island effect. On top of that, stations in low altitudes, especially in valleys, will experience in clear sky nights much lower temperatures than others in higher altitudes or alternatively proximity to the seashore. The seasonal variations of RMSE over DOY (Figure 5b and Figure 6) show large variations in the spring and autumn when the synoptic circulation patterns change from steady summer patterns [24] to more variable winter patterns.
In terms of runtime, the models run on a server running Rocky 9.3 Linux with an Intel(R) Xeon(R) E5-2650 v4 2.20 GHz CPU, 128 GB RAM and an NVIDIA GTX1080Ti GPU. Code run using Python version 3.9.18, keras 3.1.1 (for the NN models) and scikit-learn 1.4.1 (for the XGBoost models). The XGBoost hourly models took on average ~10 s, while the NN models took roughly 20 min to run. Similarly, the running time for the XGBoost daily models took less than 2 s to train the models, while the NN models required over a minute to run.
4.3. Methodology
Results when applying the LOGO evaluation methodology reveal higher RMSE (lower model precision) compared to the evaluation based on the conventional train/test approach as frequently employed in prior studies. It seems as if, despite the exclusion of station-specific features, our models demonstrate challenges in achieving robust generalization to unseen data points. This underscores the importance of adopting the LOGO methodology for reporting downscaling evaluation results. It also underscores the need for further research aimed at enhancing the adaptability of machine learning models to improve their generalization capabilities in such settings.
5. Conclusions
In this study, we successfully addressed the limitations of coarse spatial resolution global climate models, such as ERA5 and CMIP6, through the implementation of machine learning-driven downscaling techniques to enhance the resolution of near-surface air temperature (Ta) data. Leveraging a diverse array of features, including satellite data, climate model outputs, and digital elevation models, we developed accurate downscaling models, with the Deep Learning model proving most effective. The downscaled Ta is sensitive to small scale topographic features and to the effects of land cover that are missing from the larger scale climate models’ Ta (ERA5, CMIP6), which is very much needed for many applications such as climate services.
We strongly advocate for the adoption of the “leaving one group out” (LOGO) evaluation methodology when testing and reporting model results, as it provides a robust validation approach enhancing the reliability of findings in climate-related studies. Additionally, we are committed to sharing our models and data with the academic community, facilitating further research and a deeper understanding of local climate dynamics. These resources offer invaluable insights for climate adaptation strategies and informed decision-making processes. The corresponding code and data of this work are publicly shared online.
Author Contributions
Conceptualization, A.B. and I.M.L.; methodology, A.B., O.G. and I.M.L.; software, A.B.; validation, A.B., O.G. and I.M.L.; formal analysis, A.B., O.G. and I.M.L.; investigation, A.B., O.G. and I.M.L.; resources, A.B. and I.M.L.; data curation, A.B.; writing—original draft preparation, A.B., O.G. and I.M.L.; writing—review and editing, A.B., O.G. and I.M.L.; visualization, A.B.; supervision, O.G. and I.M.L.; project administration, I.M.L.; funding acquisition, O.G. and I.M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Chief Scientist of the Israeli Ministry of Agriculture, grant numbers 20-01-0058 and 18-17-0012.
Data Availability Statement
The code and data for this work are available at https://github.com/estipollak/Downscaling-Near-Surface-Air-Temperature accessed on 26 March 2024).
Acknowledgments
The authors thank Esti Polak for her assistance in organizing the code and making it suitable to be publicly available on GitHub.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- De Natale, F.; Alilla, R.; Parisse, B.; Nardi, P. A bibliometric analysis on drought and heat indices in agriculture. Agric. For. Meteorol. 2023, 341, 109626. [Google Scholar] [CrossRef]
- Li, D.; Nanseki, T.; Chomei, Y.; Kuang, J. A Review of Smart Agriculture and Production Practices in Japanese Large-Scale Rice Farming. J. Sci. Food Agric. 2022, 103, 1609–1620. [Google Scholar] [CrossRef] [PubMed]
- Dandrifosse, S.; Jago, A.; Huart, J.P.; Michaud, V.; Planchon, V.; Rosillon, D. Automatic quality control of weather data for timely decisions in agriculture. Smart Agric. Technol. 2024; in press. [Google Scholar] [CrossRef]
- Zhou, B.; Erell, E.; Hough, I.; Rosenblatt, J.; Just, A.C.; Novack, V.; Kloog, I. Estimating near-surface air temperature across Israel using a machine learning based hybrid approach. Int. J. Climatol. 2020, 40, 14. [Google Scholar] [CrossRef]
- Tsao, T.M.; Hwang, J.-S.; Chen, C.-Y.; Lin, S.-T.; Tsai, M.-J.; Su, T.-C. Urban climate and cardiovascular health: Focused on seasonal variation of urban temperature, relative humidity, and PM2.5 air pollution. Ecotoxicol. Environ. Safety 2023, 263, 115358. [Google Scholar] [CrossRef] [PubMed]
- Di Napoli, C.; Barnard, C.; Prudhomme, C.; Cloke, H.L.; Pappenberger, F. ERA5-HEAT: A global gridded historical dataset of human thermal comfort indices from climate reanalysis. Geosci. Data J. 2021, 8, 2–10. [Google Scholar] [CrossRef]
- Thrasher, B.; Wang, W.; Michaelis, A.; Melton, F.; Lee, T.; Nemani, R. NASA Global Daily Downscaled Projections, CMIP6. Sci. Data 2022, 9, 262. [Google Scholar] [CrossRef]
- Lensky, I.M.; Dayan, U.; Helman, D. Synoptic circulation impact on the near-surface temperature difference outweighs that of the seasonal signal in the Eastern Mediterranean. J. Geophys. Res. Atmos. 2018, 123, 11333–11347. [Google Scholar] [CrossRef]
- Lensky, I.M.; Dayan, U. Satellite observations of land surface temperature patterns induced by synoptic circulation. Int. J. Climatol. 2015, 35, 189–195. [Google Scholar] [CrossRef]
- Hemond, H.F.; Fechner, E.J. Chemical Fate and Transport in the Environment; Academic Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Zhang, T.; Zhou, Y.; Zhao, K.; Zhu, Z.; Chen, G.; Hu, J.; Wang, L. A global dataset of daily maximum and minimum near-surface air temperature at 1 km resolution over land (2003–2020). Earth Syst. Sci. Data 2022, 14, 5637–5649. [Google Scholar] [CrossRef]
- Sebbar, B.-E.; Khabba, S.; Merlin, O.; Simonneaux, V.; El Hachimi, C.; Kharrou, M.H.; Chehbouni, A. Machine-Learning-Based Downscaling of Hourly ERA5-Land Air Temperature over Mountainous Regions. Atmosphere 2023, 14, 610. [Google Scholar] [CrossRef]
- Afshari, A.; Vogel, J.; Chockalingam, G. Statistical Downscaling of SEVIRI Land Surface Temperature to WRF Near-Surface Air Temperature Using a Deep Learning Model. Remote Sens. 2023, 15, 4447. [Google Scholar] [CrossRef]
- Mouatadid, S.; Easterbrook, S.; Erler, A.R. A Machine Learning Approach to Non-uniform Spatial Downscaling of Climate Variables. In Proceedings of the IEEE International Conference on Data Mining Workshops, ICDMW, New Orleans, LA, USA, 18–21 November 2017; pp. 332–341. [Google Scholar] [CrossRef]
- Karaman, Ç.H.; Akyürek, Z. Evaluation of near-surface air temperature reanalysis datasets and downscaling with machine learning based Random Forest method for complex terrain of Turkey. Adv. Space Res. 2023, 71, 5256–5281. [Google Scholar] [CrossRef]
- Arumugam, P.; Patel, N.R.; Kumar, V. Estimation of air temperature using the temperature/vegetation index approach over Andhra Pradesh and Karnataka. Environ. Earth Sci. 2022, 81, 79. [Google Scholar] [CrossRef]
- Lensky, I.M.; Dayan, U. Detection of Finescale Climatic Features from Satellites and Implications for Agricultural Planning. Bull. Amer. Meteor. Soc. 2011, 92, 1131–1136. [Google Scholar] [CrossRef]
- 10 & 1-Minutes Data (API). Israel Meteorological Service. Available online: https://ims.gov.il/en/ObservationDataAPI (accessed on 26 March 2023).
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Shiff, S.; Helman, D.; Lensky, I.M. Worldwide continuous gap-filled MODIS land surface temperature dataset. Sci. Data 2021, 8, 74. [Google Scholar] [CrossRef]
- Mo, Y.; Xu, Y.; Liu, Y.; Xin, Y.; Zhu, S. Comparison of gap-filling methods for producing all-weather daily remotely sensed near-surface air temperature. Remote Sens. Environ. 2023, 296, 113732. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Chakraborty, D.; Hazem, E. Advanced machine learning techniques for building performance simulation: A comparative analysis. J. Build. Perform. Simulation 2018, 12, 193–207. [Google Scholar] [CrossRef]
- Bitan, A.; Sa’Aroni, H. The horizontal and vertical extension of the Persian Gulf pressure trough. Int. J. Climatol. 1992, 12, 733–747. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).