Next Article in Journal
Arctic Greening Trends: Change Points in Satellite-Derived Normalized Difference Vegetation Indexes and Their Correlation with Climate Variables over the Last Two Decades
Previous Article in Journal
Estimation and Evaluation of 15 Minute, 40 Meter Surface Upward Longwave Radiation Downscaled from the Geostationary FY-4B AGRI
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 16
Issue 7
10.3390/rs16071159
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Derivation of 3D Coseismic Displacement Field from Integrated Azimuth and LOS Displacements for the 2018 Hualien Earthquake

by
Li-Chieh J. Lin
1,
Ray Y. Chuang
1,*,
Chih-Heng Lu
1,2,
Kuo-En Ching
3 and
Chien-Liang Chen
4
1
Department of Geography, National Taiwan University, Taipei 106, Taiwan
2
Research Center for Environmental Changes, Academia Sinica, Taipei 115, Taiwan
3
Department of Geomatics, National Cheng Kung University, Tainan 701, Taiwan
4
Geological Survey and Mining Management Agency, Ministry of Economic Affairs, New Taipei City 235, Taiwan
*
Author to whom correspondence should be addressed.
Remote Sens. 2024, 16(7), 1159; https://doi.org/10.3390/rs16071159
Submission received: 12 January 2024 / Revised: 22 February 2024 / Accepted: 20 March 2024 / Published: 27 March 2024
Browse Figures
Versions Notes

Abstract

:
A 3D surface deformation field for an earthquake can aid in understanding fault behaviors and earthquake mechanisms. However, SAR-based 3D surface deformation estimates are often limited by insufficient observations and hampered by various error sources. In this study, we demonstrate the derivation of a 3D coseismic displacement field from different InSAR processing algorithms. The azimuth displacements from Multiple Aperture Interferometry (MAI) and Pixel Offset Tracking (POT) were integrated to ensure reliable displacements at low coherent areas. The 3D displacement field was inverted pixel-by-pixel by Line-of-Sight (LOS) displacement and integrated azimuth displacement. The results showed that MAI and POT could compensate for the weaknesses of each algorithm. Also, pixels with less than three sets of observations showed higher noise levels. Such noisy pixels were removed by a denoising criterion proposed herein. For the vertical direction, the proportion of pixels inverted with two sets of azimuth and one set of LOS displacements was 26.1%. After denoising, the proportion dropped to 2.4% due to the insufficiency of LOS displacements. This shows that the viewing angle influences the overall performance of 3D surface displacement inversion. Implementing various displacement vectors should reduce such limitations.

Graphical Abstract

1. Introduction

Earthquakes are major hazardous events due to releasing accumulated crustal strain with destructive surface motion, causing building collapse and numerous casualties [1]. In addition to the heavy fatalities, earthquakes are also one of the main processes resulting in surface deformation and significant topographic changes [2,3]. Currently, such coseismic deformation is commonly estimated by terrestrial geodesy [4,5,6] and space-borne SAR imagery, which was first demonstrated for the 1992 Landers earthquake by measuring the coseismic surface displacements along the Line-of-Sight (LOS) direction [7]. Since then, SAR imagery has become one of the main observational approaches for monitoring varied crustal activities [8,9,10,11].
In order to characterize coseismic deformation and fault behaviors, a 3D coseismic displacement field can help to reveal the overall deformation pattern associated with the faulting characteristics [12,13,14]. In addition to the surface displacements due to fault movement, such deformation often exhibits complicated deformation behaviors such as off-fault deformation [15,16] and multi-fault triggering [17,18]. Having an accurate 3D surface displacement field can help to better assess the effect of an earthquake event, making it crucial for seismic hazard mitigation [12].
To obtain a 3D coseismic displacement field, it takes more than one InSAR processing algorithm and/or one interferometric pair. Differential Interferometric Synthetic Aperture Radar (DInSAR) estimates surface displacements along the LOS direction, which is highly sensitive to the deformation in the east–west (EW) and up–down (UD) directions but less resolvable in the north–south (NS) direction [7]. Therefore, it is inadequate to solve for 3D displacements by solely using LOS measurements. An exceptional case is the 2002 Nenana Mountain earthquake due to oblique viewing angles at high latitudes [19]. Along with the development of the DInSAR technique, Pixel Offset Tracking (POT), Multiple Aperture Interferometry (MAI), and Burst Overlap Interferometry (BOI) were consecutively proposed to detect surface displacements along the azimuth direction, which are highly sensitive to the NS direction, little to the EW direction, and free of vertical motion [20,21,22]. Combining at least three sets of observations in the range and range directions, one can invert the 3D displacement adequately [23].
In addition to the insufficient observations, different errors may affect the resolved 3D surface displacements. Algorithms relying on the phase property of radar echoes often have accuracy as high as a few centimeters [7,22,24]. However, for places with low or incoherent backscatters, such algorithms might yield erroneous results or fail to resolve surface displacements. On the other hand, algorithms such as POT, which is more amplitude-dependent, could still correctly resolve surface displacements even with low pixel coherence [25]. Nevertheless, the theoretical accuracy of POT is a fraction of the pixel size [20]; thus, it often falls in the range of dozens of centimeters. Therefore, it is also important to examine how coherence affects the estimates of 3D coseismic displacements.
In this study, we took the 2018 Hualien, Taiwan, earthquake as a test area to systematically examine the ability to resolve 3D coseismic displacements by combining different SAR algorithms and the influence of pixel coherence in the 3D estimates. Because the Hualien earthquake has been well-studied and its surface deformation has been constrained by geodetic data, it provides an opportunity for us to examine different algorithms for 3D deformation [26,27,28,29,30,31,32]. We then proposed a method to integrate observations derived from different methods for resolving 3D coseismic deformation. Additionally, for the apparent noisy pixels shown in the displacement results, we proposed a denoising criterion in this study for noise removal.

2. Data and Materials

2.1. SAR Images

In this study, we used ALOS-2 and Sentinel-1 SAR images (Table 1) to generate 3D surface displacements. The ALOS-2 and Sentinel-1 data were provided by the Japan Aerospace Exploration Agency (JAXA) and European Space Agency (ESA), respectively. ALOS-2 images were the main data source for surface displacement recovery due to the longer wavelength (~24.1 cm), which lowers the effects of decorrelation and phase aliasing. On the contrary, Sentinel-1 images have a wavelength of about 5.6 cm, which was reported as not successfully resolving the surface displacement of the 2018 Hualien earthquake by using the DInSAR technique [27]. The imaging mode of Sentinel-1 is Terrain Observation with Progressive Scans (TOPS), which acquires data in overlapping bursts. These overlapping bursts could be used to solve for surface displacement along the azimuth direction through the BOI algorithm [22]. However, the overlapping area was only a few kilometers wide, which was too narrow to be used in later 3D displacement inversion.

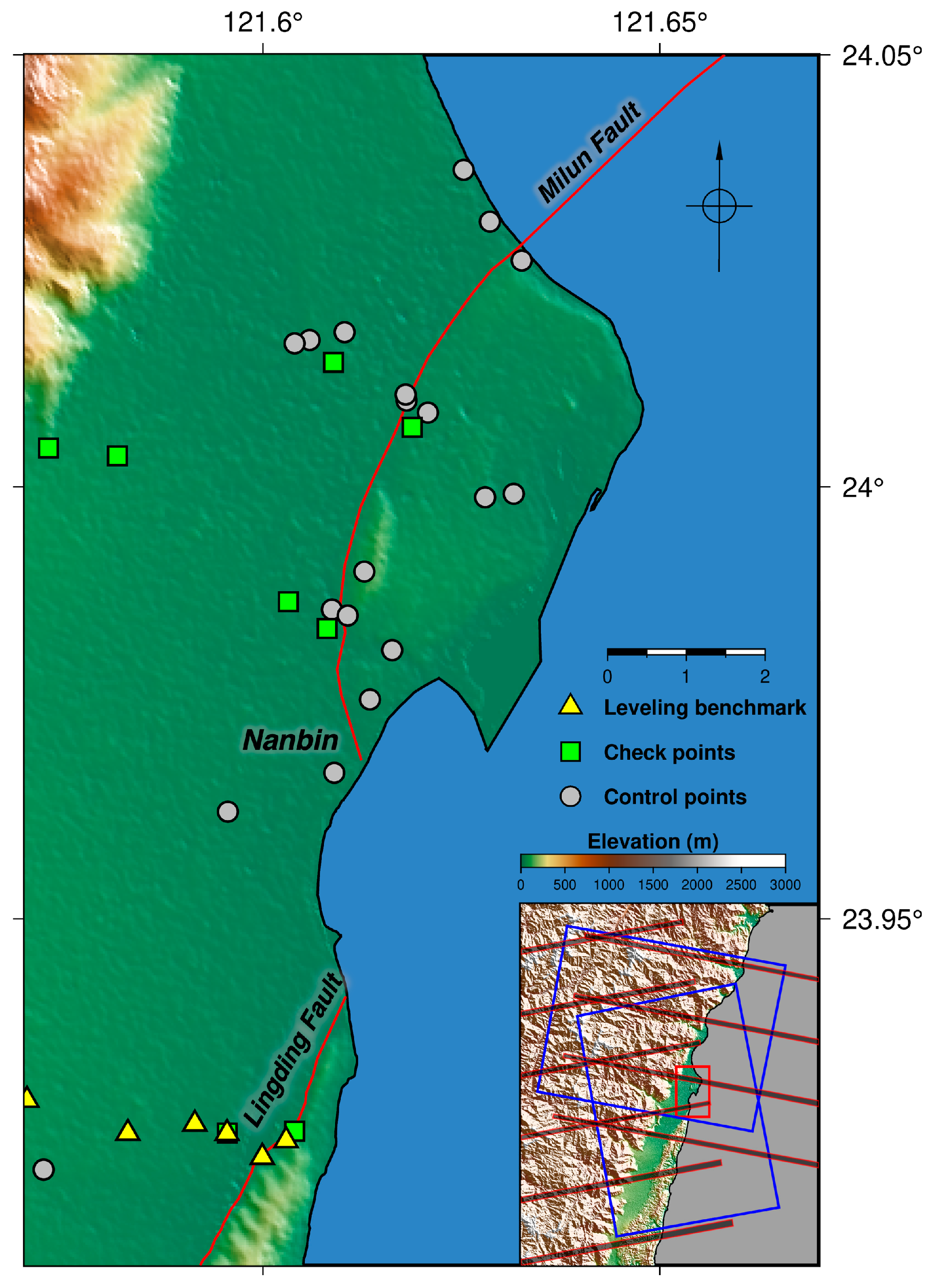
2.2. GPS and Leveling Data

The distribution of GPS stations, leveling benchmarks, SAR image coverage, and inverted displacement area is shown in Figure 1. GPS data served as control points and check points to constrain SAR-derived coseismic displacements and to examine the overall RMSE, respectively. The GPS data were provided by the Geological Survey and Mining Management Agency (GSMMA) in Taiwan and some were collected from [27]. Continuous GPS time series were fitted with a polynomial function to estimate the secular velocity, coseismic, postseismic displacement, and seasonal variations [33]. The coseismic component that resided in campaign ones was extracted by subtracting the long-term trend estimated with linear regression. We chose GPS stations that served as control points relatively even in the SAR image coverage to ensure good displacement constraints.
Leveling data were also provided by GSMMA with annual benchmark measurements. This particular survey line was exceptionally important for detecting the coseismic motion across surface rupture. The signals induced by tectonic motion were estimated and eliminated by the secular GPS velocity from the nearest station. The coseismic displacement was calculated by the difference between post- and pre-seismic benchmark records.

3. Methods

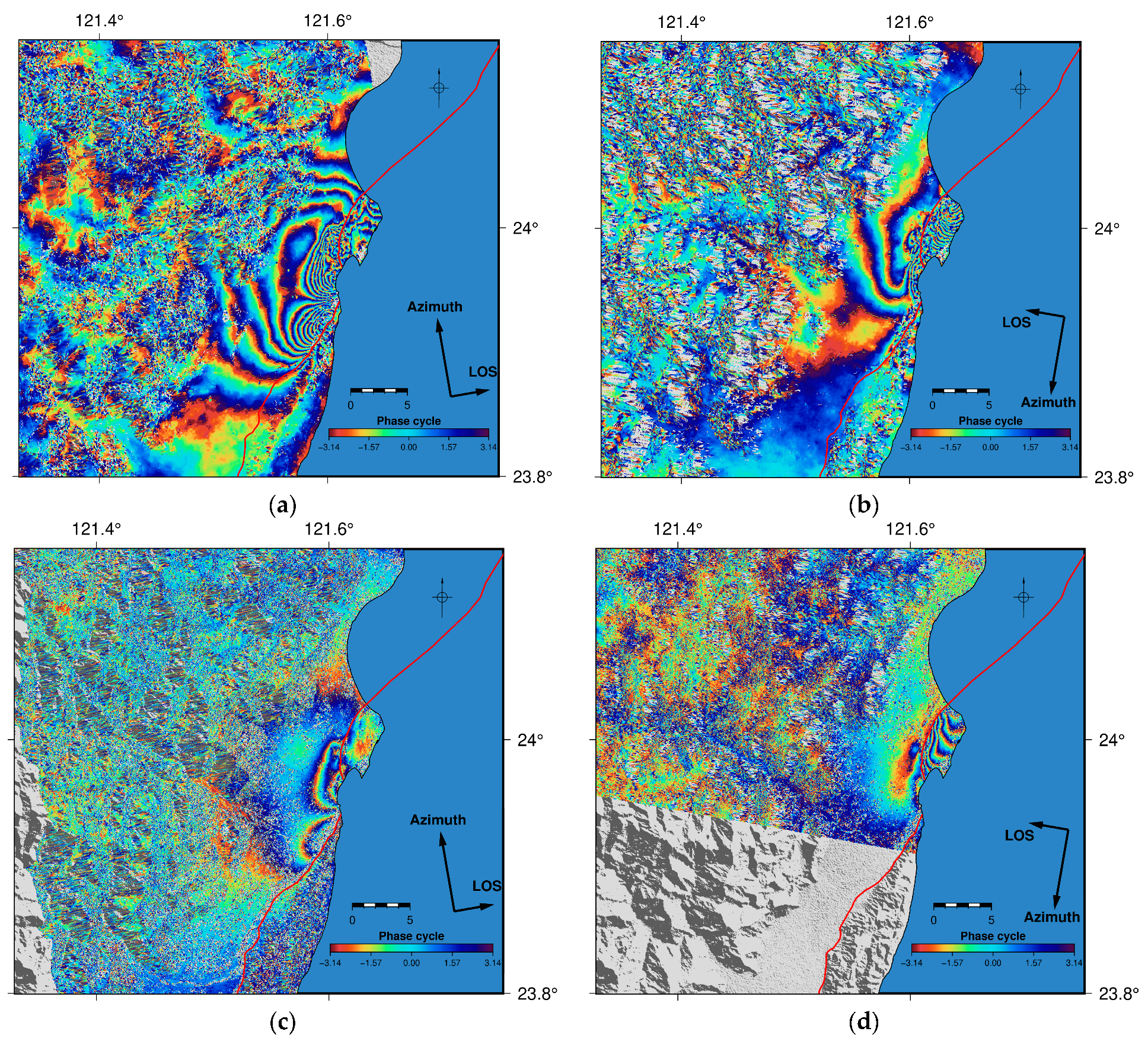
3.1. SAR-Based Surface Displacement Retrieval

We used open-source software GMTSAR (v6.1) [35,36] to process SAR images. ALOS-2 images were processed with DInSAR, MAI, and POT algorithms, and the ionospheric error was removed by split-spectrum method with semi-gird-searched filtering size [37,38] (Figure S1). No apparent tropospheric-associated pattern was observed in either interferogram. The zenith wet delay model had little to no displacement gradient within the research site. Therefore, taking both the interferograms and the zenith wet delay model into account, the tropospheric error was assumed negligible. We split half of the aperture to form forward-looking and backward-looking images to calculate the azimuth displacements based on the double difference of forward and backward interferograms [21]. As for POT, it is always a trade-off between image size and search window size. We used grid search for the optimal input parameters for POT by calculating the resulting RMSE between SAR-derived displacements and GPS observations (Figure S2). Lastly, for the implementation of BOI on Sentinel-1 images, we calculated the phase shift within the burst overlapping area along the azimuth direction with the Enhanced Spectral Diversity method (ESD). Assuming no clock error or ionospheric perturbation, the resulting azimuth shift should be mainly from coseismic motion [39]. However, the coverage of the BOI result was not large enough to reveal the overall deformation pattern (Figure 2); therefore, we did not further incorporate the BOI result either for 3D displacement inversion or for azimuth displacement integration.

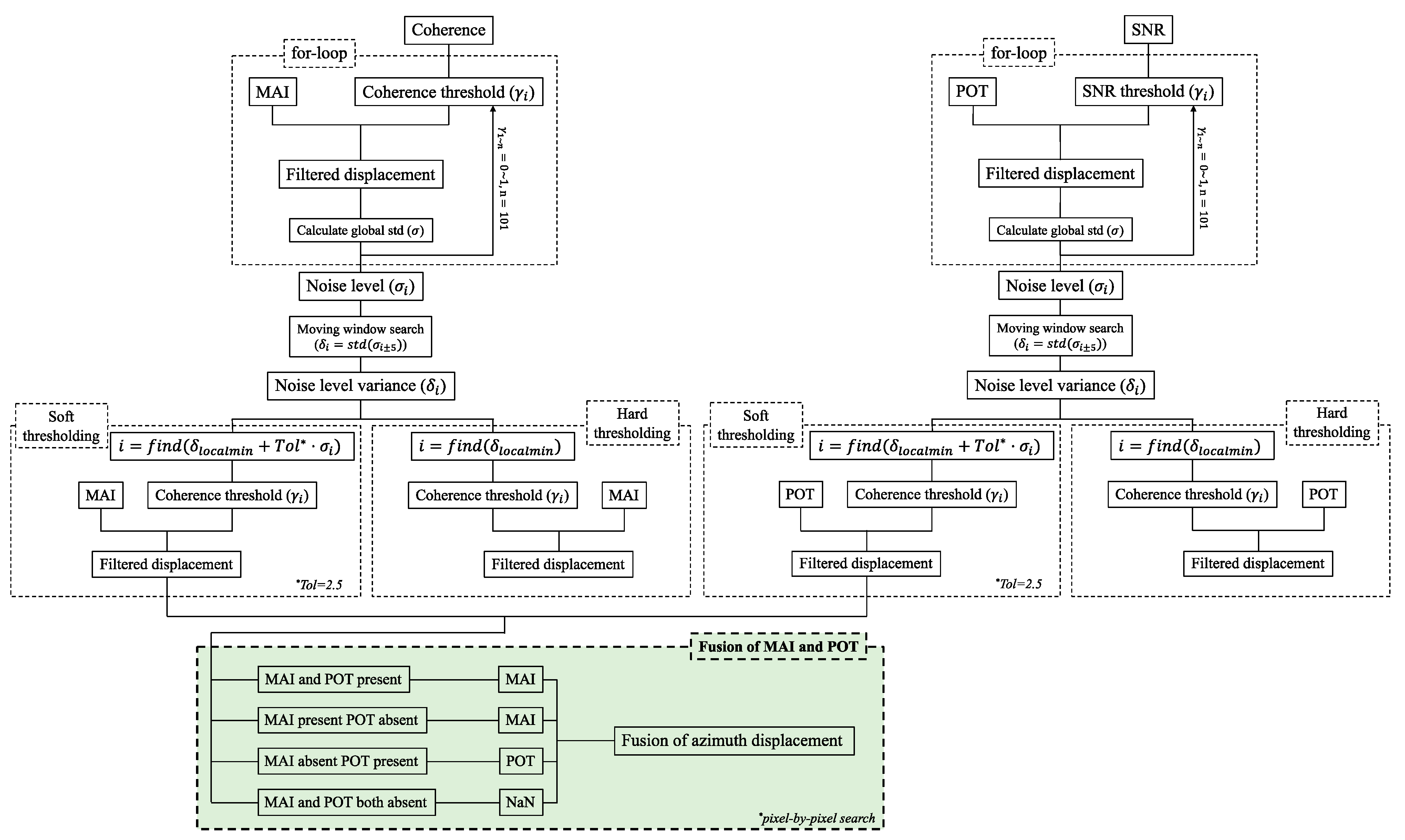
3.2. Azimuth Displacement Integration

Azimuth displacements were obtained from the MAI and POT algorithms using ALOS-2 images. The azimuth displacement integration process is shown in Figure 2. Firstly, the noisy pixels in raw azimuth displacement from MAI and POT were masked out with interferometric coherence and Signal-to-Noise ratio (SNR), respectively. We determined the coherence and SNR thresholds by exploring the characteristics of the global standard deviation from the remaining pixels given different masking thresholds. We performed 101 times of iterations and individually masked out pixels using thresholds from 0 to 1 with increments of 0.01. For each iteration, the remaining pixels were used to calculate the global standard deviation, also named noise level (σ). Then, the noise level would be further used to determine the noise level variance (δ) by calculating the standard deviation of noise levels with a moving window size of 11. Each noise level variance was determined by the standard deviation of 5 noise levels before and after the current step. Finally, the threshold was determined by the local minima of the noise level variance series (Figure 3 insets). It is noted that the goal of this initial masking was to reduce noise and at the same time to maintain as much data as possible. Therefore, we adopted “Soft-thresholding” to keep more data available by accepting a tolerance of noise level. For our case here, it was set to 2.5 for both MAI and POT results.
After masking out the noisy pixels, all POT results were upsampled to the same spatial resolution as MAI ones. This step was to make the two datasets have the same spatial resolutions. However, the upsampling might introduce artificial high-frequency errors. These induced errors were greatly removed by the denoising criterion proposed in this study. It is discussed in further detail in Section 4.3. The integration process was completed in a pixel-by-pixel sense, whereby, if both MAI and POT results were present in one pixel, then the MAI result would be used. If only one displacement result was present, then it remained unchanged. Lastly, if both results were absent, then the pixel would be assigned NaN. The MAI result was more favored due to its higher theoretical accuracy than POT’s. This integration choice was to ensure higher accuracy for the final integrated azimuth displacement field.

3.3. 3D Displacement Inversion

The 3D displacement inversion was completed by using the method proposed in [23]. Since the LOS direction consisted of the EW, NS, and UD directions, the LOS vector could be decomposed into the three according vectors given sufficient constraints. The azimuth displacements were only sensitive to horizontal motion, which could only be decomposed into the EW and NS directions. A simple linear system can be constructed based on satellite viewing and orbiting geometry. For our case shown here, which was an overdetermined system, the final solution was solved using least-squares optimization.
[ A z i A A z i D L O S A L O S D ] = [ s i n α A c o s α A 0 s i n α D c o s α D 0 − s i n θ A c o s α A − s i n θ D c o s α D s i n θ A s i n α A s i n θ D s i n α D c o s θ A c o s θ D ] ⋅ [ E N U ]
where subscripts A and D denote ascending and descending tracks. α is the satellite inclination angle, and θ is the satellite looking angle.
However, since we completed the inversion in a pixel-by-pixel sense, there were not always four equations for solving the three unknowns at every pixel. If only three equations were present, then the solution would be unique and could be solved sufficiently. If there were only two azimuth displacements, then only the EW and NS displacements would be solved. Similarly, only the EW and UD displacements would be solved if the pixel contained solely LOS displacements. Here, since the LOS displacements were not sensitive to the NS movements, the NS component was neglected, leaving two unknowns to be solved. Lastly, we discarded pixels with one azimuth and one LOS displacement or one displacement only because they were not invertible.

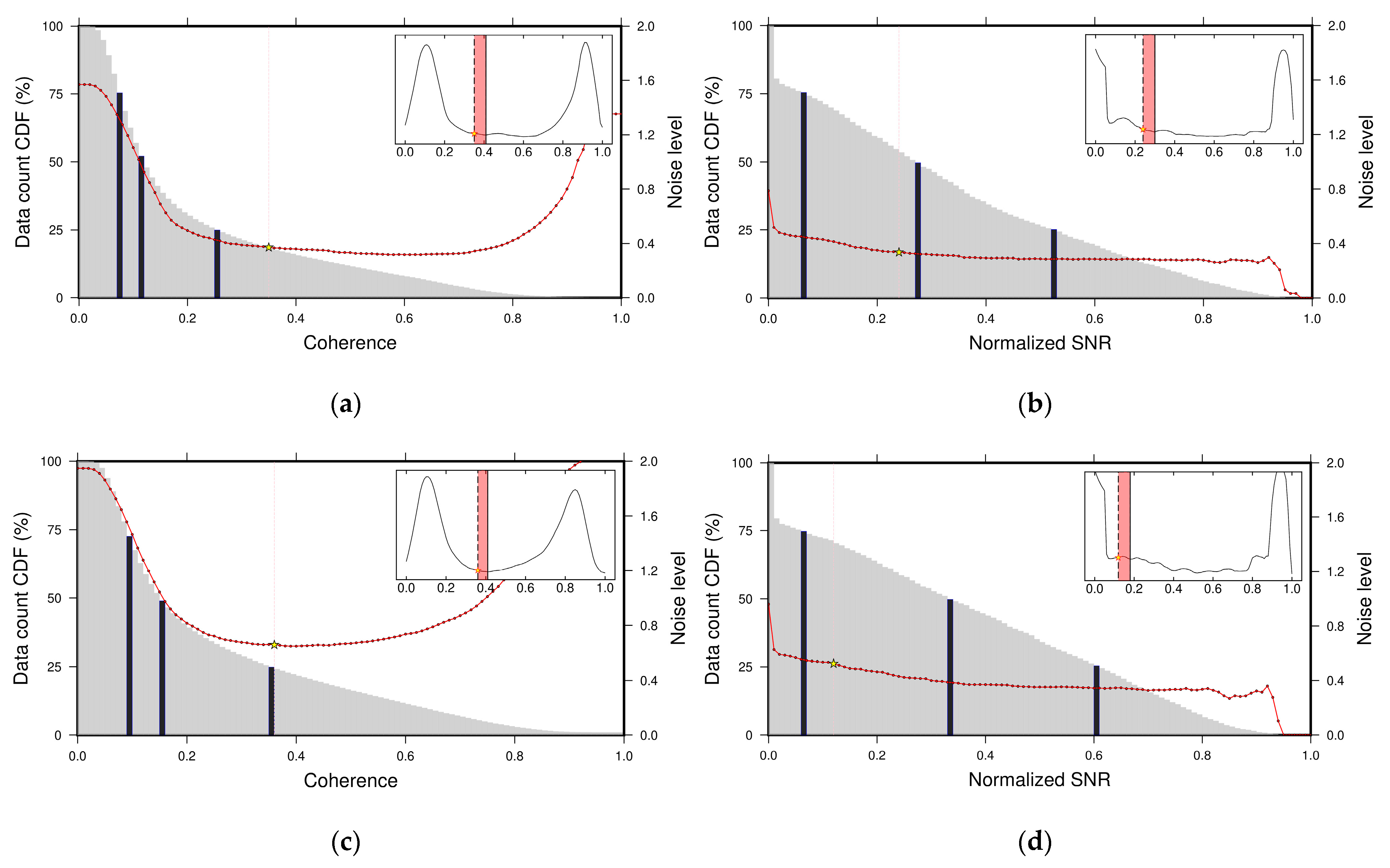
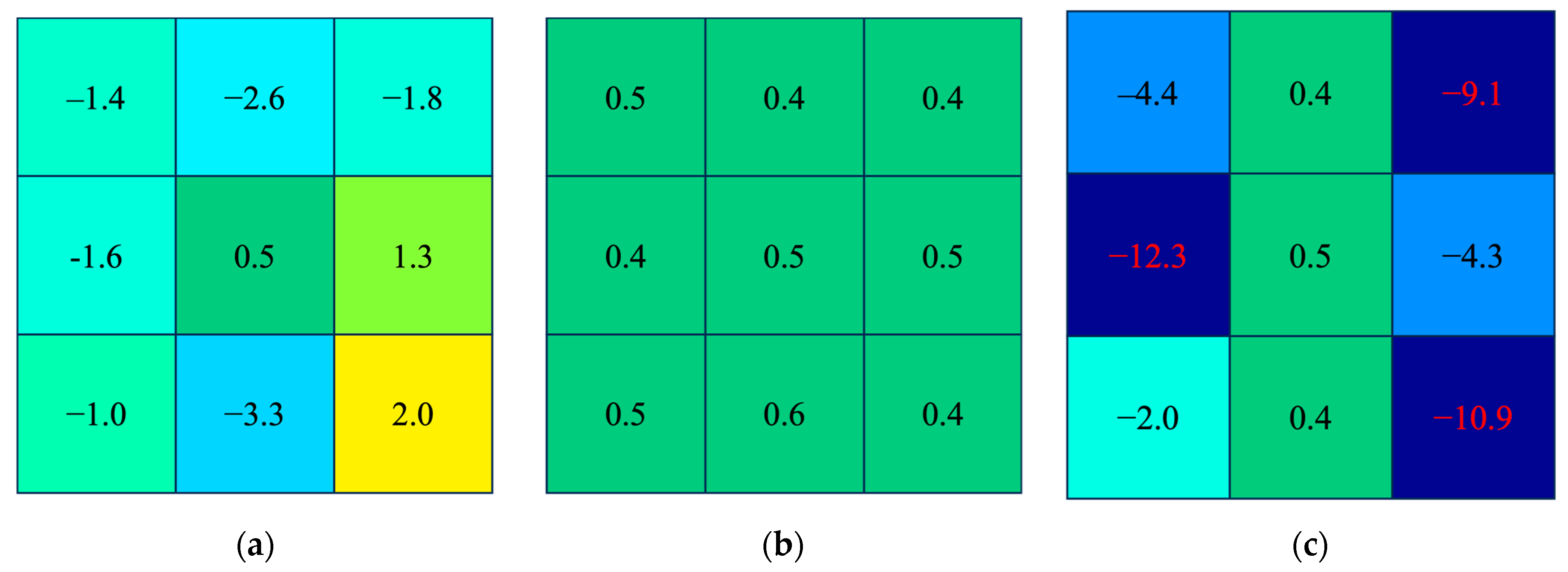
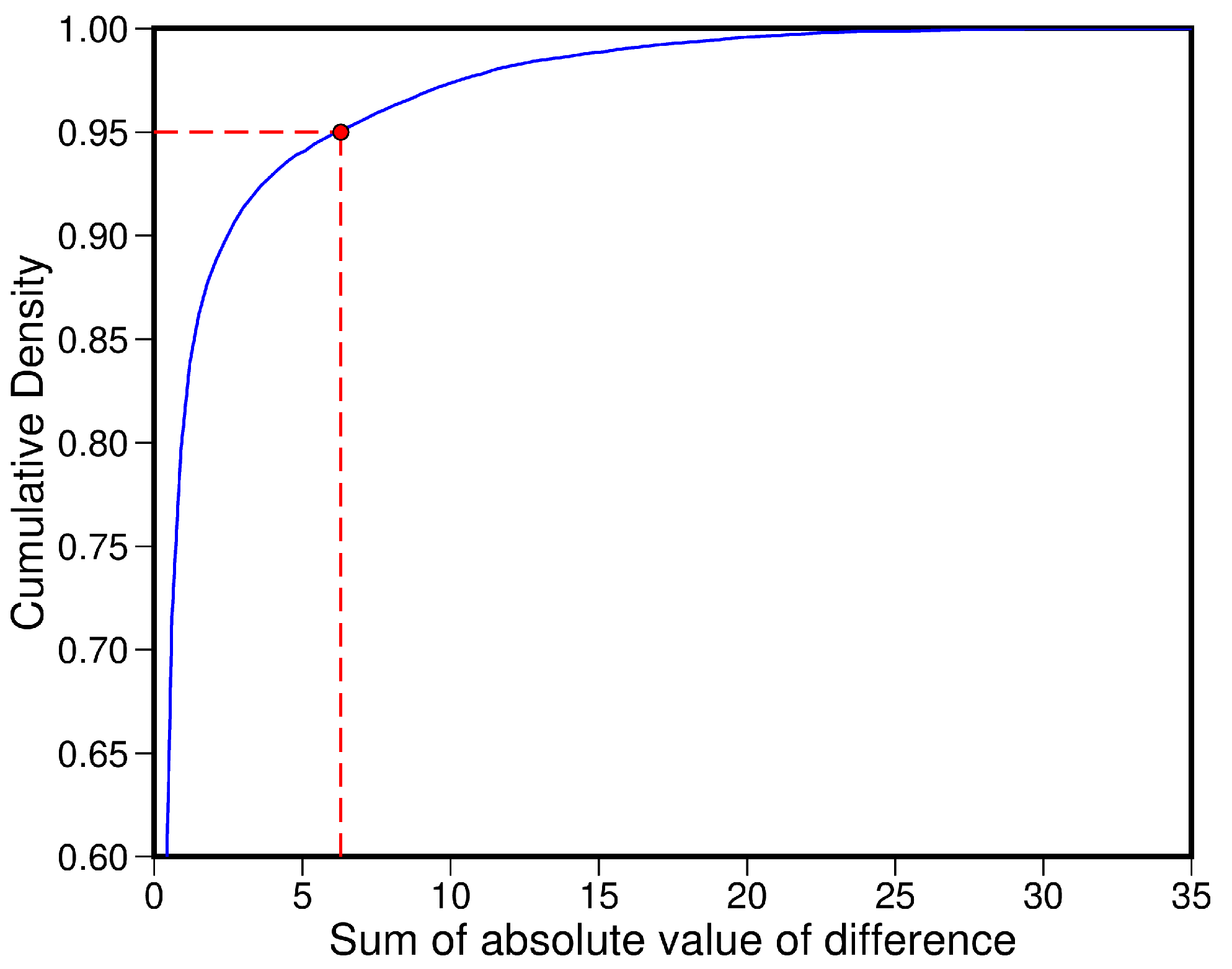
3.4. Denoising Criterion

SAR-based displacement fields often contained noise, which was commonly observed in MAI and POT results. Figure 4a,c are examples of noisy pixels observed in displacement fields. Figure 4b is the noise-free area where all pixel values are similar, while the left and right panels show areas containing noise that have a random distribution of pixel values or unrealistic values. Obviously, a simple denoising strategy like masking unrealistic values would not be enough since noisy pixels did not necessarily have unrealistic values. Manually removing noise would be too time-consuming and could introduce a certain degree of human bias. Therefore, it cannot be used for operational use due to the lack of automation and objectivity. Median filters or equivalent low-pass filters could cope with noise effects by smoothing out the overall image, but the filtering would blur the overall image, which would obscure the fault traces that are essential for recognizing where the fault boundary was.
Here, we proposed a novel method for removing noise and maintaining the spatial resolution without any low-pass filtering. First, a moving window of self-defined (we set the window size to 3 × 3) size slid through the whole image to calculate the sum of absolute value of difference between the center pixel with its adjacent pixels at each step. The sum of difference (γ) was provided by
γ = ∑ ( i , j ) ( 3 , 3 ) | N 22 − N i j |
where N is the pixel value, subscripts i,j are the row and column indices.
The sum of difference indicated whether the current pixel was a noise or a signal. If noise was dominant within the window, then γ would be large. On the other hand, γ would be small if the pixels in the current window had similar values. Therefore, the larger γ was, the noisier the pixel was. Next, we calculated the CDF of γ and took the value at 95% CDF as the masking threshold (Figure 5). Pixels with a sum of difference higher than the masking threshold would be masked out. Since the threshold was set at 95% CDF, approximately 5% of the data containing the most noise would be masked out. This denoising procedure was designed to be repeated until the noise was removed satisfactorily.

4. Results

4.1. SAR-Derived Surface Displacement

Coseismic interferograms are shown in Figure 6. Higher density of fringes is observed in the Sentinel-1 results due to the shorter radar wavelength (~5.6 cm). In contrast, ALOS-2 is an L-band SAR system, which has a wavelength nearly four times longer than the C-band, showing fewer fringes than Sentinel-1. Both interferograms could be used to extract surface displacement through phase unwrapping. However, previous studies showed that Sentinel-1 results were contaminated by phase aliasing and phase decorrelation, which would further induce phase unwrapping errors [27]. Therefore, we unwrapped interferograms from ALOS-2 to obtain the LOS displacement for both tracks.
The MAI, POT, and BOI results reveal coseismic surface motion along the azimuth direction (Figure 7). The deformation pattern agrees with both the faulting mechanism of the Milun and Lingding faults as well as the terrestrial geodetic survey after the earthquake occurrence [28,34]. The coseismic motion was sinistral along these two faults and was well-imaged by both Sentinel-1 and ALOS-2 images. However, BOI can only solve for the azimuth offset at the burst overlapping areas, which are only a few kilometers in width. Although the BOI result demonstrates sinistral motion, the coverage was insufficient for further 3D displacement inversions. Thus, the BOI displacements were discarded.

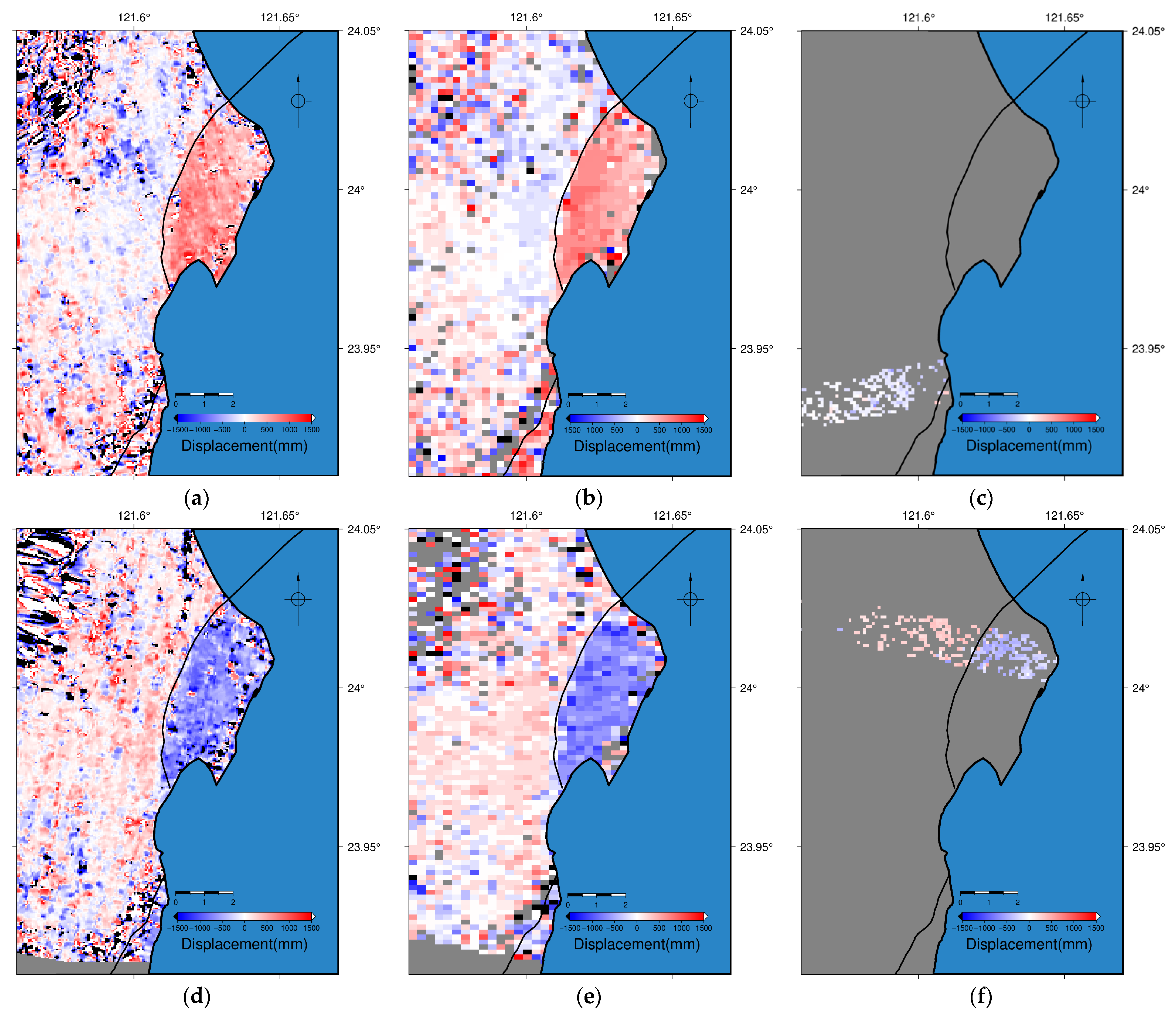
4.2. Integrated Azimuth Displacement

Integrated azimuth displacement was conducted via the method proposed in Section 3.2 using the MAI and POT results. The BOI results also revealed the azimuth offset; however, the coverage was not large enough for the integration stage. Figure 8 shows the integrated azimuth displacements for both ascending and descending tracks and the displacement type within each pixel. Urban areas often promise good surface displacement retrieval with their high interferometric coherence. On the other hand, places with low coherence, such as vegetated areas or mountainous regions, often prohibit correct displacement recovery. Therefore, the integrated azimuth displacement field contained MAI results mostly for the urban area in Hualien, and outskirts areas for POT ones, especially east of the Lingding fault.

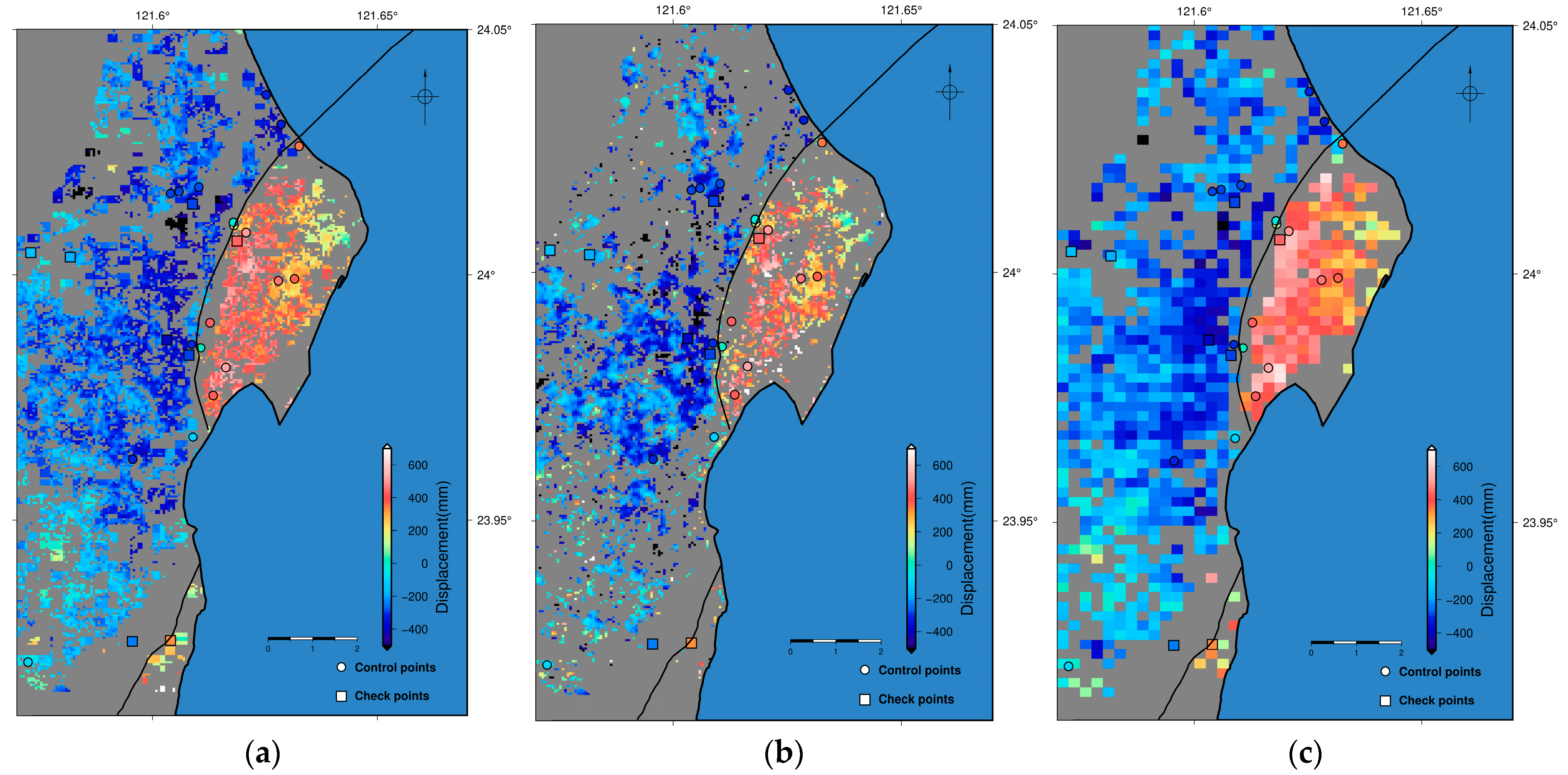
4.3. 3D Displacement Field

We decomposed the LOS and azimuth displacements using the method proposed by [12]. The 3D displacement was inverted with two LOS and two integrated azimuth displacements. Pixels that had less than four inputs were handled with the method elaborated in Section 3.3. Figure 9 shows the 3D displacement field, which contains high-frequency noise that resulted from the upsampled POT result. This noise was well-removed by the denoising criterion proposed in Section 3.4, with nine times for the EW direction, twelve times for the NS direction, and eight times for the UD direction. The iteration times were determined by the local minima of the noise levels. The artifacts were removed and the denoised displacement field showed a much cleaner and clearer deformation pattern. The hanging wall of the Milun fault showed clockwise rotational motion with vertical uplift. Left-lateral displacements were observed along the Milun and Lingding faults. Lastly, subsidence was observed in the Nanbin area.

5. Discussion

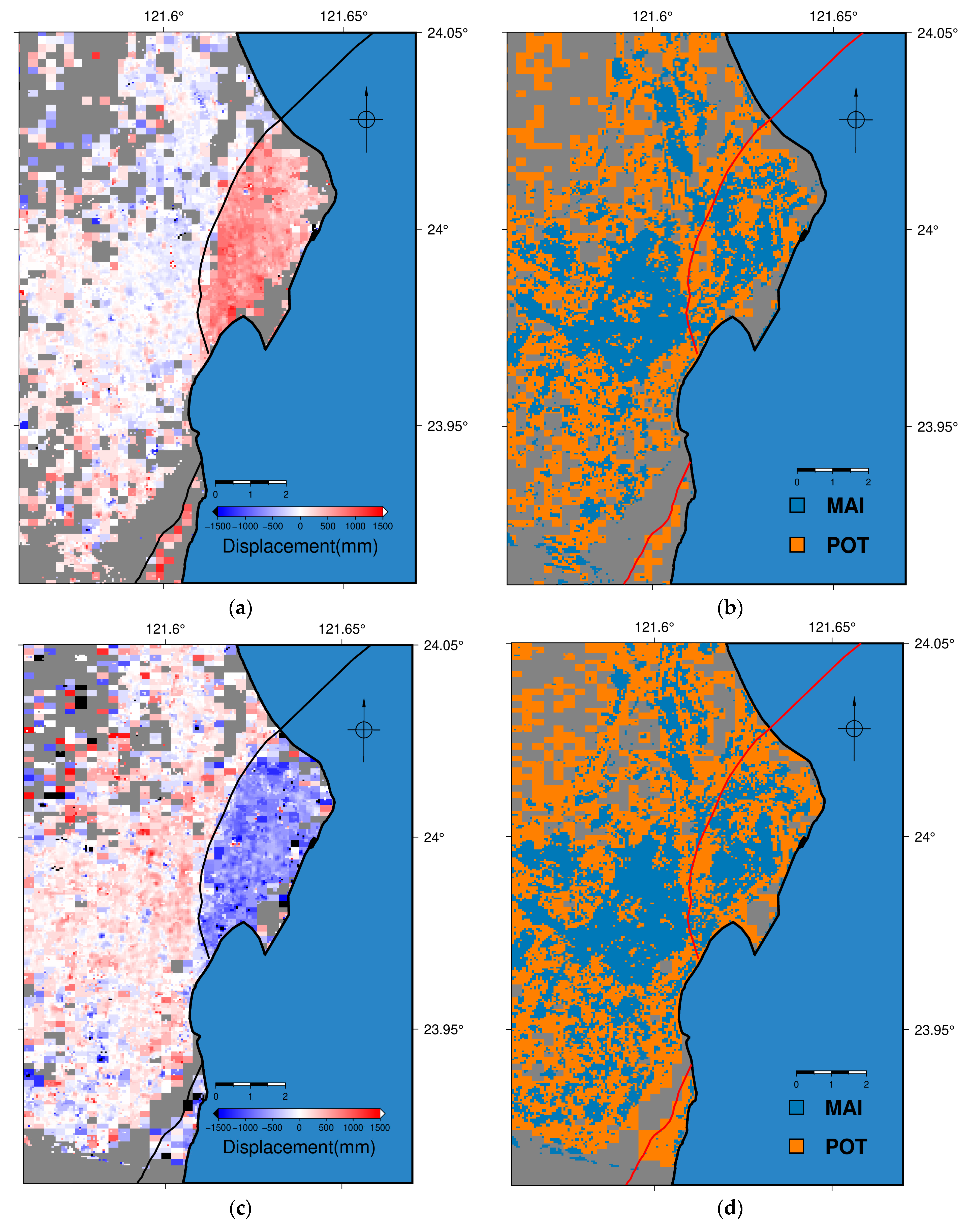
5.1. Comparison between Different Versions of 3D Displacement Fields

Aside from inverting the 3D displacement field with the LOS displacements and integrated azimuth displacements (Version 1), we created two other 3D displacement fields by using the LOS displacements derived from the MAI (Version 2) and derived from the POT (Version 3) methods (Figure 10). One distinct difference between Versions 1, 2, and 3 is the final spatial resolution. The difference is about four to five times finer for Version 1 and 2 than for Version 3 (Table 2). Typically, the POT algorithm involves pixel averaging to avoid extremely high spatial frequency noise. This would result in lower spatial resolution. Although all three versions of the 3D displacement field can capture the first-order deformation pattern, some details were obscured in Version 3 due to the low spatial resolution.
We estimated the uncertainties of the displacements in each direction by GPS displacements (Table 2). The result shows that the displacements in the EW and UD directions for all three versions have the lowest uncertainty compared with the displacements in the NS direction. It is expected and manifested by the high accuracy of DInSAR and the high proportion of the EW and UD directions contributing to the LOS displacement. The EW and UD displacements are highly LOS-dependent, while the NS displacements are highly aligned with azimuth displacement. Therefore, the uncertainty in the NS direction is higher than for the EW and UD components. It is noted that the EW error of Version 3 is abnormally high because of the sampling of unwanted noisy pixels when calculating the RMSE. The overall uncertainty in the EW direction in Version 3 should be less than 10 cm due to the dependence of the LOS displacements. Although MAI has a theoretical accuracy of a few to tens of centimeters [13], which is higher than the accuracy of the POT method, it shows that the NS uncertainty of Version 2 is larger than Version 3. There could be two possible reasons. The first one is that, in GMTSAR processing, a certain degree of filtering and averaging were conducted during the POT calculation. This would reduce the noise contribution, thus lowering the overall uncertainty. The second one is that, following the first reason, since there are more noisy pixels in MAI than POT, the higher uncertainty in the NS direction in Version 2 might result from sampling some noisy pixels while calculating RMSE based on GPS. Lastly, the uncertainty of Version 1 was a combined result of Versions 2 and 3, especially in the NS direction.
The first-order deformation pattern is consistent for all three versions of the NS displacements (Figure 11). Note that these NS displacements were GPS-constrained, so they appeared differently in Figure 9. There is a difference in the east of the Lingding fault. The NS displacements in the east of the Lingding fault were resolved more satisfactorily in Version 1 than in Versions 2 and 3 in terms of pixel coverage. The interferometric coherence is low in the east of the fault where much vegetation is present. Therefore, the low coherence prevented phase-related algorithms from successfully estimating 3D displacements at the specific region. In such conditions, POT could still yield good results since it is less affected by pixel coherence. By combining the POT and MAI results, one could both maintain the pixel resolution, which could portray the fault trace boundaries, and retain good displacement results at less coherent areas.

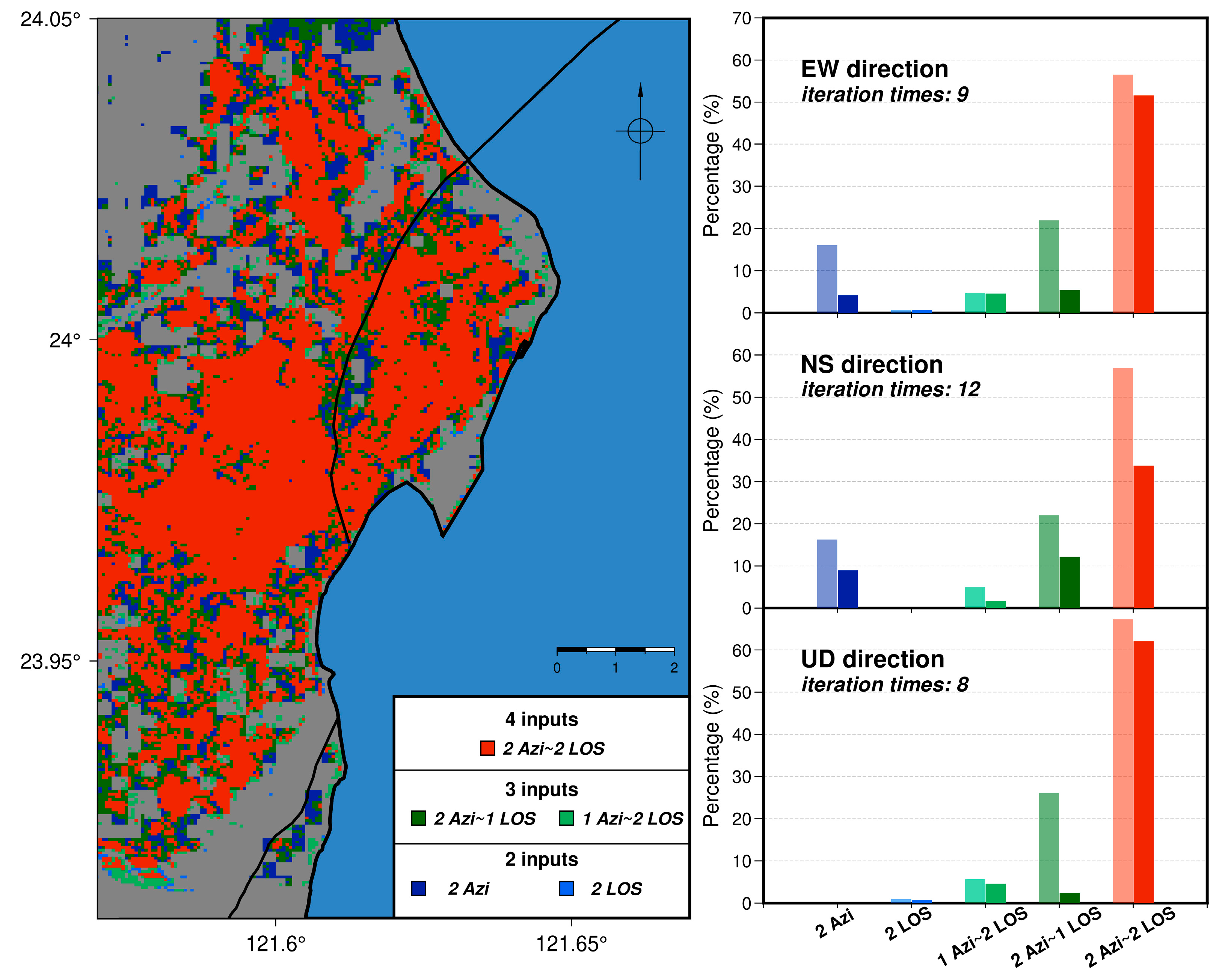
5.2. Performance of Denoising

The inverted 3D displacement fields are based on several combinations of inputs: two inputs (two Azi or two LOS), three inputs (two Azi + one LOS or one Azi + two LOS), and four inputs (two Azi + two LOS). Theoretically, pixels inverted from four inputs have more constraints than three inputs and two inputs. Figure 12 shows the inversion input for Version 1 and the proportion before and after denoising. More than half of the pixels were inverted from four inputs, around 20% were obtained from three inputs, and the rest were derived from two inputs. It should be noted that the UD direction could not be inverted from two azimuth displacements since the azimuth displacements contain no vertical motion. Therefore, the proportion for the UD direction by using two sets of azimuth displacements was 0. For the EW and UD directions, the denoised pixels were mostly derived from two and three sets of the inputs. Especially in the UD direction, pixels inverted from two sets of the azimuth displacements and one set of the LOS displacements were largely removed compared to those obtained from one set of the azimuth displacements and two sets of the LOS displacements. This is because the UD direction is highly dependent on the LOS displacements, whereas the displacements in the azimuth direction are insensitive to vertical displacement. Having more LOS inputs can reduce the ambiguity of the UD direction decomposition. Also, in the EW direction, pixels from two sets of the LOS inputs were more than one set of the LOS inputs. Similar to the UD direction, the displacements in the EW direction were more dependent on the LOS observations than displacements in the azimuth direction. Lastly, for the NS direction, based on the denoised results, it seems like the noise was relatively more evenly distributed among these five types. One reason might be because of the uncertainty of the surface displacements in the azimuth direction from SAR images. Although MAI and POT can obtain azimuth displacements, which are highly sensitive to the NS direction, the inherent ambiguity in the azimuth surface motion detection resulted in a relatively stronger noise level in the NS decomposition. Therefore, the removed pixels were dependent on the original azimuth displacement inputs. If the input azimuth displacements are noisy, then the inverted displacement field is very likely to be noisy as well.
Adapting the methods to integrate the azimuth displacements in this study may induce artificial errors due to upsampling. This might not be observed in the integrated azimuth displacement fields (Figure 8) but could be readily observed after 3D decomposition (Figure 9). These errors must be removed before further analysis, such as fault slip models or analyzing fault behaviors. Using the proposed denoising criterion could successfully remove such erroneous pixels and retain the overall deformation patterns and spatial resolution (Figure 9). This denoising method could also be applied to computing other displacement fields for removing unwanted pixels without any low-pass filtering.
As illustrated in the previous sections, other denoising strategies might involve applying low-pass filtering, spatial smoothing, or setting weighting to each pixel during inversion. Low-pass filtering could efficiently reduce the effect of noise but also contaminate signals with the value of noisy pixels. In addition, low-pass filtering would blur the overall image, which would not be ideal for analyzing deformation behaviors. Set weightings during inversions could also reduce noise effects. However, it is sometimes not easy to determine the weights. All the above methods are noise reduction, meaning that the noise effect is only “reduced” but not removed. The method we proposed here is noise “removal”, which picks out noisy pixels and retains the good ones without altering them. However, we do note that there are several limitations to our method. One is the mis-removal of pixels adjacent to sharp displacement boundaries such as surface ruptures. Another limitation is that the identification of noise relies on the noisy pixel to be adjacent to other pixels. If not, the sum of difference from this noisy pixel cannot be calculated. Therefore, this isolated noisy pixel will be preserved from being identified and removed regardless of how many iterations are being executed. With regard to this situation, a certain degree of manual inspection should take place to remove them accordingly.

6. Conclusions

In this study, we examined different SAR algorithms for resolving 3D surface displacements and proposed a method to decompose the 3D displacement field using LOS displacements with an integrated azimuth displacement field. Compared with the results using LOS with solely MAI or POT, the 3D displacement field using our method provides both high spatial resolution and solid displacement at low coherence areas. The uncertainty also demonstrates the success of this method. We suggest that MAI and POT can make up for the weaknesses of each other. By combining them, the high spatial resolution of MAI and the surface displacements at less coherent areas from POT can co-exist in the integrated azimuth displacement field. The artifacts induced from upsampling the POT results can be removed via the denoising criterion proposed in this study. The proposed denoising criterion can efficiently “remove” noise rather than reduce the effects stemming from noise. Although the denoising method was tested in this case, it still requires further examination to guarantee its robustness.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs16071159/s1, Figure S1: Ionospheric error semi-grid-searched filtering size result; Figure S2: Grid-searched Pixel-Offset-Tracking (POT) result.

Author Contributions

Conceptualization, R.Y.C.; methodology, L.-C.J.L.; software, L.-C.J.L. and C.-H.L.; validation, R.Y.C.; formal analysis, L.-C.J.L.; investigation, L.-C.J.L.; resources, R.Y.C.; data curation, R.Y.C., K.-E.C. and C.-L.C.; writing—original draft preparation, L.-C.J.L.; writing—review and editing, R.Y.C.; visualization, L.-C.J.L.; supervision, R.Y.C.; project administration, R.Y.C.; funding acquisition, R.Y.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Ministry of Science and Technology (National Science and Technology Council) with grant number 110-2119-M-002-008 and 112-2119-M-008-009.

Data Availability Statement

All data will be made available upon request.

Acknowledgments

We thank Taiwan Geodetic Model for providing GNSS data. We thank European Space Agency for providing Sentinel-1 data. We thank Japan Aerospace Exploration Agency and 2nd Research Announcement on the Earth Observations for providing ALOS-2 data. We thank Taiwan Earthquake Model for providing active structure data. We thank Central Geological Survey for providing leveling data. All figures were generated via GMT5 software (v5.4.5).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Fan, X.; Scaringi, G.; Korup, O.; West, A.J.; van Westen, C.J.; Tanyas, H.; Hovius, N.; Hales, T.C.; Jibson, R.W.; Allstadt, K.E.; et al. Earthquake-induced chains of geologic hazards: Patterns, mechanisms, and impacts. Rev. Geophys. 2019, 57, 421–503. [Google Scholar] [CrossRef]
  2. Huang, Y.; Yu, M. Review of soil liquefaction characteristics during major earthquakes of the twenty-first century. Nat. Hazards 2013, 65, 2375–2384. [Google Scholar] [CrossRef]
  3. Huang, M.H.; Fielding, E.J.; Liang, C.; Milillo, P.; Bekaert, D.; Dreger, D.; Salzer, J. Coseismic deformation and triggered landslides of the 2016 Mw 6.2 Amatrice earthquake in Italy. Geophys. Res. Lett. 2017, 44, 1266–1274. [Google Scholar] [CrossRef]
  4. Yu, E.; Segall, P. Slip in the 1868 Hayward earthquake from the analysis of historical triangulation data. J. Geophys. Res. Solid Earth 1996, 101, 16101–16118. [Google Scholar] [CrossRef]
  5. Marshall, G.A.; Stein, R.S.; Thatcher, W. Faulting geometry and slip from co-seismic elevation changes: The 18 October 1989, Loma Prieta, California, earthquake. Bull. Seismol. Soc. Am. 1991, 81, 1660–1693. [Google Scholar] [CrossRef]
  6. Bock, Y.; Melgar, D. Physical applications of GPS geodesy: A review. Rep. Prog. Phys. 2016, 79, 106801. [Google Scholar] [CrossRef]
  7. Massonnet, D.; Rossi, M.; Carmona, C.; Adragna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The displacement field of the Landers earthquake mapped by radar interferometry. Nature 1993, 364, 138–142. [Google Scholar] [CrossRef]
  8. Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
  9. Bürgmann, R.; Rosen, P.A.; Fielding, E.J. Synthetic aperture radar interferometry to measure Earth’s surface topography and its deformation. Annu. Rev. Earth Planet. Sci. 2000, 28, 169–209. [Google Scholar] [CrossRef]
  10. Simons, M.; Rosen, P.A. Interferometric synthetic aperture radar geodesy. Geodesy 2007, 3, 391–446. [Google Scholar] [CrossRef]
  11. Biggs, J.; Wright, T.J. How satellite InSAR has grown from opportunistic science to routine monitoring over the last decade. Nat. Commun. 2020, 11, 3863. [Google Scholar] [CrossRef] [PubMed]
  12. González, P.J.; Fernandez, J.; Camacho, A.G. Coseismic three-dimensional displacements determined using SAR data: Theory and an application test. Pure Appl. Geophys. 2009, 166, 1403–1424. [Google Scholar] [CrossRef]
  13. Hu, J.; Li, Z.W.; Ding, X.L.; Zhu, J.J.; Zhang, L.; Sun, Q. Resolving three-dimensional surface displacements from InSAR measurements: A review. Earth-Sci. Rev. 2014, 133, 1–17. [Google Scholar] [CrossRef]
  14. Merryman Boncori, J.P. Measuring coseismic deformation with spaceborne synthetic aperture radar: A review. Front. Earth Sci. 2019, 7, 16. [Google Scholar] [CrossRef]
  15. Lu, C.H.; Lin, Y.S.; Chuang, R.Y. Pixel offset fusion of SAR and optical images for 3-D coseismic surface deformation. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1049–1053. [Google Scholar] [CrossRef]
  16. Carboni, F.; Porreca, M.; Valerio, E.; Mariarosaria, M.; De Luca, C.; Azzaro, S.; Ercoli, M.; Barchi, M.R. Surface ruptures and off-fault deformation of the October 2016 central Italy earthquakes from DInSAR data. Sci. Rep. 2022, 12, 3172. [Google Scholar] [CrossRef] [PubMed]
  17. Hamling, I.J.; Hreinsdóttir, S.; Clark, K.; Elliott, J.; Liang, C.; Fielding, E.; Litchfield, N.; Villamor, P.; Wallace, L.; Wright, T.J.; et al. Complex multifault rupture during the 2016 Mw 7.8 Kaikōura earthquake, New Zealand. Science 2017, 356, 154. [Google Scholar] [CrossRef]
  18. Diederichs, A.; Nissen, E.K.; Lajoie, L.J.; Langridge, R.M.; Malireddi, S.R.; Clark, K.J.; Hamling, I.J.; Tagliasacchi, A. Unusual kinematics of the Papatea fault (2016 Kaikōura earthquake) suggest anelastic rupture. Sci. Adv. 2019, 5, 10. [Google Scholar] [CrossRef]
  19. Wright, T.J.; Lu, Z.; Wicks, C. Source model for the Mw 6.7, 23 October 2002, Nenana Mountain Earthquake (Alaska) from InSAR. Geophys. Res. Lett. 2003, 30, 18. [Google Scholar] [CrossRef]
  20. Fialko, Y.; Simons, M.; Agnew, D. The complete (3-D) surface displacement field in the epicentral area of the 1999 Mw7. 1 Hector Mine earthquake, California, from space geodetic observations. Geophys. Res. Lett. 2001, 28, 17. [Google Scholar] [CrossRef]
  21. Bechor, N.B.; Zebker, H.A. Measuring two-dimensional movements using a single InSAR pair. Geophys. Res. Lett. 2006, 33, 16. [Google Scholar] [CrossRef]
  22. Grandin, R.; Klein, E.; Métois, M.; Vigny, C. Three-dimensional displacement field of the 2015 Mw8. 3 Illapel earthquake (Chile) from across-and along-track Sentinel-1 TOPS interferometry. Geophys. Res. Lett. 2016, 43, 2552–2561. [Google Scholar] [CrossRef]
  23. Wright, T.J.; Parsons, B.E.; Lu, Z. Toward mapping surface deformation in three dimensions using InSAR. Geophys. Res. Lett. 2004, 31, 1. [Google Scholar] [CrossRef]
  24. Jung, H.S.; Lee, W.J.; Zhang, L. Theoretical accuracy of along-track displacement measurements from multiple-aperture interferometry (MAI). Sensors 2014, 14, 17703–17724. [Google Scholar] [CrossRef] [PubMed]
  25. Wang, T.; Jónsson, S. Improved SAR amplitude image offset measurements for deriving three-dimensional coseismic displacements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3271–3278. [Google Scholar] [CrossRef]
  26. Huang, M.H.; Huang, H.H. The complexity of the 2018 Mw 6.4 Hualien earthquake in east Taiwan. Geophys. Res. Lett. 2018, 45, 13–249. [Google Scholar] [CrossRef]
  27. Yen, J.Y.; Lu, C.H.; Dorsey, R.J.; Kuo-Chen, H.; Chang, C.P.; Wang, C.C.; Chuang, R.Y.; Kuo, Y.T.; Chiu, C.Y.; Chang, Y.H.; et al. Insights into seismogenic deformation during the 2018 Hualien, Taiwan, earthquake sequence from InSAR, GPS, and modeling. Seismol. Res. Lett. 2019, 90, 78–87. [Google Scholar] [CrossRef]
  28. Wu, B.L.; Yen, J.Y.; Huang, S.Y.; Kuo, Y.T.; Chang, W.Y. Surface deformation of 0206 Hualien earthquake revealed by the integrated network of RTK GPS. Terr. Atmos. Ocean. Sci. 2019, 30, 301–310. [Google Scholar] [CrossRef]
  29. Lin, Y.S.; Chuang, R.Y.; Yen, J.Y.; Chen, Y.C.; Kuo, Y.T.; Wu, B.L.; Huang, S.Y.; Yang, C.J. Mapping surface breakages of the 2018 Hualien earthquake by using UAS photogrammetry. Terr. Atmos. Ocean Sci. 2019, 30, 3. [Google Scholar] [CrossRef]
  30. Huang, S.Y.; Yen, J.Y.; Wu, B.L.; Yen, I.C.; Chuang, R.Y. Investigating the Milun Fault: The coseismic surface rupture zone of the 2018/02/06 M L 6.2 Hualien earthquake, Taiwan. Terr. Atmos. Ocean Sci. 2019, 30, 3. [Google Scholar] [CrossRef]
  31. Lo, Y.C.; Yue, H.; Sun, J.; Zhao, L.; Li, M. The 2018 Mw6. 4 Hualien earthquake: Dynamic slip partitioning reveals the spatial transition from mountain building to subduction. Earth Planet. Sci. Lett. 2019, 524, 115729. [Google Scholar] [CrossRef]
  32. Kuo, Y.T.; Wang, Y.; Hollingsworth, J.; Huang, S.Y.; Chuang, R.Y.; Lu, C.H.; Hsu, Y.C.; Tung, H.; Yen, J.Y.; Chang, C.P. Shallow fault rupture of the Milun fault in the 2018 Mw 6.4 Hualien earthquake: A high-resolution approach from optical correlation of Pléiades satellite imagery. Seismol. Res. Lett. 2019, 90, 97–107. [Google Scholar] [CrossRef]
  33. Nikolaidis, R. Observation of Geodetic and Seismic Deformation with the Global Positioning System. Ph.D. Thesis, University of California, San Diego, CA, USA, 2002. Available online: https://www.proquest.com/dissertations-theses/observation-geodetic-seismic-deformation-with/docview/304798351/se-2 (accessed on 5 August 2023).
  34. Shyu, J.B.H.; Chuang, Y.R.; Chen, Y.L.; Lee, Y.R.; Cheng, C.T. A New On-Land Seismogenic Structure Source Database from the Taiwan Earthquake Model (TEM) Project for Seismic Hazard Analysis of Taiwan. Terr. Atmos. Ocean Sci. 2016, 27, 311–323. [Google Scholar] [CrossRef]
  35. Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. Open radar interferometry software for mapping surface deformation. Eos. Trans. AGU 2011, 92, 234. [Google Scholar] [CrossRef]
  36. Sandwell, D.; Mellors, R.; Tong, X.; Xu, X.; Wei, M.; Wessel, P. GMTSAR: An InSAR Processing System Based on Generic Mapping Tools; Scripps Institution of Oceanography: San Diego, CA, USA, 2016; Available online: https://escholarship.org/uc/item/8zq2c02m (accessed on 5 August 2023).
  37. Gomba, G.; Parizzi, A.; De Zan, F.; Eineder, M.; Bamler, R. Toward operational compensation of ionospheric effects in SAR interferograms: The split-spectrum method. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1446–1461. [Google Scholar] [CrossRef]
  38. Fattahi, H.; Simons, M.; Agram, P. InSAR time-series estimation of the ionospheric phase delay: An extension of the split range-spectrum technique. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5984–5996. [Google Scholar] [CrossRef]
  39. Wang, K.; Xu, X.; Fialko, Y. Improving burst alignment in TOPS interferometry with bivariate enhanced spectral diversity. IEEE Trans. Geosci. Remote Sens. 2017, 14, 2423–2427. [Google Scholar] [CrossRef]
Remotesensing 16 01159 g001
Figure 1. Geography of the study area. Yellow triangles are leveling benchmarks. Green squares denote GPS records serving as check points, while gray circles are GPS records used to constrain SAR-derived displacement. Red lines are the two identified active faults in this region [34]. Inset shows the SAR image coverage. Blue rectangles are ascending and descending ALOS-2 image coverage. Black-shaded bars are burst overlapping areas in Sentinel-1 images.
Figure 1. Geography of the study area. Yellow triangles are leveling benchmarks. Green squares denote GPS records serving as check points, while gray circles are GPS records used to constrain SAR-derived displacement. Red lines are the two identified active faults in this region [34]. Inset shows the SAR image coverage. Blue rectangles are ascending and descending ALOS-2 image coverage. Black-shaded bars are burst overlapping areas in Sentinel-1 images.
Remotesensing 16 01159 g001
Remotesensing 16 01159 g002
Figure 2. The process of integrating azimuth displacement fields. See main text for detailed explanation.
Figure 2. The process of integrating azimuth displacement fields. See main text for detailed explanation.
Remotesensing 16 01159 g002
Remotesensing 16 01159 g003
Figure 3. The search of masking thresholds for MAI and POT results. X-axis is the coherence/SNR thresholds. Y-axis is the Cumulative Distribution Function (CDF) of data counts. The gray shadings are the CDFs of pixel counts under each threshold. Blue bars are the 1st, 2nd, and 3rd quantiles of CDF. Red curves are the noise level defined by the global standard deviation. Yellow stars are the final threshold value based on soft thresholding. The insets are the noise level variance. X-axis is the coherence/SNR threshold and Y-axis is the noise level variance. The red shading is the 2.5 standard deviation of the noise level at the threshold inferred using hard thresholding. (a) The search of the threshold for ascending MAI result; (b) the search of the threshold for ascending POT result; (c,d) are the same as (a,b) but in descending track.
Figure 3. The search of masking thresholds for MAI and POT results. X-axis is the coherence/SNR thresholds. Y-axis is the Cumulative Distribution Function (CDF) of data counts. The gray shadings are the CDFs of pixel counts under each threshold. Blue bars are the 1st, 2nd, and 3rd quantiles of CDF. Red curves are the noise level defined by the global standard deviation. Yellow stars are the final threshold value based on soft thresholding. The insets are the noise level variance. X-axis is the coherence/SNR threshold and Y-axis is the noise level variance. The red shading is the 2.5 standard deviation of the noise level at the threshold inferred using hard thresholding. (a) The search of the threshold for ascending MAI result; (b) the search of the threshold for ascending POT result; (c,d) are the same as (a,b) but in descending track.
Remotesensing 16 01159 g003
Remotesensing 16 01159 g004
Figure 4. Examples of noise-present and noise-free data matrices. Numbers in the boxes are the pixel values. Red numbers are unrealistic values. Color fills represent the values of the boxes in “jet” color palette; cool colors are negative and warm colors are positive. (a) Shows the value of pixels are inconsistent with neighboring pixels; (b) represents the noise-free matrix in which all pixels are within the similar pixel value; (c) has both inconsistent pixel values and unrealistic values.
Figure 4. Examples of noise-present and noise-free data matrices. Numbers in the boxes are the pixel values. Red numbers are unrealistic values. Color fills represent the values of the boxes in “jet” color palette; cool colors are negative and warm colors are positive. (a) Shows the value of pixels are inconsistent with neighboring pixels; (b) represents the noise-free matrix in which all pixels are within the similar pixel value; (c) has both inconsistent pixel values and unrealistic values.
Remotesensing 16 01159 g004
Remotesensing 16 01159 g005
Figure 5. An example of CDF for sum of difference γ. In this example, the threshold for the sum of difference will be 6.3.
Figure 5. An example of CDF for sum of difference γ. In this example, the threshold for the sum of difference will be 6.3.
Remotesensing 16 01159 g005
Remotesensing 16 01159 g006
Figure 6. Interferograms of Sentinel-1 and ALOS-2 images. Red lines are the two main active faults mapped in Figure 1; the Milun and the Lingding fault (Same for figures below). (a) Interferogram of Sentinel-1 in the ascending track; (b) interferogram of Sentinel-1 in the descending track; (c,d) are the same as (a,b) but interferograms are of ALOS-2 images.
Figure 6. Interferograms of Sentinel-1 and ALOS-2 images. Red lines are the two main active faults mapped in Figure 1; the Milun and the Lingding fault (Same for figures below). (a) Interferogram of Sentinel-1 in the ascending track; (b) interferogram of Sentinel-1 in the descending track; (c,d) are the same as (a,b) but interferograms are of ALOS-2 images.
Remotesensing 16 01159 g006
Remotesensing 16 01159 g007
Figure 7. Azimuth displacements from MAI, POT, and BOI algorithms. Warm colors denote surface moving away from satellite, while cool colors represent surface moving towards satellite. Black solid lines are the Milun fault and the Lingding fault. (a–c) Azimuth displacement in the ascending track using MAI, POT, and BOI, respectively; (d–f) are the same as (a–c) but in the descending track.
Figure 7. Azimuth displacements from MAI, POT, and BOI algorithms. Warm colors denote surface moving away from satellite, while cool colors represent surface moving towards satellite. Black solid lines are the Milun fault and the Lingding fault. (a–c) Azimuth displacement in the ascending track using MAI, POT, and BOI, respectively; (d–f) are the same as (a–c) but in the descending track.
Remotesensing 16 01159 g007
Remotesensing 16 01159 g008
Figure 8. Integrated azimuth displacement and the displacement type. The color sense is the same as in Figure 8. (a) Integrated azimuth displacement in the ascending track; (b) the displacement type of each pixel. Blue denotes MAI results and orange represents POT ones; (c,d) are the same as (a,b) but in the descending track.
Figure 8. Integrated azimuth displacement and the displacement type. The color sense is the same as in Figure 8. (a) Integrated azimuth displacement in the ascending track; (b) the displacement type of each pixel. Blue denotes MAI results and orange represents POT ones; (c,d) are the same as (a,b) but in the descending track.
Remotesensing 16 01159 g008
Remotesensing 16 01159 g009aRemotesensing 16 01159 g009b
Figure 9. Original 3D displacement fields, denoise iterations, and denoised 3D displacement fields. Circles and squares are GPS stations used to constrain and evaluate the displacement fields. (a–c) EW, NS, and UD displacements with positive values moving to the east, north, and up; (d) the denoising iteration times. The blue, red, and black curves represent EW, NS, and UD directions. Yellow stars are the selected thresholds by the local minima of noise levels. (e–g) Are the same as (a–c) but denoised with the selected iteration times.
Figure 9. Original 3D displacement fields, denoise iterations, and denoised 3D displacement fields. Circles and squares are GPS stations used to constrain and evaluate the displacement fields. (a–c) EW, NS, and UD displacements with positive values moving to the east, north, and up; (d) the denoising iteration times. The blue, red, and black curves represent EW, NS, and UD directions. Yellow stars are the selected thresholds by the local minima of noise levels. (e–g) Are the same as (a–c) but denoised with the selected iteration times.
Remotesensing 16 01159 g009aRemotesensing 16 01159 g009b
Remotesensing 16 01159 g010
Figure 10. Different versions of 3D displacement fields. Warm colors represent surface uplift, while cool colors mean surface subsidence. Arrows are horizontal motions. Triangles denote leveling benchmarks. Circles and squares are control and check points used to constrain and evaluate the 3D displacement fields. The three components were all GPS-constrained. (a) The 3D displacement of Version 1; (b) the 3D displacement field of Version 2; (c) the 3D displacement field of Version 3.
Figure 10. Different versions of 3D displacement fields. Warm colors represent surface uplift, while cool colors mean surface subsidence. Arrows are horizontal motions. Triangles denote leveling benchmarks. Circles and squares are control and check points used to constrain and evaluate the 3D displacement fields. The three components were all GPS-constrained. (a) The 3D displacement of Version 1; (b) the 3D displacement field of Version 2; (c) the 3D displacement field of Version 3.
Remotesensing 16 01159 g010
Remotesensing 16 01159 g011
Figure 11. GPS-constrained NS displacement of Versions 1, 2, and 3. Circles and squares are GPS stations used to constrain and evaluate the displacement fields. Note that these NS displacements are constrained with GPS records, which appear differently to those in Figure 10. (a) NS displacement of Version 1; (b) NS displacement of Version 2; (c) NS displacement of Version 3.
Figure 11. GPS-constrained NS displacement of Versions 1, 2, and 3. Circles and squares are GPS stations used to constrain and evaluate the displacement fields. Note that these NS displacements are constrained with GPS records, which appear differently to those in Figure 10. (a) NS displacement of Version 1; (b) NS displacement of Version 2; (c) NS displacement of Version 3.
Remotesensing 16 01159 g011
Remotesensing 16 01159 g012
Figure 12. Inversion inputs for Version 1 and the ratio of inversion types. The left panel is the in-version inputs for Version 1. Red is four inputs, green denotes 3 inputs, and blue represents 2 in-puts. The right panels are the inversion type percentages before and after denoising. The coloring sense is the same as the left panel. Light colors represent percentages of pre-denoising and dark colors denote percentages of post-denoising. Top right panel is the EW direction, middle right panel is the NS direction, and bottom right panel is the UD direction.
Figure 12. Inversion inputs for Version 1 and the ratio of inversion types. The left panel is the in-version inputs for Version 1. Red is four inputs, green denotes 3 inputs, and blue represents 2 in-puts. The right panels are the inversion type percentages before and after denoising. The coloring sense is the same as the left panel. Light colors represent percentages of pre-denoising and dark colors denote percentages of post-denoising. Top right panel is the EW direction, middle right panel is the NS direction, and bottom right panel is the UD direction.
Remotesensing 16 01159 g012
Table 1. List of SAR data used in this study.
Table 1. List of SAR data used in this study.
SatelliteOrbitReference DateAligned DateScan ModeWavelength
Sentinel-1Ascending3 February 201815 February 2018TOPSC-band
Descending5 February 201811 February 2018TOPSC-band
ALOS-2Ascending5 November 2016 10 February 2018Stripmap-HBQ 1L-band
Descending18 June 2017 11 February 2018Stripmap-FBD 2L-band
1 HBQ: high-sensitive mode quad polarization. 2 FBD: fine mode dual polarization.
Table 2. RMSE and spatial resolution of 3D displacement fields.
Table 2. RMSE and spatial resolution of 3D displacement fields.
VersionEW Error 1NS Error 1UD Error 1X Spacing 2Y Spacing 2
DInSAR + Integrated azimuth displacement (1)2.29.54.361.646.2
DInSAR + MAI (2)2.019.82.761.646.2
DInSAR + POT (3)48.611.63.2279.0212.7
1 Unit: cm; 2 unit: m.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Lin, L.-C.J.; Chuang, R.Y.; Lu, C.-H.; Ching, K.-E.; Chen, C.-L. Derivation of 3D Coseismic Displacement Field from Integrated Azimuth and LOS Displacements for the 2018 Hualien Earthquake. Remote Sens. 2024, 16, 1159. https://doi.org/10.3390/rs16071159

AMA Style

Lin L-CJ, Chuang RY, Lu C-H, Ching K-E, Chen C-L. Derivation of 3D Coseismic Displacement Field from Integrated Azimuth and LOS Displacements for the 2018 Hualien Earthquake. Remote Sensing. 2024; 16(7):1159. https://doi.org/10.3390/rs16071159

Chicago/Turabian Style

Lin, Li-Chieh J., Ray Y. Chuang, Chih-Heng Lu, Kuo-En Ching, and Chien-Liang Chen. 2024. "Derivation of 3D Coseismic Displacement Field from Integrated Azimuth and LOS Displacements for the 2018 Hualien Earthquake" Remote Sensing 16, no. 7: 1159. https://doi.org/10.3390/rs16071159

APA Style

Lin, L. -C. J., Chuang, R. Y., Lu, C. -H., Ching, K. -E., & Chen, C. -L. (2024). Derivation of 3D Coseismic Displacement Field from Integrated Azimuth and LOS Displacements for the 2018 Hualien Earthquake. Remote Sensing, 16(7), 1159. https://doi.org/10.3390/rs16071159

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop