Estimation and Evaluation of 15 Minute, 40 Meter Surface Upward Longwave Radiation Downscaled from the Geostationary FY-4B AGRI
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
2.2.1. GaoFen5-02 VIMI Data
2.2.2. FengYun-4B AGRI Level 1 Data
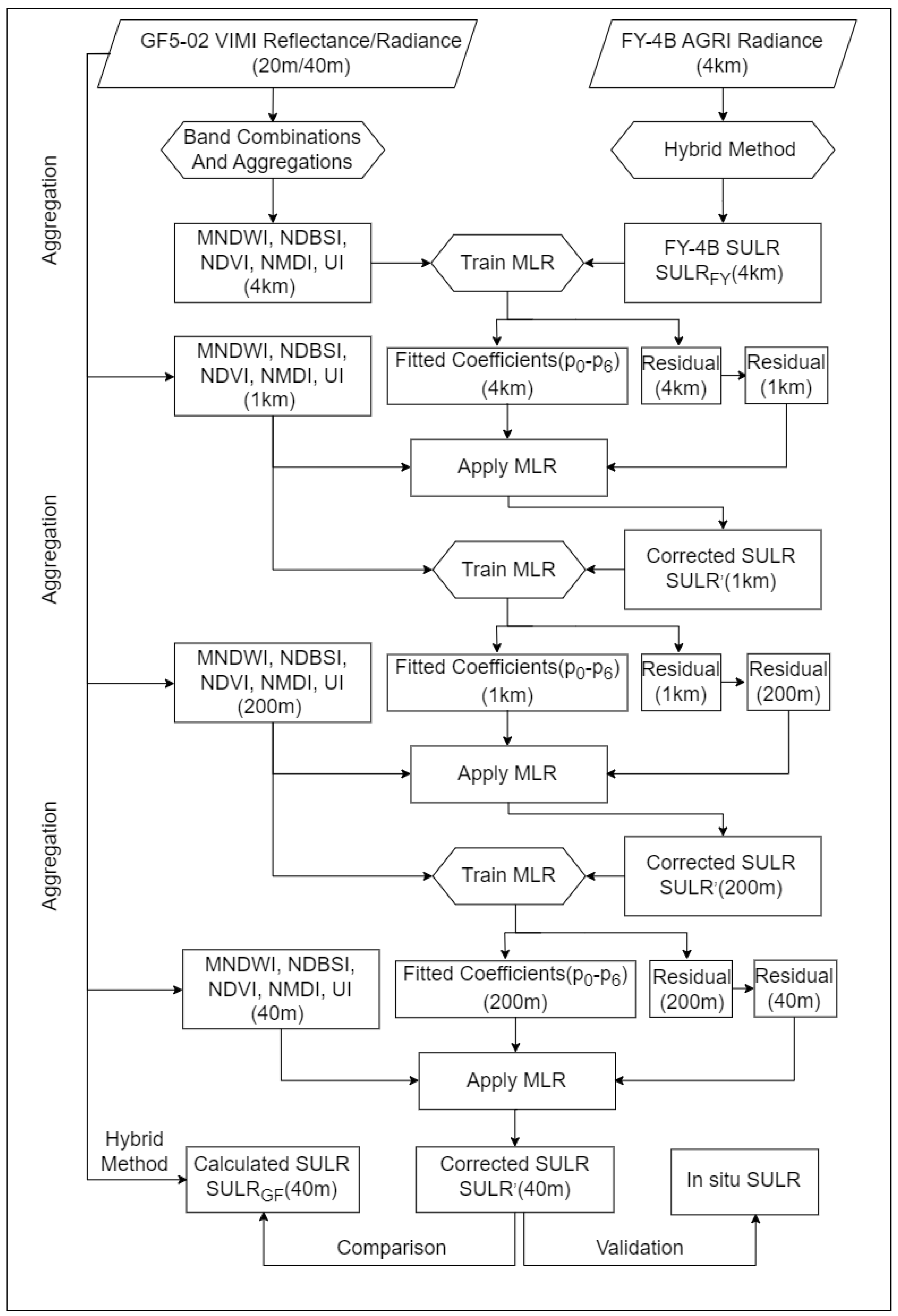
3. Methodology
3.1. Hybrid Algorithm for Estimating SULR
3.2. Surface Factors and Downscaling the Model Selection
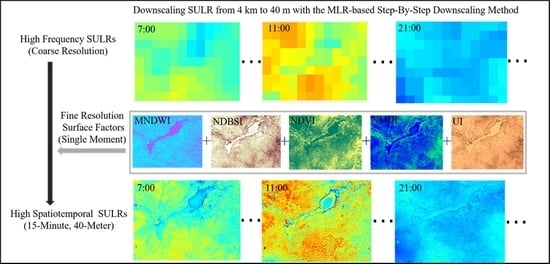
3.3. MLR-Based Step-by-Step Downscaling Strategy
3.4. Evaluation Strategy
4. Results and Evaluation
4.1. Step-by-Step Downscaled SULR Results
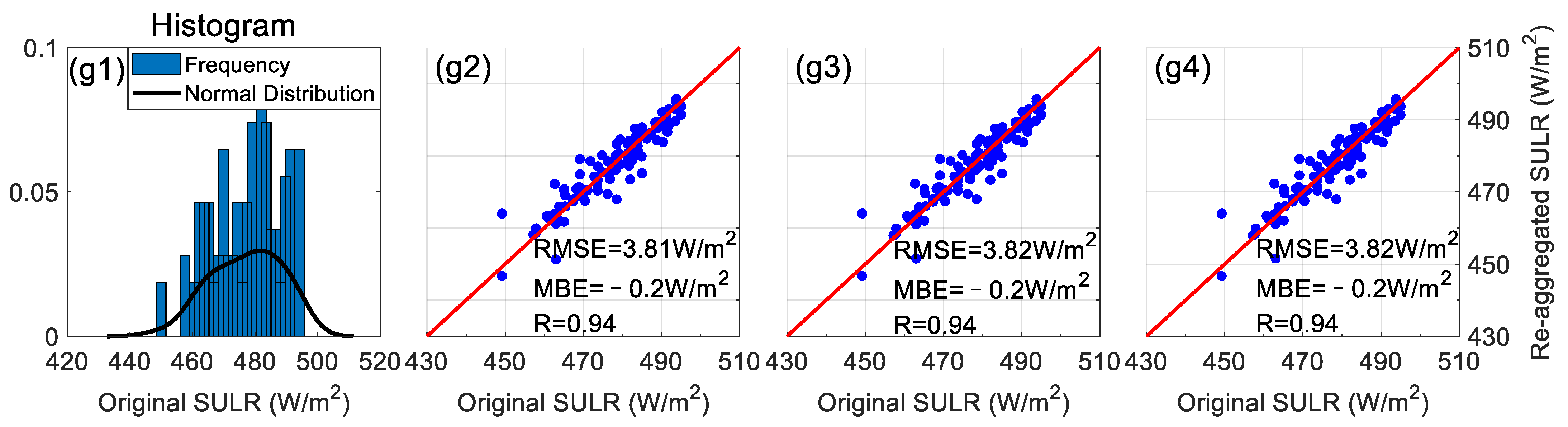
4.2. Hour-by-Hour Downscaled SULR Results

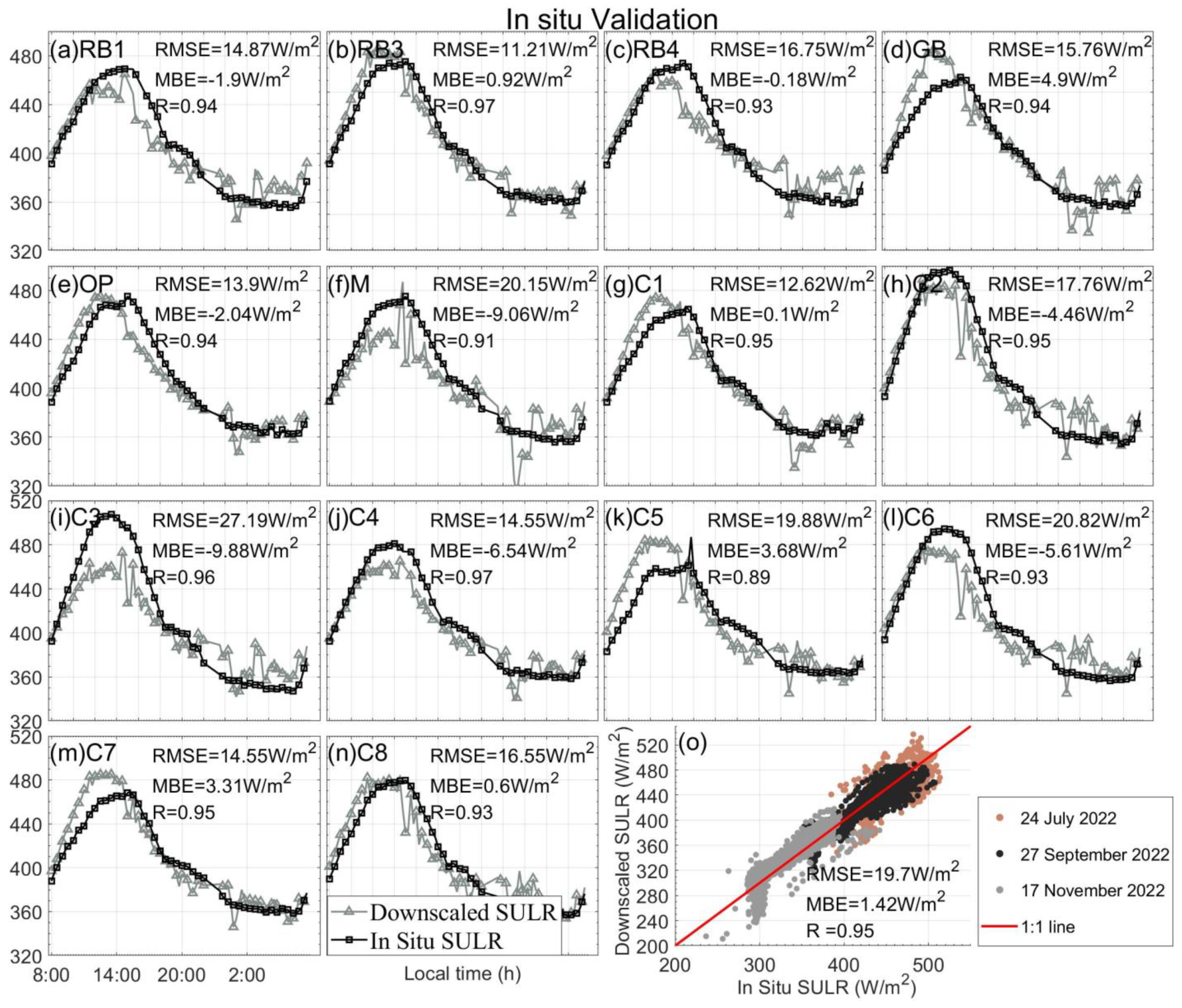
4.3. Point-by-Point Validation Using the SULR Measured In Situ
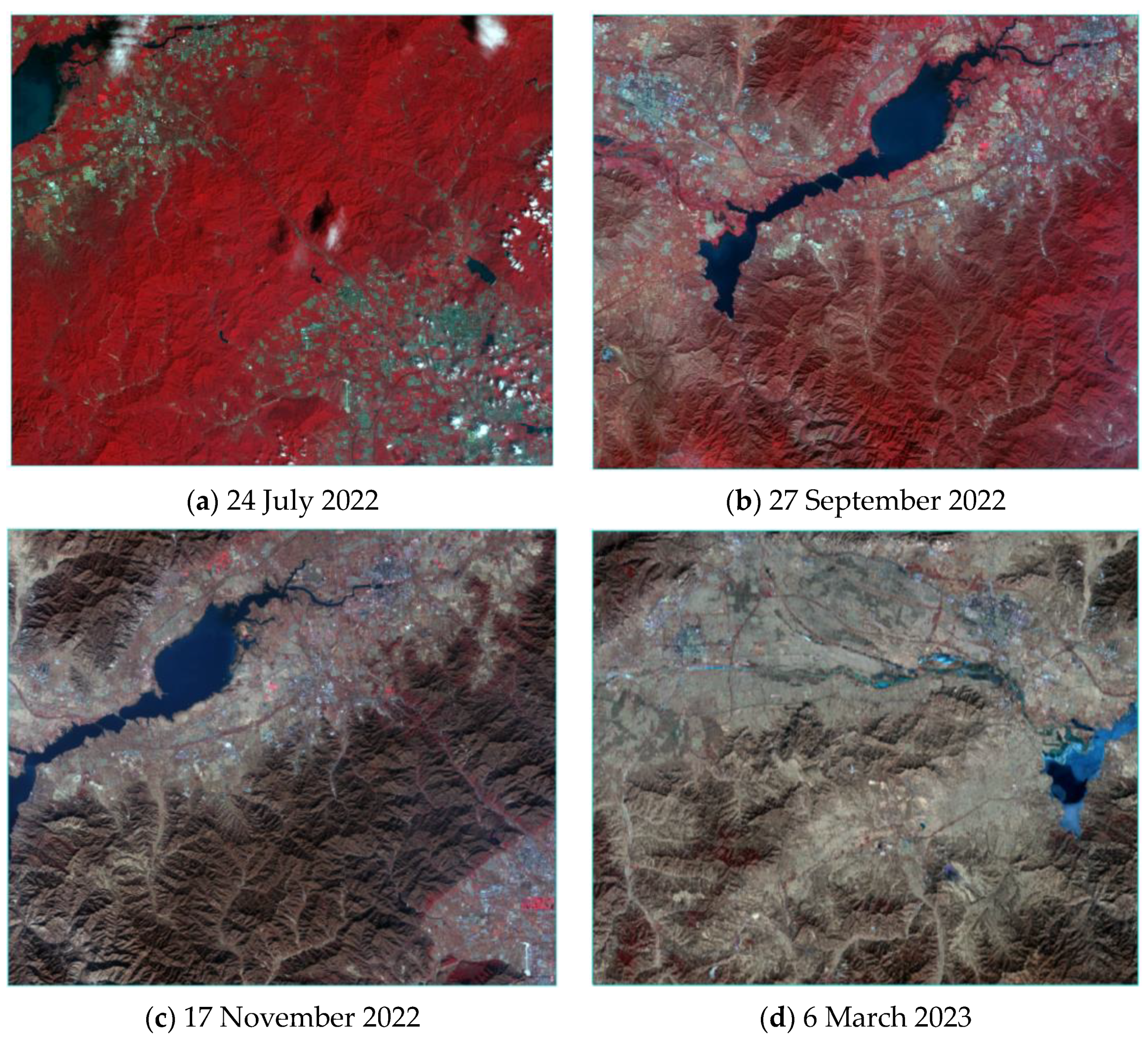
4.4. Image-to-Image Comparison Using the Calculated GF5-02 SULR
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liang, S.; Wang, K.; Zhang, X.; Wild, M. Review on Estimation of Land Surface Radiation and Energy Budgets From Ground Measurement, Remote Sensing and Model Simulations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 225–240. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S. Global Estimates for High-Spatial-Resolution Clear-Sky Land Surface Upwelling Longwave Radiation From MODIS Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4115–4129. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, B.-H. Retrieval of Daytime Surface Upward Longwave Radiation Under All-Sky Conditions With Remote Sensing and Meteorological Reanalysis Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Tang, B.; Li, Z.-L. Estimation of Instantaneous Net Surface Longwave Radiation from MODIS Cloud-Free Data. Remote Sens. Environ. 2008, 112, 3482–3492. [Google Scholar] [CrossRef]
- Jiao, Z.; Yan, G.; Zhao, J.; Wang, T.; Chen, L. Estimation of Surface Upward Longwave Radiation from MODIS and VIIRS Clear-Sky Data in the Tibetan Plateau. Remote Sens. Environ. 2015, 162, 221–237. [Google Scholar] [CrossRef]
- Sellers, P.J.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; et al. Modeling the Exchanges of Energy, Water, and Carbon Between Continents and the Atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Diak, G.R.; Mecikalski, J.R.; Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Torn, R.D.; DeWolf, R.L. Estimating Land Surface Energy Budgets From Space: Review and Current Efforts at the University of Wisconsin—Madison and USDA–ARS. Bull. Am. Meteorol. Soc. 2004, 85, 65–78. [Google Scholar] [CrossRef]
- Hu, T.; Du, Y.; Cao, B.; Li, H.; Bian, Z.; Sun, D.; Liu, Q. Estimation of Upward Longwave Radiation From Vegetated Surfaces Considering Thermal Directionality. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6644–6658. [Google Scholar] [CrossRef]
- Ge, N.; Zhong, L.; Ma, Y.; Fu, Y.; Zou, M.; Cheng, M.; Wang, X.; Huang, Z. Estimations of Land Surface Characteristic Parameters and Turbulent Heat Fluxes over the Tibetan Plateau Based on FY-4A/AGRI Data. Adv. Atmos. Sci. 2021, 38, 1299–1314. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, X.; Liang, S.; Yang, H.; Zhou, G. Estimation of Clear-sky Land Surface Longwave Radiation from MODIS Data Products by Merging Multiple Models. J. Geophys. Res. Atmos. 2012, 117, 2012JD017567. [Google Scholar] [CrossRef]
- Zhan, W.; Chen, Y.; Zhou, J.; Li, J.; Liu, W. Sharpening Thermal Imageries: A Generalized Theoretical Framework From an Assimilation Perspective. IEEE Trans. Geosci. Remote Sens. 2011, 49, 773–789. [Google Scholar] [CrossRef]
- Nie, J.; Wu, J.; Yang, X.; Liu, M.; Zhang, J.; Zhou, L. Downscaling Land Surface Temperature Based on Relationship between Surface Temperature and Vegetation Index. Acta Ecol. Sin. 2011, 187, 259–272. [Google Scholar]
- Quan, J.; Zhan, W.; Chen, Y.; Liu, W. Downscaling Remotely Sensed Land Surface Temperatures: A Comparison of Typical Methods. J. Remote Sens. 2013, 17, 361–387. [Google Scholar]
- Wang, Y.; Xie, D.; Li, Y. Downscaling Remotely Sensed Land Surface Temperature over Urban Areas Using Trend Surface of Spectral Index. J. Remote Sens. 2014, 18, 13. [Google Scholar]
- Hua, J.; Zhu, S.; Zhang, G. Downscaling Land Surface Temperature Based on Random Forest Algorithm. Remote Sens. Land Resour. 2018, 30, 78–86. [Google Scholar]
- Yu, F.; Zhu, S.; Zhang, G.; Zhu, J.; Zhang, N.; Xu, Y. A Downscaling Method for Land Surface Air Temperature of ERA5 Reanalysis Dataset under Complex Terrain Conditions in Mountainous Areas. J. Geosci. 2022, 24, 750–765. [Google Scholar]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating Subpixel Surface Temperatures and Energy Fluxes from the Vegetation Index–Radiometric Temperature Relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Neale, C.M.U. A Vegetation Index Based Technique for Spatial Sharpening of Thermal Imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
- Zhu, S.; Guan, H.; Millington, A.C.; Zhang, G. Disaggregation of Land Surface Temperature over a Heterogeneous Urban and Surrounding Suburban Area: A Case Study in Shanghai, China. Int. J. Remote Sens. 2013, 34, 1707–1723. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling Land Surface Temperatures at Regional Scales with Random Forest Regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Wang, Z.; Qin, Q.; Sun, Y. Downscaling of Remotely Sensed Land Surface Temperature with the BP Neural Network. Remote Sens. Technol. Appl. 2018, 33, 793–802. [Google Scholar]
- Dong, P.; Zhan, W.; Wang, C.; Jiang, S.; Du, H.; Liu, Z.; Chen, Y.; Li, L.; Wang, S.; Ji, Y. Simple yet Efficient Downscaling of Land Surface Temperatures by Suitably Integrating Kernel- and Fusion-Based Methods. ISPRS J. Photogramm. Remote Sens. 2023, 205, 317–333. [Google Scholar] [CrossRef]
- Hu, Y.; Tang, R.; Jiang, X.; Li, Z.-L.; Jiang, Y.; Liu, M.; Gao, C.; Zhou, X. A Physical Method for Downscaling Land Surface Temperatures Using Surface Energy Balance Theory. Remote Sens. Environ. 2023, 286, 113421. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, N.; Cheng, J.; Xu, S. A Stepwise Downscaling Method for Generating High-Resolution Land Surface Temperature from AMSR-E Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5669–5691. [Google Scholar] [CrossRef]
- Li, X.; Zhang, G.; Zhu, S.; Xu, Y. Step-By-Step Downscaling of Land Surface Temperature Considering Urban Spatial Morphological Parameters. Remote Sens. 2022, 14, 3038. [Google Scholar] [CrossRef]
- Jung, H.-S.; Lee, K.-T.; Zo, I.-S. Calculation Algorithm of Upward Longwave Radiation Based on Surface Types. Asia-Pac. J. Atmos. Sci. 2020, 56, 291–306. [Google Scholar] [CrossRef]
- Wang, C.; Tang, B.-H.; Huo, X.; Li, Z.-L. New Method to Estimate Surface Upwelling Long-Wave Radiation from MODIS Cloud-Free Data. Opt. Express 2017, 25, A574. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Cheng, J. Estimation of High Spatial-Resolution Clear-Sky Land Surface-Upwelling Longwave Radiation from VIIRS/S-NPP Data. Remote Sens. 2018, 10, 253. [Google Scholar] [CrossRef]
- Qin, B.; Cao, B.; Li, H.; Bian, Z.; Hu, T.; Du, Y.; Yang, Y.; Xiao, Q.; Liu, Q. Evaluation of Six High-Spatial Resolution Clear-Sky Surface Upward Longwave Radiation Estimation Methods with MODIS. Remote Sens. 2020, 12, 1834. [Google Scholar] [CrossRef]
- Dong, P.; Gao, L.; Zhan, W.; Liu, Z.; Li, J.; Lai, J.; Li, H.; Huang, F.; Tamang, S.K.; Zhao, L. Global Comparison of Diverse Scaling Factors and Regression Models for Downscaling Landsat-8 Thermal Data. ISPRS J. Photogramm. Remote Sens. 2020, 169, 44–56. [Google Scholar] [CrossRef]
- Sánchez, J.M.; Galve, J.M.; Nieto, H.; Guzinski, R. Assessment of High-Resolution LST Derived From the Synergy of Sentinel-2 and Sentinel-3 in Agricultural Areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 916–928. [Google Scholar] [CrossRef]
- Zhu, X.; Song, X.; Leng, P.; Hu, R. Spatial Downscaling of Land Surface Temperature with the Multi-Scale Geographically Weighted Regression. J. Remote Sens. 2021, 25, 18. [Google Scholar] [CrossRef]
- Yoo, C.; Im, J.; Park, S.; Cho, D. Spatial Downscaling of MODIS Land Surface Temperature: Recent Research Trends, Challenges, and Future Directions. Korean J. Remote Sens. 2020, 36, 609–626. [Google Scholar] [CrossRef]
- Li, H.; Li, R.; Tu, H.; Cao, B.; Liu, F.; Bian, Z.; Hu, T.; Du, Y.; Sun, L.; Liu, Q. An Operational Split-Window Algorithm for Generating Long-Term Land Surface Temperature Products From Chinese Fengyun-3 Series Satellite Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Wang, W.; Liang, S.; Augustine, J.A. Estimating High Spatial Resolution Clear-Sky Land Surface Upwelling Longwave Radiation from MODIS Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1559–1570. [Google Scholar] [CrossRef]
- Zeng, Q.; Cheng, J.; Dong, L. Assessment of the Long-Term High-Spatial-Resolution Global LAnd Surface Satellite (GLASS) Surface Longwave Radiation Product Using Ground Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2032–2055. [Google Scholar] [CrossRef]
- Zeng, Q.; Cheng, J.; Guo, M. A Comprehensive Evaluation of Three Global Surface Longwave Radiation Products. Remote Sens. 2023, 15, 2955. [Google Scholar] [CrossRef]
- Qin, B.; Cao, B.; Roujean, J.-L.; Gastellu-Etchegorry, J.-P.; Ermida, S.L.; Bian, Z.; Du, Y.; Hu, T.; Li, H.; Xiao, Q.; et al. A Thermal Radiation Directionality Correction Method for the Surface Upward Longwave Radiation of Geostationary Satellite Based on a Time-Evolving Kernel-Driven Model. Remote Sens. Environ. 2023, 294, 113599. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L. Spatial Downscaling of MODIS Land Surface Temperatures Using Geographically Weighted Regression: Case Study in Northern China. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6458–6469. [Google Scholar] [CrossRef]
- Cao, B.; Liu, Q.; Du, Y.; Roujean, J.-L.; Gastellu-Etchegorry, J.-P.; Trigo, I.F.; Zhan, W.; Yu, Y.; Cheng, J.; Jacob, F.; et al. A Review of Earth Surface Thermal Radiation Directionality Observing and Modeling: Historical Development, Current Status and Perspectives. Remote Sens. Environ. 2019, 232, 111304. [Google Scholar] [CrossRef]
- Hu, T.; Roujean, J.-L.; Cao, B.; Mallick, K.; Boulet, G.; Li, H.; Xu, Z.; Du, Y.; Liu, Q. Correction for LST Directionality Impact on the Estimation of Surface Upwelling Longwave Radiation over Vegetated Surfaces at the Satellite Scale. Remote Sens. Environ. 2023, 295, 113649. [Google Scholar] [CrossRef]

| VZA | 0° | 10° | 20° | 30° | 40° | 50° | 60° | |
|---|---|---|---|---|---|---|---|---|
| FY-4B AGRI | a0 | 86.0905 | 86.4723 | 87.6620 | 89.7995 | 93.1742 | 98.3240 | 106.2046 |
| a1 | −2.4927 | −2.5541 | −2.7384 | −3.0441 | −3.4589 | −3.9184 | −4.1643 | |
| a2 | 105.9331 | 106.7086 | 109.0992 | 113.3028 | 119.7131 | 129.0193 | 142.3019 | |
| a3 | −68.9081 | −69.7235 | −72.2442 | −76.7023 | −83.5696 | −93.7132 | −108.6330 | |
| RMSE (W/m2) | 6.65 | 6.71 | 6.91 | 7.27 | 7.86 | 8.82 | 10.48 | |
| GF5-02 VIMI | b0 | −38.0897 | −38.4436 | −39.5298 | −41.4500 | −44.4164 | −48.8187 | −55.5221 |
| b1 | 21.8166 | 22.0164 | 22.6375 | 23.7702 | 25.6111 | 28.5709 | 33.6638 | |
| b2 | 104.2309 | 104.8645 | 106.8184 | 110.2269 | 115.3711 | 122.7523 | 132.9230 | |
| b3 | −53.2957 | −53.8959 | −55.7607 | −59.0569 | −64.1387 | −71.6837 | −82.6188 | |
| b4 | 66.9902 | 67.2557 | 68.0969 | 69.6449 | 72.1708 | 76.1867 | 82.4844 | |
| RMSE (W/m2) | 6.03 | 6.09 | 6.26 | 6.59 | 7.13 | 8.05 | 9.65 |
| Index | Description | Formula |
|---|---|---|
| MNDWI | Improves the normalized difference water body index to highlight water | |
| NDBSI | Indicates the degree of dryness of the ground surface | |
| NDVI | Highlights the vegetation information | |
| NMDI | Indicates the vegetation moisture | |
| UI | Highlights the urban information |
| Section | Time |
|---|---|
| 4.1 Step-by-step downscaled SULR results | 11:15 in local time on 27 September 2022 (i.e., the same as the GF5-02 imaging time of a specific day) (Figure 4) |
| 4.2 Hour-by-hour downscaled SULR results | 08:00, 08:15, 08:30…24:00 on 27 September 2022 00:15, 00:30…07:45 on 28 September 2022 in local time (i.e., the same as the FY-4B imaging time of a specific day) (Figure 5) |
| 4.3 Point-by-point validation using the SULR measured in situ | The same time as in Section 4.2 for all 14 stations separately (Figure 6a–n); The same time as in Section 4.2 for all 14 stations together on 24 July 2022, 27 September 2022, and 17 November 2022 (Figure 6o) |
| 4.4 Image-to-image comparison using the calculated GF5-02 SULR | 11:15 in local time on 24 July 2022, 27 September 2022, 17 November 2022, and 6 March 2023 (i.e., the same as all the GF5-02 imaging times of four specific days) (Figure 7) |
| 24 July 2022 | 27 September 2022 | 17 November 2022 | 6 March 2023 | |
|---|---|---|---|---|
| RMSD (W/m2) | 23.21 | 24.22) | 24.10 | 27.90 |
| MBE (W/m2) | −11.46 | −3.00 | 6.53 | 4.68 |
| R | 0.42 | 0.38 | 0.41 | 0.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, L.; Cao, B.; Na, Q.; Qin, B.; Bai, J.; Du, Y.; Li, H.; Bian, Z.; Xiao, Q.; Liu, Q. Estimation and Evaluation of 15 Minute, 40 Meter Surface Upward Longwave Radiation Downscaled from the Geostationary FY-4B AGRI. Remote Sens. 2024, 16, 1158. https://doi.org/10.3390/rs16071158
Zheng L, Cao B, Na Q, Qin B, Bai J, Du Y, Li H, Bian Z, Xiao Q, Liu Q. Estimation and Evaluation of 15 Minute, 40 Meter Surface Upward Longwave Radiation Downscaled from the Geostationary FY-4B AGRI. Remote Sensing. 2024; 16(7):1158. https://doi.org/10.3390/rs16071158
Chicago/Turabian StyleZheng, Limeng, Biao Cao, Qiang Na, Boxiong Qin, Junhua Bai, Yongming Du, Hua Li, Zunjian Bian, Qing Xiao, and Qinhuo Liu. 2024. "Estimation and Evaluation of 15 Minute, 40 Meter Surface Upward Longwave Radiation Downscaled from the Geostationary FY-4B AGRI" Remote Sensing 16, no. 7: 1158. https://doi.org/10.3390/rs16071158
APA StyleZheng, L., Cao, B., Na, Q., Qin, B., Bai, J., Du, Y., Li, H., Bian, Z., Xiao, Q., & Liu, Q. (2024). Estimation and Evaluation of 15 Minute, 40 Meter Surface Upward Longwave Radiation Downscaled from the Geostationary FY-4B AGRI. Remote Sensing, 16(7), 1158. https://doi.org/10.3390/rs16071158