1. Introduction
Lake water levels fluctuate because of natural climatic–hydrological forcings and artificial manipulation [
1,
2]. In natural lakes, water levels vary based on precipitation, evaporation, catchment size and characteristics, and outflow [
3,
4,
5]. Water-level fluctuations in managed lakes primarily depend upon timing, magnitude, and rate of water withdrawal and refilling processes to meet water budget and human needs, although they are mediated by catchment and climate characteristics [
6]. As such, short-term (i.e., hourly, daily) and long-term (i.e., seasonal, inter-annual) variability in lake water levels may differ significantly between natural lakes and lakes with control structures [
2,
7].
Winter water-level drawdowns (WDs) are an example of artificial lake management practices that manipulate water levels. WDs are primarily used to reduce invasive macrophytes, provide flood storage, and protect shoreline infrastructure from ice damage [
2,
8,
9]. The artificial manipulation of water levels, coupled with global climate change, can impact the littoral zone habitat, water quality, and overall ecological integrity of lakes [
2,
10]. While the ecological impacts are still debated, WDs provide an important tool for managers to maintain recreational access, protect shoreline infrastructure, and combat invasive macrophytes that can overwhelm shallow lake habitats [
11]. In the northeast United States, WD is practiced not only as a matter of lake management but is integral to regional environmental stewardship and community well-being [
2]. In this region, WDs usually start in early autumn when the water levels of lakes are lowered until they reach a target level prior to ice cover, and then, the refilling process starts in the spring after ice-out [
2,
11,
12]. However, the timing, magnitude, and duration of WDs vary among lakes and across years [
2], and quantifying such spatiotemporal variability in water levels using in situ data alone is impractical for lakes in a wide geographic region. A regional analysis of WDs can provide key insights into how lake managers are responding to multiple pressures, including climate change, invasive species, and shoreline development.
Satellite remote sensing techniques provide near-real-time, cost-effective, and large-scale monitoring capability of water resources [
13,
14] that can overcome in situ data limitations. Satellite altimeters (e.g., Jason satellite series, Sentinel 3 altimeter, Icesat satellite series) have been used to derive water levels of lakes [
15,
16]. However, satellite altimeters do not cover all inland lakes (i.e., limited to large lakes) and have low revisit frequency (~1 month). Therefore, several studies have used either optical or synthetic aperture radar (SAR) data to study spatial variability in surface water area extent, which can be used as a surrogate for water level [
13,
17,
18,
19]. Optical sensors (e.g., Landsat-series satellites) provide long-term data archives (last three decades) every 16 days, but cloud-affected images create data gaps that may be problematic in continuous monitoring of surface water dynamics. Moreover, optical sensors can differentiate various surface water features (aquatic vegetation, ice cover, suspended sediments, algae bloom, etc.) using their spectral bands [
20,
21,
22]. SAR sensors have the advantage of providing data in almost all weather using their longer wavelength (microwave) and facilitate gap-free continuous monitoring at their respective temporal resolutions [
23,
24]. Application of SAR data was limited in the past because of a lack of open-access data, time-intensive data processing, and the complexity involved in data interpretation by non-expert users [
25,
26,
27]; however, recent advances have overcome these challenges.
The recent advancement in cloud computing platforms such as Google Earth Engine (GEE) has enabled quick processing of satellite data without downloading and storing the data on local machines [
27,
28]. GEE is a web-based platform that hosts freely available satellite data and provides a JavaScript Application Programming Interface (API) as well as a Python API for accessing and processing satellite data on a global scale [
27]. Global satellite data from the National Aeronautics and Space Administration (NASA) (Landsat series: Landsat 8, Landsat 9) and the European Union’s Copernicus program (Sentinel series: Sentinel 1, Sentinel 2) are promptly made available on the GEE platform within days of acquisition of new scenes. Leveraging the cloud storage and cloud computing powers of GEE allow for quick and routine monitoring of inland water bodies and, therefore, the mapping of WD lakes across a wide geographic region.
The objective of this study was to develop a multi-sensor, cloud-based framework to characterize WD lakes. We used the computational power of the GEE platform to process and analyze the multi-sensor satellite data, including data from both optical sensors and SAR sensors. Satellite data were compared to in situ water-level data from 21 lakes in Massachusetts (MA), USA, from 2016–2021 to assess the accuracy of satellite-based characterization of WD lakes among the three satellite sensors. The satellite data were used to characterize WD lakes > 0.3 km2 across the entire state, resulting in a statewide WD frequency map for 166 lakes for five years (2016–2021). This study involved calculating various WD metrics, such as start date, duration, magnitude, and the area of lakebed exposed. We also evaluated WD metrics’ interannual variability in relation to precipitation patterns. The web-based tool along with its findings and results from this study could aid in decision-making processes regarding WD guidelines, aiming to mitigate potential negative impacts associated with WDs.
2. Methods
2.1. Study Area
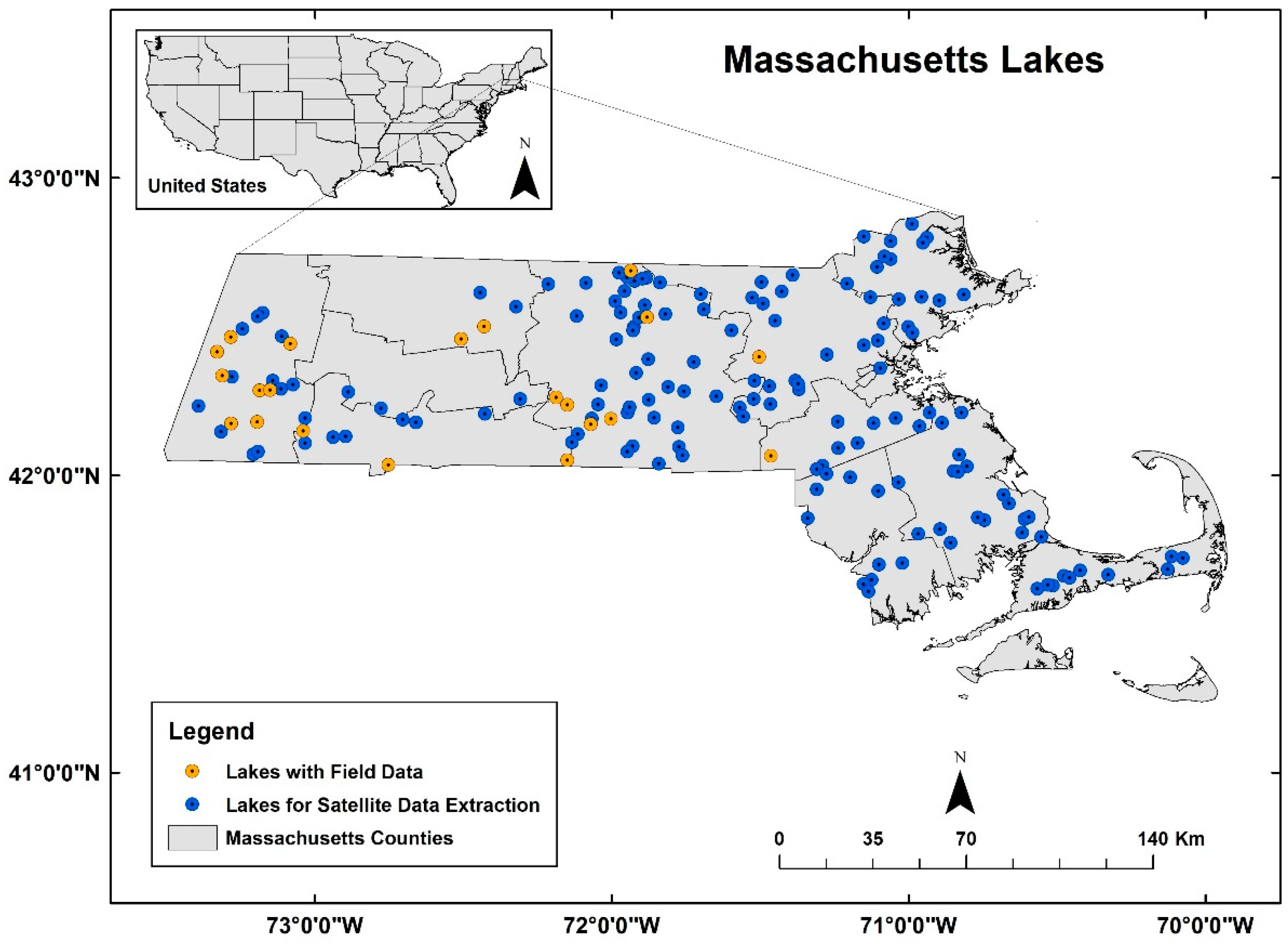
This study focused on lakes in Massachusetts, located in the northeastern United States (
Figure 1). This region experiences a humid continental climate with warm, wet summers and cold, snowy winters [
29]. Precipitation in the region is generally evenly distributed throughout the year except for the wet season, with an annual average rainfall of 1016–1270 mm [
30]. River flows in the region are typically characterized by higher flows during leaf-off periods (~November through April) and spring snowmelt and lower flows during summer months [
31,
32]. Natural lakes in Massachusetts fill during the high spring flows and gradually decline during the drier summer–fall months as evapotranspiration exceeds precipitation inputs [
33,
34]. Most WD lakes implement drawdowns in the fall by releasing water downstream when river flows are lowest. Past research indicates that the timing of these drawdowns, which coincide with the region’s seasonal precipitation and temperature patterns, can significantly impact physical habitat structure and macrophytes in Massachusetts lakes [
35].
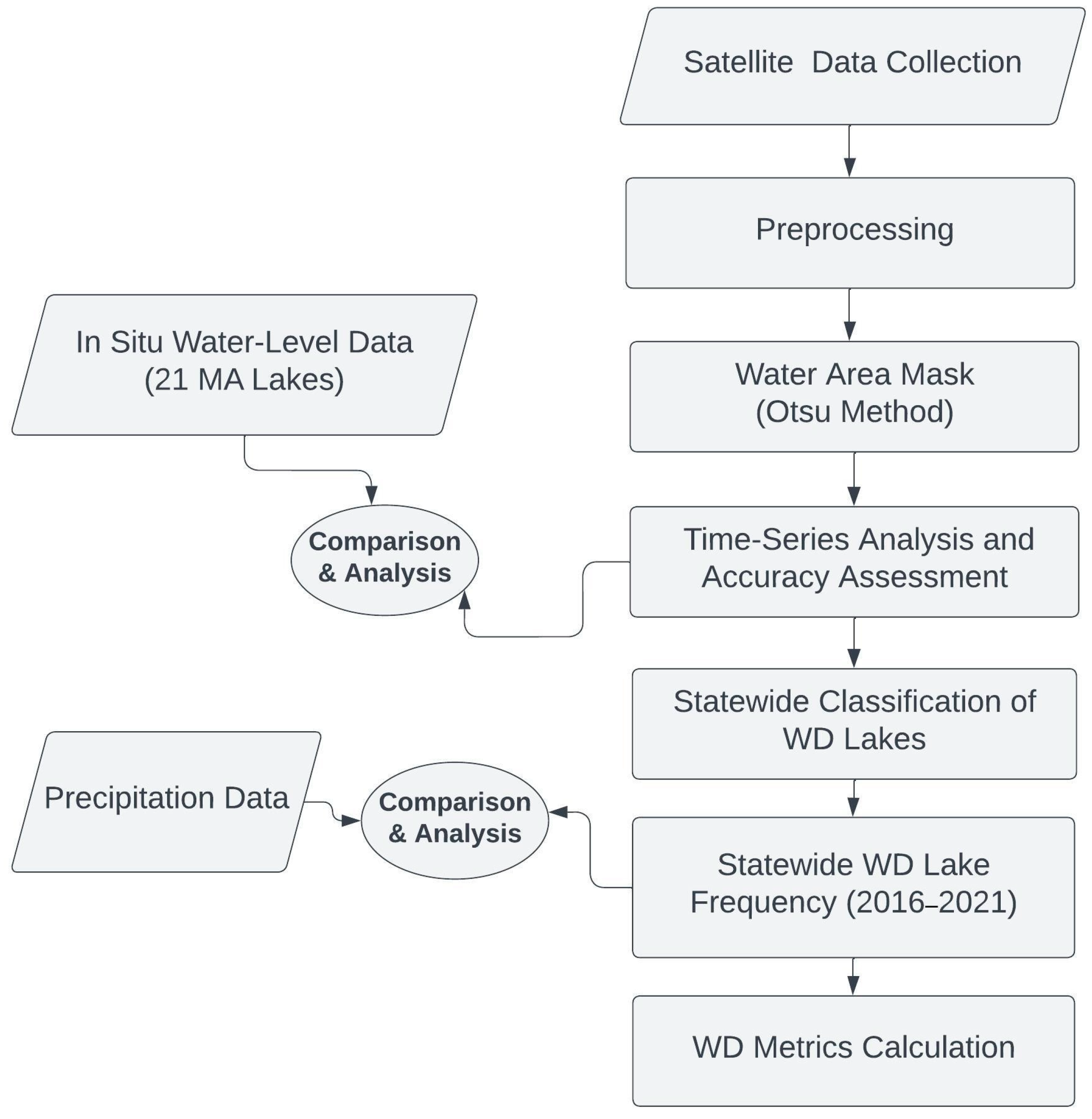
The overall methods including data collection, processing, and analysis steps involved to achieve the objectives of this study are shown in
Figure 2. The detailed descriptions of each component are presented in the following subsections.
2.2. Satellite Data Collection and Preprocessing
This study utilized two optical sensors (Landsat 8-Operational Land Imager (LS8-OLI) and Sentinel 2A/B-Multi Spectral Instrument (S2-MSI)) and one SAR sensor (Sentinel 1A/B-SAR (S1-SAR)) to generate surface water area data (
Table 1). To avoid the data download process, we used an online image processing platform (Google Earth Engine, GEE) to process and analyze the data derived from all three satellite sensors.
Top-of-atmosphere (TOA) reflectance (RTOA) level-1 data from both optical sensors (LS8-OLI and S2-MSI) were used as input for preprocessing within the GEE platform. For the S1-SAR sensor, C-band Ground Range Detected (GRD) raw data were already processed using the Sentinel 1 toolbox to produce calibrated, ortho-corrected scenes before they were made available to users on the Google Earth Engine platform. The preprocessing steps for optical sensors included cloud masking (for LS8-OLI and S2-MSI), resampling pixels to a common spatial resolution (30 m). The preprocessing steps for S1-SAR included spatial resampling at 30 m and speckle filtering. Both S2-MSI and S1-SAR sensors have multiple spatial resolutions and, therefore, spatial resampling was required to have a consistent spatial resolution. We resampled S1-SAR and S2-MSI pixels at a 30 m spatial resolution to have consistent comparison with respect to the LS8-OLI sensor’s spatial resolution. Cloud masking was performed using quality assurance bands available in both optical sensors.
The S1-SAR data available in GEE have two polarization modes, i.e., VV (vertical transmit/vertical receive) and VH (vertical transmit/horizontal receive). We used backscattering coefficients (dB) from only VV polarization mode because previous studies have found VV mode more suitable for surface water classification than VH mode [
36]. SAR sensors like the Sentinel 1 emit microwave pulses and measure the intensity of backscattered energy returning to the sensor. The strength of the backscatter signal depends on surface properties like roughness, moisture content, and structure [
37,
38]. For open water bodies like lakes, the smooth surface acts as a specular reflector that reflects most of the incident radar pulses away from the sensor, resulting in a very low backscatter and dark tone in SAR imagery [
39]. In contrast, vegetation, urban areas, and bare land have higher surface roughness, leading to diffuse scattering of radar pulses in multiple directions, including back to the sensor [
40], resulting in higher backscatter intensity and brighter tone compared to water. The raw S1-SAR data contain speckle noises which may result in misclassification of water area. To remove the speckle noises, a 100 m circular buffer was used within the GEE platform and pixels within that buffer were averaged.
2.3. Water Area Mask (Otsu Method)
Following preprocessing, we used an automated surface water classification algorithm known as “Otsu” [
41] to classify water and non-water regions. The Otsu algorithm is an unsupervised method that was originally developed to select a threshold for the reduction of a gray-scale image to a binary image containing two classes. The Otsu method is a complex, iterative process that selects an optimal threshold value separating two classes so that the between-class variance is maximized. To implement Otsu thresholding efficiently, we utilized JavaScript code developed by Zhou et al. [
42] within the GEE platform. The code implements the Otsu method in a simplified and efficient way by using the following steps: (a) it converts the input image to a gray-scale image and calculates the histogram of pixel values; (b) it iterates over all possible threshold values and computes the between-class variance for each value; and (c) it selects the threshold value that maximizes the between-class variance and returns it as the optimal threshold. The code simplifies the original algorithm by avoiding the use of complex mathematical formulas and matrix operations. Instead, it leverages the built-in functions of the Google Earth Engine platform, such as ee.Image.reduceRegion and ee.Image.select, which are optimized for large-scale image processing. The Otsu code by Zhou et al. [
42] was written for S1-SAR data and, thus, we modified the Otsu code for optical sensors (LS8-OLI and S2-MSI) using the short-wave infrared (SWIR) band as input image. In the SWIR band, water absorbs the incoming solar light strongly, and a bimodal histogram is observed. In addition, the SWIR band is also less affected by turbid water and atmospheric noise compared to the near-infrared (NIR) band used in initial studies for surface water area classification. We used the optimal threshold computed by the Otsu method in a conditional expression to classify water areas below that optimal threshold value. The surface water area was derived by counting the number of water pixels and multiplying that value to each pixel area (30 m × 30 m = 0.0009 km
2).
2.4. Time-Series Analysis and Accuracy Assessment
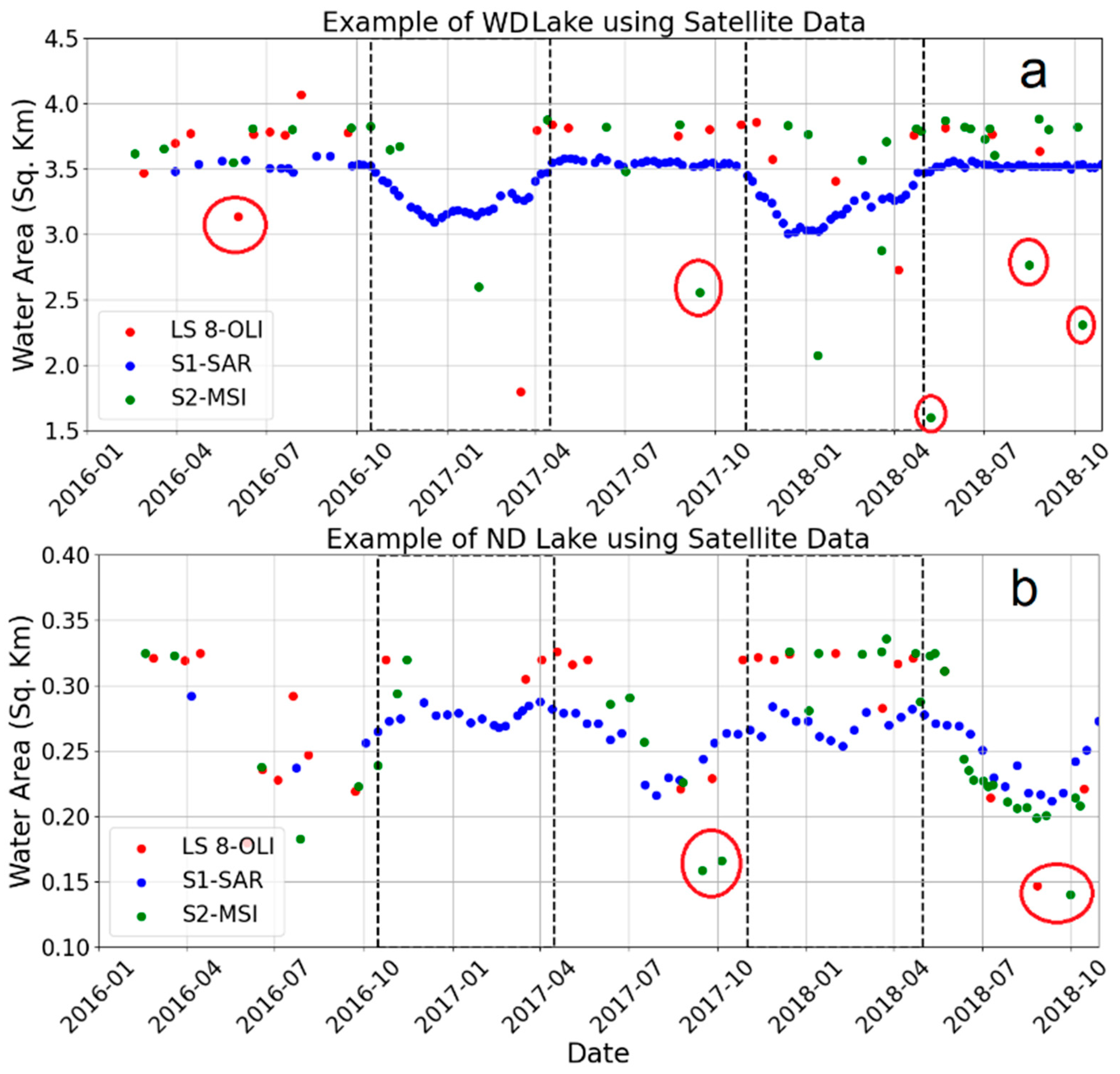
To differentiate WD and non-drawdown lakes, we extracted surface water area time-series (2016–2021) data from both optical and SAR sensors. We selected 2016–2021 for data extraction because data from both optical and SAR sensors were available during this period, allowing us to compare the time-series results from all three sensors (LS8-OLI, S2-MSI, and S1-SAR). Using these three sensors, we compared the trend between satellite-derived surface water area and in situ water level. We used all the available common dates between satellite and in situ data to compare surface water area time series derived from satellite data and 24 h mean in situ water-level data for 21 MA lakes. To compare in situ water-level data with satellite-derived surface water area, bihourly water-level data were averaged for 24 h to obtain the mean daily water level.
To assess accuracy, we first found the total number of matched dates between the available satellite images and in situ logger data during the study period for each of the 21 lakes. We then qualitatively examined the alignment in the patterns and trends between the satellite-derived surface water area time series and the in situ water-level time series. We looked for consistent increases and decreases that aligned between the two datasets, indicative of accurate capture of water-level fluctuations. We assessed accuracy of the satellite data by comparing the magnitude and spatiotemporal trend of surface water area to those of in situ relative water-level data. In situ water-level data were available from 18 WD lakes and 3 non-drawdown (ND) lakes in MA (
Figure 2; [
2]). Lakes varied in surface area (0.19–4.21 km
2), mean depth (1.5–7.6 m), and maximum depth (3.0–25.7 m). The data were collected using pressure transducers (Onset HOBO U20L-01, Bourne, MA) bihourly for 3–4 years (2014–2018). More details on in situ water-level data can be found in Carmignani et al. [
2].
We assessed how lake size, shape, and shoreline slope affected the surface water area trend when compared to in situ water-level time-series data. Some lakes were very narrow in shape (Hamilton), some with dendritic geometry (Wyman) and some with wide surface area (Stockbridge, Richmond, Wyola). For shoreline slope, we used digital bathymetry maps of lakes (
Supplementary Materials Figure S1) to interpret the surface water area fluctuation observed in satellite maps. Surface water spatiotemporal maps were produced in the GEE platform for selective WD lakes before, during, and after winter drawdown.
2.5. Statewide Classification of WD Lakes
Using the US Fish and Wildlife Service National Wetland shapefile of lakes, we extracted surface water area data from October 2014 to October 2021 for all MA lakes >0.3 km
2 (166 lakes) using S1-SAR data in the GEE platform. We empirically determined the 0.3 km
2 threshold by evaluating the accuracy of the satellite-derived water area measurements against in situ water-level data for a subset of MA lakes ranging in size from 0.1 km
2 to 15 km
2. Other studies have also found that accuracy of satellite-based lake water area extraction decreases for smaller water bodies without specifying any size threshold [
43,
44,
45]. While the 0.3 km
2 cutoff was suitable for reliably monitoring water level fluctuations in our MA lake dataset, further accuracy assessments would be required to determine an appropriate minimum lake size threshold if applying this method in other geographic regions. After applying the 0.3 km
2 cutoff, we exported the time-series surface water area data from the GEE platform in .csv format for further analysis.
To differentiate WD lakes from ND lakes, Carmignani et al. [
2] divided each annual cycle (April to March) of in situ water-level data into summer (April to September) and winter (October to March) periods. They found that WD lakes exhibited significantly lower water levels during the winter compared to summer, while ND lakes showed the opposite seasonal pattern. We implemented a similar seasonality-based classification idea in an automated way using a machine learning technique which takes time-series data as input to classify WD lakes. We used K-nearest neighbor (KNN) to classify the time series of WD and ND lakes. This method can handle large datasets and automates the WD lake characterization process. To implement this classification algorithm, we used a Python library package, tslearn (
https://github.com/tslearn-team/tslearn, accessed on 1 December 2022).
To implement the KNN classification model, continuous time-series data were required as input. Therefore, we used linear interpolation between the actual Sentinel 1 observation dates (~6 days) to generate daily surface water extent values for each lake. This allowed creation of a consistent time-step series across all lakes for model implementation. While interpolation introduces some uncertainty on days without true observations, we chose linear interpolation as a simple method to create a continuous dataset while minimizing assumption of non-linear changes between observations. Importantly, the ~6 days revisit frequency still captured the major seasonal fluctuations in water levels critical for distinguishing winter drawdown. We excluded outliers in the time-series data using a 95% confidence interval and standardized the data using a normalization method (min–max).
To classify the lakes with in situ data, we used a 7-fold cross validation approach to maximize the data for model training. We used a stratified sampling approach based on the WD and ND classes of the lakes to ensure a balanced representation of both classes in the training and testing datasets. Out of 44 WD lake samples (10 lakes × 2 yrs = 20; 8 lakes × 3 yrs = 24), we used 30 samples for training and 14 samples for testing. Out of eight ND lake samples (2 lakes × 3 yrs = 6; 1 lake × 2 yrs = 2), we used five samples for training and three samples for testing. Cross-validation was performed using the test dataset (WD = 14, ND = 3) in seven iterations. We divided the test dataset of 17 total lakes (WD = 14, ND = 3) into 7 groups, each containing 3 lakes (2 WD and 1 ND lake). For each fold, the 3 lakes were held out for model testing while the remaining 14 lakes were used for model training. In each iteration, we used 49 samples for training and 3 samples for testing. We used different test samples in each of the seven iterations to cover all test samples. The accuracy results were then averaged across the seven folds. We also examined the effect of the time window on classification accuracy. Time windows included 12 months, 6 months (August to December), and 3 months (October to December). We followed the same procedure: three test samples at a time and averaging the accuracy across seven iterations for the time-window experiments.
For satellite data classification, we selected 38 known lakes (WD = 24; ND = 14) with either WD history or no history of WD based on a survey result conducted by Carmignani et al. [
2]. We used 5 years (April 2016–March 2021) of surface water area time-series data for training and testing the accuracy of the classification model. For training, we used a total of 140 samples (WD = 90 samples (18 lakes × 5 yrs); ND = 50 samples (10 lakes × 5 yrs)) and for testing, we used a total of 50 samples (WD = 30 samples (6 lakes × 5 yrs); ND = 20 samples (4 lakes × 5 yrs)). We used a combination of lakes in both training and testing datasets to avoid any site-specific bias in the result. Similar to in situ analysis, we used 12-month, 6-month, and 3-month time series during the classification. Once we finalized the best time window for satellite-based classification, we combined the accurately classified WD and ND lakes samples from both training and testing datasets to create a master training dataset for classifying all 166 lakes in MA.
To our knowledge, this study represents the first application of machine learning techniques to satellite data for statewide mapping and classification of WD versus ND lakes. While past studies have focused on manual classification of individual or small groups of lakes, our method allowed efficient classification of drawdown status across 166 lakes in Massachusetts.
2.6. Statewide WD Lake Frequency (2016–2021) and Precipitation Data
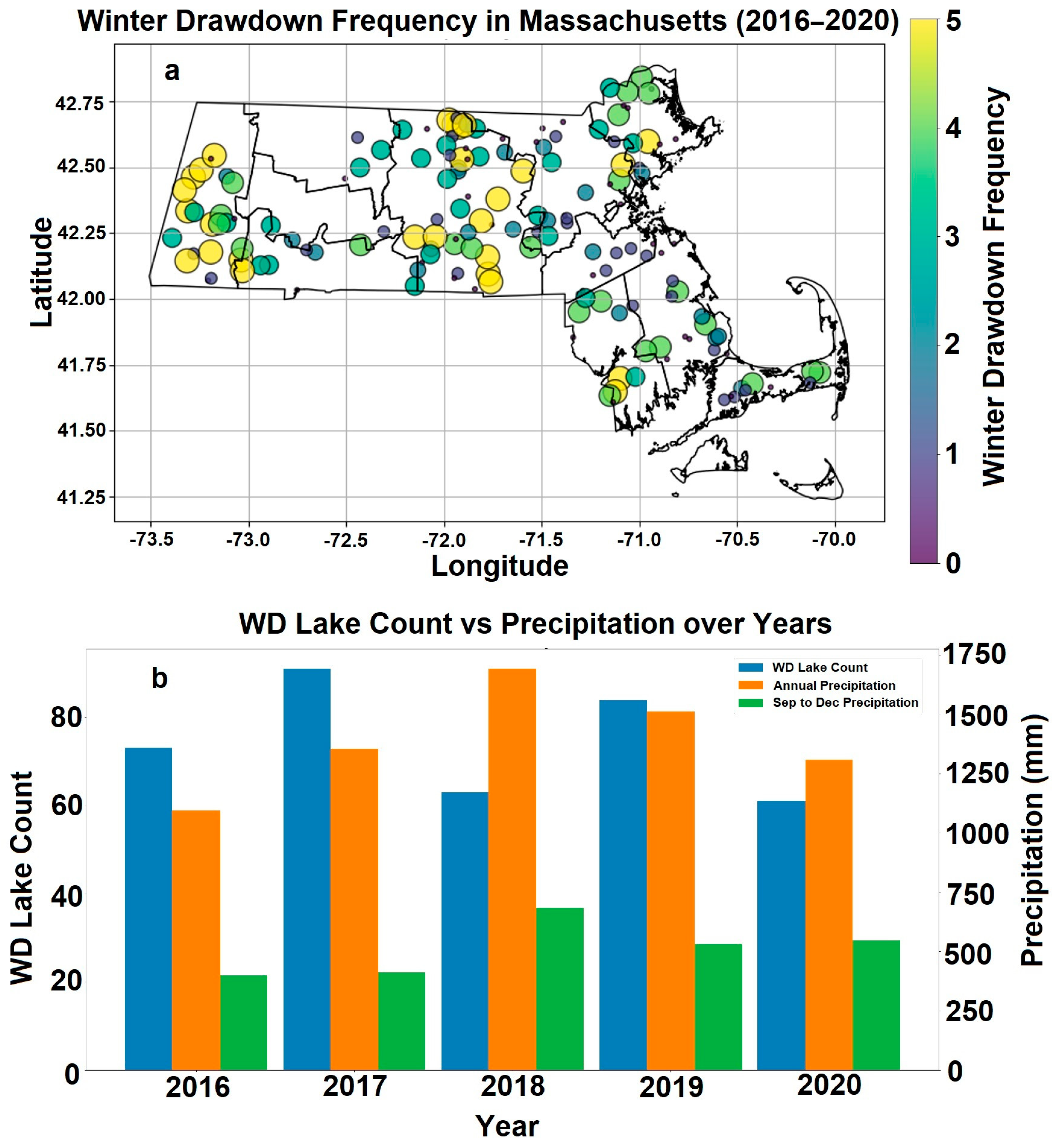
We created a statewide WD frequency map for 166 lakes using satellite-based classification data between 2016–2021. The multi-year statewide frequency mapping provides novel insights into the spatial patterns and prevalence of winter drawdown practices not feasible through analysis of individual lakes. The annual classification for each lake was performed by implementing the ML-based time-series algorithm based on the tslearn package [
46]. This algorithm can capture the shape and similarity of time-series data, but it may not account for the seasonality and trend of the data. Therefore, we applied some post-processing steps to filter out the false-positive WD lakes using the seasonality and trend information. We calculated the slope of the water level between 1 October and 1 December for each year, which is the expected period of water-level decrease for WD lakes. If the slope was positive, indicating an increasing water level, we reclassified the lake as a ND lake. We also reclassified the lakes with WD starting dates beyond 31 January as ND lakes, because winter drawdown operations usually end by the end of January. We performed these post-processing steps to improve the accuracy of classification of WD lakes. These post-processing steps were simple and easy to implement compared to complex preprocessing techniques such as deseasonalization and detrending the time-series data. In addition, WD lakes exhibit a distinct seasonal decline in water levels during fall–winter months, while ND lakes do not show this sharp downward trend. Removing the seasonal component through deseasonalization may eliminate this key differentiation in hydrologic regimes that the model uses for classification. Likewise, not detrending retains the directionality and magnitude of water-level changes that distinguish drawdown versus non-drawdown lakes. However, exploring preprocessing techniques as an option to potentially improve classification is an area for future refinement.
To assess the effect of precipitation on WD frequency, precipitation data for MA were downloaded from NASA’s Giovanni web interface for 2016–2020. The GPM monthly precipitation product (GPM_3IMERGM_07) was downloaded for the entire state and then county-wide data were extracted using MA county shapefiles to exclude data from islands. We extracted both annual (12 month) precipitation and precipitation data for September to December for each of the five years.
2.7. WD Metrics Calculation
A unique aspect of this study was the development of methods to automatically calculate key WD metrics including timing, duration, magnitude, and lake area exposure using satellite-derived lake water levels. Automatic calculation of these metrics allowed efficient quantification of drawdown characteristics across many lakes and years. We calculated WD metrics for each of the five years for WD lakes using the MA time-series data (see, as an example,
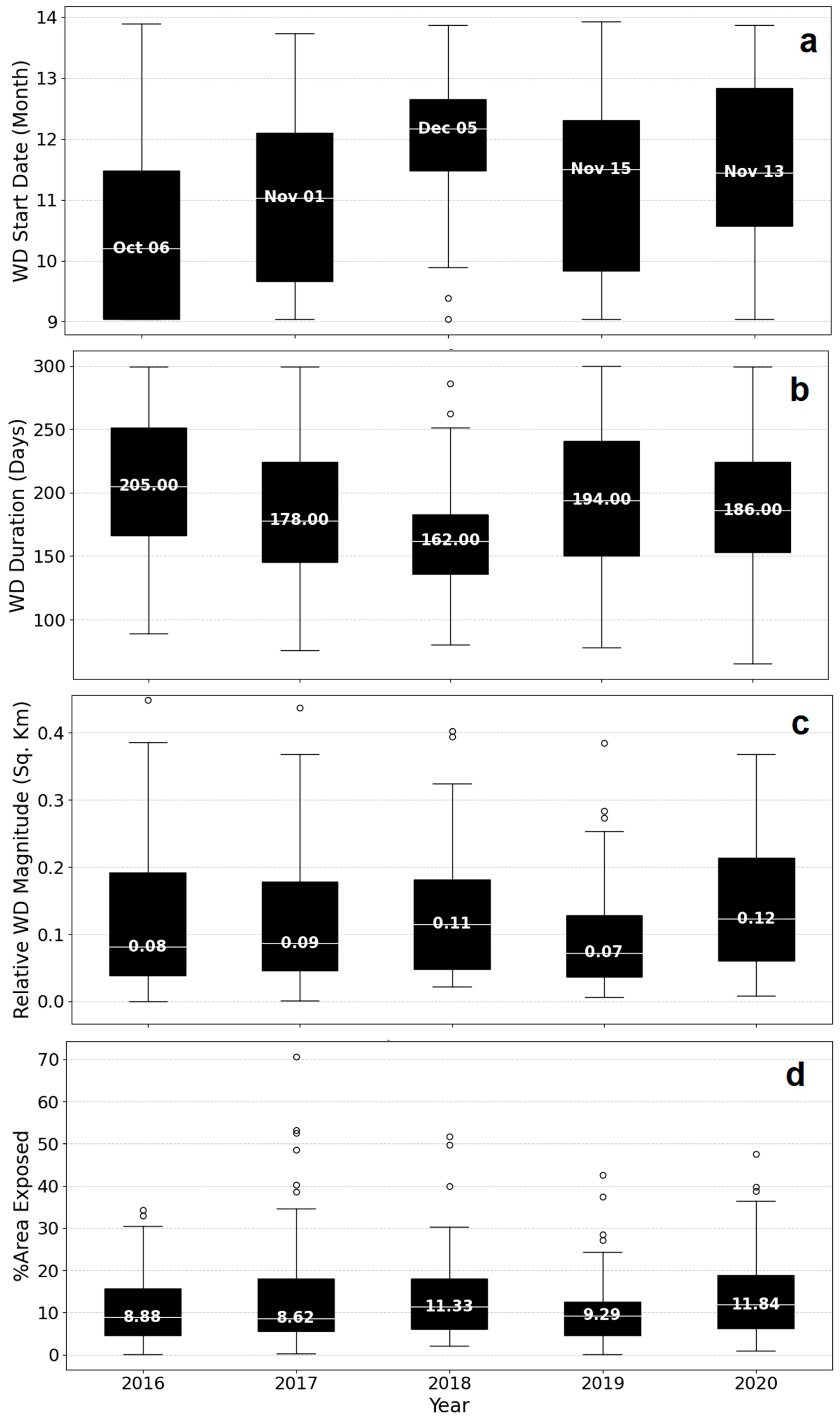
Supplementary Materials Figure S2). To determine WD metrics, we used 1 September as the starting window to exclude any drawdown happening before this date. We used a criterion of a consistent decline in water level until it reached the lowest level to determine the start of WD. Within such a consistent decline, we derived the first date of such a consistent decline as the WD starting date. Then, to find out the relative WD magnitude, we first determined the reference pool level (RPL) for each year and the lowest magnitude during the WD phase. To determine the RPL, we used a time window of 1 week before and after the maximum value post-lowest water level and then computed the median value within that 14-day window (±1 week of maximum value). We subtracted the lowest water level from the RPL value to derive the relative WD magnitude for each lake and for each year. We considered the first time when the water level reached the RPL after WD as the end of WD. WD duration was calculated as the difference between the end of WD and the start of WD. Finally, we computed the percentage of lake area exposed (%LAE) during the WD phase as Equation (1). We created boxplots for each metric across five years to show the annual variability as well as the variability across WD lakes. Correlation analysis was also used to show relationships among metrics and variability within and across years.
where %LAE = percentage of lake area exposed at lowest water level,
WA (
RPL) = water area at reference pool level, and
WA (
Lowest level) = water area at the lowest winter water level.
4. Discussion
Our study demonstrated the utility of freely available multi-sensor satellite data in the GEE platform for characterizing winter water-level drawdowns across lakes in Massachusetts. Among the three sensors compared, S1-SAR provided the most consistent and gap-free time-series data to differentiate drawdown and non-drawdown lakes compared to optical sensors which were prone to cloud cover and sun glint effects. The machine learning-based time-series analysis accurately classified drawdown and non-drawdown lakes using both in situ and S1-SAR data when a 3-month period (October–December) was used. Leveraging GEE and machine learning approaches, we were able to conduct a comprehensive analysis of statewide lakes (166 lakes > 0.3 km2) and identified drawdown frequency and WD metrics over a 5-year period. Interannual variability in metrics suggested that WD is primarily a managed activity rather than driven by precipitation variability. The same approach can be extended to broader areas and regions to assess the impacts of WD on lake ecosystems and water resources.
4.1. Effectiveness of Sensors for Capturing Water Area and Water-Level Fluctuations
We conducted a robust accuracy assessment of different satellite sensors for capturing water-level variations during the challenging winter season. Our analysis identified Sentinel 1-SAR as the most reliable for capturing winter water-level variations indicative of drawdown practices. Our results demonstrated some of the major advantages of SAR over optical sensors for mapping surface water extent under problematic conditions like cloud cover, sun glint, and ice cover. Optical sensors like Landsat and Sentinel 2 have been used widely for water body mapping [
48,
49] but are limited by an inability to penetrate cloud cover. Several studies have shown SAR provides consistent water extraction unaffected by clouds or sunlight angle [
19,
26]. Our analysis matched these past findings, with frequent cloud gaps and sun glint artifacts in the Landsat and Sentinel 2 time series. SAR has also been found to better characterize lakes during ice cover compared to optical data [
50,
51], though accuracy declines once the lake fully freezes over [
52,
53,
54] and it results in overestimation of water area due to specular reflection from a smooth surface. A hybrid approach incorporating optical and SAR data could help address this limitation during winter. Overall, Sentinel 1 provided consistent time-series data on surface water extent changes that served as a proxy for relative water-level fluctuations in lakes during fall drawdown and spring refill periods.
The time-series analysis of surface water extent changes derived from S1-SAR aligned well with in situ logger data. The relationship between satellite-derived surface water area and relative in situ water-level fluctuations has been assessed in multiple past studies [
43,
55,
56]. Strong correlations are typically found for lakes with gradual slope shorelines, low shoreline-to-surface-area ratios, and well-defined boundaries [
43,
57]. The small discrepancies between SAR-derived area and in situ water levels could be attributed to factors such as wind, shoreline slope, frozen lake surface, size and shape of the lake, in situ data logger deployment location, and drawdown magnitude [
43,
57,
58]. Shoreline slope influences the extent of water-level change that is detectable through area change. For instance,
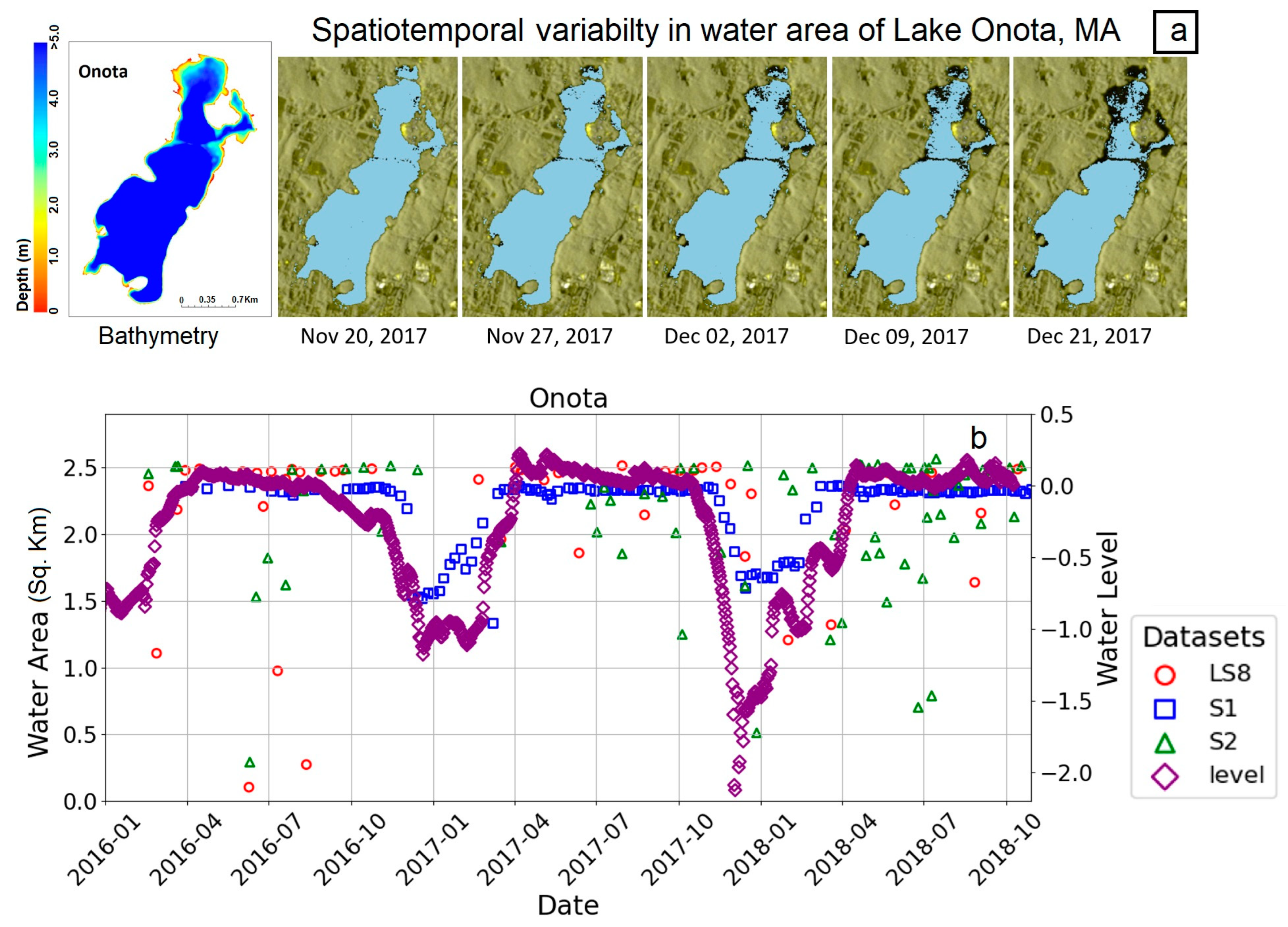
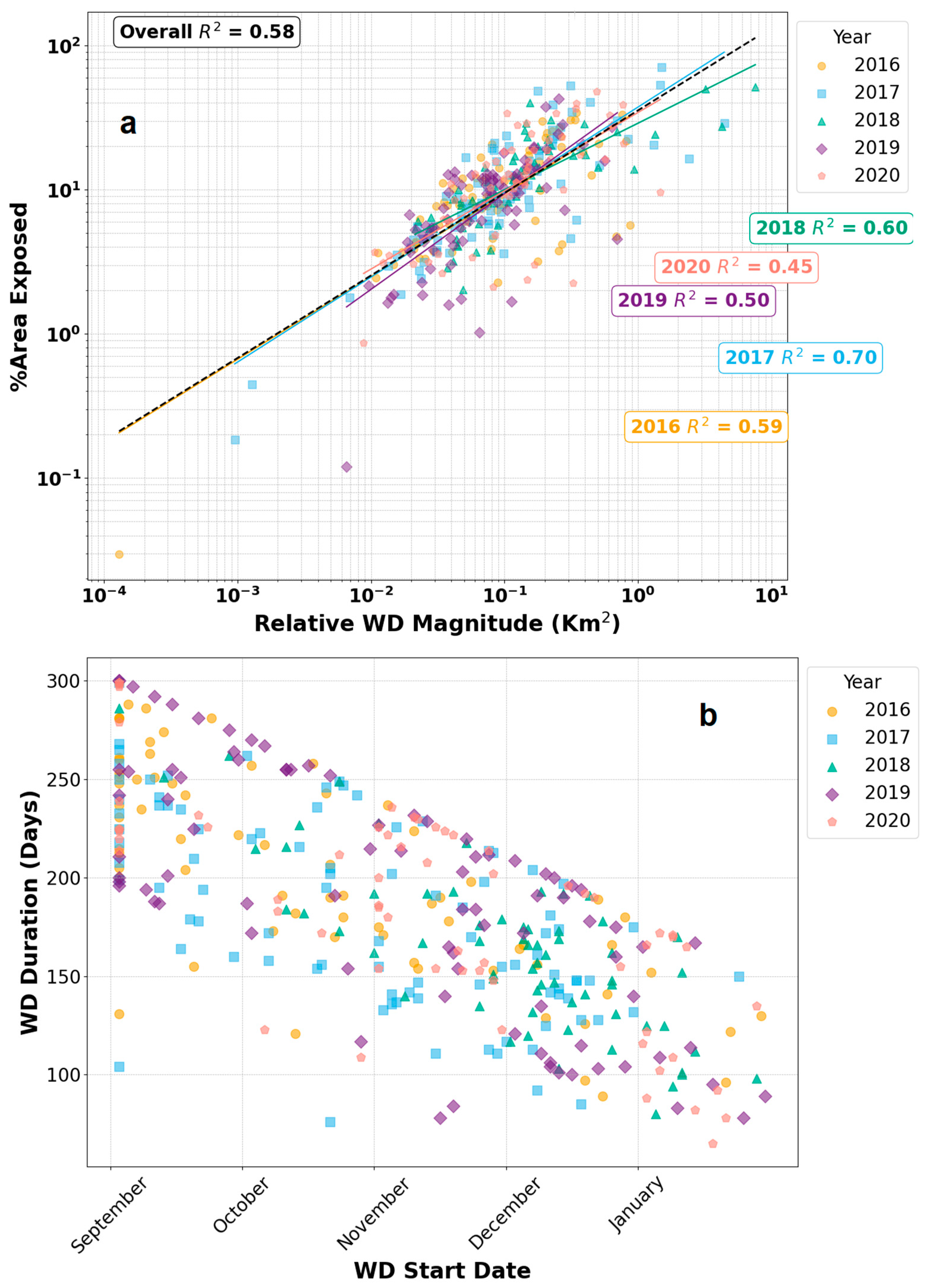
Figure 5b shows significantly lower areal change compared to the relative water-level fluctuation. Steeper slopes result in smaller areal changes relative to water level fluctuations. Moderate sloping shorelines are more suitable for detecting gradual water-level changes [
58]. Additionally, frozen lake surfaces can mask the open water–ice boundary used to estimate area as water levels decline under ice.
Busker et al. [
43] observed lower accuracy for smaller waterbodies but mentioned that along with size, there are many other factors which may contribute to accuracy such as surrounding topography, surface waves, winter ice coverage, and shape of the water body. Keys and Scott [
57] found that lakes with dendritic geometry resulted in poor results compared to lakes with well-defined boundaries. We also observed the effect of size, shape, and shoreline slope effect on accuracy when comparing satellite-derived results with in situ water-level measurements for 21 lakes in MA. For example, lakes with smaller size (<0.3 km
2) (Cranberry Meadow, Silver, Brookhaven) showed more random fluctuations in water area and did not align with in situ water level, whereas lakes with relatively larger size (Otis, Onota, Stockbridge, Goose, Garfield, Richmond, Ashmere) aligned well with in situ water-level fluctuations. For some moderately sized lakes (0.4 to 0.9 km
2) with steeper bathymetry sloping (Buel, Watatic, Quacumquasit), water area did not show a similar trend compared to that observed in in situ water levels. In addition, the nature of the shoreline bathymetric gradient can also introduce lag between satellite-derived water area and in situ water levels. This is mainly because small water-level drops may not expose much area until a certain depth threshold is crossed. We observed a time lag between the satellite-derived surface water area recovery and the in situ water-level recovery in spring (e.g.,
Figure 5b). This time lag varies from lake to lake based on lake size, bathymetric profile, and shoreline slope of the lakes. The primary physical reason for such variable time lag could be the in situ sensor deployment location because in situ sensors provide measurements at a discrete point location, while satellite imagery provides water area variations for overall lakes. If water levels are increasing first in shallow, near-shore regions distant from the sensor, this could introduce a lag before the in situ gauge starts to record the rising water. Lakes with dendritic geometry (Wyman, Boon) and narrow shape (Hamilton) also showed poor alignment with in situ water levels. Though there exist the above factors which may affect the accuracy of satellite-derived water-level fluctuations, nonetheless, the S1-SAR observations provided indicative relative changes in lake water levels useful for assessing winter drawdown practices.
4.2. WD Frequency in MA Lakes
Using the extracted water area time-series data, a machine learning approach was implemented to classify WD versus ND lakes based on their seasonal water-level fluctuation patterns. Using both in situ and satellite training data, the classification accuracy was highest when using just a 3-month (October–December) time window compared to longer 6- and 12-month periods. The 6-month and 12-month time window classifications could be affected by drawdown during summertime and may result in misclassification of ND lakes as WD lakes (false positive). The 3-month window (October–December) captures the active drawdown phase when water levels steadily decline in WD lakes in MA in contrast to ND lakes that show seasonal variability but not large directional changes during fall–winter months [
2]. Potential uncertainty exists from the linear interpolation used to create daily water extent values between actual Sentinel 1 observation dates. Future work could incorporate methods to estimate non-linear changes during intervals between satellite observation dates. A limitation of the machine learning model’s development was the imbalance between the number of WD and ND samples available for training and testing the classification. The disproportionate sample sizes between classes may have biased the accuracy results in favor of the majority WD class. While we used cross-validation approaches to account for the imbalance, it may have introduced some bias favoring the majority WD class. Increasing the ND sample size in future could improve accuracy, particularly the false-positive rate. However, the overall accuracy achieved even with imbalance classes demonstrates the potential of machine learning for automated WD classification using remote sensing time-series data.
The statewide mapping indicated that drawdowns are widely practiced across MA. Over 75% of lakes >0.3 km
2 had at least one WD during the five study years, indicating it is a common management practice. There was high interannual variability in the number of lakes conducting drawdowns each year, which cannot be explained by precipitation alone. These results concur with the findings of Carmignani et al. [
2] who concluded that drawdowns are primarily based on management decisions rather than climate factors. Although our study did not survey lake managers, documented reasons for conducting drawdowns include aquatic plant control, fisheries management, infrastructure maintenance, and waterfront access [
35]. Additional social surveys across private and public lake managers could provide further insights into motivations behind drawdown decisions each year.
4.3. Variability in WD Characteristics in MA Lakes
The WD metrics provide new insights into the characteristics of this artificial hydrologic alteration across MA lakes. A few studies have analyzed drawdown trends for groups of lakes in particular regions [
2,
59]. Some drawdown studies have calculated similar water-level metrics using in situ data [
1,
2], but the remote sensing-derived measurements allow assessment at broader scales. Quantifying drawdown timing, magnitude, duration, and lake exposure area provides tangible metrics for evaluating ecological impacts and comparing across years and lakes [
35].
Our analysis of WD metrics revealed high interannual variability in magnitude of drawdowns and lake area exposure. We observed an interesting relationship between precipitation, water-level drawdown magnitude, and lake area exposure in studied lakes over the 5-year study period. The positive association observed between precipitation and drawdown magnitude suggests that higher rainfall leads to greater water inputs and rising lake levels prior to drawdown, subsequently enabling larger drawdowns. This is evidenced by the highest precipitation, drawdown magnitudes, and among-lake variability in 2018, followed by declines in 2019. However, the rebound in drawdown magnitude from 2019 to 2020 despite declining precipitation illustrates that other factors beyond rainfall also govern drawdown dynamics. Specifically, while precipitation governs water inputs, drawdown on lake water for irrigation, municipal use, and hydroelectric generation may drive drawdown magnitude.
In contrast to drawdown magnitude, we did not see a significant relationship between precipitation and lake area exposure during drawdowns. Exposure remained relatively stable across all five years, with the lowest exposure again in 2019. This suggests area exposure may be controlled more by the morphology of lake basins and maximum drawdown depths, rather than by precipitation inputs. Furthermore, the lack of a relationship between precipitation and lake area exposure indicates that drawdown regulations successfully maintain a consistent exposed area, despite varying water levels. Overall, our findings highlight that both climate and human factors regulate lake water balances and interact to drive interannual variation in drawdown magnitude, underscoring the complexity of predicting lake responses to future environmental change. A priority for future research could be quantifying water consumption and evaluating how shifting human demand interacts with climate to control lake water levels and ecological impacts of drawdowns. Metrics like exposure area help translate the water-level changes to a habitat context. The exposure of up to 30% of lake areas for months at a time may have ecological impacts.
Considerable interannual variability was also observed in drawdown start date and duration, which correlated with precipitation patterns. While managers ultimately decide when to lower water levels each year, total annual precipitation and specifically fall precipitation appeared to influence drawdown start date and duration. Median start date showed an increasing trend between 2016–2018 aligned with precipitation patterns. This suggests that wetter conditions could delay the onset of drawdowns. In contrast, duration declined with increasing precipitation, indicating earlier refilling of lakes in wetter years. This indicates that natural hydrologic conditions mediate aspects of drawdown implementation; however, these relationships need to be interpreted cautiously given the short five-year study period. As more satellite data become available, they can strengthen the analysis of relationships between climate, management practices, and drawdown characteristics.
4.4. Web Application Interface
To facilitate broader access and use of the satellite-derived lake characterization technique outlined in this study, we developed an interactive web application leveraging the GEE platform [
60]. This interface allows users to visualize and download the remotely sensed time series of lake water areas and corresponding water-level estimates for over 10,000 lakes across the northeast and upper Midwest United States. By leveraging cloud computing capabilities, the tool provides rapid access to consistently processed satellite imagery with just a few clicks. Users can zoom to a lake of interest, specify a date range, and immediately generate plots and download data. While currently limited to partner states, the application code could be adapted to monitor additional regions. Detailed documentation on the interface capabilities, underlying methodology, and potential limitations can be accessed at this link (
https://tinyurl.com/yxnernxv, accessed on 1 December 2023). Overall, this web-based decision support tool represents an innovative approach to openly share and apply the remote sensing-derived water-level data to address diverse freshwater science and management needs.