Spatial Resolution Enhancement of Vegetation Indexes via Fusion of Hyperspectral and Multispectral Satellite Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Hyperspectral and Multispectral Scanners from Space
2.2. A Review of Hyper-Sharpening
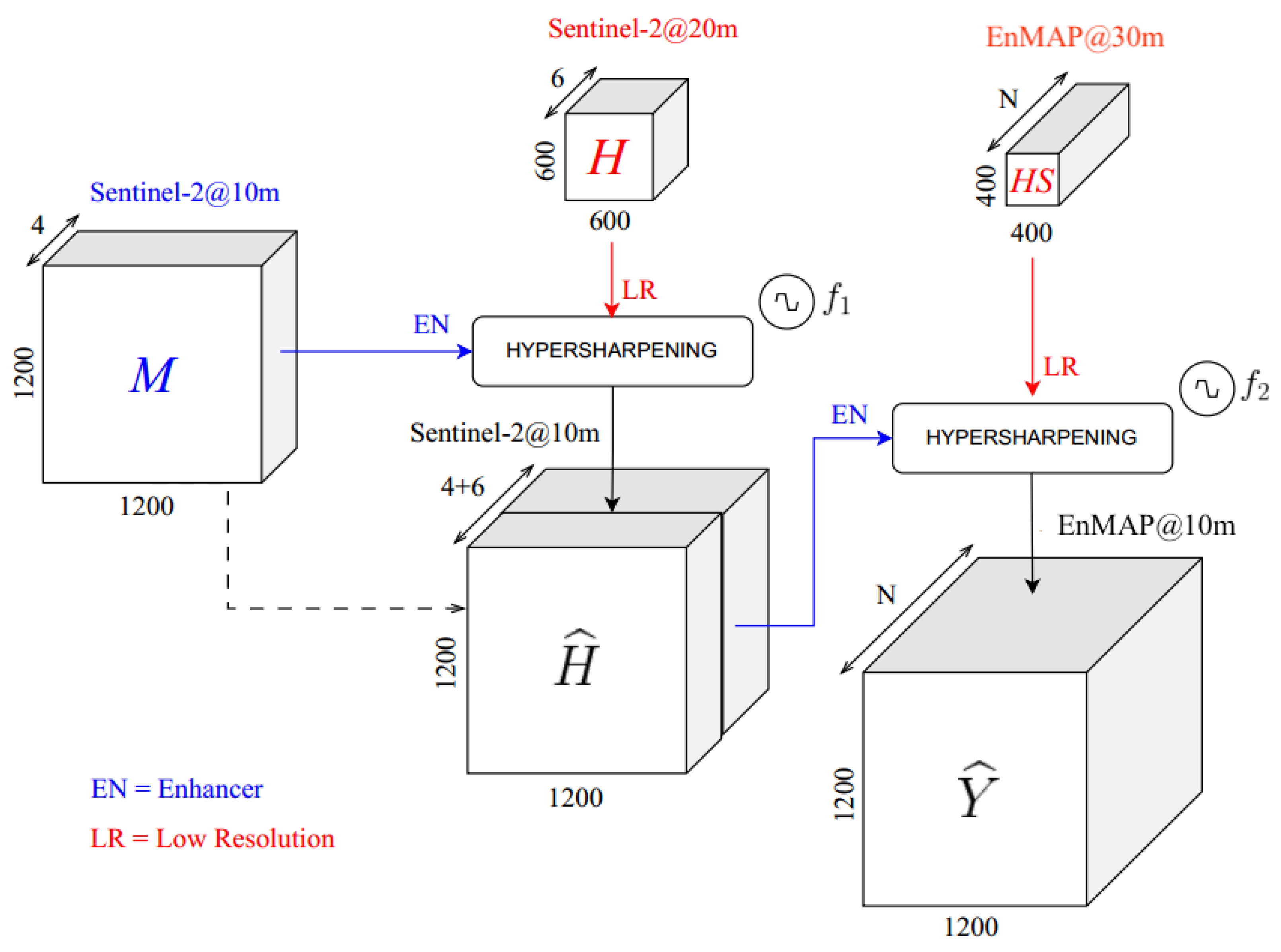
2.3. Flowchart of the Proposed Method
- The N 30 m HS bands, EnMAP in the present case, are hyper-sharpened at 10 m by means of a combination of the 10 m Sentinel-2 bands, four original and six hyper-sharpened, as described in Step 1. Each 30 m HS band is spatially enhanced at 10 m according to the hyper-sharpening protocol in Equations (1)–(4).
2.4. Statistical Quality Assessment of the Fused Dataset
2.5. Extraction of Biophysical Parameters from HS and MS Data
3. Results
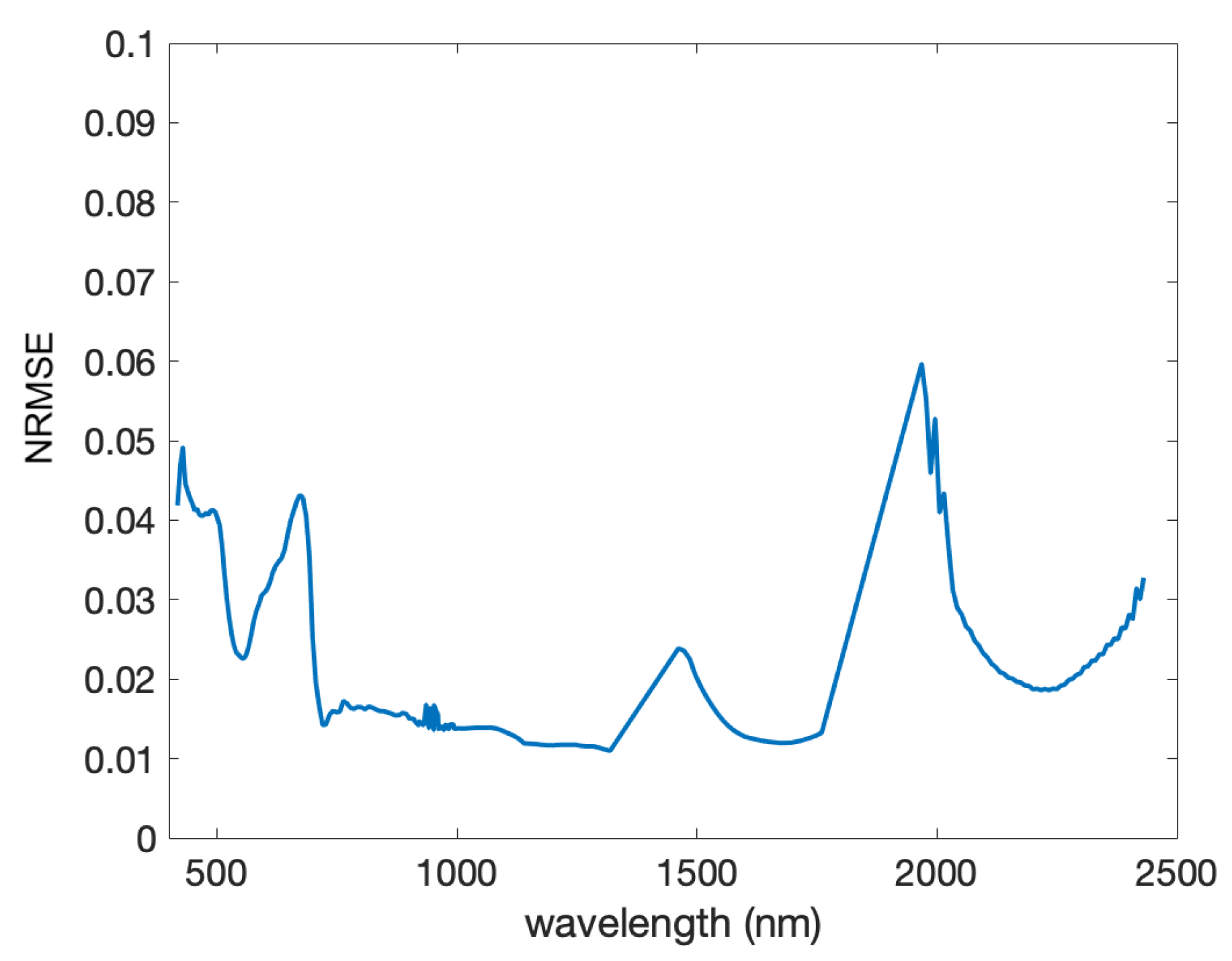
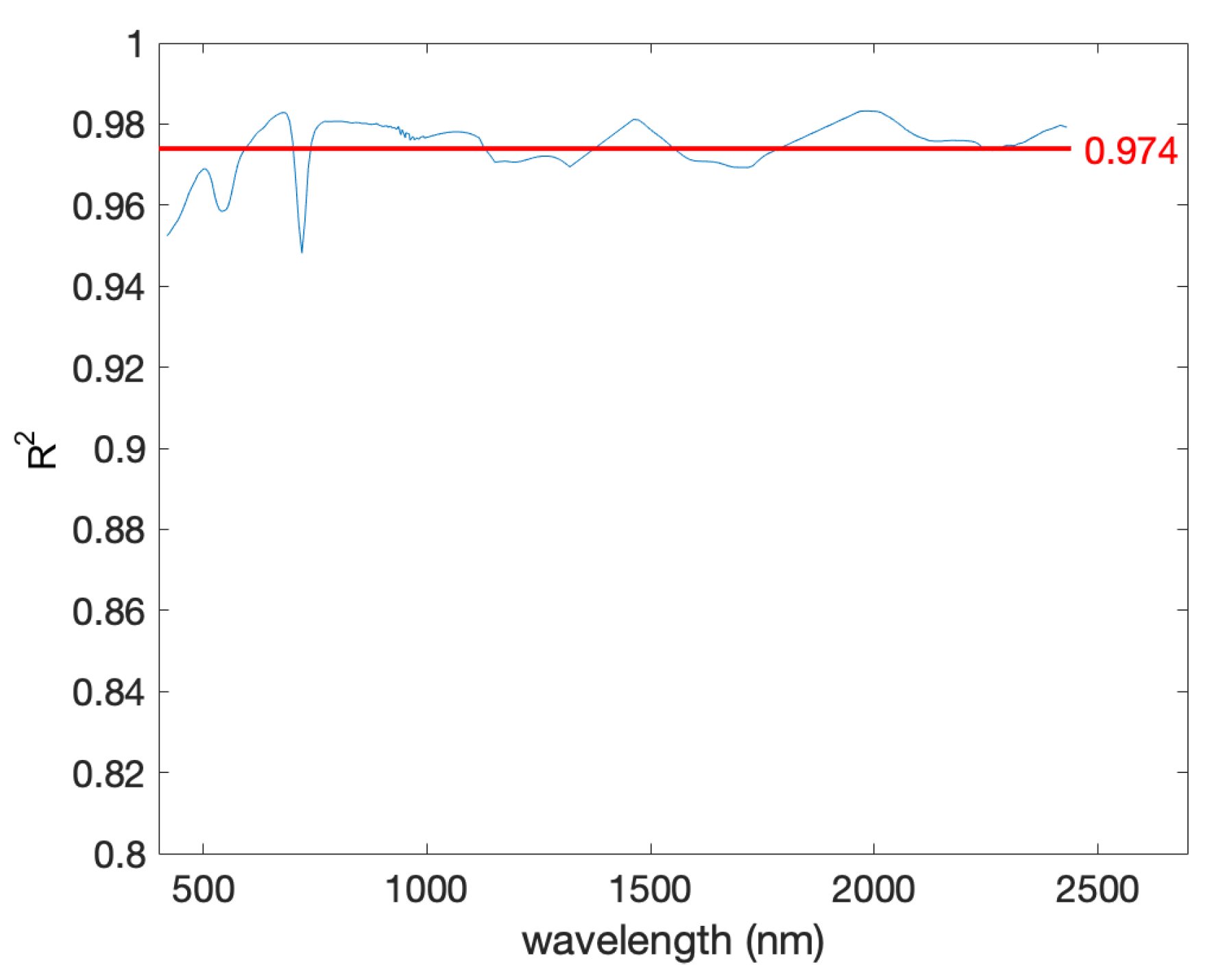
3.1. Fusion Simulations
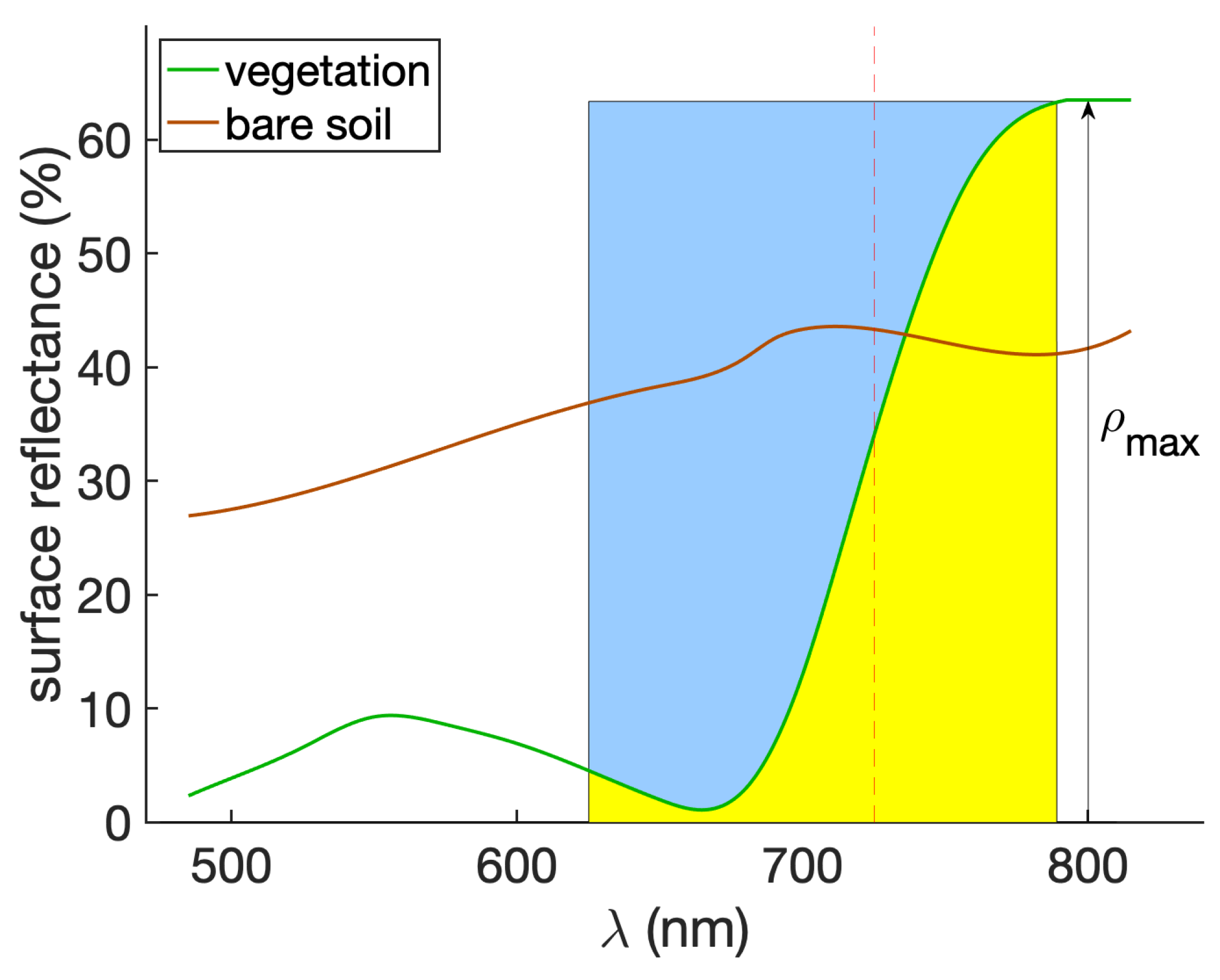
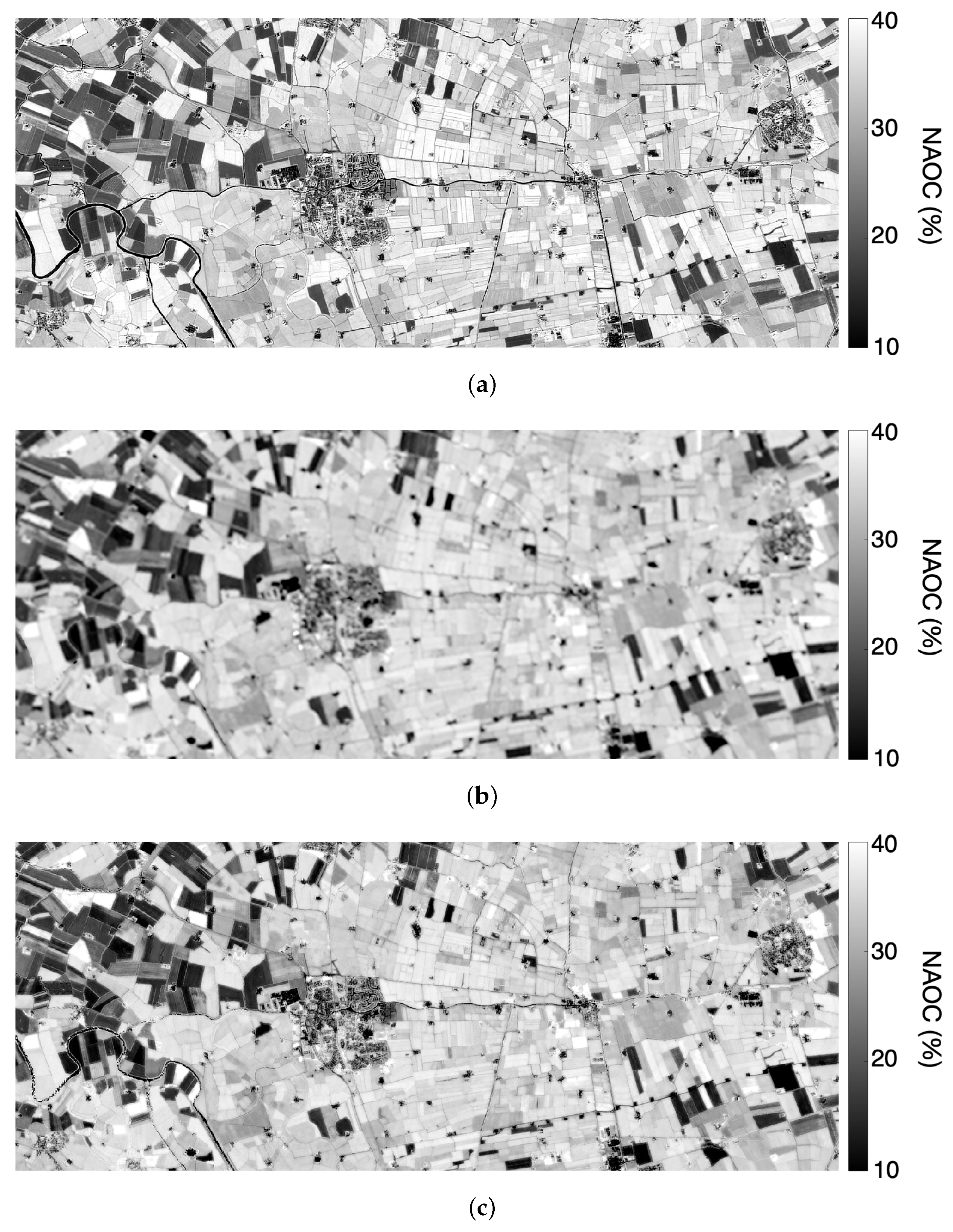
3.2. Extraction of Vegetation Indexes
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cho, M.A.; Skidmore, A.K. A new technique for extracting the red edge position from hyperspectral data: The linear extrapolation method. Remote Sens. Environ. 2006, 101, 181–193. [Google Scholar] [CrossRef]
- Delegido, J.; Alonso, L.; González, G.; Moreno, J. Estimating chlorophyll content of crops from hyperspectral data using a normalized area over reflectance curve (NAOC). Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 165–174. [Google Scholar] [CrossRef]
- Herrmann, I.; Pimstein, A.; Karnieli, A.; Cohen, Y.; Alchanatis, V.; Bonfil, D. LAI assessment of wheat and potato crops by VENµS and Sentinel-2 bands. Remote Sens. Environ. 2011, 115, 2141–2151. [Google Scholar] [CrossRef]
- Vivone, G. Multispectral and hyperspectral image fusion in remote sensing: A survey. Inform. Fusion 2023, 89, 405–417. [Google Scholar] [CrossRef]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A. Remote Sensing Image Fusion; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Selva, M.; Aiazzi, B.; Butera, F.; Chiarantini, L.; Baronti, S. Hyper-sharpening: A first approach on SIM-GA data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3008–3024. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Lastri, C. Crisp and fuzzy adaptive spectral predictions for lossless and near-lossless compression of hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2007, 4, 532–536. [Google Scholar] [CrossRef]
- Karoui, M.S.; Deville, Y.; Benhalouche, F.Z.; Boukerch, I. Hypersharpening by joint-criterion nonnegative matrix factorization. IEEE Geosci. Remote Sens. Lett. 2017, 55, 1660–1670. [Google Scholar] [CrossRef]
- Selva, M.; Santurri, L.; Baronti, S. Improving hypersharpening for WorldView-3 data. IEEE Geosci. Remote Sens. Lett. 2019, 16, 987–991. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, J.; Yu, X.; Tang, W.; Li, T.; Zhang, Y. Hyper-sharpening based on spectral modulation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1534–1548. [Google Scholar] [CrossRef]
- Restaino, R.; Vivone, G.; Addesso, P.; Chanussot, J. Hyperspectral sharpening approaches using satellite multiplatform data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 578–596. [Google Scholar] [CrossRef]
- Sihvonen, T.; Duma, Z.S.; Haario, H.; Reinikainen, S.P. Spectral profile partial least-squares (SP-PLS): Local multivariate pansharpening on spectral profiles. ISPRS Open J. Photogramm. Remote Sens. 2023, 10, 100049. [Google Scholar] [CrossRef]
- Johnson, B. Effects of pansharpening on vegetation indices. ISPRS Int. J. Geo-Inf. 2014, 3, 507–522. [Google Scholar] [CrossRef]
- Garzelli, A.; Aiazzi, B.; Alparone, L.; Lolli, S.; Vivone, G. Multispectral pansharpening with radiative transfer-based detail-injection modeling for preserving changes in vegetation cover. Remote Sens. 2018, 10, 1308. [Google Scholar] [CrossRef]
- Middleton, E.M.; Campbell, P.K.E.; Ong, L.; Landis, D.R.; Zhang, Q.; Neigh, C.S.; Huemmrich, K.F.; Ungar, S.G.; Mandl, D.J.; Frye, S.W.; et al. Hyperion: The first global orbital spectrometer, earth observing-1 (EO-1) satellite (2000–2017). In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3039–3042. [Google Scholar] [CrossRef]
- Cogliati, S.; Sarti, F.; Chiarantini, L.; Cosi, M.; Lorusso, R.; Lopinto, E.; Miglietta, F.; Genesio, L.; Guanter, L.; Damm, A.; et al. The PRISMA imaging spectroscopy mission: Overview and first performance analysis. Remote Sens. Environ. 2021, 262, 112499. [Google Scholar] [CrossRef]
- Storch, T.; Honold, H.P.; Chabrillat, S.; Habermeyer, M.; Tucker, P.; Brell, M.; Ohndorf, A.; Wirth, K.; Betz, M.; Kuchler, M.; et al. The EnMAP imaging spectroscopy mission towards operations. Remote Sens. Environ. 2023, 294, 113632. [Google Scholar] [CrossRef]
- Aguirre-Gutiérrez, J.; Rifai, S.; Shenkin, A.; Oliveras, I.; Bentley, L.P.; Svátek, M.; Girardin, C.A.; Both, S.; Riutta, T.; Berenguer, E.; et al. Pantropical modelling of canopy functional traits using Sentinel-2 remote sensing data. Remote Sens. Environ. 2021, 252, 112122. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Garzelli, A.; Santurri, L. Blind correction of local misalignments between multispectral and panchromatic images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1625–1629. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. Advantages of Laplacian pyramids over ”à trous” wavelet transforms for pansharpening of multispectral images. In Proceedings of the Image and Signal Processing for Remote Sensing XVIII; Bruzzone, L., Ed.; International Society for Optics and Photonics; SPIE: Bellingham, WA, USA, 2012; Volume 8537, pp. 12–21. [Google Scholar] [CrossRef]
- Arienzo, A.; Aiazzi, B.; Alparone, L.; Garzelli, A. Reproducibility of pansharpening methods and quality indexes versus data formats. Remote Sens. 2021, 13, 4399. [Google Scholar] [CrossRef]
- Pacifici, F.; Longbotham, N.; Emery, W.J. The importance of physical quantities for the analysis of multitemporal and multiangular optical very high spatial resolution images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6241–6256. [Google Scholar] [CrossRef]
- Lolli, S.; Di Girolamo, P. Principal component analysis approach to evaluate instrument performances in developing a cost-effective reliable instrument network for atmospheric measurements. J. Atmos. Ocean. Technol. 2015, 32, 1642–1649. [Google Scholar] [CrossRef]
- Lolli, S.; Sauvage, L.; Loaec, S.; Lardier, M. EZ LidarTM: A new compact autonomous eye-safe scanning aerosol Lidar for extinction measurements and PBL height detection. Validation of the performances against other instruments and intercomparison campaigns. Opt. Pura Apl. 2011, 44, 33–41. [Google Scholar]
- Ciofini, M.; Lapucci, A.; Lolli, S. Diffractive optical components for high power laser beam sampling. J. Opt. Pure Appl. Opt. 2003, 5, 186–191. [Google Scholar] [CrossRef]
- Chavez, P.S., Jr. Image-based atmospheric corrections–Revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1036. [Google Scholar]
- Fu, Q.; Liou, K.N. On the correlated k-distribution method for radiative transfer in nonhomogeneous atmospheres. J. Atmos. Sci. 1992, 49, 2139–2156. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Argenti, F.; Baronti, S. Wavelet and pyramid techniques for multisensor data fusion: A performance comparison varying with scale ratios. In Proceedings of the Image and Signal Processing for Remote Sensing V; Serpico, S.B., Ed.; International Society for Optics and Photonics; SPIE: Bellingham, WA, USA, 1999; Volume 3871, pp. 251–262. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O.; Benediktsson, J.A. Quantitative quality evaluation of pansharpened imagery: Consistency versus synthesis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1247–1259. [Google Scholar] [CrossRef]
- Guan, X.; Li, F.; Zhang, X.; Ma, M.; Mei, S. Assessing full-resolution pansharpening quality: A comparative study of methods and measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 6860–6875. [Google Scholar] [CrossRef]
- Arienzo, A.; Vivone, G.; Garzelli, A.; Alparone, L.; Chanussot, J. Full-resolution quality assessment of pansharpening: Theoretical and hands-on approaches. IEEE Geosci. Remote Sens. Mag. 2022, 10, 2–35. [Google Scholar] [CrossRef]
- Alparone, L.; Garzelli, A.; Vivone, G. Spatial consistency for full-scale assessment of pansharpening. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 5132–5134. [Google Scholar]
- Thenkabail, P.S.; Smith, R.B.; De Pauw, E. Hyperspectral vegetation indices and their relationships with agricultural crop characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar] [CrossRef]
- Miraglio, T.; Adeline, K.; Huesca, M.; Ustin, S.; Briottet, X. Assessing vegetation traits estimates accuracies from the future SBG and biodiversity hyperspectral missions over two Mediterranean forests. Int. J. Remote Sens. 2022, 43, 3537–3562. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Garzelli, A.; Zoppetti, C.; Arienzo, A.; Alparone, L. Spatial resolution enhancement of PRISMA hyperspectral data via nested hypersharpening with Sentinel-2 multispectral data. In Proceedings of the 2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 5997–6000. [Google Scholar] [CrossRef]
- Tagliabue, G.; Boschetti, M.; Bramati, G.; Candiani, G.; Colombo, R.; Nutini, F.; Pompilio, L.; Rivera-Caicedo, J.P.; Rossi, M.; Rossini, M.; et al. Hybrid retrieval of crop traits from multi-temporal PRISMA hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2022, 187, 362–377. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Chen, J.; Chen, X.; Zhu, X.; Qiu, Y.; Song, H.; Rao, Y.; Zhang, C.; Cao, X.; Cui, X. Sensitivity of six typical spatiotemporal fusion methods to different influential factors: A comparative study for a normalized difference vegetation index time series reconstruction. Remote Sens. Environ. 2021, 252, 112130. [Google Scholar] [CrossRef]
- Wang, Q.; Atkinson, P.M. Spatio-temporal fusion for daily Sentinel-2 images. Remote Sens. Environ. 2018, 204, 31–42. [Google Scholar] [CrossRef]





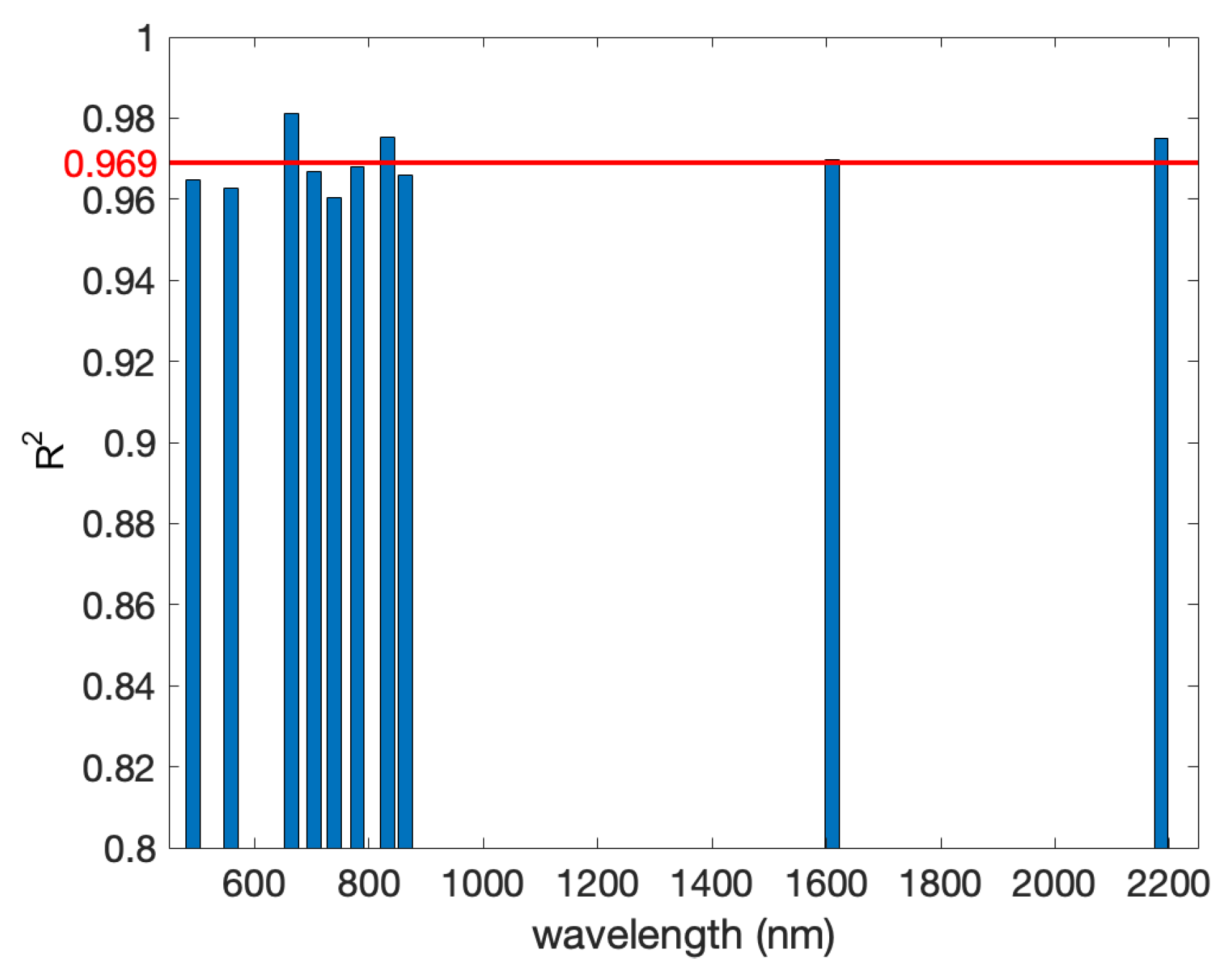



| S2 Band | B4 | B5 | B6 | B7 | B8 |
|---|---|---|---|---|---|
| resolution (m) | 10 | 20 | 20 | 20 | 10 |
| center (nm) | 665 | 705 | 740 | 783 | 842 |
| (nm) | 30 | 15 | 15 | 20 | 115 |
| (a) | (b) | (c) | ||||||
|---|---|---|---|---|---|---|---|---|
| pure | 0.013 | 4.48 | pure | 0.012 | 4.41 | pure | 0.003 | 0.79 |
| mixed | 0.034 | 16.78 | mixed | 0.019 | 16.58 | mixed | 0.011 | 3.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alparone, L.; Arienzo, A.; Garzelli, A. Spatial Resolution Enhancement of Vegetation Indexes via Fusion of Hyperspectral and Multispectral Satellite Data. Remote Sens. 2024, 16, 875. https://doi.org/10.3390/rs16050875
Alparone L, Arienzo A, Garzelli A. Spatial Resolution Enhancement of Vegetation Indexes via Fusion of Hyperspectral and Multispectral Satellite Data. Remote Sensing. 2024; 16(5):875. https://doi.org/10.3390/rs16050875
Chicago/Turabian StyleAlparone, Luciano, Alberto Arienzo, and Andrea Garzelli. 2024. "Spatial Resolution Enhancement of Vegetation Indexes via Fusion of Hyperspectral and Multispectral Satellite Data" Remote Sensing 16, no. 5: 875. https://doi.org/10.3390/rs16050875
APA StyleAlparone, L., Arienzo, A., & Garzelli, A. (2024). Spatial Resolution Enhancement of Vegetation Indexes via Fusion of Hyperspectral and Multispectral Satellite Data. Remote Sensing, 16(5), 875. https://doi.org/10.3390/rs16050875











