Abstract
Drought can have significant impacts on forests, with long periods of water scarcity leading to water stress in trees and possible damages to their eco-physiological functions. Satellite-based remote sensing offers a valuable tool for monitoring and assessing drought conditions over large and remote forested regions. The objective of this study is to evaluate the hydrological consistency in the context of drought of precipitation, soil moisture, evapotranspiration, and land surface temperature observations against in situ measurements in a number of well-monitored sites in New Zealand. Results showed that drought indicators were better captured from soil moisture observations compared to precipitation satellite observations. Nevertheless, we found statistically significant causality relationships between the multi-sensor satellite observations (median p-values ranging from 0.001 to 0.019), with spatial resolution appearing to be an important aspect for the adequate estimation of drought characteristics. Understanding the limitations and capabilities of satellite observations is crucial for improving the accuracy of forest drought monitoring, which, in turn, will aid in sustainable forest management and the development of mitigation and adaptation strategies in the face of changing climate conditions.
1. Introduction
Drought can have significant impacts on forests, with long periods of water scarcity leading to water stress in trees and possible damages to their eco-physiological functions [1]. While trees can somewhat control their water loss through stomatal regulation, dry conditions and the associated prolonged rising temperatures can lead to greater tree mortality and increased vulnerability [2]. There are also indirect impacts of drought on forests, including pest outbreaks and wildfires [3]. As climate change alters the frequency and magnitude of these disturbances and potentially exacerbates these impacts, the monitoring of drought and understanding of its mechanisms becomes important for adapting forest management to mitigate the associated adverse impacts. Particularly for planted forests, understanding the locations of higher and lower drought risk areas in the forest allows for more cost-effective management planning [4]. Satellite observations have been widely used to provide valuable information on different drought characteristics, especially as they can estimate the spatial and temporal development of drought events over regional to continental scales [5]. Multi-sensor remote sensing offers several advantages for monitoring drought, including potentially better capturing the complexity of process interactions and diversity of drought impacts [6]. Currently, satellite observations are being used for monitoring different aspects of drought and calculating many indicators of drought, with some being satellite-specific (e.g., [7]).
Precipitation plays a crucial role as the primary variable for the identification of meteorological droughts [8]. Nonetheless, there are many challenges associated with the lack of consistency between multi-sensor or even single-sensor data products (e.g., [9]). To address this issue, a number of studies have been performed to evaluate and/or compare different precipitation datasets at regional to global scales (e.g., [10]), with most results indicating that multi-sensor approaches are advantageous for drought monitoring [11]. Soil moisture is another important variable that defines agricultural drought, and therefore its observations have been widely used in agricultural and water resources applications (e.g., [12]). Both active and passive microwave sensors have been used to monitor drought conditions and soil wetness [13], although they are limited by a shallow soil penetration depth of less than 5 cm. Thermal stress, which can be a proxy for drought conditions, particularly during an event’s onset [14], can be inferred from observations of land surface temperature. The remote sensing of land surface temperature has a long history with numerous sensors, although issues such as atmospheric correction can complicate the application for drought monitoring [15]. Nonetheless, the combination of land surface temperature observations with different vegetation indices has been successfully applied to quantify soil water content [16]. Vegetation indices have also been used on their own to monitor drought conditions via observing vegetation health. The primary index used for this purpose is the normalized difference vegetation index (NDVI), although it has many limitations, including atmospheric effects, saturation issues, and soil brightness [17]. An alternative index that was developed to overcome some of those issues and is being used in drought-related applications is the enhanced vegetation index (EVI) [18]. Evapotranspiration contains information on land–atmosphere interface processes, and therefore such observations can be used to estimate drought characteristics [19]. As evapotranspiration is not directly observed from satellite sensors, a number of different algorithms have been developed that incorporate a suite of additional data (meteorological, radiation, etc.) into semi-empirical models. Finally, observations of total water storage that can also provide information on groundwater storage have been used to characterize hydrological drought. The Gravity Recovery and Climate Experiment (GRACE) and interferometric synthetic aperture radar sensors have been used for drought monitoring [20], although they each have their limitations, including a very coarse spatial resolution for the former or signal coherence for the latter.
With drought having multiple facets, the use of multiple sensors to observe different variables related to drought characteristics becomes a viable option. However, this multiplicity of data sources brings with it the challenge of ensuring the harmonization and reliability of observations [21]. Inaccuracies and discrepancies in data derived from different sensors, particularly in terms of spatial scales, can propagate through the estimation of drought indicators. Consequently, the need to comprehensively evaluate the hydrological consistency across multiple sensors becomes important [22], especially in forested environments that present additional complexities for drought estimation.
Some of these complexities include the subtle effects to forests caused by drought (wilting, reduced needle density, etc.), the diversity in plant species with different drought tolerance levels, and the effects of the different types of drought, such as soil moisture, precipitation, and temperature stress [23]. Therefore, the objective of this study is to evaluate the hydrological consistency in the context of drought of precipitation, soil moisture, evapotranspiration, and land surface temperature observations against in situ measurements in a number of forested sites. This assessment of the hydrological consistency is two-fold and includes the validation of multiple products observing the same variable or drought indicator as well as the evaluation of the dependence relationship and causality between observations of different variables that describe the hydrological processes controlling drought.
2. Methods
2.1. Study Sites
Seven sites throughout New Zealand were used for this study, located in planted forests where soil moisture sensors and meteorological stations were installed. All forests are managed for commercial forestry with the same species, Pinus radiata (D. Don), with ages ranging from 5 to 20 years (Table 1). These sites were used in an earlier study [24]. Regarding long-term climatic patterns, these sites have an annual total precipitation ranging from 345 to 1420 mm, and annual mean daily temperature ranging from 10.1 to 13.7 °C (Table 1). Four of the sites (Puruki, Central Kaingaroa, Southern Kaingaroa, and Rangipo) are situated in the central region of the North Island (see Figure 1) on volcanic Andisols (Table 1). Two sites (Ashley and Balmoral) are located in the east central part of the South Island (see Figure 1) on Inceptisols developed from alluvial parent material, while the last site (Tokoiti) is located on Alfisols developed from schist-derived parent material (Table 1). All sites have canopy closure (proportion of sky obscured by canopy), and the forest cover fractions of each site relative to the intrinsic resolution of SMAP pixels (33 km) range from about 35% for Ashley and Balmoral to 48% for Puruki, 53% for Tokoiti, 58% for S. Kaingaroa, and 64% for C. Kaingaroa and Rangipo. Additionally, all sites are on topographically complex terrain with slopes being mostly moderate (Ashley being the only very steep site) but with large variability, with the exception of the Balmoral site which is flat.

Table 1.
Description and characteristics of the physiography, geography, and climatology for each forest study site.
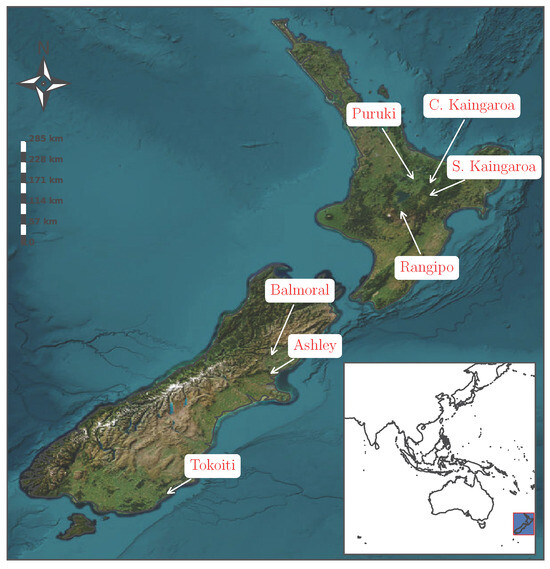
Figure 1.
Map of New Zealand and the forested sites with ground measurements that were used in this study (inset map of larger region is included).
Soil volumetric water content was measured by 10HS Soil Moisture Smart Sensors (Onset Corporation, Borne, MA, USA) originally developed by Decagon Devices, now Meter Group (Pullman, WA, USA). The sensors use capacitance (amount of electric charge stored) to measure the dielectric constant of 1100 of the surrounding soil medium at 70 . The probe converts capacitance values into a proportional single voltage value, which directly correlates to volumetric water content with an empirical equation [25] and provides average water content along its length [26]. The data can be used to understand changes in soil moisture content and the direction of the flow of moisture through the soil and how these vary both spatially and temporally [27]. The manufacturer’s default equation was used with an accuracy of ±0.03 m3/m3 and its accuracy and performance were demonstrated on a range of mineral soils [28]. Sensors were installed horizontally at 5 cm below the mineral soil surface at Southern Kaingaroa (15 stations), Puruki (23 stations), and Balmoral (9 stations). At the other four sites, one sensor was installed at a 45° angle, which provided an average soil moisture for approximately the top 10 cm. Temperature and precipitation data were collected using Onset’s 12-bit Temp/RH Smart Sensors and Rain Gauge tipping bucket that has a minimum precipitation detection rate of 0.2 mm. Sensors were either connected to an Onset HOBO U30-NRC metrological station data logger or an Onset HOBO microstation data logger. Measurements were taken at 5-min intervals at the Central and Southern Kaingaroa, and at 15 min intervals at the other sites.
2.2. Satellite Observations
Table 2 lists the observational datasets that were used in this study along with their primary characteristics (variable observed, spatial and temporal resolutions). Precipitation observations were acquired from two sources: the Global Precipitation Measurement (GPM) satellite mission and the Climate Hazards Group Infrared Precipitation with Station (CHIRPS) datasets. GPM is a joint NASA/JAXA mission comprising a constellation of sensors with a dual-frequency radar and a microwave imager as the core observatory, and provides global precipitation products at relatively high spatial (0.1°) and temporal (30 min) resolutions. The algorithm processing these observations is the Integrated Multi-Satellite Retrievals for GPM (IMERG) [29], and here we used the IMERG late run data product (version 6). CHIRPS is a quasi-global and long-term daily precipitation dataset with high spatial resolution (0.05°) derived from infrared cold cloud duration (CCD) observations [30]. Both GPM and CHIRPS precipitation estimates have been evaluated globally and regionally (e.g., [9,31]) as well as in a variety of contexts, including drought identification and estimation (e.g., [32,33]).

Table 2.
List and characteristics (resolution and variable) of satellite observation datasets used in this study.
Soil moisture observations were obtained at multiple resolutions from the Soil Moisture Active Passive (SMAP) satellite mission [34]. Although there has been a long history of microwave sensors providing soil moisture observations, the attenuation and scattering characteristics of vegetation at their operating frequencies (e.g., C-band) limited their applicability in forested environments. The lower frequency (L-band) of SMAP can overcome some of those limitations and has been shown to produce accurate estimates of soil moisture in forests (e.g., [24]). In addition, there have been numerous studies that have evaluated the potential for using SMAP soil moisture observations to monitor drought characteristics (e.g., [12,35]). The SMAP data products that we used in this study include the SPL3SMP_E Enhanced Level-3 soil moisture and the SPL2SMAP_S Level-2 product, which combines SMAP and Sentinel-1 measurements to derive soil moisture at 3 and 1 km. The 9 km product samples the coarser brightness temperature (TB) measurements from the SMAP radiometer (∼36 km) on a 9 km grid using the Backus–Gilbert approach and inverts them to a soil moisture estimate [36]. On the other hand, the 3 and 1 km products merge the SMAP radiometer and Sentinel-1 C-band synthetic aperture radar (SAR) observations to downscale TB and then invert it to soil moisture [37]. A limitation of this algorithm is that the SMAP temporal coverage is degraded due to the narrower width of the Sentinel-1 swath, which reduces the spatial overlap between the two sensors, leading to an approximate 12-day observation frequency.
A number of different earth observation datasets are derived from Moderate Resolution Imaging Spectroradiometer (MODIS) measurements, and, for this study, we used the land surface temperature (LST) and evapotranspiration data products. The MODIS sensors have 36 spectral bands in the visible, near-infrared, and thermal infrared portions of the electromagnetic spectrum and have been used for a multitude of earth science applications in the past two decades [38]. The land surface temperature data products (MOD11A1.061 from Terra used here) provide daily observations globally at a 1 km spatial resolution with a validation accuracy of the order of 1–2 °C under clear-sky conditions [39]. Land surface temperature is retrieved from emissivity and other land surface/atmospheric parameters with split-window algorithms [40], and although there have been efforts to ameliorate the effects of cloud cover (i.e., missing data) (e.g., [41]), we did not employ any of those approaches in the data used here. The evapotranspiration data product from MODIS (MOD16A2.061 from Terra used here) is an 8-day composite dataset with a 500 m spatial resolution, and is derived from a set of semi-empirical equations that are based on the Penman–Monteith model [42]. In addition to the satellite observations, the MOD16 algorithm uses regional meteorological data and parameter calibration, with the latter leading to potentially sub-optimal performance in certain regions and land covers [43].
All satellite datasets were acquired using the earthaccess Python library for NASA Earthdata APIs and the earthengine-api Python interface to the Google Earth Engine.
2.3. Assessing Hydrologic Consistency
Drought affects different parts of the water cycle and generally falls on the spectrum of meteorological, agricultural, hydrological, and socioeconomic in terms of drivers and impacts [44]. Consequently, many hydro-meteorological variables and a number of different indices have been used to characterize different aspects of drought. The former include precipitation, soil moisture, and runoff, while the latter are numerical representations that describe drought features such as magnitude, severity, duration, extent, etc., and can be based on uni- or multi-variate calculations [45,46].
As the objective of this study is the evaluation of the consistency of different remotely sensed observations related to drought characteristics, we calculate a number of indices related to each variable observed by each sensor and compare them against ground-based estimates. The standardized precipitation index (SPI) measures the deviation of precipitation from its long-term average and provides a standardized measure of drought severity. The SPI can be calculated for different duration (1 to 24 months usually) [47] with a non-parametric approach that transforms precipitation to a z-score [48]. The other precipitation-based indicator of drought that we calculated was the duration of dry spells [49], which were defined as the number of consecutive days with zero precipitation. Although there are studies that have defined dry spells using different precipitation thresholds (e.g., [50]), we argue that a non-zero threshold value is subjective and could be sensor-dependent.
Soil moisture is a key indicator of water availability in forested environments, and therefore we examined the drydown rates, moisture content during summer months, and probability distribution of soil moisture. A drydown can be defined as a period of a sustained decrease in soil moisture [51], and quantifying it can provide insights on soil hydraulic properties and land–atmosphere feedback mechanisms, although spatial heterogeneity and coupled soil–vegetation–climate dynamics appear to dominate the drydown signal at larger observation scales (e.g., remotely sensed) [52,53]. In order to identify drydown periods, we adapted the approach from McColl et al. [54] by finding periods in each time series where the total decrease in soil moisture was at least 5% of the observed range. Subsequently, we selected only periods with a duration longer than 1 day and calculated the drydown rate as the change in soil moisture (expressed as percent volumetric content) divided by the duration in days. When comparing estimated drydown rates between different datasets (ground- and satellite-based), the drydown periods will most likely not be identical. Therefore, we aligned the drydown events identified in the satellite and ground observation time series by matching periods of soil moisture decreases in the two time series that were within 7 days of each other in terms of starting date. Another important indicator for forest health during dry periods is the number of days that soil moisture is below a certain threshold (e.g., critical drying threshold [55]). For our study sites, we selected a threshold value of 0.2 cm3cm−3 as it corresponds to “very dry” conditions [56]. The number of days below that threshold was then calculated from the ground measurements and both SMAP and SMAP/Sentinel observations between December and March of each year as this is typically the driest period [57]. Finally, we examined the agreement between the probability distributions of soil moisture in terms of the empirical CDF as the latter can be used to define drought severity for different events [58]. There are a number of different metrics used to evaluate the agreement between distributions [59], but here we chose to use the two-sample Kolmogorov–Smirnov statistic, which is non-parametric and quantifies the distance between the cumulative distributions of two samples [60].
We evaluated the consistency of satellite land surface temperature and evapotranspiration from MODIS by directly comparing against estimates from ground measurements, as well as assessing their variability with soil moisture. The objective of this analysis was the evaluation of the relationship between land surface temperature and evapotranspiration with soil moisture and particularly soil water deficits. Many studies have shown the use of land surface temperature as a proxy for soil moisture during drought conditions (e.g., [61]), and therefore a simple correlation analysis should suffice as an initial verification of that relationship from satellite observations. A similar assessment was performed with satellite evapotranspiration from MODIS and soil moisture from SMAP, but we also compared the former with ground-based estimates of evapotranspiration calculated using the Priestley–Taylor method [62]. Although the MODIS evapotranspiration is calculated based on a Penmann–Monteith method, we used the Priestley–Taylor method to compute the ground-based estimates as it has comparatively reduced data requirements and has been shown to be effective in forested environments [63,64]. A summary of the indices that were calculated for and the datasets used in this assessment is shown in Figure 2.
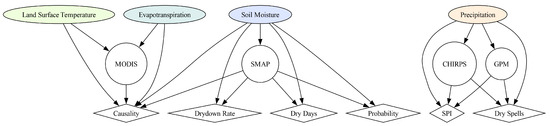
Figure 2.
Diagram of the variables, satellite datasets, and drought indicators/analyses performed in the assessment of multi-sensor hydrologic consistency at the studied forested sites.
The calculation of some of the aforementioned drought indices from satellite observations and subsequent comparison with ground-based estimates can be problematic due to missing data in the former. In particular, the number of dry summer days and the empirical CDF for soil moisture could not be calculated for the SMAP/Sentinel observations due to their temporal frequency. Therefore, we applied an imputation method based on Gaussian process regression to interpolate the missing data in the soil moisture time series. Although there are many methods for time series imputation [65], Gaussian process regression is a non-parametric, kernel-based method that can be used for interpolation [66]. Figure 3 shows an example of applying the imputation method on the ground soil moisture measurements sampled at the SMAP/Sentinel observation days and then comparing the interpolated (“Prediction”) and the actual (“Truth”) time series. Although the imputation is not able to capture some of the short-scale variability, it does provide a realistic estimate with relative root mean squared errors less than 10% when tested across the study sites.
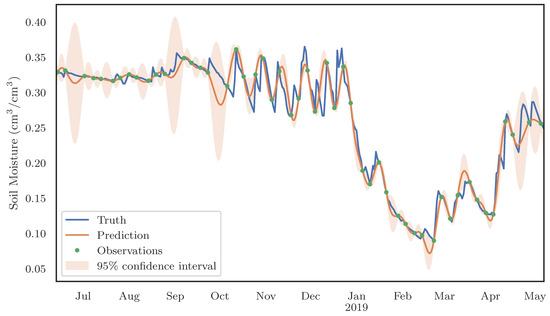
Figure 3.
Validation example of the time series imputation approach at the Ashley forest site. The actual daily time series is derived from the ground measurements at the site, with the observations being subsampled to match the SMAP/Sentinel observation frequency. The prediction time series was then generated from the observations and a Gaussian process model along with the 95% confidence intervals.
Finally, we evaluated the potential causality relationships between satellite observations of precipitation, soil moisture, land surface temperature, and evapotranspiration using the Granger causality statistical test. The Granger causality test has been widely used in many disciplines and essentially quantifies the dependence when regressing two variables for different time lags [67]. This statistical test is used to determine the direction of causality between two time series variables by regressing each variable with the other’s lagged values. If the coefficients of the regression equation are different from zero to a specific statistical significance level, then there is a causal relationship between the variables [68]. The regression can be performed with a vector auto-regressive model after choosing the maximum time lag. Here, we compute and evaluate the statistical significance of the test for both the ground measurements and the satellite observations using the Sciki-learn Python machine learning library.
3. Results
3.1. Precipitation
In contrast to floods, droughts are slower phenomena with persistence, and therefore an initial comparison of satellite precipitation for characterizing drought can be performed at the monthly scale. We aggregated the daily satellite observations of precipitation to monthly values and compared them against ground measurements (aggregated from sub-daily to monthly). In order to focus on dry conditions, we evaluated the satellite observations only for months when precipitation was less than the mean precipitation for each site (based on the in situ measurements). Figure 4 shows a scatter plot of monthly in situ precipitation against satellite precipitation for both GPM and CHIRPS during months with below-average precipitation. Both satellite datasets perform relatively poorly when compared to the ground measurements, with values that range from 0.01 to 0.37 for CHIRPS and 0.01 to 0.32 for GPM. That performance appears to be consistent across all the study sites, with a mean of 0.09 and 0.11 for CHIRPS and GPM, respectively. If we do not apply the filtering of months with below-average precipitation (i.e., include all months), the error metric improves to an average of 0.31 (CHIRPS) and 0.32 (GPM) across the study sites.
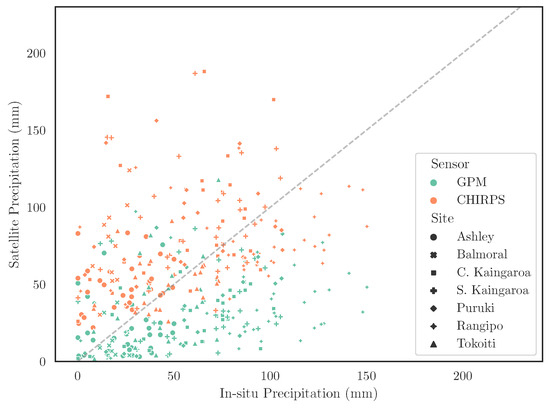
Figure 4.
Comparison of in situ and satellite (both CHIRPS and GPM datasets) monthly precipitation amounts for all study sites when in situ measurements were below each site’s respective mean.
In contrast to the comparison of precipitation amounts, a more direct comparison for drought identification is the SPI. Figure 5 shows a comparison of time series of the 3-month SPI (SPI-3) between the satellite and in situ observations at each study site. There is significant disagreement between both the satellite and the in situ observations but also between the two satellite datasets. The SPI calculated from CHIRPS observations did exhibit the highest correlations with in situ observations for two of the sites (Balmoral and S. Kaingaroa) albeit they were only 0.23 to 0.34, with the mean correlation being 0.11 across all sites. The correlation of SPI calculated from GPM observations has an average of 0.02, with four of the sites (Rangipo, Balmoral, C. Kaingaroa, and Puruki) actually having negative correlations. These results are in contrast to the correlations of the precipitation amounts, with the average correlations being 0.55 and 0.52 for CHIRPS and GPM, respectively. When SPI is calculated for a 6-month duration, results do improve, with the highest correlations being 0.73 for Balmoral (CHIRPS) and 0.56 for C. Kaingaroa (GPM), although the average correlations remain relatively low (0.24 and 0.12 for CHIRPS and GPM, respectively).
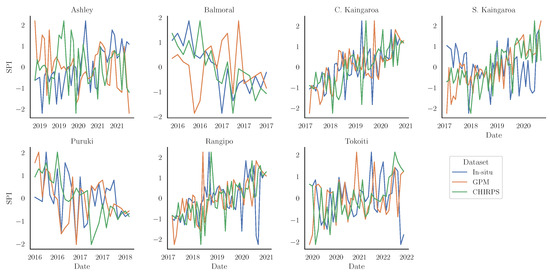
Figure 5.
Comparison of SPI-3 time series derived from in situ, GPM, and CHIRPS observations at each study site.
Figure 6 shows the average duration of dry spells (i.e., consecutive days with zero precipitation) per month for each site and all three datasets (in situ, GPM, and CHIRPS). The Ashley and Balmoral forest sites do show relative agreement between the satellite datasets, at least when compared to the rest of the study sites. The difference in the satellite-estimated dry spell duration from the ones estimated from ground observations is ~5 and ~4 days for those two sites, but CHIRPS consistently overestimates duration for all other sites. The root mean squared error (RMSE) for duration ranged from 2.0 to 5.9 days for GPM, and 4.8 to 9.9 days for CHIRPS. On the other hand, when comparing the monthly time series of dry spell duration, the correlations between the satellite and ground-based estimates ranged from 0.12 to 0.52 for GPM (mean of 0.37) and −0.44 to 0.21 for CHIRPS (mean of 0.01).
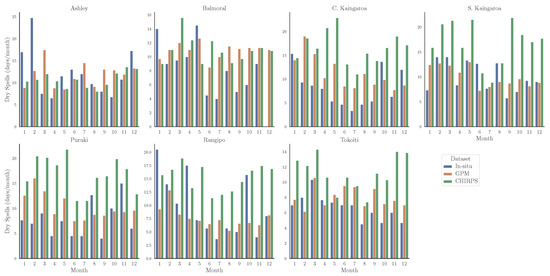
Figure 6.
Comparison of the number of dry spells per month as derived from in situ, GPM, and CHIRPS observations at each study site. Dry spells were defined as the number of consecutive days with zero precipitation per month.
3.2. Soil Moisture
Figure 7 shows scatter plots of the drydown rates estimated at each study site from the ground measurements versus the ones estimated from the satellite observations. The calculation of the drydown rates can be affected by the temporal resolution of the satellite datasets. Although the time series matching procedure ensures to a reasonable degree that the same events are identified, the frequency of the 1 and 3 km SMAP observations could lead to an overestimation of the duration of the drydown event. With the exception of the Rangipo and the Tokoiti sites, where the mean duration was 6.8 and 5.6 days, all other sites had a mean duration between 9.9 and 24.6 days, making the comparison with the SMAP 1 and 3 km datasets appropriate. Overall, the drydown rates calculated from the SMAP observations exhibit disagreement with the ground-based estimates to varying degrees. It is clear, however, that the finer spatial resolution estimates (SMAP/Sentinel data products) are closer to the ground-based estimates when compared to the SMAP 9 km data product. In particular, the average across the study sites for the 9 km SMAP product is 0.03, whereas it is 0.07 for the 3 km SMAP/Sentinel dataset and 0.06 for the 1 km SMAP/Sentinel dataset. In terms of RMSE, the average over the study sites was 0.01 for the SMAP/Sentinel dataset and 0.02 for the SMAP dataset. Apart from C. Kaingaroa, at each of the sites there was at least one of the satellite datasets that had a RMSE less than . The SMAP 9 km dataset only satisfied the RMSE threshold for Balmoral, which was the only site where the 1 km dataset exceeded that RMSE value; the 3 km product, on the other hand, exceeded it for only Tokoiti and C. Kaingaroa.
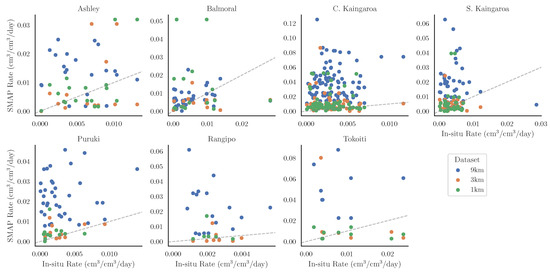
Figure 7.
Comparison of estimated soil moisture drydown rates between in situ (x-axis), SMAP (9 km resolution, y-axis) and SMAP/Sentinel (3 and 1 km resolution, y-axis) observations at each study site. Drydown events were identified for each dataset and rates were calculated and aligned between the in situ and satellite observations.
The number of summer days with “very dry” soil columns in the study sites showed very good agreement overall with the ground observations. Figure 8 shows a scatter plot of the summer days with soil moisture less than calculated from ground measurements and satellite observations for the different satellite products. The only outlier relative to the 1:1 line is the summer 2018 for the SMAP/Sentinel dataset, when the number of summer “very dry” days was 9 (1 km) and 11 (3 km) versus 60 (in situ). The correlations were relatively high, with being 0.93 for the SMAP 9 km dataset and 0.85 and 0.83 for the SMAP/Sentinel 3 and 1 km datasets. Similarly, the difference from the ground measurements in terms of RMSE was 10.2, 14.3, and 15.0 days for the 9, 3, and 1 km datasets.
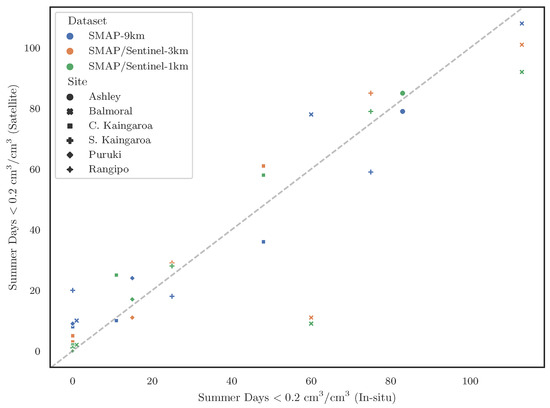
Figure 8.
Comparison of summer days with soil moisture below a 0.2 threshold computed from in situ (x-axis) and SMAP satellite observations (y-axis).
Finally, we examine the probability distributions of soil moisture from the ground measurements and the satellite observations, shown in Figure 9 for each study site. The distributions of soil moisture show a general qualitative agreement between the SMAP/Sentinel datasets and the ground measurements. With the exception of the S. Kaingaroa and Ashley Forest sites, the SMAP dataset shows relatively poor agreement with the in situ empirical CDF. These results are reflected in the values of the Kolmogorov–Smirnov (K-S) statistic, which is closer to 0 if the distributions agree and 1 if they disagree. The SMAP dataset has a statistic of 0.06 for the S. Kaingaroa site and 0.22 and 0.29 for Ashley and Balmoral, but over 0.44 for the rest of the sites, with the average being 0.41 for all sites. The SMAP/Sentinel datasets, on the other hand, had average scores of 0.19 (3 km) and 0.27 (1 km), with the best-performing site being S. Kaingaroa and the worst being Rangipo (both) and Tokoiti (just the 1 km product).
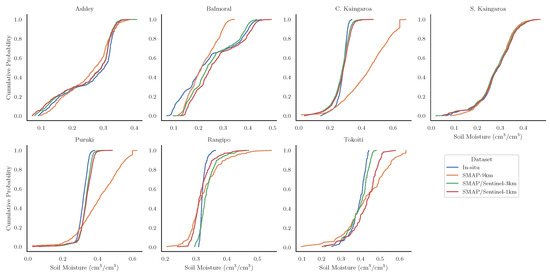
Figure 9.
Comparison of empirical CDFs calculated from in situ and SMAP satellite observations (including the SMAP-E and SMAP/Sentinel data products) of soil moisture at each study site.
3.3. Land Surface Temperature
Although ground measurements of land surface temperature were not available, we can evaluate the MODIS observations against measurements of 2 m air temperature at the study sites. The correlations ranged from 0.70 (Puruki) to 0.87 (C. Kaingaroa), with an average correlation of 0.79, suggesting that the satellite observations captured the variability in temperature. More importantly, we assessed how consistent the MODIS land surface temperature observations were with soil moisture observations. Figure 10 shows time series plots of SMAP soil moisture and MODIS land surface temperature for each study site. Although results were similar for the SMAP/Sentinel observations, we opted to use the SMAP 9 km product for this assessment as its temporal resolution matches better with that of the MODIS data. There is a relatively strong inverse relationship between the satellite soil moisture and land surface temperature. The correlations are the lowest for the Rangipo (−0.33) and Tokoiti (−0.23) sites, which are also the ones with the smallest sample size. In contrast, the other sites have much higher anti-correlations, which are −0.83 (Ashley), −0.78 (Puruki and C. Kaingaroa), −0.74 (S. Kaingaroa), and −0.71 (Balmoral). When the same analysis is performed with the ground soil moisture measurements, the satellite land surface temperature exhibits a similar negative correlation but weaker than the one with the SMAP observations. The correlations in that case range from −0.42 (Balmoral) to −0.71 (Ashley), with an average of −0.51.
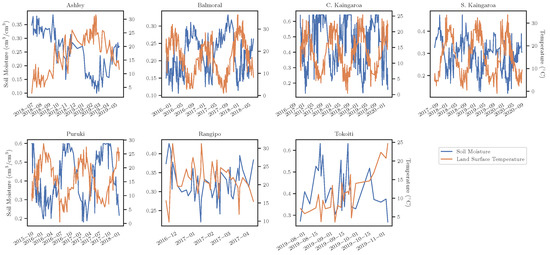
Figure 10.
Relationship between the time series of SMAP soil moisture (left y-axis) and MODIS land surface temperature (right y-axis) at each study site.
3.4. Evapotranspiration
We compared the ground-based estimates of evapotranspiration with the MODIS satellite dataset, with Figure 11 showing their scatter plot for all the forest sites. There is a relatively large bias in the MODIS observations when compared with the ground-based estimates of . Nevertheless, the two datasets have a relatively high degree of agreement, as the average is 0.79, ranging from 0.73 (Tokoiti) to 0.84 (Rangipo).
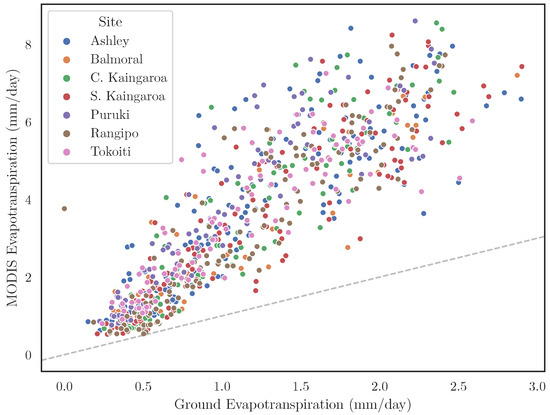
Figure 11.
Comparison of evapotranspiration at each study site estimated from the MODIS satellite observations (y-axis) and in situ measurements (x-axis).
When examining the relationship between the satellite observations of evapotranspiration (MODIS) and soil moisture (SMAP 9 km), we have a similar result to the land surface temperature comparison. There is a relatively strong inverse relationship between the two datasets, with correlations that range from −0.56 (Balmoral) to −0.79 (C. Kaingaroa). Two exceptions to those correlations were the Rangipo and Tokoiti sites, which have correlations of −0.37 and −0.11, respectively. These lower (in absolute value) correlations could be attributed to the smaller sample size of coincident observations, but do result in an average correlation of −0.57. Figure 12 shows a scatter plot between SMAP soil moisture and MODIS evapotranspiration along with regression lines and their 95% confidence intervals. Results with the SMAP/Sentinel products also exhibited a negative relationship with the MODIS observations, although it was not as strong, with average correlations of −0.44 (1 km) and −0.40 (3 km) that can be attributed to the smaller sample size.
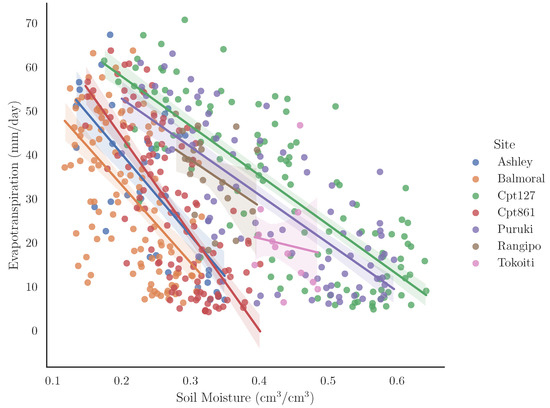
Figure 12.
Scatter plots and linear fit between SMAP satellite soil moisture (x-axis) and MODIS evapotranspiration (y-axis) showing the relationship between these two datasets at the study sites. Confidence intervals (90%) for each of the linear fits are also shown.
3.5. Causality Tests
We computed the p-values of the Granger causality test with a maximum lag of 15 days for the relationship of precipitation, evapotranspiration, and temperature with soil moisture. Figure 13 shows the p-values of the Granger test for the three examined relationships and each study site. The dependence was evaluated using both satellite observations and ground measurements, with the only caveat being that air temperature measurements were used for the ground soil moisture–temperature relationship instead of the unavailable land surface temperature. With few exceptions, the causality test was statistically significant at the 95% level for all relationships. The median p-values for the satellite observations were 0.050 for evapotranspiration, 0.001 for precipitation, and 0.019 for land surface temperature. On the other hand, the median p-values for ground measurements were 0.0003 for evapotranspiration, 0.000002 for precipitation, and 0.0012 for temperature. Some of the higher p-values could be attributable to the sample size effects, e.g., Rangipo and Tokoiti for soil moisture with precipitation and temperature. The worst p-value was found for the Rangipo site and the soil moisture/temperature relationship (both ground and satellite observations). Overall, the statistically significant unidirectional relationship between soil moisture and the other variables quantitatively confirms the results from the previously made comparisons, showing that satellite observations have a relatively high degree of consistency despite limitations with some of the drought indicators.
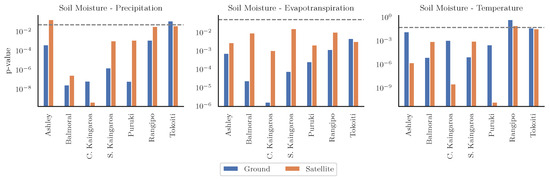
Figure 13.
p-values of the Granger causality hypothesis F-test for both ground and satellite observations of soil moisture with observations of precipitation, evapotranspiration, and land surface temperature. The dashed line signifies the 95% significance level.
4. Discussion
The characterization of meteorological drought from satellite observations appears to be somewhat problematic. The comparison of rainfall amounts with ground measurements revealed relatively large errors even at the monthly scale. Although the calculated drought indicators such as SPI and dry spell duration did not show differences as significant as the amount comparison, they were still inadequate for reproducing drought characteristics. In terms of the drought indicators, the record length could also be affecting the calculation of the SPI, especially at shorter time scales [69]. The sites in this study do represent a fairly challenging environment for sensing precipitation both in terms of topography and land cover. In addition, the scale discrepancy between the 5–10 km resolution of the satellite observations with the ground-based measurements could also be attributed to the disagreements in rainfall amounts [70].
The scale discrepancy between satellite and ground observations is a pervasive issue across all observational datasets used here that can be challenging to amend [71]. This was also evident in the soil-moisture-related comparisons of drydown rates and probability distributions, with the higher resolution SMAP/Sentinel products outperforming the coarser SMAP observations. The number of dry summer days, which is a very important metric for managing forest resources, on the other hand, was captured accurately by all SMAP soil moisture observations. These results are also supported by a number of previous studies that found that SMAP soil moisture can be a valuable indicator of drought conditions either in terms of moisture content [72], soil moisture dynamics [73], probability distributions [74], and threshold-based drought detection [75].
Evapotranspiration estimates from satellite observations showed good correspondence with estimates from ground measurements, with high correlations. There was a relatively large bias though but, overall, the performance of the MODIS product was on par with results from other studies [43].
Most importantly, the satellite observations appear to be hydrologically consistent, particularly when examining the relationships between soil moisture and evapotranspiration or land surface temperature. Although this is the first such result in forested environments, it is in agreement with other studies that examined the relationship of SMAP soil moisture with evapotranspiration and land surface temperature [76]. The inverse relationship between them was evident at the temporal frequency of the satellite observations, with periods of drier soil conditions directly corresponding to periods of higher land surface temperature and higher lagged evapotranspiration. These relationships were quantitatively confirmed using a Granger causality test, which showed statistically significant causal relationships at the 5% level (with very few exceptions) between soil moisture and the precipitation, land surface temperature, and evapotranspiration.
Although there are many more drought indices that we could have calculated to evaluate the hydrological consistency of the satellite observations (e.g., [77,78,79]), we selected a subset of either widely used ones (e.g., SPI) or ones that are important for forest resources (e.g., drydown rates). Two exceptions of some widely used indices that we did not focus on in this study were the leaf area index (LAI) and normalized difference vegetation index (NDVI). The results were inconsistent and, as there were no direct in situ observations to compare them against, we opted to exclude them from the analysis here, although we have included them in Appendix A.
5. Conclusions
Droughts in forested environments are increasingly recognized as a critical component of global climate change, affecting ecosystem services. Satellite-based remote sensing offers a valuable tool for monitoring and assessing drought conditions over large and remote forested regions. However, the consistency and accuracy of satellite observations in quantifying forest drought remain subject to various sources of uncertainty, including sensor characteristics, data processing, and spatial heterogeneity. We performed an assessment of the consistency of satellite observations of drought from multiple sensors in a number of well-monitored sites in New Zealand. Results showed that drought indicators were better captured from soil moisture observations compared to precipitation satellite observations. Nonetheless, we found statistically significant causality relationships between the multi-sensor satellite observations, with spatial resolution appearing to be an important aspect for the adequate estimation of drought characteristics. Causality was tested for the relationship of precipitation, evapotranspiration, and temperature with soil moisture. With a few sites being the exception, relationships were found to be statistically significant at the 95% level, with stronger relationships between soil moisture and precipitation.
The findings of this study, particularly the ability to quantify the dry summer days, can have implications for the utilization of satellite-based drought information in forest management, ecosystem modeling, and climate change assessments. Understanding the limitations and capabilities of satellite observations is crucial for improving the accuracy of forest drought monitoring, which, in turn, will aid in sustainable forest management and the development of mitigation and adaptation strategies in the face of changing climate conditions. Lastly, the methodology presented in this study is not necessarily limited to forested areas but could be applied for evaluating multi-sensor satellite observations for drought estimation in other types of landscape.
Author Contributions
Conceptualization, K.M.A.; methodology, K.M.A. and D.M.; software, K.M.A.; validation, K.M.A., P.C.-L., N.D. and D.M.; formal analysis, K.M.A.; investigation, K.M.A.; resources, K.M.A. and D.M.; data curation, P.C.-L. and B.H.; writing—original draft preparation, K.M.A.; writing—review and editing, K.M.A., D.M., B.H. and N.D.; visualization, K.M.A.; supervision, K.M.A.; project administration, D.M.; funding acquisition, D.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Business, Innovation and Employment of New Zealand Endeavour Fund grant number C04X1905.
Data Availability Statement
The data presented in this study are openly available in https://dx.doi.org/10.6084/m9.figshare.24899733 (accessed on 18 February 2024).
Conflicts of Interest
Author Dean Meason and Priscilla Corbett-Lad were employed by the company Scion-New Zealand Forest Research Institure Ltd. And author Barbara Höck was employed by the company Candleford Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A
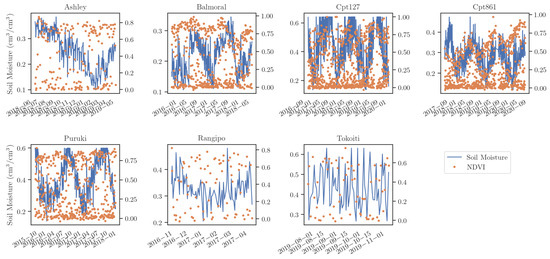
Figure A1.
Time series of satellite soil moisture observations from SMAP (left y-axis) and NDVI observations from MODIS (right y-axis) for all study sites.
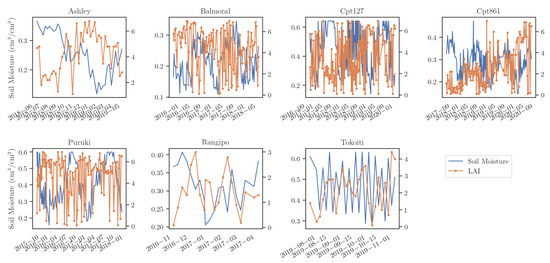
Figure A2.
Time series of satellite soil moisture observations from SMAP (left y-axis) and LAI observations from MODIS (right y-axis) for all study sites.
References
- Brodribb, T.J.; Powers, J.; Cochard, H.; Choat, B. Hanging by a Thread? Forests and Drought. Science 2020, 368, 261–266. [Google Scholar] [CrossRef]
- Choat, B.; Jansen, S.; Brodribb, T.J.; Cochard, H.; Delzon, S.; Bhaskar, R.; Bucci, S.J.; Feild, T.S.; Gleason, S.M.; Hacke, U.G.; et al. Global Convergence in the Vulnerability of Forests to Drought. Nature 2012, 491, 752–755. [Google Scholar] [CrossRef] [PubMed]
- Norman, S.P.; Koch, F.H.; Hargrove, W.W. Review of Broad-Scale Drought Monitoring of Forests: Toward an Integrated Data Mining Approach. For. Ecol. Manag. 2016, 380, 346–358. [Google Scholar] [CrossRef]
- Lucas-Borja, M.E.; Andivia, E.; Candel-Pérez, D.; Linares, J.C.; Camarero, J.J. Long Term Forest Management Drives Drought Resilience in Mediterranean Black Pine Forest. Trees 2021, 35, 1651–1662. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Farahmand, A.; Melton, F.S.; Teixeira, J.; Anderson, M.C.; Wardlow, B.D.; Hain, C.R. Remote Sensing of Drought: Progress, Challenges and Opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef]
- Jiao, W.; Wang, L.; McCabe, M.F. Multi-Sensor Remote Sensing for Drought Characterization: Current Status, Opportunities and a Roadmap for the Future. Remote Sens. Environ. 2021, 256, 112313. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, S.; Zhang, H.; Bai, Y.; Zhang, J. Monitoring Drought Using Composite Drought Indices Based on Remote Sensing. Sci. Total Environ. 2020, 711, 134585. [Google Scholar] [CrossRef]
- Keyantash, J.; Dracup, J.A. The Quantification of Drought: An Evaluation of Drought Indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Pradhan, R.K.; Markonis, Y.; Vargas Godoy, M.R.; Villalba-Pradas, A.; Andreadis, K.M.; Nikolopoulos, E.I.; Papalexiou, S.M.; Rahim, A.; Tapiador, F.J.; Hanel, M. Review of GPM IMERG Performance: A Global Perspective. Remote Sens. Environ. 2022, 268, 112754. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-Scale Evaluation of 22 Precipitation Datasets Using Gauge Observations and Hydrological Modeling. In Satellite Precipitation Measurement; Levizzani, V., Kidd, C., Kirschbaum, D.B., Kummerow, C.D., Nakamura, K., Turk, F.J., Eds.; Advances in Global Change Research, Springer International Publishing: Cham, Switzerland, 2020; Volume 2, pp. 625–653. [Google Scholar] [CrossRef]
- Hinge, G.; Mohamed, M.M.; Long, D.; Hamouda, M.A. Meta-Analysis in Using Satellite Precipitation Products for Drought Monitoring: Lessons Learnt and Way Forward. Remote Sens. 2021, 13, 4353. [Google Scholar] [CrossRef]
- Mladenova, I.E.; Bolten, J.D.; Crow, W.T.; Sazib, N.; Cosh, M.H.; Tucker, C.J.; Reynolds, C. Evaluating the Operational Application of SMAP for Global Agricultural Drought Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3387–3397. [Google Scholar] [CrossRef]
- Zhu, Q.; Luo, Y.; Xu, Y.P.; Tian, Y.; Yang, T. Satellite Soil Moisture for Agricultural Drought Monitoring: Assessment of SMAP-Derived Soil Water Deficit Index in Xiang River Basin, China. Remote Sens. 2019, 11, 362. [Google Scholar] [CrossRef]
- Seyednasrollah, B.; Domec, J.C.; Clark, J.S. Spatiotemporal Sensitivity of Thermal Stress for Monitoring Canopy Hydrological Stress in near Real-Time. Agric. For. Meteorol. 2019, 269–270, 220–230. [Google Scholar] [CrossRef]
- Hu, T.; Renzullo, L.J.; van Dijk, A.I.J.M.; He, J.; Tian, S.; Xu, Z.; Zhou, J.; Liu, T.; Liu, Q. Monitoring Agricultural Drought in Australia Using MTSAT-2 Land Surface Temperature Retrievals. Remote Sens. Environ. 2020, 236, 111419. [Google Scholar] [CrossRef]
- Karnieli, A.; Agam, N.; Pinker, R.T.; Anderson, M.; Imhoff, M.L.; Gutman, G.G.; Panov, N.; Goldberg, A. Use of NDVI and Land Surface Temperature for Drought Assessment: Merits and Limitations. J. Clim. 2010, 23, 618–633. [Google Scholar] [CrossRef]
- West, H.; Quinn, N.; Horswell, M. Remote Sensing for Drought Monitoring & Impact Assessment: Progress, Past Challenges and Future Opportunities. Remote Sens. Environ. 2019, 232, 111291. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a Two-Band Enhanced Vegetation Index without a Blue Band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Yang, Y.; Anderson, M.C.; Gao, F.; Wood, J.D.; Gu, L.; Hain, C. Studying Drought-Induced Forest Mortality Using High Spatiotemporal Resolution Evapotranspiration Data from Thermal Satellite Imaging. Remote Sens. Environ. 2021, 265, 112640. [Google Scholar] [CrossRef]
- Ojha, C.; Werth, S.; Shirzaei, M. Recovery of Aquifer-Systems in Southwest US Following 2012–2015 Drought: Evidence from InSAR, GRACE and Groundwater Level Data. J. Hydrol. 2020, 587, 124943. [Google Scholar] [CrossRef]
- Sánchez, N.; González-Zamora, Á.; Martínez-Fernández, J.; Piles, M.; Pablos, M. Integrated Remote Sensing Approach to Global Agricultural Drought Monitoring. Agric. For. Meteorol. 2018, 259, 141–153. [Google Scholar] [CrossRef]
- McCabe, M.F.; Wood, E.F.; Wójcik, R.; Pan, M.; Sheffield, J.; Gao, H.; Su, H. Hydrological Consistency Using Multi-Sensor Remote Sensing Data for Water and Energy Cycle Studies. Remote Sens. Environ. 2008, 112, 430–444. [Google Scholar] [CrossRef]
- Zhao, J.; Feng, H.; Xu, T.; Xiao, J.; Guerrieri, R.; Liu, S.; Wu, X.; He, X.; He, X. Physiological and Environmental Control on Ecosystem Water Use Efficiency in Response to Drought across the Northern Hemisphere. Sci. Total Environ. 2021, 758, 143599. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Meason, D.F.; Höck, B.; Lad, P.; Das, N. Evaluation of Multiscale SMAP Soil Moisture Products in Forested Environments. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Sakaki, T.; Limsuwat, A.; Smits, K.M.; Illangasekare, T.H. Empirical Two-Point α -Mixing Model for Calibrating the ECH2 O EC-5 Soil Moisture Sensor in Sands. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Fares, A.; Polyakov, V. Advances in Crop Water Management Using Capacitive Water Sensors. In Advances in Agronomy; Academic Press: Cambridge, MA, USA, 2006; Volume 90, pp. 43–77. [Google Scholar] [CrossRef]
- Wiekenkamp, I.; Huisman, J.A.; Bogena, H.R.; Lin, H.S.; Vereecken, H. Spatial and Temporal Occurrence of Preferential Flow in a Forested Headwater Catchment. J. Hydrol. 2016, 534, 139–149. [Google Scholar] [CrossRef]
- Kizito, F.; Campbell, C.S.; Campbell, G.S.; Cobos, D.R.; Teare, B.L.; Carter, B.; Hopmans, J.W. Frequency, Electrical Conductivity and Temperature Analysis of a Low-Cost Capacitance Soil Moisture Sensor. J. Hydrol. 2008, 352, 367–378. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Integrated Multi-satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In Satellite Precipitation Measurement: Volume 1; Levizzani, V., Kidd, C., Kirschbaum, D.B., Kummerow, C.D., Nakamura, K., Turk, F.J., Eds.; Advances in Global Change Research, Springer International Publishing: Cham, Switzerland, 2020; pp. 343–353. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS Satellite Rainfall Estimates over Eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, W.; Yu, Z. Evaluating the Drought-Monitoring Utility of GPM and TRMM Precipitation Products over Mainland China. Remote Sens. 2021, 13, 4153. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Liu, T.; Ndayisaba, F.; He, D.; Kurban, A.; De Maeyer, P. Meteorological Drought Analysis in the Lower Mekong Basin Using Satellite-Based Long-Term CHIRPS Product. Sustainability 2017, 9, 901. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Wu, Z.; Qiu, J.; Crow, W.T.; Wang, D.; Wang, Z.; Zhang, X. Investigating the Efficacy of the SMAP Downscaled Soil Moisture Product for Drought Monitoring Based on Information Theory. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1604–1616. [Google Scholar] [CrossRef]
- Chan, S.; Bindlish, R.; O’Neill, P.; Jackson, T.; Njoku, E.; Dunbar, S.; Chaubell, J.; Piepmeier, J.; Yueh, S.; Entekhabi, D.; et al. Development and assessment of the SMAP enhanced passive soil moisture product. Remote Sens. Environ. 2018, 204, 931–941. [Google Scholar] [CrossRef]
- Das, N.N.; Entekhabi, D.; Dunbar, R.S.; Chaubell, M.J.; Colliander, A.; Yueh, S.; Jagdhuber, T.; Chen, F.; Crow, W.; O’Neill, P.E.; et al. The SMAP and Copernicus Sentinel 1A/B microwave active-passive high resolution surface soil moisture product. Remote Sens. Environ. 2019, 233, 111380. [Google Scholar] [CrossRef]
- Zhao, Q.; Yu, L.; Du, Z.; Peng, D.; Hao, P.; Zhang, Y.; Gong, P. An Overview of the Applications of Earth Observation Satellite Data: Impacts and Future Trends. Remote Sens. 2022, 14, 1863. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Li, H.; Göttsche, F.M.; Wu, H.; Zhao, W.; Leng, P.; Zhang, X.; Coll, C. Validation of Collection 6 MODIS Land Surface Temperature Product Using in Situ Measurements. Remote Sens. Environ. 2019, 225, 16–29. [Google Scholar] [CrossRef]
- Mao, K.B.; Ma, Y.; Tan, X.L.; Shen, X.Y.; Liu, G.; Li, Z.L.; Chen, J.M.; Xia, L. Global Surface Temperature Change Analysis Based on MODIS Data in Recent Twelve Years. Adv. Space Res. 2017, 59, 503–512. [Google Scholar] [CrossRef]
- Yu, P.; Zhao, T.; Shi, J.; Ran, Y.; Jia, L.; Ji, D.; Xue, H. Global Spatiotemporally Continuous MODIS Land Surface Temperature Dataset. Sci. Data 2022, 9, 143. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS Global Terrestrial Evapotranspiration Algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Zhang, K.; Zhu, G.; Ma, J.; Yang, Y.; Shang, S.; Gu, C. Parameter Analysis and Estimates for the MODIS Evapotranspiration Algorithm and Multiscale Verification. Water Resour. Res. 2019, 55, 2211–2231. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The Drought Phenomenon: The Role of Definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Drought Characterization from a Multivariate Perspective: A Review. J. Hydrol. 2015, 527, 668–678. [Google Scholar] [CrossRef]
- Heim, R.R. A Review of Twentieth-Century Drought Indices Used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1166. [Google Scholar] [CrossRef]
- Jalayer, S.; Sharifi, A.; Abbasi-Moghadam, D.; Tariq, A.; Qin, S. Assessment of Spatiotemporal Characteristic of Droughts Using In Situ and Remote Sensing-Based Drought Indices. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1483–1502. [Google Scholar] [CrossRef]
- Farahmand, A.; AghaKouchak, A. A Generalized Framework for Deriving Nonparametric Standardized Drought Indicators. Adv. Water Resour. 2015, 76, 140–145. [Google Scholar] [CrossRef]
- Mishra, A.; Liu, S.C. Changes in Precipitation Pattern and Risk of Drought over India in the Context of Global Warming. J. Geophys. Res. Atmos. 2014, 119, 7833–7841. [Google Scholar] [CrossRef]
- Martin-Vide, J.; Gomez, L. Regionalization of Peninsular Spain Based on the Length of Dry Spells. Int. J. Climatol. 1999, 19, 537–555. [Google Scholar] [CrossRef]
- Laio, F.; Porporato, A.; Ridolfi, L.; Rodriguez-Iturbe, I. Plants in Water-Controlled Ecosystems: Active Role in Hydrologic Processes and Response to Water Stress: II. Probabilistic Soil Moisture Dynamics. Adv. Water Resour. 2001, 24, 707–723. [Google Scholar] [CrossRef]
- Gaur, N.; Mohanty, B.P. A Nomograph to Incorporate Geophysical Heterogeneity in Soil Moisture Downscaling. Water Resour. Res. 2019, 55, 34–54. [Google Scholar] [CrossRef]
- Sehgal, V.; Gaur, N.; Mohanty, B.P. Global Surface Soil Moisture Drydown Patterns. Water Resour. Res. 2021, 57, e2020WR027588. [Google Scholar] [CrossRef]
- McColl, K.A.; Wang, W.; Peng, B.; Akbar, R.; Short Gianotti, D.J.; Lu, H.; Pan, M.; Entekhabi, D. Global Characterization of Surface Soil Moisture Drydowns. Geophys. Res. Lett. 2017, 44, 3682–3690. [Google Scholar] [CrossRef]
- Belmonte, A.; Ts. Sankey, T.; Biederman, J.; Bradford, J.B.; Kolb, T. Soil Moisture Response to Seasonal Drought Conditions and Post-Thinning Forest Structure. Ecohydrology 2022, 15, e2406. [Google Scholar] [CrossRef]
- Gao, Y.; Markkanen, T.; Aurela, M.; Mammarella, I.; Thum, T.; Tsuruta, A.; Yang, H.; Aalto, T. Response of Water Use Efficiency to Summer Drought in a Boreal Scots Pine Forest in Finland. Biogeosciences 2017, 14, 4409–4422. [Google Scholar] [CrossRef]
- Salinger, M.J.; Porteous, A.S. New Zealand Climate: Patterns of Drought 1941/42–2012/13. Weather Clim. 2014, 34, 2–19. [Google Scholar] [CrossRef]
- Steinemann, A.; Iacobellis, S.F.; Cayan, D.R. Developing and Evaluating Drought Indicators for Decision-Making. J. Hydrometeorol. 2015, 16, 1793–1803. [Google Scholar] [CrossRef]
- Loikith, P.C.; Waliser, D.E.; Lee, H.; Kim, J.; Neelin, J.D.; Lintner, B.R.; McGinnis, S.; Mattmann, C.A.; Mearns, L.O. Surface Temperature Probability Distributions in the NARCCAP Hindcast Experiment: Evaluation Methodology, Metrics, and Results. J. Clim. 2015, 28, 978–997. [Google Scholar] [CrossRef]
- Daniel, W.W. Applied Nonparametric Statistics, 2nd ed.; Duxbury Classic Series; Duxbury: Pacific Grove, CA, USA, 1990. [Google Scholar]
- Cammalleri, C.; Vogt, J. On the Role of Land Surface Temperature as Proxy of Soil Moisture Status for Drought Monitoring in Europe. Remote Sens. 2015, 7, 16849–16864. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Sawano, S.; Hotta, N.; Tanaka, N.; Tsuboyama, Y.; Suzuki, M. Development of a Simple Forest Evapotranspiration Model Using a Process-Oriented Model as a Reference to Parameterize Data from a Wide Range of Environmental Conditions. Ecol. Model. 2015, 309–310, 93–109. [Google Scholar] [CrossRef]
- Shi, T.; Guan, D.; Wang, A.; Wu, J.; Jin, C.; Han, S. Comparison of Three Models to Estimate Evapotranspiration for a Temperate Mixed Forest. Hydrol. Process. 2008, 22, 3431–3443. [Google Scholar] [CrossRef]
- Ben Aissia, M.A.; Chebana, F.; Ouarda, T.B.M.J. Multivariate Missing Data in Hydrology—Review and Applications. Adv. Water Resour. 2017, 110, 299–309. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar] [CrossRef]
- Jiang, B.; Liang, S.; Yuan, W. Observational Evidence for Impacts of Vegetation Change on Local Surface Climate over Northern China Using the Granger Causality Test. J. Geophys. Res. Biogeosci. 2015, 120, 1–12. [Google Scholar] [CrossRef]
- Shojaie, A.; Fox, E.B. Granger Causality: A Review and Recent Advances. Annu. Rev. Stat. Its Appl. 2022, 9, 289–319. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Hayes, M.J.; Wilhite, D.A.; Svoboda, M.D. The Effect of the Length of Record on the Standardized Precipitation Index Calculation. Int. J. Clim. 2005, 25, 505–520. [Google Scholar] [CrossRef]
- Derin, Y.; Anagnostou, E.; Berne, A.; Borga, M.; Boudevillain, B.; Buytaert, W.; Chang, C.H.; Chen, H.; Delrieu, G.; Hsu, Y.C.; et al. Evaluation of GPM-era Global Satellite Precipitation Products over Multiple Complex Terrain Regions. Remote Sens. 2019, 11, 2936. [Google Scholar] [CrossRef]
- Huang, G.; Li, X.; Huang, C.; Liu, S.; Ma, Y.; Chen, H. Representativeness Errors of Point-Scale Ground-Based Solar Radiation Measurements in the Validation of Remote Sensing Products. Remote Sens. Environ. 2016, 181, 198–206. [Google Scholar] [CrossRef]
- Ayres, E.; Colliander, A.; Cosh, M.H.; Roberti, J.A.; Simkin, S.; Genazzio, M.A. Validation of SMAP Soil Moisture at Terrestrial National Ecological Observatory Network (NEON) Sites Show Potential for Soil Moisture Retrieval in Forested Areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10903–10918. [Google Scholar] [CrossRef]
- Eswar, R.; Das, N.N.; Poulsen, C.; Behrangi, A.; Swigart, J.; Svoboda, M.; Entekhabi, D.; Yueh, S.; Doorn, B.; Entin, J. SMAP Soil Moisture Change as an Indicator of Drought Conditions. Remote Sens. 2018, 10, 788. [Google Scholar] [CrossRef]
- Sadri, S.; Wood, E.F.; Pan, M. Developing a Drought-Monitoring Index for the Contiguous US Using SMAP. Hydrol. Earth Syst. Sci. 2018, 22, 6611–6626. [Google Scholar] [CrossRef]
- Ford, T.W.; Quiring, S.M. Comparison of Contemporary In Situ, Model, and Satellite Remote Sensing Soil Moisture With a Focus on Drought Monitoring. Water Resour. Res. 2019, 55, 1565–1582. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Senay, G.B.; Morisette, J.T. Evaluating New SMAP Soil Moisture for Drought Monitoring in the Rangelands of the US High Plains. Rangelands 2016, 38, 183–190. [Google Scholar] [CrossRef]
- Sahbeni, G.; Pleynet, J.B.; Jarocki, K. A Spatiotemporal Analysis of Precipitation Anomalies Using Rainfall Gini Index between 1980 and 2022. Atmos. Sci. Lett. 2023, 24, e1161. [Google Scholar] [CrossRef]
- Rassl, A.; Michel, D.; Hirschi, M.; Duguay-Tetzlaff, A.; Seneviratne, S.I. Climatological Drought Monitoring in Switzerland Using EUMETSAT SAF Satellite Data. Remote Sens. 2022, 14, 5961. [Google Scholar] [CrossRef]
- Cammalleri, C.; Arias-Muñoz, C.; Barbosa, P.; de Jager, A.; Magni, D.; Masante, D.; Mazzeschi, M.; McCormick, N.; Naumann, G.; Spinoni, J.; et al. A Revision of the Combined Drought Indicator (CDI) Used in the European Drought Observatory (EDO). Nat. Hazards Earth Syst. Sci. 2021, 21, 481–495. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).