Rainfall Erosivity Characteristics during 1961–2100 in the Loess Plateau, China
Abstract
1. Introduction
2. Materials and Methods
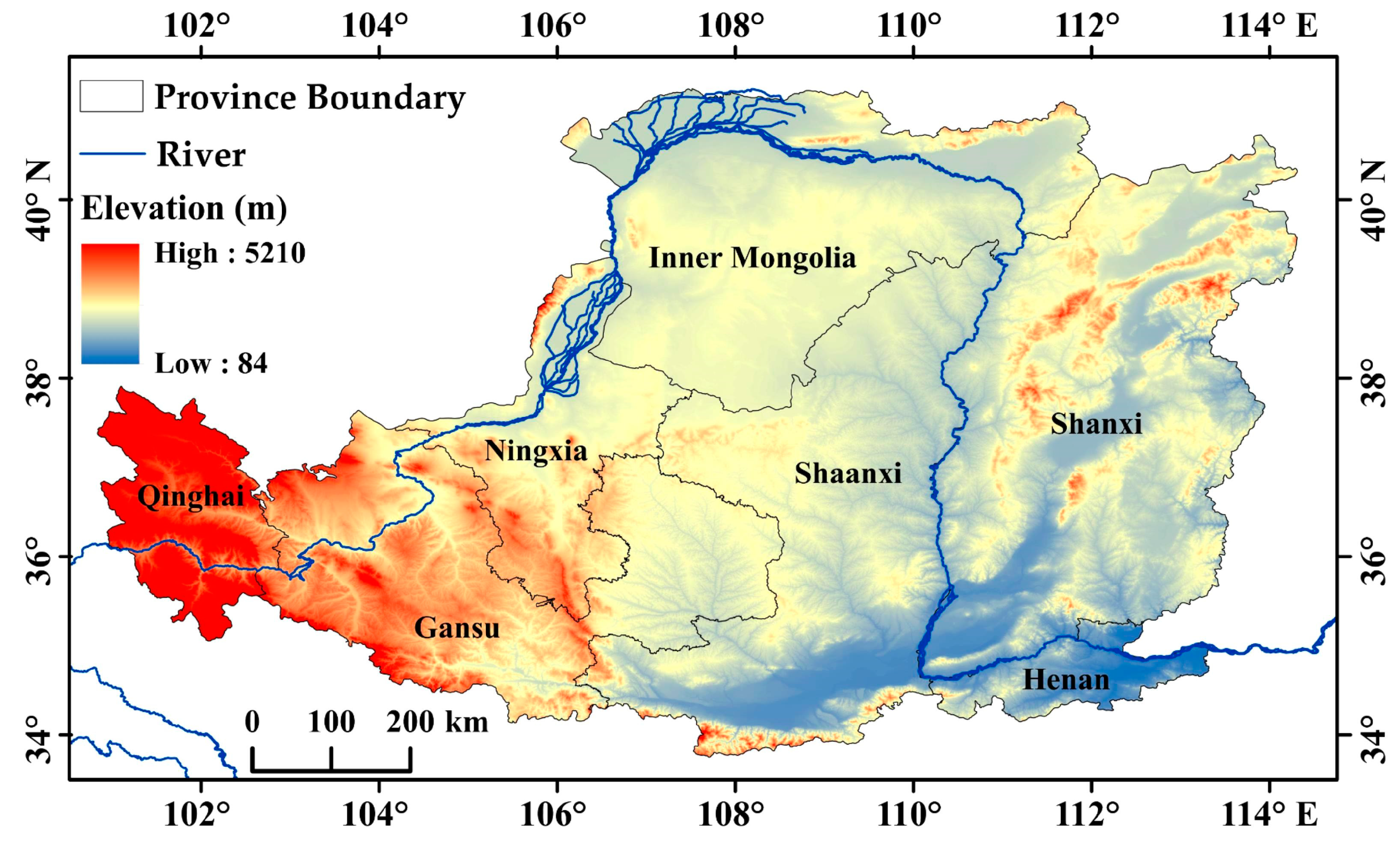
2.1. Study Area
2.2. Data
2.3. Methods
2.3.1. Statistical Downscaling
2.3.2. Multi-Model Ensemble (MME)
2.3.3. Evaluation of the Multi-Model Adaptability
2.3.4. Rainfall Erosivity Calculations
2.3.5. Change Trend and Significance Test
2.3.6. Coefficient of Variation (COV)
3. Results
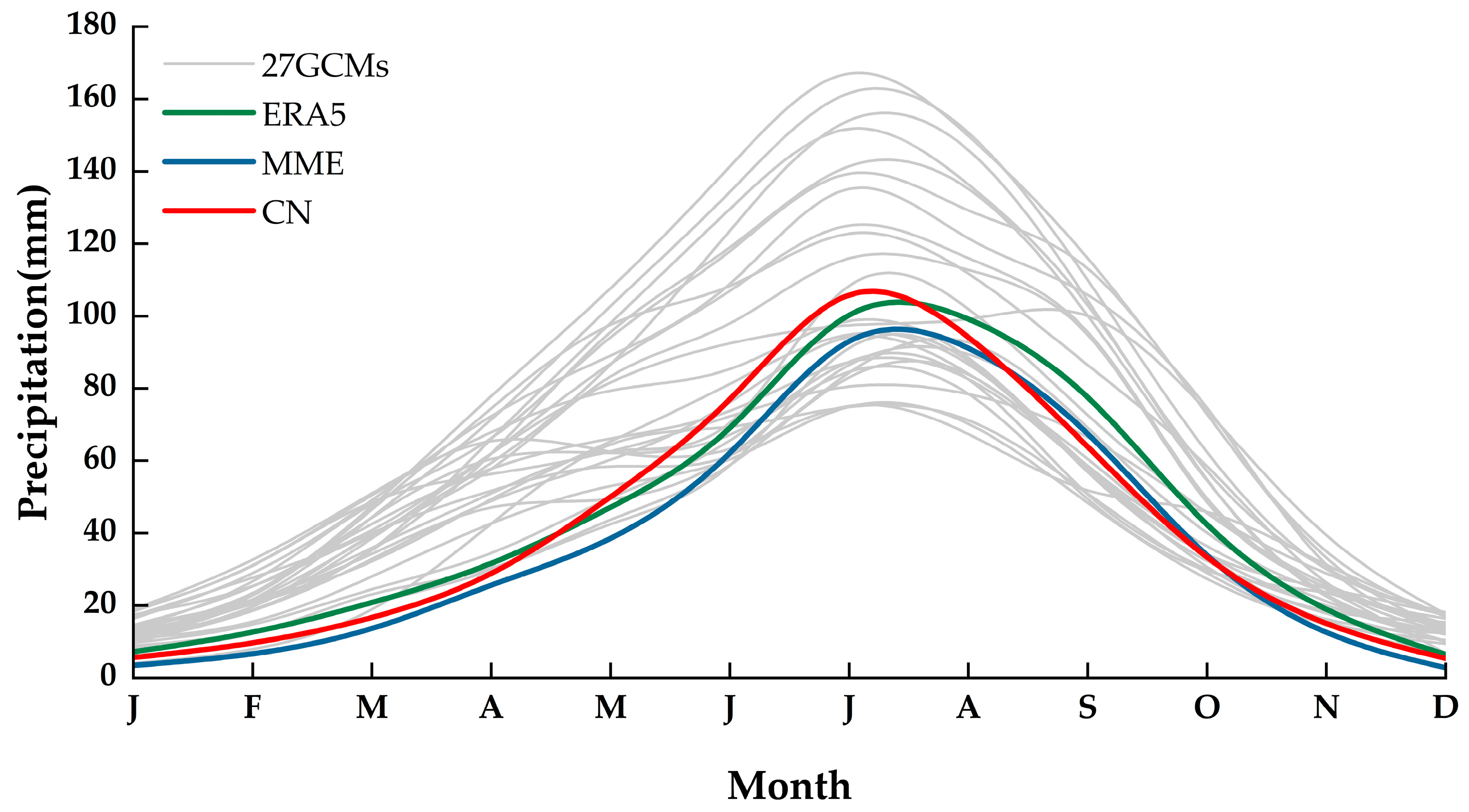
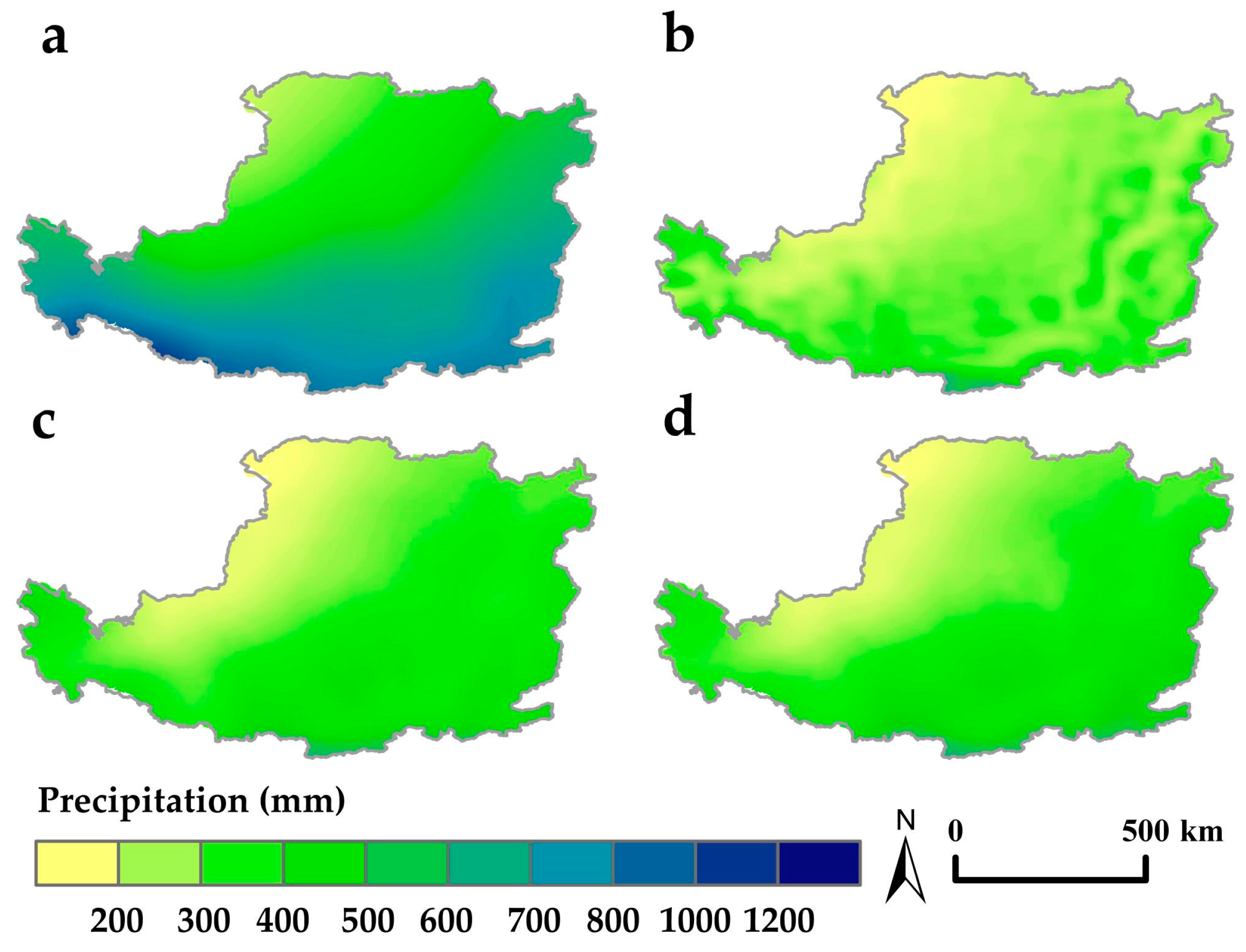
3.1. Evaluation of Precipitation under the Multi-Model Ensemble Mean
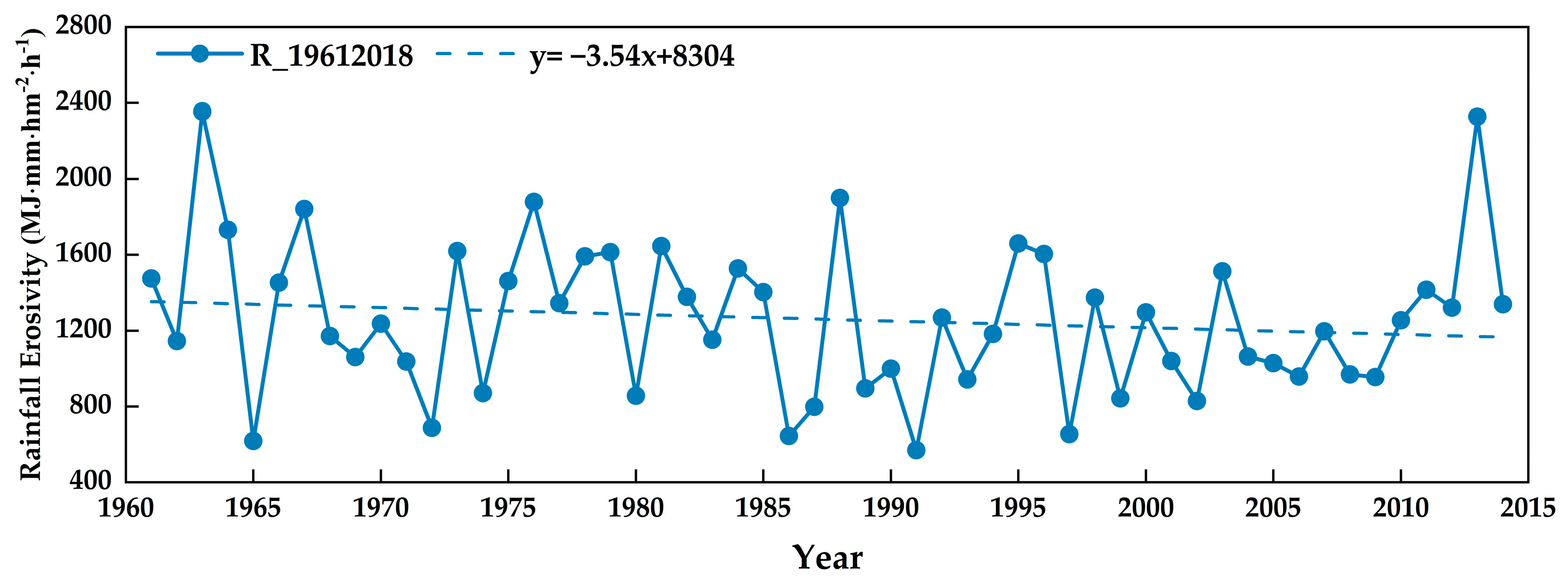
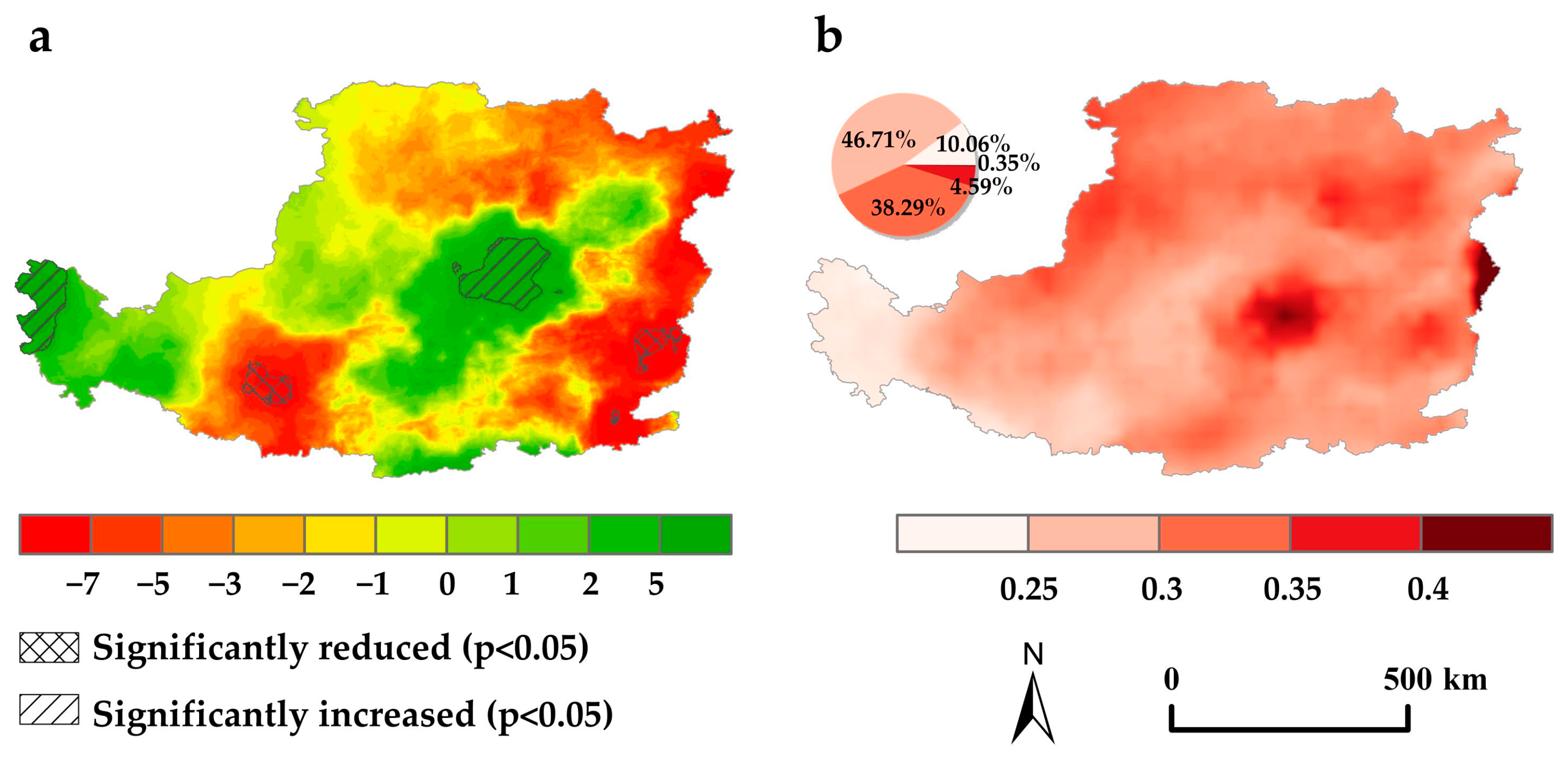
3.2. Characteristics of Rainfall Erosivity from 1961 to 2014
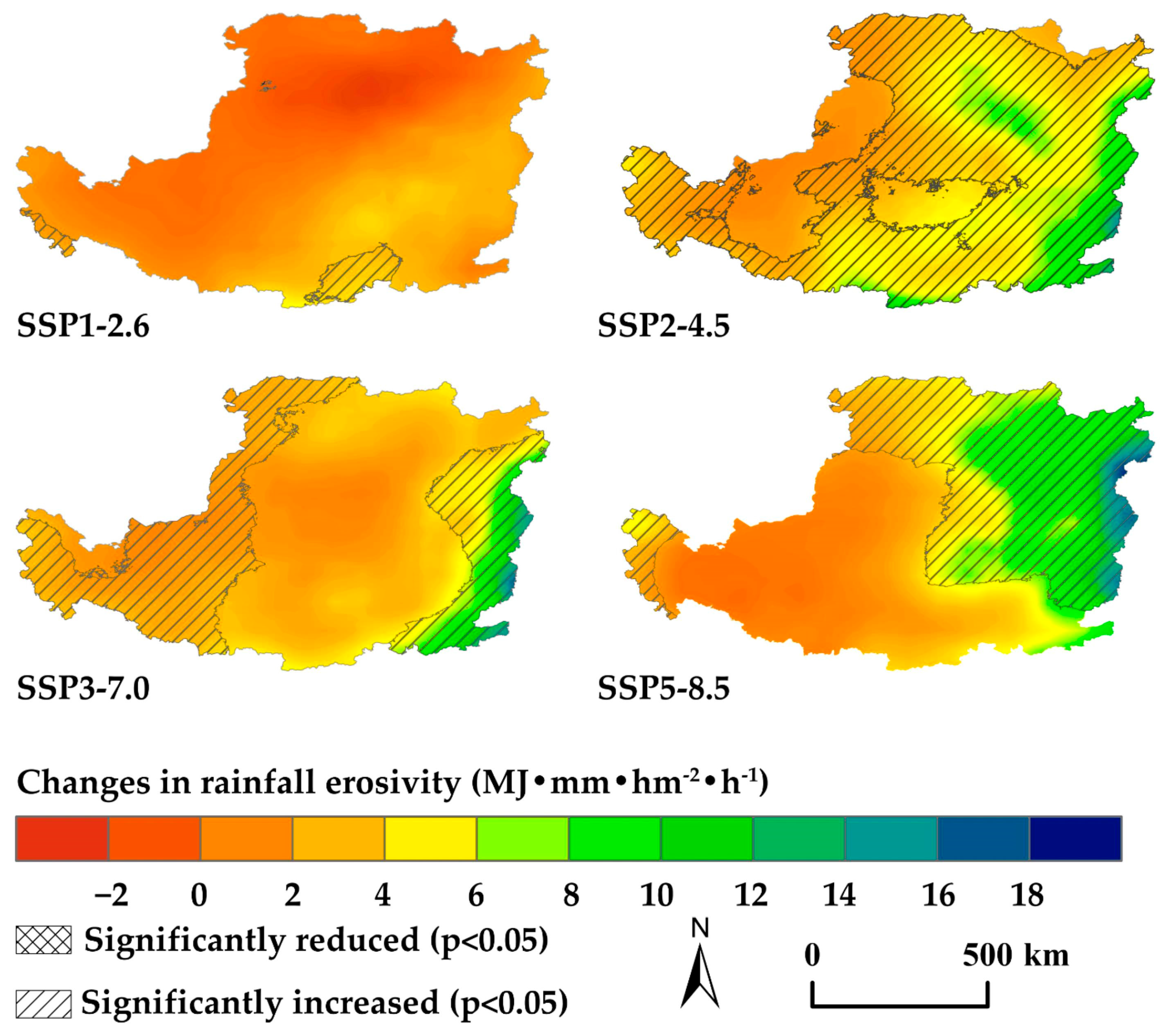
3.3. Estimation of the Future Rainfall Erosivity
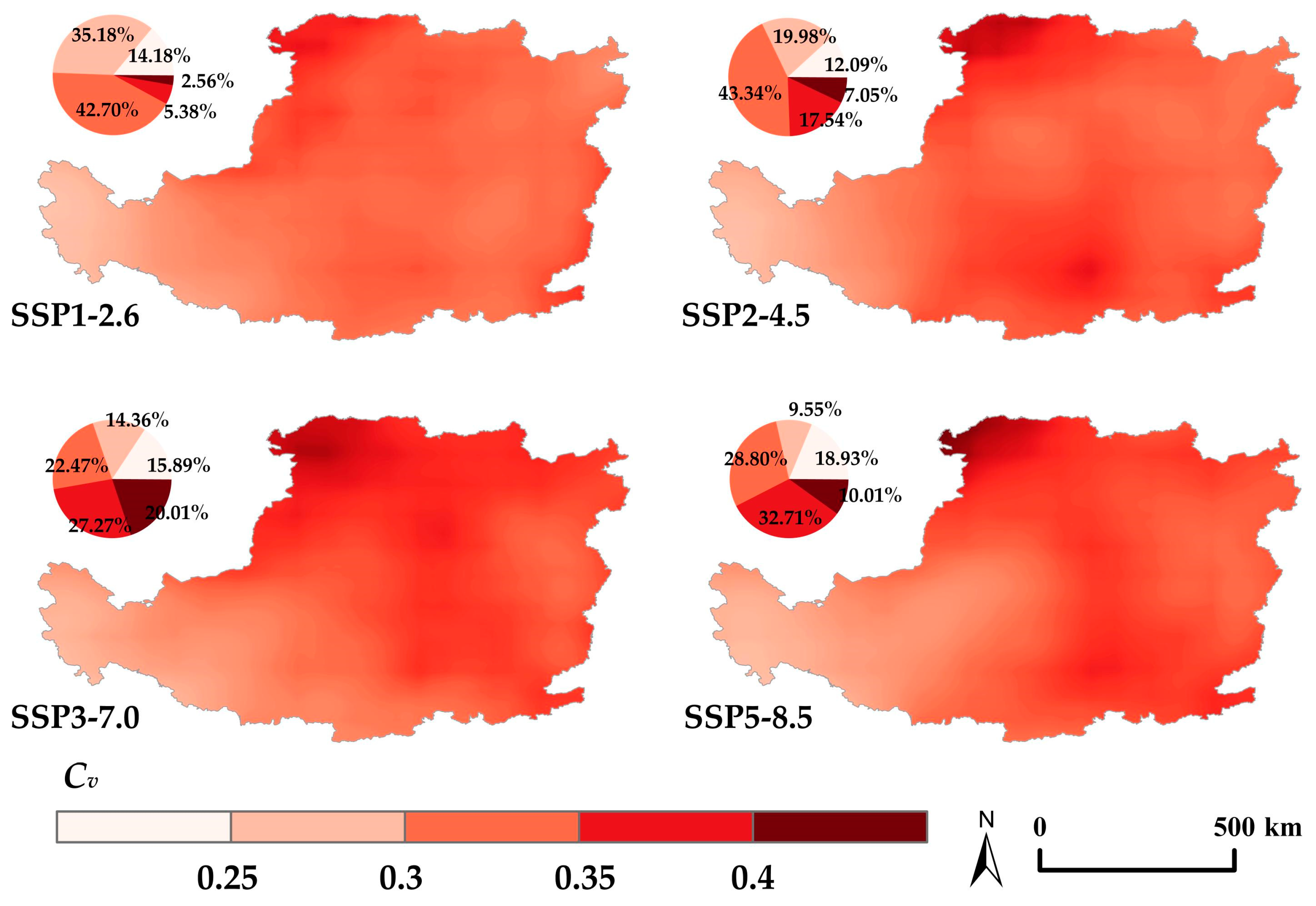
3.4. Analysis of Variability
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, X.; Yang, Q.; Zhu, H.; Wang, L.; Wang, C.; Pang, G.; Du, C.; Mubeen, M.; Waleed, M.; Hussain, S. Quantitative Evaluation of Soil Water and Wind Erosion Rates in Pakistan. Remote Sens. 2023, 15, 2404. [Google Scholar] [CrossRef]
- Amundson, R.; Berhe, A.A.; Hopmans, J.W.; Olson, C.; Sztein, A.E.; Sparks, D.L. Soil and Human Security in the 21st Century. Science 2015, 348, 1261071. [Google Scholar] [CrossRef]
- Takhellambam, B.S.; Srivastava, P.; Lamba, J.; McGehee, R.P.; Kumar, H.; Tian, D. Projected Mid-Century Rainfall Erosivity under Climate Change over the Southeastern United States. Sci. Total Environ. 2023, 865, 161119. [Google Scholar] [CrossRef]
- Grillakis, M.G.; Polykretis, C.; Alexakis, D.D. Past and Projected Climate Change Impacts on Rainfall Erosivity: Advancing Our Knowledge for the Eastern Mediterranean Island of Crete. CATENA 2020, 193, 104625. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Matthews, F.; Liakos, L.; Bezak, N.; Diodato, N.; Ballabio, C. Global Rainfall Erosivity Projections for 2050 and 2070. J. Hydrol. 2022, 610, 127865. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, Y.; Zhou, X.; Zhang, Y. Climate and Human Impact Together Drive Changes in Ecosystem Multifunction-ality in the Drylands of China. Appl. Soil Ecol. 2024, 193, 105163. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Montanari, A. Global and Regional Increase of Precipitation Extremes Under Global Warming. Water Resour. Res. 2019, 55, 4901–4914. [Google Scholar] [CrossRef]
- Neelin, J.D.; Sahany, S.; Stechmann, S.N.; Bernstein, D.N. Global Warming Precipitation Accumulation Increases above the Current-Climate Cutoff Scale. Proc. Natl. Acad. Sci. USA 2017, 114, 1258–1263. [Google Scholar] [CrossRef] [PubMed]
- Guhathakurta, P.; Sreejith, O.P.; Menon, P.A. Impact of Climate Change on Extreme Rainfall Events and Flood Risk in India. J. Earth Syst. Sci. 2011, 120, 359–373. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, F.; Liu, W.; Flanagan, D.C. Spatial Distribution and Temporal Trends of Extreme Temperature and Precipitation Events on the Loess Plateau of China during 1961–2007. Quat. Int. 2010, 226, 92–100. [Google Scholar] [CrossRef]
- Hoomehr, S.; Schwartz, J.S.; Yoder, D.C. Potential Changes in Rainfall Erosivity under GCM Climate Change Scenarios for the Southern Appalachian Region, USA. CATENA 2016, 136, 141–151. [Google Scholar] [CrossRef]
- Wang, W.; Yin, S.; Gao, G.; Papalexiou, S.M.; Wang, Z. Increasing Trends in Rainfall Erosivity in the Yellow River Basin from 1971 to 2020. J. Hydrol. 2022, 610, 127851. [Google Scholar] [CrossRef]
- Chang, Y.; Lei, H.; Zhou, F.; Yang, D. Spatial and Temporal Variations of Rainfall Erosivity in the Middle Yellow River Basin Based on Hourly Rainfall Data. CATENA 2022, 216, 106406. [Google Scholar] [CrossRef]
- Xu, X.; Yan, Y.; Dai, Q.; Yi, X.; Hu, Z.; Cen, L. Spatial and Temporal Dynamics of Rainfall Erosivity in the Karst Region of Southwest China: Interannual and Seasonal Changes. CATENA 2023, 221, 106763. [Google Scholar] [CrossRef]
- Kilic, O.M.; Gunal, H. Spatial-Temporal Changes in Rainfall Erosivity in Turkey Using CMIP5 Global Climate Change Scenario. Arab. J. Geosci. 2021, 14, 1079. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Meusburger, K.; Spinoni, J.; Alewell, C.; Borrelli, P. Towards Estimates of Future Rainfall Erosivity in Europe Based on REDES and WorldClim Datasets. J. Hydrol. 2017, 548, 251–262. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Yang, X.; Ji, F.; Liu, D.L.; Yu, Q. Extreme Rainfall, Rainfall Erosivity, and Hillslope Erosion in Australian Alpine Region and Their Future Changes. Int. J. Climatol. 2020, 40, 1213–1227. [Google Scholar] [CrossRef]
- Li, D.; Qi, Y.; Zhou, T. Changes in Rainfall Erosivity over Mainland China under Stabilized 1.5 °C and 2 °C Warming Futures. J. Hydrol. 2021, 603, 126996. [Google Scholar] [CrossRef]
- Mondal, A.; Khare, D.; Kundu, S. Change in Rainfall Erosivity in the Past and Future Due to Climate Change in the Central Part of India. Int. Soil Water Conserv. Res. 2016, 4, 186–194. [Google Scholar] [CrossRef]
- Tebaldi, C.; Debeire, K.; Eyring, V.; Fischer, E.; Fyfe, J.; Friedlingstein, P.; Knutti, R.; Lowe, J.; O’Neill, B.; Sanderson, B.; et al. Climate Model Projections from the Scenario Model Intercomparison Project (ScenarioMIP) of CMIP6. Earth Syst. Dynam. 2021, 12, 253–293. [Google Scholar] [CrossRef]
- Xin, X.; Wu, T.; Zhang, J.; Yao, J.; Fang, Y. Comparison of CMIP6 and CMIP5 Simulations of Precipitation in China and the East Asian Summer Monsoon. Int. J. Climatol. 2020, 40, 6423–6440. [Google Scholar] [CrossRef]
- Diaz-Nieto, J.; Wilby, R.L. A Comparison of Statistical Downscaling and Climate Change Factor Methods: Impacts on Low Flows in the River Thames, United Kingdom. Clim. Change 2005, 69, 245–268. [Google Scholar] [CrossRef]
- Mosier, T.M.; Hill, D.F.; Sharp, K.V. 30-Arcsecond Monthly Climate Surfaces with Global Land Coverage: 30-ARCSECOND Global Climate Surfaces. Int. J. Climatol. 2014, 34, 2175–2188. [Google Scholar] [CrossRef]
- Fan, X.; Jiang, L.; Gou, J. Statistical Downscaling and Projection of Future Temperatures across the Loess Plateau, China. Weather Clim. Extrem. 2021, 32, 100328. [Google Scholar] [CrossRef]
- Peng, S.; Gang, C.; Cao, Y.; Chen, Y. Assessment of Climate Change Trends over the Loess Plateau in China from 1901 to 2100: Assessment of Climate Change Trends over the Loess Plateau. Int. J. Clim. 2018, 38, 2250–2264. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Tebaldi, C.; van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.-F.; Lowe, J.; et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- Wu, J.; Gao, X.; Giorgi, F.; Chen, D. Changes of Effective Temperature and Cold/Hot Days in Late Decades over China Based on a High Resolution Gridded Observation Dataset: Changes of Effective Temperature and Cold/Hot Days over China. Int. J. Clim. 2017, 37, 788–800. [Google Scholar] [CrossRef]
- Bi, D.; Dix, M.; Marsland, S.; O’Farrell, S.; Sullivan, A.; Bodman, R.; Law, R.; Harman, I.; Srbinovsky, J.; Rashid, H.A.; et al. Configuration and Spin-up of ACCESS-CM2, the New Generation Australian Community Climate and Earth System Simulator Coupled Model. J. South. Hemisph. Earth Syst. Sci. 2020, 70, 225–251. [Google Scholar] [CrossRef]
- Ziehn, T.; Chamberlain, M.A.; Law, R.M.; Lenton, A.; Bodman, R.W.; Dix, M.; Stevens, L.; Wang, Y.-P.; Srbinovsky, J. The Australian Earth System Model: ACCESS-ESM1.5. J. South. Hemisph. Earth Syst. Sci. 2020, 70, 193–214. [Google Scholar] [CrossRef]
- Semmler, T.; Danilov, S.; Gierz, P.; Goessling, H.F.; Hegewald, J.; Hinrichs, C.; Koldunov, N.; Khosravi, N.; Mu, L.; Rackow, T.; et al. Simulations for CMIP6 with the AWI Climate Model AWI-CM-1-1. J. Adv. Model Earth Syst. 2020, 12, e2019MS002009. [Google Scholar] [CrossRef]
- Wu, T.; Lu, Y.; Fang, Y.; Xin, X.; Li, L.; Li, W.; Jie, W.; Zhang, J.; Liu, Y.; Zhang, L.; et al. The Beijing Climate Center Climate System Model (BCC-CSM): The Main Progress from CMIP5 to CMIP6. Geosci. Model Dev. 2019, 12, 1573–1600. [Google Scholar] [CrossRef]
- Xin, Y.; Dai, Y.; Li, J.; Rong, X.; Zhang, G. Coupling the Common Land Model to ECHAM5 Atmospheric General Circulation Model. J. Meteorol. Res. 2019, 33, 251–263. [Google Scholar] [CrossRef]
- Swart, N.C.; Cole, J.N.S.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Hanna, S.; et al. The Canadian Earth System Model Version 5 (CanESM5.0.3). Geosci. Model Dev. 2019, 12, 4823–4873. [Google Scholar] [CrossRef]
- Sigmond, M.; Anstey, J.; Arora, V.; Digby, R.; Gillett, N.; Kharin, V.; Merryfield, W.; Reader, C.; Scinocca, J.; Swart, N.; et al. Improvements in the Canadian Earth System Model (CanESM) through Systematic Model Analysis: CanESM5.0 and CanESM5.1. Clim. Earth Syst. Model. 2023, 16, 6553–6591. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, M.; Jin, J.; Fei, K.; Ji, D.; Wu, C.; Zhu, J.; He, J.; Chai, Z.; Xie, J.; et al. Description and Climate Simulation Performance of CAS-ESM Version 2. J. Adv. Model Earth Syst. 2020, 12, e2020MS002210. [Google Scholar] [CrossRef]
- Gettelman, A.; Mills, M.J.; Kinnison, D.E.; Garcia, R.R.; Smith, A.K.; Marsh, D.R.; Tilmes, S.; Vitt, F.; Bardeen, C.G.; McInerny, J.; et al. The Whole Atmosphere Community Climate Model Version 6 (WACCM6). JGR Atmos. 2019, 124, 12380–12403. [Google Scholar] [CrossRef]
- Cherchi, A.; Fogli, P.G.; Lovato, T.; Peano, D.; Iovino, D.; Gualdi, S.; Masina, S.; Scoccimarro, E.; Materia, S.; Bellucci, A.; et al. Global Mean Climate and Main Patterns of Variability in the CMCC-CM2 Coupled Model. J. Adv. Model. Earth Syst. 2018, 11, 2018MS001369. [Google Scholar] [CrossRef]
- Lovato, T.; Peano, D.; Butenschön, M.; Materia, S.; Iovino, D.; Scoccimarro, E.; Fogli, P.G.; Cherchi, A.; Bellucci, A.; Gualdi, S.; et al. CMIP6 Simulations with the CMCC Earth System Model (CMCC-ESM2). J. Adv. Model Earth Syst. 2022, 14, e2021MS002814. [Google Scholar] [CrossRef]
- Döscher, R.; Acosta, M.; Alessandri, A.; Anthoni, P.; Arsouze, T.; Bergman, T.; Bernardello, R.; Boussetta, S.; Caron, L.-P.; Carver, G.; et al. The EC-Earth3 Earth System Model for the Coupled Model Intercomparison Project 6. Geosci. Model Dev. 2022, 15, 2973–3020. [Google Scholar] [CrossRef]
- Wyser, K.; Kjellström, E.; Koenigk, T.; Martins, H.; Döscher, R. Warmer Climate Projections in EC-Earth3-Veg: The Role of Changes in the Greenhouse Gas Concentrations from CMIP5 to CMIP6. Environ. Res. Lett. 2020, 15, 054020. [Google Scholar] [CrossRef]
- He, B.; Yu, Y.; Bao, Q.; Lin, P.; Liu, H.; Li, J.; Wang, L.; Liu, Y.; Wu, G.; Chen, K.; et al. CAS FGOALS-F3-L Model Dataset Descriptions for CMIP6 DECK Experiments. Atmos. Ocean. Sci. Lett. 2020, 13, 582–588. [Google Scholar] [CrossRef]
- Li, L.; Yu, Y.; Tang, Y.; Lin, P.; Xie, J.; Song, M.; Dong, L.; Zhou, T.; Liu, L.; Wang, L.; et al. The Flexible Global Ocean-Atmosphere-Land System Model Grid-Point Version 3 (FGOALS-g3): Description and Evaluation. J. Adv. Model Earth Syst. 2020, 12, e2019MS002012. [Google Scholar] [CrossRef]
- Krishnan, R.; Swapna, P.; Vellore, R.; Narayanasetti, S.; Prajeesh, A.G.; Choudhury, A.D.; Singh, M.; Sabin, T.P.; Sanjay, J. The IITM Earth System Model (ESM): Development and Future Roadmap. In Current Trends in the Representation of Physical Processes in Weather and Climate Models; Randall, D.A., Srinivasan, J., Nanjundiah, R.S., Mukhopadhyay, P., Eds.; Springer Atmospheric Sciences; Springer: Singapore, 2019; pp. 183–195. ISBN 9789811333958. [Google Scholar]
- Volodin, E.M.; Mortikov, E.V.; Kostrykin, S.V.; Galin, V.Y.; Lykossov, V.N.; Gritsun, A.S.; Diansky, N.A.; Gusev, A.V.; Iakovlev, N.G.; Shestakova, A.A.; et al. Simulation of the Modern Climate Using the INM-CM48 Climate Model. Russ. J. Numer. Anal. Math. Model. 2018, 33, 367–374. [Google Scholar] [CrossRef]
- Volodin, E.M.; Mortikov, E.V.; Kostrykin, S.V.; Galin, V.Y.; Lykosov, V.N.; Gritsun, A.S.; Diansky, N.A.; Gusev, A.V.; Yakovlev, N.G. Simulation of Modern Climate with the New Version of the INM RAS Climate Model. Izv. Atmos. Ocean. Phys. 2017, 53, 142–155. [Google Scholar] [CrossRef]
- Boucher, O.; Servonnat, J.; Albright, A.L.; Aumont, O.; Balkanski, Y.; Bastrikov, V.; Bekki, S.; Bonnet, R.; Bony, S.; Bopp, L.; et al. Presentation and Evaluation of the IPSL-CM6A-LR Climate Model. J. Adv. Model Earth Syst. 2020, 12, e2019MS002010. [Google Scholar] [CrossRef]
- Lee, J.; Kim, J.; Sun, M.-A.; Kim, B.-H.; Moon, H.; Sung, H.M.; Kim, J.; Byun, Y.-H. Evaluation of the Korea Meteorological Administration Advanced Community Earth-System Model (K-ACE). Asia-Pac. J. Atmos. Sci. 2020, 56, 381–395. [Google Scholar] [CrossRef]
- Tatebe, H.; Ogura, T.; Nitta, T.; Komuro, Y.; Ogochi, K.; Takemura, T.; Sudo, K.; Sekiguchi, M.; Abe, M.; Saito, F.; et al. Description and Basic Evaluation of Simulated Mean State, Internal Variability, and Climate Sensitivity in MIROC6. Geosci. Model Dev. 2019, 12, 2727–2765. [Google Scholar] [CrossRef]
- Müller, W.A.; Jungclaus, J.H.; Mauritsen, T.; Baehr, J.; Bittner, M.; Budich, R.; Bunzel, F.; Esch, M.; Ghosh, R.; Haak, H.; et al. A Higher-resolution Version of the Max Planck Institute Earth System Model (MPI-ESM1.2-HR). J. Adv. Model. Earth Syst. 2018, 10, 1383–1413. [Google Scholar] [CrossRef]
- Mauritsen, T.; Bader, J.; Becker, T.; Behrens, J.; Bittner, M.; Brokopf, R.; Brovkin, V.; Claussen, M.; Crueger, T.; Esch, M.; et al. Developments in the MPI-M Earth System Model Version 1.2 (MPI-ESM1.2) and Its Response to Increasing CO2. J. Adv. Model Earth Syst. 2019, 11, 998–1038. [Google Scholar] [CrossRef]
- Yukimoto, S.; Kawai, H.; Koshiro, T.; Oshima, N.; Yoshida, K.; Urakawa, S.; Tsujino, H.; Deushi, M.; Tanaka, T.; Hosaka, M.; et al. The Meteorological Research Institute Earth System Model Version 2.0, MRI-ESM2.0: Description and Basic Evaluation of the Physical Component. J. Meteorol. Soc. Jpn. 2019, 97, 931–965. [Google Scholar] [CrossRef]
- Tjiputra, J.F.; Schwinger, J.; Bentsen, M.; Morée, A.L.; Gao, S.; Bethke, I.; Heinze, C.; Goris, N.; Gupta, A.; He, Y.-C.; et al. Ocean Biogeochemistry in the Norwegian Earth System Model Version 2 (NorESM2). Geosci. Model Dev. 2020, 13, 2393–2431. [Google Scholar] [CrossRef]
- Wang, Y.; Hsu, H.; Chen, C.; Tseng, W.; Hsu, P.; Lin, C.; Chen, Y.; Jiang, L.; Lee, Y.; Liang, H.; et al. Performance of the Taiwan Earth System Model in Simulating Climate Variability Compared with Observations and CMIP6 Model Simulations. J. Adv. Model Earth Syst. 2021, 13, e2020MS002353. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, D.; Zhang, L.; Zou, X.; Song, X. Comparison of Three Statistical Downscaling Methods and Ensemble Downscaling Method Based on Bayesian Model Averaging in Upper Hanjiang River Basin, China. Adv. Meteorol. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Navarro-Racines, C.; Tarapues, J.; Thornton, P.; Jarvis, A.; Ramirez-Villegas, J. High-Resolution and Bias-Corrected CMIP5 Projections for Climate Change Impact Assessments. Sci. Data 2020, 7, 7. [Google Scholar] [CrossRef] [PubMed]
- Peng, S.; Ding, Y.; Wen, Z.; Chen, Y.; Cao, Y.; Ren, J. Spatiotemporal Change and Trend Analysis of Potential Evapotranspiration over the Loess Plateau of China during 2011–2100. Agric. For. Meteorol. 2017, 233, 183–194. [Google Scholar] [CrossRef]
- Jose, D.M.; Vincent, A.M.; Dwarakish, G.S. Improving Multiple Model Ensemble Predictions of Daily Precipitation and Temperature through Machine Learning Techniques. Sci. Rep. 2022, 12, 4678. [Google Scholar] [CrossRef] [PubMed]
- Lei, X.; Xu, C.; Liu, F.; Song, L.; Cao, L.; Suo, N. Evaluation of CMIP6 Models and Multi-Model Ensemble for Extreme Precipitation over Arid Central Asia. Remote Sens. 2023, 15, 2376. [Google Scholar] [CrossRef]
- Chen, W.; Jiang, Z.; Li, L. Probabilistic Projections of Climate Change over China under the SRES A1B Scenario Using 28 AOGCMs. J. Clim. 2011, 24, 4741–4756. [Google Scholar] [CrossRef]
- Zhang, W.; Fu, J. Rainfall Erosivity Estimation Under Different Rainfall Amount. Resour. Sci. 2003, 25, 37–43. [Google Scholar]
- Gao, G.; Zhang, J.; Liu, Y.; Ning, Z.; Fu, B.; Sivapalan, M. Spatio-Temporal Patterns of the Effects of Precipitation Variability and Land Use/Cover Changes on Long-Term Changes in Sediment Yield in the Loess Plateau, China. Hydrol. Earth Syst. Sci. 2017, 21, 4363–4378. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.; Piao, S.; Lü, Y.; Ciais, P.; Feng, X.; Wang, Y. Reduced Sediment Transport in the Yellow River Due to Anthropogenic Changes. Nat. Geosci. 2016, 9, 38–41. [Google Scholar] [CrossRef]
- Ullah, R.; Khan, J.; Ullah, I.; Khan, F.; Lee, Y. Investigating Drought and Flood Evolution Based on Remote Sensing Data Products over the Punjab Region in Pakistan. Remote Sens. 2023, 15, 1680. [Google Scholar] [CrossRef]
- Yan, R.; Zhang, X.; Yan, S.; Chen, H. Estimating Soil Erosion Response to Land Use/Cover Change in a Catchment of the Loess Plateau, China. Int. Soil Water Conserv. Res. 2018, 6, 13–22. [Google Scholar] [CrossRef]
- Qin, W.; Guo, Q.; Zuo, C.; Shan, Z.; Ma, L.; Sun, G. Spatial Distribution and Temporal Trends of Rainfall Erosivity in Mainland China for 1951–2010. CATENA 2016, 147, 177–186. [Google Scholar] [CrossRef]
- Gao, G.; Han, Z.; Yin, S.; Huang, D.; Wang, W. Characteristics of Rainfall Erosivity During 1961 2017 and lts Change Projections in Future in the Yellow River Basin. J. Basic Sci. Eng. 2021, 29, 575–590. [Google Scholar] [CrossRef]
- Li, Z.; Liu, T.; Huang, Y.; Peng, J.; Ling, Y. Evaluation of the CMIP6 Precipitation Simulations Over Global Land. Earth’s Future 2022, 10, e2021EF002500. [Google Scholar] [CrossRef]
- Kou, P.; Xu, Q.; Jin, Z.; Yunus, A.P.; Luo, X.; Liu, M. Complex Anthropogenic Interaction on Vegetation Greening in the Chinese Loess Plateau. Sci. Total Environ. 2021, 778, 146065. [Google Scholar] [CrossRef]

| Test Level | Scenario Name | Forcing Category | 2100 Forcing (W·m−2) | SSP |
|---|---|---|---|---|
| Tier-1 | SSP1-2.6 | Low | 2.6 | 1 |
| SSP2-4.5 | Medium | 4.5 | 2 | |
| SSP3-7.0 | High | 7.0 | 3 | |
| SSP5-8.5 | High | 8.5 | 5 |
| NO | Model | Institution and References |
|---|---|---|
| 1 | ACCESS-CM2 | Commonwealth Scientific and Industrial Research Organization, Australia [28] |
| 2 | ACCESS-ESM1-5 | Commonwealth Scientific and Industrial Research Organization, Australia [29] |
| 3 | AWI-CM-1-1-MR | Alfred Wegener Institute, Helmholtz Centre for Polar and Marine Research, Germany [30] |
| 4 | BCC-CSM2-MR | Beijing Climate Center, China [31] |
| 5 | CAMS-CSM1-0 | Chinese Academy of Meteorological Sciences, China [32] |
| 6 | CanESM5 | Canadian Centre for Climate Modelling and Analysis,Canada [33] |
| 7 | CanESM5-1 | Canadian Centre for Climate Modelling and Analysis, Canada [34] |
| 8 | CAS-ESM2-0 | Chinese Academy of Sciences, China [35] |
| 9 | CESM2-WACCM | National Center for Atmospheric Research, USA [36] |
| 10 | CMCC-CM2-SR5 | Fondazione Centro Euro-Mediterraneo sui Cambiamenti Climatici, Italy [37] |
| 11 | CMCC-ESM2 | Centro Euro-Mediterraneo sui Cambiamenti Climatici, Italy [38] |
| 12 | EC-Earth3 | EC-Earth consortium, Europe [39] |
| 13 | EC-Earth3-Veg | EC-Earth consortium, Europe [40] |
| 14 | EC-Earth-Veg-LR | EC-Earth consortium, Europe [40] |
| 15 | FGOALS-f3-L | Chinese Academy of Sciences, China [41] |
| 16 | FGOALS-g3 | Chinese Academy of Sciences, China [42] |
| 17 | IITM-ESM | Indian Institute of Tropical Meteorology, India [43] |
| 18 | INM-CM4-8 | Institute for Numerical Mathematics, Russia [44] |
| 19 | INM-CM5-0 | Institute for Numerical Mathematics, Russia [45] |
| 20 | IPSL-CM6A-LR | Institut Pierre Simon Laplace, France [46] |
| 21 | KACE-1-0-G | National Institute of Meteorological Sciences-Korea Met. Administration, Korea [47] |
| 22 | MIROC6 | Japan Agency for Marine–Earth Science and Technology, Japan [48] |
| 23 | MPI-ESM1-2-HR | Max Planck Institute for Meteorology, Germany [49] |
| 24 | MPI-ESM1-2-LR | Max Planck Institute for Meteorology, Germany [50] |
| 25 | MRI-ESM2-0 | Meteorological Research Institute, Japan [51] |
| 26 | NorESM2-LM | Norwegian Climate Centre, Norway [52] |
| 27 | TaiESM1 | Norwegian Climate Centre, Norway [53] |
| NAME | R2 | MAE (mm) | RMSE (mm) | Wi | Rank | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Before | After | ERA5 | Before | After | ERA5 | Before | After | ERA5 | |||
| ACCESS-CM2 | 0.62 | 0.64 | 0.66 | 18.68 | 15.74 | 15.84 | 25.11 | 24.15 | 24.49 | 1.88 | 21 |
| ACCESS-ESM1-5 | 0.72 | 0.73 | 0.72 | 18.18 | 13.95 | 15.33 | 22.83 | 20.8 | 21.71 | 13.92 | 9 |
| AWI-CM-1-1-MR | 0.61 | 0.63 | 0.66 | 18.63 | 16.98 | 17.74 | 25.31 | 24.28 | 24.58 | 0.93 | 25 |
| BCC-CSM2-MR | 0.72 | 0.72 | 0.68 | 15.6 | 14.28 | 16.47 | 21.4 | 20.82 | 23.49 | 8.65 | 13 |
| CAMS-CSM1-0 | 0.34 | 0.58 | 0.65 | 25.37 | 18.13 | 18.29 | 31.77 | 27.93 | 25.83 | 0 | 27 |
| CanESM5 | 0.62 | 0.65 | 0.67 | 23.34 | 16.6 | 16.04 | 31.95 | 25.22 | 23.57 | 1.5 | 22 |
| CanESM5-1 | 0.62 | 0.68 | 0.66 | 23.97 | 16.95 | 16.99 | 33.29 | 25.66 | 24.32 | 1.5 | 23 |
| CAS-ESM2-0 | 0.58 | 0.73 | 0.74 | 25.75 | 14.01 | 15.28 | 32.75 | 20.67 | 21.18 | 14.74 | 7 |
| CESM2-WACCM | 0.72 | 0.76 | 0.72 | 29.85 | 14.42 | 15.58 | 40.17 | 21.42 | 21.99 | 10.61 | 11 |
| CMCC-CM2-SR5 | 0.79 | 0.79 | 0.82 | 38.83 | 12.68 | 13.17 | 49 | 18.52 | 18.36 | 100 | 1 |
| CMCC-ESM2 | 0.79 | 0.81 | 0.79 | 34.83 | 13.71 | 14.42 | 44.37 | 19.37 | 19.93 | 60.03 | 2 |
| EC-Earth3 | 0.66 | 0.77 | 0.67 | 16.39 | 14.04 | 17.50 | 25.46 | 18.58 | 25.62 | 31.48 | 4 |
| EC-Earth3-Veg | 0.65 | 0.73 | 0.72 | 15.99 | 14.21 | 15.47 | 24.22 | 20 | 22.32 | 14.74 | 8 |
| EC-Earth-Veg-LR | 0.73 | 0.74 | 0.71 | 14.55 | 13.63 | 16.41 | 21.25 | 19.39 | 22.41 | 31.48 | 5 |
| FGOALS-f3-L | 0.65 | 0.65 | 0.63 | 16.24 | 15.36 | 17.60 | 24.81 | 22.62 | 25.89 | 3.48 | 16 |
| FGOALS-g3 | 0.65 | 0.71 | 0.70 | 15.62 | 14.79 | 16.07 | 22.73 | 21.61 | 22.57 | 5.26 | 15 |
| IITM-ESM | 0.53 | 0.62 | 0.69 | 21.51 | 16.41 | 16.33 | 27.33 | 24.99 | 23.33 | 1.14 | 24 |
| INM-CM4-8 | 0.75 | 0.76 | 0.77 | 31.79 | 14.01 | 15.26 | 39.33 | 20.58 | 21.11 | 18.8 | 6 |
| INM-CM5-0 | 0.67 | 0.68 | 0.69 | 31.38 | 15.59 | 16.36 | 39.18 | 23 | 23.26 | 3.48 | 17 |
| IPSL-CM6A-LR | 0.71 | 0.73 | 0.74 | 15.23 | 14.3 | 15.78 | 21.77 | 19.94 | 21.50 | 11.8 | 10 |
| KACE-1-0-G | 0.64 | 0.65 | 0.68 | 17.25 | 16.29 | 16.66 | 24.73 | 22.99 | 23.85 | 2.3 | 20 |
| MIROC6 | 0.68 | 0.72 | 0.73 | 25.84 | 14.57 | 15.53 | 33.7 | 21.14 | 21.53 | 7.09 | 14 |
| MPI-ESM1-2-HR | 0.53 | 0.6 | 0.68 | 19.6 | 17.79 | 18.09 | 27.2 | 26.35 | 24.59 | 0.25 | 26 |
| MPI-ESM1-2-LR | 0.53 | 0.66 | 0.68 | 23.08 | 15.52 | 16.26 | 29.44 | 23.88 | 23.43 | 2.94 | 18 |
| MRI-ESM2-0 | 0.51 | 0.66 | 0.56 | 17.77 | 16.74 | 18.65 | 31.07 | 22.91 | 29.74 | 2.61 | 19 |
| NorESM2-LM | 0.71 | 0.74 | 0.73 | 27.95 | 14.54 | 15.49 | 37.63 | 21.23 | 21.20 | 9.09 | 12 |
| TaiESM1 | 0.77 | 0.8 | 0.77 | 29.63 | 13.47 | 14.75 | 38.81 | 19.48 | 20.28 | 52.63 | 3 |
| MME | 0.89 | 0.93 | 0.87 | 20.97 | 11.03 | 12.12 | 26.79 | 15.88 | 16.52 | × | × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Xiao, P.; Hao, S.; Wang, Z. Rainfall Erosivity Characteristics during 1961–2100 in the Loess Plateau, China. Remote Sens. 2024, 16, 661. https://doi.org/10.3390/rs16040661
Li X, Xiao P, Hao S, Wang Z. Rainfall Erosivity Characteristics during 1961–2100 in the Loess Plateau, China. Remote Sensing. 2024; 16(4):661. https://doi.org/10.3390/rs16040661
Chicago/Turabian StyleLi, Xiuping, Peiqing Xiao, Shilong Hao, and Zhihui Wang. 2024. "Rainfall Erosivity Characteristics during 1961–2100 in the Loess Plateau, China" Remote Sensing 16, no. 4: 661. https://doi.org/10.3390/rs16040661
APA StyleLi, X., Xiao, P., Hao, S., & Wang, Z. (2024). Rainfall Erosivity Characteristics during 1961–2100 in the Loess Plateau, China. Remote Sensing, 16(4), 661. https://doi.org/10.3390/rs16040661









