Abstract
Accurate identification and segmentation of individual tree points are crucial for assessing forest spatial distribution, understanding tree growth and structure, and managing forest resources. Traditional methods based on Canopy Height Models (CHM) are simple yet prone to over- and/or under-segmentation. To deal with this problem, this paper introduces a novel approach that combines marker-controlled watershed segmentation with a spectral clustering algorithm. Initially, we determined the local maxima within a series of variable windows according to the lower bound of the prediction interval of the regression equation between tree crown radius and tree height to preliminarily segment individual trees. Subsequently, using this geometric shape analysis method, the under-segmented trees were identified. For these trees, vertical tree crown profile analysis was performed in multiple directions to detect potential treetops which were then considered as inputs for spectral clustering optimization. Our experiments across six plots showed that our method markedly surpasses traditional approaches, achieving an average Recall of 0.854, a Precision of 0.937, and an F1-score of 0.892.
1. Introduction
Forests represent one of Earth’s most invaluable natural assets, serving a pivotal role in maintaining ecological equilibrium, regulating climate, safeguarding land and water resources, and offering secure habitats for rare and endangered species, among other vital functions [1,2,3,4]. However, with the expansion of human activity and the influence of climate change, forests are under increasingly serious threats. In light of these challenges, ensuring enhanced protection and efficient management of forest resources has become of paramount importance [5,6]. The traditional forest resources inventory method highly depends on site surveying [7,8]. This method is time-consuming and labor-intensive, making it challenging to be applied to a large-scale forest inventory. However, the Light Detecting and Ranging (LiDAR) technology can acquire tens of millions of tree points in a few seconds, thereby making it an ideal technology for accurate forest resource surveys [9,10]. LiDAR can acquire large-scale three-dimensional terrain and vegetation structure data [11,12], and this process is not susceptible to the influence of climate or topographical limitations. Therefore, the application of LiDAR cannot only improve the efficiency of data collection but also substantially improve the data precision while minimizing missing data. Individual trees are the elementary units of forest resources. Attributes of individual trees, such as tree species, location, height, diameter of breast height (DBH), crown width, and other relevant metrics, serve as a solid basis for quantifying forest spatial distribution, assessing forest biodiversity, and estimating forest biomass [13,14,15,16,17]. Therefore, LiDAR-based forest inventory at the individual tree level relies highly on the accurate segmentation of individual trees from large-scale forest point clouds, which constitutes a prominent area of interest in the remote sensing, photogrammetry, and computer vision communities.
The segmentation of individual tree points from LiDAR point clouds can be roughly categorized into three methodologies: CHM (Canopy Height Model)-based method, point-based method, and deep learning-based method.
1.1. CHM-Based Method
The CHM-based method initially involves converting the 3D point cloud into a 2D CHM image. It then identifies the treetops by searching from local maxima in the image and proceeds to segment the crown area with the CHM using image segmentation techniques. The most frequently used individual tree segmentation methods using the CHM images are the watershed method [18] and the region growing method [19]. The most critical step in both of these methods is the search for local maxima from the CHM images, which relies heavily on the size of the search window. For example, Hyyppa et al. [20] utilized the local maxima within a fixed-size 3 × 3 search window as seed points for a subsequent region growing method to segment individual trees. Yang et al. [17] used the local maxima within a fixed-size 5 × 5 search window as the marker points to conduct the watershed individual tree segmentation algorithm. To accurately identify the local maxima within the CHM images, Gaussian smoothing has been applied to the CHM images prior to performing watershed segmentation.
Due to the various sizes and shapes of tree crowns, the use of a fixed-size search window can potentially result in over- and/or under-segmentation. To deal with this problem, Popescu and Wynne [21] detected the local maxima from the CHM image using a strategy of a sequence of variable window sizes, which are derived based on the linear regression between the size of tree crown radius and tree height. Similarly, Chen et al. [22] established a nonlinear regression equation between the tree crown and height to determine the sequence of variable window sizes according to a lower bound of the prediction interval of the regression model. Subsequently, they employed a marker-controlled watershed algorithm to segment individual trees. In a similar approach, Zhen et al. [23] have proposed the searching of local maxima within the variable windows as the seed points of the region growing algorithm. Recently, Hui et al. [24] estimated varying crown widths of trees by analyzing gradient magnitudes to identify diverse treetops corresponding to different crown sizes. They used the treetops-guided watershed segmentation method to segment tree crowns.
In summary, the CHM-based method proves to be a simple and efficient approach for segmenting dominant tree crowns within complex forest environments. However, it is noted that the generation of the CHM images through rasterizing 3D point clouds can inevitably result in a substantial loss of information. This loss makes it challenging to detect subdominant tree crowns within the rasterized 2D CHM images. In general, the CHM-based method is well-suited for segmenting forests with a simple canopy structure and clear crown boundaries, such as coniferous forests. However, when applying this method to broad-leafed forests characterized by intricate canopy structure, high vegetation density, and significant occlusion of adjacent tree crowns, over- and/or under-segmentation may occur.
1.2. Point-Based Method
The point-based method aims to explore the potential geometric features of individual trees from LiDAR point clouds of trees. The representative algorithms, including various clustering algorithms [25,26,27,28] and Graph-cut optimization methods [29,30], have been extensively utilized to recognize each individual tree within large-scale tree point clouds. For instance, Gupta et al. [31] compared the effectiveness of the K-means in selecting seed points randomly versus using local maxima strategies within normalized Digital Surface Models (nDSM). Their performance evaluation results have shown that individual tree segmentation supported by the local maxima K-means outperforms random seed point selection. The K-means algorithm, a centroid-based clustering algorithm, calculates the distance from each individual tree point to a centroid for appropriate tree instance assignment. This method is simple to implement and works effectively for segmenting trees with simple, non-overlapping crown structures, such as those present on the sides of streets. However, it does not perform well with trees having complex structures and non-convex crown contours.
In contrast, the Meanshift algorithm is better suited for irregular tree shapes. For example, Dai et al. [32] initially used the Meanshift algorithm for individual tree segmentation. In particular, they estimated the kernel bandwidth from the spatial distribution of individual tree point clouds and then refined it using geometric and spectral information of tree points. This approach improved segmentation, particularly for under-segmented tree clusters, but did not work well with non-uniform tree crown sizes. To address this issue, Yan et al. [33] developed an adaptive Meanshift individual tree points segmentation approach that estimated the kernel bandwidth automatically by analyzing multi-directional canopy vertical structures and shapes beginning from the global maximum. Furthermore, Lei et al. [34] improved this by employing an adaptive kernel bandwidth Meanshift algorithm. In particular, they determined the kernel bandwidths for both horizontal and vertical directions based on the correlations between crown width and tree height, as well as between crown height and tree height.
Unlike the K-means and Meanshift methods, the spectral clustering algorithm is not so much constrained by the shapes of tree clusters and the spatial distribution of point clouds. Motivated by this, Heinzel et al. [28] initially identified tree trunks depending on morphology and then applied the spectral clustering algorithm to individual tree segmentation, taking the extracted tree trunks as a prior. However, the high computational complexity of the spectral clustering algorithm poses challenges for its use in large-scale forest point clouds. To address this issue, Pang et al. [35] presented a novel Nyström spectral clustering algorithm tailed for voxelized tree points, thereby significantly enhancing the computational efficiency.
Graph-cut optimization offers a robust solution to detect and distinguish individual trees from canopy point clouds. Williams et al. [29] introduced a multiclass graph-cut technique to delineate tree crowns from airborne LiDAR point clouds. This method utilized local 3D geometric and density information, combined with knowledge of crown allometries, for segmenting tree crowns. It effectively identified trees in the upper and middle layers of the canopy but struggled to recognize smaller trees. Yang et al. [30] presented a hierarchical minimum cut method to discriminate individual trees from terrestrial laser point clouds of five plots in a boreal coniferous forest. Their first step was to identify trunk and non-trunk seed points, using them to construct an undirected, weighted graph. Tree crown segmentation was then achieved through a global optimization based on this graph.
1.3. Deep Learning-Based Method
This method utilizes deep learning feature encoding to infer individual trees from forest images or tree point clouds. Recently, it has garnered increased attention for individual tree segmentation, demonstrating precise tree recognition in complex scenarios [36,37,38]. In fact, the region-based convolutional neural network (R-CNN) has been considered a pioneering solution for object detection which provides crucial technical support for extracting individual trees from forest images and LiDAR point clouds. For instance, Wang et al. [39] combined Faster R-CNN with a traditional region growing algorithm to segment individual rubber trees. Firstly, they have rasterized front and side tree trunk point clouds within a certain size of the voxels into two-dimensional depth images. Then, the Faster R-CNN was utilized to identify the locations of each individual rubber tree, followed by fined-grained individual tree segmentation using the region growing algorithm. Similarly, You et al. [19] employed Faster R-CNN to detect each individual tree in mangrove forests using unmanned aerial vehicle (UAV) point-derived images, including vertical density, maximum height, and average intensity to train their model. However, the usefulness of their method was limited to tree detection rather than detailed instance segmentation [40]. To accurately capture crown contours, Dersch et al. [41] introduced a new instance tree segmentation model called DETR with the Transformer architecture using CHM images, point density images, and average intensity images for training. However, these models often overlook the 3D vertical structure information of the point clouds. To deal with this problem, Luo et al. [42] primarily sliced the point cloud vertically, creating images for each slice with density, height, and local height gradient. After that, they presented a multi-channel representation to encode the image information of each slice. By fusing multi-channel features, they proposed a multi-branch network to achieve individual tree point segmentation in UAV LiDAR point clouds. In a different approach, Chen et al. [43] employed PointNet to directly encode point cloud features. In particular, they used the voxels to organize the raw point clouds based on tree crown width. After training PointNet to identify tree crowns within each voxel, they refined crown boundaries by analyzing height gradient.
Although the deep learning-based individual tree segmentation surpasses CHM-based and point-based methods in precision and accuracy [41,43,44], most works require converting 3D point clouds into 2D images. This conversion leads to a significant loss of point cloud information and weakens the quality of spatial feature representation. Additionally, deep learning models typically require extensive labeled datasets for training, while acquiring large-scale and high-quality single tree labels is time-consuming, labor-intensive, and costly. Another challenge is the difficulty in adapting these models to forests with diverse species, shapes, and sizes. For example, Windrim et al. [45] demonstrated that in the high point density Carabost dataset, the CHM-based watershed segmentation algorithm outperformed the R-CNN method. Similarly, You et al. [19] found no significant performance differences between Faster R-CNN segmentation and CHM-based watershed segmentation or region growing algorithms in high-density forest stands. CHM-based methods need to rasterize point clouds to CHM images, which leads to a significant loss of 3D structural information. Furthermore, inappropriate settings for CHM resolution and the search window for local maxima can lead to under- and over-segmentation. Although the point-based methods can directly process point clouds, they usually require high time and space complexity, making them less suitable for large-scale forest scenarios.
1.4. Studies Objectives and Expected Results
In this paper, our goal is to accurately differentiate individual trees within broad-leafed and coniferous forest scenes using airborne LiDAR point clouds while addressing the challenge of over- and/or under-segmentation. To accomplish this, we propose a hybrid method that integrates a Canopy Height Model (CHM)-based marker-controlled watershed method with a point-based spectral clustering optimization method. Our approach is designed to tackle the intricate task of segmenting individual trees from airborne laser point clouds, capitalizing on the 3D forest structure information inherent in point clouds and the efficiency of CHM-based methods. The marker-controlled watershed method obtains initial individual tree clusters, and subsequently, spectral clustering is employed to refine these clusters. This refinement process specifically targets under-segmented clusters, thereby enhancing the accuracy of individual tree segmentation in both coniferous and broad-leafed scenes. The proposed hybrid method synergizes the strengths of 3D forest structure information and the effectiveness of CHM-based techniques, contributing to an improved and robust individual tree segmentation approach for airborne LiDAR point clouds.
2. Methodology
2.1. Datasets
In this study, we have selected two publicly available datasets, namely, NEWFOR and OpenTopography, for experimentation. NEWFOR [46] is a project funded by the Alpine Space Program, which primarily aimed at obtaining forest resource information through LiDAR and UAV remote sensing. Subsequently, this information was utilized to optimize forest resource management using Geographic Information System (GIS) techniques. This dataset encompasses 14 sample plots from four European countries within the Alpine region, covering diverse forest types and structures. All sample plots provide airborne LiDAR point clouds collected by different sensors, Digital Terrain Models (DTMs) with spatial resolutions of either 0.5 m or 1.0 m, and ground reference data containing individual tree position and height.
OpenTopography [47] is another dataset sponsored by the National Science Foundation (NSF) in the United States of America. It provides high-resolution terrain data acquired through airborne LiDAR and photogrammetric technology. This dataset primarily supports research related to Earth sciences, such as geomorphology, GIS, and land use dynamics. Specifically, the LiDAR dataset created from the 2018 Yosemite Illilouette Creek LiDAR Survey was collected by the National Center for Airborne Laser Mapping (NCALM). This dataset covers 75.68 of Yosemite National Park, California, with a data point density of approximately 20.97 .
NEWFOR comprises seven plots with a data point density of around 10 , one plot with around 20 , and six plots with 30 or higher. Considering the balance and complementarity of point density among the sample plots, we have selected two plots with a density of around 10 , one plot with about 20 , and two plots with 30 or higher from the NEWFOR. Additionally, one plot with about 20 is obtained from the OpenTopography, resulting in a total of six experimental plots. These plots are categorized into three complexity levels—simple, medium, and complex—based upon their point cloud densities. In addition, although NEWFOR has provided the field measurement data such as tree locations and tree heights, they do not perfectly match with the actual point clouds. Previous research efforts have shown that there will be more significant errors within the given field measurement data for a sample plot characterized by low overall point cloud density but high trunk density [5]. To ensure more reliable validation results, we have obtained the reference data (location, height, and crown diameter) by manually segmenting the individual trees in the open source software CloudCompare (https://www.cloudcompare.org/ (accessed on 5 February, 2024)). Relevant information about the sample plots is detailed in Table 1.

Table 1.
Tree information data for the six sample plots.
2.2. Workflow Description
We propose a method for individual tree point segmentation, which combines marker-controlled watershed segmentation with a spectral clustering algorithm. The complete workflow of the proposed methodology is illustrated in Figure 1 and consists of two steps, namely, marker-controlled watershed coarse segmentation and spectral clustering optimization. In the first step, we identify local maxima within the rasterized CHM image, using variable window sizes to explore the distinct location of treetops. The identified treetops are fed into the marker-controlled watershed segmentation module to obtain the coarse segmentation of individual trees. During the second step, we address the issue of severe under-segmentation by optimizing the coarse segmentation results. Within each under-segmented region, we perform a vertical tree crown profile analysis in multiple directions to infer the potential treetops. These inferred treetops serve as seed points for subsequent spectral clustering optimization. After the optimization process, the non-dominant small trees can be detected within the under-segmented regions.
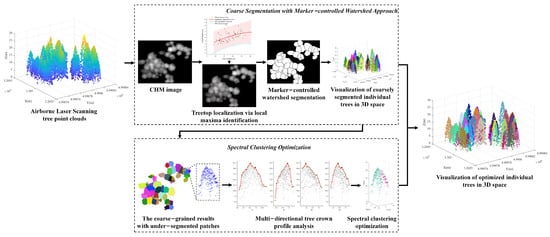
Figure 1.
Illustration of the workflow of the proposed methodology.
2.3. Marker-Controlled Watershed Segmentation of Individual Tree Points
The watershed algorithm [48] is a widely used method for image segmentation, implemented based on mathematical morphology and initially applied in the field of computer vision. Its underlying principle can be described as follows. The image is considered as a topographic surface, where the grayscale values of image pixels are interpreted as elevations on the surface, and it assumes that each region with a lower elevation has a water source. As water continuously rises until it is about to converge in adjacent regions, dams are constructed between them to prevent merging, forming what is known as a watershed [49]. The watershed divides the entire topographic surface into multiple catchment basins, where each basin corresponds to the segmented cluster in our case.
It is noted, however, that by directly applying the watershed algorithm to CHMs for individual tree segmentation, this may lead to significant over-segmentation, especially when dealing with irregular tree crown structures in broad-leafed forest. Despite the Gaussian smoothing applied during the preprocessing stage to reduce some noise and local maxima, over-segmentation issues can still persist. The marker-controlled watershed segmentation algorithm [22] is an effective solution to address this problem, as it segments each tree cluster guided solely by the provided markers, rather than considering all local maxima in the CHMs image, thereby mitigating over-segmentation.
In our study, we identify local maxima within variable window sizes in CHM images to serve as markers for individual treetops. To be specific, we initially determine a sequence of variable windows based on the relationship between tree crown radius and tree height. After that, morphological dilation operations are employed to search the local maxima in CHM images, progressing from the largest sliding window to the smallest. The local maxima derived from the different sliding windows are aggregated and considered as the set of markers for treetops. The relationship between tree crown radius and tree height for variable sliding windows is determined through regression analysis using tree height and crown observations from sample plots. To identify the most appropriate regression models, we develop both linear and nonlinear models, including quadratic, power, exponential, and logarithmic models. The optimal model is then selected based on the best fit to observations. Here, the quadratic model performed best, achieving an of 0.56. The regression models relating tree height to crown radius for our six sample plots are listed in Table 2.

Table 2.
The regression equation and the fitted equation for the lower prediction interval.
It should be noted that the quadratic regression model estimations of tree crown radius presented in Table 2 can effectively make a trade-off between under- and over-segmentation. This relationship is illustrated in Figure 2, taking the 64 reference trees in Plot_1, for example, where the red curve illustrates the relationships between tree crown radius and tree height. However, the scattered sample points beneath the red curve exhibit predicted tree crown values slightly larger than their actual observations. In this case, under-segmentation may occur. This implies that each segmented region may contain multiple trees, thereby resulting in the omission of some non-dominant trees. To mitigate this problem, inspired by the work of Chen et al. [22], we utilize the lower bound of the prediction interval indicated by the dashed blue curve in Figure 2 as our final estimations. Moreover, if the predicted value is negative, we substitute it with the minimum crown radius observed in the sample plot. It is important to underline that the tree crown estimation represented by the dashed blue curve decreases as the prediction interval widens, potentially increasing the risk of over-segmented regions. Therefore, the selection of a suitable prediction interval is very critical. We design five prediction intervals corresponding to the confidence levels of 80%, 85%, 90%, 95%, and 99%. For each of them, the CHMs with a resolution of 0.3 m, 0.4 m, 0.5 m, and 0.6 m are, respectively, generated based on the raw point cloud. Additionally, we sequentially apply the Gaussian filter with kernel sizes of 3 × 3, 5 × 5, and 7 × 7 to smooth CHMs with different resolutions. Finally, the optimal prediction intervals for the six sample plots are chosen based upon the accuracy of the segmented results, as was also detailed in Table 2.
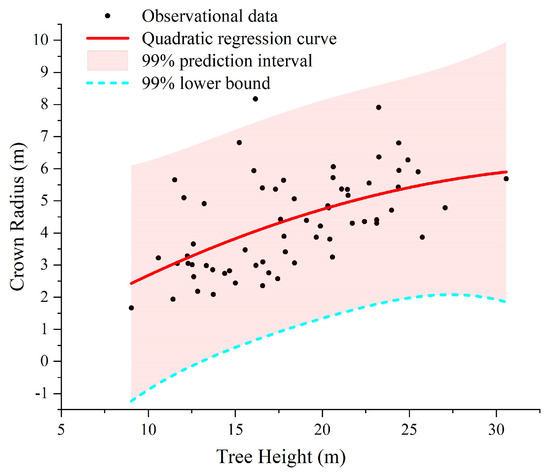
Figure 2.
Crown radius vs. tree height performance for Plot_1 data.
The treetops can be identified by the morphological dilation operations within variable-sized sliding windows. These windows are determined by regressing the different sizes of tree crowns using the proposed quadratic regression model. Guided by these treetop markers, the Figure 3 presents the results of coarse individual tree segmentation achieved through the mark-controlled watershed segmentation algorithm. Figure 3a illustrates the detected treetops represented by the red point set in the Gaussian-smoothed CHM (GCHM) images. Subsequently, we invert the GCHM, where the treetop markers become local minima. We perform marker-controlled watershed segmentation based on the inverted GCHM images, as shown in Figure 3b. It should be noted that the marker-controlled watershed CHM segments should be transformed into the original 3D tree point clouds according to the rasterization relationship between the point clouds and pixels within the GCHM, as illustrated in Figure 3c,d.
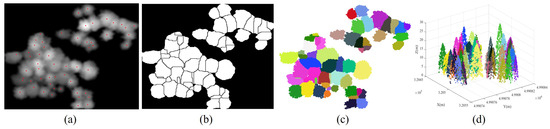
Figure 3.
The marker-controlled watershed segmentation result for Plot_1. Subfigure (a) represents the identified treetops, highlighted with red points. In subfigure (b), the segmented results of the inverted GCHM images are depicted using the marker-controlled watershed segmentation algorithm. Subfigures (c,d) showcase the individually segmented tree points.
2.4. Segmented Patch Recognition
After marker-controlled watershed segmentation, tree point clouds are segmented into a set of patches categorized into three semantic groups, namely, over-segmented patches, under-segmented patches, and correctly segmented patches. In this paper, we adopt a hierarchical strategy to discern the semantics of these patches. To be specific, we initially distinguish the correctly segmented patches and over-segmented patches, followed by the identification of under-segmented patches. To improve the quality of the three patch types, the following three recognition strategies have been employed.
- (1)
- Correctly segmented patches: The complete individual tree exhibits an almost conical shape, with the treetop positioned centrally within the tree crown, denoting its highest point. This characteristic is particularly evident in needle-leaf trees [24]. When the tree point clouds are projected onto the XOY plane, the contour of the projected 2D point clouds resembles nearly a circle [17,32]. Additionally, the tips of trees are positioned approximately at the centers of these circular-like shapes. In contrast, the contours of projected under-segmented patches, encompassing multiple trees, tend to resemble an elliptic shape [17,32]. In such cases, the projected points of the tree tips noticeably deviate from the intersection of the short and long axes of the ellipse, as demonstrated in Figure 4.
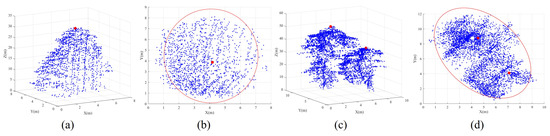 Figure 4. The differentiation in shapes is evident between correctly segmented patches and under-segmented patches. Subfigures (a,b) represent the correctly segmented patch in 3D and projected 2D views. Subfigures (c,d) illustrate the under-segmented patches in a 3D and 2D projection. Note that blue points represent tree point clouds, red points signify treetops, and the red circle or oval delineates the outer contour of the projected tree crowns.To accurately describe the projected contour shapes, we utilize the principal component analysis (PCA) to derive the dominant direction and its orthogonal counterpart for the projected patch points on the XOY plane, as illustrated in Figure 5. After that, we establish a new coordinate system with as the X-axis and as the Y-axis. The projected highest point indicated by the red point serves as a pivotal point within the patch, allowing us to vertically and horizontally divide the patch into four regions. As shown in Figure 5, four parameters, namely, , , , and , easily characterize the shapes of these four areas. In addition, two parameters, denoted as and , represent the length and width of the axis-aligned bounding box of the patch. Based on the above shape parameters, for a correctly segmented patch, the contour of the projected patch points should approximate a circle, and the highest point representing the treetop should be approximately at the circle’s center. This implies that and , and , as well as and should be approximately equal. The value of is used to determine whether the patch contour is circular. The expressions of and are employed to determine if the treetop points are suited at the center of the projected patch. In other words, a coarsely segmented patch can be classified as correctly segmented if it satisfies the condition &&&&, where is the threshold for these three types of distance differences.
Figure 4. The differentiation in shapes is evident between correctly segmented patches and under-segmented patches. Subfigures (a,b) represent the correctly segmented patch in 3D and projected 2D views. Subfigures (c,d) illustrate the under-segmented patches in a 3D and 2D projection. Note that blue points represent tree point clouds, red points signify treetops, and the red circle or oval delineates the outer contour of the projected tree crowns.To accurately describe the projected contour shapes, we utilize the principal component analysis (PCA) to derive the dominant direction and its orthogonal counterpart for the projected patch points on the XOY plane, as illustrated in Figure 5. After that, we establish a new coordinate system with as the X-axis and as the Y-axis. The projected highest point indicated by the red point serves as a pivotal point within the patch, allowing us to vertically and horizontally divide the patch into four regions. As shown in Figure 5, four parameters, namely, , , , and , easily characterize the shapes of these four areas. In addition, two parameters, denoted as and , represent the length and width of the axis-aligned bounding box of the patch. Based on the above shape parameters, for a correctly segmented patch, the contour of the projected patch points should approximate a circle, and the highest point representing the treetop should be approximately at the circle’s center. This implies that and , and , as well as and should be approximately equal. The value of is used to determine whether the patch contour is circular. The expressions of and are employed to determine if the treetop points are suited at the center of the projected patch. In other words, a coarsely segmented patch can be classified as correctly segmented if it satisfies the condition &&&&, where is the threshold for these three types of distance differences.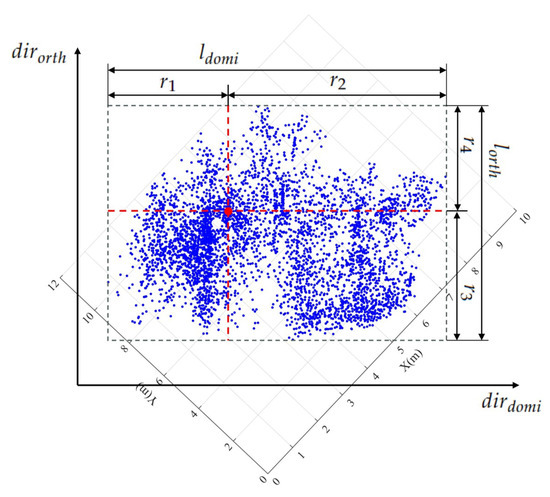 Figure 5. Descriptions of segmented patch shapes are provided through PCA-derived geometric parameters. The red point within each segmented patch signifies the highest elevation, while the black dashed rectangle indicates the minimum bounding box aligned with the two dominant PCA-derived directions of the projected segmented patches.
Figure 5. Descriptions of segmented patch shapes are provided through PCA-derived geometric parameters. The red point within each segmented patch signifies the highest elevation, while the black dashed rectangle indicates the minimum bounding box aligned with the two dominant PCA-derived directions of the projected segmented patches. - (2)
- Over-segmented patches: In our marker-controlled watershed algorithm, treetops are systematically identified in a hierarchical manner using a sequence of variable-sized sliding windows, ranging from the largest to the smallest. Once a treetop is identified within a large window, no other treetops are sought within the region of the current window, even in the subsequent iterations with smaller sliding windows. This masking strategy proves particularly effective in preventing over-segmentation. Additionally, as previously mentioned, the Gaussian smoothing strategy is employed before implementing the CHM segmentation, thereby noticeably reducing the occurrence of the over-segmented patches. As a result of these, our coarse segmented patches exhibit a limited ratio of over-segmented patches. As shown in Figure 6, these instances predominantly show at the periphery of tree crowns, typically attributed to branches protruding from the edge of large trees. As a result, each over-segmented patch contains only a small number of point clouds. Therefore, we construct a histogram for the patches based on the number of enclosed point clouds within each patch. Through histogram analysis, patches that fall below a specified threshold of included tree points are identified as over-segmented patches. Due to the relatively small number of points within over-segmented patches generated during the watershed segmentation stage in our proposed method, their impact on the final segmentation evaluation can be considered negligible. However, in our practical implementation, points from over-segmented patches are assigned to their nearest correctly segmented patches based on a nearest-neighbor principle.
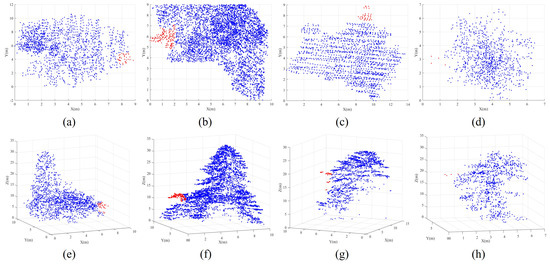 Figure 6. Illustrations of experimental over-segmented patches. The top row comprising subfigures (a–d) represents the projected patches, while the bottom row encompassing subfigures (e–h) denotes the 3D segmented patches. The over-segmented patches, denoted by the red points, are mistakenly classified as individual trees. However, they should be associated with their adjacent blue patch as an integral part of the adjacent patch.
Figure 6. Illustrations of experimental over-segmented patches. The top row comprising subfigures (a–d) represents the projected patches, while the bottom row encompassing subfigures (e–h) denotes the 3D segmented patches. The over-segmented patches, denoted by the red points, are mistakenly classified as individual trees. However, they should be associated with their adjacent blue patch as an integral part of the adjacent patch. - (3)
- Under-segmented patches: Once correctly segmented and over-segmented patches have been correctly identified, the remaining patches are categorized as under-segmented patches. In our paper, we refine these under-segmented patches through spectral clustering optimization, as detailed in Section 2.5. It is noteworthy that under- and over-segmentation constitute the primary factors influencing the accuracy of individual tree segmentation. For our study here, because the minimal number of over-segmented patches generated during the watershed segmentation stage in our proposed method, their impact on the final segmentation evaluation is relatively negligible. Consequently, we do not optimize these over-segmented patches in this study.
2.5. Spectral Clustering Optimization of Under-Segmented Patches
To refine the segmentation of under-segmented patches, we employ a spectral clustering optimization algorithm to infer the potential small trees within these regions. This involves determining the number and the positions of potential trees within under-segmented patches, which are then employed as prior knowledge to guide the spectral clustering optimization process.
2.5.1. Treetop Identification Based on Vertical Tree Crown Profile Analysis in Multiple Directions
We use the vertical tree crown profile analysis to determine both the number of trees and their respective treetops within each under-segmented patch. Taking as an example the tree crown profile on the XOZ plane, as depicted in Figure 7, we initially project the tree point clouds within each under-segmented patch onto the XOZ plane, resulting in a set of projected 2D patch points, as illustrated in Figure 7a. The projection extent of these 2D patch points along the X-axis is divided into predefined fixed intervals. Within each interval, the highest 2D patch point on the Z-axis is considered the corresponding z-coordinate for that interval. Repeating this process for each interval yields a sequence of 2D points, which produces the vertical crown profile on the XOZ plane by connecting these points in sequential order, as depicted in Figure 7b. We further apply Gaussian filtering to smooth the vertical crown profile and then use the zero-crossing of the first derivative method to identify potential treetops from this profile.
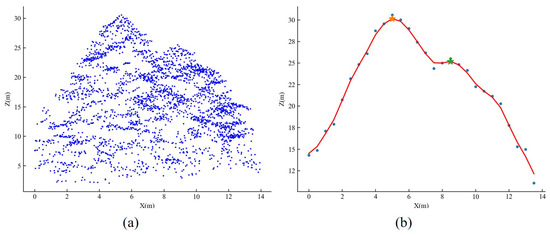
Figure 7.
Treetop identification by analyzing tree crown profile within the under-segmented patch. Subfigure (a) represents the projected point clouds onto the XOZ plane within the under-segmented patch. Subfigure (b) denotes the generated tree crown profile on the XOZ plane. Note that the yellow and green stars indicate two peaks/treetops of the profile.
A single vertical tree crown profile is insufficient for identifying potential treetops within under-segmented patches. To address this problem, treetop identification is comprehensively analyzed using two [50] or multiple [17] tree crown profiles to enhance the reliability of detected trees. Inspired by these approaches, we propose a strategy of analyzing vertical tree crown profiles in multi-directions to minimize projection occlusion and improve treetop detection accuracy. Specifically, we generate a sequence of vertical projection planes by rotating around the central axis, ranging from 0° to 180° according to a fixed rotation angle interval denoted as t. These planes serve as the canvas onto which we project under-segmented patch point clouds, with the expectation of extracting tree crown profiles. Through the decomposition of these canopy profiles and a comprehensive analysis of the results from each, we identify the real potential trees with each under-segmented patch. It is worth noting that the number of projection directions is determined by the angle interval t. As t increases, the number of projection directions decreases. To evaluate the impact of the number of projection directions on the optimized segmentation, we conduct experiments setting t at 90°, 60°, 45°, 30°, and 15°.
Taking t = 45° as an example to illustrate the entire process, as shown in Figure 8, four projection planes are generated by rotating a fixed angle of 45° with the pivot point at “O”. Notably, the tree crown profiles from the 0° and 45° generation planes reveal a solitary treetop. Conversely, the distinctive feature of hosting multiple trees becomes pronounced in the 90° and 135° canopy profiles. Two components, indicated by the positions of two red stars, are accurately identified. The analysis of profiles from multi-directional planes contributes significantly to the discovery of non-dominant trees, which are challenging to identify when using a limited number of projection planes, such as XOZ or YOZ planes.
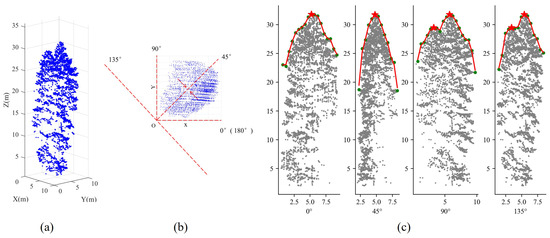
Figure 8.
Analysis of profile based on multi-directional crown projection. Subfigure (a) represents the 3D point cloud of an under-segmented patch. Subfigure (b) depicts a 2D top view illustrating multi-directional crown projection. Blue points represent the 2D point cloud, red dashed lines denote various projection directions, and red arrows indicate the projection process at a 45° angle. Subfigure (c) demonstrates the analysis of tree crown profiles in four projection planes. Gray points depict the projected point cloud, green points represent profile points, and red stars highlight potential treetops.
Although we have conducted a meticulous analysis of tree crown profiles derived from multi-directional projection planes, we still encounter the problem of the presence of pseudo treetops. Failure to appropriately eliminate these pseudo treetops poses the risk of over-segmentation during subsequent under-segmented patch optimization. To deal with this problem, we calculate two metrics, namely, horizontal intra-Euclidean distance and marginal Euclidean distance to remove these pseudo treetops. The intra-Euclidean horizontal distance refers to the distance from the dominant tree’s treetop to any other detected non-dominant treetops, while the marginal Euclidean distance denotes the minimum distance from the detected non-dominant treetops to their 2D patch boundary/edge.
In practice, if the intra-Euclidean distance is considerably smaller than a predefined threshold, the non-dominant treetops are deemed pseudo points and are thus consequently eliminated. Meanwhile, if the margin Euclidean distance is less than another predefined threshold, the non-dominant treetops are considered pseudo points and are also removed. Figure 9 illustrates this process, showing the identification and removal of a pseudo treetop through the analysis of a 90° tree crown profile, as demonstrated in Figure 9b. By the proposed two-threshold metric comparison, pseudo trees are combined with their corresponding dominant tree points (see Figure 9d), thereby effectively preventing over-segmentation in the subsequent spectral clustering optimization.
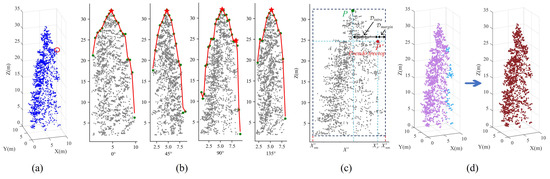
Figure 9.
Illustration of the pseudo treetops removal by comparing two metrics, and , against their predefined thresholds. Subfigure (a) represents patch point clouds. Subfigure (b) shows tree crown profiles are generated from four directional planes. Subfigure (c) demonstrates pseudo treetop removal by comparison of the two metrics. Subfigure (d) indicates the combination of pseudo tree point clouds with their corresponding dominant tree points.
2.5.2. Spectral Clustering Optimization
Spectral clustering, stemming from spectral graph theory and originally implemented in computer vision [51] to tackle 2D image segmentation issues [52], has evolved to address the segmentation of 3D point clouds in contemporary applications [35]. The spectral clustering method effectively transforms the clustering problem into a graph partitioning problem. Initially, an undirected weighted graph is constructed, wherein each point represents a vertex, and the similarity value between any pair of points is utilized as the weight of the connecting edge. Subsequently, the optimized process facilitates the segmentation of the undirected weighted graph into multiple disconnected subgraphs. In our specific method, to reduce the computational complexity, we employ voxelization on the under-segmented patch point clouds. Only non-empty voxels are utilized to construct the weighted graph denoted as , where V represents the set of nodes consisting of the non-empty voxels, E denotes the set of edges connecting any two voxels, and W represents the set of weights indicating similarity between any two voxels. Considering the potential tree-like shapes within under-segmented patches, we utilize the Gaussian similarity function to mathematically represent the graph weights as:
where represents the weight between two voxels i and j; and represent the horizontal and vertical distances between any pair of voxels i and j; and is determined as , where and indicate the horizontal distance from i and j to their respective individual treetops and . , , and serve as weighting coefficients for the distances , , and , allowing control over the sensitivity of the weights. The parameter r represents the maximum horizontal distance. If the distance between two voxels exceeds r, their similarity is considered zero, i.e., . The values of , , and are set to the maximum values of , , and . Distinct values of r are assigned for different under-segmented patches based on the radius/size of the patches.
The goal of spectral clustering is the partitioning of the graph into multiple disconnected subgraphs, with the aim of maximizing similarity among voxels within each subgraph while minimizing it between different subgraphs. We divided G into k subsets, denoted as , by utilizing multi-way normalized cut. The corresponding objective function (2) is as follows:
where is the complement of , represents the sum of the weight of nodes in and , and represents the sum of the weight of nodes in and all the nodes in the graph. Unfortunately, minimizing Equation (2) is an NP-hard problem, and as a result, only approximate solutions are employed [52,53]. Following the optimization of the under-segmented patches, distinct non-dominant trees are revealed, as illustrated in Figure 10.
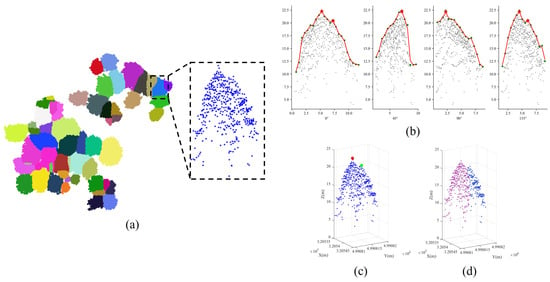
Figure 10.
Illustration of the spectral clustering optimization process for under-segmented patches. Subfigure (a) represents the marker-controlled watershed segmentation result (Plot_1), with the dashed box indicating the under-segmented patch. Subfigure (b) shows vertical tree crown profiles are extracted at multi-directional planes. Through the analysis of these profiles, two treetops are discovered, as denoted in subfigure (c). After spectral clustering optimization, two trees are successfully identified within the under-segmented patch, as denoted in subfigure (d).
2.6. Evaluation Metrics
Evaluation of each tree segmentation is performed at the individual tree level by matching the trees detected by the proposed method with the trees in the reference dataset. The evaluation metrics are calculated based on the numbers of True Positives (), False Positives (), and False Negatives (). refers to the detected trees that are correctly matching with the reference trees, indicating correct segmentation. refers to a reference tree being incorrectly segmented into multiple individual trees in the experimental result, indicating over-segmentation. refers to a reference tree being incorrectly segmented as a part of the adjacent trees, indicating under-segmentation. If the number of reference trees is denoted as and the detected trees as , then and . Utilizing these values, four evaluation metrics, , , , and F1-score [17,30,54,55] have been calculated as follows:
where denotes the tree extraction rate, measuring the capability to detect trees; signifies the ratio of correctly extracted trees to all reference trees, offering an indirect insight into the extent of under-segmentation. indicates the ratio of correctly extracted trees to all detected trees, providing an indirect measure of the degree of over-segmentation. F1-score considers both and , representing the overall accuracy of individual tree segmentation. The ranges for , , and F1-score are from 0 to 1, where higher values signify higher accuracy in tree segmentation.
3. Performance Evaluation Results
3.1. Quantitative Evaluation of Marker-Controlled Watershed Individual Tree Segmentation
To quantitatively assess the performance of the marker-controlled watershed segmentation, we calculated the evaluation metrics for the segmentation results of the six plots, and the specific outcomes are listed in Table 3. As indicated in the table, the average F1-score for the six plots is 0.860, with a maximum of 0.919 and a minimum of 0.785. Overall, both and are relatively low, especially the , with an average of only 0.780, suggesting a notable presence of under-segmentation during the watershed segmentation stage. It is important to note that the for each plot is quite high, averaging 0.965. This implies that in the stage of watershed segmentation, the detection of most potential trees is achieved, and the occurrence of over-segmentation is rare.

Table 3.
Performance evaluation of the watershed segmentation results across six plots.
3.2. Evaluation of Semantic Recognition for Segmented Patches
Following the individual tree segmentation using the marker-controlled watershed algorithm, we conducted semantic recognition on the segmented patches and categorized them into correctly segmented patches, over-segmented patches, and under-segmented patches. The optimization phase merely focuses on the under-segmented patches; therefore, we combine the correctly segmented patches and over-segmented patches into non-under-segmented patches. The recognition results for Plot_1 are shown in Figure 11. The patches in Figure 11a represent 56 individual trees segmented through the marker-controlled watershed algorithm, while Figure 11b illustrates 24 identified under-segmented patches. Additionally, Figure 11c depicts the confusion matrix for under-segmented patches and non-under-segmented patches classification results. The of Plot_1 stands at 0.714. The reason for the relatively lower is due to some non-under-segmented patches being categorized as under-segmented patches. However, it is noted that the of under-segmented patches has reached up to 0.9. This indicates that the proposed semantic recognition method exhibits a strong capability in identifying genuinely under-segmented patches, providing an opportunity for these under-segmented patches to be optimized in the subsequent phase.
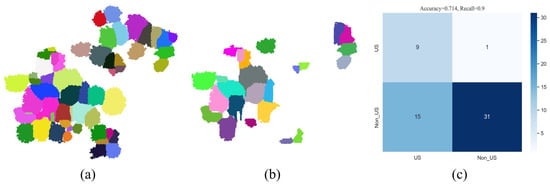
Figure 11.
Illustration of the performance results for the semantic recognition (Plot_1). Subfigure (a) represents the result of marker-controlled watershed segmentation. Subfigure (b) shows the recognized under-segmented patches. Subfigure (c) denotes the confusion matrix for under-segmented patches and non-under-segmented patches classification (US stands for under-segmented patches, Non_US stands for non-under-segmented patches).
3.3. Quantitative Evaluation of Individual Tree Segmentation after Spectral Clustering Optimization
After identifying under-segmented patches, we utilized vertical tree crown profile analysis in multiple directions to determine the numbers and locations of potential treetops within these patches. Subsequently, the spectral clustering algorithm was employed to optimize the under-segmented patches. Figure 12 illustrates the segmentation result of Plot_1 and provides a comparison of selected under-segmented patches before and after optimization.
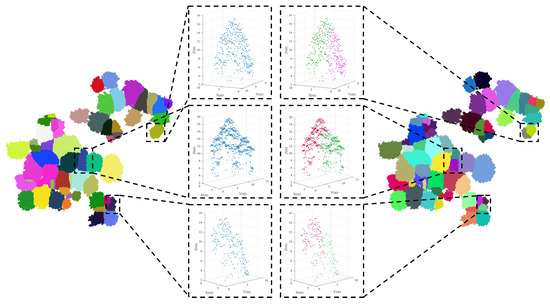
Figure 12.
Illustration of the final individual tree segmentation result (Plot_1). The left shows the initial segmentation result of the marker-controlled watershed. The middle displays a comparison of some under-segmented patches before and after spectral clustering optimization. The right exhibits the final segmentation result.
Figure 13 displays the segmentation results obtained by the proposed method across six different plots. Table 4 outlines the four evaluation metrics for the segmentation results. The average value of each metric is greater than 0.85, with an average F1-score of 0.892. It is evident that satisfactory segmentation results were achieved for all six plots. The average of the six plots is 0.913, indicating that the proposed method does not result in significant over-segmentation. This is further evident from the . Metric as the average is 0.931, with a minimum value of 0.889, indicating an extremely low occurrence of over-segmentation in the results of all plots. Some plots exhibit lower than Precision, indicating a higher occurrence of under-segmentation compared to over-segmentation. These instances of under-segmentation are primarily observed in Plot_4, Plot_5, and Plot_6, mainly due to the presence of understory vegetation. Particularly in Plot_6, the number of understory trees constitutes 20% of the total trees.
Figure 13.
The segmentation results of six plots (different trees displayed in random colors). Subfigures (a–f) represent Plot_1 to Plot_6, respectively.

Table 4.
Evaluation metrics of segmentation results for six plots.
We further evaluated the individual tree segmentation results of different forest types. In the six plots, Plot_3 and Plot_4 represent coniferous forests, while the remaining four plots consist of mixed forests containing both coniferous and broad-leafed tree species. Table 3 displays the initial segmentation accuracy metrics during the watershed segmentation stage for the six plots. The average for the two coniferous forest plots is 0.821, the is 0.983, and the F1-score is 0.894. For the four mixed forest plots, the average is 0.759, the is 0.956, and the F1-score is 0.845. Similarly, Table 4 presents the segmentation accuracy metrics after spectral clustering optimization for the six plots. The average for the two coniferous forest plots is 0.865, the is 0.973, and the F1-score is 0.915. On the other hand, for the four mixed forest plots, the average is 0.849, the is 0.919, and the F1-score is 0.881. It is evident that, whether in the initial segmentation stage or after optimization, every accuracy metric for coniferous forests surpasses that of mixed forests. This indicates that the segmentation performance in coniferous forests is superior to that in mixed forests. The relatively lower in mixed forests can be attributed to the presence of substantial understory forests in these two plots. The lower in mixed forests is influenced by two factors. Firstly, the complex tree crown structures of broad-leafed tree species in mixed forests affect the detection of tree treetops, and secondly, the irregular crown shapes of broad-leafed tree species impede the recognition of under-segmented patches, as discussed in detail in Section 4.4. Although the segmentation performance of the proposed method is comparatively lower in mixed forests, the method performs significantly better in handling mixed forests containing broad-leafed tree species compared to the other two well-known methods of individual tree segmentation, as it will become evident in Section 4.5.
Similarly, we compared the individual tree segmentation results of different plot complexities. Figure 14 illustrates the corresponding evaluation metrics. It can be observed that the accuracy metrics generally exhibit a declining trend. Specifically, as plot complexity increases, the accuracy of individual tree segmentation decreases. The F1-score decreases from 0.930 to 0.832, decreases from 1.003 to 0.845, and decreases from 0.931 to 0.767. Notably, the decrease in is close to 20%, indicating that as plot complexity increases, there are more under-segmented patches. It is worth noting that initially increases and then decreases. Specifically, medium plots exhibit the highest , and the complex plots exhibit the lowest . This is primarily because medium plots (Plot_3 and Plot_4) are both coniferous forests, where the conical-shaped tree crown profiles are distinct, enabling accurate detection of treetops. Conversely, the complex plots (Plot_5 and Plot_6) are both mixed forests, where the complex tree crown structures of broad-leafed trees affect the detection of treetops.
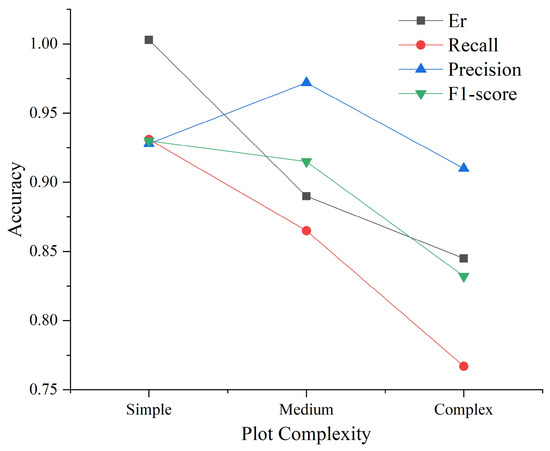
Figure 14.
Comparison of accuracy for different plot complexities.
4. Discussion and Comparisons
4.1. Impact of Variable Window on Watershed Segmentation
To determine the appropriate variable window size for marker-controlled watershed segmentation, we designed five prediction intervals with confidence levels of 80%, 85%, 90%, 95%, and 99%. Sensitivity analysis was conducted on how the lower bound of each prediction interval, acting as a window radius, affected the watershed segmentation results under different configurations. As mentioned in Section 2.3, the different configurations include varying resolutions of the CHMs and different sizes of Gaussian smoothing windows. Table 5 presents the results of the marker-controlled watershed individual tree segmentation for Plot_1.

Table 5.
Segmentation results of marker-controlled watershed (Plot_1).
From the results presented in Table 5, we have summarized the average evaluation metrics of watershed segmentation results based on different prediction intervals, as shown in Figure 15, where it can be observed that as the prediction interval increases, continues to ascend, while steadily descends. Moreover, the F1-score initially ascends and subsequently stabilizes. The 95% and 99% prediction intervals exhibit the highest F1-score values. This implies that window sizes determined by the lower bounds of the 95% and 99% prediction intervals, derived from the non-linear regression between tree crown radius and tree height, both yield optimal segmentation results. The conclusion drawn from the lower bound of the 95% prediction interval aligns with the works of Chen et al. [22] and Zhen et al. [23]. However, what is different is that the 99% prediction interval lower bound we designed also acquires favorable segmentation results. As shown in Table 5, the largest F1-score reaches up to 0.883, falling within the 99% prediction interval. Among these six sample plots, five of them indicate the 99% prediction interval as the optimal interval, with only one favoring the 95% prediction interval, as detailed in Table 2. It is important to note that as the prediction interval increases from 80% to 95%, the trends of and are reversed. Moreover, remains lower than , suggesting a higher proportion of under-segmentation than over-segmentation in the segmentation results within these prediction intervals. Within the 99% prediction interval, even though the average is slightly higher than the average , all the corresponding to the larger F1-score (greater than 0.840) are lower than . Due to the second phase of the proposed method focusing on the under-segmentation optimization, the initial segmentation results with a higher proportion of under-segmentation than over-segmentation are advantageous to the proposed method.
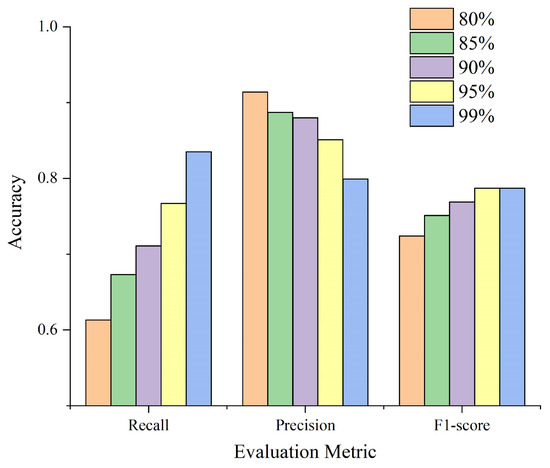
Figure 15.
The average accuracy with different lower bounds of prediction intervals as the window radius.
To demonstrate the effectiveness of the variable window, we further compared the watershed segmentation results based on variable windows with those based on fixed windows. The specific comparison results of the six plots can be found in Table 6. Fixed windows of sizes 3 × 3, 5 × 5, and 7 × 7 are employed. The quantitative comparison in Table 6 reveals that within the fixed window, except for Plot_2, the F1-scores of the other five plots gradually increase as the window sizes increase. This indicates there is an overall improvement in the accuracy of individual tree segmentation with the increase in window size. Although the F1-score from the variable window is comparable to the optimal F1-score in the fixed window, the for each plot in the variable window is notably high, ranging from a minimum of 0.946 to a maximum of 0.983. In other words, within the segmentation results based on the variable window, the proportion of over-segmentation for each plot is very minimal. In the proposed method, the goal of marker-controlled watershed segmentation is to accurately segment the majority of individual trees rapidly, rather than directly obtaining the segmentation results. Therefore, our requirement for watershed segmentation is to minimize the proportion of over-segmentation, while the under-segmented patches will be optimized through spectral clustering. Consequently, for the proposed method, choosing a variable window proves superior to a fixed window.

Table 6.
Performance comparison results between variable window and fixed window approaches.
4.2. Impact of Projection Directions on Treetops Detection
As described in Section 2.5.1, the proposed method detects treetops through vertical tree crown profile analysis in multiple directions, where the number of projection directions is determined by angular intervals. We have summarized the four evaluation metrics for the segmentation results of Plot_1 with different angle intervals (90°, 60°, 45°, 30°, and 15°), as shown in Figure 16. It can be observed that the remains nearly unchanged across different angular intervals. This suggests that the number of correctly extracted treetops remains consistent. When , with the reduction of the angle interval, Er decreases, while Precision and F1-score increase. This indicates that the decrease in the number of extracted pseudo treetops leads to a reduction in over-segmentation. When , with the reduction of the angle interval, Er continuously increases, while Precision and F1-score continuously decrease. This suggests that with smaller angle intervals, more pseudo treetops are extracted, resulting in more over-segmentation and thereby reducing the overall segmentation accuracy. When , the segmentation result performs best, with maximum and F1-score.
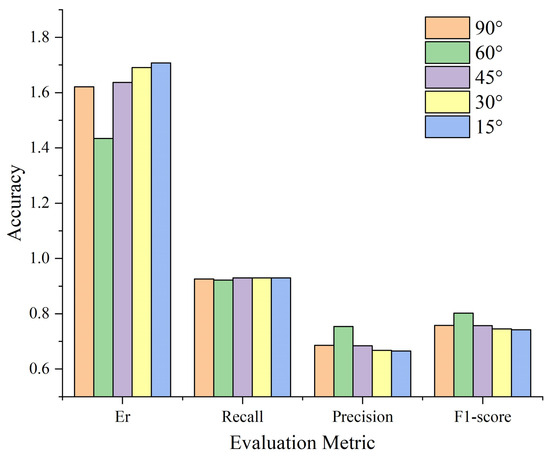
Figure 16.
Evaluation metrics based on different angle intervals (Plot_1).
Yan et al. [50] identified potential treetops based on tree crown profile analysis at two directions (t = 90°) and used these treetops as input into the Normalized Cut (NCut) algorithm to optimize the under-segmented patches. Our research shows that using only two directions does indeed result in better , reducing the proportion of under-segmentation. Nevertheless, a moderate increase in the number of projection directions can more effectively describe the crown profile of the under-segmented patches, thereby improving the overall segmentation accuracy. Due to the inconsistent spatial distribution of individual trees and varying tree crown structures within different plots, the occlusion of adjacent tree crowns differs across different projection directions. It is challenging to determine which projection directions can better describe the crown profile of the under-segmented patches. Therefore, a vertical tree crown profile analysis in multiple directions is necessary. However, it is crucial to judiciously select the number of projection directions, as an excessive increase in the number of projection directions may elevate the risk of over-segmentation.
4.3. Impact of Treetops Detection on Spectral Clustering Optimization
Aside from high computational complexity, a pivotal challenge restricting the application of the spectral clustering algorithm is the accurate selection of the number of clusters. The eigengap heuristic method is specifically devised to determine the optimal number of clusters in spectral clustering, relying on disparities among the eigenvalues derived from the similarity matrix [29,35]. Specifically, if the first k eigenvalues are all small, and there is a significant difference between the -th eigenvalue and the k-th eigenvalue, then the number of clusters is chosen as k. In this paper, we determined the potential treetops of the under-segmented patches by vertical tree crown profile analysis in multiple directions. To evaluate the effectiveness of the proposed method, we performed a further quantitative comparison between our method and the eigengap heuristic in spectral clustering optimization for under-segmented patches. Table 7 presents the results of the two methods. It is observed that except for Plot_5, the F1-scores of treetops-guided spectral clustering are higher than those of eigengap heuristic spectral clustering across the other five plots. In other words, between the two methods, the proposed treetops-guided spectral clustering performs better during the optimization phase. This is primarily because after watershed segmentation, the under-segmented patches tend to exhibit intersecting tree crowns, resulting in less distinct differences in eigenvalues. This, in turn, affects the accuracy of the eigengap heuristic in selecting the number of individual trees. The proposed method, however, directly conducts tree crown profile analysis on the under-segmented patches, accurately determining the potential treetops and enhancing the segmentation accuracy.

Table 7.
Performance of eigangap heuristic and treetops-guided spectral clustering.
4.4. Analysis of Failed Optimization Segmentation
The proposed method has successfully resolved the majority of under-segmented patches, as depicted in Figure 17, where these under-segmented patches have been accurately segmented. However, there are still some under-segmented patches that were not effectively segmented in the optimization phase. These failure cases primarily include the following scenarios:
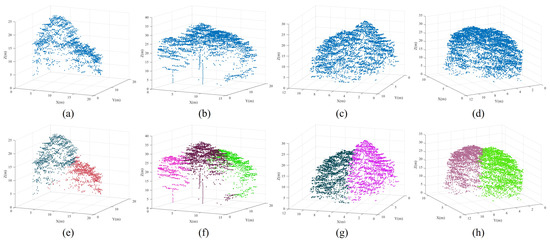
Figure 17.
Illustration of typical optimization results for under-segmented patches. The top row encompassing subfigures (a–d) represents under-segmented patches, while the bottom row comprising subfigures (e–h) denotes segmentation results after optimization.
(1) The potential treetops were not detected, resulting in no change in under-segmented patches before and after optimization (see Figure 18a,d).
Figure 18.
Illustration of typical optimization failures. Subfigures (a,d) correspond to Case (1). Subfigures (b,e) correspond to Case (2). Subfigures (c,f) correspond to Case (3).
(2) The detected pseudo treetops resulted in over-segmentation (see Figure 18b,e).
(3) The potential treetops were successfully detected, but the under-segmented patches were not optimized correctly(see Figure 18c,f).
Table 8 presents statistical data for the three failure cases across all plots. It is evident that Case (1) constitutes a primary aspect of failed optimization segmentation. These failures are attributed to the undetected potential treetops within the under-segmented patches. These patches often consist of a small tree beneath a larger tree or a small tree positioned closely adjacent to the crown edge of a larger tree. After projection, these under-segmented patches often exhibit only one peak in the fitting curve of the projected profile. Consequently, there is no change in these patches before and after optimization (see Figure 18a,d). The plots where Case (1) occurs more frequently are Plot_4, Plot_5, and Plot_6. The failures in Plot_4 primarily arise from the treetops of the small trees being adjacent to the edges of the large tree crowns. The failures in Plot_5 and Plot_6 are due to the presence of understory forests. Case (2) is primarily due to the irregularity of the tree crown structure. In some broad-leafed tree species, certain protruding branches within the tree crown are often mistakenly identified as treetops. Even with the addition of two threshold metrics, these pseudo treetops cannot be entirely avoided. It is worth noting that within the over-segmented patches during the optimization phase, a portion of them stem from originally independent trees (see Figure 18b,e). This occurs because these individual trees fail to meet the shape parameter requirements outlined in Section 2.4 and are mistakenly identified as under-segmented patches during the semantic recognition phase. This also indicates that the extraction results of under-segmented patches have a certain impact on the optimization result. Cases (1) and (2) encompass 99% of the failure cases, primarily due to the inadequate detection of potential treetops within the under-segmented patches. In other words, if the potential treetops are accurately identified, spectral clustering can effectively achieve accurate segmentation of these patches. However, due to the irregular spatial distribution of the point cloud and the non-convex tree crowns, some under-segmented patches cannot be correctly optimized. Consequently, Case (3) may still arise (see Figure 18c,f), with a very low probability.

Table 8.
Statistics of failure cases.
4.5. Method Comparison
To validate the effectiveness of the proposed method, we tested two other methods for individual tree segmentation and compared the results with those of our proposed method. These two methods include the marker-controlled watershed algorithm (MCWA) and Nyström-based spectral clustering (NSC). MCWA was initially introduced by Chen et al. [22], and we implemented it using the MATLAB programming language. NSC, described by Pang et al. [35], is an improved spectral clustering on the supervoxelized point cloud, and the algorithm is implemented in the Python programming language.
The comparison of the average evaluation metrics for different methods is shown in Table 9. It is evident that the proposed method demonstrates higher and compared to the other two methods. This indicates that employing the proposed method results in the least amount of under-segmentation and over-segmentation. Notably, the of the proposed method is 20% higher than the average of the other two methods, effectively reducing the occurrence of over-segmentation in the results. Although the values of of these three methods are around 1, the proposed method exhibits the highest and , suggesting a tendency in the other two methods to extract more erroneous trees. Regarding the F1-score, the proposed method achieves the highest value, surpassing the average of the other two methods by 15%. In summary, compared to the other two methods, the proposed method can achieve better individual tree segmentation results.

Table 9.
Comparison of average evaluation metrics for the different methods.
Figure 19 illustrates the , , , and F1-score of different methods across the six sample plots. In terms of , as shown in Figure 19a, our newly proposed method and MCWA exhibit similar performance, outperforming NSC significantly. NSC tends to inaccurately segment more trees in Plot_1, Plot_2, and Plot_3. In terms of , as shown in Figure 19b, the proposed method performs slightly better than MCWA in all plots except Plot_6 and outperforms NSC in all plots except Plot_2. Therefore, the average of the proposed method is higher across all plots compared to the other two methods. In terms of , as shown in Figure 19c, the proposed method obtains the highest , indicating its ability to maintain the lowest rate of false positives in all six plots. In terms of F1-score, as shown in Figure 19d, it is evident that our method attains the highest F1-score in each plot, with all F1-score exceeding 0.8. These findings highlight the significant advantage of the proposed method in individual tree segmentation.
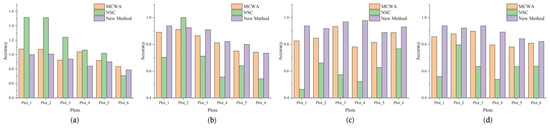
Figure 19.
Comparison of the three methods in six plots. Subfigure (a) represents Er. Subfigure (b) represents Recall. Subfigure (c) represents Precision. Subfigure (d) represents F1-score.
To better evaluate the proposed method, we further compared the implementation efficiency of these three methods. All the methods were executed on the same laptop computer with an AMD Ryzen 7 5800H CPU and 16 GB RAM, running the 64-bit Windows 11 operating system. The comparative result is shown in Table 10. We can find that MCWA exhibits the shortest processing time among the six plots. This is primarily attributed to the watershed algorithm operating on the rasterized CHM, which is highly efficient in handling pixel-to-pixel relationships. NSC has the longest processing time, primarily because it directly segments the point cloud. Particularly, the Mean Shift voxelization process requires multiple iterations to compute the density gradient of each data point. Compared to NSC, the proposed method demonstrates a faster processing speed. This is because most individual trees are already extracted during the marker-controlled watershed segmentation phase, and only a small amount of under-segmented patches require spectral clustering optimization. Although the processing time of the proposed method is a bit longer than MCWA, our segmentation results surpass those of MCWA, as observed from Table 9.

Table 10.
Efficiency comparison for different methods (measured in seconds).
5. Conclusions
In this study, an individual tree segmentation method based on ALS data was proposed and its performance was thoroughly evaluated. It consists of three stages involving a individual tree point segmentation by marker-controlled watershed algorithm, semantic recognition of segmented patches, and spectral clustering optimization segmentation focusing on under-segmented patches. Six sample plots of three different point densities were selected as a case study. Various performance evaluation results have shown that the proposed method can achieve a highly precise individual tree segmentation. Compared to the other two classic segmentation methods, our method possesses the highest of 0.854, of 0.937, and F1-score of 0.892. By leveraging the efficiency of the CHM-based method and the advantages of the point-based method in capturing point cloud features, satisfactory segmentation results can be attainable across sample plots with diverse point densities and structures.
However, some limitations persist. Firstly, in the stage of marker-controlled watershed segmentation, treetop markers were searched using variable window sizes calculated by a regression equation between tree crown radius and tree height. The specific regression equation may not be generalizable to other sample plots or different types of forests. Secondly, after watershed segmentation, the correctly segmented patches were recognized based on the shape feature of horizontal projection profiles, which might be limited by complex canopy structures or broad-leafed forests with significant vertical spatial variation. Lastly, achieving satisfactory segmentation for the understory of multi-layered forests remains challenging. Future studies might consider incorporating morphological features of individual trees from various projection directions to improve semantic recognition accuracy. Additionally, leveraging deep learning to extract deep features from the canopy point cloud could aid in scenarios with complex vertical structures.
Author Contributions
Y.L. conceived the original idea of the study and drafted the manuscript. D.C. defined the main research objectives and methods, and managed the project. S.F., J.N. and M.S. contributed to the revision of the manuscript. P.T.M. and J.P. assisted in conducting the experiments and performing the experimental analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 42271450 and Grant 41971415; and in part by the Key Laboratory of Land Satellite Remote-Sensing Applications, Ministry of Natural Resources of the People’s Republic of China, under grant KLSMNR-G202209. This work was performed while Dr. Dong Chen acted as an awardee of the 2021 Qinglan Project, sponsored by Jiangsu Province, China.
Data Availability Statement
Two datasets including NEWFOR and OpenTopography that support the research can be accessed openly. The NEWFOR dataset is accessible via the link https://www.newfor.net/download-newfor-single-tree-detection-benchmark-dataset/ (accessed on 5 February 2024), and the OpenTopography dataset can be accessed through the link https://portal.opentopography.org/lidarDataset?opentopoID=OTLAS.042021.6340.1 (accessed on 5 February 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yu, X.; Kukko, A.; Kaartinen, H.; Wang, Y.; Liang, X.; Matikainen, L.; Hyyppä, J. Comparing features of single and multi-photon lidar in boreal forests. ISPRS J. Photogramm. Remote Sens. 2020, 168, 268–276. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Li, Z.; Zhao, Y.; Wang, R.; Habib, A. Optimization Method of Airborne LiDAR Individual Tree Segmentation Based on Gaussian Mixture Model. Remote Sens. 2022, 14, 6167. [Google Scholar] [CrossRef]
- Hao, Y.; Widagdo, F.R.A.; Liu, X.; Liu, Y.; Dong, L.; Li, F. A hierarchical region-merging algorithm for 3-d segmentation of individual trees using UAV-LiDAR point clouds. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef]
- Xu, X.; Iuricich, F.; De Floriani, L. A topology-based approach to individual tree segmentation from airborne LiDAR data. GeoInformatica 2023, 27, 759–788. [Google Scholar] [CrossRef]
- Ma, Q.; Lin, J.; Ju, Y.; Li, W.; Liang, L.; Guo, Q. Individual structure mapping over six million trees for New York City USA. Sci. Data 2023, 10, 102. [Google Scholar] [CrossRef]
- Newnham, G.J.; Armston, J.D.; Calders, K.; Disney, M.I.; Lovell, J.L.; Schaaf, C.B.; Strahler, A.H.; Danson, F.M. Terrestrial laser scanning for plot-scale forest measurement. Curr. For. Rep. 2015, 1, 239–251. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Liu, L.; Lim, S.; Shen, X.; Yebra, M. A hybrid method for segmenting individual trees from airborne lidar data. Comput. Electron. Agric. 2019, 163, 104871. [Google Scholar] [CrossRef]
- Lu, X.; Guo, Q.; Li, W.; Flanagan, J. A bottom-up approach to segment individual deciduous trees using leaf-off lidar point cloud data. ISPRS J. Photogramm. Remote Sens. 2014, 94, 1–12. [Google Scholar] [CrossRef]
- Bigdeli, B.; Amirkolaee, H.A.; Pahlavani, P. DTM extraction under forest canopy using LiDAR data and a modified invasive weed optimization algorithm. Remote Sens. Environ. 2018, 216, 289–300. [Google Scholar] [CrossRef]
- Hui, Z.; Jin, S.; Xia, Y.; Nie, Y.; Xie, X.; Li, N. A mean shift segmentation morphological filter for airborne LiDAR DTM extraction under forest canopy. Opt. Laser Technol. 2021, 136, 106728. [Google Scholar] [CrossRef]
- Indirabai, I.; Nair, M.H.; Jaishanker, R.N.; Nidamanuri, R.R. Terrestrial laser scanner based 3D reconstruction of trees and retrieval of leaf area index in a forest environment. Ecol. Inform. 2019, 53, 100986. [Google Scholar] [CrossRef]
- Chang, L.; Fan, H.; Zhu, N.; Dong, Z. A Two-stage Approach for Individual Tree Segmentation from TLS Point Clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8682–8693. [Google Scholar] [CrossRef]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. Yolov4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Yun, T.; Jiang, K.; Li, G.; Eichhorn, M.P.; Fan, J.; Liu, F.; Chen, B.; An, F.; Cao, L. Individual tree crown segmentation from airborne LiDAR data using a novel Gaussian filter and energy function minimization-based approach. Remote Sens. Environ. 2021, 256, 112307. [Google Scholar] [CrossRef]
- Yang, J.; Kang, Z.; Cheng, S.; Yang, Z.; Akwensi, P.H. An individual tree segmentation method based on watershed algorithm and three-dimensional spatial distribution analysis from airborne LiDAR point clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1055–1067. [Google Scholar] [CrossRef]
- Li, Y.; Xie, D.; Wang, Y.; Jin, S.; Zhou, K.; Zhang, Z.; Li, W.; Zhang, W.; Mu, X.; Yan, G. Individual tree segmentation of airborne and UAV LiDAR point clouds based on the watershed and optimized connection center evolution clustering. Ecol. Evol. 2023, 13, e10297. [Google Scholar] [CrossRef]
- You, H.; Liu, Y.; Lei, P.; Qin, Z.; You, Q. Segmentation of individual mangrove trees using UAV-based LiDAR data. Ecol. Inform. 2023, 77, 102200. [Google Scholar] [CrossRef]
- Hyyppa, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. IEEE Trans. Geosci. Remote Sens. 2001, 39, 969–975. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the trees in the forest. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating individual trees in a savanna woodland using small footprint lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Impact of tree-oriented growth order in marker-controlled region growing for individual tree crown delineation using airborne laser scanner (ALS) data. Remote Sens. 2014, 6, 555–579. [Google Scholar] [CrossRef]
- Hui, Z.; Cheng, P.; Yang, B.; Zhou, G. Multi-level self-adaptive individual tree detection for coniferous forest using airborne LiDAR. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103028. [Google Scholar] [CrossRef]
- Cao, Y.; Ball, J.G.; Coomes, D.A.; Steinmeier, L.; Knapp, N.; Wilkes, P.; Disney, M.; Calders, K.; Burt, A.; Lin, Y.; et al. Tree segmentation in airborne laser scanning data is only accurate for canopy trees. bioRxiv 2022. [Google Scholar] [CrossRef]
- Ferraz, A.; Bretar, F.; Jacquemoud, S.; Gonçalves, G.; Pereira, L.; Tomé, M.; Soares, P. 3-D mapping of a multi-layered Mediterranean forest using ALS data. Remote Sens. Environ. 2012, 121, 210–223. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Meyer, V. Lidar detection of individual tree size in tropical forests. Remote Sens. Environ. 2016, 183, 318–333. [Google Scholar] [CrossRef]
- Heinzel, J.; Huber, M.O. Constrained spectral clustering of individual trees in dense forest using terrestrial laser scanning data. Remote Sens. 2018, 10, 1056. [Google Scholar] [CrossRef]
- Williams, J.; Schönlieb, C.B.; Swinfield, T.; Lee, J.; Cai, X.; Qie, L.; Coomes, D.A. 3D segmentation of trees through a flexible multiclass graph cut algorithm. IEEE Trans. Geosci. Remote Sens. 2019, 58, 754–776. [Google Scholar] [CrossRef]
- Yang, B.; Dai, W.; Dong, Z.; Liu, Y. Automatic forest mapping at individual tree levels from terrestrial laser scanning point clouds with a hierarchical minimum cut method. Remote Sens. 2016, 8, 372. [Google Scholar] [CrossRef]
- Gupta, S.; Weinacker, H.; Koch, B. Comparative analysis of clustering-based approaches for 3-D single tree detection using airborne fullwave lidar data. Remote Sens. 2010, 2, 968–989. [Google Scholar] [CrossRef]
- Dai, W.; Yang, B.; Dong, Z.; Shaker, A. A new method for 3D individual tree extraction using multispectral airborne LiDAR point clouds. ISPRS J. Photogramm. Remote Sens. 2018, 144, 400–411. [Google Scholar] [CrossRef]
- Yan, W.; Guan, H.; Cao, L.; Yu, Y.; Li, C.; Lu, J. A self-adaptive mean shift tree-segmentation method using UAV LiDAR data. Remote Sens. 2020, 12, 515. [Google Scholar] [CrossRef]
- Lei, L.; Yin, T.; Chai, G.; Li, Y.; Wang, Y.; Jia, X.; Zhang, X. A novel algorithm of individual tree crowns segmentation considering three-dimensional canopy attributes using UAV oblique photos. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102893. [Google Scholar] [CrossRef]
- Pang, Y.; Wang, W.; Du, L.; Zhang, Z.; Liang, X.; Li, Y.; Wang, Z. Nyström-based spectral clustering using airborne LiDAR point cloud data for individual tree segmentation. Int. J. Digit. Earth 2021, 14, 1452–1476. [Google Scholar] [CrossRef]
- Bryson, M.; Wang, F.; Allworth, J. Using Synthetic Tree Data in Deep Learning-Based Tree Segmentation Using LiDAR Point Clouds. Remote Sens. 2023, 15, 2380. [Google Scholar] [CrossRef]
- Jiang, T.; Liu, S.; Zhang, Q.; Xu, X.; Sun, J.; Wang, Y. Segmentation of individual trees in urban MLS point clouds using a deep learning framework based on cylindrical convolution network. Int. J. Appl. Earth Obs. Geoinf. 2023, 123, 103473. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Liu, X.; Yu, H. Towards Intricate Stand Structure: A Novel Individual Tree Segmentation Method for ALS Point Cloud Based on Extreme Offset Deep Learning. Appl. Sci. 2023, 13, 6853. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Cao, L.; An, F.; Chen, B.; Xue, L.; Yun, T. Individual rubber tree segmentation based on ground-based LiDAR data and faster R-CNN of deep learning. Forests 2019, 10, 793. [Google Scholar] [CrossRef]
- Sun, C.; Huang, C.; Zhang, H.; Chen, B.; An, F.; Wang, L.; Yun, T. Individual tree crown segmentation and crown width extraction from a heightmap derived from aerial laser scanning data using a deep learning framework. Front. Plant Sci. 2022, 13, 914974. [Google Scholar] [CrossRef]
- Dersch, S.; Schöttl, A.; Krzystek, P.; Heurich, M. Towards complete tree crown delineation by instance segmentation with Mask R–CNN and DETR using UAV-based multispectral imagery and lidar data. ISPRS Open J. Photogramm. Remote Sens. 2023, 8, 100037. [Google Scholar] [CrossRef]
- Luo, Z.; Zhang, Z.; Li, W.; Chen, Y.; Wang, C.; Nurunnabi, A.A.M.; Li, J. Detection of individual trees in UAV LiDAR point clouds using a deep learning framework based on multichannel representation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, K.; Zhu, Y.; Wang, X.; Yun, T. Individual tree crown segmentation directly from UAV-borne LiDAR data using the PointNet of deep learning. Forests 2021, 12, 131. [Google Scholar] [CrossRef]
- Liu, Y.; You, H.; Tang, X.; You, Q.; Huang, Y.; Chen, J. Study on Individual Tree Segmentation of Different Tree Species Using Different Segmentation Algorithms Based on 3D UAV Data. Forests 2023, 14, 1327. [Google Scholar] [CrossRef]
- Windrim, L.; Bryson, M. Detection, segmentation, and model fitting of individual tree stems from airborne laser scanning of forests using deep learning. Remote Sens. 2020, 12, 1469. [Google Scholar] [CrossRef]
- Eysn, L.; Hollaus, M.; Lindberg, E.; Berger, F.; Monnet, J.M.; Dalponte, M.; Kobal, M.; Pellegrini, M.; Lingua, E.; Mongus, D.; et al. A benchmark of lidar-based single tree detection methods using heterogeneous forest data from the alpine space. Forests 2015, 6, 1721–1747. [Google Scholar] [CrossRef]
- Thompson, S. Illilouette Creek Basin Lidar Survey, Yosemite Valley, CA 2018. National Center for Airborne Laser Mapping (NCALM). Distributed by OpenTopography. 2021. Available online: https://doi.org/10.5069/G96M351N (accessed on 5 February 2024).
- Beucher, S.; Meyer, F. The morphological approach to segmentation: The watershed transformation. In Mathematical Morphology in Image Processing; CRC Press: Boca Raton, FL, USA, 2018; pp. 433–481. [Google Scholar]
- Vincent, L.; Soille, P. Watersheds in digital spaces: An efficient algorithm based on immersion simulations. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 583–598. [Google Scholar] [CrossRef]
- Yan, W.; Guan, H.; Cao, L.; Yu, Y.; Gao, S.; Lu, J. An automated hierarchical approach for three-dimensional segmentation of single trees using UAV LiDAR data. Remote Sens. 2018, 10, 1999. [Google Scholar] [CrossRef]
- Malik, J.; Belongie, S.; Leung, T.; Shi, J. Contour and texture analysis for image segmentation. Int. J. Comput. Vis. 2001, 43, 7–27. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Yin, D.; Wang, L. How to assess the accuracy of the individual tree-based forest inventory derived from remotely sensed data: A review. Int. J. Remote Sens. 2016, 37, 4521–4553. [Google Scholar] [CrossRef]
- Yin, D.; Wang, L. Individual mangrove tree measurement using UAV-based LiDAR data: Possibilities and challenges. Remote Sens. Environ. 2019, 223, 34–49. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).