Estimation of Signal Distortion Bias Using Geometry-Free Linear Combinations
Abstract
1. Introduction
2. Materials and Methods
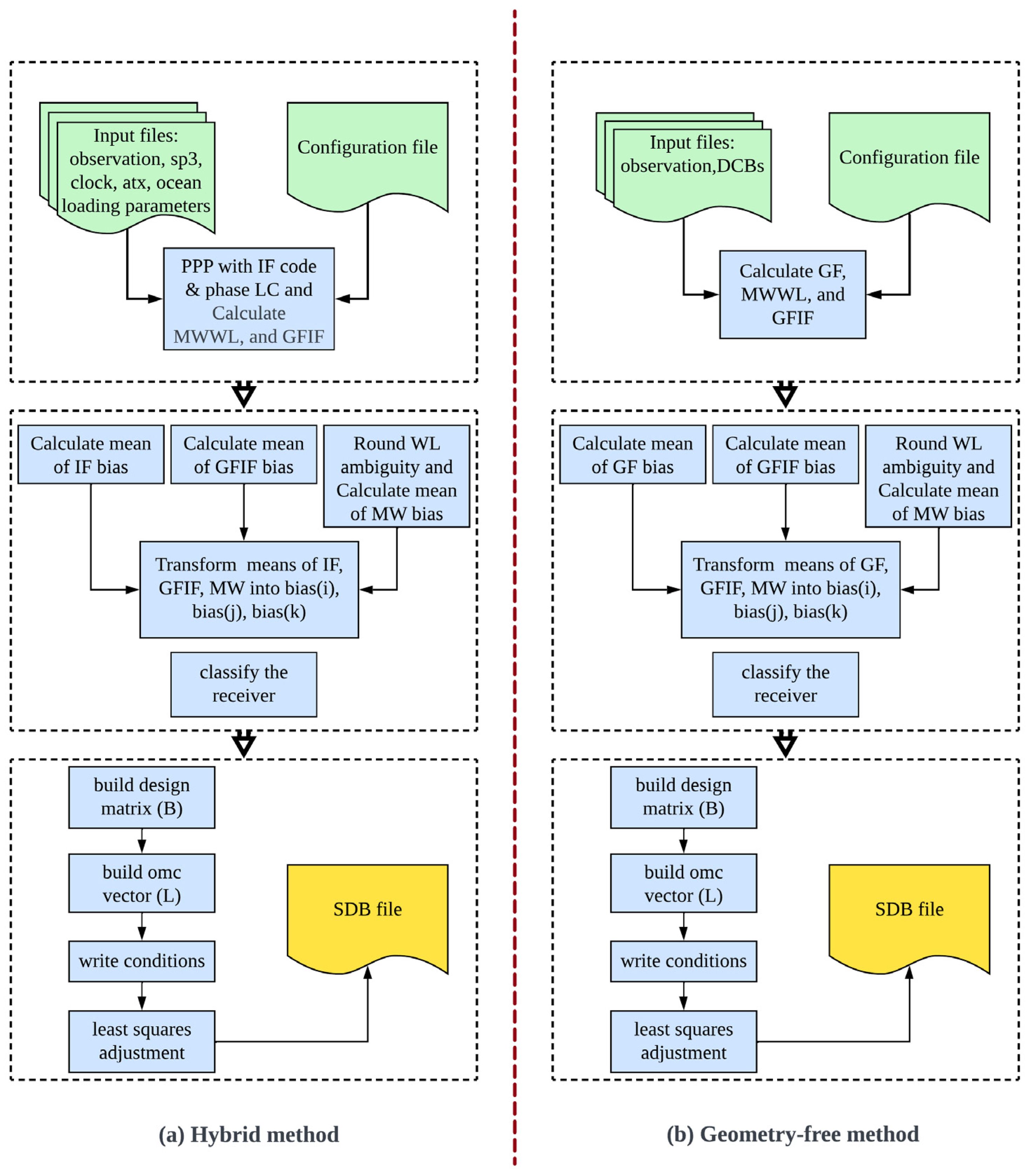
2.1. Hybrid Method
2.2. Geometry-Free Method
2.3. Theoretical Analysis
2.4. Data and Flowchart of Both Methods
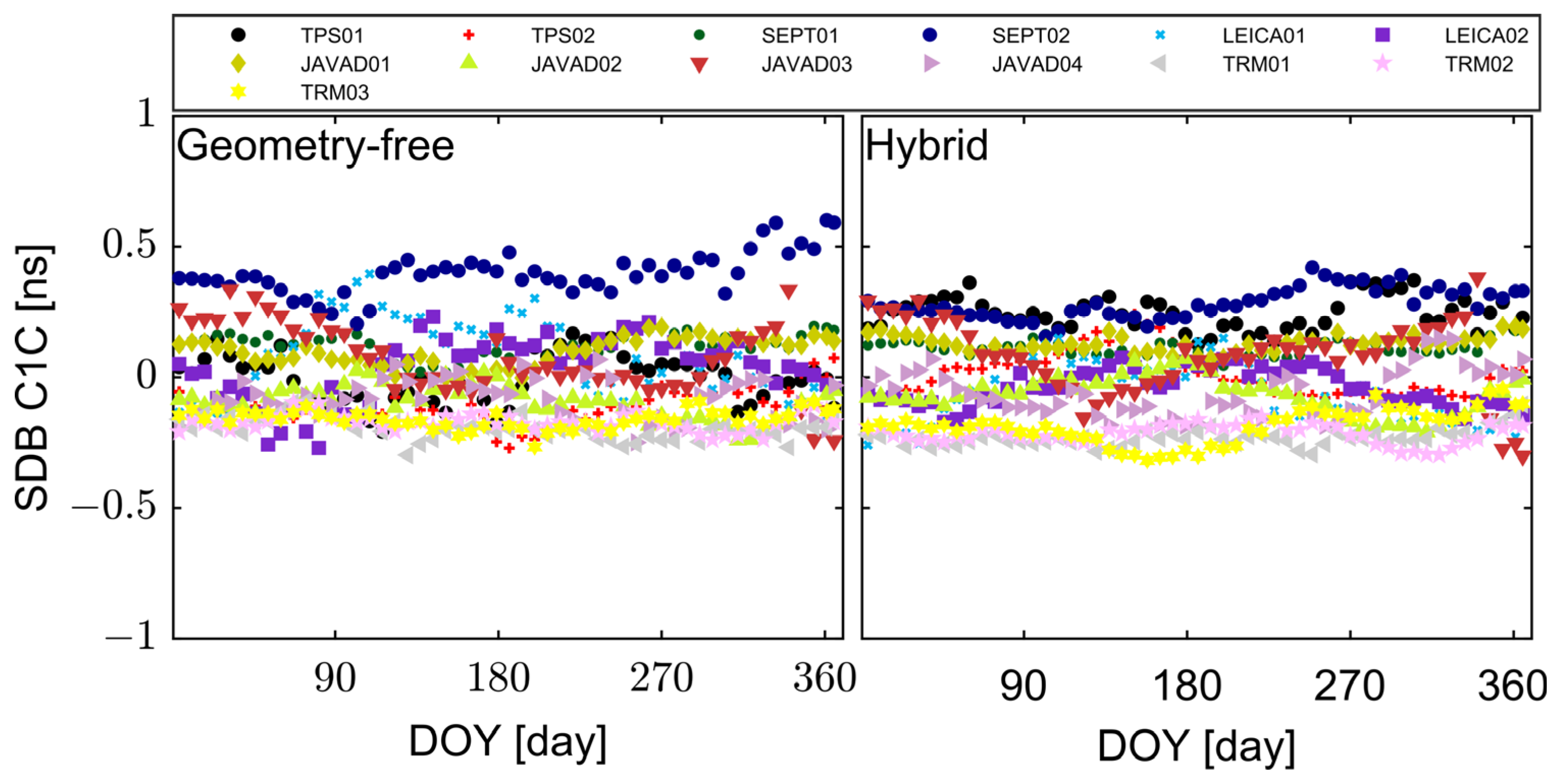
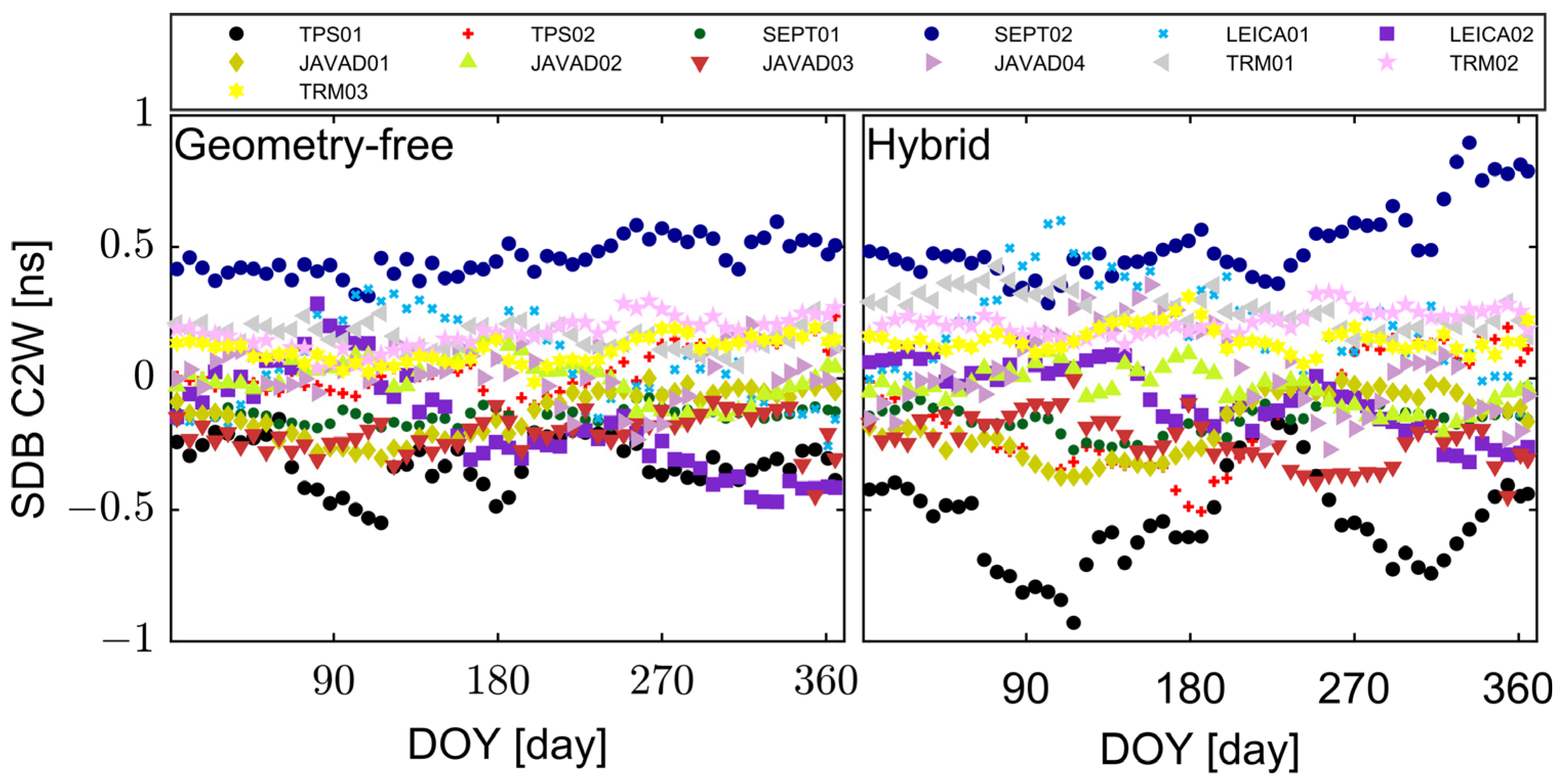
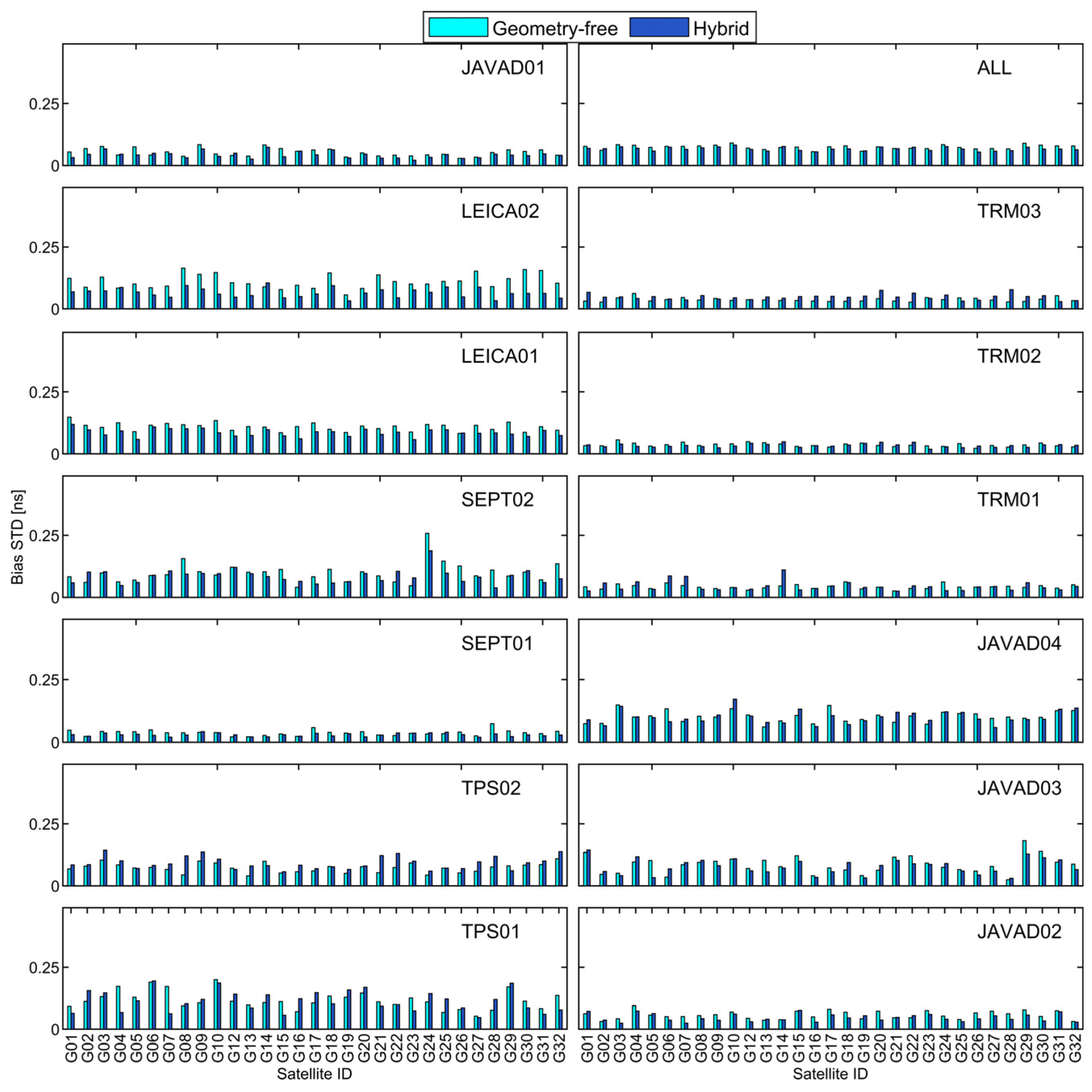
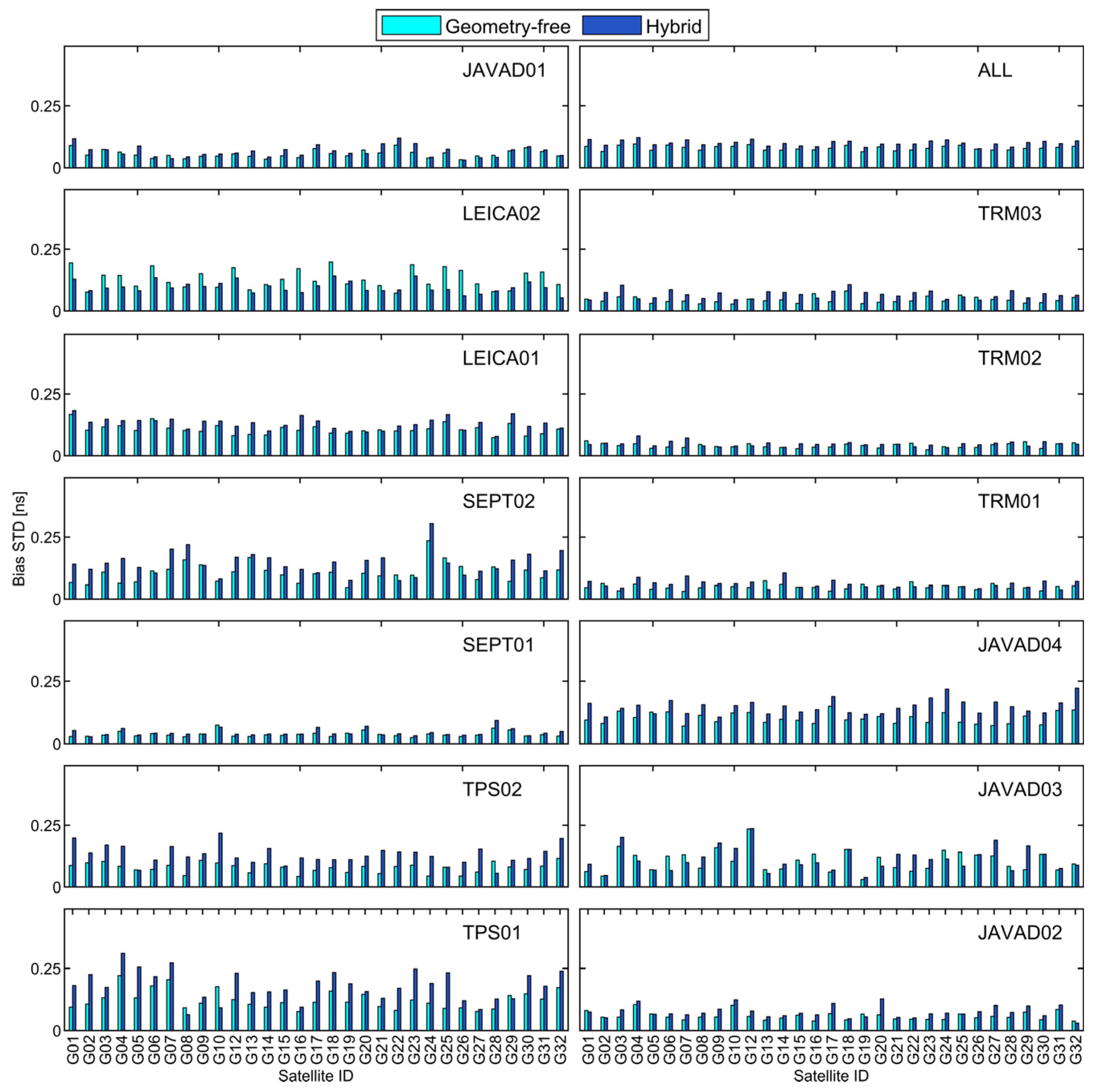
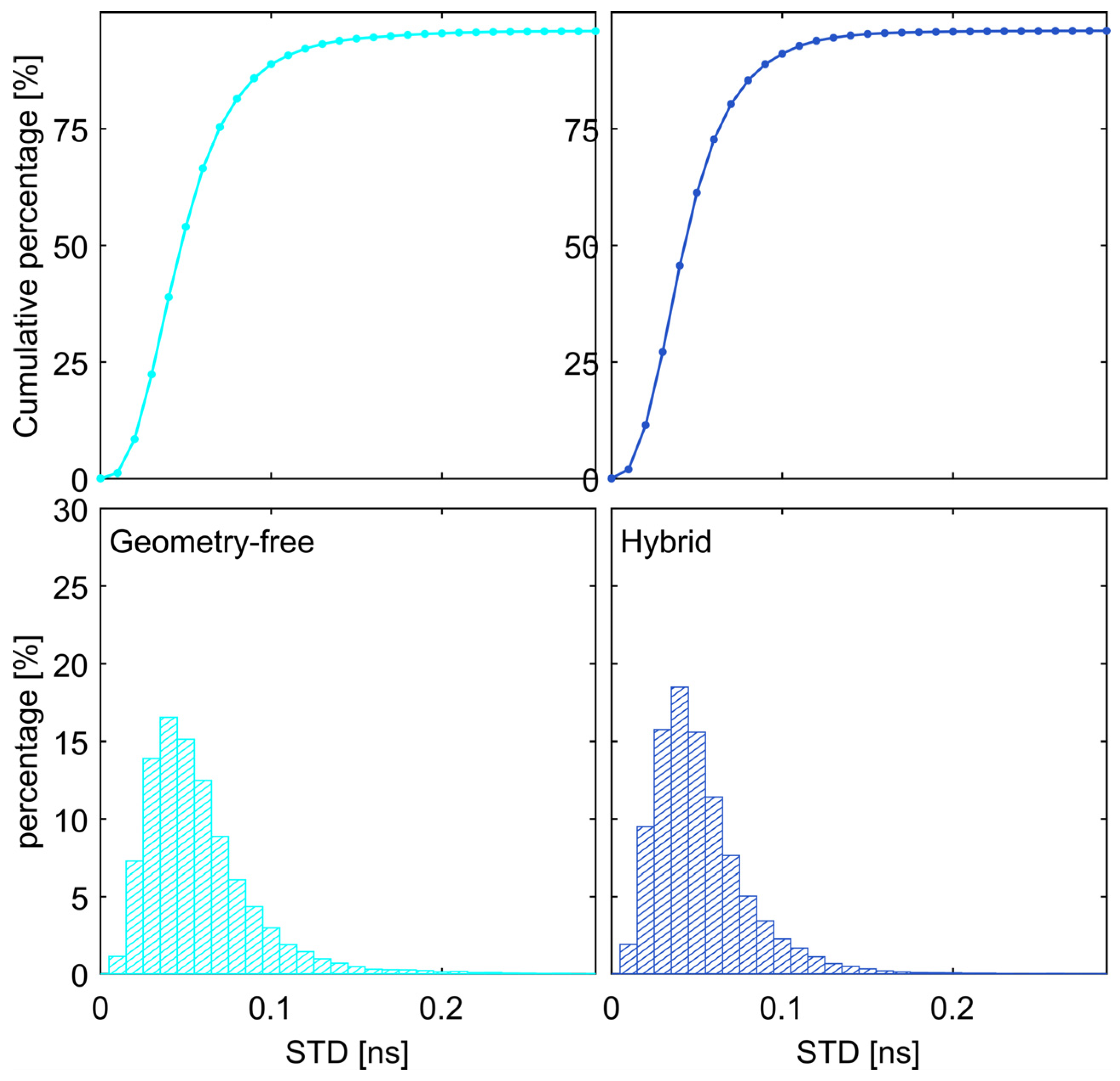
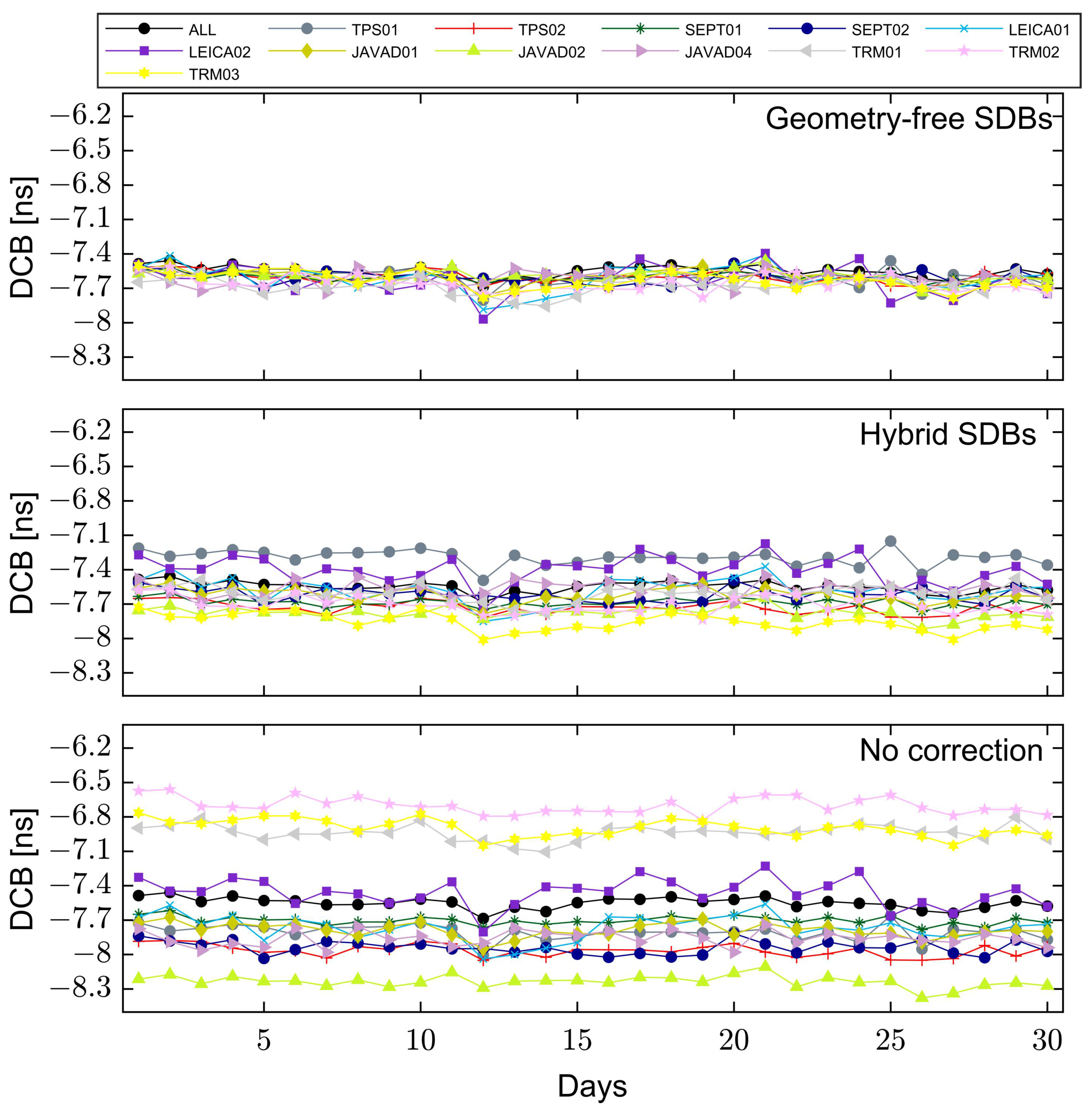
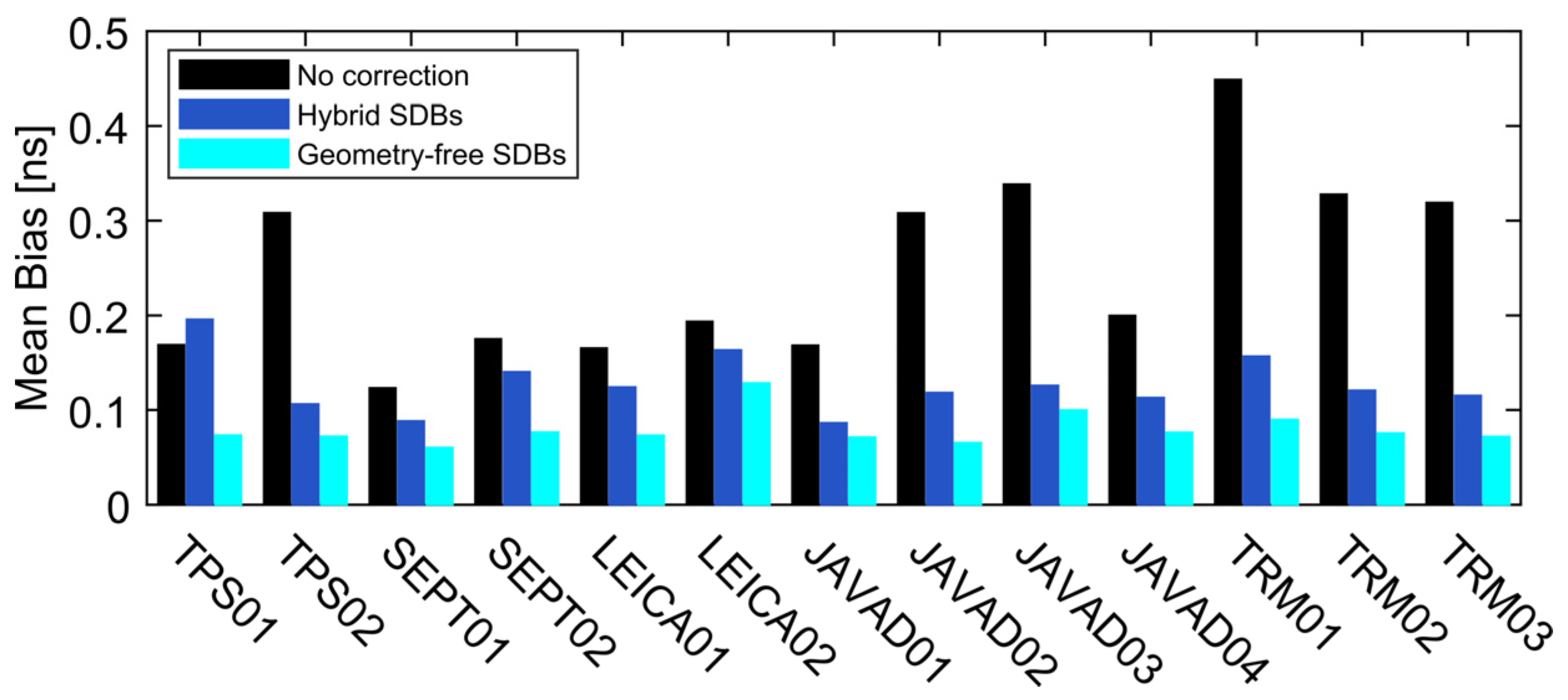
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Phelts, R.E.; Akos, D.M.; Enge, P. Robust signal quality monitoring and detection of evil waveforms. In Proceedings of the 13th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2000), Salt Lake City, UT, USA, 19–22 September 2000. [Google Scholar]
- Pini, M.; Akos, D.M.; Esterhuizen, S.; Mitelman, A. Analysis of GNSS signals as observed via a high gain parabolic antenna. In Proceedings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, 13–16 September 2005. [Google Scholar]
- Hauschild, A.; Montenbruck, O. A study on the dependency of GNSS pseudorange biases on correlator spacing. GPS Solut. 2014, 20, 159–171. [Google Scholar] [CrossRef]
- Mi, X.; Sheng, C.; El-Mowafy, A.; Zhang, B. Characteristics of receiver-related biases between BDS-3 and BDS-2 for five frequencies including inter-system biases, differential code biases, and differential phase biases. GPS Solut. 2021, 25, 113. [Google Scholar] [CrossRef]
- Gong, X.; Zheng, F.; Gu, S.; Zhang, Z.; Lou, Y. The long-term characteristics of GNSS signal distortion biases and their empirical corrections. GPS Solut. 2022, 26, 52. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, Z.; Gong, X.; Zheng, F.; Gu, S.; Shi, C. Estimating GPS satellite and receiver differential code bias based on signal distortion bias calibration. GPS Solut. 2023, 27, 48. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P. Differential code bias estimation using multi-GNSS observations and global ionosphere maps. Navig. J. Inst. Navig. 2014, 61, 191–201. [Google Scholar] [CrossRef]
- Hauschild, A.; Steigenberger, P.; Montenbruck, O. Inter-receiver GNSS pseudorange biases and their effect on clock and DCB estimation. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019. [Google Scholar]
- Cui, B.; Li, P.; Wang, J.; Ge, M.; Schuh, H. Calibrating receiver-type-dependent wide-lane uncalibrated phase delay biases for PPP integer ambiguity resolution. J. Geod. 2021, 95, 82. [Google Scholar] [CrossRef]
- Gong, X.; Lou, Y.; Zheng, F.; Gu, S.; Shi, C.; Liu, J.; Jing, G. Evaluation and calibration of BeiDou receiver-related pseudorange biases. GPS Solut. 2018, 22, 98. [Google Scholar] [CrossRef]
- Zhang, Y.; Kubo, N.; Chen, J.; Wang, A. Calibration and analysis of BDS receiver-dependent code biases. J. Geod. 2021, 95, 1–14. [Google Scholar] [CrossRef]
- Zheng, F.; Gong, X.; Lou, Y.; Gu, S.; Jing, G.; Shi, C. Calibration of BeiDou triple-frequency receiver-related pseudorange biases and their application in BDS precise positioning and ambiguity resolution. Sensors 2019, 19, 3500. [Google Scholar] [CrossRef] [PubMed]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)–achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
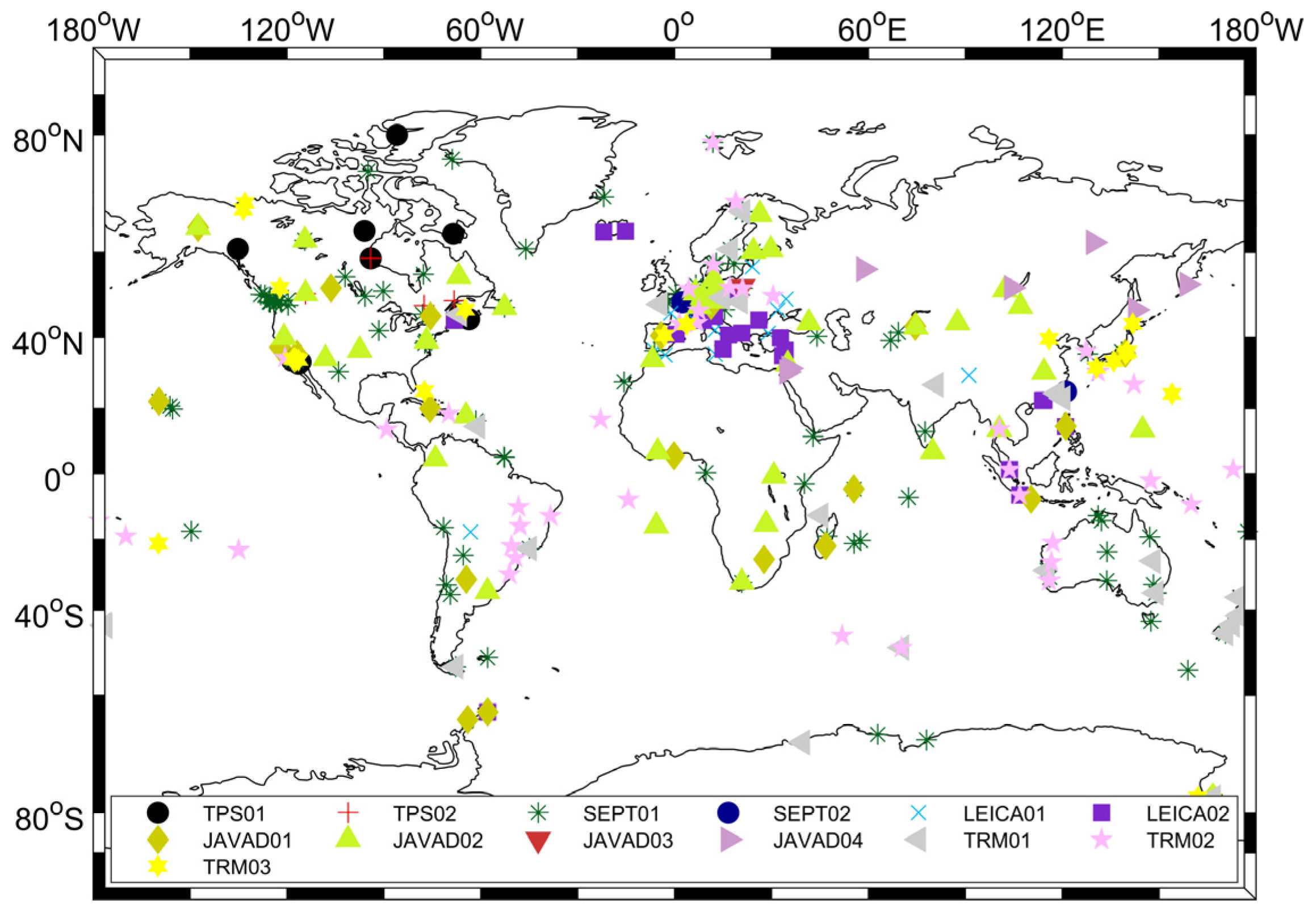
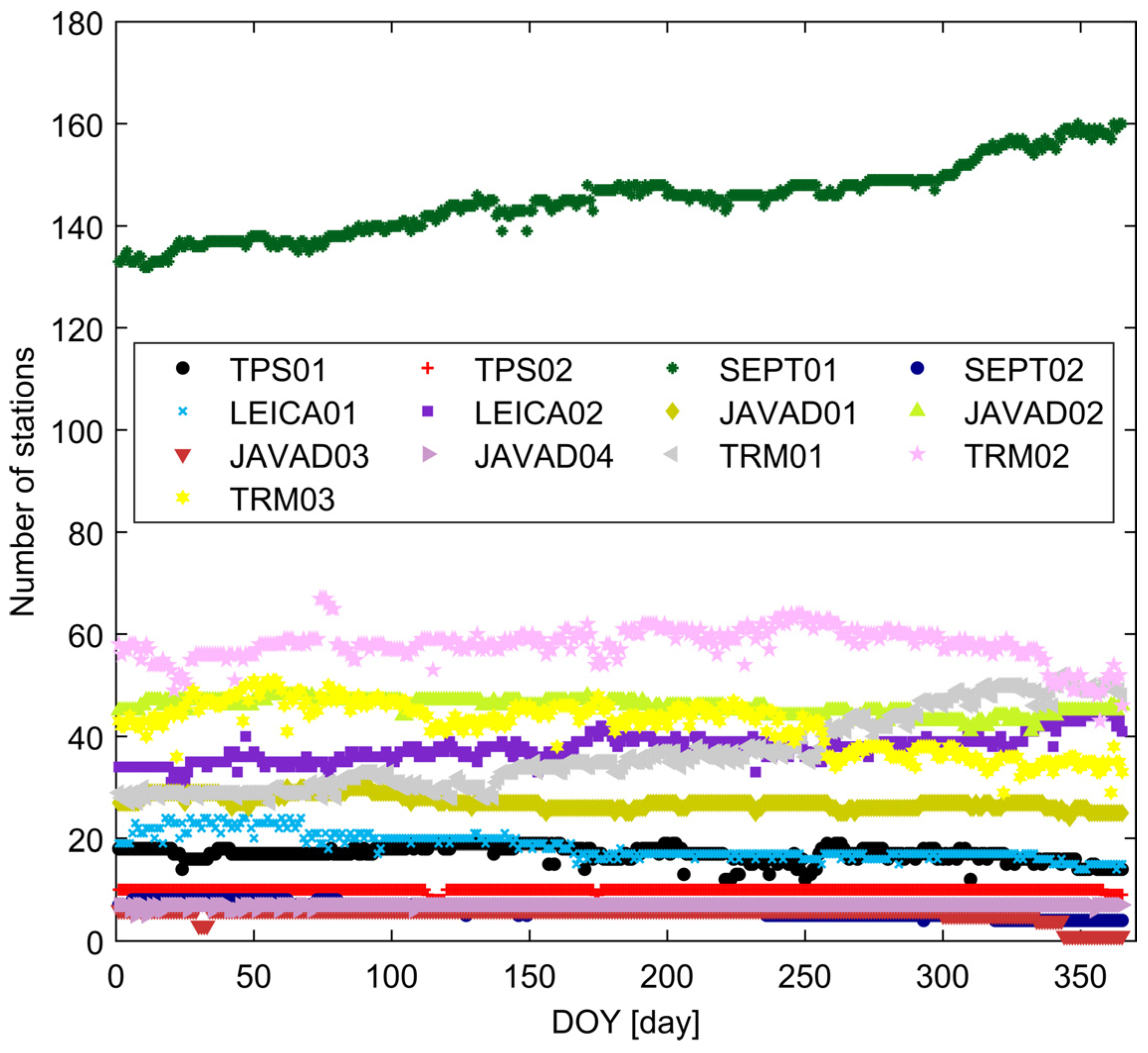
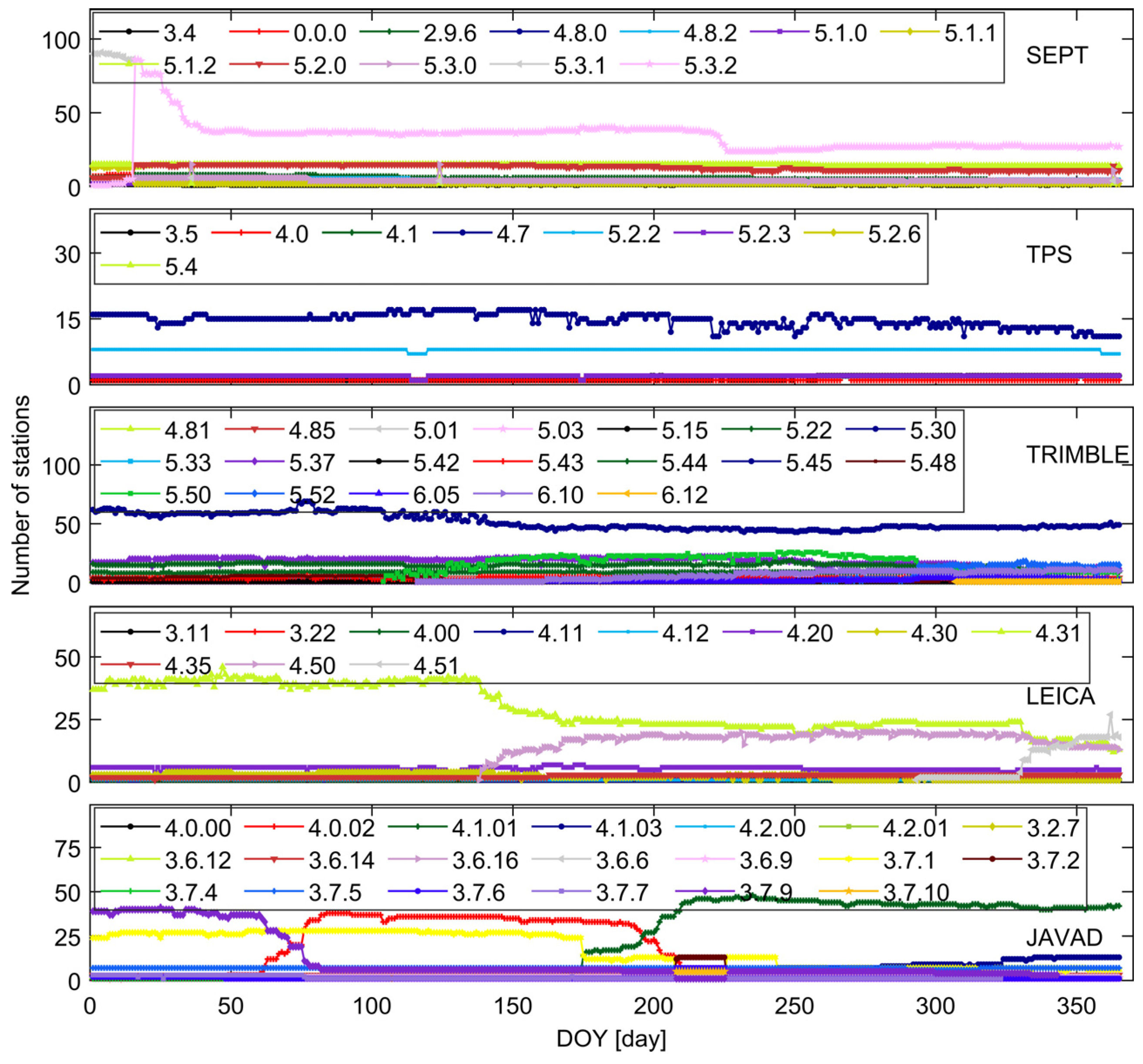



| Group Name | Receiver Brand | Receiver Model |
|---|---|---|
| TPS01 | TPS | NET-G3A |
| TPS02 | NET-G5 | |
| SEPT01 | SEPT | POLARX5TR/POLARX5/ASTERX4 |
| SEPT02 | POLARX4TR/POLARX4 | |
| LEICA01 | LEICA | GR25/GR10 |
| LEICA02 | GR50/GR30 | |
| JAVAD01 | JAVAD | TRE_G3TH DELTA/TR_G3TH/TRE_G2T DELTA |
| JAVAD02 | TRE_3N DELTA/TRE_3 DELTA/TRE_3 | |
| JAVAD03 | TRE_G3T DELTA | |
| JAVAD04 * | - | |
| TRM01 | TRIMBLE | ALLOY |
| TRM02 | NETR9 | |
| TRM03 * | - |
| Items | Models |
|---|---|
| Observations | IF observables, MWWL observables, and GFIF observables |
| Interval | 30 s |
| Elevation cutoff angle | 15° |
| Ionospheric effect | IF observables are utilized to mitigate the first-order ionospheric effect |
| Troposphere delay | The dry tropospheric delay is modeled, while the wet tropospheric delay is estimated as an unknown |
| Phase center offset and variations | Igs14.atx |
| Weighting scheme | Elevation-based is used |
| Items | Models |
|---|---|
| Observations | GF observables, MWWL observables, and GFIF observables |
| Interval | 30 s |
| Elevation cutoff angle | 15° |
| Ionospheric effect | Mitigated by using final global ionospheric maps |
| Satellite and receiver DCB | Estimated by MDCB MATLAB code |
| Weighting scheme | Elevation-based is used |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abou Galala, M.; Chen, W. Estimation of Signal Distortion Bias Using Geometry-Free Linear Combinations. Remote Sens. 2024, 16, 4463. https://doi.org/10.3390/rs16234463
Abou Galala M, Chen W. Estimation of Signal Distortion Bias Using Geometry-Free Linear Combinations. Remote Sensing. 2024; 16(23):4463. https://doi.org/10.3390/rs16234463
Chicago/Turabian StyleAbou Galala, Mohammed, and Wu Chen. 2024. "Estimation of Signal Distortion Bias Using Geometry-Free Linear Combinations" Remote Sensing 16, no. 23: 4463. https://doi.org/10.3390/rs16234463
APA StyleAbou Galala, M., & Chen, W. (2024). Estimation of Signal Distortion Bias Using Geometry-Free Linear Combinations. Remote Sensing, 16(23), 4463. https://doi.org/10.3390/rs16234463








