Intelligent QLFEKF Integrated Navigation for the SSBE Cruise Phase Based on X-Ray Pulsar/Solar and Target Planetary Doppler Information Fusion

Abstract

The Solar System Boundary Exploration (SSBE) mission is the focal point for future far-reaching space exploration. Due to the SSBE having many scientific difficulties that need to be studied, such as a super long space exploratory distance, a super long flight time in orbit, and a significant communication data delay between the ground and the probe, the probe must have sufficient intelligence to realize intelligent autonomous navigation. Traditional navigation schemes have been unable to provide high-accuracy autonomous intelligent navigation for the probe independent of the ground. Therefore, high-accuracy intelligent astronomical integrated navigation would provide new methods and technologies for the navigation of the SSBE probe. The probe of the SSBE is disturbed by multiple sources of solar light pressure and a complex, unknown environment during its long cruise operation while in orbit. In order to ensure the high-accuracy position state and velocity state error estimation for the probe in the cruise phase, an autonomous intelligent integrated navigation scheme based on the X-ray pulsar/solar and target planetary Doppler velocity measurements is proposed. The reinforcement Q-learning method is introduced, and the reward mechanism is designed for trial-and-error tuning of state and observation noise error covariance parameters. The federated extended Kalman filter (FEKF) based on the Q-learning (QLFEKF) navigation algorithm is proposed to achieve high-accuracy state estimations of the autonomous intelligence navigation system for the SSBE probe cruise phase. The main advantage of the QLFEKF is that Q-learning combined with the conventional federated filtering method could optimize the state parameters in real-time and obtain high position and velocity state estimation (PVSE) accuracy. Compared with the conventional FEKF integrated navigation algorithm, the PVSE navigation accuracy of the federated filter integrated based the Q-learning navigation algorithm is improved by 55.84% and 37.04%, respectively, demonstrating the higher accuracy and greater capability of the raised autonomous intelligent integrated navigation algorithm. The simulation results show that the intelligent integrated navigation algorithm based on QLFEKF has higher navigation accuracy and is able to satisfy the demands of autonomous high accuracy for the SSBE cruise phase.

1. Introduction

The exploration of the extremely distant, extremely dark, and extremely cold regions at the solar system boundary is a hot point in deep space exploration. After the human exploration of the Moon and Mars, which has progressively expanded to the solar system boundary, further space exploration could continuously open new windows for humans’ understanding of the universe [1]. There are only a limited number of deep space missions that continue to explore the solar system boundary after completing the scheduled exploration mission, such as Pioneer 10–11 [2,3,4], Voyager 1–2 [5,6], and New Horizons [7,8]. With the continuous extension of the field of deep space exploration, China has put forward the SSBE program, which could build the capability of the probe to reach the whole area of the solar system and realize super long-distance detection from internal celestial bodies to interstellar space, providing us with the capability to independently explore interplanetary far-reaching space [1,9]. Due to the characteristics of unknown and varied exploration environments, super long space exploratory distances, super long orbital flight times, and significant communication data delays between the SSBE and the ground, the implementation of the exploration mission is very difficult [10]. Because the probe is so far from the ground, it cannot rely on traditional navigation methods, such as the radio station aeronautical ground, very long baseline interferometry (VLBI), and tracking telemetry and command (TT&C) communication networks to provide real-time and high-accuracy navigation information, which presents new challenges to ultra-long-distance autonomous high-accuracy navigation [11,12].

Regarding the solar system boundary probe, reliance on local ground-based tracking navigation would no longer be applicable and could not be used for autonomous real-time and high-accuracy navigation of the probe at great distances from the ground [12]. In order to improve the autonomous operation capability of the probe in orbit, autonomous navigation technology that is independent of ground navigation measurements has been actively studied in depth. X-ray pulsar navigation (XNAV) is a new kind of autonomous celestial navigation technology that can be applied to both near-Earth and deep space [13,14,15]. Based on the three X-ray pulsars, the autonomous position determination of the deep space probe could be realized. By collecting the X-ray radiation signals from the X-ray pulsar with the X-ray detector, the pulse time-of-arrival (TOA) can be obtained. The arrival time of the pulse reaching the detector and the time to reach the solar system barycenter (SSB) are predicted, which can determine the position of the probe by characterizing its position direction along the X-ray pulsar [16,17]. Reichley et al. [18] and Downs [19] stated that the position of the spacecraft is determined through the measurement of the phase of a periodic signal, and they speculated for the first time that the X-ray pulsar could be used to determine the time and position of the spacecraft in orbit [15]. Runnels et al. [20] proposed a method to estimate the comprehensive six DOF position navigation and time solutions for the deep space exploration spacecraft, which relied on the measurement of the arrival time and angles of the X-ray photons from the X-ray pulsars and other bright stars. Gao et al. [21] proposed differential XNAV based on the time difference of the pulse arrival, which analyzed the impact of the ephemeris errors on correcting the photon TOA and observation equations, and three Mars orbits with different altitudes were simulated to validate the efficacy of the navigation scheme and its suitability for the different heights from the Martian surface. When the detector moves relative to stellar objects in far-reaching space exploration, the measured stellar objects spectrum also undergoes Doppler frequency offset, which reflects the velocity of the probe relative to the stellar objects [22]. The radial velocity of the probe relative to the navigation stellar objects can be calculated based on the Doppler frequency offset of the probe with respect to the stellar object, and then the velocity state of the probe can be estimated. Yim et al. [23] adopted Doppler measurements generated by the relative motion of the spacecraft and Sun as the key measurement, which realized the autonomous navigation of the spacecraft for deep space exploration, but the positioning accuracy is not particularly high. Ning et al. [24] introduced the celestial navigation algorithm assisted by the differential Doppler measurements, which used the difference between Doppler radial velocity measured in two adjacent observation periods as the measured value to mitigate the effects of solar spectrum frequency instability and enhance autonomous celestial navigation accuracy.

Since deep space probes operate in long-endurance, highly dynamic, and extreme environments, it is difficult for the single navigation pattern to satisfy the navigation demands of excellent accuracy and great dependability for the deep space probe. The integrated navigation formed by the combination of multiple navigation modes is an irresistible trend for deep space exploration navigation systems in the future. Liu et al. [25] proposed an autonomous integrated navigation scheme based on Doppler/XNAV, and the Doppler autonomous navigation provides high-accuracy velocity error estimation information by measuring the radial velocity information relative to the Sun. The complementary of the two navigation methods can make up for the problem of low-accuracy navigation caused by shrinking the pulse signal receiving area size for the X-ray pulsar detection sensor. Pan et al. [26] used the stability of the solar Doppler differential navigation to put forward the solar time difference of arrival (TDOA)/Doppler difference joint observation and integrate it with Mars angle navigation. This approach allows fully observable Mars angle and solar light joint observation navigation, providing higher accuracy and stability of the navigation. Cui et al. [27] proposed the integrated navigation scheme based on the X-ray pulsars and Doppler to advance the error estimation precision of the probe during the final approach phase entry state of Mars exploration, and the navigation scheme adopted the X-ray pulsar observations and Doppler velocity measurements to complement each other to eliminate the problem of the reduced velocity state estimation performance of the XNAV for this phase.

During the design of the autonomous navigation system for the SSBE cruise phase, compared with other filtering estimators [28,29], the extended Kalman filter (EKF) is the preferred state estimator for the cruise phase navigation system because of the nonlinearity of the orbital dynamics model [30]. The EKF is widely used in various scenarios involving navigation systems and has a very stable navigation performance [31,32]. This state estimation algorithm has also been favored by researchers from the field of astronomical autonomous navigation. In addition, for the navigation system, the measurement noise is usually based on the measurement error of the sensor used in actual tasks. The environment disturbances mainly come from micrometeoroids, cosmic rays, and solar wind in the space environment, which all have an impact on the navigation accuracy of the deep space probe, and it is necessary to set the noise according to the scene in the different phases during the simulation analysis. Kang et al. [33] combined Doppler velocity measurements and the XNAV and proposed the integrated navigation method of the Doppler velocity measurements based on the double measurement model and X-ray pulsar. The EKF was used to achieve continuous high-accuracy state estimation, which effectively suppressed the accumulative state errors in the Doppler velocity measurements and improved the PVSE precision of the autonomous navigation system for the deep space exploration spacecraft. To enhance the autonomous navigation capability of the deep space probes, many FEKF integrated navigation methods based on multiple measurement models have been proposed [34]. Yang et al. [35] applied the XNAV and ultraviolet sensor to measure the position, velocity, and attitude of the deep space probe. The researchers also designed the FEKF integrated navigation system based on the X-ray pulsar and ultraviolet sensor, and the system could perform clock time prediction, attitude determination, and orbit determination concurrently during the deep space probe in-orbit flight. It could supply high-precision error state estimations. In order to eliminate the influence of the unstable solar spectra on Doppler velocity measurements and given that Doppler difference navigation might accumulate position errors over time, Liu et al. [36] combined the solar Doppler difference velocity measurement and the XNAV method to propose integrated X-ray pulsar/Doppler differential velocity measurement navigation based on FEKF for deep space exploration. This method has high robustness for Doppler velocity measurement deviation brought by the solar spectral instability and also ensures high-accuracy state estimation of the deep space probe in orbit.

The intelligent autonomous navigation algorithm combined with the reinforcement Q-learning algorithm has been favored by researchers at present [37]. In particular, it has a very good application in estimating the accuracy of in-orbit spacecraft, providing high precision for spacecraft navigation systems [38]. Xiong et al. [39] proposed the state error estimation algorithm that combines the reinforcement Q-learning algorithm and the EKF and tried to use reinforcement learning (RL) to restrain the influence of the uncertain noise error covariance matrix on the estimation performance of the EKF navigation algorithm, in which the covariance adaptive adjustment strategy based on Q-learning was designed to enhance the state estimation performance of the autonomous nonlinear navigation systems for the spacecraft. In addition, they also adopted the astronomical integrated navigation based on an ultraviolet earth sensor and optical interferometer and introduced QLEKF to integrate the information from the two measurements to estimate the position, velocity, and attitude state error of the spacecraft [40]. They also assessed the optical path delay bias in the optical interferometer, and the proposed QLEKF demonstrates superior estimation performance compared to the conventional EKF. Nemati et al. [41] adopted RL to enhance the position estimation of the spacecraft and proposed the state estimation algorithm based on the combination of RL and the Kalman filter to acquire the optimal solution of the state and observation noise covariance, which improved the PVSE accuracy for the spacecraft navigation. Xiong et al. [42] recently developed an improved Q-learning EKF optical autonomous navigation based on their own previous research by measuring the line of sight (LOS) direction of the non-cooperative spacecraft targets, which improved the PVSE precision of the spacecraft navigation based on the space target LOS by fine-tunning the process noise error covariance matrix filtering parameters.

Based on the above research conducted by others, this paper presents a combined navigation scheme based on the X-ray pulsar and two-dimensional Doppler velocity measurements to improve the high accuracy of autonomous integrated navigation for the SSBE cruise phase, which can make up for the accumulated position estimation error in the Doppler velocity measurements. The FEKF algorithm is designed to correct the position information obtained from the two-dimensional Doppler velocity-measuring in real-time by the position information estimation of the XNAV, and eliminate the accumulated position errors caused by Doppler velocity-measuring at the same time. The Q-learning-based FEKF integrated navigation algorithm was developed, enabling real-time parameter tuning and fine-tuning the state and observation noise error parameters for this navigation system according to the operational state environment of the probe during the cruising phase. The research is different from the X-ray pulsar and the Doppler velocity dual measurement model integrated navigation given by [33] in that the federation filter composed of the primary filter and sub-filter is adopted to realize the information fusion of multiple navigation modes and guarantee the estimation performance of autonomous integrated navigation. Compared with the above research [39,40,41,42], the intelligent Q-learning algorithm used to tune the parameters of the state and observation noise covariance is also improved accordingly. The reward mechanism and Q-table of the reinforcement Q-learning is designed according to the sub-filter characteristics of the federated filter, and the iterative period of the Q-learning is taken as the algorithm to evaluate the cumulative reward. The optimal state and observation noise covariance parameters are obtained by adjusting the grid size of the Q-table and the learning parameters. The proposed intelligent integrated navigation method based on QLFEKF has the potential to realize high precision and autonomy.

The main research work for this paper involves in-depth research on the high accuracy and feasibility of the intelligent integrated navigation for the cruise phase of the SSBE based on the X-ray pulsar/solar and target planetary Doppler velocity measurements of the QLFEKF algorithm. This paper is divided into six sections. After the introduction of the first section, the orbital dynamics model and the integrated navigation measurement model based on the X-ray pulsar and two-dimensional Doppler velocity measurements of the cruise phase are modeled in Section 2, and the state and measurement equations intelligent navigation for the cruise phase are given. In Section 3, the navigation information obtained from the fusion state estimation algorithm based on QLFEKF is developed with the combination of reinforcement Q-learning and the conventional Kalman filter. In Section 4, the performance of the QLFEKF-based intelligent integrated navigation using X-ray pulsar/solar and target planetary Doppler velocity measurements is simulated and analyzed. The results are compared with the EKF and the FEKF integrated navigation algorithms. The high accuracy performance of the suggested intelligent integrated navigation algorithm is confirmed with simulation and analysis. Finally, the conclusions are presented in Section 5.

2. System Models of Integrated Navigation

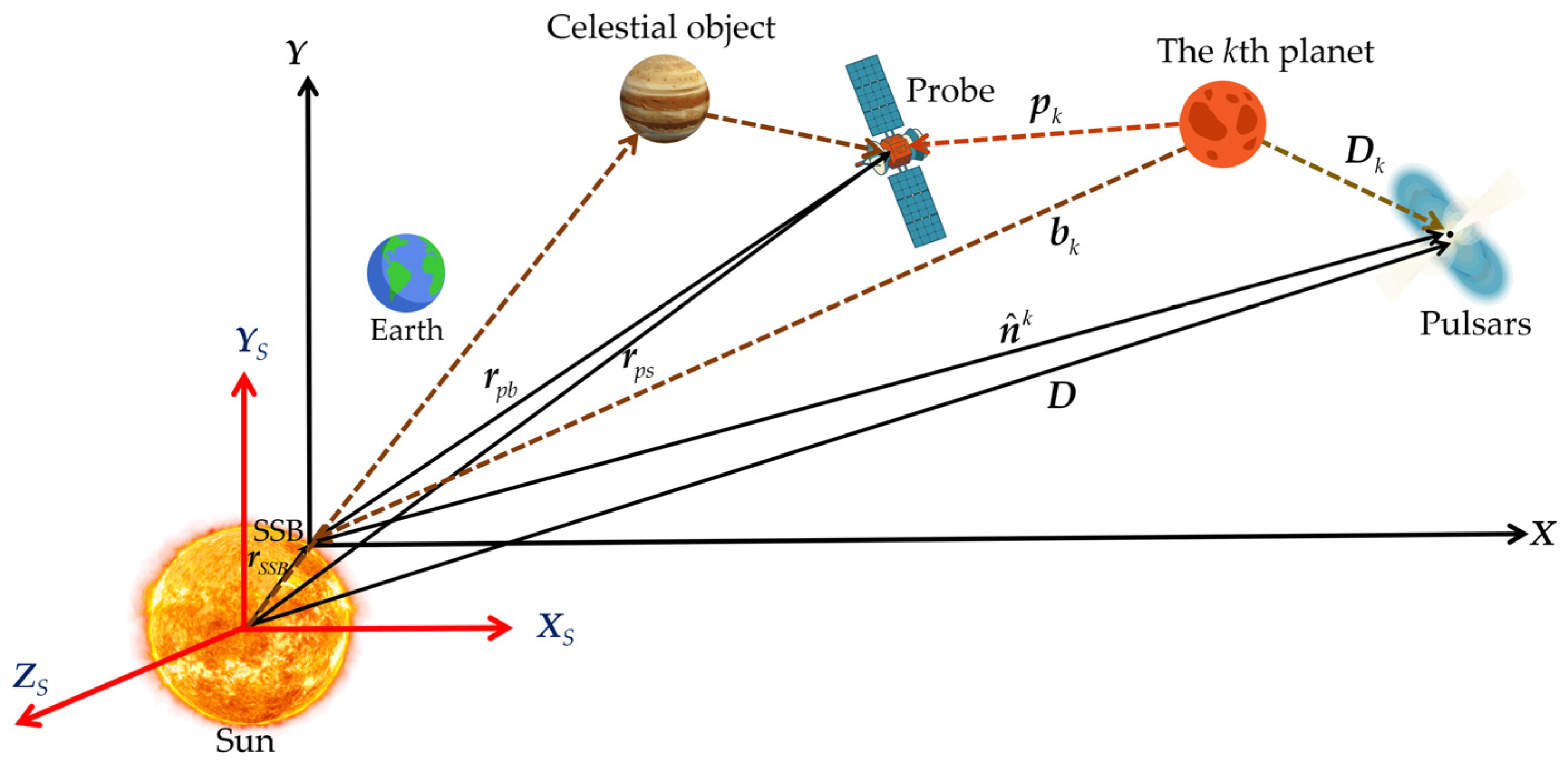
2.1. Integrated Navigation Dynamics Model

The heliocentric inertial coordinate system is chosen [43]. The orbit dynamics model [44] of the navigation system during the cruise phase for the SSBE with the Sun as the center and the large planet as the gravitational perturbations [45] is established as follows:

$$\left\{\begin{array}{l}\dot{\mathit{r}}=\mathit{v}\hfill \\ \dot{\mathit{v}}=-{\mu }_s{\displaystyle \frac{{\mathit{r}}_{ps}}{{\mathit{r}}_{ps}^3}}-{\displaystyle \sum _i^{N_p}{\mu }_i}\left[{\displaystyle \frac{{\mathit{r}}_{pi}}{r_{pi}^3}}-{\displaystyle \frac{{\mathit{r}}_{si}}{r_{si}^3}}\right]+\alpha \hfill \end{array}\right.$$

(1)

where $\mathit{r}={\left[\begin{array}{ccc}x& y& z\end{array}\right]}^T$ and $\mathit{v}={\left[\begin{array}{ccc}\dot{x}& \dot{y}& \dot{z}\end{array}\right]}^T$ are the vector of the position and velocity for the SSBE probe in the system of heliocentric inertial coordinate, respectively. µ_s is the constant of heliocentric attraction. r_ps is the vector of the relative position between the heliocentric and the SSBE probe. The gravitational constant is denoted as µ_i for the ith perturbation planet object. The vector of the relative position between the ith perturbation planet object and the probe is denoted by r_pi. The vector of the relative position between the ith perturbation planet and the heliocentric in the inertial system is denoted by r_si, ${\mathit{r}}_{si}={\mathit{r}}_{pi}+r$. N_p represents the number of planetary targets for perturbing planets. α represents a variety of disturbances in the cruise phase environment that are not modeled and can be treated as process noise.

The orbit dynamic model for the cruise phase of the Earth-to-Jupiter is expressed as follows [46].

$$\left\{\begin{array}{l}\dot{x}=v_x\\ \dot{y}=v_y\\ \dot{z}=v_z\\ {\dot{v}}_x=-{\mu }_s{\displaystyle \frac{x}{r_{ps}^3}}-{\mu }_j\left[{\displaystyle \frac{x-x_j}{r_{pj}^3}}+{\displaystyle \frac{x_j}{r_{sj}^3}}\right]-{\mu }_m\left[{\displaystyle \frac{x-x_m}{r_{pm}^3}}+{\displaystyle \frac{x_m}{r_{sm}^3}}\right]-{\mu }_e\left[{\displaystyle \frac{x-x_e}{r_{pe}^3}}+{\displaystyle \frac{x_e}{r_{se}^3}}\right]+w_x\\ {\dot{v}}_y=-{\mu }_s{\displaystyle \frac{y}{r_{ps}^3}}-{\mu }_j\left[{\displaystyle \frac{y-y_j}{r_{pj}^3}}+{\displaystyle \frac{y_j}{r_{sj}^3}}\right]-{\mu }_m\left[{\displaystyle \frac{y-y_m}{r_{pm}^3}}+{\displaystyle \frac{y_m}{r_{sm}^3}}\right]-{\mu }_e\left[{\displaystyle \frac{y-y_e}{r_{pe}^3}}+{\displaystyle \frac{y_e}{r_{se}^3}}\right]+w_y\\ {\dot{v}}_z=-{\mu }_s{\displaystyle \frac{z}{r_{ps}^3}}-{\mu }_j\left[{\displaystyle \frac{z-z_j}{r_{pj}^3}}+{\displaystyle \frac{z_j}{r_{sj}^3}}\right]-{\mu }_m\left[{\displaystyle \frac{z-z_m}{r_{pm}^3}}+{\displaystyle \frac{z_m}{r_{sm}^3}}\right]-{\mu }_e\left[{\displaystyle \frac{z-z_e}{r_{pe}^3}}+{\displaystyle \frac{z_e}{r_{se}^3}}\right]+w_z\end{array}\right.$$

(2)

Here, (x_j, y_j, z_j), (x_m, y_m, z_m), and (x_e, y_e, z_e) are the position vectors of Jupiter, Mars, and Earth, respectively. The relative positions between the center of mass of Jupiter, Mars, and Earth and the probe are denoted as r_pj, r_pm, and r_pe, respectively. The relative positions between the center of mass of Jupiter, Mars, and Earth and the heliocentric are denoted as r_sj, r_sm, and r_se, respectively.

The state variable $\mathit{X}={\left[\begin{array}{cc}{\mathit{r}}^T& {\mathit{v}}^T\end{array}\right]}^T$ is selected. The above orbital dynamics model is converted into the equation of state of the system as follows:

$$\mathit{X}\left(t\right)=f\left[\mathit{X}\left(t\right),t\right]+\mathit{\omega }\left(t\right)$$

(3)

where ω(t) is the perturbation force that is not modeled considering solar radiation pressure and other planetary bodies, ω(t) = [0, 0, 0, ω_x, ω_y, ω_z]^T. Compared to the perturbations of Sun, Jupiter, Mars, and Earth, ω_x, ω_y, and ω_z are very small and can be treated as the error noise of the system state in the dynamic model of the cruise phase. It is simplified to the state error covariance ${\widehat{\mathit{Q}}}_k$ with the zero mean white noise, ${\widehat{\mathit{Q}}}_k={\left[{\widehat{\mathit{Q}}}_{rk},{\widehat{\mathit{Q}}}_{vk}\right]}^T$.

2.2. Integrated Navigation Measurement Model

2.2.1. Navigation Measurement Model Based on X-Ray Pulsar

The X-ray pulsar navigation measurement uses the pulse TOA as the navigation measurement information, which is suitable for the probe on the SSBE mission that is an in-orbit operation for a long period of time [47]. The X-ray pulsars provide a unique pulse signal that can be detected by the X-ray sensor mounted on the probe. Figure 1 presents the fundamental principle of the X-ray pulsar measurement of the pulse TOA. The X-ray pulsar measurement is the difference between the pulse TOA observed by the X-ray sensor on the probe and the pulse TOA predicted by the pulse arrival time model on the SSB [48]. $t_{ps}^k$ is the pulse TOA of the kth X-ray pulsar measured from the probe, and $t_{SSB}^k$ is the time it takes the pulse of the kth X-ray pulsar to reach the SSB. ${\widehat{\mathit{n}}}^k$ is the line of sight direction vector of the kth pulsar along the SSB, it can be considered constant throughout the solar system [49]. r_pb is the position vector of the probe with respect to the SSB, r_pb = r_ps − r_SSB. Here, r_SSB is the position vector of the SSB relative to the center of Sun, which could be provided by the JPL DE441 ephemeris tables. c is the speed at which light travels. The offset projection reflected on $t_{SSB}^k-t_{ps}^k$ could be used to estimate the position of the probe in the following expression [27].

$$t_{SSB}^k-t_{ps}^k={\displaystyle \frac{{\widehat{\mathit{n}}}^k\cdot {\mathit{r}}_{pb}}{c}}$$

(4)

The TDOA between the pulse of the X-ray pulsar and the SSB could be used as the observation value. Considering the influences of the general relativistic effect, the time conversion model from the probe to the SSB is obtained as follows [49].

$$\begin{array}{ll}{t}_{SSB}^k-t_{ps}^k=& {\displaystyle \frac{1}{c}}{\widehat{\mathit{n}}}^k\cdot {\mathit{r}}_{pb}+{\displaystyle \frac{1}{2c{D}_0^k}}\left[{\left({\widehat{\mathit{n}}}^k\cdot {\mathit{r}}_{pb}\right)}^2+2\left({\widehat{\mathit{n}}}^k\cdot b\right)\left({\widehat{\mathit{n}}}^k\cdot {\mathit{r}}_{pb}\right)\right.\\ & \left.-2\left(\mathit{b}\cdot {\mathit{r}}_{pb}\right)-{\mathit{r}}_{pb}^2\right]+{\displaystyle \frac{2{\mu }_S}{c^3}}\ln \left|{\displaystyle \frac{{\widehat{\mathit{n}}}^k\cdot {\mathit{r}}_{pb}+‖{\mathit{r}}_{pb}‖}{{\widehat{\mathit{n}}}^k\cdot \mathit{b}+‖\mathit{b}‖}}+1\right|\end{array}$$

(5)

Here, $D_0^k$ is the range from the kth X-ray pulsar to the SSB. b is the position vector from the SSB to the heliocentric, b = r_SSB. k is the number of pulsars applied for navigation estimates, k = 1, 2, …, m. When three X-ray pulsars are observed simultaneously, the high-precision three-dimensional position estimation information could be obtained.

Assume the XNAV measurement value is ${\mathit{Z}}^X\left(t\right)$, which can be expressed as follows:

$${\mathit{Z}}^X\left(t\right)={\left[c\left(t_{SSB}^1-t_{ps}^1\right),c\left(t_{SSB}^2-t_{ps}^2\right),\cdots ,c\left(t_{SSB}^k-t_{ps}^k\right)\right]}^T$$

(6)

The observed quantity of the X-ray pulsar measurement can be expressed as follows:

$${\mathit{Z}}^X\left(t\right)={\mathit{h}}^X\left[\mathit{X}\left(t\right),t\right]+\mathit{v}\left(t\right)$$

(7)

where $\mathit{v}\left(t\right)$ is measurement noise. ${\mathit{h}}^X\left[\mathit{X}\left(t\right),t\right]$ is the XNAV measurement model, and the measurement model for multi-pulsar navigation [36] can be expressed as follows:

$${\mathit{h}}^X\left[\mathit{X}\left(t\right),t\right]={\left[{\mathit{h}}_1\left[\mathit{X}\left(t\right),t\right],\cdots ,{\mathit{h}}_i\left[\mathit{X}\left(t\right),t\right],\cdots ,{\mathit{h}}_k\left[\mathit{X}\left(t\right),t\right]\right]}^T$$

(8)

where ${\mathit{h}}_k\left[\mathit{X}\left(t\right),t\right]$ is the XNAV measurement equation for the k-th X-ray pulsar.

$$\begin{array}{ll}{\mathit{h}}^X\left[\mathit{X}\left(t\right),t\right]& =c\cdot \left(t_{SSB}-t_{SC}\right)={\widehat{\mathit{n}}}^k\cdot {\mathit{r}}_{pb}+{\displaystyle \frac{1}{2D_0^k}}\left[{\left({\widehat{\mathit{n}}}^k\cdot {\mathit{r}}_{pb}\right)}^2\right.+2\left({\widehat{\mathit{n}}}^k\cdot \mathit{b}\right)\left({\widehat{\mathit{n}}}^k\cdot {\mathit{r}}_{pb}\right)\\ & \left.-2\left(\mathit{b}\cdot {\mathit{r}}_{pb}\right)-{\mathit{r}}_{pb}^2\right]+{\displaystyle \frac{2{\mu }_S}{c^2}}\ln \left|{\displaystyle \frac{{\widehat{\mathit{n}}}^k\cdot {\mathit{r}}_{pb}+‖{\mathit{r}}_{pb}‖}{{\widehat{\mathit{n}}}^k\cdot \mathit{b}+‖\mathit{b}‖}}+1\right|\end{array}$$

(9)

The corresponding measurement matrix can be expressed as follows:

$${\mathit{H}}^X={\displaystyle \frac{\partial {\mathit{h}}^X\left[\mathit{X}\left(t\right),t\right]}{\partial \mathit{X}}}=\left[{\widehat{\mathit{n}}}^1,\cdots ,{\widehat{\mathit{n}}}^i,\cdots {\widehat{\mathit{n}}}^k\right]$$

(10)

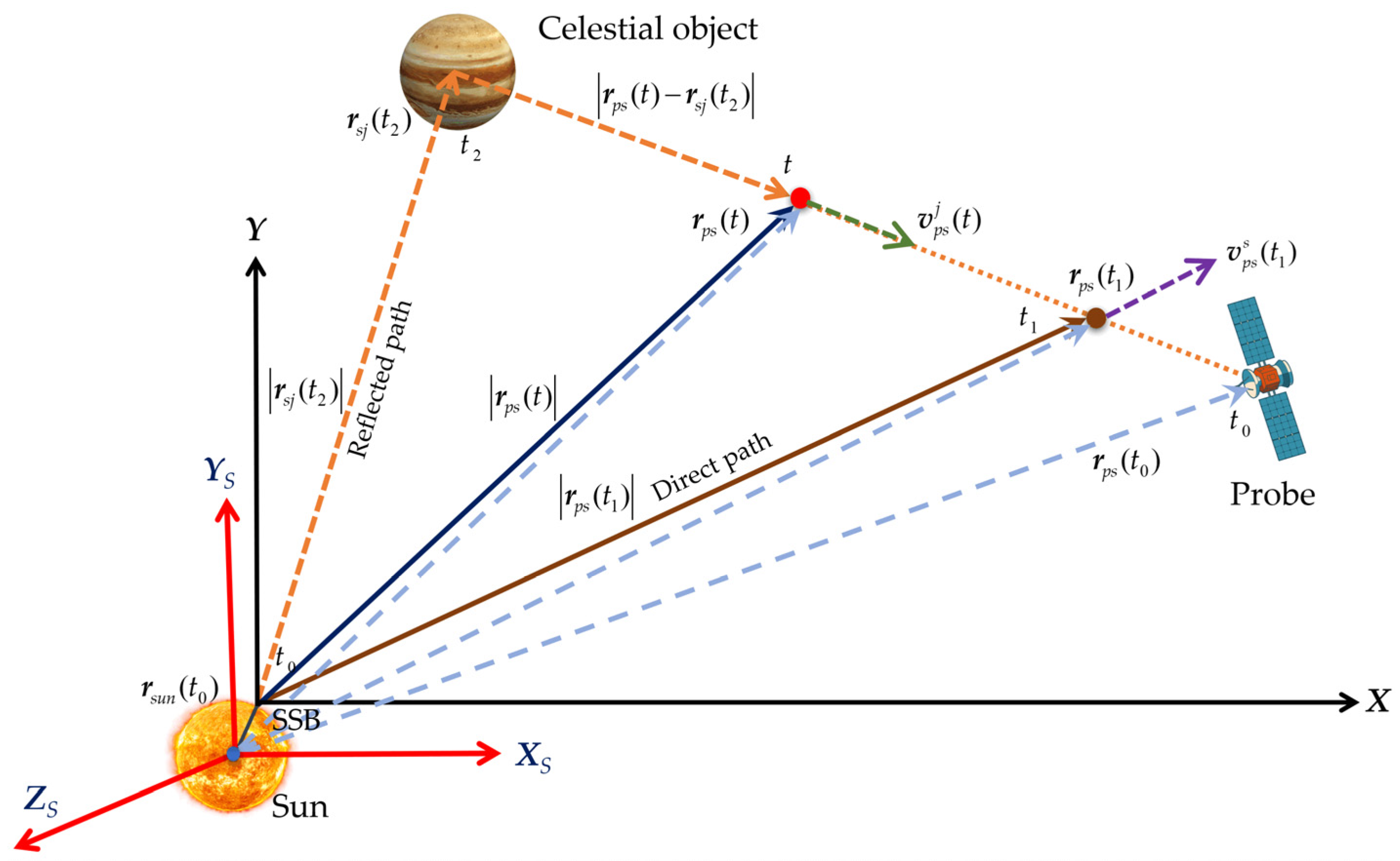
2.2.2. Navigation Measurements Model Based on Two-Dimensional Doppler Velocity

Two-dimensional Doppler velocity measurement means that the two spectrometers on the probe separately measure two radial velocities from the probe relative to Sun and the planetary target object, which are used as the velocity measurement information for the SSBE cruise phase. We adopt the two-dimensional Doppler velocity measurement based on the Sun and the target planetary bodies to compensate for the defect of the velocity estimation accuracy of the XNAV and enhance the state estimation precision for the cruise phase navigation.

The basic principle of Doppler velocity measurements based on the solar/target planetary object is shown in Figure 2. Assume that two solar photons leave the Sun at t₀ and are captured by the spectrometer on board the probe through two paths. One is received by spectrometer 1 facing the Sun at time t₁, and the position of the probe at this time is r_ps (t₁). The other one arrives at Jupiter at time t₂, where the position of Jupiter is r_sj(t₂). After it is reflected, it is received by the spectrometer 2 facing Jupiter at time t [33]. The times t₁, t₂, and t can be obtained by numerical calculations, corresponding to the velocity v_ps (t₁), v_ps (t₂), and v_ps (t) of the probe.

In the cruise phase orbit, the positions r_ps (t₀) and r_ps (t₁) of the probe at time t₀ and t₁ can be approximated as follows:

$${\mathit{r}}_{ps}\left(t_1\right)={\mathit{r}}_{ps}\left(t_0\right)+{\mathit{v}}_{ps}\left(t_0\right)\left(t_1-t_0\right)+{\displaystyle \frac{1}{2}}{\mathit{a}}_{ps}{\left(t_1-t_0\right)}^2$$

(11)

where the acceleration vector for the probe is denoted by a_ps. In the temporal interval t₀ ~ t₁, the distance traveled by the solar photon after departure from Sun is derived as follows:

$$c\left(t_1-t_0\right)=\left|{\mathit{r}}_{ps}\left(t_1\right)\right|=\left|{\mathit{r}}_{ps}\left(t_0\right)+{\mathit{v}}_{ps}\left(t_0\right)\left(t_1-t_0\right)+{\displaystyle \frac{1}{2}}{\mathit{a}}_{ps}{\left(t_1-t_0\right)}^2\right|$$

(12)

Similarly, the time t and t₂ can be calculated as follows:

$$\begin{array}{ll}c\left(t_1-t_0\right)& =\left|{\mathit{r}}_{sj}\left(t_2\right)\right|\\ c\left(t-t_0\right)& =\left|{\mathit{r}}_{sj}\left(t_2\right)\right|+\left|{\mathit{r}}_{ps}\left(t\right)-{\mathit{r}}_{sj}\left(t_2\right)\right|\\ & =\left|{\mathit{r}}_{sj}\left(t_2\right)\right|+\left|{\mathit{r}}_{ps}\left(t_0\right)+{\mathit{v}}_{ps}\left(t_0\right)\left(t-t_0\right)+{\displaystyle \frac{1}{2}}{\mathit{a}}_{ps}{\left(t_1-t_0\right)}^2-{\mathit{r}}_{sj}\left(t_2\right)\right|\end{array}$$

(13)

(1)

Solar Doppler radial velocity measurement

The radial velocity relative to the Sun and the target planetary object measured by the two spectrometers on board the probe is based on the Doppler shift principle, which can be directly used as navigation measurement information [33,36]. According to the position vector r_ps and velocity vector v_ps of the probe, its radial velocity ${\mathit{v}}_{ps}^s$ relative to the Sun can be determined as follows:

$${\mathit{v}}_{ps}^s={\displaystyle \frac{{\mathit{r}}_{ps}\left(t\right)\cdot {\mathit{v}}_{ps}\left(t\right)}{\left|{\mathit{r}}_{ps}\left(t\right)\right|}}+{\mathit{\omega }}_1\left(t\right)$$

(14)

where ${\mathit{\omega }}_1\left(t\right)$ is the Doppler measurement noise of spectrometer 1 facing the Sun. Based on the above analysis, the Doppler radial velocity measurement model of the probe relative to Sun is described as follows

$${\mathit{Z}}_D^S\left(t\right)={\mathit{h}}_D^S\left[\mathit{X}\left(t\right),t\right]+{\mathit{\omega }}_1\left(t\right)$$

(15)

The measurement equation of the Doppler radial velocity from the probe relative to the Sun is represented as follows:

$${\mathit{h}}_D^S\left[\mathit{X}\left(t\right),t\right]={\displaystyle \frac{{\mathit{r}}_{psx}\cdot {\mathit{v}}_{psx}+{\mathit{r}}_{psy}\cdot {\mathit{v}}_{psy}+{\mathit{r}}_{psz}\cdot {\mathit{v}}_{psz}}{\sqrt{{\mathit{r}}_{psx}^2+{\mathit{r}}_{psy}^2+{\mathit{r}}_{psz}^2}}}$$

(16)

The following expression can be used to represent the corresponding matrix of the observed values.

$${\mathit{H}}_D^S={\displaystyle \frac{\partial {\mathit{h}}_D^S\left[\mathit{X}\left(t\right),t\right]}{\partial \mathit{X}}}=\left[\begin{array}{c}{\displaystyle \frac{{\mathit{v}}_{ps}}{\left|{\mathit{r}}_{ps}\right|}}-{\displaystyle \frac{{\mathit{r}}_{ps}\cdot {\mathit{v}}_{ps}}{{\left|{\mathit{r}}_{ps}\right|}^3}}{\mathit{r}}_{ps}\\ {\displaystyle \frac{{\mathit{r}}_{ps}}{\left|{\mathit{r}}_{ps}\right|}}\end{array}\right]$$

(17)

(2)

Target planetary object Doppler radial velocity measurement

The radial velocity of the probe with respect to Jupiter can be measured by the spectrometer 2 facing Jupiter on the probe, for which the radial velocity measurement of the probe with respect to Jupiter can be measured.

The radial velocity measurement model measured by the probe relative to Jupiter is expressed as follows:

$${\mathit{Z}}_D^S\left(t\right)={\mathit{h}}_J^D\left[\mathit{X}\left(t\right),t\right]+{\mathit{\omega }}_2\left(t\right)$$

(18)

where ${\mathit{\omega }}_2\left(t\right)$ is the Doppler measurement noise of the spectrometer 2 oriented toward Jupiter. The corresponding velocity observation equation is expressed as follows:

$${\mathit{h}}_J^D\left[\mathit{X}\left(t\right),t\right]={\displaystyle \frac{\left({\mathit{r}}_{ps}-{\mathit{r}}_{js}\right)\cdot \left({\mathit{v}}_{ps}-{\mathit{v}}_{js}\right)}{\left|{\mathit{r}}_{ps}-{\mathit{r}}_{js}\right|}}$$

(19)

where r_js and v_js represent the position and velocity vectors of the probe, respectively, when the Sun photon arrives at Jupiter.

This measurement model corresponds to the observation matrix is expressed as follows:

$${\mathit{H}}_J^D={\displaystyle \frac{\partial h_J^D\left[\mathit{X}\left(t\right),t\right]}{\partial \mathit{X}}}=\left[\begin{array}{c}{\displaystyle \frac{{\mathit{v}}_{ps}-{\mathit{v}}_{js}}{\left|\mathit{r}{\mathit{r}}_{ps}-{\mathit{r}}_{js}\right|}}-{\displaystyle \frac{\left({\mathit{r}}_{ps}-{\mathit{r}}_{js}\right)\cdot \left({\mathit{v}}_{ps}-{\mathit{v}}_{js}\right)}{{\left|{\mathit{r}}_{ps}-{\mathit{r}}_{js}\right|}^3}}\left({\mathit{r}}_{ps}-{\mathit{r}}_{js}\right)\\ {\displaystyle \frac{{\mathit{r}}_{ps}-{\mathit{r}}_{js}}{\left|{\mathit{r}}_{ps}-{\mathit{r}}_{js}\right|}}\end{array}\right]$$

(20)

3. Intelligent Integrated Navigation Q-Learning FEKF Algorithm

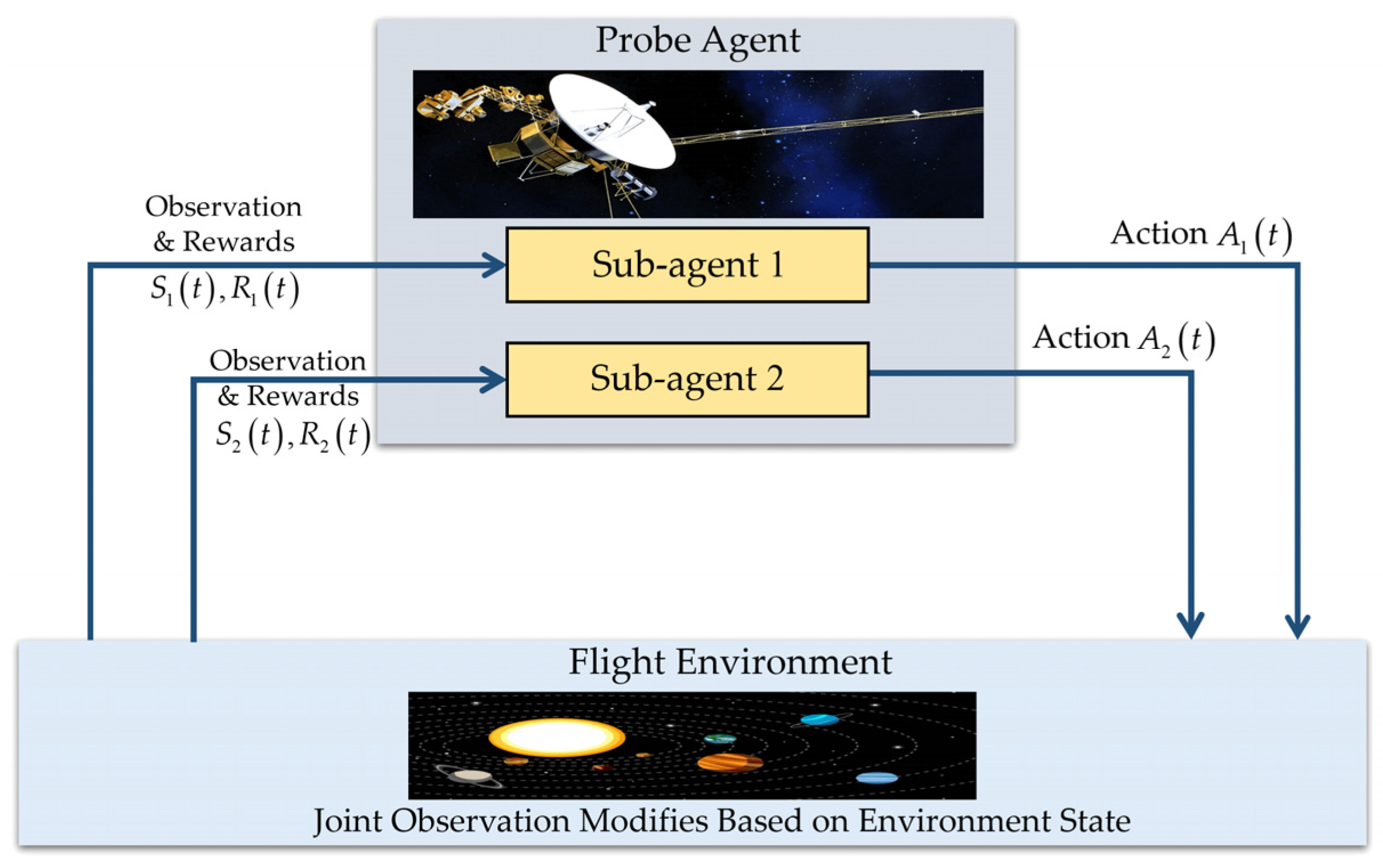
3.1. Navigation Information Fusion with the Q-Learning

In the integrated navigation scheme of the SSBE based on pulsar and solar/target planetary objects presented in the previous section, the state equation and the observational equation of the system are both nonlinear. The orbital dynamics model of the cruise phase for the SSBE shown as Equation (2) is adopted as the state transition model to forecast the next state of the probe, and it can be seen that both the X-ray pulse and solar/target planetary object Doppler velocity measurements are adopted as the measurement model for the navigation system. The EKF algorithm has a good performance for optimal state estimation for nonlinear navigation systems. The FEKF based on RL is adopted to evaluate the position and velocity for the navigation system integrating X-ray pulsar and two-dimensional Doppler velocity measurements in this research. However, the state estimation performance of the conventional federated EKF depends on the suitable state and observation noise error covariance matrices. Based on this, we attempt to combine the reinforcement Q-learning with the federated EKF, which searches for the best state and observation noise error covariance through continuous interactive trial-and-error with the environment and optimizes the error of state estimation by the QLFEKF algorithm. It can improve the navigation error precision for the probe cruise phase during long orbit run.

One of the RL methods that is most frequently applied is Q-learning [50,51,52]. With the development of intelligent autonomous navigation research, Q-learning has been applied more and more in the navigation system design [39,41]. Since the Q-learning is essential for adaptive trial-and-error optimization of the state and observation noise error covariance matrices, we briefly describe the fusion of enhanced Q-learning and navigation information. The intelligent information interaction with the operating environment for the probe agent (PA) is presented in Figure 3. The real-time in-orbit flight environment status for the probe is characterized by the state s. The various measuring instruments have their own state in the flight environment. The environment-based state of the pulsar detector is s₁(t), and the environment-based state of Doppler velocimetry spectrometer is s₂(t). The on-orbit state prediction of the PAs is characterized by the Doppler velocity spectrometer and the X-ray pulsar detector. The PA moves from the current states s₁(t) and s₂(t) to the next state and takes the corresponding actions a₁(t) and a₂(t), while receiving the corresponding rewards R₁(t) and R₂(t) from the environmental information as feedback for performing the corresponding actions in that state. In the current operational environment state in-orbit, the reward represents the good or bad action performed by the PA to choose the next state.

The PA updates its state, selects the best action in real-time according to the ε-greedy strategy, and calculates the cumulative reward. The state and observation noise matrices Q_k (t₁) and R_k (t₁), respectively, are used as the observed state s_k (t₁) for the integrated navigation sub-filter EKF in the SSBE cruise phase. When the PA enters the next operational environment state (performing action a_k (t₂)), the Q_k (t₁) and R_k (t₁) are transferred to Q_k (t₂) and R_k (t₂) (current state s_k (t₂)). The reward could be generated during the process of state transition, evaluating the PVSE errors during the cruise phase for the probe. The positive reward could reinforce the action to choose the more proper observation noise covariance error matrix. The cumulative update rules for the reward R(s_k, a_k) are as follows:

$$R\left(s_k,a_k\right)=R\left(s_{k-1},a_{k-1}\right)+{\displaystyle \frac{1}{TtCy}}\left\{{\left[{\left({\tilde{\mathit{y}}}_{ps,k}^{Tr}\right)}^T{\left({\widehat{\mathit{R}}}_k\right)}^{-1}{\tilde{\mathit{y}}}_{ps,k}^{Ex}\right]}^{-1}-R\left(s_{k-1},a_{k-1}\right)\right\}$$

(21)

where $R\left(s_{k-1},a_{k-1}\right)$ is the cumulative reward after the selection action performed in the previous state. ItCy is the learning reward iteration cycle. ${\widehat{\mathit{R}}}_k$ is the observation noise error covariance matrix corresponding to the current state. ${\left({\tilde{\mathit{y}}}_{ps,k}^{Tr}\right)}^T$ and ${\tilde{\mathit{y}}}_{ps,k}^{Ex}$ are the deviation (measurement residual) between the actual observed value and observed update value obtained by the stateful estimation calculation for the conventional EKF and searching EKF, respectively, and are closely associated with the observation noise error covariance adopted for the QLFEKF.

The accumulation of rewards is assessed using the Q-value. The reward is updated in each iteration cycle in the Q-learning algorithm, and the Q-value also is updated accordingly. The updating rules of the Q-value are expressed as follows:

$$Q\left(s_k,a_k\right)=\left(1-\alpha \right)Q\left(s_k,a_k\right)+\alpha \left[R\left(s_k,a_k\right)+\gamma \underset{a_{k+1}}{\max }Q(s_{k+1},a_{k+1})\right]$$

(22)

where Q (s_k, a_k) is the performance of performing action a_k based on flight environment state s_k for the agent. α is the learning rate, $\alpha \in \left(0,1\right]$. γ is the discount factor, $\gamma \in \left(0,1\right]$. Each time the state s changes, the corresponding action a is selected to obtain the corresponding cumulative reward R, and a corresponding Q-value is calculated. The Q-value represents the superiority of choosing action a in state s. When the Q-value corresponding to action a is greater than the Q-value corresponding to other actions that can be selected in this state, action a is the optimum selection for the current state.

The Q-table is introduced to combine Q-learning with the traditional navigation filtering method. By constructing collections for state S and collections for actions A, the Q-learning table with the grid specification M × N is established. The Q-table is utilized to determine the appropriate noise covariance matrix to enhance the efficiency of the intelligent integrated navigation system during the cruise phase. The PA tries to search the optimal state and observation noise covariance based on the Q-value calculated by the cumulative reward to optimize the federated filter. The set of states and corresponding action sets for the QLFEKF are shown in Figure 4. The process noise error covariance matrix is denoted as ${\mathit{Q}}_k^{(i)}=\left\{{\mathit{Q}}_{rk}^{(i)},{\mathit{Q}}_{vk}^{(i)}\right\}$, i = 1, 2, …, m. ${\mathit{Q}}_{rk}^{(i)}$ and ${\mathit{Q}}_{vk}^{(i)}$ represent the position and velocity state noise covariance information, respectively. The measurement noise error covariance matrix is denoted as ${\mathit{R}}_k^{(j)}=\left\{{\mathit{R}}_{pk}^{(j)},{\mathit{R}}_{dk}^{(j)}\right\}$ j = 1, 2, …, n. ${\mathit{R}}_{pk}^{(j)}$ and ${\mathit{R}}_{dk}^{(j)}$ represent the measurement error covariance information of the pulsar detectors and Doppler spectrometers, respectively. The state set of the Q-table is represented as ${\mathit{S}}^{(ij)}=\left\{{\mathit{Q}}_{rk}^{(i)},{\mathit{Q}}_{vk}^{(i)},{\mathit{R}}_{pk}^{(j)},{\mathit{R}}_{dk}^{(j)}\right\}$, which is distributed in a grid of M rows and N columns. These are divided into three state types, including corner regions (such as S⁽¹¹⁾, S^(m1), S⁽¹ⁿ⁾, and S^(mn)), edge regions (such as S⁽ⁱ¹⁾, S^(1j), S⁽ⁱⁿ⁾, and S^(mj), i ≠ 1, m − 1, j ≠ 1, n − 1) and the central region (S^(ij), i ≠ 1, m − 1 and j ≠ 1, n − 1). The process of state transition defines the actions A set with up direction (↑), down direction (↓), left direction (←), and right direction (→), which is represented by A = {0 ↑, 1 ↓, 2 ←, 3 →}. The actions that could be selected for the corner regions (top left, bottom left, top right, bottom right) are A_{corner_tl} = {1, 3}, A_{corner_bl} = {0, 3}, A_{corner_tr} = {1, 2}, and A_{corner_br} = {0, 2}; the edge regions (up, down, left, right) are A_{edge_u} = {1, 2, 3}, A_{edge_d} = {0, 2, 3}, A_{edge_l} = {0, 1, 3}, and A_{edge_r} = {0, 1, 2}; and the central region is A_center = {0, 1, 2, 3}.

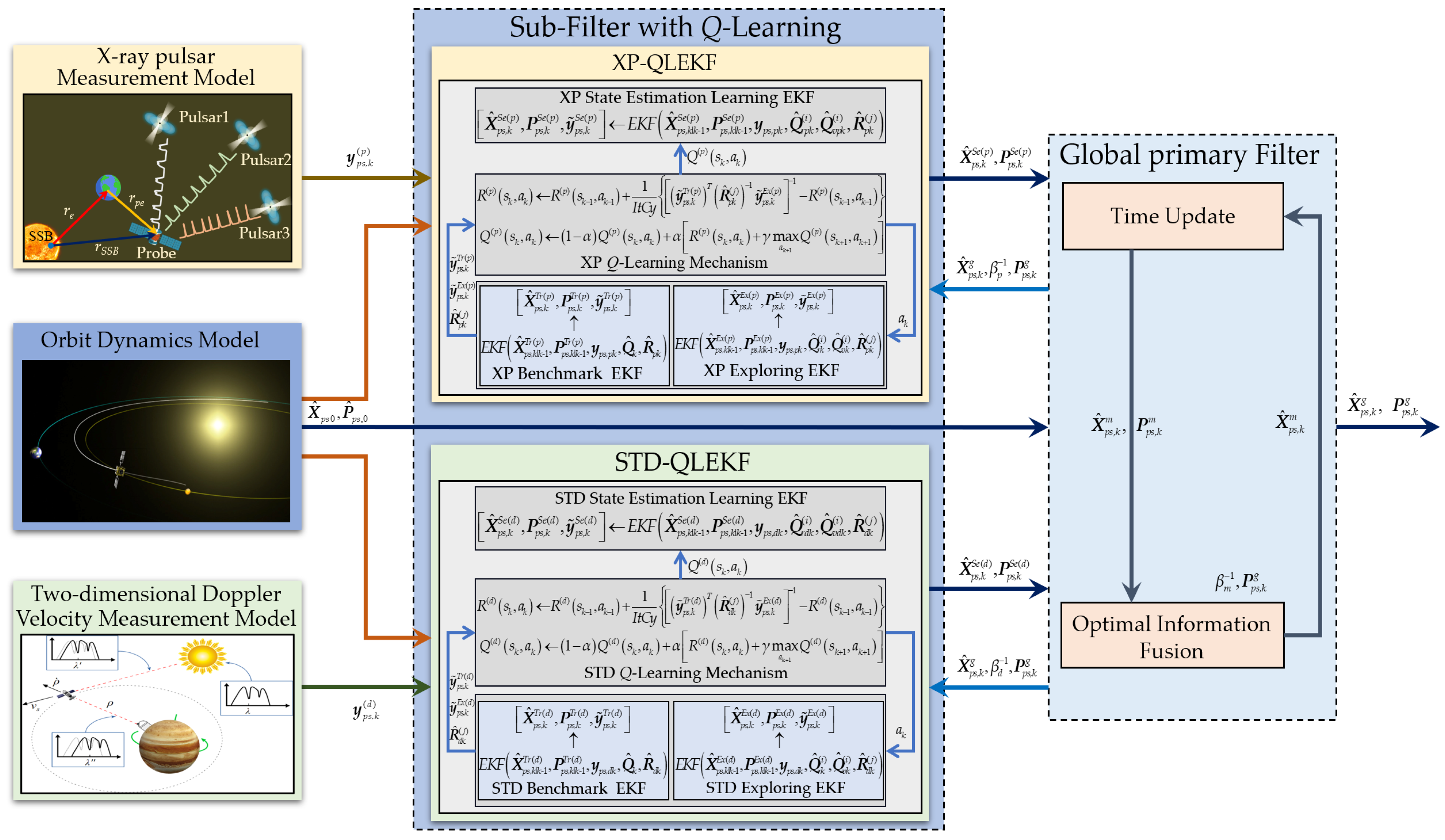
3.2. Design of the Q-Learning-Based FKF for Intelligent Integrated Navigation

The Q-learning-based FEKF navigation algorithm is designed based on the dynamics and measurement model established in Section 2.1 and Section 2.2, and the updated cumulative reward criteria of the Q-learning shown in Equation (21). The Q-learning and federated EKF are deeply integrated, and the X-ray pulsar and Doppler velocity measurement sub-filter parameters are trial-and-error and fine-tuned to improve the PVSE precision of the intelligent integrated navigation for the cruise phase. The state process and observation noise error covariance matrices related to the dynamic and measurement model are both crucial filtering parameters that affect the state estimation precision and performance for the intelligent integrated FEKF navigation system. Thus, the QLFEKF algorithm is adopted to adjust the state and observation noise error covariance matrices in real-time to accurately assess the PVSE precision of the in-orbit operation probe during the cruise phase.

According to the above description, the implementation process of the QLFEKF is given in Algorithm 1.

Algorithm 1: The Q-learning-based FEKF algorithm of the intelligent integrated navigation system
Input:	Initial state estimation ${\widehat{\mathit{X}}}_{ps,0}$, error covariance matrix Pps,0, predetermined set of the noise covariance matrix error initial values ${\widehat{\mathit{Q}}}_0,{\widehat{\mathit{Q}}}_{p0},{\widehat{\mathit{Q}}}_{d0}$, and learning parameter α, γ, ε
Step 1:	Initialize variables, ${\widehat{\mathit{X}}}_{ps,0}^{Tr\left(p\right)}={\widehat{\mathit{X}}}_{ps,0}^{Ex\left(p\right)}={\widehat{\mathit{X}}}_{ps,0}^{Se\left(p\right)}\leftarrow {\widehat{\mathit{X}}}_{ps,0},{\widehat{\mathit{X}}}_{ps,0}^{Tr\left(d\right)}={\widehat{\mathit{X}}}_{ps,0}^{Ex\left(d\right)}={\widehat{\mathit{X}}}_{ps,0}^{Se\left(d\right)}\leftarrow {\widehat{\mathit{X}}}_{ps,0},{\widehat{\mathit{X}}}_{ps,0}^g\leftarrow {\widehat{\mathit{X}}}_{ps,0},$${\mathit{P}}_{ps,0}^{Tr}={\mathit{P}}_{ps,0}^{Ex}={\mathit{P}}_{ps,0}^{Se}\leftarrow {\mathit{P}}_{ps,0},{\mathit{P}}_{ps,0}^g\leftarrow {\mathit{P}}_{ps,0}$
Step 2:	Time index initialization $k\leftarrow 0$
Step 3:	For the specified time of the navigation
Step 4:	Set state and action, for all construct state sets $s\in \mathit{S}$, the action set $a\in \mathit{A}$
Step 5:	Environment state initialization $s_k\leftarrow s_0$, Q-value $Q^{(p)}(s_k,a_k)\leftarrow 0,R^{(p)}\left(s_k,a_k\right)\leftarrow 0$, and reward initialization $Q^{(d)}(s_k,a_k)\leftarrow 0,R^{(d)}\left(s_k,a_k\right)\leftarrow 0$
Step 6:	Set the initial noise error covariance matrix ${\widehat{\mathit{Q}}}_{rk}\leftarrow {\widehat{\mathit{Q}}}_{r0},{\widehat{\mathit{Q}}}_{vk}\leftarrow {\widehat{\mathit{Q}}}_{v0}$, and ${\widehat{\mathit{Q}}}_k\leftarrow [{\widehat{\mathit{Q}}}_{rk},{\widehat{\mathit{Q}}}_{vk}]$; ${\widehat{\mathit{R}}}_{pk}\leftarrow {\widehat{\mathit{R}}}_{p0},{\widehat{\mathit{R}}}_{dk}\leftarrow {\widehat{\mathit{R}}}_{d0}$
Step 7:	Generated randomly the noise error covariance matrix ${\widehat{\mathit{Q}}}_{rk}^{(i)}\in \left[{\underset{\_}{q}}_{rk}\ast {\widehat{\mathit{Q}}}_{r0},{\overline{q}}_{rk}\ast {\widehat{\mathit{Q}}}_{r0}\right]$,${\widehat{\mathit{Q}}}_{vk}^{(i)}\in \left[{\underset{\_}{q}}_{vk}\ast {\widehat{\mathit{Q}}}_{v0},{\overline{q}}_{vk}\ast {\widehat{\mathit{Q}}}_{v0}\right],{\widehat{\mathit{R}}}_{pk}\in \left[{\underset{\_}{r}}_{pk}\ast {\widehat{\mathit{R}}}_{p0},{\overline{r}}_{pk}\ast {\widehat{\mathit{R}}}_{p0}\right],{\widehat{\mathit{R}}}_{dk}\in \left[{\underset{\_}{r}}_{dk}\ast {\widehat{\mathit{R}}}_{d0},{\overline{r}}_{dk}\ast {\widehat{\mathit{R}}}_{d0}\right]$
Step 8:	ε-greedy strategy ak ← ε-greedy (sk, A, Q (sk, ak), ε) choose action ak for state sk
Step 9:	Execute action ak and observe arrived the next states ${s^{\prime }}_k$
Step 10:	For each time step ItCy = 1, 2, …, T in one iteration, do
Step 11:	k ← k + 1
Step 12:	$\left[{\widehat{\mathit{X}}}_{ps,k}^{Tr(p)},{\mathit{P}}_{ps,k}^{Tr(p)},{\tilde{\mathit{y}}}_{ps,k}^{Tr(p)}\right]\leftarrow EKF\left({\widehat{\mathit{X}}}_{ps,k|k-1}^{Tr(p)},{\mathit{P}}_{ps,k|k-1}^{Tr(p)},{\mathit{y}}_{ps,pk},{\widehat{\mathit{Q}}}_k,{\widehat{\mathit{R}}}_{pk}\right)⊳$XP benchmark     $\left[{\widehat{\mathit{X}}}_{ps,k}^{Tr(d)},{\mathit{P}}_{ps,k}^{Tr(d)},{\tilde{\mathit{y}}}_{ps,k}^{Tr(d)}\right]\leftarrow EKF\left({\widehat{\mathit{X}}}_{ps,k|k-1}^{Tr(d)},{\mathit{P}}_{ps,k|k-1}^{Tr(d)},{\mathit{y}}_{ps,dk},{\widehat{\mathit{Q}}}_k,{\widehat{\mathit{R}}}_{dk}\right)⊳$STD benchmark
Step 13:	${\widehat{\mathit{Q}}}_{rk}^{(i)},{\widehat{\mathit{Q}}}_{vk}^{(i)},{\widehat{\mathit{R}}}_{pk}^{(j)}$ and ${\widehat{\mathit{R}}}_{dk}^{(j)}$ are determined according to the current state sk
Step 14:	$\left[{\widehat{\mathit{X}}}_{ps,k}^{Ex(p)},{\mathit{P}}_{ps,k}^{Ex(p)},{\tilde{\mathit{y}}}_{ps,k}^{Ex(p)}\right]\leftarrow EKF\left({\widehat{\mathit{X}}}_{ps,k|k-1}^{Ex(p)},{\mathit{P}}_{ps,k|k-1}^{Ex(p)},{\mathit{y}}_{ps,pk},{\widehat{\mathit{Q}}}_{rk}^{(i)},{\widehat{\mathit{Q}}}_{vk}^{(i)},{\widehat{\mathit{R}}}_{pk}^{(j)}\right)⊳$XP searching     $\left[{\widehat{\mathit{X}}}_{ps,k}^{Ex(d)},{\mathit{P}}_{ps,k}^{Ex(d)},{\tilde{\mathit{y}}}_{ps,k}^{Ex(d)}\right]\leftarrow EKF\left({\widehat{\mathit{X}}}_{ps,k|k-1}^{Ex(d)},{\mathit{P}}_{ps,k|k-1}^{Ex(d)},{\mathit{y}}_{ps,dk},{\widehat{\mathit{Q}}}_{rk}^{(i)},{\widehat{\mathit{Q}}}_{vk}^{(i)},{\widehat{\mathit{R}}}_{dk}^{(j)}\right)⊳$STD searching
Step 15:	$R^{(p)}\left(s_k,a_k\right)\leftarrow R^{(p)}\left(s_{k-1},a_{k-1}\right)+{\displaystyle \frac{1}{ItCy}}\left\{{\left[{\left({\tilde{\mathit{y}}}_{ps,k}^{Tr(p)}\right)}^T{\left({\widehat{\mathit{R}}}_{pk}^{(j)}\right)}^{-1}{\tilde{\mathit{y}}}_{ps,k}^{Ex(p)}\right]}^{-1}-R^{(p)}\left(s_{k-1},a_{k-1}\right)\right\}⊳$XP rewards     $R^{(d)}\left(s_k,a_k\right)\leftarrow R^{(d)}\left(s_{k-1},a_{k-1}\right)+{\displaystyle \frac{1}{ItCy}}\left\{{\left[{\left({\tilde{\mathit{y}}}_{ps,k}^{Tr(d)}\right)}^T{\left({\widehat{\mathit{R}}}_{dk}^{(j)}\right)}^{-1}{\tilde{\mathit{y}}}_{ps,k}^{Ex(d)}\right]}^{-1}-R^{(d)}\left(s_{k-1},a_{k-1}\right)\right\}⊳$STD rewards
Step 16:	$\begin{array}{l}{\mathit{P}}_{ps,k-1}^{Se(p)}\leftarrow {\beta }_p^{-1}{\mathit{P}}_{ps,k-1}^g,{\widehat{\mathit{Q}}}_{rpk}^{(i)}\leftarrow {\beta }_p^{-1}{\widehat{\mathit{Q}}}_{rk}^{(i)},{\widehat{\mathit{Q}}}_{vpk}^{(i)}\leftarrow {\beta }_p^{-1}{\widehat{\mathit{Q}}}_{vk}^{(i)}\\ {\mathit{P}}_{ps,k-1}^{Se(d)}\leftarrow {\beta }_d^{-1}{\mathit{P}}_{ps,k-1}^g,{\widehat{\mathit{Q}}}_{rdk}^{(i)}\leftarrow {\beta }_d^{-1}{\widehat{\mathit{Q}}}_{rk}^{(i)},{\widehat{\mathit{Q}}}_{vdk}^{(i)}\leftarrow {\beta }_d^{-1}{\widehat{\mathit{Q}}}_{vk}^{(i)}\\ {\mathit{P}}_{ps,k-1}^m\leftarrow {\beta }_m^{-1}{\mathit{P}}_{ps,k-1}^g,{\widehat{\mathit{Q}}}_k^m\leftarrow {\beta }_m^{-1}{\widehat{\mathit{Q}}}_k\\ {\widehat{\mathit{X}}}_{ps,k-1}^{Se(p)}\leftarrow {\widehat{\mathit{X}}}_{ps,k-1}^g,{\widehat{\mathit{X}}}_{ps,k-1}^{Se(d)}\leftarrow {\widehat{\mathit{X}}}_{ps,k-1}^g,{\widehat{\mathit{X}}}_{ps,k-1}^m\leftarrow {\widehat{\mathit{X}}}_{ps,k-1}^g\end{array}$$⊳$Information distribution weight
Step 17:	$\begin{array}{l}{\widehat{\mathit{X}}}_{ps,k|k-1}^{Se(p)}\leftarrow {\Phi }_{ps,k|k-1}^{Se(p)}{\widehat{\mathit{X}}}_{ps,k-1}^{Se(p)},{\mathit{P}}_{ps,k|k-1}^{Se(p)}\leftarrow {\Phi }_{ps,k|k-1}^{Se(p)}{\mathit{P}}_{ps,k-1}^{Se(p)}{\left({\Phi }_{ps,k|k-1}^{Se(p)}\right)}^T+{\widehat{\mathit{Q}}}_{pk}^{Se(i)}\\ {\widehat{\mathit{X}}}_{ps,k|k-1}^{Se(d)}\leftarrow {\Phi }_{ps,k|k-1}^{Se(d)}{\widehat{\mathit{X}}}_{ps,k-1}^{Se(d)},{\mathit{P}}_{ps,k|k-1}^{Se(d)}\leftarrow {\Phi }_{ps,k|k-1}^{Se(d)}{\mathit{P}}_{ps,k-1}^{Se(d)}{\left({\Phi }_{ps,k|k-1}^{Se(d)}\right)}^T+{\widehat{\mathit{Q}}}_{dk}^{Se(i)}\\ {\widehat{\mathit{X}}}_{ps,k|k-1}^m\leftarrow {\Phi }_{ps,k|k-1}^m{\widehat{\mathit{X}}}_{ps,k-1}^m,{\mathit{P}}_{ps,k|k-1}^m\leftarrow {\Phi }_{ps,k|k-1}^m{\mathit{P}}_{ps,k-1}^m{\left({\Phi }_{ps,k|k-1}^m\right)}^T+{\widehat{\mathit{Q}}}_k^m\end{array}$$⊳$Time update
Step 18:	$\left[{\widehat{\mathit{X}}}_{ps,k}^{Se(p)},{\mathit{P}}_{ps,k}^{Se(p)},{\tilde{\mathit{y}}}_{ps,k}^{Se(p)}\right]\leftarrow EKF\left({\widehat{\mathit{X}}}_{ps,k|k-1}^{Se(p)},{\mathit{P}}_{ps,k|k-1}^{Se(p)},{\mathit{y}}_{ps,pk},{\widehat{\mathit{Q}}}_{rpk}^{(i)},{\widehat{\mathit{Q}}}_{vpk}^{(i)},{\widehat{\mathit{R}}}_{pk}^{(j)}\right)⊳$XP measurement update     $\left[{\widehat{\mathit{X}}}_{ps,k}^{Se(d)},{\mathit{P}}_{ps,k}^{Se(d)},{\tilde{\mathit{y}}}_{ps,k}^{Se(d)}\right]\leftarrow EKF\left({\widehat{\mathit{X}}}_{ps,k|k-1}^{Se(d)},{\mathit{P}}_{ps,k|k-1}^{Se(d)},{\mathit{y}}_{ps,dk},{\widehat{\mathit{Q}}}_{rdk}^{(i)},{\widehat{\mathit{Q}}}_{vdk}^{(i)},{\widehat{\mathit{R}}}_{dk}^{(j)}\right)⊳$STD measurement update
Step 19:	$\begin{array}{l}{\mathit{P}}_{ps,k}^g\leftarrow {\left[{\left({\mathit{P}}_{ps,k}^{Se(p)}\right)}^{-1}+{\left({\mathit{P}}_{ps,k}^{Se(d)}\right)}^{-1}+{\left({\mathit{P}}_{ps,k}^m\right)}^{-1}\right]}^{-1}\\ {\widehat{\mathit{X}}}_{ps,k}^g\leftarrow {\mathit{P}}_{ps,k}^g\left[{\left({\mathit{P}}_{ps,k}^{Se(p)}\right)}^{-1}{\widehat{\mathit{X}}}_{ps,k}^{Se(p)}+{\left({\mathit{P}}_{ps,k}^{Se(d)}\right)}^{-1}{\widehat{\mathit{X}}}_{ps,k}^{Se(d)}+{\left({\mathit{P}}_{ps,k}^m\right)}^{-1}{\widehat{\mathit{X}}}_{ps,k}^m\right]\end{array}$$⊳$Information fusion
Step 20:	End for
Step 21:	$Q^{(p)}\left(s_k,a_k\right)\leftarrow \left(1-\alpha \right)Q^{(p)}\left(s_k,a_k\right)+\alpha \left[R^{(p)}\left(s_k,a_k\right)+\gamma \underset{a_{k+1}}{max}{Q}^{(p)}\left(s_{k+1},a_{k+1}\right)\right]⊳$XP Q-value   $Q^{(d)}\left(s_k,a_k\right)\leftarrow \left(1-\alpha \right)Q^{(d)}\left(s_k,a_k\right)+\alpha \left[R^{(d)}\left(s_k,a_k\right)+\gamma \underset{a_{k+1}}{max}{Q}^{(d)}\left(s_{k+1},a_{k+1}\right)\right]⊳$STD Q-value
Step 22:	Set ${s^{\prime }}_k$ as the current state $s_k\leftarrow {s^{\prime }}_k$
Step 23:	$R^{(p)}\left(s_k,a_k\right)\leftarrow 0,R^{(d)}\left(s_k,a_k\right)\leftarrow 0⊳$Reset reward
Step 24:	${\widehat{\mathit{X}}}_{ps,k}^{Ex(p)}\leftarrow {\widehat{\mathit{X}}}_{ps,k}^{Tr(p)},{\mathit{P}}_{ps,k}^{Ex(p)}\leftarrow {\mathit{P}}_{ps,k}^{Tr(p)},{\widehat{\mathit{X}}}_{ps,k}^{Ex(d)}\leftarrow {\widehat{\mathit{X}}}_{ps,k}^{Tr(d)},{\mathit{P}}_{ps,k}^{Ex(d)}\leftarrow {\mathit{P}}_{ps,k}^{Tr(d)}$ Reset searching EKF
Step 25:	End for
Output:	Return as state estimate ${\widehat{\mathit{X}}}_{ps,k}\leftarrow {\widehat{\mathit{X}}}_{ps,k}^g$ and ${\mathit{P}}_{ps,k}\leftarrow {\mathit{P}}_{ps,k}^g$

In Algorithm 1, the initial information includes the estimation error covariance matrix ${\widehat{\mathit{X}}}_{ps,0}$, the state noise error covariance matrix ${\widehat{\mathit{Q}}}_0=\left({\widehat{\mathit{Q}}}_{r0},{\widehat{\mathit{Q}}}_{v0}\right)$ of the system, and the observation noise error covariance matrix $\left({\widehat{\mathit{R}}}_{p0},{\widehat{\mathit{R}}}_{d0}\right)$ at the initial time. α represents the learning rate of the Q-learning, γ represents the learning rate of the Q-learning, and ε represents the action selection probability of the Q-learning, which can be applied to regulate the performance of the learning for the reinforcement Q-learning. The specific time of the navigation in step 3 refers to the navigation time for the cruise phase. In step 7, the state process (including PVSE) and observation (including the X-ray pulsar detector and two Doppler velocity-measuring spectrometers) noise error covariance matrix are randomly generated within the set range corresponding to the initial values of the noise error covariance matrix. ${\underset{\_}{q}}_{rk}$ and ${\overline{q}}_{rk}$ are the upper edge and lower edge bounds for the position state noise covariance matrix of the system error, respectively. ${\underset{\_}{q}}_{vk}$ and ${\overline{q}}_{vk}$ are the upper edge and lower edge bounds for the velocity state noise covariance matrix of the system error, respectively. The ε-greed strategy is involved in step 8, which is determined by the cumulative rewards [R^(p)(s_k, a_k), R^(d)(s_k, a_k)] and Q-values [Q^(p)(s_k, a_k), Q^(d)(s_k, a_k)] calculated from different state s_k and action a_k. The PA selects the random action according to the probability of choice action ε and selects the action to maximize the Q-value with the probability of the (1 − ε). The learning strategy has good stability for the PA to select the most suitable noise covariance matrix. ItCy is the period of time for the calculation of cumulative rewards. If ItCy is small, the weight and cumulative rewards for each update will be large, so the design of the ItCy should not be too small.

In step 12, ${\widehat{\mathit{X}}}_{ps,k}^{Tr(p)}$ and ${\widehat{\mathit{X}}}_{ps,k}^{Tr(d)}$ represent the state estimate values corresponding the sub-filter in the benchmark EKF for the X-ray pulsar and Doppler, respectively. ${\mathit{P}}_{ps,k}^{Tr(p)}$ and ${\mathit{P}}_{ps,k}^{Tr(d)}$ represent the state transition matrix corresponding to the benchmark EKF, respectively. ${\tilde{\mathit{y}}}_{ps,k}^{Tr(p)}$ and ${\tilde{\mathit{y}}}_{ps,k}^{Tr(d)}$ represent the measured innovation information corresponding to the benchmark EKF, respectively. Innovation information in the benchmark EKF and search EKF are important parameters of the Q-learning reward evaluation. ${\widehat{\mathit{Q}}}_{rk}^{\left(i\right)}$, ${\widehat{\mathit{Q}}}_{vk}^{\left(i\right)}$, ${\widehat{\mathit{R}}}_{pk}^{\left(j\right)}$, and ${\widehat{\mathit{R}}}_{dk}^{\left(j\right)}$ are determined according to the current state s_k. In step 14, ${\widehat{\mathit{X}}}_{ps,k}^{Ex(p)}$ and ${\widehat{\mathit{X}}}_{ps,k}^{Ex(d)}$ are state estimates for the searching EKF in the X-ray pulsars sub-filters and Doppler sub-filters, respectively. ${\mathit{P}}_{ps,k}^{Ex(p)}$ and ${\mathit{P}}_{ps,k}^{Ex(d)}$ represent the state transition matrix corresponding to the searching EKF, respectively. ${\tilde{\mathit{y}}}_{ps,k}^{Ex(p)}$ and ${\tilde{\mathit{y}}}_{ps,k}^{Ex(d)}$ represent the measurement innovation information corresponding to the searching EKF, respectively. In step 15, the cumulative reward of the QLEKF based on the X-ray pulsar and Doppler during the iteration period is calculated, and the Q-value is determined according to the sizes of the reward $R^{(p)}\left(s_k,a_k\right)$ and $R^{(d)}\left(s_k,a_k\right)$. A positive reward is received for suitable ${\widehat{\mathit{Q}}}_{rk}^{\left(i\right)}$, ${\widehat{\mathit{Q}}}_{vk}^{\left(i\right)}$, ${\widehat{\mathit{R}}}_{pk}^{\left(j\right)}$, and ${\widehat{\mathit{R}}}_{dk}^{\left(j\right)}$, and a negative reward is received for unsuitable ${\widehat{\mathit{Q}}}_{rk}^{\left(i\right)}$, ${\widehat{\mathit{Q}}}_{vk}^{\left(i\right)}$, ${\widehat{\mathit{R}}}_{pk}^{\left(j\right)}$, and ${\widehat{\mathit{R}}}_{dk}^{\left(j\right)}$. In step 16, the weights of the X-ray pulsar, Doppler sub-filter, and the main filter are designed and distributed information. In steps 17 and 18, the corresponding time information update and measurement information update of federated filtering are mainly carried out. ${\widehat{\mathit{X}}}_{ps,k}^{Se(p)}$ and ${\widehat{\mathit{X}}}_{ps,k}^{Se(d)}$ are the state estimates for the measurement updated EKF for the X-ray pulsars sub-filters and Doppler sub-filters, respectively. ${\mathit{P}}_{ps,k}^{Se(p)}$ and ${\mathit{P}}_{ps,k}^{Se(d)}$ are the state transition matrices corresponding to the measurement update EKF, respectively. ${\tilde{\mathit{y}}}_{ps,k}^{Se(p)}$ and ${\tilde{\mathit{y}}}_{ps,k}^{Se(d)}$ are the measurement innovation information corresponding to the measurement update EKF, respectively. In step 19, information fusion is performed on the state estimation of the sub-filter based on the X-ray pulsar, the sub-filter based on Doppler and the main filter. The detailed design process of the federated filtering algorithm in steps 16~19 are given below. The cumulative rewards are gained at the end of the iteration cycle. The value of the Q-value is calculated according to the cumulative reward from the innovation information of filtering, and the corresponding Q-value for each set of the state-action pair (s_k, a_k) is stored in the Q-table. According to the Q-values corresponding to different actions in the current state, the best action is selected to reach the next best state, and the corresponding selection locates the state and observation noise variance matrices.

The structure diagram of the Q-learning-based FEKF intelligent integrated navigation system is shown in Figure 5. The observation information of the X-ray pulsar and Doppler velocity-measuring is fused by the QLFEKF. The reinforcement Q-learning-based EKF is used as the sub-filter for the X-ray pulsar and Doppler velocity-measuring navigation system, and each sub-filter is composed of the benchmark filter, searching filter, and state estimation learning filter. The two sub-filters work in parallel, the output locally optimal state estimates ${\widehat{\mathit{X}}}_{ps,k}^{Se(p)}$ and ${\widehat{\mathit{X}}}_{ps,k}^{Se(d)}$ as well as the error covariance matrices ${\mathit{P}}_{ps,k}^{Se(p)}$ and ${\mathit{P}}_{ps,k}^{Se(d)}$, which are used as inputs to the global master-filter for information fusion periodically. Finally, the global optimal state estimation ${\widehat{\mathit{X}}}_{ps,k}^g$ and error covariance ${\mathit{P}}_{ps,k}^g$ are obtained. The global primary filter system performs fusion estimation according to the estimation information of the sub-filter system and assigns the fusion estimation information to the sub-filter according to the design weight by using the information distribution principle. The single-step intelligent federated filtering process is realized to obtain the current state estimation information.

The information distribution process is that the global main filter and two sub-filters allocate state estimation information according to a certain weight. The information distribution principle between the main filter and each sub-filter is as follows:

$$\left\{\begin{array}{l}{\widehat{\mathit{Q}}}_{nk}^{(i)}={\beta }_n^{-1}{\widehat{\mathit{Q}}}_k^{(i)},{\widehat{\mathit{Q}}}_k^m={\beta }_m^{-1}{\widehat{\mathit{Q}}}_k\\ {\mathit{P}}_{ps,k}^{Se(n)}={\beta }_n^{-1}{\mathit{P}}_{ps,k}^g,{\mathit{P}}_{ps,k}^m={\beta }_m^{-1}{\mathit{P}}_{ps,k}^g\\ {\widehat{\mathit{X}}}_{ps,k}^{Se(n)}={\widehat{\mathit{X}}}_{ps,k}^g,{\widehat{\mathit{X}}}_{ps,k}^m={\widehat{\mathit{X}}}_{ps,k}^g\end{array}\right.,n=p,d$$

(23)

where ${\beta }_m$ and ${\beta }_n$ are the information distribution coefficients of the parallel sub-filter and primary filter, respectively, ${\beta }_m,{\beta }_n\in \left(0,1\right],n=1,2,\cdots$. Here the principle of conservation of the information distribution is satisfied, ${\displaystyle \sum ^n{\beta }_m+{\beta }_n}=1$.

The QLFEKF information update includes time update and measurement update, in which the update of time is updated autonomously in the parallel sub-filter and primary filter, the specific update process is as follows:

$$\left\{\begin{array}{l}{\widehat{\mathit{X}}}_{ps,k|k-1}^{Se(n)}={\Phi }_{ps,k|k-1}^{Se(n)}{\widehat{\mathit{X}}}_{ps,k-1}^{Se(p)}\\ {\mathit{P}}_{ps,k|k-1}^{Se(n)}={\Phi }_{\mathit{p}s,k|k-1}^{Se(n)}{\mathit{P}}_{ps,k-1}^{Se(n)}{\left({\Phi }_{ps,k|k-1}^{Se(n)}\right)}^T+{\widehat{\mathit{Q}}}_{nk}^{(i)}\\ {\widehat{\mathit{X}}}_{ps,k|k-1}^m={\Phi }_{ps,k|k-1}^m{\widehat{\mathit{X}}}_{ps,k-1}^m\\ {\mathit{P}}_{ps,k|k-1}^m={\Phi }_{ps,k|k-1}^m{\mathit{P}}_{ps,k-1}^m{\left({\Phi }_{ps,k|k-1}^m\right)}^T+{\widehat{\mathit{Q}}}_k^m\end{array}\right.$$

(24)

Since there is not measurement information in the global main filter, the measurement information is located in the parallel sub-filter and is only carried out in the state estimation learning filter in the sub-filter. The specific update process is described as follows:

$$\left\{\begin{array}{l}{K}_k^{Se(n)}={\mathit{P}}_{ps,k}^{Se(n)}{\left(H_{ps,k}^{Se(n)}\right)}^T{\left[H_{ps,k}^{Se(n)}{\mathit{P}}_{ps,k|k-1}^{Se(n)}{\left(H_{ps,k}^{Se(n)}\right)}^T+{\widehat{\mathit{R}}}_{pk}^n\right]}^{-1}\\ {\widehat{\mathit{X}}}_{ps,k}^{Se(n)}={\widehat{\mathit{X}}}_{ps,k|k-1}^{Se(n)}+K_k^{Se(n)}{\mathit{y}}_{ps,nk}\\ {\mathit{P}}_{ps,k}^{Se(n)}=\left[I-K_k^{Se(n)}{H}_{ps,k}^{Se(n)}\right]{\mathit{P}}_{ps,k|k-1}^{Se(n)}{\left[I-K_k^{Se(n)}{H}_{ps,k}^{Se(n)}\right]}^T+K_k^{Se(n)}{\widehat{\mathit{R}}}_{pk}^n{\left(K_k^{Se(n)}\right)}^T\end{array}\right.$$

(25)

The federated EKF fuses the information of the state estimates ${\widehat{\mathit{X}}}_{ps,k}^{Se(p)}$ and ${\widehat{\mathit{X}}}_{ps,k}^{Se(d)}$ as well as the error covariance matrices ${\mathit{P}}_{ps,k}^{Se(p)}$ and ${\mathit{P}}_{ps,k}^{Se(d)}$ of the two sub-filters and the main filter. The optimal global state estimation is obtained as follows:

$$\left\{\begin{array}{l}{\widehat{\mathit{X}}}_{ps,k}^g={\left[{\displaystyle \sum _{n=p,d}^n{\left({\mathit{P}}_{ps,k}^{Se(n)}\right)}^{-1}}+{\left({\mathit{P}}_{ps,k}^m\right)}^{-1}\right]}^{-1}\\ {\mathit{P}}_{ps,k}^g={\mathit{P}}_{ps,k}^g\left[{\displaystyle \sum _{n=p,d}^n\left[{\left({\mathit{P}}_{ps,k}^{Se(n)}\right)}^{-1}{\widehat{\mathit{X}}}_{ps,k}^{Se(n)}\right]}+{\left({\mathit{P}}_{ps,k}^m\right)}^{-1}{\widehat{\mathit{X}}}_{ps,k}^m\right]\end{array}\right.$$

(26)

The output result of the QLFEKF algorithm is the global state estimate, including the PVSE ${\widehat{\mathit{X}}}_{ps,k}$ and corresponding state error estimate covariance ${\mathit{P}}_{ps,k}$.

$$\left\{\begin{array}{l}{\widehat{\mathit{X}}}_{ps,k}={\widehat{\mathit{X}}}_{ps,k}^g\\ {\mathit{P}}_{ps,k}={\mathit{P}}_{ps,k}^g\end{array}\right.$$

(27)

4. Simulation and Results Analysis

The high-accuracy, effectiveness, and feasibility of the autonomous intelligent integrated navigation method is an important index to improve the autonomous operation ability of the cruise phase for the SSB probe. In order to further analyze the performance for this presented method, which is compared with the integrated navigation FEKF algorithm to verify the high accuracy of the state estimation of the X-ray pulsar/solar and target planetary Doppler velocity-measuring intelligent integrated navigation algorithm based on the QLFEKF.

4.1. Simulation Initial Conditions

This section presents the initial position state and velocity sate parameters of the probe cruise phase for the solution of the orbital dynamics model at the beginning. The initial simulation conditions are shown in

Table 1. Initial state orbit parameters for the probe.

Simulation Conditions	Parameters Value
Initial position values	[53,107,871.00559; 137,626,318.36608; −10,143.24541] km
Initial velocity values	[−14.01219; 35.86413; 0.42128] km/s
Initial state errors	δX0 = [δrx, δry, δrz, δvx, δvy, δvz]T δrx = δry = δrz = 1.0 × 102 km, δvx = δvy = δvz = 2.0 × 10−3 km/s
Initial state estimation covariance	$P_0=diag\left(\left[\delta r_x^2,\delta r_y^2,\delta r_z^2,\delta v_x^2,\delta v_y^2,\delta v_z^2\right]\right)$
Initial state process noise covariance	$Q_0=diag\left(\left[q_1^2,q_1^2,q_1^2,q_2^2,q_2^2,q_2^2\right]\right)$, q1 = 2.0 × 10−3 km; q2 = 3.0 × 10−6 km/s

as follows. The simulation time is from 1 September 2026 12:00:00:00.000 UTCG to 7 September 2026 12:00:00:00.000 UTCG. Thus, the total simulation time is 6 days.

Three X-ray pulsars are considered as one of the measurement models for intelligent integrated navigation, namely PSR B1937+21, PSR B0531+21, and PSR J1821-24. Their specific parameters are shown in

Table 2. The corresponding parameters of the selected X-ray pulsars.

Pulsars Name	RAD (°)	DEC (°)	D0 (kpc)	P (10−3 s)	W (10−3 s)	Fx (ph/cm2/s)	Pf (%)
PSR B1937+21	294.92	21.580	3.6	1.56	0.021	4.99 × 10−5	86
PSR B0531+21	83.63	22.014	2.0	33.5	1.670	1.54	70
PSR J1821-24	276.13	−24.870	5.5	3.05	0.055	1.93 × 10−4	98

. The X-ray pulsar detector has an effective area of 1 m². The vector of the position for the SSB relative to the solar center of mass is calculated by the ephemeris DE441 from the Jet Propulsion Laboratory (JPL). According to the approximate calculation formula of the pulsar observation noise [53,54], the standard deviations of the measurement noise for three X-ray pulsars are p₁ = 0.42060 km, p₂ = 0.14070 km, and p₃ = 0.44488 km, respectively.

The initial conditions of the relevant parameters for the X-ray pulsars and solar/target planetary Doppler measurement model that would be adopted in the simulation are listed in

Table 3. The corresponding parameters of the measurement models.

Initial Condition	Parameters Name	Parameters Value
XNAV Measurement	Number of detectors	3
	Effective area of the detectors	1 m2
	Measurement noise variance matrix	${\widehat{R}}_{p0}=diag\left(\left[p_1^2,p_2^2,p_3^2\right]\right){\mathrm{km}}^2$
Solar/target planetary Doppler measurement	Number of the spectrometers	2
	Accuracy of the spectrometers	d1 = d2 = 10−6 km/s
	Velocity measurement navigation measurement noise variance matrix	${\widehat{R}}_{d0}=diag\left(\left[d_1^2,d_2^2\right]\right){\left(\mathrm{km}/\mathrm{s}\right)}^2$

and mainly include the relevant initial measurement parameter characteristics of the X-ray pulsar detectors and Doppler spectrometers.

In the QLFEKF algorithm, reinforcement Q-learning is adopted to tune the parameters of the state and observation noise error covariance matrices and to obtain the optimum state and observation noise error covariance matrices. The parameters tuned by the reinforcement Q-learning include α, γ, and ε. Set the size of the appropriate Q-learning grid to M × N = 20 × 20. In the case of the specific range of the ${\widehat{\mathit{Q}}}_{rk}^{\left(i\right)}$, ${\widehat{\mathit{Q}}}_{vk}^{\left(i\right)}$, ${\widehat{\mathit{R}}}_{pk}^{\left(j\right)}$, and ${\widehat{\mathit{R}}}_{dk}^{\left(j\right)}$, the larger scale grid could search more fully and cover more area. The root mean squared error (RMSE) [54] is adopted as the evaluation indicator to implement precision analysis of the PVSE for the probe’s cruise phase. The relevant design parameters for the QLFEKF algorithm are summarized in

Table 4. The design parameters of the QLFEKF algorithm.

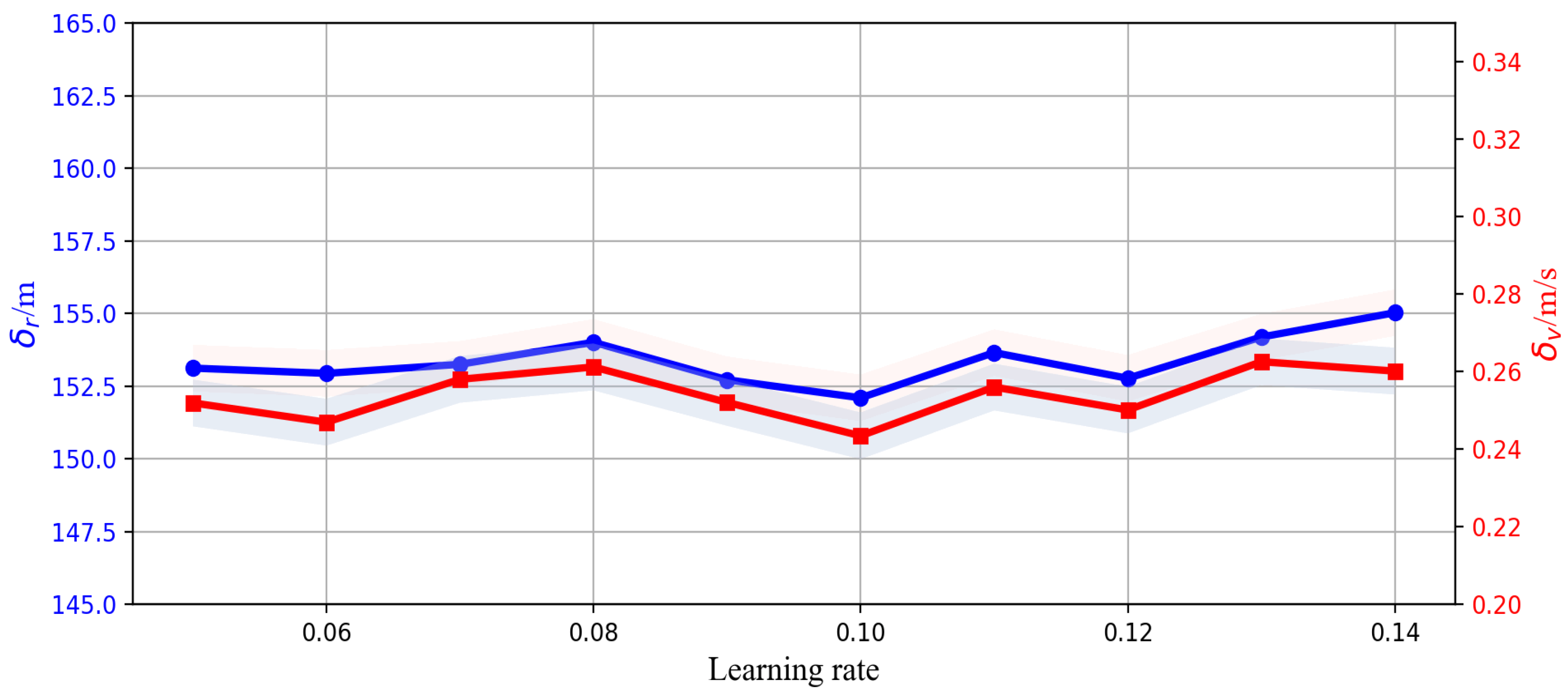
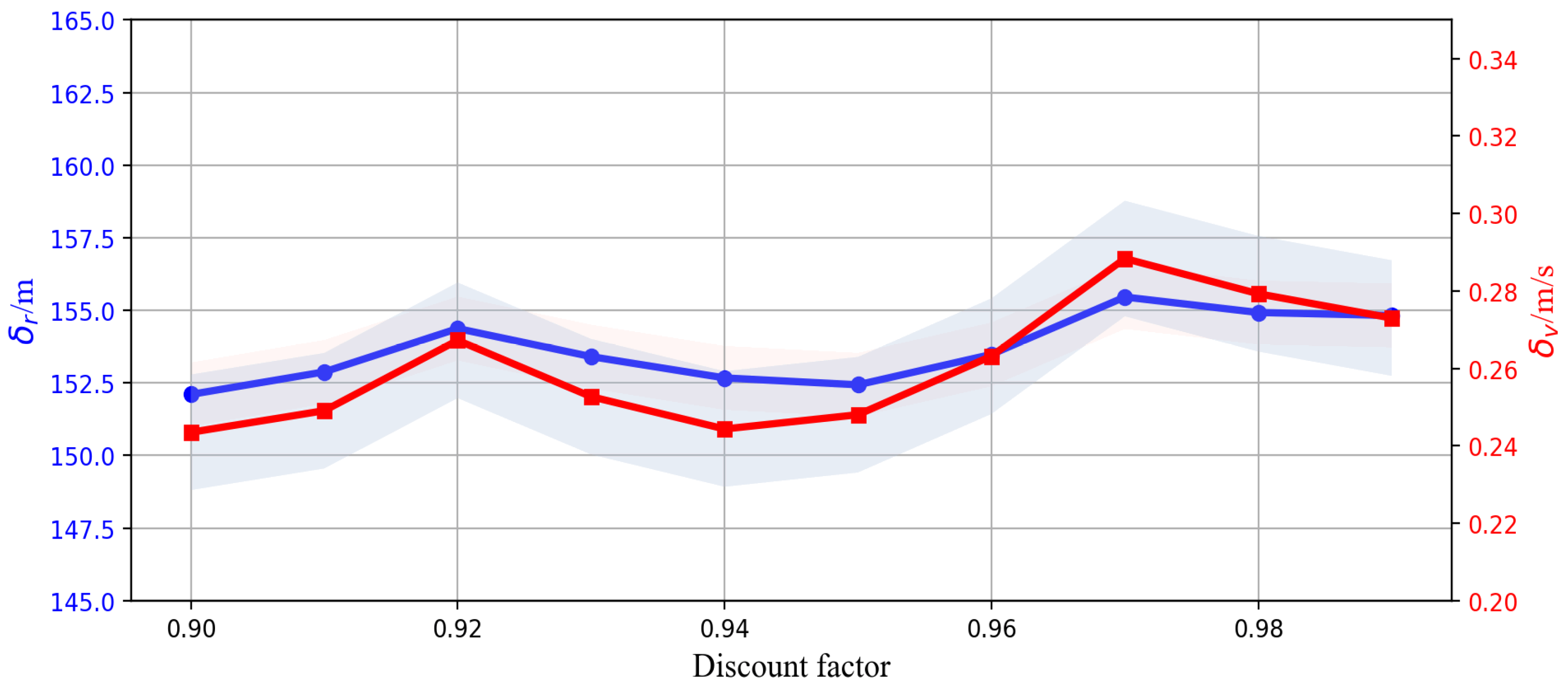
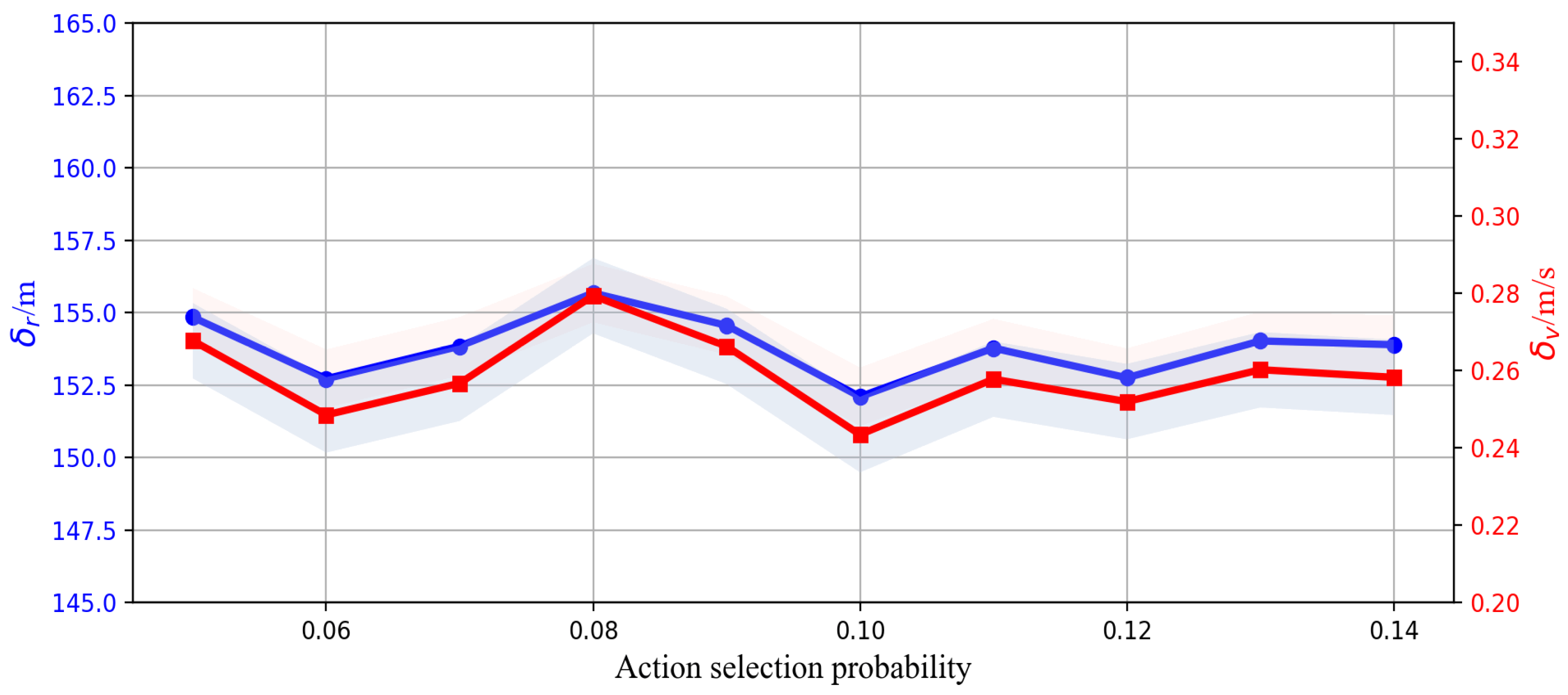
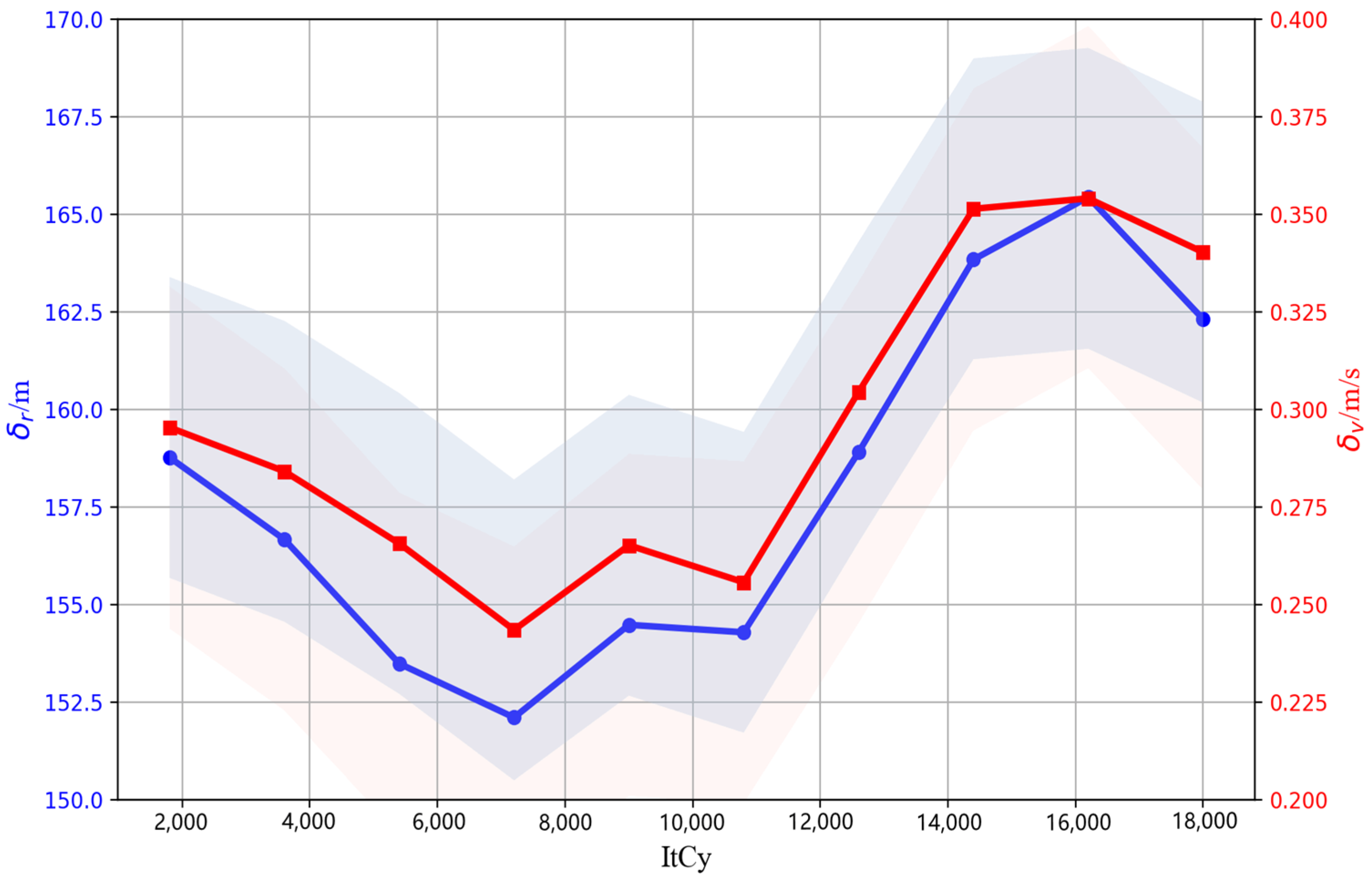
Parameter Name		Value
Learning rate, discount factor, and greedy values	α	0.1
	γ	0.9
	ε	0.1
The upper edge and lower edge bounds of ${\widehat{\mathit{Q}}}_{rk}^{\left(i\right)}$, ${\widehat{\mathit{Q}}}_{vk}^{\left(i\right)}$, ${\widehat{\mathit{R}}}_{pk}^{\left(j\right)}$, and ${\widehat{\mathit{R}}}_{dk}^{\left(j\right)}$	$\left[\begin{array}{cc}{\underset{\_}{q}}_{rk}& {\overline{q}}_{rk}\end{array}\right]$	[1/202 1/102]
	$\left[\begin{array}{cc}{\underset{\_}{q}}_{vk}& {\overline{q}}_{vk}\end{array}\right]$	[1/102 102]
	$\left[\begin{array}{cc}{\underset{\_}{r}}_{pk}& {\overline{r}}_{pk}\end{array}\right]$	[1/102 1]
	$\left[\begin{array}{cc}{\underset{\_}{r}}_{dk}& {\overline{r}}_{dk}\end{array}\right]$	[1/102 1/101]

as follows.

4.2. Simulation and Analysis

The X-ray pulsar/solar and target planetary Doppler velocity measurement based the Q-learning federation EKF (STD/XP-QLFEKF) is compared with the navigation state estimates of precision of the X-ray pulsar/solar and target planetary Doppler velocity measurement-based EKF (STD/XP-EKF) and the X-ray pulsar/solar and target planetary Doppler velocity measurement-based federated EKF (STD/XP-FEKF). The RMSE of the PVES of the cruise phase for the probe is used as the evaluation indicator of the navigation accuracy.

Figure 6 and Figure 7 show the RMSE curves of the position estimation error and the three-axis position estimation error of the three integrated navigation algorithms. It can be seen from the figure that the QLFEKF algorithm shows high accuracy position estimation performance with an error accuracy of 10² m. This shows that QLFEKF can adaptively choose the appropriate process states and observation (the X-ray pulsar detector measurement errors and spectrometer measurement errors) noise error covariance matrix by using the cumulative reward mechanism of the Q-learning through its interaction with the flight environment.

The stability of the position for the three integrated navigation algorithms has corresponding fluctuations, which are caused by eliminating the accumulated position errors caused by Doppler velocity measurements. However, compared with the position state estimation of the STD/XP-EKF navigation algorithm and STD/XP-FEKF navigation algorithm, the stability of the STD/XP-QLFEKF position state estimation is better. This result shows that the Q-learning algorithm has a good convergence effect in the process of parameter tuning, which ensures that the probe can operate continuously and stably in the cruise phase with high precision.

From Figure 8 and Figure 9, it is seen that the velocity estimation precision of the STD/XP-QLFEKF algorithm is about 10⁻¹ m/s, which is much higher than that of the STD/XP-EKF algorithm and the STD/XP-FEKF algorithm. It can be indicated that the state error estimation precision of the FEKF is better than that of the EKF, which reflects the superiority of the federated filter in the fusion of various measurement information. The FEKF combined with the Q-learning algorithm can distribute the position, velocity, and state transition information from different measurement models according to the weighted proportions, and it ensures that the information fusion of various navigation measurement models can obtain high-accuracy position state and velocity state error estimations based on the time update and measurement update. In addition, we could see that the precision convergence of the intelligent navigation system based on X-ray pulsar/solar and target planetary Doppler velocity measurements is very stable.

Based on the simulated analysis mentioned above, it verifies that the proposed STD/XP-QLFEKF intelligent integrated navigation is very appropriate for the considered intelligent integrated navigation for the cruise phase of the SSBE.

Table 5. The PVSE RMSE errors (3σ) of the integrated navigation system.

Filter Algorithm	Position Estimation Accuracy (m)				Velocity Estimation Accuracy (m/s)
	rx	ry	rz	r	vx	vy	vz	v
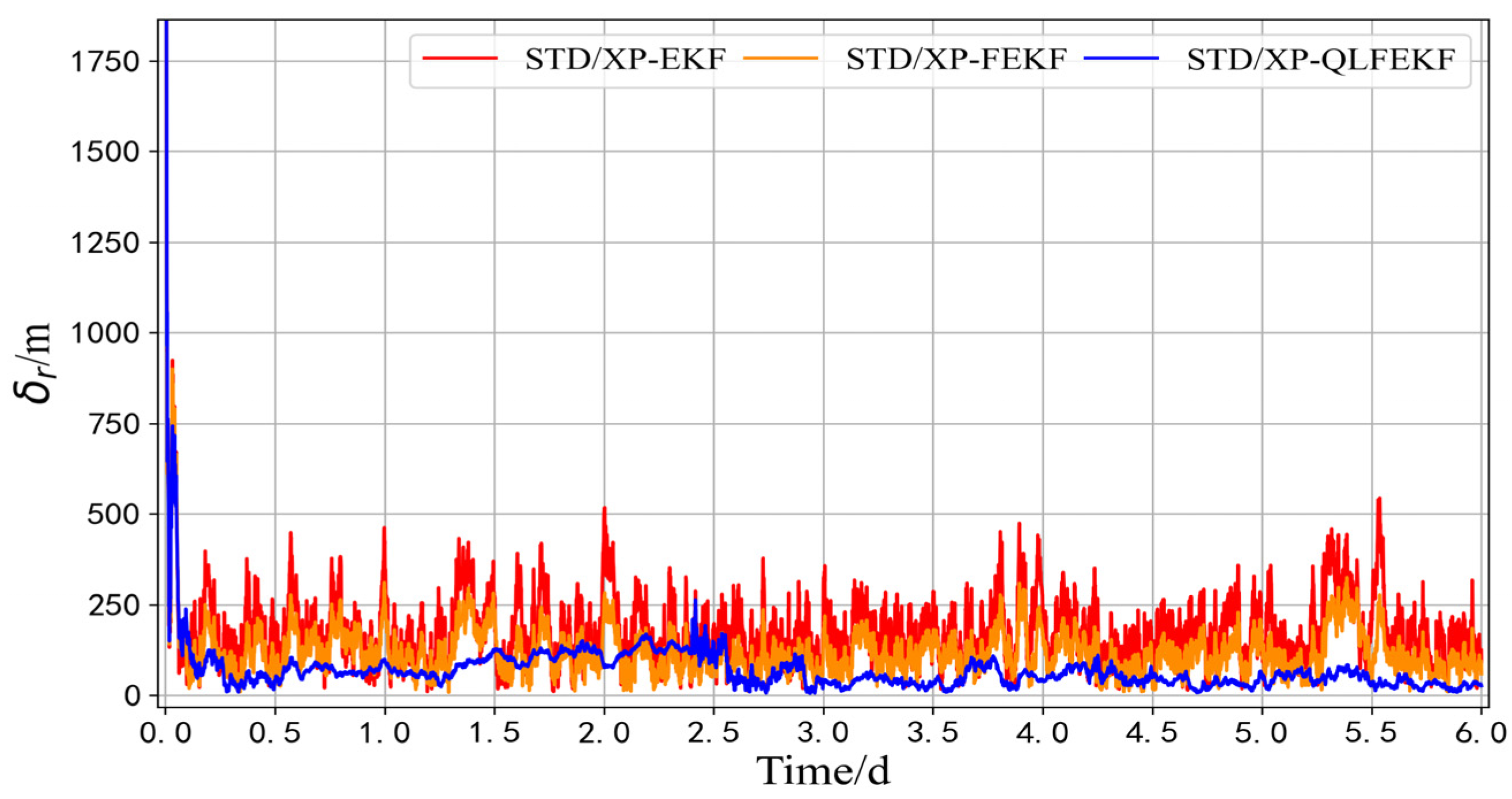
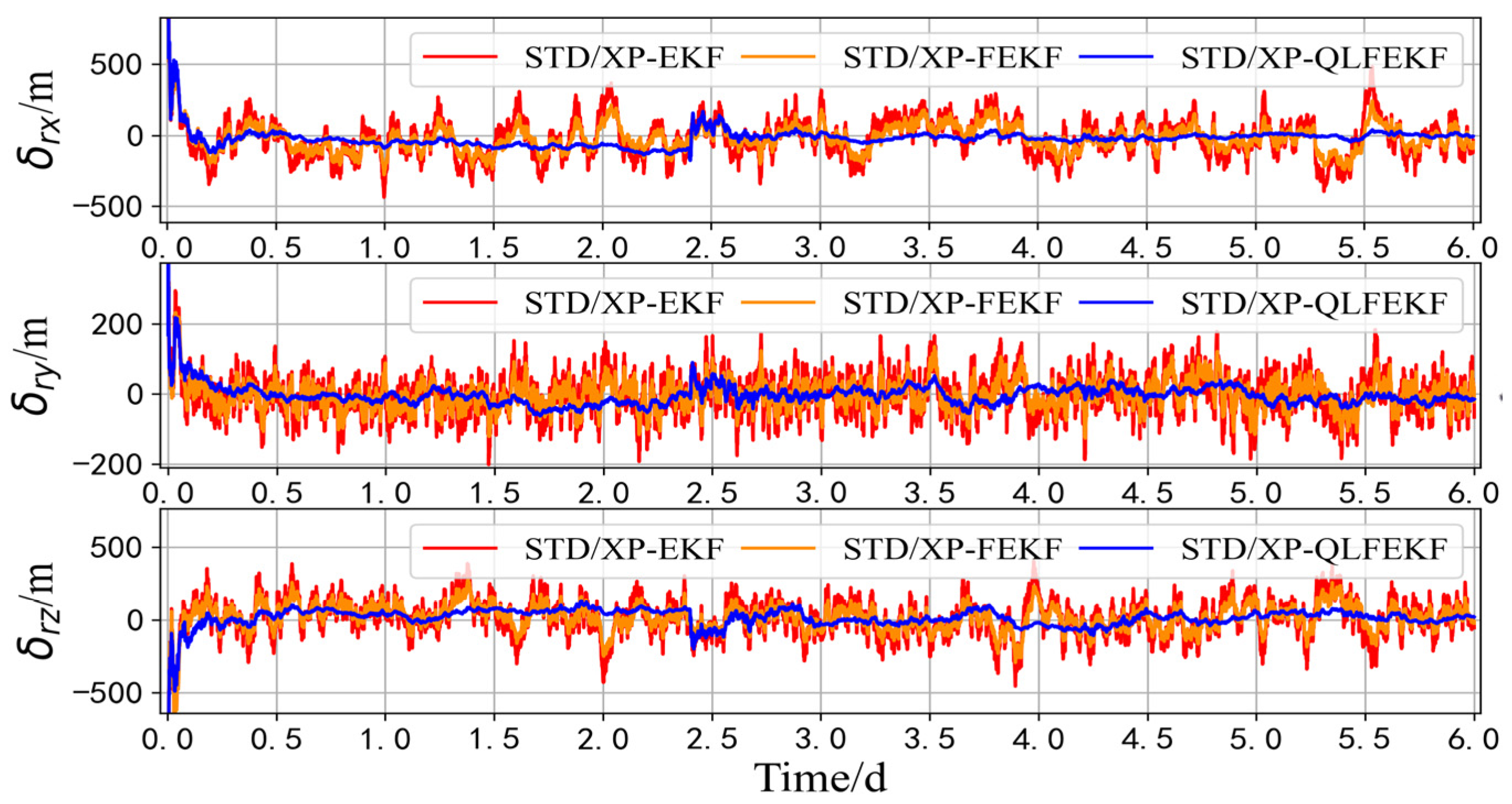
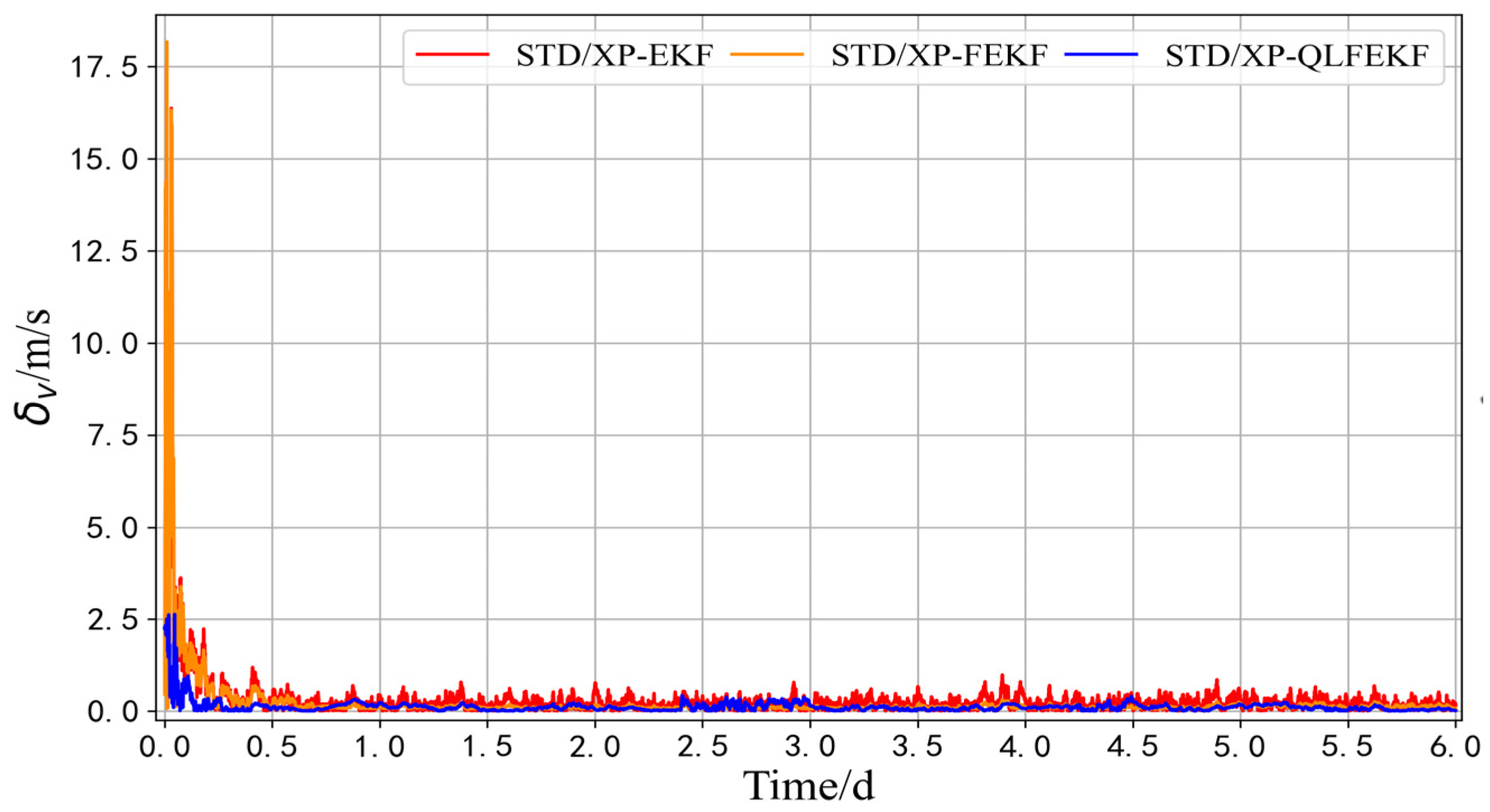
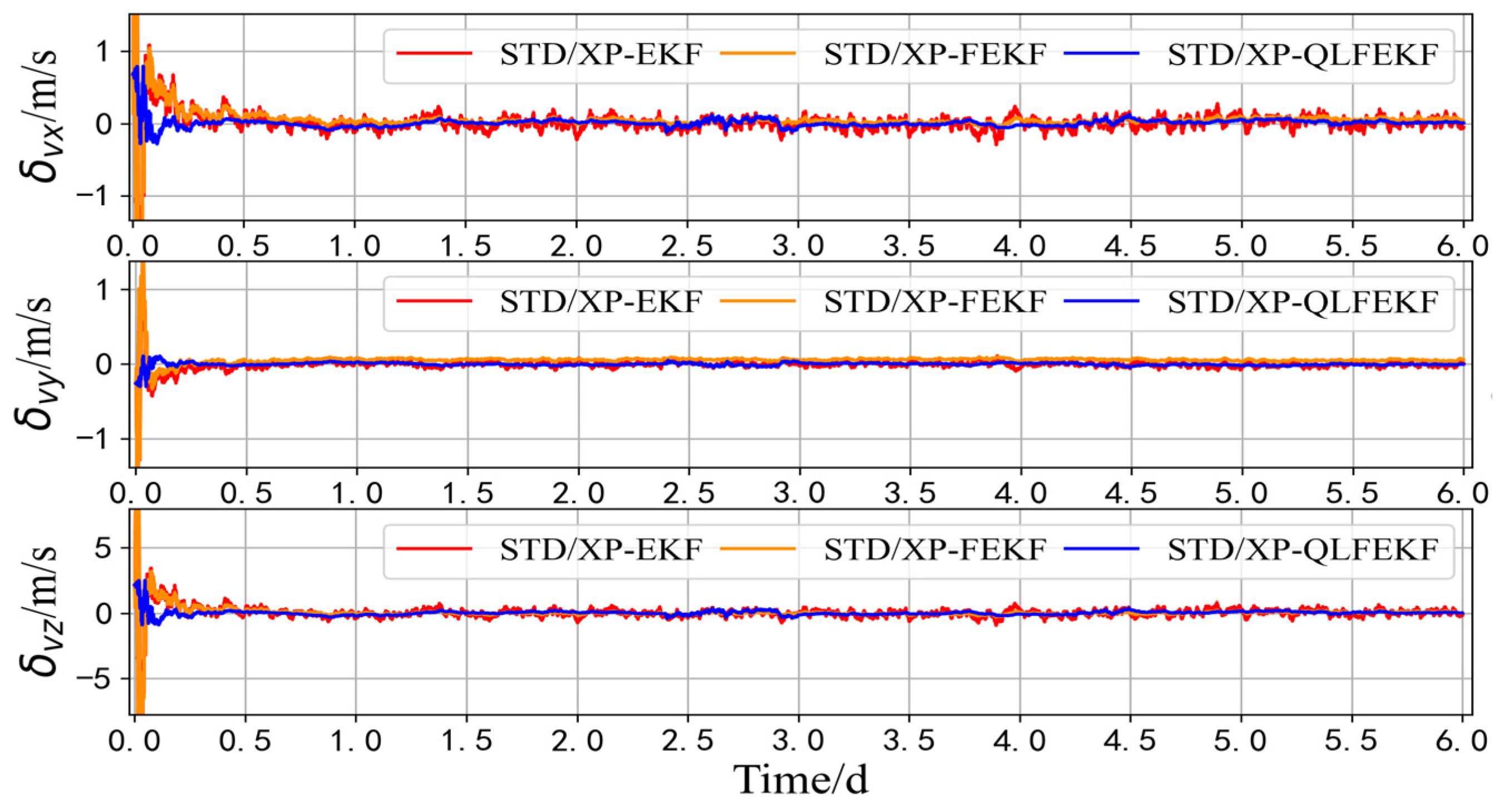
STD/XP-EKF	414.797	174.586	380.772	443.560	0.196	0.089	0.610	0.630
STD/XP-FEKF	335.289	132.138	279.342	351.803	0.169	0.158	0.289	0.386
STD/XP-QLFEKF	148.075	65.095	78.936	152.101	0.086	0.104	0.150	0.243
Navigation accuracy improvement rate	55.84%	50.73%	71.74%	56.76%	49.11%	34.18%	48.10%	37.04%

below shows the comparison of the position state and velocity state estimation RMSE errors (3σ) for the above three integrated navigation algorithms.

From Table 5 above, it can be seen that the position estimation RMSE error (3σ) accuracy is 443.560 m and the velocity state RMSE (3σ) precision is 0.630 m/s for the STD/XP-EKF. The PVES RMSE (3σ) precision of the STD/XP-FEKF are 351.803 m and 0.386 m/s, respectively. Based on the proposed STD/XP-QLFEKF algorithm in the paper, the PVSE RMSE error (3σ) accuracy of the cruise phase for the probe is 152.101 m and 0.243 m/s, respectively. By comparing the accuracy of the PVSE errors (3σ) between the STD/XP-QLFEKF and STD/XP-FEKF algorithms, the accuracy of the STD/XP-QLFEKF algorithm has been greatly improved. According to statistical analysis, the PVSE precision improvement capability of the STD/XP-QLFEKF algorithm is 55.84% and 37.04%, respectively. This is because the Q-learning algorithm can dynamically adjust the process and observation noise error covariance by periodically iterating according to the real-time in-orbit operating state after receiving different measurement state information. The cumulative reward is obtained through continuous iterations in each iteration cycle (ItCy). The Q-value of the corresponding state (${\widehat{\mathit{Q}}}_{rk}^{\left(i\right)}$, ${\widehat{\mathit{Q}}}_{vk}^{\left(i\right)}$, ${\widehat{\mathit{R}}}_{pk}^{\left(j\right)}$, and ${\widehat{\mathit{R}}}_{dk}^{\left(j\right)}$) position in the Q-table is calculated according to the cumulative reward value, and the appropriate information parameters are selected to the maximum extent through continuous trial-and-error to guarantee the performance superiority of the STD/XP-QLFEKF algorithm.

Next, the range of the related parameters (including α, γ, and ε) for the reinforcement Q-learning is set to evaluate the effects on the related learning parameters on the precision of the PVES error of the STD/XP-QLFEKF. The following sets the range of the Q-learning parameters involved above when the three learning parameters are changed in the range of $\alpha \in \left[0.05 0.14\right]$, $\gamma \in \left[0.90 0.99\right]$, and $\epsilon \in \left[0.05 0.14\right]$, and the RMSE errors (3σ) for position state and velocity state estimation of the STD/XP-QLFEKF algorithm are shown in Figure 10, Figure 11 and Figure 12, respectively.

From Figure 10, Figure 11 and Figure 12, it can be seen that the change of the Q-learning design parameters has relatively little influence on the PVES error precision for the STD/XP-QLFEKF algorithm. The simulation results show that the STD/XP-QLFEKF is insensitive to the changes in the navigation PVSE errors within the range of the above α, γ, and ε, and the small changes of navigation accuracy estimation errors caused by the changes of the Q-learning parameters can be ignored in the process of intelligent navigation algorithm design.

In addition, in the process of the STD/XP-QLFEKF algorithm reward mechanism design, we take the iteration period as a function of reward accumulation, and the setting of the iteration period has a certain influence on the calculation results of the reward accumulation. The following is the simulation and analysis of the PVES error corresponding different iteration cycles of the Q-learning of the QLFEKF algorithm. The influence of the different iteration cycles of reinforcement Q-learning on the accuracy of PVSE errors in the probe cruise phase is shown in Figure 13.

The simulation results show that when the iteration cycle of the Q-learning in STD/XP-QLFEKF algorithm is 7200 s, the position state and velocity state estimation precision for the intelligent integrated navigation is higher. Therefore, the cumulative reward calculation of the Q-learning algorithm is carried out according to the iteration cycle (ItCy = 2.0 h) in this research to ensure the high precision of the state error estimation of the intelligent integrated navigation system for the cruise phase of the SSBE.

5. Conclusions

Intelligent, high-accuracy integrated navigation for the cruise phase of the SSBE is deeply studied in this paper. The single navigation mode could not meet the high-precision and high-reliability requirements of the navigation system for a probe operating in long-endurance, highly dynamic, and extreme environments. In order to improve the navigation accuracy of the PVSE for the cruise phase of the probe, the QLFEKF based on the X-ray pulsar/solar and target planetary Doppler velocity measurement intelligent integrated navigation algorithm is proposed. The integrated navigation algorithm can compensate for the accumulated position estimation error of Doppler velocity measurements. The navigation system adopts the federation filter composed of the sub-filter and main filter to realize the information fusion of the various navigation modes and ensure the estimation performance of the intelligent integrated navigation system. At the same time, the cumulative reward mechanism of the reinforcement Q-learning algorithm is designed according to the sub-filter characteristics of the federated filter, and the iterative period of the Q-learning algorithm is used as an index to judge the cumulative reward. The process and measurement noise covariance matrices are carried out by tuning the parameters by traversing the Q-table. The simulation and analysis show that compare with the STD/XP-EKF and the STD/XP-FEKF, the STD/XP-QLFEKF algorithm has higher navigation accuracy, and its PVSE RMSE error (3σ) accuracy can reach 152.101 m and 0.243 m/s, respectively. The different values of the three learning parameters (α, γ, and ε) for the QLFEKF algorithm are insensitive to the PVSE errors, and slight changes in the estimation errors of the navigation accuracy caused by changes in the Q-learning parameters can be ignored. Of course, it is necessary to consider the iterative period parameters related to the cumulative rewards of Q-learning in the QLFEKF algorithm. As a function of the reward accumulation, the iterative period has a certain influence on reward accumulation and thus affects the PVSE accuracy of the navigation system. It is important to choose the appropriate cumulative reward iteration cycle. Therefore, the QLEKF based on the intelligent X-ray pulsar/solar and target planetary Doppler velocity measurement integrated navigation system has high accuracy, which can fully fulfill the high accuracy demands for the cruise phase of the SSBE probe.

In future work, the combination of reinforcement learning and traditional navigation methods will be further studied, and deep neural networks will be added to reinforcement learning to provide interpretability for intelligent integrated navigation methods and improve the flexibility of navigation system parameter setting. The fusion of multisource intelligent information of the integrated navigation measurement models would be simultaneously carried out to further improve the information fusion accuracy and efficiency of information obtained from various navigation measurements. It provides theoretical and technical support for the interpretability of the multistage, intelligent, and highly accurate integrated navigation of the SSBE.