Abstract
Interferometric synthetic aperture radar (InSAR) processing techniques have been widely used to derive surface deformation or retrieve terrain elevation. Over the development of the past few decades, most research has mainly focused on its application, new techniques for improved accuracy, or the investigation of a particular error source and its correction method. Therefore, a thorough discussion about each error source and its influence on InSAR-derived products is rarely addressed. Additionally, InSAR is a challenging topic for beginners to learn due to the intricate mathematics and the necessary signal processing knowledge required to grasp the core concepts. This results in the fact that existing papers about InSAR are easy to understand for those with a technical background but difficult for those without. To cope with the two issues, this paper aims to provide an organized, comprehensive, and easily understandable review of the InSAR error budget. In order to assist readers of various backgrounds in comprehending the concepts, we describe the error sources in plain language, use the most fundamental math, offer clear examples, and exhibit numerical and visual comparisons. In this paper, InSAR-related errors are categorized as intrinsic height errors or location-induced errors. Intrinsic height errors are further divided into two subcategories (i.e., systematic and random error). These errors can result in an incorrect number of phase fringes and introduce unwanted phase noise into the output interferograms, respectively. Location-induced errors are the projection errors caused by the slant-ranging attribute of the SAR systems and include foreshortening, layover, and shadow effects. The main focus of this work is on systematic and random error, as well as their effects on InSAR-derived topographic and deformation products. Furthermore, because the effects of systematic and random errors are greatly dependent on radar wavelengths, different bands are utilized for comparison, including L-band, S-band, C-band, and X-band scenarios. As examples, we used the parameters of the upcoming NISAR operation to represent L-band and S-band, ERS-1 and Sentinel-1 to represent C-band, and TerraSAR-X to represent X-band. This paper seeks to bridge this knowledge gap by presenting an approachable exploration of InSAR error sources and their implications. This robust and accessible analysis of the InSAR error budget is especially pertinent as more SAR data products are made available (e.g., NISAR, ICEYE, Capella, Umbra, etc.) and the SAR user-base continues to expand. Finally, a commentary is offered to explore the error sources that were not included in this work, as well as to present our thoughts and conclusions.
1. Introduction
The interferometric synthetic aperture radar (InSAR) technique has proven to be an excellent and reliable approach to measuring and map land surface topography since the early 1970s (e.g., [1,2,3,4]). Spaceborne SAR systems possess the capability of obtaining radar images over wide areas of up to hundreds of kilometers under all-weather conditions at relatively low costs when compared to ground surveying or conventional aerial systems [5,6]. Due to the merits of spaceborne SAR, mission programs in the 1990s, such as the European Remote Sensing Satellites series (ERS-1, ERS-2) or the Canadian Radarsat program, have initiated a large number of studies and methodological investigations into the application of topographic mapping [7,8,9,10]. In 1989, the first demonstration of the potential of Differential InSAR (DInSAR) was proposed for surface deformation mapping at a centimeter or sub-centimeter accuracy [11,12]. This opened the door for a variety of applications using the DInSAR technique, including seismic deformation [13,14,15], glacier motion [11,16,17,18], volcanic eruption [19,20,21], landslides [22], and land subsidence [23,24,25,26].
The principle of InSAR is based on the extraction of ground surface data to generate topography or deformation products through phase differencing between two acquisitions [27]. The workflow of both applications is very similar, including image coregistration, interferogram generation, phase filtering, phase unwrapping, phase to elevation/displacement, and lastly, geometric correction. The primary distinction between the two applications is that the topographic information is preserved during the interferogram generation phase for topographic mapping but is removed for deformation mapping. Early InSAR research extensively explored possibilities regarding the application of InSAR techniques, and it also revealed multiple error sources connected to imaging geometry, propagation path, and InSAR processing [28,29,30,31,32]. These error sources make the interpretation of interferograms difficult and thus might limit users’ understanding of the resulting InSAR products without an in-depth knowledge of the InSAR technique.
Early InSAR literature derived different error sources. The first effort was made by Li and Goldstein [29] who presented an error model including signal-to-noise ratios (SNR), number of looks, pixel misregistration, and baseline decorrelation. Later on, Rodriguez and Martin [30] provided a more extended view towards the topic and separated the errors into two types: (1) intrinsic height error and (2) location-induced error. Intrinsic height error occurs because of the errors in estimating the measured heights, while location-induced error refers to the fact that the measured heights are spatially mis-projected [30]. Later in the same year, Zebker and Villasenor [32] published a paper concentrated on factors leading to InSAR decorrelation. These factors encompassed (1) thermal noise, causing thermal decorrelation; (2) lack of parallelism between radar flight tracks resulting in decorrelation due to target rotation concerning radar look location; (3) spatial baseline noise leading to baseline decorrelation; and (4) surficial changes contributing to both temporal and volume decorrelation. Subsequently, many research works discussed the impact of tropospheric delay as it was found to be one of the most significant error sources for InSAR measurements [7,14,31,33,34]. It was not until 2001 that Hanssen [28] provided an organized and more comprehensive view of the overall error budget and proposed several models to describe the influence of each contributor. Hanssen created empirical and stochastic models to analyze the most important error sources for repeat-pass radar interferometry. Nevertheless, while the substance is excellent, it was a math-heavy research paper that is difficult for novices to understand.
In the evolution of InSAR research, pivotal work from Li and Goldstein [29], Rodriguez and Martin [30], Zebker and Villasenor [32], and Hanssen [28] have significantly contributed to our understanding of error sources. Beyond the references cited, there are numerous other papers that discuss InSAR phase errors and/or decorrelations (e.g., [35,36,37,38,39]). However, these works often only focus on specific error sources (e.g., tropospheric delay or decorrelations). Moreover, the intricate mathematical formulations found in many existing studies pose challenges for novices seeking comprehension. Despite the wealth of prior research on InSAR error sources, there remains a lack of a clear and easily digestible categorization for all error sources. Addressing this gap and building upon the foundational work of Rodriguez and Martin [30], we classified errors into two primary categories: intrinsic height errors (Section 2.1) and location-induced errors (Section 2.2), predicated on their association with InSAR estimation or imaging location. Additionally, we introduced a new categorization within intrinsic height errors, further dividing them into systematic errors (Section 3) and random errors (Section 4) based on their manifestation under coherent conditions. The organizational structure for each error source is visually represented in Figure 1. This innovative categorization aims to furnish a comprehensive and accessible framework for comprehending InSAR error sources. This paper retains essential equations for a fundamental understanding and provides a comparative analysis of error sources across different radar bands. Our aim is to offer the best entry point for novices seeking to grasp InSAR error sources without the unnecessary complexity found in previous literature. The paper focuses on the emergence of error sources, simplifying concepts for beginners, while preserving essential equations needed for estimation. Additionally, it provides a comprehensive picture of all error sources, comparing different radar bands to illustrate how wavelengths alter the effect of each error origin. This makes our paper the ideal starting point for novices to learn about InSAR.
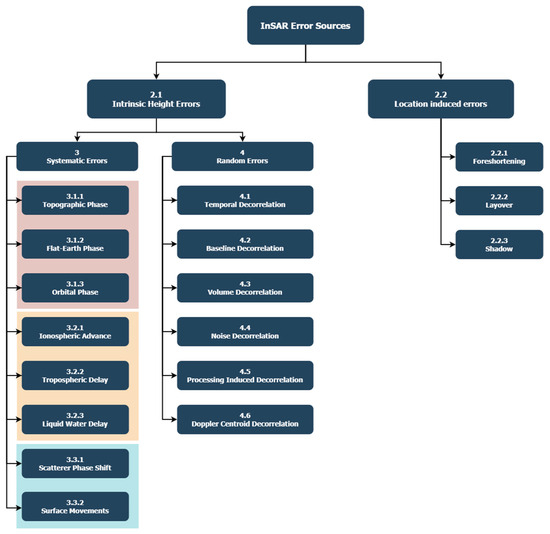
Figure 1.
The structure of the error sources with their respective sections in this article.
A profound comprehension of error sources is imperative not only for understanding the inherent limitations and potential inaccuracies in InSAR-derived products but also for actively enhancing study outcomes’ accuracy and reliability. Notably, research [40] has showcased significant variations in Digital Elevation Models (DEMs) resulting from equivalent InSAR workflows over the same area of interest. Consequently, users of InSAR data products must grasp these error sources to optimize their workflows effectively. The intricate InSAR error budget, spanning the entire imaging system, often challenges users in identifying causes of poor-quality outputs. A thorough understanding of potential error causes and effects is essential for researchers to accurately explain their findings and minimize processing workflow errors. While this article provides valuable insights into these matters, it is crucial to recognize that a comprehensive analysis of each specific error source goes beyond the current scope and may require dedicated research efforts. Additionally, it is important to note that specific examples of SAR phase interpretation are beyond the scope of this paper. While these components are vital for making informed decisions during InSAR processing, the objective of this paper is to establish a foundational understanding of the overarching landscape of InSAR error sources, laying the groundwork for more focused investigations in subsequent studies. In summary, we seek to sort and explain the different error sources with notable clarity so that readers can build a comprehensive view of the total InSAR error budget. The impacts of different error types vary depending on the sensor wavelength. Having stated that, this work will concentrate on Sentinel-1 C-band cases while also comparing them to other bands. This paper provides a thorough explanation for readers who are not familiar with InSAR techniques and will also provide the fundamental knowledge of InSAR error sources for those who wish to advance their skills in InSAR phase interpretation.
2. Intrinsic Height Errors and Location-Induced Errors
Error sources can exert their influence on InSAR measurements through two primary pathways. The first pathway results in direct inaccuracies in the derived output InSAR measurements. In specific terms, this pertains to errors in estimating either the surface height or the displacements, depending on whether the InSAR technique is employed to derive digital elevation models (DEMs) or assess surface deformation. This first set of error sources is referred to as intrinsic height errors [30]. On the other hand, the second error pathway does not alter the fundamental value of the output InSAR measurement itself. Instead, it leads to the misrepresentation of the actual position of the true topographic features within the radar image. This second set of errors is known as location-induced errors [30].
2.1. Intrinsic Height Errors
Intrinsic height inaccuracies are caused by issues in determining topographic height [30]. In other words, intrinsic height errors cause inaccuracies that result in erroneous measurements and are separate from errors related to incorrect positioning. These height errors are the main focus of this paper.
For a repeat-pass interferometry SAR system, two single-look complex (SLC) SAR images are acquired from similar positions in space over the same terrain. The interferogram is formed by cross-multiplying two SAR images and deriving the phase difference between the two SLC SAR images. A SAR interferogram is a superposition of the different phase components, including the topographic phase (Δφtopo), flat-Earth phase (Δφflat), orbital phase (Δφorb), tropospheric delay (Δφtropo), ionospheric advance (Δφiono), liquid water delay (Δφliq), scatterer’s phase shift (Δφscatt), deformation phase (Δφdefo), and the noise phase (Δφnoise) (Equation (1)) [27,41,42,43].
If the goal of the InSAR measurement is topographic mapping, then the topographic phase is the phase of interest, and all others will produce measurement error. Similarly, if the goal is deformation mapping, only the deformation phase is of importance, then all other components will contribute to inaccuracies. As a consequence, one of the most crucial components of InSAR processing is to remove as much undesired phase noise as possible in order to acquire accurate measurements. If each undesirable phase term is not appropriately eliminated from the overall phase variation, the unwanted phase will be mistaken as topographic/deformation phase, thereby resulting in inaccurate measurements.
Interferometric SAR only works under coherent conditions [44,45] in which the received backscatter is correlated between the two SAR images [28]. The signal in each interferogram pixel is composed of two parts: the coherent portion that generates fringe patterns; and the incoherent portion that appears as phase noise [35,46]. The intrinsic height errors can therefore be further categorized into two types: (1) systematic errors and (2) random errors. Systematic errors exist in the coherent portion of Equation (1) (i.e., Δφtopo, Δφflat, Δφorb, Δφtropo, Δφiono, Δφliq, Δφscatt, and Δφdefo). Random errors are the sources that contribute to phase noise (represented as Δφnoise in Equation (1)). When the phase variation caused by a scatterer’s movement and/or surface deformation are incoherent, Δφscatt and Δφdefo can also contribute to random errors. The systematic errors influence the accuracy while the random errors determine the precision of the interferometric system [30].
2.2. Location-Induced Errors
Location-induced error refers to the situation in which real topographic features are not projected to the correct location in the radar image [30]. The imaging principle of SAR systems is reliant on measuring the time delay between two different ground scatterers and determining their relative distance in radar images. Due to the inherent oblique observation geometry of all SAR imaging systems, areas where local terrain slope exists produce topographic displacement in the range direction of the SAR images [47,48]. Whether or not ground features are distorted or are simply not recorded depends upon the relationships between incidence angle, local terrain slope, and perpendicular baseline. This distorted effect is commonly known as geometric distortion, or geo-location error. Geometric distortion includes foreshortening, layover, and shadow [49]. Figure 2 displays how radar echoes record ground information on the image plane and how they create three distinct geometric distortions, which are separately represented in red (foreshortening), green (layover), and blue (shadow).
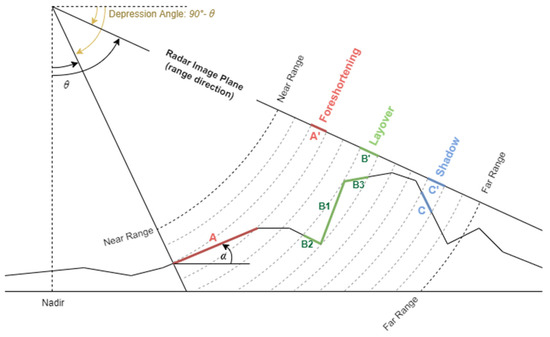
Figure 2.
Geometric distortion (or geo-location error) of imaging radar systems (modified from [28], Figure 2.9, and [50] Figure 2.4). Radar echoes are recorded between each concentric circle segment. The two darker concentric circle dashed lines represent the near range and far range, respectively. θ is the incidence angle and α is the local terrain slope. The three types of geometric distortion are shown in red (foreshortening), green (layover), and blue (shadow) separately.
2.2.1. Foreshortening
Foreshortening is a distortion inherent in radar imaging [51]. Foreshortening can occur even on flat terrain. It can be observed that if the local terrain slope α increases, terrain A in Figure 2 lying within two concentric curves will be lengthened accordingly. The signals within the segment of terrain (A) are projected to radar image plane (A’). Since the range difference within A is lengthened by the terrain slope, the signal will be compressed in plane A’ and thus foreshortened. If α rises and approaches incidence angle θ, more terrain will be recorded between two radar echoes, resulting in more compression in the range direction and thereby symmetric fore-slope patterns which lean toward the sensor in SAR images.
Foreshortening occurs when α is smaller than θ. Given the same area of interest, a larger incidence angle implies a greater likelihood that the slope angle will be smaller than the incidence angle, resulting in a greater likelihood of foreshortening effects. Foreshortening is the most common geometric distortion type because most of the imaged topography falls within the geometric condition of foreshortening, i.e., α < θ, except for very steep terrain and areas in backslope.
2.2.2. Layover
For a layover situation, the radar echo hits the top (B1 and B3) of the terrain before the bottom (B2). Therefore, B1 and B3 are recorded first in the image plane and then B2, which is the reverse of the ordering on the ground. The echo includes signals from the top and bottom as well as fore-slope and/or back-slope which are projected to the radar image plane (B’). As the signals are out of order and mixed together, it is ambiguous and makes target detection challenging [48]. Similar to foreshortening, the layover pattern in radar images leans toward the sensor, but it creates brighter features (i.e., higher intensity backscatter) within the images.
The geometric condition of layover is α > θ. In other words, once the local terrain slope exceeds the incidence angle, foreshortening turns into layover. Consequently, as the incidence angle rises, it will be more difficult for layover to occur. In general, if the local terrain slope is over 40°, it is highly likely that layover will occur for both ERS-1 and Sentinel-1 SAR platforms. Both the local terrain slope and the incidence angle need to be very steep to observe the layover effect.
2.2.3. Shadow
Shadow typically happens at the back-slope of the terrain. However, due to the oblique observation geometry, not all areas at the back side are indetectable. Here, we define the slopes at the back side of the terrain with a negative sign. The condition of shadow effect occurs when α < −(90° − θ), meaning radar shadow occurs when the slope angles are smaller than the negative of the depression angle [52]. Also, large ground features or artificial construction which block radar waves from illuminating the surface could result in shadow effect [47].
The terrain segment C is located at the back side of the terrain, so when C is projected to image plane (C’), it appears dark as there was essentially no feature exposed to radar illumination. The existence of shadow hinders image interpretation. The way to limit shadow areas is to reduce the incidence angle. However, smaller incidence angle produces more areas of layover as a drawback.
2.2.4. Overall
It is impossible to prevent geometric distortion from occurring, thus combining radar images from both ascending and descending orbits is one solution to acquire complete surface information over a given terrain [50]. It is important to be aware of which geometric distortions are present in the study area. By knowing this information beforehand, one could adjust the region of interest or apply other means to prevent or mitigate interference from geometric distortion.
3. Systematic Errors
Systematic errors are derived from coherent phase variations external to the desired phase. For terrain mapping, the topographic phase is the desired component, while the deformation phase component is desired for deformation monitoring applications. Systematic errors come from the systematic phase shifts which occur in interferograms. The phase shifts generated by undesirable coherent phase variations superimpose noise onto interferograms and generate unwanted phase fringes. If the additional fringes are misinterpreted as the desired topographic/deformation phase component, then the resulting measurement would include the contribution from these redundant phase shifts and undermine the accuracy of the measured values. For example, if the InSAR measurement captured five fringes for a deformation mapping application, but only three of the fringes were caused by actual surface deformation (the desired signal) and the other two fringes were caused by tropospheric delay (the undesired signal), the measured deformation accuracy would be reduced as two fringes were misinterpreted as true deformation phase variation.
In this paper, systematic errors are classified into three categories based on the origin of the phase shift: viewing geometry (from space), propagation path (atmosphere), and scatterer motions (ground surface). The viewing geometry consists of three phase components: (1) flat-Earth phase, (2) orbital phase, and (3) topographic phase. The propagation path consists of three components: (1) ionospheric advance, (2) tropospheric delay, and (3) liquid water delay. Scatterer movement accounts for (1) scatterer phase shift and (2) surface movement.
3.1. Viewing Geometry (Space)
3.1.1. Topographic Phase
Topographic phase signals include the topographic phase (an artifact of elevation differences) and flat-earth phase (an artifact of the side-looking radar). The topographic phase allows for reconstruction of the surface topography from the two-dimensional phase field measurements due to the viewing geometry and the accurate spatial coupling of the two imaging orbits [31]. This is the desired phase component for DEM generation. However, it is an undesirable phase component for deformation mapping. Equation (2) shows the calculation for the topographic phase, where h is topographic height. divided by is the conversion factor from pseudo range to phase delay, which will always exist in the phase terms. The most influential component is perpendicular baseline (). The reason is closely related to the height sensitivity of the interferometer, namely, height ambiguity, which symbolizes the elevation difference corresponding to a fringe () of change (i.e., height per phase cycle) [28]. The calculation for height ambiguity is given in Equation (3), where symbolizes the height ambiguity [27,28]. A longer perpendicular baseline leads to less height ambiguity. Reduced height ambiguity indicates that a fringe is more sensitive to elevation change, making it ideal for DEM generation but not for deformation mapping. On the other hand, a shorter perpendicular baseline leads to significant height uncertainty. A high degree of height ambiguity suggests that a fringe is insensitive to elevation change, making it useful for deformation mapping but not DEM generation.
This explains why Sentinel-1 is unsuitable for topographic mapping, as its orbital tube was not designed for DEM generation [53,54]. Sentinel-1 orbit maintenance strategy provides modest orbital InSAR baselines in the order of 150 m [55]; hence, baselines of Sentinel-1 image pairs are often too narrow to achieve a preferred height ambiguity. In principle, the best baselines for topographic mapping are between 150 and 300 m, whereas baselines below 50 m are recommended for deformation mapping [35]. One issue to keep in mind is that while a larger perpendicular baseline is preferred for DEM production in order to provide higher sensitivity of the InSAR phase to height variation, the value should not be more than the critical baseline (Bc) in order to avoid excessive decorrelation noise. Longer perpendicular baselines increase baseline decorrelation [12], particularly in places with moderate to severe slopes (e.g., [56]), as well as volume decorrelation, since the longer baseline increases the sensitivity of the coherence and the InSAR phase to vegetation characteristics.
Height ambiguity is an important value for DEM generation as it is used to translate the number of fringes to the measured topographic height. Here, we use the parameters of C-band Sentinel-1 as an example. Suppose the wavelength is 0.0555 m, slant range is 780,000 m, incident angle is , and perpendicular baseline is 150 m. Using Equation (3), we could derive a height ambiguity of 74 m/fringe. If there are four fringes in the interferogram, this indicates that the topographic height is m. As a result, a lower height ambiguity provides a more accurate translation from the number of fringes to the measured elevation, but a large ambiguity height (say, above 500 m/fringe) is unlikely to offer meaningful information for areas where the elevation gradient is less than 500 m.
Table 1 compares the baselines of different satellite constellations, revised from Braun [57]. Range of height ambiguity (m) is calculated using Equation (3) given the parameters of each SAR system. The lowest limit of the Sentinel-1 and TerraSAR-X/TanDEM-X baselines is set to 10 m for calculation purposes. However, we note that values lower than 10 m are possible. Sentinel-1 baselines are often less than 150 m, with values as low as 50 m or less being frequent [58], making the sensor unsuitable for topographic mapping but ideal for deformation mapping. A thorough literature review on the topic targeted at Sentinel-1 was discussed in Braun [57]. ERS and ENVISAT both have extremely high perpendicular baselines, which provides enough height ambiguity for DEM generation (successful example, e.g., [59]).

Table 1.
Range of perpendicular baseline and height ambiguity for different satellite operations [57,60].
The topographic phase is often eliminated for deformation mapping applications using an arbitrary reference surface (usually Shuttle Radar Topography Mission, SRTM). Nevertheless, if the reference surface is not correct (not up to date, low spatial resolution, or low vertical accuracy) or if the InSAR geometric parameters (i.e., system altitude, baseline, and orbit position) are inaccurate, there will be topographic phase residuals that will substantially impact the output deformation product. As a result, an accurate DEM and geometric parameters are deemed critical for properly detecting minor deformation. Some common ways to reduce topographic residuals include stacking interferograms [61], small baseline subset (SBAS) processing [62,63,64], or Multiple Aperture SAR Interferometry (MAI) [63,65].
3.1.2. Flat-Earth Phase
Flat-Earth phase is part of the topographic phase signal. It is the phase component of the reference Earth surface and is also called the reference plane phase. Since a flat altitude profile instead of the real topography is initially used for interferogram generation, the resulting interferogram needs to be compensated for the ellipsoid or geoid model of the Earth [35].
The “flat-Earth” pattern results from the small change of two viewing geometries (or shift in orbital trajectory) between two imaging acquisitions [31,46]. Being a long-wavelength phase contribution, the pattern appears as dense stripes on interferograms. Normally, the difference in look angle across a swath of 6000 pixels can generate hundreds of fringes [46]. Due to orbital inaccuracies, the stripes occur in both the range and azimuth directions [66]. These dense stripes can severely obscure other phase variation information and add a significant load to later phase filtering and unwrapping. Therefore, flat-Earth phase is often removed during the initial stages of InSAR processing.
The fringe frequency (fϕ) is given by Equation (4) [28]. Fringe frequency (cycle/m) is not a fixed value. It is composed of the perpendicular baseline (B⊥), slant range (R), wavelength (λ), incidence angle (θ), and local terrain slope (α). The perpendicular baseline and local terrain slope are the most critical components in determining the density of fringe frequency. Recall that the flat-Earth phase results from the shift in orbital trajectory. A greater shift suggests a wider perpendicular baseline and, as a result, a denser flat-Earth fringe frequency.
In addition to the parameters in Equation (4) that can impact the density of the flat-Earth-phase fringes, additional factors such as system altitude error and baseline error play a role in changing the fringe frequency [29,30,67]. System altitude error, hereafter altitude error, refers to the differences in system altitude estimation and true system altitude, also known as altitude indetermination. Baseline error refers to the differences in baseline estimation and true baseline, also known as baseline indetermination. The formation of altitude error and baseline error occurs due to the limitations in determining InSAR geometric parameters [68,69,70,71,72].
The errors in altitude and baseline not only pose additional errors on the flat-Earth phase but also on the topographic phase component. In the flat-Earth phase, the altitude error superimposes an additive lower-order polynomial fringe (a linear tilt) in the range direction, and a height shift in the topographic phase, which is dependent on local topography [29,30]. In the flat-Earth phase, the baseline error superimposes an additive lower-order polynomial fringe (a quadratic surface distortion) in the range direction and a height shift based on local topography in the topographic phase [29,30,35]. Reducing the impact of altitude error and baseline error can be achieved by either having more precise geometric parameters or applying tie points in the area of interest [30]. A minimum of two tie points is necessary for the correction of altitude error, and at least three are required for the correction of baseline error [30].
3.1.3. Orbital Phase
Orbital phase arises from the differences between orbit estimation and the true orbit position, often referred to as orbit indetermination or orbit error [73]. Similar to altitude error and baseline error, the error in orbit estimation emerges due to the imperfect InSAR geometric parameters. The impact of orbit error becomes evident when these parameters are employed to correct the flat-Earth phase through a process known as phase flattening. In cases where orbit parameters lack precision, the correction becomes imperfect, resulting in residual flat-Earth phase error [46,74]. Consequently, the orbital phase represents the remaining part of the flat-Earth phase after applying phase flattening [46]. These forms of phase error exhibit gradual changes over large spatial scales, earning them the label of “long wavelength phase contribution”. This term is aptly descriptive as the phase error displays smooth variation across large spatial extents.
Since the topographic phase persists in the interferograms for DEM generation, the orbital phase is difficult to see and measure due to its relatively small scale [74]. However, if the InSAR approach is used for deformation mapping, the topographic phase is subtracted from the interferograms, resulting in two outcomes. First, the topographic phase residuals will be present as the removal of the topographic phase also incorporates orbital parameters. Second, the flat-Earth phase residuals will be more prominent in the interferograms because the topographic phase is removed [74].
Fattahi and Amelung [75] conducted an experiment to investigate the influence of orbital errors and compare them with theoretical influences. The result has shown that the impact of orbit errors is significantly smaller than expected [75]. The authors outlined the worst-case range and azimuth uncertainties of the velocity gradients resulting from orbital errors for several satellite operations (Table 2). Modern satellites, such as TerraSAR-X and Sentinel-1, have much more precise orbit determination than older platforms, which constrains the influence of orbit errors to an extremely small extent (e.g., below 1 mm/year over 100 km). Because the impact is so minor, orbital phase is usually ignored.

Table 2.
Range and azimuth uncertainties of the velocity gradients caused by orbital errors for each satellite in mm yr−1 100 km−1 (modified from [75]).
3.2. Propagation Path (Atmosphere)
When microwave signals propagate through the atmosphere, they enter the exosphere, thermosphere (contains the ionosphere in its lowest portion), mesosphere, stratosphere, and then the troposphere, respectively. In this process, a couple of propagation impairments occur due to different physical reasons, including phase delay or advance, signal attenuation, signal depolarization, tropospheric refractive fading, and ionospheric signal scintillations [76]. These propagation impairments influence InSAR measurements in different ways with varying magnitudes. Nevertheless, because phase delay or advance is the primary cause of systematic error in InSAR-derived measurements, this section focuses on phase delay or advance.
Since the refractivity index of the mediums in the ionosphere and troposphere differs slightly from that of a vacuum, wave velocity decreases or increases, resulting in phase advances in the ionosphere and phase delays in the troposphere [77]. The errors caused by this effect are called clock timing errors [30]. Phase advance or delay can be characterized by the dimensionless refractivity index, N [28,78], and is composed of four different elements: hydrostatic component, wet component, ionospheric component, and liquid component (Equation (5)) [79,80,81].
In Equation (5), k1, k2′, and k3 are empirical constants [80]; P is total atmospheric pressure in hPa; T is temperature in Kelvin; e is the partial pressure of water vapor in hPa; k1 is 77.6 K hPa−1; k2′ is 23.3 K hPa−1; k3 is 3.75 × 105 K2 hPa−1; ne is the electron number density per cubic meter; f is radar frequency in GHz; and W is the liquid water content in g/m3.
The signal delay induced by the hydrostatic and wet components is known as tropospheric delay, the signal delay caused by the liquid component is known as liquid water delay, and the signal advance generated by the ionospheric component is known as an ionospheric advance. Tropospheric delays and ionospheric advances both cause phase patterns at various scales ranging from short wavelength to long wavelength artifacts. Both error sources are more substantial than the liquid water delay in most cases [28]. As liquid water delay accounts for relatively much smaller delays, it is usually ignored during InSAR processing and analysis.
It should be noted that the term “advance” is used in this article to distinguish it from the “delay” that occurs within the troposphere. Since the phase velocity in the ionosphere is greater than in a vacuum, there is a phase advance along the propagation route rather than the delay seen in the troposphere [82,83]. In other words, the increased total electron content along the propagation path in the ionosphere will result in a decreased observed range, so the phase is “advanced” [28]. Due to the fact that the phase is advanced in the ionosphere but delayed in the troposphere, the sign of the ionospheric component in Equation (5) is negative, whereas the other components (all of which occur within the troposphere) are positive. To avoid using misleading language, we will refer to the phenomenon that occurred within the ionosphere as “ionospheric advance” rather than “ionospheric delay”, as was commonly reported in prior research.
Additionally, it is essential to acknowledge that the “phase delay or advance” that occurs during a single acquisition does not generate errors in interferograms, but rather the differences between two acquisitions. For example, if we assume the signal delay or advance in the first and second acquisitions were both 6 mm, there are virtually no atmospheric effects in this set of images. If the variation (difference between two acquisitions) exists with a value other than zero, the difference will create extra fringe patterns in the interferogram, resulting in a systematic error in the InSAR measurements. As a result, the errors caused by ionospheric advance, tropospheric delay, and liquid water delay are strongly reliant on the mediums’ spatiotemporal variability.
3.2.1. Ionospheric Advance
In contrast with neutral atmosphere (mesosphere, stratosphere, and troposphere), the ionosphere is the portion of the atmosphere where ionization occurs as molecules and atoms absorb strong shortwave solar energy [84]. During the process of ionization, molecules or atoms lose electrons and become positively charged ions and the electrons are released from ionization [84]. Therefore, there are a lot of free electrons in the ionosphere. The number of free electrons is represented by the electron density (electrons/m3), and the integral of the electron density along the propagation path within the ionosphere is represented by the total electron content, TEC (TECu or 1016 electrons/m2).
There are several resulting influences which are dependent on TEC when microwave signals propagate through the ionosphere. The influences include group delay (corresponding to a phase advance with the same magnitude but an opposite sign), Faraday rotation, defocusing of SAR images, and an extra shift between SAR images in the azimuth direction [28,85]. Scintillation on SAR imaging is an effect which is unrelated to TEC but can also occur within the ionosphere [85]. Unlike the troposphere, there are limited refractions between radar microwaves and the mediums in the ionosphere. This is because radio frequencies exceeding the plasma frequency (typically between 2 and 20 MHz) could directly pass through the ionosphere without significant reflection and refraction [76]. Further, the frequencies of radar microwaves are between 0.4 and 10 GHz from P-band to X-band, which are far higher than the plasma frequency.
Though being free from the influence of refraction within the ionosphere, Faraday rotation occurs in this layer and can depolarize the transmitting signals. As Faraday rotation only causes significant influences on applications which are related to the utilization of the polarimetric characteristics of the SAR systems [76], it will not be discussed in this paper. Therefore, group delay (or phase advance) and extra shift in azimuth direction are the main focus in this subsection.
As free electrons are a dispersive medium, different frequencies of waves travel at different velocities in the ionosphere [85]. Therefore, a wave-front phase advance, induced by the gradients in the ionospheric electron density, is dependent on the carrier frequencies of the microwave signals. The zenith ionospheric advance () in meters is given in Equation (6) [86], where TECs represents the total electron content along the propagation path in TECu, f is radar frequency in GHz, and 40.28 is a constant with the unit m3/s2 [87]. The ionospheric phase advance can be derived as Equation (7). In Equation (6), ionospheric advance is inversely proportional to the square of radar wave frequency due to the dispersive (frequency dependent) nature of the electrons [85]. As a result, L-band SAR systems are severely susceptible to ionospheric distortions owing to their low frequencies [88].
The errors resulting from ionospheric effect are determined by the spatiotemporal variations of TECs between two acquisitions, thereafter ∆TECs [89,90,91,92,93,94]. ∆TECs is strongly related to the ionization process as the stronger the process is, the more free electrons will be created in the ionosphere [95]. Also, when higher TECs is associated with stronger spatial variation, ∆TECs will be reasonably larger as well.
The ionization level is highest in the equatorial regions due to strong solar radiation resulting from small solar zenith angles and due to the equatorial anomaly resulting from the fountain effect [85,88,96]. As the solar zenith angle ascends with the increase in latitude, the ionization level decreases, so the variation of TECs in the mid-latitude regions is smaller and less variable (27; 41). When the latitude approaches the polar regions, the ionization process becomes active again due to the aurora effect, but the ionization level in the high-latitude regions is not as strong as in the equatorial regions [85,88].
In addition to geographic location that influences the ionization process in the ionosphere, other factors such as time of day, season, solar cycle, and geomagnetic activity are also strongly related to the ∆TECs [97,98]. A study was conducted to inspect the variation of TEC based on the observation data at Taoyuan, Taiwan (24.954°N, 121.165°E), from 2002 to 2014 [83]. According to their results, the following summarizes the variations of TEC: (1) The diurnal variation shows the lowest TEC happened at 5 a.m. (5.51 TECu) and the highest value between 2 p.m. and 4 p.m. local time (48.92 TECu); (2) the seasonal variation shows the lowest TEC between June and July (18 TECu) and between December and January (20 TECu), while the highest TEC is between March and April (33 TECu); and (3) the solar activity cycles, which happen around every 11 years, show the lowest TEC between 2008 and 2009 (10 TECu) and the highest TEC in 2002 (70–80 TECu). Although the observations in Taiwan from 2002 to 2014 cannot be generalized to the rest of the globe, the study provides the readers with a complete overview of different variations in terms of magnitude and fluctuations.
As the InSAR technique is often applied to image pairs with short time intervals, the diurnal variation is crucial. In order to limit the influence of the ionospheric effect, image acquisition in the morning hours is more desirable. Consider Sentinel-1: descending orbiting images are preferable to ascending orbiting images because descending orbiting images are acquired in the early mornings and ascending orbiting images in the late afternoons [88].
Another study arranged TEC characteristics of 47 pairs of Sentienl-1 ascending nodes from 2016 to 2017, in which the study area covered about 3° of latitudinal extent from 22°N to 25°N in Taiwan [99]. In this study, about 38.3% of image pairs obtain |∆TECs| of less than 2 TECu, 36.2% of image pairs obtain between 2 and 5 TECu, 17% of image pairs obtain between 5 and 10 TECu, and 8.5% of image pairs possess |∆ TECs| of more than 10 TECu. The numbers shown here are for reference purposes to showcase a rough reasonable range of ∆TECs. About 75% of image pairs have TEC variation within 5 TECu; thus, 0 to 5 TECu can be considered as a reasonable variation range for normal situations. However, it is clear that ∆TECs is highly variated, as stated in the previous paragraphs. So, one should be aware that this variation can drift to a certain degree depending on the geographical location, latitudinal extents, acquisition time, etc.
Table 3 organizes the impact of the spatiotemporal variation of 1 TECu at L-band, S-band, C-band, and X-band frequencies [28,83]. The third row demonstrates how many phase shifts would be generated by 1 TECu variation at different SAR frequencies. The calculation can essentially be achieved with Equation (7) with a small modification, changing to so the unit will be , i.e., numbers of phase cycles. The variation of 1 TECu can result in 2.11 phase cycles at L-band, 1.07 at S-band, 0.5 at C-band frequency, and 0.28 at X-band frequency [28,83,85]. The fourth row displays the quantity of zenith ionospheric advances resulting from 1 TECu in millimeters. The values are calculated with Equation (6). The sign is negative because an increase in TEC leads to a phase advance [86]. The zenith ionospheric advance () at L-band frequency is −250 mm, which is about 4, 19, and 61 times larger than at S-band, C-band, and X-band frequencies, respectively [85].

Table 3.
The impact of 1 TECu spatiotemporal variation in the ionosphere at L-band, S-band, C-band, and X -band frequencies (modified from [83]).
Figure 3 depicts the effect of TECu’s spatiotemporal fluctuation when it spans from 0 to 15 TECu. Note that the zenith advance (the right subplot) is shown in meters. When the variance is 15 TECu, the zenith advance is nearly 4 m in L-band, 1 m in S-band, and less than 0.25 m in C- and X-band.
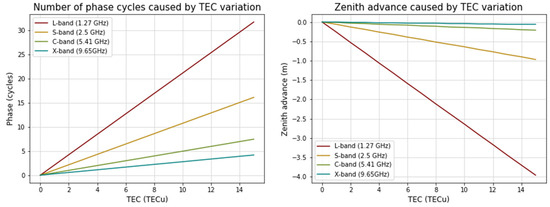
Figure 3.
The impact of the spatiotemporal variation of 0 to 15 TECu at L-band, S-band, C-band, and X-band frequencies. The left subplot shows how many phase shifts would be generated at the given TEC variation (modified from [83]). The right subplot shows how much zenith advance in meters is caused at the given TEC variation. The sign is negative because an increase in TEC leads to a phase advance.
Spatiotemporal ionospheric fluctuations can translate into notable height errors (pertaining to DEM generation) or deformation errors (pertaining to deformation mapping). This translation entails a multiplication of various contributing factors, as expounded upon in the work by Feng et al. [83]. For instance, with a perpendicular baseline of 200 m, even a modest 1 TECu of spatiotemporal fluctuation in the ionosphere can give rise to substantial errors in the measured topographic heights and surface displacements across different frequency bands. Feng et al. [83] quantified these effects and revealed errors of 445.92, 24.62, and 7.72 m in topographic heights, as well as 38, 2, and 0.7 cm in observed surface deformation at L-, C-, and X-band frequencies, respectively.
Although 1 TECu of variation could bring in devastating contamination for L-band sensors, the damage it causes on C-band sensors is not negligible either. Liao’s study [99] has shown that 75% of image pairs in that study have the |∆ TECs| within ±5 TECu. The range reaches up to 2.5 phase shifts and corresponds to 123.1 m of topographic height errors even at the C-band frequency. Other studies also have found that fringe patterns caused by ionospheric effects may be seen in some interferograms obtained with C-band Sentinel-1 and Radarsat images [88,100], especially when the latitudinal range of the study area is large (>50 km) and ionospheric anomalies are present [28,99]. Consequently, it is advised that in such cases, ionospheric advance should not be overlooked, even for C-band systems, and that ionospheric artifact correction be performed as an essential step during InSAR processing [88].
3.2.2. Tropospheric Delay
When radar waves travel through the troposphere, they are refracted and scattered by molecules as well as solid and liquid particles floating in the atmosphere. The refractivity index, N, deviates from unity (i.e., 1) owing to the polarizability of the molecules and the particles in the air [76]. Accordingly, the three terms that impact the refractivity inside the troposphere, including the hydrostatic term, moist term, and liquid term, may be generated based on the molecules and their polarizability [76,81,101]:
- Hydrostatic term: The dry constituents (primarily non-polar nitrogen and oxygen molecules) have an induced dipole moment when interacting with radar microwaves. This means the molecules are polarized, and during the precise moment of polarization, the center of charges is displaced towards the direction of the electric field. Since sometimes the dry constituents include non-polar water vapor, the “hydrostatic delay” is a more precise term than “dry delay”, which is misleading [102].
- Wet term: The wet constituents (mainly polar water vapor molecules) have an induced dipole moment when interacting with radar microwaves.
- Liquid water term: the water molecules (polar liquid water molecules) have a permanent dipole moment when interacting with radar microwaves.
The three terms characterize the delays happening in the troposphere. Tropospheric delays are the addition of delays caused by the hydrostatic term and the wet term. The delay induced by the liquid water term causes liquid water delay (explain in Section 3.2.3). Unlike free electrons in the ionosphere, tropospheric media are nondispersive. Therefore, tropospheric delays are independent of the carrier frequency. The tropospheric phase can be written as Equation (8), where is ground surface height, and is the height of the tropopause (which varies spatially). As a reference, the tropopause in the tropics is about 17 km, at middle latitudes about 11 km, and in polar regions is about 9 km [84]. Although most tropospheric delays happen within the lower troposphere [102], the integral water vapor along the propagation path within the whole troposphere should be obtained to accurately calculate the tropospheric phase. Since the refractivity index N is a very small number, the value is scaled by a factor of 10−6 by definition [77]. Also, as the microwave propagates through the atmosphere along the slant range, the calculation of the delay should be multiplied by the reciprocal of the cosine of incidence angle.
Since microwave wavelengths are inherently sensitive to phase changes, the same amount of signal delay will produce larger phase shifts in short-wavelength sensors than in long-wavelength sensors. For instance, a phase variation caused by spatiotemporal variations of 40 mm/km can result in 2.6 phase cycles for X-band wavelength, 1.4 phase cycles for C-band wavelength, 0.67 phase cycles for S-band wavelength, and 0.3 phase cycle for L-band wavelength. Therefore, phase variations are inversely proportional to microwave wavelength. This calculation is achieved with Equation (9), by which we could convert the number of spatiotemporal variations in mm to the number of phase cycles. Figure 4 depicts the number of phase cycles produced when the spatiotemporal variation ranges from 0 to 120 mm/km. When the spatiotemporal variations are 120 mm/km, it causes eight times more phase shifts in the X-band than in the L-band.
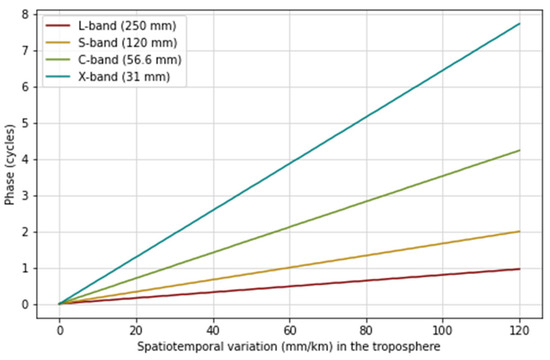
Figure 4.
The impact of the spatiotemporal variation in the troposphere at L-band, S-band, C-band, and X-band wavelengths. The tropospheric effect has a significantly larger influence on shorter-wavelength sensors.
Delay induced by the hydrostatic term is parameterized by total atmospheric pressure, and the resulting hydrostatic delay in zenith direction is defined by surface height (z0), latitude (Φ), and total surface pressure (Ps), given in Equation (10) [28,102,103]. The hydrostatic fringe pattern is smooth and the impact is minimal because the delay induced by the hydrostatic component is just a few millimeters throughout the entire interferogram. Since the spatial fluctuation of total surface pressure is negligible in flat terrain, the impact may be ignored if the frame is less than 50 km [28,43,77]. However, in regions with significant topography, the hydrostatic component is correlated with surface elevation, so the delay should not be ignored [25,104].
The wet term is much more spatially variable compared to the hydrostatic term and is the dominant contributor for tropospheric delays. Therefore, precipitable water vapor (PWV) in millimeters is defined as integrated precipitable water vapor from the surface to the tropopause [102]. This is given by Equation (11), where ρ1 is density of liquid water (106 g/m3) and ρv is density of water vapor (kg/m2) [28]. To acquire the density of liquid water and water vapor, one needs temperature, pressure of water vapor, and saturation vapor pressure information. The zenith delay produced by the wet component is proportional to PWV [105,106], given by Equation (12) [28].
Tropospheric delays are made up of a large range of phase variation between two acquisitions due to the fact that weather conditions can change rapidly and that both the wet and hydrostatic components are topographically dependent. In general, a typical range for tropospheric delay variation is between 8 and 64 mm, equivalent to a 0.3–2.3 phase shift for C-band sensors, but values can rise to more than 120 mm during extreme weather events such as storms, resulting in a large 4.2 phase shift on interferograms [28]. Obviously, tropospheric delay appears to have a significant influence on the observed phase changes. Therefore, it has been one of the most prominent InSAR subjects studied, and numerous correction strategies have been developed. To name a few, common correction methods include ground meteorological observations [103,107], GPS observations [102,108,109,110,111,112,113], weather models [114,115,116,117], and optical sensors [116,118,119].
3.2.3. Liquid Water Delay
In addition to dry neutral atmosphere and water vapor, there are also solid and liquid particles suspended within the atmosphere, such as ice crystals and liquid water droplets, which are the components of clouds [120]. When interacting with a radar wave, liquid water forms a secondary wave front owing to the dielectric medium, and subsequently the undisturbed and secondary wave fronts interfere with each other, resulting in a phase shift [28,76]. Consequently, the refractivity induced by the dielectric medium is related to the liquid water content W (g/m3) as well as the thickness of the cloud layer L (km) regardless of the shape of cloud droplets. The zenith liquid water delay () in mm is given in Equation (13) [28].
The variables W and L fluctuate according to different cloud types (see [120]: 131–133 for cloud classification). Since the values for W and L vary from different literature [28,76,121,122], we categorize two groups for simplification: nonprecipitating clouds and precipitating clouds (including drizzle and rain). Liquid water content for nonprecipitating clouds ranges between 0.1 and 1 g/m3, and for rain clouds, it can exceed 2 g/m3 [123]. To define the range of liquid water content for precipitating clouds, we set a general range of 0.5–3 g/m3 after referencing different literature [28,122,123]. As for the cloud layer, the vertical extent of the cloud could be up to 12 km for the most severe and extreme weather conditions such as thunderstorms [120]. The other values specified for the cloud layer column referenced [76]. Table 4 arranges the overall information and calculates the zenith liquid delay for each group. The zenith liquid water delay () is calculated based on the given range of liquid water content and cloud layer.

Table 4.
Calculation for zenith liquid delay for two groups: nonprecipitating clouds and precipitating clouds (reference the parameters from [28,120,123].
Non-precipitating clouds only induce up to 3 mm of liquid water delay. For situations such as lighter precipitation (drizzle or light rain), say W = 0.5–2 and L = 0.5–2, the resulting liquid delay is within 6 mm, which could produce a noticeable 0.2 phase cycle for C-band sensors and an unnoticeable 0.05 phase cycle for L-band sensors. More drastic situations are clouds of vertical developments where the extents extend to several kilometers in height, such as cumulus congestus and cumulonimbus. These clouds can produce heavy precipitation and are sometimes accompanied by lightning and thunder [120]. In such scenarios, say W > 2 and L > 8, liquid water could result in more than 20 mm of signal delay, corresponding to 0.7 phase shift for C-band sensors and 0.16 phase shift for L-band sensors. Although radar remote sensing is known for “seeing through” clouds and being operable during all weather conditions, and this is always considered one of its best merits over optical sensors, this does not mean that the effects of clouds and rain are negligible in all situations for radar measurements.
In the past, phase delay contributed from liquid water has rarely been considered mainly due to two reasons. First, it is assumed that condensed water such as clouds and precipitation do not exist in the atmosphere under the clear gas hypothesis [28]. Second, the contribution from liquid water delay is as little as only 1–5% of the amount of wet delay since the droplets are too small to cause much scattering [28,79]. However, it is apparent that this hypothesis is not realistic since clouds are an important and prevalent weather phenomenon. Moreover, although phase shifts caused by cloud droplets only produce limited signal delay in interferograms, it is only limited to the conditions of no precipitation. The delay caused by precipitation clouds could climb to a few millimeters, which can be influential for C-band and X-band sensors. In severe weather conditions, cumulus congestus clouds and cumulonimbus clouds can bring in more than 20 mm of delay and can be destructive.
In addition to the errors caused by the liquid water delay itself, ignoring the liquid water delay will lead to a slight overestimation in computing PWV because the refractivity caused by scattering will be interpreted as being caused by water vapor [79]. The value of overestimation is defined as a quarter of a function of rain rate (mm/h) and temperature (K; see Figure A-1 in [79]). For regions where the temperature is higher than 0 °C and the rain rate is lower than 16 mm/h, the overestimation of PWV is less than 5% [79]. Although the overestimation is subtle, it serves as an additional error source if liquid water delay is ignored.
To sum up, the signal delay of C-band sensors caused by liquid water is limited under good weather conditions, especially when no clouds are present in the atmosphere. In this case, liquid water delay can be ignored. Nevertheless, if the weather worsens with increased liquid water content and cloud layer (cloudy sky, drizzle, or light rain), liquid water delay should be considered based on the required accuracy of the application. If the weather condition is severe (strong precipitation or thunderstorm), the influence from liquid water delay must be considered. Note that clouds and precipitation also modulate the observed water vapor quantities, so water vapor concentration is relatively high. As a result, regardless of the weather condition, water vapor (the medium for wet delay) is always the most dominant driving force of the delays [28].
The errors caused by the medium along the propagation path is one of the most complicated and significant contributions. Here we summarize the sources of the artifacts that occur along the propagation path (Table 5).

Table 5.
Summary of the sources of errors that occur along the propagation path.
3.3. Scatterer Movement (Ground Surface)
3.3.1. Scatterer Phase Shift
There are two kinds of changes in point scatterers within the time interval of two acquisitions: one is random motion in which the scatterers move independently from each other and are not spatiotemporally correlated; and the other is when the scatterers move in the same direction together [27,32]. The random movements create phase noise as a result of volume decorrelation or temporal decorrelation, as stated in Section 4. On the other hand, the latter circumstance introduces a systematic phase offset and is therefore classified as a systematic error.
A change in a point scatterer can relate to a change in its dielectric constant. This can be influenced by factors such as density, wetness, particle size, shape, and roughness [124]. These alterations cause variations in backscattering and, as a result, phase shifts. For example, if a soil swells by a few millimeters and the effect is visible from a radar sensor, the systematic change of the point scatterers would contribute extra phase shifts to the interferogram. Scatterer phase shift is rarely addressed as a systematic error source because of its minor contribution, but also because scatterer movement is frequently more random than being spatially correlated. For example, a field of vegetation acquired at two separate dates is likely to have larger volume decorrelation and temporal decorrelation, even if the plant or soil moisture change produced a slight phase shift.
3.3.2. Surface Movements
The other cause for a scatterer’s movement are small surface motions. This is the desired phase information for deformation mapping and undesirable phase information for topographic mapping. The traditional approach to calculating surface motion is the differential InSAR (DInSAR) technique, first proposed by Gabriel et al. [12]. Surface movements resolvable via the DInSAR method include (but are not limited to) volcanic/dike injections, land subsidence, glacier flow, and seismic deformation. The deformation phase component can be calculated by Equation (14), where is the motion along the line-of-sight (LOS) direction. The translation from the number of fringes to the measured deformation is directly related to the sensor wavelength, as a phase cycle corresponds to displacement of half of the wavelength. Therefore, a fringe in an L-band interferogram means a deformation of 12.5 cm, in a C-band means a deformation of 2.8 cm, and in an X-band means a deformation of 1.55 cm (Table 6).

Table 6.
The translation from number of fringes to the measured deformation.
Because these kinds of movements are spatiotemporally correlated, when such incidences happen, this will induce an additional phase shift to the total phase variation if the displacement happens along the LOS direction. However, as the magnitude of the displacements and the spatial scale of the incidences can vary widely, not every surface motion is detectable if it exceeds the limits of the deformation gradient and/or the spatial scale [46]. The detectable area is confined by five boundary lines: (1) upper gradient limit, (2) cycle-slicing limit, and (3) small-gradient limit are the boundary lines for the deformation gradient, while (4) pixel size limit and (5) swath width limit are for enclosing the detectable spatial ranges. The cost of exceeding the boundary lines could be as minor as not being able to detect the surface movements or the possibility of misinterpretation, but also could be as large as causing decorrelation or phase discontinuity. The following paragraphs will elaborate on the five boundary lines in detail.
The limit of upper deformation gradient comes from the constraint of phase variations within a pixel. The phase difference of one pixel between two SAR images must not exceed one fringe of a round trip range shift of one wavelength per pixel as a fundamental criterion for interferometry [46]. If the phase variation exceeds this limit, such as through abrupt changes in topography, the pixels will become incoherent. We could define the upper gradient limit using Equation (15), where fϕ is fringe frequency (cycle/m) given in Equation (4). The expression uses half of wavelength since one fringe corresponds to half of a wavelength’s displacement.
To calculate the upper gradient limit, the critical baseline (Bc) should be applied to Equation (4). The critical baseline is given in Equation (16), where is range single bandwidth in Hz. The definition of critical baseline could be understood from two perspectives. First, as seen from the imaging geometry, Bc is defined as the maximum permissible change in look angle between two acquisitions. The coherence necessary for effective InSAR analysis will be sustained as long as this angular value is not exceeded [32]. Second, as seen from the imaging plane, Bc is defined as the maximum phase change (2π, or a fringe) within a resolution cell [29,30]. The fringe frequency calculated with the critical baseline is formed in Equation (17). By putting Equation (17) back to Equation (15), we can derive the upper gradient limit as Equation (18). Consequently, to calculate the upper gradient limit for any sensor, information on the range single bandwidth and the wavelength of the sensor are required.
Following Equation (18), the calculations of the upper gradient limits for ERS-1, Sentinel-1, TerraSAR-X, and NISAR are presented in Table 7. The upper gradient limit for ERS-1 is 3 × 10−3, which meets the statements in Massonnet and Feigl [46]. This limit means that the displacement (in the range direction) is only detectable below 30 cm every 100 m. Since the range single bandwidth of Sentinel-1 are all larger than ERS-1, the upper gradient limit is about 2–4 times larger. In other words, Sentinel-1 is capable of measuring 2–4 times larger surface motions than ERS-1. TerraSAR-X has a shorter wavelength (X-band) but a much larger range single bandwidth (150 MHz and 300 MHz), resulting in higher upper gradient limits. NISAR has two distinct wavelengths: S-band, and L-band. Both wavelengths are intended to offer a wide variety of possible range bandwidths (10, 25, 37.5, 75 MHz for S-band; and 5, 20, 40, 80 MHz for L-band). We selected 75 MHz for S-band and 80 MHz for L-band sensors to show the maximum capability of detectable deformation for NISAR. The specification of NISAR could measure about-20-times-larger surface motion than ERS-1. It is evident from this table that radar satellite technology has evolved significantly over the past 30 years.

Table 7.
Calculation for the upper gradient limit (ERS-1, Sentinel-1, TerraSAR-X, and NISAR).
The lower gradient limit is characterized by two bottom lines: cycle-slicing limit and small-gradient limit. The upper gradient limit represents the maximum border of the phase change inside one pixel as one fringe, where the cycle slicing limit specifies the minimal phase change where incoherent noise within a pixel does not overwhelm the displacement information. In general, phase differences of less than one-tenth of a fringe are challenging to identify [46]. The cycle-slicing limit could be defined as Equation (19). Consequently, the cycle slicing limit is about 12.5 mm for L-band, 6 mm for S-band sensors, 2.8 mm for C-band, and 1.6 mm for X-band (Table 8). In other words, surface motion is detectable for C-band sensors if the motion is larger than 2.8 mm. Unlike the upper and lower gradient limits, the cycle-slicing limit is a fixed value for a sensor and does not vary with different spatial scales. Therefore, no matter how large or small the image frame is, the cycle-slicing limit for C-band sensors is around 2.8 mm. Wavelength is the decisive factor for the cycle-slicing limit. Longer wavelengths uplift the limit while shorter wavelengths lower it. Accordingly, the cycle-slicing limit of L-band sensors is about 4–5 times larger than that of C-band, meaning tiny surface displacements are less detectable for L-band. On the other hand, X-band possesses better sensitivity over small surface motions, with a cycle-slicing limit at 1.6 mm.

Table 8.
Range of list of symbols and their corresponding values for each satellite (calculation for cycle-slicing limit).
The other bottom line is the small-gradient limit, which is formed because of the mixture of all long wavelength error sources. These sources include the flat-Earth phase, the uncertainty of orbital inaccuracies (orbital error), long wavelength atmospheric gradients, and long wavelength displacements [28,46]. Since the fringe patterns of the long wavelength signals are similar, the phase variation caused by long wavelength displacements can easily be misinterpreted as other longer wavelength errors [125,126]. For the application of deformation mapping, the similarities cause bias in the estimation of the correct deformation. For the application of topographic mapping, this leads to misinterpretation as well as problems of solving the errors correctly based on their sources. As defined by Massonnet and Feigl [46], the small-gradient limit that will cause misinterpretation is about 10−7. The value is unitless and it means long wavelength displacements need to be at least larger than 0.01 mm per 100 m to be distinguished from other long wavelength error sources. The value of 10−7 comes from 0.01 mm divided by 100 m.
The limits of the spatial scale are pixel size limit and swath width limit. The two limits restrict the spatial extent of observable displacement to the dimension as small as a pixel size but could also be as large as the swath width [46]. For example, a surface motion that is only 5 m wide in spatial scale is not detectable in a pixel size of 20 m. However, to observe a geophysical phenomenon, the spatial extent of the occurrence needs to be at least 200 m in the real world (corresponding to about 10 pixels). Thus, the pixel size limit is simply the spatial resolution and only depicts the physical constraint of the detectability of a sensor but is not enough for interpreting geophysical phenomena. The pixel size limit is about 20 m for both ERS-1 and Sentinel-1, about 3 m for TerraSAR-X in Stripmap mode, 16 m for TerraSAR-X in ScanSAR mode, and about 5–30 m for NISAR. Contrary to the pixel size limit, the swath width limit is the maximum detectable spatial limit. Displacements that occur at a scale larger than the width of a swath are not observable; thus, the swath width forms the maximum spatial detectability limit. This limit is 100 km for ERS-1 and about 83 km for a subswath of Sentinel-1, 30 km for TerraSAR-X in Stripmap mode, 100 km for TerraSAR-X in ScanSAR mode, and 240 km for NISAR. It is possible to merge three subswaths together for Sentinel-1 imagery, so the limit could be expanded to 250 km if the three subswaths are combined.
Figure 5 delineates the five detectability limits of ERS-1, Sentinel-1, TerraSAR-X (Stripmap mode and ScanSAR mode), and NISAR (S-band and L-band), modified from [28,46]. The light-yellow color (the area enclosed by the polygon) illustrates the detectable area. To be detected via interferometry and be coherent between two images, a signal needs to fall within the detectable area. Overall, since both ERS-1 and Sentinel-1 use C-band sensors, the boundary lines and detectable area are similar in their values and shape, but the upper gradient limit and swath width limit of Sentinel-1 are slightly larger than those of ERS-1. NISAR has apparently higher cycle-slicing limit because of their larger wavelengths, and this implies that they are relatively worse at detecting small motions. The swath width limit notably affects the actual size of the detectable area since it essentially symbolizes the size of the scan area of a swath. The plots display the x- and y-axes in log scale, so while the size of the region does not appear to change much, their true sizes are considerably different. The detectable area is about 15 km2 for ERS-1 and about 330 km2 for Sentinel-1. The subswath of the TerraSAR-X Stripmap mode is only 30 km, leading it to having the smallest detectable area of 7 km2, while the TerraSAR-X ScanSAR mode has a detectable area of 155 km2. NISAR has a much larger detectable area owing to its wide 240 km subswath. The detectable area for the NISAR S-band is 907 km2, and for L-band it is 1828 km2.
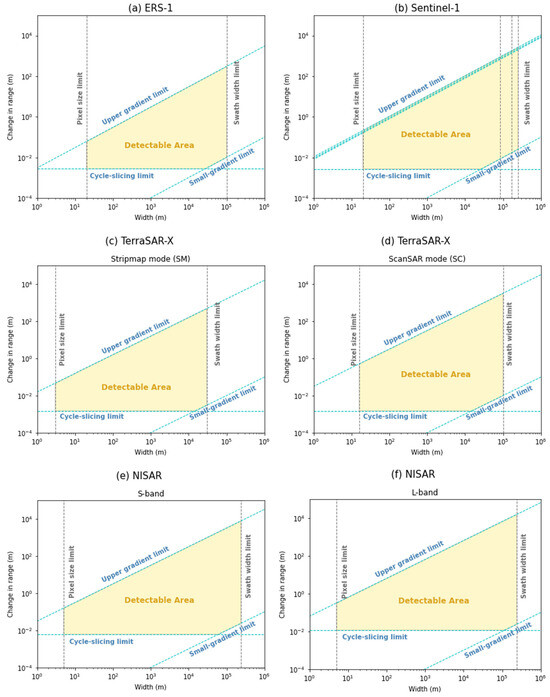
Figure 5.
Detectability for surface movements for (a) ERS-1, (b) Sentinel-1, (c) TerraSAR-X Stripmap mode, (d) TerraSAR-X ScanSAR mode, (e) NISAR S-band, and (f) NISAR L-band, modified from [28,46]. The y-axis shows the magnitude of the surface movements in the range direction, which can be translated to phase gradients. The boundary lines for the magnitude of the surface movements include upper gradient limit, cycle-slicing limit, and small gradient limit, demonstrated in dashed light blue lines. There are three upper gradient limits for Sentinel-1. From top to bottom, they represent the limit of swath 1, swath 2, and swath 3, respectively. The cycle-slicing limit is defined as λ/20, as mentioned in Equation (19). The x-axis shows the spatial scale from 1 m to 106 m. The spatial limitation is characterized by the pixel size limit and the swath width limit, demonstrated by dashed light-gray lines. There are three swath width limits for Sentinel-1. From left to right, they represent the case of using one subswath, two subswaths, and three subswaths, respectively. The light-yellow background color illustrates the detectable area.
The characteristics of each limit are arranged in Table 9 for the reader’s information. The fourth column of Table 9 supplements the geophysical phenomenon that has the possibility of falling out of the detectable area according to [28,46].

Table 9.
Five boundary lines of detectable area and their characteristics.
4. Random Errors
Phase noises are represented as Δφnoise in Equation (1). Phase noise, also known as speckle noise, is the drawback of coherent SAR systems since the functionality of SAR systems relies on coherent scattered signals [45]. Figure 6 demonstrates the InSAR imaging geometry and the SAR signal in detail, where ∆R is the range difference between two acquisitions, H is satellite altitude, and h is topographic height. If the returning waves of both acquisitions oscillate “in phase”, the resulting signal is coherent. If the waves oscillate “out of phase”, the resulting signal is incoherent [127]. Therefore, the returned scattering information (s) recorded in each pixel from the first and second interferometric SAR image is composed of the coherent part (c) and the incoherent part (n), as expressed in Equation (20) [39,128]. Subscript 1 or 2 symbolizes the information acquired during the first and second acquisition.
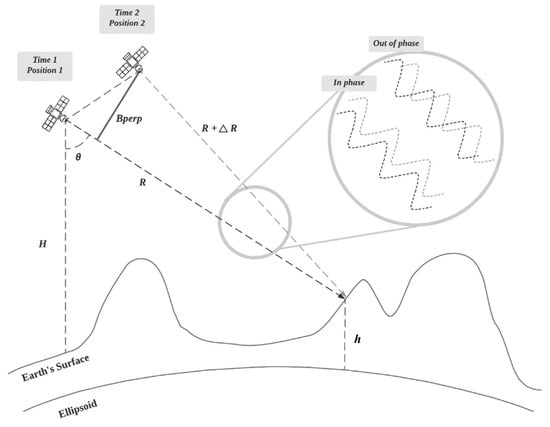
Figure 6.
Imaging geometry of interferometry SAR, revised from [129].
To quantify phase noise and evaluate the quality of an interferogram, the complex correlation coefficient (γ) is defined as Equation (21) [28,36,39,128]. The magnitude of the correlation, i.e., |γ|, is often referred to as “coherence”, which can be used as a measure of phase noise [38]. In Equation (21), s* is the complex conjugate of s, and ⟨∙⟩ means ensemble average. For simplicity, γ is termed coherence hereafter.
Coherence is between 0 and 1. A coherence value equal to 0 indicates that the wave oscillation is fully out of phase; hence, there is no correlation at the given pixel between two SAR images. A coherence value equal to 1 indicates that the condition is completely coherent, and the signals are completely in phase. If the interferogram is covered by low-coherence pixels, they will obscure the useful information in the interferogram, by which the interferogram will start to be grainy, and the fringes will become unrecognizable [35,46]. This not only impedes the interpretation of interferograms but also presents difficulties in retrieving useful phase information and imposes adverse effects on phase unwrapping (PU).
Phase unwrapping is one of the most important steps in InSAR processing as it calculates the absolute phase values from the original wrapped phase [2,27,69,130]. The consequence of PU is decisive for the quality of the final InSAR results. However, PU is an error-prone process mainly due to the existence of phase noise and steep terrain slopes [28,131]. Current PU processing methods involve the path of integration, so the local errors caused by phase noise can easily propagate along the path of integration. If the InSAR processing continues after an erroneous PU calculation, the errors will again propagate throughout the rest of the InSAR workflow and will ultimately undermine the precision of the InSAR measurements. Coherence should be maximized in order to reduce phase noise and prevent PU errors.
Coherence is determined by several different correlation components. The temporal correlation (γtemp) describes the correlation induced by the temporal interval between acquisitions. The baseline correlation (γB) describes the correlation affected by different observing geometries. The volumetric correlation (γvolume) is the correlation influenced by the vertical extent of the scatterers. The noise correlation (γSNR) is the correlation influenced by receiver thermal noise inside of the radar system. The processing-induced correlation (γprocessing) is the correlation influenced by the InSAR processing procedures. Lastly, the doppler centroid correlation (γDC) is influenced by the displacement of the Doppler centroids between two images [28,32,36,38]. Coherence can be calculated as a product of all the aforementioned components, as shown in Equation (22) [30,32]. A critical range of coherence between 0.15 and 0.2 was proposed to judge if useful phase information could be retrieved from an interferogram [39,132]. When the coherence is above the critical range, phase information can be constructed, and the fringe pattern will become more recognizable and readable as the coherence increases. When the coherence lies within the range, it is possible to recover phase information but with higher risks of failure. It is likely not possible to retrieve phase information if the coherence value is below the range [39,132].
Decorrelation, or loss of coherence, is more often used to discuss the physical reason why correlation decreases. It is defined as , where X is the subscripts of each coherence component, i.e., temp, B, volume, SNR, processing, and DC [38]. An increased decorrelation value refers to an increased interferometric phase noise variance. The decorrelation sources are seen as the cause of random errors in the signal. The following paragraphs will elaborate on each decorrelation factor in more detail.
4.1. Temporal Decorrelation ()
Repeat pass SAR systems are susceptible to any changes between two acquisitions [133,134]. That said, the time interval between the acquisitions is the primary factor that causes temporal decorrelation [32]. Everything (e.g., vegetation growth, weather) that can vary between acquisitions are secondary factors and will possibly induce temporal decorrelation. Temporal decorrelation would not occur without the existence of the time interval between two acquisitions. Therefore, it is a specific error cause for all repeat-pass InSAR systems. Once a time difference between two acquisitions exists, many conditions (e.g., changes in moisture, turbulence) will change at various degrees depending on how long the time interval is and the wavelength of the SAR sensor.
The potential changes during the time interval include weather conditions, scatterer movements, surface movements, and surface type. Because the majority of the changes between time intervals are systematic, they do not contribute to temporal decorrelation but are regarded as systematic error causes [32]. For example, a change in weather condition could contribute to atmospheric phase shifts, scatterer motions may be systematic or random, and surface movements often generate systematic phase shifts. Surface type, on the other hand, is the element that reveals how much a specific land cover type varies over time, resulting in loss of coherence. As a result, temporal decorrelation is frequently expressed as the result of the combination of time interval and surface type [28].
Temporal decorrelation can be seen as a function of land cover types owing to different physical properties [32,135]. Urban regions and forested areas are two of the most prevalent examples. Urban areas are less susceptible to temporal decorrelation because buildings are theoretically immobilized and remain stationary for long periods of time. In contrast, vegetated landscapes are more affected by temporal decorrelation due to the subtle movement of the leaves as well as the natural growth cycles of vegetation. Vegetated canopies are also subject to volumetric decorrelation, which makes it more difficult to inspect and quantify temporal decorrelation in vegetated areas [32,136,137,138]. Consequently, it is often suggested to prevent selecting vegetated areas as study sites to simplify the error sources and to enhance the overall coherence.
The triggers that activate these temporal changes on the land surface include wind, precipitation, seasons (phenology and cultivation cycles), anthropogenic activities (e.g., agriculture and construction), and natural hazards (e.g., landslides, eruption, floods). These triggers transform the landscape at varying scales [135]. Also, since their occurrences are stochastic and non-stationary, temporal decorrelation is the most challenging decorrelation component to be modeled and analyzed. Several studies have tried to model temporal decorrelation [32,137,139,140,141]. The significance of understanding, analyzing, and modeling temporal decorrelation is not only in separating different sources of decorrelation but also in benefiting change detection studies for natural hazard assessment [142,143,144].
Despite the complexity involved in quantifying temporal decorrelation, it is one of the most essential contributions for random noise as the coherence decreases rapidly when the time interval increases. This is especially true if the physical properties of the land cover type allow for the temporal triggers discussed above (e.g., natural surface). Therefore, a shorter time interval is necessary to limit the influence of temporal decorrelation. Braun [57] demonstrated the influence of temporal decorrelation on Sentinel-1 imagery. The study has shown that an increase in temporal baseline from 6 to 18 days results in a mean coherence loss of 19.2%. The largest coherence decrease occurred in non-forested vegetation areas (i.e., 30.6%), then in agricultural regions and water bodies (i.e., 20%), while the coherence in urban regions remained above 0.5 [57].
Given the same surface change over a period of time, temporal decorrelation occurs with varying severity for each SAR sensor. A longer wavelength platform is less sensitive to small changes of scattering properties, so L-band and S-band sensors are less susceptible to temporal decorrelation, while C-band and X-band sensors are easily contaminated by phase noises caused by temporal decorrelation [28,32,34,39,145,146,147]. Zebker and Villasenor [32] showed that to achieve complete decorrelation, it requires 10 cm RMS motion of scatterers for L-band sensors, while it only needs 2–3 cm for C-band sensors. That said, it is about four times easier for C-band sensors to completely lose coherence than L-band sensors.
4.2. Baseline/Geometric/Spatial Decorrelation ()
The antenna separation between two repeat SAR acquisitions in space is the baseline of the SAR geometry, and the orthogonal vector of which to the look direction is called the perpendicular baseline (see Figure 6 for InSAR imaging geometry and perpendicular baseline). The difference in two viewing geometries provides the opportunity to observe the topography since the backscattered radar wave contains a different ground reflectivity spectrum for each observation [127]. The reflectivity spectrum difference is defined by a shift and stretch of the imaged terrain spectrum; i.e., the identical spectral components in the first spectrum have a frequency shift in the second spectrum [127]. This is the frequency shift (or spectral shift) that causes decorrelation. The longer the perpendicular baseline, corresponding to a larger spectral shift, the lower the correlation between two SAR images. Once the shift exceeds the range single bandwidth (denoted as BR), the two images will be completely decorrelated because of the zero overlap between two spectrums. With this restraint, the critical baseline (Bc, see Equation (16)) is defined as the maximum effective baseline where the overlap and correlation exist.
The length of the perpendicular baseline is one major factor that causes a frequency shift in the range direction. However, there are minor factors that could also lead to frequency shifts (e.g., steepness of the terrain slope and the gradient of the surface displacements) [28]. We mentioned that steep terrain slopes are a major contributor to the loss of coherence; here, we demonstrate why: steep slopes increase the spectral shift, resulting in less overlap. To consider the influence of terrain slope (α) on frequency shift (∆f), Gatelli [127] has demonstrated that spectral shift is a function of the local angle (Equation (23)). Terrain slope ranges from −90° to 90°, where the positive angles (α = 0°~90°) mean that the slope is facing the sensor, and the negative angles (α = −90°~0°) mean a backslope relative to the sensor. Equation (23) shows that ∆f is dependent on perpendicular baseline, local terrain slope, and incident angle. Suppose the perpendicular baseline is fixed (−600 m for ERS-1 as a reproduction of Gatelli [127], and −100 m for Sentinel-1 as a reasonable value for using Sentinel-1), the relationship between the local terrain slope and the frequency shift can be visualized (Figure 7). The parameters used for the ERS-1 frequency shift calculation are retrieved from Gatelli [127], and the parameters set for Sentinel-1 (IW1, IW2, and IW3), TerraSAR-X (Stripmap mode and ScanSAR mode), and NISAR (S-band and L-band) are selected within their reasonable range (Table 10). With the frequency shift calculated from Equation (23), one could derive the coherence for baseline term by Equation (24).
Figure 7.
Frequency shift as a function of the local terrain slope in the case of ERS-1, Sentinel-1 (IW1/IW2/IW3), TerraSAR-X (Stripmap mode and ScanSAR mode), and NISAR (S-band and L-band). The horizontal red dashed lines symbolize the range single bandwidth. The pink background color shows the blind angle area where the frequency shift exceeds the single range bandwidth. The slopes within the blind angle area (pink) will directly lead to a complete loss of coherence (decorrelation). The light yellow, light green, and light gray background colors represent the area of angles where layover, foreshortening, and shadow occurs, respectively. The area without a colored background means the terrain slope is not subject to the influence of geometric decorrelation (blind angle area) nor geometric distortion (layover, foreshortening, and shadow).

Table 10.
Set of parameters used to calculate the frequency shift in Figure 7.
Frequency shift is directly related to the overlap between two spectra. When the frequency shift (the black curves in Figure 7) equals 0 (indicated by the horizontal black dashed line), the overlap is 100%. However, when the frequency shift matches the range single bandwidth (indicated by horizontal red dashed lines), the overlap is 0. Once the frequency shift exceeds the range single bandwidth, i.e., , there is no overlap in the range direction between both the primary and secondary images. This implies a complete loss of correlation between the two images, i.e., γB = 0. The frequency shift can surge to infinity when the local terrain slope approaches the incident angle (indicated by the vertical black line). Blind angles (pink background) are local slope angles close to the incidence angle that cause the frequency shift to exceed the range single bandwidth. Baseline decorrelation occurs within this local slope range [127]. ERS-1 has the broadest blind angle range (about incidence angle ), owing to its extremely low-range single bandwidth (16 MHz). This suggests that ERS-1 (with the given parameters) is the most vulnerable to geometric decorrelation. Note that the blind angles in subplots (b), (c), (d), (g), and (h) are quite narrow (about incidence angle ), making them less noticeable, but they do exist.
In addition to range single bandwidth, the other most influential factor that impacts the blind angle range is the perpendicular baseline. Figure 8 demonstrates the frequency shift plot with NISAR S-band parameters at varying perpendicular baselines (i.e., −500 m, −1000 m, −5000 m, and −10,000 m). When the perpendicular baseline increases, so does the blind angle range, and the frequency shift curve becomes more rounded. When comparing the −500 m (Figure 8a) and −10,000 m (Figure 8d) scenarios, the frequency shift remains very close to zero until the local terrain slope approaches the incidence angle when the perpendicular baseline is −500 m. In contrast, the frequency shift rapidly increases as the slope increases when the perpendicular baseline is −10,000 m. This shows that baseline correlation is more likely to reduce under longer perpendicular baselines. Therefore, coming back to Figure 7, Sentinel-1 and NISAR L-band are two SAR system designs that are less likely to experience geometric decorrelation due to their narrower perpendicular baselines. We note that other systems can have wider blind angles when their baselines are higher than the values set for the derivation of this figure (i.e., Table 10).
Figure 8.
Frequency shift as a function of the local terrain slope in the case of NISAR S-band with four different perpendicular baselines (−500 m, −1000 m, −5000 m, and −10,000 m). The colored lines and regions in these subplots follow the same meanings as in Figure 7.
The third factor that influences the blind angle is wavelength. Large wavelengths can obtain narrower blind angles, while short wavelengths lead to wider blind angles. This is the main reason why TerraSAR-X shows a noticeably larger range of blind angles despite its significantly larger single-range bandwidth. The range of blind angles in subplot (e) is about incidence angle , and in subplot (f), it is about incidence angle .
4.3. Volume Decorrelation ()
The baseline decorrelation (previous subsection) was derived with an assumption that the returned signal comprised only surface scattering (Figure 9 Left) [30,36,127,148]. However, different media are more conductive to volume scattering (e.g., vegetation, sand, and icy terrain) (Figure 9 Right) [30,36,127,149,150].
Figure 9.
Illustration of volume decorrelation. A stands for antenna. The subscript 1 and 2 symbolize the first and second acquisition. ∆z is the vertical vector of the scattering layer. B is baseline between A1 and A2. B⊥ is perpendicular baseline. (Left) Interferometry viewing geometry with the assumption that the returned signal is only comprised of surface scattering. (Right) Interferometry viewing geometry which considers the influence of a scattering layer.
The ability of the radar signal to penetrate the ground surface is determined by the incident wavelength as well as the dielectric constant of the scattering medium. The vertical vector (∆z) of the penetration within a resolution cell causes dispersion of the scatterers [69], so the vertical vector is the decisive factor for volume decorrelation. As the backscatter phase from a given pixel is extended over a larger projected area along the vertical vector, a thicker scattering layer leads to more severe loss of coherence until it reaches a critical thickness (∆zc). This is defined in Equation (25), where volume correlation becomes 0 (Equation (26)) [36,127].
4.4. Noise Decorrelation ()
Noise decorrelation is related to the signal-to-noise Ratio (SNR) [32]. The SNR is calculated by the ratio of the target signal (S) to noise power (N, Equation (27)) [32]. The noise contribution of this term mainly comes from receiver thermal noise and jammer noise [151]. Receiver thermal noise is formed when the temperature of the internal radar receiver interferes with the target signal. Jammer noise introduces noise into the radar receiver through the antenna and interferes with the target signal [151,152]. Both receiver thermal noise and jammer noise reduce SNR and cause difficulty in detecting target signals. Low SNR values result in decreased coherence or high decorrelation (Equation (28)). SNR over the entire radar image is not necessarily uniform and is spatially variable over the scene. This variability is dependent on the strength of the backscattered signal. For example, noise decorrelation is dominant in radar shadow areas as no signal is returned from these areas. Therefore, the correlation in shadow areas is zero.
4.5. Processing-Induced Decorrelation ()
Processing-induced decorrelation differs from all other error causes identified thus far. The errors in the aforementioned scenarios are caused by the sensor, orbit positioning, propagation path, or surface/scatterer motion. Processing-induced decorrelation is introduced during InSAR processing. The two most prevalent forms are interpolation error and coregistration error.
Resampling is the first step in InSAR processing which helps to coregister the first image onto the second one. To resample radar images, an interpolation kernel is applied for the purpose of convolution. Different interpolation kernels create aliasing terms at varying scales and are treated as interpolation noises [153] which reduce coherence.
Coregistration is one of the most important steps in InSAR processing. In this step, two radar images are aligned so that an interferogram can be properly generated in subsequent steps. Good alignment symbolizes optimal coherence conditions. On the other hand, misalignment reduces coherence. A shift of an entire resolution cell will result in a complete loss of coherence since it means there is no overlap within the resolution cells between the two radar scans. Consequently, subpixel coregistration accuracy is required to obtain coherent interferometric products.
As the algorithms applied for InSAR processing have been developed for several decades, the interpolation error and coregistration error are subtle enough to be ignored. For example, the cubic convolution method can achieve mean total coherence at over 0.99, and a coregistration accuracy of 0.1 resolution cell can achieve a mean total coherence at 0.96 [28]. For the equations to calculate mean total coherence, one can reference Hanssen [28].
4.6. Doppler Centroid Decorrelation Decorrelation ()
Doppler centroid decorrelation is the equivalent of geometric decorrelation but in the azimuth (or along-track) direction [28]. Doppler centroid (fDC) is related to the frequency of the azimuth beam center. Ideally, the Doppler centroid is zero. However, due to the Earth’s rotation, the center of the illuminating beam on the ground varies while the satellite is orbiting. The difference of Doppler centroid (∆fDC) between the primary and secondary images would cause a mismatch of two spectrums in the azimuth direction, and a lack of spectrum overlap will reduce the coherence (γDC), thereby resulting in Doppler centroid decorrelation [55]. Similar to geometric decorrelation, the coherence factor γDC decreases as the difference of Doppler centroid increases (e.g., Equation (29), where BA is the bandwidth in azimuth direction) [28].
One way to avoid Doppler centroid decorrelation is by filtering the bursts of two images to a common bandwidth which is known as azimuth spectral shift filtering (or azimuth filtering). The drawback of this method is that the azimuth resolution is downgraded [55]. However, Doppler centroid decorrelation generally creates a very limited coherence drop due to that the advanced attitude steering capabilities of modern spaceborne satellites. The yaw-steering mode applied on ERS-1/2 back in 1991 was already capable of minimizing the effect of Doppler centroid decorrelation without azimuth filtering [28,154]. The zero-Doppler attitude steering mode that is applied during Sentinel-1 operation is a significant improvement from the ERS-1/2 era as the zero-Doppler attitude steering mode combines yaw-steering with an additional pitch-steering to reduce the Doppler centroid to 0 Hz. Studies have assessed and proven that Sentinel-1 possesses an excellent attitude steering system, which means no azimuth filtering is necessary unless pre-processed SLC images are used or many interferograms need to be stacked [28,55].
5. Conclusions
In this paper, we have provided a comprehensive review of the error budget within the InSAR processing technique. Our aim was to address two critical issues: the lack of thorough discussion about each error source and their influence on InSAR-derived products; and the difficulty for novices in grasping the intricate mathematics and signal processing knowledge associated with InSAR workflows. We classified InSAR-related errors into two main categories, namely, intrinsic height errors and location-induced errors, with further subdivisions into systematic and random errors for intrinsic height errors. Our focus primarily revolved around systematic and random errors and their impact on InSAR-derived topographic and deformation products. Throughout the paper, we strived to make the content easily understandable by using plain language, fundamental mathematical concepts, and numerical and visual comparisons. We have also emphasized the influence of radar wavelengths by comparing different SAR bands. These include L-band, S-band, C-band, and X-band, using representative SAR platforms as examples (i.e., ERS-1, Sentinel-1, TerraSAR-X, and the upcoming NISAR mission).
In conclusion, this review provides valuable insights into the error sources of InSAR processing and their implications for the accuracy of derived products. By offering an organized, comprehensive, and easily understandable discussion, we hope to bridge the gap between technical and non-technical audiences, thereby making InSAR more accessible to a wider range of readers and data users. Additionally, we acknowledge that there may be error sources not covered in this work, and we encourage further exploration in future research. Some minor error sources that were not included in this paper incluide approximation errors, some InSAR processing constants, as well as terms that are minimal and neglected (e.g., Faraday rotation). Moreover, the most important error which merits further discussion stems from phase unwrapping (PU), which results from phase noise. Compared to systematic errors, it is much more complicated to formulate how random errors hinder the PU process, lead to further PU errors, and jeopardize the overall accuracy of the InSAR-derived products. Further, PU is another topic that has been heavily discussed in the InSAR literature since the 1970s. The advances in different PU methods can help to solve the current error-prone PU problem and help track how phase noise introduces error into the final InSAR products.
Overall, this paper contributes to the existing body of knowledge on InSAR processing by shedding light on the error budget and facilitating a deeper understanding of the challenges involved. We believe that our efforts will aid both researchers and InSAR practitioners in improving the accuracy of their InSAR-derived data products, ultimately advancing the applications and potential of this valuable remote sensing technique.
Author Contributions
Conceptualization, Y.-Y.W.; methodology, Y.-Y.W.; software, Y.-Y.W.; validation, Y.-Y.W.; formal analysis, Y.-Y.W.; investigation, Y.-Y.W.; resources, Y.-Y.W.; data curation, Y.-Y.W.; writing—original draft preparation, Y.-Y.W.; writing—review and editing, A.M.; visualization, Y.-Y.W.; supervision, A.M.; project administration, A.M.; funding acquisition, A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
There is no data involved in this review paper. The Python code that is used to create figures will not be shared.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Elachi, C.; Bicknell, T.; Jordan, R.L.; Wu, C. Spaceborne synthetic-aperture imaging radars: Applications, techniques, and technology. Proc. IEEE 1982, 70, 1174–1209. [Google Scholar] [CrossRef]
- Graham, L.C. Synthetic interferometer radar for topographic mapping. Proc. IEEE 1974, 62, 763–768. [Google Scholar] [CrossRef]
- Richman, D. Three Dimensional, Azimuth-Correcting Mapping Radar. U.S. Patent 4321601A, 23 March 1982. [Google Scholar]
- Zisk, S.H. A new, earth-based radar technique for the measurement of lunar topography. Moon 1972, 4, 296–306. [Google Scholar] [CrossRef]
- Mercer, B. DEMs created from airborne IFSAR—An update. Int. Arch. Photogramm. Remote Sens. 2004, 35, 841–848. [Google Scholar]
- Nelson, A.; Reuter, H.I.; Gessler, P. DEM production methods and sources. Dev. Soil Sci. 2009, 33, 65–85. [Google Scholar]
- Gens, R.; Van Genderen, J.L. Review Article SAR interferometry—Issues, techniques, applications. Int. J. Remote Sens. 1996, 17, 1803–1835. [Google Scholar] [CrossRef]
- Hartl, P. Application of interferometric SAR-data of the ERS-1 mission for high resolution topographic terrain mapping. Geo-Inf.-Syst. 1991, 4, 8–14. [Google Scholar]
- Hartl, P.; Thiel, K.H. Radar interferometry—Basic concepts and applications. ISPRS 1993, 29, 207–233. [Google Scholar]
- Hartle, P. Application of SAR interferometry with ERS-1 in the Antarctic. Earth Obs. Q. 1994, 43, 1–4. [Google Scholar]
- Fahnestock, M.; Bindschadler, R.; Kwok, R.; Jezek, K. Greenland ice sheet surface properties and ice dynamics from ERS-1 SAR imagery. Science 1993, 262, 1530–1534. [Google Scholar] [CrossRef]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. Solid Earth 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Jónsson, S.; Segall, P.; Pedersen, R.; Björnsson, G. Post-earthquake ground movements correlated to pore-pressure transients. Nature 2003, 424, 179–183. [Google Scholar] [CrossRef] [PubMed]
- Massonnet, D.; Rossi, M.; Carmona, C.; Adragna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The displacement field of the Landers earthquake mapped by radar interferometry. Nature 1993, 364, 138–142. [Google Scholar] [CrossRef]
- Wright, T.J.; Parsons, B.; England, P.C.; Fielding, E.J. InSAR observations of low slip rates on the major faults of western Tibet. Science 2004, 305, 236–239. [Google Scholar] [CrossRef] [PubMed]
- Feigl, K.L.; Sergent, A.; Jacq, D. Estimation of an earthquake focal mechanism from a satellite radar interferogram: Application to the December 4, 1992 Landers aftershock. Geophys. Res. Lett. 1995, 22, 1037–1040. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Engelhardt, H.; Kamb, B.; Frolich, R.M. Satellite radar interferometry for monitoring ice sheet motion: Application to an Antarctic ice stream. Science 1993, 262, 1525–1530. [Google Scholar] [CrossRef] [PubMed]
- Joughin, I.R.; Kwok, R.; Fahnestock, M.A. Interferometric estimation of three-dimensional ice-flow using ascending and descending passes. IEEE Trans. Geosci. Remote Sens. 1998, 36, 25–37. [Google Scholar] [CrossRef]
- Briole, P.; Massonnet, D.; Delacourt, C. Post-eruptive deformation associated with the 1986–87 and 1989 lava flows of Etna detected by radar interferometry. Geophys. Res. Lett. 1997, 24, 37–40. [Google Scholar] [CrossRef]
- Massonnet, D.; Briole, P.; Arnaud, A. Deflation of Mount Etna monitored by spaceborne radar interferometry. Nature 1995, 375, 567–570. [Google Scholar] [CrossRef]
- Wicks Jr, C.; Thatcher, W.; Dzurisin, D. Migration of fluids beneath Yellowstone caldera inferred from satellite radar interferometry. Science 1998, 282, 458–462. [Google Scholar] [CrossRef]
- Hilley, G.E.; Burgmann, R.; Ferretti, A.; Novali, F.; Rocca, F. Dynamics of slow-moving landslides from permanent scatterer analysis. Science 2004, 304, 1952–1955. [Google Scholar] [CrossRef] [PubMed]
- Bawden, G.W.; Thatcher, W.; Stein, R.S.; Hudnut, K.W.; Peltzer, G. Tectonic contraction across Los Angeles after removal of groundwater pumping effects. Nature 2001, 412, 812–815. [Google Scholar] [CrossRef] [PubMed]
- Carnec, C.; Delacourt, C. Three years of mining subsidence monitored by SAR interferometry, near Gardanne, France. J. Appl. Geophys. 2000, 43, 43–54. [Google Scholar] [CrossRef]
- Ding, X.L.; Liu, G.X.; Li, Z.W.; Li, Z.L.; Chen, Y.Q. Ground subsidence monitoring in Hong Kong with satellite SAR interferometry. Photogramm. Eng. Remote Sens. 2004, 70, 1151–1156. [Google Scholar] [CrossRef]
- Massonnet, D.; Holzer, T.; Vadon, H. Land subsidence caused by the East Mesa geothermal field, California, observed using SAR interferometry. Geophys. Res. Lett. 1997, 24, 901–904. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Boston, NY, USA, 2001. [Google Scholar]
- Li, F.K.; Goldstein, R.M. Studies of multibaseline spaceborne interferometric synthetic aperture radars. IEEE Trans. Geosci. Remote Sens. 1990, 28, 88–97. [Google Scholar] [CrossRef]
- Rodriguez, E.; Martin, J.M. Theory and design of interferometric synthetic aperture radars. IEEE Proc. F Radar Signal Process. 1992, 139, 147–159. [Google Scholar] [CrossRef]
- Zebker, A.; Rosen, P.A. Atmospheric Artifacts in Interferometric SARSurface Deformation Topografic Maps. J. Geophys. Res. Solid Earth 1996. [Google Scholar]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Goldstein, R. Atmospheric limitations to repeat-track radar interferometry. Geophys. Res. Lett. 1995, 22, 2517–2520. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Zebker, H.A.; Webb, F.H.; Fielding, E.J. Surface deformation and coherence measurements of Kilauea Volcano, Hawaii, from SIR-C radar interferometry. J. Geophys. Res. Planets 1996, 101, 23109–23125. [Google Scholar] [CrossRef]
- Ferretti, A.; Monti-Guarnieri, A.; Prati, C.; Rocca, F. InSAR Principles: Guidelines for SAR Interferometry Processing and Interpretation (TM-19, February 2007); European Space Agency (ESA): Paris, France, 2007. [Google Scholar]
- Hoen, E.W.; Zebker, H.A. Penetration depths inferred from interferometric volume decorrelation observed over the Greenland ice sheet. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2571–2583. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing; Mcgraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Simons, M.; Rosen, P.A. Interferometric synthetic aperture radar geodesy. Geodesy 2007, 3, 391–446. [Google Scholar]
- Wei, M.; Sandwell, D.T. Decorrelation of L-band and C-band interferometry over vegetated areas in California. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2942–2952. [Google Scholar]
- Wu, Y.Y.; Ren, H. Regression analysis of errors of sar-based dems and controlling factors. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2021, XLIII-B5, 51–57. [Google Scholar] [CrossRef]
- Braun, A. Sentinel-1 Toolbox: DEM generation with Sentinel-1 Workflow and Challenges. Open Geosci. 2020, 13, 532–569. [Google Scholar] [CrossRef]
- Pepe, A.; Calò, F. A review of interferometric synthetic aperture RADAR (InSAR) multi-track approaches for the retrieval of Earth’s surface displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef]
- Tarayre, H.; Massonnet, D. Atmospheric propagation heterogeneities revealed by ERS-1 interferometry. Geophys. Res. Lett. 1996, 23, 989–992. [Google Scholar] [CrossRef]
- Jensen, H.; Graham, L.C.; Porcello, L.J.; Leith, E.N. Side-looking airborne radar. Sci. Am. 1977, 237, 84–95. [Google Scholar] [CrossRef]
- Porcello, L.J.; Massey, N.G.; Innes, R.B.; Marks, J.M. Speckle reduction in synthetic-aperture radars. JOSA 1976, 66, 1305–1311. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Corner, W.R.; Rees, W.G. The simulation of geometric distortion in a synthetic aperture radar image of Alpine terrain. In Proceedings of the 1995 International Geoscience and Remote Sensing Symposium, IGARSS’95. Quantitative Remote Sensing for Science and Applications, Firenze, Italy, 10–14 July 1995; IEEE: Toulouse, France, 1995; pp. 1515–1517. [Google Scholar]
- Rho, S.H.; Song, W.Y.; Kim, J.; Kwag, Y.K. Geolocation error correction method for SAR image using ground control. In Proceedings of the 2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Seoul, Republic of Korea, 26–30 September 2011; IEEE: Toulouse, France, 2011; pp. 1–4. [Google Scholar]
- Bayer, T.; Winter, R.; Schreier, G. Terrain influences in SAR backscatter and attempts to their correction. IEEE Trans. Geosci. Remote Sens. 1991, 29, 451–462. [Google Scholar] [CrossRef]
- Flores-Anderson, A.I.; Herndon, K.E.; Thapa, R.B.; Cherrington, E. The SAR Handbook: Comprehensive Methodologies for Forest Monitoring and Biomass Estimation; NASA Technical Reports Server: Cleveland, OH, USA, 2019.
- MacDonald, H.C. Geologic Evaluation of Radar Imagery from Darien Province, Panama; Defense Technical Information Center: Fort Belvoir, VA, USA, 1969. [Google Scholar]
- Lewis, A.J.; Macdonald, H.C. Interpretive and mosaicking problems of SLAR imagery. Remote Sens. Environ. 1970, 1, 231–236. [Google Scholar] [CrossRef]
- Barat, I.; Prats-Iraola, P.; Duesmann, B.; Geudtner, D. Sentinel-1: Link between orbit control and interferometric SAR baselines performance. In Proceedings of the 25th International Symposium on Space Flight Dynamics, Munich, Germany, 19–23 October 2015; pp. 19–23. [Google Scholar]
- Noviello, C.; Verde, S.; Zamparelli, V.; Fornaro, G.; Pauciullo, A.; Reale, D.; Nicodemo, G.; Ferlisi, S.; Gulla, G.; Peduto, D. Monitoring buildings at landslide risk with SAR: A methodology based on the use of multipass interferometric data. IEEE Geosci. Remote Sens. Mag. 2020, 8, 91–119. [Google Scholar] [CrossRef]
- Yagüe-Martínez, N.; Prats-Iraola, P.; Gonzalez, F.R.; Brcic, R.; Shau, R.; Geudtner, D.; Eineder, M.; Bamler, R. Interferometric processing of Sentinel-1 TOPS data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2220–2234. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Fransson, J.E.S.; Wegmüller, U. Complementarity of X-, C-, and L-band SAR backscatter observations to retrieve forest stem volume in boreal forest. Remote Sens. 2019, 11, 1563. [Google Scholar] [CrossRef]
- Braun, A. Retrieval of digital elevation models from Sentinel-1 radar data–open applications, techniques, and limitations. Open Geosci. 2021, 13, 532–569. [Google Scholar] [CrossRef]
- Prats-Iraola, P.; Rodriguez-Cassola, M.; De Zan, F.; Scheiber, R.; López-Dekker, P.; Barat, I.; Geudtner, D. Role of the orbital tube in interferometric spaceborne SAR missions. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1486–1490. [Google Scholar] [CrossRef]
- Wegmüller, U.; Santoro, M.; Werner, C.; Strozzi, T.; Wiesmann, A.; Lengert, W. DEM generation using ERS–ENVISAT interferometry. J. Appl. Geophys. 2009, 69, 51–58. [Google Scholar] [CrossRef]
- Santoro, M.; Wegmuller, U.; Askne, J.I.H. Signatures of ERS–Envisat interferometric SAR coherence and phase of short vegetation: An analysis in the case of maize fields. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1702–1713. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Price, E.J. Phase gradient approach to stacking interferograms. J. Geophys. Res. Solid Earth 1998, 103, 30183–30204. [Google Scholar] [CrossRef]
- Gaber, A.; Darwish, N.; Koch, M. Minimizing the residual topography effect on interferograms to improve DInSAR results: Estimating land subsidence in Port-Said City, Egypt. Remote Sens. 2017, 9, 752. [Google Scholar] [CrossRef]
- He, L.; Wu, L.; Liu, S.; Wang, Z.; Su, C.; Liu, S.-N. Mapping two-dimensional deformation field time-series of large slope by coupling DInSAR-SBAS with MAI-SBAS. Remote Sens. 2015, 7, 12440–12458. [Google Scholar] [CrossRef]
- Pawluszek-Filipiak, K.; Borkowski, A. Integration of DInSAR and SBAS Techniques to determine mining-related deformations using sentinel-1 data: The case study of Rydułtowy mine in Poland. Remote Sens. 2020, 12, 242. [Google Scholar] [CrossRef]
- Jung, H.-S.; Won, J.-S.; Kim, S.-W. An improvement of the performance of multiple-aperture SAR interferometry (MAI). IEEE Trans. Geosci. Remote Sens. 2009, 47, 2859–2869. [Google Scholar] [CrossRef]
- Zeng, Q.; Li, X.; Gao, L.; Liu, Y. An improvement to flattening in interferometric SAR processing. In Proceedings of the Remote Sensing of the Environment: 15th National Symposium on Remote Sensing of China, Guiyan City, China, 19–23 August 2005; International Society for Optics and Photonics: San Diego, CA, USA, 2006; p. 62000D. [Google Scholar]
- Tkachenko, A.I. GPS-correction in the problem of low-orbit spacecraft navigation. J. Comput. Syst. Sci. Int. 2009, 48, 447. [Google Scholar] [CrossRef]
- Rizzoli, P.; Martone, M.; Gonzalez, C.; Wecklich, C.; Tridon, D.B.; Bräutigam, B.; Bachmann, M.; Schulze, D.; Fritz, T.; Huber, M. Generation and performance assessment of the global TanDEM-X digital elevation model. ISPRS J. Photogramm. Remote Sens. 2017, 132, 119–139. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Tian, X.; Malhotra, R.; Xu, B.; Qi, H.; Ma, Y. Modeling orbital error in InSAR interferogram using frequency and spatial domain based methods. Remote Sens. 2018, 10, 508. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, J.; Fu, H.; Feng, G.; Wang, C. Modeling and robust estimation for the residual motion error in airborne SAR interferometry. IEEE Geosci. Remote Sens. Lett. 2018, 16, 65–69. [Google Scholar] [CrossRef]
- Yoon, Y.T.; Eineder, M.; Yague-Martinez, N.; Montenbruck, O. TerraSAR-X precise trajectory estimation and quality assessment. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1859–1868. [Google Scholar] [CrossRef]
- Liao, M.; Balz, T.; Rocca, F.; Li, D. Paradigm changes in Surface-Motion estimation from SAR: Lessons from 16 years of Sino-European cooperation in the dragon program. IEEE Geosci. Remote Sens. Mag. 2020, 8, 8–21. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, Y.; Fu, H.; Zhu, J.; Yu, Y.; Li, R.; Zhang, S.; Qu, Z.; Hu, S. Parameterized Modeling and Calibration for Orbital Error in TanDEM-X Bistatic SAR Interferometry over Complex Terrain Areas. Remote Sens. 2021, 13, 5124. [Google Scholar] [CrossRef]
- Fattahi, H.; Amelung, F. InSAR uncertainty due to orbital errors. Geophys. J. Int. 2014, 199, 549–560. [Google Scholar] [CrossRef]
- Barclay, L. Propagation of Radiowaves; IET: Stevenage, UK, 2003. [Google Scholar]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. Solid Earth 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Wright, T.; Fielding, E.; Parsons, B. Triggered slip: Observations of the 17 August 1999 Izmit (Turkey) earthquake using radar interferometry. Geophys. Res. Lett. 2001, 28, 1079–1082. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System. J. Geophys. Res. Atmos. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Smith, E.K.; Weintraub, S. The constants in the equation for atmospheric refractive index at radio frequencies. Proc. IRE 1953, 41, 1035–1037. [Google Scholar] [CrossRef]
- Thayer, G.D. An improved equation for the radio refractive index of air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Belcher, D.P. Theoretical limits on SAR imposed by the ionosphere. IET Radar Sonar Navig. 2008, 2, 435–448. [Google Scholar] [CrossRef]
- Feng, J.; Zhen, W.; Wu, Z. Ionospheric effects on repeat-pass SAR interferometry. Adv. Space Res. 2017, 60, 1504–1515. [Google Scholar] [CrossRef]
- Lutgens, F.K.; Tarbuck, E.J.; Tusa, D. The Atmosphere; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Fattahi, H.; Simons, M.; Agram, P. InSAR time-series estimation of the ionospheric phase delay: An extension of the split range-spectrum technique. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5984–5996. [Google Scholar] [CrossRef]
- Gomba, G.; Parizzi, A.; De Zan, F.; Eineder, M.; Bamler, R. Toward operational compensation of ionospheric effects in SAR interferograms: The split-spectrum method. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1446–1461. [Google Scholar] [CrossRef]
- Jakowski, N.; Bettac, H.-D.; Jungstand, A. Ionospheric corrections for radar altimetry and geodetic positioning techniques. In Proceedings of the Symposium on Refraction of Transatmospheric Signals in Geodesy, The Hague, The Netherlands, 19–22 May 1992. [Google Scholar]
- Gomba, G.; González, F.R.; De Zan, F. Ionospheric phase screen compensation for the Sentinel-1 TOPS and ALOS-2 ScanSAR modes. IEEE Trans. Geosci. Remote Sens. 2016, 55, 223–235. [Google Scholar] [CrossRef]
- Gray, A.L.; Mattar, K.E.; Sofko, G. Influence of ionospheric electron density fluctuations on satellite radar interferometry. Geophys. Res. Lett. 2000, 27, 1451–1454. [Google Scholar] [CrossRef]
- Jakowski, N.; Stankov, S.M.; Schlueter, S.; Klaehn, D. On developing a new ionospheric perturbation index for space weather operations. Adv. Space Res. 2006, 38, 2596–2600. [Google Scholar] [CrossRef]
- Mattar, K.E.; Gray, A.L. Reducing ionospheric electron density errors in satellite radar interferometry applications. Can. J. Remote Sens. 2002, 28, 593–600. [Google Scholar] [CrossRef]
- Meyer, F.; Bamler, R.; Jakowski, N.; Fritz, T. The potential of low-frequency SAR systems for mapping ionospheric TEC distributions. IEEE Geosci. Remote Sens. Lett. 2006, 3, 560–564. [Google Scholar] [CrossRef]
- Rignot, E.J.M. Effect of Faraday rotation on L-band interferometric and polarimetric synthetic-aperture radar data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 383–390. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Chen, C. Measurement and mitigation of the ionosphere in L-band interferometric SAR data. In Proceedings of the 2010 IEEE Radar Conference, Arlington, VA, USA, 10–14 May 2010; IEEE: Toulouse, France, 2010; pp. 1459–1463. [Google Scholar]
- Rodger, A.S.; Jarvis, M.J. Ionospheric research 50 years ago, today and tomorrow. J. Atmos. Sol. Terr. Phys. 2000, 62, 1629–1645. [Google Scholar] [CrossRef]
- Appleton, E.V. Two anomalies in the ionosphere. Nature 1946, 157, 691. [Google Scholar] [CrossRef]
- Bremer, J. Investigations of long-term trends in the ionosphere with world-wide ionosonde observations. Adv. Radio Sci. 2005, 2, 253–258. [Google Scholar] [CrossRef]
- Laštovička, J. Long-Term Trends in the Upper Atmosphere–Recent Progress. In Aeronomy of the Earth’s Atmosphere and Ionosphere; Springer: Berlin/Heidelberg, Germany, 2011; pp. 395–406. [Google Scholar]
- Liao, W.-T.; Tseng, K.-H.; Lee, I.-T.; Liibusk, A.; Lee, J.-C.; Liu, J.-Y.; Chang, C.-P.; Lin, Y.-C. Sentinel-1 interferometry with ionospheric correction from global and local TEC maps for land displacement detection in Taiwan. Adv. Space Res. 2020, 65, 1447–1465. [Google Scholar] [CrossRef]
- Nagler, T.; Rott, H.; Hetzenecker, M.; Wuite, J.; Potin, P. The Sentinel-1 mission: New opportunities for ice sheet observations. Remote Sens. 2015, 7, 9371–9389. [Google Scholar] [CrossRef]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Elliott, J.R.; Biggs, J.; Parsons, B.; Wright, T.J. InSAR slip rate determination on the Altyn Tagh Fault, northern Tibet, in the presence of topographically correlated atmospheric delays. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Hogg, D.C.; Guiraud, F.O.; Decker, M.T. Measurement of excess radio transmission length on earth-space paths. Astron. Astrophys. 1981, 95, 304–307. [Google Scholar]
- Resch, G.M. Water vapor radiometry in geodetic applications. In Geodetic Refraction: Effects of Electromagnetic Wave Propagation through the Atmosphere; Springer: Berlin/Heidelberg, Germany, 1984; pp. 53–84. [Google Scholar]
- Hopfield, H.S. Tropospheric effect on electromagnetically measured range: Prediction from surface weather data. Radio Sci. 1971, 6, 357–367. [Google Scholar] [CrossRef]
- Bock, Y.; Williams, S. Integrated satellite interferometry in southern California. Eos Trans. Am. Geophys. Union 1997, 78, 293–300. [Google Scholar] [CrossRef]
- Janssen, V.; Ge, L.; Rizos, C. Tropospheric corrections to SAR interferometry from GPS observations. GPS Solut. 2004, 8, 140–151. [Google Scholar] [CrossRef]
- Li, Z.; Fielding, E.J.; Cross, P.; Muller, J. Interferometric synthetic aperture radar atmospheric correction: GPS topography-dependent turbulence model. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Löfgren, J.S.; Björndahl, F.; Moore, A.W.; Webb, F.H.; Fielding, E.J.; Fishbein, E.F. Tropospheric correction for InSAR using interpolated ECMWF data and GPS zenith total delay from the Southern California integrated GPS network. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; IEEE: Toulouse, France, 2010; pp. 4503–4506. [Google Scholar]
- Onn, F.; Zebker, H.A. Correction for interferometric synthetic aperture radar atmospheric phase artifacts using time series of zenith wet delay observations from a GPS network. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Williams, S.; Bock, Y.; Fang, P. Integrated satellite interferometry: Tropospheric noise, GPS estimates and implications for interferometric synthetic aperture radar products. J. Geophys. Res. Solid Earth 1998, 103, 27051–27067. [Google Scholar] [CrossRef]
- Foster, J.; Brooks, B.; Cherubini, T.; Shacat, C.; Businger, S.; Werner, C.L. Mitigating atmospheric noise for InSAR using a high resolution weather model. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Liu, S.; Hanssen, R.; Mika, Á. On the value of high-resolution weather models for atmospheric mitigation in SAR interferometry. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; IEEE: Toulouse, France, 2009; p. II-749. [Google Scholar]
- Puysségur, B.; Michel, R.; Avouac, J. Tropospheric phase delay in interferometric synthetic aperture radar estimated from meteorological model and multispectral imagery. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Wadge, G.; Webley, P.W.; Stevens, N.F. Correcting InSAR data for tropospheric path effects over volcanoes using dynamic atmospheric models. In Proceedings of the FRINGE 2003 Workshop (ESA SP-550), Frascati, Italy, 1–5 December 2003; pp. 1–5. [Google Scholar]
- Li, Z. Correction of Atmospheric Water Vapour Effects on Repeat-Pass SAR Interferometry Using GPS, MODIS and MERIS Data. Ph.D. Thesis, University of London, London, UK, University College London (United Kingdom), London, UK, 2005. [Google Scholar]
- Li, Z.; Fielding, E.J.; Cross, P.; Muller, J. Interferometric synthetic aperture radar atmospheric correction: Medium resolution imaging spectrometer and advanced synthetic aperture radar integration. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Frederick, K.L.; Edward, J.T.; Dennis, G.T. The Atmosphere: An Introduction to Meteorology; Prentice Hall: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- Hess, M.; Koepke, P.; Schult, I. Optical properties of aerosols and clouds: The software package OPAC. Bull. Am. Meteorol. Soc. 1998, 79, 831–844. [Google Scholar] [CrossRef]
- Thompson, A. Simulating the Adiabatic Ascent of Atmospheric Air Parcels using the Cloud Chamber; Department of Meteorology, Penn State: University Park, PA, USA, 2007; pp. 121–123. [Google Scholar]
- Liebe, H.J.; Manabe, T.; Hufford, G.A. Millimeter-wave attenuation and delay rates due to fog/cloud conditions. IEEE Trans. Antennas Propag. 1989, 37, 1612–1617. [Google Scholar] [CrossRef]
- Guneriussen, T.; Hogda, K.A.; Johnsen, H.; Lauknes, I. InSAR for estimation of changes in snow water equivalent of dry snow. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2101–2108. [Google Scholar] [CrossRef]
- Biggs, J.; Wright, T.; Lu, Z.; Parsons, B. Multi-interferogram method for measuring interseismic deformation: Denali Fault, Alaska. Geophys. J. Int. 2007, 170, 1165–1179. [Google Scholar] [CrossRef]
- Lohman, R.B.; Simons, M. Some thoughts on the use of InSAR data to constrain models of surface deformation: Noise structure and data downsampling. Geochem. Geophys. Geosyst. 2005, 6, 6. [Google Scholar] [CrossRef]
- Gatelli, F.; Guamieri, A.M.; Parizzi, F.; Pasquali, P.; Prati, C.; Rocca, F. The wavenumber shift in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1994, 32, 855–865. [Google Scholar] [CrossRef]
- Lee, J.-S.; Hoppel, K.W.; Mango, S.A.; Miller, A.R. Intensity and phase statistics of multilook polarimetric and interferometric SAR imagery. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1017–1028. [Google Scholar]
- Braun, A. Radar Satellite Imagery for Humanitarian Response. Bridging the Gap between Technology and Application. Ph.D. Thesis, Universität Tübingen, Tübingen, Germany, 2019. [Google Scholar]
- Zebker, H.A.; Goldstein, R.M. Topographic mapping from interferometric synthetic aperture radar observations. J. Geophys. Res. Solid Earth 1986, 91, 4993–4999. [Google Scholar] [CrossRef]
- Yu, H.; Lan, Y.; Yuan, Z.; Xu, J.; Lee, H. Phase unwrapping in InSAR: A review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 40–58. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Myer, D.; Mellors, R.; Shimada, M.; Brooks, B.; Foster, J. Accuracy and resolution of ALOS interferometry: Vector deformation maps of the Father’s Day intrusion at Kilauea. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3524–3534. [Google Scholar] [CrossRef]
- Papathanassiou, K.P.; Cloude, S.R. The effect of temporal decorrelation on the inversion of forest parameters from Pol-InSAR data. In Proceedings of the International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; p. III-1429. [Google Scholar]
- Santoro, M.; Askne, J.I.H.; Wegmuller, U.; Werner, C.L. Observations, modeling, and applications of ERS-ENVISAT coherence over land surfaces. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2600–2611. [Google Scholar] [CrossRef]
- Ahmed, R.; Siqueira, P.; Hensley, S.; Chapman, B.; Bergen, K. A survey of temporal decorrelation from spaceborne L-Band repeat-pass InSAR. Remote Sens. Environ. 2011, 115, 2887–2896. [Google Scholar] [CrossRef]
- Durden, S.L.; Van Zyl, J.J.; Zebker, H.A. Modeling and observation of the radar polarization signature of forested areas. IEEE Trans. Geosci. Remote Sens. 1989, 27, 290–301. [Google Scholar] [CrossRef]
- Lavalle, M.; Simard, M.; Hensley, S. A temporal decorrelation model for polarimetric radar interferometers. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2880–2888. [Google Scholar] [CrossRef]
- Richards, J.A.; Woodgate, P.W.; Skidmore, A.K. An explanation of enhanced radar backscattering from flooded forests. Int. J. Remote Sens. 1987, 8, 1093–1100. [Google Scholar] [CrossRef]
- Jung, J.; Kim, D.; Lavalle, M.; Yun, S.-H. Coherent change detection using InSAR temporal decorrelation model: A case study for volcanic ash detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5765–5775. [Google Scholar] [CrossRef]
- Lavalle, M.; Hensley, S. Extraction of structural and dynamic properties of forests from polarimetric-interferometric SAR data affected by temporal decorrelation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4752–4767. [Google Scholar] [CrossRef]
- Rocca, F. Modeling interferogram stacks. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3289–3299. [Google Scholar] [CrossRef]
- Gamba, P.; Dell’Acqua, F.; Trianni, G. Rapid damage detection in the Bam area using multitemporal SAR and exploiting ancillary data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1582–1589. [Google Scholar] [CrossRef]
- Matsuoka, M.; Yamazaki, F. Use of satellite SAR intensity imagery for detecting building areas damaged due to earthquakes. Earthq. Spectra 2004, 20, 975–994. [Google Scholar] [CrossRef]
- Yonezawa, C.; Takeuchi, S. Decorrelation of SAR data by urban damages caused by the 1995 Hyogoken-nanbu earthquake. Int. J. Remote Sens. 2001, 22, 1585–1600. [Google Scholar] [CrossRef]
- Morishita, Y.; Hanssen, R.F. Deformation parameter estimation in low coherence areas using a multisatellite InSAR approach. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4275–4283. [Google Scholar] [CrossRef]
- Parizzi, A.; Cong, X.; Eineder, M. First Results from Multifrequency Interferometry. A Comparison of Different Decorrelation Time Constants at L, C, and X Band; ESA Scientific Publications: Paris, France, 2009; pp. 1–5. [Google Scholar]
- Tanase, M.A.; Santoro, M.; Wegmüller, U.; de la Riva, J.; Pérez-Cabello, F. Properties of X-, C-and L-band repeat-pass interferometric SAR coherence in Mediterranean pine forests affected by fires. Remote Sens. Environ. 2010, 114, 2182–2194. [Google Scholar] [CrossRef]
- Piau, P.; Bruniquel, J.; Cael, J.-C.; Deschaux, M.; Lopes, A. Analysis of the resolution of a multitemporal SAR System. In Proceedings of the IGARSS’93—IEEE International Geoscience and Remote Sensing Symposium, Tokyo, Japan, 18–21 August 1993; IEEE: Toulouse, France, 1993; pp. 1196–1199. [Google Scholar]
- Hagberg, J.O.; Ulander, L.M.H.; Askne, J. Repeat-pass SAR interferometry over forested terrain. IEEE Trans. Geosci. Remote Sens. 1995, 33, 331–340. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Moghaddam, M.; Yoder, B.J. Forest vertical structure from multibaseline interferometric radar for studying growth and productivity. In Proceedings of the IGARSS’97—1997 IEEE International Geoscience and Remote Sensing Symposium Proceedings. Remote Sensing—A Scientific Vision for Sustainable Development, Singapore, 3–8 August 1997; IEEE: Toulouse, France, 1997; pp. 1884–1886. [Google Scholar]
- Richards, M.A.; Scheer, J.; Holm, W.A.; Melvin, W.L. Principles of Modern Radar; Citeseer: University Park, PA, USA, 2010. [Google Scholar]
- Schleher, D.C. Electronic Warfare in the Information Age; Artech House, Inc.: Norwood, MA, USA, 1999. [Google Scholar]
- Bamler, R.; Hanssen, R. Decorrelation induced by interpolation errors in InSAR processing. In Proceedings of the IGARSS’97. 1997 IEEE International Geoscience and Remote Sensing Symposium Proceedings. Remote Sensing—A Scientific Vision for Sustainable Development, Singapore, 3–8 August 1997; IEEE: Toulouse, France, 1997; pp. 1710–1712. [Google Scholar]
- Just, D.; Schattler, B. Doppler-characteristics of the ERS-1 yaw steering mode. In Proceedings of the IGARSS’92 International Geoscience and Remote Sensing Symposium, Houston, TX, USA, 26–29 May 1992; IEEE: Toulouse, France, 1992; pp. 1349–1352. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).