A Persistent Scatterer Point Selection Method for Deformation Monitoring of Under-Construction Cross-Sea Bridges Using Statistical Theory and GMM-EM Algorithm
Abstract
1. Introduction
2. Materials and Methods
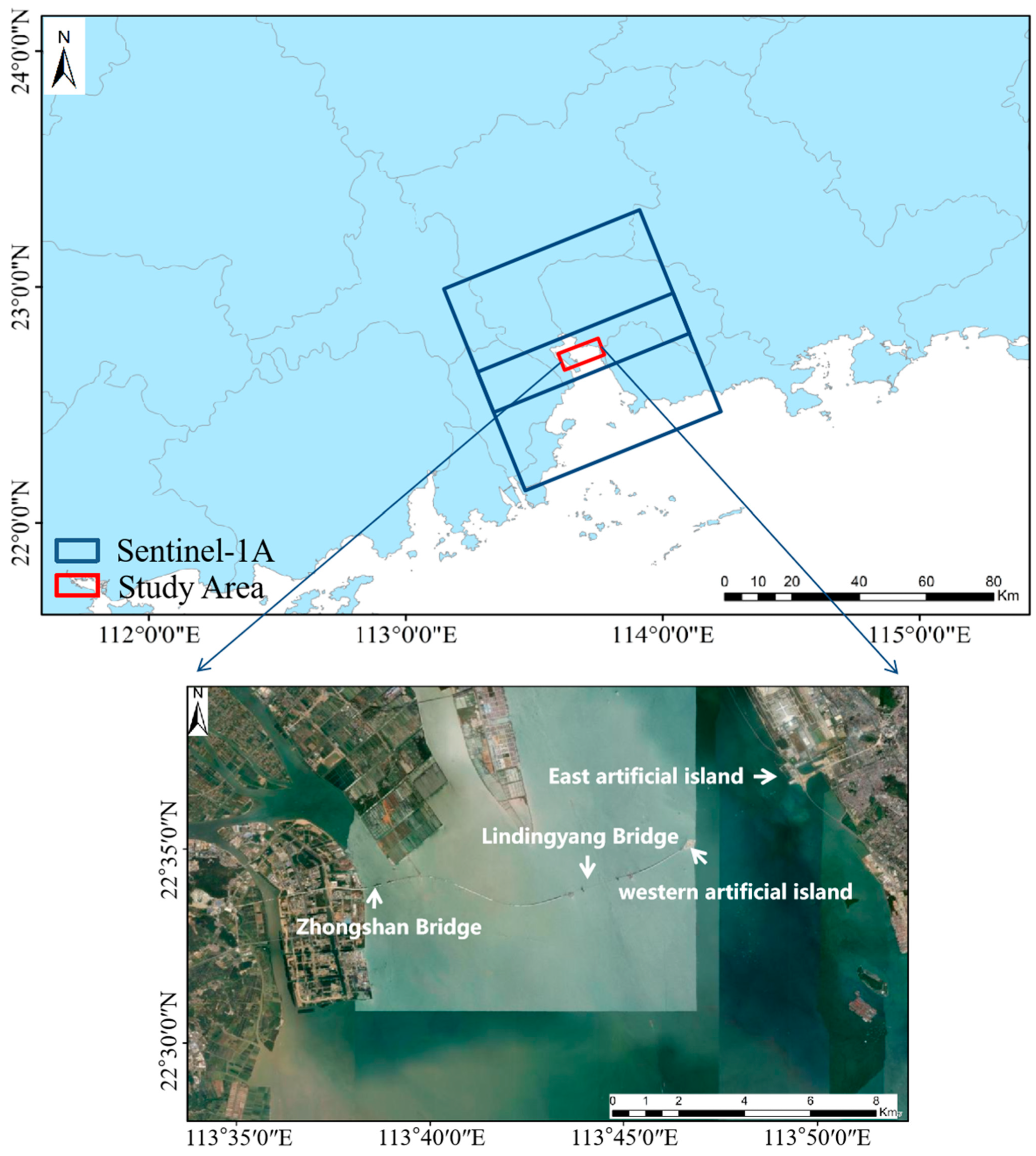
2.1. Study Area
2.2. Data Source and Preprocessing
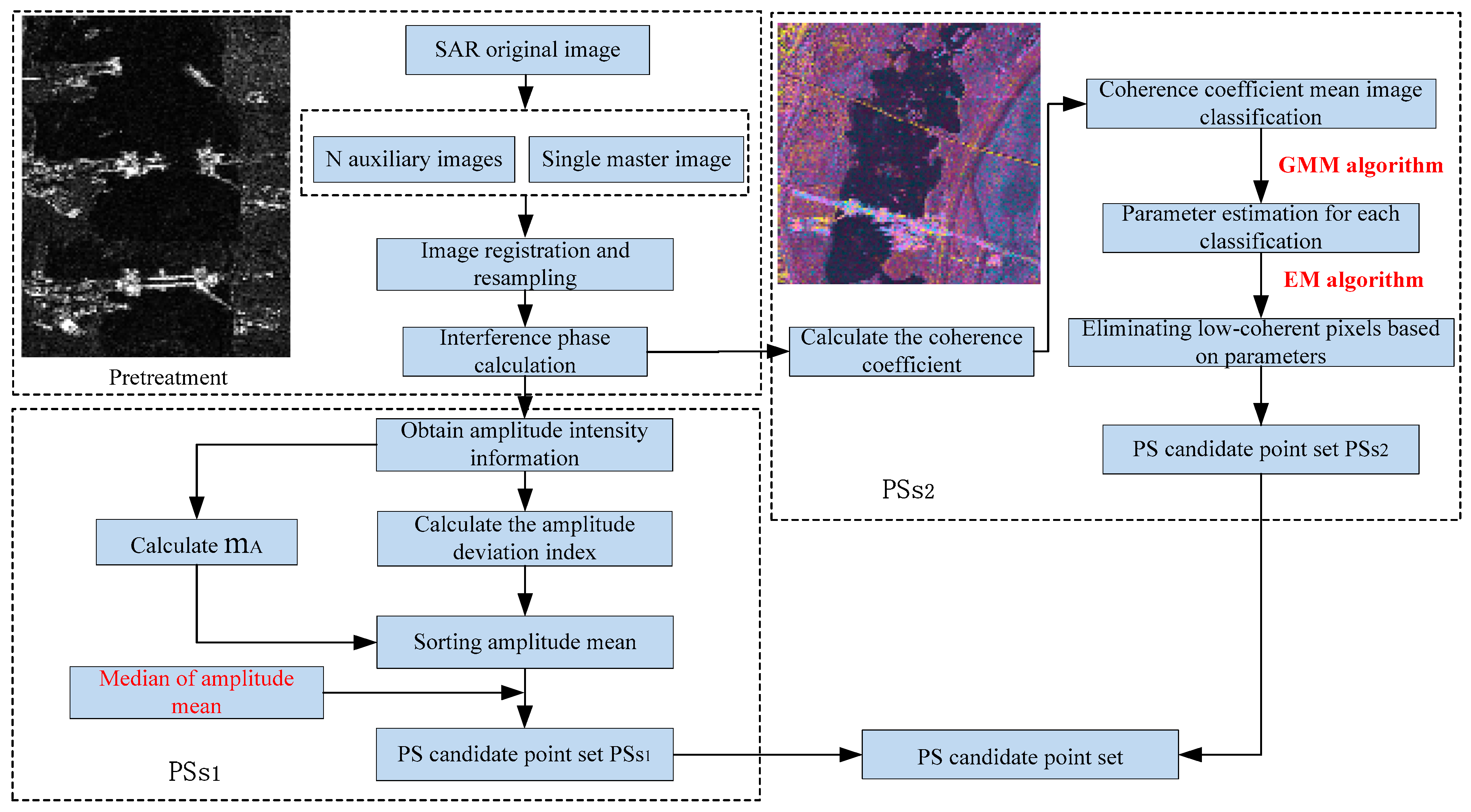
2.3. A Persistent Scatterer Points Selection Method for Deformation Monitoring of Under-Construction Cross-Sea Bridges Using Statistical Theory and GMM-EM Algorithm
2.3.1. PS Point Selection Based on Statistical Theory
2.3.2. PS Point Selection Based on GMM-EM Algorithm
- (1)
- To attain a homogeneous coherent area, N + 1 time-series SAR images were divided into a master image and N slave images, yielding N interference image pairs. The coherence coefficient (γ) of each pixel in the interference image pairs is expressed as follows:
- (2)
- To eliminate pixels in the low coherence area while retaining those in the high coherence area, this study derived initialization parameters Ø(0) for low, medium, and high mixed components based on the distribution characteristics of the coherence coefficient in the mean coherence coefficient image. Subsequently, the posterior probability of each component was calculated by adding the probabilities of the three components across all pixels. The optimal solution for each parameter was obtained iteratively using the EM algorithm. The process is as follows:
- ①
- Parameter initialization
- ②
- Parameter estimation
- ③
- Parameter maximization
2.3.3. PS Point Selection Based on Statistical Theory and GMM-EM Algorithm
- (1)
- Amplitude values and amplitude dispersion indices were computed based on the amplitude images of the study area. A threshold for the amplitude dispersion index was established to conduct the initial screening of PS points. The amplitude average of the initially screened PS candidate points was then sorted, with the median of this sequence chosen as the threshold for the second screening. The candidate points obtained at this stage are denoted as PSS1.
- (2)
- Using the GMM-EM algorithm, coherence coefficients of ground scattering units were statistically analyzed and classified to extract coherence coefficient features of interferometric pairs. High-coherence pixel points were selected based on the Gaussian parameters of each category of pixel points. The candidate points acquired in this phase are referred to as PSS2.
- (3)
- PSS1 and PSS2 were merged using set theory, providing the foundation for subsequent calculations and establishing the components of the interferometric phase. The deformation phase was inverted, thereby yielding deformation information for the study area.
3. Results
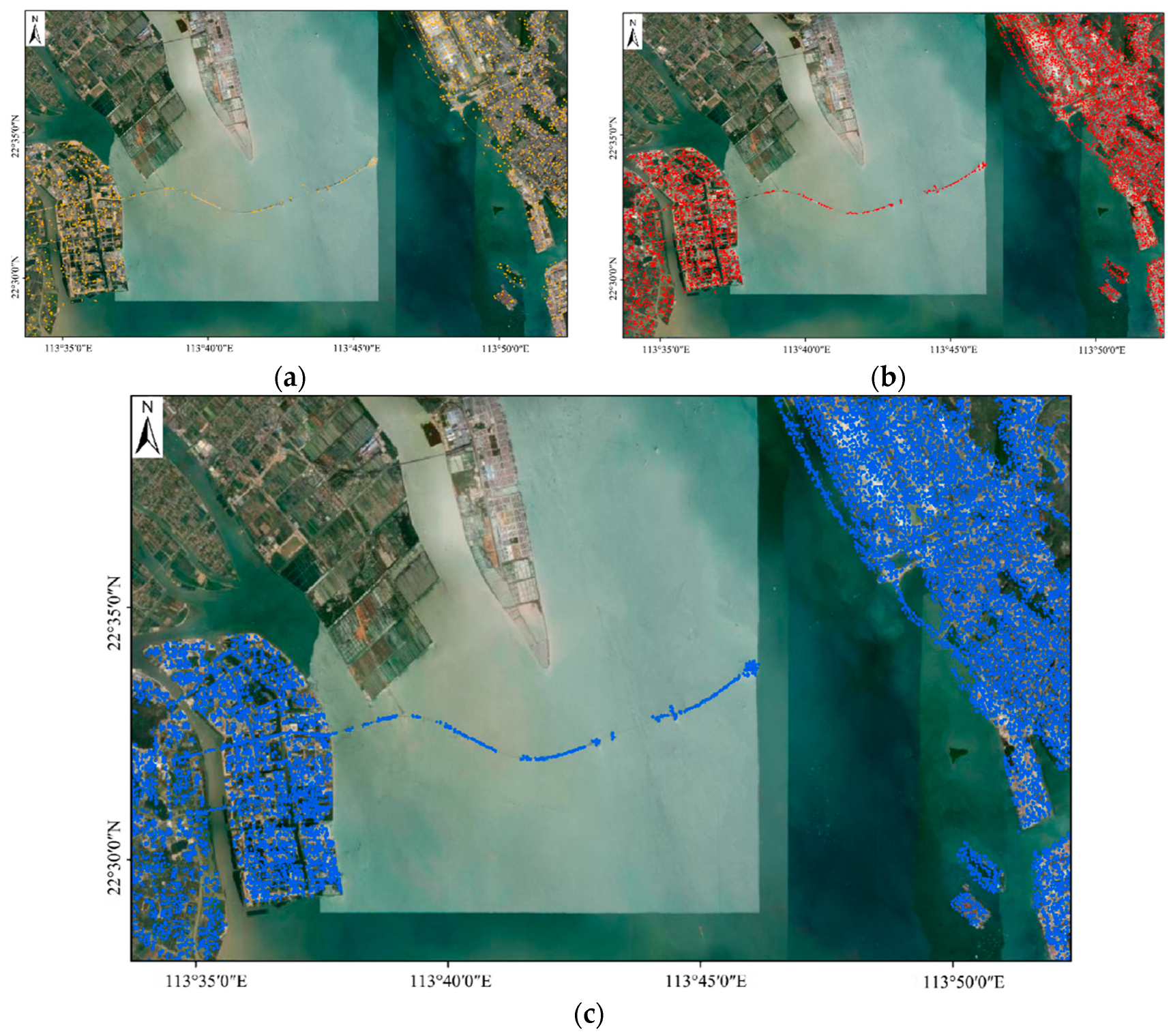
3.1. Analysis of PS Point Identification Results
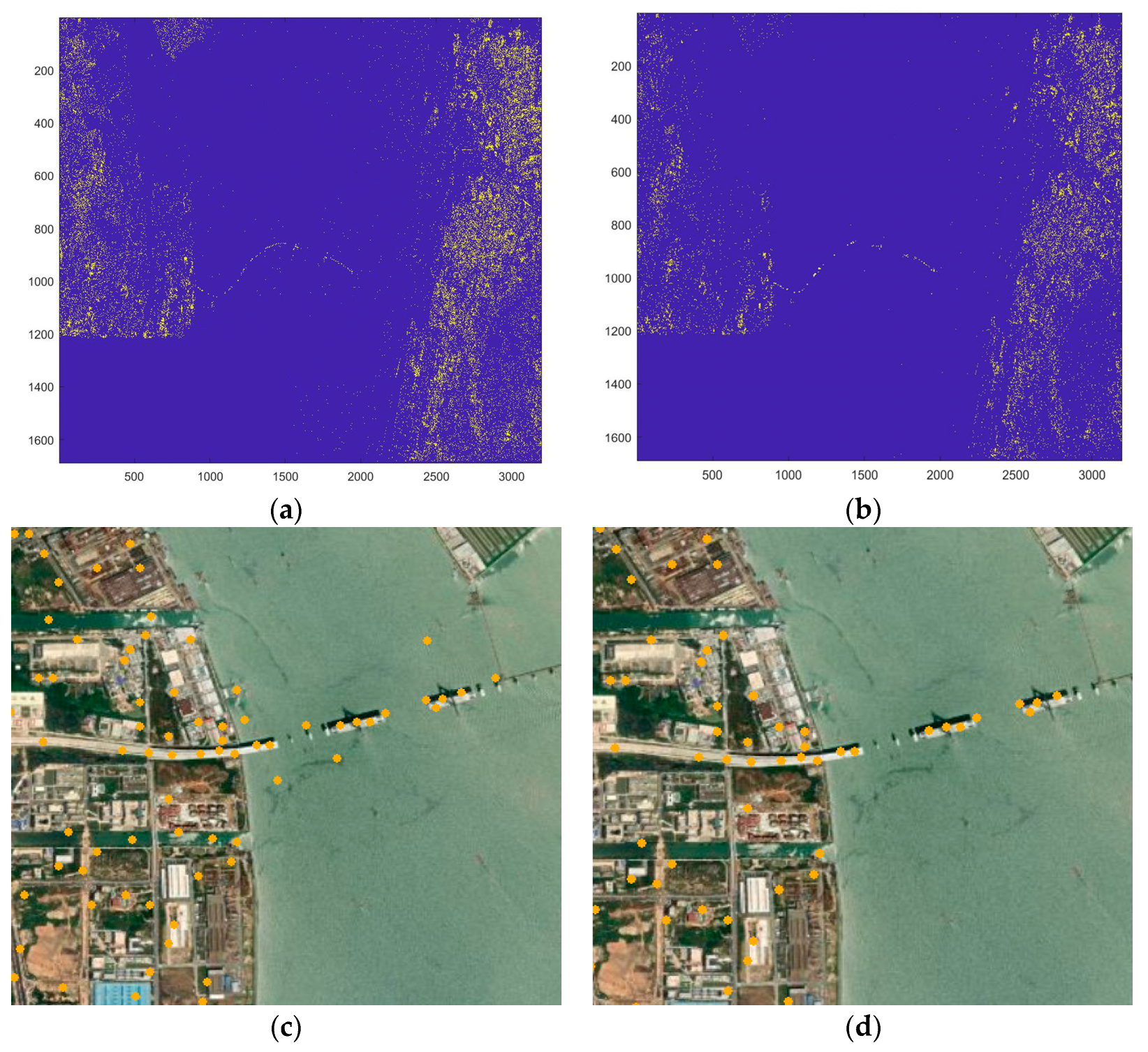
3.1.1. Analysis of PS Point Identification Results Based on Statistical Theory
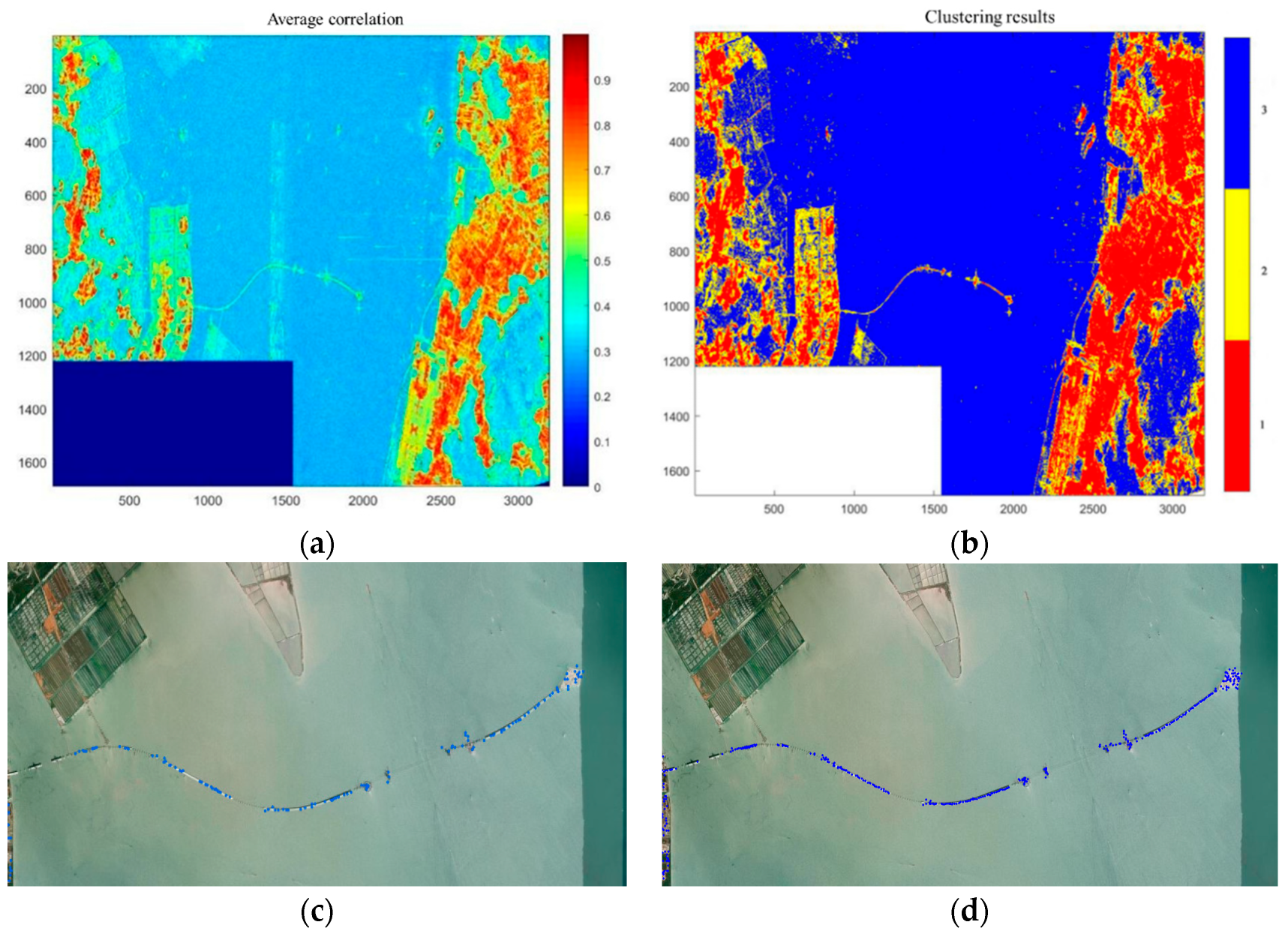
3.1.2. Analysis of PS Point Identification Results Based on GMM-EM Method
3.1.3. Analysis of PS Point Identification Results Based on Statistical Theory and GMM-EM Method
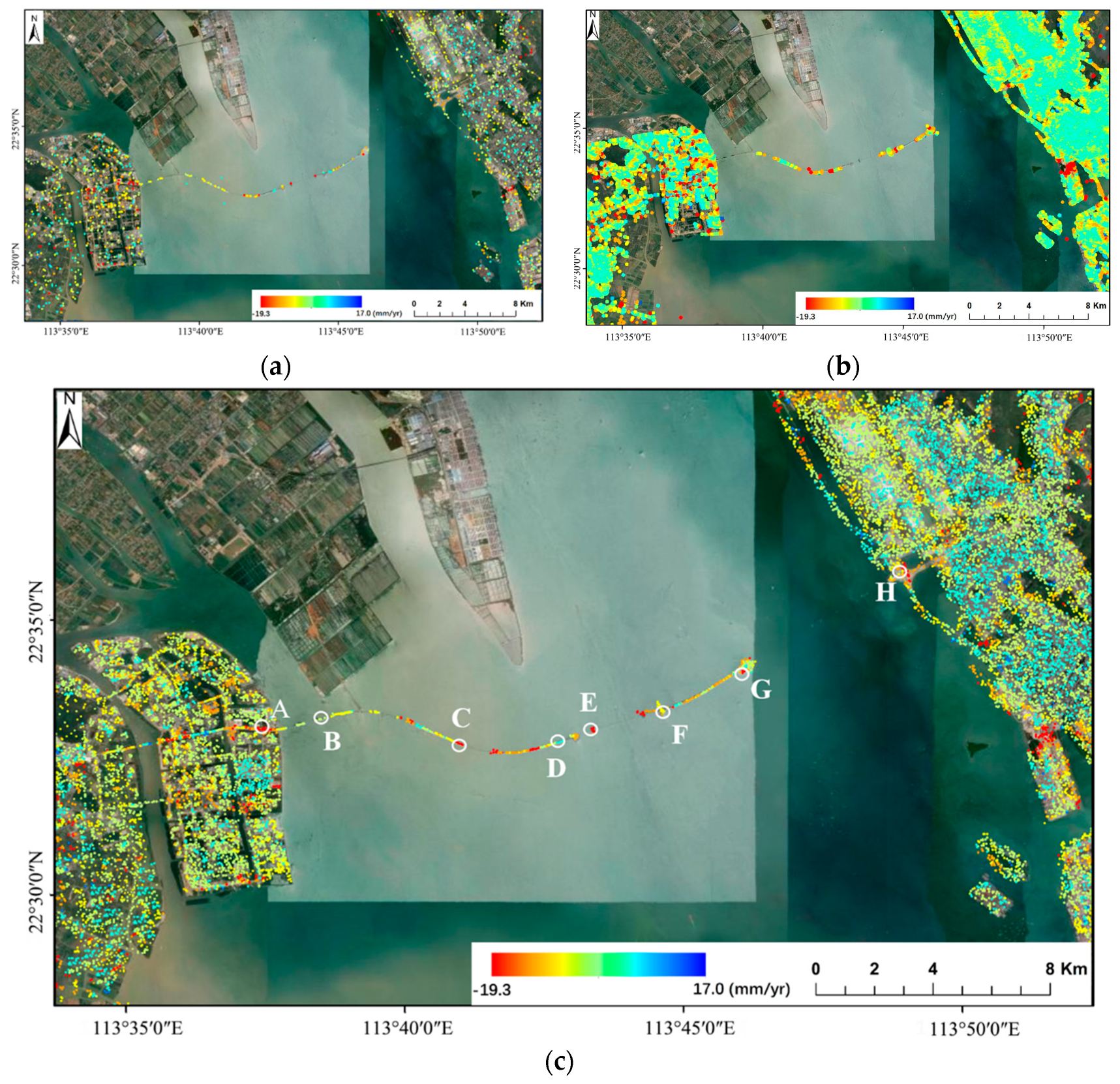
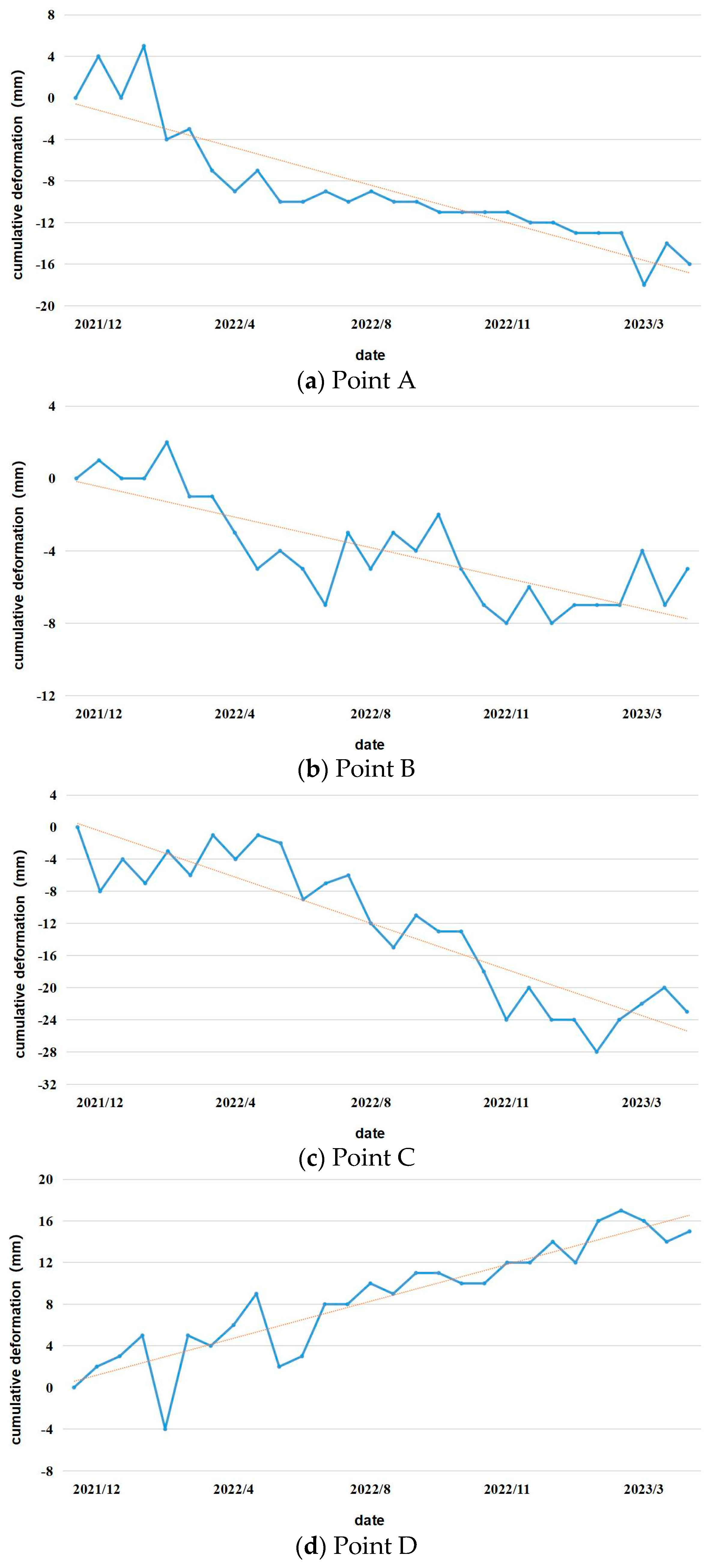
3.2. Deformation Analysis of Under-Construction Cross-Sea Bridges and Adjacent Engineering Areas
4. Discussion
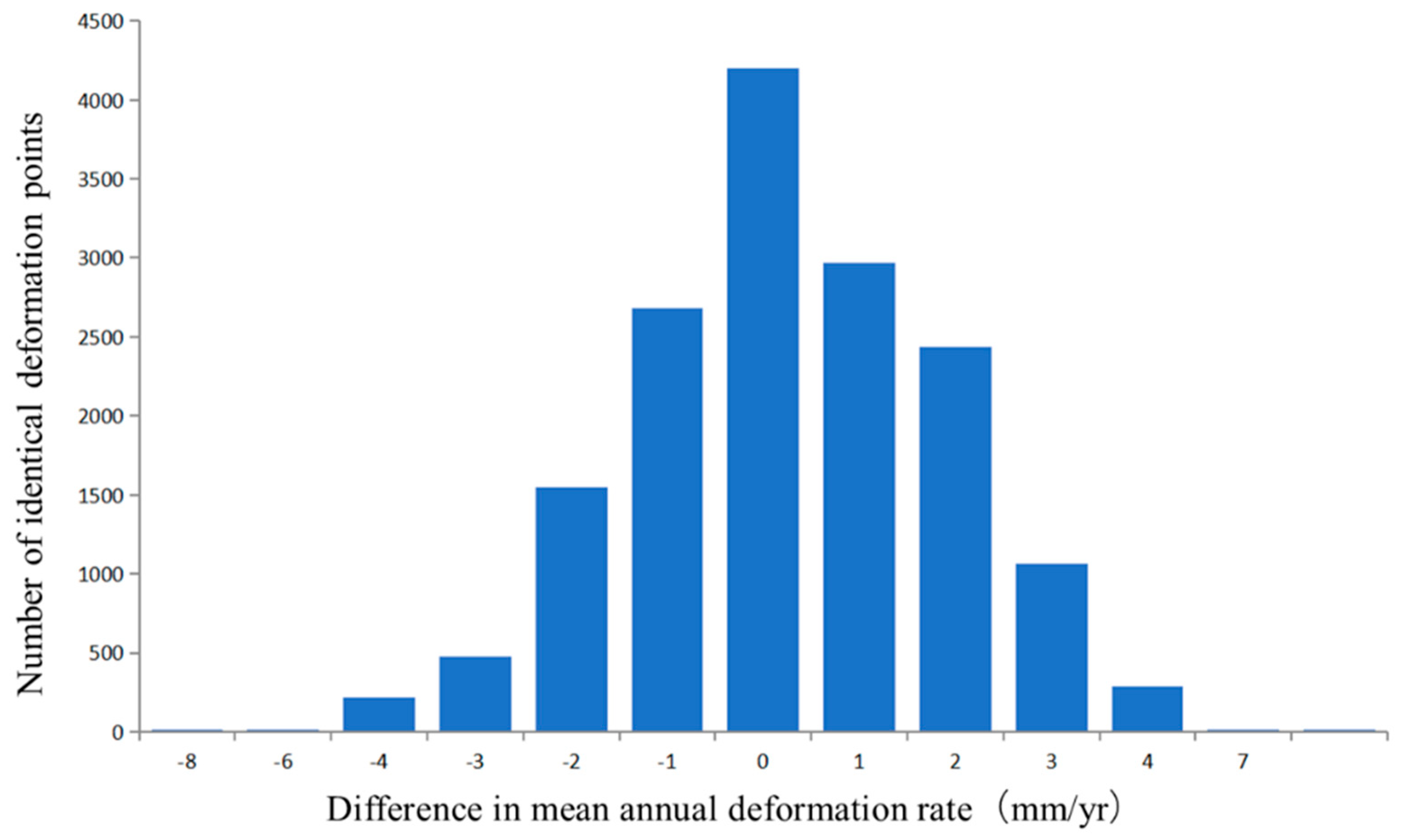
4.1. Comparative Analysis of Results
4.2. Analysis of Deformation Causes
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, H.H.; Li, B.Q.; Xiao, Y.; Sun, J.Y.; Chen, C.; Jin, G.Y.; Liu, Y.Y. Surface Subsidence over a Coastal City Using SBAS-InSAR with Sentinel-1A Data: A Case of Nansha District, China. Remote Sens. 2023, 16, 55. [Google Scholar] [CrossRef]
- Lubczynski, M.W.; Leblanc, M.; Batelaan, O. Remote sensing and hydrogeophysics give a new impetus to integrated hydrological models: A review. J. Hydrol. 2024, 633, 130901. [Google Scholar] [CrossRef]
- Tonelli, D.; Caspani, V.F.; Valentini, A.; et a Rocca, A.; Torboli, R.; Vitti, A.; Perissin, D.; Zonta, D. Interpretation of Bridge Health Monitoring Data from Satellite InSAR Technology. Remote Sens. 2023, 15, 5242. [Google Scholar] [CrossRef]
- He, Y.; Chen, Y.; Wang, W.; Yan, H.; Zhang, L.; Liu, T. TS-InSAR analysis for monitoring ground deformation in Lanzhou New District, the loess Plateau of China, from 2017 to 2019. Adv. Space Res. 2021, 67, 1267–1283. [Google Scholar] [CrossRef]
- Lazecky, M.; Hlavacova, I.; Bakon, M.; Sousa, J.J.; Perissin, D.; Patricio, G. Bridge displacements monitoring using space-borne X-band SAR interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 205–210. [Google Scholar] [CrossRef]
- D’Amico, F.; Gagliardi, V.; Ciampoli, L.B.; Tosti, F. Integration of InSAR and GPR techniques for monitoring transition areas in railway bridges. NDT E Int. 2020, 115, 102291. [Google Scholar] [CrossRef]
- Schlögl, M.; Widhalm, B.; Avian, M. Comprehensive time-series analysis of bridge deformation using differential satellite radar interferometry based on Sentinel-1. ISPRS J. Photogramm. Remote Sens. 2021, 172, 132–146. [Google Scholar] [CrossRef]
- Wang, H.; Li, A.; Li, J. Progressive finite element model calibration of a long-span suspension bridge based on ambient vibration and static measurements. Eng. Struct. 2010, 32, 2546–2556. [Google Scholar] [CrossRef]
- Qin, X.; Ding, X.; Liao, M.; Zhang, L.; Wang, C. A bridge-tailored multi-temporal DInSAR approach for remote exploration of deformation characteristics and mechanisms of complexly structured bridges. ISPRS J. Photogramm. Remote Sens. 2019, 156, 27–50. [Google Scholar] [CrossRef]
- Qin, X.; Li, Q.; Ding, X.; Xie, L.; Wang, C.; Liao, M.; Zhang, L.; Zhang, B.; Xiong, S. A structure knowledge-synthetic aperture radar interferometry integration method for high-precision deformation monitoring and risk identification of sea-crossing bridges. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102476. [Google Scholar] [CrossRef]
- Xiong, S.; Wang, C.; Qin, X.; Zhang, B.; Li, Q. Time-Series Analysis on Persistent Scatter-Interferometric Synthetic Aperture Radar (PS-InSAR) Derived Displacements of the Hong Kong–Zhuhai–Macao Bridge (HZMB) from Sentinel-1A Observations. Remote Sens. 2021, 13, 546. [Google Scholar] [CrossRef]
- Hoppe, E.J.; Novali, F.; Rucci, A.; Fumagalli, A.; Del Conte, S.; Falorni, G.; Toro, N. Deformation monitoring of posttensioned bridges using high-resolution satellite remote sensing. J. Bridge Eng. 2019, 24, 04019115. [Google Scholar] [CrossRef]
- Yang, M.; Wang, R.; Li, M.; Liao, M. A PSI targets characterization approach to interpreting surface displacement signals: A case study of the Shanghai metro tunnels. Remote Sens. Environ. 2022, 280, 113150. [Google Scholar] [CrossRef]
- Ma, P.; Liu, Y.; Wang, W.; Lin, H. Optimization of PSInSAR networks with application to TomoSAR for full detection of single and double persistent scatterers. Remote Sens. Lett. 2019, 10, 717–725. [Google Scholar] [CrossRef]
- Blekas, K.; Likas, A.; Galatsanos, N.P.; Lagaris, I.E. A spatially constrained mixture model for image segmentation. IEEE Trans. Neural Netw. 2005, 16, 494–498. [Google Scholar] [CrossRef] [PubMed]
- Balakrishnan, N.; Leiva, V.; Sanhueza, A.; Vilca, F. Estimation in the Birnbaum-Saunders distribution based on scale-mixture of normals and the EM-algorithm. SORT-Stat. Oper. Res. Trans. 2009, 33, 171–192. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, L.; Tang, M.; Liao, M.; Xu, Q.; Gong, J.; Ao, M. Mapping landslide surface displacements with time series SAR interferometry by combining persistent and distributed scatterers: A case study of Jiaju landslide in Danba, China. Remote Sens. Environ. 2018, 205, 180–198. [Google Scholar] [CrossRef]
- Falabella, F.; Serio, C.; Masiello, G.; Zhao, Q.; Pepe, A. A Multigrid InSAR Technique for Joint Analyses at Single-Look and Multi-Look Scales. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3086271. [Google Scholar] [CrossRef]
- Sousa, J.J.; Hooper, A.J.; Hanssen, R.F.; Bastos, L.C.; Ruiz, A.M. Persistent scatterer InSAR: A comparison of methodologies based on a model of temporal deformation vs. spatial correlation selection criteria. Remote Sens. Environ. 2011, 115, 2652–2663. [Google Scholar] [CrossRef]
- Guccione, P.; Zonno, M.; Mascolo, L.; D’Introno, S. Persistent point scatterer statistical analysis for X-band SAR data: The Cosmo-SkyMed case study. Int. J. Remote Sens. 2014, 35, 127–148. [Google Scholar] [CrossRef]
- Fan, H.; Liu, Y.; Xu, Y.; Yang, H. Surface subsidence monitoring with an improved distributed scatterer interferometric SAR time series method in a filling mining area. Geocarto Int. 2022, 37, 8979–9001. [Google Scholar] [CrossRef]
- Guo, W.; Ke, C.; Fan, Y. Glacier changes on the East Pamirs Plateau: Based on SAR interference data. J. Geo-Inf. Sci. 2019, 21, 1790–1801. [Google Scholar]
- Hara, K.; Liu, W.; Yamazaki, F. Monitoring of Volcanic Activity in Kuchinoerabu Island from ALOS-2 Data. J. Remote Sens. Soc. Jpn. 2016, 36, 338–347. [Google Scholar]
- Besag, J. On the statistical analysis of dirty pictures. J. R. Stat. Soc. Ser. B Stat. Methodol. 1986, 48, 259–279. [Google Scholar] [CrossRef]
- Zheng, M.; Cai, Q.; Qin, M.; Yue, T. A New Approach to Accuracy Assessment of Classifications of Remotely Sensed Data. J. Remote Sens. 2006, 10, 39–48. [Google Scholar]
- Wang, P.; Zhu, H.; Ling, X. Intravascular optical coherence tomography image segmentation based on Gaussian mixture model and adaptive fourth-order PDE. Signal Image Video Process. 2020, 14, 29–37. [Google Scholar] [CrossRef]
- Tan, W.; Li, J.; Hou, T.; Huang, P.; Qi, Y.; Xu, W.; Chen, Y. A New Permanent Scatterer Selection Method Based on Gaussian Mixture Model for Micro-Deformation Monitoring Radar Images. Sensors 2024, 24, 1809. [Google Scholar] [CrossRef] [PubMed]
- Sarker, M.S.; Kamal, A.M.; Rahman, M.Z.; Faruki Fahim, A.K. Land subsidence monitoring using InSAR technique in the southwestern region of Bangladesh. Geomat. Nat. Hazards Risk 2024, 15, 2333795. [Google Scholar] [CrossRef]
- Maruo, N.; Susaki, J.; Boonyatee, T.; Kishida, K. Detection of gaps between land and building surface displacement by PSInSAR and SBAS analysis using L-band PALSAR data. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5994–5997. [Google Scholar]
- Yao, J.; Yao, X.; Liu, X. Landslide detection and mapping based on SBAS-InSAR and PS-InSAR: A case study in Gongjue County, Tibet, China. Remote Sens. 2022, 14, 4728. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, C.; Wu, Z.; Zhang, Z.; Yang, S.; Yang, W. Monitoring and analysis of ground subsidence in Shanghai based on PS-InSAR and SBAS-InSAR technologies. Sci. Rep. 2023, 13, 8031. [Google Scholar] [CrossRef] [PubMed]
- Dai, X.H.; Yuan, J.Y.; Chen, L.Z.; Huang, Y.L.; Yu, Y.M. Study on the influence of structural form on the displacement response of suspension bridge beam end. Road 2024, 69, 122–130. [Google Scholar]

| Parameter Name | Sentinel-1A |
|---|---|
| Band | C |
| Product type | SLC |
| Polarization mode | VV |
| Sensor mode | IW |
| Orbital direction | Ascending orbit |
| Spatial resolution | 20 m |
| Image number | 28 |
| Date range | December 2021–May 2023 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Xu, Z.; Zhang, X.; Ma, W.; He, S. A Persistent Scatterer Point Selection Method for Deformation Monitoring of Under-Construction Cross-Sea Bridges Using Statistical Theory and GMM-EM Algorithm. Remote Sens. 2024, 16, 2197. https://doi.org/10.3390/rs16122197
Li J, Xu Z, Zhang X, Ma W, He S. A Persistent Scatterer Point Selection Method for Deformation Monitoring of Under-Construction Cross-Sea Bridges Using Statistical Theory and GMM-EM Algorithm. Remote Sensing. 2024; 16(12):2197. https://doi.org/10.3390/rs16122197
Chicago/Turabian StyleLi, Jianyong, Zidong Xu, Xuedong Zhang, Weiyu Ma, and Shuguang He. 2024. "A Persistent Scatterer Point Selection Method for Deformation Monitoring of Under-Construction Cross-Sea Bridges Using Statistical Theory and GMM-EM Algorithm" Remote Sensing 16, no. 12: 2197. https://doi.org/10.3390/rs16122197
APA StyleLi, J., Xu, Z., Zhang, X., Ma, W., & He, S. (2024). A Persistent Scatterer Point Selection Method for Deformation Monitoring of Under-Construction Cross-Sea Bridges Using Statistical Theory and GMM-EM Algorithm. Remote Sensing, 16(12), 2197. https://doi.org/10.3390/rs16122197







