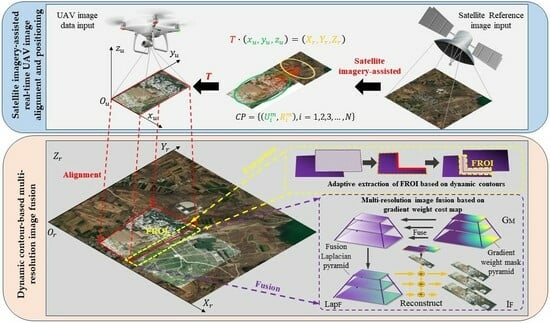
SatellStitch: Satellite Imagery-Assisted UAV Image Seamless Stitching for Emergency Response without GCP and GNSS
Abstract
1. Introduction
1.1. Optimal Stitch Line
1.2. Image Feature Information-Based Method
1.3. Image Fusion
- Using high-precision satellite imagery without the need for GCP and GNSS support overcomes the problem of error accumulation in traditional image stitching strategies and achieves absolute positioning and fast stitching of UAV images;
- A dynamic fast positioning and elimination method of gap is proposed. It breaks through the technical bottleneck that the effect of the traditional seamless processing method is limited by the degree of overlap between frames and alignment accuracy and improves the quality of stitched images.
2. Methodology
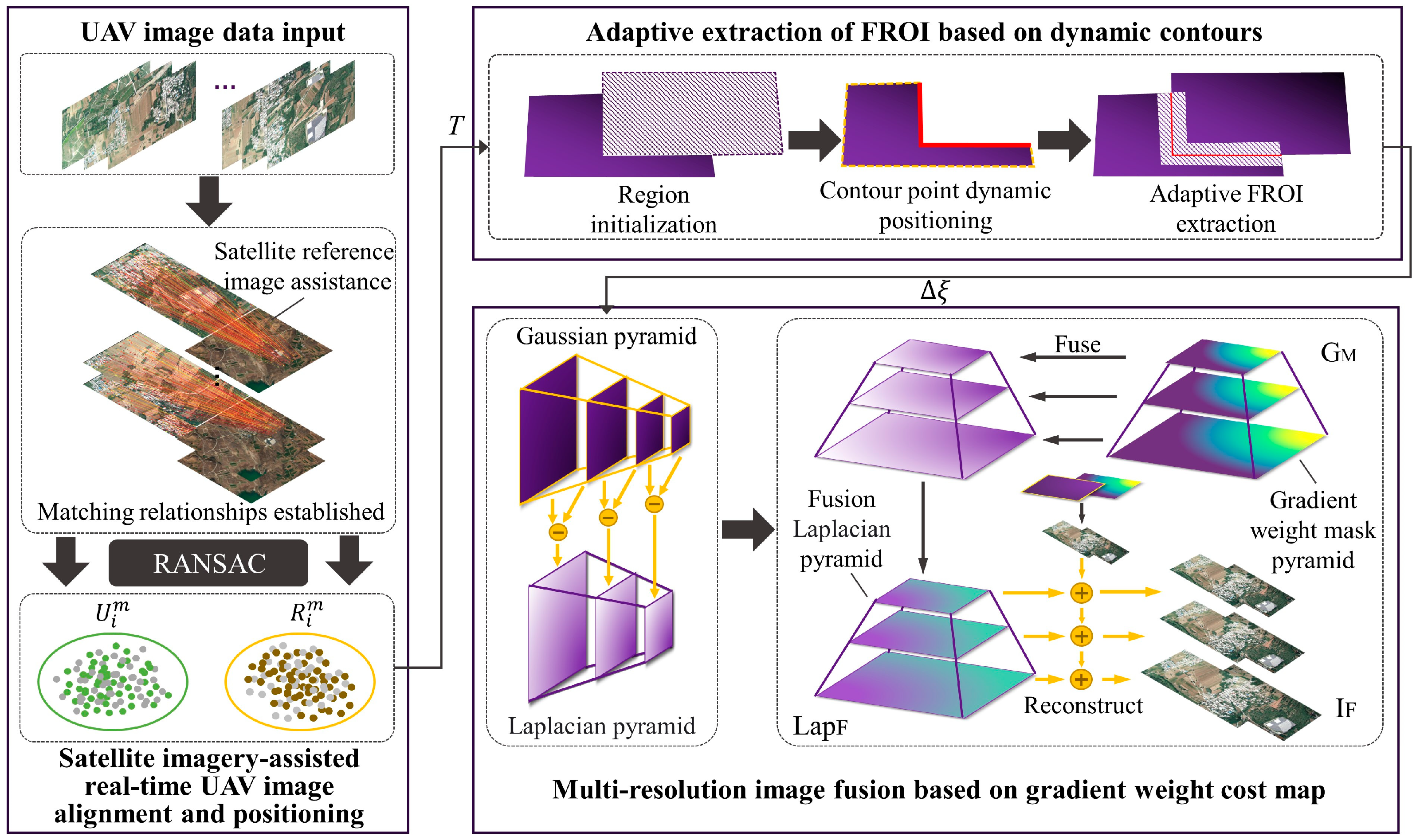
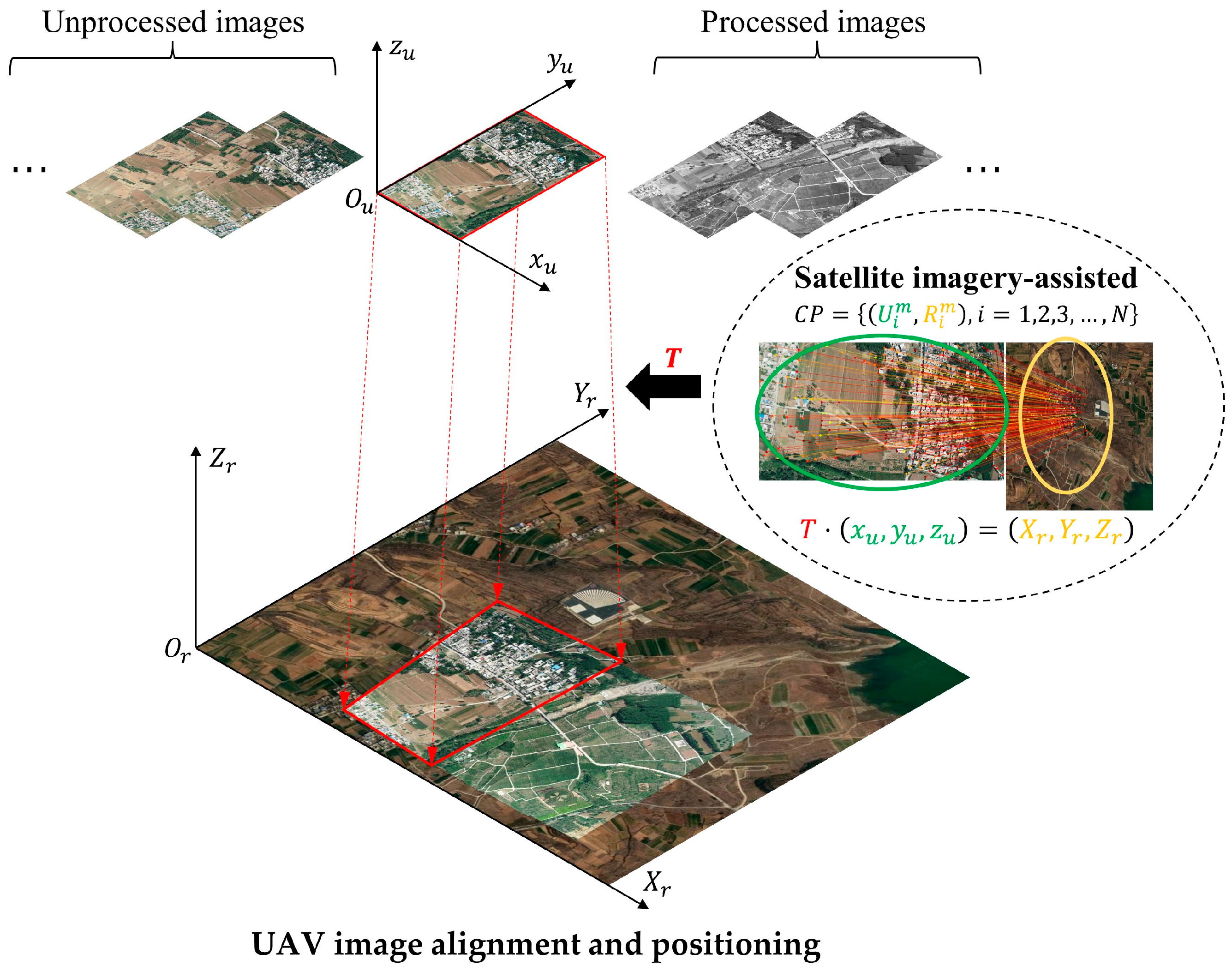
2.1. Satellite Imagery-Assisted Real-Time UAV Image Alignment and Positioning
2.2. Adaptive Extraction of FROI Based on Dynamic Contours
2.2.1. Dynamic Contour-Based Geometric Positioning of the Stitching Area
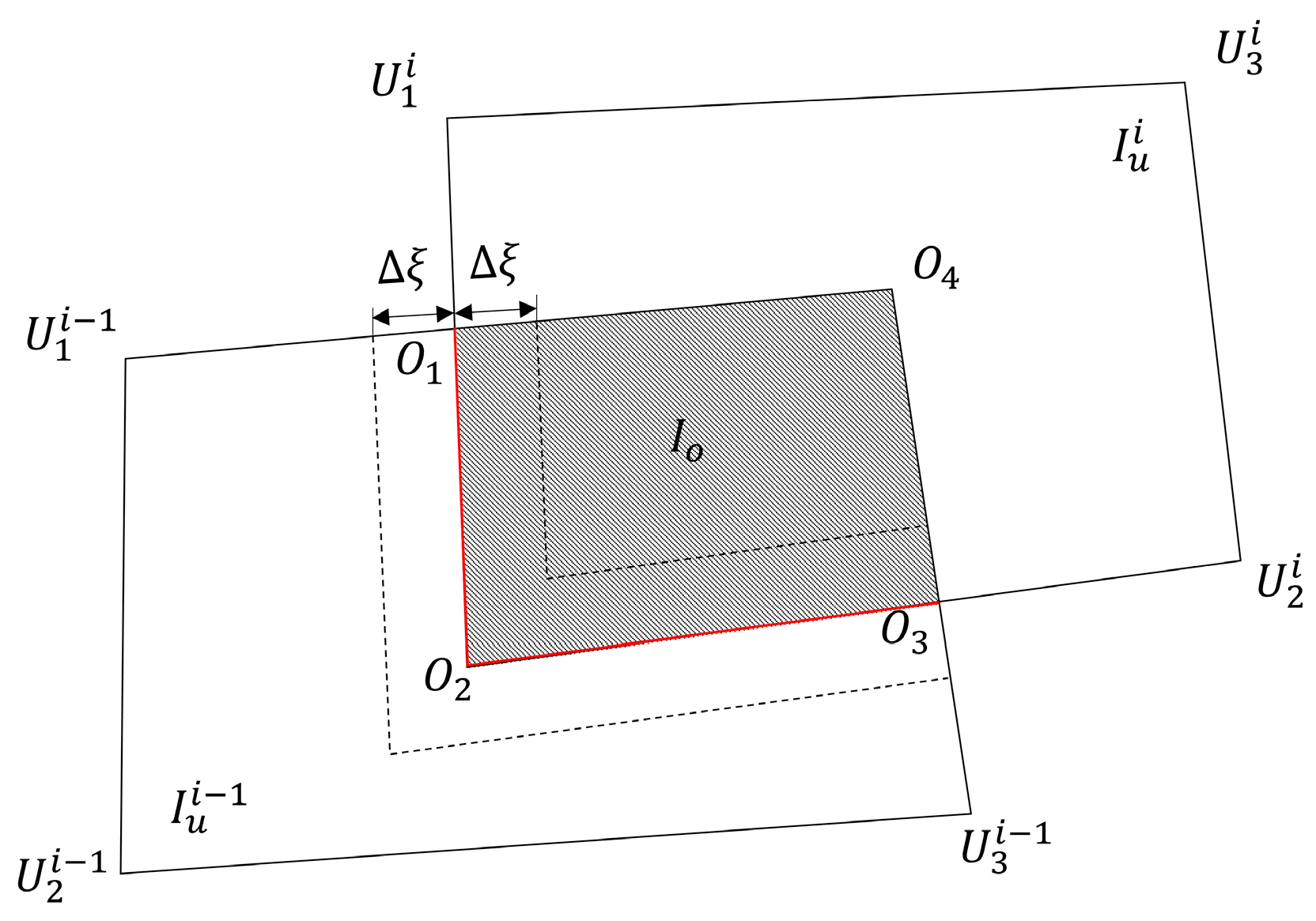
- Region initialization. Assign the region using the position information obtained from the alignment. The pixels in the overlapping area are judged according to the inter-frame boundary relationship, and the pixels are assigned a value of 0 to obtain the boundary contour polygon area;
- Contour point set extraction. The initialized polygon area is binarized and geometrically analyzed to extract a set of contour points including the gap boundary points, which can be expressed aswhere indicates the set of extracted contour points, indicates the contour line point, and represent the non-gap and gap parts of the boundary contour, respectively and represents the integration along the boundary contour;
- Dynamic geometric positioning. The acquired set of contour points is aligned with the image frames to be stitched, and the gaps are positioned directly according to the boundary geometry. This process is repeated for each frame to be stitched to achieve dynamic and fast positioning of the stitched area between frames.
2.2.2. Adaptive FROI Extraction
- The coordinates of the four image corner points are obtained using the matching relationship established with satellite reference images. By means of boundary intersection, the adjacent image boundary intersection ( = 0, 1, …, ) is obtained, where n is the number of boundary intersection points;
- The area of the single image and the area of the overlapping area between adjacent images are calculated separately. The formula for calculating the area is given as follows:where ( = 0, 1, …, ) and ( = 0, 1, …, ) is the horizontal coordinate of the adjacent corner point, ( = 0, 1, …, ) and ( = 0, 1, …, ) is the vertical coordinate of the adjacent corner point, and is the number of corner points;
- Solve for the degree of overlap between adjacent images, which is calculated as follows:where is the area of the ith image to be stitched. Since the stitching method uses incremental stitching, in practice the previous frame of the stitching is the group of images, so for simplicity, the overlap solution is based directly on the area of the image to be stitched;
- Solve for the adaptation factor based on . The formula is as follows:where ( = 0, 1, …, ) and ( = 0, 1, …, ) are the horizontal coordinates of the corner points adjacent to the image overlap region , and ( = 0, 1, …, ) and ( = 0, 1, …, ) are the vertical coordinates of the corner points adjacent to the image overlap region . The adaptive factor is solved by taking the maximum overlap length in the fore-and-aft overlap and side overlap, ensuring that it can meet the fusion requirements in both directions at the same time.
2.3. Multi-Resolution Image Fusion Based on Gradient Weight Cost Map
2.3.1. Gradient Weight Cost Map Calculation
- Image binarization processing. The image to be fused is converted to HSV color space, and the HSV threshold is extracted by an adjuster to decide on the trade-off of image information to obtain a binary image on a two-dimensional plane. This binary image can be considered to contain only two types of pixels: the target (the region containing the valid image information is defined as , where the FROI region is defined as , ) and the background, where the target pixel value is set to 255 and the background pixel value is set to 0. The formula for the binarization process is as follows:
- Noise reduction filtering. Noise reduction is completed by using a Gaussian filter to process the noise points that appear after the image binarization processing;
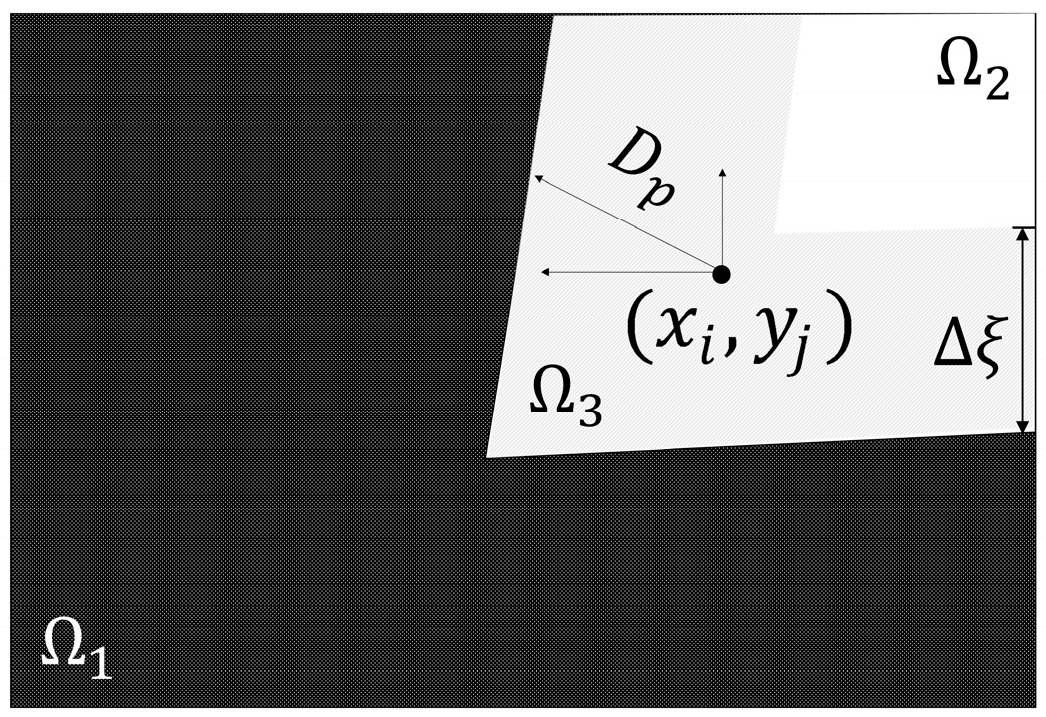
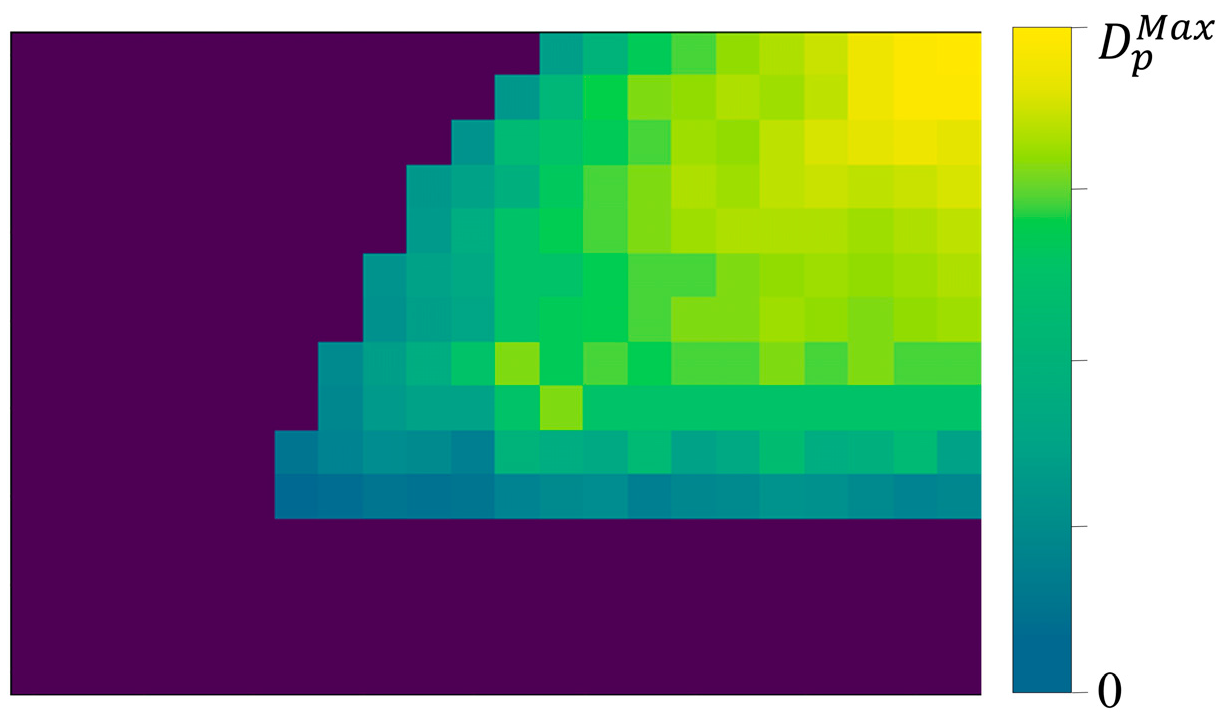
- Distance transformation calculation. The distance of each non-zero pixel in the image from its own nearest zero is calculated using the distance transformation function as shown in Figure 4. At this time, the gray value in the pixel represents the distance between the pixel and the nearest background pixel. Common distance transformation functions are as follows:where is the nearest background pixel; i.e., ; is the target pixel within the FROI, and , is the distance factor of pixel . The schematic diagram of is shown in Figure 5;
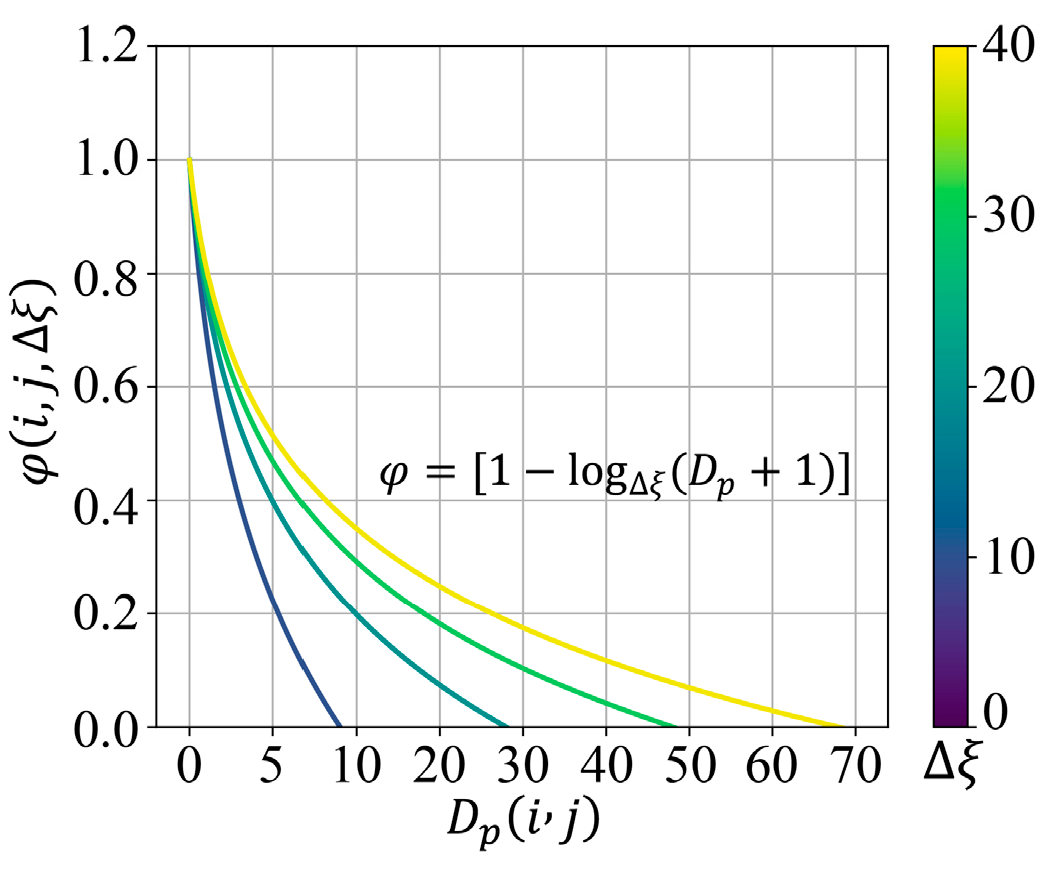
- Weight normalization. The distance grayscale map obtained from the calculation is normalized; i.e., the distance value is replaced by a pixel value to achieve a smooth transition of the pixel value within the stitching seam , to obtain a gradient weight cost map of the image to be fused. The normalization process is as follows:where is the normalized pixel weight, is the weight function, and a graph of the weight function is shown in Figure 6. The larger the value of , the smoother the trend of the weights. is determined by both the distance factor and the adaptive factor , making the weights suitable for both limiting image detail loss and eliminating exposure differences. A schematic diagram of the normalized weight result is shown in Figure 7.
2.3.2. Improved Multi-Resolution Pyramid Fusion
- Extract the FROI of the image to be stitched and the group of stitched images, which perform a Gaussian pyramid decomposition to obtain and , respectively, with the following decomposition rules:where is the lth layer image, and are the height and width of the lth layer image, N is the total number of Gaussian pyramid levels, and is a two-dimensional weight function;
- Laplacian pyramid decomposition is performed on the FROIs of the image to be stitched and the group of stitched images to obtain and . The decomposition rules are:where is the interpolated enlargement of the lth layer image , and the interpolated image is the same size as the l-1st layer image . Subtracting from its interpolated image yields the corresponding Laplacian pyramid layer l-1 image , which can be expressed as follows:
- The gradient weight cost map of the FROI is solved as mask input, Gaussian pyramid decomposition is performed to obtain , and at this time the Gaussian image has the same number of layers as the Laplacian image and to be fused;
- On each layer, , are fused according to the fusion rules of the current layer to achieve a smooth transition of pixel values in the FROI and to obtain a Laplacian pyramid of the fused image, where the fusion rules are as follows:where is the fused image Laplacian pyramid lth layer image, is the gradient weight cost map mask Gaussian pyramid lth layer image, and are the FROIs Laplacian pyramid lth layer image of the image to be stitched and the group of stitched images;
- The reconstruction of the high-resolution fused image is repeated by interpolating and expanding the fused Laplacian pyramid from the top layer and summing the images from the lower layers. The reconstruction process can be expressed as follows:where is the reconstructed fused image pyramid lth layer image, is the fused image Laplacian pyramid lth layer image, and is the image interpolation enlargement result.
3. Experiments and Results
3.1. Data Sets
3.2. Experimental Details
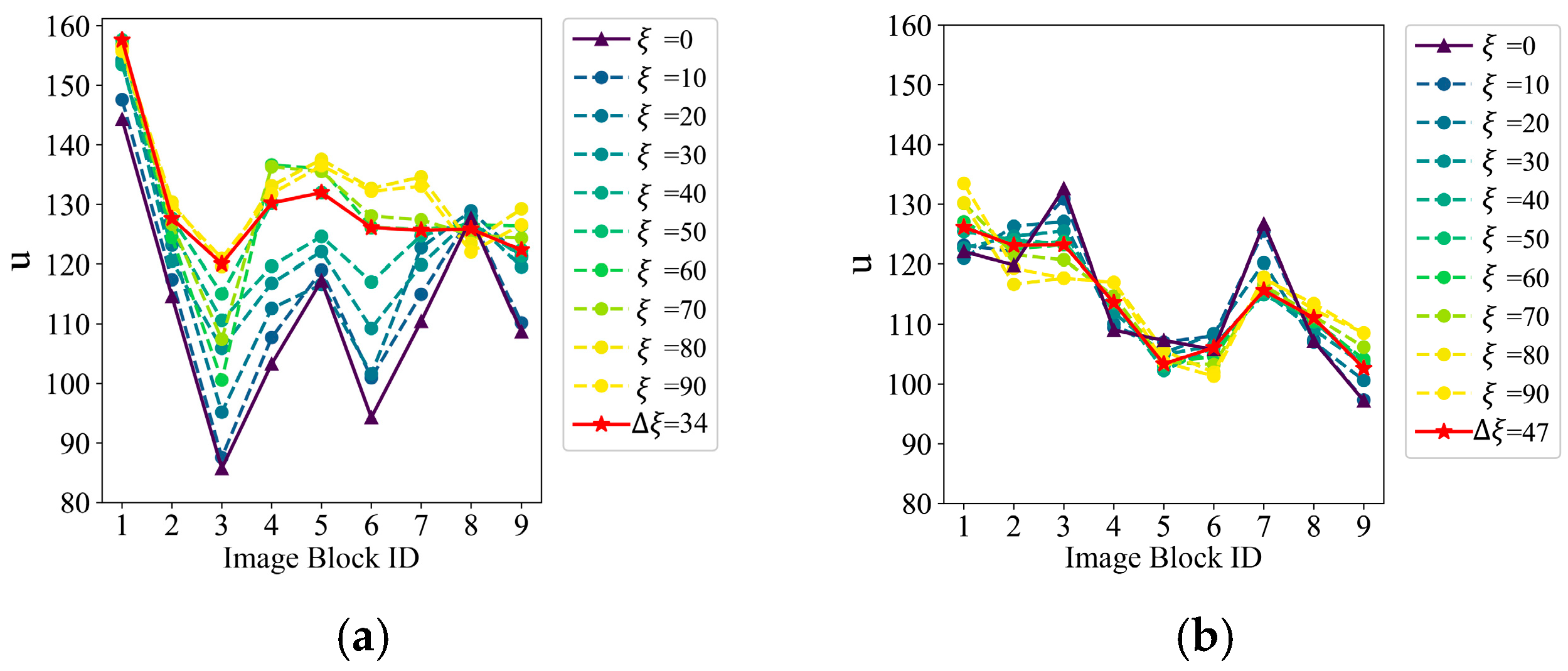
3.3. FROI Adaptive Experiment
3.4. Fusion Experiment
3.5. Image Stitching Experiment
4. Discussion
5. Conclusions
- The UAV fast-stitch image map stitching strategy assisted by satellite reference images effectively solves the cumulative error problem of the traditional method. Without the support of GCPs and GNSS, the UAV image alignment can be absolutely positioned, which can meet the application requirements of UAV emergency mapping;
- The dynamic contour-based multi-resolution image fusion algorithm achieves the simultaneous resolution of stitching-gap and ghosting problems. The smoothing ability of hue and exposure differences is remarkable, and the quality of the stitched image is effectively improved.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, H.; Qin, R.; Chen, X. Unmanned Aerial Vehicle for Remote Sensing Applications—A Review. Remote Sens. 2019, 11, 1443. [Google Scholar] [CrossRef]
- Bu, S.; Zhao, Y.; Wan, G.; Liu, Z. Map2DFusion: Real-Time Incremental UAV Image Mosaicing Based on Monocular SLAM. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; IEEE: Daejeon, Republic of Korea, 2016; pp. 4564–4571. [Google Scholar]
- Zhao, Y.; Cheng, Y.; Zhang, X.; Xu, S.; Bu, S.; Jiang, H.; Han, P.; Li, K.; Wan, G. Real-Time Orthophoto Mosaicing on Mobile Devices for Sequential Aerial Images with Low Overlap. Remote Sens. 2020, 12, 3739. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, L.; Liu, Y. Robust hierarchical structure from motion for large-scale unstructured image sets. ISPRS J. Photogramm. Remote Sen. 2021, 181, 367–384. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, K.; Sun, P. Homogenization of daily precipitable water vapor time series derived from GNSS observations over China. Adv. Space Res. 2023, 72, 1751–1763. [Google Scholar] [CrossRef]
- Ren, M.; Li, J.; Song, L.; Li, H.; Xu, T. MLP-Based Efficient Stitching Method for UAV Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zeng, W.; Deng, Q.; Zhao, X. A method for stitching remote sensing images with Delaunay triangle feature constraints. Geocarto. Int. 2023, 38, 2285356. [Google Scholar] [CrossRef]
- Cui, Z.; Tang, R.; Wei, J. UAV Image Stitching With Transformer and Small Grid Reformation. IEEE Geosci. Remote Sen. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Tang, W.; Jia, F.; Wang, X. An improved adaptive triangular mesh-based image warping method. Front. Neurorobot. 2023, 16, 1042429. [Google Scholar] [CrossRef]
- Li, R.; Gao, P.; Cai, X.; Chen, X.; Wei, J.; Cheng, Y.; Zhao, H. A Real-Time Incremental Video Mosaic Framework for UAV Remote Sensing. Remote Sens. 2023, 15, 2127. [Google Scholar] [CrossRef]
- Nie, L.; Lin, C.; Liao, K.; Liu, S.; Zhao, Y. Unsupervised Deep Image Stitching: Reconstructing Stitched Features to Images. IEEE Trans. Image Process. 2021, 30, 6184–6197. [Google Scholar] [CrossRef]
- Huang, C.; Pan, X.; Cheng, J.; Song, J. Deep Image Registration With Depth-Aware Homography Estimation. IEEE Signal Process. Lett. 2023, 30, 6–10. [Google Scholar] [CrossRef]
- Yan, N.; Mei, Y.; Xu, L. Deep learning on image stitching with multi-viewpoint images: A survey. Neural Process. Lett. 2023, 55, 3863–3898. [Google Scholar] [CrossRef]
- Zhang, W.; Guo, B.; Li, M.; Liao, X.; Li, W. Improved Seam-Line Searching Algorithm for UAV Image Mosaic with Optical Flow. Sensors 2018, 18, 1214. [Google Scholar] [CrossRef] [PubMed]
- Pan, W.; Li, A.; Wu, Y. Research on seamless image stitching based on fast marching method. IET Image Process. 2023, 12, 885–893. [Google Scholar] [CrossRef]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active Contour Models. Int. J. Comput. Vis. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A Note on Two Problems in Connexion with Graphs. Numerische Mathematik. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Dong, Q.; Liu, J. Seamline Determination Based on PKGC Segmentation for Remote Sensing Image Mosaicking. Sensors 2017, 17, 1721. [Google Scholar] [CrossRef]
- Duplaquet, M.-L. Building Large Image Mosaics with Invisible Seam Lines. In Visual Information Processing VII, Proceedings of the Aerospace/Defense Sensing and Controls, Orlando, FL, USA, 13–17 April 1998; Park, S.K., Juday, R.D., Eds.; SPIE: Bellingham, WA, USA, 1998; pp. 369–377. [Google Scholar]
- Li, X.; Hui, N.; Shen, H.; Fu, Y.; Zhang, L. A Robust Mosaicking Procedure for High Spatial Resolution Remote Sensing Images. ISPRS J. Photogramm. Remote Sens. 2015, 109, 108–125. [Google Scholar] [CrossRef]
- Kwata, V.; Schödl, A.; Essa, I.; Turk, G.; Bobick, A. Graphcut Textures: Image and Video Synthesis Using Graph. ACM Trans. Graph. 2003, 22, 277–286. [Google Scholar] [CrossRef]
- Qu, Z.; Wang, T.; An, S.; Liu, L. Image Seamless Stitching and Straightening Based on the Image Block. IET Image Process. 2018, 12, 1361–1369. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, G.; Song, R.; Xie, Y.; Luo, M.; Yue, T. Continuous Space Ant Colony Algorithm for Automatic Selection of Orthophoto Mosaic Seamline Network. ISPRS J. Photogramm. Remote Sens. 2022, 186, 201–217. [Google Scholar] [CrossRef]
- Gao, K.; Liu, B.; Yu, X. Unsupervised meta learning with multiview constraints for hyperspectral image small sample set classification. IEEE Trans. Image Process. 2022, 31, 3449–3462. [Google Scholar] [CrossRef] [PubMed]
- Xue, Z.; Tan, X.; Yu, X. Deep hierarchical vision transformer for hyperspectral and LiDAR data classification. IEEE Trans. Image Process. 2022, 31, 3095–3110. [Google Scholar] [CrossRef]
- Huang, W.; Sun, Q.; Yu, A. Leveraging Deep Convolutional Neural Network for Point Symbol Recognition in Scanned Topographic Maps. ISPRS Int. J. Geo-Inf. 2023, 12, 128. [Google Scholar] [CrossRef]
- Li, J.; Guo, W.; Liu, H. Predicting User Activity Intensity Using Geographic Interactions Based on Social Media Check-In Data. ISPRS Int. J. Geo-Inf. 2021, 10, 555. [Google Scholar] [CrossRef]
- Yu, A.; Guo, W.; Liu, B. Attention aware cost volume pyramid based multi-view stereo network for 3d reconstruction. ISPRS J. Photogramm. Remote Sens. 2021, 175, 448–460. [Google Scholar] [CrossRef]
- Li, L.; Yao, J.; Liu, Y.; Yuan, W.; Shi, S.; Yuan, S. Optimal Seamline Detection for Orthoimage Mosaicking by Combining Deep Convolutional Neural Network and Graph Cuts. Remote Sens. 2017, 9, 701. [Google Scholar] [CrossRef]
- Yu, A.; Quan, Y.; Yu, R. Deep Learning Methods for Semantic Segmentation in Remote Sensing with Small Data: A Survey. Remote Sens. 2023, 15, 4987. [Google Scholar] [CrossRef]
- Gao, K.; Yu, A.; You, X. Cross-Domain Multi-Prototypes with Contradictory Structure Learning for Semi-Supervised Domain Adaptation Segmentation of Remote Sensing Images. Remote Sens. 2023, 15, 3398. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, Y.; Yang, X.; Guo, G.M. A Fast Mosaic Algorithm of UAV Images Based on Dense SIFT Feature Matching. J. Geo-Inf. Sci. 2019, 21, 588–599. [Google Scholar]
- Zhu, S.; Qian, Z. The Seam-line Removal under Mosaicking of Remotely Sensed Images. J. Remote Sens. 2002, 6, 183–187. [Google Scholar]
- Chen, Y.; Zhan, D. Image Seamline Removal Method Based on JND Model. J. Electron. Inf. Technol. 2017, 39, 2404–2412. [Google Scholar]
- Bai, X.; Gu, S.; Zhou, F.; Xue, B. Weighted Image Fusion Based on Multi-Scale Top-Hat Transform: Algorithms and a Comparison Study. Optik 2013, 124, 1660–1668. [Google Scholar] [CrossRef]
- Szeliski, R. Video Mosaics for Virtual Environments. IEEE Comput. Graph. Appl. 1996, 16, 22–30. [Google Scholar] [CrossRef]
- Cai, H.; Wu, X.; Zhuo, L.; Huang, Z.; Wang, X. Fast SIFT Image Stitching Algorithm Combining Edge Detection. Infrared Laser Eng. 2018, 47, 449–455. [Google Scholar]
- Wang, D.; Liu, H.; Li, K.; Zhou, W. An Image Fusion Algorithm Based on Trigonometric Functions. Infrared Technol. 2017, 39, 53–57. [Google Scholar]
- Brown, M.; Lowe, D.G. Automatic Panoramic Image Stitching Using Invariant Features. Int. J. Comput. Vis. 2007, 74, 59–73. [Google Scholar] [CrossRef]
- Aslantas, V.; Bendes, E.; Toprak, A.N.; Kurban, R. A Comparison of Image Fusion Methods on Visible, Thermal and Multi-Focus Images for Surveillance Applications. In Proceedings of the 4th International Conference on Imaging for Crime Detection and Prevention 2011 (ICDP 2011), London, UK, 3–4 November 2011; IET: London, UK, 2011; pp. 1–6. [Google Scholar]
- Burt, P.J.; Adelson, E.H. A Multiresolution Spline with Application to Image Mosaics. ACM Trans. Graph. 1983, 2, 217–236. [Google Scholar] [CrossRef]
- Liu, Y.; Mo, F.; Tao, P. Matching multi-source optical satellite imagery exploiting a multi-stage approach. Remote Sens. 2017, 9, 1249. [Google Scholar] [CrossRef]
- Fan, Z.; Liu, Y.; Liu, Y. 3MRS: An Effective Coarse-to-Fine Matching Method for Multimodal Remote Sensing Imagery. Remote Sens. 2022, 14, 478. [Google Scholar] [CrossRef]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. SuperPoint: Self-Supervised Interest Point Detection and Description. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; IEEE: Salt Lake City, UT, USA, 2018; pp. 337–33712. [Google Scholar]
- Sarlin, P.-E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. SuperGlue: Learning Feature Matching with Graph Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; IEEE: Seattle, WA, USA, 2020; pp. 4937–4946. [Google Scholar]
- Vallet, J.; Panissod, F.; Strecha, C.; Tracol, M. Photogrammetric Performance of an Ultra Light Weight Swinglet “UAV”. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXVIII-1/C22, 253–258. [Google Scholar] [CrossRef]










| PSNR/dB | Image Quality Standards |
|---|---|
| PSNR ≥ 40 | Superb picture quality, virtually the same as the original |
| PSNR | Good picture quality, very similar to the original |
| PSNR | Poor picture quality with significant distortion |
| PSNR | Very poor picture quality with unacceptable image distortion |
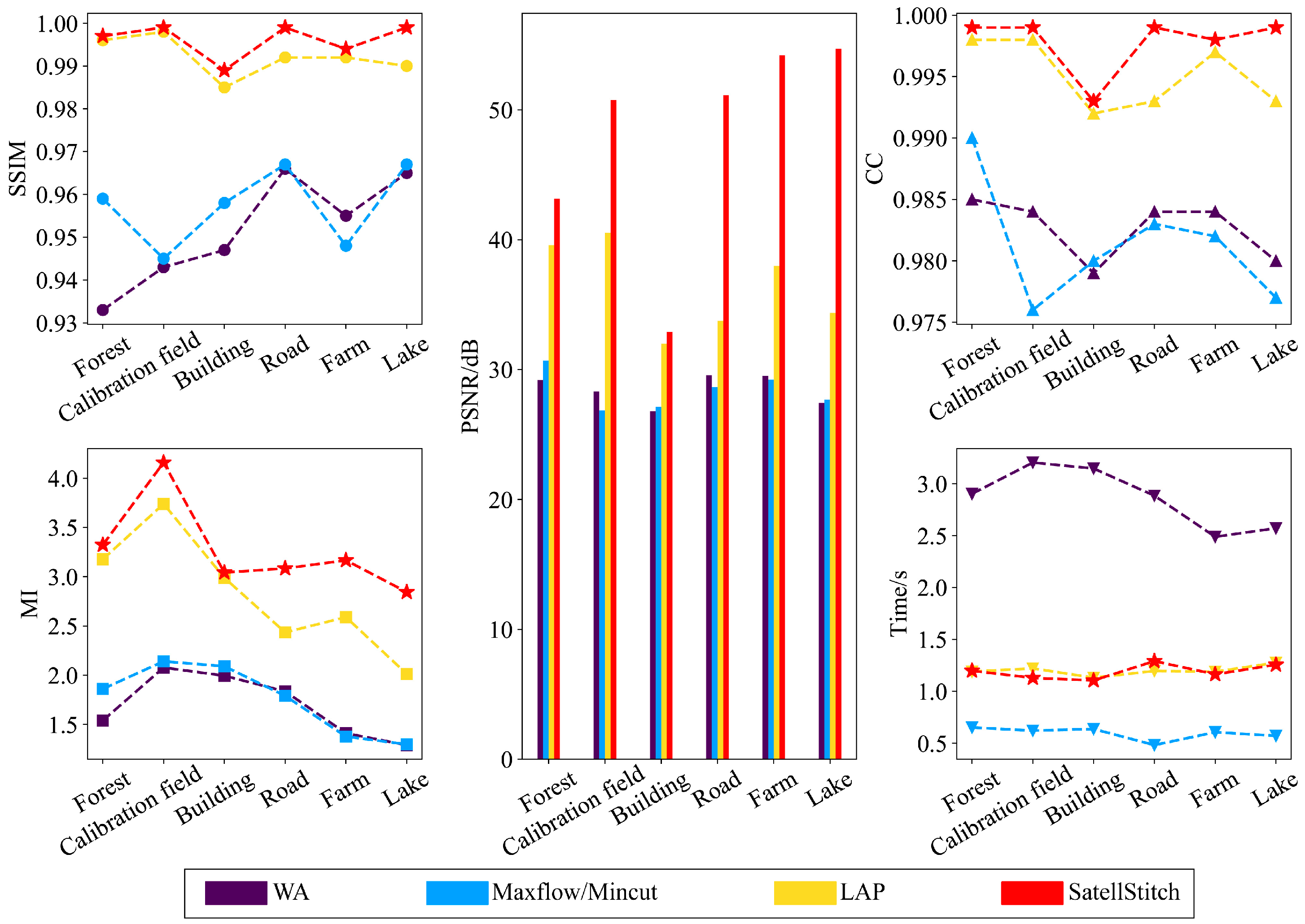
| Evaluation Indicators | Method | Forest | Calibration Field | Building | Road | Farm | Lake |
|---|---|---|---|---|---|---|---|
| PSNR/dB | WA | 29.202 | 28.319 | 26.806 | 29.569 | 29.507 | 27.438 |
| Maxflow/Mincut | 30.695 | 26.846 | 27.148 | 28.665 | 29.224 | 27.684 | |
| LAP | 39.589 | 40.542 | 31.985 | 33.752 | 37.992 | 34.369 | |
| SatellStitch | 43.155 | 50.751 | 32.916 | 51.131 | 54.187 | 54.695 | |
| SSIM | WA | 0.933 | 0.943 | 0.947 | 0.966 | 0.955 | 0.965 |
| Maxflow/Mincut | 0.959 | 0.945 | 0.958 | 0.967 | 0.948 | 0.967 | |
| LAP | 0.996 | 0.998 | 0.985 | 0.992 | 0.992 | 0.990 | |
| SatellStitch | 0.997 | 0.999 | 0.989 | 0.999 | 0.994 | 0.999 | |
| MI | WA | 1.540 | 2.078 | 1.995 | 1.836 | 1.411 | 1.291 |
| Maxflow/Mincut | 1.861 | 2.141 | 2.091 | 1.791 | 1.378 | 1.298 | |
| LAP | 3.177 | 3.739 | 2.989 | 2.435 | 2.590 | 2.013 | |
| SatellStitch | 3.323 | 4.159 | 3.043 | 3.084 | 3.167 | 2.844 | |
| CC | WA | 0.985 | 0.984 | 0.979 | 0.984 | 0.984 | 0.980 |
| Maxflow/Mincut | 0.990 | 0.976 | 0.980 | 0.983 | 0.982 | 0.977 | |
| LAP | 0.998 | 0.998 | 0.992 | 0.993 | 0.997 | 0.993 | |
| SatellStitch | 0.999 | 0.999 | 0.993 | 0.999 | 0.998 | 0.999 | |
| Time/s | WA | 2.903 | 3.204 | 3.147 | 2.885 | 2.489 | 2.571 |
| Maxflow/Mincut | 0.652 | 0.621 | 0.637 | 0.482 | 0.606 | 0.571 | |
| LAP | 1.190 | 1.221 | 1.131 | 1.196 | 1.189 | 1.276 | |
| SatellStitch | 1.198 | 1.129 | 1.105 | 1.291 | 1.164 | 1.256 |
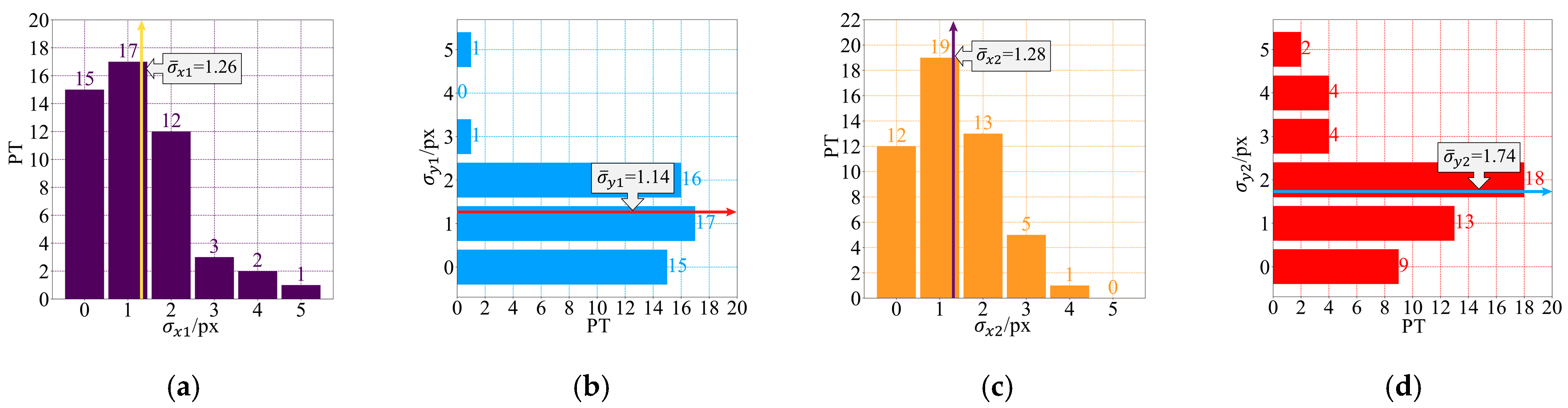
| Data | Number of Images | (pixels) | (pixels) |
|---|---|---|---|
| Data I | 61 | 1.26 | 1.14 |
| Data II | 25 | 1.28 | 1.74 |
| Data | SatellStitch | Pix4DMapper | |||
|---|---|---|---|---|---|
| (s) | (s) | (s) | (s) | ||
| Data I | 0.93 | 0.27 | 1.28 | 2.48/151.37 | 6.58/401 |
| Data II | 0.91 | 0.22 | 1.12 | 2.25/56.25 | 2.76/69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Lan, C.; Xu, Q.; Wang, L.; Gao, T.; Yao, F.; Hou, H. SatellStitch: Satellite Imagery-Assisted UAV Image Seamless Stitching for Emergency Response without GCP and GNSS. Remote Sens. 2024, 16, 309. https://doi.org/10.3390/rs16020309
Wei Z, Lan C, Xu Q, Wang L, Gao T, Yao F, Hou H. SatellStitch: Satellite Imagery-Assisted UAV Image Seamless Stitching for Emergency Response without GCP and GNSS. Remote Sensing. 2024; 16(2):309. https://doi.org/10.3390/rs16020309
Chicago/Turabian StyleWei, Zijun, Chaozhen Lan, Qing Xu, Longhao Wang, Tian Gao, Fushan Yao, and Huitai Hou. 2024. "SatellStitch: Satellite Imagery-Assisted UAV Image Seamless Stitching for Emergency Response without GCP and GNSS" Remote Sensing 16, no. 2: 309. https://doi.org/10.3390/rs16020309
APA StyleWei, Z., Lan, C., Xu, Q., Wang, L., Gao, T., Yao, F., & Hou, H. (2024). SatellStitch: Satellite Imagery-Assisted UAV Image Seamless Stitching for Emergency Response without GCP and GNSS. Remote Sensing, 16(2), 309. https://doi.org/10.3390/rs16020309