A Focusing Method of Buildings for Airborne Circular SAR
Abstract
1. Introduction
- A detailed analysis about the range errors that lead to azimuth defocusing for CSAR buildings imaging, and an analytical relationship between the azimuth focusing quality and the height of the scatterer away from the imaging plane are given for the first time. This analytical relationship can be independently used as a criterion to judge whether a good focusing CSAR image can be achieved by using BP algorithm on a certain height plane or not.
- An focusing method based on BP algorithm is proposed for CSAR buildings imaging. The proposed method can improve the focusing quality of the buildings with large height in the CSAR mode.
- The proposed method is used to process the airborne CSAR real data, and the improved imaging results of high-rise buildings are achieved. It is a good reference for the subsequent real data processing under similar scenarios.
2. Problem Statement
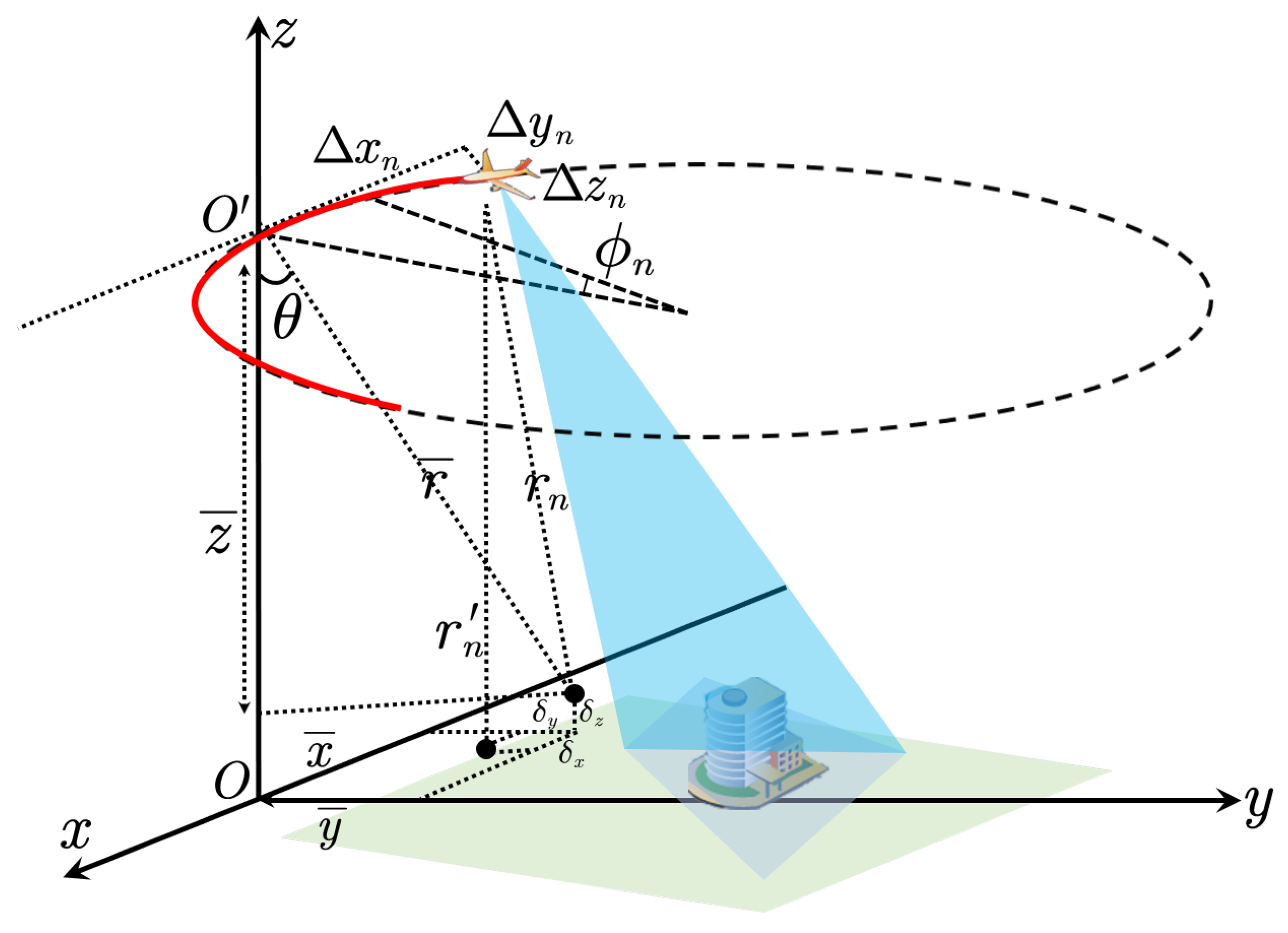
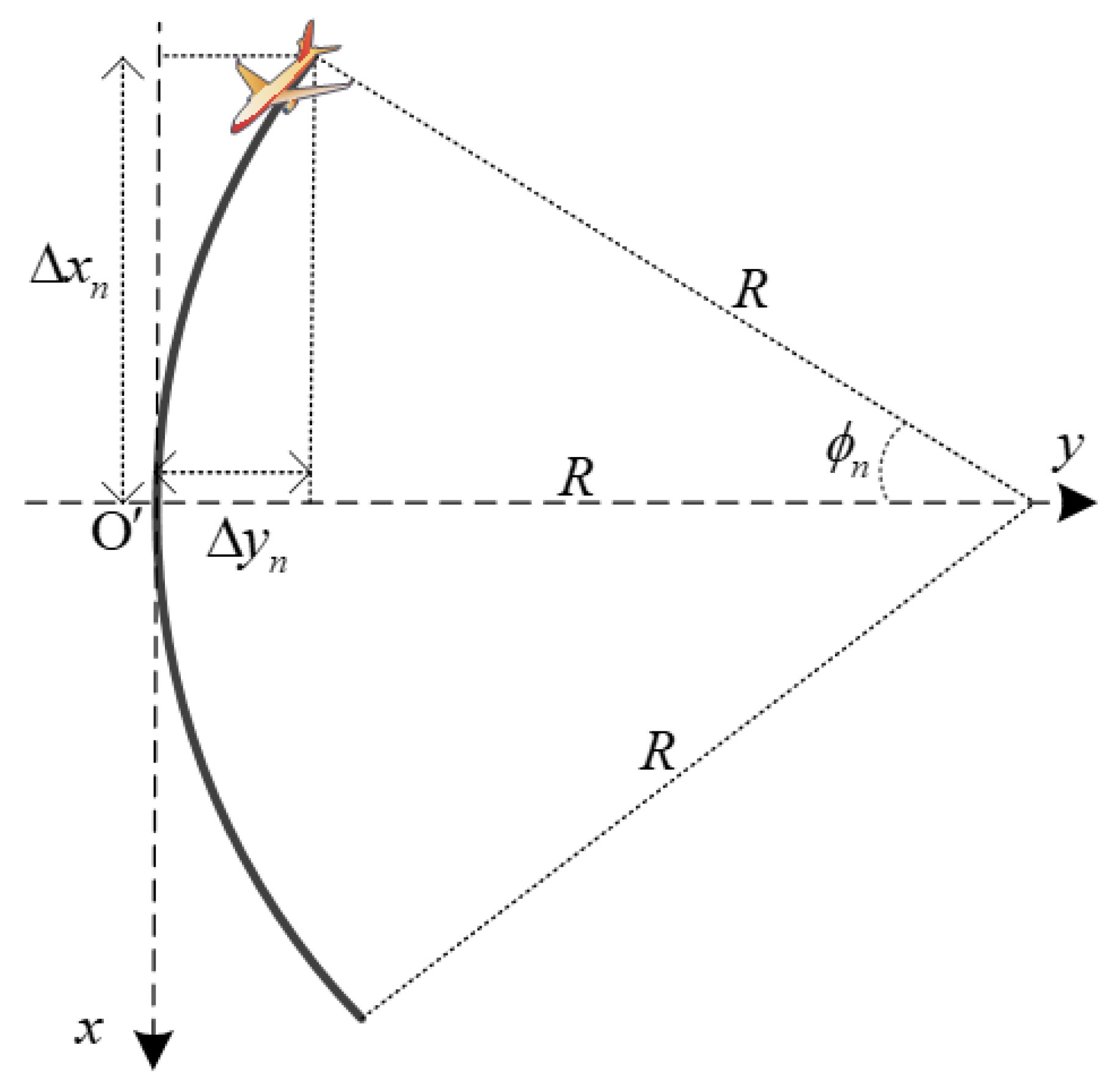
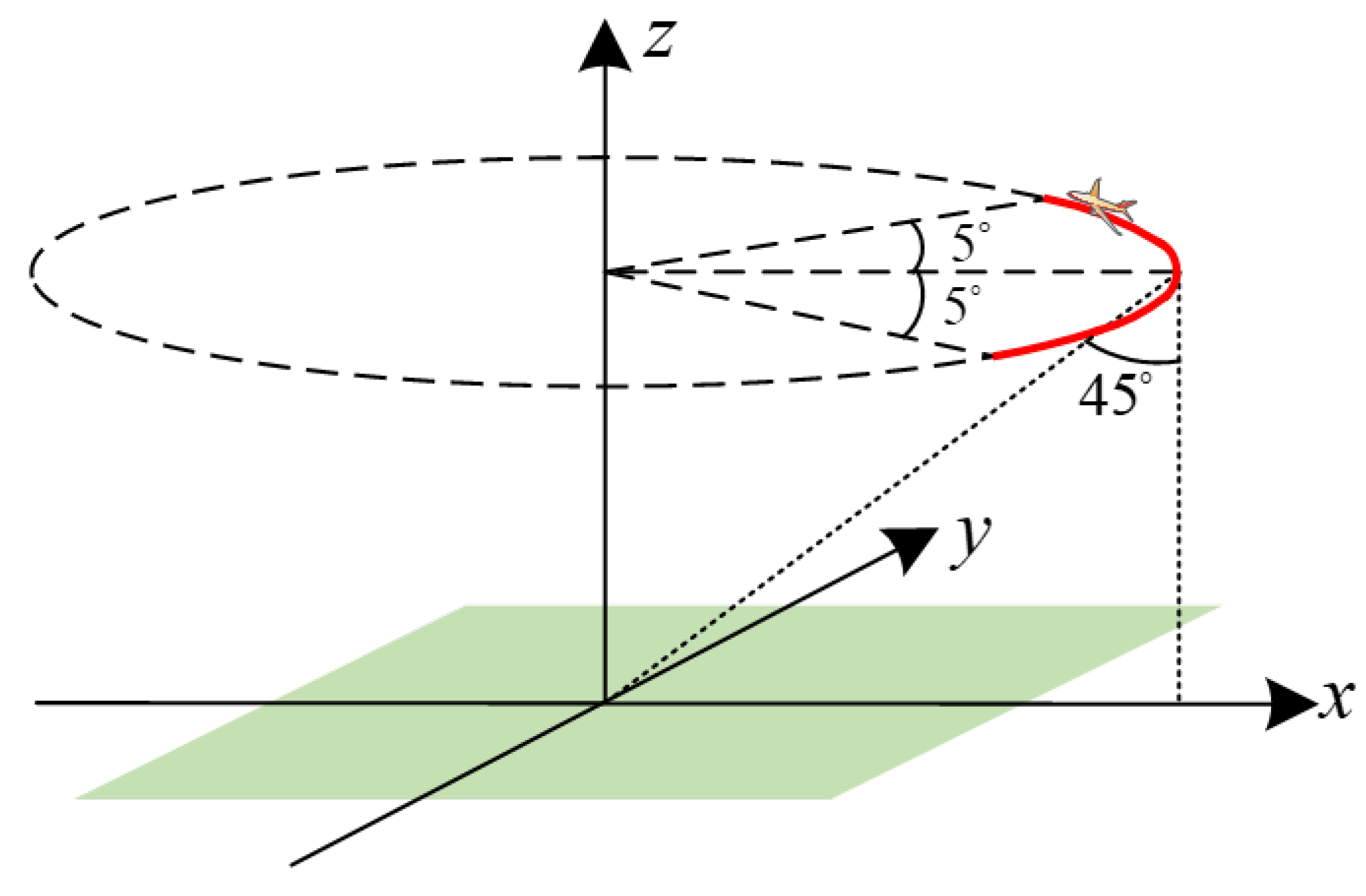
2.1. Imaging Geometry and Signal Model
2.2. Analysis on the Range Errors in Buildings Focusing
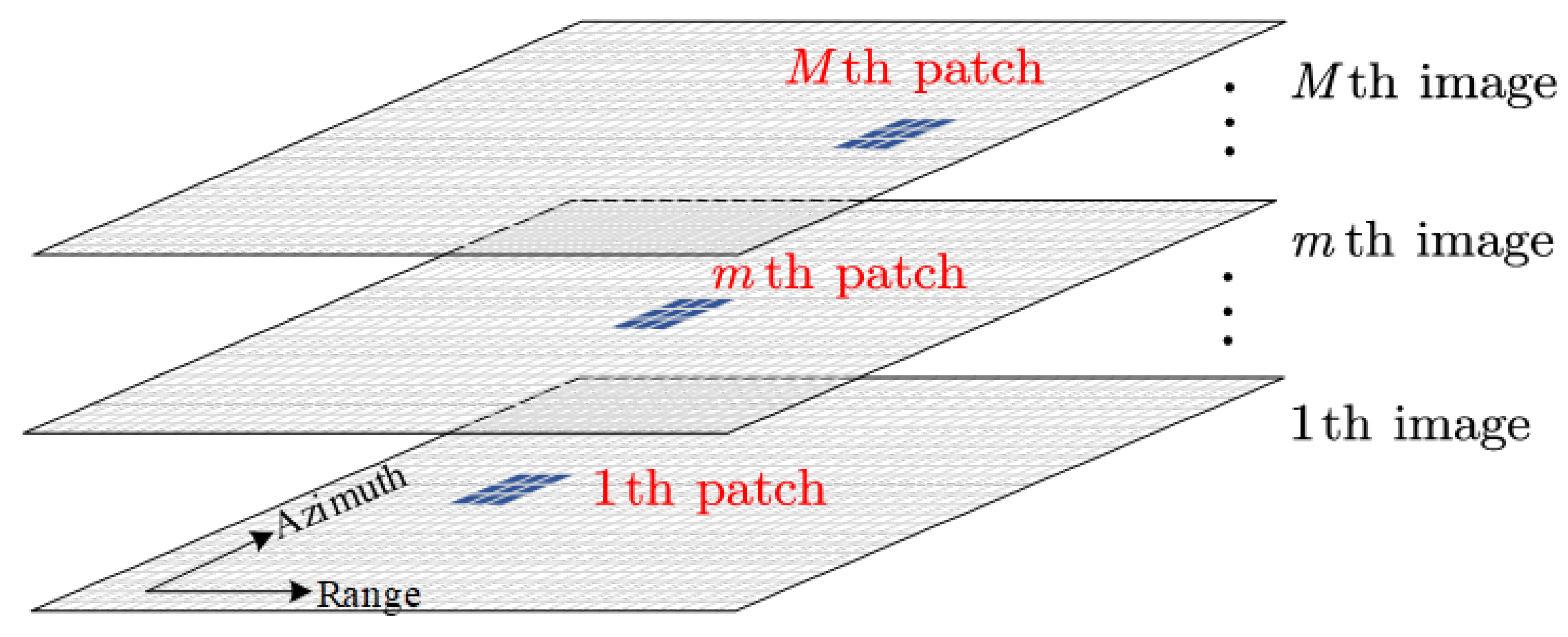
3. Method
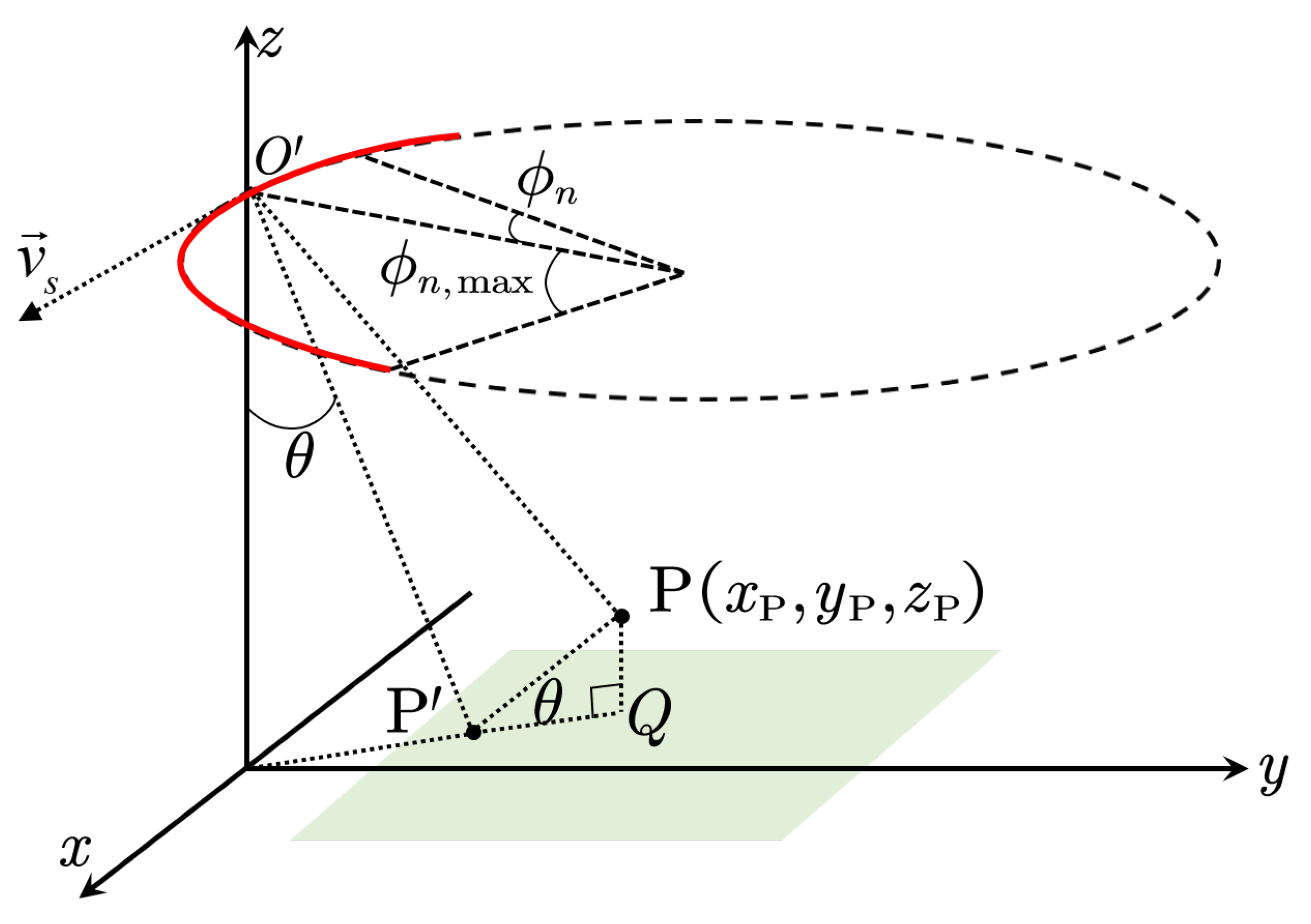
3.1. Position Tracking of the Scatterer on Different Planes
3.2. Offsets Estimation Based on Local Focusing Evaluation
3.3. Processing Flow of the Proposed Method and Computational Complexity Analysis
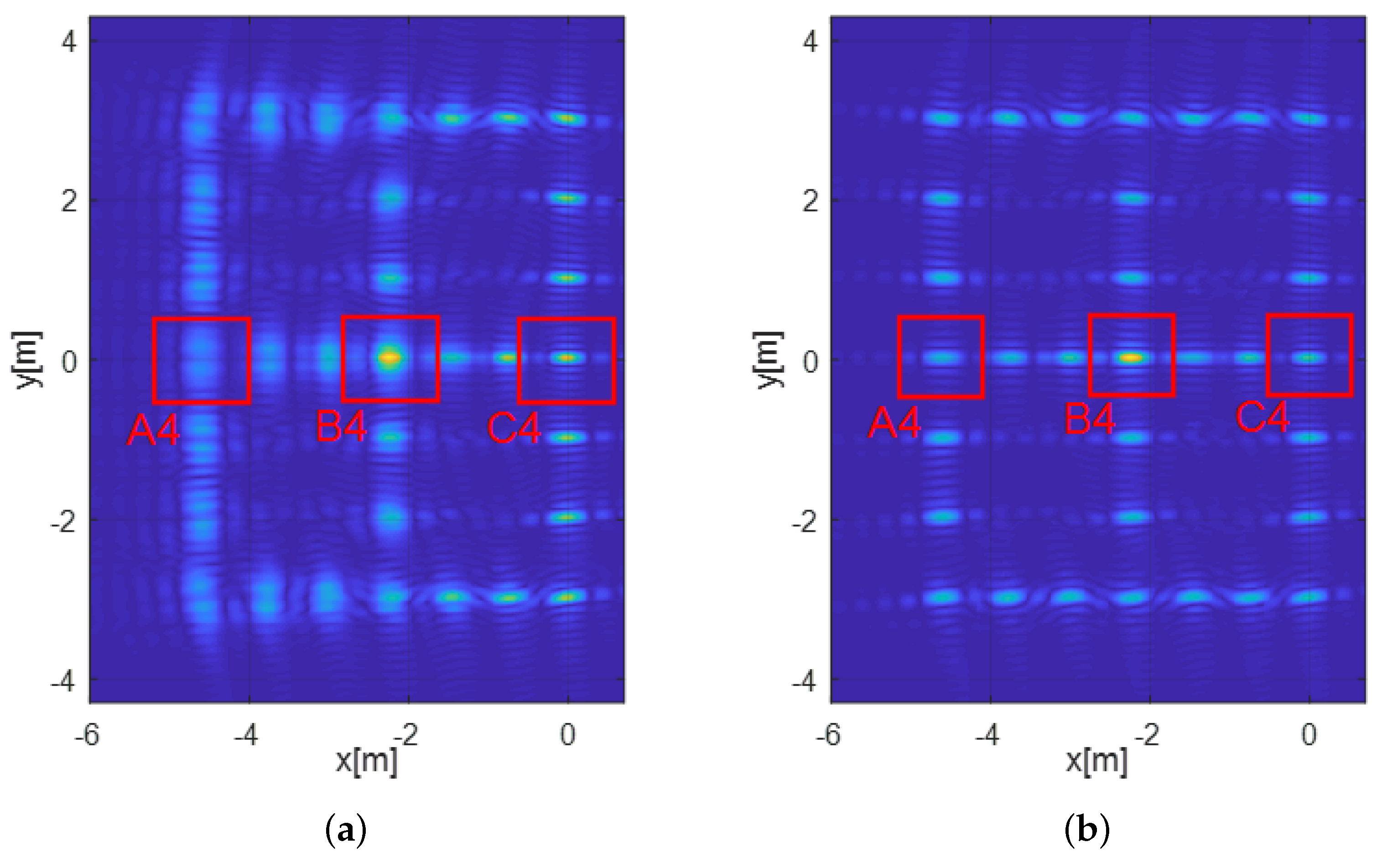
4. Experimental Results
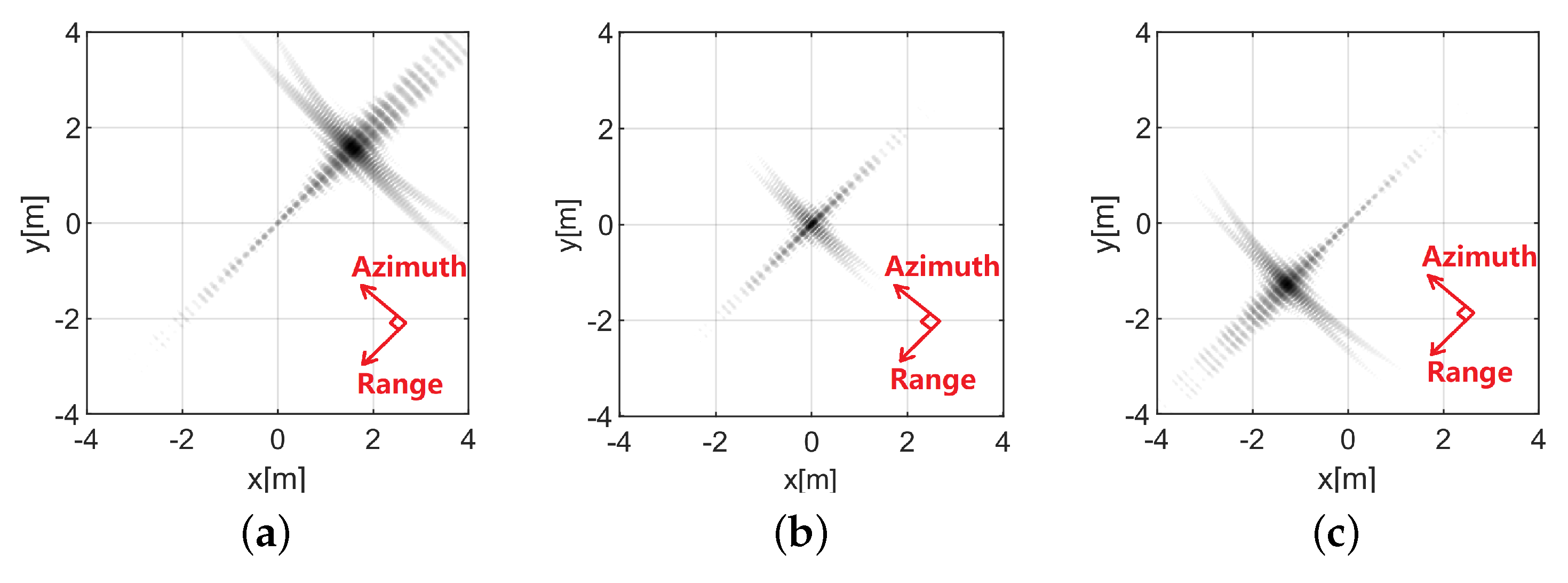
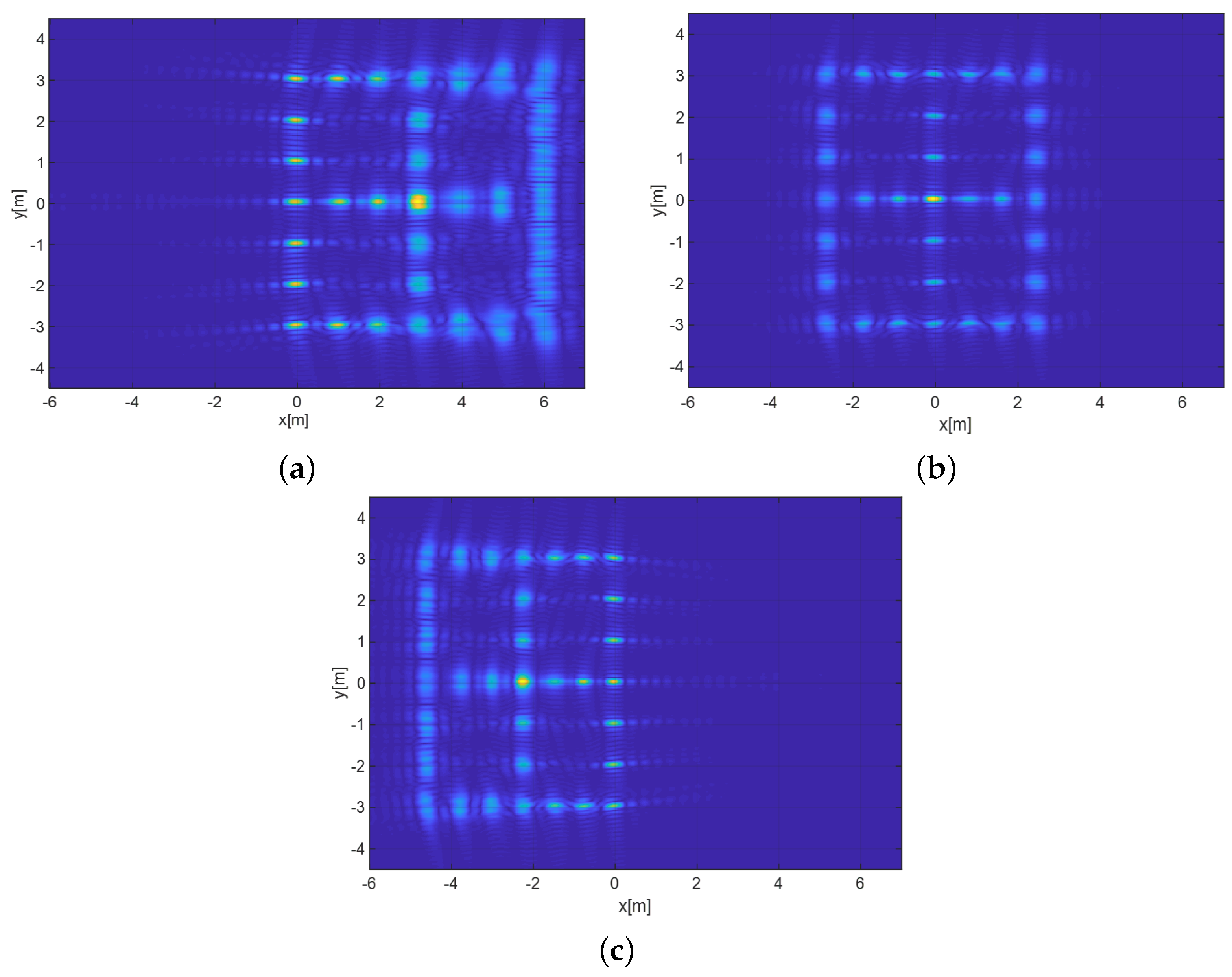
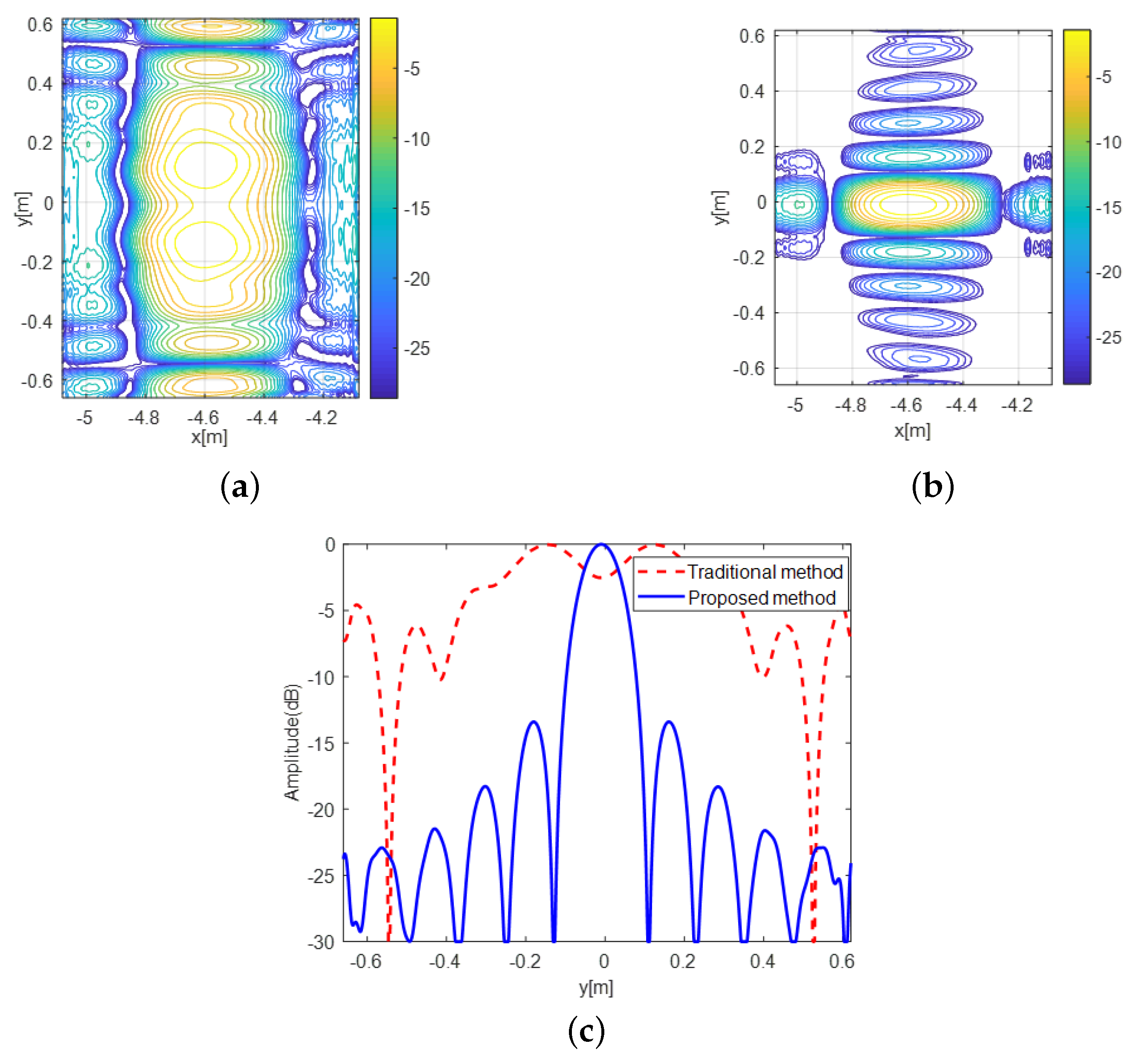
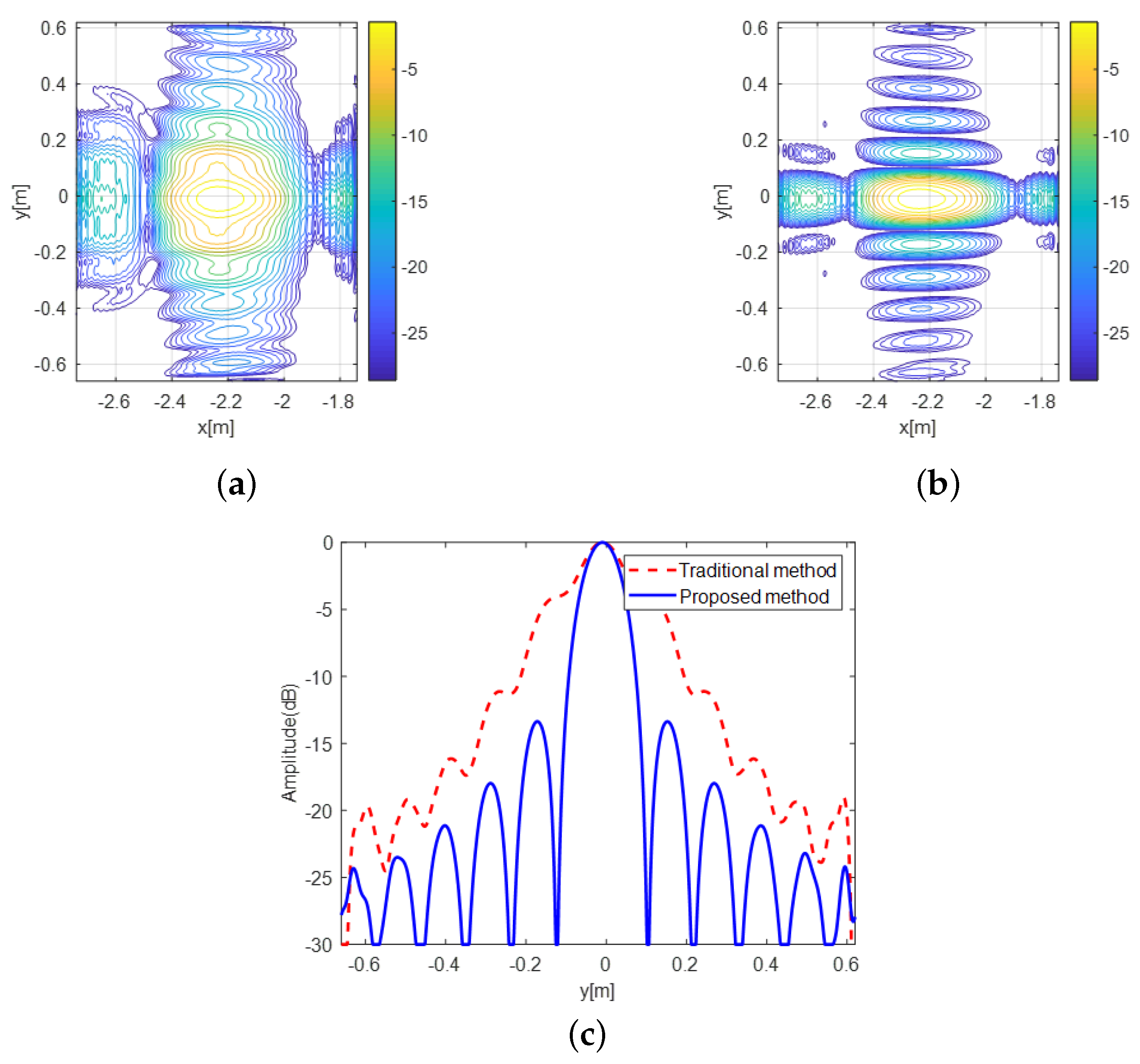
4.1. Simulated Data
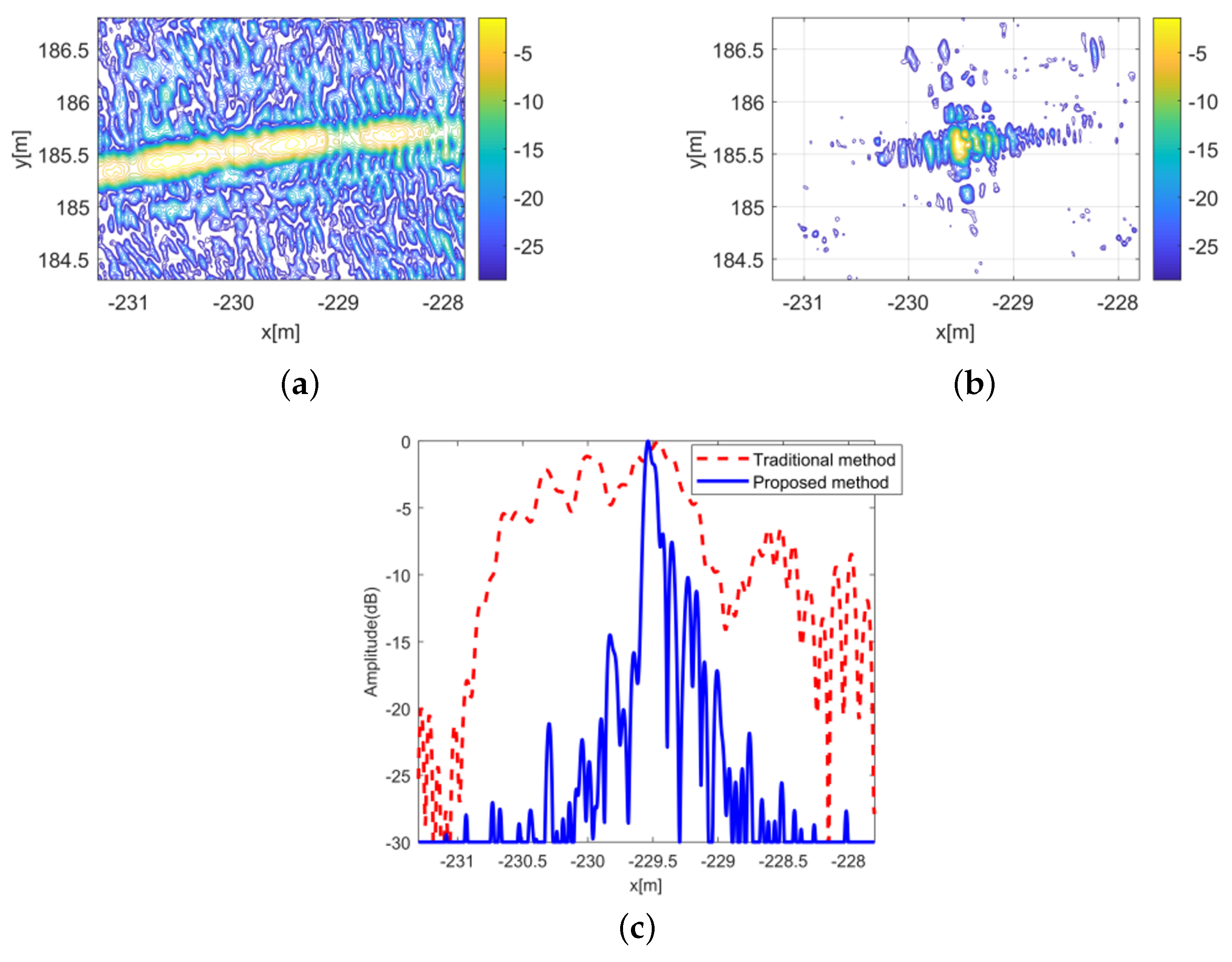
4.2. Real Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Chen, J.; Li, M.; Yu, H.; Xing, M. Full-aperture processing of airborne microwave photonic SAR raw data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5218812. [Google Scholar] [CrossRef]
- Rambour, C.; Budillon, A.; Johnsy, A.C.; Denis, L.; Tupin, F.; Schirinzi, G. From interferometric to tomographic SAR: A review of synthetic aperture radar tomography-processing techniques for scatterer unmixing in urban areas. IEEE Geosci. Remote Sens. Mag. 2020, 8, 6–29. [Google Scholar] [CrossRef]
- Kechagias-Stamatis, O.; Aouf, N. Automatic target recognition on synthetic aperture radar imagery: A survey. IEEE Aerosp. Electron. Syst. Mag. 2021, 36, 56–81. [Google Scholar] [CrossRef]
- Soumekh, M. Reconnaissance with slant plane circular SAR imaging. IEEE Trans. Image Process. 1996, 5, 1252–1265. [Google Scholar] [CrossRef] [PubMed]
- Ishimaru, A.; Chan, T.; Kuga, Y. An imaging technique using confocal circular synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1524–1530. [Google Scholar] [CrossRef]
- Cantalloube, H.; Koeniguer, E.C. Assessment of physical limitations of high resolution on targets at X band from circular SAR experiments. In Proceedings of the 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2–5 June 2008; pp. 1–4. [Google Scholar]
- Austin, C.D.; Ertin, E.; Moses, R.L. Sparse signal methods for 3-D radar imaging. IEEE J. Sel. Topics Signal Process. 2011, 5, 408–423. [Google Scholar] [CrossRef]
- Palm, S.; Sommer, R.; Janssen, D.; Tessmann, A.; Stilla, U. Airborne circular W-band SAR for multiple aspect urban site monitoring. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6996–7016. [Google Scholar] [CrossRef]
- Ponce, O.; Prats-Iraola, P.; Pinheiro, M.; Rodrigues-Cassola, M.; Scheiber, R.; Reigber, A.; Moreira, A. Fully polarimetric high resolution 3-D imaging with circular SAR at L-band. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3074–3090. [Google Scholar] [CrossRef]
- Palm, S.; Stilla, U. 3-D point cloud generation from airborne single-pass and single-channel circular SAR data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8398–8417. [Google Scholar] [CrossRef]
- Lin, Y.; Hong, W.; Tan, W.; Wang, Y.; Wu, Y. Interferometric circular SAR method for three-dimensional imaging. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1026–1030. [Google Scholar] [CrossRef]
- Bao, Q.; Lin, Y.; Hong, W.; Shen, W.; Zhao, Y.; Peng, X. Holographic SAR tomography image reconstruction by combination of adaptive imaging and sparse Bayesian inference. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1248–1252. [Google Scholar] [CrossRef]
- Feng, D.; An, D.; Chen, L.; Huang, X. Holographic SAR tomography 3-D reconstruction based on iterative adaptive approach and generalized likelihood ratio test. IEEE Trans. Geosci. Remote Sens. 2021, 59, 305–315. [Google Scholar] [CrossRef]
- Ponce, O.; Prats-Iraola, P.; Scheiber, R.; Reigber, A.; Moreira, A. First airborne demonstration of holographic SAR tomography with fully polarimetric multicircular acquisitions at L-band. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6170–6196. [Google Scholar] [CrossRef]
- Ertin, E.; Moses, R.L.; Potter, L.C. Interferometric methods for three-dimensional target reconstruction with multipass circular SAR. IET Radar Sonar Navigat. 2010, 4, 464–473. [Google Scholar] [CrossRef]
- An, D.; Huang, X.; Jin, T.; Zhou, Z. Extended nonlinear chirp scaling algorithm for high-resolution highly squint SAR data focusing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3595–3609. [Google Scholar] [CrossRef]
- Jia, G.; Buchroithner, M.F.; Chang, W.; Liu, Z. Fourier-based 2-D imaging algorithm for circular synthetic aperture radar: Analysis and application. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2016, 9, 475–489. [Google Scholar] [CrossRef]
- Feng, D.; An, D.; Huang, X. An extended fast factorized back projection algorithm for missile-borne bistatic forward-looking SAR imaging. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2724–2734. [Google Scholar] [CrossRef]
- Hu, X.; Xie, H.; Zhang, L.; Hu, J.; He, J.; Yi, S.; Jiang, H.; Xie, K. Fast factorized backprojection algorithm in orthogonal elliptical coordinate system for ocean scenes imaging using geosynchronous spaceborne-airborne VHF UWB bistatic SAR. Remote Sens. 2023, 15, 2215. [Google Scholar] [CrossRef]
- Ulander, L.M.H.; Hellsten, H.; Stenstrom, G. Synthetic aperture radar processing using fast factorized back-projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef]
- Duersch, M.I.; Long, D.G. Analysis of time-domain back-projection for stripmap SAR. Int. J. Remote Sens. 2015, 36, 2010–2036. [Google Scholar] [CrossRef]
- Cantalloube, H.M.-J. Circular SAR imaging of not planar targets. Limitations of the “height from focus” paradigm. In Proceedings of the IEEE International Symposium on Geoscience and Remote Sensing (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 3671–3674. [Google Scholar]
- Ertin, E.; Austin, C.D.; Sharma, S.; Moses, R.L.; Potter, L.C. GOTCHA experience report: Three-dimensional SAR imaging with complete circular apertures. Proc. SPIE 2007, 6568, 656802. [Google Scholar]
- Ponce, O.; Prats-Iraola, P.; Scheiber, R.; Reigber, A.; Moreira, A.; Aguilera, E. Polarimetric 3-D reconstruction from multicircular SAR at P-band. IEEE Geosci. Remote Sens. Lett. 2014, 11, 803–807. [Google Scholar] [CrossRef]
- Cao, N.; Lee, H.; Zaugg, E.; Shrestha, R.; Carter, W.E.; Glennie, C.; Lu, Z.; Yu, H. Estimation of residual motion errors in airborne SAR interferometry based on time-domain backprojection and multisquint techniques. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2397–2407. [Google Scholar] [CrossRef]
- Chen, J.; Xing, M.; Yu, H.; Liang, B.; Peng, J.; Sun, G.C. Motion compensation/autofocus in airborne synthetic aperture radar: A review. IEEE Geosci. Remote Sens. Mag. 2022, 10, 185–206. [Google Scholar] [CrossRef]
- Luo, Y.; Qiu, X.; Dong, Q.; Fu, K. A robust stereo positioning solution for multiview spaceborne SAR images based on the range-doppler model. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4008705. [Google Scholar] [CrossRef]
- Aghababaee, H.; Fornaro, G.; Schirinzi, G. Phase calibration based on phase derivative constrained optimization in multibaseline SAR tomography. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6779–6791. [Google Scholar] [CrossRef]
- Ash, J.N. An autofocus method for backprojection imagery in synthetic aperture radar. IEEE Geosci. Remote Sens. Lett. 2012, 9, 104–108. [Google Scholar] [CrossRef]


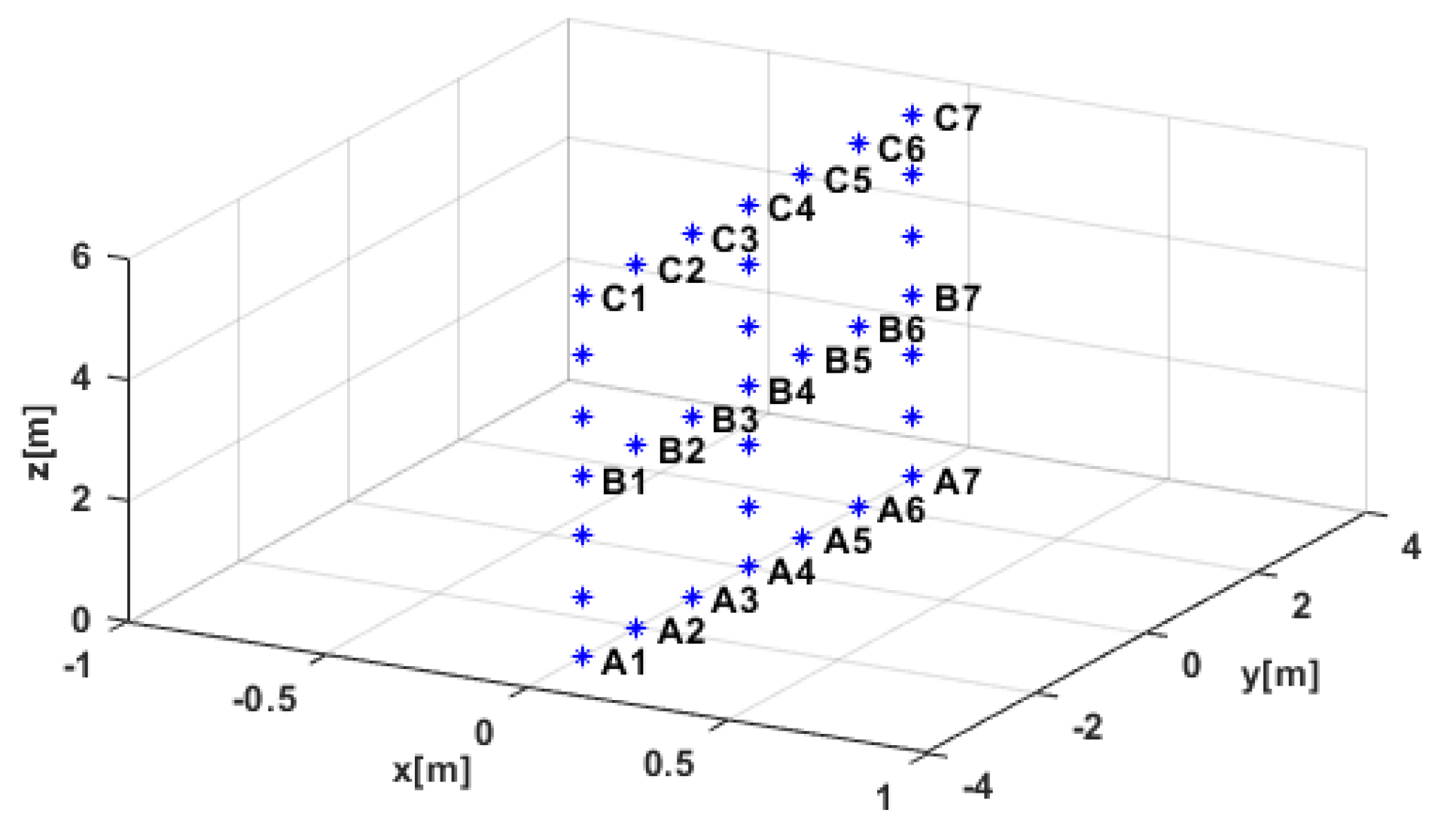





| Parameters | Values |
|---|---|
| Center frequency | 10 GHz |
| Signal bandwidth | 600 MHz |
| Chirp Duration | 1 us |
| Azimuth accumulation angel | 10 degrees |
| Elevation angle | 45 degrees |
| Scene size | 20 m × 20 m () |
| Measured Parameters | Methods | A4 | B4 | C4 |
|---|---|---|---|---|
| Resolutions (in meters) | Traditional | 0.528 | 0.140 | 0.088 |
| Proposed | 0.104 | 0.100 | 0.088 | |
| Theoretical | 0.105 | 0.097 | 0.090 | |
| PSLR (in dB) | Traditional | −0.016 | −11.115 | −13.285 |
| Proposed | −13.404 | −13.360 | −13.235 | |
| ISLR (in dB) | Tradional | 1.920 | −10.481 | −10.600 |
| Proposed | −10.723 | −10.743 | −10.546 |
| Parameters | Values |
|---|---|
| Radar operating band | Ku-band |
| Signal bandwidth | 1200 MHz |
| Chirp duration | 200 us |
| Elevation angle | 48 degrees |
| Mean flight height | 1975 m |
| Mean flight radius | 2192 m |
| Measured Parameters | Methods | D1 | D2 |
|---|---|---|---|
| Resolutions (in meters) | Traditional | 1.065 | 0.609 |
| Proposed | 0.090 | 0.075 | |
| PSLR (in dB) | Traditional | −4.677 | −3.948 |
| Proposed | −7.568 | −8.273 | |
| ISLR (in dB) | Tradional | 1.742 | 2.113 |
| Proposed | −5.487 | −5.359 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, D.; An, D.; Wang, J.; Chen, L.; Huang, X. A Focusing Method of Buildings for Airborne Circular SAR. Remote Sens. 2024, 16, 253. https://doi.org/10.3390/rs16020253
Feng D, An D, Wang J, Chen L, Huang X. A Focusing Method of Buildings for Airborne Circular SAR. Remote Sensing. 2024; 16(2):253. https://doi.org/10.3390/rs16020253
Chicago/Turabian StyleFeng, Dong, Daoxiang An, Jian Wang, Leping Chen, and Xiaotao Huang. 2024. "A Focusing Method of Buildings for Airborne Circular SAR" Remote Sensing 16, no. 2: 253. https://doi.org/10.3390/rs16020253
APA StyleFeng, D., An, D., Wang, J., Chen, L., & Huang, X. (2024). A Focusing Method of Buildings for Airborne Circular SAR. Remote Sensing, 16(2), 253. https://doi.org/10.3390/rs16020253






