Early Mission Calibration Performance of NOAA-21 VIIRS Reflective Solar Bands
Abstract
1. Introduction
2. Radiometric Calibration Methodology
3. Screen Functions Derived from Calibration Data Collected at Both the Yaw Maneuver and Regular Times
4. Results
4.1. Screen Functions
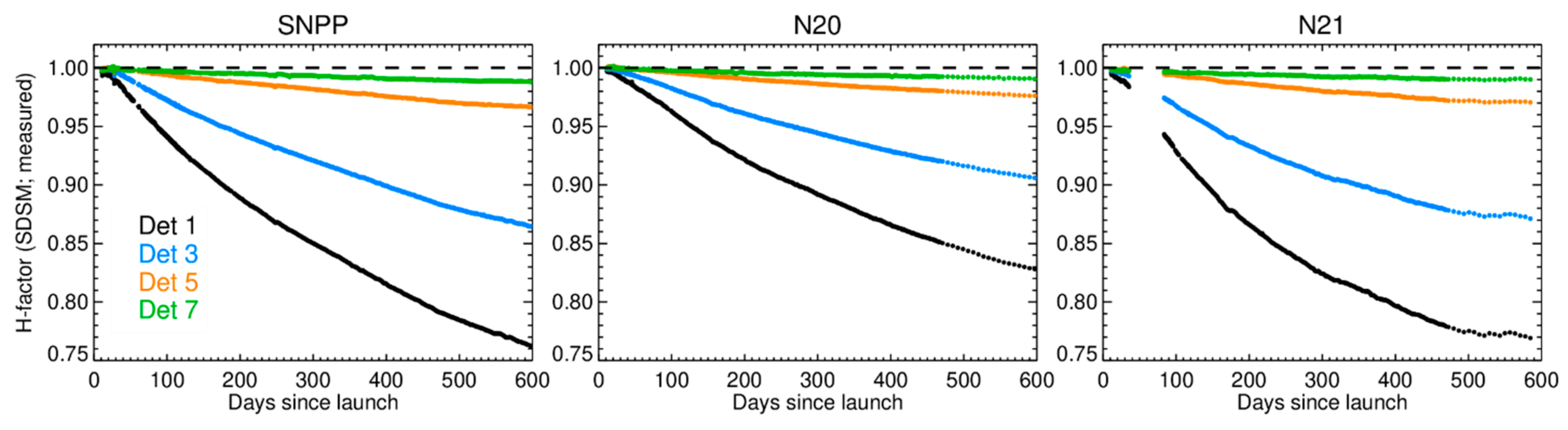
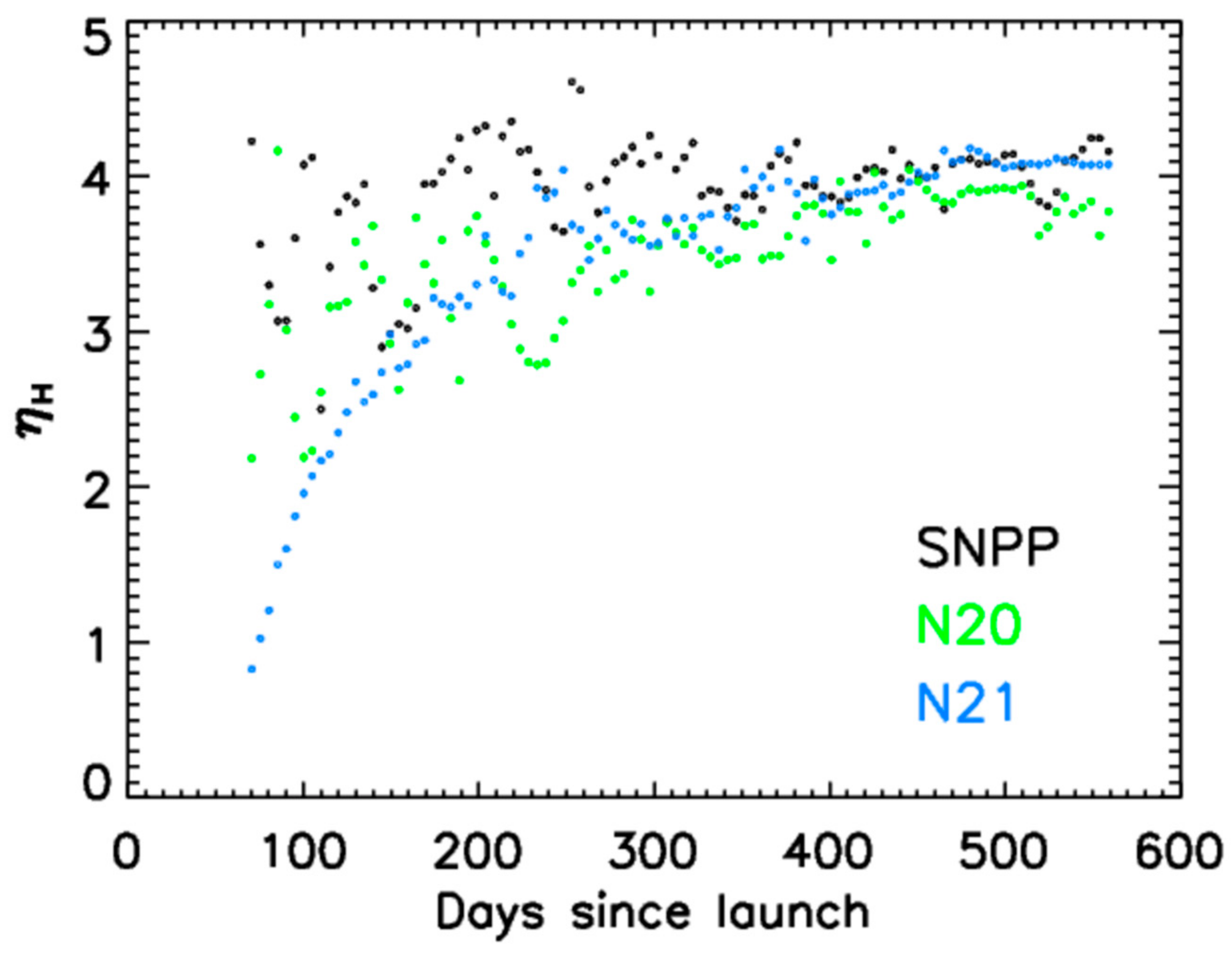
4.2. SDSM and SD Radiometric Calibration Performance
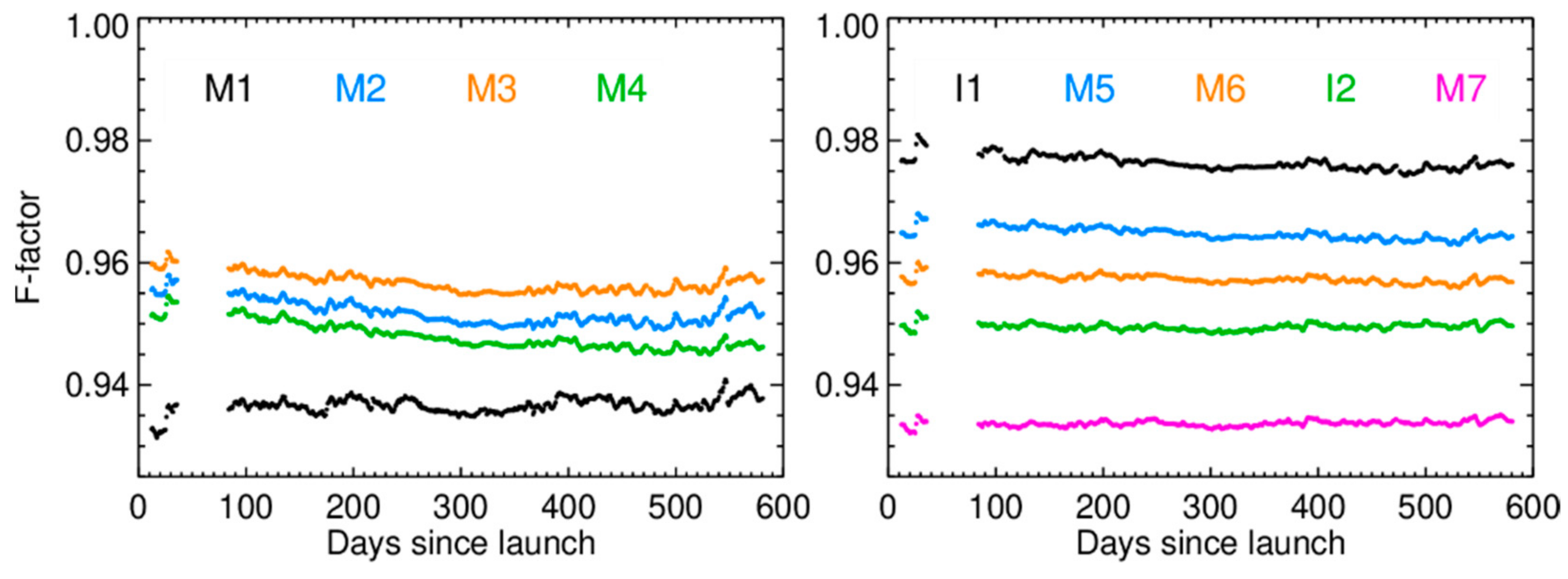
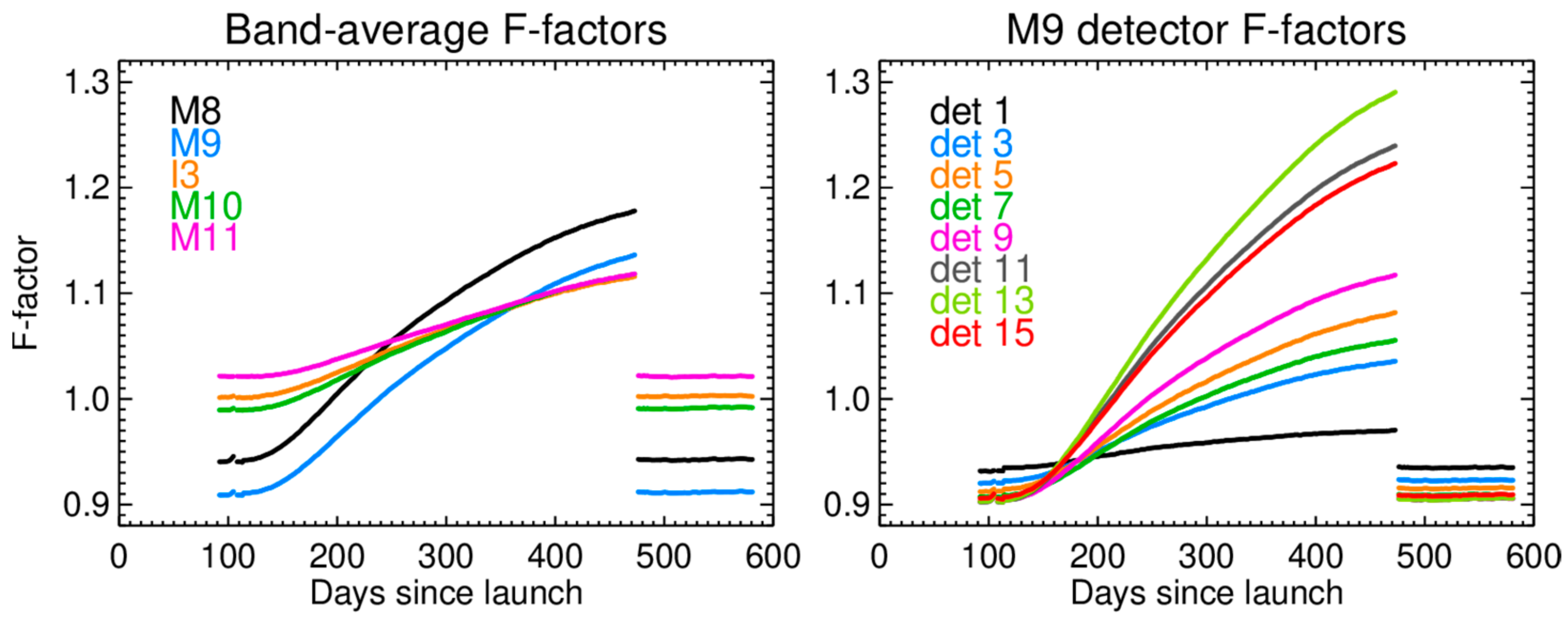
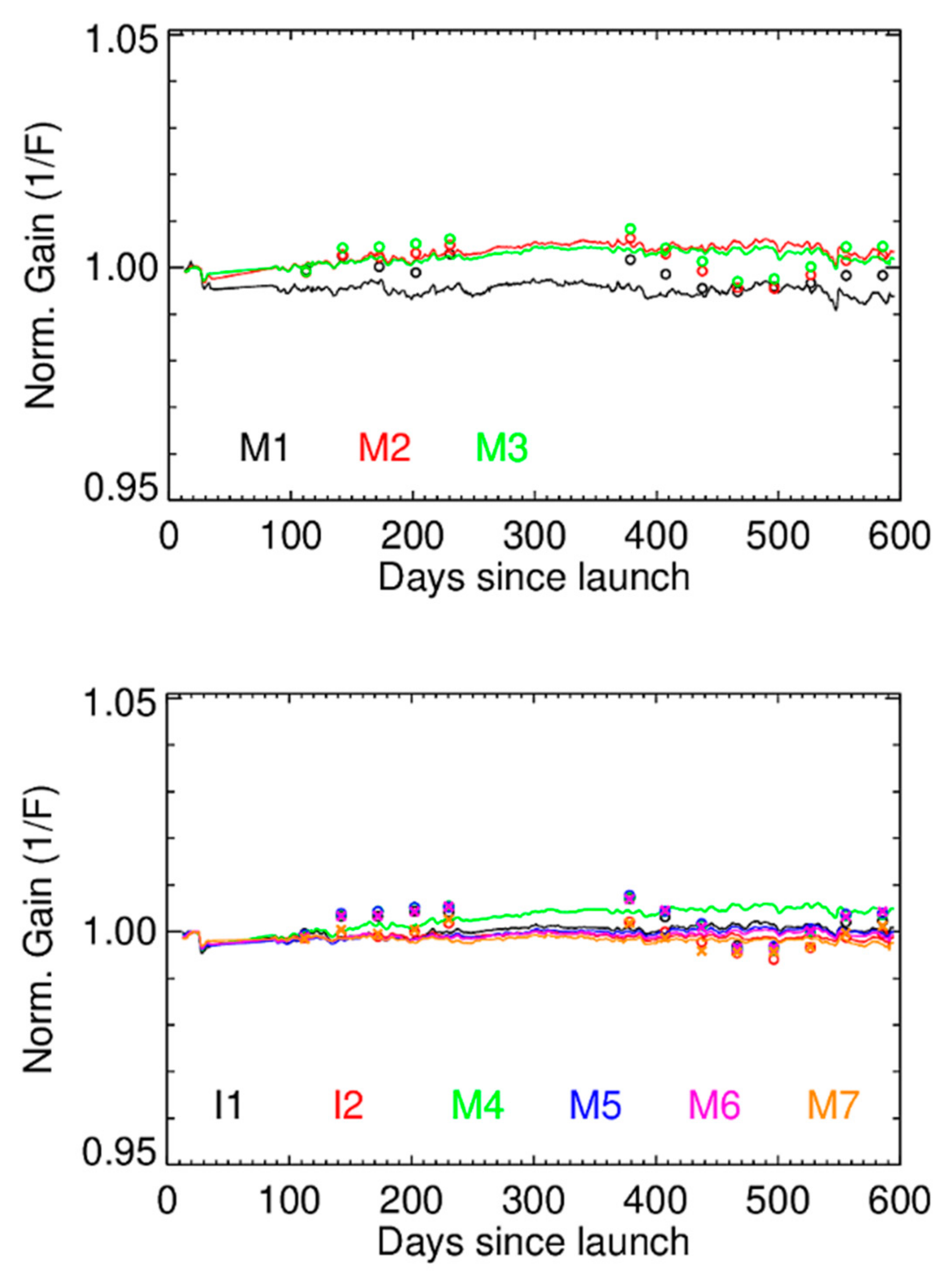
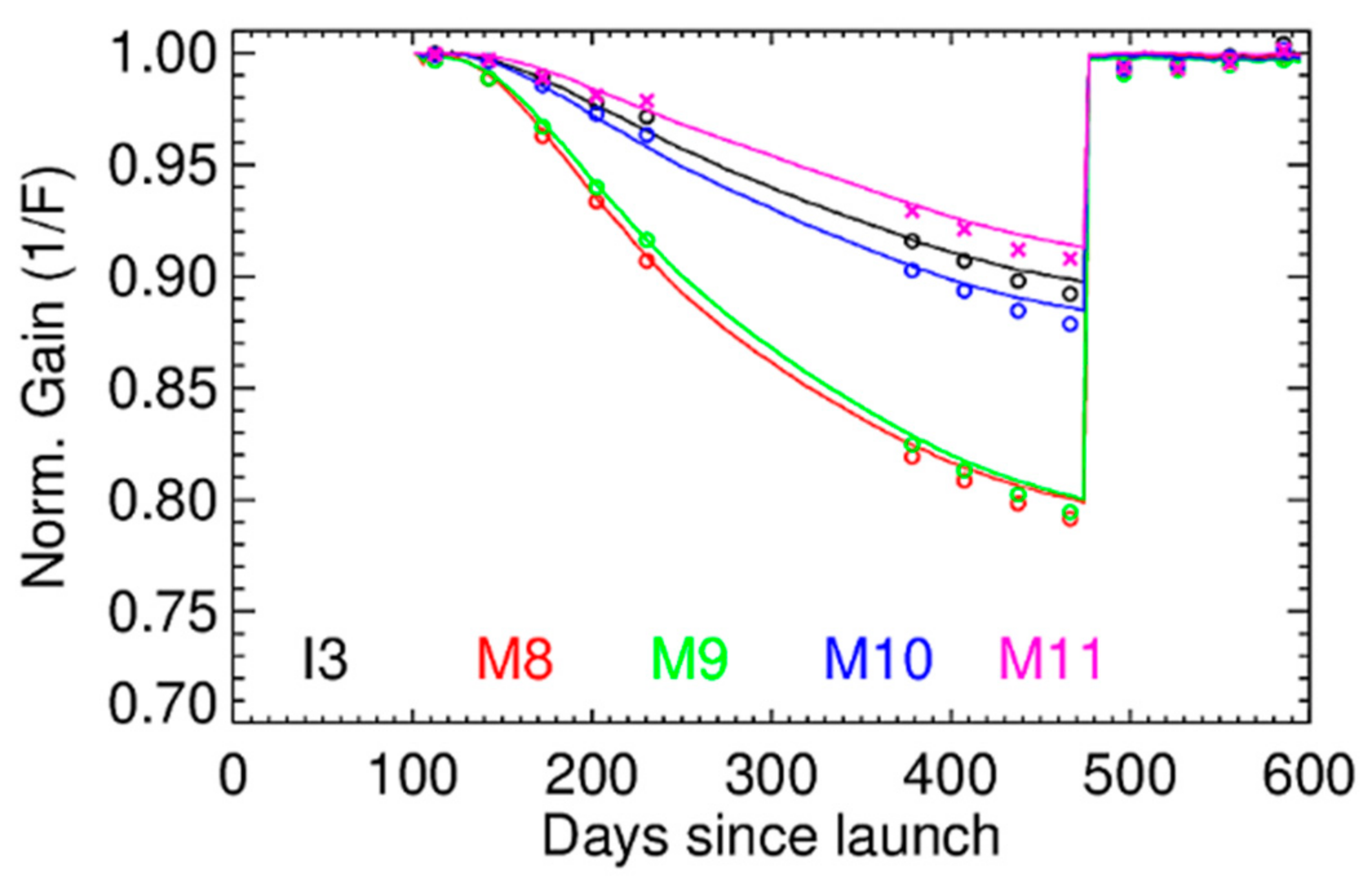
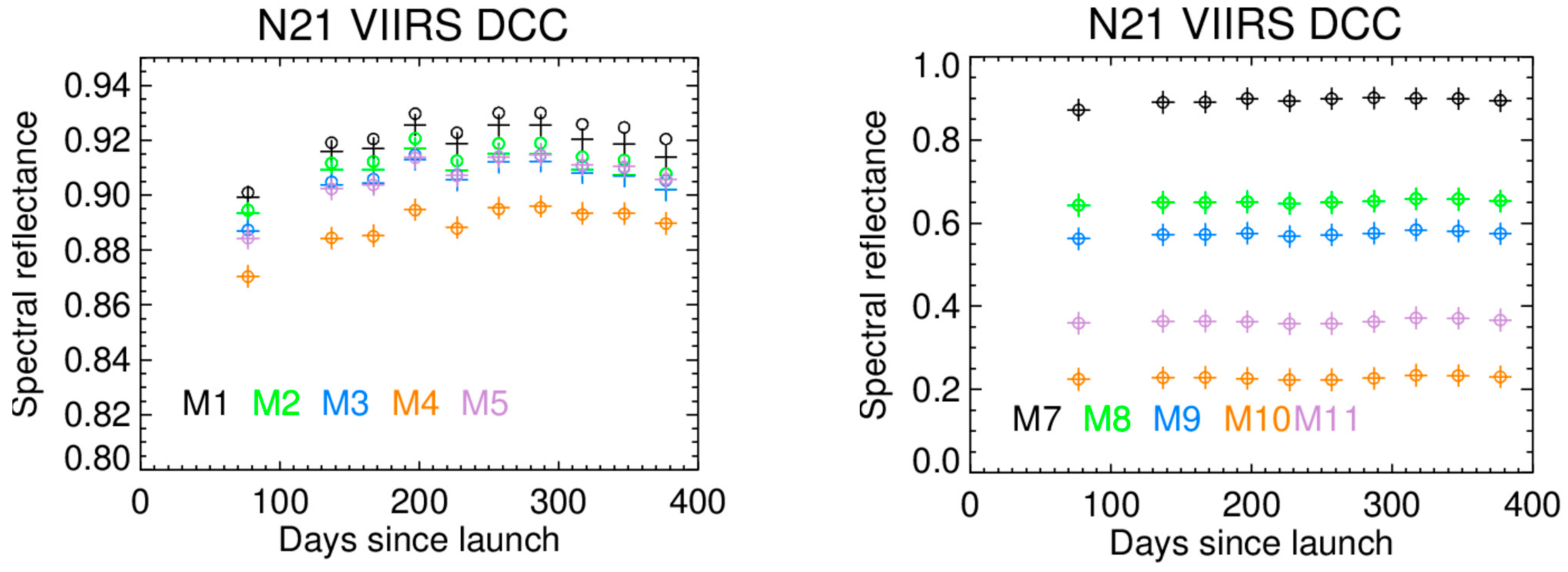
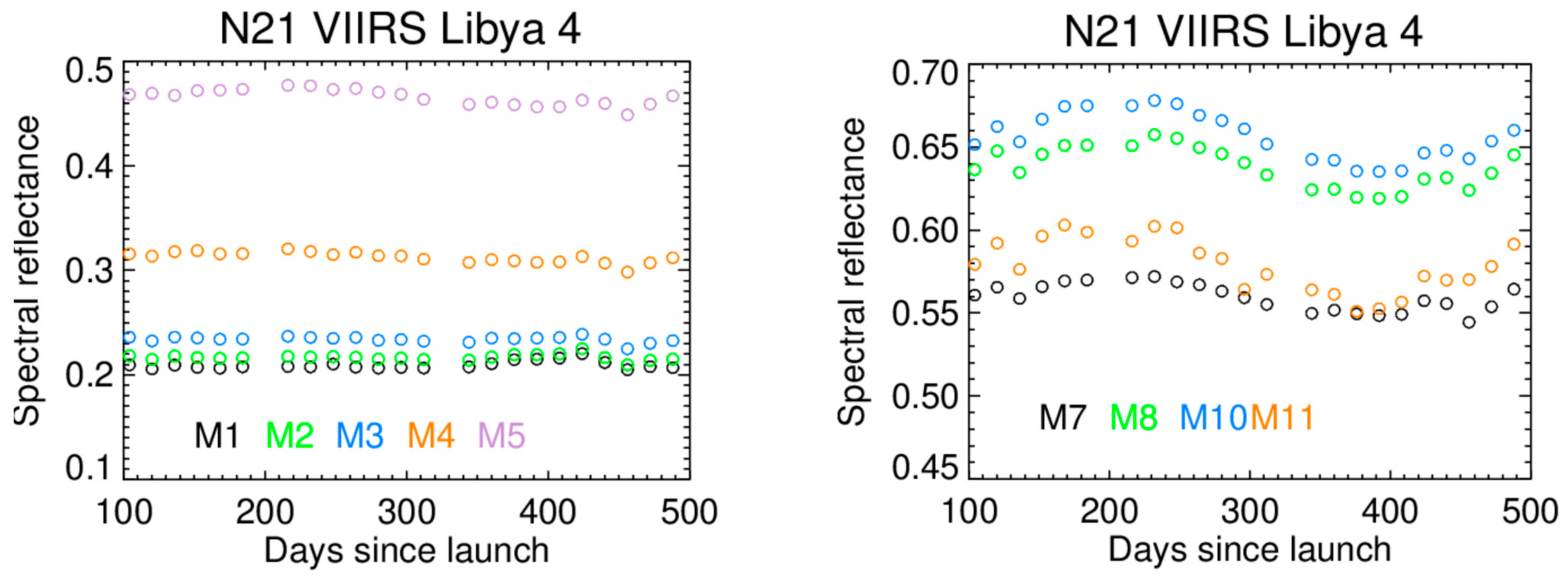
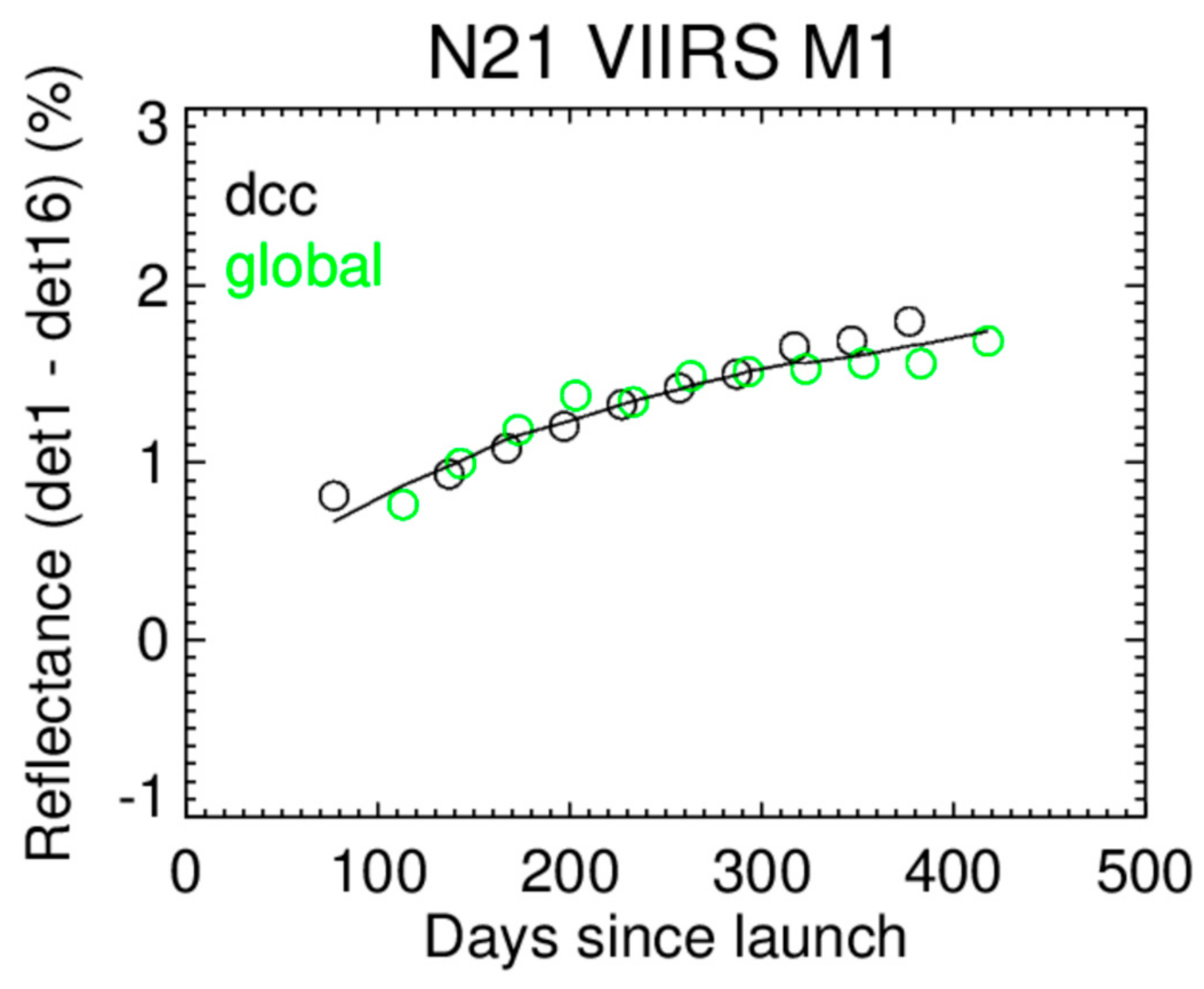
4.3. RSB Radiometric Gain Performance
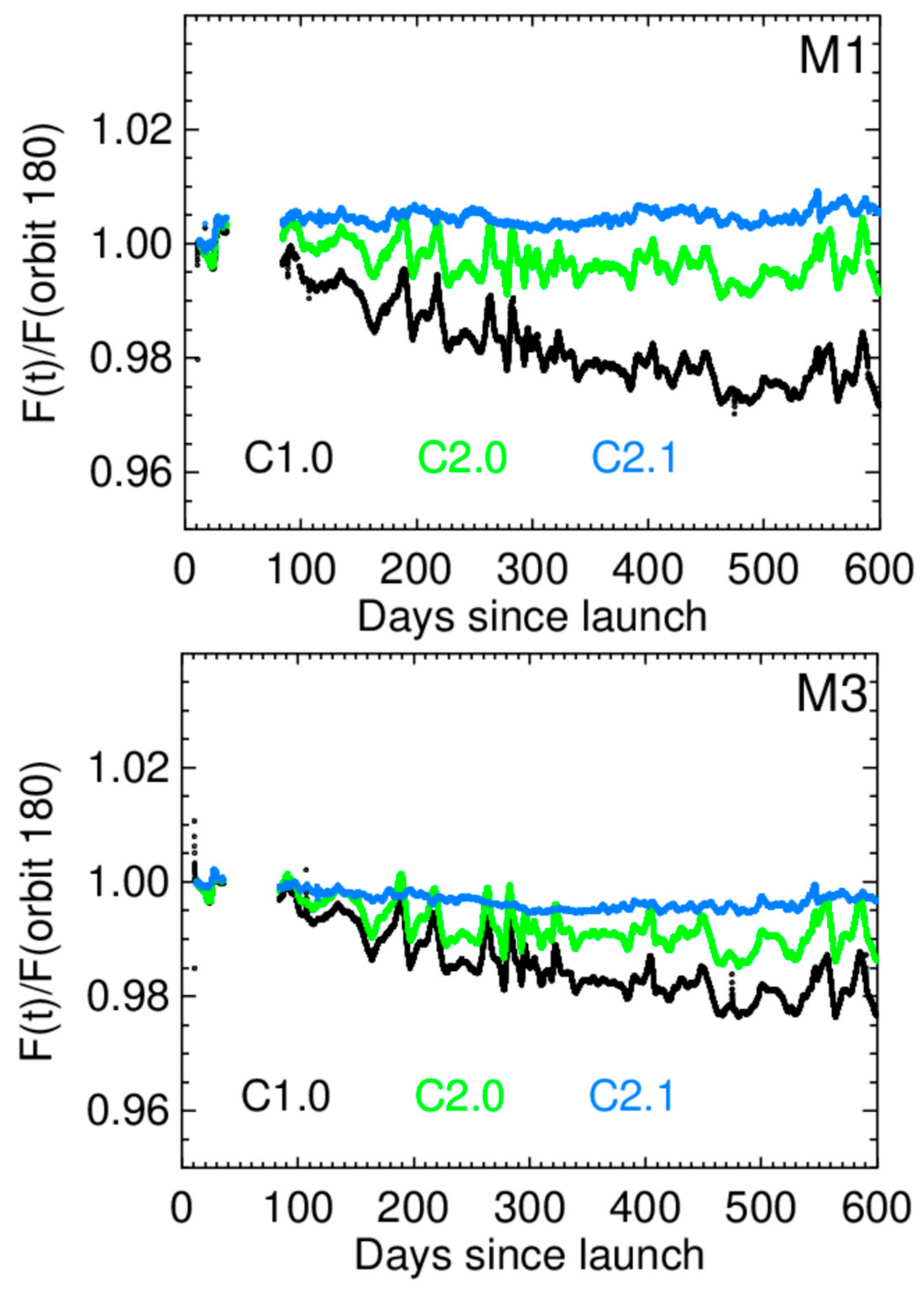
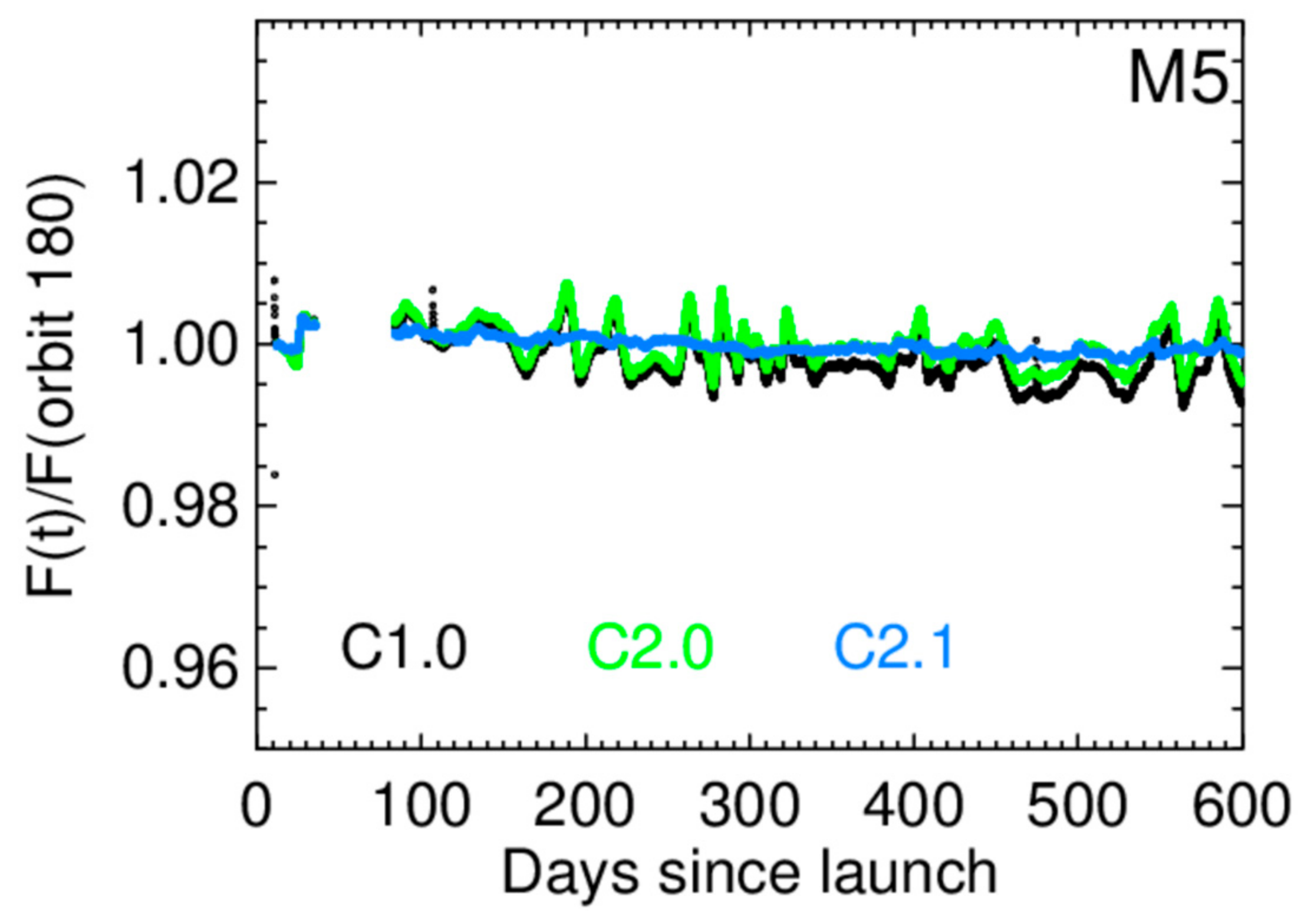
5. Striping Assessment and Mitigation
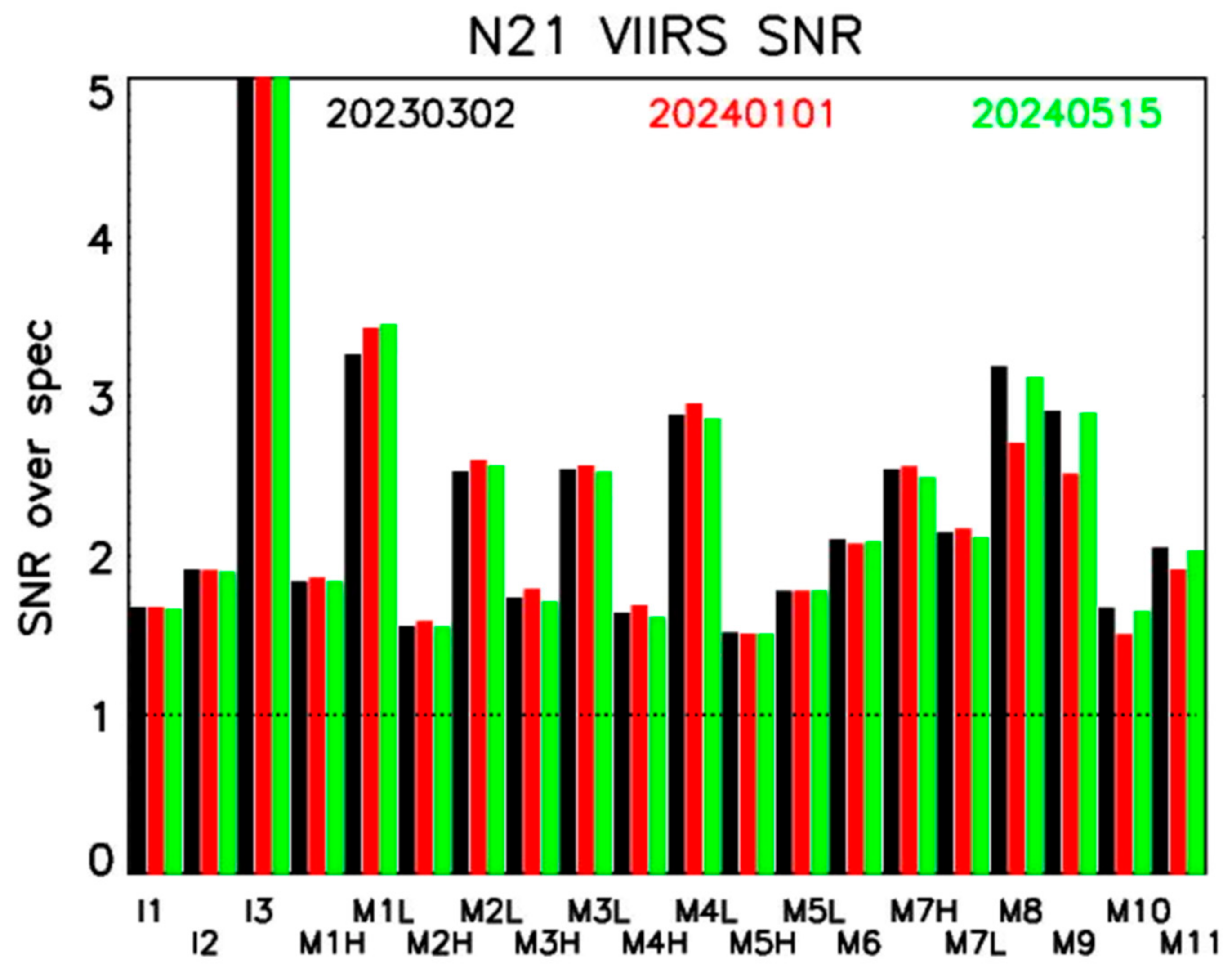
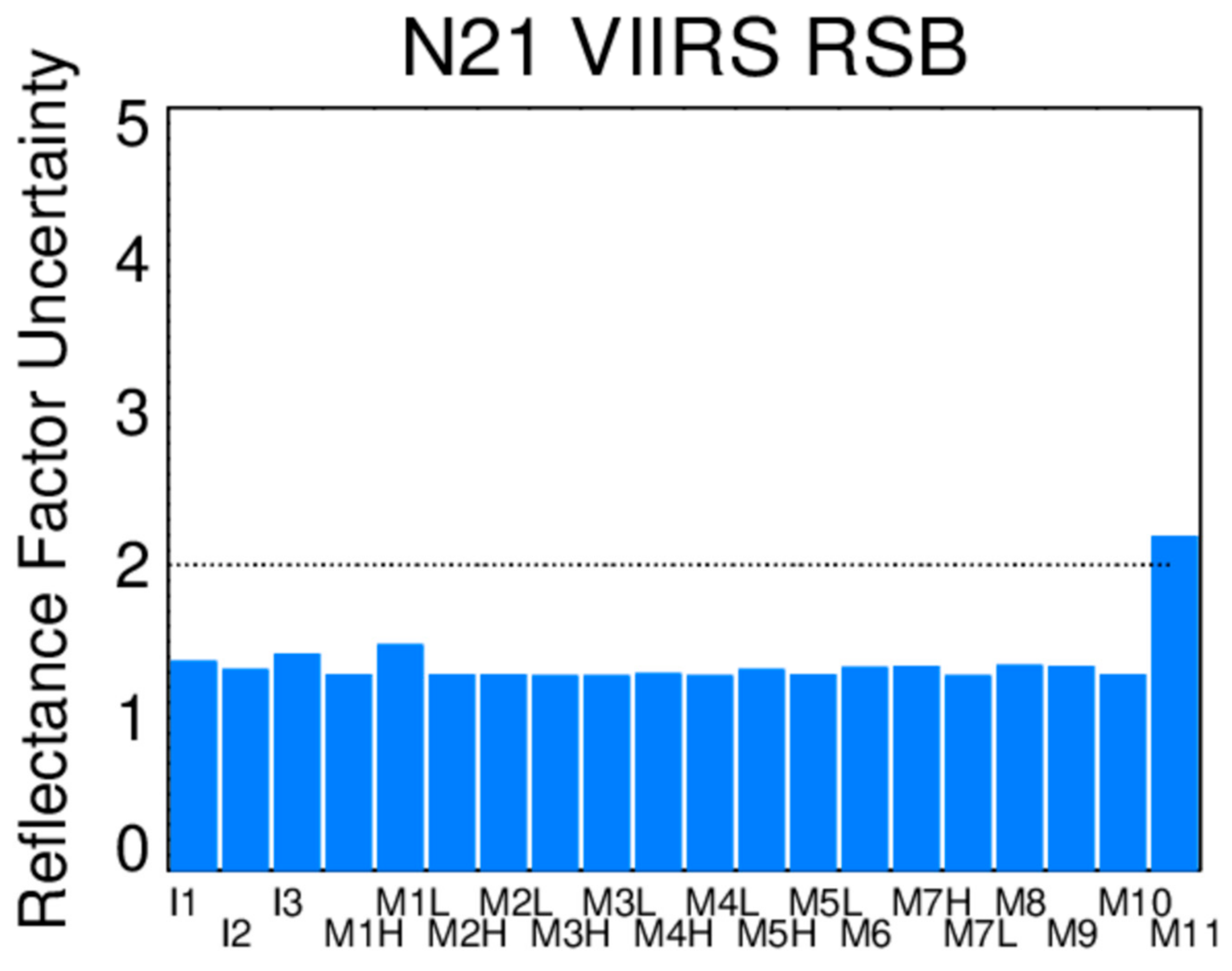
6. L1B Reflectance Factor Uncertainty Estimate: SNR and Bias
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
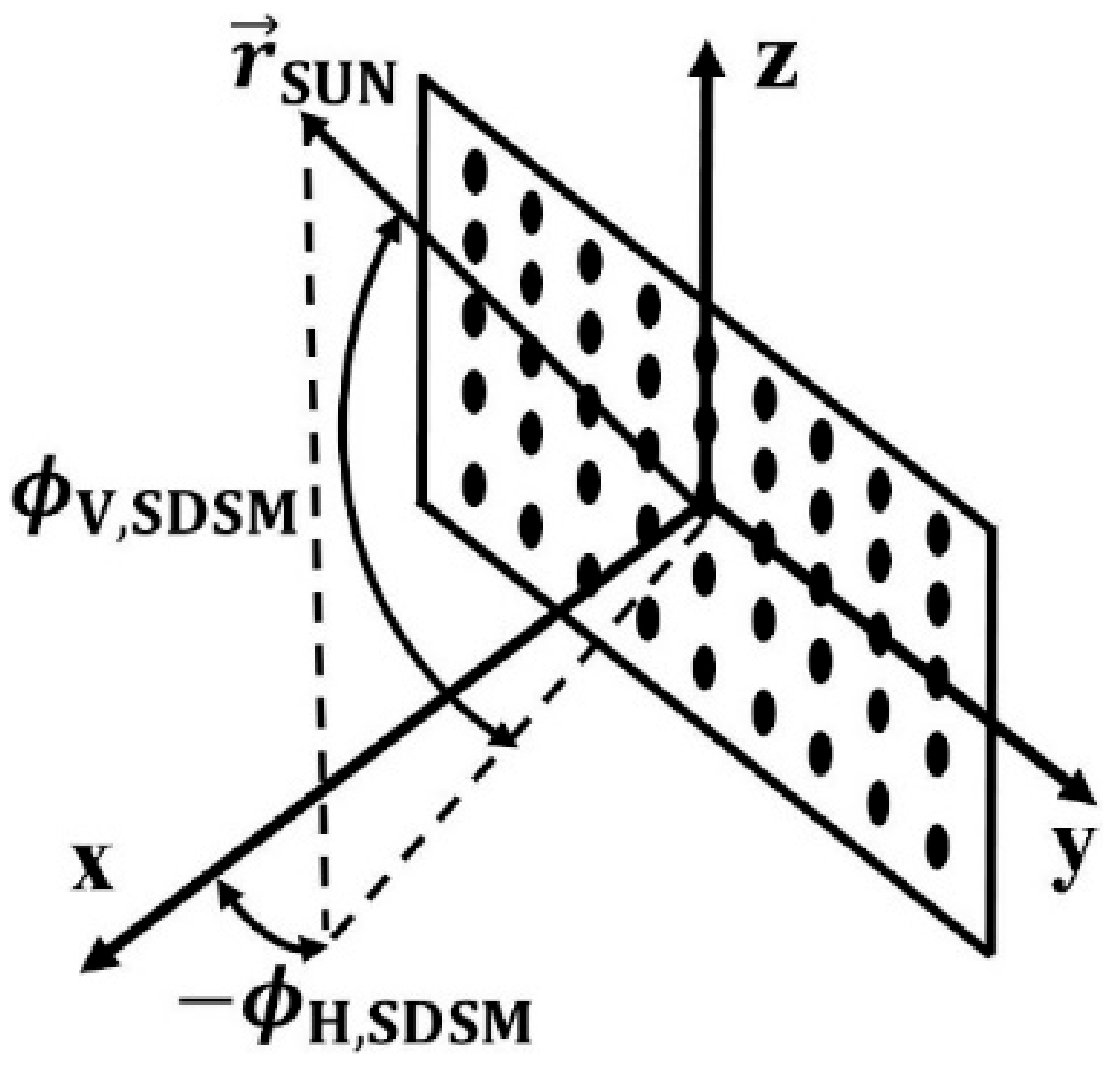
Appendix A. Definitions of the VIIRS SDSM Screen and VIIRS Coordinate Systems
Appendix B
| Acronyms | Definitions |
|---|---|
| AOI | Angle of incidence with respect to the half-angle mirror surface |
| Angle of incidence with respect to the half-angle mirror surface when the telescope aims at the solar diffuser | |
| Angle of incidence with respect to the half-angle mirror surface when the telescope aims at the Earth | |
| BRDF | Bidirectional reflectance distribution function |
| Bidirectional reflectance distribution function for the telescope solar diffuser view | |
| Bidirectional reflectance distribution function for the solar diffuser stability monitor solar diffuser view | |
| DC | Solar diffuser stability monitor detector count without background subtraction |
| dc | Solar diffuser stability monitor detector count with background subtraction |
| Background-subtracted digital count for the solar diffuser stability monitor detector solar diffuser view | |
| Background-subtracted digital count for the solar diffuser stability monitor detector Sun view | |
| Background-subtracted digital count for the solar diffuser stability monitor detector Sun view with temperature impact removed | |
| Background-subtracted digital count for the solar diffuser stability monitor detector Sun view with temperature impact, distance between the Sun and the VIIRS, and the SDSM screen transmittance impacts removed, defined by Equation (15) | |
| DCC | Deep convective cloud |
| DN | Reflective solar band detector digital number without background subtraction |
| dn | Reflective solar band detector digital number with background subtracted |
| Distance between the VIIRS and the Sun | |
| F-factor | A correction factor for the scene spectral radiance calculated by using the dn quadratic polynomial, defined by Equation (1) |
| F-factor derived from lunar views | |
| HAM | Half-angle mirror which reflects sunlight collected by the telescope to the aft optics |
| Solar diffuser BRDF on-orbit change factor for the telescope solar diffuser view | |
| True solar diffuser BRDF on-orbit change factor for the solar diffuser stability monitor solar diffuser view, typically found by deconvolving defined below | |
| Measured solar diffuser BRDF on-orbit change factor for the solar diffuser stability monitor solar diffuser view without deconvolution | |
| Spectral irradiance for the Moon calculated from the Robotic Lunar Observatory model developed by the US Geological Survey, weighted by the relative spectral response function of the band | |
| I-band | Imaging band: nominal nadir resolution of 375 m |
| JPSS | Joint Polar Satellite System (between NASA and NOAA) |
| L | Scene spectral radiance |
| Spectral radiance provided by the solar diffuser for the telescope solar diffuser view | |
| Typical Earth-view spectral radiance for a band | |
| L1B | Level-1 B: geometrically and radiometrically calibrated Earth-view spectral radiance and reflectance |
| LUT | Lookup table: a table which the L1B code reads to produce spectral radiance and reflectance |
| Band central wavelength for a band denoted by B | |
| Band central wavelength for a solar diffuser stability monitor detector with its index denoted by d | |
| M-band | Moderate-resolution band: nominal nadir resolution of 750 m |
| Nagg | Number of frames to aggregate for forming a pixel in Level-1B products |
| NSCAN | Number of scans that have the entire lunar image captured by the detector array in a band |
| N21 | NOAA-21 |
| ΩB | VIIRS RSB detector object view solid angle before aggregation |
| Solar angle | |
| Solar azimuth angle with respect to the SD surface normal vector | |
| Solar azimuth angle with respect to the SDSM screen normal vector in the SDSM screen coordinate system defined in Appendix A | |
| Solar spectral power | |
| Angle between the solar vector and the SD surface plane | |
| Top-of-the-atmosphere spectral reflectance | |
| ROLO | Robotic Lunar Observatory model developed by the US Geological Survey |
| RSB | Reflective solar band |
| RSR | Relative spectral response function of a band |
| RTA | Rotating telescope assembly: the VIIRS telescope, the first component in the VIIRS optical path |
| SD | Solar diffuser |
| SDSM | Solar diffuser stability monitor |
| SNPP | Suomi National Polar-orbiting Partnership |
| SV | Space view port, providing a dark scene |
| SWIR | Shortwave infrared |
| SDSM screen’s relative effective transmittance | |
| Product of the solar diffuser screen’s relative effective transmittance and the BRDF for the SDSM solar diffuser view | |
| Relative product of the solar diffuser screen transmittance and the BRDF for the telescope solar diffuser view | |
| Product of the solar diffuser screen transmittance and the BRDF for the telescope solar diffuser view | |
| tmid | Time associated with a data point that is about the middle in a data time sequence |
| Angle between the solar vector and Earth surface normal vector | |
| Angle of incidence with respect to the half-angle mirror when the telescope aims at the Earth | |
| Angle of incidence with respect to the half-angle mirror when the telescope aims at the solar diffuser | |
| Tbulkhead | Bulkhead temperature in Kelvin |
| TOA | Top-of-the-atmosphere |
| VIIRS | Visible Infrared Imaging Radiometer Suite |
Appendix C
| Band | λB (μm) | ||
|---|---|---|---|
| I1 | 0.20 | 0.12 | 0.638 |
| I2 | 0.25 | 0.42 | 0.862 |
| I3 | 0.0 | 5.65 | 1.601 |
| M1 | 0.23 | 0.03 | 0.411 |
| M2 | 0.17 | 0.04 | 0.443 |
| M3 | 0.13 | 0.05 | 0.486 |
| M4 | 0.10 | 0.07 | 0.551 |
| M5 | 0.11 | 0.16 | 0.671 |
| M6 | 0.14 | 0.25 | 0.745 |
| M7 | 0.18 | 0.42 | 0.862 |
| M8 | 0.0 | 1.88 | 1.238 |
| M9 | 0.0 | 2.94 | 1.375 |
| M10 | 0.0 | 5.63 | 1.601 |
| M11 | 0.0 | 23.4 | 2.257 |
References
- Wolfe, R.; Lin, G.; Nishihama, M.; Tewari, K.; Tilton, J.; Isaacman, A. Suomi NPP VIIRS prelaunch and on-orbit geometric calibration and characterization. J. Geophy. Res. Atmos. 2013, 118, 11508–11521. [Google Scholar] [CrossRef]
- Lin, G.; Wolfe, R.; Tilton, J. Trending of SNPP ephemeris and its implications on VIIRS geometric performance. Proc. SPIE 2016, 9972, 485–495. [Google Scholar] [CrossRef]
- Schueler, C.; Clement, J.; Ardanuy, P.; Welsch, C.; De Luccia, F.; Swenson, H. NPOESS VIIRS sensor design overview. Proc. SPIE 2012, 4483, 11–23. [Google Scholar] [CrossRef]
- Murphy, R.; Ardanuy, P.; De Luccia, F.; Clement, J.; Schueler, C. The visible infrared imaging radiometer suite. In Earth Science Satellite Remote Sensing; Qu, J., Gao, W., Kafatos, M., Murphy, R., Salomonson, V., Eds.; Springer-Verlag: New York, NY, USA, 2006; Volume 1, pp. 199–223. [Google Scholar]
- Joint Polar Satellite System (JPSS) VIIRS Radiometric Calibration Algorithm Theoretical Basis Document (ATBD); NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2013.
- Cao, C.; Zhang, B.; Shao, X.; Wang, W.; Uprety, S.; Choi, T.; Blonski, S.; Gu, Y.; Bai, Y.; Lin, L.; et al. Mission-Long Recalibrated Science Quality Suomi NPP VIIRS Radiometric Dataset Using Advanced Algorithms for Time Series Studies. Remote Sens. 2021, 13, 1075. [Google Scholar] [CrossRef]
- Zhou, L.; Divakarla, M.; Liu, X.; Layns, A.; Goldberg, M. An Overview of the Science Performances and Calibration/Validation of Joint Polar Satellite System Operational Products. Remote Sens. 2019, 11, 698. [Google Scholar] [CrossRef]
- Oudrari, H.; McIntire, J.; Xiong, X.; Butler, J.; Ji, Q.; Schwarting, T.; Angal, A. An Overall Assessment of JPSS-2 VIIRS Radiometric Performance Based on Pre-Launch Testing. Remote Sens. 2018, 10, 1921. [Google Scholar] [CrossRef]
- Angal, A.; Moyer, D.; Ji, Q.; McIntire, J.; Oudrari, H.; Xiong, X. Prelaunch characterization and performance of JPSS-2 VIIRS reflective solar bands. Proc. SPIE 2018, 10764, 1076403. [Google Scholar] [CrossRef]
- Moyer, D.; Angal, A.; Ji, Q.; McIntire, J.; Xiong, X. JPSS-2 VIIRS Pre-Launch Reflective Solar Band Testing and Performance. Remote Sens. 2022, 14, 6353. [Google Scholar] [CrossRef]
- Lei, N.; Wang, Z.; Xiong, X. On-orbit Radiometric Calibration of Suomi NPP VIIRS Reflective Solar Bands through Observations of a Sunlit Solar Diffuser Panel. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5983–5990. [Google Scholar] [CrossRef]
- Twedt, K.; Lei, N.; Xiong, X.; Angal, A.; Li, S.; Chang, T.; Sun, J. On-Orbit Calibration and Performance of NOAA-20 VIIRS Reflective Solar Bands. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1001413. [Google Scholar] [CrossRef]
- Choi, T.; Cao, C.; Shao, X.; Wang, W. S-NPP VIIRS Lunar Calibrations over 10 Years in Reflective Solar Bands (RSB). Remote Sens. 2022, 14, 3367. [Google Scholar] [CrossRef]
- Choi, T.; Cao, C.; Blonski, S.; Shao, X.; Wang, W. NOAA-20 VIIRS On-orbit Reflective Solar Band Radiometric Calibration Five-Year Update. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1000610. [Google Scholar] [CrossRef]
- Eplee, R.; Turpie, K.; Meister, G.; Patt, F.; Franz, B.; Bailey, S. On-orbit calibration of the Suomi National Polar-Orbiting Partnership Visible Infrared Imaging Radiometer Suite for ocean color applications. Appl. Opt. 2015, 54, 1984–2006. [Google Scholar] [CrossRef] [PubMed]
- Fulbright, J.; Lei, N.; Efremova, B.; Xiong, X. Suomi-NPP VIIRS Solar Diffuser Stability Monitor Performance. IEEE Trans. Geosci. Remote Sens. 2016, 54, 631–639. [Google Scholar] [CrossRef]
- Lei, N. Examining the angular dependence of the SNPP VIIRS Solar Diffuser bidirectional reflectance distribution function degradation factor: I. VCST Tech. Rep. 2014, 2014_006. [Google Scholar]
- Lei, N.; Chiang, K.; Xiong, X. Examination of the angular dependence of the SNPP VIIRS solar diffuser BRDF degradation factor. Proc. SPIE 2014, 9218, 550–562. [Google Scholar] [CrossRef]
- Lei, N.; Xiong, X. Impacts of the Angular Dependence of the Solar Diffuser BRDF Degradation Factor on the SNPP VIIRS Reflective Solar Band On-Orbit Radiometric Calibration. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1537–1543. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M. Visible Infrared Imaging Radiometer Suite solar diffuser calibration and its challenges using a solar diffuser stability monitor. Appl. Opt. 2014, 53, 8571–8584. [Google Scholar] [CrossRef]
- Klein, S.; Murgai, V.; Johnson, L. Solar Attenuation Screen Transmittance, Modulation, and Albedo for JPSS J2. Proc. SPIE 2019, 11127, 61–68. [Google Scholar] [CrossRef]
- Valencia, A.; Klein, S.; Murgai, V. Solar Attenuation Screen Transmittance, Modulation, and Albedo for JPSS J3 and J4. Proc. SPIE 2020, 11501, 115010V. [Google Scholar] [CrossRef]
- McIntire, J.; Moyer, D.; Efremova, B.; Oudrari, H.; Xiong, X. On-orbit Characterization of S-NPP VIIRS Transmission Functions. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2354–2892. [Google Scholar] [CrossRef]
- Sun, J.; Chu, M.; Wang, M. On-orbit characterization of the VIIRS solar diffuser and attenuation screens for NOAA-20 using yaw measurements. Appl. Opt. 2018, 57, 6605–6619. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Lei, N. JPSS-2 VIIRS Post-Launch Test (PLT) CSE6: Yaw Maneuver Analysis. VCST Tech. Rep. 2023, 2023_028. [Google Scholar]
- Lei, N.; Chen, X.; Xiong, X. Determination of the SNPP VIIRS SDSM Screen Relative Transmittance from Both Yaw Maneuver and Regular On-Orbit Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1390–1398. [Google Scholar] [CrossRef]
- Lei, N.; Xiong, X. Products of the SNPP VIIRS SD Screen Transmittance and the SD BRDFs from Both Yaw Maneuver and Regular On-orbit Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1975–1987. [Google Scholar] [CrossRef]
- Lei, N.; Xiong, X. Determination of NOAA-20 VIIRS screen transmittance functions with both yaw maneuver and regular on-orbit calibration data. J. Appl. Opt. 2020, 59, 2992–3001. [Google Scholar] [CrossRef]
- Xiong, X.; Butler, J.; Chiang, K.; Efremova, B.; Fulbright, J.; Lei, N.; McIntire, J.; Oudrari, H.; Sun, J.; Wang, Z.; et al. VIIRS on-orbit calibration methodology and performance. J. Geophys. Res. Atmos. 2014, 119, 5065–5078. [Google Scholar] [CrossRef]
- Lei, N.; Xiong, X.; Wang, Z.; Li, S.; Twedt, K. SNPP VIIRS RSB on-orbit radiometric calibration algorithms Version 2.0 and the performances, part 1: The algorithms. J. Appl. Remote Sens. 2020, 14, 047501. [Google Scholar] [CrossRef]
- Lei, N.; Twedt, K.; Xiong, X.; Angal, A. Performance of NOAA-20 VIIRS Solar Diffuser and Solar Diffuser Stability Monitor. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7180–7188. [Google Scholar] [CrossRef]
- Wu, A.; Xiong, X.; Cao, C. Assessment of stability of the response versus scan angle for the S-NPP VIIRS reflective solar bands using pseudo-invariant desert and Dome C sites. Proc. SPIE 2017, 10423, 432–440. [Google Scholar] [CrossRef]
- Murgai, V.; Klein, S. Spectralon® Solar Diffuser BRDF Extrapolation to 2.25 microns for JPSS J1, J2 and J3. Proc. SPIE 2019, 11127, 75–85. [Google Scholar] [CrossRef]
- Kieffer, H.H. Photometric Stability of the Lunar Surface. Icarus 1997, 130, 323–327. [Google Scholar] [CrossRef]
- Kieffer, H.H.; Stone, T.C. The Spectral Irradiance of the Moon. Astron. J. 2005, 129, 2887–2901. [Google Scholar] [CrossRef]
- Xiong, X.; Sun, J.; Fulbright, J.; Wang, Z.; Butler, J. Lunar Calibration and Performance for S-NPP VIIRS Reflective Solar Bands. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1052–1061. [Google Scholar] [CrossRef]
- Lei, N.; Xiong, X. Suomi NPP VIIRS Solar Diffuser BRDF Degradation Factor at Short Wave Infrared Band Wavelengths. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6212–6216. [Google Scholar] [CrossRef]
- Lei, N.; Xiong, X.; Li, S.; Twedt, K. SNPP VIIRS solar vector orientation knowledge error revealed by solar diffuser stability monitor sun views. J. Appl. Remote Sens. 2024, 18, 027502. [Google Scholar] [CrossRef]
- Choi, T.; Blonski, S.; Shao, X.; Wang, W. Preliminary assessment of the NOAA-21 VIIRS on-orbit Reflective Solar Band calibration and performance. Proc. SPIE 2023, 12685, 243–256. [Google Scholar] [CrossRef]
- De Luccia, F.; Moyer, D.; Johnson, E.; Rausch, K.; Lei, N.; Chiang, K.; Xiong, X.; Fulbright, J.; Hass, E.; Iona, G. Discovery and characterization of on-orbit degradation of the Visible Infrared Imaging Radiometer Suite (VIIRS) Rotating Telescope Assembly (RTA). Proc. SPIE 2012, 8510, 477–493. [Google Scholar] [CrossRef]
- Lei, N.; Xiong, X.; Wang, Z.; Li, S.; Twedt, K. SNPP VIIRS RSB on-orbit radiometric calibration algorithms Version 2.0 and the performances, part 2: The performances. J. Appl. Remote Sens. 2020, 14, 047502. [Google Scholar] [CrossRef]
- Coddington, O.M.; Richard, E.C.; Harber, D.; Pilewskie, P.; Woods, T.N.; Chance, K.; Liu, X.; Sun, K. The TSIS-1 Hybrid Solar Reference Spectrum. Geophys. Res. Lett. 2020, 48, e2020GL091709. [Google Scholar] [CrossRef]
- Bhatt, R.; Doelling, D.R.; Coddington, O.; Scarino, B.; Gopalan, A.; Haney, C. Quantifying the Impact of Solar Spectra on the Inter-Calibration of Satellite Instruments. Remote Sens. 2021, 13, 1438. [Google Scholar] [CrossRef]
- Kurucz, R. High resolution irradiance spectrum from 300 to 1000 nm. MassAFRL Transmission Meeting. 15–16 June 2005. Available online: https://arxiv.org/pdf/astro-ph/0605029.pdf (accessed on 19 September 2024).
- Thuillier, G.; Hersé, M.; Labs, D.; Foujols, T.; Peetermans, W.; Gillotay, D.; Simon, P.C.; Mandel, H. The solar spectral irradiance from 200 to 2400 nm as measured by the SOLSPEC spectrometer from the ATLAS and EURECA missions. Sol. Phys. 2003, 214, 1–22. [Google Scholar] [CrossRef]
- Lei, N.; Xiong, X.; Guenther, B. Modeling the Detector Radiometric Gains of the Suomi NPP VIIRS Reflective Solar Bands. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1565–1573. [Google Scholar] [CrossRef]
- Iona, G.; Butler, J.; Guenther, B.; Johnson, E.; Kennedy, B.; Kent, C.; Lambeck, R.; Waluschka, E.; Xiong, X. VIIRS on-orbit optical anomaly: Investigation, analysis, root cause determination and lessons learned. Proc. SPIE 2012, 8510, 506–520. [Google Scholar] [CrossRef]
- Li, Y.; Xiong, X.; McIntire, J.; Angal, A.; Gusev, S.; Chiang, K. Early Calibration and Performance Assessments of NOAA-20 VIIRS Thermal Emissive Bands. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9242–9251. [Google Scholar] [CrossRef]
- Mishra, N.; Helder, D.; Angal, A.; Choi, J.; Xiong, X. Absolute Calibration of Optical Satellite Sensors Using Libya 4 Pseudo Invariant Calibration Site. Remote Sens. 2014, 6, 1327–1346. [Google Scholar] [CrossRef]
- Wu, A.; Xiong, X.; Mu, Q.; Angal, A.; Bhatt, R.; Shea, Y. Early Radiometric Assessment of NOAA-21 Visible Infrared Imaging Radiometer Suite Reflective Solar Bands Using Vicarious Techniques. Remote Sens. 2024, 16, 2528. [Google Scholar] [CrossRef]
- David, R. Doelling, Daniel Morstad, Benjamin R. Scarino, Rajendra Bhatt, and Arun Gopalan. The Characterization of Deep Convective Clouds as an Invariant Calibration Target and as a Visible Calibration Technique. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1147–1158. [Google Scholar] [CrossRef]
- Lei, N.; Xiong, X.; Mu, Q.; Li, S.; Chang, T. Positional Dependence of SNPP VIIRS Solar Diffuser BRDF Change Factor. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8056–8061. [Google Scholar] [CrossRef]
- Lei, N.; Li, S.; Wilson, T.; Mu, Q.; Geng, X.; Twedt, K.; Angal, A.; Chang, T. NASA VCST N20 VIIRS VisNIR band L1B de-striping. VCST Tech. Memo 2023, 2023_005. [Google Scholar]
- Moeller, C.; Schwarting, T.; McCorkel, J.; Moyer, D.; McIntire, J. The JPSS-2 VIIRS version 2 at-launch relative spectral response characterization. Proc. SPIE 2019, 11127, 46–60. [Google Scholar] [CrossRef]
- Twedt, K.; Lei, N.; Xiong, X. On-orbit noise characterization of the SNPP VIIRS reflective solar bands. Proc. SPIE 2017, 10402, 598–606. [Google Scholar] [CrossRef]
- McIntire, J.; Moyer, D.; Chang, T.; Oudrari, H.; Xiong, X. Pre-Launch JPSS-2 VIIRS Response versus Scan Angle Characterization. Remote Sens. 2017, 9, 1300. [Google Scholar] [CrossRef]
- Moyer, D.; McIntire, J.; Oudrari, H.; McCarthy, J.; Xiong, X.; De Luccia, F. JPSS-1 VIIRS Pre-Launch Response Versus Scan Angle Testing and Performance. Remote Sens. 2016, 8, 141. [Google Scholar] [CrossRef]
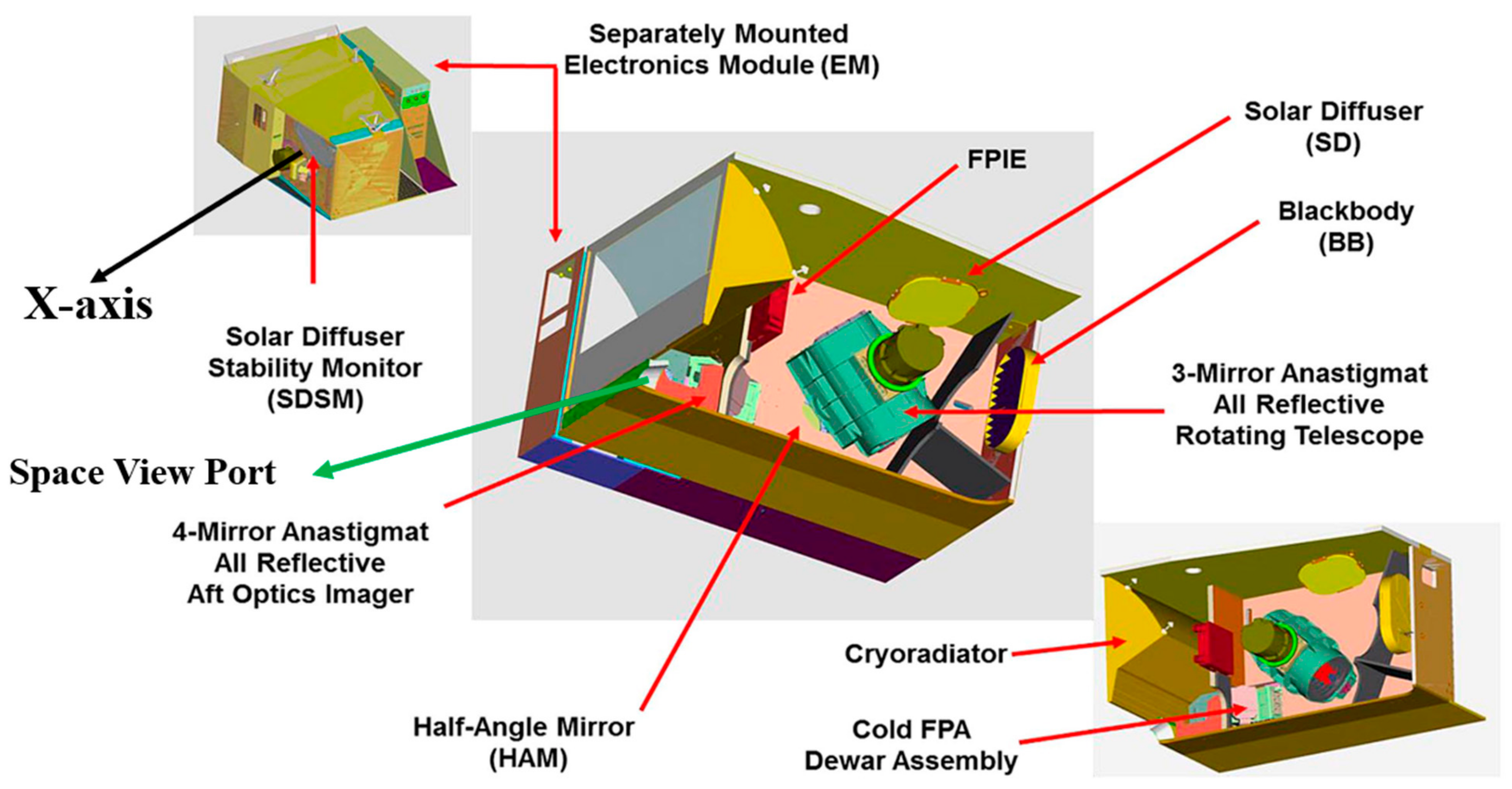

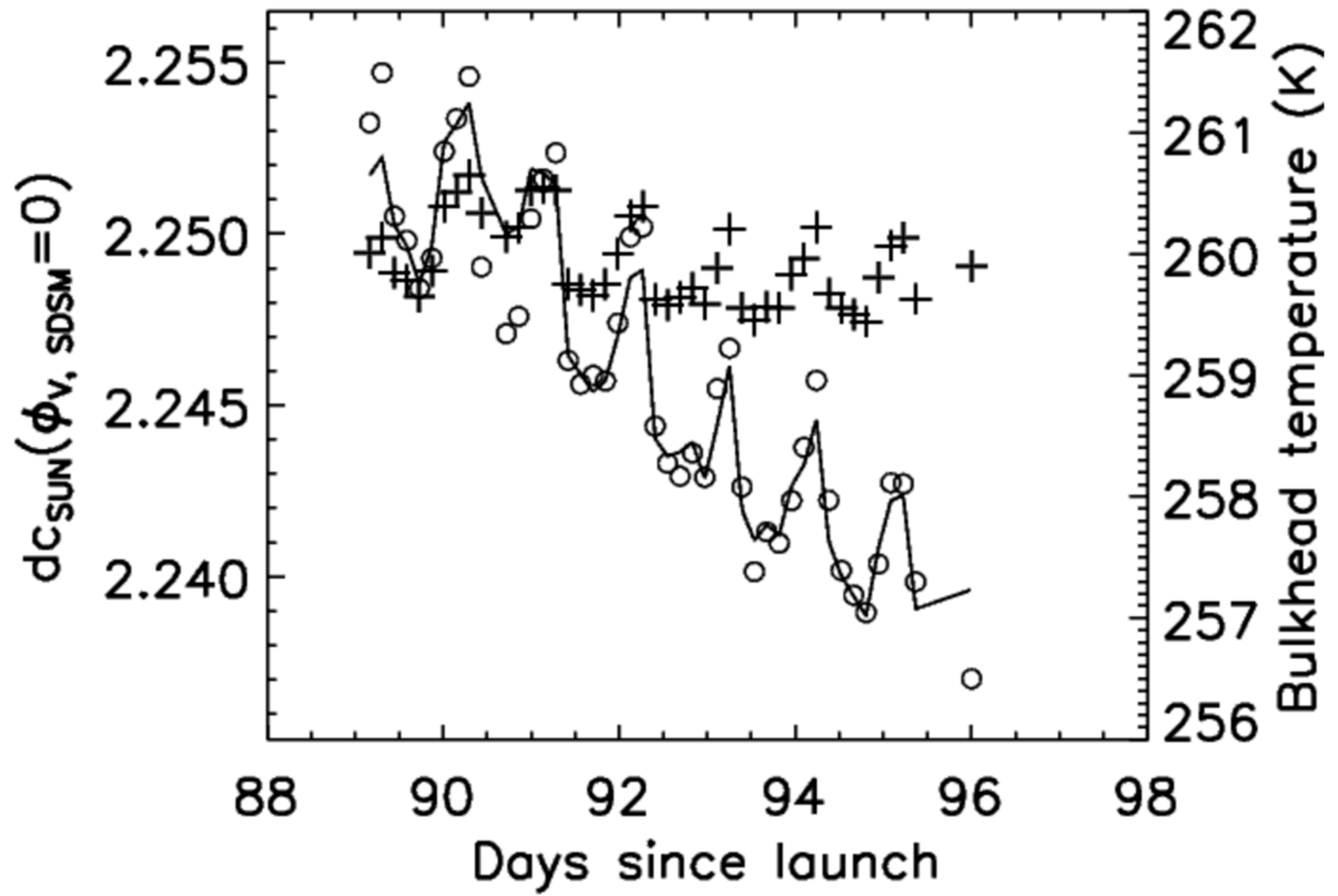
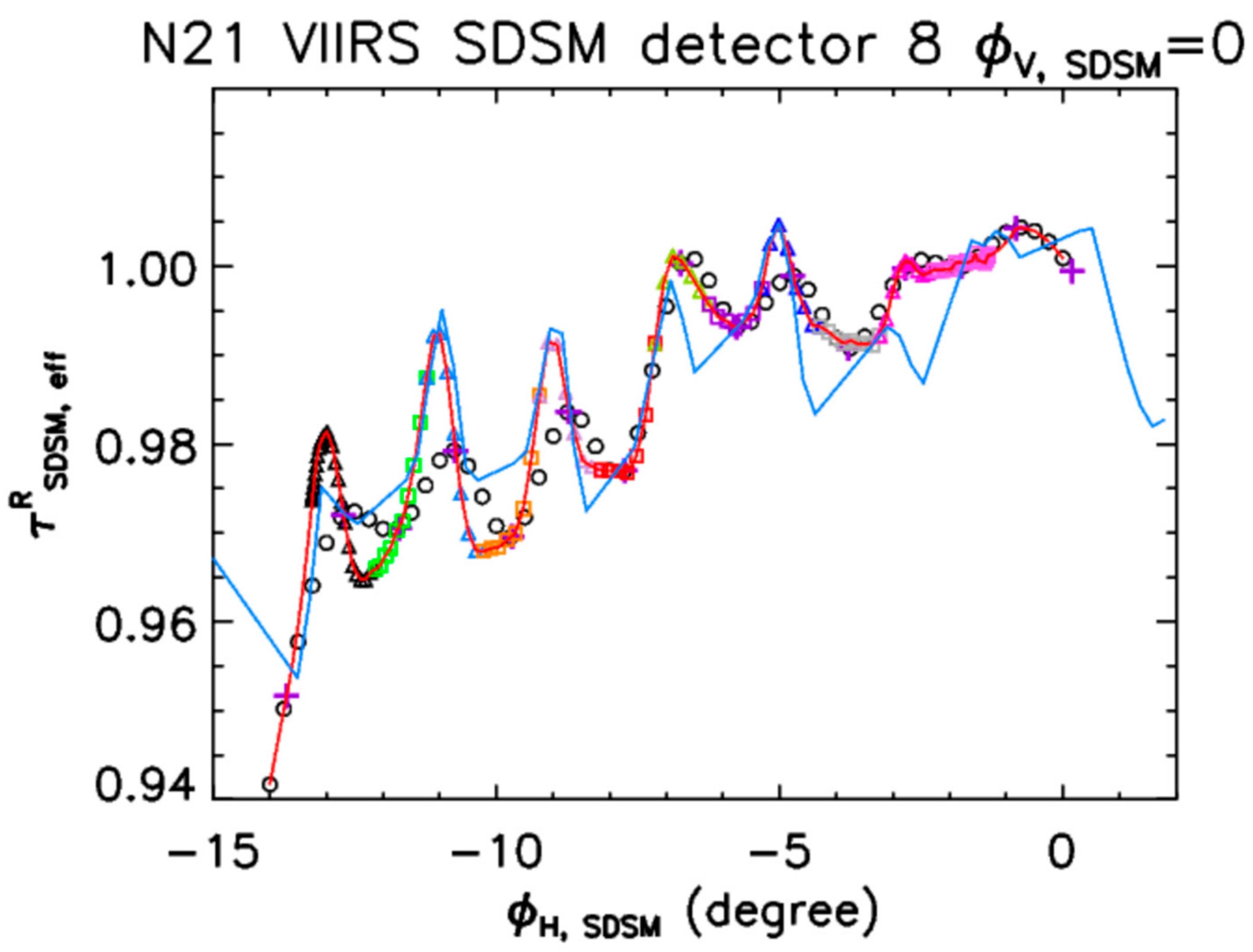
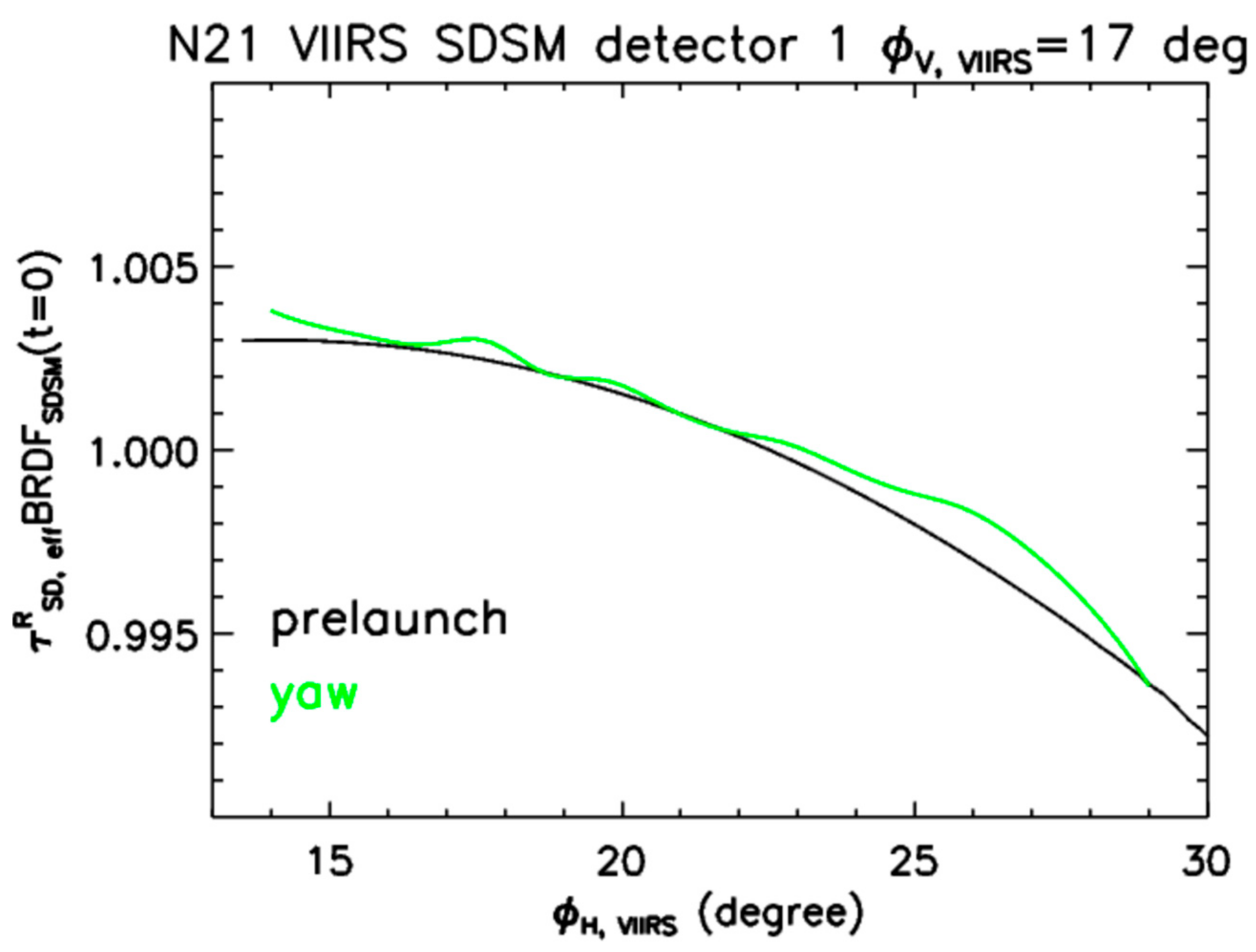
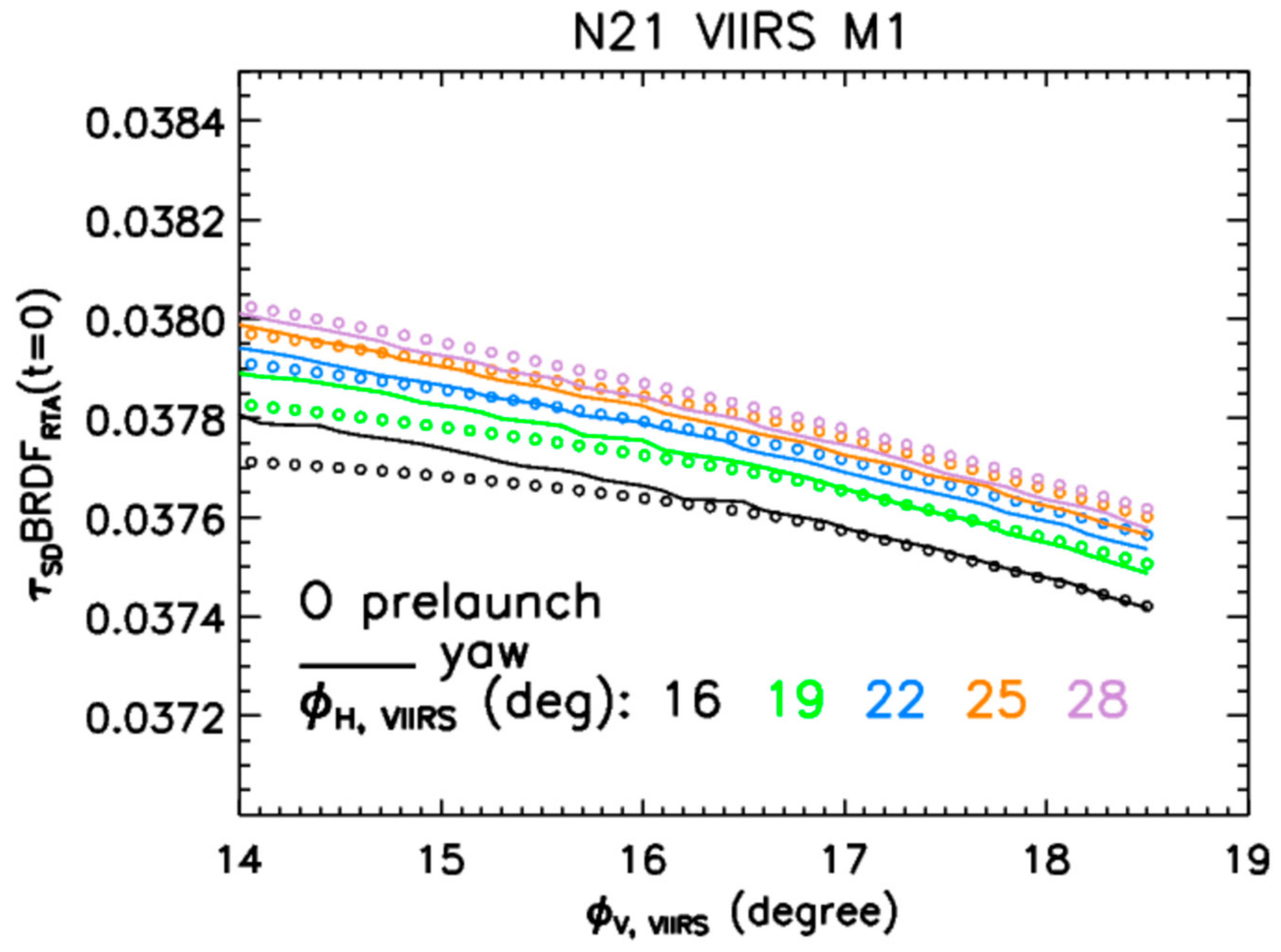
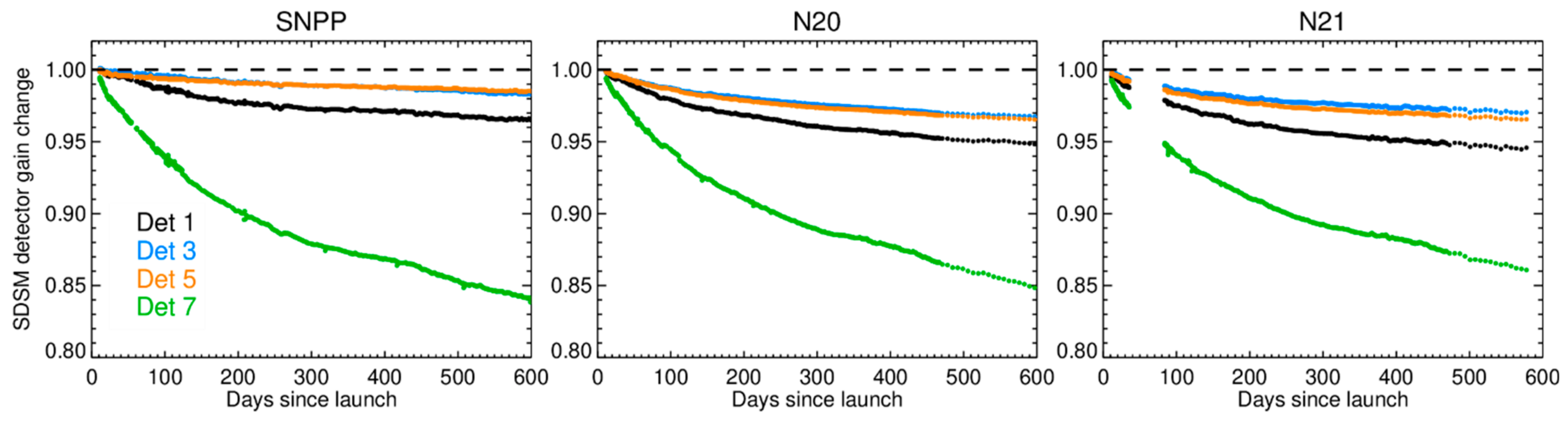
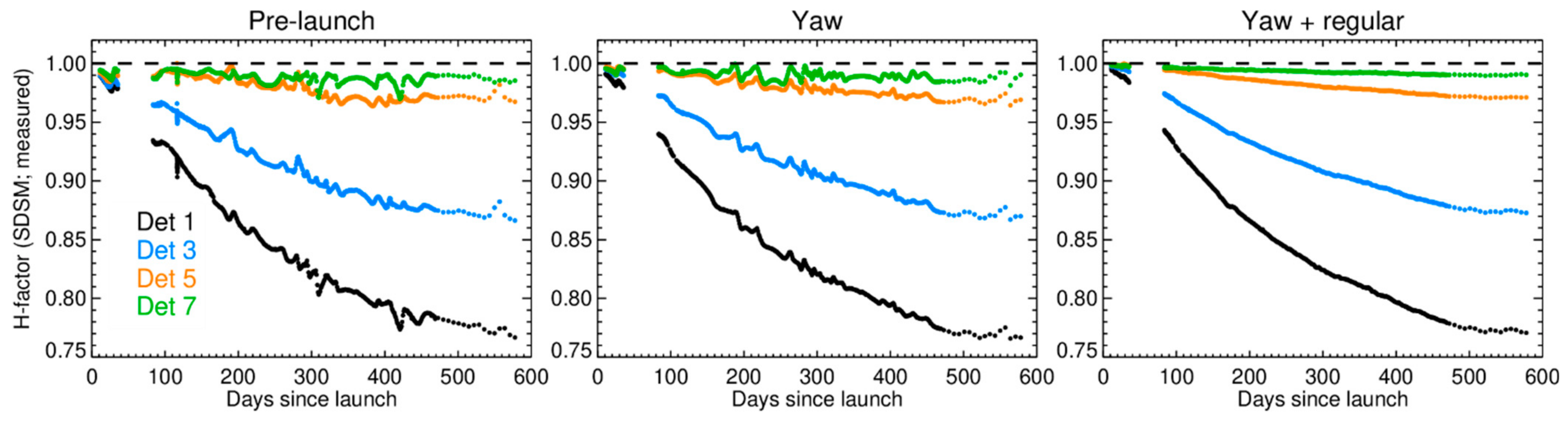



| Band | Center Wavelength (nm) | Bandwidth (nm) | SNR Spec | Lmin | Ltyp | Lmax |
|---|---|---|---|---|---|---|
| I1 | 640 | 80 | 119 | 5 | 22 | 718 |
| I2 | 865 | 39 | 150 | 10.3 | 25 | 349 |
| I3 | 1610 | 60 | 6 | 1.2 | 7.3 | 72.5 |
| M1HG | 412 | 20 | 352 | 30 | 44.9 | 135 |
| M1LG | 316 | 135 | 155 | 615 | ||
| M2HG | 445 | 18 | 380 | 26 | 40 | 127 |
| M2LG | 409 | 127 | 146 | 687 | ||
| M3HG | 488 | 20 | 416 | 22 | 32 | 107 |
| M3LG | 414 | 107 | 123 | 702 | ||
| M4HG | 555 | 20 | 362 | 12 | 21 | 78 |
| M4LG | 315 | 78 | 90 | 667 | ||
| M5HG | 672 | 20 | 242 | 8.6 | 10 | 59 |
| M5LG | 360 | 59 | 68 | 651 | ||
| M6 | 746 | 15 | 199 | 5.3 | 9.6 | 41 |
| M7HG | 885 | 39 | 215 | 3.4 | 6.4 | 29 |
| M7LG | 340 | 29 | 33.4 | 349 | ||
| M8 | 1240 | 20 | 74 | 3.5 | 5.4 | 164.9 |
| M9 | 1378 | 15 | 83 | 0.6 | 6 | 77.1 |
| M10 | 1610 | 60 | 342 | 1.2 | 7.3 | 71.2 |
| M11 | 2250 | 50 | 90 | 0.12 | 1.0 | 31.8 |
| Description | Mission Day | Orbit | Start Date/Time | End Date/Time |
|---|---|---|---|---|
| Launch | 001 | - | 10 November 2022_09:49z | Lift off 1:49 PST/4:49 EST |
| SDSM first measurement, 5 min every orbit (started 3 min too early) | 011 | 149 | 20 November 2022 | - |
| SDSM timing corrected by extending measurement from 5 to 8 min | 012 | 160 | 21 November 2022 | - |
| SDSM measurement reduced back to 5 min | 022 | 307 | 1 December 2022 | |
| Nadir aperture door open | 026 | 360 | 5 December 2022_17:37z | - |
| SDSM operation change to once every other orbit | 029 | 405 | 8 December 2022 | |
| N21 Ka-band transmitter (KaTX-1) anomaly | 037 | 508 | 16 December 2022_02:49z | - |
| N21 Ka-band transmitter #2 (KaTX-2) activated after 48 days | 085 | 2 February 2023_15:22:52z | ||
| Cryoradiator cooler door open | 091 | 8 February 2023_15:46z | - | |
| Cold focal plane assembly CFPA) (stable) | 093 | - | 10 February 2023_02:30z | |
| SDSM operation change to once daily (36 cycles) | 097 | 14 February 2023 | ||
| Mid-mission outgassing | 106–108 | 1485–1519 | 23 February /2023_14:25:42z | 25 February 2023_08:45:03z |
| CFPA return to nominal 82K (stable) | 109 | 1528 | - | 26 February /2023_01:10z |
| CFPA change from 82K to 80K (only LWIR heater controls both CFPAs) | 114 | 1610–1611 | 3 March 2023_19:33:23z | 3 March 2023_20:29:20z |
| Yaw maneuvers 14 orbits yaw + 1 middle orbit, no yaw; SDSM, 5 min | 117 | 1649–1663 | 6 March 2023_13:22:30z | 7 March 2023_13:14:33z |
| Pitch maneuver (deep space view) | 121 | 1705 | 10 March 2023_11:37:05z | 10 March /2023_12:10:51z |
| CFPA return to nominal 80K stable | 121 | 1711 | - | 10 March 2023_22:42z |
| Mid-mission outgassing #2 | 474–476 | 6715–6743 | 26 February 2024_15:05:21z | 28 February 2024_13:57:45z |
| VIIRS in active mode | 475 | 6733 | 27 february 2024_21:00:00z | - |
| CFPA return to nominal 80K stable | 477 | 6753 | - | 29 February 2024_07:30z |
| Collections/AS #s | RSB Calibration Algorithms |
|---|---|
| 1.0 | Screen functions from the yaw maneuvers, Thuillier solar spectral power, HRTA = , HRTA(SWIR) = 1 |
| 2.0/5200c | Screen functions from the yaw maneuvers, Thuillier solar spectral power, SDSM-measured H-factor without RSR deconvolution and a multiplicative factor that is the mean of F(HRTA; SNPP)/F( and F(HRTA; N20)/F(, (M11) is 1.061 of the prelaunch value |
| 2.1/5201 | Screen functions from both the yaw maneuver and a small portion of regular times, TSIS-1 solar spectral power, SDSM-measured H-factor without RSR deconvolution and a multiplicative factor that is F(HRTA; SNPP)/F(, wavelength power law for at the SWIR wavelengths, HRTA(SWIR)= (SWIR), (M11) is 1.061 of the prelaunch value, M4 low-gain c-coefficients updated, VisNIR band striping mitigated |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, N.; Xiong, X.; Twedt, K.; Li, S.; Chang, T.; Mu, Q.; Angal, A. Early Mission Calibration Performance of NOAA-21 VIIRS Reflective Solar Bands. Remote Sens. 2024, 16, 3557. https://doi.org/10.3390/rs16193557
Lei N, Xiong X, Twedt K, Li S, Chang T, Mu Q, Angal A. Early Mission Calibration Performance of NOAA-21 VIIRS Reflective Solar Bands. Remote Sensing. 2024; 16(19):3557. https://doi.org/10.3390/rs16193557
Chicago/Turabian StyleLei, Ning, Xiaoxiong Xiong, Kevin Twedt, Sherry Li, Tiejun Chang, Qiaozhen Mu, and Amit Angal. 2024. "Early Mission Calibration Performance of NOAA-21 VIIRS Reflective Solar Bands" Remote Sensing 16, no. 19: 3557. https://doi.org/10.3390/rs16193557
APA StyleLei, N., Xiong, X., Twedt, K., Li, S., Chang, T., Mu, Q., & Angal, A. (2024). Early Mission Calibration Performance of NOAA-21 VIIRS Reflective Solar Bands. Remote Sensing, 16(19), 3557. https://doi.org/10.3390/rs16193557







