Analysis of Spatiotemporal Changes in Energy Consumption Carbon Emissions at District and County Levels Based on Nighttime Light Data—A Case Study of Jiangsu Province in China
Abstract
1. Introduction
2. Data and Study Area
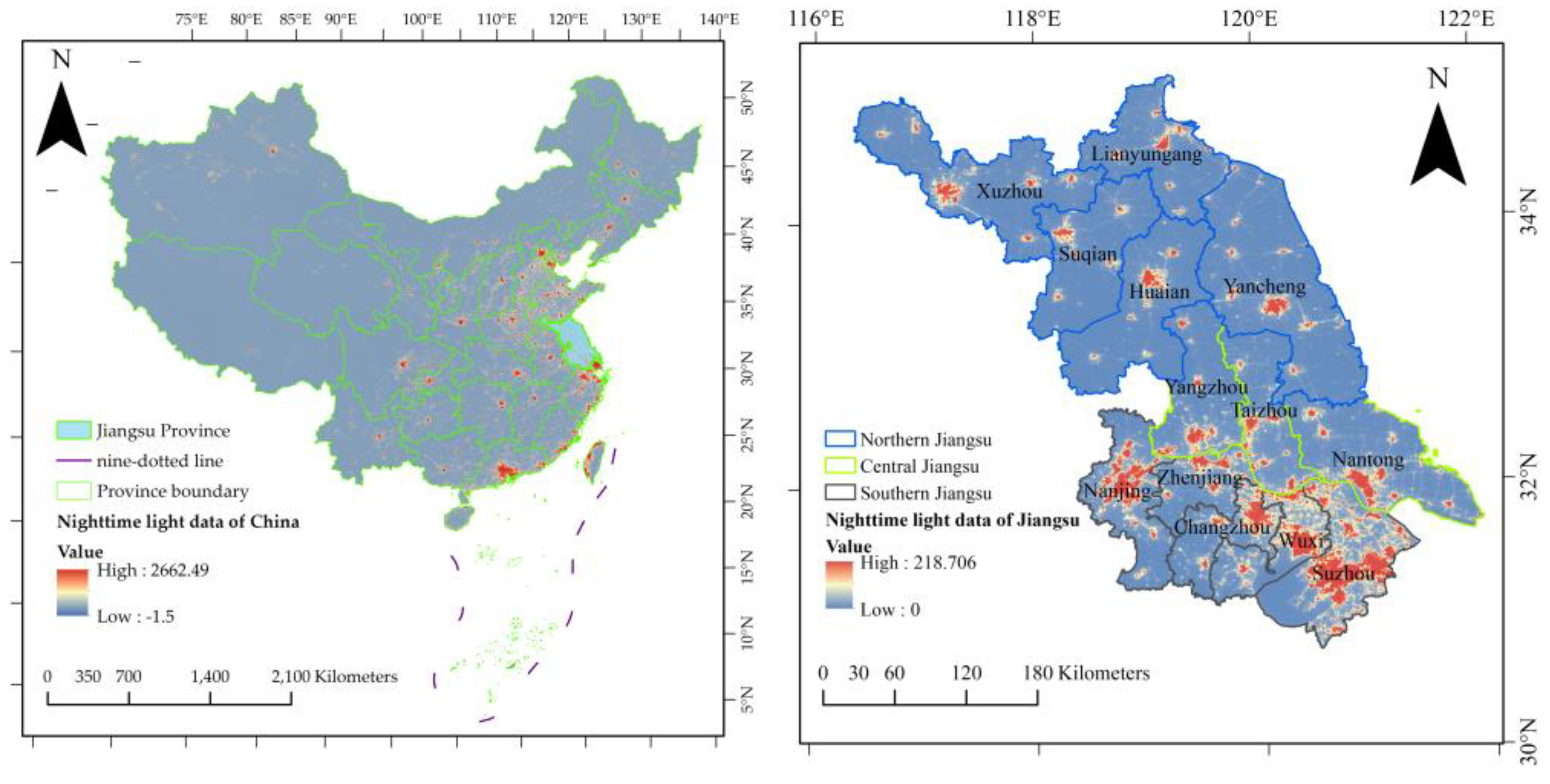
2.1. Study Area
2.2. Data
3. Calculation of County-Level ECCE Based on NTL Data
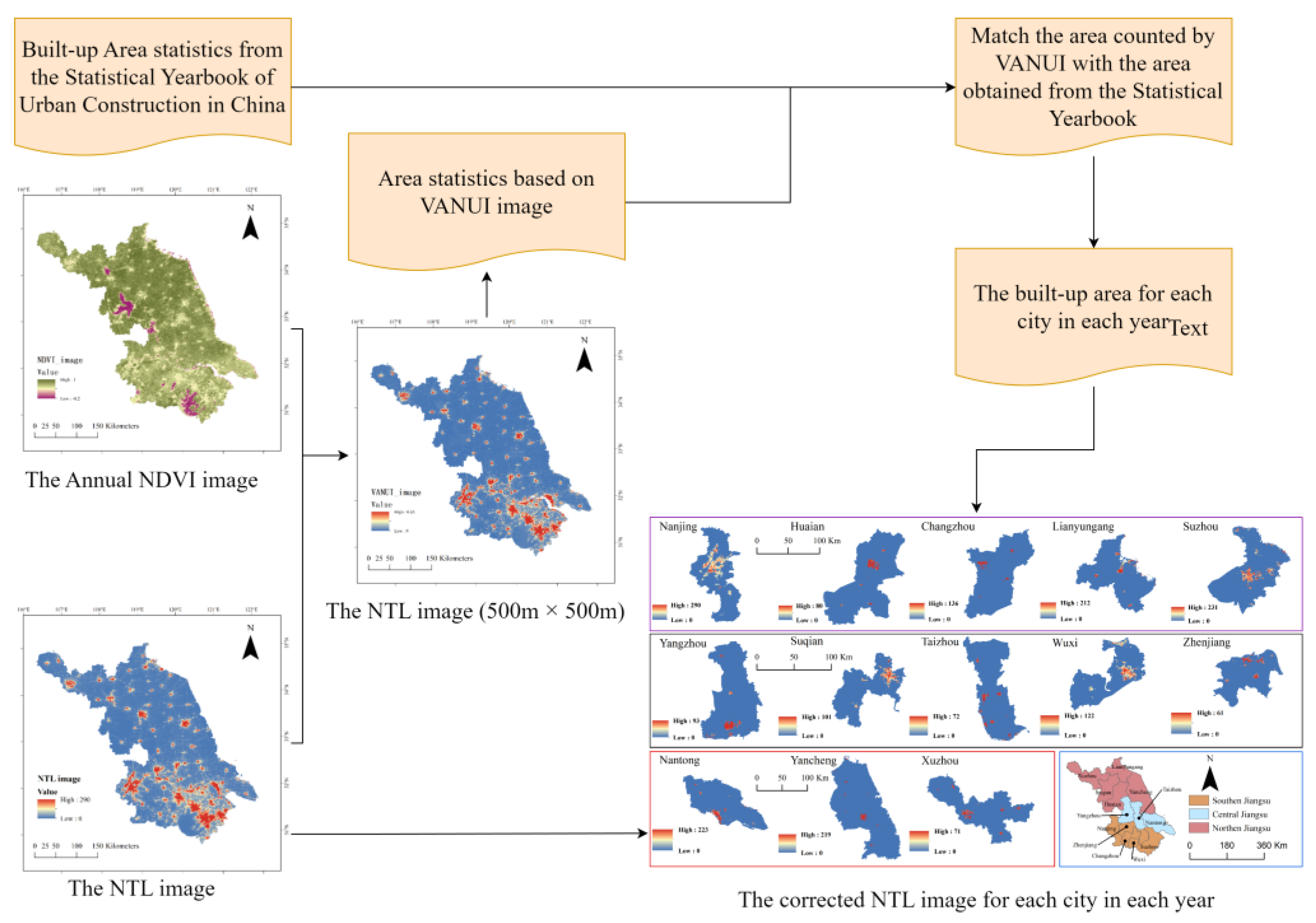
3.1. The Night-Light Time (NTL) Data Calibration Processing
3.1.1. The VANUI Index to Eliminate the “Saturation Effect”
3.1.2. Extraction of Urban Built-Up Areas in NTL Data
3.2. Calculation of City Level Energy Consumption Carbon Emissions (ECCE)
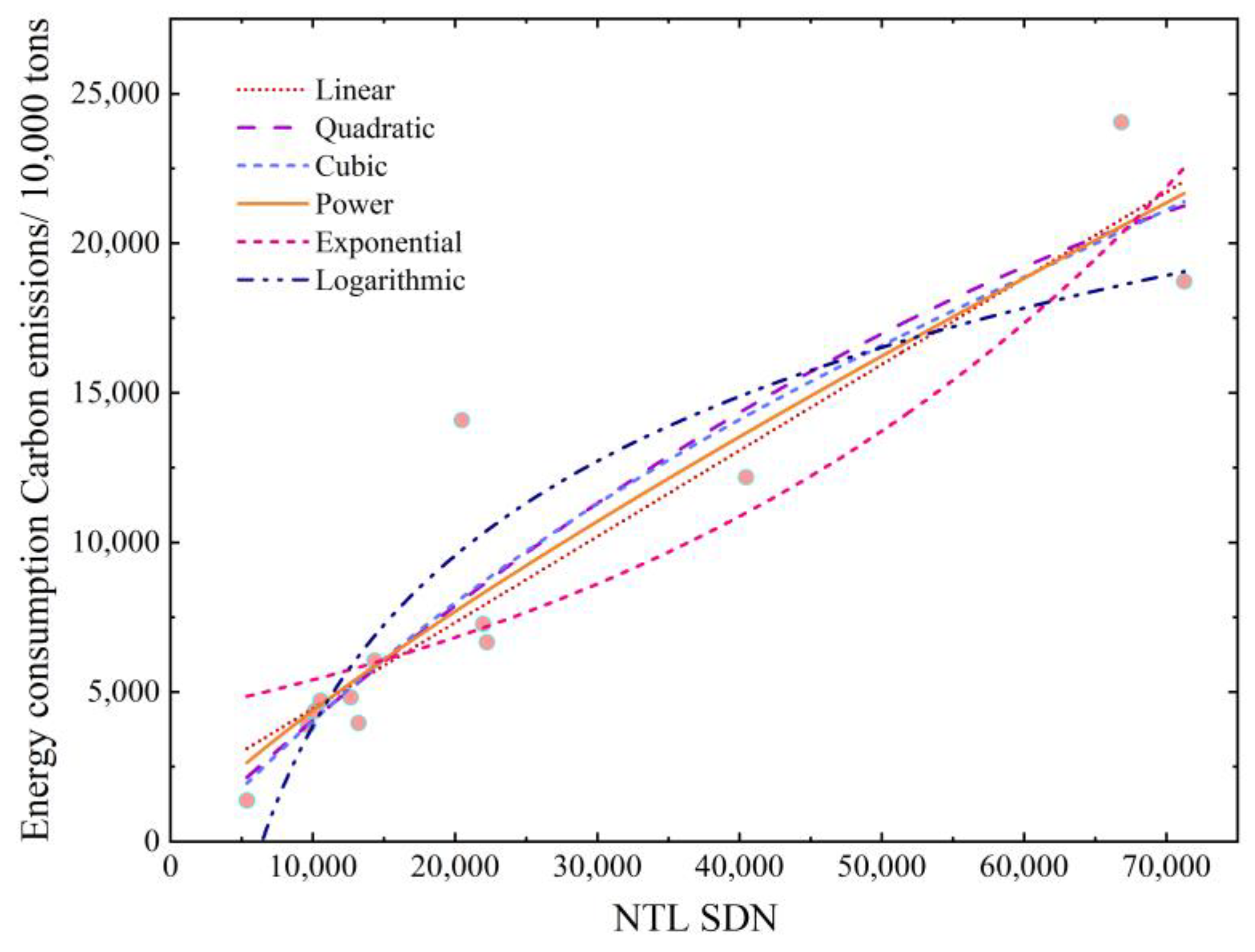
3.3. Correlation of NTL with ECCE
3.4. Simulation Model of Carbon Emissions from Energy Consumption Based on Night-Time Light Data
4. Analysis of Changes in Energy Consumption Carbon Emissions Based on Estimates of Nighttime Light Data
4.1. Carbon Intensity of Energy Consumption (ECCE Intensity)
4.2. Characterization of Time-Trends in ECCE
4.3. Characterization of Spatial Auto-Correlation of ECCE
4.3.1. Characterization of Spatial Auto-Correlation Based on the Global Moran’s I Index
4.3.2. Characterization of Spatial Auto-Correlation Based on the Local Moran’s I Index
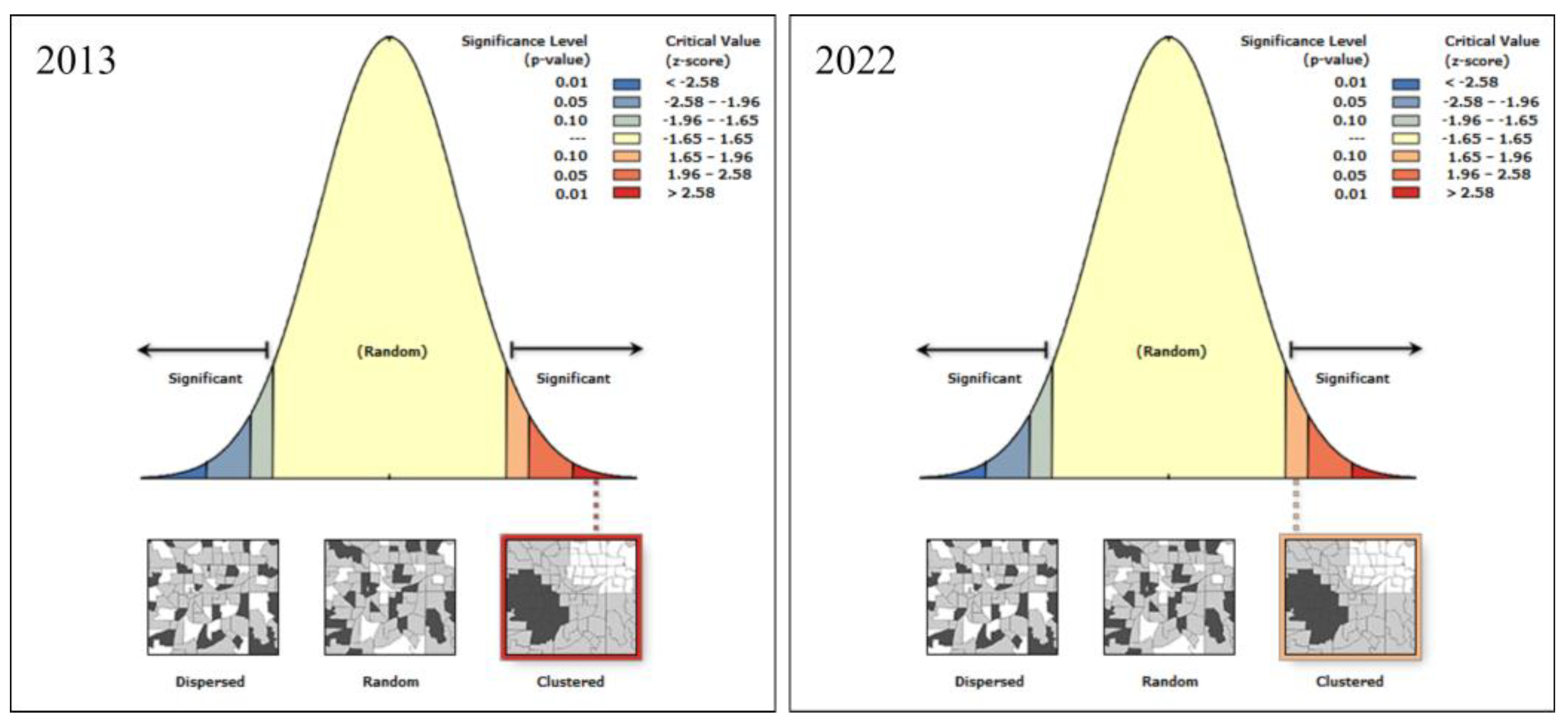
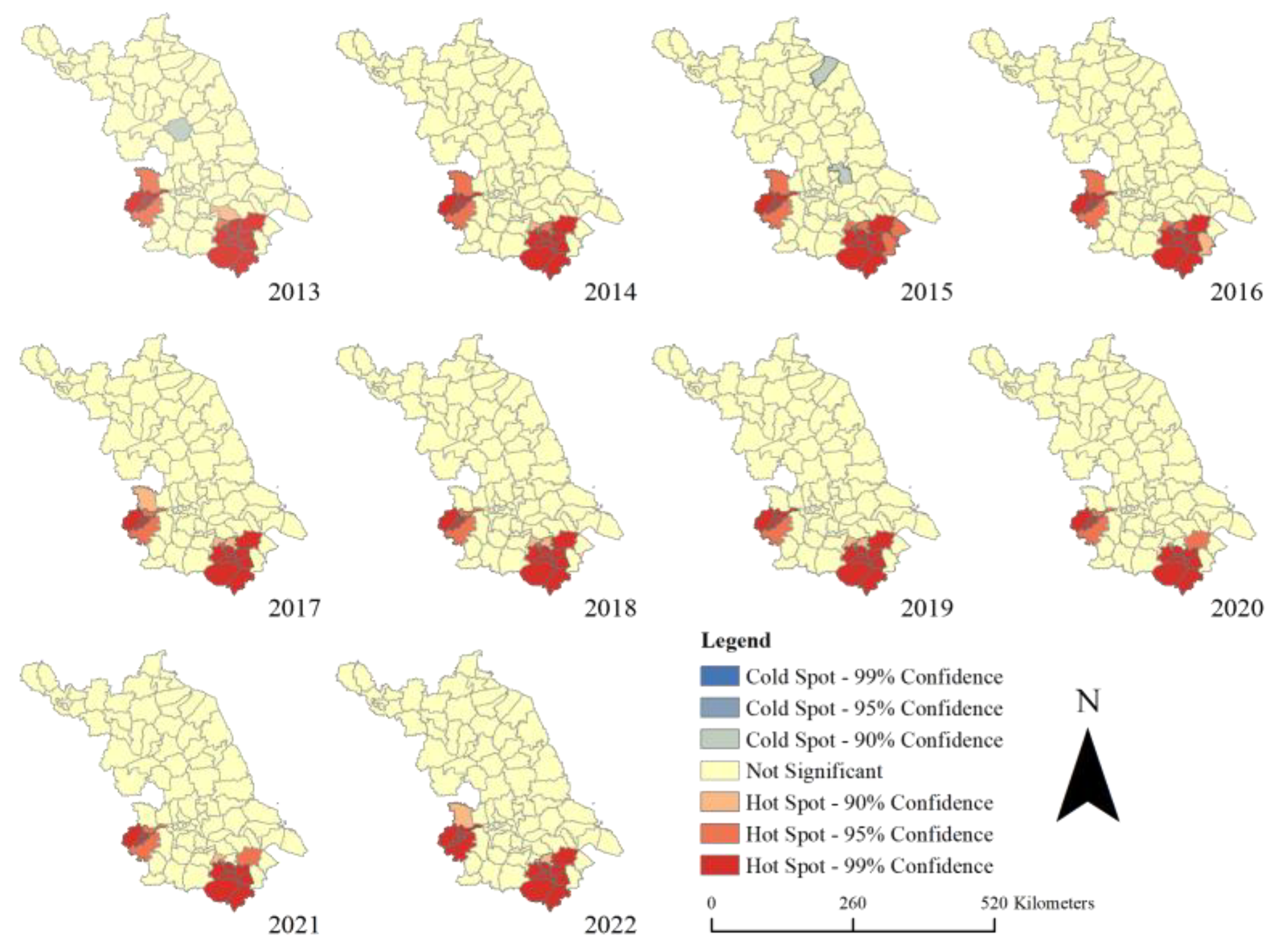
4.3.3. Characterization of Spatial Auto-Correlation Based on Local Index
5. Result
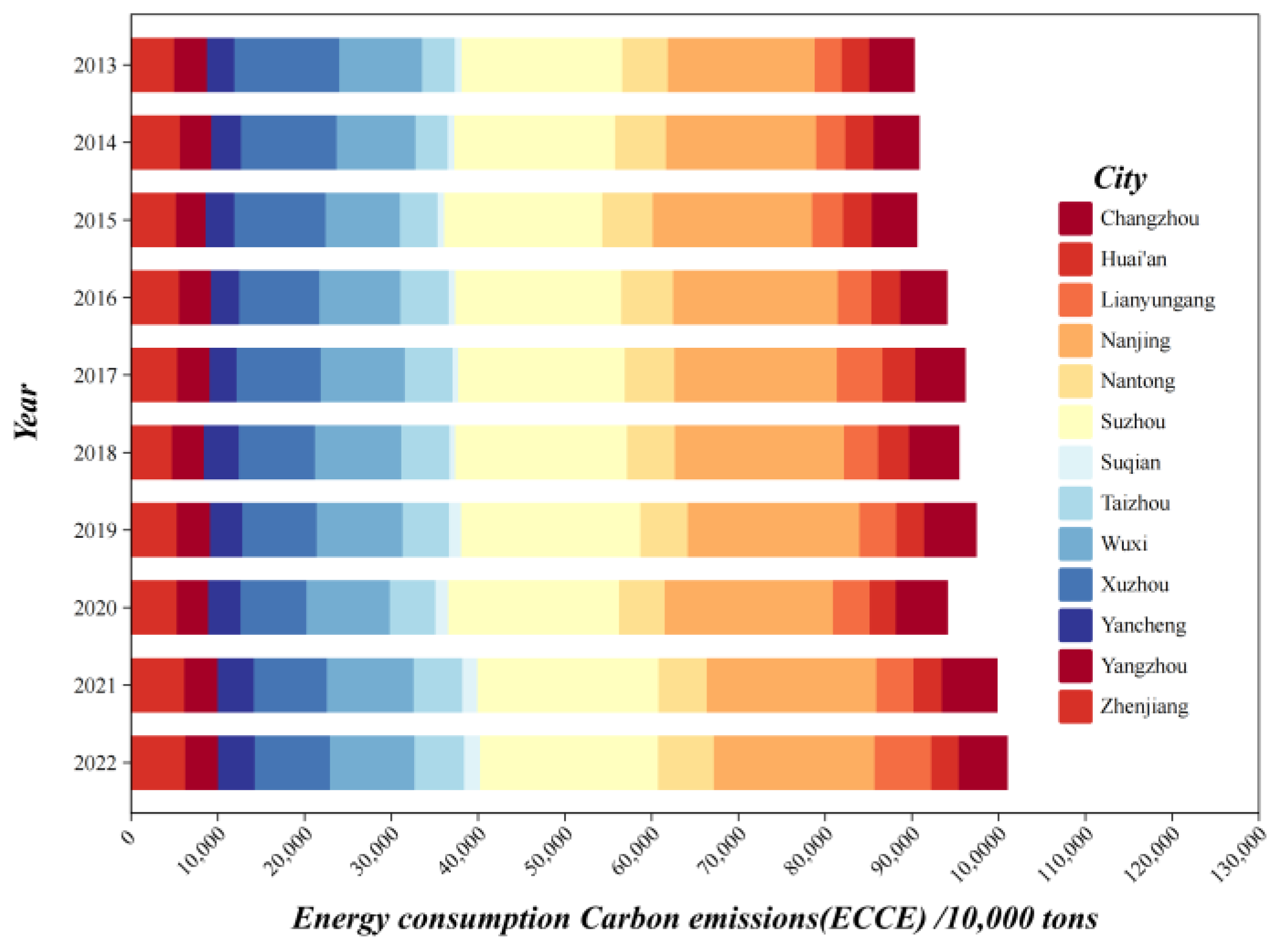
5.1. The Accounting Result of ECCE
5.2. Calculation of the Correlation between NTL Data and ECCE and Model Fitting Results
5.3. Fundamental Characterization of ECCE
5.3.1. Fundamental Characterization of Total ECCE in Jiangsu Province
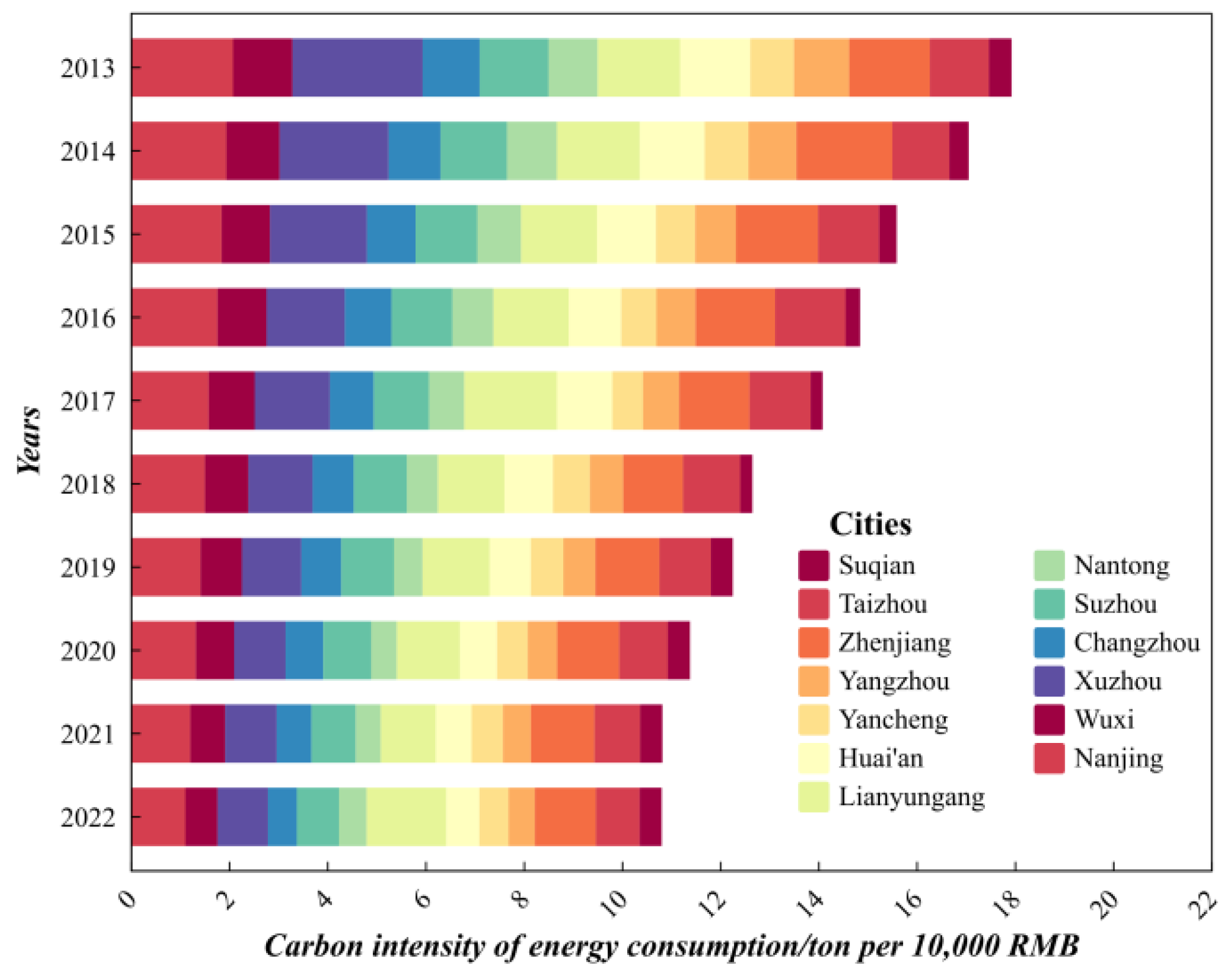
5.3.2. Characterization of ECCE Intensity in Jiangsu Province
5.4. Results of Temporal Variation Analyses
5.5. Results of Spatial Variation Analyses
5.5.1. Results of the Global Moran’s I Index
5.5.2. Results of the Local Moran’s I Index
5.5.3. Results of the Local Index
6. Discussion
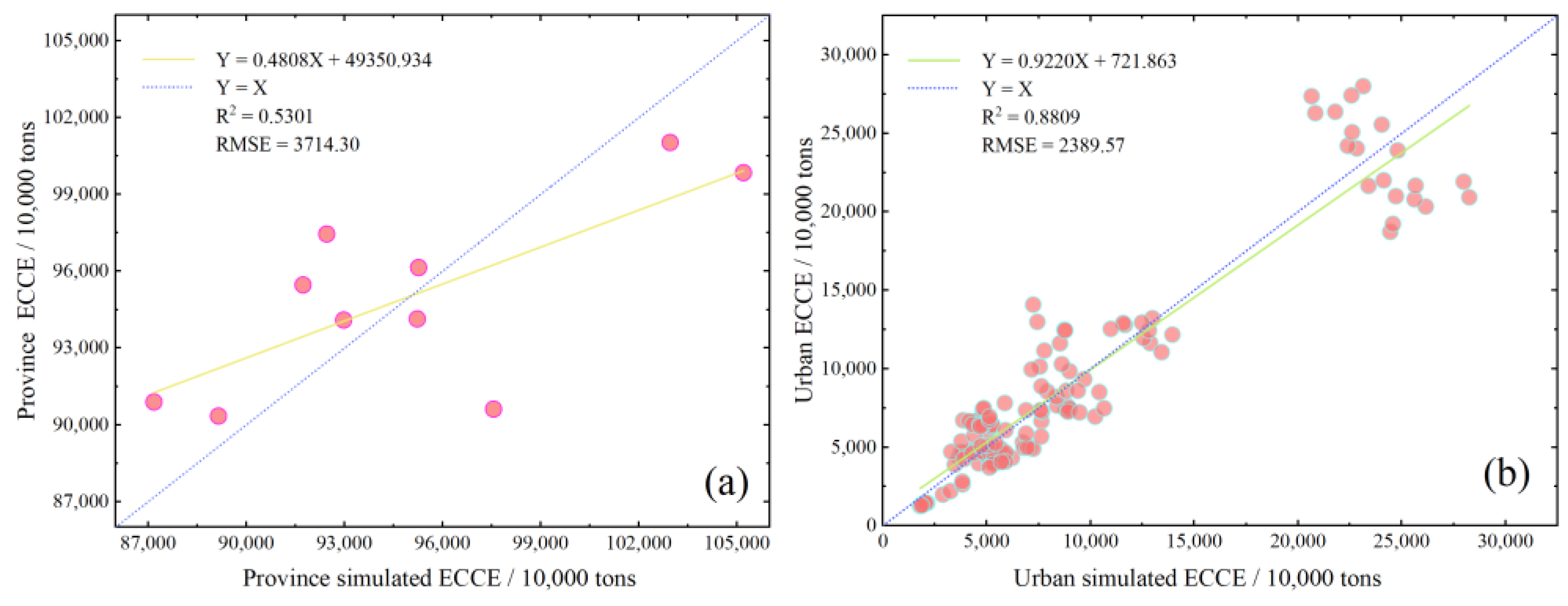
6.1. Reliability Validation of Estimating ECCE Based on NTL Data
6.2. Spatiotemporal Patterns of Energy Consumption Carbon Emissions in Jiangsu Province
6.3. The Policy Suggestion for Energy Conservation and Emission Reduction
6.4. Limitations
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wei, Y.; Wang, L.; Liao, H.; Wang, K.; Murty, T.; Yan, J. Responsibility accounting in carbon allocation: A global perspective. Appl. Energy 2014, 130, 122–133. [Google Scholar] [CrossRef]
- Lu, H.; Liu, G. Spatial effects of carbon dioxide emissions from residential energy consumption: A county-level study using enhanced nocturnal lighting. Appl. Energy 2014, 131, 297–306. [Google Scholar] [CrossRef]
- Qiu, R.; Han, G.; Li, X.; Xiao, J.; Liu, J.; Wang, S.; Li, S.; Gong, W. Contrasting responses of relationship between solar-induced fluorescence and gross primary production to drought across aridity gradients. Remote Sens. Environ. 2024, 302, 113984. [Google Scholar] [CrossRef]
- Al-Ghussain, L. Global warming: Review on driving forces and mitigation. Environ. Prog. Sustain. 2019, 38, 13–21. [Google Scholar] [CrossRef]
- He, C.; Ma, Q.; Li, T.; Yang, Y.; Liu, Z. Spatiotemporal dynamics of electric power consumption in Chinese Mainland from 1995 to 2008 modeled using DMSP/OLS stable nighttime lights data. J. Geogr. Sci. 2012, 22, 125–136. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, Z.; Ye, X.; Wei, Y.D. Spatiotemporal dynamics of carbon intensity from energy consumption in China. J. Geogr. Sci. 2014, 24, 631–650. [Google Scholar] [CrossRef]
- Wang, N.; Chang, Y.-C. The development of policy instruments in supporting low-carbon governance in China. Renew. Sust. Energ. Rev. 2014, 35, 126–135. [Google Scholar] [CrossRef]
- Fang, J.; Yu, G.; Liu, L.; Hu, S.; Chapin, F.S., III. Climate change, human impacts, and carbon sequestration in China. Proc. Nat. Acad. Sci. USA 2018, 115, 4015–4020. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, F.; Zheng, J. Estimation of Greenhouse Gas Emissions from the EU, US, China, and India up to 2060 in Comparison with Their Pledges under the Paris Agreement. Sustainability 2017, 9, 1587. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y.; Chen, X.; He, R.; Guan, Y.; Gu, Y.; Chen, Y. Crop Production Pushes up Greenhouse Gases Emissions in China: Evidence from Carbon Footprint Analysis Based on National Statistics Data. Sustainability 2019, 11, 4931. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, K.; Fan, J.; Zhao, H. Progress of research on energy-related carbon emission accounting methods at the prefectural and county levels. Prog. Geogr. 2023, 42, 1406–1419. [Google Scholar] [CrossRef]
- Wu, Q.; Gu, S. Discerning drivers and future reduction paths of energy-related CO2 emissions in China: Combining EKC with three-layer LMDI. Environ. Sci. Pollut. Res. 2021, 28, 36611–36625. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, Z.; Zhang, J. Analysis of carbon emission performance and regional differences in Chinas eight economic regions: Based on the super-efficiency SBM model and the Theil index. PLoS ONE 2021, 16, e0250994. [Google Scholar] [CrossRef]
- Han, G.; Huang, Y.; Shi, T.; Zhang, H.; Li, S.; Zhang, H.; Chen, W.; Liu, J.; Gong, W. Quantifying CO2 emissions of power plants with Aerosols and Carbon Dioxide Lidar onboard DQ-1. Remote Sens. Environ. 2024, 313, 114368. [Google Scholar] [CrossRef]
- Liu, B.; Ma, X.; Guo, J.; Wen, R.; Li, H.; Jin, S.; Ma, Y.; Guo, X.; Gong, W. Extending the wind profile beyond the surface layer by combining physical and machine learning approaches. Atmos. Chem. Phys. 2024, 24, 4047–4063. [Google Scholar] [CrossRef]
- Han, G.; Pei, Z.; Shi, T.; Mao, H.; Li, S.; Mao, F.; Ma, X.; Zhang, X.; Gong, W. Unveiling Unprecedented Methane Hotspots in China’s Leading Coal Production Hub: A Satellite Mapping Revelation. Geophys. Res. Lett. 2024, 51, e2024GL109065. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Ziskin, D.; Baugh, K.E.; Tuttle, B.T.; Ghosh, T.; Pack, D.W.; Erwin, E.H.; Zhizhin, M. A Fifteen Year Record of Global Natural Gas Flaring Derived from Satellite Data. Energies 2009, 2, 595–622. [Google Scholar] [CrossRef]
- Ma, T.; Zhou, C.; Pei, T.; Haynie, S.; Fan, J. Quantitative estimation of urbanization dynamics using time series of DMSP/OLS nighttime light data: A comparative case study from China’s cities. Remote Sens. Environ. 2012, 124, 99–107. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, B.; Song, W.; Liu, H.; Wu, Q.; Shi, K.; Wu, J. A new approach for detecting urban centers and their spatial structure with nighttime light remote sensing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6305–6319. [Google Scholar] [CrossRef]
- Zhuo, L.; Zheng, J.; Zhang, X.; Li, J.; Liu, L. An improved method of night-time light saturation reduction based on EVI. Int. J. Remote Sens. 2015, 36, 4114–4130. [Google Scholar] [CrossRef]
- Zhang, Q.; Schaaf, C.; Seto, K.C. The Vegetation Adjusted NTL Urban Index: A new approach to reduce saturation and increase variation in nighttime luminosity. Remote Sens. Environ. 2013, 129, 32–41. [Google Scholar] [CrossRef]
- He, C.; Liu, Z.; Tian, J.; Ma, Q. Urban expansion dynamics and natural habitat loss in China: A multiscale landscape perspective. Glob. Chang. Biol. 2014, 20, 2886–2902. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; He, C.; Liu, Z.; Dou, Y. How did urban land expand in China between 1992 and 2015? A multi-scale landscape analysis. PLoS ONE 2016, 11, e0154839. [Google Scholar] [CrossRef] [PubMed]
- Jean, N.; Burke, M.; Xie, M.; Davis, W.M.; Lobell, D.B.; Ermon, S. Combining satellite imagery and machine learning to predict poverty. Science 2016, 353, 790–794. [Google Scholar] [CrossRef]
- Li, C.; Jia, J.; Wu, F.; Zuo, L.; Cui, X. County-level intensity of carbon emissions from crop farming in China during 2000–2019. Sci. Data 2024, 11, 457. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Li, P.; Gao, J. Spatiotemporal patterns and influencing factors of carbon emissions in the Pan-Yangtze River Delta region, 1990–2014. Prog. Geogr. 2016, 12, 1472–1482. [Google Scholar] [CrossRef][Green Version]
- Ou, J.; Liu, X.; Wang, S.; Xie, R.; Li, X. Investigating the differentiated impacts of socioeconomic factors and urban forms on CO2 emissions: Empirical evidence from Chinese cities of different developmental levels. J. Clean. Prod. 2019, 226, 601–614. [Google Scholar] [CrossRef]
- Su, Y.; Chen, X.; Ye, Y.; Wu, Q.; Zhang, H.; Huang, N.; Kuang, Y. The characteristics and mechanisms of carbon emissions from energy consumption in China using DMSP/OLS night light imageries. Acta Geogr. Sin. 2013, 68, 1513–1526. [Google Scholar] [CrossRef]
- Zhou, S.; Wei, L.; Lu, Z.; Lu, Z. A technical framework for integrating carbon emission peaking factors into the industrial green transformation planning of a city cluster in China. J. Clean. Prod. 2022, 344, 131091. [Google Scholar] [CrossRef]
- Zhu, K.; Tu, M.; Li, Y. Did Polycentric and Compact Structure Reduce Carbon Emissions? A Spatial Panel Data Analysis of 286 Chinese Cities from 2002 to 2019. Land 2022, 11, 185. [Google Scholar] [CrossRef]
- Li, L.; Shan, Y.L.; Lei, Y.L.; Wu, S.M.; Yu, X.; Lin, X.Y.; Chen, Y.P. Decoupling of economic growth and emissions in China’s cities: A case study of the Central Plains urban agglomeration. Appl. Energy 2019, 244, 36–45. [Google Scholar] [CrossRef]
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Cui, M.; Levinson, D. Interaction between Development Intensity: An Evaluation of Alternative Spatial Weight Matrices. Urban Sci. 2023, 7, 22. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The Analysis of Spatial Association by Use of Distance Statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Chen, J.; Gao, M.; Cheng, S.; Hou, W.; Song, M.; Liu, X.; Liu, Y.; Shan, Y. County-level CO2 emissions and sequestration in China during 1997–2017. Sci. Data 2020, 7, 391. [Google Scholar] [CrossRef]
- Meng, H.; Zhang, X.; Du, X.; Du, K. Spatiotemporal Heterogeneity of the Characteristics and Influencing Factors of Energy-Consumption-Related Carbon Emissions in Jiangsu Province Based on DMSP-OLS and NPP-VIIRS. Land 2023, 12, 1369. [Google Scholar] [CrossRef]
- Li, M.; Liu, H.; Yu, S.; Wang, J.; Miao, Y.; Wang, C. Estimating the Decoupling between Net Carbon Emissions and Construction Land and Its Driving Factors: Evidence from Shandong Province, China. Int. J. Environ. Res. Public Health 2022, 19, 8910. [Google Scholar] [CrossRef]
- Cui, Y.; Zha, H.; Jiang, L.; Zhang, M.; Shi, K. Luojia 1–01 Data Outperform Suomi-NPP VIIRS Data in Estimating CO2 Emissions in the Service, Industrial, and Urban Residential Sectors. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3000905. [Google Scholar] [CrossRef]



| Data | Time | Data Sources | Data Utilization |
|---|---|---|---|
| NPP-VIIRS Nighttime light (NTL) data | 2013–2022 | Earth Observation Group | simulate the energy consumption carbon emissions |
| Annual Normalized Difference Vegetation Index (NDVI) | NASA Earth data Search/MODIS | calibrate and extract the NTL data | |
| Built-up area data of each city in Jiangsu Province | Statistical Yearbook of Urban Construction in China | extract the NTL data values | |
| Energy consumption statistics of Jiangsu Province | Statistical Yearbook of Jiangsu Province and the Statistical Yearbooks of each city in Jiangsu Province | calculate the energy consumption carbon emissions |
| Type of Energy | Conversion Standard Coal (t Standard Coal/t) | Carbon Emission Factor (104 Carbon/104 Standard Coal) |
|---|---|---|
| Raw Coal | 0.7143 | 0.7559 |
| Coke | 0.9714 | 0.855 |
| Crude Oil | 1.4286 | 0.5857 |
| Gasoline | 1.4714 | 0.5538 |
| Kerosene | 1.4714 | 0.5714 |
| Diesel oil | 1.4571 | 0.5921 |
| Fuel Oil | 1.4286 | 0.6185 |
| Natural Gas | 1.33 | 0.4483 |
| Liquefied Natural Gas | 1.7143 | 0.5124 |
| Liquefied petroleum gas | 1.6198 | 0.5042 |
| Heat | 0.03412 | 0.67 |
| Electricity | 3.45 | 0.272 |
| Model Type | Formula |
|---|---|
| Linear | |
| logarithmic | |
| quadratic | |
| cubic | |
| exponential | |
| power |
| Type of Change | Classification Criteria |
|---|---|
| Rapid decrease | <x − 1.5d |
| Slow decrease | x − 1.5d ~ x − 0.5d |
| Essentially unchanged | x − 0.5d ~ x + 0.5d |
| Slow increase | X + 0.5d ~ x + 1.5d |
| Rapid increase | >x + 1.5d |
| Z-Score | p-Value | Confidence Level | Distribution |
|---|---|---|---|
| z < −2.58 | <0.01 | 99% | Discrete |
| −2.58 ≤ z < −1.96 | <0.05 | 95% | Discrete |
| −1.96 ≤ z < −1.65 | <0.10 | 90% | Discrete |
| 1.65 < z ≤ 1.96 | <0.10 | 90% | Gathering |
| 1.96 < z ≤ 2.58 | <0.05 | 95% | Gathering |
| z > 2.58 | <0.01 | 99% | Gathering |
| −1.65 ≤ z ≤ 1.65 | >0.01 | / | Random |
| Clustering Features | Norm | |
|---|---|---|
| Moran’s I Index | Z-Score | |
| High-High | Positive | Positive |
| Low-High | Positive | Positive |
| Low-Low | Negative | Negative |
| High-Low | Negative | Negative |
| HSHS | MSHS | SHS | IS | SCS | MSCS | |
|---|---|---|---|---|---|---|
| Z-score | Positive | Positive | Positive | / | Negative | Negative |
| p-value | 0.001 | 0.01 | 0.05 | 0.05 | 0.05 | 0.01 |
| City | Years | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | |
| Zhenjiang | 4962 | 5602 | 5164 | 5559 | 5320 | 4691 | 5311 | 5286 | 6164 | 6241 |
| Yangzhou | 3788 | 3662 | 3409 | 3628 | 3740 | 3711 | 3778 | 3605 | 3782 | 3795 |
| Yancheng | 3132 | 3398 | 3337 | 3261 | 3122 | 4044 | 3760 | 3706 | 4224 | 4217 |
| Xuzhou | 12,121 | 11,042 | 10,531 | 9269 | 9699 | 8785 | 8532 | 7627 | 8409 | 8692 |
| Wuxi | 9552 | 9060 | 8539 | 9329 | 9666 | 9902 | 9930 | 9602 | 9995 | 9734 |
| Taizhou | 3745 | 3711 | 4342 | 5573 | 5505 | 5550 | 5358 | 5234 | 5607 | 5703 |
| Suqian | 812 | 800 | 800 | 733 | 663 | 708 | 1372 | 1479 | 1751 | 1843 |
| Suzhou | 18,493 | 18,533 | 18,180 | 19,165 | 19,178 | 19,766 | 20,670 | 19,735 | 20,862 | 20,529 |
| Nantong | 5237 | 5846 | 5798 | 5963 | 5749 | 5514 | 5445 | 5213 | 5583 | 6391 |
| Nanjing | 16,982 | 17,323 | 18,411 | 18,972 | 18,711 | 19,486 | 19,783 | 19,425 | 19,548 | 18,574 |
| Lianyungang | 3069 | 3355 | 3559 | 3889 | 5251 | 3960 | 4269 | 4205 | 4254 | 6497 |
| Huai’an | 3201 | 3279 | 3320 | 3312 | 3780 | 3587 | 3228 | 3037 | 3278 | 3200 |
| Changzhou | 5255 | 5288 | 5229 | 5447 | 5768 | 5767 | 6023 | 5987 | 6399 | 5616 |
| SUM | 90,351 | 90,898 | 90,619 | 94,100 | 96,151 | 95,472 | 97,459 | 94,141 | 99,855 | 101,034 |
| Years | Pearson’s | Significance |
|---|---|---|
| 2013 | 0.929 | 0.000 |
| 2014 | 0.941 | 0.000 |
| 2015 | 0.957 | 0.000 |
| 2016 | 0.957 | 0.000 |
| 2017 | 0.944 | 0.000 |
| 2018 | 0.960 | 0.000 |
| 2019 | 0.945 | 0.000 |
| 2020 | 0.928 | 0.000 |
| 2021 | 0.919 | 0.000 |
| 2022 | 0.906 | 0.000 |
| Model | Models Summary | |
|---|---|---|
| R2 | Significance | |
| linear | 0.862 | 0.000 |
| logarithmic | 0.838 | 0.000 |
| quadratic | 0.872 | 0.000 |
| cubic | 0.872 | 0.000 |
| power | 0.883 | 0.000 |
| Exponential | 0.714 | 0.000 |
| Years | Fitting Function | R2 |
|---|---|---|
| 2013 | Y = 0.453674 × X0.968901 | 0.883 |
| 2014 | Y = 0.437251 × X0.980557 | 0.866 |
| 2015 | Y = 0.584471 × X0.952287 | 0.866 |
| 2016 | Y = 0.347497 × X0.998623 | 0.827 |
| 2017 | Y = 0.373649 × X0.983689 | 0.885 |
| 2018 | Y = 0.229900 × X1.024459 | 0.921 |
| 2019 | Y = 0.193272 × X1.032601 | 0.892 |
| 2020 | Y = 0.281682 × X0.995149 | 0.861 |
| 2021 | Y = 0.360764 × X0.970502 | 0.844 |
| 2022 | Y = 0.326374 × X0.968624 | 0.814 |
| Type of Change | District and County Names | SUM |
|---|---|---|
| Rapid decrease | Liuhe, Qingjiangpu, Huqiu, Kunshan, Wujiang, Xinwu, Quanshan | 7 |
| Slow decrease | Jianye, Gulou (Nanjing), Changshu, Gusu, Taicang, Sihong, Binhu, Liangxi, Xishan, Tongshan, Yizheng, Jingkou, Runzhou | 13 |
| Essentially unchanged | Shuyang, Lianyun, Gaoyou, Haimen, Haizhou, Tianning, Xinyi, Suyu, Gaogang, Peixian, Jinhu, Suining, Zhonglou, Xinghua, Jiangyin, Ganyu, Hai’an, Dongtai, Jintan, Donghai, Yangzhong, Qinhuai, Dafeng, Gouyun, Yixing, Fengxian, Binhai, Qidong, Huaiyin, Gannan, Huishan, Xiangshui, Jiangyan, Wujin, Siyang, Tongzhou, Xinbei, Liyang, Jurong, Danyang, Jiangdu, Hailing, Rugao, Rudong, Xuyi, Yuhuatai, Sheyang, Jingjiang, Dantu, Qixia, Baoying, Lianshui, Hongze, Zhangjiagang, Gaochun, Funing, Xuanwu, Jiawang, Jianhu, Yunlong, Gulou (Xuzhou) | 61 |
| Slow increase | Yandu, Guangling, Lishui, Wuzhong, Pizhou, Taixing, Huai’an | 7 |
| Rapid increase | Tinghu, Pukou, Chongchuan, Ganjiang, Jiangning, Xiangcheng, Sucheng | 7 |
| Years | Moran’s I Index | Z-Score | p-Value |
|---|---|---|---|
| 2013 | 0.3363 | 3.4716 | 0.0005 |
| 2014 | 0.2933 | 3.0923 | 0.0020 |
| 2015 | 0.2544 | 2.6320 | 0.0085 |
| 2016 | 0.2671 | 2.7847 | 0.0054 |
| 2017 | 0.1907 | 2.0572 | 0.0397 |
| 2018 | 0.1942 | 2.0825 | 0.0373 |
| 2019 | 0.1908 | 2.0362 | 0.0417 |
| 2020 | 0.1383 | 1.5218 | 0.1281 |
| 2021 | 0.1663 | 1.7888 | 0.0737 |
| 2022 | 0.1711 | 1.8323 | 0.0669 |
| Norm (%) | Years | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | |
| RE | −1.33 | −4.09 | 7.66 | −1.2 | −0.92 | −3.92 | −5.13 | 1.15 | 5.35 | 1.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, C.; Mei, Y.; Liang, A. Analysis of Spatiotemporal Changes in Energy Consumption Carbon Emissions at District and County Levels Based on Nighttime Light Data—A Case Study of Jiangsu Province in China. Remote Sens. 2024, 16, 3514. https://doi.org/10.3390/rs16183514
Xiang C, Mei Y, Liang A. Analysis of Spatiotemporal Changes in Energy Consumption Carbon Emissions at District and County Levels Based on Nighttime Light Data—A Case Study of Jiangsu Province in China. Remote Sensing. 2024; 16(18):3514. https://doi.org/10.3390/rs16183514
Chicago/Turabian StyleXiang, Chengzhi, Yong Mei, and Ailin Liang. 2024. "Analysis of Spatiotemporal Changes in Energy Consumption Carbon Emissions at District and County Levels Based on Nighttime Light Data—A Case Study of Jiangsu Province in China" Remote Sensing 16, no. 18: 3514. https://doi.org/10.3390/rs16183514
APA StyleXiang, C., Mei, Y., & Liang, A. (2024). Analysis of Spatiotemporal Changes in Energy Consumption Carbon Emissions at District and County Levels Based on Nighttime Light Data—A Case Study of Jiangsu Province in China. Remote Sensing, 16(18), 3514. https://doi.org/10.3390/rs16183514






